Comparative Analysis Using Multiple Regression Models for Forecasting Photovoltaic Power Generation
Abstract
1. Introduction
1.1. Motivation and Contribution
- Realistic time series dataset is harvested from PV panels (with sensors) and installed on multiple buildings of the SHARDA University campus.
- A comparative study and a performance analysis of the LR, SVR, KNR, DTR, RFR, GBR, and MPR for power prediction are tested.
- A discussion of numerous case studies for PV power is presented to identify the important features favoring power prediction.

1.2. Acronyms Used
1.3. Structure of the Article
2. Literature Survey
3. Testbed and Dataset Description
3.1. DAQ Unit
3.2. DMU
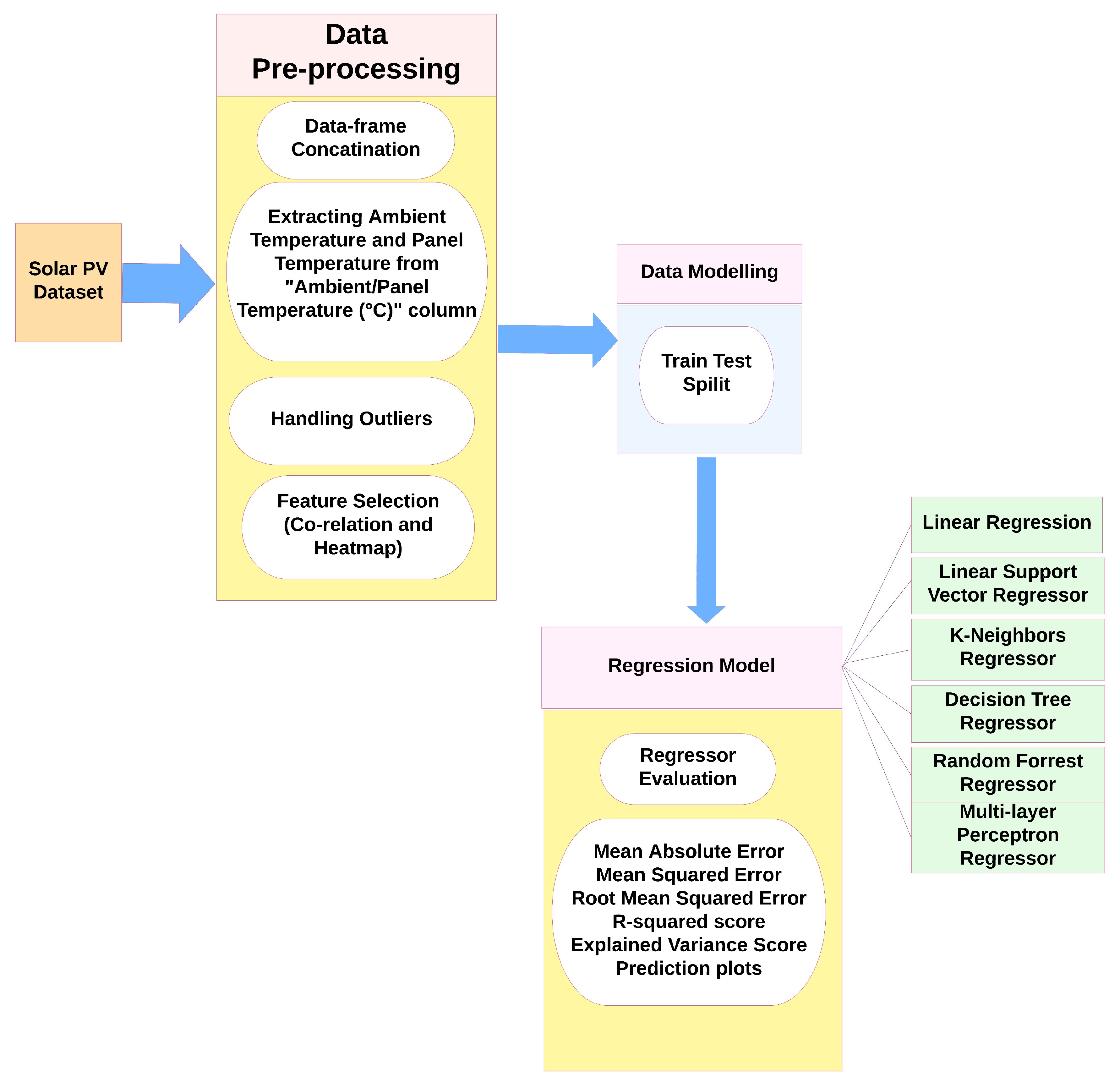
4. Proposed Regression Methodology
4.1. PV Dataset
4.2. Data Pre-Processing
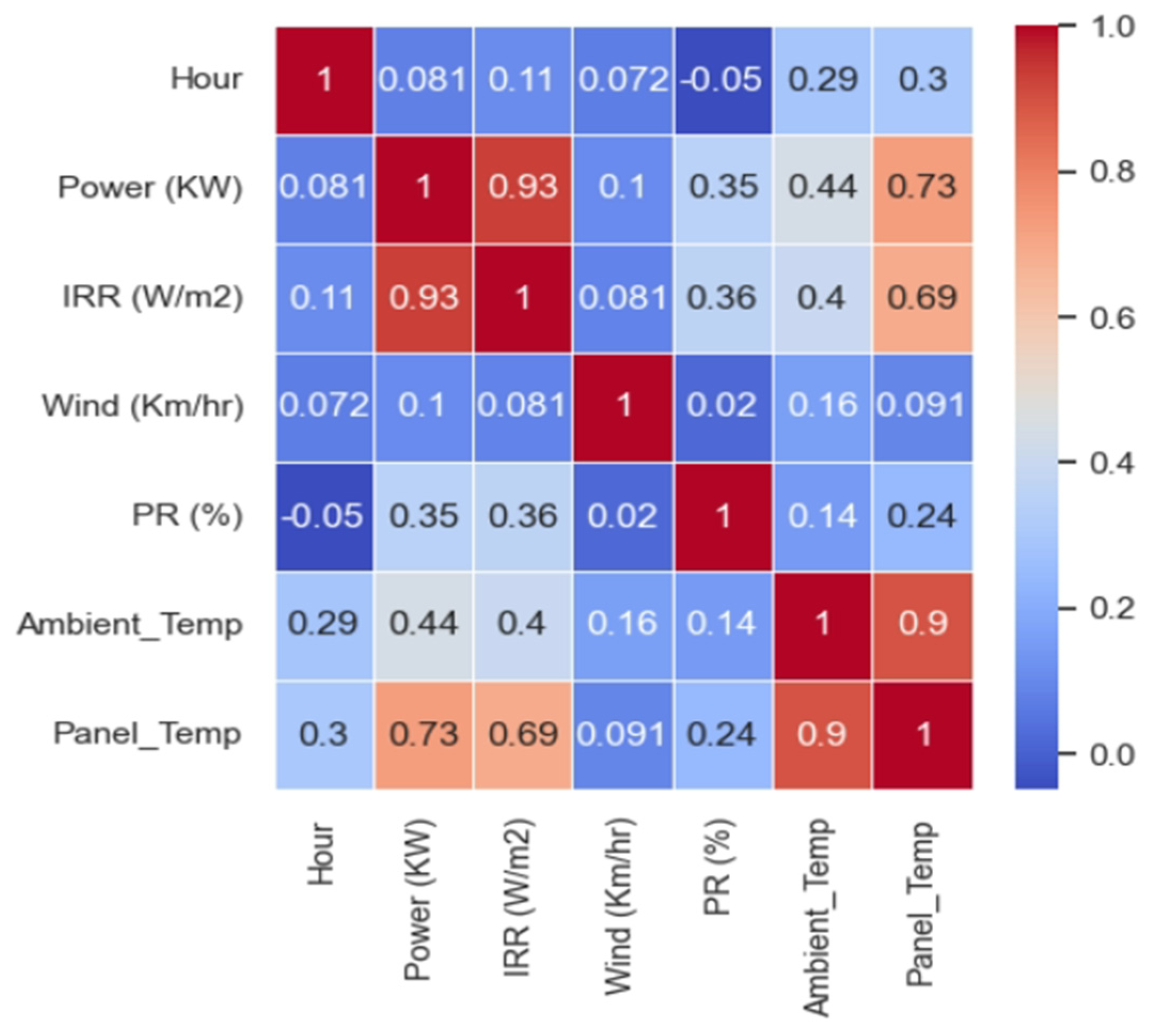
4.3. Data Modelling
4.4. Regression Models
4.4.1. Linear Regression
4.4.2. Support Vector Regressor
4.4.3. K-Neighbor Regressor
4.4.4. Decision Tree Regressor
- represents predicted output for the input a using a decision tree.
- Ci is the constant value associated with the leaf node i.
4.4.5. Random Forest Regressor
- Pick m predictors randomly from the p covariates.
- Choose the top predictor for the split section out of the m identified predictors.
- Divide this location (node) into two minor nodes by establishing specific decision-making guidelines.
- is the predicted output for the input X;
- B is the total number of trees left (base learners right) in the RFR
- is the prdiction of the b-the decision tree in the forest for input X.
4.4.6. Gradient Boosting Regressor
4.4.7. Multilayer Perceptron Regressor
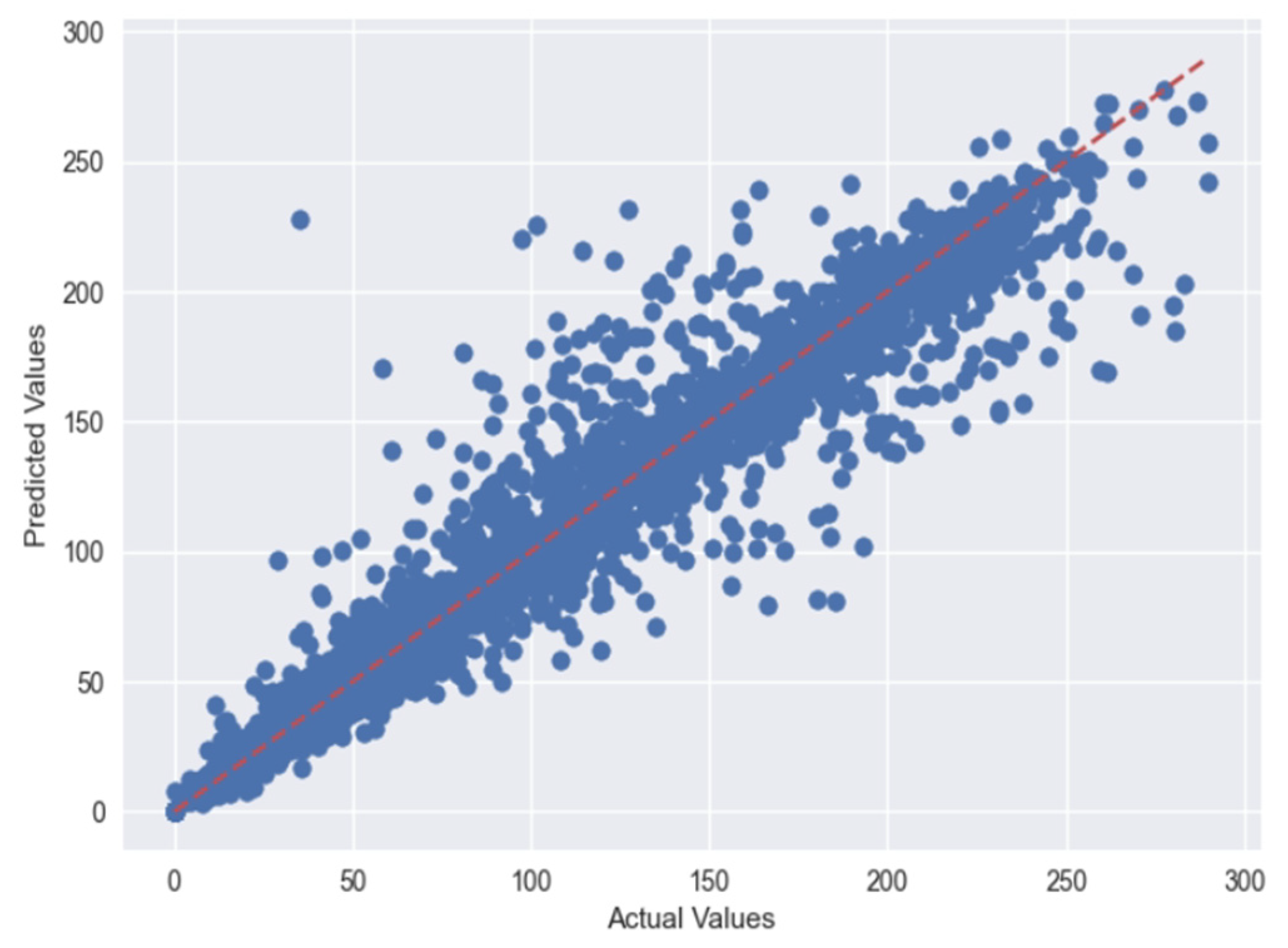
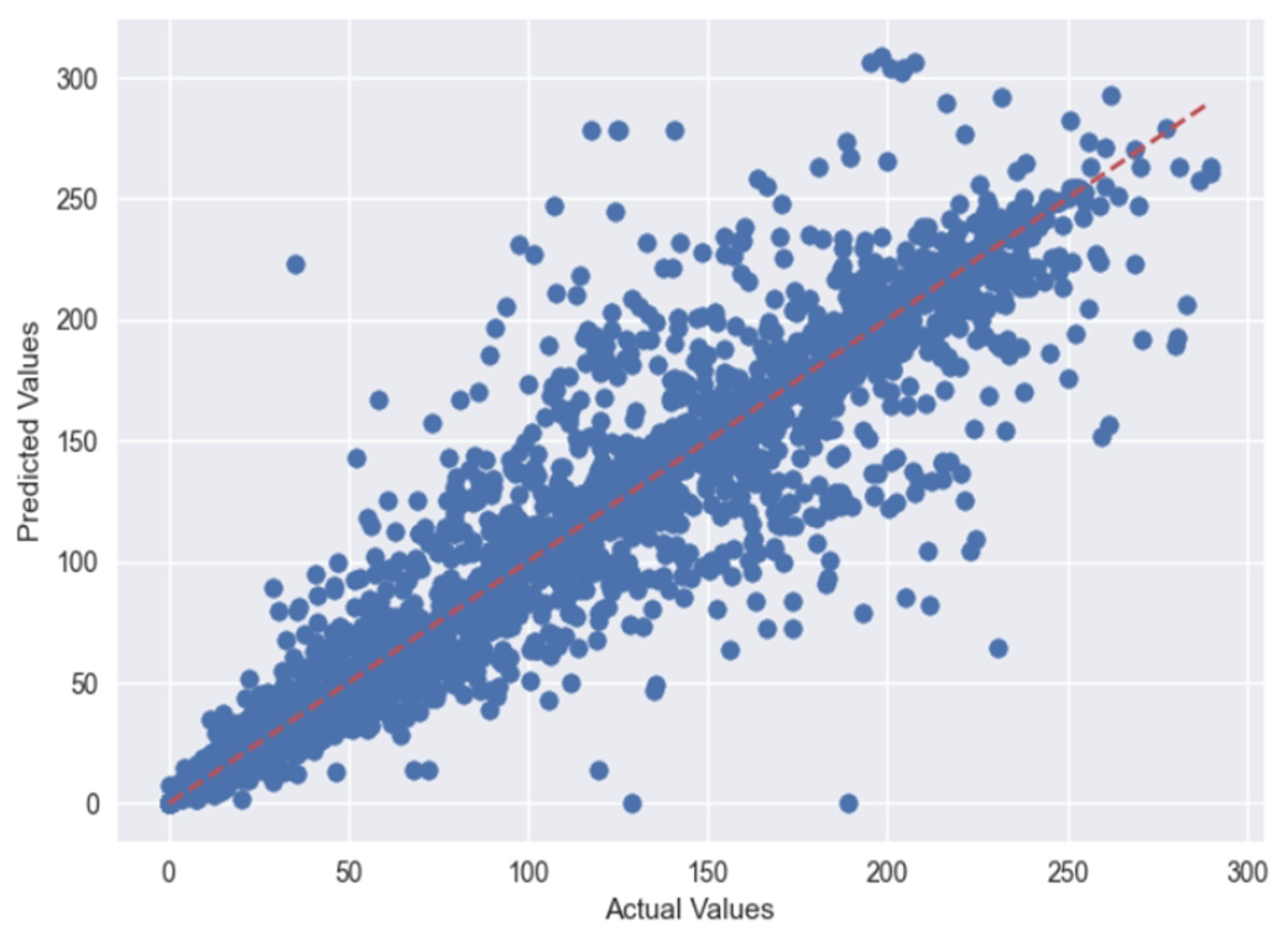
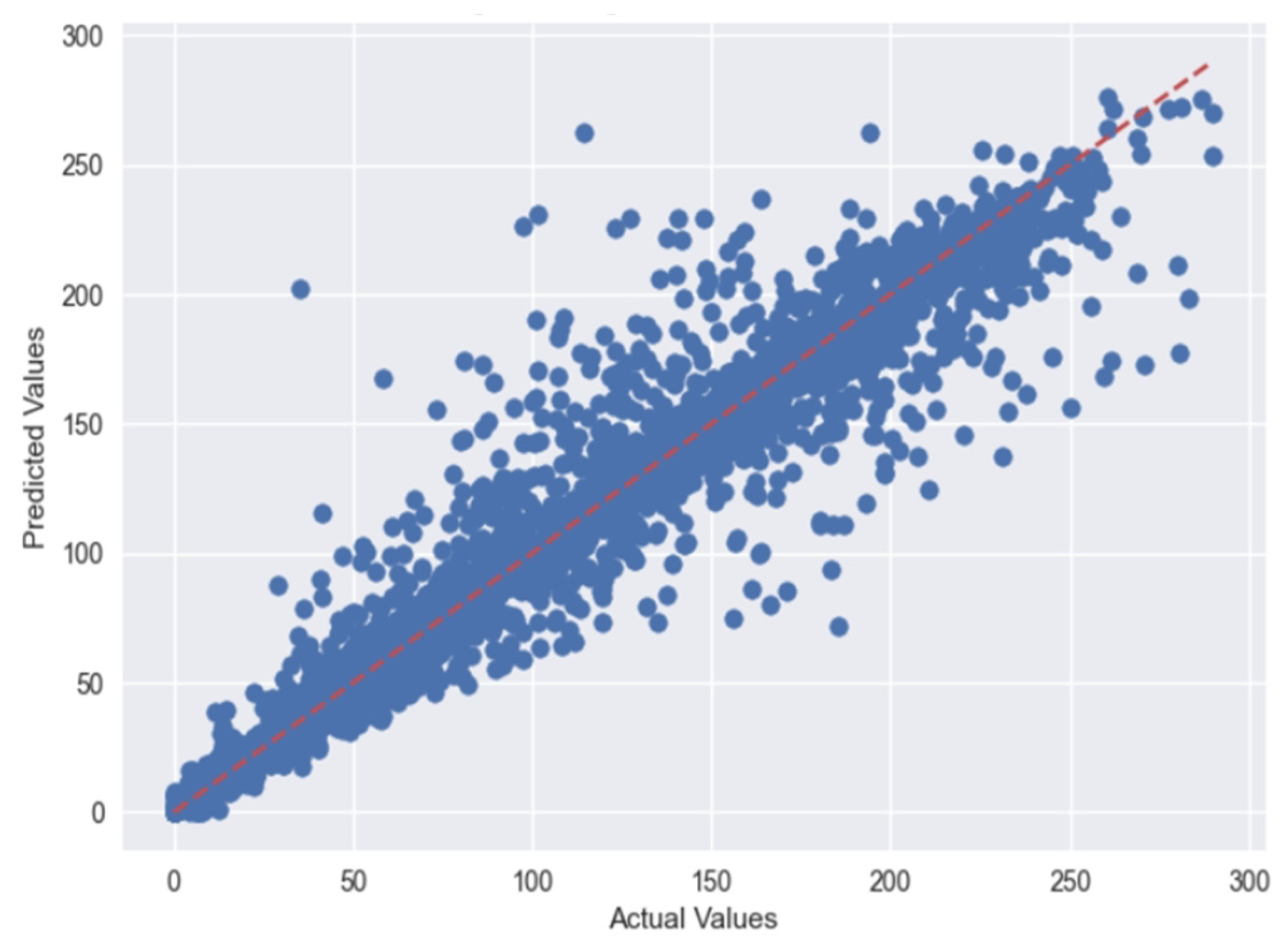
5. Results
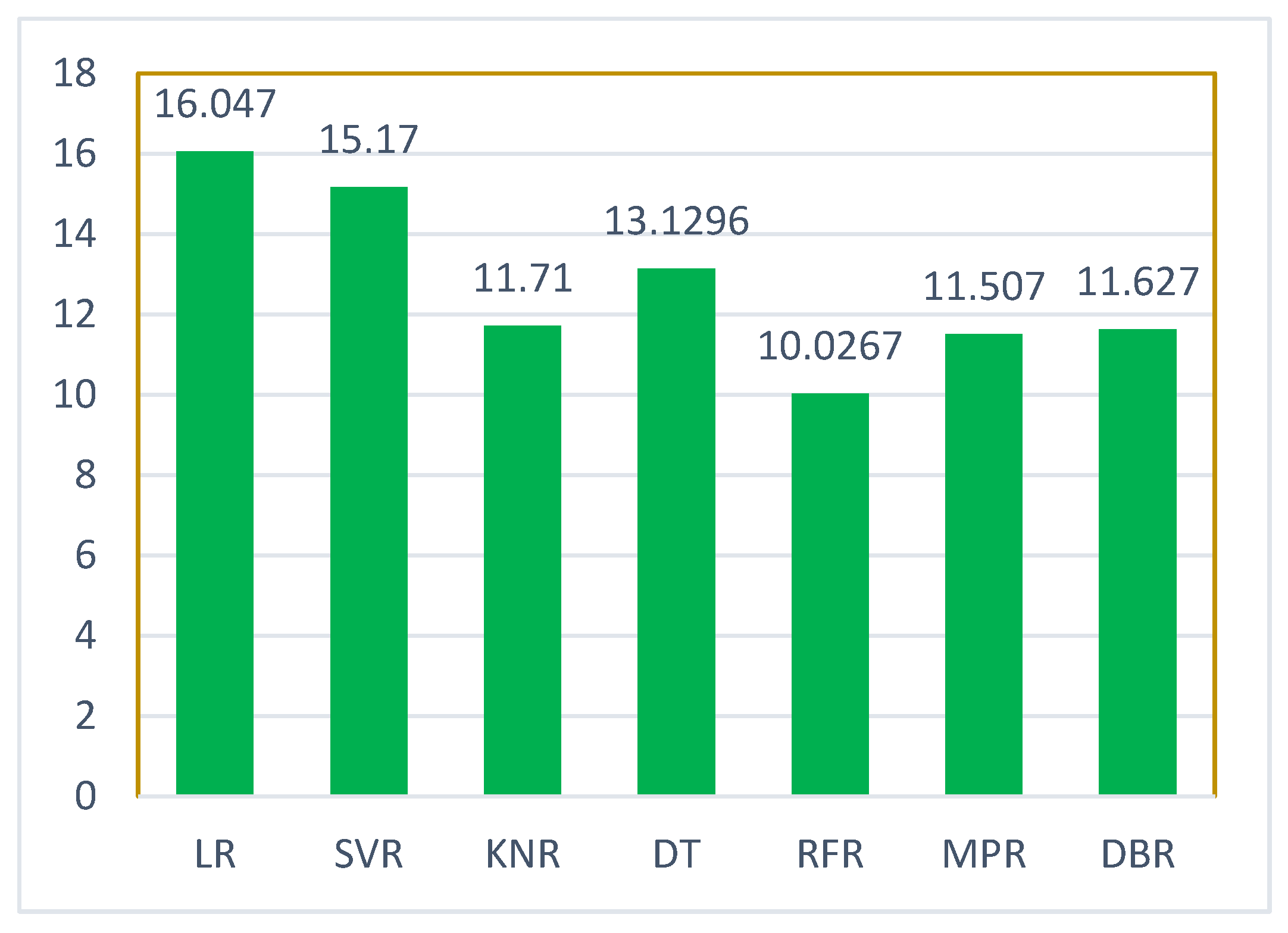
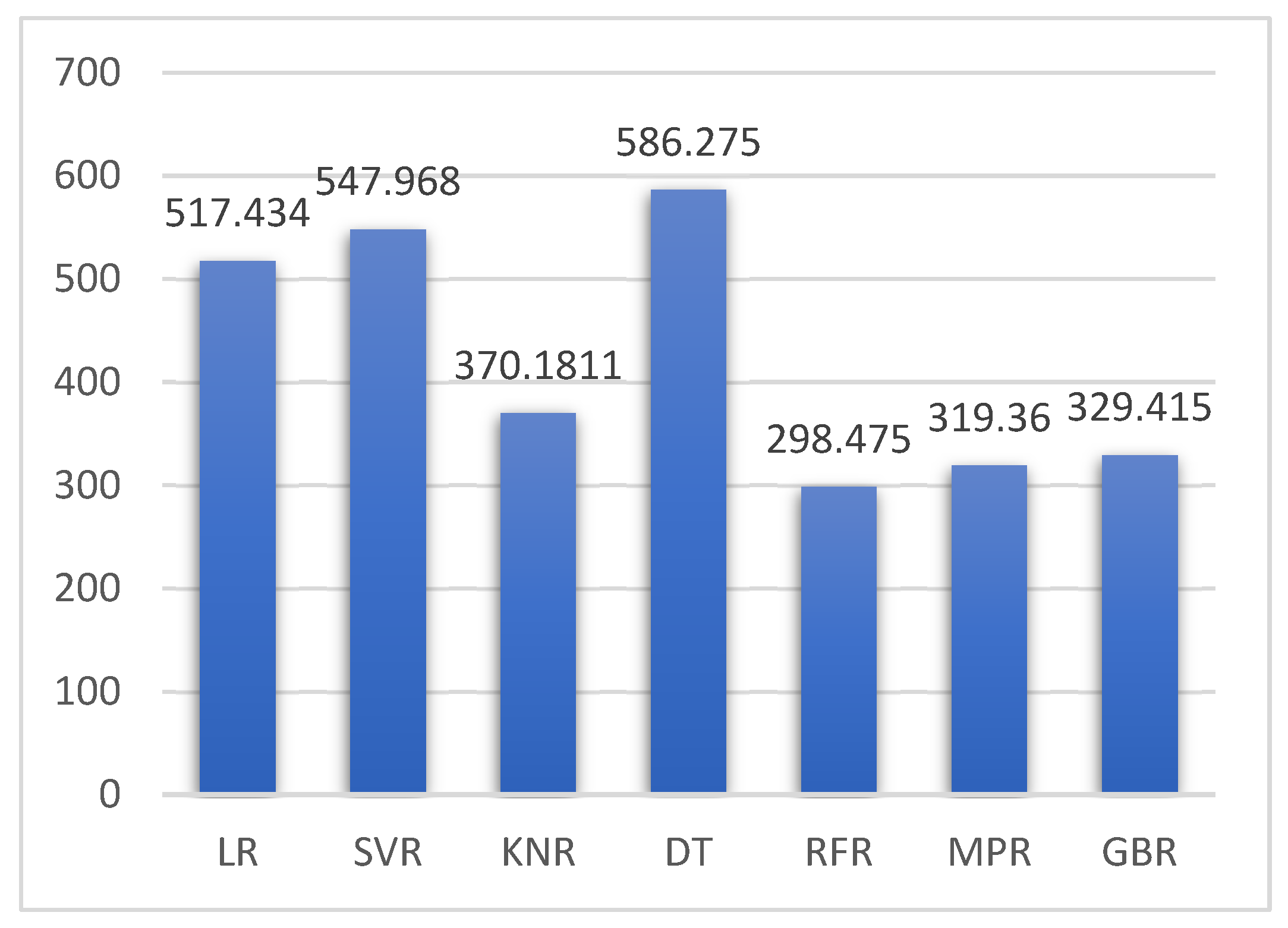
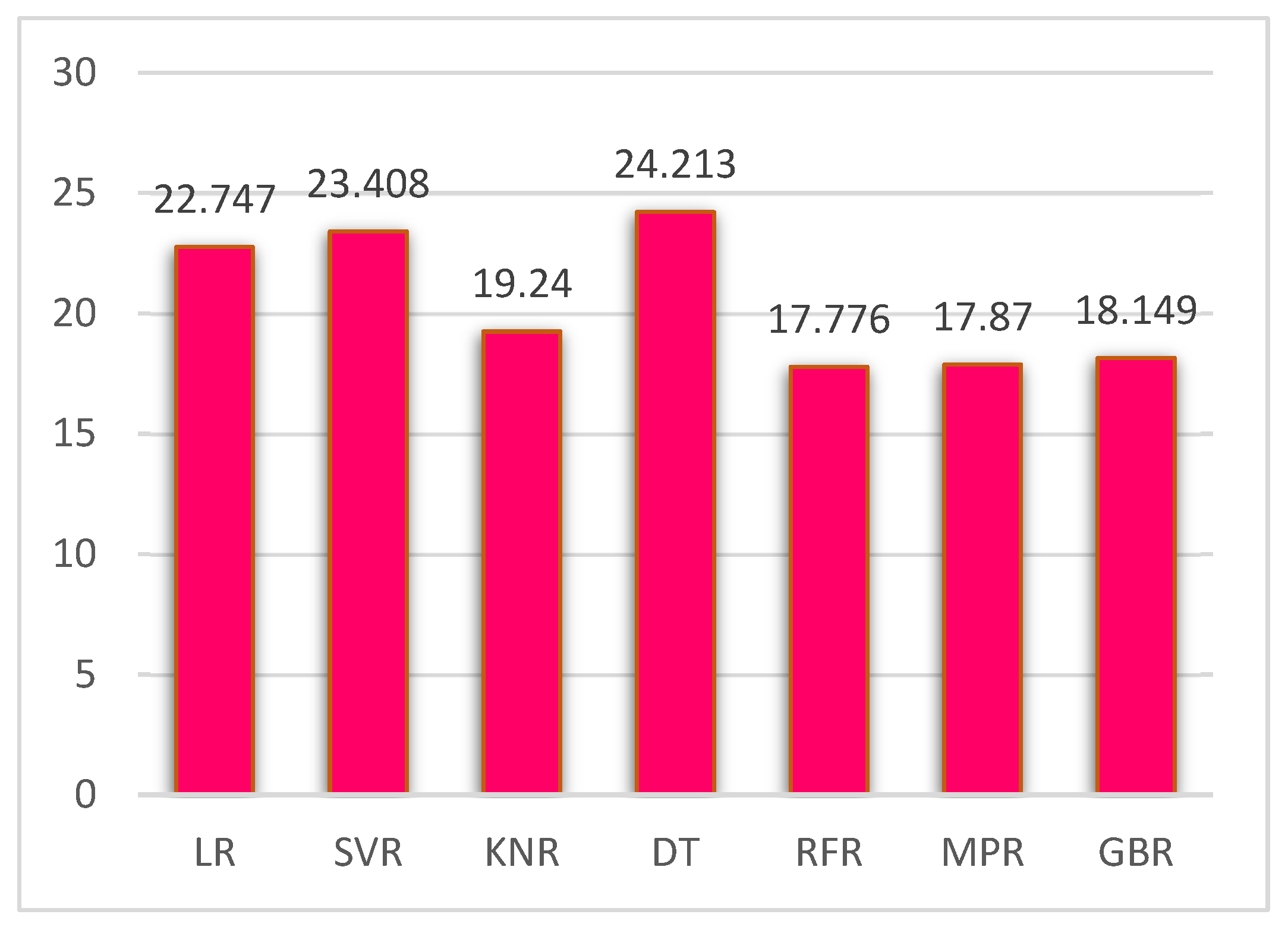
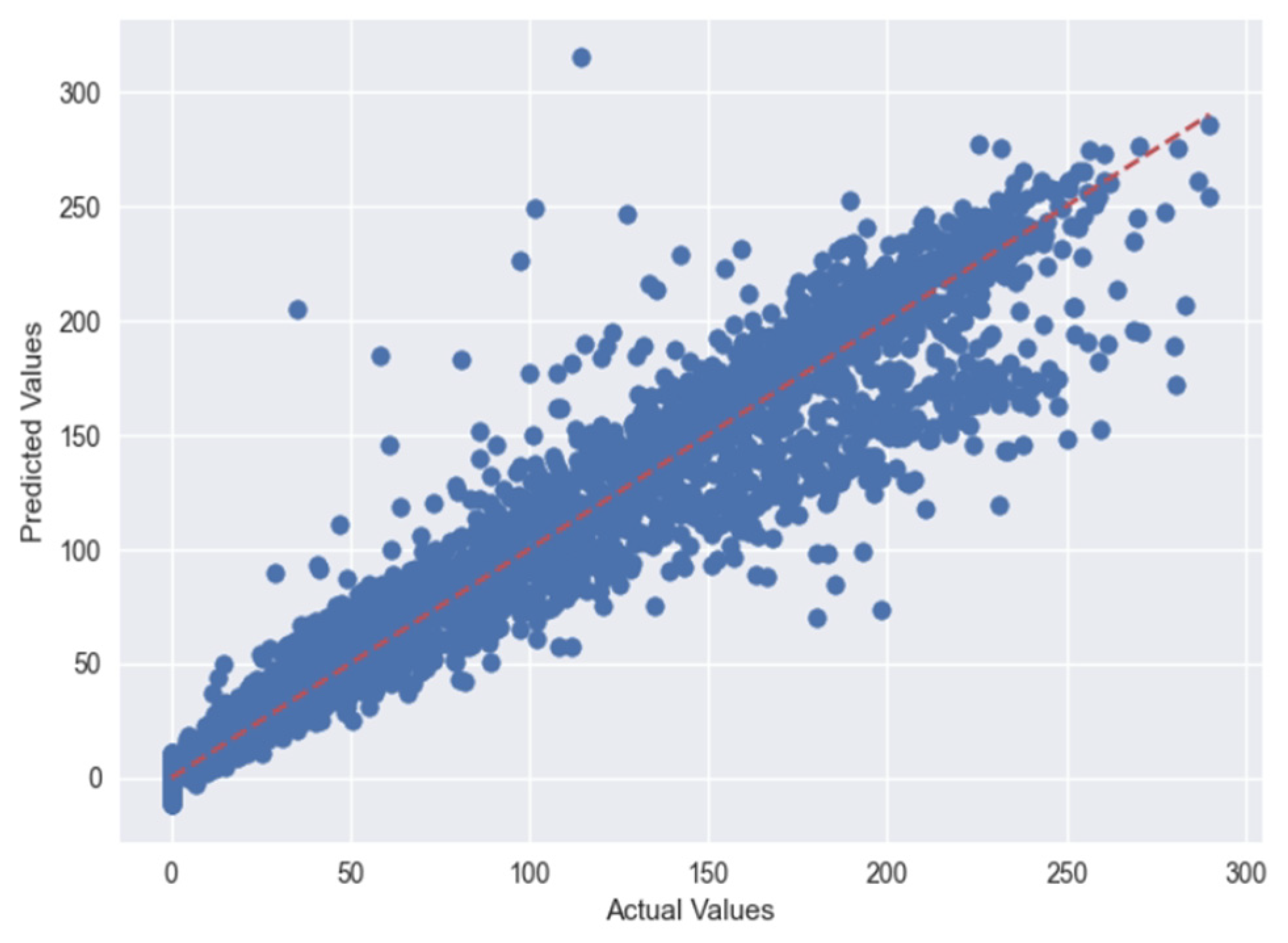
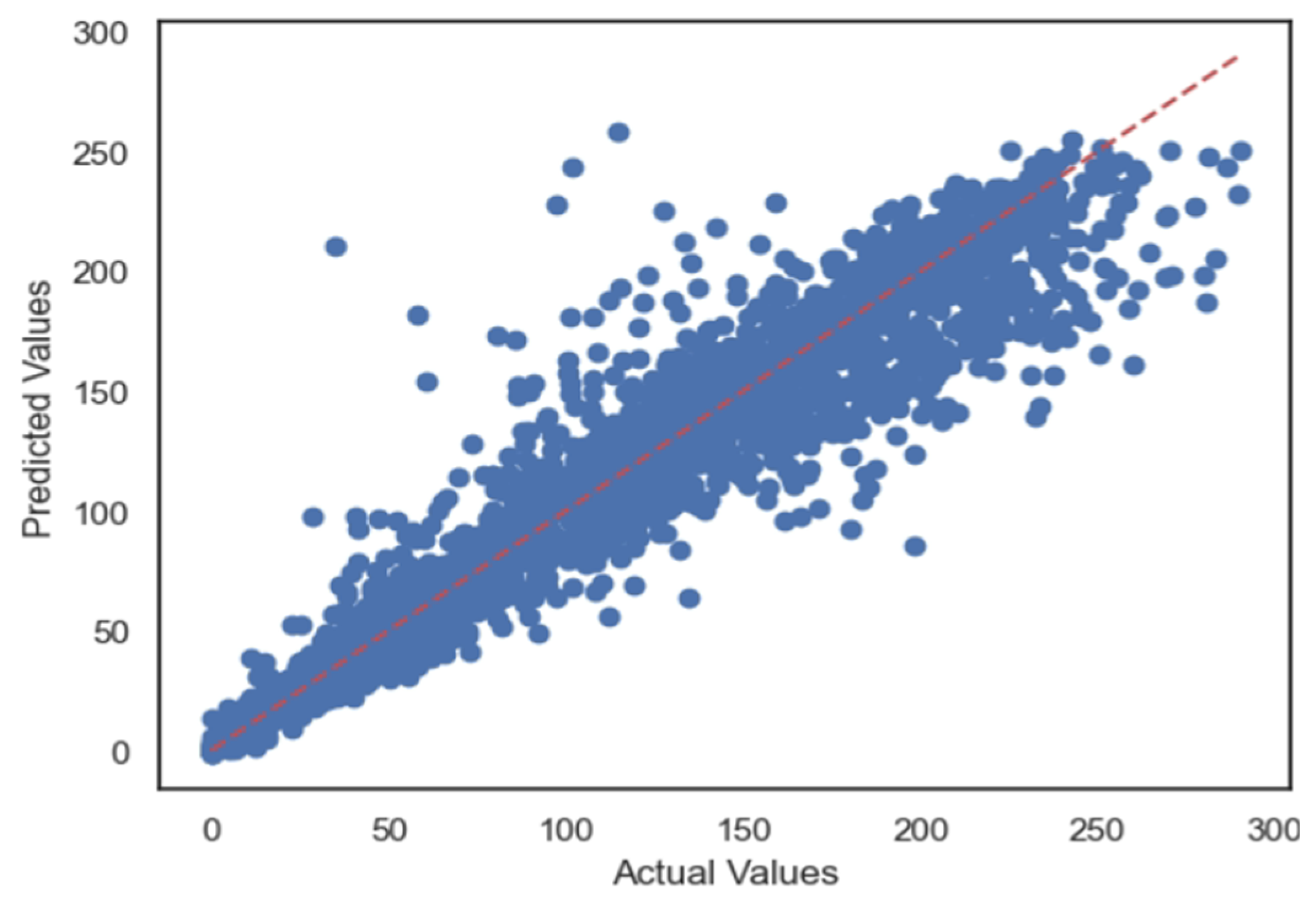
5.1. Case 1:—Data Frame with All Features
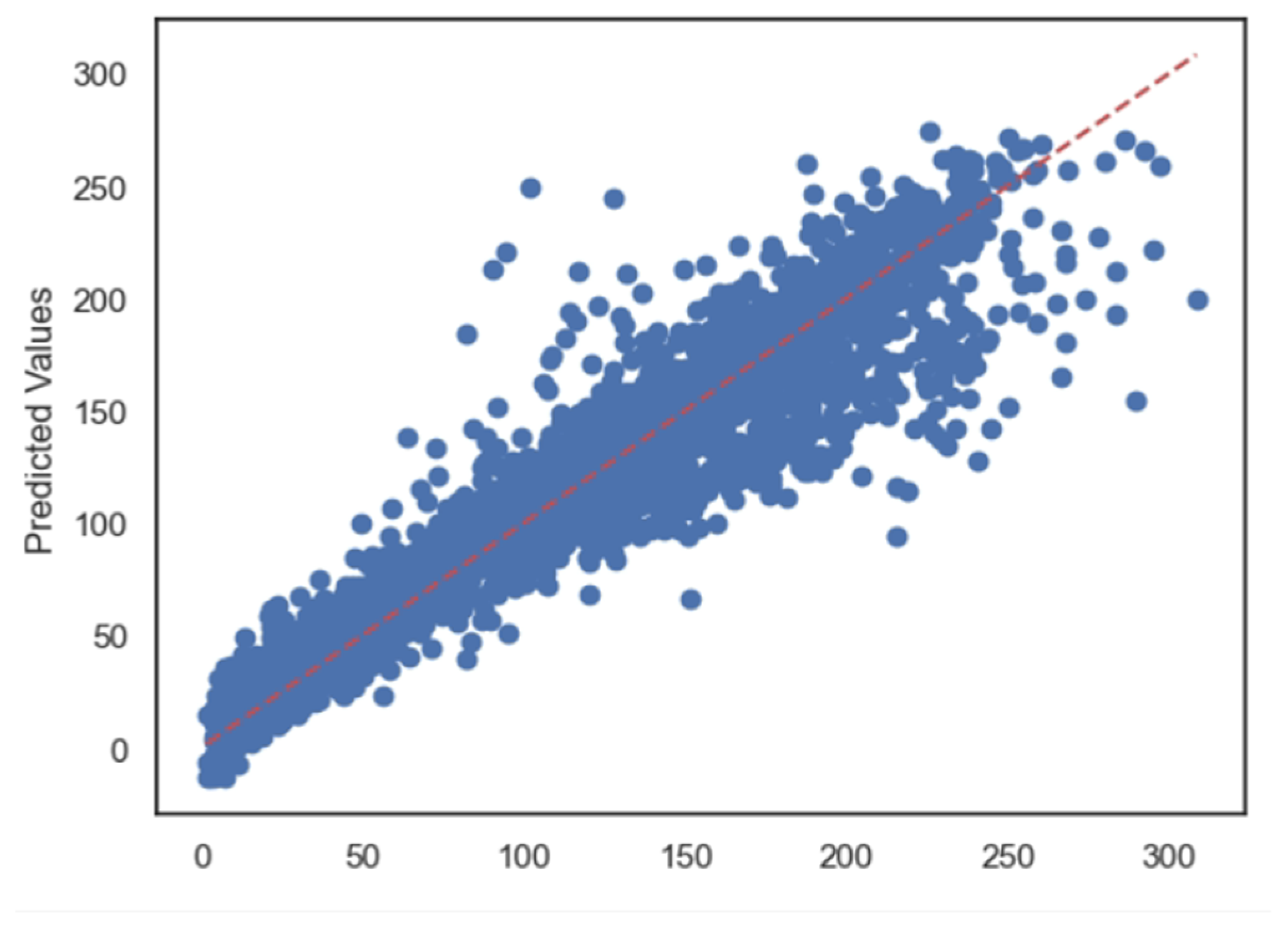
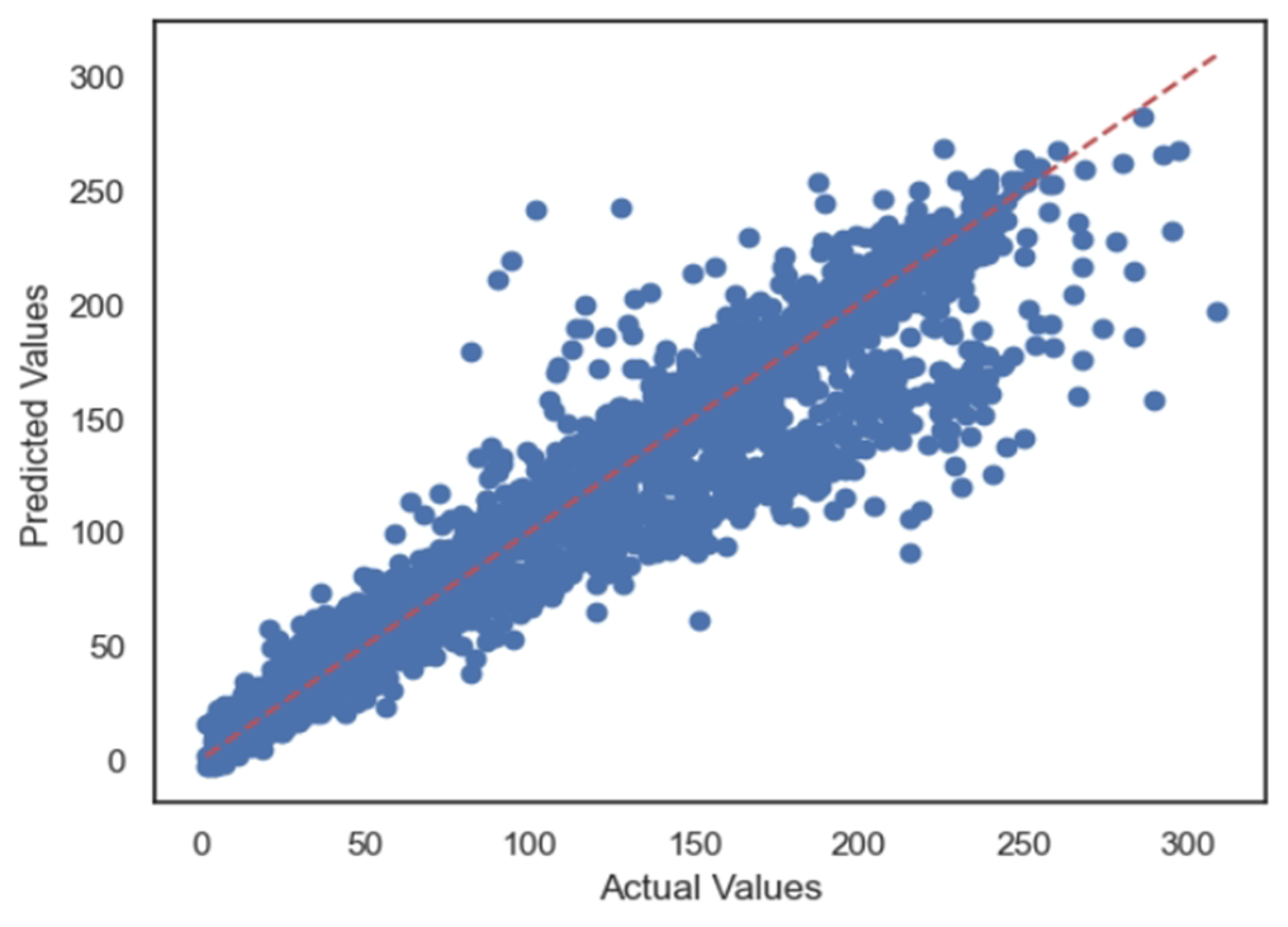
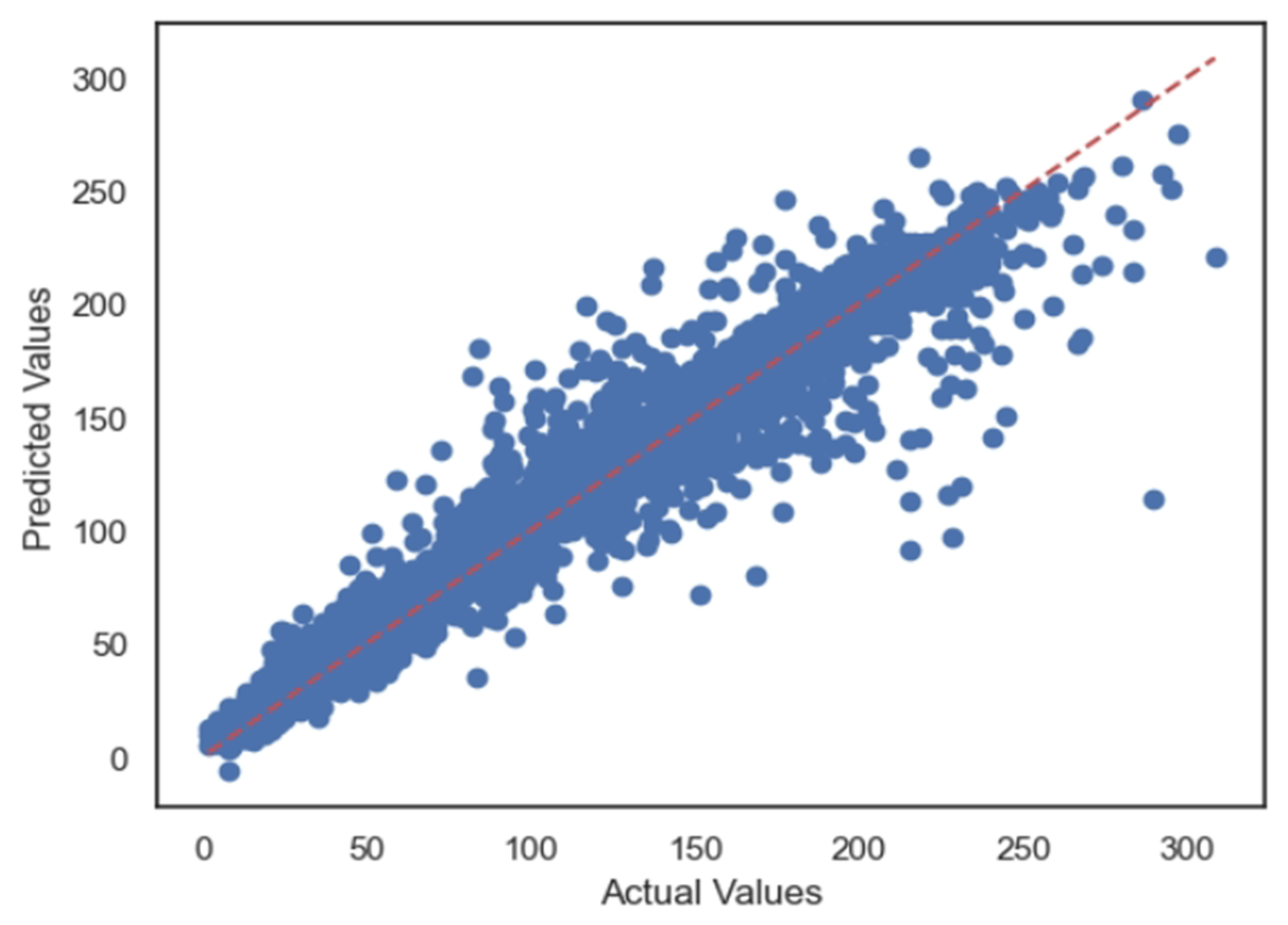
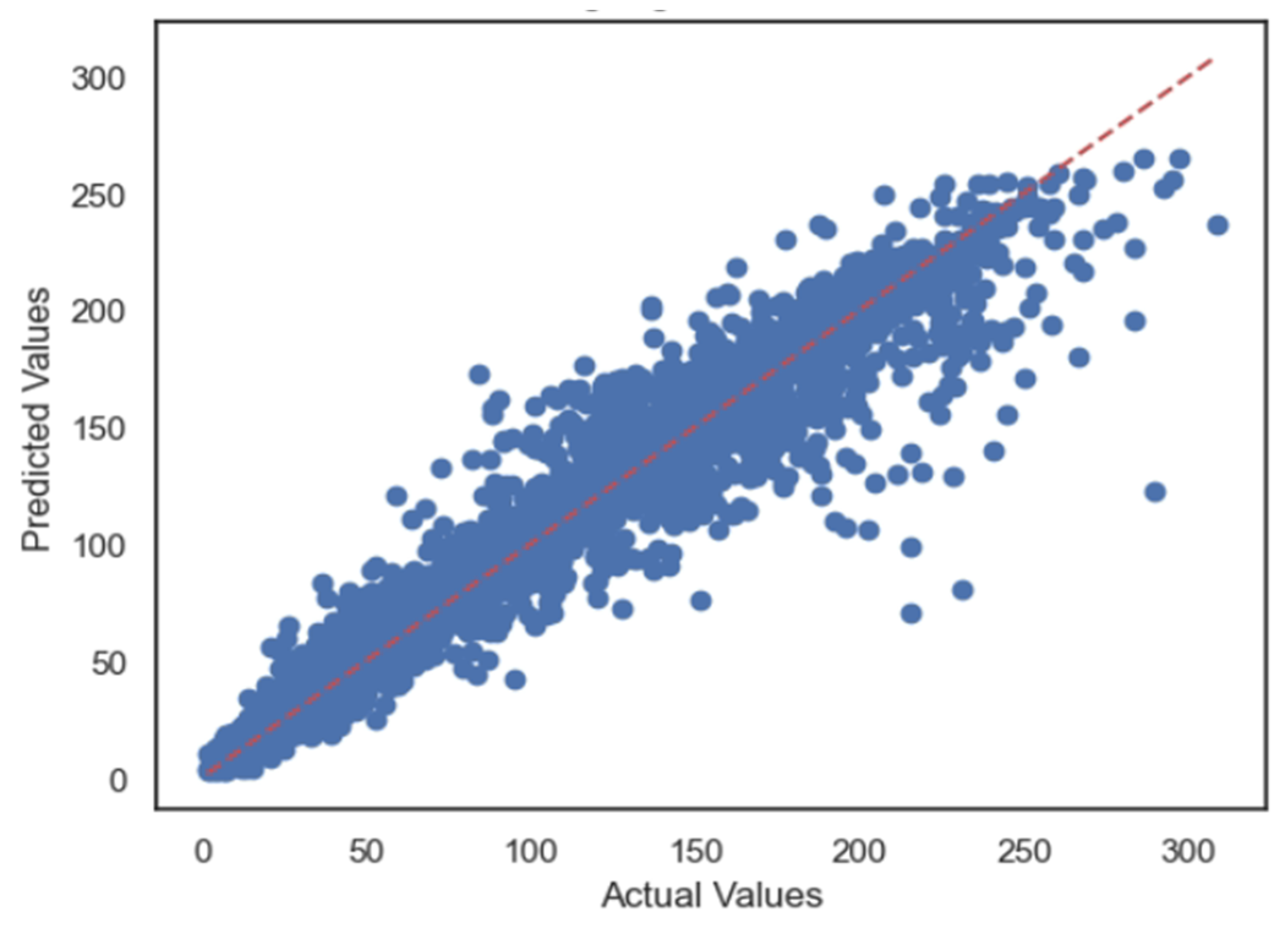
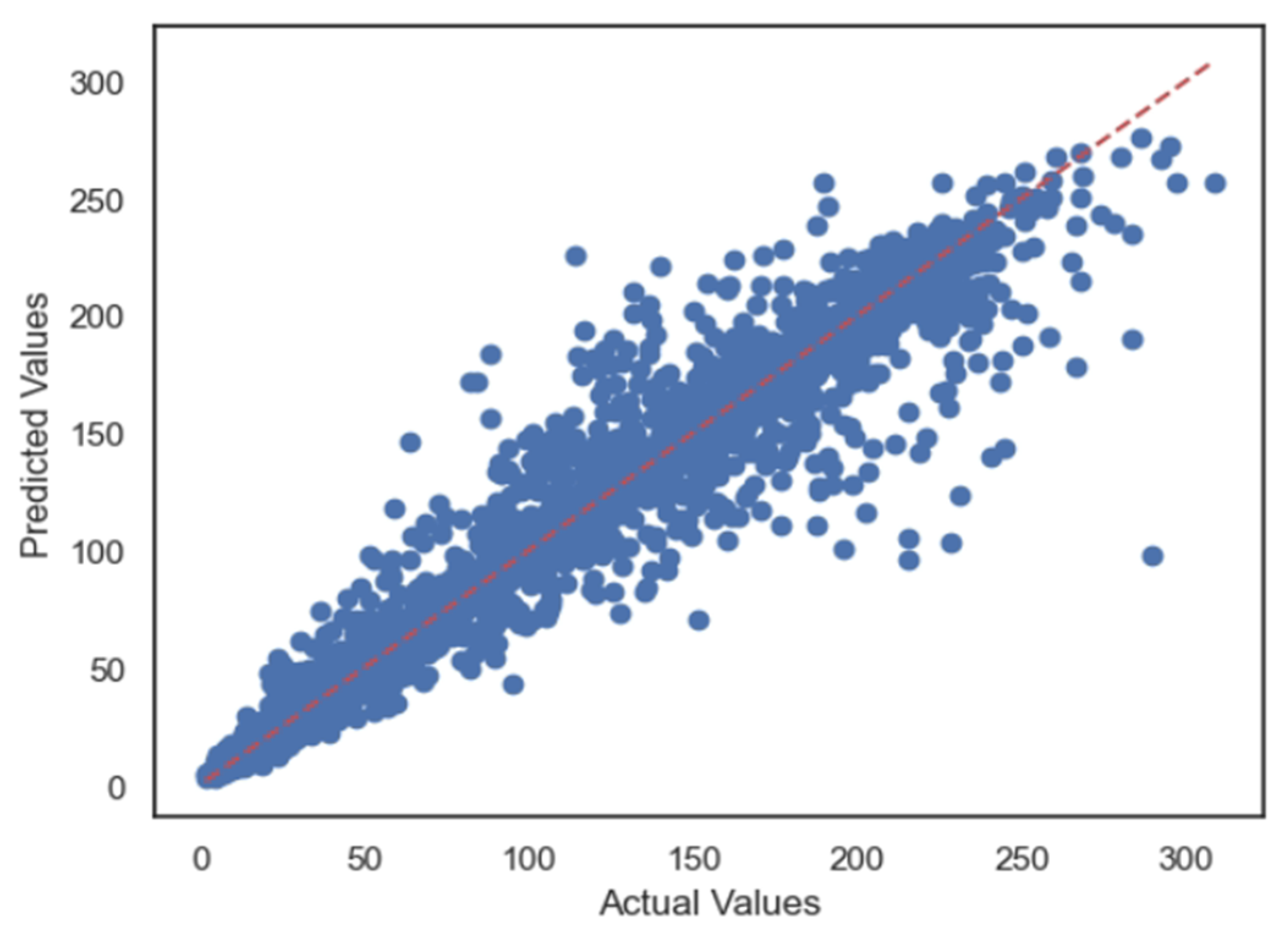
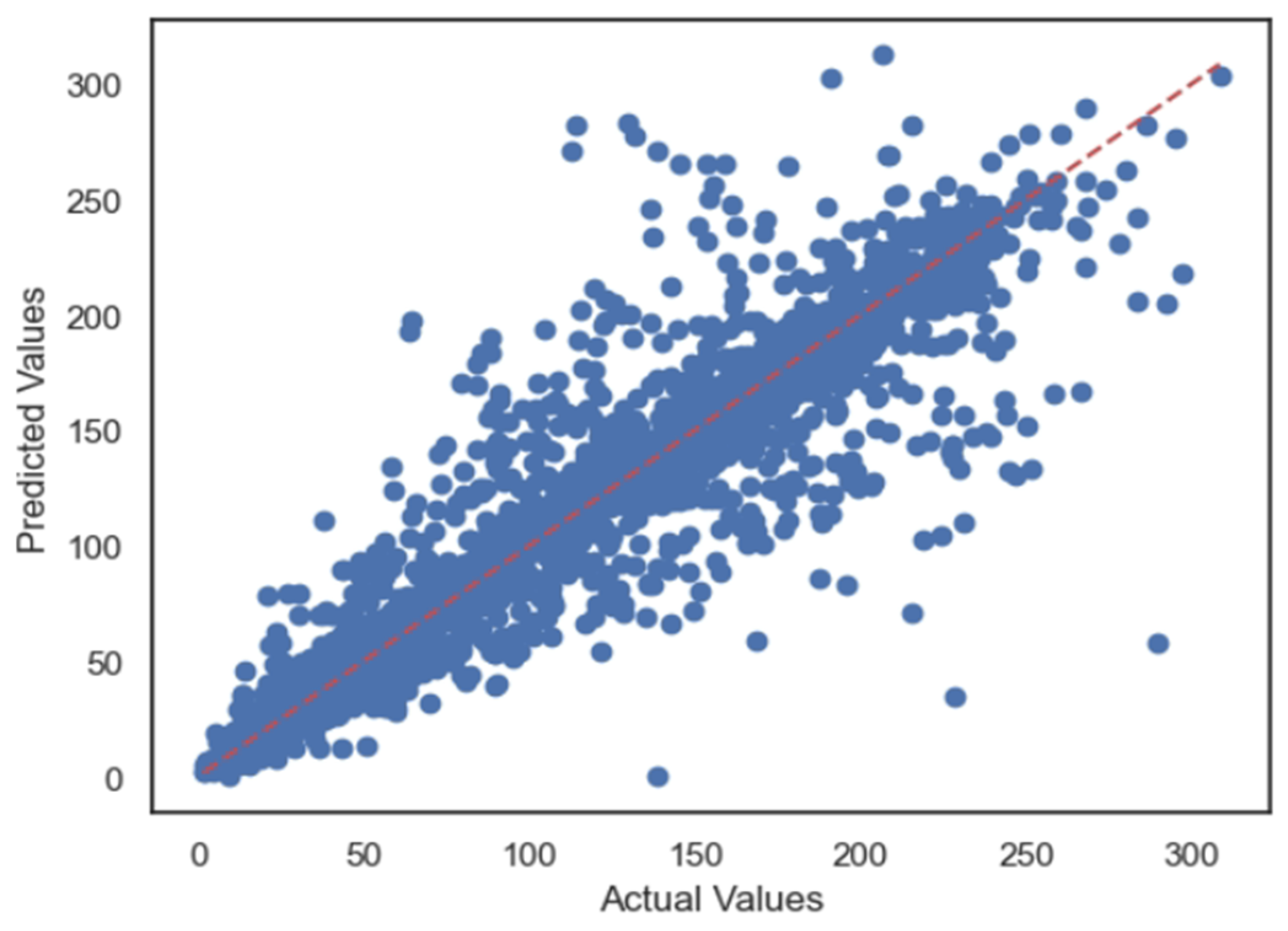
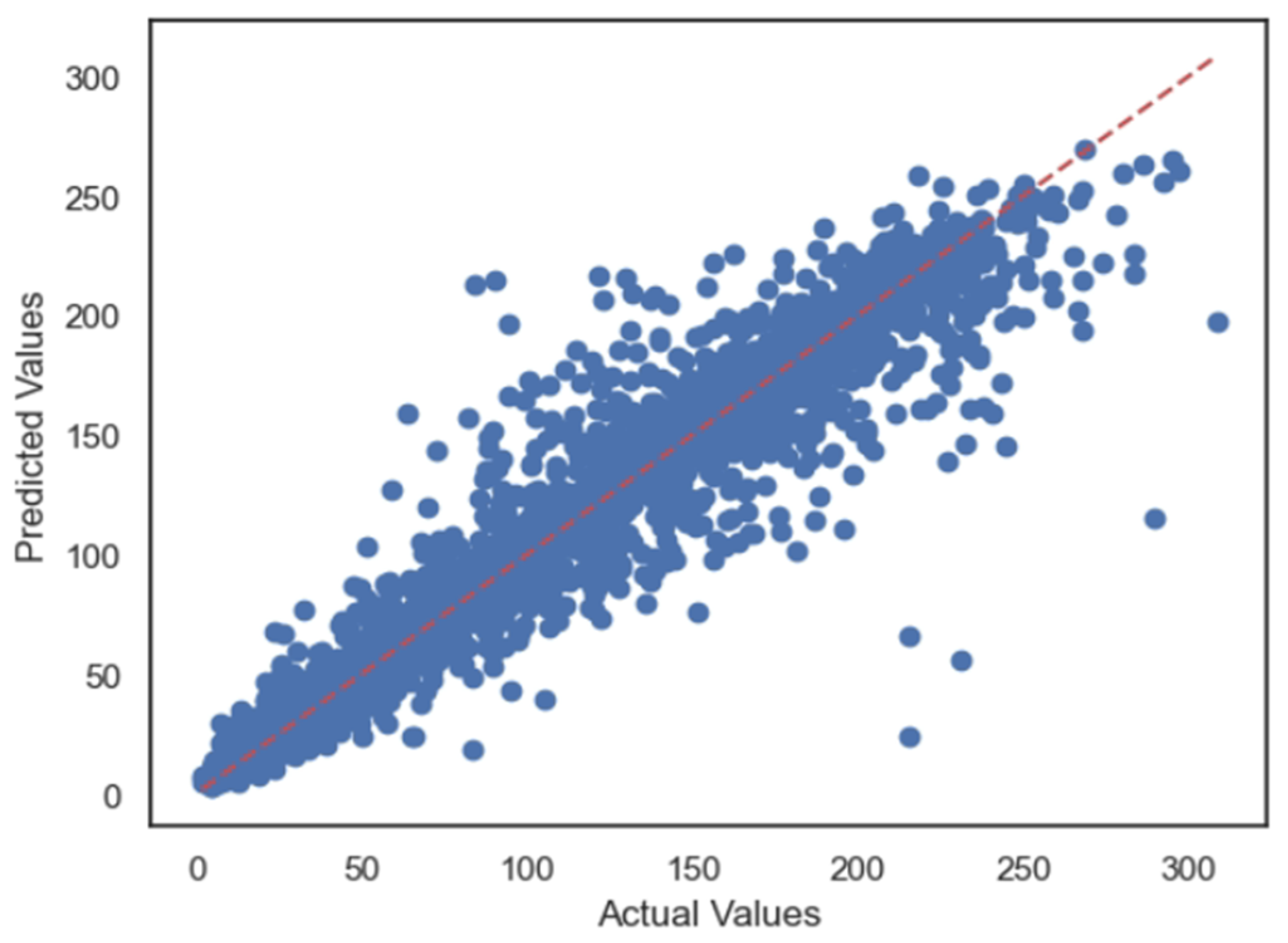
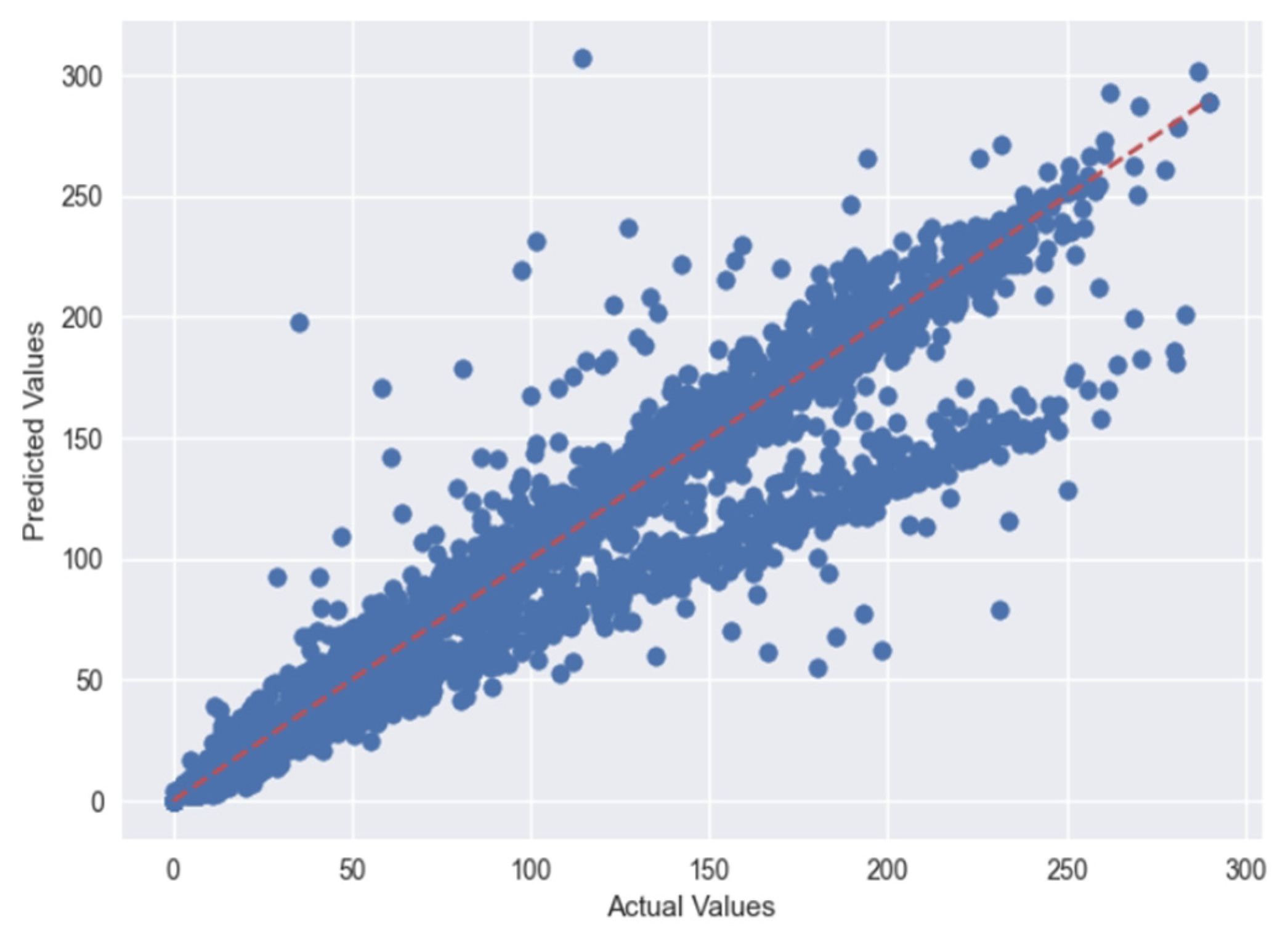
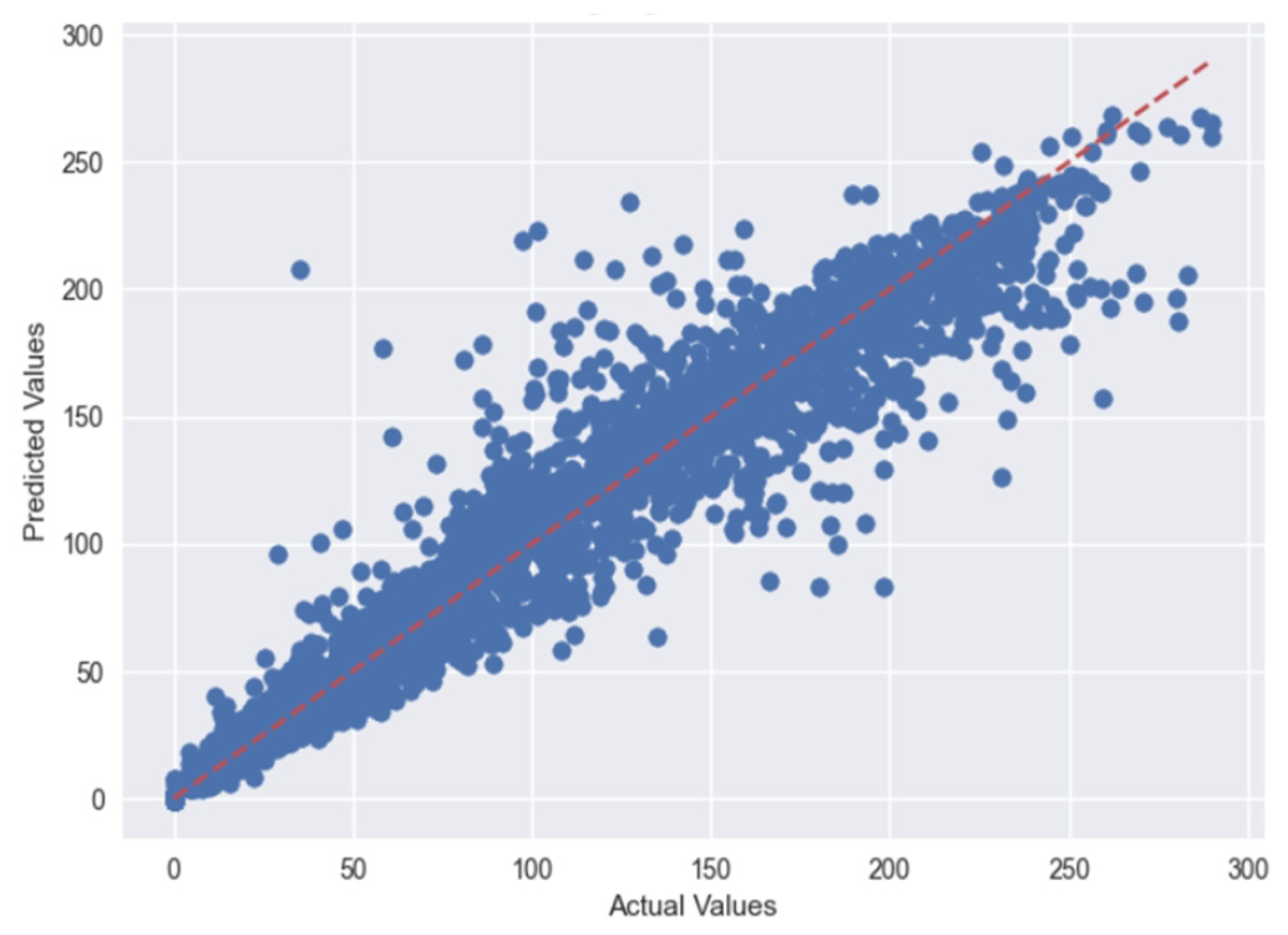
5.2. Case 2:—Data Frame without Wind (Km/h) and PR% Features
6. Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kuzlu, M.; Cali, U.; Sharma, V.; Güler, Ö. Gaining insight into solar photovoltaic power generation forecasting utilizing explainable artificial intelligence tools. IEEE Access 2020, 8, 187814–187823. [Google Scholar] [CrossRef]
- Behera, M.K.; Majumder, I.; Nayak, N. Solar photovoltaic power forecasting using optimized modified extreme learning machine technique. Eng. Sci. Technol. Int. J. 2018, 21, 428–438. [Google Scholar] [CrossRef]
- Yang, H.-T.; Huang, C.-M.; Huang, Y.-C.; Pai, Y.-S. A weather-based hybrid method for 1-day ahead hourly forecasting of solar power output. IEEE Trans. Sustain. Energy 2014, 5, 917–926. [Google Scholar] [CrossRef]
- Zhou, H.; Rao, M.; Chuang, K.T. Artificial intelligence approach to energy management and control in the HVAC process: An evaluation, development and discussion. Dev. Chem. Eng. Miner. Process. 1993, 1, 42–51. [Google Scholar] [CrossRef]
- De Benedetti, M.; Leonardi, F.; Messina, F.; Santoro, C.; Vasilakos, A. Anomaly detection and predictive maintenance for photovoltaic systems. Neurocomputing 2018, 310, 59–68. [Google Scholar] [CrossRef]
- Elsaraiti, M.; Merabet, A. A comparative analysis of the arima and lstm predictive models and their effectiveness for predicting wind speed. Energies 2021, 14, 6782. [Google Scholar] [CrossRef]
- Lee, S.; Nengroo, S.H.; Jin, H.; Doh, Y.; Lee, C.; Heo, T.; Har, D. Anomaly detection of smart metering system for power management with battery storage system/electric vehicle. ETRI J. 2023, 45, 650–665. [Google Scholar] [CrossRef]
- Etxegarai, G.; López, A.; Aginako, N.; Rodríguez, F. An analysis of different deep learning neural networks for intra-hour solar irradiation forecasting to compute solar photovoltaic generators’ energy production. Energy Sustain. Dev. 2022, 68, 1–17. [Google Scholar] [CrossRef]
- Javanmard, M.E.; Ghaderi, S. A hybrid model with applying machine learning algorithms and optimization model to forecast greenhouse gas emissions with energy market data. Sustain. Cities Soc. 2022, 82, 103886. [Google Scholar] [CrossRef]
- Shedbalkar, K.H.; More, D. Bayesian Regression for Solar Power Forecasting. In Proceedings of the 2022 2nd International Conference on Artificial Intelligence and Signal Processing (AISP), Vijayawada, India, 12–14 February 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1–4. [Google Scholar]
- Nengroo, S.H.; Kamran, M.A.; Ali, M.U.; Kim, D.-H.; Kim, M.-S.; Hussain, A.; Kim, H.J. Dual battery storage system: An optimized strategy for the utilization of renewable photovoltaic energy in the United Kingdom. Electronics 2018, 7, 177. [Google Scholar] [CrossRef]
- Dash, P.; Majumder, I.; Nayak, N.; Bisoi, R. Point and interval solar power forecasting using hybrid empirical wavelet transform and robust wavelet kernel ridge regression. Nat. Resour. Res. 2020, 29, 2813–2841. [Google Scholar] [CrossRef]
- Nengroo, S.H.; Lee, S.; Jin, H.; Har, D. Optimal Scheduling of Energy Storage for Power System with Capability of Sensing Short-Term Future solar Power Production. In Proceedings of the 2021 11th International Conference on Power and Energy Systems (ICPES), Shanghai, China, 18–20 December 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 172–177. [Google Scholar]
- Alfadda, A.; Adhikari, R.; Kuzlu, M.; Rahman, S. Hour-ahead solar power forecasting using SVR based approach. In Proceedings of the 2017 IEEE Power & Energy Society Innovative Smart Grid Technologies Conference (ISGT), Washington, DC, USA, 23–26 April 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1–5. [Google Scholar]
- Persson, C.; Bacher, P.; Shiga, T.; Madsen, H. Multi-site solar power forecasting using gradient boosted regression trees. Sol. Energy 2017, 150, 423–436. [Google Scholar] [CrossRef]
- Abuella, M.; Chowdhury, B. Solar power forecasting using support vector regression. arXiv 2017, arXiv:1703.09851. [Google Scholar]
- Huang, J.; Perry, M. A semi-empirical approach using gradient boosting and k-nearest neighbors regression for GEFCom2014 probabilistic solar power forecasting. Int. J. Forecast. 2016, 32, 1081–1086. [Google Scholar] [CrossRef]
- Lin, K.-P.; Pai, P.-F. Solar power output forecasting using evolutionary seasonal decomposition least-square support vector regression. J. Clean. Prod. 2016, 134, 456–462. [Google Scholar] [CrossRef]
- Bacher, P.; Madsen, H.; Nielsen, H.A. Online short-term solar power forecasting. Sol. Energy 2009, 83, 1772–1783. [Google Scholar] [CrossRef]
- Nengroo, S.H.; Jin, H.; Kim, I.; Har, D. Special Issue on Future Intelligent Transportation System (ITS) for Tomorrow and Beyond. Appl. Sci. 2022, 12, 5994. [Google Scholar] [CrossRef]
- Jin, H.; Nengroo, S.H.; Kim, I.; Har, D. Special issue on advanced wireless sensor networks for emerging applications. Appl. Sci. 2022, 12, 7315. [Google Scholar] [CrossRef]
- Al-Qahtani, F.H.; Crone, S.F. Multivariate k-nearest neighbour regression for time series data—A novel algorithm for forecasting UK electricity demand. In Proceedings of the 2013 International Joint Conference on Neural Networks (IJCNN), Dallas, TX, USA, 4–9 August 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 1–8. [Google Scholar]
- El hadj Youssef, W.; Abdelli, A.; Kharroubi, F.; Dridi, F.; Khriji, L.; Ahshan, R.; Machhout, M.; Nengroo, S.H.; Lee, S. A Secure Chaos-Based Lightweight Cryptosystem for the Internet of Things. IEEE Access 2023, 11, 123279–123294. [Google Scholar] [CrossRef]
- Jin, H.; Nengroo, S.H.; Lee, S.; Har, D. Power Management of Microgrid Integrated with Electric Vehicles in Residential Parking Station. In Proceedings of the 2021 10th International Conference on Renewable Energy Research and Application (ICRERA), Istanbul, Turkey, 26–29 September 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 65–70. [Google Scholar]
- Lee, S.; Nengroo, S.H.; Jin, H.; Doh, Y.; Lee, C.; Heo, T.; Har, D. Power management in smart residential building with deep learning model for occupancy detection by usage pattern of electric appliances. In Proceedings of the 2023 5th International Electronics Communication Conference, Osaka City, Japan, 21–23 July 2023; pp. 84–92. [Google Scholar]
- Lee, S.; Jin, H.; Nengroo, S.H.; Doh, Y.; Lee, C.; Heo, T.; Har, D. Smart Metering System Capable of Anomaly Detection by Bi-directional LSTM Autoencoder. In Proceedings of the 2022 IEEE International Conference on Consumer Electronics (ICCE), Las Vegas, NV, USA, 7–9 January 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1–6. [Google Scholar]
- Lee, S.; Nengroo, S.H.; Jung, Y.; Kim, S.; Kwon, S.; Shin, Y.; Lee, J.; Doh, Y.; Heo, T.; Har, D. Factory Energy Management by Steam Energy Cluster Modeling in Paper-Making. In Proceedings of the 2023 11th International Conference on Smart Grid (icSmartGrid), Paris, France, 4–7 June 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 1–5. [Google Scholar]
- Rifat, M.S.H.; Niloy, M.A.; Rizvi, M.F.; Ahmed, A.; Ahshan, R.; Nengroo, S.H.; Lee, S. Application of Binary Slime Mould Algorithm for Solving Unit Commitment Problem. IEEE Access 2023, 11, 45279–45300. [Google Scholar] [CrossRef]
- Lai-Dang, Q.-V.; Nengroo, S.H.; Jin, H. Learning dense features for point cloud registration using a graph attention network. Appl. Sci. 2022, 12, 7023. [Google Scholar] [CrossRef]
- Munawar, U.; Wang, Z. A framework of using machine learning approaches for short-term solar power forecasting. J. Electr. Eng. Technol. 2020, 15, 561–569. [Google Scholar] [CrossRef]
- Mishra, M.; Dash, P.B.; Nayak, J.; Naik, B.; Swain, S.K. Deep learning and wavelet transform integrated approach for short-term solar power prediction. Measurement 2020, 166, 108250. [Google Scholar] [CrossRef]
- Aslam, M.; Lee, S.-J.; Khang, S.-H.; Hong, S. Two-stage attention over LSTM with Bayesian optimization for day-ahead solar power forecasting. IEEE Access 2021, 9, 107387–107398. [Google Scholar] [CrossRef]

| Acronym | Full Form |
|---|---|
| ANN | Artificial Neural Network |
| XAI | Extensible Artificial Intelligence |
| LSTM | Long Short-Term Memory |
| CNN | Convolutional Neural Network |
| ARIMA | Autoregressive Integrated Moving Average |
| PV | Photovoltaic |
| MLP | Multi-layer Perceptron Regressor |
| SARIMA | Seasonal Autoregressive Integrated Moving Average |
| SARIMAX | Seasonal Auto-Regressive Integrated Moving Average with Exogenous Factors |
| LR | Linear Regression |
| LAN | Local Area Network |
| SVR | Support Vector Regressor |
| Case Studies | Methodologies | Regression Models Used | Dataset Description | Testbed Description |
|---|---|---|---|---|
| [8] | The study proposes two deep learning methods for irradiance predictions for the next hour. | LSTM and CNN networks are used. | - | - |
| [9] | To tackle the consequences of carbon dioxide and other pollutants, this work has provided a hybrid machine learning and quantitative programming approach that has a high rate of approximation and is used with sparse data. | The nine methods of ANN, autoregressive, ARIMA, SARIMA, SARIMAX, random forest, SVR, K-nearest neighbors, and LSTM were used to predict the harmful emissions of each gas. | - | - |
| [10] | The findings of PV power generation forecasts using linear, ridge, and Bayesian regression methods are presented in this work. | Linear regression, Ridge regression, and Bayesian regression. | The data collection approach uses the data records at 15 min intervals. | Skymet W.S.P.L. |
| [11] | According to the distinctions and commonalities, the paper sorts the nomenclature of PV energy forecast approaches, optimizers, and prediction frameworks into various groups. | The difficulties and probable paths for future study in PV power forecasting using machine learning algorithms are discussed by the authors. | Challenges faced in forecasting structure. | - |
| [12] | For point-to-point and intermediate modeling of PV power in the context of a smart grid ecosystem, a viable composite empirical wavelet transform (EWT)-based modified resilient Mexican hat wavelet kernel ridge regression (RMHWK) approach has been suggested. | EWT (empirical wavelet transform) and RKRR (robust Kernel Ridge regressor) methods are used by the researchers. | - | 1 Megawatt PV Plant data of Odisha, India, validated using a dataset from Florida, USA. |
| [13] | Initially a time-series-based PV power projection (SPF) structure is developed using the nearby meteorology station’s forecasted weather data and its time component. For the proposed SPF, the long short-term memory (LSTM) method is applied in consideration of the data correlations in the data dimensions. | Long short-term memory (LSTM) with Gaussian process regression. | - | - |
| [14] | The paper suggests an overall regression neural network (GRNN) built around Grey Wolf optimization (GWO), which is anticipated to deliver better precise forecasts with faster computation. | To achieve meteorological aggregation and training the neural network. With GWO model, an autonomous map (SOM) is implemented. | Xiamen University Tan Kah Kee College, Zhangzhou China, and National Kaohsiung University of Science and Technology, Kaohsiung Taiwan. | Fifty-three thousand records each year are collected from various PV plants. |
| [15] | The weighted Gaussian procedure regression strategy is used in this investigation, and a novel method is suggested where data points with an elevated outlier likelihood are given a lower weight. | For data with large dimensions, a density-based local outlier identification approach is presented to make up for the degradation of the Euclidean distance outcome. | Dataset by Nanyang Technical University. | The testbed used in the research has six panel systems, distributed at various locations in a tropical rainforest region of Singapore. |
| [16] | This work involves performing hour-ahead PV power generation predictions. | Support vector regressor. Lasso regression and polynomial regression. | Data collected for 15 months are used in the study. | Virginia Tech Research Centre. |
| [17] | In this study, a non-parametric predictive machine learning method for PV electric power generation and forecasting in an anticipated timeframe of one to six hours is presented. To develop a gradient-boosted regression tree (GBRT) framework, 42 unique PV roofing setups, past power production, and pertinent climatic data are used. | Gradient-boosted regression tree and multi-site modelling. | - | Data has been collected from 46 distinctive PV installations. |
| [18] | To simulate the real-world practice of energy projections, the research provides a support vector regression approach to generate PV power estimates on an ongoing schedule for 24 h, extending over an entire calendar year. | Support vector regressor. | The dataset used in the research is from the Global Energy Forecasting Competition in the year 2014. | Precise PV power units installed in Australia. |
| [19] | The authors of the manuscript propose a strategy that employs the gradient boosting technique for reliable planning. | Gradient boost and k-nearest neighbor. | GEFCom 2014. | - |
| [20] | To project weekly PV power output, this study creates a genetic intermittent decomposition least-square support vector regression (ESDLS-SVR). | Least-square support vector regression, ARIMA, SARIMA, and GRNN. | Dataset by the Ministry of Science and Technology of the Republic of China incorporating Taiwan. | - |
| [21] | The manuscript introduces an online platform for power forecasting in PV systems used in various applications. This article is used to forecast hourly PV power estimates over 36 h spans. | Autoregressive models. | Data of a 15 min timelapse are used. | 21 PV systems installed on building rooftops. |
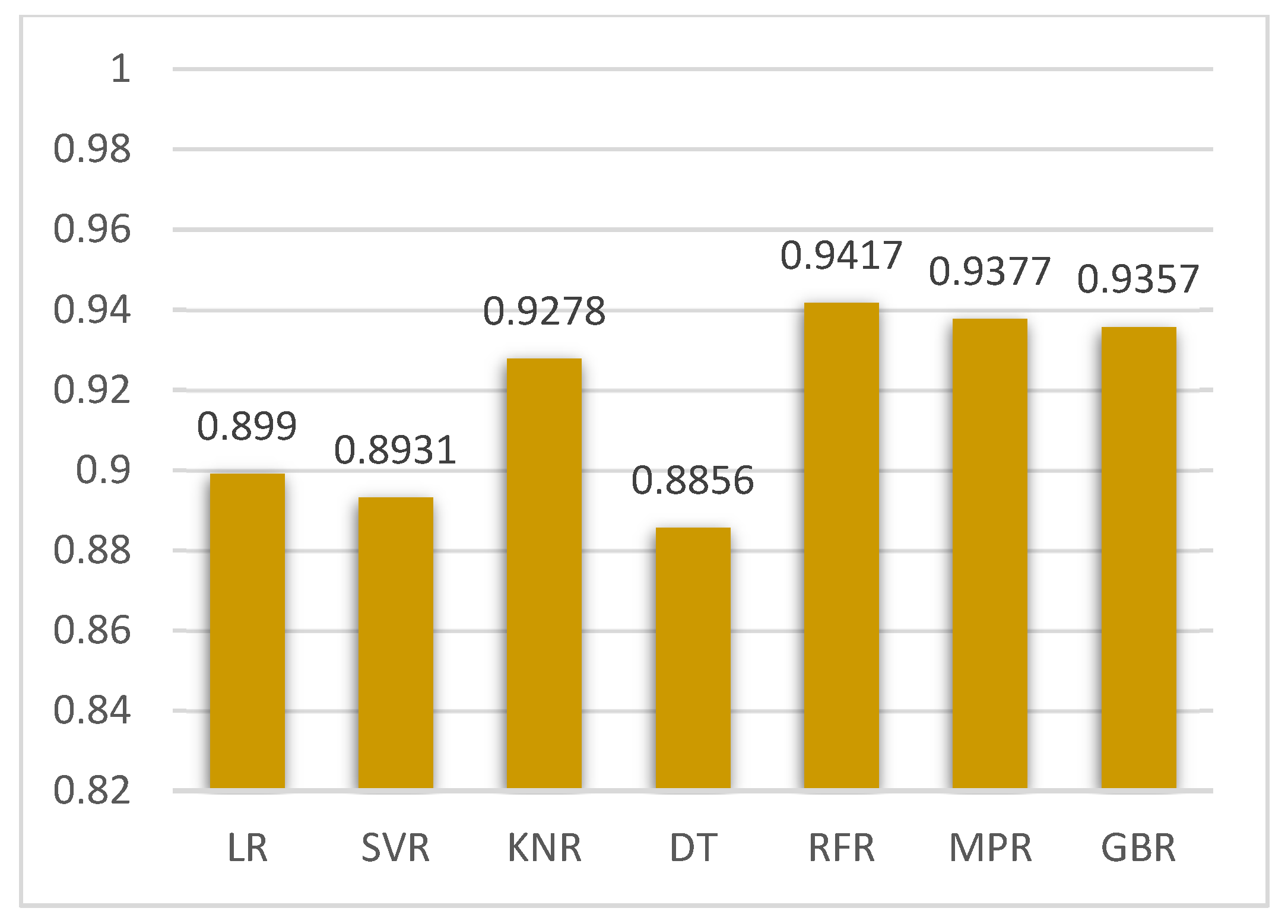
| Regression Method | MAE | MSE | RMSE | R2 Score |
|---|---|---|---|---|
| LR | 16.047 | 517.434 | 22.747 | 0.8990 |
| SVR | 15.170 | 547.968 | 23.408 | 0.8931 |
| KNR | 11.710 | 370.1811 | 19.2400 | 0.9278 |
| DTR | 13.1296 | 586.275 | 24.213 | 0.8856 |
| random forest regression | 10.0267 | 298.475 | 17.776 | 0.9417 |
| MLP | 11.507 | 319.36 | 17.870 | 0.9377 |
| GBR | 11.627 | 329.415 | 18.149 | 0.9357 |
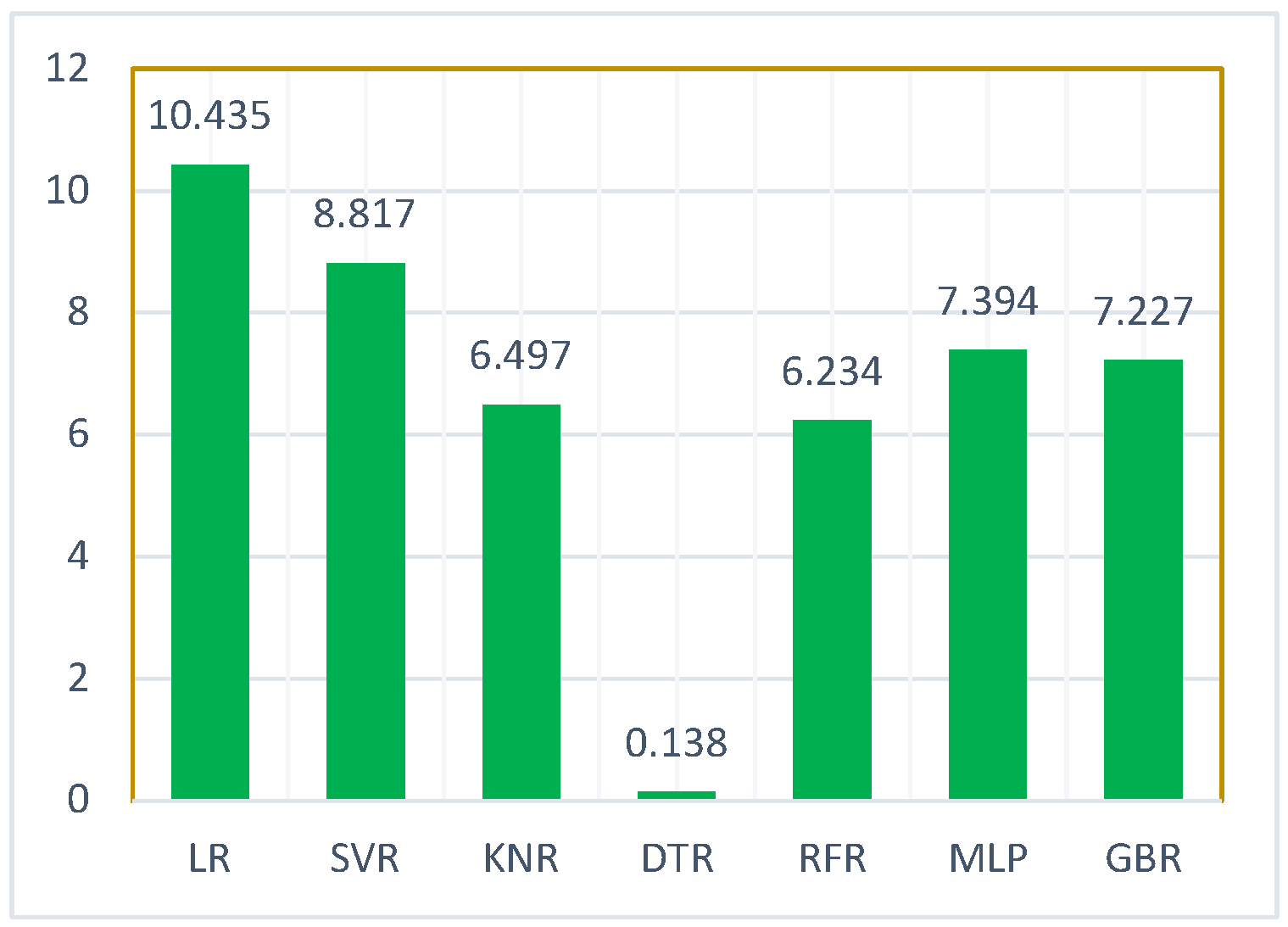
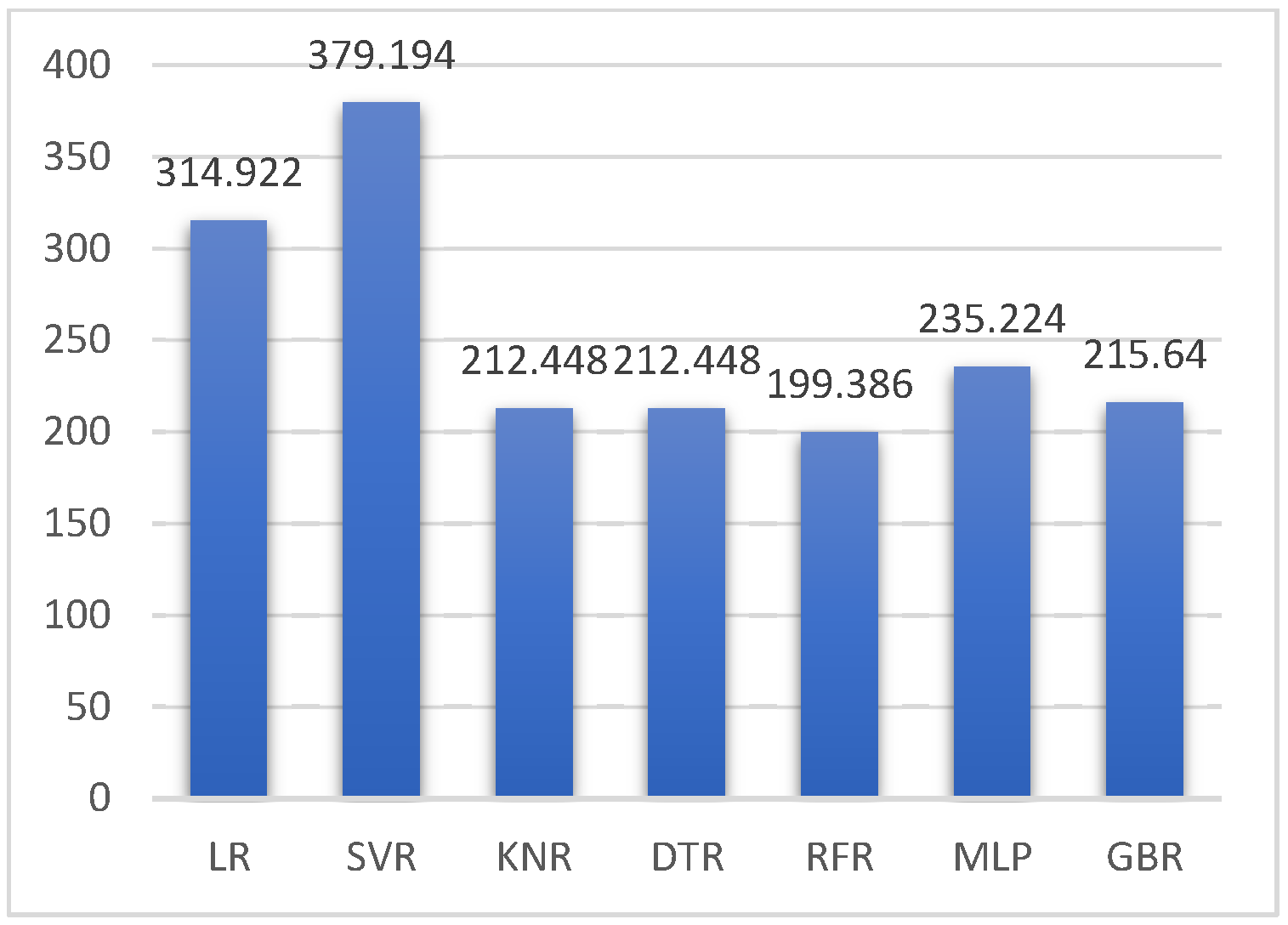
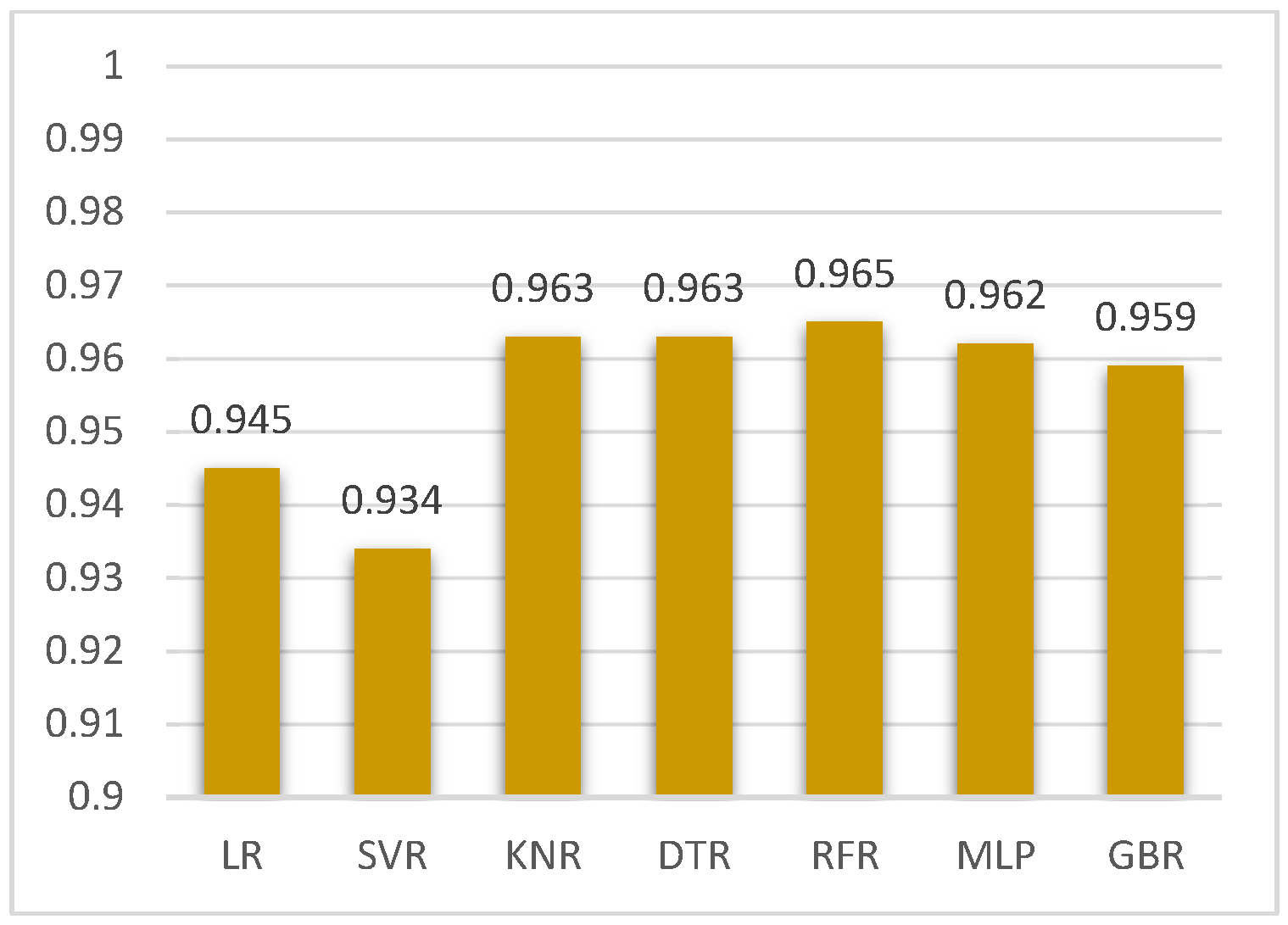
| Regression Method | MAE | MSE | RMSE | R2 Score |
|---|---|---|---|---|
| LR | 10.435 | 314.922 | 17.746 | 0.945 |
| SVR | 8.817 | 379.194 | 19.472 | 0.934 |
| KNR | 6.497 | 212.448 | 14.575 | 0.963 |
| DTR | 0.138 | 212.448 | 14.575 | 0.963 |
| random forest regression | 6.234 | 199.386 | 14.120 | 0.965 |
| MLP | 7.394 | 235.224 | 15.337 | 0.962 |
| GBR | 7.227 | 215.640 | 14.684 | 0.959 |
| Case Study | Feature Selection Method | Regression Type | Features Used | Maximum R2 | Dataset Used |
|---|---|---|---|---|---|
| [30] | Tree-based feature importance and principal component analysis. | Artificial neural network and random forest. | Temperature, humidity, day, and time. | 0.9355 | Metrological data of Hawaii United States of America (2016) |
| [31] | Wavelet transformation-based decomposition technique. | WT-LSTM, LSTM, Ridge regression, Lasso regression and elastic-net regression. | Cloudy index, visibility, temperature, dew point, humidity, wind speed, atmospheric, pressure, altimeter, PV output power. | 0.9505 | Urbana Champaign, Illinois |
| [32] | Correlation heatmap and Bayesian optimization. | LSTM | 41 different features are used with variation. | 0.8917 | German dataset |
| Proposed Model | Pearson’s correlation and heatmap. | LR, | Hour, power, IRR (W/m2), wind km/h, ambient temperature, and panel temperature. | 0.9650 | SHARDA University PV Dataset (2022 Edition) |
| SVR, | |||||
| KNR, | |||||
| DTR, | |||||
| RFR, | |||||
| GBR, and | |||||
| MLP |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdullah, B.U.D.; Khanday, S.A.; Islam, N.U.; Lata, S.; Fatima, H.; Nengroo, S.H. Comparative Analysis Using Multiple Regression Models for Forecasting Photovoltaic Power Generation. Energies 2024, 17, 1564. https://doi.org/10.3390/en17071564
Abdullah BUD, Khanday SA, Islam NU, Lata S, Fatima H, Nengroo SH. Comparative Analysis Using Multiple Regression Models for Forecasting Photovoltaic Power Generation. Energies. 2024; 17(7):1564. https://doi.org/10.3390/en17071564
Chicago/Turabian StyleAbdullah, Burhan U Din, Shahbaz Ahmad Khanday, Nair Ul Islam, Suman Lata, Hoor Fatima, and Sarvar Hussain Nengroo. 2024. "Comparative Analysis Using Multiple Regression Models for Forecasting Photovoltaic Power Generation" Energies 17, no. 7: 1564. https://doi.org/10.3390/en17071564
APA StyleAbdullah, B. U. D., Khanday, S. A., Islam, N. U., Lata, S., Fatima, H., & Nengroo, S. H. (2024). Comparative Analysis Using Multiple Regression Models for Forecasting Photovoltaic Power Generation. Energies, 17(7), 1564. https://doi.org/10.3390/en17071564







