Reservoir Porosity Prediction Based on BiLSTM-AM Optimized by Improved Pelican Optimization Algorithm
Abstract
1. Introduction
2. Principle and Modeling
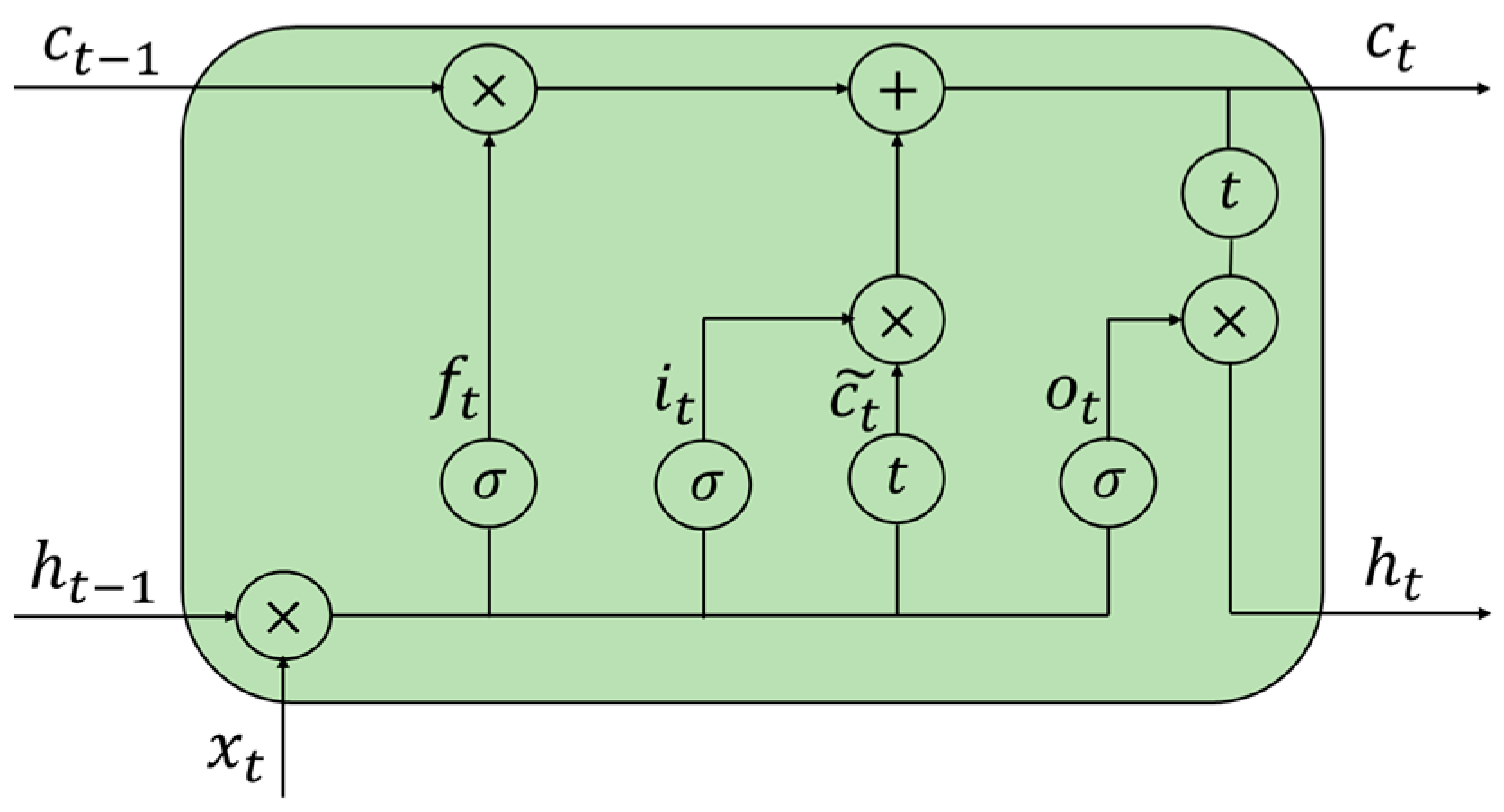
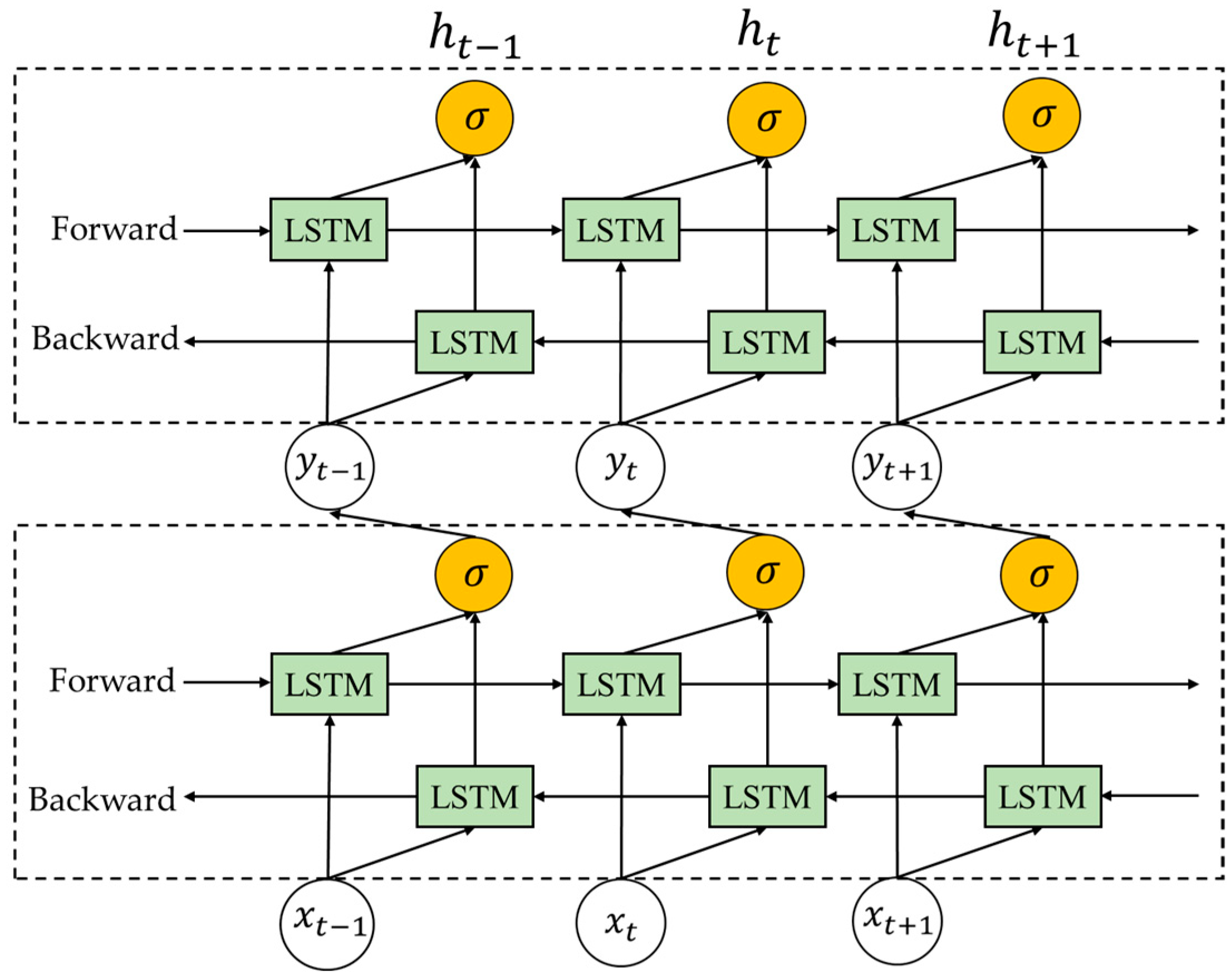
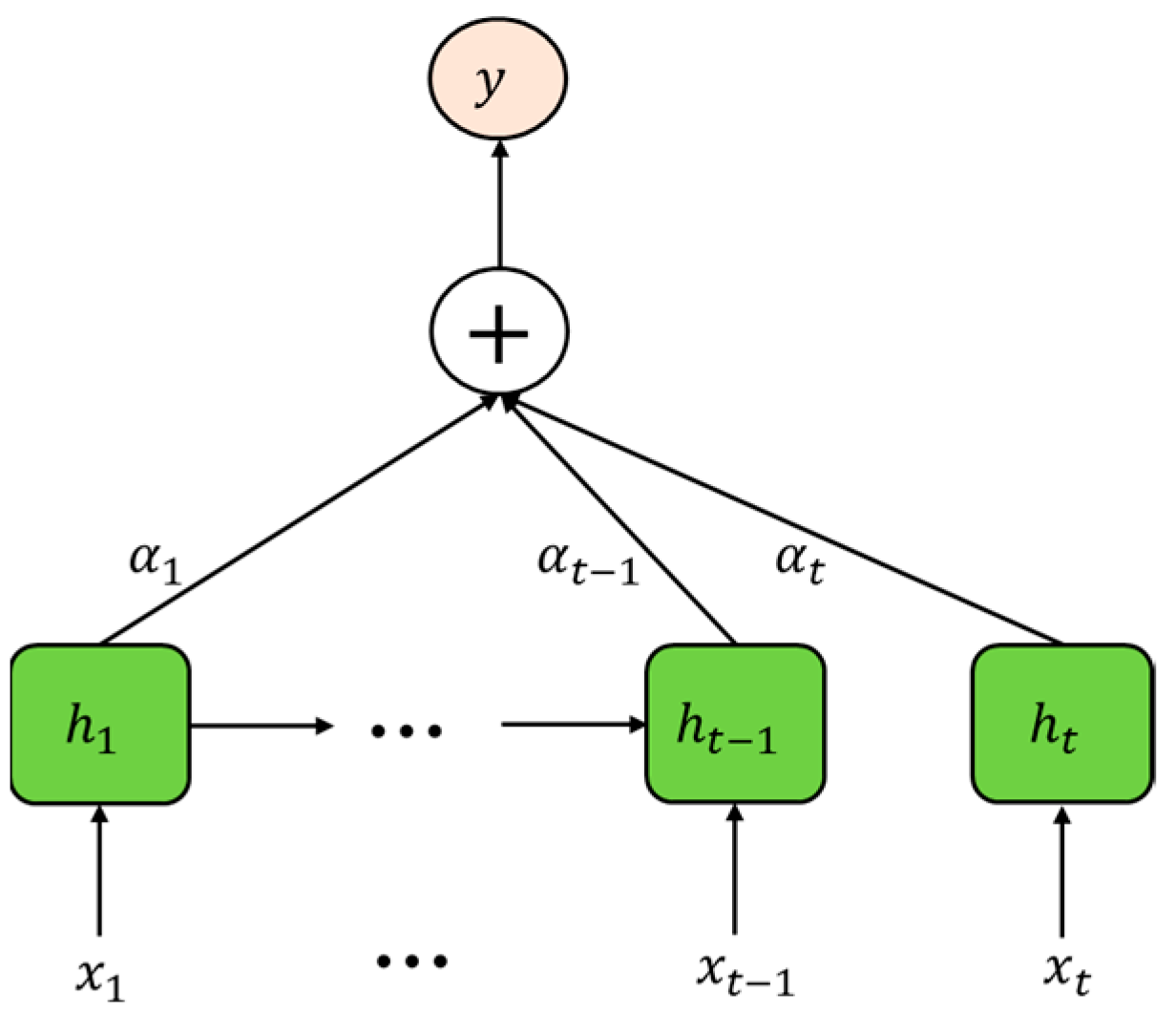
2.1. Principle of BiLSTM-AM
2.2. Pelican Optimization Algorithm
2.2.1. Moving towards Prey (Exploration Phase)
2.2.2. Winging on the Water Surface (Exploitation Phase)
2.3. Improvement of POA
2.3.1. Nonlinear Inertia Weight Factor
2.3.2. Cauchy Mutation
2.3.3. Sparrow Warning Mechanism
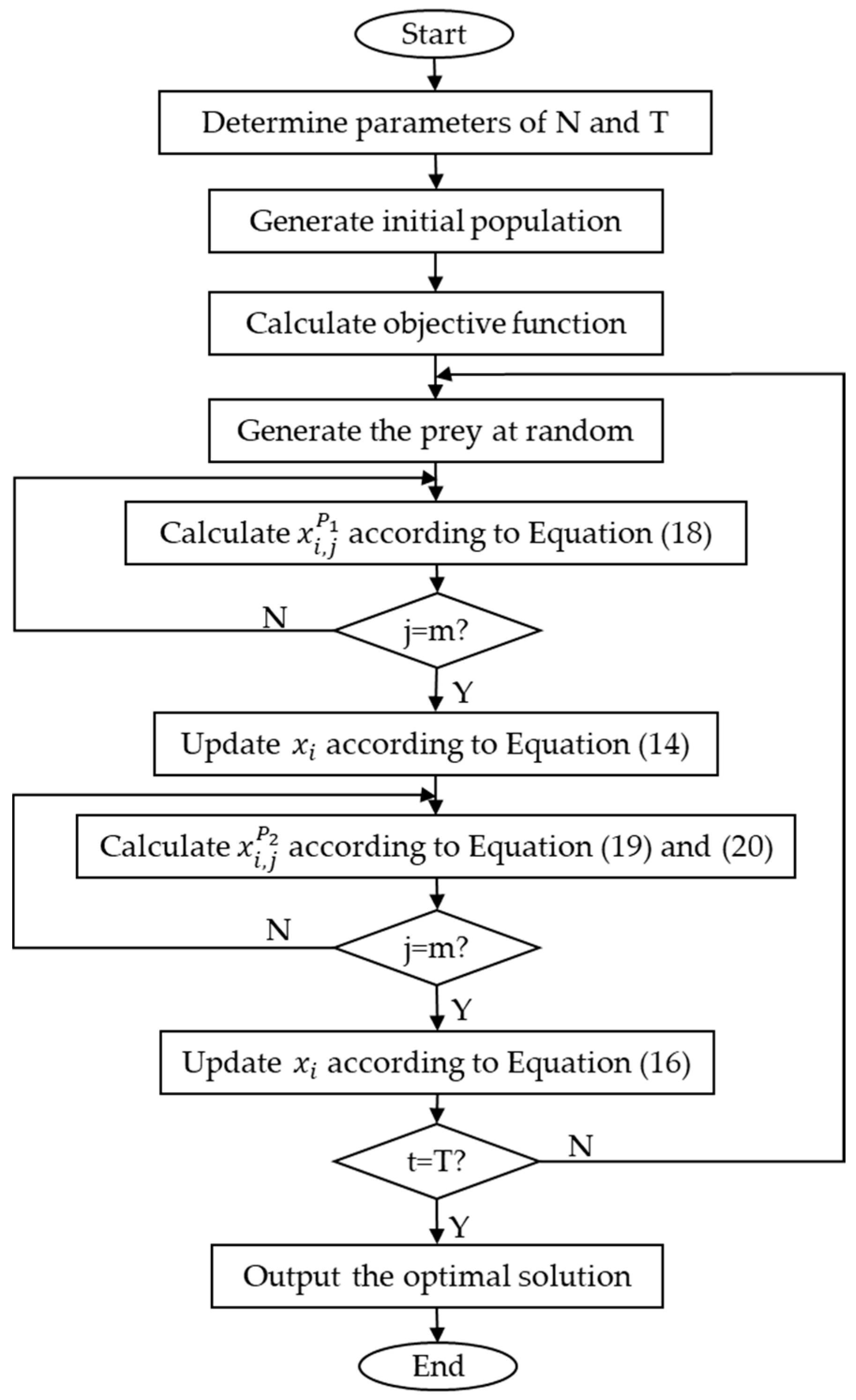
2.3.4. IPOA Calculation Flow
- Step 1: set population size , maximum number of iterations .
- Step 2: generate initial population.
- Step 3: calculate objective function.
- Step 4: generate the prey at random.
- Step 5: calculate according to Equation (18).
- Step 6: update the position according to Equation (14).
- Step 7: calculate according to Equations (19) and (20).
- Step 8: update the position according to Equation (16).
- Step 9: determine whether the end condition is reached; if so, jump to the next step; otherwise, jump to step 4.
- Step 10: output the optimal solution.
3. IPOA Performance Test
3.1. Exploration and Exploitation Analysis
3.2. Comparative Analysis of Algorithm Convergence Curves
3.3. Statistical Analysis Rank-Sum Test
4. Practical Application and Result Analysis
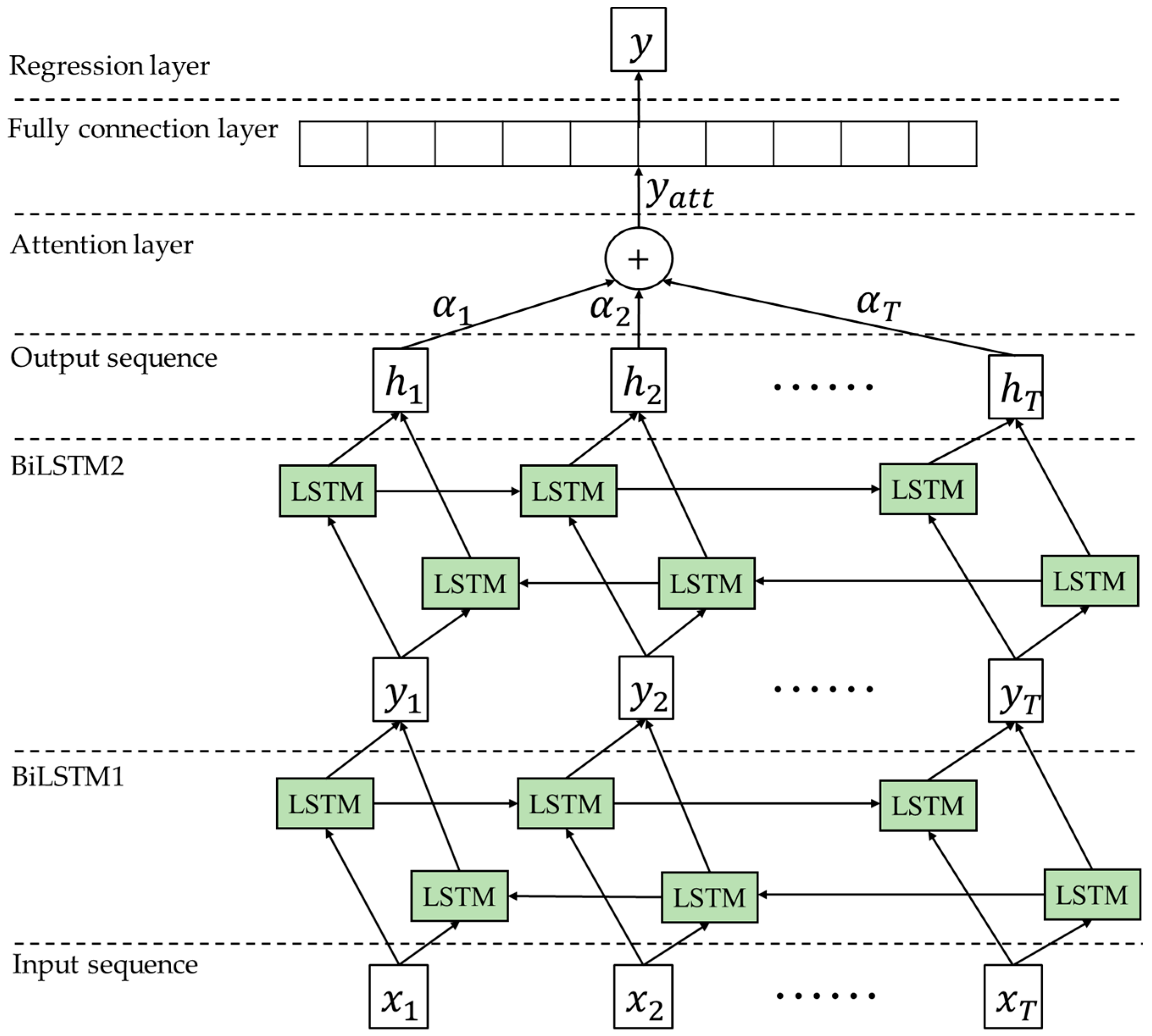
4.1. Construction of BiLSTM-AM Based on IPOA
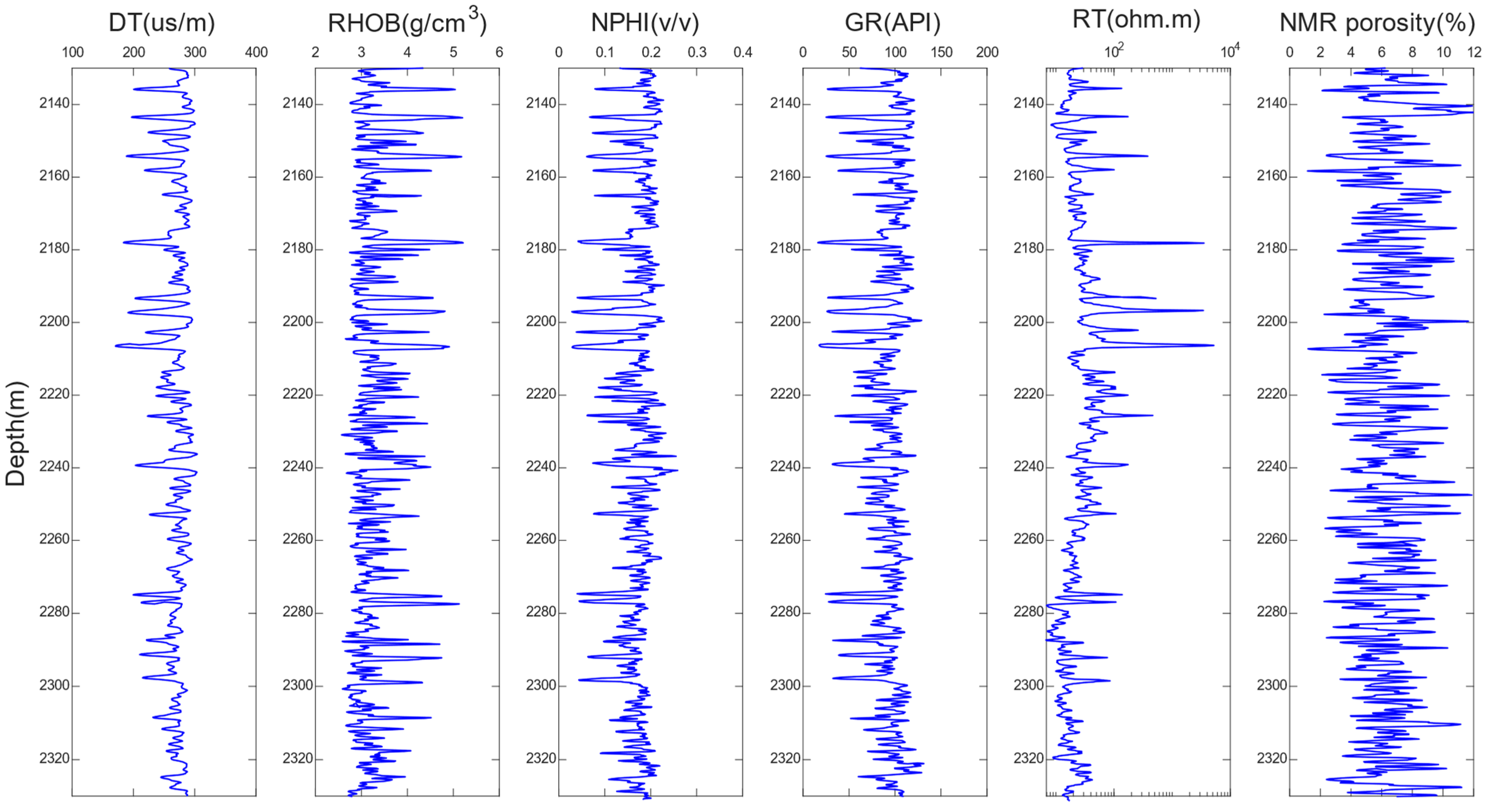
4.2. Data Preparation
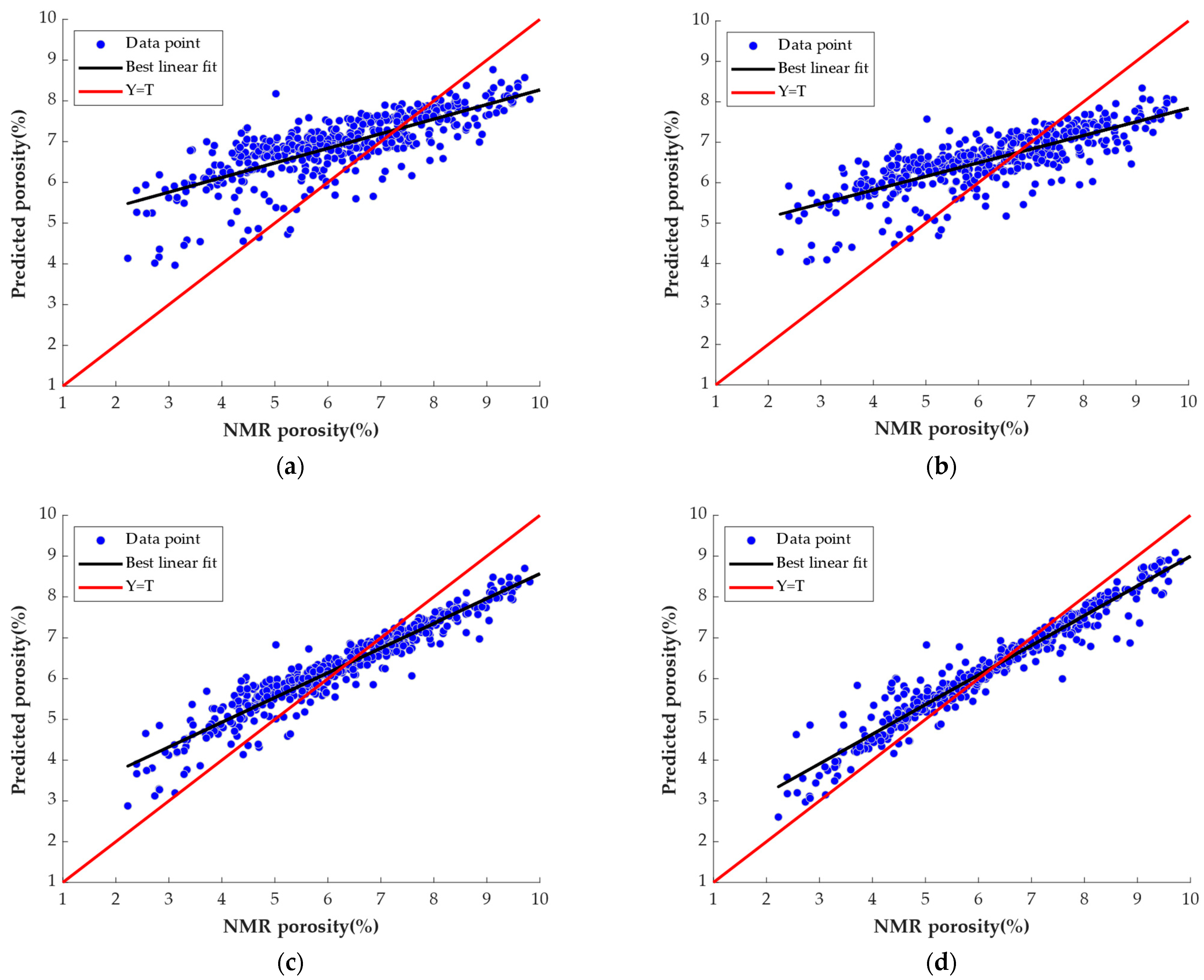
4.3. Analysis of Prediction Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, Y.K. Automatic microseismic event picking via unsupervised machine learning. Geophys. J. Int. 2020, 3, 1750–1764. [Google Scholar] [CrossRef]
- Chen, W.; Yang, L.Q.; Zha, B.; Zhang, M.; Chen, Y.K. Deep learning reservoir porosity prediction based on multilayer long short-term memory network. Geophysics 2020, 85, 213–225. [Google Scholar] [CrossRef]
- Jia, B.; Xian, C.G.; Jia, W.F.; Su, J.Z. Improved Petrophysical Property Evaluation of Shaly Sand Reservoirs Using Modified Grey Wolf Intelligence Algorithm. Comput. Geosci. 2023, 27, 537–549. [Google Scholar] [CrossRef]
- Chen, Y.K.; Zhang, G.Y.; Bai, M.; Zu, S.H.; Guan, Z.; Zhang, M. Automatic waveform classification and arrival picking based on convolutional neural network. Earth Space Sci. 2019, 6, 1244–1261. [Google Scholar] [CrossRef]
- Silva, A.A.; Neto, I.A.L.; Roseane, M. Misságia.; Ceia, M.A.; Carrasquilla, A.G.; Archilha, N.L. Artificial neural networks to support petrographic classification of carbonate-siliciclastic rocks using well logs and textural information. J. Appl. Geophys. 2015, 117, 118–125. [Google Scholar] [CrossRef]
- Mohebbi, A.; Kamalpour, R.; Keyvanloo, K.; Sarrafi, A. The prediction of permeability from well logging data based on reservoir zoning, using artificial neural networks in one of an iranian heterogeneous oil reservoir. Liq. Fuels Technol. 2012, 30, 1998–2007. [Google Scholar] [CrossRef]
- Zheng, J.; Lu, J.R.; Peng, S.P.; Jiang, T.Q. An automatic microseismic or acoustic emission arrival identification scheme with deep recurrent neural networks. Geophys. J. Int. 2017, 212, 389–1397. [Google Scholar] [CrossRef]
- Zhang, G.; Wang, Z.; Chen, Y. Deep learning for seismic lithology prediction. Geophys. J. Int. 2018, 215, 1368–1387. [Google Scholar] [CrossRef]
- Zu, S.; Cao, J.; Qu, S.; Chen, Y. Iterative deblending for simultaneous source data using the deep neural network. Geophysics 2020, 85, 131–141. [Google Scholar] [CrossRef]
- Duan, Y.X.; Xu, D.S.; Sun, Q.F.; Li, Y. Research and Application on DBN for Well Log Interpretation. J. Appl. Sci. 2018, 36, 689–697. [Google Scholar]
- Zhang, D.X.; Chen, Y.T.; Jin, M. Synthetic well logs generation via Recurrent Neural Networks. Pet. Explor. Dev. 2018, 45, 629–639. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Liu, Z.; Zhang, Y.; Zheng, X.; Xie, J. Degradation-trend-dependent remaining useful life prediction for bearing with BiLSTM and attention mechanism. In Proceedings of the IEEE 10th Data Driven Control and Learning Systems Conference, Suzhou, China, 14–16 May 2021; pp. 1177–1182. [Google Scholar]
- Wang, Y.; Jia, P.; Peng, X. BinVulDet: Detecting vulnerability in binary program via decompiled pseudo code and BiLSTM-attention. Comput. Secur. 2023, 125, 103023. [Google Scholar] [CrossRef]
- Trojovsk, P.; Dehghani, M. Pelican Optimization Algorithm: A Novel Nature-Inspired Algorithm for Engineering Applications. Sensors 2022, 22, 855. [Google Scholar] [CrossRef] [PubMed]
- Seyyedabbasi, A.; Kiani, F. Sand Cat swarm optimization: A nature-inspired algorithm to solve global optimization problems. Eng. Comput. 2022, 39, 2627–2651. [Google Scholar] [CrossRef]
- Kiani, F.; Nematzadeh, S.; Anka, F.A.; Findikli, M.A. Chaotic Sand Cat Swarm Optimization. Mathematics 2023, 11, 2340. [Google Scholar] [CrossRef]
- Xue, J.; Shen, B. Dung beetle optimizer: A new meta-heuristic algorithm for global optimization. J. Supercomput. 2022, 79, 7305–7336. [Google Scholar] [CrossRef]
- Xue, J.; Shen, B. A novel swarm intelligence optimization approach: Sparrow search algorithm. Syst. Sci. Control Eng. 2020, 8, 22–34. [Google Scholar] [CrossRef]
- Awadallah, M.A.; Al-Betar, M.A.; Doush, I.A. Recent Versions and Applications of Sparrow Search Algorithm. Arch. Comput. Methods Eng. 2023, 30, 2831–2858. [Google Scholar] [CrossRef] [PubMed]
- Seyedali, M.; Andrew, L. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar]
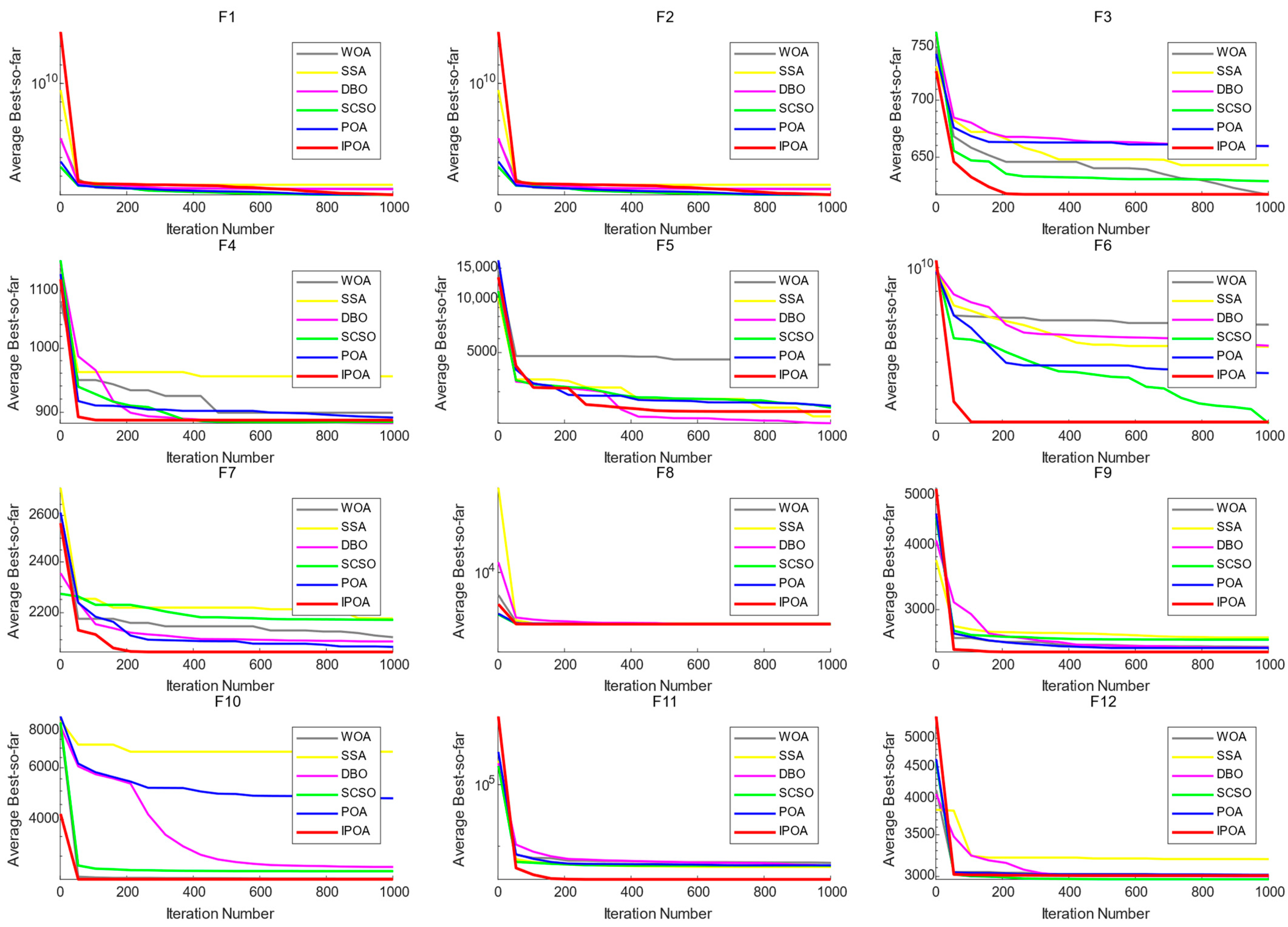


| Funciton | IPOA | POA | SCSO | DBO | SSA | WOA |
|---|---|---|---|---|---|---|
| F1 | 3.29 × 102 | 7.34 × 102 | 3.07 × 103 | 3.68 × 103 | 5.26 × 103 | 4.12 × 103 |
| (1.37 × 102) | (8.84 × 102) | (2.36 × 103) | (1.90 × 103) | (2.25 × 103) | (2.26 × 103) | |
| F2 | 4.22 × 102 | 4.28 × 102 | 4.45 × 102 | 4.55 × 102 | 4.66 × 102 | 4.58 × 102 |
| (2.95 × 101) | (3.04 × 101) | (3.54 × 101) | (3.43 × 101) | (3.62 × 101) | (3.18 × 101) | |
| F3 | 6.06 × 102 | 6.19 × 102 | 6.17 × 102 | 6.24 × 102 | 6.22 × 102 | 6.10 × 102 |
| (4.72 × 100) | (9.68 × 100) | (1.06 × 101) | (5.54 × 100) | (1.07 × 101) | (5.55 × 100) | |
| F4 | 8.13 × 102 | 8.19 × 102 | 8.28 × 102 | 8.23 × 102 | 8.47 × 102 | 8.31 × 102 |
| (6.59 × 100) | (4.44 × 100) | (5.17 × 100) | (6.56 × 100) | (7.25 × 100) | (1.04 × 101) | |
| F5 | 1.16 × 103 | 1.09 × 103 | 1.13 × 103 | 1.05 × 103 | 9.79 × 102 | 1.02 × 103 |
| (2.21 × 102) | (1.21 × 102) | (2.01 × 102) | (7.86 × 101) | (4.88 × 101) | (1.14 × 102) | |
| F6 | 4.57 × 102 | 2.79 ×103 | 4.48 × 103 | 2.23 × 103 | 5.17 × 104 | 1.43 × 104 |
| (2.44 × 102) | (1.40 × 103) | (2.23 × 103) | (5.67 × 102) | (3.63 × 104) | (1.43 × 104) | |
| F7 | 2.03 × 103 | 2.03 × 103 | 2.05 × 103 | 2.05 × 103 | 2.08 × 103 | 2.05 × 103 |
| (9.43 × 100) | (1.06 × 101) | (2.26 × 101) | (1.17 × 101) | (3.70 × 101) | (2.42 × 101) | |
| F8 | 2.22 × 103 | 2.22 × 103 | 2.23 × 103 | 2.23 × 103 | 2.25 × 103 | 2.23 × 103 |
| (2.06 ×100) | (7.45 × 100) | (4.11 × 100) | (7.87 × 100) | (2.23 × 101) | (3.82 × 100) | |
| F9 | 2.53 × 103 | 2.54 × 103 | 2.59 × 103 | 2.56 × 103 | 2.64 × 103 | 2.60 × 103 |
| (1.92 × 10−1) | (2.77 × 101) | (4.48 × 101) | (1.42 × 101) | (4.39 × 101) | (3.04 × 101) | |
| F10 | 2.50 × 103 | 2.55 × 103 | 2.56 × 103 | 2.54 × 103 | 2.64 × 103 | 2.57 × 103 |
| (6.53 × 101) | (6.24 × 101) | (6.51 × 101) | (3.84 × 100) | (4.22 × 101) | (6.34 × 101) | |
| F11 | 2.71 × 103 | 2.77 × 103 | 2.88 × 103 | 2.81 × 103 | 3.27 × 103 | 3.03 × 103 |
| (1.37 × 102) | (1.62 × 102) | (2.12 × 102) | (6.53 × 101) | (2.78 × 102) | (2.21 × 102) | |
| F12 | 2.87 × 103 | 2.87 × 103 | 2.88 × 103 | 2.87 × 103 | 2.87 × 103 | 2.87 × 103 |
| (5.68 × 100) | (1.09 × 101) | (1.91 × 101) | (3.85 × 100) | (9.04 × 100) | (9.47 × 100) |
| Funciton | IPOA vs. POA | IPOA vs. SCSO | IPOA vs. DBO | IPOA vs. SSA | IPOA vs. WOA | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| P | h | P | h | P | h | P | h | P | h | |
| F1 | 1.29 × 10−9 | + | 8.15 × 10−11 | + | 3.02 × 10−11 | + | 3.34 × 10−11 | + | 3.69 × 10−11 | + |
| F2 | 3.48 × 10−2 | + | 1.85 × 10−3 | + | 1.63 × 10−5 | + | 3.81 × 10−6 | + | 1.67 × 10−4 | + |
| F3 | 6.01 × 10−8 | + | 4.42 × 10−6 | + | 4.50 × 10−11 | + | 1.17 × 10−9 | + | 5.57 × 10−3 | + |
| F4 | 9.88 × 10−3 | + | 6.91 × 10−4 | + | 7.28 × 10−11 | + | 1.20 × 10−10 | + | 4.85 × 10−3 | + |
| F5 | 6.52 × 10−1 | − | 9.00 × 10−1 | − | 3.87 × 10−1 | − | 2.71 × 10−2 | + | 8.50 × 10−2 | − |
| F6 | 8.12 × 10−4 | + | 1.00 × 10−3 | + | 7.22 × 10−6 | + | 6.70 × 10−11 | + | 1.41 × 10−9 | + |
| F7 | 6.57 × 10−2 | − | 8.56 × 10−4 | + | 2.88 × 10−6 | + | 1.61 × 10−10 | + | 1.95 × 10−3 | + |
| F8 | 2.01 × 10−4 | + | 3.82 × 10−9 | + | 6.07 × 10−11 | + | 3.02 × 10−11 | + | 1.33 × 10−10 | + |
| F9 | 9.67 × 10−9 | + | 5.04 × 10−11 | + | 2.25 × 10−11 | + | 2.25 × 10−11 | + | 2.25 × 10−11 | + |
| F10 | 6.31 × 10−3 | + | 9.82 × 10−3 | + | 9.33 × 10−2 | − | 6.01 × 10−8 | + | 9.47 × 10−1 | − |
| F11 | 2.60 × 10−3 | + | 1.17 × 10−4 | + | 3.33 × 10−3 | + | 9.62 × 10−10 | + | 5.99 × 10−7 | + |
| F12 | 2.64 × 10−2 | + | 4.19 × 10−2 | + | 5.97 × 10−5 | + | 1.34 × 10−5 | + | 3.40 × 10−2 | + |
| Model | RMSE | MAE |
|---|---|---|
| BPNN | 1.1217 | 1.0338 |
| GRU | 0.9712 | 0.9025 |
| LSTM | 0.7421 | 0.6918 |
| IPOA-BiLSTM-AM | 0.5736 | 0.4313 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiao, L.; He, N.; Cui, Y.; Zhu, J.; Xiao, K. Reservoir Porosity Prediction Based on BiLSTM-AM Optimized by Improved Pelican Optimization Algorithm. Energies 2024, 17, 1479. https://doi.org/10.3390/en17061479
Qiao L, He N, Cui Y, Zhu J, Xiao K. Reservoir Porosity Prediction Based on BiLSTM-AM Optimized by Improved Pelican Optimization Algorithm. Energies. 2024; 17(6):1479. https://doi.org/10.3390/en17061479
Chicago/Turabian StyleQiao, Lei, Nansi He, You Cui, Jichang Zhu, and Kun Xiao. 2024. "Reservoir Porosity Prediction Based on BiLSTM-AM Optimized by Improved Pelican Optimization Algorithm" Energies 17, no. 6: 1479. https://doi.org/10.3390/en17061479
APA StyleQiao, L., He, N., Cui, Y., Zhu, J., & Xiao, K. (2024). Reservoir Porosity Prediction Based on BiLSTM-AM Optimized by Improved Pelican Optimization Algorithm. Energies, 17(6), 1479. https://doi.org/10.3390/en17061479





