Research on Adaptive Droop Control Strategy for a Solar-Storage DC Microgrid

Abstract

When the solar-storage DC microgrid operates in islanded mode, the battery needs to stabilize the bus voltage and keep the state of charge (SOC) balanced in order to extend the service life of the battery and the islanded operation time. When there are multiple energy storage units in the DC microgrid, it is necessary to solve the problem of unbalanced circulation and the state of charge between batteries using a reasonable droop control method. In this paper, firstly, the DC–DC charging and discharging circuit of the battery is designed, and the unbalanced SOC of the battery caused by the different impedances of the line is analyzed. Secondly, an adaptive droop control method is proposed to solve the problems of SOC imbalance and current circulation between the batteries. Thirdly, based on MATLAB/SIMULINK R2021b simulation software, the proposed control method is modeled and simulated. Compared with the traditional droop control, the effectiveness of the proposed method is validated.

1. Introduction

With the depletion of fossil fuels, the application of new energy is increasing day by day. As a clean and abundant energy source, the application of solar energy in photovoltaic power generation modules has increased greatly in recent years [1,2,3]. The photovoltaic power generation module emits electric energy in the form of DC; the DC microgrid uses the DC bus, which eliminates the inverter and rectifier when connecting the photovoltaic power generation module, battery, and DC load, so the DC microgrid basically improves the efficiency of the system [4,5].

Due to the random and intermittent characteristics of photovoltaic power generation, in the islanded mode, the photovoltaic power generation module works in the maximum power point tracking (MPPT) mode, and the DC bus voltage stability is mainly maintained by the energy storage unit [6]. Compared with the large power grid, the capacity and rated power of the battery in the energy storage unit are limited. In order to stabilize the DC bus voltage, the control strategy of the battery is very important [7].

In recent years, scholars have conducted extensive research on the control of energy storage units in DC microgrids. As for the circulation problem, in refs. [8,9], the papers point out that the circulation is caused by different line resistances, but the influence of line resistance on the state of charge (SOC) of the battery was not further discussed. The SOC of a battery is used to reflect the remaining available capacity of the battery, which is numerically defined as the ratio of the remaining capacity of the battery to the total capacity of the battery.

In ref. [10], the paper proposes a droop control method that includes the rise coefficient and droop coefficient, which can solve the circulation and SOC imbalance problem. However, the rise coefficient and droop coefficient are both fixed and cannot adapt to various dynamic changes in the DC microgrid. In ref. [11], the paper proposes an adaptive droop coefficient, which can improve the problem of large voltage deviation between two DC sources under a heavy load, but the current deviation is aggravated under a light load. Meanwhile, this method cannot solve the problem of SOC imbalance. In refs. [12,13,14], a droop control method based on battery charging and discharging power was adopted to balance the battery SOC and the charging and discharging power in order to solve the imbalance of the battery’s SOC. In refs. [15,16], adaptive droop control is adopted, and the droop coefficient is inversely proportional to the n power of SOC to change the droop coefficient in real-time so as to achieve SOC balance in the discharge process of the energy storage unit, but the charging situation and circulation problems are not considered. Subsequently, further research was carried out in ref. [17] to supplement and design the method of the charge state equilibrium during the charging process. Previous studies failed to take into account both the circulation problem and the state of charge problem of droop control under a light load. This paper proposes an improved droop control to solve the above two problems at the same time.

Based on the above analysis, in this paper, an improved adaptive droop control is proposed based on the DC–DC bidirectional charge and discharge circuit, which improves the current deviation between the two batteries when the traditional droop control is too large and solves the problem of SOC imbalance and the circulation of the battery. Compared with the traditional balanced SOC method, the proposed method can participate in the suppression of circulation, and it only needs to provide the local information of the device itself, which is convenient for control. Finally, MATLAB/SIMULINK is used to build a DC microgrid model with two storage batteries, and the method is verified.

In the following sections, starting from the introduction of the droop control principle, the improved droop control method is elaborated on step by step on how to suppress the circulation between batteries and eliminate the imbalance of the state of charge. Section 2 contains the traditional droop control principle; Section 3 discusses SOC imbalance and circulation problems; Section 4 comprises the improved adaptive droop control; Section 5 includes simulation verification; and Section 6 provides the conclusions.

2. Traditional Droop Control Principle

The load distribution method of the DC microgrid generally adopts I-U or P-U droop control. In order to directly reflect the correlation between the residual capacity of the energy storage unit and DC voltage, the I-U droop control method is adopted in this paper, and its expression is as follows:

$$u=u^{*}-ki$$

(1)

where $u$ is the output voltage of the DC–DC converter; $i$ is the output current; $u^{*}$ is the reference voltage; and $k$ is the droop coefficient.

In order to improve the redundancy and reliability of the microgrid, N groups of distributed energy storage units with equal or similar capacities are connected in parallel to the DC bus through the DC–DC converter, as shown in Figure 1. $D_i$ and $D_j$ are any two groups of the distributed energy storage unit (DESU). $R_{linei}$ and $R_{linej}$ are the equivalent line impedance from the corresponding energy storage unit to the point of common coupling (PCC), respectively. $u_{PCC}$ is the DC bus voltage; $i_{load}$ is the total load current.

The state of the charge of the energy storage unit represents the current output capacity of the energy storage unit, and its expression is as follows:

$${E_{SOC}}_i=E_{{soc}_i}^{*}-\frac{l\int i_{i}dt}{C_e}$$

(2)

where $E_{SOCi}^{*}$ is the initial charging state of $D_i$; $E_{SOCi}$ indicates the current charged state of $D_i$. $C_e$ is the capacity of the energy storage unit and $l$ is the voltage ratio between the output and input of the converter.

Through the derivation of (2), the rate of change in $E_{SOC}$ can be obtained as follows:

$$d{E_{SOC}}_i=-l{i}_i/C_e$$

(3)

Here, (3) shows that the larger the energy storage discharge current, the larger the negative change rate of $E_{SOC}$, and the faster the decline rate of the charged state. The higher the charging current, the higher the forward change rate of $E_{SOC}$, and the faster the rise rate of the charged state. When the system is stable, and if the SOC of the energy storage unit is balanced, the change rate of $E_{SOC}$ is the same; that is, the accurate distribution of the converter output current is a necessary condition for SOC balancing. According to Figure 1, the expression of the current emitted by each converter is as follows:

$$i_i=\frac{u_i-u_{PCC}}{R_{linei}}$$

(4)

By substituting (1) into (4), we obtain the following:

$$i_i=\frac{u^{*}-u_{PCC}}{R_{linei}+k}$$

(5)

Thus, the ratio of the $E_{SOC}$ derivative between $D_i$ and $D_j$ under a traditional droop control is as follows:

$$\frac{d{E_{SOC}}_i}{d{E_{SOC}}_j}=\frac{R_{linej}+k}{R_{linei}+k}$$

(6)

According to (6), when there are multiple DG units in the DC microgrid that can change the output power to stabilize the DC bus voltage, the power quota can be allocated by setting the droop coefficient.

However, when $R_{linei}$ is not equal to $R_{linej}$, the necessary conditions for the equilibrium of the state of charge of each energy storage unit cannot be met, so the SOC of each DESU cannot be balanced under the traditional droop control; this is why we propose an improved droop method in this paper.

3. SOC Imbalance and Circulation Problems

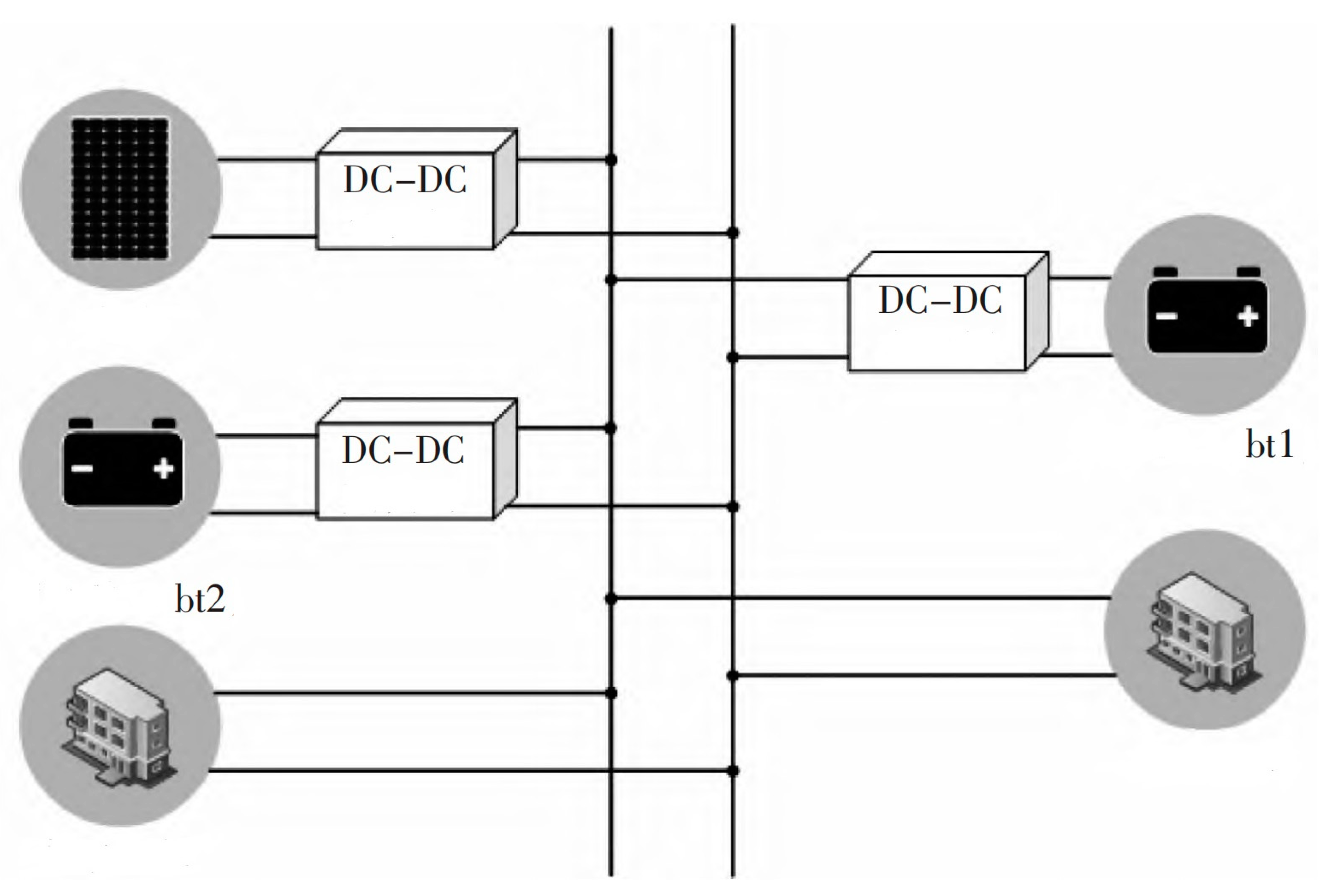
The topology of the optical storage DC microgrid is shown in Figure 2. The topology is composed of photovoltaic power generation modules, batteries, loads, and DC–DC converters. Two batteries and photovoltaic power modules are connected in parallel to the DC bus to provide power to the load. The output power of the photovoltaic power generation module varies according to the light intensity and temperature.

When the output power of the photovoltaic power generation module is higher than the load power demand, the bus voltage increases. Otherwise, the bus voltage is reduced. When the bus voltage is higher than the rated voltage, the battery is charged. When the bus voltage is lower than the rated voltage, the battery is discharged. In this way, the bus voltage is stable, and all batteries are charged and discharged at the same time.

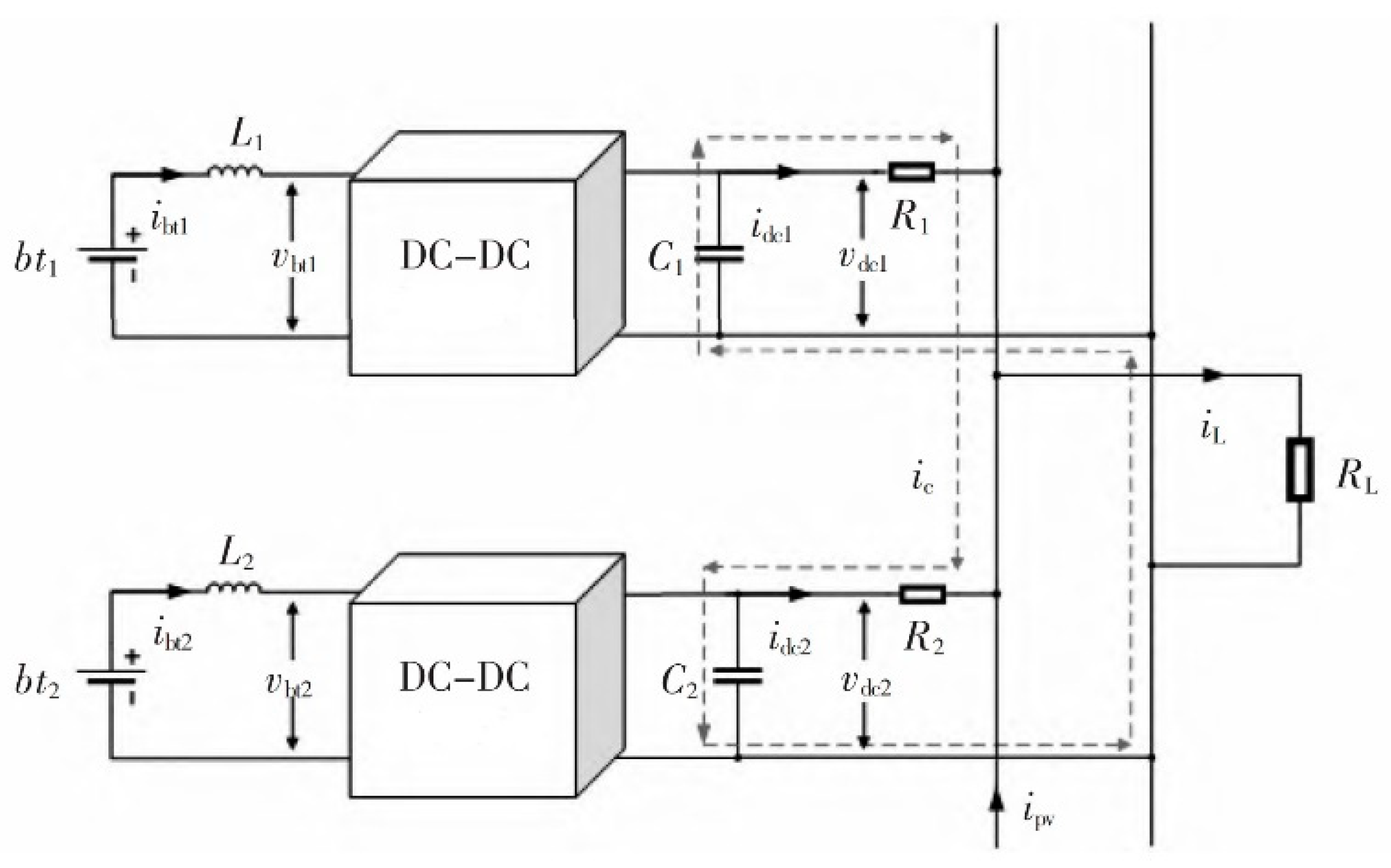
Multiple batteries in microgrids can bring higher stability to the grid, but there is also the problem of the battery’s SOC imbalance. As for the causes of the SOC imbalance between batteries in the microgrid, this paper makes a quantitative analysis. Taking two parallel batteries discharging at the same time as an example, the parallel topology of two batteries is shown in Figure 3.

In the figure, $v_{dc1}$ and $v_{dc2}$ represent the output voltage of converters 1 and 2; $i_{dc1}$ and $i_{dc2}$ represent the output voltage of converters 1 and 2; $R_1$ and $R_2$ are line resistors 1 and 2; $v_{bt1}$, $v_{bt2}$, $i_{bt1}$, $i_{bt2}$ are the output voltage and output current of battery 1 and 2, respectively; $R_L$ is the load; $i_L$ is the current flowing through the load; $i_c$ is the circulation of converter 1 to converter 2; and $C_1$, $C_2$, L₁, and L₂ are filter capacitors and inductors, respectively.

Based on Kirchhoff’s voltage law (KVL), the voltage, current of each battery, and bus current are obtained.

$$v_{dc1}=i_{dc1}{R}_1+i_L{R}_L$$

(7)

$$v_{dc2}=i_{dc2}{R}_2+i_L{R}_L$$

(8)

$$i_L=i_{dc1}+i_{dc2+}{i}_{pv}$$

(9)

The circulating current i_c is given by the following equation:

$$i_c=\frac{v_{dc1}-v_{dc2}}{R_1+R_2}=\frac{i_{dc1R_1}-i_{dc2}{R}_2}{R_1+R_2}$$

(10)

It can be seen that the circulating current $i_c$ is not zero if the two-line resistance $\mathrm{v}\mathrm{a}\mathrm{l}\mathrm{u}\mathrm{e}\mathrm{s} R_1$ and $R_2$ are not the same.

Because the power loss of the converter is very small and negligible compared with the power of the photovoltaic power module and the battery power, it can be obtained according to the equal power of the two ends of the converter:

$$i_{btj}=\frac{i_{dcj}{v}_{dcj}}{v_{btj}}$$

(11)

where j = 1,2, according to Coulomb’s law, and the equation of the battery’s SOC is as follows:

$${SOC}_j={SOC}_{j,t=0}-\frac{1}{C_{btj}}\int i_{btj}dt={SOC}_{j,t=0}-\frac{1}{C_{btj}}\int \frac{i_{dcj}{v}_{dcj}}{v_{btj}}dt$$

(12)

where ${SoC}_{j,t=0}$ is the initial SOC value of the JTH battery; $C_{btj}$ indicates the rated capacity of the JTH battery.

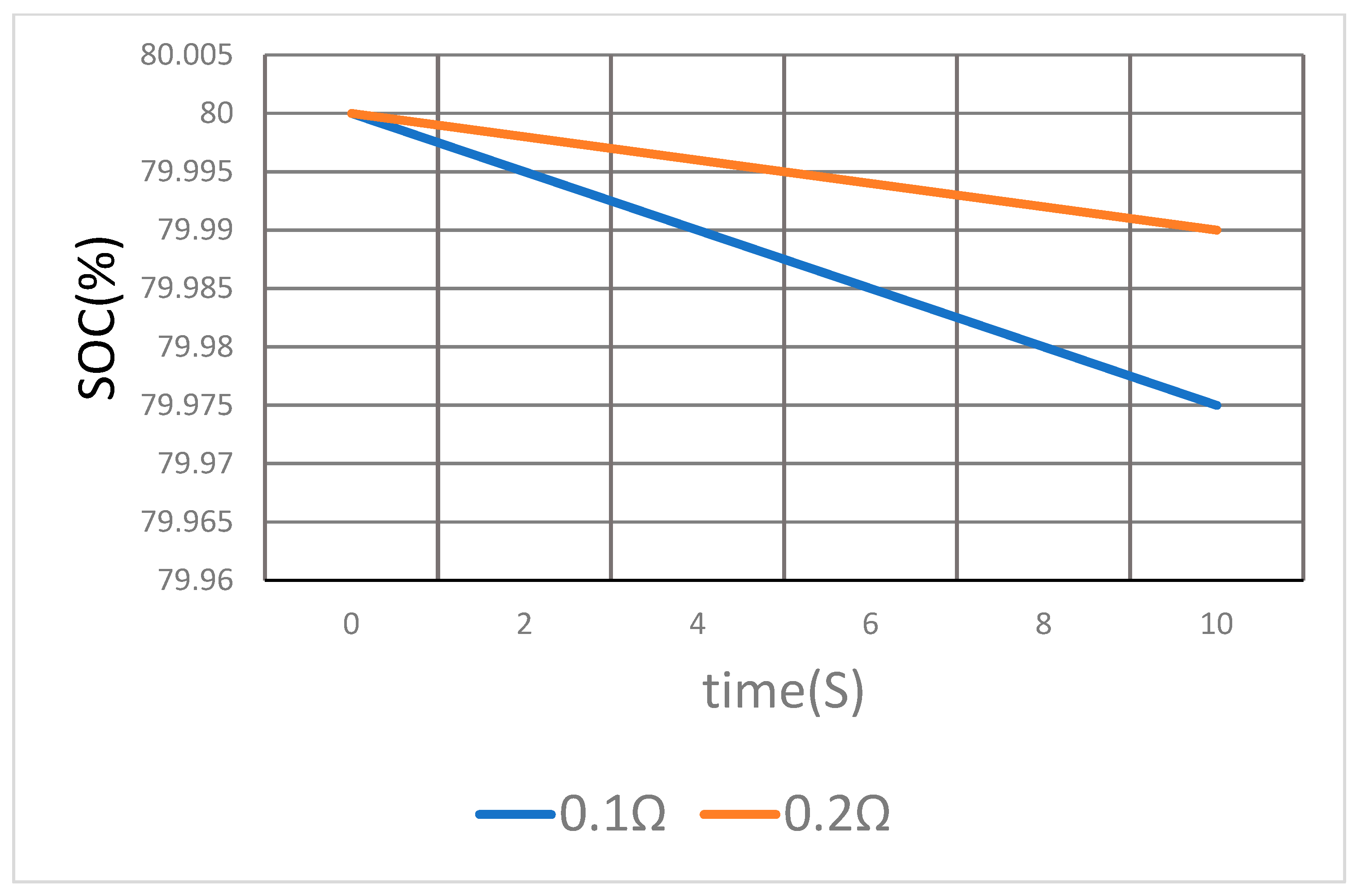
It can be seen from (7) to (12) that an unequal line resistance causes unequal $i_{btj}$, resulting in the unbalanced SOC of the battery, and the quantitative calculation of the SOC of each battery is realized. Figure 4 shows the SOC comparison of two batteries. The initial SOC of two batteries of the same specifications is 80%, and the line resistance values are 0.1 Ω and 0.2 Ω, respectively.

As can be seen from Figure 4, when charging from time 0, the battery’s SOC is 79.975% and 79.99%, respectively, at 10 s, indicating that the different line resistance will lead to the battery’s SOC imbalance.

4. DC–DC Charging and Discharging Circuit

The bidirectional DC–DC conversion circuit contains two fully controlled devices, and controlling the on-time of the two transistors can realize the bidirectional energy flow because the bidirectional DC–DC conversion circuit has the characteristics of the energy reverse transmission of electrical energy, so it is widely used in places where energy storage devices need to be installed. Its schematic diagram is shown in Figure 5.

When energy is transferred from the power supply side to the storage side, at this time, mosfet2 is controllable, mosfet1 is in the off-state, and the bidirectional DC–DC converter works in the BUCK mode. When mosfet2 is turned on, the power supply is powered by inductor L, capacitor C, and the battery. When mosfet2 is turned off, the anti-parallel diode of mosfet1 is on, and the inductance is discharged through the diode and the battery.

When energy is transferred from the battery to the power supply side, at this time, mosfet2 is in the off-state, mosfet1 is controllable on and off, and the bidirectional DC–DC converter works in the BOOST mode. When mosfet1 is turned on, the battery side supplies power to the load through inductors and capacitors. When mosfet1 is turned off, the anti-parallel diode of mosfet2 is switched on, and the battery and inductor discharge to the capacitor through the diode at the same time.

According to the above analysis, the bidirectional converter can realize the bidirectional flow of energy, so the circuit is called the bidirectional DC–DC conversion circuit. In view of the simple structure of this circuit, which is easy to control and can realize the characteristics of bidirectional energy flow, it is often used in the DC microgrid; the method is to add a bidirectional DC–DC converter between the energy storage device and the DC bus, and its role is to connect the battery to the DC bus, by controlling its on-trigger time, to achieve the charge and discharge control of the battery.

5. Improved Adaptive Droop Control

Adaptive control is a kind of control in which the system automatically changes the control parameters and corrects the original scheme to ensure the best state of the system when the conditions change indeterminably. In the photovoltaic DC microgrid, due to the changes in the load power and the power of the photovoltaic power generation module, and even the transmission line due to the differences in ambient temperature and humidity, the system control parameters change so that the charging state of the energy storage unit deviates. The traditional adaptive droop method uses the droop coefficient inversely proportional to the n power of SOC and changes the droop coefficient in real-time to achieve a SOC balance in the discharge process of the energy storage unit. 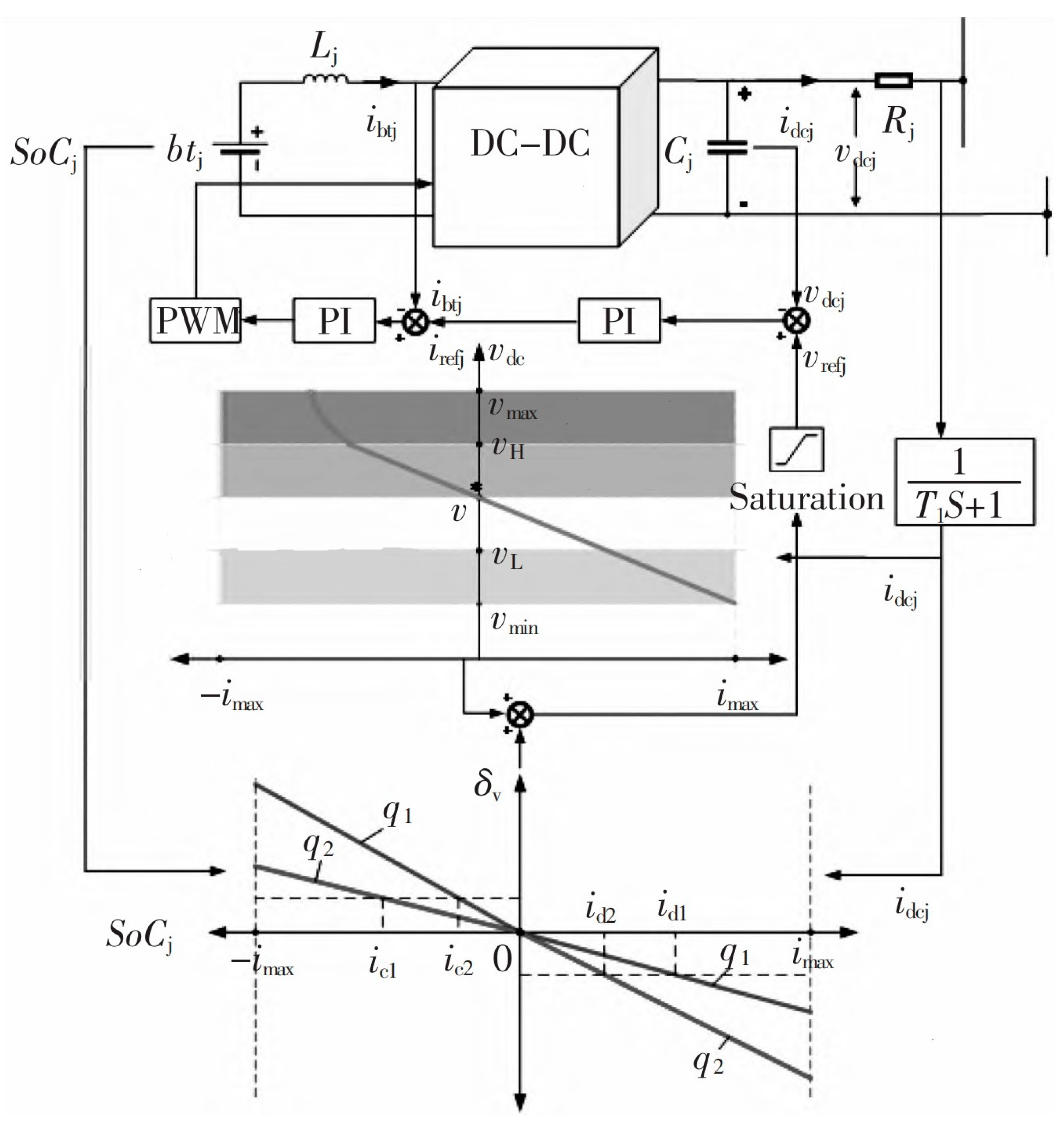Figure 6 shows the schematic diagram of the battery adaptive droop control. This figure includes two rings of proportional-integral (PI) feedback control and a droop control section.

The droop control link calculates the reference voltage $v_{ref}$ and provides it to the PI feedback control link. $v_{ref}$ is mainly composed of three parts; one part is the control component introduced to balance the SOC, one part is the control component introduced to suppress the circulation, and the other part is the DC bus voltage rating. The bottom coordinate of Figure 5 is the balance SOC control component; the fourth quadrant represents the battery discharge, and the second quadrant represents the battery charging. The magnitude of the control component is the inverse of the product of the output current of the converter and the droop parameter q; the detailed control principle is described below. The coordinates in the middle of Figure 6 are the sum of the circulation suppression component and the rated voltage component of the DC bus, the working principle of which is explained in detail below. The PI feedback control part is mainly to achieve accurate voltage tracking, including the voltage outer ring and the current inner ring. The outer voltage ring contains a PI controller, which can make the input and output voltage $v_{dc}$ of the energy storage unit quickly track its reference value $v_{ref}$. The current inner ring contains a PI controller, which increases the damping of the system, makes the system more stable, and prevents excessive current fluctuations when the battery is charged and discharged.

The improved adaptive droop control proposed in this paper is divided into the following two parts: circulation suppression and SOC balance. It can not only suppress the circulation between the storage battery and the SOC imbalance of the two batteries but also solve the problem of the circulation increasing under the light load by setting the adaptive droop coefficient. The energy storage unit is mainly composed of a battery and a bidirectional buck–boost converter.

The improved adaptive droop control expression is as follows:

$$v_{refj}=v^{*}-k_j{i}_{dcj}-q_j{i}_{dcj}$$

(13)

where $v^{*}$ is the voltage rating of the DC bus, $k_j$ is the adaptive droop coeffcient of the circulation suppression ring joint, and $q_j$ is the adaptive droop coefficient of the balanced SOC link.

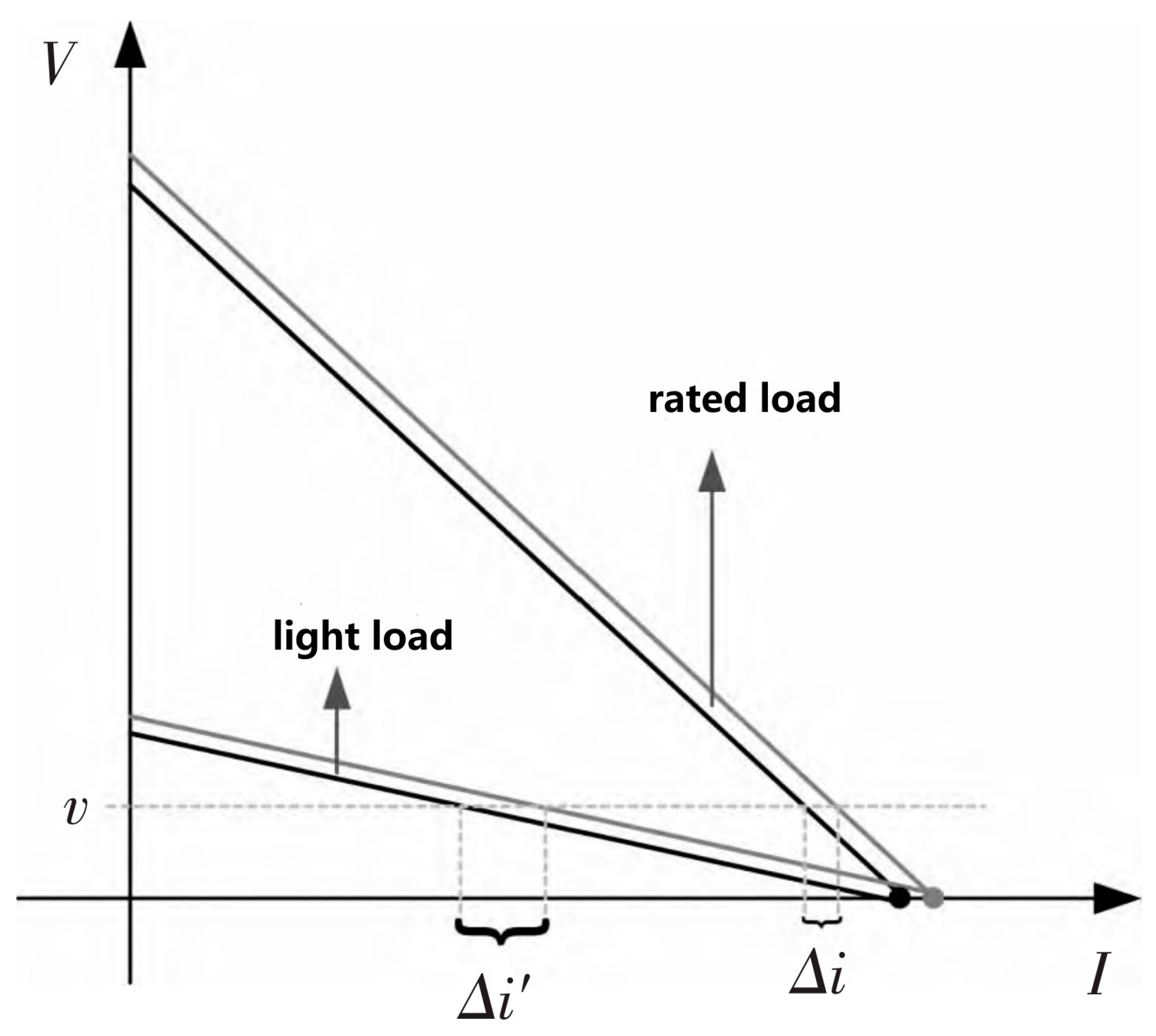
5.1. Circulation Inhibition

Figure 6 shows the current deviation of the two batteries under the traditional droop control method (the droop coefficient is a fixed value) for the light load and rated load. The current deviation of the light load is $\mathsf{\Delta }{i}^{\prime }$, and the current deviation of the rated load is $\mathsf{\Delta }i$.

As can be seen from Figure 7, $\mathsf{\Delta }{i}^{\prime }$ > $\mathsf{\Delta }i$, it indicates that the traditional droop control has insufficient ability to restrain the circulation under the light load condition. As the power consumption of the light load is lower than that of the normal load, the bus voltage rises accordingly. In order to improve the shortcomings of traditional droop control, this paper adjusts the droop coefficient in real-time according to the uptick value of $v_{dcj}$, and the design of $k_j$ as follows:

$$k_j=\frac{h(v_{maxj}-v_{minj})}{2·i_{maxj}}$$

(14)

$$h=1+m(v_{dcj}-v_H)$$

(15)

where m is a positive real number when $v_{dcj}$ > $v_H$, $v_{dcj}$ is in the high-voltage region, then m = 1; when $v_{dcj}$ ≤ $v_H$, m = 0. $v_{dcj}$ is not allowed to exceed ±5% of the rated voltage; $v_{max}$ and $v_{min}$ are the maximum and minimum values of $v_{dcj}$ respectively; $i_{max}$, −$i_{max}$ are the maximum and minimum values of $i_{dcj}$ respectively, and the maximum discharge current and maximum charging current of the JTH battery unit are represented. The circulation suppression in Figure 6 is the adaptive droop curve in this paper; the first quadrant represents discharge, and the second quadrant represents charging. When the load is light, it causes the bus voltage to rise $v_{dcj}$ > $v_H$, and $k_j$ starts real-time adjustment at this time.

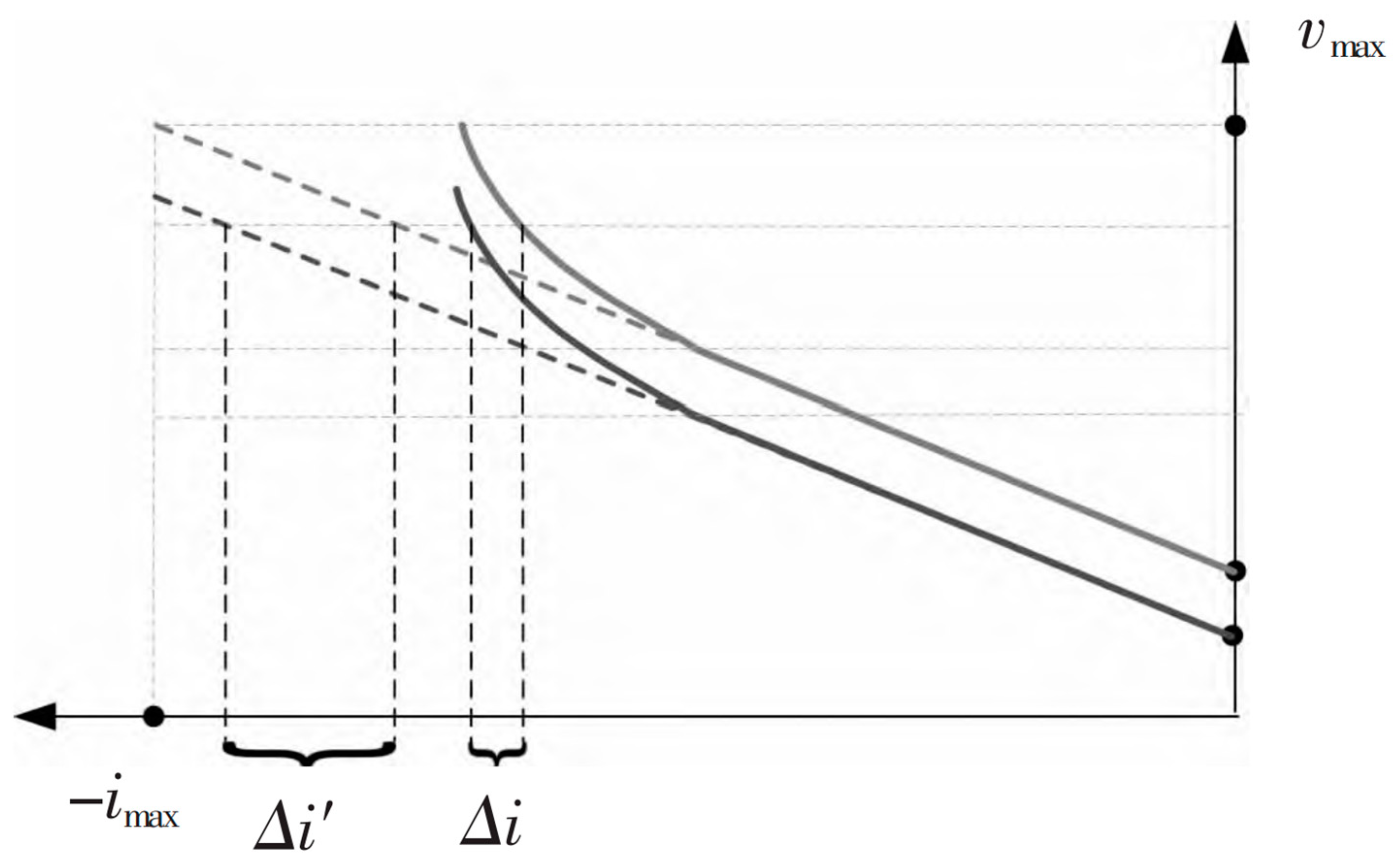
Figure 8 is the second quadrant of the droop control curve, which shows the current deviation comparison between the modified and traditional droop control. The solid line is the droop control curve proposed in this paper, and the dashed line is the traditional droop control curve.

As can be seen from Figure 8, under a light load, the current difference $\mathsf{\Delta }i$ of improved droop control is significantly smaller than the current difference $\mathsf{\Delta }{i}^{\prime }$ of the traditional droop control.

5.2. Balance Dual Battery SOC

The droop coefficient $q_j$ of the balanced dual battery ${SoC}_j$ is adjusted adaptively according to SOC. The output current of each battery is proportional to the battery SOC, and the input current is inversely proportional to the battery SOC.

$$q_j=\left\{\begin{array}{c}{k}_c{SoC}_j^n, charge\\ \frac{k_d}{{SoC}_j^n},discharge\end{array}\right.$$

(16)

When charging, the higher the ${SoC}_j$, the lower the input current, and the lower the ${SoC}_j$, the higher the input current. When discharging, the higher the ${SoC}_j$, the higher the output current, and the lower the ${SoC}_j$, the lower the output current, so that the battery’s SOC is balanced.

In the balanced SoC section in Figure 6, the fourth quadrant represents discharge, and the second quadrant represents charging, where ${SOC}_1$ > ${SOC}_2$; when charging, $q_1$ > $q_2$, so |$i_{c2}$| > |$i_{c1}$|; and when discharging, $q_2$ > $q_1$, so |$i_{d1}$| > |$i_{d2}$|.

In (16), n is a positive integer. When n is larger, the SOC balance speed is faster, but the output power of the converter increases with the increase in n. In order to avoid exceeding the rated power of the converter, n = 3 is taken. The value ranges of $k_c$ and $k_d$ are shown in (17).

$${\mathsf{\Delta }v}_{dc}=\left\{\begin{array}{ll}{(k}_c{SoC}_{max}^n)i_{max}& {\mathsf{\Delta }v}_{dc}={\mathsf{\Delta }v}_{dcmax}\\ {(k}_c{SoC}_{min}^n)i_{-max}& {\mathsf{\Delta }v}_{dc}={\mathsf{\Delta }v}_{dcmin}\\ \left(\frac{k_d}{{SoC}_{min}^n}\right)i_{max}& \mathsf{\Delta }vdc={\mathsf{\Delta }v}_{dcmax}\\ \left(\frac{k_d}{{SoC}_{max}^n}\right)i_{-max}& \mathsf{\Delta }vdc={\mathsf{\Delta }v}_{dcmin}\end{array}\right.$$

(17)

The bus voltage rating is 800 V, and the allowable fluctuation range is 5%, that is, ${\mathsf{\Delta }\mathrm{v}}_{\mathrm{d}\mathrm{c}\mathrm{m}\mathrm{a}\mathrm{x}}$ = 40 V, ${\mathsf{\Delta }\mathrm{v}}_{\mathrm{d}\mathrm{c}\mathrm{m}\mathrm{i}\mathrm{n}}$ = −40 V; $i_{max}$ = 100 A, $i_{-max}$ = −100 A. The SOC ranges from 20% to 80%.

6. Simulation Verification

In order to verify the effectiveness of the proposed method, Matlab/Simulink software is used to simulate and analyze the rated load and light load, respectively.

The simulation parameters are as follows. The photovoltaic module model is built according to the working principle of the photovoltaic module when the light intensity is 1000 W/${\mathrm{m}}^2$, the temperature is 25 °C, and the maximum output power is 120 kW. The capacity of the two batteries is 10 Ah, the end voltage is 500 V, and the initial ${SoC}_{1,t=0}$ and ${SoC}_{2,t=0}$ are 80% and 75%, respectively. The normal SOC working value ranges from 20% to 80%. The two-line resistance values are $R_1$ = 0.1 Ω and $R_2$ = 0.2 Ω. The power consumption at the rated load $R_L$ is 60 kW, the rated bus voltages are $v^{*}$ = 800 V and $v_H$ = 830 V, and the allowable fluctuation value of the bus voltage is ±5% of the rated value. The PI controller parameters are P = 0.1 and I = 0.2, the PWM carrier frequency is 2 kHz, and the droop control parameters are $k_c$ = 1 and $k_d$ = 0.1 when h = 1 and k = 0.6. In traditional droop control, the droop coefficient is a fixed value of 0.6.

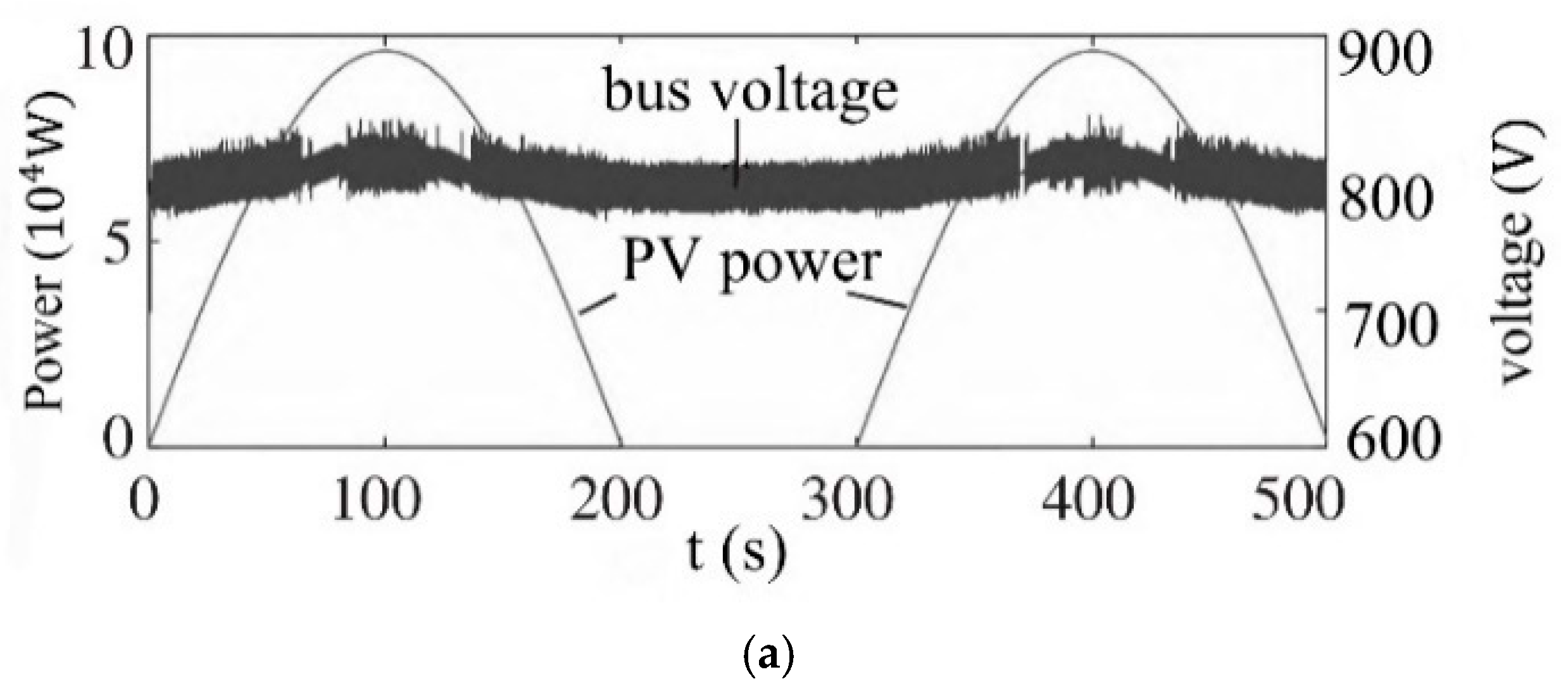
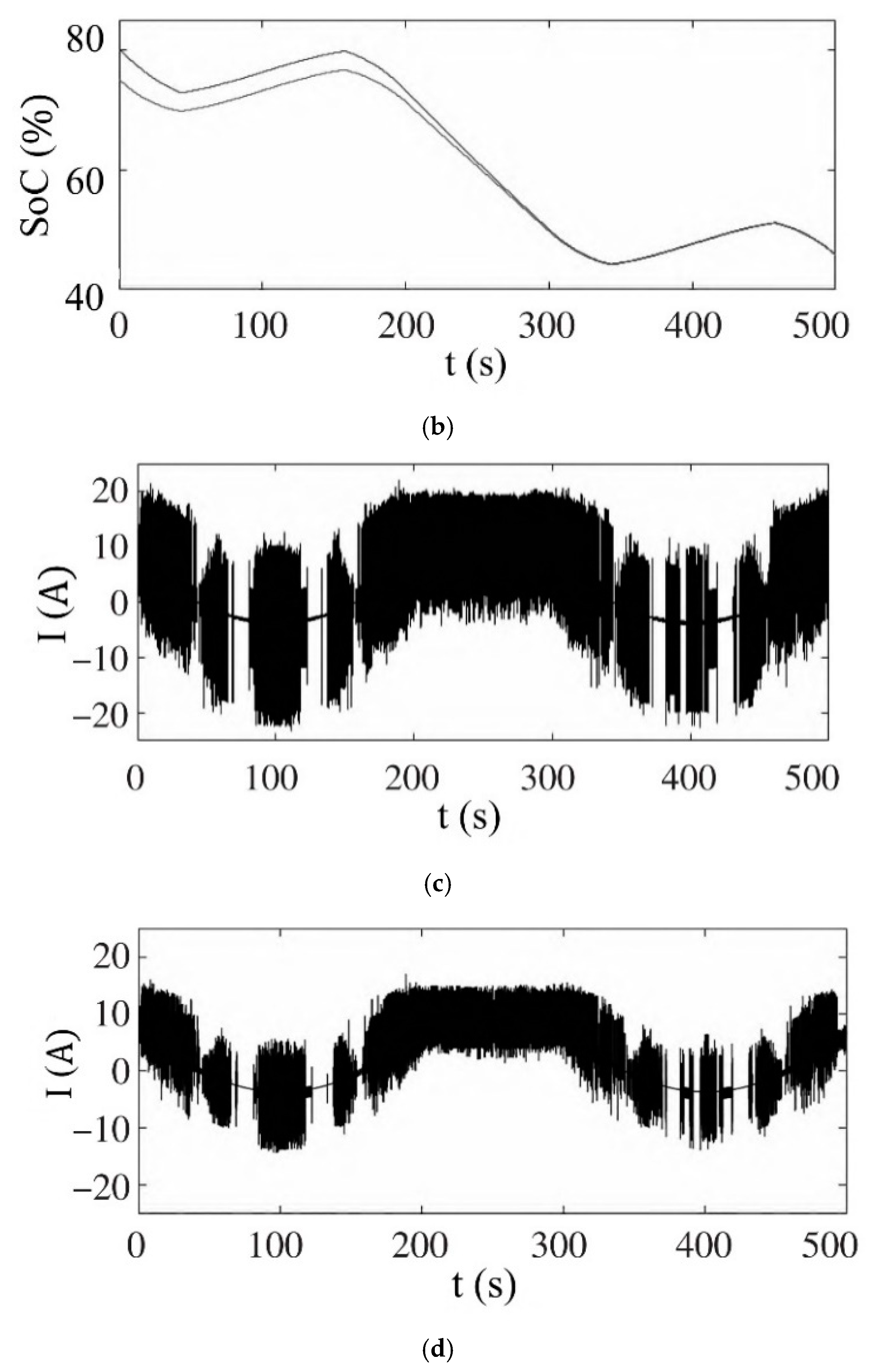
Figure 9a shows the simulation results at a rated load. As can be seen, the photovoltaic power module is controlled by the MPPT mode, and the output power changes with the light intensity. For 0–200 s, the photovoltaic output power ranges from low to high and then low; for 200~300 s, the photovoltaic output power is 0; for 300~500 s it changes again into the daytime. When the photovoltaic output power is greater than the load power of 60 kW, the bus voltage rises; when the photovoltaic output power is less than the load power of 60 kW, the bus voltage drops. When the bus voltage is higher than 800 V, the battery is charged, and the accumulator is discharged. It can be seen that the bus voltage can be well-stabilized at a fixed value of 800 V. The voltage fluctuation range is within 3.5%, the maximum value is 827 V, and the minimum value is 771 V.

Figure 9b shows the SOC changes in the two batteries, which should be controlled by the control method proposed in this paper. The initial SOC of the two batteries is 80% and 75%, respectively, and the double storage pool is charged and discharged with the change in the bus voltage. According to Figure 9c,d, the circulation of the improved balanced SOC method is smaller, and its mean square error value is 5.219, while that of the traditional method is 5.582, and the circulation is reduced by 7%. Therefore, the improved balanced SOC method proposed in this paper has a better circulation inhibition effect.

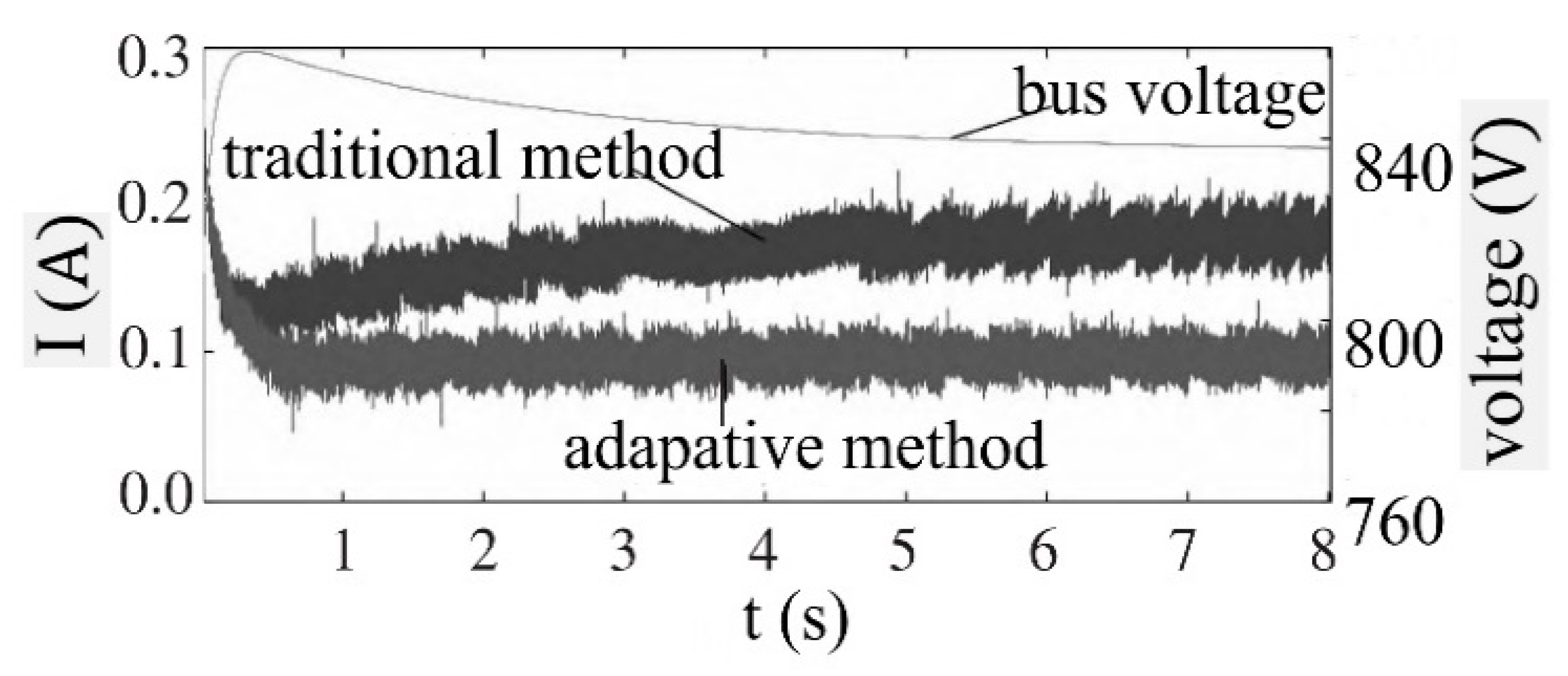
In order to demonstrate the superiority of the proposed method under a light load, the load power consumption is set at 30 kW for simulation verification. Figure 10 shows the circulation between two batteries under a light load with the traditional droop control method and the method proposed in this paper.

As can be seen from Figure 10, the output power of the PV power module is greater than the power consumed by the direct current load, resulting in a bus voltage higher than 830 V, and the bus voltage was greater than $v_H$ during the simulated true time, indicating that it was in the high-voltage area. The droop coefficient $k_j$ of the droop control proposed in this paper was adjusted in real-time according to the bus voltage, and the mean square deviation of the circulation was 0.098, while the mean-square deviation of the traditional droop control was 0.164.

7. Conclusions

The problem of the unbalanced circulation and SOC caused by unequal line resistance is analyzed in this paper, and an improved droop control method is proposed, in which the adaptive droop coefficient of circulation suppression is adjusted in real-time according to the bus voltage, and the adaptive droop coefficient of the balanced SOC is adjusted in real-time according to the charging state of the battery. With control by this method, the voltage fluctuation range is within 3.5%. Compared to the traditional method, this method can reduce the mean square error of circulation by 7%, and the reduction value can reach 40% under light load; the effect is clear, and finally, the SOC can reach equilibrium.

The simulation verifies that the battery charging and discharging logic designed in this paper can effectively stabilize the bus voltage and solve the problem of unbalanced circulation and SOC. Compared to the circulation suppression link of the traditional method, the control method in this paper had a good effect under the condition of light load and can effectively inhibit the circulation between two batteries. Previous studies on droop control either did not consider the influence of line resistance on battery charge status, or the droop control parameters were fixed, which could not adapt to various dynamic changes in the DC microgrid, or, in order to improve the circulation problem under a heavy load, it aggravated the circulation problem under a light load and did not consider the SOC balance problem of the energy storage unit. The problems of circulation and SOC balance are solved in this paper. Finally, the superiority of the proposed method is verified via a simulation. However, this paper does not consider the problem that when the transmission line is long, the line impedance is large, and the busbar voltage deviates too much. In future research, voltage compensation should be considered to solve this problem.