Abstract
The building sector, known for its high energy consumption, needs to reduce its energy use due to rising greenhouse gas emissions. To attain this goal, a projection for domestic energy usage is needed. This work optimizes short-term load forecasting (STLF) in the building sector while considering several variables (energy consumption/generation, weather information, etc.) that impact energy use. It performs a comparative analysis of various machine learning (ML) models based on different data resolutions and time steps ahead (15 min, 30 min, and 1 h with 4-step-, 2-step-, and 1-step-ahead, respectively) to identify the most accurate prediction method. Performance assessment showed that models like histogram gradient-boosting regression (HGBR), light gradient-boosting machine regression (LGBMR), extra trees regression (ETR), ridge regression (RR), Bayesian ridge regression (BRR), and categorical boosting regression (CBR) outperformed others, each for a specific resolution. Model performance was reported using , root mean square error (RMSE), coefficient of variation of RMSE (CVRMSE), normalized RMSE (NRMSE), mean absolute error (MAE), and execution time. The best overall model performance indicated that the resampled 1 h 1-step-ahead prediction was more accurate than the 15 min 4-step-ahead and the 30 min 2-step-ahead predictions. Findings reveal that data preparation is vital for the accuracy of prediction models and should be model-adjusted.
1. Introduction
Energy use and surrounding issues are critically important today as these challenges directly impact society’s wellbeing and security [1]. Among the three main economic sectors described as having very high energy consumption, buildings have been identified to contribute a large share of this consumption [2]. According to the International Energy Agency (IEA) report 2021, energy use in buildings has significantly increased from 115 EJ in 2010 to 135 EJ in 2021. The latter represents 30% of global final energy consumption, with electricity accounting for 35% of building energy use and a significant amount catering to space cooling needs [3]. Because people spend most of their time in buildings, homes, and offices, they rely heavily on heating and cooling systems. Electricity and heat generated for use in buildings account for substantial carbon emissions in the energy industry. In residential houses, electricity use is growing faster than any other energy source and is projected to increase through 2050, regardless of the efficiency gains.
A power grid that relies heavily on renewable energy is one of the most essential steps toward carbon neutrality [4]. According to estimates, 60% of the world’s power will be generated from renewable energy by 2035 [5]. This growth in renewable energy generations and their sporadic nature has made it necessary to have smart grids and microgrids to ensure power system stability, operability, and reliability [6,7]. The developed variability in the energy demanded and power generated, introduced by several power sources, particularly solar and wind, is causing an impending transition in the power systems and infrastructure. Several strategies have been conceived and implemented to lessen the adverse ramping effects, such as demand response (DR), resource allocation, total energy forecasting, peer-to-peer energy transfer, microgrids, and bigger storage capabilities.
Accurate energy forecasting makes managing imbalances between energy production and consumption easier and supports smart grid architecture procedures like demand response management (DRM) [8]. DR allows households to actively participate in efforts to improve power system reliability and emissions reduction [9]. Proper implementation of DR programs requires forecasting households’ energy requirements. To assess the impact of both current and prospective energy plans, stakeholders in the energy sectors, such as the distribution system operators (DSOs) and aggregators, rely on prediction algorithms to anticipate demand and supply. The power sectors use long-term load requirement forecasts to guide current investments and planning while using short-term energy forecasts to ensure supply and dependability [10].
The development of powerful prediction tools for building energy consumption has been facilitated by the rapid growth of the Internet of Things (IoT) and artificial intelligence (AI) technologies exploiting data contained in complex information networks [11]. Energy recommendation systems continue to be deployed and implemented to foster energy-saving behavior and reduce carbon emissions [12]. These systems can propose models for short-term load forecasting (STLF) for various buildings, considering their physical and operational characteristics and time series data on energy consumption.
Load forecasting has transitioned over the years and has become a pillar for energy planning and operation. However, load forecasting for buildings does not receive the necessary attention from the power engineering community. The growing impacts of smart meters have driven the attention of building engineers, researchers, and practitioners to building load forecasting primarily to pursue operational excellence. This study aims to use different machine learning (ML) algorithms for very-short-term load forecasting (VSTLF) of energy requirements in a household and evaluate the performance of algorithms on different time resolutions (15 min, 30 min, and 1 h) to observe the errors in the predictions.
VSTLF has found high relevance in energy load forecasting (ELF). Hence, this paper elaborates on short-term ELF, comparing the performance of different traditional models on the same data with different features like data time resolution and forecasting time steps [13]. The study explores the effect of different time steps on the prediction models’ performance by resampling the data into 30 min and 1 h time steps. While analyzing the resampled datasets, the models were compared to their 1 h ahead predictions using 1, 2, and 4 steps for each resolution. The results showed that the most accurate prediction was achieved with the resampled 1 h 1-step-ahead prediction, outperforming the 15 min 4-step-ahead and the 30 min 2-step-ahead predictions.
The study reveals the relevance of energy forecasting in transitioning from conventional to sustainable, smart buildings with greater control over their energy resources by spelling out the importance of high-performing ML prediction models.
2. Background
The design and operation of power systems rely on ELF. To monitor and balance future energy generation with consumption, DSOs use forecasting as a tool. It lets utility providers predict electricity usage and plan for future power loads. Given the rapidly changing infrastructure for energy distribution and its growing capabilities, the need for precise predictions for quicker response times and resource allocation is very apparent. It can be generalized that ELF is essential for the proper and continuous operation of power systems. Compared to other types of loads, the accuracy of residential ELF has proven challenging due to many uncertainties.
In the past, it was a usual practice to forecast residential energy usage by estimating the hourly average electricity usage of many households [14]. This gives the ability to predict peak electricity demand times and allows power system operators to switch on additional power plants to avoid severe electrical shortages. Recently, buildings have incorporated solar panels, wind turbines, and battery storage, which require accurate ELF for proper implementation [15]. The nature of renewable energy sources necessitates accurate forecasting of residential electricity consumption at disaggregated levels.
Energy consumption forecasting would be straightforward if the process depended only on the energy data. In reality, this is not the case. Energy use also relies heavily on several other factors, including the environment and the weather. Household energy consumption patterns vary according to temperature, humidity, time of day, occupancy level, and socioeconomic characteristics. Researchers have reported several factors significantly affecting the energy consumption in residential buildings. In [16], the number of bedrooms accounts for almost 35% of the difference in the electricity consumption of houses in Leicester and Sheffield, United Kingdom.
Similarly, another study revealed that the number of rooms per house is the most significant factor influencing energy consumption [17]. While this is obvious, at the city and national levels, population density is directly linked to aggregated energy consumption [18]. These variables are very related. The higher the number of rooms in a house, the higher the number of occupants in the building, hence the higher the use of electrical appliances. These factors can be directly linked to household spaces, which is also a significant factor. A large space area will require a large amount of heat or cooling. In the case of electric heating systems, the impact of the space area per square meter on electricity consumption was investigated [19]. Another factor that has been attributed to influence energy consumption is household income. A high-income household may imply a larger, warmer house with more appliances.
2.1. Factors Affecting Energy Use in Building
The energy behavior of a building is impacted by such factors as the weather conditions, the thermal characteristics of construction materials, the level of occupancy, occupants’ behavior and performance, and schedules of components—lighting and heating, ventilating, and air-conditioning (HVAC) systems [20].
2.1.1. Weather
The weather plays a significant role in determining how much energy buildings use. Parameters such as temperature, relative humidity, and wind speed, which define the weather conditions, vary with time. Commercial building heating and cooling loads using the external dry-bulb temperature as a weather factor were estimated [21]. To forecast monthly building energy usage, authors in [22] used the typical monthly temperatures. Their prediction is more accurate than conventional methods, which often use heating and cooling degree days. The annual heating and cooling load of nonresidential buildings was predicted based on a few weather variables, such as the monthly average of maximum and lowest temperatures, relative humidity, air pressure, and cloud cover [23]. Comparing their findings to energy simulation tools, predictions for low-mass envelope buildings were more accurate.
Time series prediction models estimate future demand using historical energy and climate data. As a result, once the weather pattern changes, the prediction error will significantly increase. The lower performance of time series predictions with changing weather conditions is considered a challenge.
2.1.2. Building Characteristics
A building’s characteristics are another critical aspect of its energy performance. These entail the physical design of the building, the shape, window-to-wall ratio, type of facade, orientation, roof and wall insulation, the number of floors, the type of window, and glazing. It is a significant but complicated factor in determining energy performance is the building. A simple method of predicting energy consumption in a residential building with a renewable energy system was conceived [19]. Appliances, hot water, and space heating were included in the definition of the total energy use of the building. A particular modeling technique was used for each component, using statistical data on average end-use consumption.
Just a few studies considered building characteristics as a predictor in the forecast models according to their reviews [24]. Using statistical ML algorithms, the effect of eight building characteristics on the cooling and heating of a building was also investigated [25]. The authors further compared the strength of each factor on the performance of a linear and nonlinear regression model to ascertain the potential of using an ML model to predict building energy load.
2.1.3. Type of Appliance Used
The number, type, and occupants’ appliance use pattern explain the household’s electricity consumption. These appliances account for up to 30% of energy use in the residential sector [26]. Appliance energy consumption can be divided into components, including HVAC equipment like air conditioners. Another study analyzed household electrical appliances, including dish and clothes washers, to determine their energy use pattern. It was demonstrated that the use of these appliances depends highly on the user and varies with time from house to house [27]. The use of these appliances also affects indoor conditions such as temperature, humidity, light, and noise.
The influence of appliances on thermal gains is very significant and relevant for highly insulated buildings in terms of a building’s energy performance [27]. The problem of predicting appliance aggregated energy use was addressed by applying four regression models: support vector regression (SVR), gradient-boosting regression (GBR), random forest (RF), and multiple linear regression (MLR) models with several combinations of features [28].
2.2. Time Series Energy Forecasting
Energy forecasting has made it possible to solve real-world issues by developing a system of predicting energy demand and production. These systems are developed by creating models that learn about past events from historical data represented by many observations, each corresponding to a specific moment in time. These sequential observations indexed by time are called time series data and are expressed as a vector of n variables. The primary goal of analyzing these time series data is to create a mathematical model to learn from available data to predict future observations. This has made time series forecasting an extensive research field in science and engineering [29].
Time series modeling and prediction are approached with linear or nonlinear forecasting models. Autoregressive (AR), moving average (MA), and autoregressive moving average (ARMA) are the three most common linear models for time series forecasting [30]. These models do not perform well for nonlinear time series. They rarely produce accurate predictions because they exhibit linear dependencies over time and assume that the time series is constant. However, there have been numerous studies on the application of AI to solve forecasting problems using nonlinear time series [31,32,33].
Four statistical models were developed to forecast aggregated appliance energy consumption for a passive house in Belgium [28]. These models were MLP, SVM with radial kernel, RF, and GBMs using R programming language. The extensive data analysis approach to the model development indicated that the best model performance was achieved with GBMs. The evaluation considered the metric values of root mean square error (RMSE), mean absolute percentage error (MAPE), and mean absolute error (MAE) and was compared with the three other employed models. In [34], authors adopted a homogeneous and heterogeneous transfer learning approach using boosting to learn a set of multiple kernel regressors. The results of this experiment on the residential dataset showed that knowledge gained from other households could significantly reduce forecasting errors.
2.3. Energy Load Forecasting
ELF can be divided into the following categories, each with a distinct goal and time frame. According to [35], short-, medium-, and long-term are the three main types of ELF in energy operations planning and control. VSTLF is the term used to describe forecasts for extremely small time frames. Using past energy loads observed on the same day to train the prediction model, they vary from one minute to one or several hours in the future (often in five-minute steps) [36]. In addition to being used in transmission lines load management, VSTLF assists in intraday power trading and handling ancillary tasks that ensure the electricity system’s stability [10].
STLF is intended to estimate electrical demand for 30 min up to two weeks [37] and is applied to the day-ahead load, energy network planning, and maintenance. STLF can improve operational safety and reduce power system costs [8].
Medium-term load forecasting (MTLF) covers one week to a couple of months up to one year in advance [10]. It allows running the power networks’ energy switching, maintenance, and outage planning [38]. Retailers and large customers need accurate long-term probabilistic energy forecasting to optimize their energy scheduling and operation and adjust in the short-term market and profitable sign agreements [10].
The time ranges covered by long-term load forecasting (LTLF) may range from one to ten years or even longer [39]. Energy management and system capacity planning heavily rely on long-term energy forecasts. The long-term annual energy demand forecast is crucial because it plays a part in developing and planning the nation’s energy mix and power system infrastructure investment.
Compared to the middle and long-term, short-term forecasts provide more accurate and precise predictions. Though studies on short-term energy have been conducted, the accuracy of forecasting performance differs due to the lack of real-time data [40,41,42]. Recently, day-ahead forecasting of residential customers’ electricity consumption has also undergone extensive analysis. Other researchers claimed that their 1-step-ahead method for STLF can be used consistently for any energy load prediction problem irrespective of the type of load forecasting. The study further suggests that forecasts depend on the context and the input data for the hypothetical energy demand [8].
2.4. Related Work
Recently, much research has been conducted on how electrical energy is used in buildings. The effect of meteorological factors on the monthly power demand in buildings has been the subject of many studies. Variables such as the daytime, weekend, month, outdoor temperature, holiday, previous day consumption, rainfall index, global solar radiation, wind speed, and occupancy have been incorporated in models for predicting electricity demand in buildings [43,44].
The electricity data of 1628 households were studied, containing information on the weather, building envelope characteristics, number of appliances, occupancy level, location, age of the building, floor area, ownership, energy-efficient light gadgets, and income level of occupants. The researcher concluded that the weather, location, floor area, number of refrigerators, and entertainment appliances were the most crucial factors affecting minimum daily consumption [45]. It was demonstrated that weather variables can be used to forecast how much electricity is used in buildings. In another study, the same author correlated the energy use efficiency in the building with the time of occupancy and attributed the low efficiency of appliance energy use with a high level of occupancy [46]. Also, data-driven prediction models were used to establish the relationship between appliance energy consumption and the predicting variables for a house in Stambruges [28]. The statistical analysis of the data collected and prediction models showed the prevalence of weather data and time information as better predictors among the variables used.
Several deep learning techniques were used to forecast the energy consumption of a building, and the long short-term memory network/gated recurrent unit (LSTM/GRU) model performed the best [47]. A strategy for predicting energy usage in residential buildings using a deep extreme ML approach was proposed by [48].
A comparative analysis of different ML models on household energy data was performed in South Korea to determine the behavioral pattern of the occupants and develop an optimal energy use plan for each house [49]. The authors applied linear regression (LR), SVR, and k-nearest neighbor (KNN) regression on the dataset using WEKA (Waikato Environment for Knowledge Analysis—a data mining tool) before using times series models, ARIMA, and vector autoregression (VAR) to forecast energy consumption. They found that ARIMA and VAR did not perform well on the test data, but better performance was recorded for SVM regression.
Examining the energy use in all German industries, including residential structures, it was reported that multiple regression was the best forecasting method [50]. Likewise, an analysis of different factors that affected home energy usage in France concluded that MLR is the best method to identify the critical factors [51]. For buildings in London, the influence of economic, sociodemographic, and building characteristics on energy consumption and using LR models was also investigated [52].
To optimize HVAC systems, a data-driven predictive control approach that combines reinforcement learning (RL) and time-series forecasting to analyze different sensor metadata was proposed [53]. This entails creating and validating sixteen architectures based on long short-term memory (LSTM) with attention, convolution, and bidirectional processing processes. The findings demonstrated that recursive prediction significantly lowers model accuracy. This effect was more noticeable in the model that predicts temperature and humidity.
The extreme weather identification and STLF model based on the bagging-extreme gradient-boosting (XGBoost) algorithm may provide an early warning on the time period and detailed value of peak demand [54]. First, the concept of bagging was presented to lower the output variance and improve the algorithm’s capacity for generalization based on the XGBoost algorithm. Next, to increase the model’s ability to follow changes in the weather, the mutual information (MI) between weather-affecting factors and load was evaluated. The extreme weather detection model was then constructed to ascertain the occurrence range of peak load, taking into account the load, weather, and timing aspects.
Furthermore, to estimate building loads, a novel hybrid technique that incorporates convolutional neural networks (CNNs), grey wolf optimization (GWO), and bidirectional long short-term memory (BiLSTM) was introduced [55]. The CNN and BiLSTM algorithms’ ideal set of parameters was obtained using the GWO. To extract the time series data feature efficiently, one-dimensional CNN was used. Four buildings with unique characteristics acted as case studies to examine the performance of the suggested technique utilizing hourly resolution data. The outcomes validated that the same method may be successfully employed on other architectures.
Home energy consumption was predicted in the United States using an MLR method [56]. Multiple regression was employed to predict building gas and electricity consumption using the average number of rooms, heating degree days, and median household income as the model inputs [57]. Finally, the number of occupants and rooms in a building were utilized as input to model an algorithm for predicting electricity consumption [58].
2.5. Challenges in Household Energy Forecasting
Anticipating energy consumption in a building is difficult due to the intricate nature of energy systems. The primary energy sources discussed in the literature are heating/cooling load, hot water, and electricity [23,43,59]. Individuals’ decision-making processes influence their electricity consumption, which is unpredictable. Each occupant’s behavior is rendered insignificant when forecasting energy consumption at an aggregated level. However, it becomes more important when forecasting is carried out at disaggregated levels. That way, noticeable variations can be observed in individual consumption, consequently introducing errors in the prediction model.
Data gathering and access are the main challenges in building ELF. Much research on individual electricity consumption forecasting uses consumer survey data or sub-metered appliances. However, this is not practically feasible on a large scale, partly due to privacy concerns. Therefore, it is crucial to conduct research in this field using data from fiscal smart meters that include integrated local weather data. A combination of several ML techniques to manage data inconsistencies from the fiscal smart meter modeling user behavior and forecast individual users’ residential electricity consumption was conceived [14]. Such studies focus on forecasting the next day’s hourly energy consumption of residential households [60].
Despite the success achieved with data-driven forecasting models, there are certain drawbacks in capturing residential consumers’ irregular but highly periodic energy habits. Generalizing occupant behavioral patterns is one of the main flaws in the current models. When only electricity consumption, calendar information, and external weather data are accessible, they reflect user behavior, climate, and seasonal variations. However, it is difficult to infer the user behavior as it is independent of these seasonal dependencies. Another study emphasized the high correlation between the occupancy profile and energy consumption relative to people’s activity. This occupancy profile predicted the electricity demand for heating and cooling appliances [61].
After exploring the main challenges in household ELF, this study addresses the urgent need to lower energy usage by presenting a novel method for optimizing short-term load forecasting (STLF). The research performs a comparative examination of multiple ML models, investigating varying data resolutions and time steps ahead, and demonstrates the specificity of each model’s performance for various resolutions. Although the study provides insightful information about the relative advantages of different models, it also emphasizes the importance of improving data preparation procedures to increase forecasting accuracy, underscoring the necessity of ongoing adaptation to attain the best outcomes.
3. Methodology
Comparative analysis of the performance of conventional ML models for predicting the energy consumption of the building under study is carried out using its historical energy consumption and weather data. The effect of engineered features and hyperparameter tuning on the model’s performance is also analyzed. The study explored the model’s performance based on different time steps, i.e., 15 min, 30 min, and 1 h. The computation stage is divided into the training stage and the test stage. The evaluation of the models is based on the estimation error and the computational time to train the model.
Having all the 1-step-ahead predictions for all three resolutions, a 1-step-ahead vs. direct multistep-ahead (i.e., 4-step and 2-step) comparison was performed to identify the best method for 1 h ahead prediction. The goal was to test the original 15 min resolution on a 4-step-ahead prediction against a 2-step-ahead resampled 30 min resolution and 1-step-ahead resampled 1 h resolution.
3.1. Dataset Description
Data from the ITI/CERTH Smart House [62], the first smart net-zero building in Thessaloniki, Greece, were explored for the experimental test. The energy data include energy consumption, photovoltaic (PV) energy generation, battery storage, and electricity price. These energy data were logged at 15 min intervals over two years between October 2018 and September 2020 by IoT devices, smart meters, and sensors. The weather data include temperature, relative humidity, wind speed, and cloud cover, which were interpolated at 15 min intervals from a local weather station. All in all, the data comprised 63,612 observations with 15 min time intervals.
3.2. Data Preprocessing
Data preprocessing is a crucial step in time series forecasting model development. This critical process determines model success. To gain insights and make predictions using ML algorithms, smart meter data need to be analyzed using robust techniques due to missing data and outliers. Data preprocessing quality directly affects forecasting model performance.
3.2.1. Handling Missing Data
Missing observations or null values pose a big problem to the learning algorithms. Making the algorithm work and connecting all the signals in the features is impossible if some values are missing. Initially, the weather data had some missing values, whichwere filled by using linear interpolation. This approach is commonly employed in time series data to fill the missing values with the preceding or succeeding ones.
3.2.2. Outliers Removal
Communication errors in data collection and storage may result in inaccurate data that exceed the normal measurable limits. Outliers, also known as anomalies, are typically data points that deviate significantly from the expected values, being either very low or very high. Outliers pose a significant risk to ML algorithms as they can potentially disrupt the patterns and rules that the algorithm has learned. To address this issue, a statistical analysis was conducted to assess the deviation of median values from the mean, as well as the difference between the 25th and 75th percentiles.
Energy Consumption: Sorting the frequency of unique values in ascending and descending order detects the outliers in the energy consumption data. These outliers were replaced by the 99.8th percentile of the energy consumption data. The frequency of the data represented by the histogram in Figure 1 shows the occurrences of different energy consumptions that range from 0–2.4 kiloWatt hour (kWh) after removing outliers. Figure 2 shows the hourly energy consumption profile. The low values in this profile represent a period of low energy consumption, reflecting the diminishing occupant’s energy use.
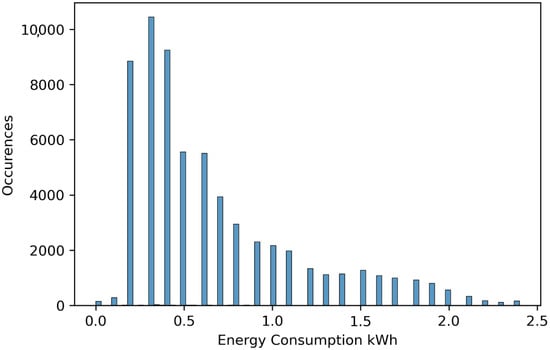
Figure 1.
Histogram of the energy consumption data.
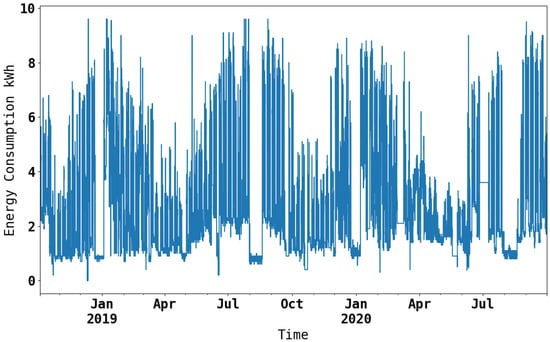
Figure 2.
Energy consumption profile aggregated per hour.
Weather data: These data feature temperature, relative humidity, wind speed, and cloud cover data. The outliers in temperature were removed by replacing the outrageous values with the 99th percentile of the data values, found to be approximately 41 °C. This is important because the temperature is fundamentally related to the energy consumption of any building.
Energy generation: The PV energy generation data contain no missing and extreme values. The 0th and 100th percentile of PV energy generation lie between 0 and 3.6 kWh. Outliers were eliminated by replacing data values exceeding the 99th percentile with the 99th percentile value of the data. The hourly energy generation profile is shown in Figure 3.
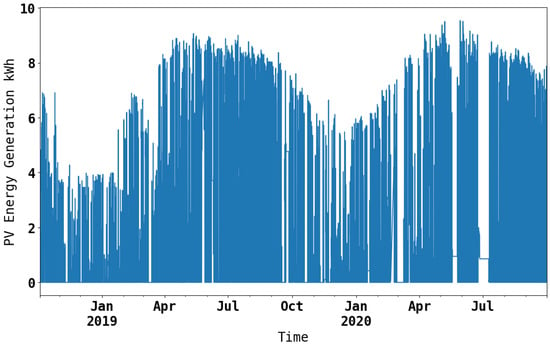
Figure 3.
PV energy generation profile aggregated per hour.
3.2.3. Data Rescaling
The performance of ML models is often affected by the scale of numeric values. Therefore, rescaling the distribution is necessary for the approach to converge more quickly and provide a more accurate result. Rescaling changes the feature values’ range, and it may also impact variance [63]. In this study, the scikit-learn “StandardScaler” was employed [64]. This preprocessing method uses min–max transformation to rescale the data from 0 to 1 by subtracting the minimum values from the current value and dividing by the range. This method was preferred because the data observations have a very small deviation from the mean values.
3.2.4. Feature Extraction and Engineering
Feature extraction highlights parts of the time series and reduces dimensionality. In this step, the time series is modified to produce a few distinctive features that will be passed as input variables for the prediction model. In addition to the energy consumption, generation, and weather data, time-related features extracted from the time series form the bulk of data for analysis. Research demonstrated that integrating time-related data improves the performance of electricity forecasting algorithms [65].
Dummy variables were created from the time-related features extracted using one hot encoding. The intention behind feature generation was to create a more complex feature matrix that could help the model achieve better results rather than building complex models.
3.3. Exploratory Data Analysis
As originally used in his book Exploratory Data Analysis (EDA), the American statistician John Tukey discussed the need for greater integration between graphical analysis and descriptive measure [66]. Visualizing observable trends in 1 h resolution can enhance comprehension of the data. Figure 2 shows that the 1 h energy consumption profile has higher energy consumption during the winter and the summer months due to high cooling and heating demands. The lower energy consumption in August and December implies periods of inactivity in the building. The PV energy generation data show a gradual increase in energy generation from January through April, as shown in Figure 3. The peak of energy generation spans from June to October due to the intense and prolonged sunlight, followed by a gradual decline until December.
3.3.1. Energy Consumption—Weather Data Relationship
Scatter plots visualize the relationship between energy consumption and weather variables. As shown in Figure 4, temperature reveals a clear pattern with energy consumption. When the ambient temperature is high or low, there is a corresponding proportion of energy consumption. Figure 5 shows the hourly mean aggregation of the energy consumption and the temperature in the dataset. This illustrates high energy consumption when the temperature is high. Daytime temperatures coincide with increased electrical energy consumption, particularly for cooling purposes. Utilizing a sliding window (SW) for the model training, as described in Section 3.4.3, necessitates a large number of parameters, rendering it impractical to showcase feature importance for numerous variables. Thus, Figure 6 shows a feature matrix that filters out and displays the most significant correlations defining the variables with the greatest impact to be used for the model training.
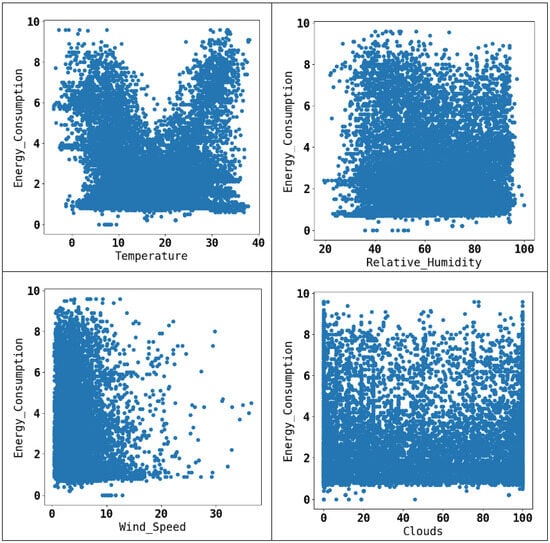
Figure 4.
Scatter plot of the weather variables.
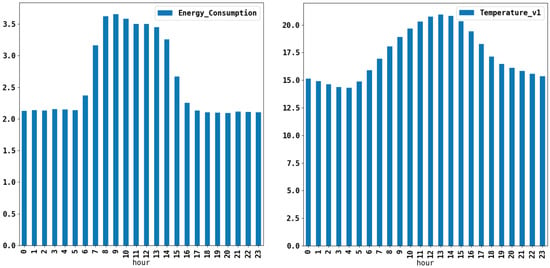
Figure 5.
Hourly aggregation of energy consumption and temperature data.
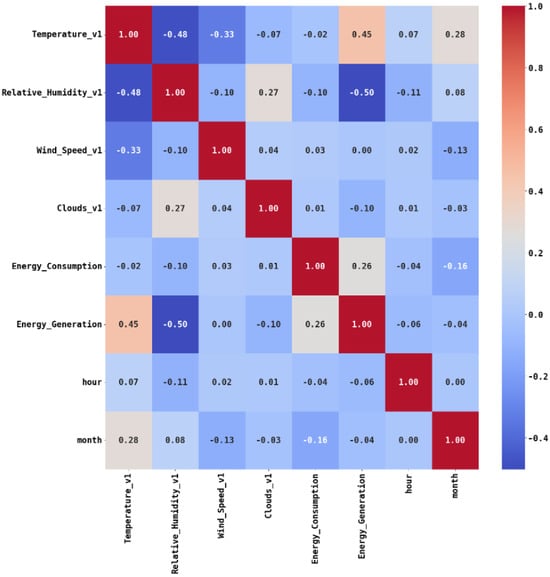
Figure 6.
Feature correlation matrix.
3.3.2. Autocorrelation Analysis
Time series data result from collecting the same repetitive observation over a period. Considering the correlation between the observations specified by the lag is essential to understanding the persistent relation in the time series data. This also helps to determine the stationarity of the dataset, as it is commonly assumed in time series problems that the data is stationary. The properties defining stationarity are the unaltered pattern in the mean, fluctuation, and autocorrelation over time. Figure 7 shows the autocorrelation plot of the hourly energy consumption in the dataset, which indicates a strong correlation between hourly energy consumption throughout the dataset. Moreover, the blue area represents a 95% confidence interval and serves as a signal of the significance threshold. Inside this area, values are statistically insignificant, while beyond this area, values are statistically significant. To establish the model’s order, we must consider all spikes that fall beyond the significance threshold (blue region).
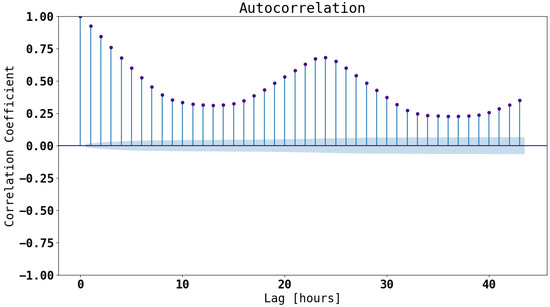
Figure 7.
Autocorrelation plot of the hourly energy consumption.
3.4. Algorithmic Modeling
Over the years, several techniques have been developed to predict building energy consumption accurately. The widely used methods include engineering, statistics, and AI.
3.4.1. Linear Models
The most fundamental regression algorithm is LR. Simple LR is used when there is only a single input variable, while MLR is applied when there are several variables, usually referred to as a matrix of features. A linear model predicts by adding the bias term (also known as the intercept term) to the weighted sum of the input features. More complexity is not required if a linear model sufficiently captures the facts. A cost function is often used to validate the performance of LR. The goal is to reduce this distance between the predictions of the linear model and the training samples.
Ridge regression (RR) is a regularized version of LR. Regularization of the linear model is an effective way to reduce the problem of overfitting. This is achieved by constraining the model and reducing the number of polynomial degrees to reduce its degree freedom and make it hard to overfit. Another regularized form of LR is the least absolute shrinkage and selection operator regression, lasso. Like RR, it adds a regularization element to the cost function [67].
Support vector regression (SVR) is based on high-dimensional feature space created by modifying the original variables and penalizing the resulting complexity with a term added to the error function. The model generated by SVR only depends on a subset of the training data because the cost function for building the model ignores any training data relatively close to the model prediction [68].
One of the main drawbacks of LR models is that they should not be used when a nonlinear relationship exists between the independent and dependent variables.
3.4.2. Tree-Based and Boosting Models
Tree-based models are a family of ML models that perform regression or classification tasks by building decision trees to classify the target variable or determine its values. Because of their capacity to handle outliers, tree models provide a major advantage over linear models. Regression trees are likely to perform better than linear models when no attributes have been found to have a linear relationship with the target variable [69]. They are robust algorithms that can successfully fit complex datasets.
RF is an ensemble of decision trees trained on several random subsets of the training via the bagging method. This method combines classification and regression by growing many decision trees in parallel [70]. Due to its simplicity, ease of usage, and straightforward interpretation, RF is one of the most popular and efficient ML algorithms currently accessible [63]. It proves very useful for data with very high dimensionality.
The extremely randomized trees ensemble, shortened as extra-trees, is a forest of extremely random trees. When growing a tree in an RF, only a random subset of the features is considered for splitting at each node. Instead of looking for the best possible thresholds like conventional decision trees, random entries can be used for each feature to make trees even more random. This method sacrifices a higher bias for a reduced variance. As a result, extra-trees are considerably faster to train than conventional RFs. This is due to the short time it takes to figure out the optimal threshold for each feature at each node of the trees.
Boosting models are ensemble methods that combine and turn several weak learners into strong learners [63]. The main concept behind most boosting techniques is to train predictors in succession, each attempting to correct the one before it. GBR operates by adding predictors to an ensemble one at a time, with each one correcting the one before it. It achieves this by fitting the new predictor to the residual errors made by the previous predictor rather than adjusting the instance weights at each iteration [63]. The prediction of building energy consumption has been made using GB in such research as simulating the energy usage of commercial buildings [71]. In forecasting commercial building energy usage [72], GB outperformed MLR and RF models implemented in comparison to it.
Extreme gradient-boosting regression (XGBR) is an optimized implementation of GB, usually used with decision trees [14,69]. This efficient, fast, and scalable machine learning method is frequently used along with neural networks. The model is enhanced so that each decision tree incorporates lessons from the one before it and influences the one after it [73]. GB models surpass other ML algorithms (such as KNN and SVMs) in accuracy and robustness [74]. A method for predicting energy usage in a large-scale scenario using GB is presented [75].
The light gradient-boosting machine regressor (LGBMR) uses one-side sampling to determine the ideal split for input data. But, unlike other boosting algorithms, the LGBMR expands on a leaf basis for developing a decision tree. The LGBMR is considered lightweight and resource-efficient compared to other gradient-boosting techniques, allowing quicker training times and lower computational demands while producing excellent accuracy [76].
3.4.3. Model Selection and Training
Model selections for prediction depend on the data available [77]. The models selected for this study consist of linear and nonlinear ML models informed by past works in ELF. The linear regression (LR), elastic net regression (ENR) [78], lasso least-angle regression (LLR) [79], RR [67], and SVR [68] were selected because of the interesting facts about them. LLR can zero out the coefficient of the parameters that are unimportant in the model by automatically selecting the best features on its own; RR regression can deal with multicollinearity in a dataset with many predictors; and SVR is effective for multifeature modeling.
The gradient models—GBR [73], XGBR [77], LGBMR [80], and categorical boosting regressor (CBR) [81]—were included as they rely on the ensembling of weaker models to obtain better performance. The tree algorithms, random forest regressor (RFR) [82], and extra trees regressor (ETR) [83] have been reported as suitable when dealing with models whose features have almost zero linear correlation with the target vector [69]. Other models utilized were histogram-based gradient-boosting regressor (HGBR) [73], bagging regressor (BR) [84], and Bayesian ridge regression (BRR) [85].
The dataset was divided horizontally into training and testing sets in proportions of 80% and 20%, respectively. This is equivalent to using approximately the first 18 months of the data to train the models and the last six months to test the models. The train–test split is in this order to avoid randomization, which results in poor performance of the model.
Since the correlation between the target variable (energy consumption) and weather features is very little, the approach adopted is to check, by trial and error method, the impact of each feature group on the model’s performance to identify the right combination of features that gives optimal performance. Having features that do not correlate with the target variable in the feature matrix impacts the model’s performance and takes a long time for the computation.
The data comprised 63,612 observations with 15 min time intervals. Resampling the data into 30 min and 1 h time steps reduces the size of the training and test sets for the experiments. Thus, the time resolution and size of the dataset affect the model’s performance and establish the best time frame for short-time load forecasting.
The selected algorithms were first trained with the default parameters, and the performance obtained formed the preliminary results. Hyperparameter optimization was employed to improve the models’ performance. The process involves tweaking the parameters. Primarily, hyperparameters are defined as ones that must be provided to the models before training because they cannot learn. Numerous methods for hyperparameter optimization have been proposed. For this study, grid search with cross-validation from the scikit-learn library [64] was employed. Furthermore, the SW technique [86] was utilized for all three resolutions, including previous observations up to one day before. This means that a 96-step SW was utilized for the 15 min resolution, a 48-step SW for the 30 min resolution, and a 24-step SW for the 1 h resolution. Figure 8 shows the chart of the experimental framework.

Figure 8.
Overview of the experimental process.
3.5. Performance Measures
The performance of prediction models is evaluated using statistical metrics, which represent the key performance indicators of the models. The common metrics used for time series models are RMSE, MAE, , CVRMSE, and NRMSE. They all quantify the variability of observations around the mean, but they are not the same, and their values are different. These metrics were rationally selected based on a combination of absolute (MAE, RMSE, time) and relative (CVRMSE, NRMSE, ) measures to comprehensively assess the models’ performance in terms of accuracy, error, computational time, and resources.
3.5.1. Root Mean Square Error (RMSE)
RMSE is a general-purpose error metric for prediction. The standard deviation of the prediction errors gives the difference between the regression line and the data points [87]. It is defined as the square root of the average squared difference of the actual and prediction values. RMSE is widely used as it is measured in the same units as the variable in question. According to its mathematical definition (Equation (1)), RMSE applies more weight to larger errors, given that the impact of a single error on the total is proportional to its square and not its magnitude [88].
where is the actual and is the forecasted value, and N is the number of values.
3.5.2. Mean Absolute Error (MAE)
Calculating MAE involves summing the absolute error values (i.e., the difference between the actual and the predicted value) and then dividing the total error by the number of observations (Equation (2)). Unlike other statistical methods, MAE considers the same weight for all errors.
where is the actual and is the forecasted value, and N is the number of values.
3.5.3. Coefficient of Determination ()
The coefficient of determination () constitutes the comparison of the variance of the errors to the variance of the data that are to be modeled. It describes the proportion of variance “explained” by the forecasting model (Equation (3)). Unlike other error-based metrics, the higher its value, the better the fit.
where is the sum of squares of residuals (errors) and is the total sum of squares (proportional to the variance of the data), is the actual energy load value, is the mean of the actual values, and is the forecasted value.
3.5.4. Coefficient of Variation of Root Mean Square Error (CVRMSE)
The CVRMSE is often used to measure relative error. It is calculated as the ratio of the RMSE to the mean of the observed values. The formula for CVRMSE is given by Equation (4):
where
: Mean of the observed values.
3.5.5. Normalized Root Mean Square Error (NRMSE)
The NRMSE is a common metric for assessing the accuracy of a model’s predictions. It is calculated as the ratio of the RMSE to the range of the observed values. The formula for NRMSE is provided in Equation (5):
where
: Mean of the observed values
Range(): Range of the observed values (max–min).
4. Results
This section presents and discusses the experimental procedure results and the models’ performance evaluation based on the evaluation metrics. The experimentation is broken down into different parts. The first part evaluates the models using a 15 min resolution (Section 4.1). The second part evaluates the models based on a 30 min resolution (Section 4.2), with the third part extending the second part with a 1 h resolution (Section 4.3). Finally, a one- vs. multistep comparison is conducted to identify the best method for 1 h ahead forecasting in Section 4.4.
Forecasting using different time series resolutions is crucial for gaining a thorough insight into trends, patterns, and anomalies across various temporal scales. This approach enhances prediction accuracy and facilitates the comparison of results for optimal outcomes [89,90].
4.1. Dataset with 15 min Resolution
The first set of experiments was carried out with processed data in the default 15 min resolution and 1-step-ahead prediction. The 10 best-performing models are illustrated in Table 1.

Table 1.
Model performance metrics for 1-step-ahead and 15 min resolution.
In addition to the training time, the table also presents the performance metrics for various regression models. HGBR and extra tree regression (ETR) stand out with high values of 0.939, indicating strong predictive performance. However, ETR has a notably longer computational time of 1759.75 s. LGBMR also performs with an of 0.938 and a relatively low computational time of 11.20 s. Regarding MAE, HGBR and LGBMR show lower errors, followed by ETR, while from an RMSE (as well as CVRMSE and NRMSE) perspective, HGBR and ETR have lower values, followed by LGBMR. After these three top-performing models, all the others provide lower but similar performance metrics in terms of , RMSE, MAE, CVRMSE, and NRMSE.
Table 2 provides results for 15 min resolution for 4-step-ahead. HGBR and LGBMR lead with an of 0.884, demonstrating robust predictive capabilities, followed by ETR and GBR. However, ETR, despite achieving a high , exhibits a significantly longer computational time of 1731.49 s, the second after RFR, which has the highest computational time of 1944.22 s. In terms of error, again, HGBR and LGBMR show lower scores, followed either by GBR (in the case of MAE) or ETR (in the case of RMSE, CVRMSE, and NRMSE).

Table 2.
Model performance metrics for 4-step-ahead and 15 min resolution.
4.2. Dataset with 30 min Resolution
With a 30 min 1-step-ahead time step, the total number of observations was reduced to half compared to the 15 min resolution. Therefore, fewer data remained for the training and test sets. Initially, models were trained and tested for 1-step-ahead (30 min ahead) forecasting, followed by a 2-step-ahead (1 h ahead) implementation.
Regarding the performance metrics with a 1-step-ahead 30 min resolution, Table 3 illustrates that GBR and HGBR stand out with high values of 0.957 and 0.956, indicating strong predictive capabilities. LGBMR also performs well, with an of 0.954. These models exhibit low RMSE, CVRMSE, NRMSE and MAE, suggesting accurate predictions. However, the computation time varies significantly, with GBR being the most time-consuming, taking 116.15 s. In general, all 10 illustrated models show good performance, indicating a strong fit to the dataset.

Table 3.
Model performance metrics for a 1-step-ahead and 30 min resolution.
Furthermore, a 2-step-ahead implementation was conducted, targeted for 1 h ahead forecasting. Table 4 showcases the performance metrics for the 10 best-performing regression models.

Table 4.
Model performance metrics for 2-step-ahead and 30 min resolution.
RR and BRR lead with high values of 0.920 and 0.919, indicating strong predictive performance. These models, along with CBR, LR, and ENR, demonstrate low RMSE and MAE, suggesting accurate predictions. GBR and ETR, although slightly less accurate, stand out negatively for their relatively high computational times of 117.95 and 373.49 s, respectively. From RR to HGBR and LGBMR, all the models in the table show generally good performance, indicating a strong fit to the dataset.
4.3. Dataset with 1 h Resolution
Resampling the dataset into 1 h resolution resulted in 17,702 observations, i.e., two times less than the 30 min dataset and four times less than the 15 min dataset. Initially, it was expected that the performance might deteriorate due to the smaller number of observations. However, the model performed better for the 1 h ahead (Table 5) compared to the first two cases (4-step-ahead for 15 min and 2-step-ahead prediction for 30 min resolutions) described in Section 4.1 and Section 4.2, respectively. This outcome can be attributed to the fact that the data were smoothened by resampling to remove some extremities, such as long periods of no energy production or low energy consumption. The resampled data take the hourly sum of energy consumption to compute the hourly resolution and the mean of the weather variables.

Table 5.
Model performance metrics for 1-step-ahead and 1 h resolution.
More detailed results are presented in Table 5, providing details regarding the 10 best-performing models. The top three of them are LGBMR, HGBR, and ETR. LGBMR is computationally efficient, taking only 1.08 s, obtaining a high score of 0.927, indicating a significant correlation between predicted and real values. Furthermore, low RMSE (0.486) (as well as CVRMSE, NRMSE) and MAE (0.252) show reliable predictions with minimal mistakes.
Similar to LGBMR, with an of 0.926, HGBR performs quite closely to the former, with RMSE (0.489), CVRMSE (0.192), and NRMSE (054) being marginally higher than those of LGBMR, with MAE (0.252) being equal. Overall, HGBR is still a robust performer, taking 5.52 s to train.
Regarding ETR, while having a high of 0.925 (very close to LGBMR and HGBR), it exhibits a slightly higher RMSE (0.493) and MAE (0.260) compared to the previous models. The computational cost is higher, taking approximately 79.93 s.
Overall, all 10 illustrated models perform well, indicating a strong fit to the 1 h resolution dataset.
4.4. Final Models’ Comparison for 1 h Ahead Forecasting
A thorough comparison of the performance metrics for the three best distinct ML models that were applied to forecasting tasks at different resolutions (15 min, 30 min, and 1 h) is shown in Table 6, as provided in Section 4.1, Section 4.2 and Section 4.3. Every row corresponds to a distinct set of resolutions, steps ahead, and regression models. Also, it is important to highlight that since the energy load target parameter was measured in kWh, downgrading the resolutions provides higher MAE and RMSE metrics for 30 min and 1 h datasets.

Table 6.
Model performance metrics comparison for 1 h ahead forecasting.
For the 4-step-ahead and 15 min resolution implementation, models HGBR, LGBMR, and ETR performed best, with shorter intervals and with a finer temporal granularity. These models have strong predictive performance, as seen by their high values. Particularly, HGBR and LGBMR have similar performance but different computation times.
For the 2-step-ahead and 30 min resolution, models RR, BRR, and CB are the best performing, with the 2-step-ahead at a slightly coarser 30 min resolution. Each of these models has a strong and comparable performance metrics. This stands in terms of , where RR performs slightly better than the others with a 2-step-ahead 30 min resolution, providing better results compared to the 4-step-ahead 15 min resolution.
For the 1-step-ahead and 1 h resolution, the models LGBMR, HGBR, and ETR are the best performing. Each of these models at the 1-step-ahead and 1 h resolution has a higher and lower CVRMSE and NRMSE compared to the two previous resolutions.
Overall, although the dataset size was resampled to 1 h resolution, results indicate higher and lower CVRMSE and NRMSE compared to the 2-step-ahead and 15 min resolution or the 2-step-ahead and 30 min resolution.
4.5. Discussion
It was observed that the models performed differently for different time resolutions on the same data. The difference in the number of observations from the original data is by half (for 30 min resolution) and a quarter (for 1 h resolution). This shows that models reported to have good prediction performance may perform poorly on different datasets, provided the preprocessing stage is performed adequately.
For time series data, our analysis shows the dependency and important predicting power of time- and calendar-related predictors in the model’s performance. In this study, several parameters were included, like the day of the week, the hour of the day, the week of the year, and the month of the year. Based on the data, the temperature is the only weather feature with the highest correlation with the target variable, and is ranked as the most important feature for all the algorithms used. This suggests that temperature is an adequate weather predictor for household energy consumption when weather data cannot be easily obtained.
Implications
Developing energy prediction models is essential to managing and improving building energy efficiency and reducing carbon emissions. In developed and developing countries, with growing populations, rising economies, and a desire for a better quality of life, energy consumption prediction in buildings is required to support national and municipal energy strategies.
Energy forecasting is capable of tracking changes in building energy usage towards the directive of the European Parliament on the energy performance of buildings, which supports nearly-zero-energy buildings. Energy consumption forecast in the buildings sector at the sub-national level, such as regions, local governments, and cities, can be used to identify areas that will be the focus of future investments, thereby enhancing the success of energy-saving measures in buildings there [77].
Forecasting energy requirements in residential buildings is part of the effort to achieve a community of high-energy-efficient buildings. It forms the core of building energy management systems, building design optimization, and retrofit evaluation. The benefits of accurate energy forecasting cut across energy consumers, generating companies and stakeholders in the distribution line, DSOs, and aggregators. Knowing the consumption and potential future consumption empowers households to manage energy use operations efficiently.
It also allows them to participate effectively in DR programs, providing recommendations for optimal energy usage and playing their end roles in energy management. If occupants or house owners know their likely consumption at a particular time, they are better informed to take precautions to curtail it to meet the DR deal. By doing so, households can contribute to the stability of the power system and the reduction of emissions.
It is advisable to utilize forecasting recommendation systems to develop building energy management systems that optimize real-time building operations management, minimize expenses, and facilitate informed decision making. Such tools serve as valuable resources for selecting forecasting models to predict building energy consumption.
This study identified the most effective models for STLF, yet such a finding is specific to the building being examined. Based on the outcome of the performance evaluation, the most effective models can be incorporated into developing a scalable model-based recommendation system. Such a system could identify the appropriate models for energy prediction in a specific building by utilizing its historical energy data during the training process. For example, a building energy model recommendation system with a meta-learning approach to automatically identify the most effective models for various building types was introduced in [91]. This methodology minimized redundant computations and promised precise modeling outcomes.
5. Conclusions
This study focused on optimizing building STLF by performing a comparative analysis of various ML models. State-of-the-art preprocessing techniques were employed for detailed data analysis, emphasizing the crucial role of data preprocessing in the accuracy of ML models. Time-related and dummy features were engineered, transforming the dataset into a supervised learning problem. Various linear, tree-based, and gradient-boosting models were utilized for energy consumption prediction in the ITI/CERTH Smart House at different resolutions (15 min, 30 min, and 1 h).
The accuracy of selected forecasting models was evaluated based on key performance metrics and training time. Notably, the best-boosting models (HGBR, LGBMR) outperformed tree-based models (ETR) for 15 min and 1 h resolutions, while both were surpassed by RR in the 30 min resolution. The overall best performance for 1-step-ahead forecasting was observed for the resampled 30 min resolution.
Additionally, a one- vs. multistep comparison identified the most effective method for 1 h ahead forecasting. Findings showed that the 1-step-ahead resampled 1 h resolution outperformed other methods, followed by the 2-step-ahead resampled 30 min resolution. Despite the reduced dataset sizes for these resampled resolutions, they exhibited a stronger fit compared to the original 4-step-ahead forecasting target with a 15 min resolution.
In the future, testing with more diverse and vast datasets can assist in ensuring our approach’s resilience and generalizability. In a more technical context, potential areas for further research are the following:
- Improve ELF data preprocessing by tailoring it to different models and investigating model-specific challenges, such as addressing multicollinearity in linear models and handling missing data for nonlinear models.
- Explore model variability by investigating alternatives to neural network approaches while considering computational costs and dataset sizes. Also, examine the potential of stacking tree-based models, especially in scenarios with limited historical data.
- Improve the model evaluation by incorporating additional regression problem evaluation metrics, such as SMAPE and MAPE, with the aim of providing an even more comprehensive analysis.
- Include building attributes that expand beyond weather-related data for a more holistic understanding of the building’s energy consumption. Consider the type of home and its physical characteristics, the number, type, and efficiency of energy-consuming devices, and the number of occupants and their energy consumption behavior.
Author Contributions
Conceptualization, P.K., A.M. (Aristeidis Mystakidis) and A.M. (Akeem Mustapha); methodology, A.M. (Akeem Mustapha), P.K. and A.M. (Aristeidis Mystakidis); validation, P.K., A.M. (Aristeidis Mystakidis) and C.T.; formal analysis, P.K. and A.M. (Aristeidis Mystakidis); investigation, A.M. (Akeem Mustapha), P.K. and C.T.; resources, P.K.; data curation, A.M. (Aristeidis Mystakidis) and A.M. (Akeem Mustapha); writing—original draft preparation, P.K. and A.M. (Akeem Mustapha); writing—review and editing, A.M. (Aristeidis Mystakidis) and P.K.; visualization, A.M. (Akeem Mustapha); supervision, P.K.; project administration, P.K. and C.T.; funding acquisition, C.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data presented in this study are available upon request from the authors. The data are not publicly available due to working on more research analyses.
Conflicts of Interest
Researchers in School of Science and Technology, International Hellenic University.
Abbreviations
The following abbreviations are used in this manuscript:
| AI | Artificial intelligence |
| AR | Autoregressive |
| ARMA | Autoregressive moving average |
| BiLSTM | Bidirectional long short-term memory |
| CNN | Convolutional neural network |
| CVRMSE | Coefficient of the variation of the root mean square error |
| DR | Demand response |
| DRM | Demand response management |
| DSO | Distribution system operator |
| EDA | Explorative data analysis |
| EJ | Exajoule |
| ELF | Energy load forecasting |
| ETR | Extra tree regression |
| GBR | Gradient-boosting regression |
| GBM | Gradient-boosting machine |
| GWO | Grey wolf optimization |
| HGBR | Histogram gradient-boosting regression |
| HVAC | Heating, ventilating, and air-conditioning |
| IEA | International Energy Agency |
| IoT | Internet of Things |
| ITI/CERTH | Information Technologies Institute/Centre for Research and Technology |
| KNN | k-nearest neighbor |
| kWh | kiloWatt hour |
| LGBMR | Light gradient-boosting machine regressor |
| LR | Linear regression |
| LSTM | Long short-term memory network |
| LSTM/GRU | Long short-term memory network/gated recurrent unit |
| LTLF | Long-term load forecasting |
| MA | Moving average |
| MAE | Mean absolute error |
| MAPE | Mean absolute percentage error |
| MI | Mutual information |
| ML | Machine learning |
| MLP | Multilayer perceptron |
| MLR | Multiple linear regression |
| MTLF | Medium-term load forecasting |
| NRMSE | Normalized root mean square error |
| nZEB | Net-zero building |
| PV | Photovoltaic |
| RF | Random forest |
| RL | Reinforcement learning |
| RMSE | Root mean square error |
| R2 | Coefficient of determination |
| SMAPE | Symmetric mean absolute percentage error |
| STLF | Short-term load forecasting |
| SVM | Support vector machine |
| SVR | Support vector regression |
| SW | Sliding window |
| VAR | Vector autoregression |
| VSTLF | Very-short-term load forecasting |
| WEKA | Waikato Environment for Knowledge Analysis |
| XGBoost | Extreme gradient boosting |
| XGBR | Extreme gradient-boosting regressor |
References
- Shahriar, M.S.; Rahman, M.S. Urban sensing and smart home energy optimisations: A machine learning approach. In Proceedings of the IoT-App 2015—2015 International Workshop On Internet of Things Towards Applications, Co-Located with SenSys 2015, Seoul, Republic of Korea, 1 November 2015; pp. 19–22. [Google Scholar] [CrossRef]
- Himeur, Y.; Alsalemi, A.; Bensaali, F.; Amira, A. Building power consumption datasets: Survey, taxonomy and future directions. Energy Build. 2020, 227, 110404. [Google Scholar] [CrossRef]
- International Energy Agency (IEA). World Energy Outlook 2022. p. 524. Available online: https://www.iea.org/reports/world-energy-outlook-2022 (accessed on 21 January 2024).
- Cai, Q.; Xu, Q.; Qing, J.; Shi, G.; Liang, Q.M. Promoting wind and photovoltaics renewable energy integration through demand response: Dynamic pricing mechanism design and economic analysis for smart residential communities. Energy 2022, 261, 125293. [Google Scholar] [CrossRef]
- McKinsey Company. Global Energy Perspective 2022—Executive Summary. 2022. Available online: https://www.mckinsey.com/~/media/McKinsey/Industries/Oil%20and%20Gas/Our%20Insights/Global%20Energy%20Perspective%202022/Global-Energy-Perspective-2022-Executive-Summary.pdf (accessed on 8 February 2024).
- Hong, T.; Fan, S. Probabilistic electric load forecasting: A tutorial review. Int. J. Forecast. 2016, 32, 914–938. [Google Scholar] [CrossRef]
- Koukaras, P.; Tjortjis, C.; Gkaidatzis, P.; Bezas, N.; Ioannidis, D.; Tzovaras, D. An interdisciplinary approach on efficient virtual microgrid to virtual microgrid energy balancing incorporating data preprocessing techniques. Computing 2021, 104, 209–250. [Google Scholar] [CrossRef]
- Koukaras, P.; Bezas, N.; Gkaidatzis, P.; Ioannidis, D.; Tzovaras, D.; Tjortjis, C. Introducing a novel approach in one-step ahead energy load forecasting. Sustain. Comput. Inform. Syst. 2021, 32, 100616. [Google Scholar] [CrossRef]
- Shakeri, M.; Shayestegan, M.; Abunima, H.; Reza, S.M.; Akhtaruzzaman, M.; Alamoud, A.R.; Sopian, K.; Amin, N. An intelligent system architecture in home energy management systems (HEMS) for efficient demand response in smart grid. Energy Build. 2017, 138, 154–164. [Google Scholar] [CrossRef]
- Ahmad, T.; Zhang, H.; Yan, B. A review on renewable energy and electricity requirement forecasting models for smart grid and buildings. Sustain. Cities Soc. 2020, 55, 102052. [Google Scholar] [CrossRef]
- Koukaras, P.; Berberidis, C.; Tjortjis, C. A Semi-supervised Learning Approach for Complex Information Networks. In Intelligent Data Communication Technologies and Internet of Things; Hemanth, J., Bestak, R., Chen, J.I.Z., Eds.; Springer: Singapore, 2021; pp. 1–13. [Google Scholar] [CrossRef]
- Himeur, Y.; Alsalemi, A.; Al-Kababji, A.; Bensaali, F.; Amira, A.; Sardianos, C.; Dimitrakopoulos, G.; Varlamis, I. A survey of recommender systems for energy efficiency in buildings: Principles, challenges and prospects. Inf. Fusion 2021, 72, 1–21. [Google Scholar] [CrossRef]
- Mystakidis, A.; Ntozi, E.; Afentoulis, K.; Koukaras, P.; Giannopoulos, G.; Bezas, N.; Gkaidatzis, P.A.; Ioannidis, D.; Tjortjis, C.; Tzovaras, D. One Step Ahead Energy Load Forecasting: A Multi-Model Approach Utilizing Machine and Deep Learning. In Proceedings of the 2022 57th International Universities Power Engineering Conference (UPEC), Istanbul, Turkey, 30 August–2 September 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Lazzari, F.; Mor, G.; Cipriano, J.; Gabaldon, E.; Grillone, B.; Chemisana, D.; Solsona, F. User behaviour models to forecast electricity consumption of residential customers based on smart metering data. Energy Rep. 2022, 8, 3680–3691. [Google Scholar] [CrossRef]
- Langevin, A.; Cheriet, M.; Gagnon, G. Efficient deep generative model for short-term household load forecasting using non-intrusive load monitoring. Sustain. Energy Grids Netw. 2023, 34, 101006. [Google Scholar] [CrossRef]
- Baker, K.J.; Rylatt, R.M. Improving the prediction of UK domestic energy-demand using annual consumption-data. Appl. Energy 2008, 85, 475–482. [Google Scholar] [CrossRef]
- Brounen, D.; Kok, N.; Quigley, J.M. Residential energy use and conservation: Economics and demographics. Eur. Econ. Rev. 2012, 56, 931–945. [Google Scholar] [CrossRef]
- Urquizo, J.; Calderón, C.; James, P. Metrics of urban morphology and their impact on energy consumption: A case study in the United Kingdom. Energy Res. Soc. Sci. 2017, 32, 193–206. [Google Scholar] [CrossRef]
- Jones, R.V.; Lomas, K.J. Determinants of high electrical energy demand in UK homes: Socio-economic and dwelling characteristics. Energy Build. 2015, 101, 24–34. [Google Scholar] [CrossRef]
- Zhao, H.X.; Magoulès, F. A review on the prediction of building energy consumption. Renew. Sustain. Energy Rev. 2012, 16, 3586–3592. [Google Scholar] [CrossRef]
- Dhar, A.; Reddy, T.A.; Clarid, D.E. A Fourier series model to predict hourly heating and cooling energy use in commercial buildings with outdoor temperature as the only weather variable. J. Sol. Energy Eng. 1999, 121, 47–53. [Google Scholar] [CrossRef]
- White, J.; Reichmuth, R. Simplified method for predicting building energy consumption using average monthly temperatures. In Proceedings of the IECEC 96, 31st Intersociety Energy Conversion Engineering Conference, Washington, DC, USA, 11–16 August 1996; Volume 3, pp. 1834–1839. [Google Scholar] [CrossRef]
- Westphal, F.S.; Lamberts, R. The use of simplified weather data to estimate thermal loads of non-residential buildings. Energy Build. 2004, 36, 847–854. [Google Scholar] [CrossRef]
- Al-Shargabi, A.A.; Almhafdy, A.; Ibrahim, D.M.; Alghieth, M.; Chiclana, F. Buildings’ energy consumption prediction models based on buildings’ characteristics: Research trends, taxonomy, and performance measures. J. Build. Eng. 2022, 54, 104577. [Google Scholar] [CrossRef]
- Tsanas, A.; Xifara, A. Accurate quantitative estimation of energy performance of residential buildings using statistical machine learning tools. Energy Build. 2012, 49, 560–567. [Google Scholar] [CrossRef]
- Cetin, K.S.; Tabares-Velasco, P.C.; Novoselac, A. Appliance daily energy use in new residential buildings: Use profiles and variation in time-of-use. Energy Build. 2014, 84, 716–726. [Google Scholar] [CrossRef]
- Ruellan, M.; Park, H.; Bennacer, R. Residential building energy demand and thermal comfort: Thermal dynamics of electrical appliances and their impact. Energy Build. 2016, 130, 46–54. [Google Scholar] [CrossRef]
- Candanedo, L.M.; Feldheim, V.; Deramaix, D. Data driven prediction models of energy use of appliances in a low-energy house. Energy Build. 2017, 140, 81–97. [Google Scholar] [CrossRef]
- Bezzar, N.E.H.; Laimeche, L.; Meraoumia, A.; Houam, L. Data analysis-based time series forecast for managing household electricity consumption. Demonstr. Math. 2022, 55, 900–921. [Google Scholar] [CrossRef]
- Hong, T.; Pinson, P.; Wang, Y.; Weron, R.; Yang, D.; Zareipour, H. Energy Forecasting: A Review and Outlook. IEEE Open Access J. Power Energy 2020, 7, 376–388. [Google Scholar] [CrossRef]
- Zhao, H. Artificial Intelligence Models for Large Scale Buildings Energy Consumption Analysis. Ph.D. Thesis, Ecole Centrale, Paris, France, 2011. [Google Scholar]
- Elbeltagi, E.; Wefki, H. Predicting energy consumption for residential buildings using ANN through parametric modeling. Energy Rep. 2021, 7, 2534–2545. [Google Scholar] [CrossRef]
- Liu, T.; Tan, Z.; Xu, C.; Chen, H.; Li, Z. Study on deep reinforcement learning techniques for building energy consumption forecasting. Energy Build. 2020, 208, 109675. [Google Scholar] [CrossRef]
- Wu, D.; Wang, B.; Precup, D.; Boulet, B. Multiple Kernel Learning-Based Transfer Regression for Electric Load Forecasting. IEEE Trans. Smart Grid 2020, 11, 1183–1192. [Google Scholar] [CrossRef]
- Arora, S.; Taylor, J.W. Rule-based autoregressive moving average models for forecasting load on special days: A case study for France. Eur. J. Oper. Res. 2018, 266, 259–268. [Google Scholar] [CrossRef]
- Guan, C.; Luh, P.B.; Michel, L.D.; Wang, Y.; Friedland, P.B. Very short-term load forecasting: Wavelet neural networks with data pre-filtering. IEEE Trans. Power Syst. 2013, 28, 30–41. [Google Scholar] [CrossRef]
- Jacob, M.; Neves, C.; Greetham, D.V. Forecasting and Assessing Risk of Individual Electricity Peaks; Springer Nature: Berlin/Heidelberg, Germany, 2020; Volume 1, pp. 1–161. [Google Scholar] [CrossRef]
- Abu-Shikhah, N.; Elkarmi, F. Medium-term electric load forecasting using singular value decomposition. Energy 2011, 36, 4259–4271. [Google Scholar] [CrossRef]
- Daneshi, H.; Shahidehpour, M.; Choobbari, A.L. Long-term load forecasting in electricity market. In Proceedings of the 2008 IEEE International Conference on Electro/Information Technology, IEEE EIT 2008 Conference, Rochester, MI, USA, 3–5 May 2008; pp. 395–400. [Google Scholar] [CrossRef]
- Ruiz-Abellón, M.C.; Fernández-Jiménez, L.A.; Guillamón, A.; Falces, A.; García-Garre, A.; Gabaldón, A. Integration of demand response and short-term forecasting for the management of prosumers’ demand and generation. Energies 2019, 13, 11. [Google Scholar] [CrossRef]
- Zheng, Z.; Chen, H.; Luo, X. A Kalman filter-based bottom-up approach for household short-term load forecast. Appl. Energy 2019, 250, 882–894. [Google Scholar] [CrossRef]
- Shaikh, A.K.; Nazir, A.; Khan, I.; Shah, A.S. Short term energy consumption forecasting using neural basis expansion analysis for interpretable time series. Sci. Rep. 2022, 12, 22562. [Google Scholar] [CrossRef] [PubMed]
- Bacher, P.; Madsen, H.; Nielsen, H.A. Online short-term heat load forecasting for single family houses. In Proceedings of the IECON Proceedings (Industrial Electronics Conference), Brussels, Belgium, 17–20 October 2013; pp. 5741–5746. [Google Scholar] [CrossRef]
- Sandels, C.; Widén, J.; Nordström, L.; Andersson, E. Day-ahead predictions of electricity consumption in a Swedish office building from weather, occupancy, and temporal data. Energy Build. 2015, 108, 279–290. [Google Scholar] [CrossRef]
- Kavousian, A.; Rajagopal, R.; Fischer, M. Determinants of residential electricity consumption: Using smart meter data to examine the effect of climate, building characteristics, appliance stock, and occupants’ behavior. Energy 2013, 55, 184–194. [Google Scholar] [CrossRef]
- Kavousian, A.; Rajagopal, R.; Fischer, M. Ranking appliance energy efficiency in households: Utilizing smart meter data and energy efficiency frontiers to estimate and identify the determinants of appliance energy efficiency in residential buildings. Energy Build. 2015, 99, 220–230. [Google Scholar] [CrossRef]
- Lee, Y.J.; Choi, H.J. Forecasting building electricity power consumption using deep learning approach. In Proceedings of the 2020 IEEE International Conference on Big Data and Smart Computing, BigComp, Busan, Republic of Korea, 19–22 February 2020; pp. 542–544. [Google Scholar] [CrossRef]
- Fayaz, M.; Kim, D. A prediction methodology of energy consumption based on deep extreme learning machine and comparative analysis in residential buildings. Electronics 2018, 7, 222. [Google Scholar] [CrossRef]
- Bilal, M.; Kim, H.; Fayaz, M.; Pawar, P. Comparative Analysis of Time Series Forecasting Approaches for Household Electricity Consumption Prediction. arXiv 2022, arXiv:2207.01019. Available online: http://arxiv.org/abs/2207.01019 (accessed on 15 January 2024).
- Tabasi, S.; Aslani, A.; Forotan, H. Prediction of Energy Consumption by Using Regression Model. Comput. Res. Prog. Appl. Sci. Eng. 2016, 2, 110–115. Available online: https://www.crpase.com/archive/CRPASE-2016-VOL%2002-ISSUE%2003-04.pdf (accessed on 8 February 2024).
- Belaïd, F. Understanding the spectrum of domestic energy consumption: Empirical evidence from France. Energy Policy 2016, 92, 220–233. [Google Scholar] [CrossRef]
- Huebner, G.; Shipworth, D.; Hamilton, I.; Chalabi, Z.; Oreszczyn, T. Understanding electricity consumption: A comparative contribution of building factors, socio-demographics, appliances, behaviours and attitudes. Appl. Energy 2016, 177, 692–702. [Google Scholar] [CrossRef]
- Zhuang, D.; Gan, V.J.; Tekler, Z.D.; Chong, A.; Tian, S.; Shi, X. Data-driven predictive control for smart HVAC system in IoT-integrated buildings with time-series forecasting and reinforcement learning. Appl. Energy 2023, 338, 120936. [Google Scholar]
- Deng, X.; Ye, A.; Zhong, J.; Xu, D.; Yang, W.; Song, Z.; Zhang, Z.; Guo, J.; Wang, T.; Tian, Y.; et al. Bagging–XGBoost algorithm based extreme weather identification and short-term load forecasting model. Energy Rep. 2022, 8, 8661–8674. [Google Scholar] [CrossRef]
- Sekhar, C.; Dahiya, R. Robust framework based on hybrid deep learning approach for short term load forecasting of building electricity demand. Energy 2023, 268, 126660. [Google Scholar]
- Fumo, N.; Biswas, M.A.R. Regression analysis for prediction of residential energy consumption. Renew. Sustain. Energy Rev. 2015, 47, 332–343. [Google Scholar] [CrossRef]
- Morris, J.; Allinson, D.; Harrison, J.; Lomas, K.J. Benchmarking and tracking domestic gas and electricity consumption at the local authority level. Energy Effic. 2016, 9, 723–743. [Google Scholar] [CrossRef][Green Version]
- Lorimer, S. A housing stock model of non-heating end-use energy in England verified by aggregate energy use data. Energy Policy 2012, 50, 419–427. [Google Scholar] [CrossRef][Green Version]
- Maltais, L.G.; Gosselin, L. Forecasting of short-term lighting and plug load electricity consumption in single residential units: Development and assessment of data-driven models for different horizons. Appl. Energy 2022, 307, 118229. [Google Scholar] [CrossRef]
- Koukaras, P.; Gkaidatzis, P.; Bezas, N.; Bragatto, T.; Carere, F.; Santori, F.; Antal, M.; Ioannidis, D.; Tjortjis, C.; Tzovaras, D. A Tri-Layer Optimization Framework for Day-Ahead Energy Scheduling Based on Cost and Discomfort Minimization. Energies 2021, 14, 3599. [Google Scholar] [CrossRef]
- Palacios-García, E.J.; Moreno-Munoz, A.; Santiago, I.; Flores-Arias, J.M.; Bellido-Outeiriño, F.J.; Moreno-Garcia, I.M. Modeling human activity in Spain for different economic sectors: The potential link between occupancy and energy usage. J. Clean. Prod. 2018, 183, 1093–1109. [Google Scholar] [CrossRef]
- ITI-CERTH. ITI Smart Home, a Digital Innovation Hub powered by ITI/CERTH. Available online: Https://smarthome.iti.gr (accessed on 5 October 2023).
- Géron, A. Hands-on Machine Learning with Scikit-Learn, Keras, and TensorFlow (2019, O’reilly); O’Reilly Media: Sebastopol, MA, USA, 2019; p. 510. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar] [CrossRef]
- Ramos, D.; Teixeira, B.; Faria, P.; Gomes, L.; Abrishambaf, O.; Vale, Z. Using diverse sensors in load forecasting in an office building to support energy management. Energy Rep. 2020, 6, 182–187. [Google Scholar] [CrossRef]
- John, P.M.; Massaron, L. Machine Learning for Dummies, 2nd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2021; pp. 1–467. [Google Scholar]
- Hoerl, A.E.; Kennard, R.W. Ridge regression: Biased estimation for nonorthogonal problems. Technometrics 1970, 12, 55–67. [Google Scholar] [CrossRef]
- Asadi, M.; TaghaviGhalesari, A.; Kumar, S. Machine learning techniques for estimation of Los Angeles abrasion value of rock aggregates. Eur. J. Environ. Civ. Eng. 2022, 26, 964–977. [Google Scholar] [CrossRef]
- Rambabu, M.; Ramakrishna, N.; Polamarasetty, P.K. Prediction and Analysis of Household Energy Consumption by Machine Learning Algorithms in Energy Management. E3S Web Conf. 2022, 350, 02002. [Google Scholar] [CrossRef]
- Gassar, A.A.A.; Yun, G.Y.; Kim, S. Data-driven approach to prediction of residential energy consumption at urban scales in London. Energy 2019, 187, 115973. [Google Scholar] [CrossRef]
- Touzani, S.; Granderson, J.; Fernandes, S. Gradient boosting machine for modeling the energy consumption of commercial buildings. Energy Build. 2018, 158, 1533–1543. [Google Scholar] [CrossRef]
- Robinson, C.; Dilkina, B.; Hubbs, J.; Zhang, W.; Guhathakurta, S.; Brown, M.A.; Pendyala, R.M. Machine learning approaches for estimating commercial building energy consumption. Appl. Energy 2017, 208, 889–904. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy Function Approximation: A Gradient Boosting Machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Yu, H.F.; Lo, H.Y.; Hsieh, H.P.; Lou, J.K.; McKenzie, T.G.; Chou, J.W.; Chung, P.H.; Ho, C.H.; Chang, C.F.; Wei, Y.H.; et al. Feature engineering and classifier ensemble for KDD cup 2010. In Proceedings of the JMLR: Workshop and Conference Proceedings, Sardinia, Italy, 13–15 May 2010; pp. 1–12. Available online: https://pslcdatashop.web.cmu.edu/KDDCup/workshop/papers/kdd2010ntu.pdf (accessed on 8 February 2024).
- Sepulveda, L.F.; Diniz, P.S.; Diniz, J.O.; Netto, S.M.; Cipriano, C.L.; Araújo, A.C.; Lemos, V.H.; Pessoa, A.C.; Quintanilha, D.B.; Almeida, J.D.; et al. Forecasting of individual electricity consumption using Optimized Gradient Boosting Regression with Modified Particle Swarm Optimization. Eng. Appl. Artif. Intell. 2021, 105, 104440. [Google Scholar] [CrossRef]
- Sun, Y.; Haghighat, F.; Fung, B.C. A review of the-state-of-the-art in data-driven approaches for building energy prediction. Energy Build. 2020, 221, 110022. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A scalable tree boosting system. In Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar] [CrossRef]
- Zou, H.; Hastie, T. Regularization and variable selection via the elastic net. J. R. Stat. Soc. Ser. B (Stat. Methodol.) 2005, 67, 301–320. [Google Scholar] [CrossRef]
- Efron, B.; Hastie, T.; Johnstone, I.; Tibshirani, R. Least angle regression. Ann. Stat. 2004, 32, 407–499. [Google Scholar] [CrossRef]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.Y. LightGBM: A Highly Efficient Gradient Boosting Decision Tree. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; Guyon, I., Luxburg, U.V., Bengio, S., Wallach, H., Fergus, R., Vishwanathan, S., Garnett, R., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2017; Volume 30. Available online: https://api.semanticscholar.org/CorpusID:3815895 (accessed on 8 February 2024).
- Prokhorenkova, L.; Gusev, G.; Vorobev, A.; Dorogush, A.V.; Gulin, A. CatBoost: Unbiased boosting with categorical features. Adv. Neural Inf. Process. Syst. 2018, 31. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Geurts, P.; Ernst, D.; Wehenkel, L. Extremely randomized trees. Mach. Learn. 2006, 63, 3–42. [Google Scholar] [CrossRef]
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef]
- MacKay, D.J.C. Bayesian interpolation. Neural Comput. 1992, 4, 415–447. [Google Scholar] [CrossRef]
- Mystakidis, A.; Stasinos, N.; Kousis, A.; Sarlis, V.; Koukaras, P.; Rousidis, D.; Kotsiopoulos, I.; Tjortjis, C. Predicting COVID-19 ICU needs using deep learning, XGBoost and random forest regression with the sliding window technique. IEEE Smart Cities 2021. Available online: https://smartcities.ieee.org/newsletter/july-2021/predicting-covid-19-icu-needs-using-deep-learning-xgboost-and-random-forest-regression-with-the-sliding-window-technique (accessed on 20 January 2024).
- Reyes, C.; Hilaire, T.; Paul, S.; Mecklenbräuker, C.F. Evaluation of the root mean square error performance of the PAST-consensus algorithm. In Proceedings of the 2010 International ITG Workshop on Smart Antennas, WSA, Bremen, Germany, 23–24 February 2010; pp. 156–160. [Google Scholar] [CrossRef]
- Mystakidis, A.; Ntozi, E.; Afentoulis, K.; Koukaras, P.; Gkaidatzis, P.; Ioannidis, D.; Tjortjis, C.; Tzovaras, D. Energy generation forecasting: Elevating performance with machine and deep learning. Computing 2023, 105, 1623–1645. [Google Scholar] [CrossRef]
- Reikard, G. Predicting solar radiation at high resolutions: A comparison of time series forecasts. Sol. Energy 2009, 83, 342–349. [Google Scholar] [CrossRef]
- Wu, X.; Shi, B.; Dong, Y.; Huang, C.; Faust, L.; Chawla, N.V. RESTFul: Resolution-Aware Forecasting of Behavioral Time Series Data. In Proceedings of the 27th ACM International Conference on Information and Knowledge Management, CIKM ’18, Torino, Italy, 22–26 October 2018; pp. 1073–1082. [Google Scholar] [CrossRef]
- Cui, C.; Wu, T.; Hu, M.; Weir, J.D.; Li, X. Short-term building energy model recommendation system: A meta-learning approach. Appl. Energy 2016, 172, 251–263. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).