Abstract
Due to concerns with air pollution and climate change, governments and transport operators around the world have engaged in transforming their fossil-fueled vehicles into electric vehicles (EVs). It is essential to build a model for the electrifying process to minimize the operation costs. This paper presents a systematic analytical approach for the electrification of a fire ambulance service station. This approach begins with the selection of suitable EVs to replace the current service vehicles. Subsequently, an in-depth analysis is conducted to determine the practical utilization of EVs at the station. The model proposes two charging strategies: immediate charging upon an EVs’ return and smart charging. Based on the chosen EVs and charging strategies, a comprehensive assessment of the load profiles for the planned EV charging station is performed. In accordance with the load profiles, a mathematical model to minimize the infrastructure and operation costs of the charging station is proposed. Various pricing schemes are compared to identify the most efficient pricing scheme for the charging station, and economic analyses of the EVs and traditional ambulance vehicles are proposed in this paper. The test results indicate that the progressive pricing scheme is well suited for immediate charging strategies, whereas smart charging should opt for the time-of-use pricing scheme. Selecting the appropriate pricing scheme has the potential to significantly reduce electric energy costs.
1. Introduction
Cars, trucks, homes, and factories all contribute to climate change by burning fossil fuels in numerous engines, furnaces, and boilers, emitting pollution that exacerbates global warming. To effectively address climate change, these machines must cease their polluting activities. Increasingly, experts advocate for replacing them with electric alternatives—vehicles, heating systems, and factories powered by clean sources such as wind, solar, or nuclear energy. In this envisioned future, a significantly larger portion of America’s energy would be derived from electricity. Moreover, overall energy consumption would decrease as electric devices tend to be more efficient than those relying on fossil fuels. For instance, while a gasoline-powered car only utilizes about 30 percent of the energy in its fuel to propel its wheels, with the majority lost as heat, an electric car utilizes around 80 percent of its energy. There are indications that the United States is already shifting towards a more electrified future. Electric vehicle sales reached record highs last year, constituting 5.8 percent of new car sales, and the administration has proposed regulations to ensure they comprise two-thirds of sales by 2032 [1].
The electrification of transportation is an essential step to reduce the air pollution. Many countries have committed to transforming their fossil-fueled vehicles into electric vehicles. In general, the electrification of transportation can be divided into three groups: official vehicles, bus fleets of bus companies, and private vehicles. The term ‘official vehicles’ refers to vehicles utilized by public-sector entities. Electrification needs to consider the operational characteristics of these vehicles and the infrastructure required. The planning of electric official vehicles should consider their duties when selecting suitable types of EVs and determining charging schemes. Electrifying buses requires a consideration of various factors, such as meeting the original service schedules, selecting charging facilities, and determining charging schedules. Private vehicle electrification allows the option of charging at home or at public charging stations.
Bus operators worldwide are encountering the transition of their fleets from fossil-fueled to electric buses. A simulation tool based on discrete event simulation to determine the vehicle, charging infrastructure, energy, and staff demand required to electrify real-world bus networks was proposed in [2]. The obtained simulation results were subsequently fed into a total cost of ownership (TCO) model. The TCO calculation demonstrated that opportunity charging has a slight cost advantage over depot charging. In [3], a method is proposed to calculate the total cost of ownership for different types of electric buses. In this model, the operating cost comprises the sum of the driver cost, energy cost, maintenance and insurance costs, and electric grid fees. The investment cost is determined based on the depreciation of chargers, batteries, and buses. The paper analyzes two charging strategies for electric buses: end stop charging, where buses are charged at the end stops, and end stop off-peak charging, where buses are charged at the end stops throughout the day except during peak hours. The method will help in identifying ways to reduce costs.
In order to enhance the cost competitiveness of electrification, it is essential to optimize the design of the battery pack and charging infrastructure to meet the specific operating conditions. A method was proposed in [4] to minimize the TCO for an electric bus fleet by selecting the optimal battery size, number of charging stations, and charging power. Energy consumption and battery aging behavior are considered, while ensuring SOC-neutral operation. The total cost of ownership for two bus depots was analyzed in [5]. Two different approaches were examined for both route planning and charging scheduling, allowing for a quantification of their respective impacts on the total costs. The test results demonstrate that optimized scheduling can have a substantial impact on costs, underscoring the importance of intelligent management systems for future electric bus depots.
A coordinated utility–transit problem formulation for the optimal design of battery electric bus systems is proposed in [6]. The proposed algorithm considers the operation requirements of both power distribution and transit networks. A real-world transit system was used to verify the proposed model. A systematic and effective approach for the feasibility check and configuration design of electrified public bus transit fleets without a complicated optimization tool is proposed in [7]. The aim is to determine the number of electric buses and their on-board battery capacities to meet the transportation service schedule. Based on the power demand profile of the public bus transit fleets, a lifecycle cost analysis is conducted to compare the electric bus options with their diesel counterparts.
Several studies [8,9,10] have concentrated on optimizing the interaction between EV charging load, renewable energy, and energy storage systems (ESS). A planning decision model for charging stations and ESS, co-optimized with a route aggregation strategy and considering uncertainties in renewable generation, is proposed in [8]. The proposed model incorporates operational energy management schemes for PV, ESS, and other components, and its effectiveness is demonstrated through numerical tests. Another study introduces day-ahead charging and discharging strategies for an electric bus charging station equipped with an energy storage system [9]. The simulation results indicate that integrating ESS enables the charging station to shift the load to off-peak periods, thereby reducing daily operational costs. Furthermore, a planning method for a fast-charging station integrated with PV and ESS in urban areas is proposed [10]. Firstly, a charging demand estimation method based on average driving speeds and multi-agent simulation is presented. Subsequently, a distributionally robust optimization (DRO) planning model, utilizing the Wasserstein metric, is developed to determine the capacities of PV and ESS.
With the increasing popularity of electric vehicles, many experts and scholars are concerned about the impact on the power grid when a large number of electric vehicles charge simultaneously. The impacts of the expected EV rollout on fuel changes, energy costs, CO2 emission reduction, and network investments in the UK are proposed in [11]. Different EV charging strategies of the expected large-scale penetration of EVs are also estimated. Test results show that smart charging and the location of EV charging have great impacts on network reinforcement costs. The impact of EVs on urban and rural distribution networks are evaluated in [12]. A wide range of practical operating scenarios are considered in this paper. The thermal capacity of the network is found to be the primary limiting factor, while voltage is the second main reason for both medium-density urban and short rural networks. A model for optimizing the charging schedule of a fleet of battery electric buses has been developed in [13]. This approach minimizes the charging costs of electric bus fleets while also accounting for battery aging and participation in vehicle-to-grid schemes. Test results suggest that, when the battery replacement cost is below a threshold of EUR 100/kWh, it may become economically viable for public transportation operators to sell excess energy back to the grid under a specific remuneration scheme.
Impacts of EV charging uncertainties on the EV charging power control participating in supplementary frequency stabilization from the perspectives of both the utility and the EV owner are investigated in [14]. The test results indicate that the number of participating EVs is the most influential parameter for frequency stabilization capability, followed by the rated charging power of EV. From the EV owner’s perspective, the energy capacity is the dominant parameter affecting the expected EV energy variance, followed by the remaining energy and available charging time. The endogenous relationships among EVs, EV charging piles, and public attention are investigated in [15]. Life cost analyses of electric and diesel bus transits are proposed in [16,17,18]. The total cost of ownership, energy efficiency, and carbon dioxide emissions are compared in these studies.
Currently, most of the literature focuses on the planning and impact analysis of electric bus charging stations and public charging stations. Few studies have addressed the electrification of official vehicles. This paper aims to fill this research gap by proposing a framework for electrifying fire ambulance vehicles. A systematic analysis approach is proposed, encompassing two charging strategies: immediate charging for returning EVs and smart charging. The first step involves selecting the appropriate type of electric vehicle to fulfill ambulance duties. Additionally, the site’s spatial arrangement needs to be considered to accommodate the charging stations and electric ambulance vehicles. Subsequently, historical practical service data on the ambulance vehicles are analyzed to estimate the load profile of the charging station after electrification. Based on the load profile, a mathematical model to minimize the infrastructure and operation costs of the charging station is proposed, and the most suitable electricity billing options for two charging strategies are identified. Additionally, economic analyses of the EVs and traditional ambulance vehicles are demonstrated in this paper.
2. The Proposed Model
Different types of transportation electrification entail distinct considerations. Electrifying bus stations requires evaluating service schedules and routes to determine the optimal placement of buses and chargers, along with devising a charging strategy aimed at minimizing overall costs, as demonstrated in [2,3,4,5,6,7,8,9,10]. Planning public electric charging stations for private EVs necessitates accounting for the unpredictable behaviors of vehicles. The randomness of EV behavior can be modeled using probability distribution functions, as illustrated in [19,20,21].
The fire ambulance service station operates with random and emergent characteristics. Security concerns must be incorporated into the planning process. A model of electrifying a fire ambulance service vehicles’ station is proposed in this section. The analytic process is demonstrated in Figure 1. A detailed description is shown below.
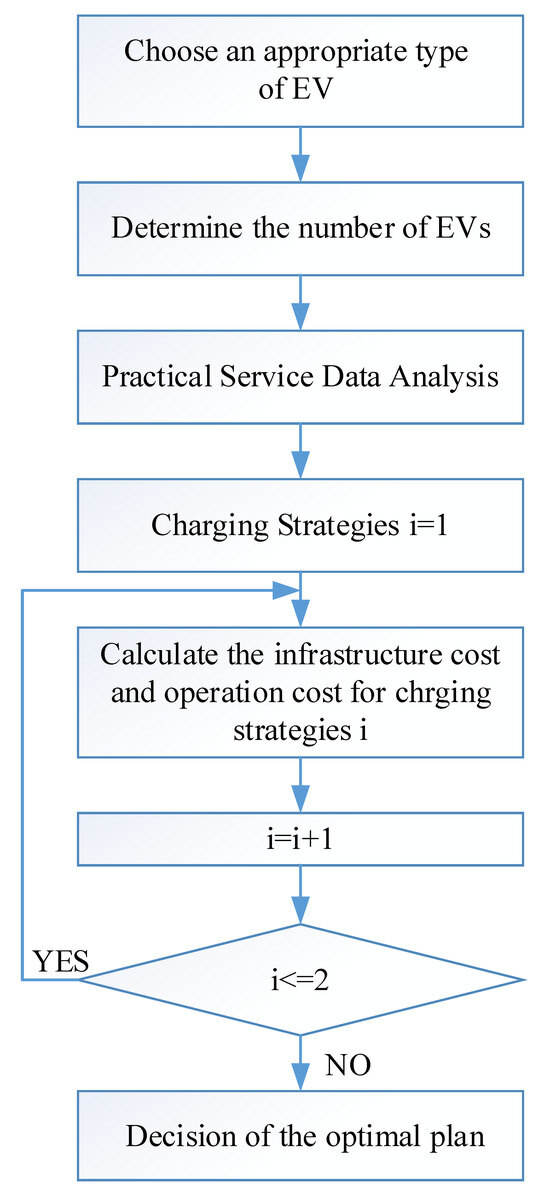
Figure 1.
The proposed model.
- 1.
- Choosing an appropriate type of EV
In 2020, Opel officially launched the Vivaro electric van, known as ‘Vivaro-e’, in the German market. The vehicle is powered by a front-mounted electric motor with a maximum output of 136 horsepower and a torque of up to 260 Nm. It can reach a top speed of 130 km per hour. The innovative 2-seat passenger bench enhances Vivaro-e’s flexibility, providing a highly competitive load volume of up to 6.6 m3 and maximum load length of up to 4 m. The standard payload is 1000 kg. Equipped with dual electric sliding doors and sensor-operated hands-free access, opening your Vivaro-e with full hands and accessing its vast load space has never been more effortless. According to the function of the ambulance vehicle, the electric vehicle Opel Vivaro-e is selected to replace the original one. Opel Vivaro-e is available with a 50 kWh battery for a range of up to 230 km. Its on-board charging power is 7.4 kW. Its energy consumption is 0.21 kWh/km [22]. This vehicle’s space and drivable distance are well suited for its use as a fire ambulance vehicle.
- 2.
- Determining the number of EVs and the infrastructure of the charging station
Different numbers of EVs will affect the infrastructure of the charging station and the charging cost. According to the land area of the site and the task needed to be performed, the minimal and maximal number of EVs are determined first. The infrastructure of this charging station and charging scheme are determined for each number of EVs. Considering this, we maintained the current quantity of electric fire ambulance vehicles after taking into account operational and site-related factors.
- 3.
- Practical service data analysis
The analysis includes the total service distance and number of services, as well as the minimum, average, maximum, and standard deviation of service distances for the three existing fire ambulance vehicles over the course of one year. Based on these analyzed service data and charging strategies, the load profile of the charging station can be derived. Detailed results are presented in the test results section.
- 4.
- Charging strategies
The model considers two charging strategies for electric ambulance vehicles: recharging them immediately upon return (Strategy 1) and recharging them during off-peak periods (Strategy 2).
- 5.
- Deciding the optimal plan
The objective function is to minimize the infrastructure cost and operation cost, as shown in Equation (1), for two charging strategies. The constraints contain the land area limitation and maintain a charging load not exceeding the rating capacity of the transformer.
where N represents the number of vehicles, VArea is the area of vehicles, Land Area indicates the area of the charging station, and Trrating is the rating capacity of the transformer.
The operation cost is related to the electricity rating scheme. There are three electricity rating schemes for the low-voltage customers in Taiwan. These three schemes are described below.
Scheme 1:
Scheme 1 employs a monthly progressive rating system. The progressive ranges are shown in Table 1. Equation (2) demonstrates the electricity cost of an energy consumption of 350 kWh in summer using scheme 1’s rating system.

Table 1.
The rating system of scheme 1.
Scheme 2:
Scheme 2 is a time-of-use rating system with two-stage electricity prices, as shown in Table 2. The peak price is NTD 4.44/kWh and NTD 4.23/kWh in the summer months and non-summer months, respectively, while the off-peak price is NTD 1.80/kWh and NTD 1.73/kWh in the summer months and non-summer months, respectively. The electricity cost is the sum of energy consumption multiplied by the corresponding electricity price in each time period.

Table 2.
The rating system of scheme 2.
Scheme 3:
Scheme 3 is a time-of-use rating system with three-stage electricity prices, as shown in Table 3. Peak, half peak, and off-peak periods are demonstrated in Table 3. For example, the peak period involves the time interval of 10:00~12:00 and 13:00~17:00 from Monday to Friday in the summer months.

Table 3.
The rating system of scheme 3.
3. Test Results
Electrifying fossil-fueled vehicles is in its initial stages in Taiwan, with the government calling upon public sectors to take the lead. An illustrative case is the transformation of a small fire department located in the township of Kaohsiung City. The first step involves the conversion of three fire ambulance vehicles within this department into electrically powered vehicles. This section presents the outcomes of electrifying these emergency vehicles, followed by an economic analysis comparing the electric vehicles (EVs) with the current usage of three traditional ambulance vehicles.
3.1. Test Results of the Electrification Process
3.1.1. Determining the Number of Electric Fire Ambulance Vehicles
As described in the proposed model, the number of vehicles should be determined first. Due to the security concern and randomness of the emergency call, the number of electric vehicles is maintained as the original number to satisfy the public requirements. Because the size of the selected EV is similar to that of the current vehicle, the original parking lot is capable of accommodating these three electric vehicles.
3.1.2. Determining the Best Rating Scheme to Minimize the Charging Cost
Table 4 shows the total service distance and service numbers, as well as the minimum, average, maximum, and standard deviation of service distances for the three current fire ambulance vehicles over the course of one year. The Opel Vivaro-e EV, capable of traveling up to 230 km on a single charge, exceeds the maximum service distance covered by the current three ambulance vehicles. The average distance for each service is 27.74 km and the energy consumption of the Opel Vivaro-e EV is 0.21 kWh/km; hence, the average energy consumption for each service duty is 5.82 kWh. The oil cost of these three fire ambulance vehicles in one year is NTD 63,340 (2010.8 USD). Figure 2 depicts the cumulative count of returning fire ambulance vehicles per hour for each month, while Figure 3 illustrates the average energy consumption per hour for each month. It is evident that fewer rescue service requests occur before dawn, with a significant increase in emergency service calls during the night.

Table 4.
The total service distance and service numbers, and the minimal, average, maximal, and standard deviation of the service distance of the current three fire ambulance vehicles in one year.

Figure 2.
The cumulative count of returning fire ambulance vehicles per hour for each month.
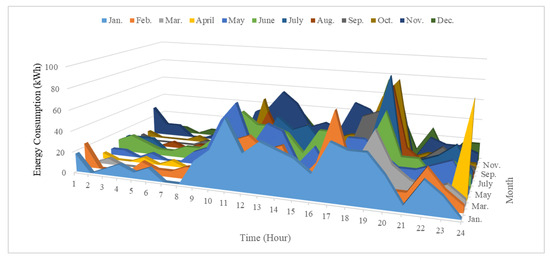
Figure 3.
The average energy consumption per hour for each month.
In the proposed model, two charging strategies for electric ambulance vehicles are analyzed: recharging them immediately upon return (Strategy 1) and recharging them during off-peak periods (Strategy 2). Strategy 1 ensures that fire service vehicles are promptly ready to meet emergency requirements. From the usage data statistics on ambulance vehicles presented in Table 4, it is observed that the average energy consumption for each service duty is 5.82 kWh, with an average number of daily missions per vehicle ranging from one to two times. Considering the battery size of the vehicles (50 kWh), it is reasonable to adopt Strategy 2 to minimize charging costs. The electricity costs associated with three candidate rating systems of two charging strategies are presented below.
- The energy cost of the scheme 1 rating system
Figure 4 shows the accumulated energy consumption for each month. The electricity cost for each month can be calculated based on the progressive rating for each month shown in Table 1. As scheme 1 does not employ a time-of-use rating system, the energy costs for charging strategies 1 and 2 are identical. Figure 5 illustrates the energy costs associated with these two charging strategies for each month. The total energy cost for one year amounts to NTD 12,986 (USD 412.254).

Figure 4.
Accumulated energy consumption for each month.
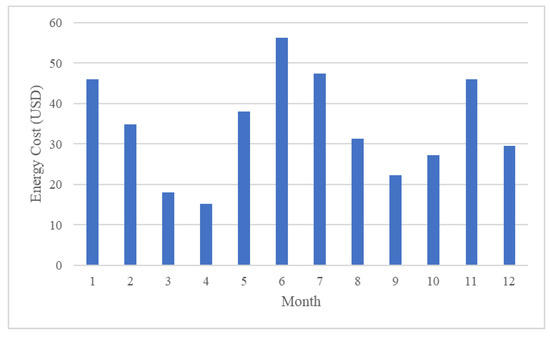
Figure 5.
Accumulated energy cost for each month for charging strategies 1 and 2.
- The energy cost of the scheme 2 rating system
- -
- Charging policy of Strategy 1
In order to calculate the electricity costs of scheme 2 and scheme 3 of the charging policy of Strategy 1, the return time of ambulance vehicles needs to be analyzed in more detail. Table 5 and Table 6 show the returning number of ambulance vehicles for different time periods of working days for summer months and non-summer months, respectively. Table 7 shows the returning number of vehicles during holidays for summer months and non-summer months.

Table 5.
The returning number for different time periods of working days for summer months.

Table 6.
The returning number for different time periods of working days for non-summer months.

Table 7.
The returning number for weekends and holidays for summer and non-summer months.
The energy consumption of peak periods and off-peak periods of working days for summer months and non-summer months of Strategy 1 can be calculated using Equations (3) and (4), respectively, and Equations (5) and (6) show the energy consumption of the half-peak periods and off-peak periods of working days of non-summer months. The energy consumption for weekends and holidays for summer months and non-summer months can be calculated using Equations (7) and (8), respectively. According to the energy rates in Table 2, the energy cost of scheme 2 for charging under Strategy 1 is shown in Equation (9).
- -
- Charging policy of Strategy 2
Based on the usage data statistics presented in Table 4, it is prudent to implement a smart charging strategy (Strategy 2) by postponing charging to off-peak periods. As indicated in Table 5, Table 6 and Table 7, the service occurrences during summer and non-summer months are 324 and 612 times, respectively. Referring to the energy rates outlined in Table 2, the energy cost for scheme 2 employing Strategy 2 is calculated as shown in Equation (10).
- The energy cost of the scheme 3 rating system
- -
- Charging policy of Strategy 1
Based on the data in Table 5, Table 6 and Table 7 and the energy rates in Table 3, the energy consumption for peak periods, half-peak periods, and off-peak periods of working days for summer months can be calculated using Equations (11)–(13), respectively. Equations (5) and (6) show the energy consumption of half-peak periods and off-peak periods of working days of non-summer months. The energy consumption for weekends and holidays for summer months and non-summer months can be calculated using Equations (7) and (8), respectively. According to the energy rates in Table 3, the energy cost of scheme 3 for charging under Strategy 1 is shown in Equation (14).
- -
- Charging policy of Strategy 2
Since the electricity prices during off-peak periods in schemes 2 and 3 are the same, the energy costs for charging under Strategy 2 under both schemes are identical. Consequently, the energy cost for Strategy 2 under scheme 2 is NTD 10,456 (USD 331.9365).
Table 8 presents the electricity costs associated with the three schemes for two charging strategies, along with the gasoline cost incurred by traditional ambulance vehicles over one year. It is evident that scheme 1 offers the lowest cost when employing Strategy 1’s charging policy, whereas scheme 2 or scheme 3 emerges as the optimal choice for charging Strategy 2. Additionally, the gasoline costs consumed by the three current ambulance vehicles exceed those under the three rating schemes for EVs.

Table 8.
Comparisons of electricity costs of the three rating schemes for two charging strategies.
3.2. The Economic Analysis of the Electric Ambulance Vehicles and Traditional Ambulance Vehicles
The operation costs of electric ambulance vehicles (EAVs) and traditional ambulance vehicles (TAVs) include the vehicle cost, energy cost, maintenance cost, and installation cost of the charging station (for EAVs only). The charger operates on AC 220 V with a rated power of 7.4 kW. These costs, shown in Table 9 [23,24,25], are used to perform an economic analysis of the total cost of EAVs and TAVs.

Table 9.
Economic analysis parameters for EAVs and TAVs.
The present value method [26] shown in Equation (15) is used to perform this financial analysis. A discount rate of 5% is applied, and the assumed lifecycle of vehicles is 10 years. Table 10 presents the present values for electric ambulance vehicles (EAVs) using two charging strategies, as well as those for traditional ambulance vehicles (TAVs). While the present value of EAVs surpasses that of TAVs, it is essential to consider that EAVs contribute to a reduction in air pollution. Moreover, vehicle electrification aligns with government policy objectives, making it imperative for businesses to proactively prepare to meet these policy requirements.
where Cveh and Cchg_sta represent the vehicle cost and charging station cost, respectively, Ceng,i and Cmain,i denote the energy cost and maintenance cost in year i, respectively, d is the discount rate, and N is the life cycle.

Table 10.
Economic analysis results for EAVs and TAVs.
4. Discussion
Fossil fuel vehicles are under consideration to be prohibited for sale in Taiwan by 2040. Establishing a structured framework for the electrification of vehicles and the implementation of charging stations is imperative. In pursuit of this goal, this paper introduces a systematic model for electrifying a fire ambulance service station. The proposed model is validated through a practical case study. A discussion regarding this paper is outlined below.
- A systematic process is proposed for programming charging stations. The process begins by selecting suitable types of electric vehicles to replace the existing fleet, followed by an evaluation of the charging station’s load profile using real-world service data. Due to the specified duty of the fire department, the number of vehicles and the chargers remain unchanged. The service distance and service numbers of the fire ambulance vehicles are analyzed over one year. These data are then utilized to calculate the energy consumption of the charging station in the event of electric ambulance vehicles being employed.
- Different forms of transportation electrification involve different considerations. Electrifying a fire ambulance service station involves distinct considerations compared with electrifying a bus service station [2,3,4,5,6,7,8,9,10]. Unlike a bus station, which operates on a fixed schedule and route, a fire ambulance service station operates with random and emergent characteristics. Following consultation with the fire bureau, the number of EAVs remains unchanged with an equal number of chargers due to security concerns and the unpredictable nature of emergency calls involving EAVs. However, after analyzing service data, implementing a smart charging strategy is deemed feasible. Although the current situation entails a fixed number of electric vehicles and chargers, it can be expanded to accommodate a variable number of electric vehicles and chargers. In fact, the authors are currently conducting a case study on electrifying the bus station using a similar model.
- While economic analyses of TAVs suggest they present a financially viable option in this study, the ongoing decrease in the costs of EVs and charging equipment, driven by the increasing adoption of EVs, will likely make EAVs increasingly competitive in the future.
5. Conclusions
This paper proposes a model for electrifying fire ambulance service stations, taking into account practical service data and charging strategies. The model aims to optimize charging station programming with the objective of minimizing infrastructure and operational costs. In this study, the number of electric ambulance vehicles and chargers remains unchanged due to security concerns. Two charging strategies, the immediate charging of returning EVs (Strategy 1) and delayed charging during off-peak periods (Strategy 2), are analyzed within the proposed model. By utilizing energy consumption data from Figure 3, the electricity costs associated with three pricing schemes for these two charging strategies are compared to determine the optimal scheme. The test results indicate that different charging strategies require distinct electricity pricing schemes. The progressive pricing scheme is suitable for Strategy 1’s charging policy, while charging under Strategy 2 should involve using the time-of-use pricing scheme to minimize energy costs. Economic analyses of electric ambulance vehicles and traditional ambulance vehicles are also demonstrated in this paper. While TAVs present an economically viable option, EAVs offer the added advantage of mitigating air pollution, aligning with the emerging trend driven by government policies promoting vehicle electrification. Hence, it is imperative to establish a standardized electrification process for conventional fossil-fueled vehicles.
Author Contributions
Y.-H.Y.: formal analysis, methodology, resources, software, and writing—original draft; R.-C.L.: conceptualization, formal analysis, methodology, resources, validation, supervision, and writing—review and editing; C.-C.K.: formal analysis, methodology, resources, software, and writing—original draft. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Popovich, N.; Plumber, B. How Electrifying Everything Became a Key Climate Solution. The New York Times (Digital Edition). 2023. Available online: https://www.nytimes.com/interactive/2023/04/14/climate/electric-car-heater-everything.html (accessed on 18 February 2024).
- Jefferies, D.; Göhlich, D. A Comprehensive TCO Evaluation Method for Electric Bus Systems Based on Discrete-Event Simulation Including Bus Scheduling and Charging Infrastructure Optimisation. World Electr. Veh. J. 2020, 11, 56. [Google Scholar] [CrossRef]
- Grauers, A.; Borén, S.; Enerbäck, O. Total Cost of Ownership Model and Significant Cost Parameters for the Design of Electric Bus Systems. Energies 2020, 13, 3262. [Google Scholar] [CrossRef]
- Teichert, O.; Chang, F.; Ongel, A.; Lienkamp, M. Joint Optimization of Vehicle Battery Pack Capacity and Charging Infrastructure for Electrified Public Bus Systems. IEEE Trans. Transp. Electrif. 2019, 5, 672–682. [Google Scholar] [CrossRef]
- Jahic, A.; Plenz, M.; Schulz, D. Impact of Route and Charging Scheduling on the Total Cost of Ownership for Electric Bus Depots. In Proceedings of the 2021 IEEE PES Innovative Smart Grid Technologies Europe, Espoo, Finland, 18–21 October 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1–6. [Google Scholar]
- El-Taweel, N.A.; Farag, H.E.Z.; Mohamed, M. Integrated Utility-Transit Model for Optimal Configuration of Battery Electric Bus Systems. IEEE Syst. J. 2020, 14, 738–747. [Google Scholar] [CrossRef]
- El-Taweel, N.A.; Farag, H.E.; Brari, G.; Zeineldin, H.; Al-Durra, A.; El-Saadany, E.F. A Systematic Approach for Design and Analysis of Electrified Public Bus Transit Fleets. IEEE Syst. J. 2021, 16, 2989–3000. [Google Scholar] [CrossRef]
- Cheng, Y.; Wang, W.; Ding, Z.; He, Z. Electric Bus Fast Charging Station Resource Planning Considering Load Aggregation and Renewable Integration. IET Renew. Power Gener. 2019, 13, 1132–1141. [Google Scholar] [CrossRef]
- Pan, J.; Wu, X.; Feng, Q.; Ji, Y. Optimization of Electric Bus Charging Station Considering Energy Storage System. In Proceedings of the 2020 8th International Conference on Power Electronics Systems and Applications, Hongkong, China, 7–10 December 2020; pp. 1–5. [Google Scholar]
- Feng, J.; Hu, Z.; Duan, X. Multi-agent Based Stochastic Programming for Planning of Fast Charging Station Integrated with Photovoltaic and Energy Storage System. In Proceedings of the 2021 IEEE IAS Industrial and Commercial Power System Asia, Chengdu, China, 18–21 July 2021; pp. 425–430. [Google Scholar]
- Calvillo, C.F.; Turner, K. Analysing the impacts of a large-scale EV rollout in the UK—How can we better inform environmental and climate policy? Energy Strategy Rev. 2020, 30, 100497. [Google Scholar] [CrossRef]
- Nutkani, I.U.; Lee, J.C. Evaluation of Electric Vehicles (EVs) Impact on Electric Grid. In Proceedings of the 2022 International Power Electronics Conference, Himeji, Japan, 15–19 May 2022; pp. 239–246. [Google Scholar]
- Manzolli, J.A.; Trovao, J.P.F.; Antunes, C.H. Electric bus coordinated charging strategy considering V2G and battery degradation. Energy 2022, 254, 124252. [Google Scholar] [CrossRef]
- Jamroen, C.; Ngmroo, I.; Dechanupaprittha, S. EVs Charging Power Control Participating in Supplementary Frequency Stabilization for Microgrids: Uncertainty and Global Sensitivity Analysis. IEEE Access 2021, 9, 111005–111019. [Google Scholar] [CrossRef]
- Ma, S.C.; Fan, Y. A deployment model of EV charging piles and its impact on EV promotion. Energy Policy 2020, 146, 111777. [Google Scholar] [CrossRef]
- Lajunen, A.; Lipman, T. Lifecycle Cost Assessment and Carbon Dioxide Emission of Diesel, Natural Gas, Hybrid Electric, Fuel Cell Hybrid and Electric Transit Buses. Energy 2016, 106, 329–342. [Google Scholar] [CrossRef]
- Lajunen, A. Lifecycle Costs and Charging Requirements of Electric Buses with Different Charging Methods. J. Clean. Prod. 2018, 172, 56–67. [Google Scholar] [CrossRef]
- Sheth, A.; Sarkar, D. Life Cycle Cost Analysis for Electric vs Diesel Bus Transit in an Indian Scenario. Int. J. Technol. 2019, 10, 105–115. [Google Scholar] [CrossRef]
- Qian, K.; Zhou, C.; Allan, M.; Yuan, Y. Modeling of Load Demand Due to EV Battery Charging in Distribution Systems. IEEE Trans. Power Syst. 2011, 26, 802–810. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, N.; Li, Z.; Shahidehpour, M. Modeling and Impact Analysis of large scale V2G Electric Vehicles on the Power Grid. In Proceedings of the IEEE PES ISGT ASIA, Tianjin, China , 21–24 May 2012 ; IEEE: Piscataway, NJ, USA, 2012; pp. 1–6. [Google Scholar]
- Leou, R.C.; Teng, J.H.; Su, C.L. Modeling and Verifying the Load Behavior of Electric Vehicle Charging Stations Based on Field Measurements. IET Gener. Transm. Distrib. 2015, 9, 1112–1119. [Google Scholar] [CrossRef]
- Available online: https://www.opel.ie/vans/vivaro-c/vivaro-e/overview.html (accessed on 18 February 2024).
- Tsai, C.H.; Hsu, J.Y.; Yeh, F.M. Cost-Effectiveness Analysis of the Operation Model of Electric Vehicle-to-Grid. J. Taiwan Energy Vol. 2021, 8, 55–77. [Google Scholar]
- Onat, N.C.; Kucukvar, M.; Tatari, O. Conventional, hybrid, plug-in hybrid or electric vehicles? State-based comparative carbon and energy footprint analysis in the United States. Appl. Energy 2015, 150, 36–49. [Google Scholar] [CrossRef]
- Smith, M.; Castellano, J. Costs Associated with Non-Residential Electric Vehicle Supply Equipment; New West Technologies, LLC for U.S. Department of Energy Vehicle Technologies Office: Landover, MD, USA, 2015. [Google Scholar]
- Hartman, J.C. Engineering Economy and the Decision-Making Process; Pearson/Prentice Hall: Upper Saddle River, NJ, USA, 2007. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).