Bi-Layer Planning of Integrated Energy System by Incorporating Power-to-Gas and Ground Source Heat Pump for Curtailed Wind Power and Economic Cost Reduction
Abstract
1. Introduction
- Establish a bi-layer optimal planning model of an integrated energy system that incorporates P2G and GSHP.
- Analyze the optimal planning results of the system in five cases, and study the scheduling performance of the system in the best case.
- Study the impact of optimization with different algorithms.
- Analyze the impact of natural gas price fluctuations on the planning results.
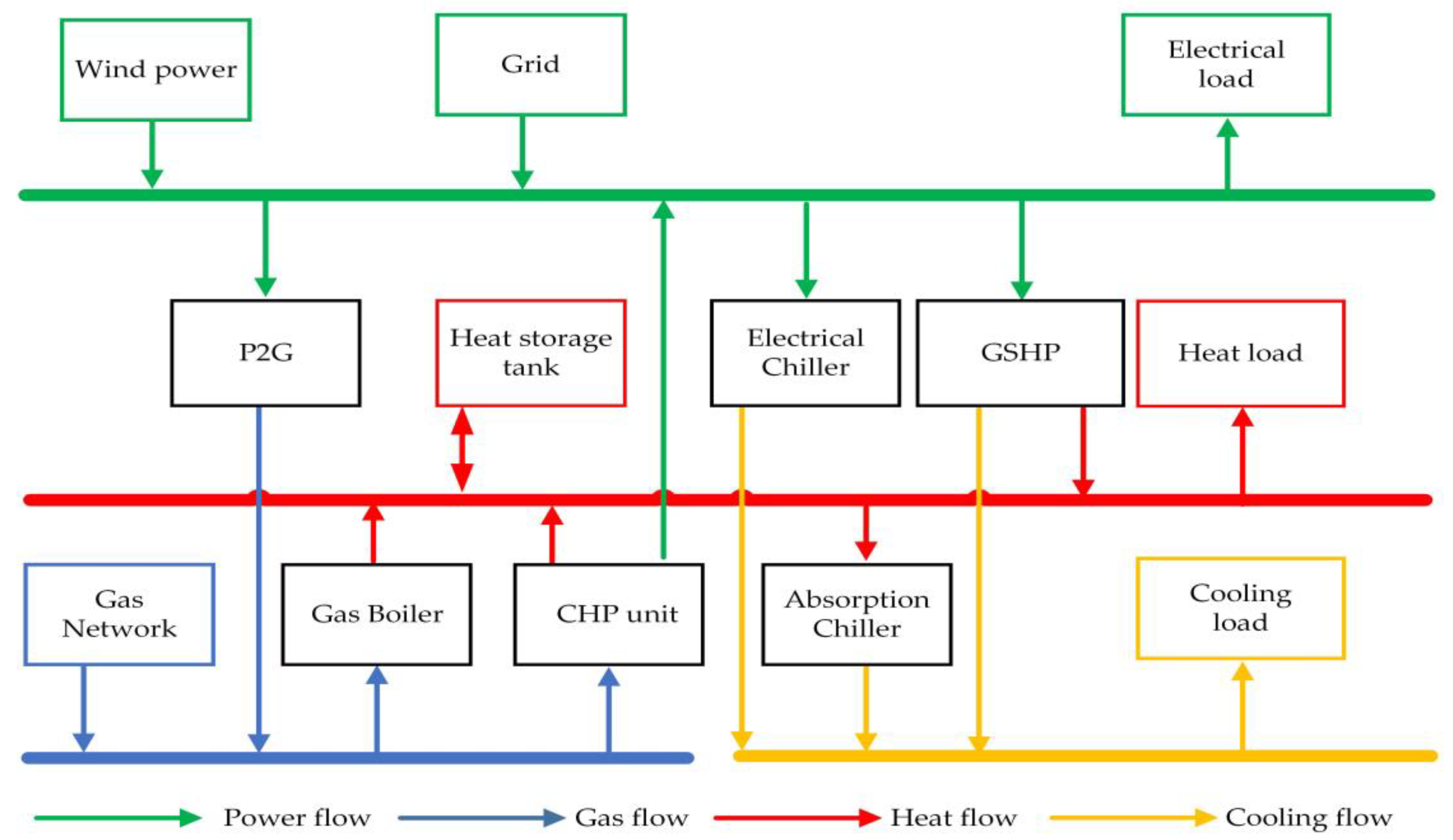
2. Structure and Model of Integrated Energy System
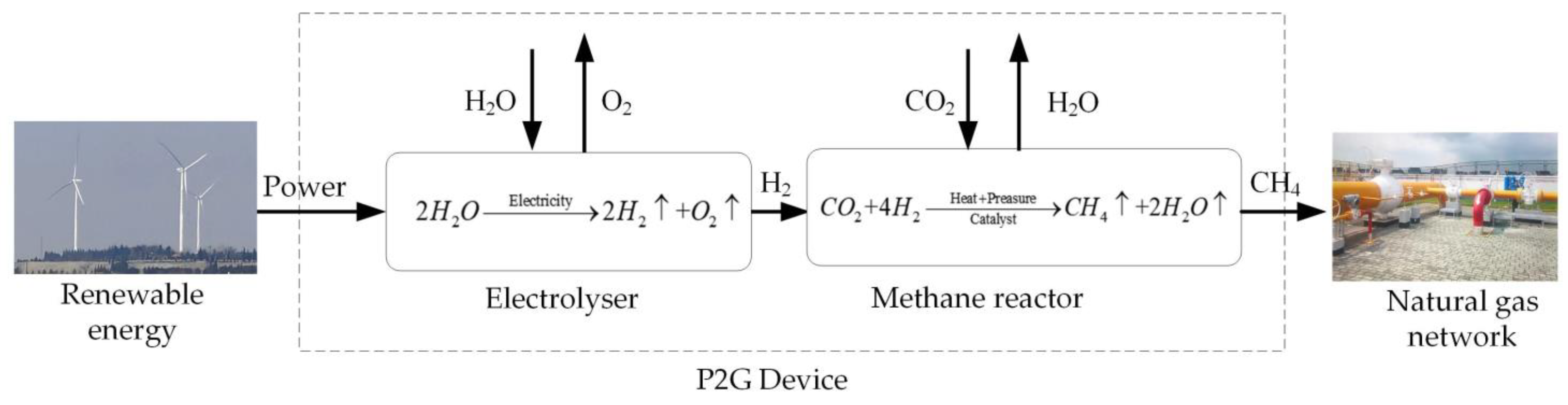
2.1. P2G Model—Electrolyser and Methane Reactor
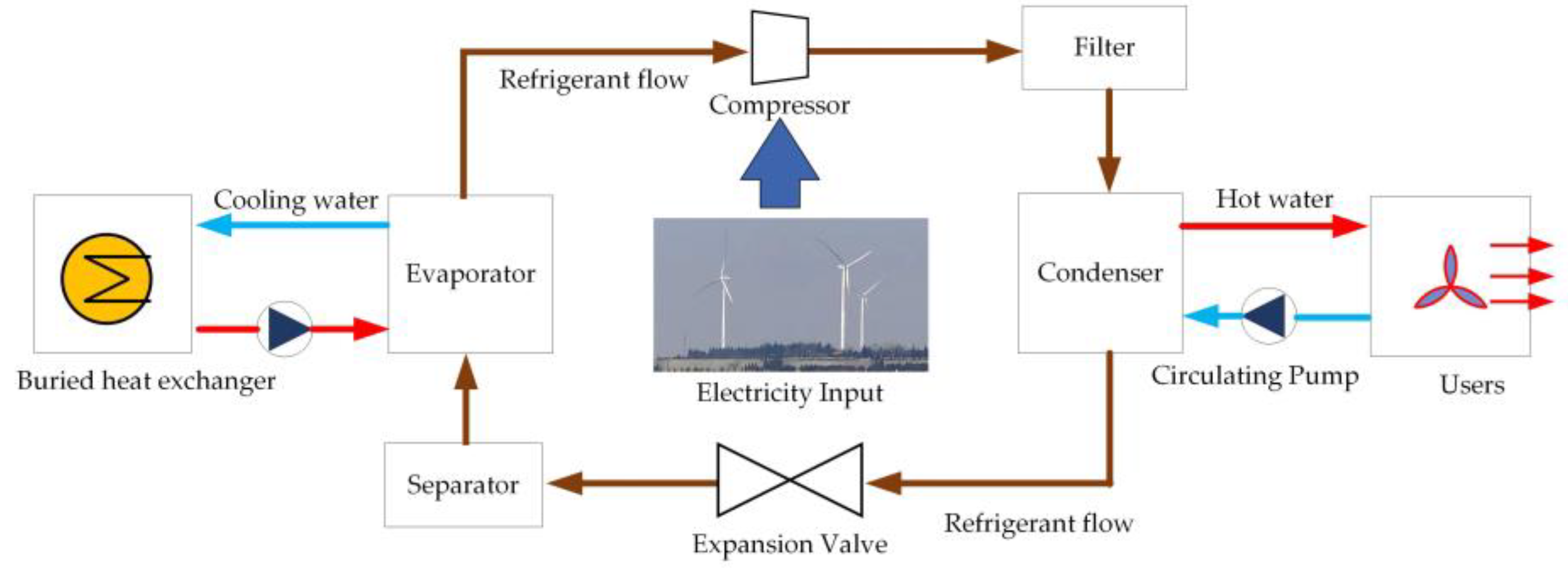
2.2. GSHP Model
2.3. CHP Model
2.4. Models of Other Devices
3. Overall Optimization Model
3.1. Objective Function of Outer-Layer Optimization Model
3.2. Objective Function of Inner-Layer Optimization Model
3.3. Constraints
3.3.1. System Power Balance Constraints
3.3.2. Capacity Constraints of Planning Devices
3.3.3. Heat Storage and Power Constraints of Heat Storage Tank
3.3.4. Power Grid and Gas Network Constraints
3.3.5. Output Constraints of the Energy Conversion Devices
4. Solution of the Bi-Layer Optimization Model
4.1. Outer-Layer Solution: The Enumeration Method, Loops, Feedback
4.2. Inner-Layer Solution: The EDIW-CPSO Algorithm
5. Case Study
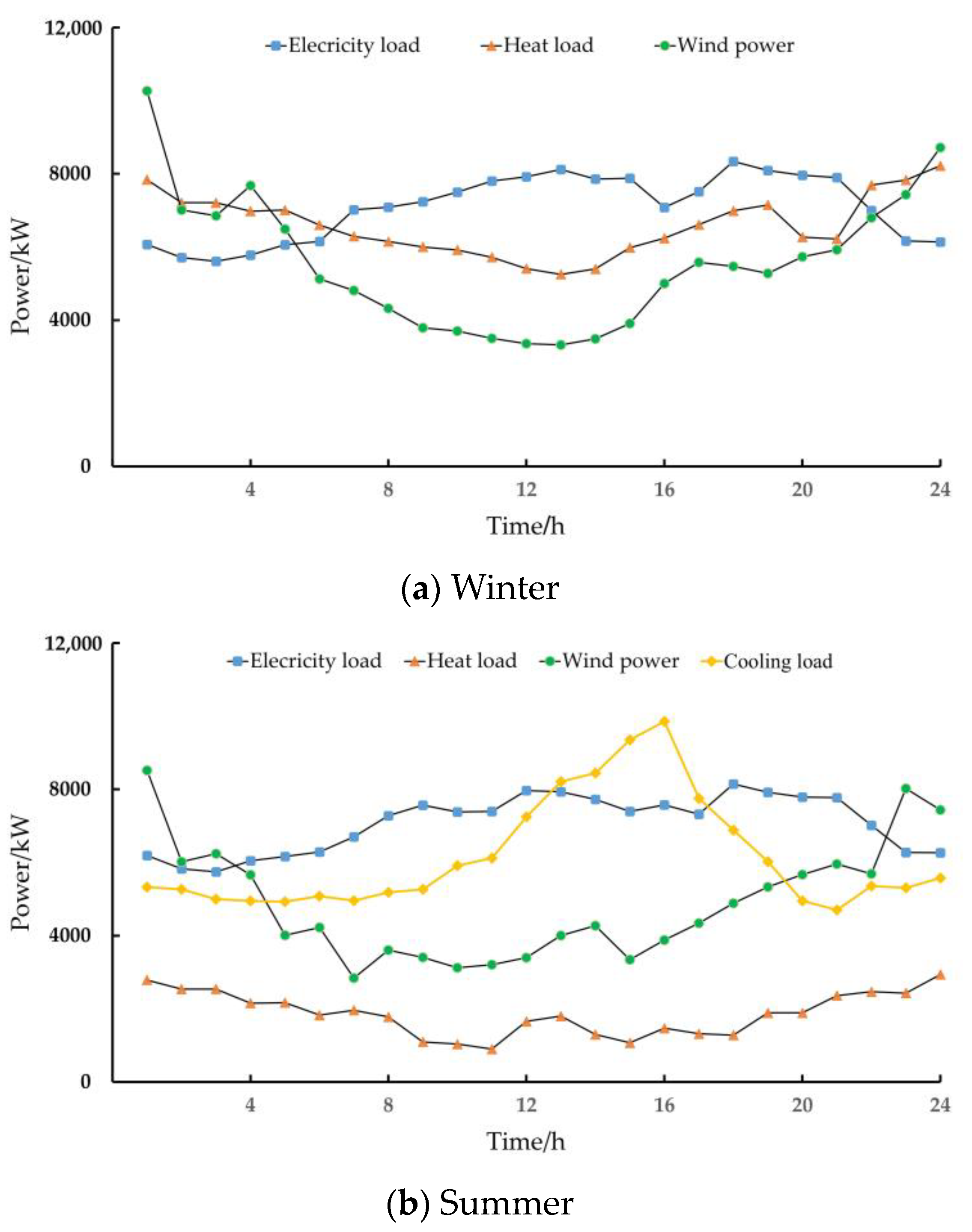
5.1. Case Information
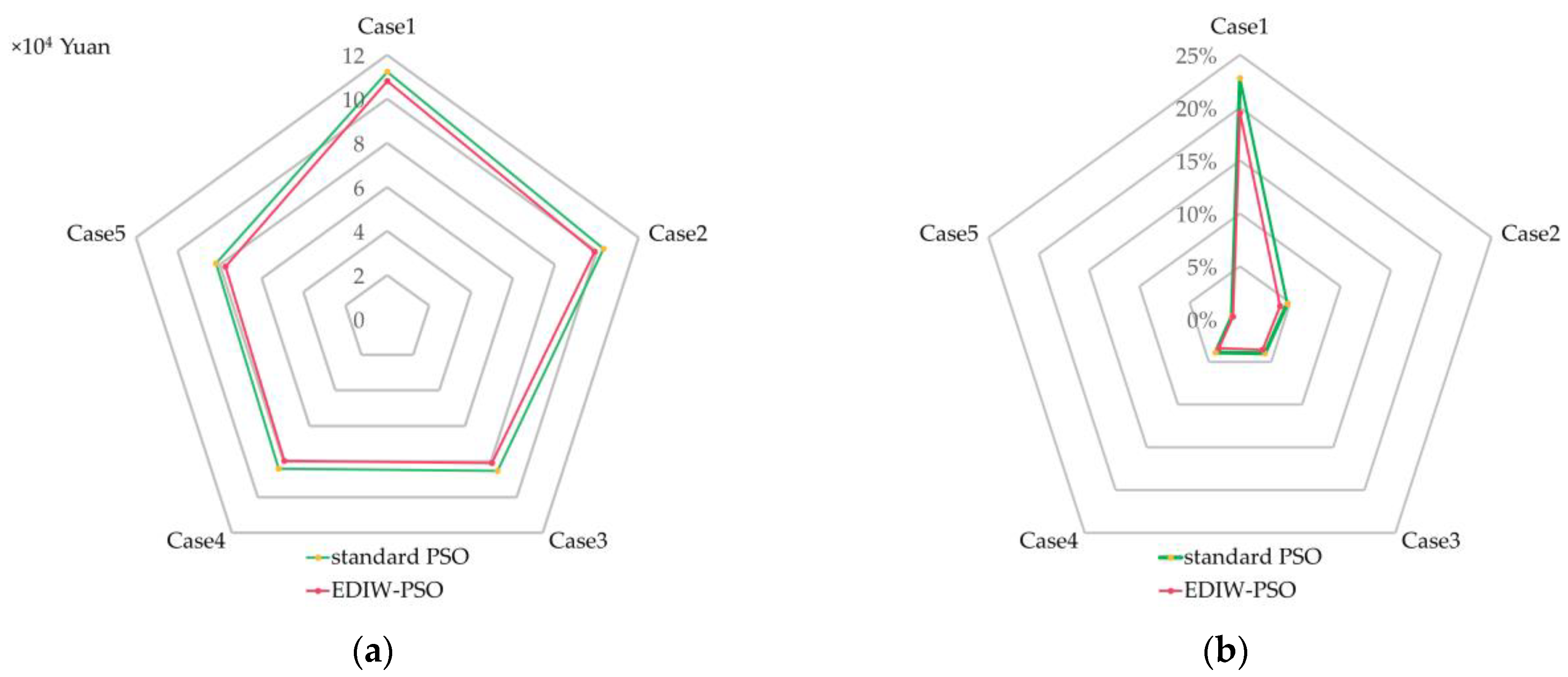
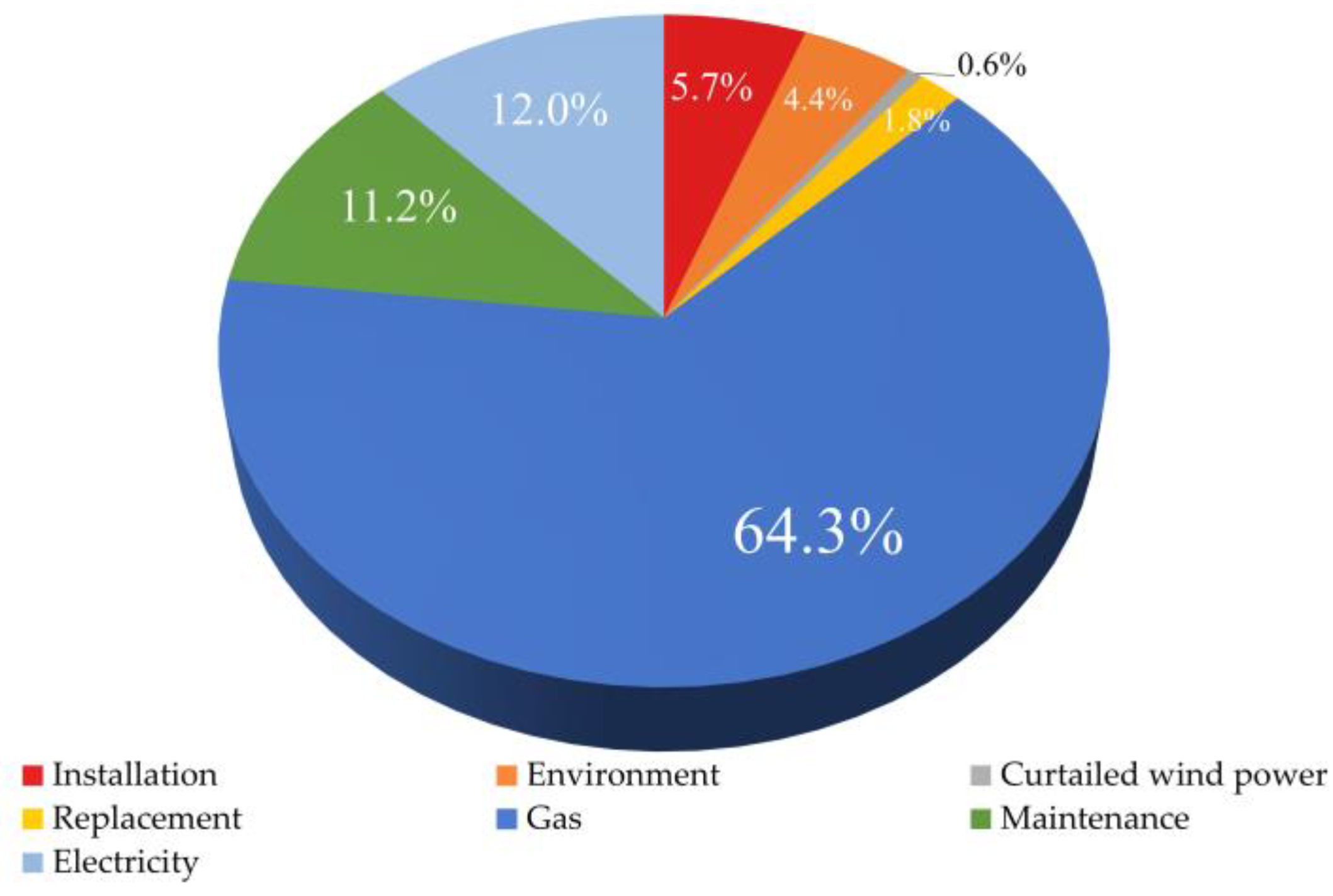
5.2. Planning Results
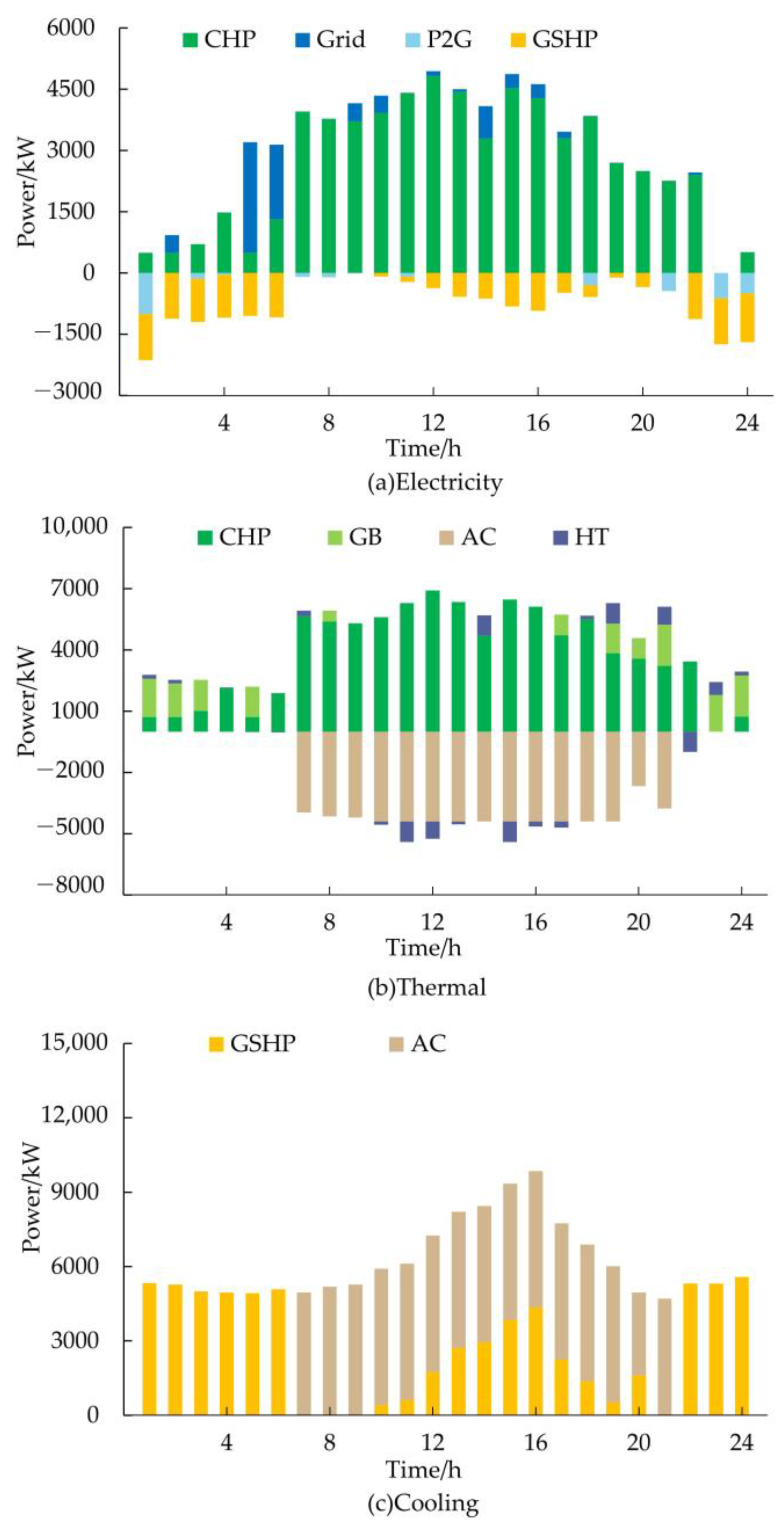
5.3. Analysis of Scheduling Results on Typical Days
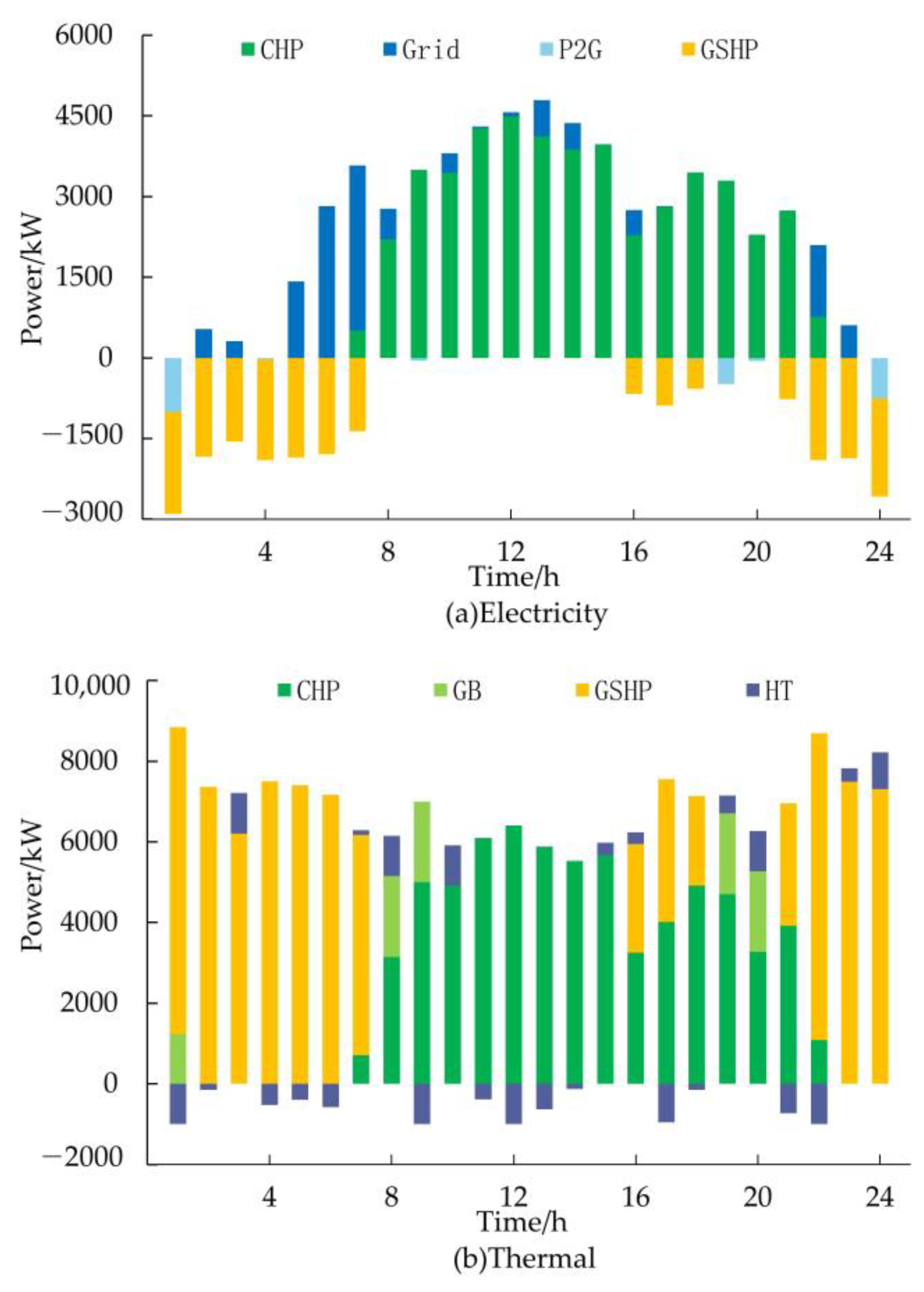
5.3.1. Scheduling on Typical Day of Winter
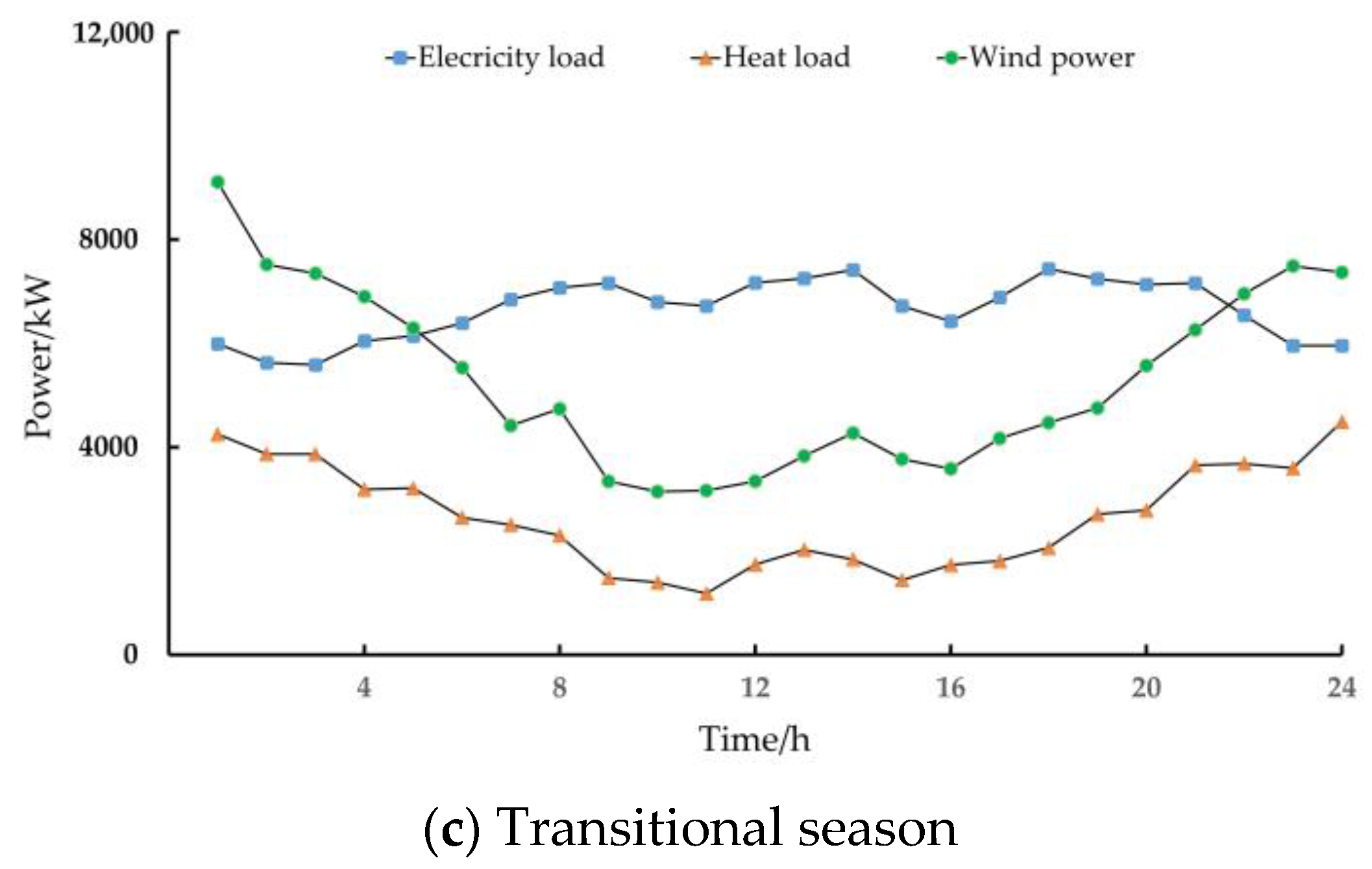
5.3.2. Scheduling on Typical Day of Transitional Season
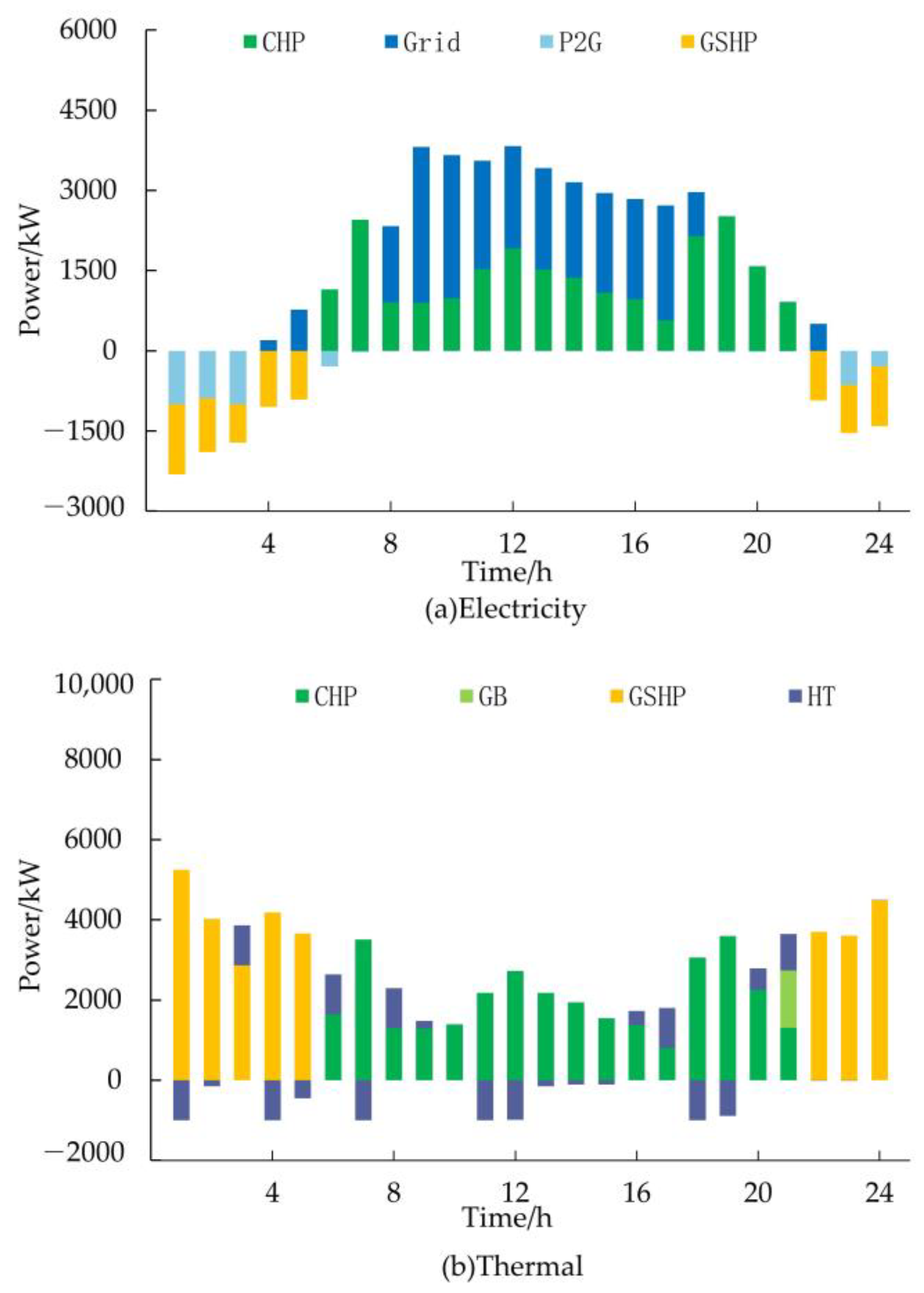
5.3.3. Scheduling on Typical Day of Summer
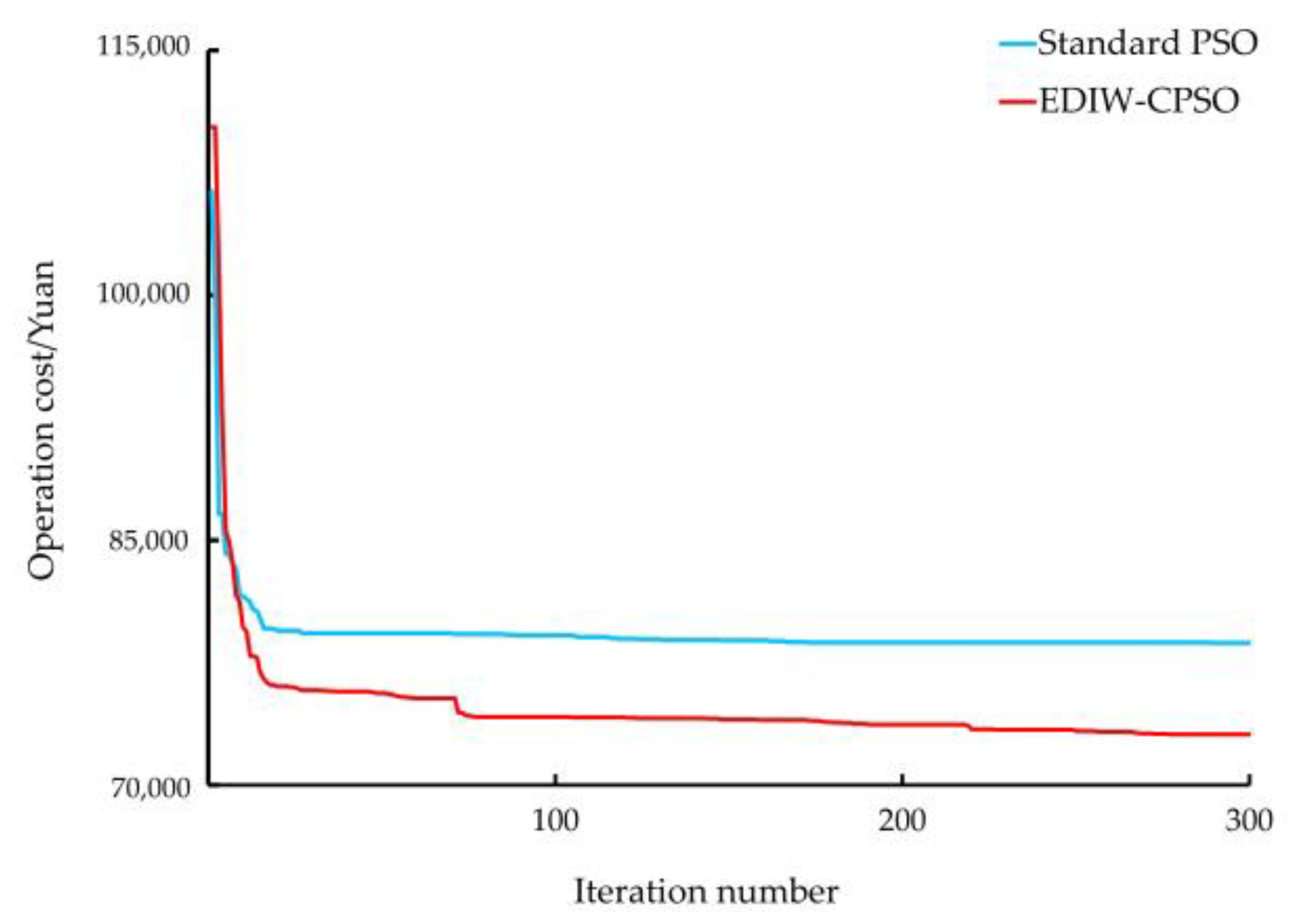
5.4. Influence of the Algorithms on Optimization
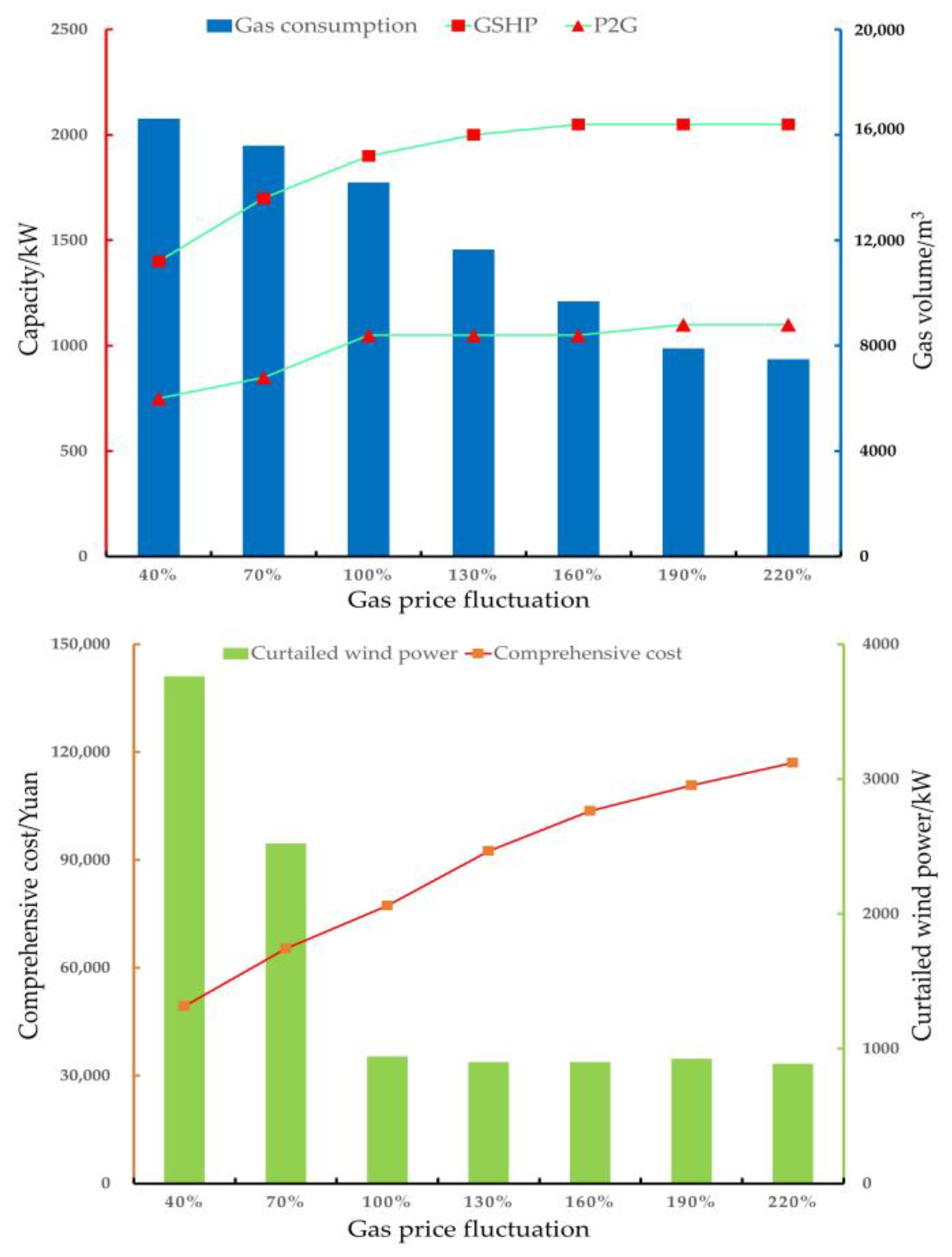
5.5. Influence of the Natural Gas Price Fluctuation on Optimization
6. Conclusions
- Among the planning cases, the improved system in case 5 has the highest installation and replacement costs, but the comprehensive cost and the ability to reduce the curtailed wind power are the best. Compared with the original system, the wind curtailment rate, gas purchase cost, operation cost, and comprehensive cost of the optimized system decreased by 18.8%, 32.3%, 33.8%, and 28.5%, respectively.
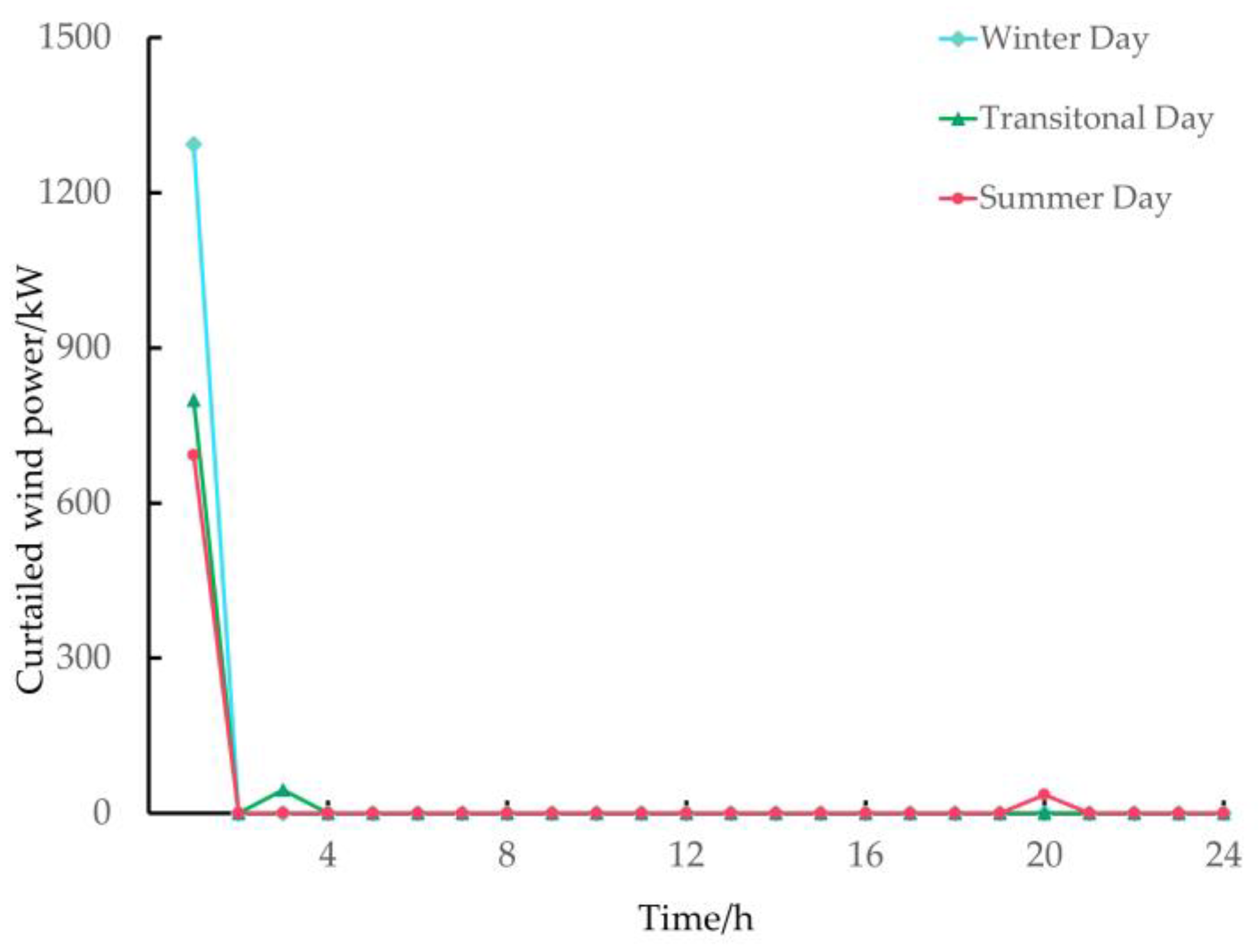
- Through analyzing the scheduling results, it can be observed that P2G and GSHP can promote the consumption of wind power during periods of abundant wind power in the system. In addition, P2G can supply gas during the peak periods of device demand, and GSHP can reduce the pressure of heat supply during the peak periods of heat load.
- Compared with the standard PSO algorithm, the EDIW-CPSO algorithm not only saves on the scheduling cost, but it also reduces the comprehensive cost and wind curtailment rate in winter. Therefore, the EDIW-CPSO algorithm can obtain better optimal scheduling results, and the corresponding planning scheme is also better.
- The fluctuation in natural gas prices affects the optimal capacities of P2G and GSHP. In the price range of 40% to 130%, the optimal capacities of two devices gradually increase. In the price range of 160% to 220%, the optimal capacities of the two devices tend to be stable. The upper limit of optimal capacity should be considered in engineering practice, and it is not cost effective to plan for too large a device capacity.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| IES | integrated energy system |
| P2G | power to gas |
| GSHP | ground source heat pump |
| CHP | combined heat and power |
| GB | gas boilers |
| GT | gas turbines |
| AC | absorption chiller |
| EC | electric chiller |
References
- He, L.; Lu, Z.; Geng, L.; Zhang, J.; Li, X.; Guo, X. Environmental economic dispatch of integrated regional energy system considering integrated demand response. Int. J. Electr. Power Energy Syst. 2020, 116, 105525. [Google Scholar] [CrossRef]
- Yu, B.; Fang, D.; Xiao, K.; Pan, Y. Drivers of renewable energy penetration and its role in power sector’s deep decarbonization towards carbon peak. Renew. Sustain. Energy Rev. 2023, 178, 113247. [Google Scholar] [CrossRef]
- Guan, Y.; Shan, Y.; Huang, Q.; Chen, H.; Wang, D.; Hubacek, K. Assessment to China’s recent emission pattern shifts. Earth’s Future 2021, 9, e2021EF002241. [Google Scholar] [CrossRef]
- Chen, X.; Kang, C.; O’Malley, M.; Xia, Q.; Bai, J.; Liu, C.; Sun, R.; Wang, W.; Li, H. Increasing the flexibility of combined heat and power for wind power integration in China: Modeling and implications. IEEE Trans. Power Syst. 2014, 30, 1848–1857. [Google Scholar] [CrossRef]
- Wu, Y.; Fu, L.; Zhang, S.; Tang, D. Study on a novel co-operated heat and power system for improving energy efficiency and flexibility of cogeneration plants. Appl. Therm. Eng. 2019, 163, 114429. [Google Scholar] [CrossRef]
- Tomin, N.; Shakirov, V.; Kozlov, A.; Sidorov, D.; Kurbatsky, V.; Rehtanz, C.; Lora, E.E. Design and optimal energy management of community microgrids with flexible renewable energy sources. Renew. Energy 2022, 183, 903–921. [Google Scholar] [CrossRef]
- Gao, C.; Zhang, Z.; Wang, P. Day-Ahead Scheduling Strategy Optimization of Electric–Thermal Integrated Energy System to Improve the Proportion of New Energy. Energies 2023, 16, 3781. [Google Scholar] [CrossRef]
- Liu, J.; Sun, W.; Yan, J. Effect of P2G on flexibility in integrated power-natural gas-heating energy systems with gas storage. Energies 2021, 14, 196. [Google Scholar] [CrossRef]
- He, C.; Wu, L.; Liu, T.; Shahidehpour, M. Robust co-optimization scheduling of electricity and natural gas systems via ADMM. IEEE Trans. Sustain. Energy 2016, 8, 658–670. [Google Scholar] [CrossRef]
- Li, Y.; Zou, Y.; Tan, Y.; Cao, Y.; Liu, X.; Shahidehpour, M.; Tian, S.; Bu, F. Optimal stochastic operation of integrated low-carbon electric power, natural gas, and heat delivery system. IEEE Trans. Sustain. Energy 2017, 9, 273–283. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, C.; Lv, H.; Liu, F.; Sheng, H.; Yang, M. Day-ahead optimal dispatch for integrated energy system considering power-to-gas and dynamic pipeline networks. IEEE Trans. Ind. Appl. 2021, 57, 3317–3328. [Google Scholar] [CrossRef]
- Wang, C.; Dong, S.; Xu, S.; Yang, M.; He, S.; Dong, X.; Liang, J. Impact of power-to-gas cost characteristics on power-gas-heating integrated system scheduling. IEEE Access 2019, 7, 17654–17662. [Google Scholar] [CrossRef]
- Sun, G.; Chen, S.; Wei, Z.; Chen, S. Multi-period integrated natural gas and electric power system probabilistic optimal power flow incorporating power-to-gas units. J. Mod. Power Syst. Clean Energy 2017, 5, 412–423. [Google Scholar] [CrossRef]
- Chen, J.; Ning, K.; Xin, X.; Shi, F.; Zhang, Q.; Li, C. Day-ahead optimal scheduling of an integrated energy system based on a piecewise self-adaptive particle swarm optimization algorithm. Energies 2022, 15, 690. [Google Scholar] [CrossRef]
- Jiang, Y.; Guo, L. Research on wind power accommodation for an electricity-heat-gas integrated microgrid system with power-to-gas. IEEE Access 2019, 7, 87118–87126. [Google Scholar] [CrossRef]
- Li, G.; Zhang, R.; Jiang, T.; Chen, H.; Bai, L.; Li, X. Security-constrained bi-level economic dispatch model for integrated natural gas and electricity systems considering wind power and power-to-gas process. Appl. Energy 2017, 194, 696–704. [Google Scholar] [CrossRef]
- Chen, Z.; Zhang, Y.; Ji, T.; Cai, Z.; Li, L.; Xu, Z. Coordinated optimal dispatch and market equilibrium of integrated electric power and natural gas networks with P2G embedded. J. Mod. Power Syst. Clean Energy 2018, 6, 495–508. [Google Scholar] [CrossRef]
- Siqin, Z.; Niu, D.; Wang, X.; Zhen, H.; Li, M.; Wang, J. A two-stage distributionally robust optimization model for P2G-CCHP microgrid considering uncertainty and carbon emission. Energy 2022, 260, 124796. [Google Scholar] [CrossRef]
- Wang, X.; Li, H. Multi-objectives combined electric heating dispatch model of wind power accommodation with heat storage device. J. Eng. 2017, 2017, 1539–1545. [Google Scholar] [CrossRef]
- Ma, Y.; Yu, Y.; Mi, Z. Accommodation of curtailed wind power by electric boilers equipped in different locations of heat-supply network for power system with CHPs. J. Mod. Power Syst. Clean Energy 2021, 9, 930–939. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhao, P.; Xu, F.; Cui, D.; Ge, W.; Chen, X.; Gu, B. Optimal dispatch strategy for a flexible integrated energy storage system for wind power accommodation. Energies 2020, 13, 1073. [Google Scholar] [CrossRef]
- Wang, J.; Chen, Y.; Dou, C.; Gao, Y.; Zhao, Z. Adjustable performance analysis of combined cooling heating and power system integrated with ground source heat pump. Energy 2018, 163, 475–489. [Google Scholar] [CrossRef]
- Zhang, Z.L.; Zhang, H.J.; Xie, B.; Zhang, X.T. Energy scheduling optimization of the integrated energy system with ground source heat pumps. J. Clean. Prod. 2022, 365, 132758. [Google Scholar] [CrossRef]
- Li, B.; Hu, P.; Zhu, N.; Lei, F.; Xing, L. Performance analysis and optimization of a CCHP-GSHP coupling system based on quantum genetic algorithm. Sustain. Cities Soc. 2019, 46, 101408. [Google Scholar] [CrossRef]
- Cui, Y.; Jiang, T.; Zhong, W.; Cui, C.; Zhao, Y. Source-load coordination economic dispatch method for regional integrated energy system considering wind power accommodation. Power Syst. Technol. 2020, 44, 2474–2483. [Google Scholar] [CrossRef]
- Sun, Q.; Gao, S.; Xie, D.; Chen, J.; Chen, Q. Optimum planning for integrated community energy system with coordination of reliability and economy. Proc. CSU-EPSA 2020, 32, 76–82. [Google Scholar] [CrossRef]
- Jin, T.; Li, N.; Qin, J.; Li, T.; Li, Y.; Pan, C. Optimization allocation of integrated energy system based on mixed integer nonlinear programming. Therm. Power Gener. China 2021, 50, 131–140. [Google Scholar] [CrossRef]
- Wang, L. Optimal Scheduling Strategy for Multi-Energy Microgrid Considering Integrated Demand Response. Energies 2023, 16, 4694. [Google Scholar] [CrossRef]
- Zeng, L.; Xu, J.; Wu, M.; Tang, J.; Wu, Q.; Wang, Q.; Fan, G. Day-ahead interval optimization for CCHP system considering uncertainty of wind power and PV. Int. J. Electr. Power Energy Syst. 2022, 138, 107895. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, Z. Day-ahead and intra-day optimal scheduling of integrated energy system considering uncertainty of source & load power forecasting. Energies 2021, 14, 2539. [Google Scholar] [CrossRef]
- Luo, Z.; Wang, J.; Xiao, N.; Yang, L.; Zhao, W.; Geng, J.; Lu, T.; Luo, M.; Dong, C. Low Carbon Economic Dispatch Optimization of Regional Integrated Energy Systems Considering Heating Network and P2G. Energies 2022, 15, 5494. [Google Scholar] [CrossRef]
- Wang, Y.; Huang, F.; Tao, S.; Ma, Y.; Ma, Y.; Liu, L.; Dong, F. Multi-objective planning of regional integrated energy system aiming at exergy efficiency and economy. Appl. Energy 2022, 306, 118120. [Google Scholar] [CrossRef]
- Bhamidi, L.; Sivasubramani, S. Optimal planning and operational strategy of a residential microgrid with demand side management. IEEE Syst. J. 2019, 14, 2624–2632. [Google Scholar] [CrossRef]
- Yang, X.; Chen, Z.; Huang, X.; Li, R.; Xu, S.; Yang, C. Robust capacity optimization methods for integrated energy systems considering demand response and thermal comfort. Energy 2021, 221, 119727. [Google Scholar] [CrossRef]
- Chai, G.; Wu, J.; Yao, L.; Zhang, Q. Operation optimization of combined cooling, heating and power microgrid based on improved dynamic inertia weighted particle swarm algorithm. Sci. Technol. Eng. 2022, 22, 1472–1479. [Google Scholar] [CrossRef]
- Lu, B.; Wei, Z.; Wei, P.; Guo, Y.; Huang, Y.; Ma, X.; Zhou, F. Optimal configuration of PtG and energy storage equipment in regional integrated energy system considering wind power consumption. Smart Power 2021, 49, 7–14+68. [Google Scholar] [CrossRef]
- Götz, M.; Lefebvre, J.; Mörs, F.; Koch, A.M.; Graf, F.; Bajohr, S.; Reimert, R.; Kolb, T. Renewable Power-to-Gas: A technological and economic review. Renew. Energy 2016, 85, 1371–1390. [Google Scholar] [CrossRef]
- Tschiggerl, K.; Sledz, C.; Topic, M. Considering environmental impacts of energy storage technologies: A life cycle assessment of power-to-gas business models. Energy 2018, 160, 1091–1100. [Google Scholar] [CrossRef]
- Ma, Z.; Xia, L.; Gong, X.; Kokogiannakis, G.; Wang, S.; Zhou, X. Recent advances and development in optimal design and control of ground source heat pump systems. Renew. Sustain. Energy Rev. 2020, 131, 110001. [Google Scholar] [CrossRef]
- Martinez, S.; Michaux, G.; Salagnac, P.; Bouvier, J.L. Micro-combined heat and power systems (micro-CHP) based on renewable energy sources. Energy Convers. Manag. 2017, 154, 262–285. [Google Scholar] [CrossRef]
- Lu, J.; Hu, H.; Bai, Y. Generalized radial basis function neural network based on an improved dynamic particle swarm optimization and AdaBoost algorithm. Neurocomputing 2015, 152, 305–315. [Google Scholar] [CrossRef]
- Yang, W.; Zhou, X.; Chen, M. New Chaotic Simplified Particle Swarm Optimization Algorithm Based on Logistic Mapping. Comput. Mod. 2019, 12, 15–20+26. [Google Scholar] [CrossRef]
- Bao, X.; Ding, W.; Song, A. Chaotic compression nonlinear particle swarm optimization algorithm for job shop scheduling problem. Mod. Manuf. Eng. 2020, 9, 15–22+52. [Google Scholar] [CrossRef]
- Xiong, J.; Jiao, Y.; Wang, M. A Day-Ahead Optimal Scheduling of Regional Integrated Energy System Considering Power to Gas. Mod. Electr. Power 2022, 39, 554–561. [Google Scholar] [CrossRef]



| Algorithm Name | Operation Cost in Winter/CNY | Operation Cost in Summer/CNY | Operation Cost in Transitional Season/CNY |
|---|---|---|---|
| Standard PSO | 78,709 | 90,634 | 55,137 |
| EDIW-CPSO | 73,120 | 85,473 | 51,713 |
| Types of Electricity Usage | Time | Price/(CNY/kW) |
|---|---|---|
| Demand valley | 00:00–07:00 | 0.43 |
| 23:00–24:00 | ||
| Normal demand | 07:00–11:00 | 0.88 |
| 16:00–19:00 | ||
| 22:00–23:00 | ||
| Demand peak | 11:00–16:00 | 1.12 |
| 19:00–22:00 |
| Device Name | Symbol | Capacity/kW | Maintenance Price/(CNY/kW) | Efficiency/% |
|---|---|---|---|---|
| Combined heating and power unit | CHP | 7000 | 0.05 | electricity 0.35/heat 0.5 |
| Heat storage tank | HS | 2000 | 0.015 | charge 0.9/loss 0.05 |
| Gas boiler | GB | 2000 | 0.01 | heat 0.9 |
| Electric chiller | EC | 1500 | 0.01 | cooling 3.1 |
| Absorption chiller | AC | 4400 | 0.005 | cooling 1.25 |
| Equipment Name | Symbol | Installation Price /(CNY/kW) | Maintenance Price /(CNY/kW) | Efficiency/% | Service Time/Year |
|---|---|---|---|---|---|
| Power to gas | P2G | 7000 | 0.03 | — | 20 |
| Ground source heat pump | GSHP | 9000 | 0.036 | Heat 4.0 Cooling 4.7 | 20 |
| Capacity of P2G/kW | Capacity of GSHP/kW | Wind Curtailment Rate | Comprehensive Cost/CNY | |
|---|---|---|---|---|
| Case 1 | 0 | 0 | 19.5% | 108,071 |
| Case 2 | 3400 | 0 | 4.0% | 99,011 |
| Case 3 | 0 | 2200 | 3.6% | 80,763 |
| Case 4 | 0 | 2350 | 3.4% | 79,510 |
| Case 5 | 1050 | 1900 | 0.7% | 77,252 |
| Case 1 | Case 2 | Case 3 | Case 4 | Case 5 | |
|---|---|---|---|---|---|
| Operation cost/CNY | 108,071 | 93,326 | 76,034 | 74,516 | 71,496 |
| Installation cost/CNY | 0 | 4334 | 3605 | 3819 | 4388 |
| Replacement cost/CNY | 0 | 1351 | 1124 | 1175 | 1368 |
| Wind curtailment cost/CNY | 13,121 | 2691 | 2422 | 2288 | 471 |
| Gas purchase cost/CNY | 73,347 | 69,523 | 51,745 | 51,091 | 49,682 |
| Comprehensive cost/CNY | 108,071 | 99,011 | 80,763 | 79,510 | 77,252 |
| Algorithm Name | Wind Curtailment Cost /CNY | Energy Purchase Cost /CNY | System Operation Cost /CNY |
|---|---|---|---|
| Standard PSO | 696 | 70,037 | 78,709 |
| EDIW-CPSO | 647 | 65,816 | 73,120 |
| Capacity of P2G/kW | Capacity of GSHP/kW | Wind Curtailment Rate | Comprehensive Cost/CNY | |
|---|---|---|---|---|
| Case 1 | 0 | 0 | 22.8% | 112,243 |
| Case 2 | 3200 | 0 | 4.7% | 103,251 |
| Case 3 | 0 | 2150 | 4.0% | 85,142 |
| Case 4 | 0 | 2250 | 3.9% | 83,930 |
| Case 5 | 950 | 1850 | 0.8% | 81,797 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, T.; Huo, T.; Li, H. Bi-Layer Planning of Integrated Energy System by Incorporating Power-to-Gas and Ground Source Heat Pump for Curtailed Wind Power and Economic Cost Reduction. Energies 2024, 17, 1447. https://doi.org/10.3390/en17061447
Wang T, Huo T, Li H. Bi-Layer Planning of Integrated Energy System by Incorporating Power-to-Gas and Ground Source Heat Pump for Curtailed Wind Power and Economic Cost Reduction. Energies. 2024; 17(6):1447. https://doi.org/10.3390/en17061447
Chicago/Turabian StyleWang, Tingling, Tianyu Huo, and Huihang Li. 2024. "Bi-Layer Planning of Integrated Energy System by Incorporating Power-to-Gas and Ground Source Heat Pump for Curtailed Wind Power and Economic Cost Reduction" Energies 17, no. 6: 1447. https://doi.org/10.3390/en17061447
APA StyleWang, T., Huo, T., & Li, H. (2024). Bi-Layer Planning of Integrated Energy System by Incorporating Power-to-Gas and Ground Source Heat Pump for Curtailed Wind Power and Economic Cost Reduction. Energies, 17(6), 1447. https://doi.org/10.3390/en17061447





