Common-Mode Voltage Reduction Method Based on Variable Sampling Frequency Finite Control Set-Model Predictive Control for PMSM Drive Systems
Abstract
1. Introduction
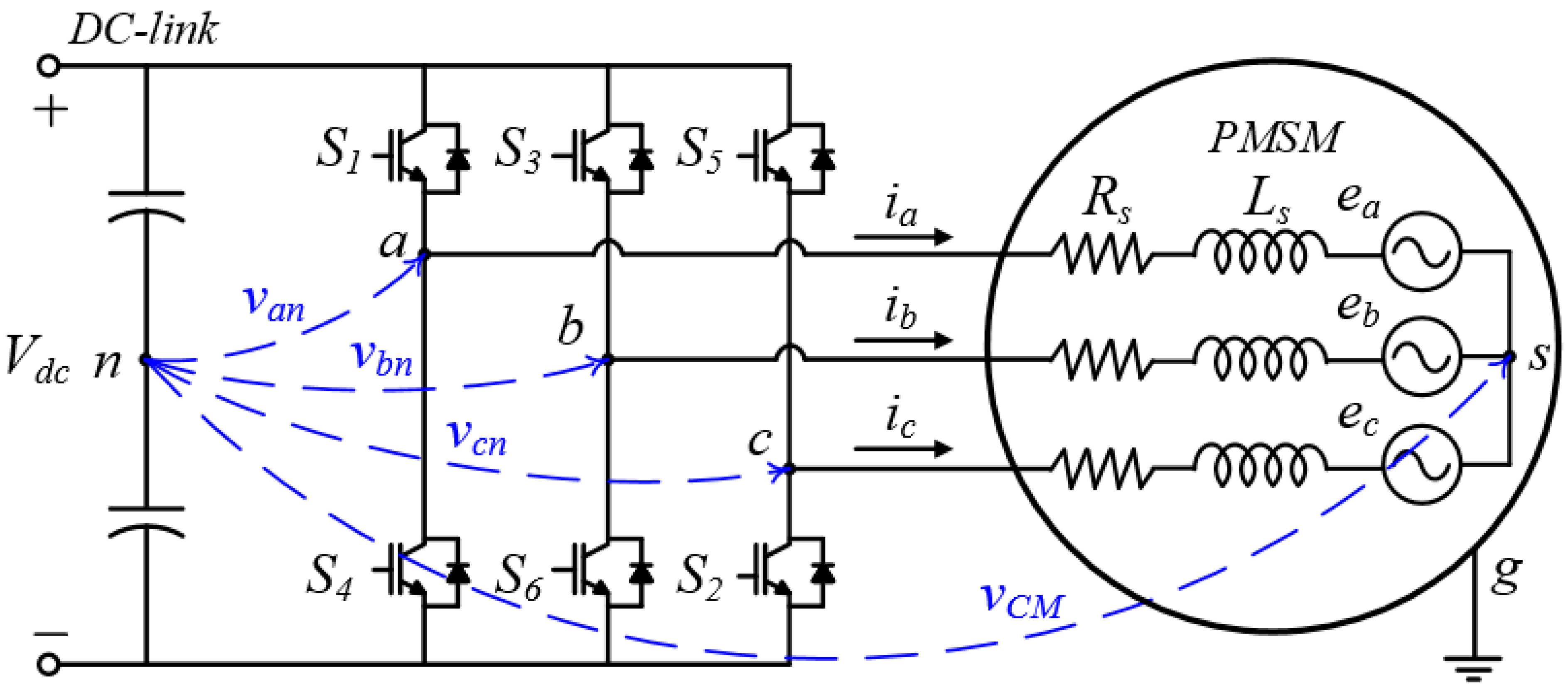
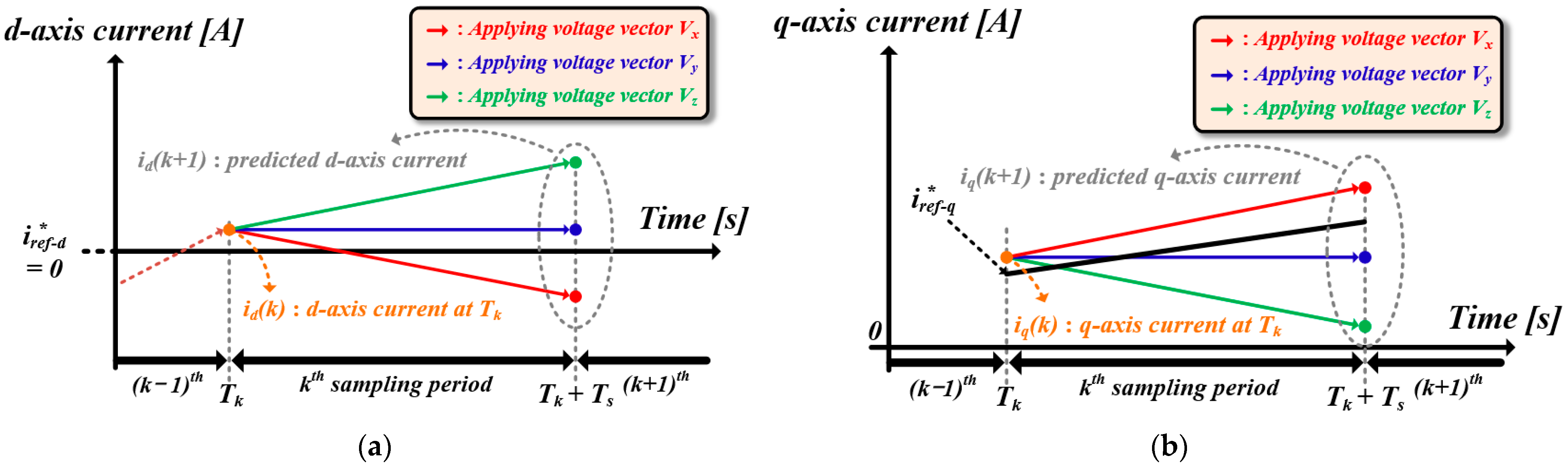
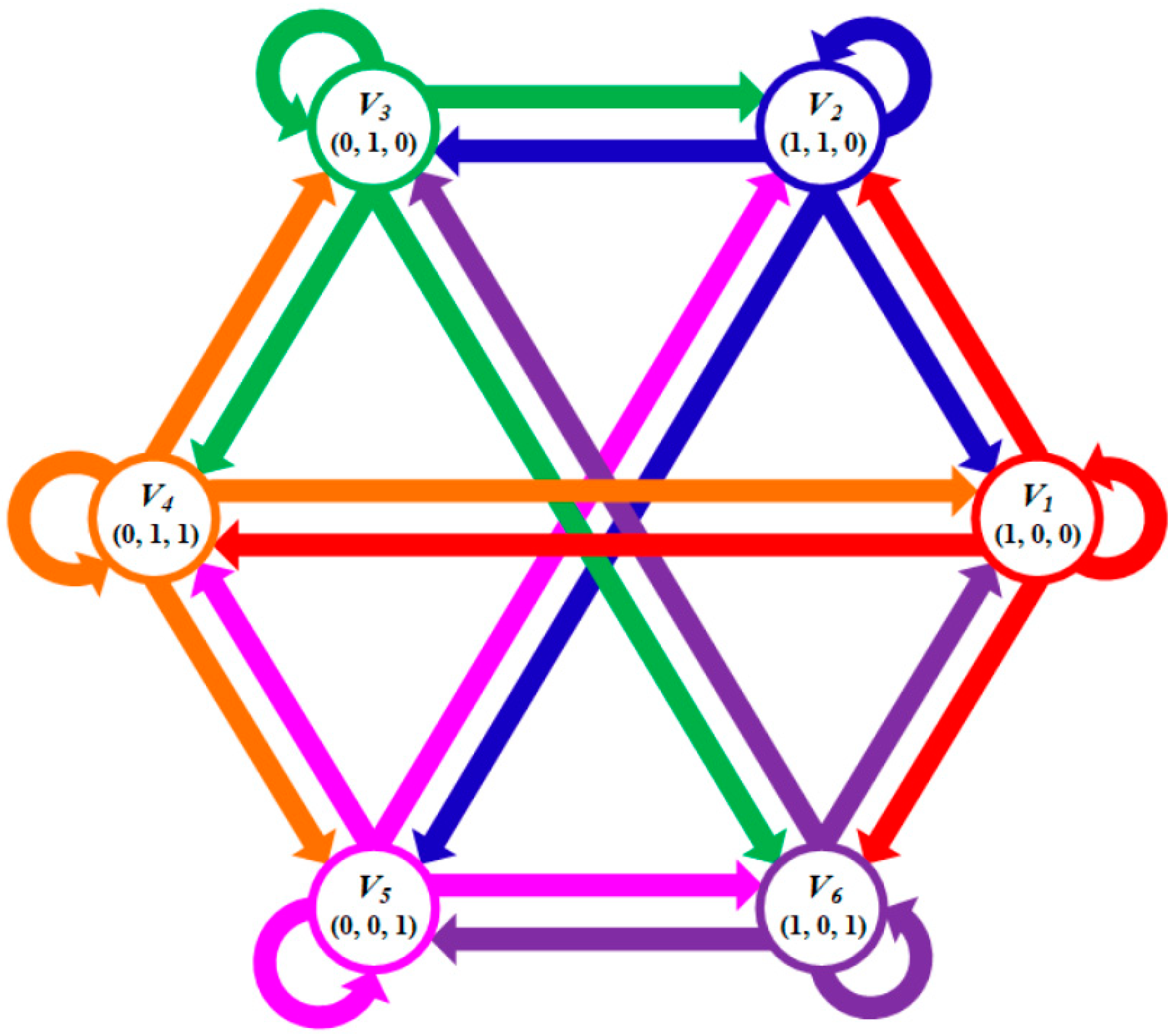
2. Review of Conventional FCS-MPC for CMV Reduction
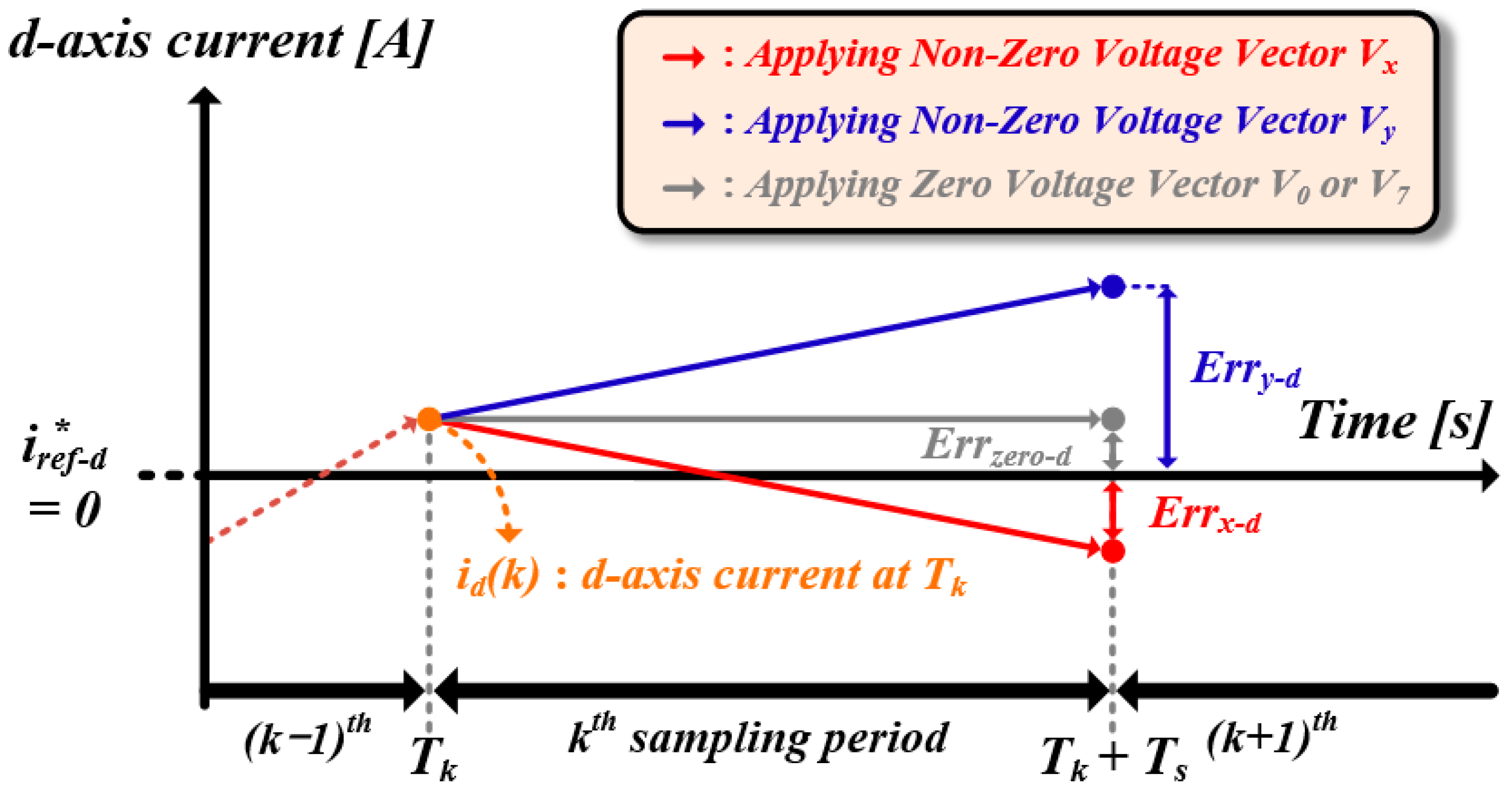
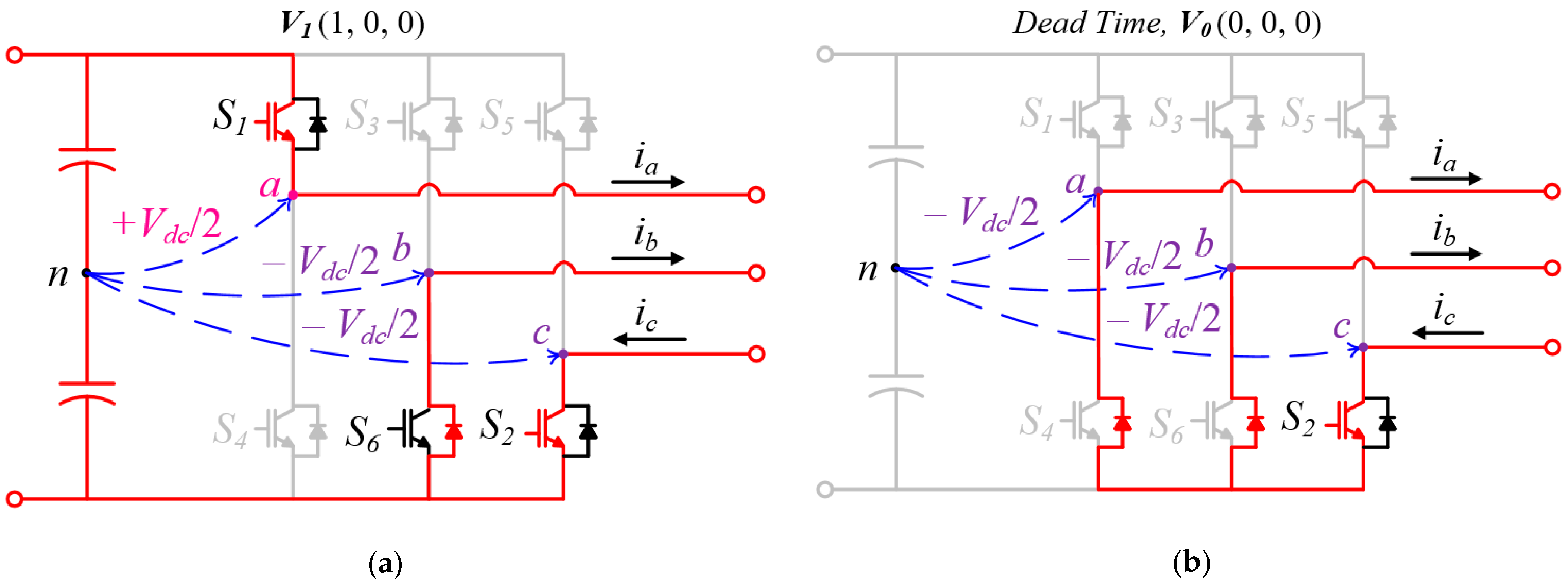
3. Consideration of the Dead Time Interval
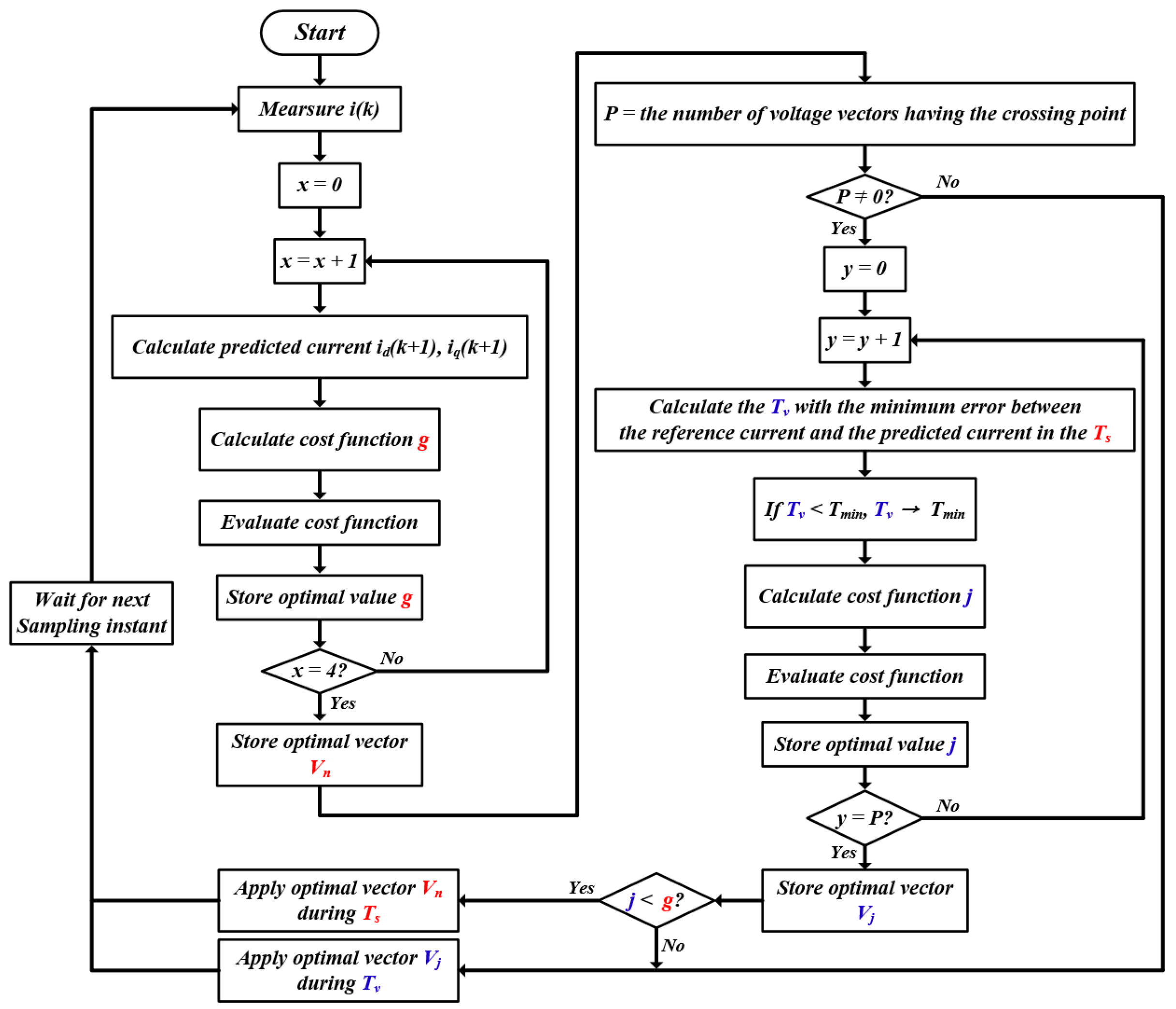
4. Proposed FCS-MPC with Variable Sampling for CMV Reduction
4.1. Minimum Value of Cost Function in Proposed Method
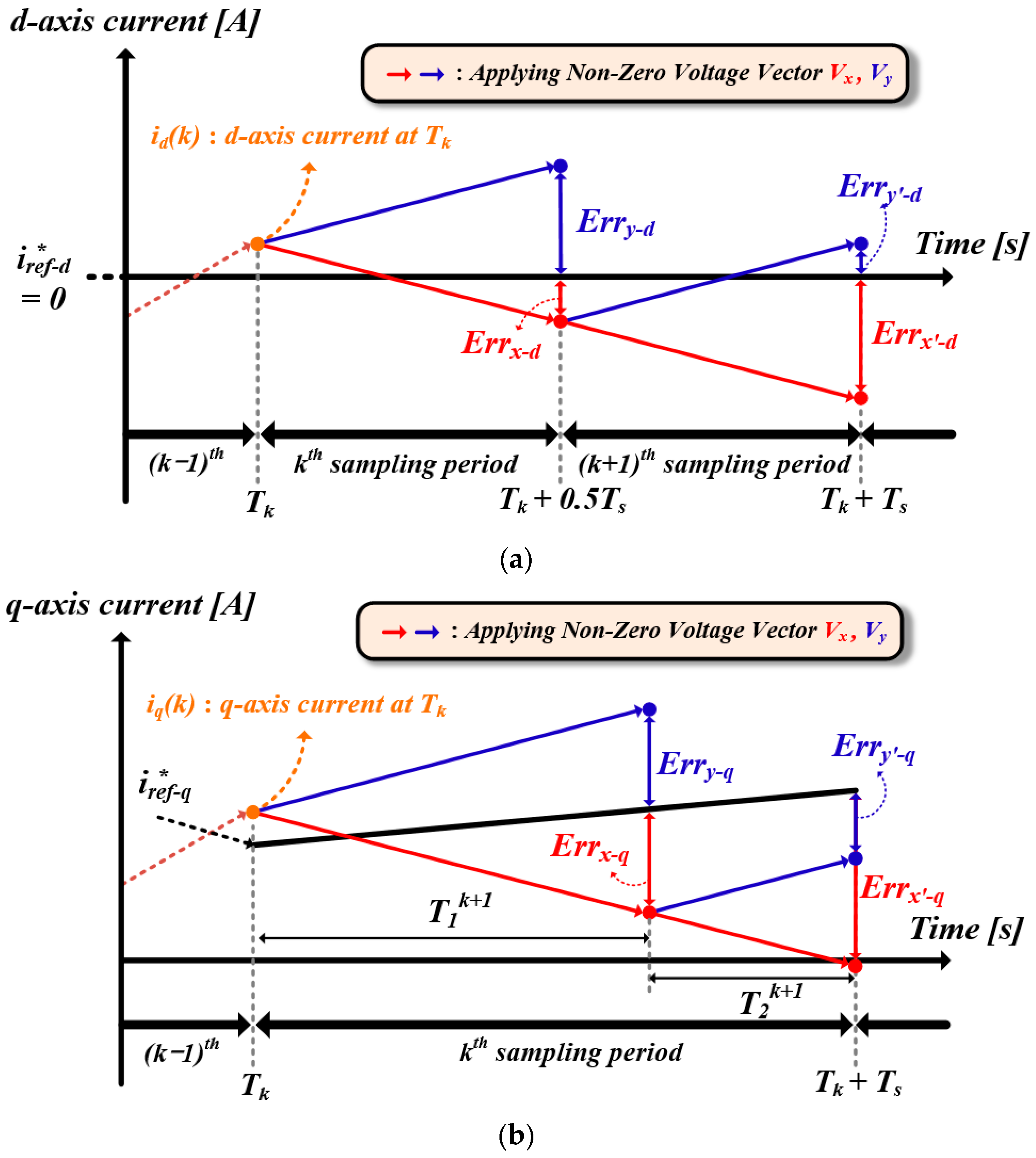
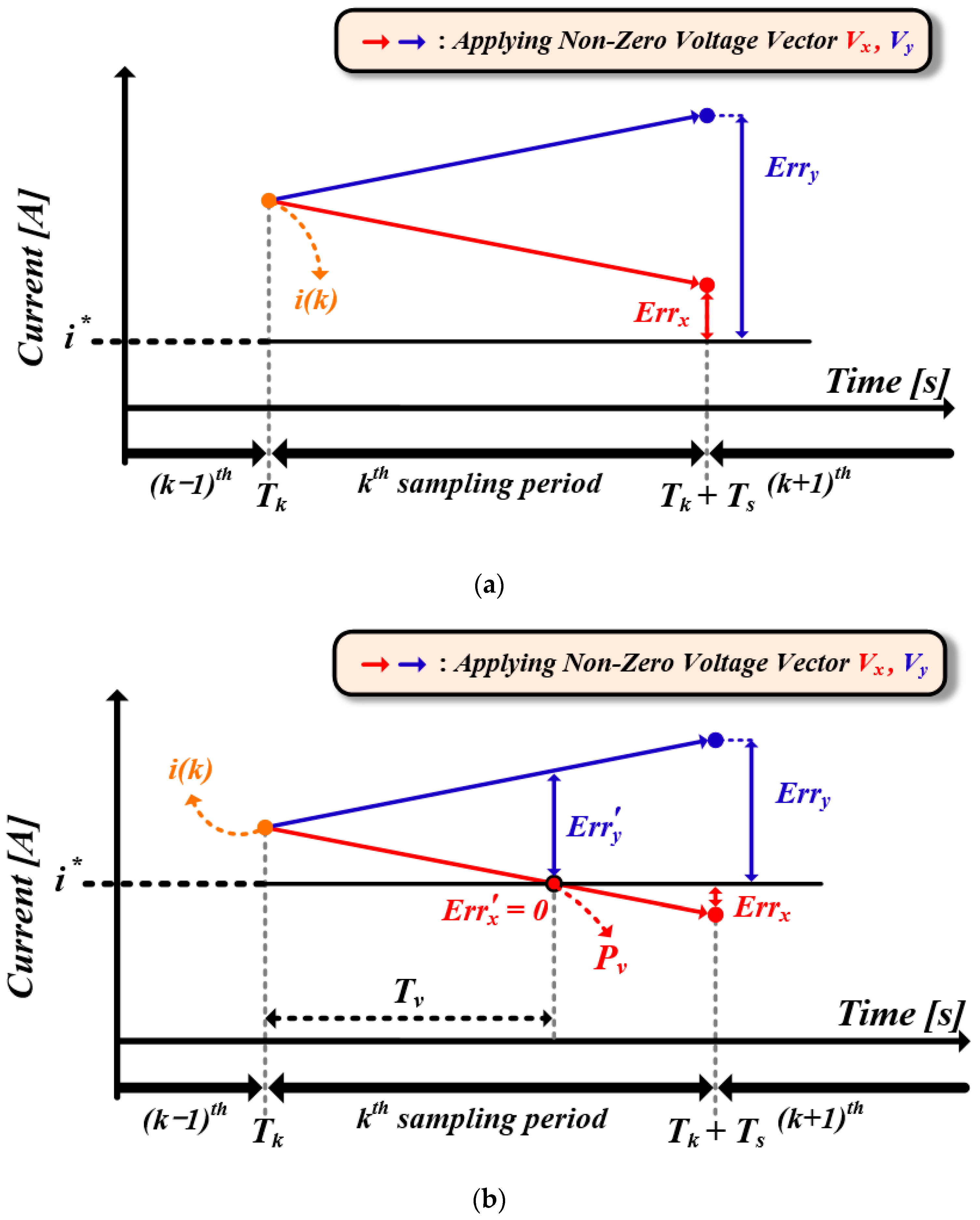
4.2. Calculation of Variable Sampling Period
4.3. Applicable Range of Variable Sampling
5. Simulation Results
5.1. FCS-MPC for Current Control
5.2. FCS-MPC Excluding ZVV
5.3. FCS-MPC Excluding ZVV with the Consideration of Dead Time (Sampling Frequencies: 10 kHz, 20 kHz)
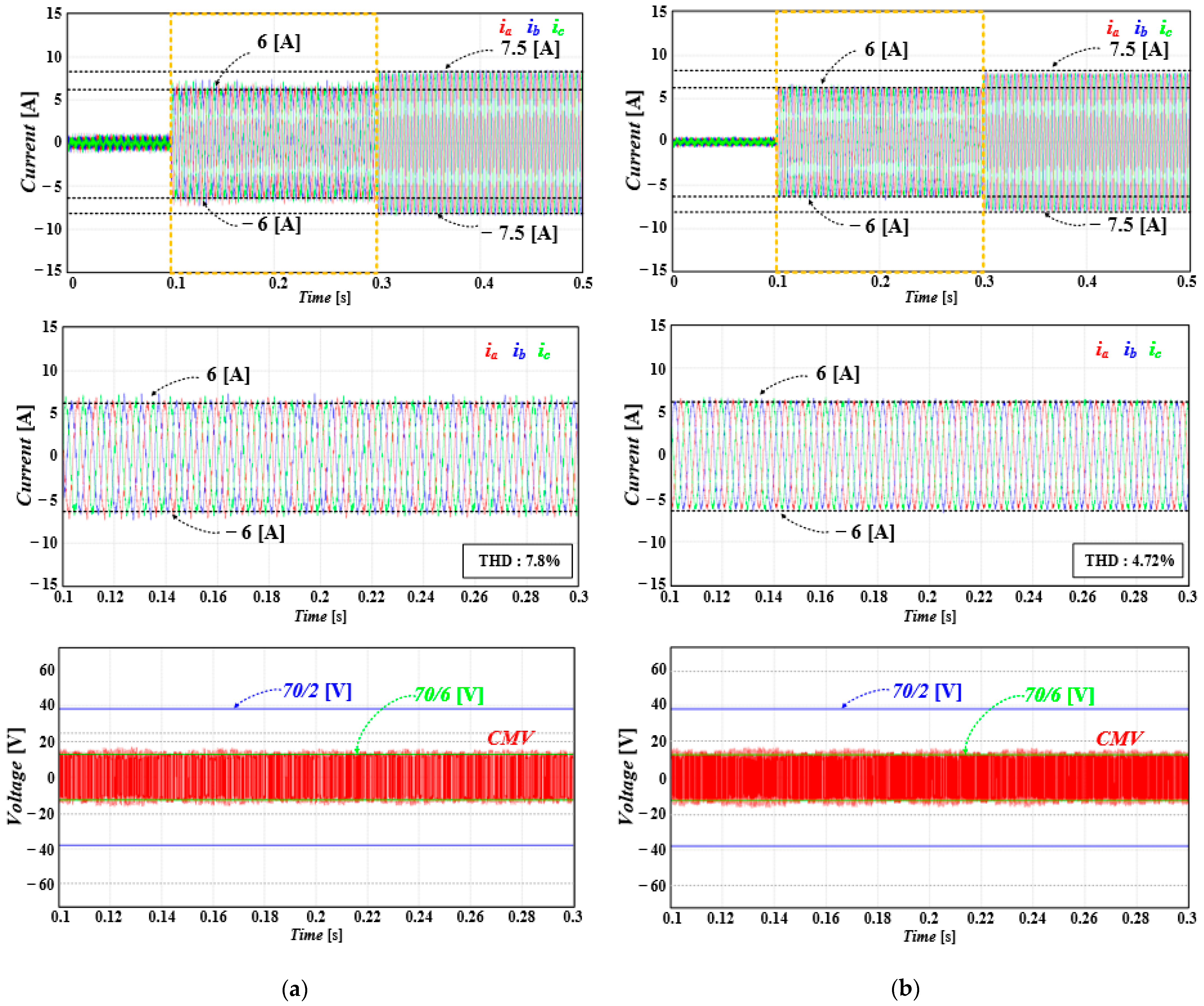
5.4. Proposed FCS-MPC for CMV Reduction with Variable Sampling Frequency
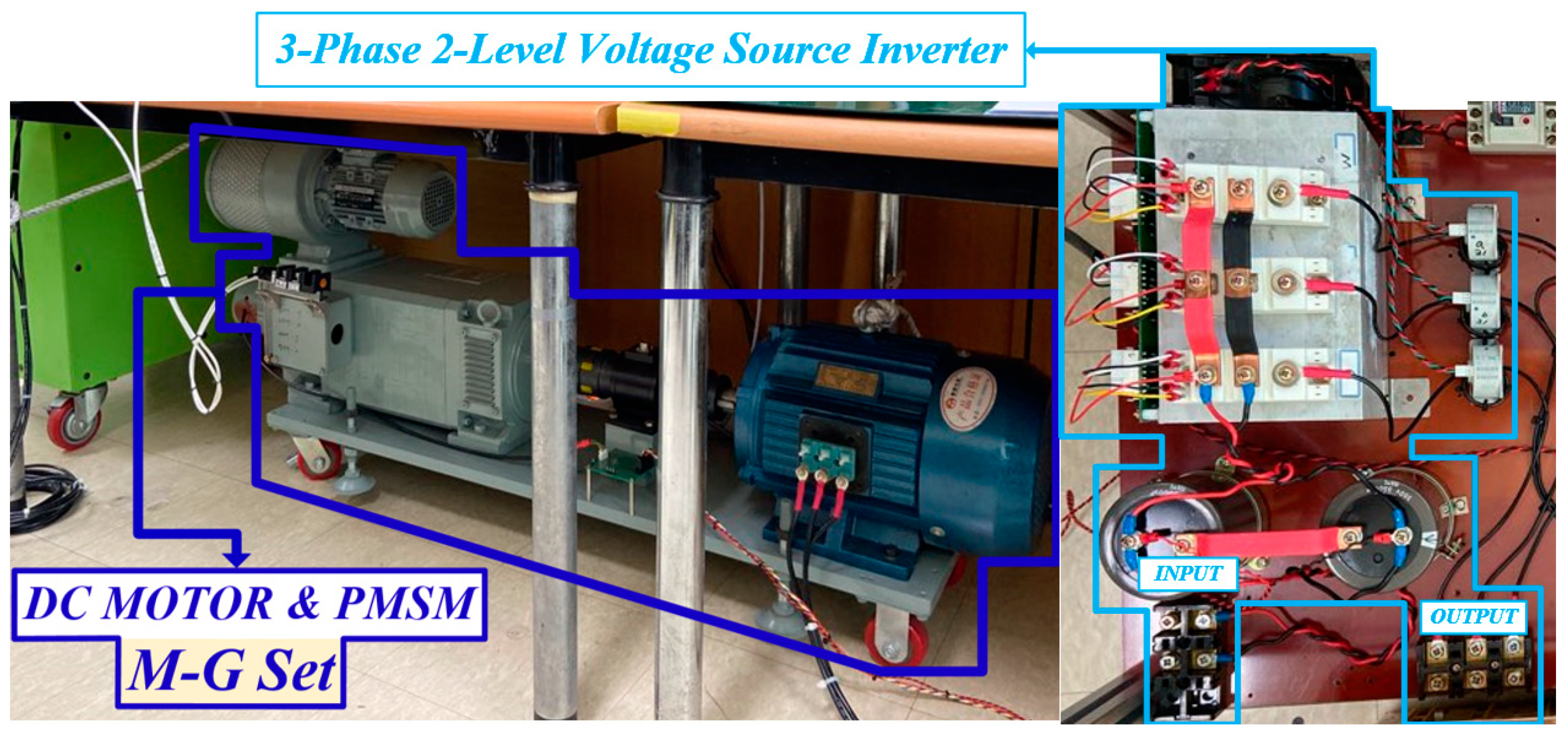
6. Experimental Results
6.1. FCS-MPC for Current Control
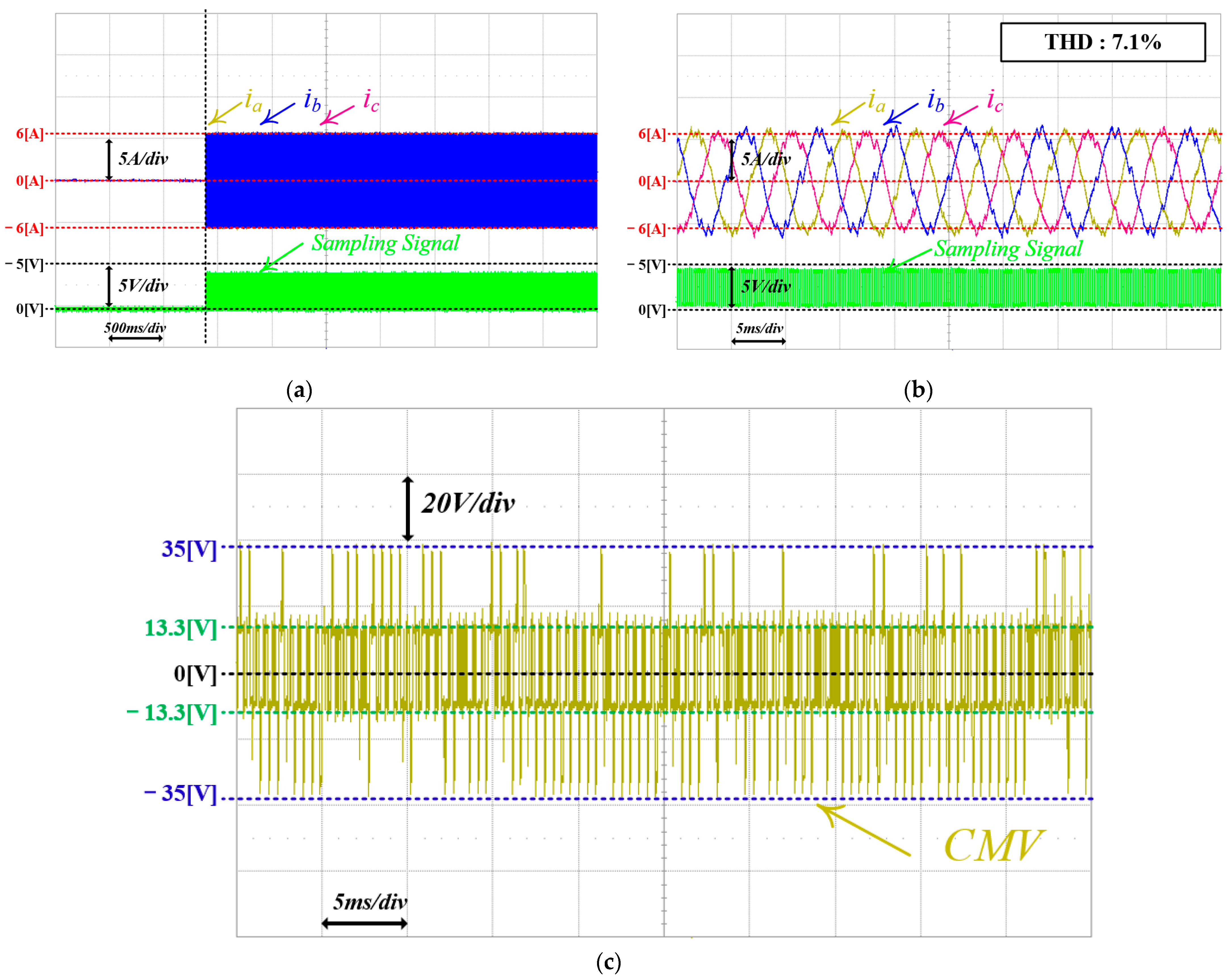
6.2. FCS-MPC Excluding ZVV
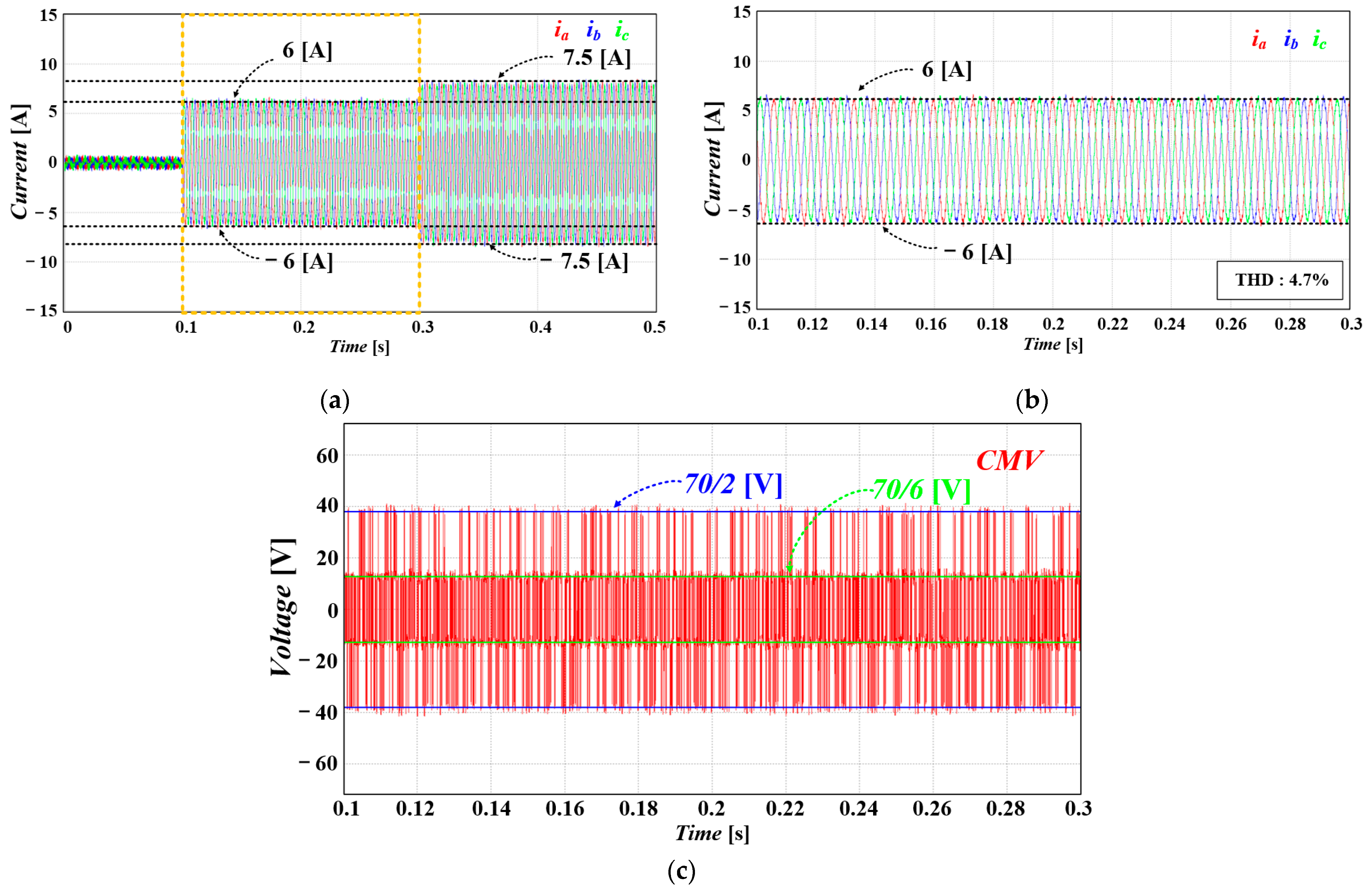
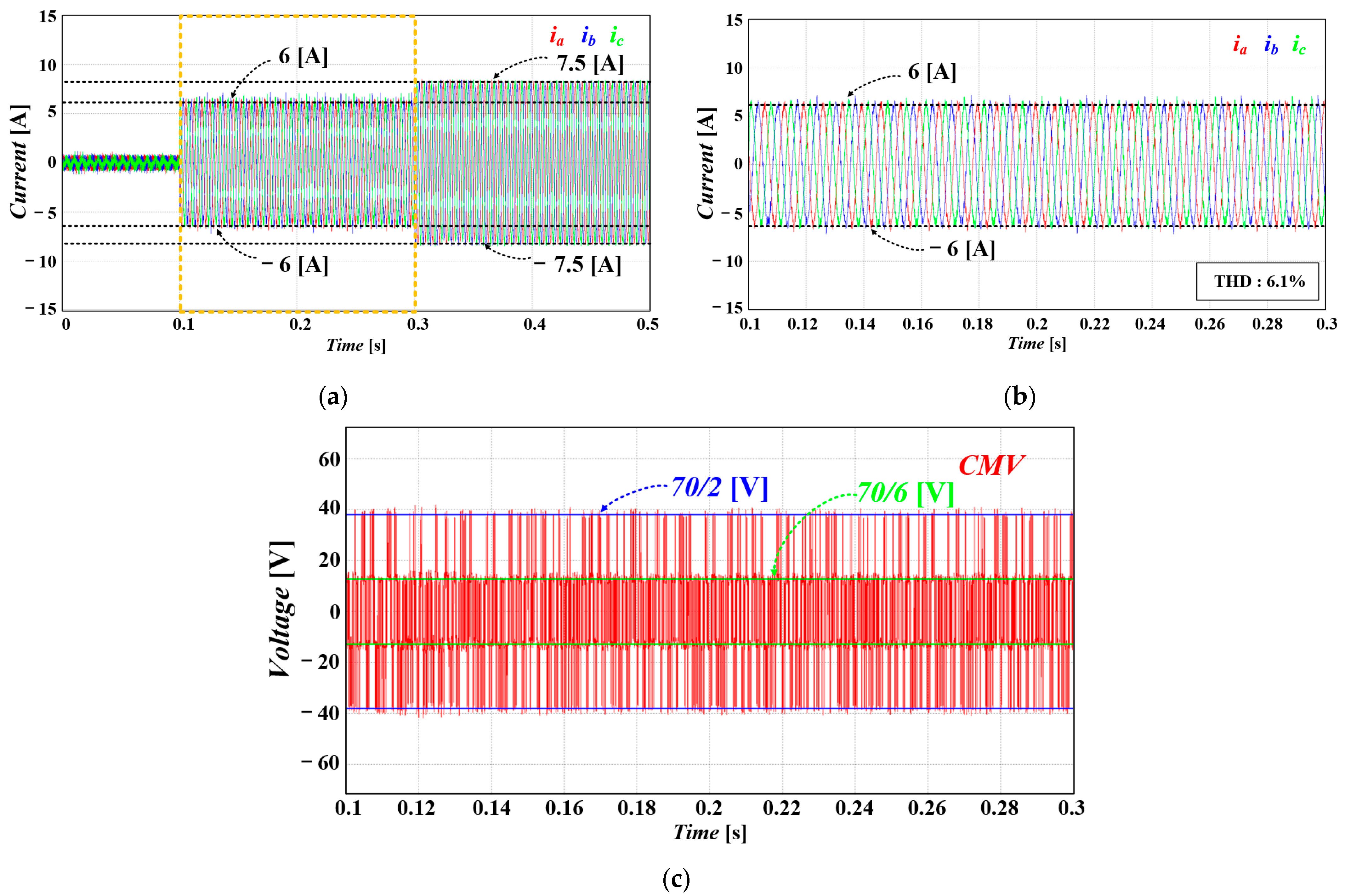
6.3. FCS-MPC Excluding ZVV with the Consideration of Dead Time Interval (Sampling Frequencies: 10 kHz, 20 kHz)
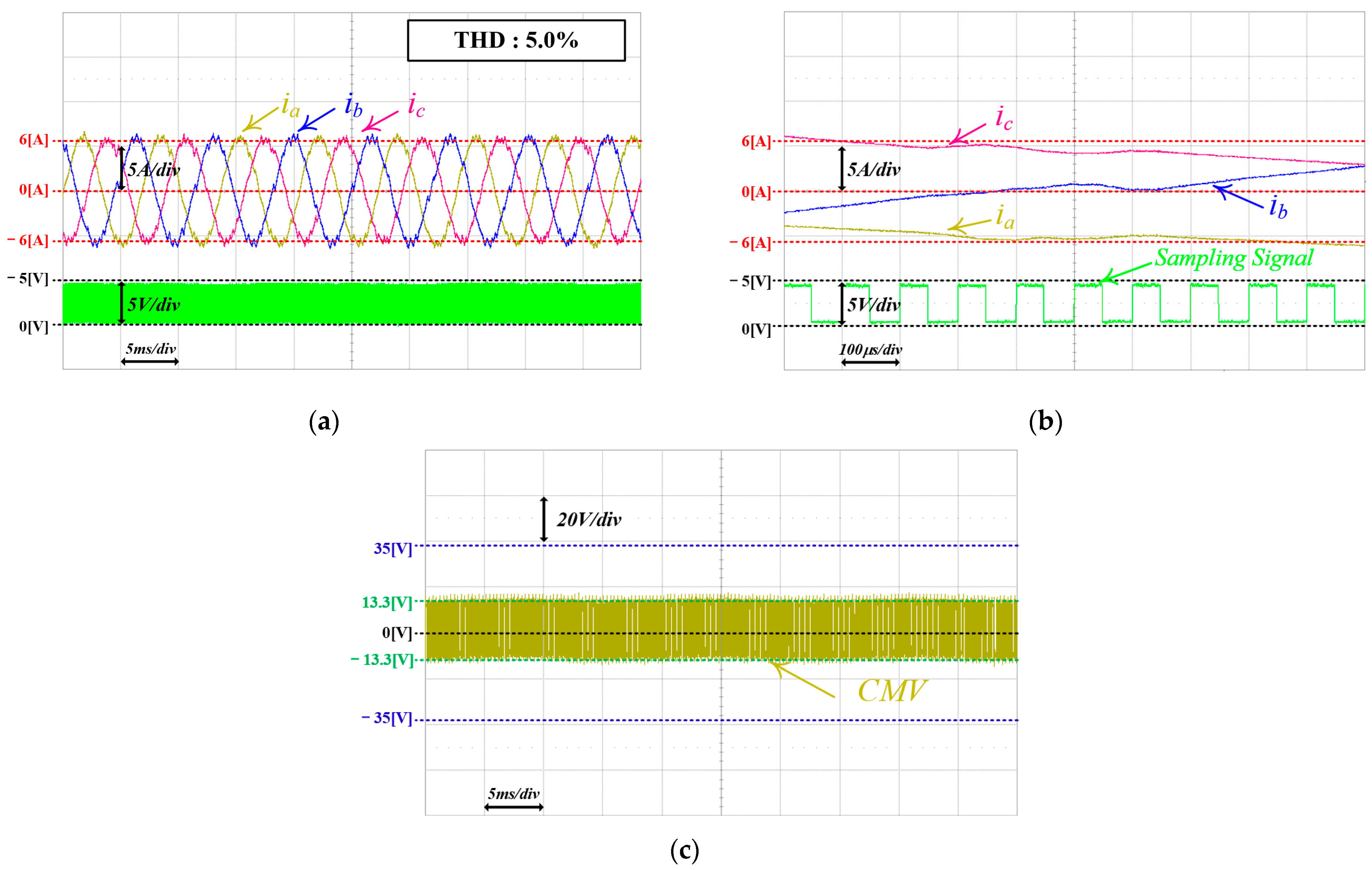
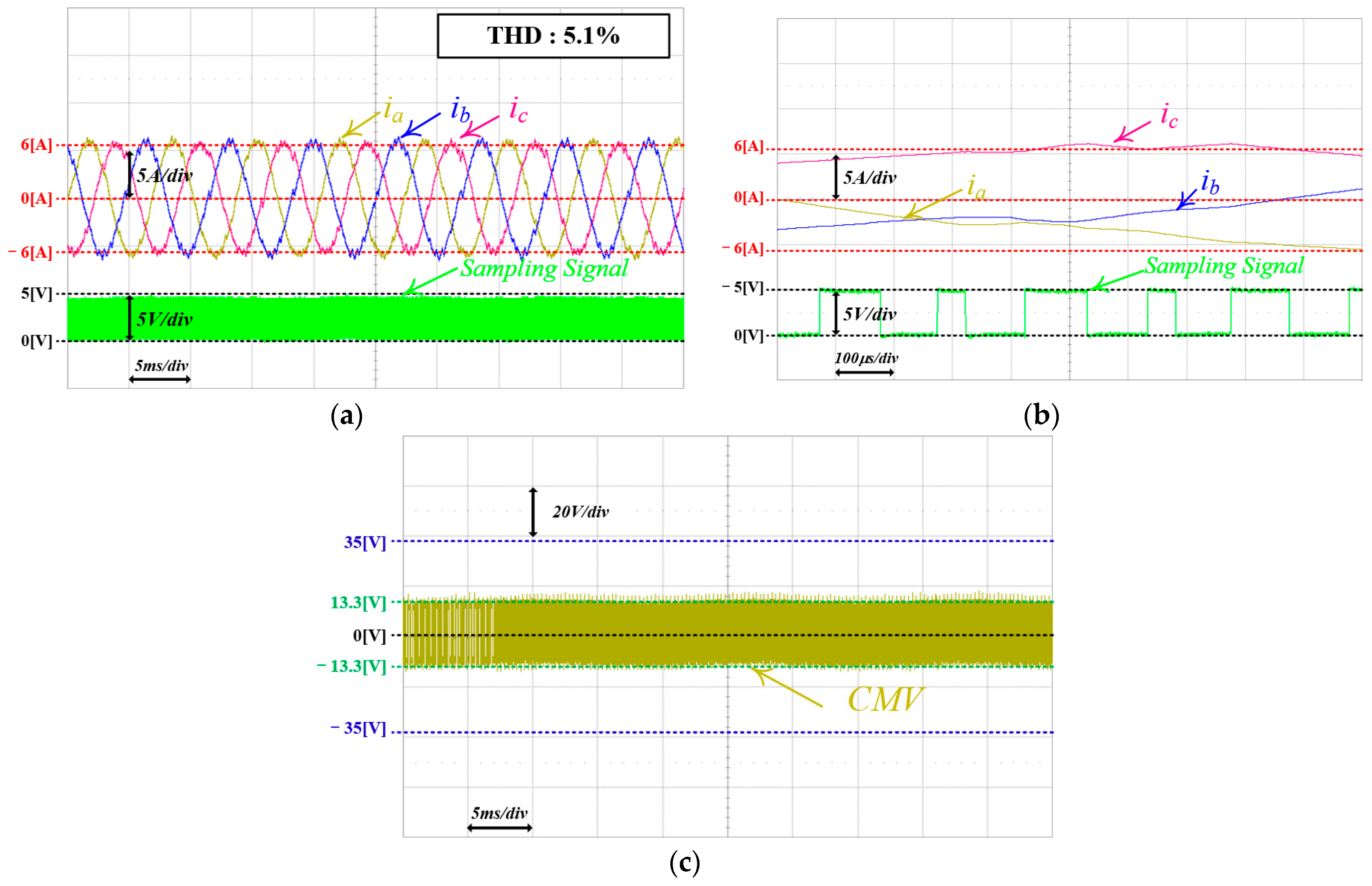
6.4. Proposed FCS-MPC for CMV Reduction with Variable Sampling Frequency
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liang, D.; Li, J.; Qu, R.; Kong, W. Adaptive Second-Order Sliding-Mode Observer for PMSM Sensorless Control Considering VSI Nonlinearity. IEEE Trans. Power Electron. 2018, 33, 8994–9004. [Google Scholar] [CrossRef]
- Amin, M.M.; Mohammed, O.A. Development of High-Performance Grid-Connected Wind Energy Conversion System for Optimum Utilization of Variable Speed Wind Turbines. IEEE Trans. Sustain. Energy 2011, 2, 235–245. [Google Scholar] [CrossRef]
- Dheer, D.K.; Vijay, A.S.; Kulkarni, O.V.; Doolla, S. Improvement of Stability Margin of Droop-Based Islanded Microgrids by Cascading of Lead Compensators. IEEE Trans. Ind. Appl. 2019, 55, 3241–3251. [Google Scholar] [CrossRef]
- Jha, S.K.; Kumar, D.; Tripathi, P.R.; Samantaray, S.R.; Kamwa, I. Demand-Side Management of Self-Sustained Droop Based Standalone Microgrid Using Conservation Voltage Reduction Strategy. IEEE Syst. J. 2023, 17, 2640–2651. [Google Scholar] [CrossRef]
- Kumar, R.; Singh, B. Grid Interactive Solar PV-Based Water Pumping Using BLDC Motor Drive. IEEE Trans. Ind. Appl. 2019, 55, 5153–5165. [Google Scholar] [CrossRef]
- Han, D.; Peng, F.Z.; Dwari, S. Advanced PWM Techniques for Multi-Level Inverters with a Multi-Level Active CM Noise Filter. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 6865–6879. [Google Scholar] [CrossRef]
- Jeong, W.-S.; Lee, Y.-S.; Lee, J.-H.; Lee, C.-H.; Won, C.-Y. Space Vector Modulation (SVM)-Based Common-Mode Current (CMC) Reduction Method of H8 Inverter for Permanent Magnet Synchronous Motor (PMSM) Drives. Energies 2022, 15, 266. [Google Scholar] [CrossRef]
- Jeong, W.-S.; Kim, S.-H.; Yi, J.; Won, C.-Y. Finite Control Set–Model Predictive Control of H8 Inverter Considering Dead-Time Effect for PMSM Drive Systems with Reduced Conducted Common-Mode EMI and Current Distortions. IEEE Trans. Power Electron. 2022, 37, 5342–5356. [Google Scholar] [CrossRef]
- Hava, A.M.; Ün, E. Performance Analysis of Reduced Common-Mode Voltage PWM Methods and Comparison with Standard PWM Methods for Three-Phase Voltage-Source Inverters. IEEE Trans. Power Electron. 2009, 24, 241–252. [Google Scholar] [CrossRef]
- Kwak, S.; Mun, S. Common-mode voltage mitigation with a predictive control method considering dead time effects of three-phase voltage source inverters. IET Power Electron. 2015, 8, 1690–1700. [Google Scholar] [CrossRef]
- Ramírez, R.O.; Baier, C.R.; Espinoza, J.; Villarroel, F. Finite Control Set MPC with Fixed Switching Frequency Applied to a Grid Connected Single-Phase Cascade H-Bridge Inverter. Energies 2020, 13, 5475. [Google Scholar] [CrossRef]
- Rivera, M. Predictive current control for a VSI with reduced common mode voltage operating at fixed switching frequency. In Proceedings of the 2015 IEEE 24th International Symposium on Industrial Electronics (ISIE), Buzios, Brazil, 3–5 June 2015; pp. 980–985. [Google Scholar] [CrossRef]
- Guo, L.; Jin, N.; Gan, C.; Xu, L.; Wang, Q. An Improved Model Predictive Control Strategy to Reduce Common-Mode Voltage for Two-Level Voltage Source Inverters Considering Dead-Time Effects. IEEE Trans. Ind. Electron. 2019, 66, 3561–3572. [Google Scholar] [CrossRef]
- Karasala, C.; Panindra, K.V.; Kumar, A.P.; Ganjikunta, S.K. Model Predictive Control of PVGCI for Reducing Common Mode Voltage and Switching Frequency. IEEE J. Emerg. Sel. Top. Power Electron. 2023, 11, 3064–3075. [Google Scholar] [CrossRef]
- Kwak, S.; Mun, S.-K. Model Predictive Control Methods to Reduce Common-Mode Voltage for Three-Phase Voltage Source Inverters. IEEE Trans. Power Electron. 2015, 30, 5019–5035. [Google Scholar] [CrossRef]
- Hoseini, S.K.; Adabi, J.; Sheikholeslami, A. Predictive Modulation Schemes to Reduce Common-mode Voltage in Three-phase Inverters-fed AC Drive Systems. IET Power Electron. 2014, 7, 840–849. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, J.; Li, J. Modeling, Analysis, and Mitigation of Load Neutral Point Voltage for Three-Phase Four-Leg Inverter. IEEE Trans. Ind. Electron. 2013, 60, 2010–2021. [Google Scholar] [CrossRef]
- Yang, Y.; Pan, J.; Wen, H.; Zhang, X.; Norambuena, M.; Xu, L.; Rodriguez, J. Computationally Efficient Model Predictive Control with Fixed Switching Frequency of Five-Level ANPC Converters. IEEE Trans. Ind. Electron. 2022, 69, 11903–11914. [Google Scholar] [CrossRef]





| VV | Switching State (Sa, Sb, Sc) 1 | CMV Level | |
|---|---|---|---|
| ZVV | V0 | (0, 0, 0) | −Vdc/2 |
| Non-ZVV | V1 | (1, 0, 0) | −Vdc/6 |
| V2 | (1, 1, 0) | +Vdc/6 | |
| V3 | (0, 1, 0) | −Vdc/6 | |
| V4 | (0, 1, 1) | +Vdc/6 | |
| V5 | (0, 0, 1) | −Vdc/6 | |
| V6 | (1, 0, 1) | +Vdc/6 | |
| ZVV | V7 | (1, 1, 1) | +Vdc/2 |
| Present VV | V1 | V2 | V3 |
| Future VV | V3, V5 | V4, V6 | V1, V5 |
| Present VV | V4 | V5 | V6 |
| Future VV | V2, V6 | V1, V3 | V2, V4 |
| Parameter | Description | Value | Unit |
|---|---|---|---|
| Vdc | DC-Link Voltage | 70 | V |
| Prate | Rated Power | 1.1 | kW |
| ωrate | Rated Speed | 1500 | rpm |
| Irate | Rated Current | 9.5 | A |
| Trate | Rated Torque | 7.0 | Nm |
| p | Number of Poles | 24 | - |
| Rs | Stator Resistance | 0.18 | Ω |
| Ls | Stator Inductance | 3.4 | mH |
| Vpk/krpm | Peak Line-to-Line Back EMF Constant | 43.5 | V/krpm |
| Methods | Current Control | Excluding ZVV | Excluding ZVV and Considering Dead Time (10 kHz) | Excluding ZVV and Considering Dead Time (20 kHz) | Variable Sampling Frequency (Proposed) |
|---|---|---|---|---|---|
| THD of Load Current | 5.4% | 7.1% | 7.9% | 5.0% | 5.1% |
| Switching State Changes | 46 | 47 | 45 | 92 | 76 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, Y.-S.; Choo, K.-M.; Lee, C.-H.; An, C.-G.; Yi, J.; Won, C.-Y. Common-Mode Voltage Reduction Method Based on Variable Sampling Frequency Finite Control Set-Model Predictive Control for PMSM Drive Systems. Energies 2024, 17, 1443. https://doi.org/10.3390/en17061443
Lee Y-S, Choo K-M, Lee C-H, An C-G, Yi J, Won C-Y. Common-Mode Voltage Reduction Method Based on Variable Sampling Frequency Finite Control Set-Model Predictive Control for PMSM Drive Systems. Energies. 2024; 17(6):1443. https://doi.org/10.3390/en17061443
Chicago/Turabian StyleLee, Yoon-Seong, Kyoung-Min Choo, Chang-Hee Lee, Chang-Gyun An, Junsin Yi, and Chung-Yuen Won. 2024. "Common-Mode Voltage Reduction Method Based on Variable Sampling Frequency Finite Control Set-Model Predictive Control for PMSM Drive Systems" Energies 17, no. 6: 1443. https://doi.org/10.3390/en17061443
APA StyleLee, Y.-S., Choo, K.-M., Lee, C.-H., An, C.-G., Yi, J., & Won, C.-Y. (2024). Common-Mode Voltage Reduction Method Based on Variable Sampling Frequency Finite Control Set-Model Predictive Control for PMSM Drive Systems. Energies, 17(6), 1443. https://doi.org/10.3390/en17061443







