Addressing Confidence in Modeling of Contrail Formation from E-Fuels in Aviation Using Large Eddy Simulation Parametrization
Abstract
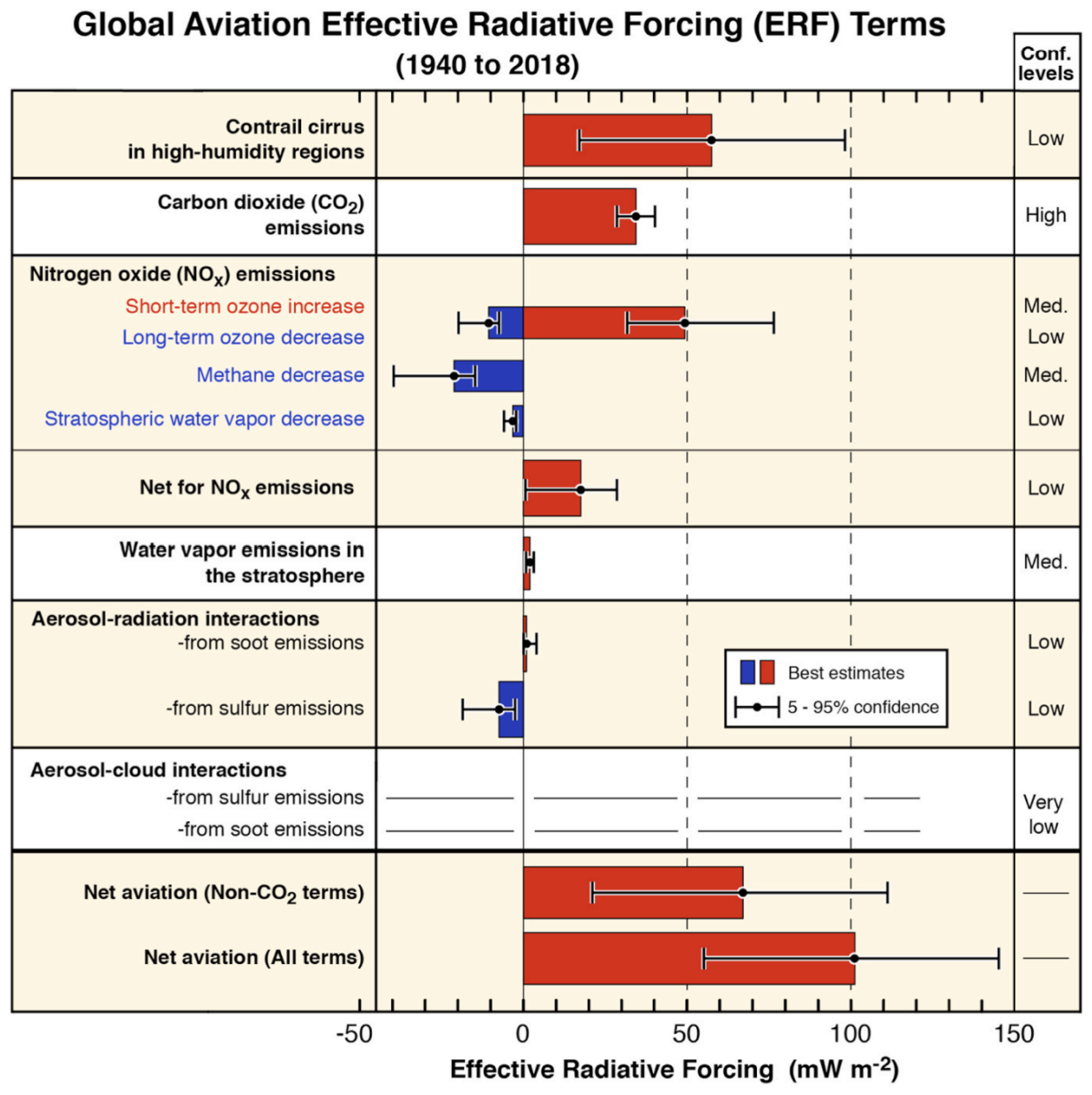
1. Introduction
2. Original Contrail Model
2.1. Contrail Formation
2.2. Early Stage Contrails
2.3. Ice Properties
2.4. Contrail Cirrus
3. LES-Based Contrail Parametrization
3.1. Compatibilization of Inputs
- Ambient temperature T, from the atmospheric data model
- Supersaturation , which is related to the ambient relative humidity
- The dimensional Brunt-Väisälä frequency
- The ice crystal emission index , which, again, is assumed to be equal to the soot emission index for soot-rich regimes
- The wingspan and the mass of the aircraft
- The mass flow of fuel per flight distance
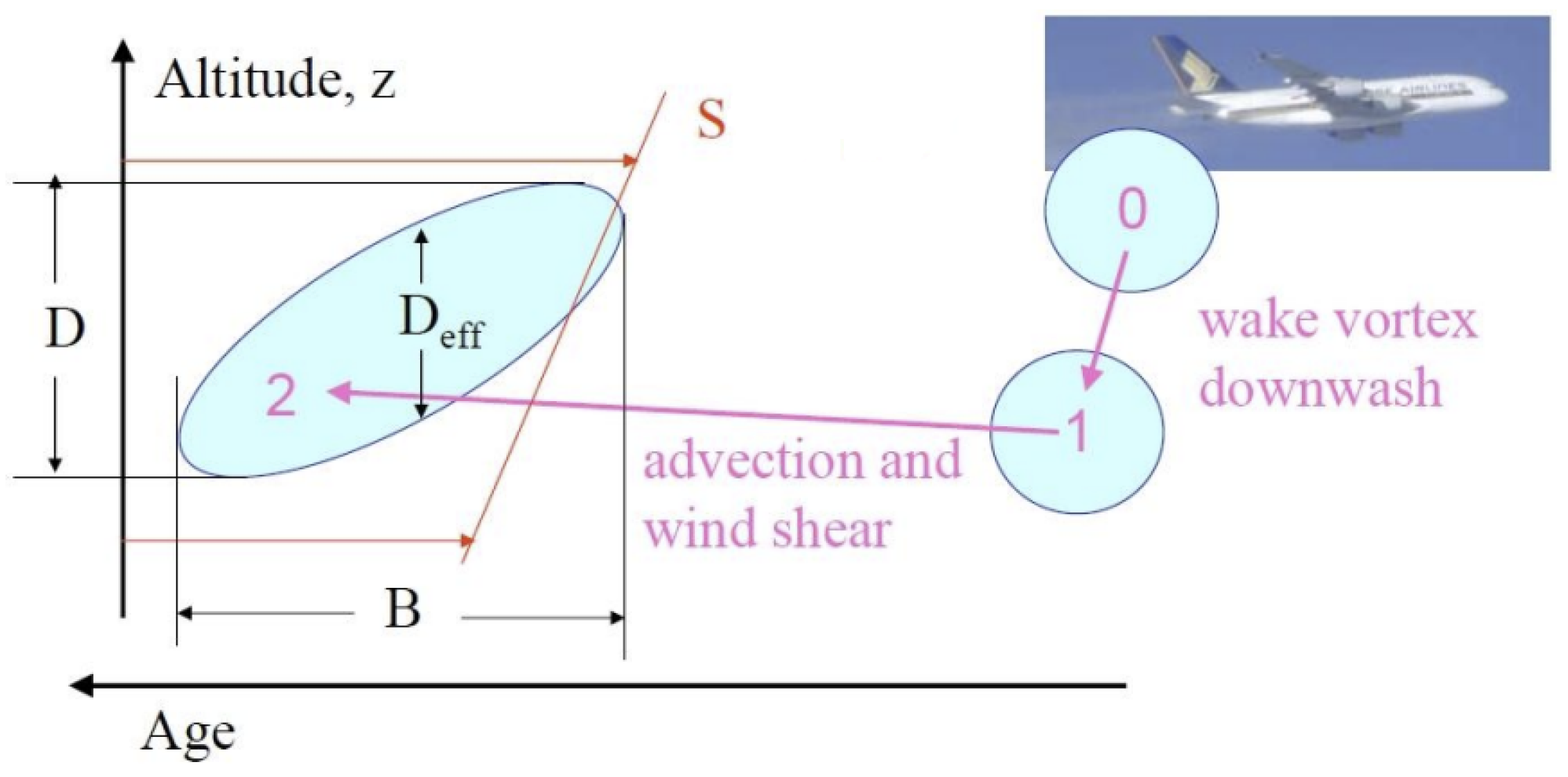
3.2. Length Scales
3.3. Ice Crystal Loss
3.4. Contrail Depth and Width
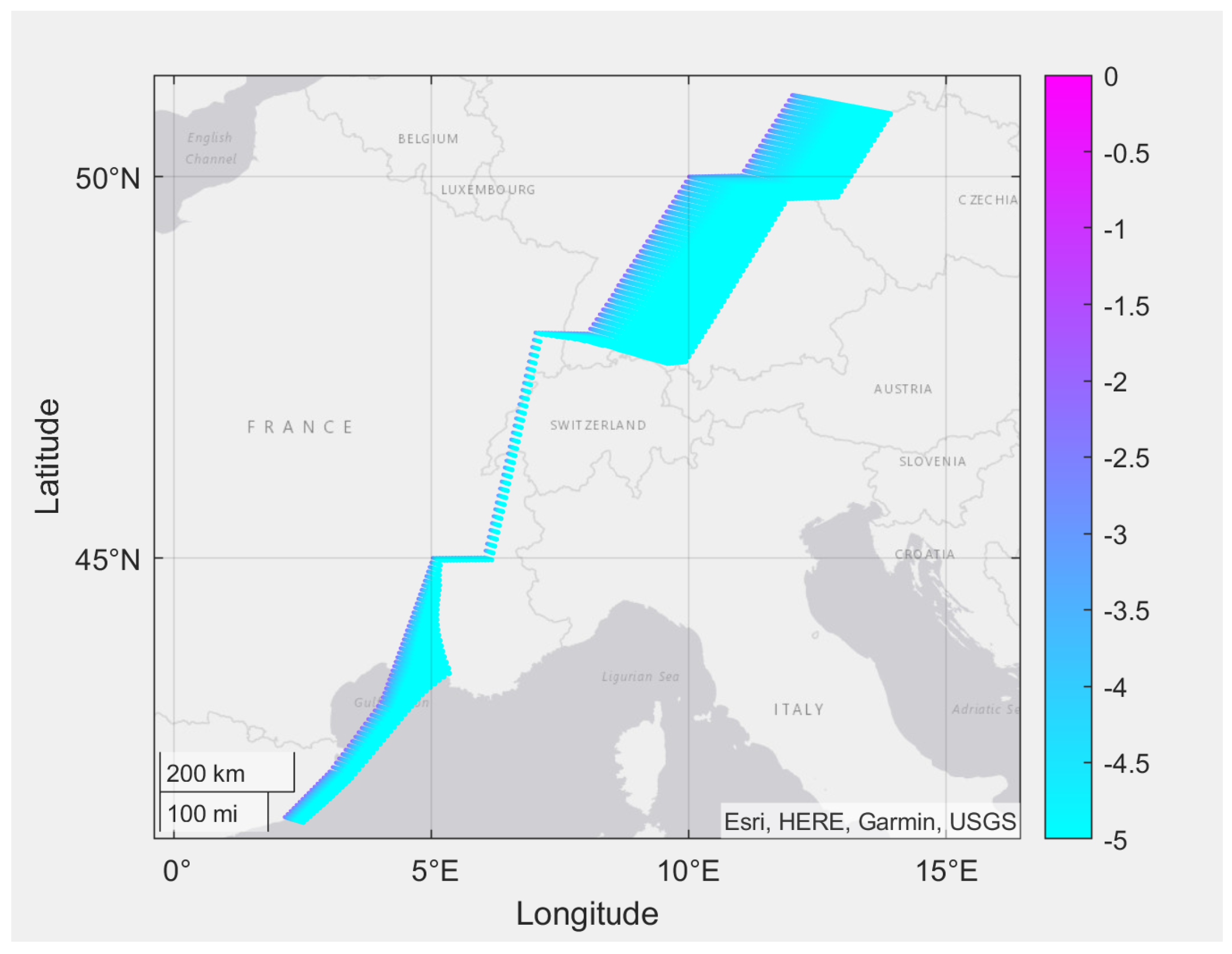
3.5. Implementation, Verification, and Validation
4. Simulation Results
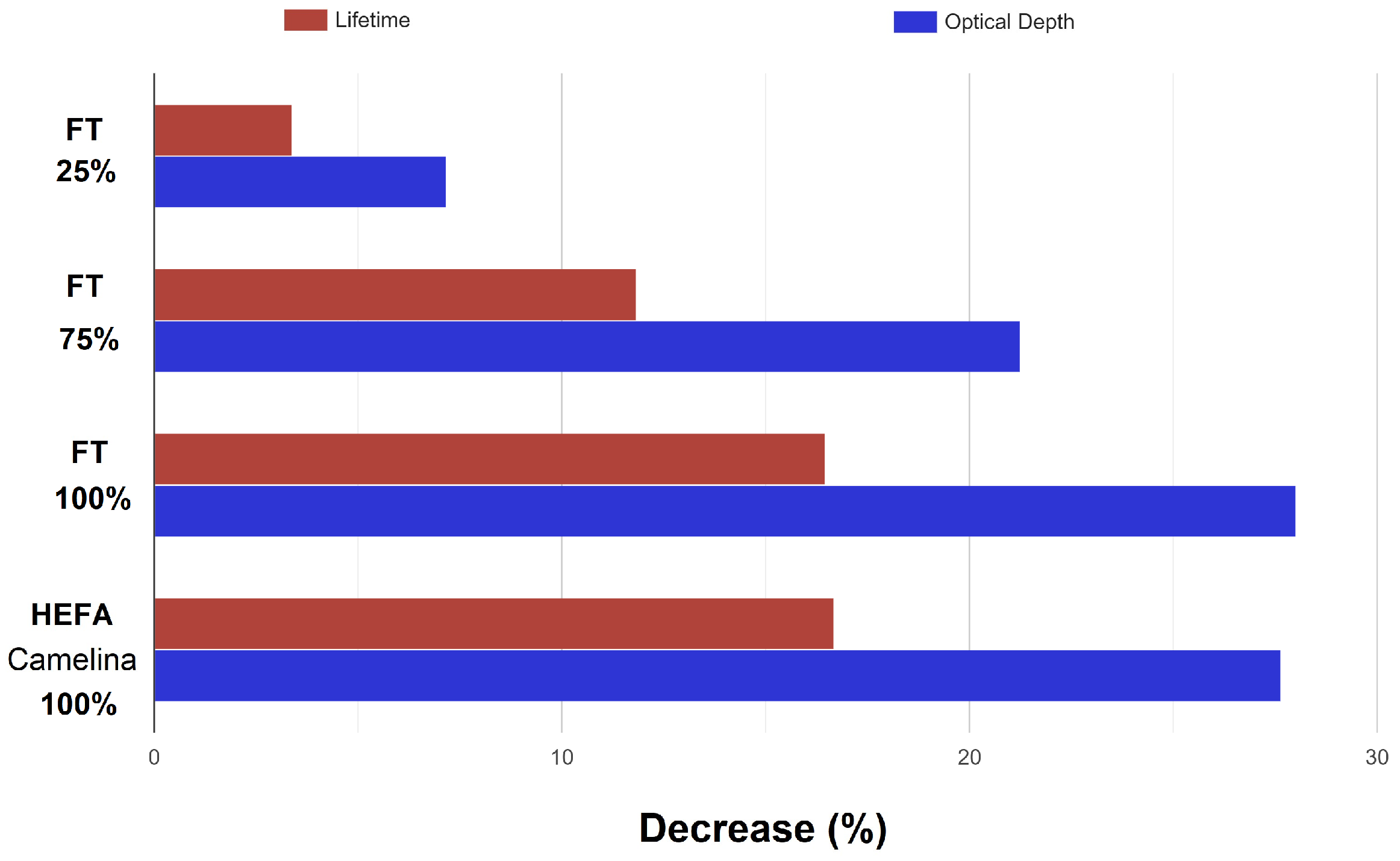
4.1. Impact of E-Fuels
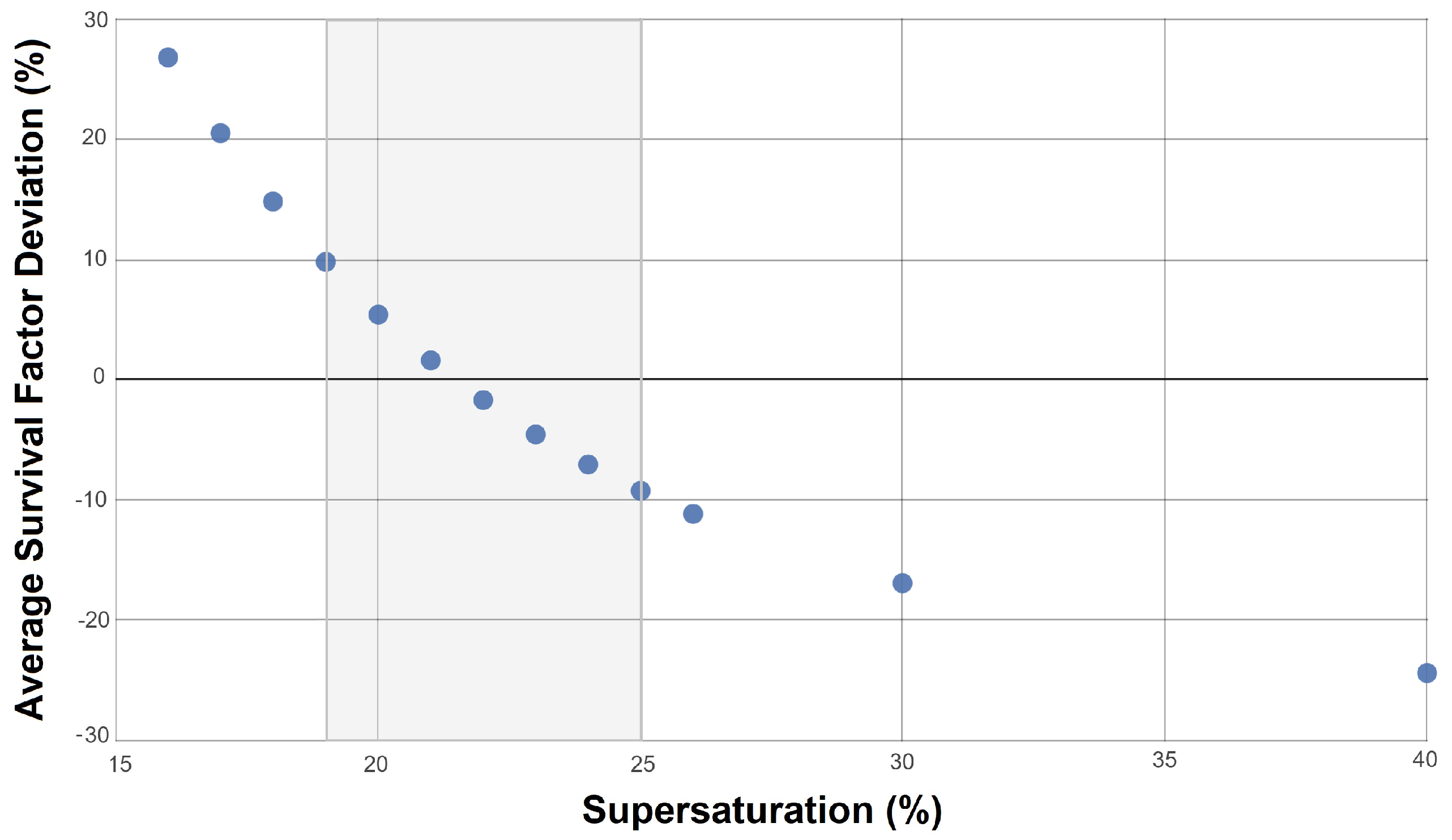
4.2. Shortcomings of the Original Contrail Model
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| CoCiP | Contrail Cirrus Prediction Model |
| CTL | Coal-to-Liquid |
| FT | Fischer–Tropsch |
| GHG | Greenhouse Gases |
| GTL | Gas-to-Liquid |
| HEFA | Hydroprocessed Esters and Fatty Acids |
| LES | Large Eddy Simulation |
| PtL | Power-to-Liquid |
| RF | Radiative Forcing |
| SAC | Schmidt–-Appleman Criterion |
| SAF | Sustainable Aviation Fuel |
| SPK | Synthetic Paraffinic Kerosene |
| TAS | True Air Speed |
| TRL | Technological Readiness Level |
| Nomenclature | |
| Propulsion efficiency | |
| Eddy dissipation rate (J/(kg s)) | |
| Initial vortex circulation (m2/s) | |
| Dry adiabatic lapse rate (K/km) | |
| Water vapor emission (kg/m) | |
| Density (kg/m3) | |
| Emitted “concentration” (kg/m3) | |
| Optical depth | |
| Non-dimensional total temperature | |
| A | Area (m2) |
| B | Contrail width (m) |
| Initial vortex separation (m) | |
| Specific heat of air at constant pressure (J/(kg K)) | |
| D | Contrail depth (m) |
| Partial water pressure at saturation (Pa) | |
| Water emission index (kg-water/kg-fuel) | |
| Ice crystal emission index (kg-fuel−1) | |
| Particle number emission index (kg-fuel−1) | |
| Fraction of surviving ice crystals | |
| G | Mixing line gradient (Pa/k) |
| g | Gravitational acceleration (m/s2) |
| Parametrized depth for a 5 min old contrail (m) | |
| I | Ice mass ratio |
| Mass flow of fuel per flight distance (kg/(s m)) | |
| Hydrogen mass ratio in the fuel | |
| Aircraft mass (kg) | |
| Molar mass of hydrogen (kg/mol) | |
| Molar mass of water (kg/mol) | |
| N | Number of ice crystals per flight distance (m−1) |
| Normalized Brunt-Väisälä frequency | |
| Brunt-Väisälä frequency (s−1) | |
| Parametrized mean ice crystal number concentration (m−3) | |
| P | Pressure (Pa) |
| Q | Fuel combustion heat (J/kg) |
| q | Absolute humidity (kg/kg) |
| Gas constant for air (J/(kg K)) | |
| Gas constant for water vapor (J/(kg K)) | |
| r | Radius (m) |
| Ambient relative humidity with respect to ice | |
| S | Vertical wind shear (s−1) |
| Wing span of aircraft (m) | |
| Ambient supersaturation | |
| T | Temperature (K) |
| t | Time (s) |
| U | Ambient relative humidity |
| Estimated horizontal spreading rate of the contrail (m/s) | |
| Parametrized width for a 5 min old contrail (m) | |
| Initial descent speed of wake vortex (m/s) | |
| z | Altitude (m) |
| Balance length scale (m) | |
| Supersaturation length scale (m) | |
| Vortex length scale (m) | |
| Emission length scale (m) |
Appendix A. Fuel Properties
| Properties | Symbol | Jet A-1 | GTL | CTL | HEFA R-8 | HEFA C |
|---|---|---|---|---|---|---|
| Net Heat of Combustion, MJ/kg | Q | 43.2 | 44.2 | 44 | 44.1 | 44.3 |
| Density at 15 °C, kg/m | 802 | 737 | 762 | 763 | 751 | |
| Viscosity at −20 °C, kg/m | v | 3.91 | 2.6 | 3.6 | 5.5 | 3.3 |
| Surface Tension at 25 °C, mm2/s | 27.4 | 23.8 | 25.2 | 25.8 | 24.8 | |
| Initial Boiling Point, °C | 151 | 146 | 149 | 156 | 151 | |
| 10% Recovered, °C | 169 | 162 | 166 | 178 | 161 | |
| 50% Recovered, °C | 199 | 169 | 180 | 218 | 182 | |
| 90% Recovered, °C | 243 | 184 | 208 | 263 | 237 | |
| Final Boiling Point, °C | 262 | 198 | 228 | 274 | 259 | |
| Hydrogen Content, % weight | 13.87 | 15.6 | 15.1 | 15.3 | 15.4 | |
| Hydrogen to Carbon Molar Ratio | 1.919 | 2.203 | 2.119 | 2.153 | 2.169 | |
| Molecular Weight, kg/kmol | M | 160.5 | 146 | 156 | 177 | 160 |
| Critical Temperature, QC | 392.3 | 346.5 | 364.5 | 394.2 | 367.1 | |
| Critical Pressure, bar | 21.88 | 20.95 | 21.27 | 17.8 | 19.79 | |
| Smoke Point, mm % | 23 | 40 | 40 | 40 | 50 |
Appendix B. LES Approach
References
- Cabrera, E.; Sousa, J.M.M. Use of Sustainable Fuels in Aviation—A Review. Energies 2022, 15, 2440. [Google Scholar] [CrossRef]
- AIN. GE Honda Aero Continues Neat SAF Tests. Available online: https://www.ainonline.com/aviation-news/business-aviation/2023-10-20/ge-honda-aero-continues-neat-saf-tests (accessed on 15 November 2023).
- AIN. Gulfstream Completes First Transatlantic Flight on 100% SAF. Available online: https://www.ainonline.com/aviation-news/business-aviation/2023-11-20/gulfstream-completes-first-transatlantic-flight-100-saf (accessed on 27 November 2023).
- Schumann, U. On conditions for contrail formation from aircraft exhausts. Meteorol. Z. 1996, 5, 4–23. [Google Scholar] [CrossRef]
- Gierens, K.; Spichtinger, P.; Schumann, U. Ice Supersaturation. In Atmospheric Physics: Background–Methods–Trends; Springer: Berlin/Heidelberg, Germany, 2012; pp. 135–150. [Google Scholar]
- Schumann, U. Formation, properties and climatic effects of contrails. Comptes Rendus Phys. 2005, 6, 549–565. [Google Scholar] [CrossRef]
- Burkhardt, U.; Kärcher, B. Global radiative forcing from contrail cirrus. Nat. Clim. Chang. 2011, 1, 54–58. [Google Scholar] [CrossRef]
- Lee, D.S.; Fahey, D.W.; Skowron, A.; Allen, M.R.; Burkhardt, U.; Chen, Q.; Doherty, S.J.; Freeman, S.; Forster, P.M.; Fuglestvedt, J.; et al. The contribution of global aviation to anthropogenic climate forcing for 2000 to 2018. Atmos. Environ. 2021, 244, 117834. [Google Scholar] [CrossRef] [PubMed]
- Schumann, U. A contrail cirrus prediction model. Geosci. Model Dev. 2012, 5, 543–580. [Google Scholar] [CrossRef]
- Schumann, U.; Baumann, R.; Baumgardner, D.; Bedka, S.T.; Duda, D.P.; Freudenthaler, V.; Gayet, J.-F.; Heymsfield, A.J.; Minnis, P.; Quante, M.; et al. Properties of individual contrails: A compilation of observations and some comparisons. Atmos. Chem. Phys. 2017, 17, 403–438. [Google Scholar] [CrossRef]
- Wong, H.-W.; Yelvington, P.E.; Timko, M.T.; Onasch, T.B.; Miake-Lye, R.C.; Zhang, J.; Waitz, I.A. Microphysical Modeling of Ground-Level Aircraft-Emitted Aerosol Formation: Roles of Sulfur-Containing Species. J. Propuls. Power 2008, 24, 590–602. [Google Scholar] [CrossRef]
- Paoli, R.; Shariff, K. Contrail Modeling and Simulation. Annu. Rev. Fluid Mech. 2016, 48, 393–427. [Google Scholar] [CrossRef]
- Kärcher, B.; Yu, F. Role of aircraft soot emissions in contrail formation. Geophys. Res. Lett. 2009, 36, 1–5. [Google Scholar] [CrossRef]
- Kärcher, B. Formation and radiative forcing of contrail cirrus. Nat. Commun. 2018, 9, 1824. [Google Scholar] [CrossRef] [PubMed]
- Grimonprez, S.; Wu, J.; Faccinetto, A.; Gosselin, S.; Riber, E.; Cuenot, B.; Cazaunau, M.; Pangui, E.; Formenti, P.; Doussin, J.-F.; et al. Hydrophilic properties of soot particles exposed to OH radicals: A possible new mechanism involved in the contrail formation. Proc. Combust. Inst. 2021, 38, 6441–6450. [Google Scholar] [CrossRef]
- Narciso, M.; Sousa, J.M.M. Influence of Sustainable Aviation Fuels on the Formation of Contrails and Their Properties. Energies 2021, 14, 5557. [Google Scholar] [CrossRef]
- Gaspar, R.M.P.; Sousa, J.M.M. Impact of alternative fuels on the operational and environmental performance of a small turbofan engine. Energy Convers. Manag. 2016, 130, 81–90. [Google Scholar] [CrossRef]
- Unterstrasser, S. Properties of young contrails—A parametrisation based on large-eddy simulations. Atmos. Chem. Phys. 2016, 16, 2059–2082. [Google Scholar] [CrossRef]
- Unterstrasser, S. Large-eddy simulation study of contrail microphysics and geometry during the vortex phase and consequences on contrail-to-cirrus transition. J. Geophys. Res. Atmos. 2014, 119, 7537–7555. [Google Scholar] [CrossRef]
- Unterstrasser, S.; Görsch, N. Aircraft-type dependency of contrail evolution. J. Geophys. Res. Atmos. 2014, 119, 14015–14027. [Google Scholar]
- Kärcher, B.; Burkhardt, U.; Unterstrasser, S.; Minnis, P. Factors controlling contrail cirrus optical depth. Atmos. Chem. Phys. 2009, 9, 6229–6254. [Google Scholar] [CrossRef]
- Kramer, S.; Andac, G.; Heyne, J.; Ellsworth, J.; Herzig, P.; Lewis, K. Perspectives on Fully Synthesized Sustainable Aviation Fuels: Direction and Opportunities. Front. Energy Res. 2022, 9, 782823. [Google Scholar] [CrossRef]
- Dekoutsidis, G.; Groß, S.; Wirth, M.; Krämer, M.; Rolf, C. Characteristics of supersaturation in mid-latitude cirrus clouds and their adjacent cloud-free air. Atmos. Chem. Phys. Discuss. 2023, 23, 3103–3117. [Google Scholar] [CrossRef]
- Sölch, I.; Kärcher, B. A large-eddy model for cirrus clouds with explicit aerosol and ice microphysics and Lagrangian ice particle tracking. Q. J. R. Meteorol. Soc. 2010, 136, 2074–2093. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cabrera, E.; de Sousa, J.M.M. Addressing Confidence in Modeling of Contrail Formation from E-Fuels in Aviation Using Large Eddy Simulation Parametrization. Energies 2024, 17, 1442. https://doi.org/10.3390/en17061442
Cabrera E, de Sousa JMM. Addressing Confidence in Modeling of Contrail Formation from E-Fuels in Aviation Using Large Eddy Simulation Parametrization. Energies. 2024; 17(6):1442. https://doi.org/10.3390/en17061442
Chicago/Turabian StyleCabrera, Eduardo, and João M. Melo de Sousa. 2024. "Addressing Confidence in Modeling of Contrail Formation from E-Fuels in Aviation Using Large Eddy Simulation Parametrization" Energies 17, no. 6: 1442. https://doi.org/10.3390/en17061442
APA StyleCabrera, E., & de Sousa, J. M. M. (2024). Addressing Confidence in Modeling of Contrail Formation from E-Fuels in Aviation Using Large Eddy Simulation Parametrization. Energies, 17(6), 1442. https://doi.org/10.3390/en17061442







