Nine-Switch Multiport Converter Applied to Battery-Powered Tramway with Reduced Leakage Current
Abstract
1. Introduction
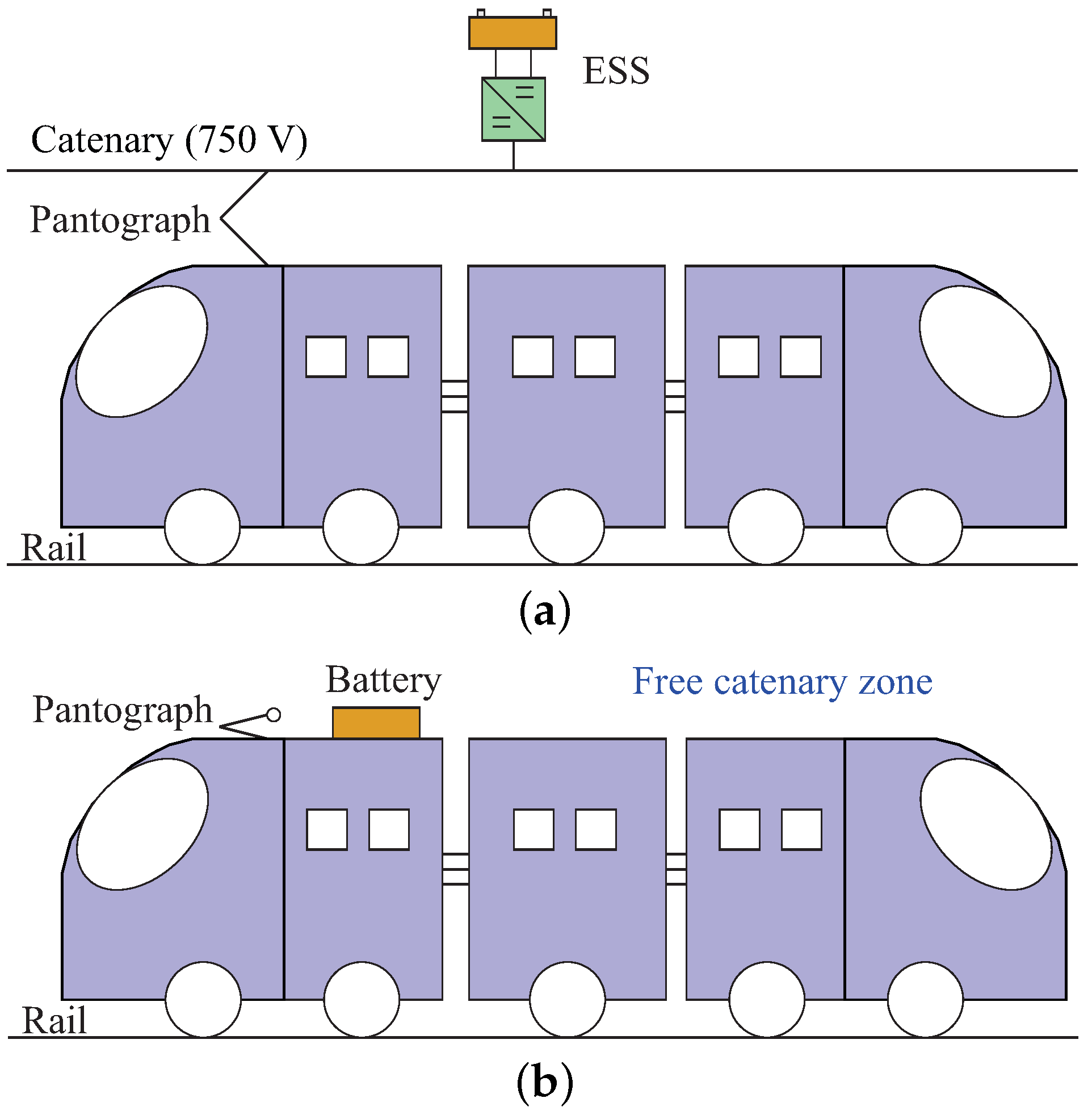
- Application of a multiport NSI converter in an electric tramway system for connecting the DC source to the AC load, resulting in a more compact solution compared to conventional topologies.
- Development of a single control scheme for regulating the battery current and voltage, enabling battery energy management. As a consequence, this eliminates the need for additional control schemes to cover regenerative braking and substation charging.
- Specification of the main characteristics of the ESS and the DC link capacitance based on the energy variation in components for real load conditions.
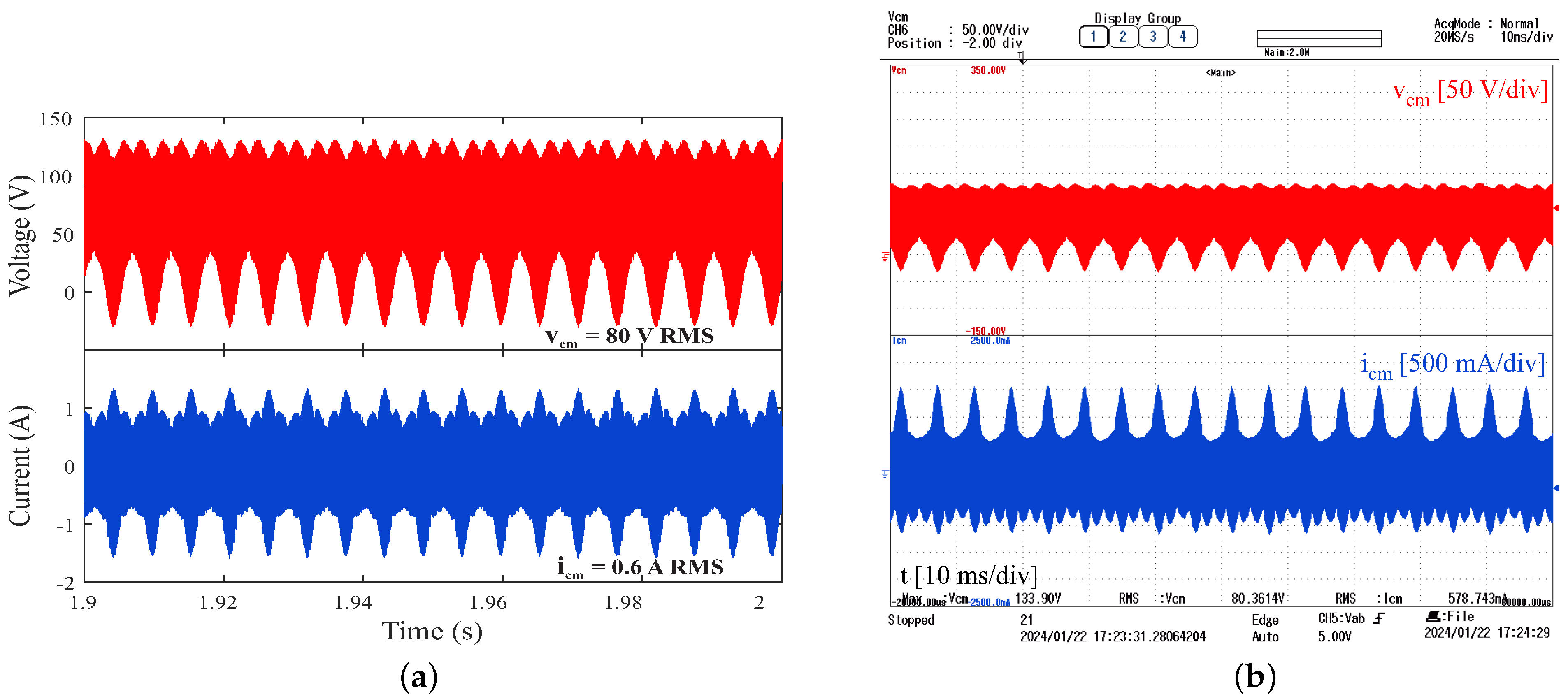
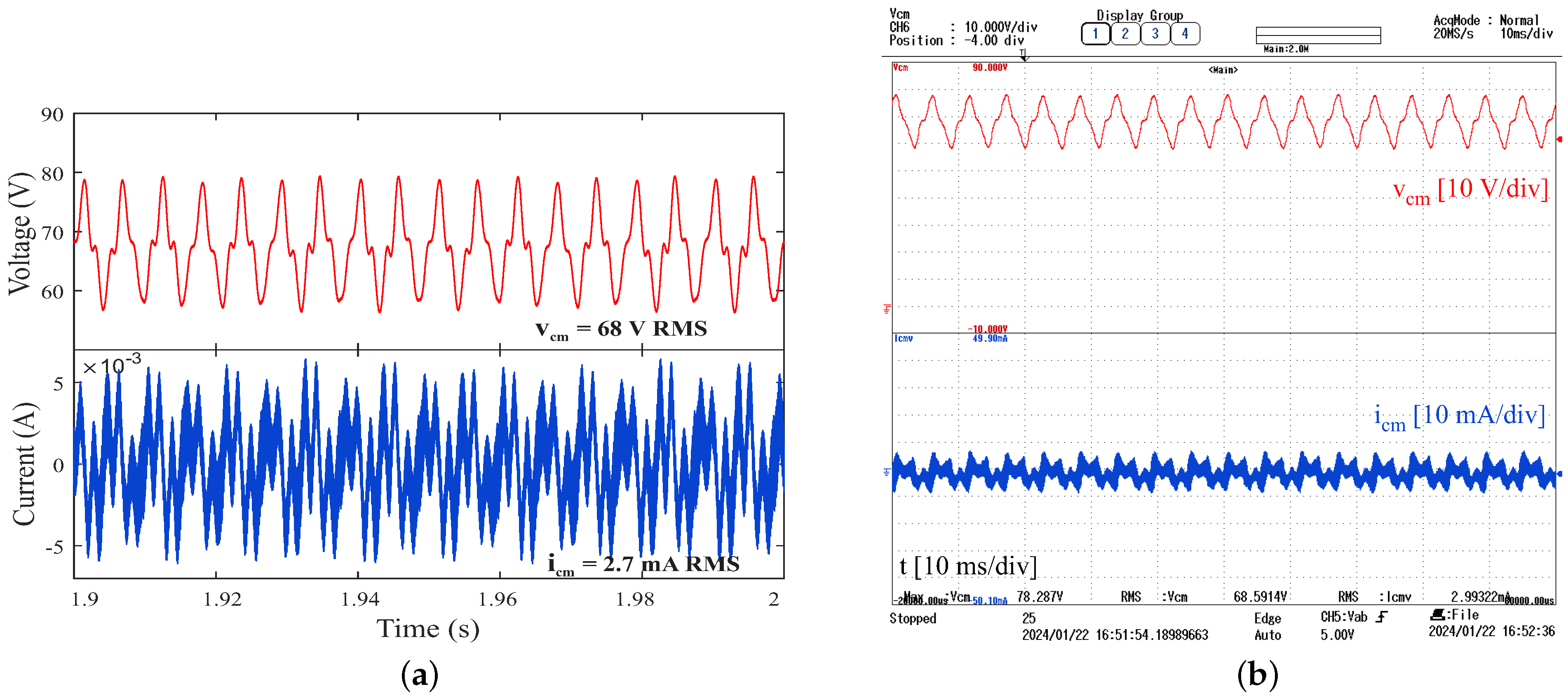
- Reduction of current leakage in the load through the use of passive filters, preventing premature wear on the motor windings and bearings.
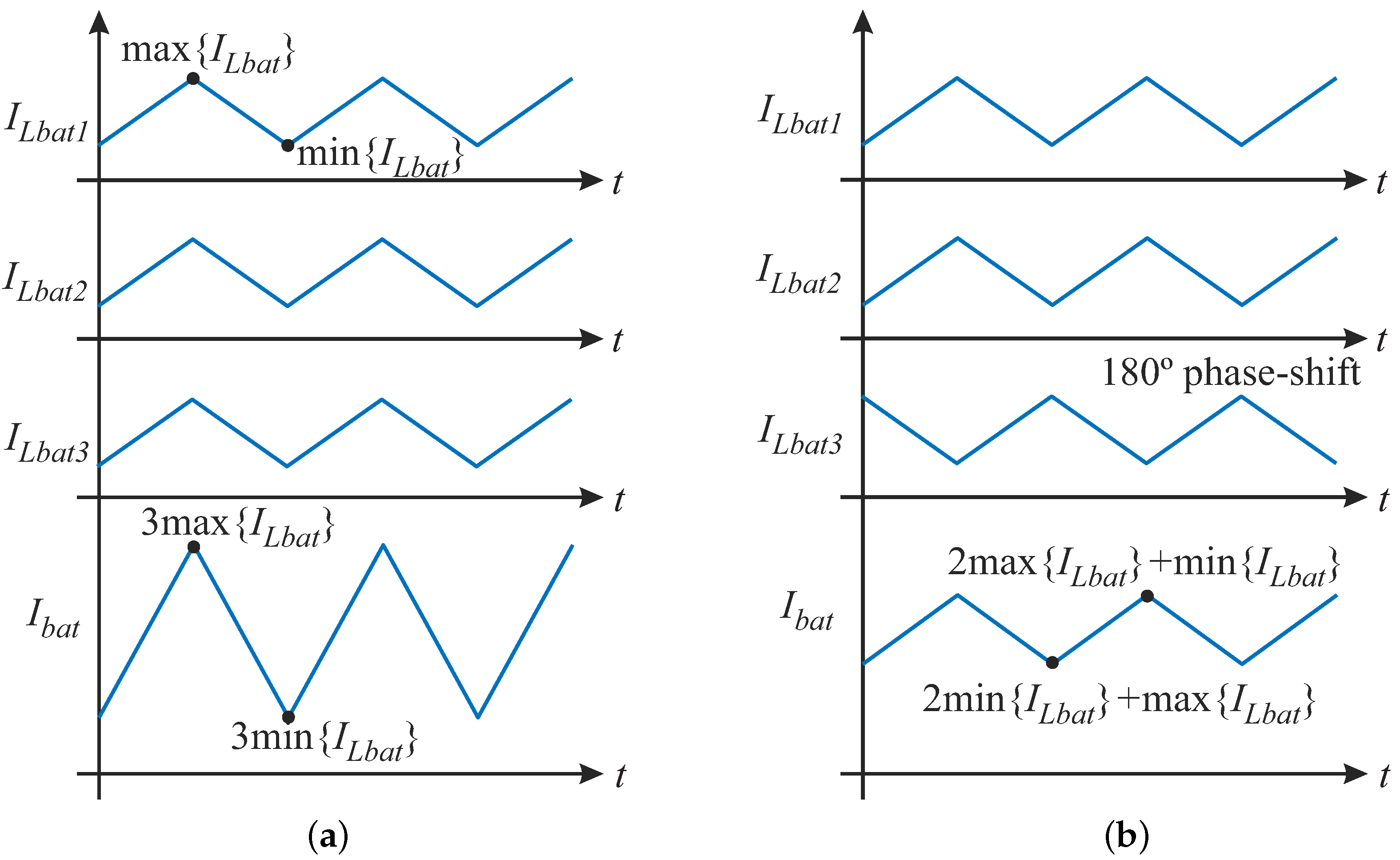
- Reduced battery current ripple through phase-shift in the triangular carrier, resulting in increased battery lifespan by reducing the strain caused by high-frequency currents.
2. Proposed Nine-Switch Multiport Scheme Applied to Battery-Powered Tramway
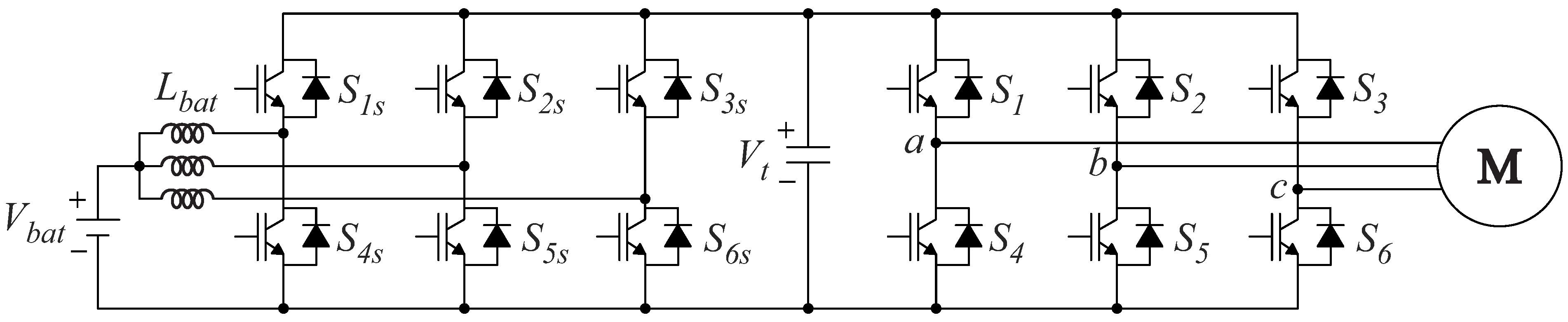
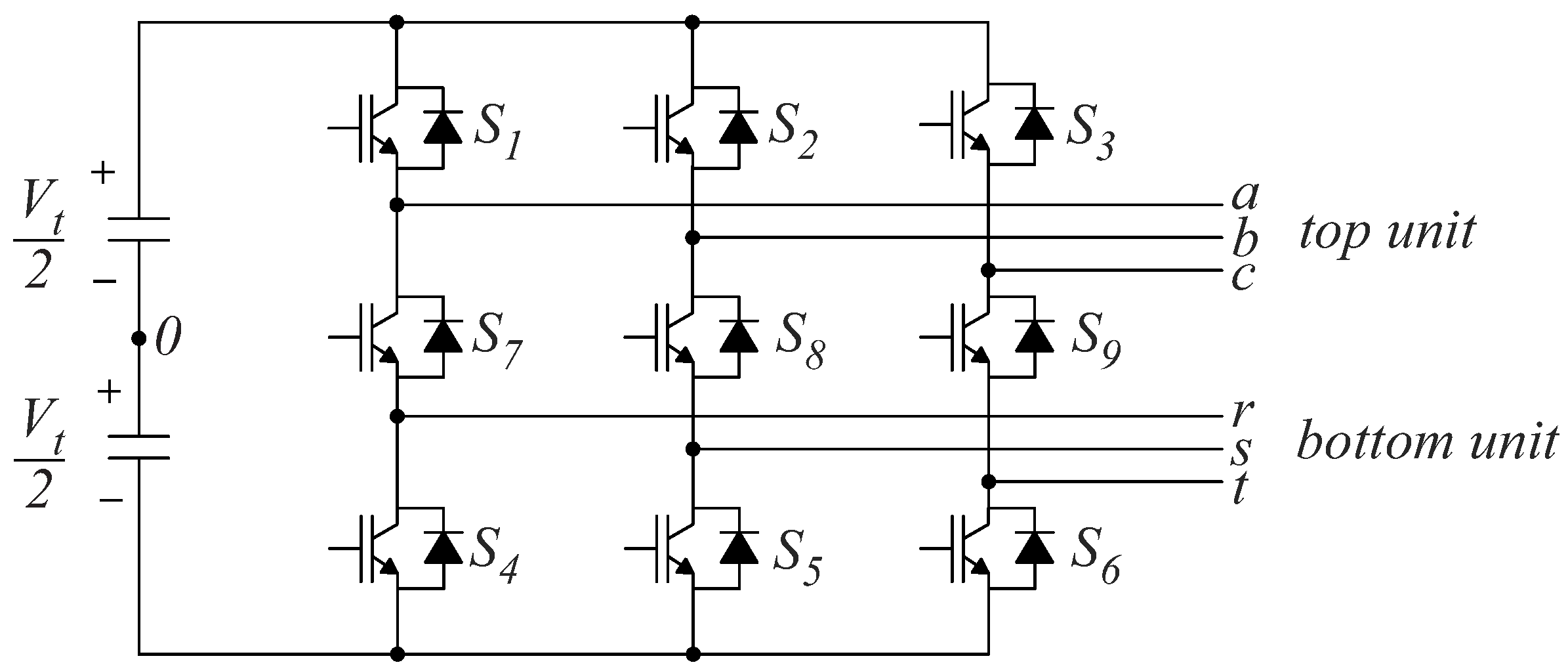
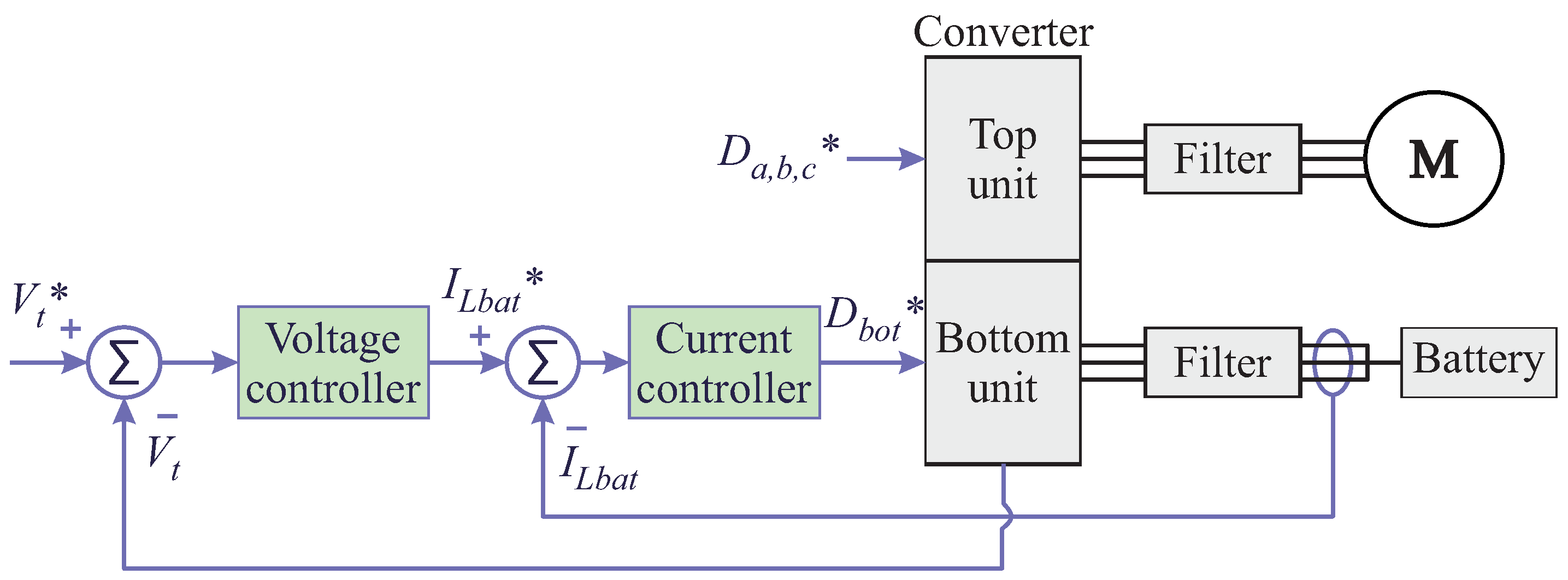
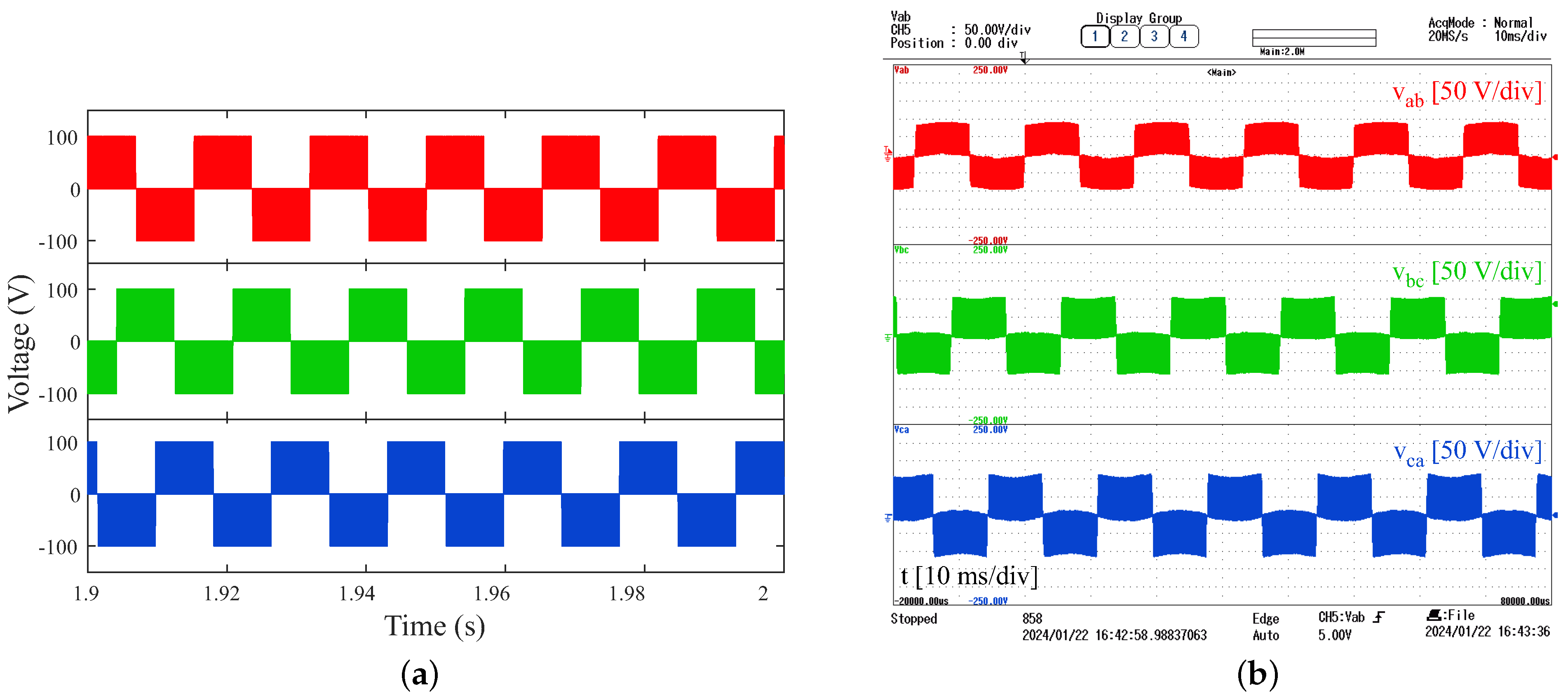
- The first port is the top unit (represented as ➀ in Figure 5), which operates as an inverter, generating the three a, b, and c voltage phases necessary for driving three-phase motors.
- The second port corresponds to the bottom unit (represented as ➁ in Figure 5), operating as a half-bridge converter responsible for managing energy from a DC power source, which is an ESS with voltage . This configuration is a modification of the traditional SSI converter, where the diodes are replaced by inductors, enabling bidirectional current flow and facilitating the battery’s ability to absorb energy from regenerative braking. It additionally includes the reference node of the NSI, enabling the circulation of current through the ESS.
- The third port (depicted as ➂ in Figure 5) comprises the DC link and the connection to the substation. When the tramway arrives at a station or garage with a recharging substation, the pantograph establishes the connection to the DC link.
3. Design of Components for the Proposed System
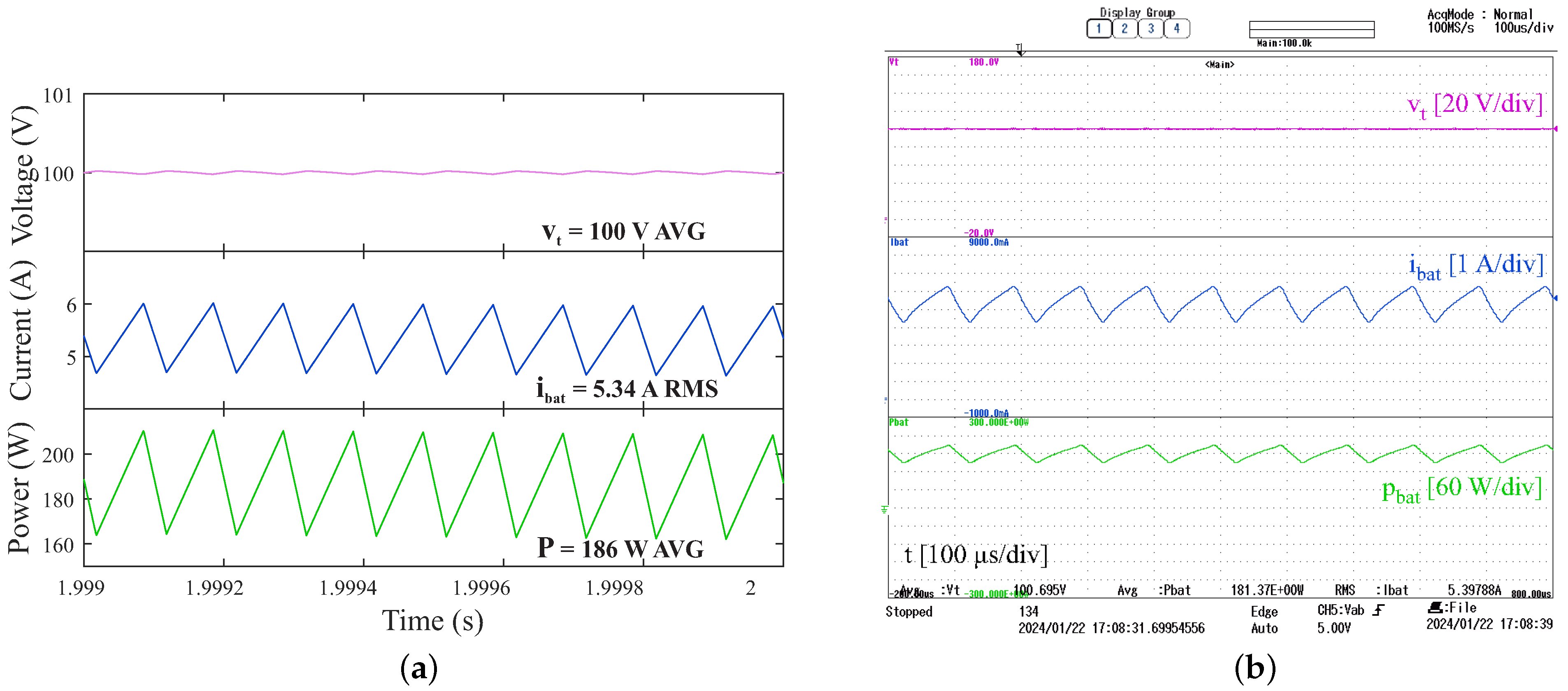
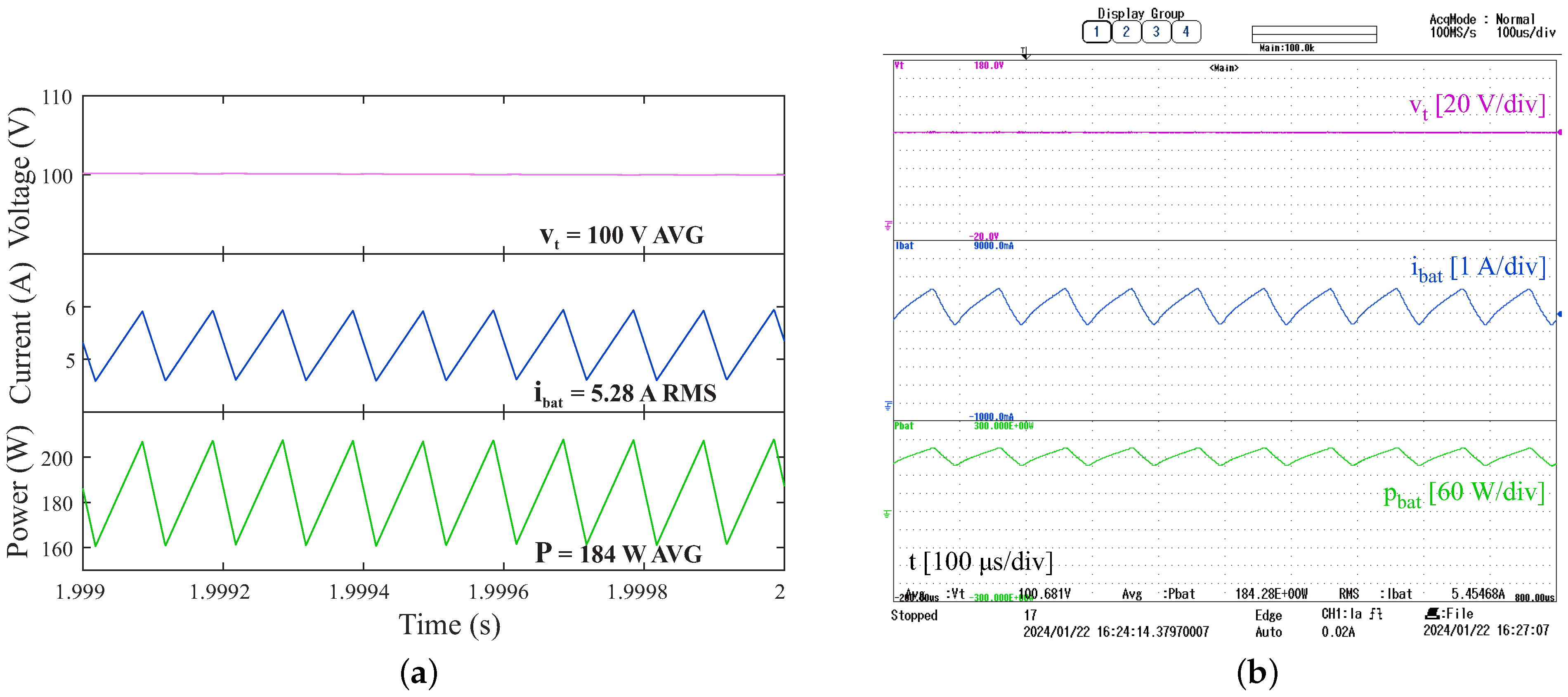
3.1. Selecting the Battery Connection Inductance
3.2. Selecting the DC Link Capacitance
- STEP 1: Set an initial capacitance for the DC link, its maximum and minimum voltage limits ( and ), and the acceptable response time for achieving capacitance energy equilibrium ().
- STEP 2: Execute the simulation and fine-tune the control parameters to achieve the shortest response time and minimal voltage fluctuation. This is evaluated for the entire load profile, considering all its abrupt variations.
- STEP 3: For the considered load profile, the system designer must track the load variations that generate the following scenarios: (i) maximum voltage level for the DC link during a transient, and () minimum voltage level for the DC link during a transient. Then, these maximum and minimum voltage levels must be measured and the response time of the control system obtained.
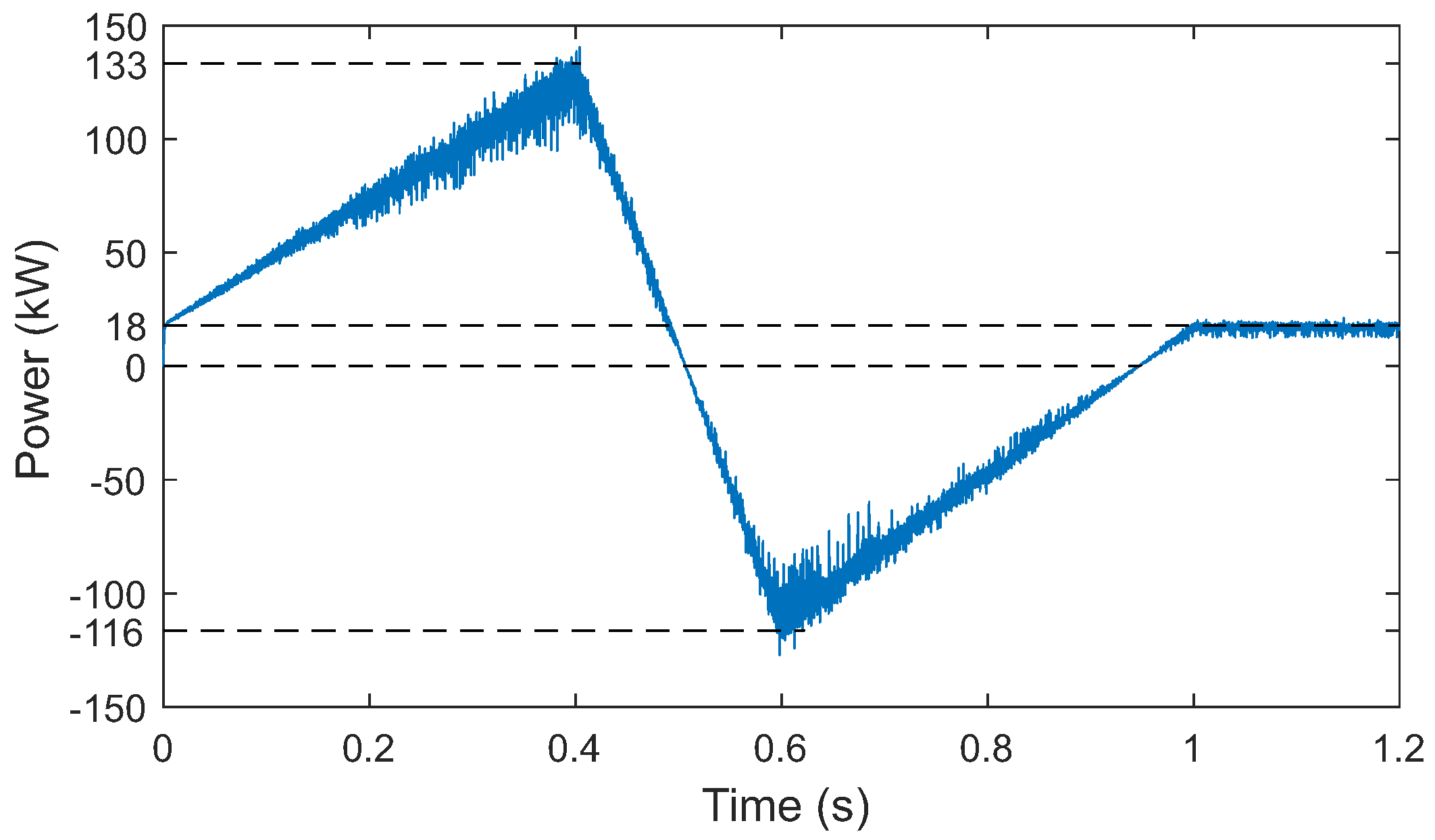
- STEP 4: Compute the maximum and minimum energy variations observed for the transients detected in the simulation of STEP 3 (referred here to as and ). Although these variables are traditionally calculated from the integral of power over time, they can be approximated by the area of the shaded triangle shown in Figure 9. Therefore, can be calculated as follows:with P and being represented in Figure 9.
- STEP 5: Use the maximum and minimum energy variations obtained in STEP 4 to compute the capacitances and for the scenarios (i) and () described in STEP 3. This can be done using the following equations:andwhere is the nominal voltage of the DC link.
- STEP 6: Choose the greater value between and as the new capacitance value, i.e.,
- STEP 7: Conduct a new simulation employing the newly determined capacitance value and repeat the control adjustment procedure.
- STEP 8: Go back to STEP 2 and repeat the subsequent steps until the capacitance value calculated in the current iteration matches that obtained in the previous iteration, ensuring that the voltage and time limits are not violated.
3.3. Defining the ESS Characteristics
3.4. Designing the LC Output Filter
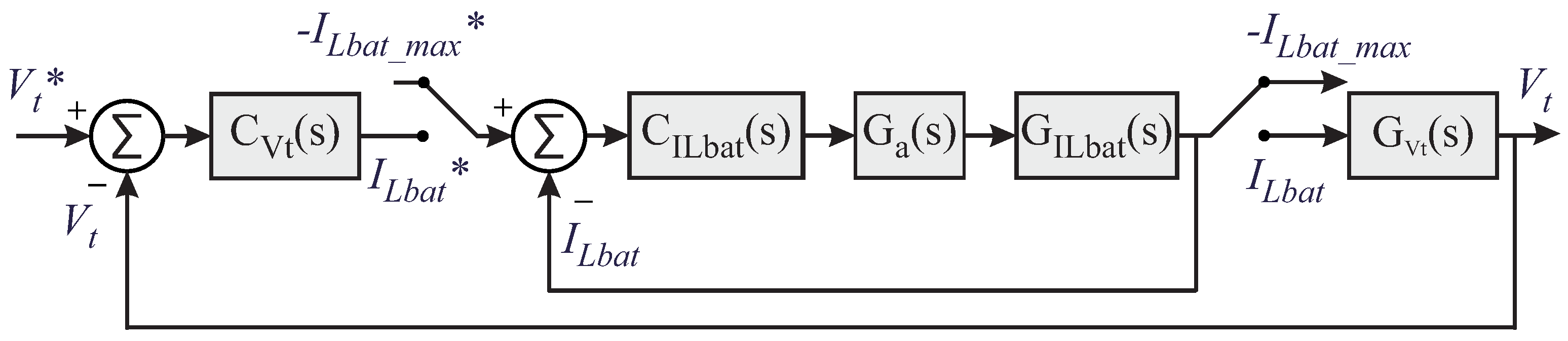
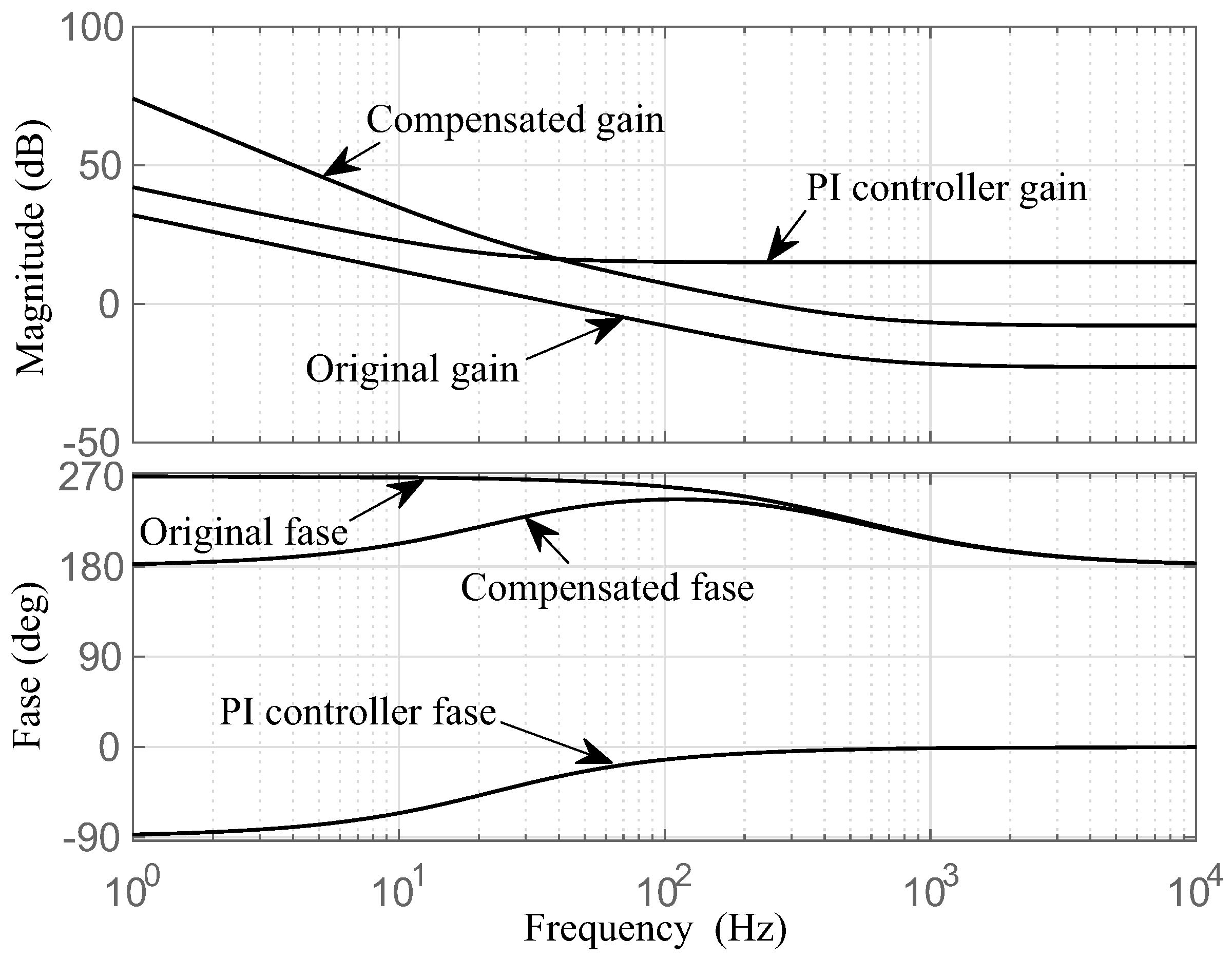
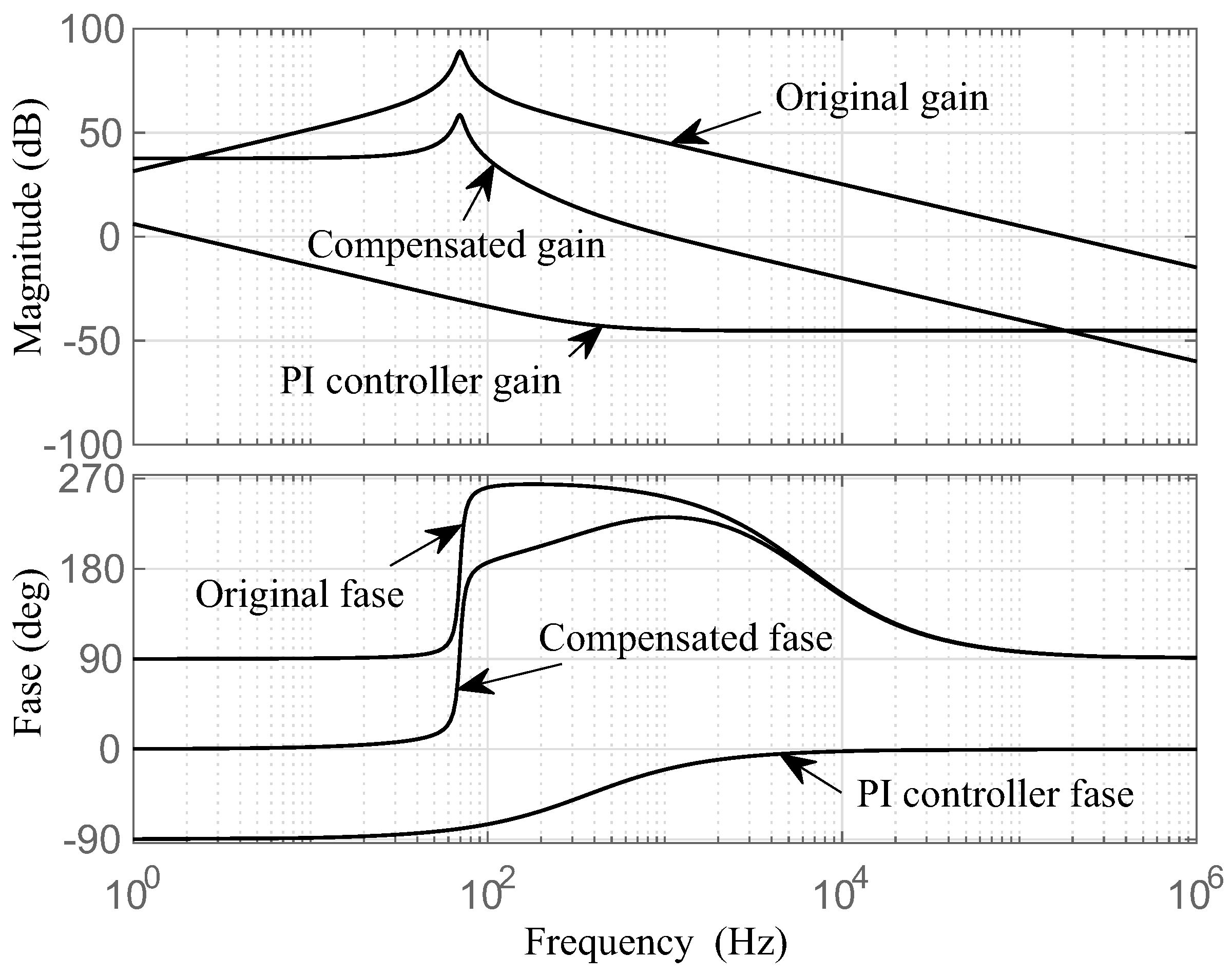
4. Design of the Control Structure for the Proposed System
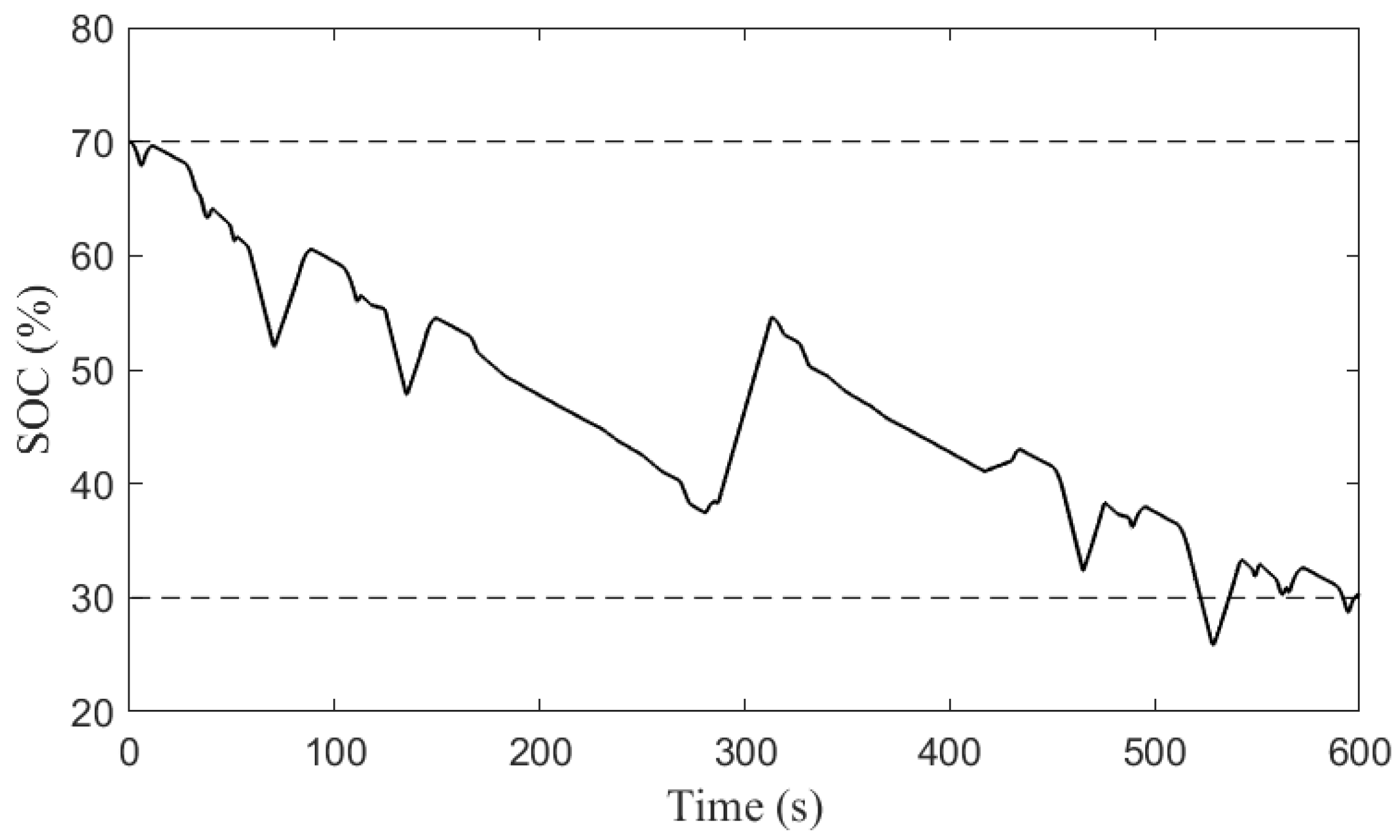
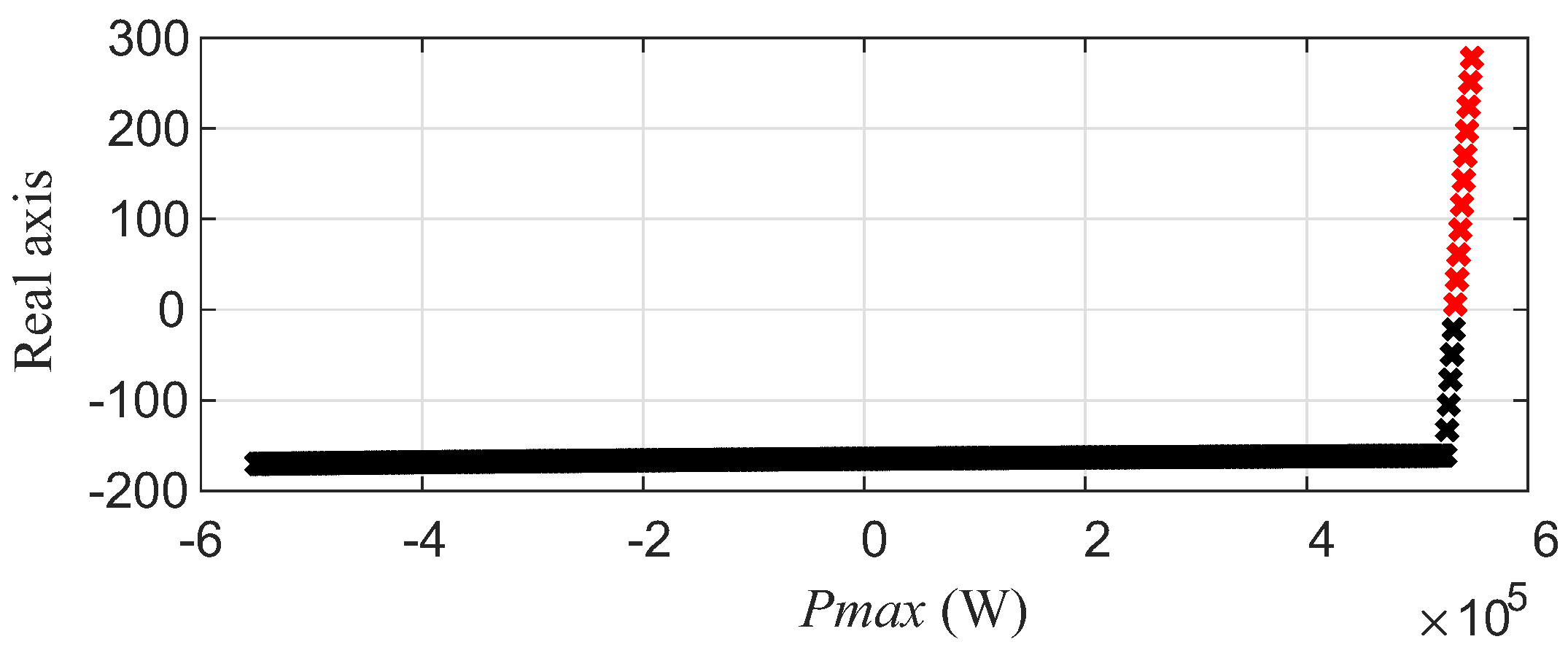
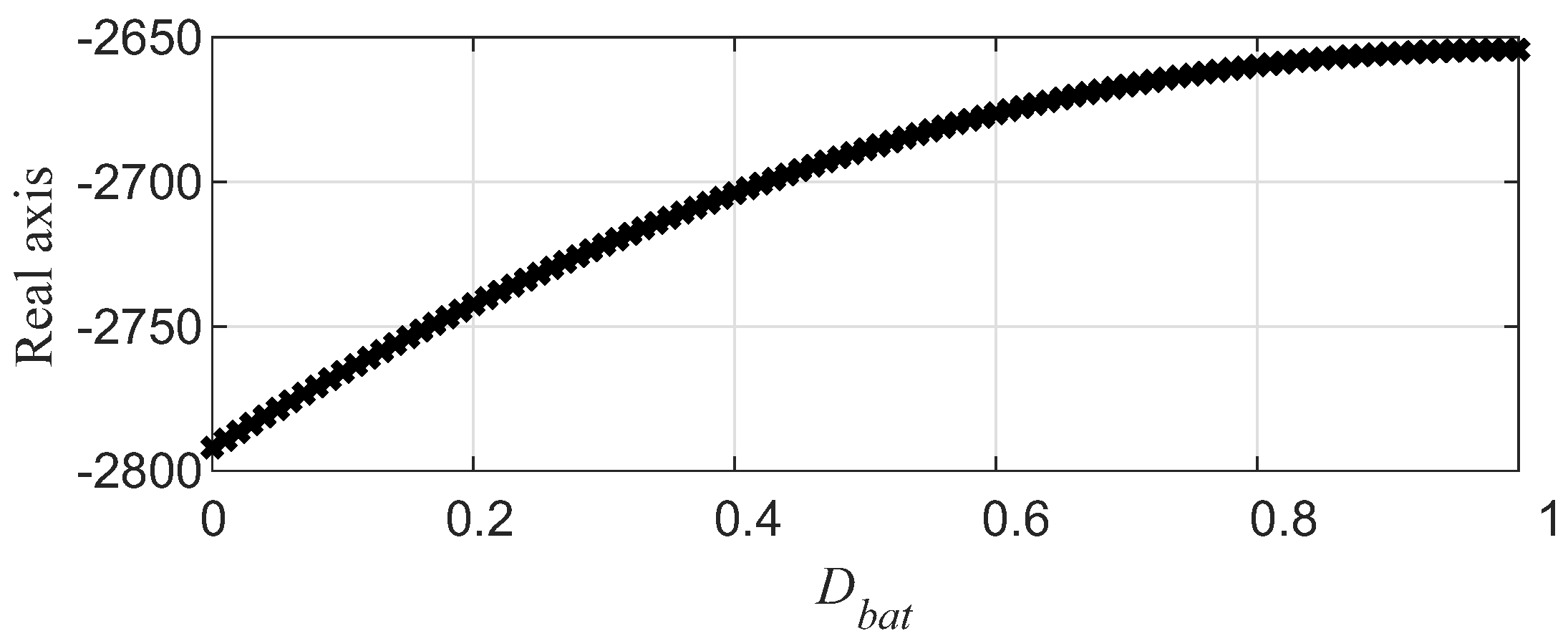
5. Simulation Results for the Real-Scale System
6. Simulation and Experimental Results of Reduced-Scale System
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AC | Alternating Current |
| CMV | Common Mode Voltage |
| CLTF | Close-Loop Transfer Function |
| DC | Direct Current |
| ESS | Energy Storage System |
| LC | Inductor and Capacitor |
| LHP | Left Half-Plane |
| NSI | Nine-Switch Inverter |
| OLTF | Open-Loop Transfer Function |
| PWM | Pulse Width Modulation |
| RHP | Right Half-Plane |
| RMS | Root Mean Square |
| SOC | State of Charge |
References
- Lee, H.; Cho, D.H. Energy Cost Minimization Based on Decentralized Reinforcement Learning with Feedback for Stable Operation of Wireless Charging Electric Tram Network. IEEE Syst. J. 2021, 15, 586–597. [Google Scholar] [CrossRef]
- Mohanraj, D.; Gopalakrishnan, J.; Chokkalingam, B.; Mihet-Popa, L. Critical Aspects of Electric Motor Drive Controllers and Mitigation of Torque Ripple—Review. IEEE Access 2022, 10, 73635–73674. [Google Scholar] [CrossRef]
- Xiao, Z.; Chen, H.; Guo, J.; Wang, Q.; Sun, P.; Feng, X. Joint Optimization of Speed and Voltage Trajectories for Hybrid Electric Trams. IEEE Trans. Ind. Appl. 2021, 57, 6427–6439. [Google Scholar] [CrossRef]
- Kim, J.; Ryu, J.; Kim, G.; Lee, J.; Chang, S.; Lee, C.; Kim, J.; Oh, Y.; Lee, H.; Kim, J. A Proposed Fast Charging and High-Power System for Wireless Railway Trains Adopting the Input Voltage Sharing Topology and the Balancing Control Scheme. IEEE Trans. Ind. Electron. 2020, 67, 6407–6417. [Google Scholar] [CrossRef]
- Brenna, M.; Foiadelli, F.; Zaninelli, D. Introduction to Railway Systems. In Electrical Railway Transportation Systems; Wiley: Hoboken, NJ, USA, 2018; pp. 1–16. [Google Scholar] [CrossRef]
- Simiyu, P.; Davidson, I.E. MVDC Railway Traction Power Systems; State-of-the Art, Opportunities, and Challenges. Energies 2021, 14, 4156. [Google Scholar] [CrossRef]
- Polater, N.; Tricoli, P. Technical Review of Traction Drive Systems for Light Railways. Energies 2022, 15, 3187. [Google Scholar] [CrossRef]
- Graber, G.; Calderaro, V.; Galdi, V.; Piccolo, A.; Lamedica, R.; Ruvio, A. Techno-economic Sizing of Auxiliary-Battery-Based Substations in DC Railway Systems. IEEE Trans. Transp. Electrif. 2018, 4, 616–625. [Google Scholar] [CrossRef]
- Xiao, Z.; Sun, P.; Wang, Q.; Zhu, Y.; Feng, X. Integrated Optimization of Speed Profiles and Power Split for a Tram with Hybrid Energy Storage Systems on a Signalized Route. Energies 2018, 11, 478. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, Z.; Li, F. Optimization of Energy Management Strategy and Sizing in Hybrid Storage System for Tram. Energies 2018, 11, 752. [Google Scholar] [CrossRef]
- Kim, J.; Kim, J.; Lee, C.; Kim, G.; Lee, H.; Lee, B. Optimal Capacity Estimation Method of the Energy Storage Mounted on a Wireless Railway Train for Energy-Sustainable Transportation. Energies 2018, 11, 986. [Google Scholar] [CrossRef]
- Arboleya, P.; Bidaguren, P.; Armendariz, U. Energy Is On Board: Energy Storage and Other Alternatives in Modern Light Railways. IEEE Electrif. Mag. 2016, 4, 30–41. [Google Scholar] [CrossRef]
- Yang, Y.; Zhang, W.; Wei, S.; Wang, Z. Optimal Sizing of On-Board Energy Storage Systems and Stationary Charging Infrastructures for a Catenary-Free Tram. Energies 2020, 13, 6227. [Google Scholar] [CrossRef]
- Radu, P.V.; Lewandowski, M.; Szelag, A. On-Board and Wayside Energy Storage Devices Applications in Urban Transport Systems—Case Study Analysis for Power Applications. Energies 2020, 13, 2013. [Google Scholar] [CrossRef]
- Garcia, P.; Fernandez, L.M.; Garcia, C.A.; Jurado, F. Energy Management System of Fuel-Cell-Battery Hybrid Tramway. IEEE Trans. Ind. Electron. 2010, 57, 4013–4023. [Google Scholar] [CrossRef]
- Chymera, M.; Renfrew, A.C.; Barnes, M.; Holden, J. Simplified Power Converter for Integrated Traction Energy Storage. IEEE Trans. Veh. Technol. 2011, 60, 1374–1383. [Google Scholar] [CrossRef]
- Jayasinghe, S.D.G.; Vilathgamuwa, D.M.; Madawala, U.K. Diode-Clamped Three-Level Inverter-Based Battery/Supercapacitor Direct Integration Scheme for Renewable Energy Systems. IEEE Trans. Power Electron. 2011, 26, 3720–3729. [Google Scholar] [CrossRef]
- İnci, M.; Büyük, M.; Demir, M.H.; İlbey, G. A review and research on fuel cell electric vehicles: Topologies, power electronic converters, energy management methods, technical challenges, marketing and future aspects. Renew. Sustain. Energy Rev. 2021, 137, 110648. [Google Scholar] [CrossRef]
- Ogasa, M.; Taguchi, Y. Power electronics technologies for a lithium ion battery tram. In Proceedings of the 2007 Power Conversion Conference, Nagoya, Japan, 2–5 April 2007; pp. 1369–1375. [Google Scholar] [CrossRef]
- Lin, Y.S.; Hu, K.W.; Yeh, T.H.; Liaw, C.M. An Electric-Vehicle IPMSM Drive With Interleaved Front-End DC/DC Converter. IEEE Trans. Veh. Technol. 2016, 65, 4493–4504. [Google Scholar] [CrossRef]
- Mande, D.; Trovão, J.P.F.; Ta, M.C.; Do, T.V. Dual-Source Bidirectional Quasi-Z-Source Inverter Development for Off-Road Electric Vehicles. World Electr. Veh. J. 2022, 13, 174. [Google Scholar] [CrossRef]
- Abdelhakim, A.; Mattavelli, P.; Spiazzi, G. Three-Phase Split-Source Inverter (SSI): Analysis and Modulation. IEEE Trans. Power Electron. 2016, 31, 7451–7461. [Google Scholar] [CrossRef]
- Thanakam, T.; Kumsuwan, Y. A Novel On-Board Battery Charger Configuration Based on Nine-Switch Converter fed Open-End Winding AC Motor Drive for Plug-In Electric Vehicles. In Proceedings of the 2021 24th International Conference on Electrical Machines and Systems (ICEMS), Gyeongju, Republic of Korea, 31 October–3 November 2021; pp. 988–991. [Google Scholar] [CrossRef]
- Salem, A.; Narimani, M. Nine-Switch Current-Source Inverter-Fed Asymmetrical Six-Phase Machines Based on Vector Space Decomposition. In Proceedings of the 2020 IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA, 11–15 October 2020; pp. 1951–1956. [Google Scholar] [CrossRef]
- Cury Alves dos Santos, S.T.; Ubaldo Guazzelli, P.R.; de Castro, A.G.; Freitas Vieira, B.; de Andrade Pinto, S.; Luis de Aguiar, M. Grid-Connected Variable Speed Driven Squirrel-Cage Induction Motor Through a Nine-Switch AC/AC Converter with Leading Power Factor. In Proceedings of the IECON 2020 the 46th Annual Conference of the IEEE Industrial Electronics Society, Singapore, 18–21 October 2020; pp. 979–984. [Google Scholar] [CrossRef]
- Abbache, M.A.; Tabbache, B.; Kheloui, A. Direct torque control of nine switches inverter—Dual induction motors. In Proceedings of the 22nd Mediterranean Conference on Control and Automation, Palermo, Italy, 16–19 June 2014; pp. 810–815. [Google Scholar] [CrossRef]
- Kandasamy, V.; Manoj, R. Grid integration of AC and DC energy resources using multi-input nine switch matrix converter. In Proceedings of the 2014 International Conference on Green Computing Communication and Electrical Engineering (ICGCCEE), Coimbatore, India, 6–8 March 2014; pp. 1–4. [Google Scholar] [CrossRef]
- Qin, Z.; Loh, P.C.; Blaabjerg, F. Power loss benchmark of nine-switch converters in three-phase online-UPS application. In Proceedings of the 2014 IEEE Energy Conversion Congress and Exposition (ECCE), Pittsburgh, PA, USA, 14–18 September 2014; pp. 1180–1187. [Google Scholar] [CrossRef]
- Dos Santos, E.C.; Jacobina, C.B.; da Silva, O.I. Six-phase machine drive system with nine-switch converter. In Proceedings of the IECON 2011—37th Annual Conference of the IEEE Industrial Electronics Society, Melbourne, VIC, Australia, 7–10 November 2011; pp. 4204–4209. [Google Scholar] [CrossRef]
- Dehghan, S.M.; Amiri, A.; Mohamadian, M.; Andersen, M.A. Modular space-vector pulse-width modulation for nine-switch converters. IET Power Electron. 2013, 6, 457–467. [Google Scholar] [CrossRef]
- Genu, L.G.B.; Limongi, L.R.; Cavalcanti, M.C.; Bradaschia, F.; Neves, F.A.S. Transformerless hybrid power filter topologies derived from nine-switch inverter. In Proceedings of the 2015 IEEE 13th Brazilian Power Electronics Conference and 1st Southern Power Electronics Conference (COBEP/SPEC), Fortaleza, Brazil, 29 November–2 December 2015; pp. 1–6. [Google Scholar] [CrossRef]
- Hou, C.C.; Wang, P.W.; Chen, C.C.; Chang, C.W. Common Mode Voltage Reduction in Four-Leg Inverter with Multicarrier PWM Scheme. In Proceedings of the 2019 10th International Conference on Power Electronics and ECCE Asia (ICPE 2019—ECCE Asia), Busan, Republic of Korea, 27–30 May 2019; pp. 3223–3228. [Google Scholar] [CrossRef]
- Dianguo, X.; Qiang, G.; Wei, W. Design of a Passive Filter to Reduce Common-Mode and Differential-Mode Voltage Generated by Voltage-Source PWM Inverter. In Proceedings of the IECON 2006—32nd Annual Conference on IEEE Industrial Electronics, Paris, France, 6–10 November 2006; pp. 2483–2487. [Google Scholar] [CrossRef]
- Hota, A.; Agarwal, V. A New H8 Inverter Topology With Low Common Mode Voltage and Phase Current THD for 3-φ Induction Motor Drive Applications. IEEE Trans. Ind. Appl. 2022, 58, 6245–6252. [Google Scholar] [CrossRef]
- Zhang, K.; Chung, H.S.H.; Wu, W. Design and Assessment of a New Active CM Filtering Architecture for PWM Inverter-Fed Motor Drive Systems. IEEE Trans. Power Electron. 2023, 38, 1819–1830. [Google Scholar] [CrossRef]
- Shen, J.X.; Sun, W.; Huang, X.Q. A DC link switch-based common mode voltage reduction scheme in PWM inverter drives. In Proceedings of the 2015 International Conference on Sustainable Mobility Applications, Renewables and Technology (SMART), Kuwait, Kuwait, 23–25 November 2015; pp. 1–7. [Google Scholar] [CrossRef]
- Porkia, H.A.; Adabi, J.; Zare, F. Reduction of Zero-Sequence and Differential-Mode Circulating Currents and Common-Mode Voltage in Parallel PWM Converters. IEEE Trans. Ind. Electron. 2023, 70, 4038–4047. [Google Scholar] [CrossRef]
- Hakami, S.S.; Halabi, L.M.; Lee, K.B. Dual-Carrier-Based PWM Method for DC-Link Capacitor Lifetime Extension in Three-Level Hybrid ANPC Inverters. IEEE Trans. Ind. Electron. 2023, 70, 3303–3314. [Google Scholar] [CrossRef]
- Hasanzad, F.; Rastegar, H.; Pichan, M. Performance analysis of reduced common-mode voltage space vector modulation techniques for three-phase four-leg voltage-source inverter. In Proceedings of the 2018 9th Annual Power Electronics, Drives Systems and Technologies Conference (PEDSTC), Tehran, Iran, 13–15 February 2018; pp. 65–70. [Google Scholar] [CrossRef]
- Liu, C.; Wu, B.; Zargari, N.R.; Xu, D.; Wang, J. A Novel Three-Phase Three-Leg AC/AC Converter Using Nine IGBTs. IEEE Trans. Power Electron. 2009, 24, 1151–1160. [Google Scholar] [CrossRef]
- Nguyen, T.; Phan Quoc, D.; Dao, N.D.; Lee, H.H. Carrier Phase-Shift PWM to Reduce Common-Mode Voltage for Three-Level T-Type NPC Inverters. J. Power Electron. 2014, 14, 1197–1207. [Google Scholar] [CrossRef]
- Erickson, R.W.; Maksimovic, D. Fundamentals of Power Electronics, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- CAF. Trams and Light Metros—Seville Metro Centro. 2022. Available online: https://www.caf.net/en/soluciones/proyectos/proyecto-detalle.php?p=70 (accessed on 14 March 2024).
- Linden, D.; Reddy, T.B. Handbook of Batteries, 3rd ed.; McGraw-Hill: New York, NY, USA, 2001. [Google Scholar]



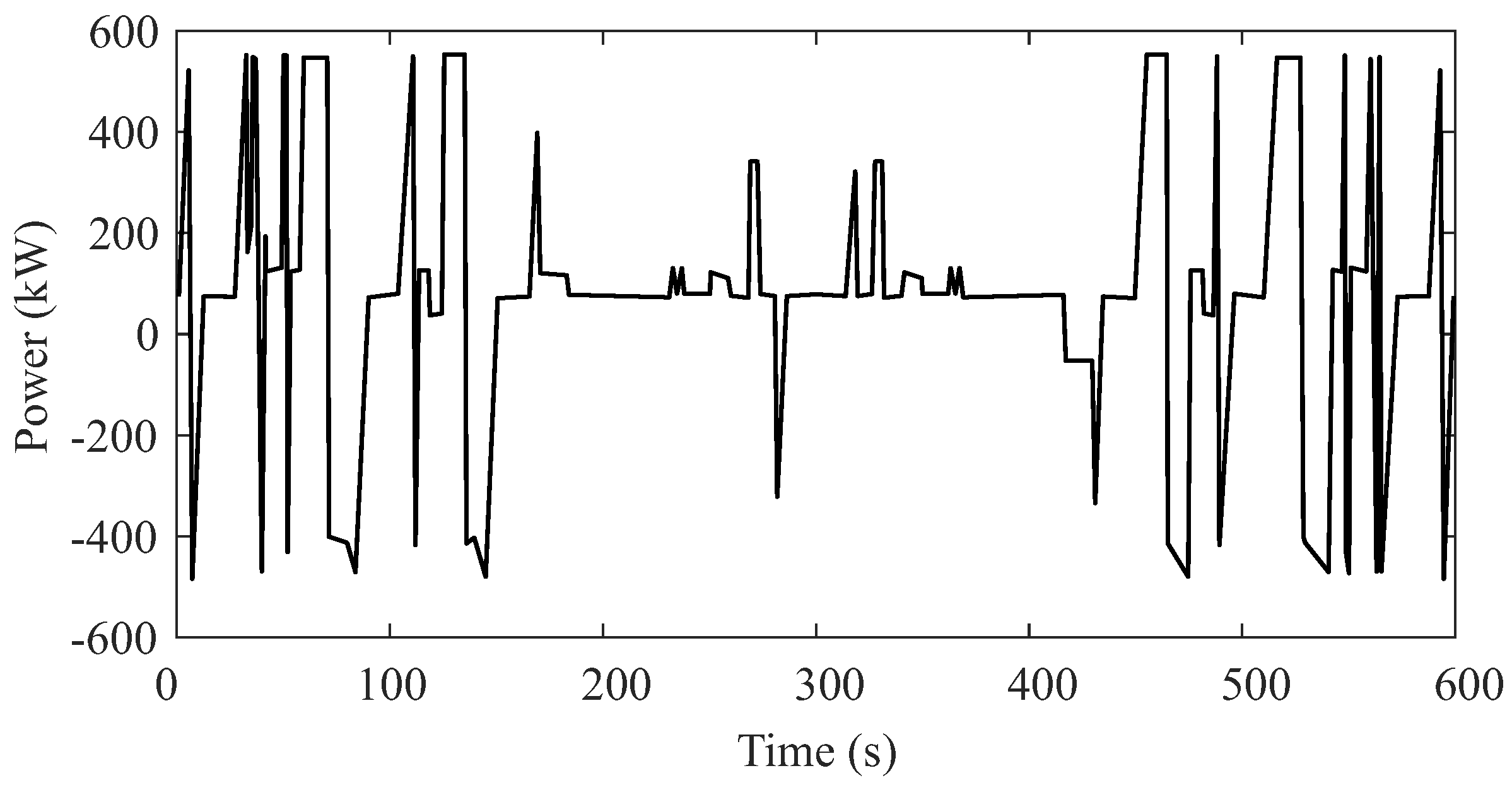
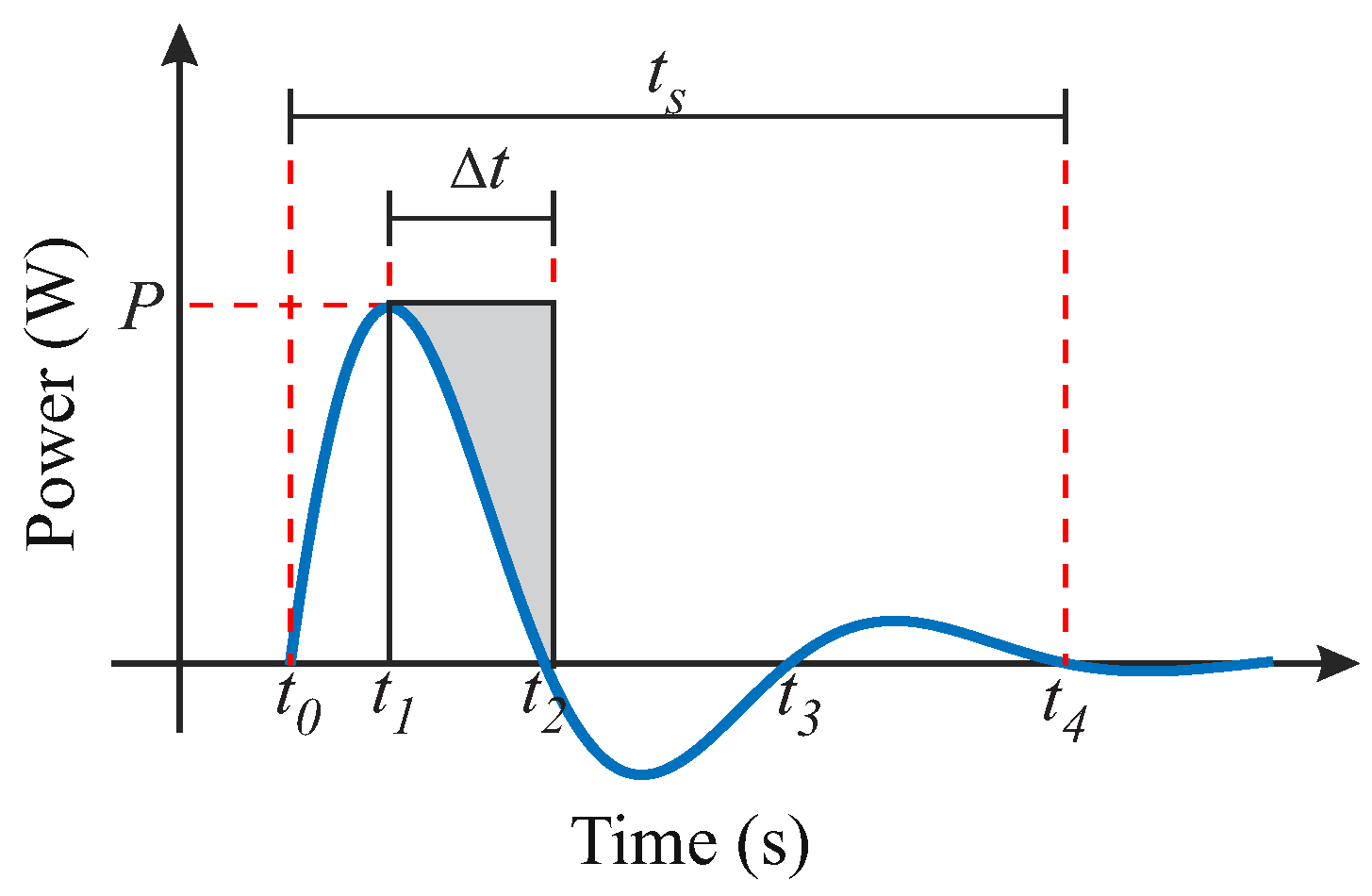
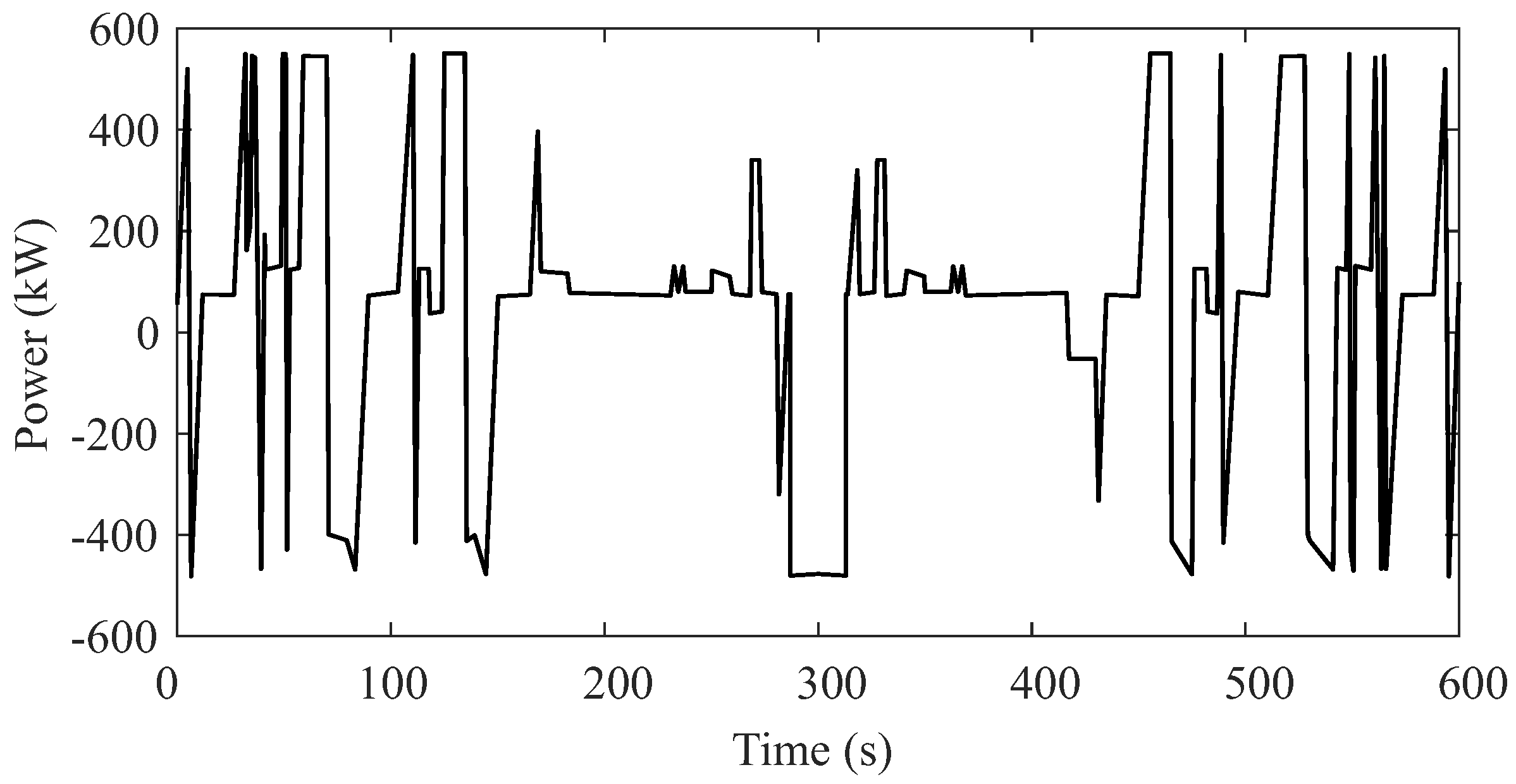
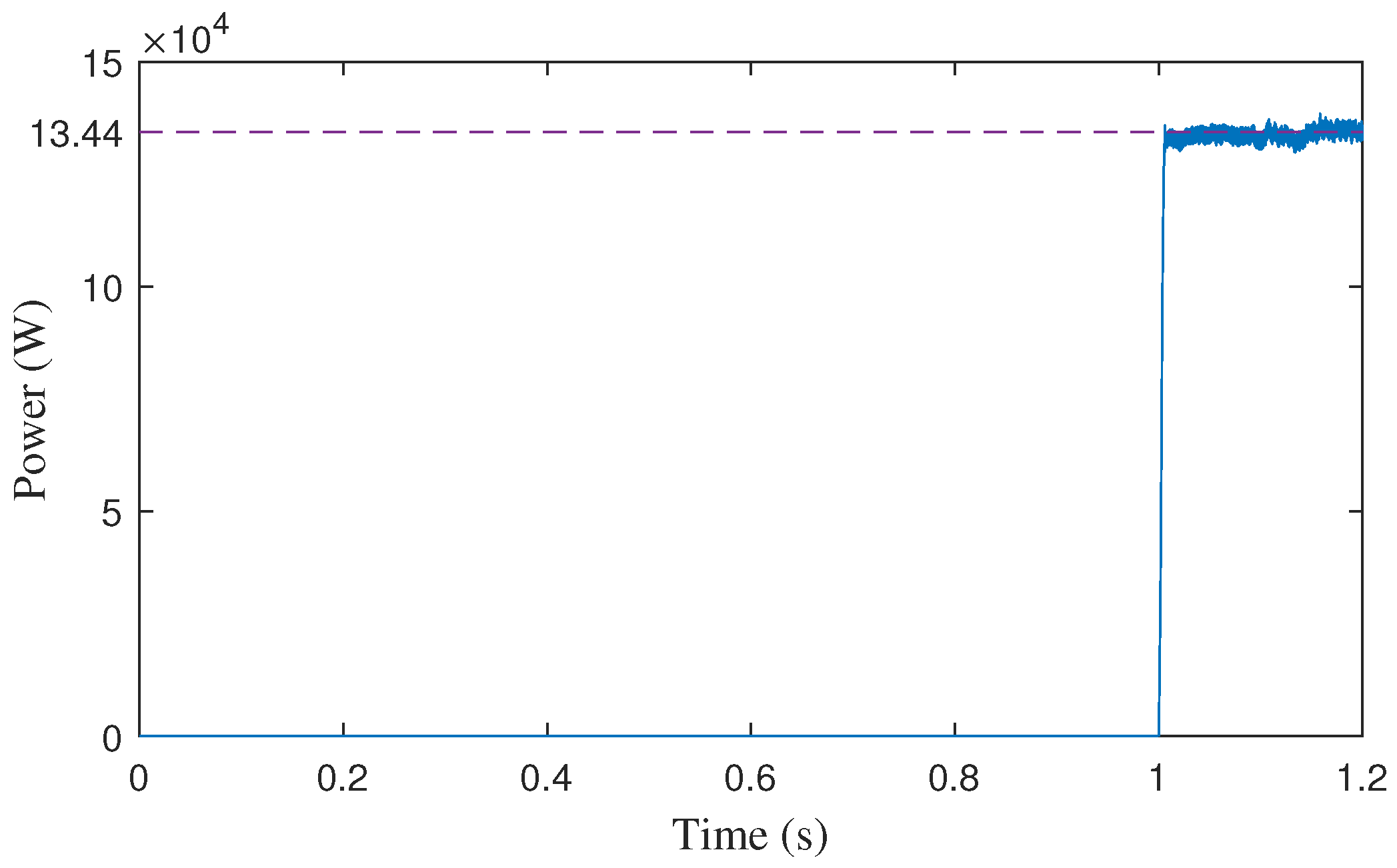
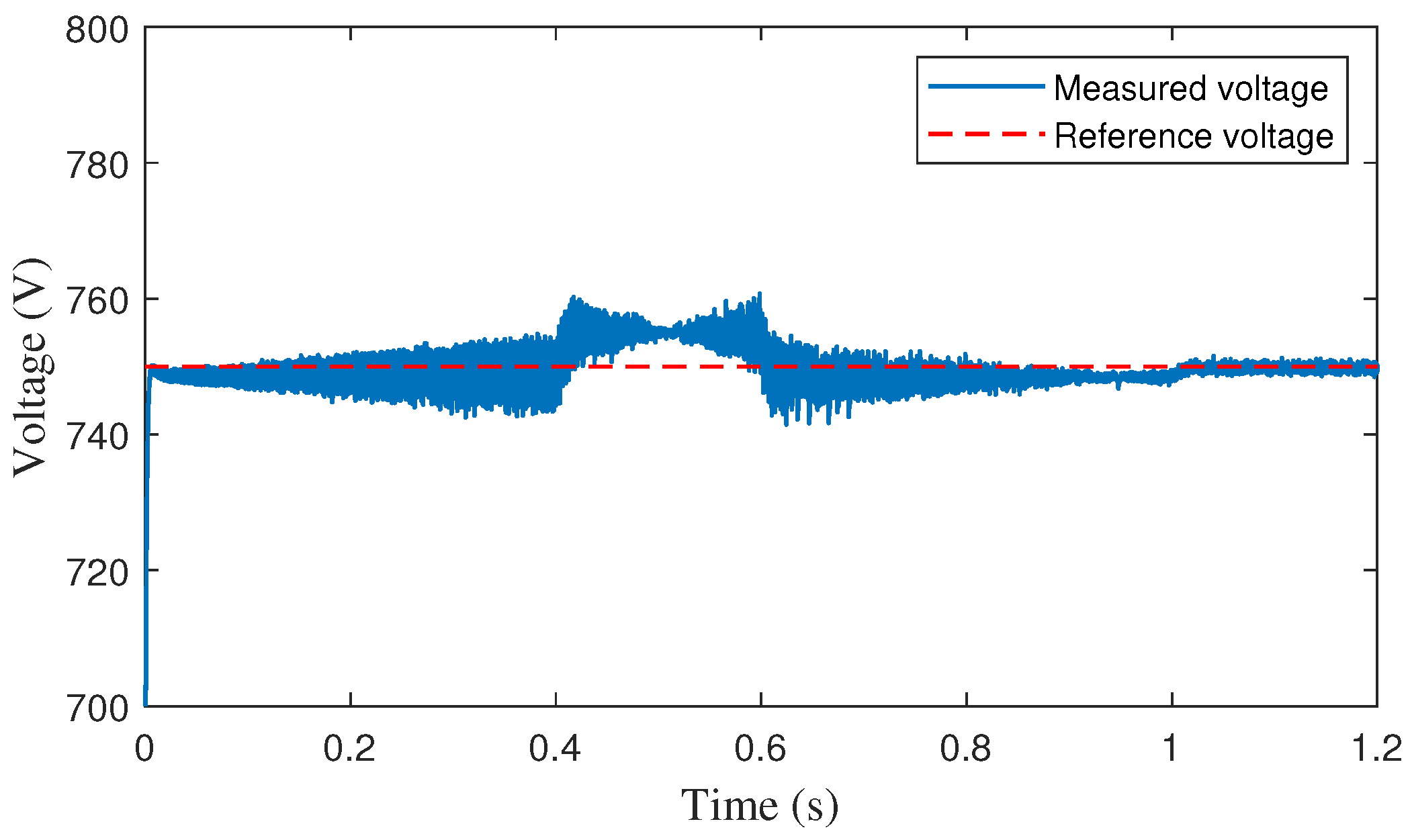
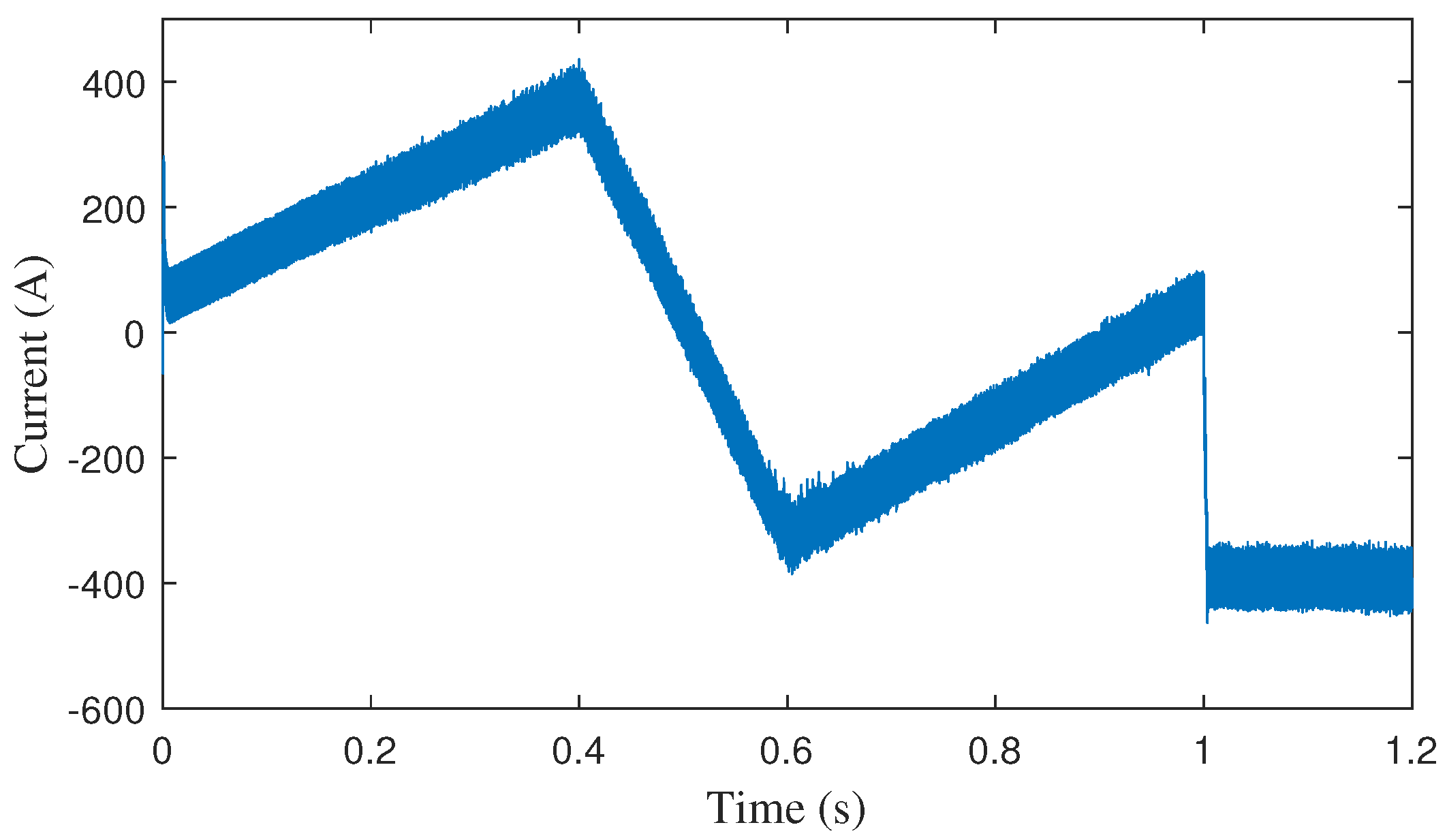
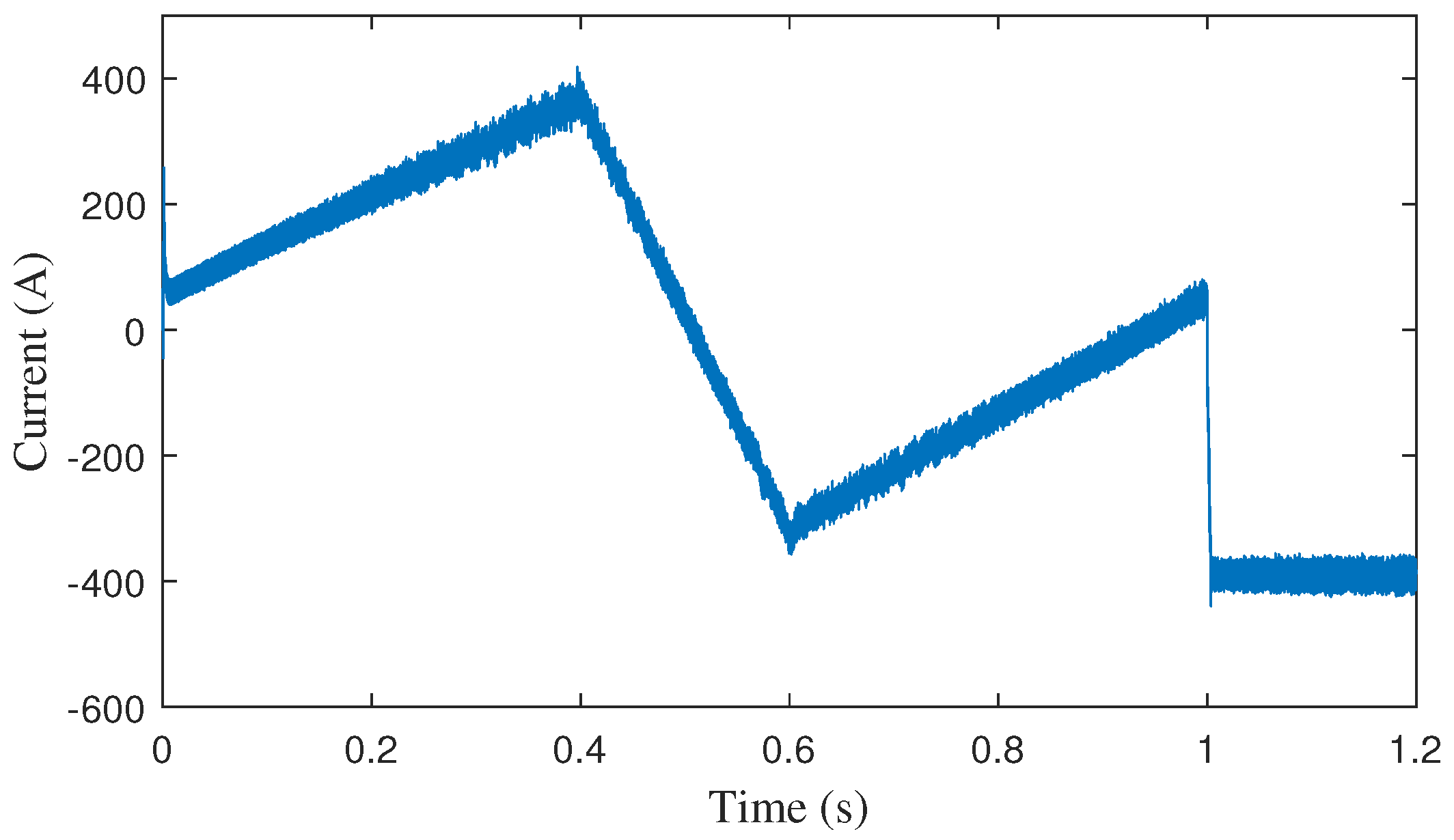
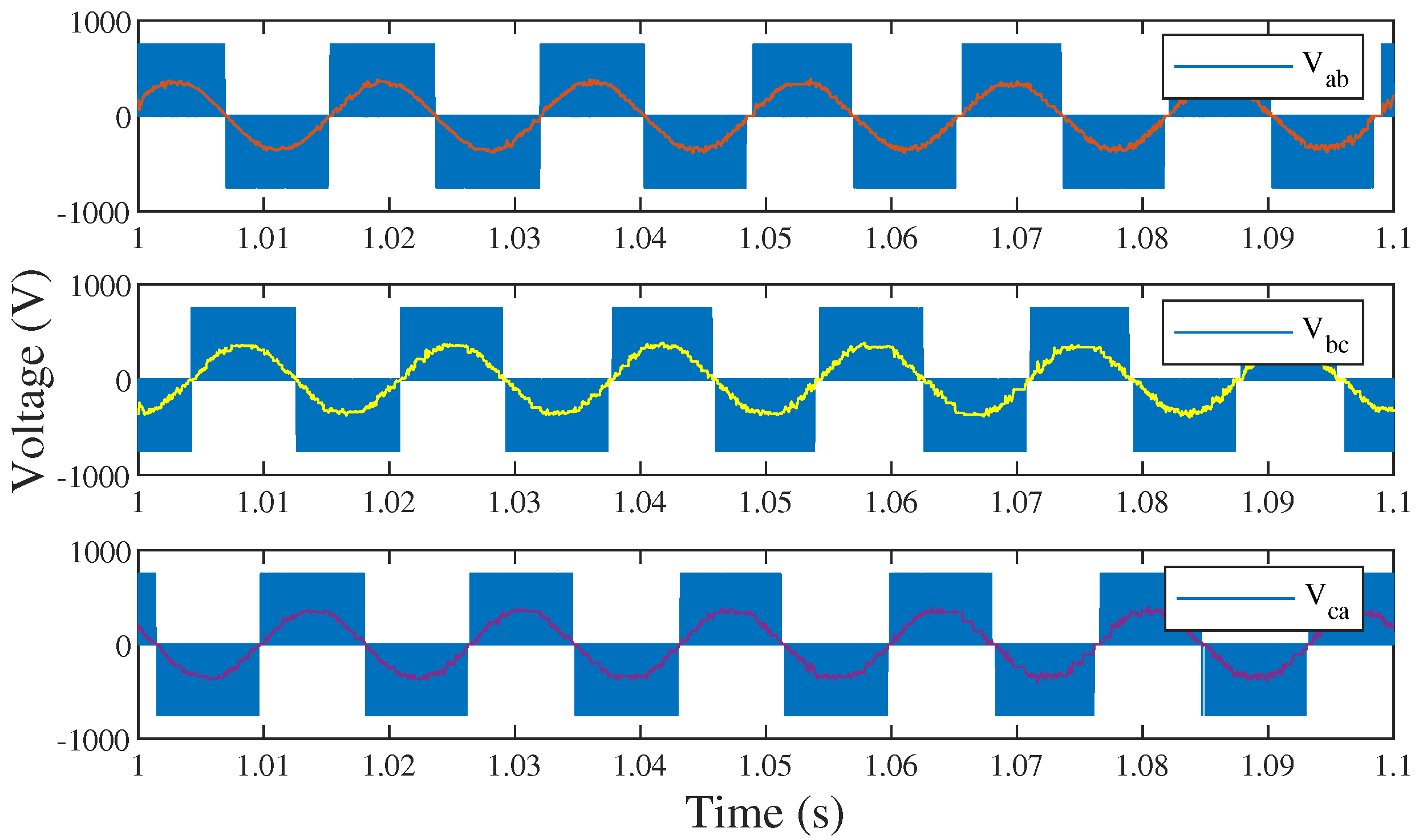
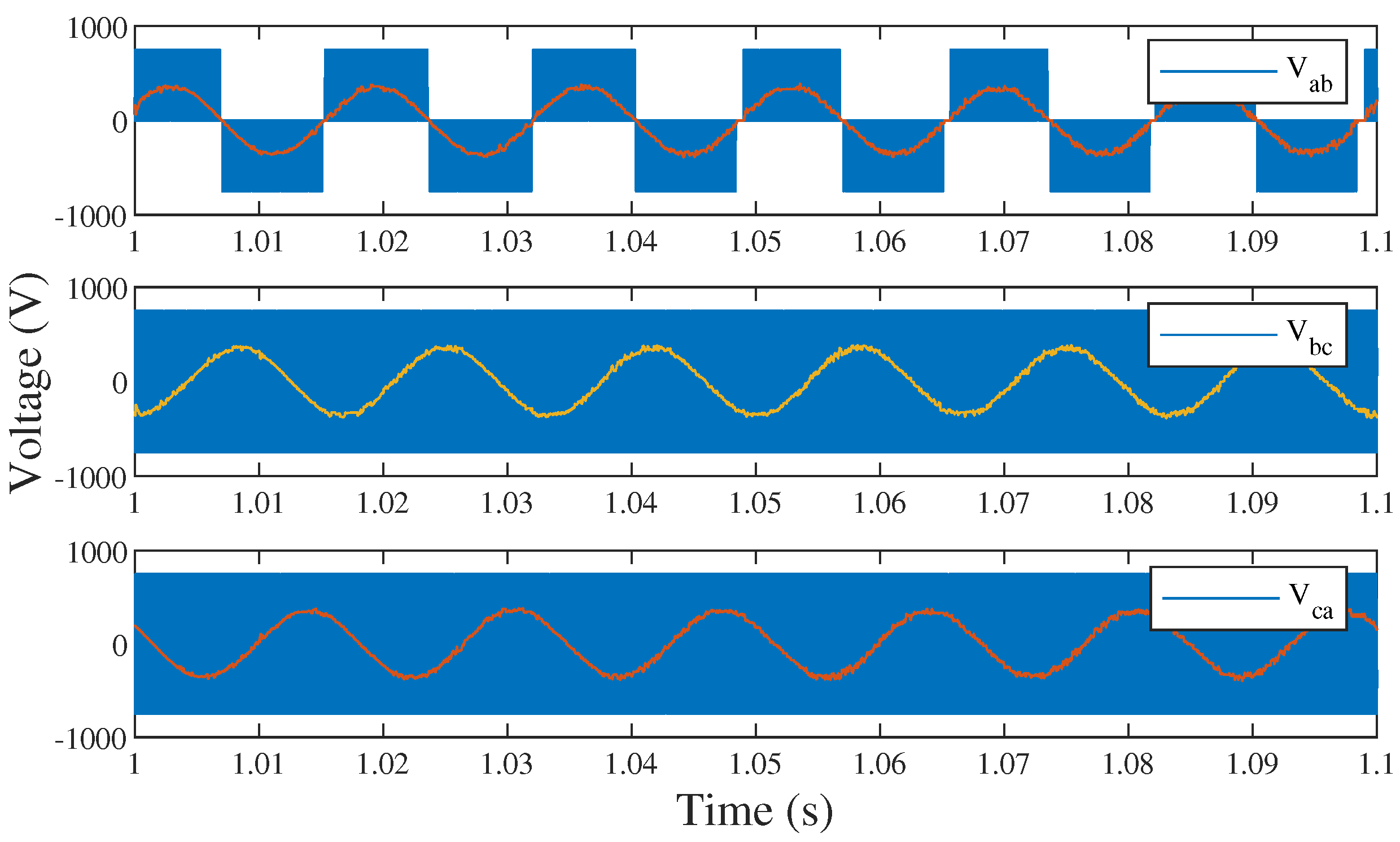
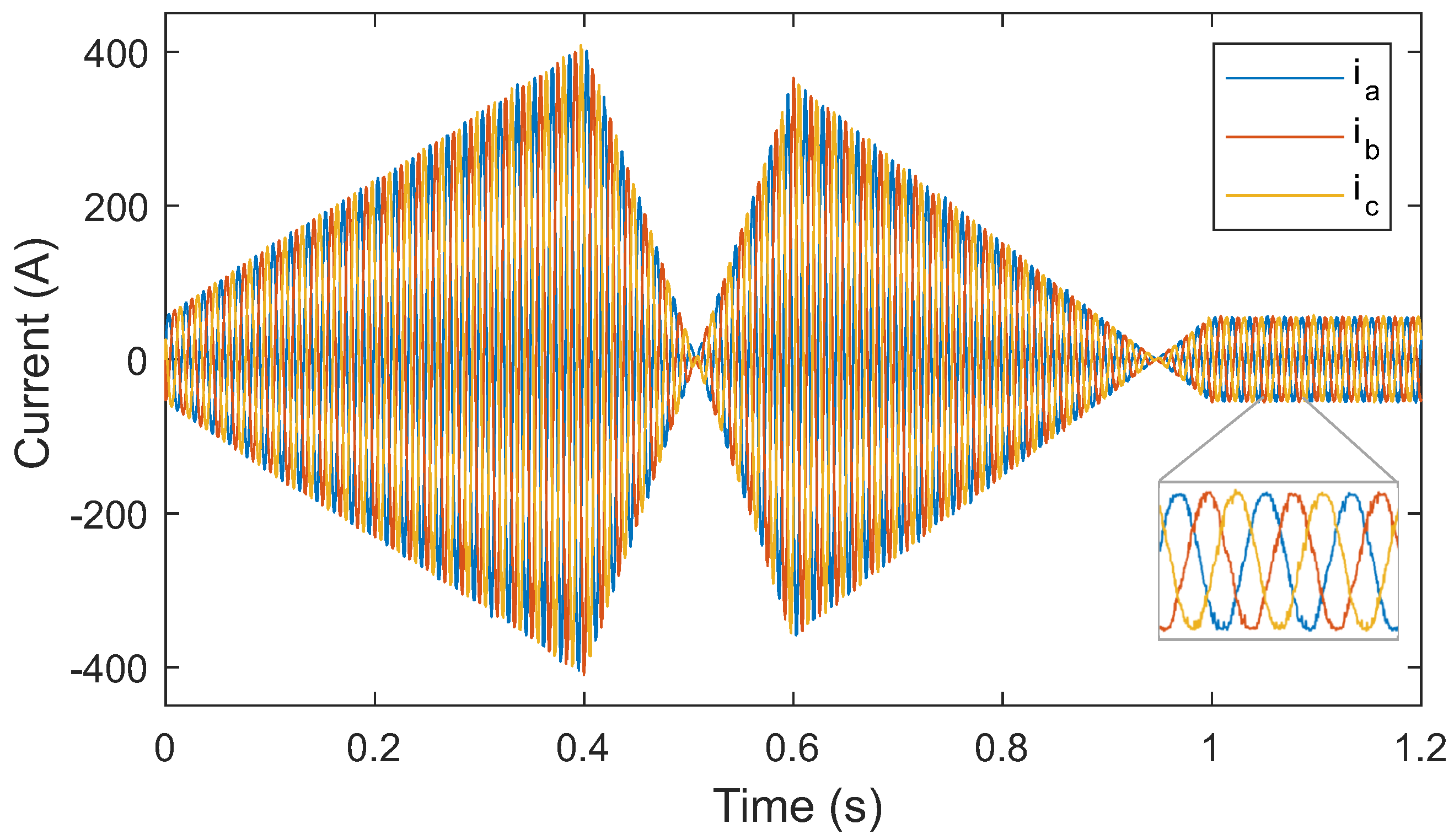

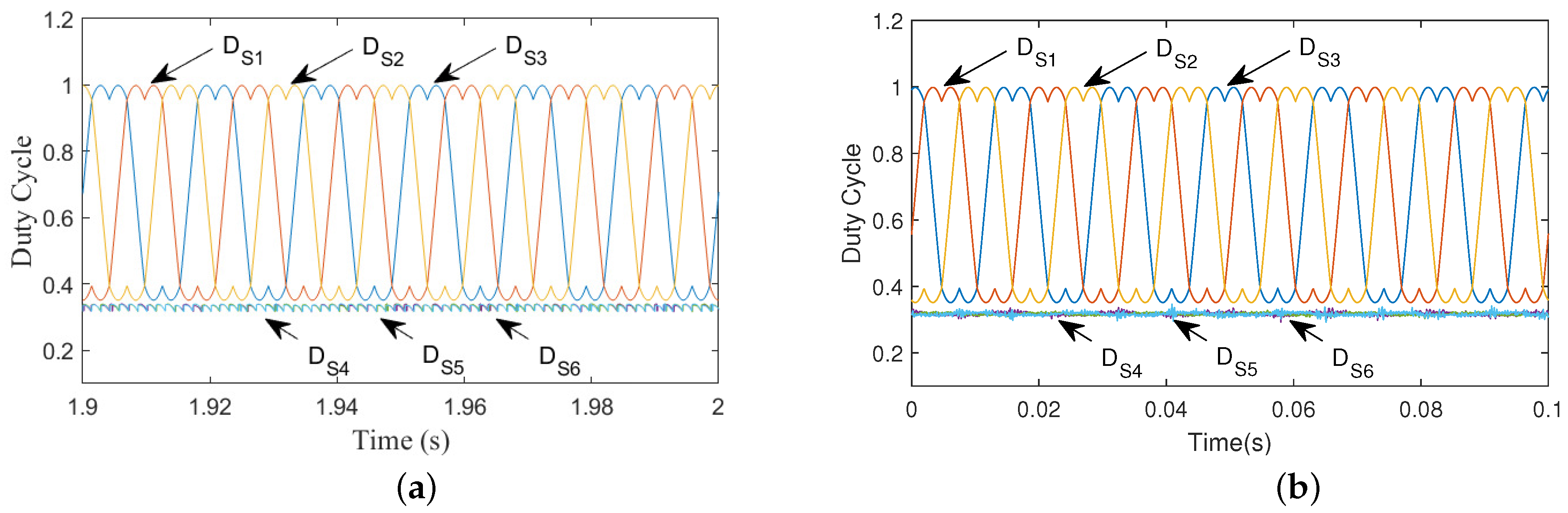

| Symbol | Parameter | Component | Value |
|---|---|---|---|
| Battery voltage | Battery | 375 V | |
| DC link voltage | Converters | 750 V | |
| Switching frequency | Converters | 10 kHz | |
| Output line voltage | Converters | 311 Vrms | |
| Input inductor current ripple | Converters | 27.2 A | |
| Average power | Battery | 192.74 kW | |
| Maximum power | Battery | 532.7 kW | |
| Minimum power | Battery | −465.9 kW | |
| Ancillary services power | Battery | 71.5 kW |
| Iteration | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| (J) | (V) | (ms) | (mF) | (J) | (V) | (ms) | (mF) | (mF) | |
| 1 | 30 | 1068 * | 1.3 | 10 | 60 | 522 * | 2 | 41 | 41 |
| 2 | 25 | 797 * | 1 | 0.688 | 45 | 708 | 3 | 1.5 | 1.5 |
| 3 | 49 | 796 * | 1.4 | 1.6 | 50 | 708 | 2.5 | 1.6 | 1.6 |
| 4 | 49 | 795 | 1.4 | 1.6 | 60 | 708 | 3 | 2 | 2 |
| 5 | 63 | 794.5 | 1.4 | 1.8 | 60 | 709 | 3 | 2 | 2 |
| Symbol | Parameter | Value |
|---|---|---|
| DC link voltage | 750 V | |
| Battery voltage | 375 V | |
| Output line voltage | 380 V | |
| Average power | 48.25 kW | |
| Maximum power | 133.2 kW | |
| Minimum power | −116.5 kW | |
| Ancillary services power | 17.9 kW | |
| Substation power | 134.4 kW | |
| Battery inductance | 750 μH | |
| DC link capacitance | 2 mF | |
| Switching frequency | 10 kHz |
| Symbol | Parameter | Value |
|---|---|---|
| IGBT | Transistor module | SKM50GB123D |
| Battery voltage | 35 V | |
| Battery inductors | 5 mH | |
| DC link voltage | 100 V | |
| DC link capacitance | 4.4 mF | |
| Switching frequency | 10 kHz | |
| Passive filter inductor | 1.26 mH | |
| Passive filter capacitor | 49.5 F | |
| R | Resistive load | 12.1 |
| Leakage capacitance | 220 nF |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Almeida, A.D.D.; Bradaschia, F.; Rech, C.; Caldeira, C.A.; Neto, R.C.; Azevedo, G.M.S. Nine-Switch Multiport Converter Applied to Battery-Powered Tramway with Reduced Leakage Current. Energies 2024, 17, 1434. https://doi.org/10.3390/en17061434
Almeida ADD, Bradaschia F, Rech C, Caldeira CA, Neto RC, Azevedo GMS. Nine-Switch Multiport Converter Applied to Battery-Powered Tramway with Reduced Leakage Current. Energies. 2024; 17(6):1434. https://doi.org/10.3390/en17061434
Chicago/Turabian StyleAlmeida, Antonio D. D., Fabrício Bradaschia, Cassiano Rech, Carolina A. Caldeira, Rafael C. Neto, and Gustavo M. S. Azevedo. 2024. "Nine-Switch Multiport Converter Applied to Battery-Powered Tramway with Reduced Leakage Current" Energies 17, no. 6: 1434. https://doi.org/10.3390/en17061434
APA StyleAlmeida, A. D. D., Bradaschia, F., Rech, C., Caldeira, C. A., Neto, R. C., & Azevedo, G. M. S. (2024). Nine-Switch Multiport Converter Applied to Battery-Powered Tramway with Reduced Leakage Current. Energies, 17(6), 1434. https://doi.org/10.3390/en17061434










