1. Introduction
The electrification and incorporation of renewable energy sources are seen today as an important solution to increase the sustainability of society [
1,
2]. This is not only important for the industrial and energy sectors but also for the water–energy nexus [
3,
4]. For example, in both urban and irrigated areas, water distribution systems (WDSs) require high energy consumption to complete a whole cycle (i.e., water capture, purification, filtering, drink and grey water treatment, distribution, and reuse), leading to high exploration costs and high energy losses [
5]. One currently viable solution to increase the energy efficiency in these systems is applying pumps working as turbines (PATs) connected to the electric grid (on-grid) to recover the excess energy that would be otherwise lost for excess pressure control during the system’s normal operation. While on-grid PAT solutions have already shown the potential to increase the system’s energy efficiency, there is still a lack of methodologies to accomplish stable and energy-efficient solutions for off-grid systems [
6,
7]. Therefore, to answer this “question”, this paper contributes a novel methodology for developing DC off-grid systems based on PATs by optimizing system energy efficiency and defining stable operational limits for different electric-hydraulic loads.
Regarding on-grid solutions, in a WDS, a pumping station should provide enough pressure to supply the farthest consumer. However, excess pressure may damage the closest consumers. Therefore, pressure-reducing valves (PRVs) are typically installed to regulate the pressure along the system. This pressure regulation produces energy losses that compromise the system’s sustainability [
8]. One solution is replacing or coupling, depending on the system restrictions, the PRV with micro hydropower solutions capable of recovering the energy losses originated by the pressure reduction.
The use of hydropower systems could be focused on classical hydraulic machines (i.e., Francis or Pelton turbines, mainly), which have higher investment costs and, in most cases, show economic unfeasibility for these types of small flow projects [
9]. Another more viable solution is using reversible systems, such as PATs, with much more positive techno-economic feasibility ratios for system owners and managers [
6,
10]. Several researchers have shown different examples of applicability in the last few years. Italy’s Casamassima water distribution system was analyzed for the possibility of recovering daily energy equal to 2300 kWh using a PAT [
11]. In [
12], a study was performed on the potential energy recovery in Merano City (Italy), showing a daily potential recovery of 338 kWh. The efficiency of the PAT booster applied in an isolated village in Normandia (France) was analyzed, reaching a daily recovered energy equal to 9.61 kWh [
13]. Different irrigation systems, which contained isolated recovery systems, were shown in the REDAWN project—Interreg (2017–2021) and in the literature review, such as the Zújar channel in Spain (2569 kWh/day) [
14] and in Italy (3500 kWh/day) [
15]. Other studies have shown the possibility of using PATs in the wastewater of oil refineries [
16]. More case studies applied to supply and irrigation networks could be consulted in the review developed by [
17]. The mentioned cases are just some examples of the applicability of PATs, which water managers can use to reach higher efficiency ratios while minimizing investment costs.
For off-grid applications, PATs could offer an energy source in remote and off-grid areas, such as isolated irrigation areas, in developed countries, and/or in isolated urban areas, such as small energy communities [
18]. This possibility led different researchers to study the PAT behavior from both hydraulic and electric phenomena. In [
19,
20], conventional pumps in water distribution systems were proposed to recover energy and increase the system’s energy efficiency. The prediction of the PAT behavior can be obtained with different methods from its pumping curves, which facilitates the selection of the PAT for a specified application [
21,
22]. CFD methods are also important tools for this task [
23,
24]. A method to select a PAT was proposed in [
25], introducing an energy exploitation coefficient and combining different previous methods. The cost analysis methods were proposed by [
26]. The use of a PAT system, both in parallel and serial, was analyzed by different authors to increase the recovered energy [
27], including the VOS strategy. In [
28,
29], the authors focused on the hydraulic and electric behaviors of the machines in terms of flow–head and flow–efficiency curves.
Despite all theoretical and experimental knowledge, the benefits of PAT systems in off-grid applications are still limited due to their highly non-linear behavior, generally associated with the lack of a constant frequency electric grid. Typically, PATs are provided with squirrel-cage induction machines due to their high robustness and lower cost [
30]. Thus, in PAT operation, these induction machines operate as generators consuming reactive power to create their air-gap rotating magnetic field. This reactive power is crucial to optimize the active power generated by the electric machine while minimizing its losses [
28,
31]. When the machine operates isolated from the grid, the induction generator must be supported by capacitors to supply the required reactive power. This is called a self-excited induction generator (SEIG). Because of the lack of a constant electric frequency, energy conversion and efficiency will depend on many factors, such as the electric load, the rotational speed, the capacitor value, and other hydraulic variables such as head, flow, and fluid properties. This originates a variable AC electric output with variable efficiency, which may compromise the supply of conventional electric loads [
32,
33,
34].
Therefore, there is currently a need to design stable off-grid electric systems based on PATs capable of supplying the electric loads with maximum efficiency. To achieve this, it is required to (a) define the PAT-SEIG operational area to maximize the energy conversion and; (b) stabilize the electric quantities (voltage and frequency) to allow the connection of conventional electric loads. One solution for stable electric quantities is creating a DC off-grid using AC/DC converters.
Following this research topic, this work proposes a new methodology based on the interaction between the hydraulic, mechanical, and electric subsystems, which is tested experimentally, to define the operation region of a PAT-SEIG system and to maximize its efficiency, creating a stable DC electric off-grid. These two objectives highly depend on the capacitor value, electric load, and rotational speed. An analytical model is developed to estimate the PAT-SEIG operation and its limits. This model will allow water managers to design and optimize an off-grid PAT-SEIG system and to define the best hydraulic machines and electronic equipment under the smart water–energy grid concept and all control elements to maximize energy conversion within the target under suitable operational limits.
The work is structured as follows:
Section 2 presents the materials used in this investigation and the proposed methodology to identify and estimate the system efficiency and operational limits.
Section 3 presents the experimental results and the accuracy of the proposed analytical model in identifying the system’s operational restriction, efficiency, and reliability.
Section 4 presents the main conclusions of this work.
2. Methodology and Methods
The proposed research methodology is divided into three parts, as shown in
Figure 1. First, experimental tests are carried out to evaluate the electric and hydraulic operational limits of a DC off-grid system based on a pump as turbine (PAT) coupled to a self-excited induction generator (SEIG, nº:06/2017, VEM motors, Thurm, Germany). The DC off-grid system is composed of a conventional pump, operating as a turbine, coupled to an induction generator, PAT-SEIG, excited by a capacitor bank and an AC/DC-DC/DC system to guarantee a stable DC voltage (
Figure 2). In this system, the energy conversion is carried from the excess of hydraulic energy into mechanical energy, mechanical to AC electrical energy, and, finally, AC electrical to DC electrical energy. Due to the multiple physics phenomena in this system, it is of utmost importance to understand the system’s operational restrictions and define design methodologies for its adequate operation.
The electric experimental characterization consists of no-load and load tests to evaluate the SEIG’s required excitation capacitors and losses and to test the DC/DC converter under variable load. After this characterization, electric load tests are performed on the SEIG-DC/DC system, with a DC motor (nº: GA3105-1ZE20-0EA1-Z, Siemens, Germany) mimicking the PAT operation. The latter allows for the identification of the electric-suitable operational area. After these, the system is coupled to the PAT and hydraulic system shown in
Figure 2. With these, the influence of the excitation capacitor and the electric load on the hydraulic operation is analyzed. Finally, the PAT-SEIG operational area is identified.
After this experimental investigation, an analytical model is proposed to estimate the electric-hydraulic operational zone of the PAT-SEIG system. This analytical model uses the SEIG’s capacitor, rotational speed, and requested load as input parameters and is capable of estimating its efficiency, electric current, voltage, and frequency. The operational domain is determined using the maximum current and voltage and the minimum voltage required to self-excite the induction generator.
2.1. Pump as Turbine (PAT)
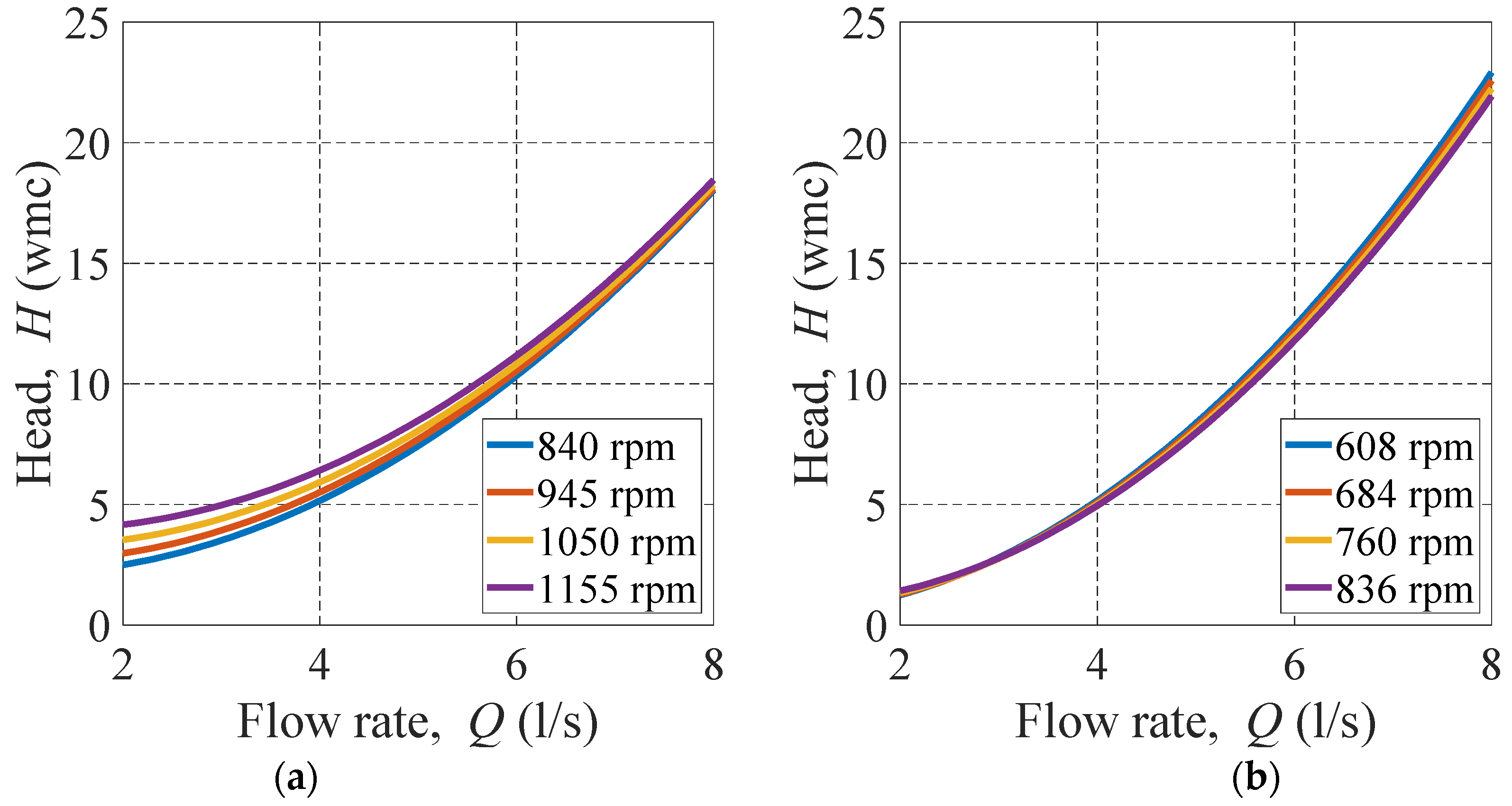
With a variable efficiency, the pump as turbine (PAT) converts the hydraulic power into mechanical power so that the SEIG can later convert it into electrical power. The experimental tests were conducted in the CERIS-Hydraulic Laboratory of Instituto Superior Técnico, University of Lisbon. This work uses two PATs, as shown in
Figure 3, with the nominal values displayed in
Table 1. PAT1 is rated at 1050 rpm and PAT2 at 760 rpm. Note that these are conventional pumps used in turbine mode.
Their characteristic curves are defined by Equations (1), (2) and (5), where
A,
B, and
C are coefficients of their
H–
Q characteristic curve,
Q is the flow in l/s;
H is the recovered head in m w.c.;
D,
E, and
F comprise the efficiency coefficients curve and
is the PAT efficiency [
35].
When the affinity laws are applied to previous equations, the new curves are defined by Equations (3) and (4)
where
is the relation between the rotational speed (
Nr) and nominal or reference rotational speed (
Nref). In the turbine mode, the relation between the head,
H, flow,
Q, and speed,
Nr, is shown in
Figure 4a,b for PAT1 and PAT2, respectively, where
A = 3.664,
B = −694.5, and
C = 314,560 for PAT1 and
A = 1.854,
B = −885.2,
C = 412,400 for PAT2. These were obtained experimentally in our laboratory.
2.2. Self-Excited Induction Generator
The squirrel-cage induction machine used as a self-excited induction generator (SEIG) is shown in
Figure 5. Its nominal parameters are presented in
Table 2. This machine is coupled to each PAT to convert the excess hydraulic energy into electricity in off-grid conditions. The SEIG is first tested in the IST Electrical Machine’s Laboratory, coupled to a DC motor mimicking the PAT operation, to evaluate the performance and limits of the electric circuit.
The energy generated by the induction machine is rectified and supplied to a DC/DC converter. In this topology, as the machine is disconnected from the grid, a source of reactive power is necessary to excite the induction machine; therefore, a capacitor bank is also installed. The capacitor value per phase required to self-excite the induction machine varies with frequency. The value of the reactive power produced by the capacitors should be the same as that consumed by the SEIG, which is mainly set by the magnetization inductance,
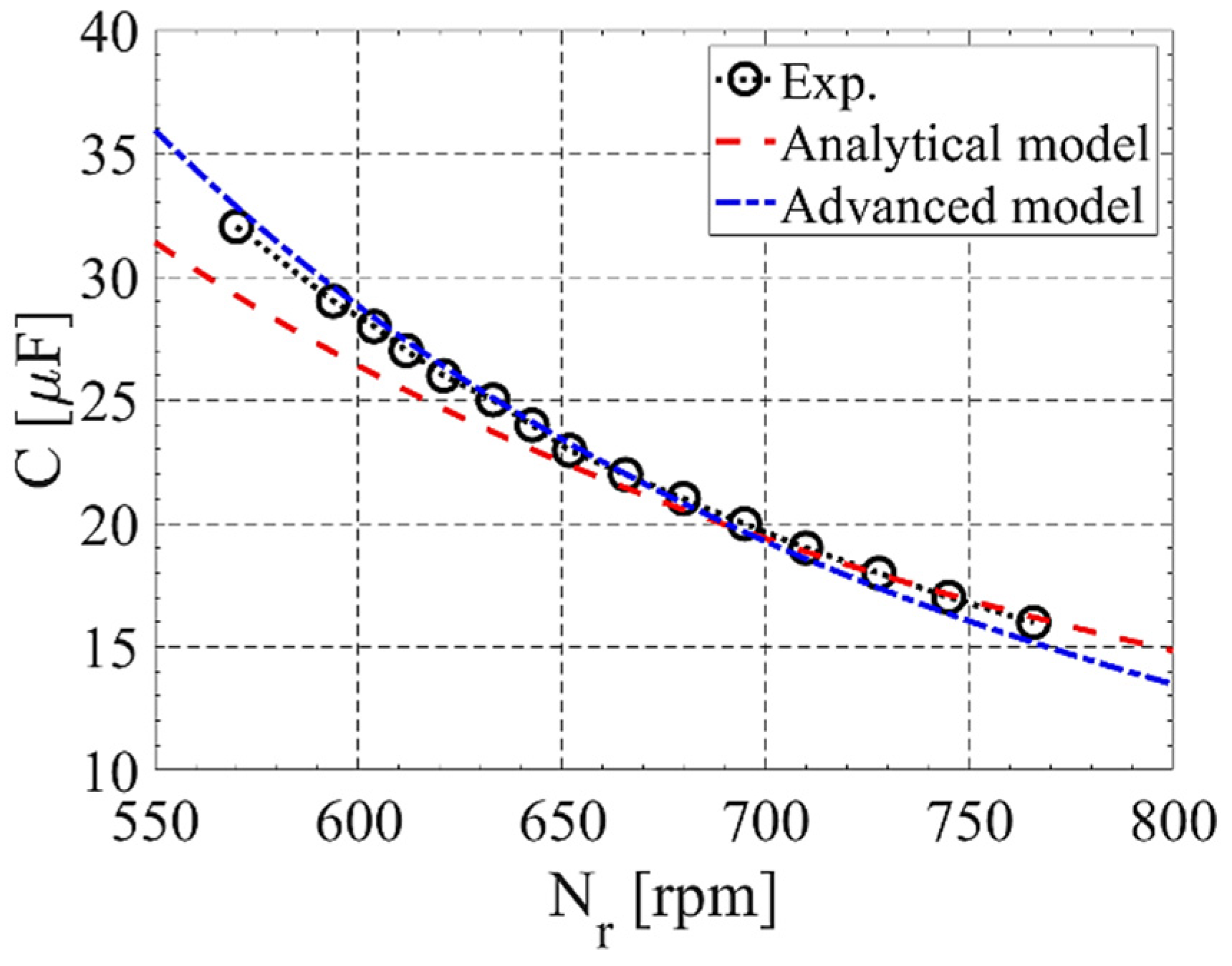
Lm. This corresponds to a resonance between the SEIG and capacitors. If the capacitor values are too high, the SEIG will saturate and overload; if these are too low, there is insufficient reactive power to excite the SEIG. Experimental tests are carried out with the SEIG to determine the values of the capacitors required for different ranges of rotational speed (
Figure 6). These are performed without load and using a DC motor as the prime mover.
A simplified method to estimate the required capacitor value is considering the SEIG’s magnetization inductance,
Lm, in parallel with the capacitor,
C, as shown in Equation (5). If there is no access to the magnetization induction value, this can be estimated based on the reactive power provided by the manufacturer (
). Other more detailed analytical models have been proposed to increase the accuracy of the capacitor required to excite the SEIG, as presented in [
4,
28], where the influence of additional parameters, such as leakage and stator and rotor resistances, can also be applied.
Experimental no-load tests are carried out to characterize the SEIG used to obtain its magnetization inductance, Lm, and iron and mechanical losses, Pfe + Pmec. From these, it is possible to estimate the correct value of capacitors required to self-excite the induction generator and to compare its behavior with the experimental results. Moreover, with the SEIG losses, it is possible to estimate the SEIG efficiency during load tests and when coupled with the PAT.
2.3. DC/DC System
Another component required to develop the DC off-grid system is a DC/DC converter capable of stable DC voltage output for a wide range of DC voltage inputs. Due to the off-grid operation, the electric frequency is not fixed, and, thus, a rectifier is used. The resonance operation between the induction generator and the capacitor bank sets the electric frequency. In addition, the SEIG’s stator voltage is not fixed as it depends on the frequency, speed, mechanical input power, and load. Therefore, the output voltage of the rectifier will vary along the PAT-SEIG system operation. The selected DC/DC converter is capable of maintaining its output voltage for a wide input voltage range (180–425 Vdc) (
Figure 7). Moreover, its output voltage can be regulated using a variable rheostat. Its main parameters are listed in
Table 3.
2.4. Experimental Tests of SEIG with DC/DC System
To understand the behavior of the DC/DC system, experimental tests are first performed on the DC/DC converter without load and under load. These tests allow for verifying its stable output voltage for the range of the admissible input voltage. In addition, the behavior of the output voltage is acquired during the activation and deactivation of the DC/DC converter to verify its time constant.
After the DC/DC converter is verified, experimental tests are carried out on the setup, and a load is connected. The electric operational region from the SEIG, DC/DC converter, and rectifier are obtained with a resistive load. The equipment necessary to carry out these tests is shown in
Figure 8. Please note that the DC motor acts as the PAT to facilitate its command during the first stage of electric tests.
The measurement apparatus consisted of AC and DC voltage, current probes, and power analyzers. The uncertainty of this equipment is 1% of the reading plus 0.02% of the full scale for the current probes and 0.2% of the reading plus 0.01% of the full scale for the voltage probe. The uncertainty of the power analyzer is 1.2% of the reading for both active and reactive powers.
2.5. Hydraulic-Electric Experiment Setup
After the verification of the electric components, experimental tests are carried out at the CERIS hydraulic laboratory to simulate the system operation in a hydraulic system. These experimental tests aim to test the system at a technological readiness level of TRL4. The experimental setup is shown in
Figure 9, composed of a flow control tank (1), recirculating pumps (2), an air vessel (3), a 20 m HDPE pipe (4), and the PAT-SEIG system (5).
The function of the flow control tank, identified as (1) in
Figure 9a, is to simulate the downstream reservoir of a micro hydro and the suction tank of a pump system, where the flow of water at lower pressure is received or is pumped, guaranteeing the minimum submergence in the pumps water intake (
Figure 10a,b). The water level is measured in this tank to estimate the low pressure at which it is stored. This reservoir is inserted inside another tank, as shown in
Figure 10b, whose function is to buffer the system in case of sudden flow rate and pressure changes. This is necessary because these possible changes can significantly affect the closed system and cannot be controlled after immediately checking out the hydraulic system’s stability. At last, the buffer can also serve as a water storage method, allowing control over the amount of water that can or cannot be pumped into the upstream reservoir for the hydropower system, (3) in
Figure 9a, to increase its pressure using an air vessel or hydropneumatic reservoir.
The recirculating pump to be used, identified as (2) in
Figure 9a,b, is signed in
Figure 11a with a red arrow. Only one pump is used since only one PAT will operate simultaneously, although the system is also prepared to operate with two PATs and the two recirculating pumps in parallel or in series. In addition, we should also highlight the valve marked in red, as it is through its operation that it is possible to regulate the amount of water to be pumped into the upstream reservoir.
The upstream reservoir is the air vessel marked as (3) in
Figure 9b and represented in
Figure 11b, as well as its flow control valve. This is intended to simulate the upstream reservoir of the hydropower system (3) in
Figure 9 and
Figure 11b, from which water is routed at high pressure towards the PAT. With the aid of the isolated valve (
Figure 11a), it is possible to fit the pressurized flow by injecting or releasing compressed air in the air vessel. This allows adjusting the pressure drop applied to the PAT and, consequently, the water flow to control the amount of hydropower available.
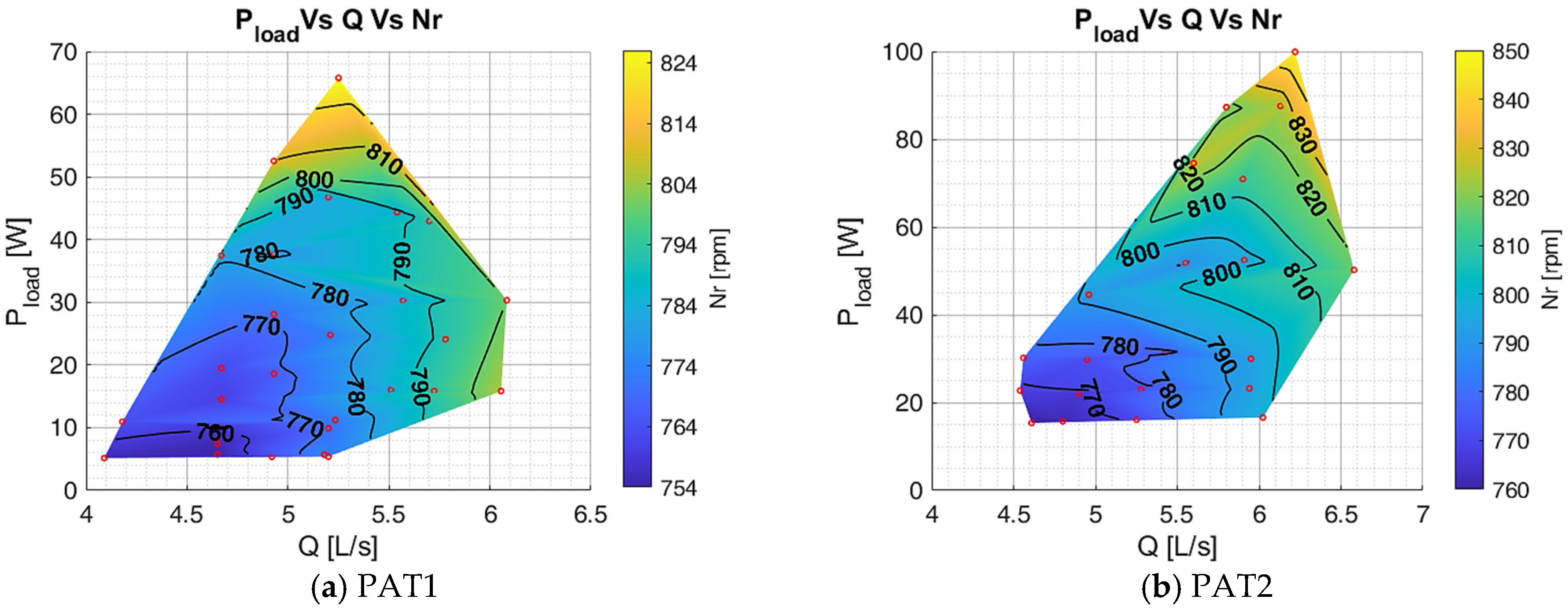
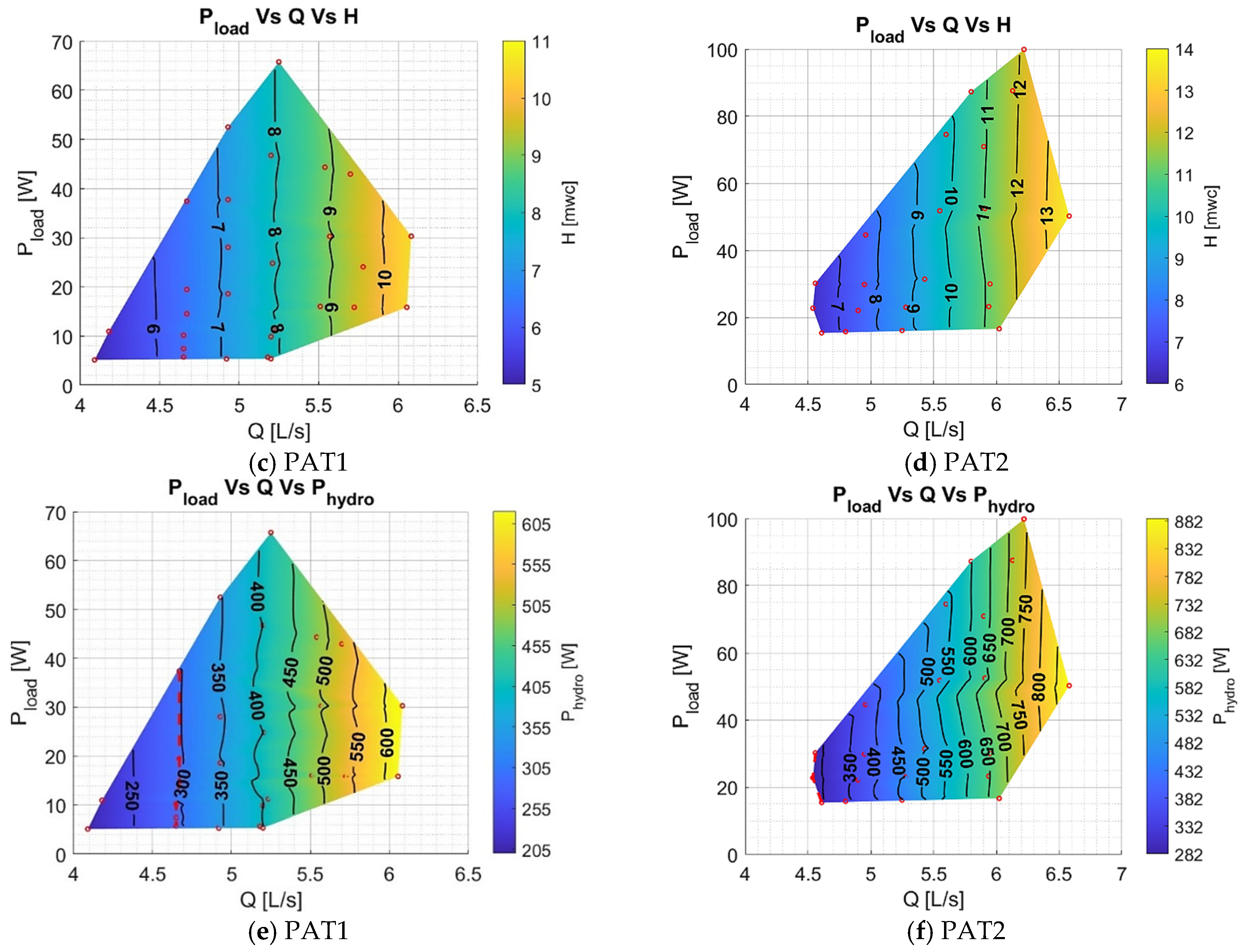
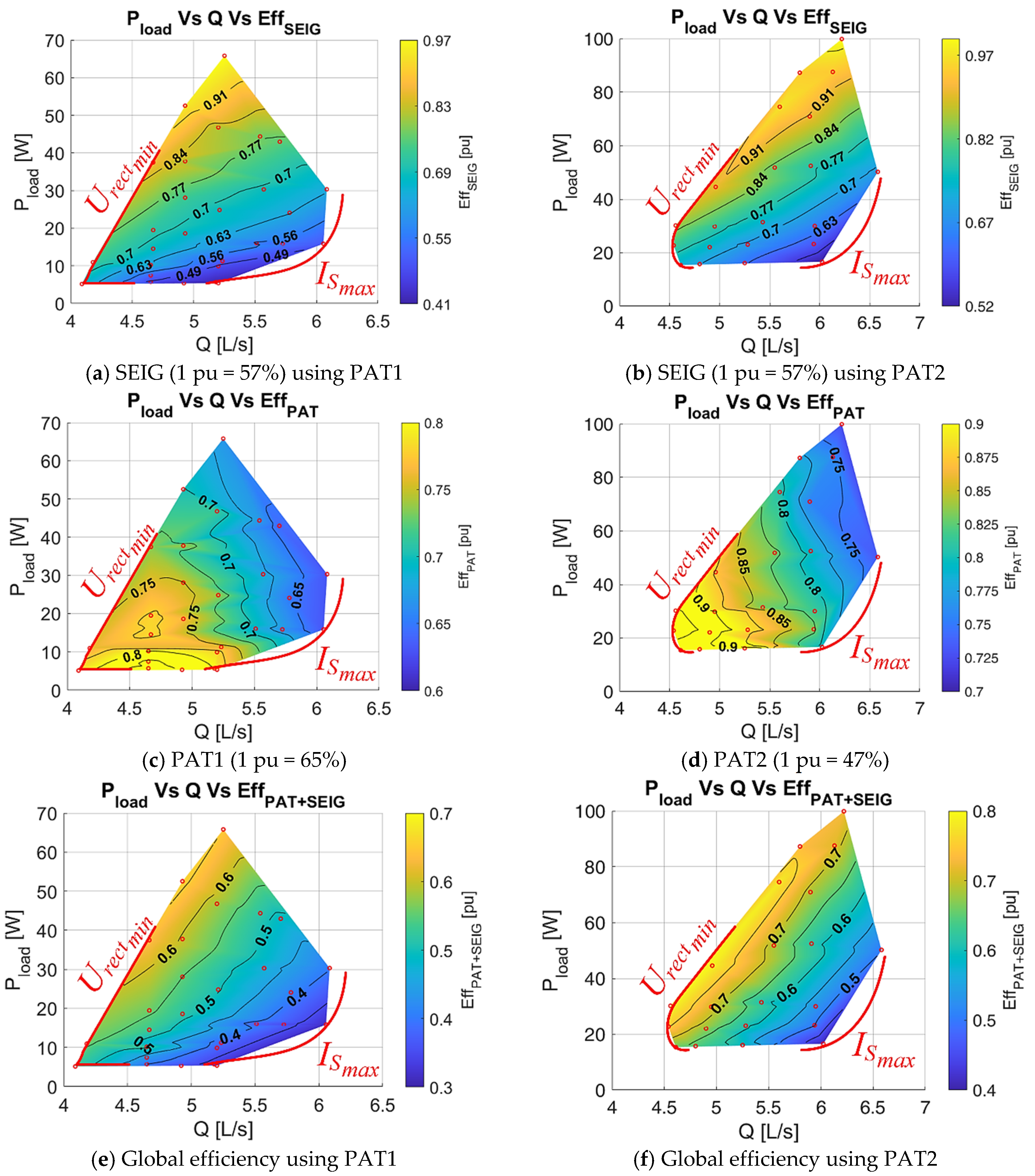
The experimental hydraulic-electric tests follow the proposed analysis tests to evaluate the system’s range operation. These measurements are used to obtain the power and the efficiency contour maps of the PAT-SEIG system to verify the same electric range of operation obtained previously but now conditioned by the hydraulic system operating conditions. Finally, the PAT, SEIG, PAT-SEIG, and the global efficiency maps of the system are computed.
2.6. Analytical Model for PAT-SEIG Operation
The proposed analytical model for estimating the PAT-SEIG operation is based on the resonance principle of the self-excited induction generator (SEIG). Due to the lack of an electrical grid in a stand-alone operation, the required reactive power for the SEIG is provided by capacitors. An excess of reactive power will saturate the SEIG and lead to overheating, and a deficiency of reactive power will lead to the loss of excitation of the SEIG. A similar effect is also presented for the active power. The mechanical power provided to the SEIG should match its losses and the electric load. Therefore, from the SEIG point of view, considering the load and capacitors, its total admittance,
Yt, should be null. The real part of the admittance is related to the active power balance and the imaginary part to the reactive one [
32]. Therefore, for an imposed SEIG rotational speed (equal to the PAT speed) and an applied capacitor value and requested load, the resonance criteria should allow the computation of the resonance electric frequency and, thus, the electric operation of the SEIG.
This can be evaluated based on the SEIG equivalent electric circuit.
Figure 12 represents the equivalent electric circuit, whose parameters are per-unit frequency, with
a =
f/
fN, where
f is the resonance electric frequency and
fN is the rated frequency. The load, stator, and rotor resistances are defined as
RL,
Rs, and
Rr′, respectively. The nominal stator, rotor, magnetization, and capacitor reactances are
,
and
, and are computed for the nominal electric frequency,
fN. The iron loss resistance is defined as
Rm. Parameter
b is the per unit rotor speed,
b =
N/
NSN, where
N is the rotational speed and
NSN is the nominal synchronous speed.
From this circuit, the total admittance,
Yt, can be computed considering the admittance of the load,
YL, capacitor,
Yc, stator,
Ys, magnetization,
Ym, and rotor,
Yr, described from (6) to (8).
Therefore, the solution of the electric resonance defined by parameter
a can be obtained by setting the real and imaginary parts of the total admittance to zero,
, and
. These solutions were obtained by these authors previously in [
32]. However, in the later work, the problem was to define the minimum capacitor value capable of exciting the SEIG. Now, the value of the capacitor is already defined; thus, only the real part of the equation is considered to find the electric resonance frequency. The solution of the per-unit frequency,
a, is obtained from (9), where parameters
D1 to
D6 are defined in
Appendix A.
Of the six possible solutions of a, only the purely real ones are considered. From the latter, the selected one corresponds to the maximum frequency. This requires an iterative process because of the non-linearity of the magnetization inductance, Lm(E/f), which depends on the magnetizing flux, i.e., on the magnetizing voltage divided by the frequency, E/f. This magnetization inductance is used to compute the magnetization reactance. Moreover, parameters a, b, and RL require an iterative process. Parameters a and b refer to the unknown electric frequency, and RL should be adjusted to keep the required electric load with the variation of the machine output voltage.
The iterative process is shown in
Figure 13. The analytical procedure starts by defining the input variables, rotational speed,
N, capacitance value,
C, and requested load active power,
Pload. Then, the method starts by defining initial values for the electric frequency,
f, and magnetization voltage,
E. With these, the per unit speed,
b, magnetization inductance,
Lm(
E/f), and load resistance,
RL, are computed. Next, the coefficients
Dk in (9) are computed, and the equation is solved to obtain the possible solutions of the per-unit frequency,
ak. The selected frequency corresponds to the maximum frequencies of those without an imaginary part. The equivalent circuit is solved with the selected frequency, and new values of the stator,
US, and magnetization voltages,
E, are computed. These are compared with the previous iterations and the convergence is checked. If no convergence is found, this cycle is repeated with the new values of the magnetization voltage,
E, and electric frequency,
f. If there are no possible real frequencies, the machine is under-excited and out of operation.
This analytical procedure estimates the SEIG efficiency and operational limits for any rotational speed input, capacitor value, and electric load.
4. Conclusions
In off-grid applications, obtaining an efficient and stable energy conversion using pumps working as turbines (PATs) coupled to self-excited induction generators (SEIGs) requires additional methodologies to maximize system efficiency and stabilize electric quantities. In this research, the proposed developed methodologies enabled, within the range of suitable operation, the creation of a stable DC voltage off-grid from a PAT-SEIG system. AC/DC and DC/DC converters were included to supply a load at constant DC voltage within a set of hydraulic, mechanical, and electrical bounds.
The operational range is essentially limited by the system’s electrical limits, namely, the minimum input voltage on the DC/DC converter and the input current on the SEIG. The choice of the capacitor value to excite the SEIG defines the speed range of the system. Therefore, selecting the best value to maximize the system’s efficiency is mandatory. Besides this, the increase in the load demanded also influences it by increasing the rotational speed and the water head for nearly constant water flow in these radial PAT impellers. The experimental methodology was verified for two sets of PAT-SEIG systems, achieving a maximum p.u. efficiency between 0.7 and 0.8 p.u.
The proposed analytical model has proved to be suitable for estimating the operational limits and efficiency of off-grid PAT-SEIG systems. This method is based on the resonance principle of the SEIG coupled to the load. The proposed analytical method was verified against experimental results with different capacitor values and presented a maximum root-mean-squared deviation of about 2.3%.
This investigation shows the capacitor value’s significance in defining the best strategy to regulate the PAT-SEIG systems to reach the maximum efficiency considering the system’s flow, available head, rotational speed, and load. Future lines of research should be aligned to define the operational control systems, considering the boundary application limits of the machines in terms of hydraulic and mechanical aspects.