Advancements and Future Directions in the Application of Machine Learning to AC Optimal Power Flow: A Critical Review
Abstract
1. Introduction
2. Problem Formulation
2.1. Objective Functions
2.1.1. Quadratic Fuel Cost
2.1.2. Real Power Loss Minimization
2.2. Constraints
2.2.1. Equality Constraints
2.2.2. Inequality Constraints
- Generator active power output
- Generator bus voltage
- Generator reactive power output
- Transformer tap settings
- Shunt VAR compensator
- Apparent power flow in transmission lines
- Voltage magnitude of load buses
3. Transformation of AC OPF Formulation for Machine Learning
4. Machine Learning Applications in OPF
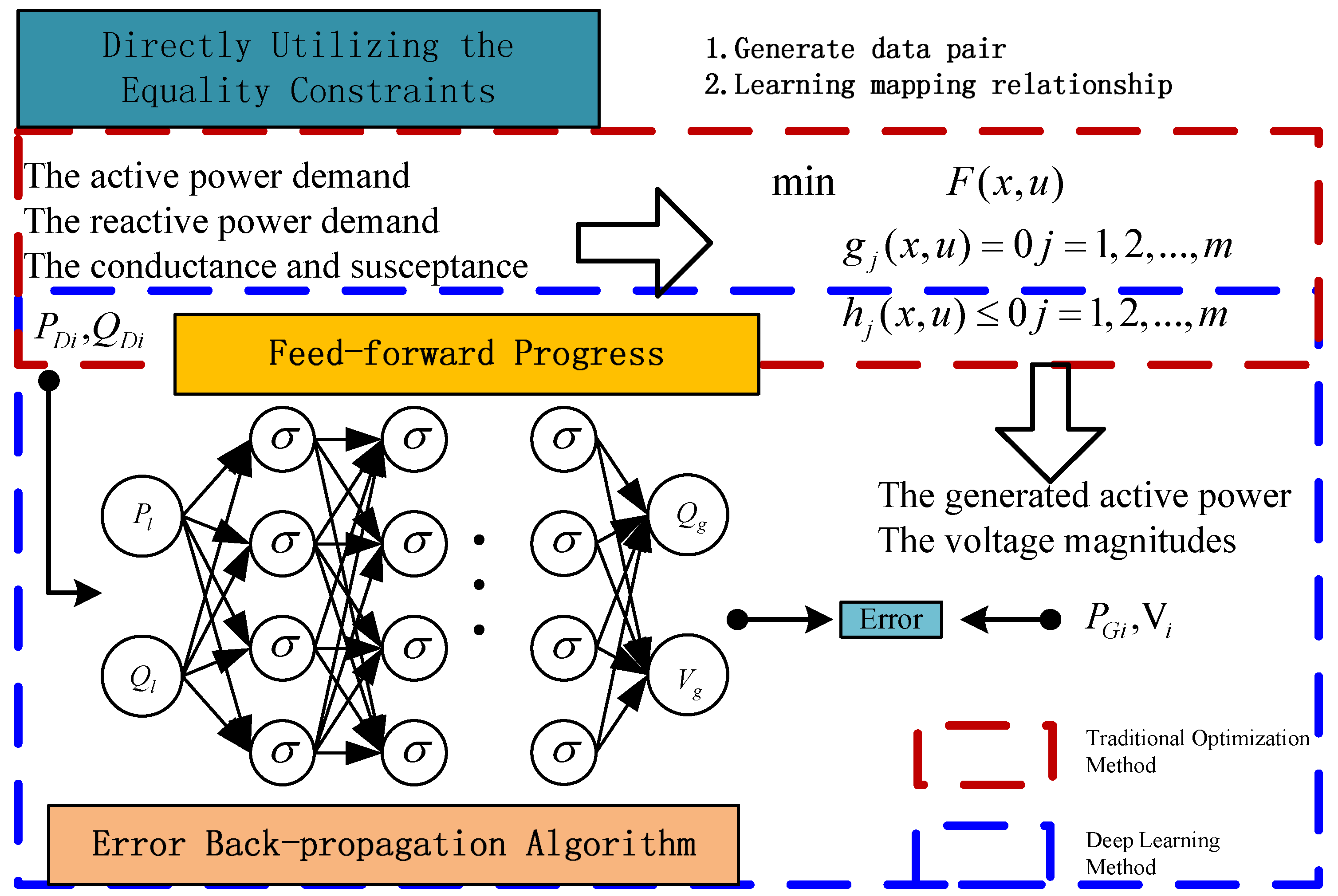
4.1. Direct Mapping of OPF Variables
4.2. Predicting Active Constraints
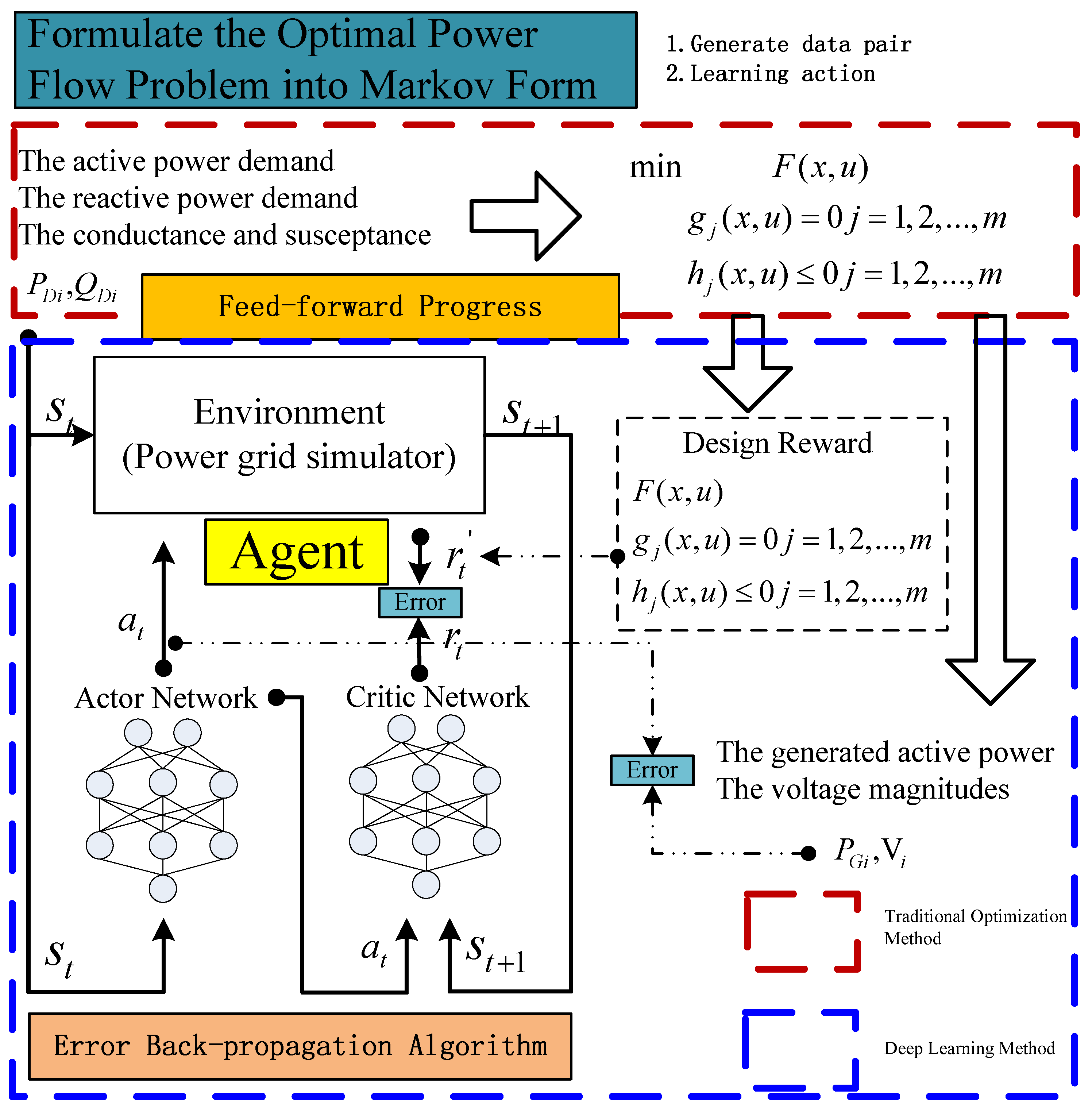
4.3. Learning Control Policy for OPF
4.4. Predicting Warm-Start Points
4.5. Learning Solution Process
5. Limitations and Path Forward
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zobaa, A.F.; Aleem, S.A.; Abdelaziz, A.Y. Classical and Recent Aspects of Power System Optimization; Academic Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Carpentier, J. Contribution a l’etude du dispatching economique. Bull. Soc. Fr. Elec. Ser. 1962, 3, 431. [Google Scholar]
- Capitanescu, F. Critical review of recent advances and further developments needed in AC optimal power flow. Electr. Power Syst. Res. 2016, 136, 57–68. [Google Scholar] [CrossRef]
- Chen, Y.; Pan, F.; Qiu, F.; Xavier, A.S.; Zheng, T.; Marwali, M.; Knueven, B.; Guan, Y.; Luh, P.B.; Wu, L.; et al. Security-constrained unit commitment for electricity market: Modeling, solution methods, and future challenges. IEEE Trans. Power Syst. 2022, 38, 4668–4681. [Google Scholar] [CrossRef]
- Conejo, A.J.; Aguado, J.A. Multi-area coordinated decentralized DC optimal power flow. IEEE Trans. Power Syst. 1998, 13, 1272–1278. [Google Scholar] [CrossRef]
- Guan, X.; Zhai, Q.; Papalexopoulos, A. Optimization based methods for unit commitment: Lagrangian relaxation versus general mixed integer programming. In Proceedings of the 2003 IEEE Power Engineering Society General Meeting (IEEE Cat. No. 03CH37491), Toronto, ON, Canada, 13–17 July 2003; Volume 2, pp. 1095–1100. [Google Scholar]
- Bixby, R.; Rothberg, E. Progress in computational mixed integer programming—A look back from the other side of the tipping point. Ann. Oper. Res. 2007, 149, 37. [Google Scholar] [CrossRef]
- Chen, Y.; Casto, A.; Wang, F.; Wang, Q.; Wang, X.; Wan, J. Improving large scale day-ahead security constrained unit commitment performance. IEEE Trans. Power Syst. 2016, 31, 4732–4743. [Google Scholar] [CrossRef]
- Wang, Q.; Yang, A.; Wen, F.; Li, J. Risk-based security-constrained economic dispatch in power systems. J. Mod. Power Syst. Clean Energy 2013, 1, 142–149. [Google Scholar] [CrossRef]
- Wang, Q.; Hodge, B.M. Enhancing Power System Operational Flexibility with Flexible Ramping Products: A Review. IEEE Trans. Ind. Inform. 2017, 13, 1652–1664. [Google Scholar] [CrossRef]
- Lu, X.; Chan, K.W.; Xia, S.; Zhou, B.; Luo, X. Security-constrained multiperiod economic dispatch with renewable energy utilizing distributionally robust optimization. IEEE Trans. Sustain. Energy 2018, 10, 768–779. [Google Scholar] [CrossRef]
- Flores-Quiroz, A.; Strunz, K. A distributed computing framework for multi-stage stochastic planning of renewable power systems with energy storage as flexibility option. Appl. Energy 2021, 291, 116736. [Google Scholar] [CrossRef]
- Li, W.; Wang, Q. Stochastic production simulation for generating capacity reliability evaluation in power systems with high renewable penetration. Energy Convers. Econ. 2020, 1, 210–220. [Google Scholar] [CrossRef]
- Faulwasser, T.; Engelmann, A.; Mühlpfordt, T.; Hagenmeyer, V. Optimal power flow: An introduction to predictive, distributed and stochastic control challenges. At-Automatisierungstechnik 2018, 66, 573–589. [Google Scholar] [CrossRef]
- Momoh, J.A.; Adapa, R.; El-Hawary, M. A review of selected optimal power flow literature to 1993. I. Nonlinear and quadratic programming approaches. IEEE Trans. Power Syst. 1999, 14, 96–104. [Google Scholar] [CrossRef]
- Momoh, J.A.; El-Hawary, M.; Adapa, R. A review of selected optimal power flow literature to 1993. II. Newton, linear programming and interior point methods. IEEE Trans. Power Syst. 1999, 14, 105–111. [Google Scholar] [CrossRef]
- Wang, Q.; McCalley, J.D.; Zheng, T.; Litvinov, E. Solving corrective risk-based security-constrained optimal power flow with Lagrangian relaxation and Benders decomposition. Int. J. Electr. Power Energy Syst. 2016, 75, 255–264. [Google Scholar] [CrossRef]
- Wang, Q.; McCalley, J.D.; Zheng, T.; Litvinov, E. A Computational Strategy to Solve Preventive Risk-Based Security-Constrained OPF. IEEE Trans. Power Syst. 2013, 28, 1666–1675. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. In Proceedings of the 31st Conference on Neural Information Processing Systems (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017; Volume 30. [Google Scholar]
- Ouyang, L.; Wu, J.; Jiang, X.; Almeida, D.; Wainwright, C.; Mishkin, P.; Zhang, C.; Agarwal, S.; Slama, K.; Ray, A.; et al. Training language models to follow instructions with human feedback. Adv. Neural Inf. Process. Syst. 2022, 35, 27730–27744. [Google Scholar]
- Knox, W.B.; Stone, P. Augmenting reinforcement learning with human feedback. In Proceedings of the ICML 2011 Workshop on New Developments in Imitation Learning, Washington, DC, USA, 2 July 2011; Volume 855, p. 3. [Google Scholar]
- Brown, T.; Mann, B.; Ryder, N.; Subbiah, M.; Kaplan, J.D.; Dhariwal, P.; Neelakantan, A.; Shyam, P.; Sastry, G.; Askell, A.; et al. Language models are few-shot learners. Adv. Neural Inf. Process. Syst. 2020, 33, 1877–1901. [Google Scholar]
- Voulodimos, A.; Doulamis, N.; Doulamis, A.; Protopapadakis, E. Deep learning for computer vision: A brief review. Comput. Intell. Neurosci. 2018, 2018, 7068349. [Google Scholar] [CrossRef] [PubMed]
- Xu, S.; Wang, J.; Shou, W.; Ngo, T.; Sadick, A.M.; Wang, X. Computer vision techniques in construction: A critical review. Arch. Comput. Methods Eng. 2021, 28, 3383–3397. [Google Scholar] [CrossRef]
- Wiley, V.; Lucas, T. Computer vision and image processing: A paper review. Int. J. Artif. Intell. Res. 2018, 2, 29–36. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, F.; Liu, K.; Mostacci, M.; Yao, Y.; Sfarra, S. Deep convolutional autoencoder thermography for artwork defect detection. Quant. Infrared Thermogr. J. 2023, 1–17. [Google Scholar] [CrossRef]
- Ibrahim, M.S.; Dong, W.; Yang, Q. Machine learning driven smart electric power systems: Current trends and new perspectives. Appl. Energy 2020, 272, 115237. [Google Scholar] [CrossRef]
- Jiang, B.; Liu, Y.; Geng, H.; Wang, Y.; Zeng, H.; Ding, J. A holistic feature selection method for enhanced short-term load forecasting of power system. IEEE Trans. Instrum. Meas. 2022, 72, 2500911. [Google Scholar] [CrossRef]
- Lei, X.; Yang, Z.; Yu, J.; Zhao, J.; Gao, Q.; Yu, H. Data-driven optimal power flow: A physics-informed machine learning approach. IEEE Trans. Power Syst. 2020, 36, 346–354. [Google Scholar] [CrossRef]
- Nellikkath, R.; Chatzivasileiadis, S. Physics-informed neural networks for ac optimal power flow. Electr. Power Syst. Res. 2022, 212, 108412. [Google Scholar] [CrossRef]
- Jiang, B.; Liu, Y.; Geng, H.; Zeng, H.; Ding, J. A Transformer Based Method with Wide Attention Range for Enhanced Short-term Load Forecasting. In Proceedings of the 2022 4th International Conference on Smart Power & Internet Energy Systems (SPIES), Beijing, China, 9–12 December 2022; pp. 1684–1690. [Google Scholar] [CrossRef]
- Nair, V.; Bartunov, S.; Gimeno, F.; Von Glehn, I.; Lichocki, P.; Lobov, I.; O’Donoghue, B.; Sonnerat, N.; Tjandraatmadja, C.; Wang, P.; et al. Solving mixed integer programs using neural networks. arXiv 2020, arXiv:2012.13349. [Google Scholar]
- Xia, Y.; Wang, J. A bi-projection neural network for solving constrained quadratic optimization problems. IEEE Trans. Neural Netw. Learn. Syst. 2015, 27, 214–224. [Google Scholar] [CrossRef]
- Lotfi, A.; Pirnia, M. Constraint-guided deep neural network for solving optimal power flow. Electr. Power Syst. Res. 2022, 211, 108353. [Google Scholar] [CrossRef]
- Pan, W.; Zhao, C.; Fan, L.; Huang, S. Efficient Optimal Power Flow Flexibility Assessment: A Machine Learning Approach. In Proceedings of the 2023 IEEE Power & Energy Society Innovative Smart Grid Technologies Conference (ISGT), Washington, DC, USA, 16–19 January 2023; pp. 1–5. [Google Scholar]
- Rahman, J.; Feng, C.; Zhang, J. Machine learning-aided security constrained optimal power flow. In Proceedings of the 2020 IEEE Power & Energy Society General Meeting (PESGM), IEEE, Montreal, QC, Canada, 2–6 August 2020; pp. 1–5. [Google Scholar]
- Rahman, J.; Feng, C.; Zhang, J. A learning-augmented approach for AC optimal power flow. Int. J. Electr. Power Energy Syst. 2021, 130, 106908. [Google Scholar] [CrossRef]
- Sun, L.; Hu, J.; Chen, H. Artificial Bee Colony Algorithm Based on-Means Clustering for Multiobjective Optimal Power Flow Problem. Math. Probl. Eng. 2015, 2015, 762853. [Google Scholar] [CrossRef]
- Hashish, M.S.; Hasanien, H.M.; Ullah, Z.; Alkuhayli, A.; Badr, A.O. Giant Trevally Optimization Approach for Probabilistic Optimal Power Flow of Power Systems Including Renewable Energy Systems Uncertainty. Sustainability 2023, 15, 13283. [Google Scholar] [CrossRef]
- Baker, K.; Bernstein, A. Joint chance constraints reduction through learning in active distribution networks. In Proceedings of the 2018 IEEE Global Conference on Signal and Information Processing (GlobalSIP), Anaheim, CA, USA, 26–29 November 2018; pp. 922–926. [Google Scholar]
- Baker, K. A learning-boosted quasi-newton method for ac optimal power flow. arXiv 2020, arXiv:2007.06074. [Google Scholar]
- Baker, K. Emulating AC OPF Solvers with Neural Networks. IEEE Trans. Power Syst. 2022, 37, 4950–4953. [Google Scholar] [CrossRef]
- Zamzam, A.S.; Fu, X.; Sidiropoulos, N.D. Data-driven learning-based optimization for distribution system state estimation. IEEE Trans. Power Syst. 2019, 34, 4796–4805. [Google Scholar] [CrossRef]
- Yu, J.; Lu, L.; Meng, X.; Karniadakis, G.E. Gradient-enhanced physics-informed neural networks for forward and inverse PDE problems. Comput. Methods Appl. Mech. Eng. 2022, 393, 114823. [Google Scholar] [CrossRef]
- Yan, Z.; Xu, Y. A hybrid data-driven method for fast solution of security-constrained optimal power flow. IEEE Trans. Power Syst. 2022, 37, 4365–4374. [Google Scholar] [CrossRef]
- Yan, Z.; Xu, Y. Real-Time Optimal Power Flow: A Lagrangian Based Deep Reinforcement Learning Approach. IEEE Trans. Power Syst. 2020, 35, 3270–3273. [Google Scholar] [CrossRef]
- Zamzam, A.S.; Baker, K. Learning Optimal Solutions for Extremely Fast AC Optimal Power Flow. In Proceedings of the 2020 IEEE International Conference on Communications, Control, and Computing Technologies for Smart Grids (SmartGridComm), Virtual, 11–13 November 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Zhou, M.; Chen, M.; Low, S.H. DeepOPF-FT: One Deep Neural Network for Multiple AC-OPF Problems with Flexible Topology. IEEE Trans. Power Syst. 2023, 38, 964–967. [Google Scholar] [CrossRef]
- Huang, B.; Wang, J. Applications of physics-informed neural networks in power systems-a review. IEEE Trans. Power Syst. 2022, 38, 572–588. [Google Scholar] [CrossRef]
- Falconer, T.; Mones, L. Leveraging power grid topology in machine learning assisted optimal power flow. IEEE Trans. Power Syst. 2022, 38, 2234–2246. [Google Scholar] [CrossRef]
- Lei, X.; Yu, J.; Aini, H.; Wu, W. Data-driven alternating current optimal power flow: A Lagrange multiplier based approach. Energy Rep. 2022, 8, 748–755. [Google Scholar] [CrossRef]
- Utama, C.; Meske, C.; Schneider, J.; Ulbrich, C. Reactive power control in photovoltaic systems through (explainable) artificial intelligence. Appl. Energy 2022, 328, 120004. [Google Scholar] [CrossRef]
- Chatzos, M.; Mak, T.W.; Van Hentenryck, P. Spatial network decomposition for fast and scalable AC-OPF learning. IEEE Trans. Power Syst. 2021, 37, 2601–2612. [Google Scholar] [CrossRef]
- Pan, X.; Chen, M.; Zhao, T.; Low, S.H. DeepOPF: A feasibility-optimized deep neural network approach for AC optimal power flow problems. IEEE Syst. J. 2022, 17, 673–683. [Google Scholar] [CrossRef]
- Zhang, L.; Chen, Y.; Zhang, B. A convex neural network solver for DCOPF with generalization guarantees. IEEE Trans. Control Netw. Syst. 2021, 9, 719–730. [Google Scholar] [CrossRef]
- Chen, Y.; Lakshminarayana, S.; Maple, C.; Poor, H.V. A meta-learning approach to the optimal power flow problem under topology reconfigurations. IEEE Open Access J. Power Energy 2022, 9, 109–120. [Google Scholar] [CrossRef]
- Deka, D.; Misra, S. Learning for DC-OPF: Classifying active sets using neural nets. In Proceedings of the 2019 IEEE Milan PowerTech, Milan, Italy, 23–27 June 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Misra, S.; Roald, L.; Ng, Y. Learning for constrained optimization: Identifying optimal active constraint sets. INFORMS J. Comput. 2022, 34, 463–480. [Google Scholar] [CrossRef]
- Ng, Y.; Misra, S.; Roald, L.A.; Backhaus, S. Statistical learning for DC optimal power flow. In Proceedings of the IEEE 2018 Power Systems Computation Conference (PSCC), Dublin, Ireland, 11–15 June 2018; pp. 1–7. [Google Scholar]
- Hasan, F.; Kargarian, A.; Mohammadi, J. Hybrid Learning Aided Inactive Constraints Filtering Algorithm to Enhance AC OPF Solution Time. IEEE Trans. Ind. Appl. 2021, 57, 1325–1334. [Google Scholar] [CrossRef]
- Liu, S.; Guo, Y.; Tang, W.; Sun, H.; Huang, W.; Hou, J. Varying Condition SCOPF Optimization Based on Deep Learning and Knowledge Graph. IEEE Trans. Power Syst. 2022, 38, 3189–3200. [Google Scholar] [CrossRef]
- Zhang, Z.J.; Mana, P.T.; Yan, D.; Sun, Y.; Molzahn, D.K. Study of Active Line Flow Constraints in DC Optimal Power Flow Problems. In Proceedings of the 2020 SoutheastCon, Raleigh, NC, USA, 28–29 March 2020; pp. 1–8. [Google Scholar] [CrossRef]
- Liu, S.; Guo, Y.; Tang, W.; Sun, H.; Huang, W. Predicting Active Constraints Set in Security-Constrained Optimal Power Flow via Deep Neural Network. In Proceedings of the 2021 IEEE Power & Energy Society General Meeting (PESGM), Washington, DC, USA, 16–29 July 2021; pp. 1–5. [Google Scholar] [CrossRef]
- Woo, J.H.; Wu, L.; Park, J.B.; Roh, J.H. Real-time optimal power flow using twin delayed deep deterministic policy gradient algorithm. IEEE Access 2020, 8, 213611–213618. [Google Scholar] [CrossRef]
- Wang, Z.; Menke, J.H.; Schäfer, F.; Braun, M.; Scheidler, A. Approximating multi-purpose AC optimal power flow with reinforcement trained artificial neural network. Energy AI 2022, 7, 100133. [Google Scholar] [CrossRef]
- Wu, S.; Hu, W.; Lu, Z.; Gu, Y.; Tian, B.; Li, H. Power System Flow Adjustment and Sample Generation Based on Deep Reinforcement Learning. J. Mod. Power Syst. Clean Energy 2020, 8, 1115–1127. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhang, B.; Xu, C.; Lan, T.; Diao, R.; Shi, D.; Wang, Z.; Lee, W.J. A Data-driven Method for Fast AC Optimal Power Flow Solutions via Deep Reinforcement Learning. J. Mod. Power Syst. Clean Energy 2020, 8, 1128–1139. [Google Scholar] [CrossRef]
- Wang, C.; Du, Y.; Chang, Y.; Guo, Z.; Huang, Y. Human–Machine Collaborative Reinforcement Learning for Power Line Flow Regulation. IEEE Trans. Ind. Inform. 2023, 1–13. [Google Scholar] [CrossRef]
- Zeng, S.; Kody, A.; Kim, Y.; Kim, K.; Molzahn, D.K. A reinforcement learning approach to parameter selection for distributed optimal power flow. Electr. Power Syst. Res. 2022, 212, 108546. [Google Scholar] [CrossRef]
- Qin, P.; Ye, J.; Hu, Q.; Song, P.; Kang, P. Deep reinforcement learning based power system optimal carbon emission flow. Front. Energy Res. 2022, 10, 1017128. [Google Scholar] [CrossRef]
- Tianjing, W.; Yong, T. Parallel deep reinforcement learning-based power flow state adjustment considering static stability constraint. IET Gener. Transm. Distrib. 2020, 14, 6276–6284. [Google Scholar] [CrossRef]
- Jeyaraj, P.R.; Asokan, S.P.; Kathiresan, A.C.; Nadar, E.R.S. Deep reinforcement learning-based network for optimized power flow in islanded DC microgrid. Electr. Eng. 2023, 105, 2805–2816. [Google Scholar] [CrossRef]
- Wang, T.; Tang, Y. An unsolvable power flow adjustment method for weak power grid based on transmission channel positioning and deep reinforcement learning. Electr. Power Syst. Res. 2022, 210, 108050. [Google Scholar] [CrossRef]
- Chow, Y.; Nachum, O.; Faust, A.; Duenez-Guzman, E.; Ghavamzadeh, M. Lyapunov-based safe policy optimization for continuous control. arXiv 2019, arXiv:1901.10031. [Google Scholar]
- Liang, Q.; Que, F.; Modiano, E. Accelerated primal-dual policy optimization for safe reinforcement learning. arXiv 2018, arXiv:1802.06480. [Google Scholar]
- Zhou, Y.; Lee, W.J.; Diao, R.; Shi, D. Deep reinforcement learning based real-time AC optimal power flow considering uncertainties. J. Mod. Power Syst. Clean Energy 2021, 10, 1098–1109. [Google Scholar] [CrossRef]
- Sayed, A.R.; Wang, C.; Anis, H.I.; Bi, T. Feasibility Constrained Online Calculation for Real-Time Optimal Power Flow: A Convex Constrained Deep Reinforcement Learning Approach. IEEE Trans. Power Syst. 2023, 38, 5215–5227. [Google Scholar] [CrossRef]
- Cao, Y.; Zhao, H.; Liang, G.; Zhao, J.; Liao, H.; Yang, C. Fast and explainable warm-start point learning for AC Optimal Power Flow using decision tree. Int. J. Electr. Power Energy Syst. 2023, 153, 109369. [Google Scholar] [CrossRef]
- Yu, J.; Li, Z.; Zhang, J.; Bai, X.; Ge, H.; Zheng, J.; Wu, Q. Efficient contingency analysis of power systems using linear power flow with generalized warm-start compensation. Int. J. Electr. Power Energy Syst. 2024, 156, 109692. [Google Scholar] [CrossRef]
- Demirovic, N.; Tesnjak, S.; Tokic, A. Hot Start and Warm start in LP based Interior Point Method and it’s Application to Multiperiod Optimal Power Flows. In Proceedings of the 2006 IEEE PES Power Systems Conference and Exposition, Atlanta, GA, USA, 29 October–1 November 2006; pp. 699–704. [Google Scholar] [CrossRef]
- Kim, Y.; Anitescu, M. A real-time optimization with warm-start of multiperiod AC optimal power flows. Electr. Power Syst. Res. 2020, 189, 106721. [Google Scholar] [CrossRef]
- Wu, Y.C.; Debs, A. Initialisation, decoupling, hot start, and warm start in direct nonlinear interior point algorithm for optimal power flows. IEE Proc.-Gener. Transm. Distrib. 2001, 148, 67–75. [Google Scholar] [CrossRef]
- Baker, K. Learning warm-start points for AC optimal power flow. In Proceedings of the 2019 IEEE 29th International Workshop on Machine Learning for Signal Processing (MLSP), Pittsburgh, PA, USA, 13–16 October 2019; pp. 1–6. [Google Scholar]
- Chen, Y.C.; Wang, J.; Domínguez-García, A.D.; Sauer, P.W. Measurement-based estimation of the power flow Jacobian matrix. IEEE Trans. Smart Grid 2015, 7, 2507–2515. [Google Scholar] [CrossRef]
- Zeng, L.; Alawneh, S.G.; Arefifar, S.A. GPU-Based Sparse Power Flow Studies with Modified Newton’s Method. IEEE Access 2021, 9, 153226–153239. [Google Scholar] [CrossRef]
- He, X.; Chu, L.; Qiu, R.; Ai, Q.; Huang, W. Data-driven estimation of the power flow jacobian matrix in high dimensional space. arXiv 2019, arXiv:1902.06211. [Google Scholar]
- Baghaee, H.R.; Mirsalim, M.; Gharehpetian, G.B.; Talebi, H.A. Generalized three phase robust load-flow for radial and meshed power systems with and without uncertainty in energy resources using dynamic radial basis functions neural networks. J. Clean. Prod. 2018, 174, 96–113. [Google Scholar] [CrossRef]
- Baghaee, H.R.; Mirsalim, M.; Gharehpetian, G.B.; Talebi, H.A. Three-phase AC/DC power-flow for balanced/unbalanced microgrids including wind/solar, droop-controlled and electronically-coupled distributed energy resources using radial basis function neural networks. IET Power Electron. 2017, 10, 313–328. [Google Scholar] [CrossRef]
- Veerasamy, V.; Abdul Wahab, N.I.; Ramachandran, R.; Kamel, S.; Othman, M.L.; Hizam, H.; Farade, R. Power flow solution using a novel generalized linear Hopfield network based on Moore–Penrose pseudoinverse. Neural Comput. Appl. 2021, 33, 11673–11689. [Google Scholar] [CrossRef]
- Li, G.; Or, S.W.; Chan, K.W. Intelligent Energy-Efficient Train Trajectory Optimization Approach Based on Supervised Reinforcement Learning for Urban Rail Transits. IEEE Access 2023, 11, 31508–31521. [Google Scholar] [CrossRef]
- Jiang, B.; Yang, H.; Liu, Y.a. Dynamic Temporal Dependency Model for Multiple Steps Ahead Short-term Load Forecasting of Power System. IEEE Trans. Ind. Appl. 2024, in press. [Google Scholar]
- Wu, J.; Tang, S.; Huang, C.; Zhang, D.; Zhao, Y. Review of attention mechanism in electric power systems. In Proceedings of the Advances in Artificial Intelligence and Security: 7th International Conference, ICAIS 2021, Dublin, Ireland, 19–23 July 2021; Proceedings, Part I 7; Springer: Berlin/Heidelberg, Germany, 2021; pp. 618–627. [Google Scholar]
- Achiam, J.; Adler, S.; Agarwal, S.; Ahmad, L.; Akkaya, I.; Aleman, F.L.; Almeida, D.; Altenschmidt, J.; Altman, S.; Anadkat, S.; et al. Gpt-4 technical report. arXiv 2023, arXiv:2303.08774. [Google Scholar]


| Method | Strength | References |
|---|---|---|
| Direct Mapping of OPF Variable | Decrease computational time | [47] |
| Incorporate physics-based rules | [30,48,49,50] | |
| Simplify the learning process | [51] | |
| Consider new energy unit | [29,52] | |
| Guarantee the solution feasibility | [34,53,54] | |
| Combine the DC OPF problem and convex ANN | [30,55,56] | |
| Predicting Active Constraints | Explore simplified OPF version | [57,58] |
| Classify active and inactive constraints | [40,58,59,60] | |
| Consider the uncertainty | [57,61] | |
| Explore the relationships among sets of con-currently active constraints | [62,63] | |
| Learning Control Policy for OPF | Apply RL into PS operation | [64,65,66,67,68,69] |
| Consider multi-object | [70] | |
| Apply RL into microgrid operation | [71,72,73] | |
| Develop model-based RL | [45,74,75] | |
| Guarantee the solution feasibility | [76,77] | |
| Predicting Warm-Start Points | Explore simplified OPF version | [78,79,80,81,82,83] |
| Enhance interpretability | [78] | |
| Learning solution process | Approximate Jacobian matrix | [41,42,84,85,86,87,88,89] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, B.; Wang, Q.; Wu, S.; Wang, Y.; Lu, G. Advancements and Future Directions in the Application of Machine Learning to AC Optimal Power Flow: A Critical Review. Energies 2024, 17, 1381. https://doi.org/10.3390/en17061381
Jiang B, Wang Q, Wu S, Wang Y, Lu G. Advancements and Future Directions in the Application of Machine Learning to AC Optimal Power Flow: A Critical Review. Energies. 2024; 17(6):1381. https://doi.org/10.3390/en17061381
Chicago/Turabian StyleJiang, Bozhen, Qin Wang, Shengyu Wu, Yidi Wang, and Gang Lu. 2024. "Advancements and Future Directions in the Application of Machine Learning to AC Optimal Power Flow: A Critical Review" Energies 17, no. 6: 1381. https://doi.org/10.3390/en17061381
APA StyleJiang, B., Wang, Q., Wu, S., Wang, Y., & Lu, G. (2024). Advancements and Future Directions in the Application of Machine Learning to AC Optimal Power Flow: A Critical Review. Energies, 17(6), 1381. https://doi.org/10.3390/en17061381







