Abstract
In this work, the design features of delta wing vortex generators (DWVGs) on the thermo-hydraulic performance of heat exchangers are investigated using machine learning. Reynolds numbers, attack angle, length, wing-to-width ratio, and relative pitch ratio of DWVGs were used as descriptor variables, with Nusselt numbers, friction factors, and performance evaluation criterion (PEC) serving as target variables. Decision tree classification revealed the pathways leading to high or low values of the performance variables. Among many of those pathways, it was found that high Reynolds numbers (between 8160 and 9800) and high attack angles (greater than or equal to 47.5°) lead to high Nusselt numbers. On the other hand, an attack angle between 41° and 60°, a Reynolds number less than 8510, and a wing-to-width ratio greater than or equal to 0.4 causes a high friction factor. Finally, the PEC is likely to enhance when the Reynolds number is higher than or equal to 10,300 and the attack angle is between 47.5° and 60°. In addition to the decision tree analysis, SHapley Additive exPlanations (SHAP) analysis (a part of explainable machine learning) was also applied to reveal the importance of design features and their positive and negative effects on the target variables. For example, for a Nusselt number as the target variable, the Reynolds number was found to be the most influential variable, followed by the attack angle and the relative pitch ratio, all of which had a positive impact on the target. It was then concluded that machine learning methods could help provide strong insights into the configuration design features of heat exchangers in DWVGs to improve their efficiency and save energy.
1. Introduction
Global energy demand is increasing together with the growing world population, and this energy is mostly provided by nonrenewable energy sources [1], which also contribute to climate change and global warming [2]. Using renewable energy resources can aid in reducing harmful gases; however, the implementation of new renewable energy programs is a slow process that is still not preferred by many countries [3]. Therefore, debate continues on the best strategies to increase the efficiency of the existing power plants and reduce their fossil fuel consumption. One of the promising methods that can be applied to existing systems that use components with high heat exchange capabilities [4] is improving the thermal performance of the heat exchangers.
Heat exchanger design may undergo significant modification based on the heat exchanger type and function. Therefore, various types of heat exchangers, such as plate-fin [5], fin tube [6], microchannel [7], double pipe [8], and shell and tube [9], have been developed so far by altering shapes, sizes, and materials and inserting different types of flow mixers into heat exchange locations. Among the studies focused on the thermal performance enhancement of heat exchangers, the majority of them include passive methods because they require no additional power and are easy to implement [10,11]. Active methods, on the other hand, require external power to generate magnetic fields [12], electric fields [13], acoustic effects [14], mechanical movements [15], and pulsations or vibrations, which is a significant disadvantage when compared to passive methods [16]. Nevertheless, some studies [17,18] included both methods to increase heat transfer. To date, various shapes of vortex generators have been proposed [19]. The fundamental purpose of adopting vortex generators in heat exchangers is that they form secondary flow by breaking the thermal boundary layer along the surface of the heat exchanger to carry heat better to the central locations of the flow. This reduces the time of heat transfer intended to be diffused through the fluid. In exchange for that, they cause pressure drop due to enhanced drag.
Joardar and Jacobi [20] conducted experimental research with winglet-type vortex generator arrays considering Reynolds numbers in the range of 220 to 970, and reported that the heat transfer coefficient was enhanced by up to 68.8% while pressure drop increased by 87.5%. They concluded that the thermal performance of fin-tube heat exchangers can be enhanced with vortex generator arrays. In another study conducted by Samadifar et al. [21], the performance of a fin-plate heat exchanger having a triangular cross-section was investigated numerically using six different vortex generators. They found that thermal performance is at its highest with rectangular-type vortex generators (RVGs) compared to others. In addition to that, 45° vortex generators demonstrated the highest heat transfer rate. Abdollahi and Shams [22] studied the effects of shape and the attack angle of winglet vortex generators in terms of heat transfer increment in a rectangular channel by combining three different methods. They used an artificial neural network (ANN), a multi-objective genetic algorithm, and computational fluid dynamics. They reported that with respect to shape comparison, RVGs show the highest heat transfer performance owing to the larger area that confronts the fluid flow. Therefore, the pressure drop with RVGs was also the highest. Gentry and Jacobi [23,24] performed similar experiments in 1997 [23] and 2002 [24] to demonstrate heat transfer enhancement using delta wing vortex generators (DWVGs) on a flat plate with the flow at a low Reynolds number. The results showed that the increment in heat transfer was 50–60% higher than that without vortex generators. In another similar study, Zhao et al. [25] found that a delta winglet–vortex generator pair in a common-flown-down arrangement put in the middle and rear of the tip surface decreased the boundary layer thickness while creating vortices between the turbulators and increasing the heat transfer by 7.4%. A detailed examination of a delta winglet vortex generator used in a solar air heater by Sawhney [26] showed that the highest possible thermal performance enhancement was 223% with the parameters set as the longitudinal pitch of three- and five-wave winglets in an experimental setup with a flow with Reynolds number of 4000. However, the friction factor dramatically increased 10.3-fold compared to the heater without a delta wing. Three-dimensional computational fluid dynamics analysis of heat exchanger performance with louvered fins was carried out by attaching delta winglet vortex generators [27]. They have reported that with the same power supply for the fan, the heat exchanger shows higher thermal performance with the delta winglet. However, a greater pressure penalty was noted due to the increased friction and barricade against flow caused by delta winglets integrated into the louvered fins. They also emphasized that some heat transfer augmentation mechanisms, such as fluid mixing, boundary layer thinning, and flow separation delay from the surface, were better when delta winglets were used.
As explained above, designing a delta winglet vortex generator to enhance the heat transfer performance of heat exchangers is quite a complex task, including several variables to optimize. At this stage, machine learning may be crucial in determining the combination of variables with the desired properties. Machine learning is a technique for discovering hidden patterns in large and complex datasets, making it simpler to comprehend the data and draw conclusions from the available dataset [28,29,30].
As a result, there is an increasing trend in the use of machine learning methods to detect the effects of the design elements of such systems. For instance, Liao et al. [31] assembled two machine learning methods, i.e., multilayer perceptron and Bayesian optimization, to obtain the optimum design of a near-field thermal radiative modulator considering the rotation angle, layer thickness, and the gap distance of the multilayer materials of modulators. In another study, Ren et al. [32] included different machine learning tools, such as reinforcement learning using proximal policy approximation (PPO) and non-Oberbeck–Boussinesq approximation (NOB). They proposed a smart active flow control system to increase the heat transfer of fluid in laminar flow conditions. Heat transfer enhancement of 76.7% was reported through extensive training. Wang and Vafai [33] used support vector regression (SVR) algorithms as a machine learning method and combined them with thermal simulation analysis to efficiently predict hotspot temperature variations in multilayer 3D chips.
In recent years, researchers have shown growing interest in using machine learning techniques in hydraulic and thermal analyses. For instance, Seal et al. [34] predicted the flow pattern images of a refrigerant, R-134a, condensation with more than 98% accuracy using convolutional neural network algorithms. They also proposed multilayer perceptron neural networks and principal component analysis for dataset visualization and decreased computational power. In another study, Farahani et al. [35] investigated the thermal performance of a microchannel heat sink in terms of the porous medium, phase change material, and shape of the microchannel using the finite volume method and group method of a data handling algorithm (GMDH). The findings demonstrated that wavy microchannels could enhance thermal performance by roughly 10.6% and 5% compared with smooth and converging microchannels. Machine learning algorithms such as ANN, random forest, AdaBoost, and extreme gradient boosting (XGBoost) were also employed by Zhou et al. [36] to predict flow condensation heat transfer coefficients in microchannels. They noted that XGBoost and ANN provided the highest accuracy of prediction among the algorithms utilized.
Other research carried out by Berber et al. [37] related to the current study focused on heat convection in a rectangular channel with curved-winglet vortex generator inserts using machine learning. They investigated the impact of the proposed novel fin geometry and attack angle in the range of 30° to 90° with varying Reynolds numbers and plate temperatures on convection heat transfer with the help of ANN algorithms. Nusselt number deviations between experimental and machine learning results were less than 4% with a prediction accuracy parameter (R2) of 0.9879. Longo et al. [38] gathered extensive data on brazed plate heat exchangers (BPHE) with various geometries and diverse refrigerant types. Next, they used this database to estimate the two-phase refrigerant diabatic flow inside these heat exchangers by using a gradient boosting machine (GBM) model.
As reviewed above, the greater part of the literature on winglet-type vortex generators focused mostly on time-consuming experimental and numerical studies, and the number of studies based on machine learning is quite limited. Machine learning methods can be used to predict feature design variables more accurately and quickly using the available data, eliminating the need for time-consuming and extensive experimental and numerical studies for the thermo-hydraulic assessment of heat exchangers used with DWVGs. Therefore, machine learning methodologies may help to determine the correlations among individual or multiple combinations of design variables of DWVGs with thermal and hydraulic performance. For that purpose, Khan et al. [39] collected experimental data on heat exchangers with delta winglet vortex generators from various publications, built a database of 300 data entries, and then employed ANN models to develop a correlation between the Reynolds numbers and the design variables of DWVGs. Accordingly, the optimum values of the variables that exhibit the highest thermal efficiency were determined.
In this study, the same database is analyzed further by explainable machine learning to reveal the individual or assembled effects of design features of DWVGs on the thermo-hydraulic performance of heat exchangers, as well as finding the pathways leading to high or low values of the performance variables. The primary goal of this research is to fill gaps in understanding the effects of design variables that are difficult to detect with the naked eye. The proposed outcomes of this study will lead to the rapid development of heat exchangers used mainly for energy conversion in terms of performance enhancement.
2. Materials and Methods
2.1. Data
The thermal performance of heat exchangers with DWVGs is affected by many variables. Based on the experimental and numerical case studies in the literature, relative pitch ratio, wing-to-width ratio, attack angle, Reynolds number, and length were chosen as descriptor variables, with friction factor, Nusselt number, and performance evaluation criterion (PEC) serving as target variables. The data used in this study were collected by Khan et al. [39] from various publications in the literature, as shown in Table 1. The database contains 300 data entries with five descriptors and three target variables. Table 2 shows all the variables and their ranges. The target variables in the database range from 0.080 to 0.527 for friction factors, 58.68 to 361.70 for Nusselt numbers, and 0.26 to 1.39 for the PEC.

Table 1.
Design features of DWVGs and ranges of variables used in the analysis [39].

Table 2.
Common design features of DWVGs found in the literature [39].
In addition, the geometric characteristics of typical DWVGs are presented in Figure 1, where w represents wing width, W is the width of the plate on which delta wings are placed, c is the length of the wing, p represents the distance between two consecutive wings along the pipe (wing pitch), L is the length of the plate, α is the angle between the wing and plate, which is called the attack angle in this study. In addition, w/W and p/W represent wing-to-width and pitch-to-width ratios, respectively.
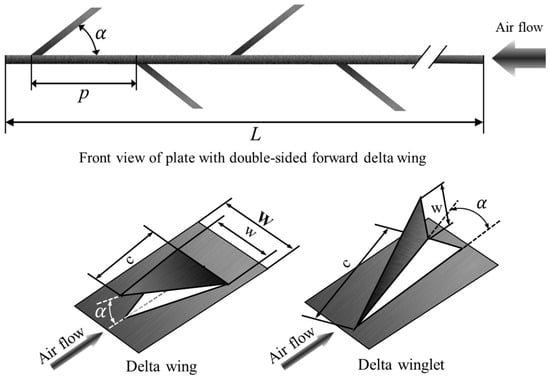
Figure 1.
Geometry of typical delta wing and winglet vortex generator inserts.
2.2. Computational Details
In this research, two different machine learning approaches were developed in a MATLAB (version 9.14.0.2206163; R2023a) environment to address two different tasks. First, the SHAP method (originating from game theory) was used as part of explainable machine learning to investigate the effects of features on the target variable [47]. It is used to calculate how much each participant contributes to a coalition or cooperative game, and as a result, this analysis can be used to evaluate the outcomes of a machine learning model. In a machine learning model, the marginal contribution of a variable to overall performance is calculated, and the results are referred to as weights. The significance of each variable is then computed according to these weights (SHAP values), and they are used to understand the outcomes of a machine learning model by determining the marginal contribution and importance of each variable [48]. The SHAP value for the ith feature of query point x is determined by the value function v as shown in Equation (1), with M representing the total number of features, being the set of all features, |S| representing the number of elements in the set S, and finally vx(S) denoting the value function of the features in set S for the query point x. A thorough explanation of the SHAP approach can be found in a recently published book [49]. The MATLAB tool “fitrnet” was used to train a feedforward, fully connected neural network for regression, and SHAP bee-swarm plots were displayed to discover the most influential variables.
Next, decision tree classification was employed to find the set of experimental conditions leading to different levels of the target variables. It should be noted that the decision tree classification method was preferred in this study because it provides highly understandable, comprehensive, and reader-friendly maps [50]. Before training the tree, the target variables were divided into three levels—low, medium, and high—and the database was randomly divided into two subsets: the training set (two-thirds of the total data) and the test set (one-third of the total data). Then, the decision trees were built using MATLAB’s “fitctree” function with the “OptimizeHyperparameters” option set to “all” to use Bayesian optimization with 5-fold cross-validation to automatically modify the minimum leaf size, the maximum number of splits, and the split criterion (Gini’s diversity index, deviation, or “twoing”) [51]. Bayesian optimization aims to optimize hyperparameter values to minimize classification error (cross-validation loss). The use of an acquisition function to determine the next point to evaluate is one of the most significant innovations in Bayesian optimization. It was reported that the acquisition function can balance sampling points with inaccurately modeled objective functions and explore regions that are not well modeled yet [52]. The minimum leaf size is a positive integer value, and each tree leaf contains at least that number of observations, whereas the maximum number of splits indicates the total number of branch nodes in the entire tree. Finally, the mathematical explanation of Gini’s diversity index, the deviance, and the twoing methods as the split criterion [53]. Equation (2) depicts the Gini index formula, while Equation (3) shows the deviance matrix, where n is the total number of classes and P is the probability that a sample will be classified as a specific class. Finally, Equation (4) provides the twoing metric, where Li represents the fraction of members of class i in the left child node after a split, Ri represents the fraction of members of class i in the right child node after a split, and PL and PR represent the proportions of observations that divide into the left and right sides, respectively.
For the optimal tree structures, confusion matrices are built for the interpretation of the performance of the decision trees with the classification metrics, as explained below.
- Precision is a quantitative measure that indicates the proportion of accurately classified samples.
- Recall is a parameter that indicates what percentage of samples in a given class are correctly classified.
- F1 score is the weighted harmonic mean of precision and recall, with a maximum value of 1 and a minimum of 0.
- Support is the number of samples in the dataset that belong to a specific class.
3. Results and Discussion
3.1. SHAP Analysis
In this part of the work, the effects of descriptor variables on thermo-hydraulic performance variables are assessed using SHAP bee-swarm plots. The variables in a bee-swarm plot are arranged according to their mean absolute SHAP values, starting from the left-hand side. A variable’s mean absolute SHAP value (measured using the same unit as the target) shows how much of an impact the variable has on the target. It should be noted that a higher mean absolute SHAP value denotes a stronger effect on the target. Furthermore, bee-swarm plots show that every dot in a variable row corresponds to a data entry and is colored based on the actual value of the variable that matches that entry. To illustrate, when the real value is high, a dot appears with various shades of green, and when the value is low, dots appear with various shades of blue.
For the Nusselt number model, the most influential descriptor variable is the Reynolds number, as it appears in the first column, and the feature has a great range of data points with different degrees of positive and negative effects on the Nusselt number. High mean SHAP values are observed when the Reynolds number increases, indicating a better heat transfer rate. The positive correlation between the Reynolds and the Nusselt numbers has been extensively reported in the literature. Indeed, the increase in Reynolds number is an indication of higher velocity together with the increased convective heat transfer coefficient with the help of rapid and better mixing. The attack angle is found to be the second-most impactful variable. Results from earlier studies [54,55,56,57,58,59,60,61,62] demonstrate a strong and consistent association between Nusselt number and attack angle as well. The Nusselt number tends to increase and decrease with regular enhancement of the attack angle. Relative pitch ratio is predicted to be the third-most impactful feature. Even though many studies noted that the decrease in relative pitch ratio is likely to increase the Nusselt number [63], the results obtained from the SHAP analysis suggest that medium values of relative pitch ratio yield higher Nusselt numbers. As opposed to the literature highlighting the enhancement of a Nusselt number when the relative pitch ratio decreases, it can be deduced from Figure 2 that both high and low values of the relative pitch ratio lower the Nusselt number.
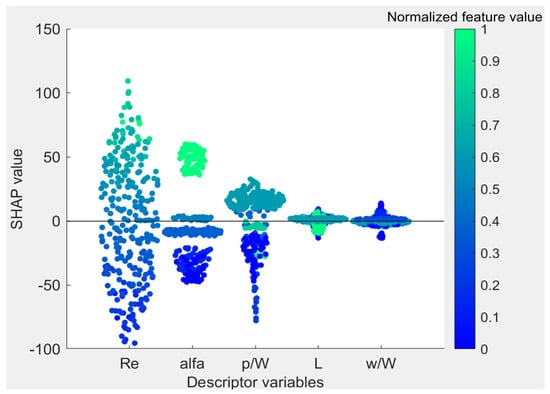
Figure 2.
SHAP summary bee-swarm plot for Nusselt number.
These results are also in accordance with the findings of the study conducted by Da Silva et al. [55]. In their numerical study, three different attack angles of 15°, 30°, and 45° of longitudinal vortex generators in the shape of rectangular and delta winglets were observed. The maximum Nusselt number was seen with both vortex generators having an attack angle of 45°. However, the optimum attack angle was suggested to be 30° for best thermo-hydraulic performance, considering both the Nusselt number and pressure penalty. Similar findings representing fluctuating Nusselt numbers by continuous increments in attack angle have also been reported by related studies by Deshmukh et al. [64] and Gonul et al. [65], who proposed optimum attack angles ranging from 30° to 60° to achieve the highest Nusselt numbers.
Another descriptor variable, pitch-to-width ratio (p/W), has varying degrees of positive and negative impact on the Nusselt number. From Figure 2, it is apparent that the Nusselt number increase may be related to the medium-range relative pitch ratio values. In addition, high values of relative pitch ratio lead to low Nusselt numbers, since they have negative mean SHAP values slightly below the reference line with zero mean SHAP value. The reduction in the relative pitch ratio can result in the enhancement of the Nusselt number, which is also mentioned in experimental studies [26,66]. This may be explained by the high versatility of either design features or the common feature ranges of DWVGs. Therefore, common relationships among such features could not be made in terms of a direct relationship between the relative pitch ratio and the Nusselt number. Finally, high or low values of wing-to-width ratio (w/W) and length can be attributed to changes in Nusselt numbers. For example, data points with both high- and low-length numbers overlap and are mostly located in the negative mean SHAP region in Figure 2. Therefore, by looking only at the SHAP summary plot, it may be presumed that a DWVG length that is too short or too long compared to the related cases causes a lower Nusselt number.
The SHAP analysis for friction factors is displayed in Figure 3. Similar to the case of the Nusselt number, the Reynolds number is located in the first column. It can be observed that a higher Reynolds number and higher wing-to-width ratio result in a higher friction factor, and conversely, lower values tend to reduce friction factor value. The findings of the present results have also been supported extensively by related experimental and numerical studies. Research conducted by Eiamsa-ard and Promvonge [41] also suggested that the increase in friction factor was driven by the increase in wing-to-width ratio. One related study [45] argued that enhancement of the friction factor may be associated with an increased wing-to-width ratio. The observation of friction factor enhancement caused by Reynolds number reduction was also seen in [67]. They also revealed the positive effect of the decrement of the features of relative pitch ratio on the friction factor and Nusselt number. Increasing the attack angle and length and decreasing the relative pitch ratio enlarges the area of vortex generators and demonstrates better thermal performance. The positive effect of the augmented heat transfer and pressure drop may be attributed to the decrease in the cross-sectional area of the fluid flow, causing an increased flow velocity and leading to durable vortices [19].
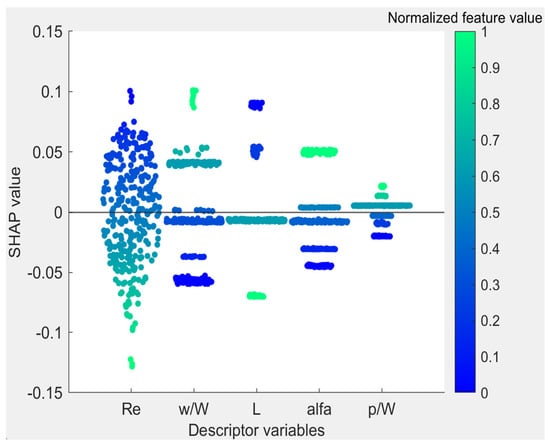
Figure 3.
SHAP Summary bee-swarm plot for friction factor.
Finally, the SHAP analysis for the PEC is displayed in Figure 4. The length is found to be the most influential design feature, with higher length values resulting in higher PEC values. The second is the attack angle, as mentioned repeatedly in this paper and many related studies. Based on the results, the positive contribution of the attack angle to the enhancement of all target variables may be seen as apparent. The relative pitch ratio is identified to be the third-most influential feature. Thermal performance can be maximized when lower Reynolds numbers and wing-to-width ratio values accompany greater length, attack angle, and relative pitch ratio. Carpio et al. [68] reported in their study that the Nusselt number and PEC also tend to increase with the increase in the Reynolds number.
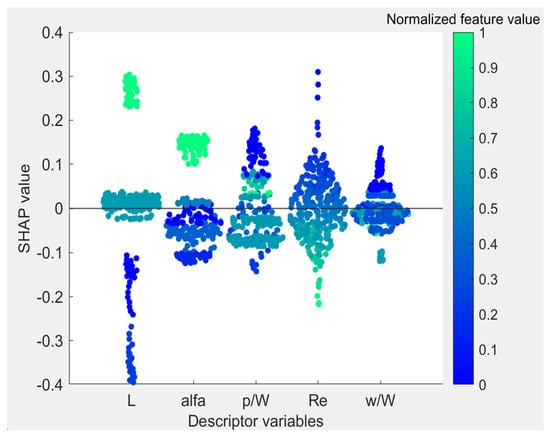
Figure 4.
SHAP Summary bee-swarm plot of PEC.
As seen in Figure 4, the configuration of a low Reynolds number and high attack angle tends to raise the PEC value. The combination of Reynolds number and attack angle was also investigated by Zhai et al. [69]. They observed a similar correlation between these features and the PEC. The current findings establish that Reynolds number adjustment and its combination with other design features are substantial determinants in achieving the highest PEC ratio; therefore, an optimum balance point must be determined between Nusselt numbers and friction factor values.
3.2. Decision Tree Analysis
As the next task, three different decision trees are built for each target variable. The different combinations of descriptor variables leading to low, medium, and high levels of target variables are investigated. In the decision tree, as shown in Figure 5, Figure 6, and Figure 7, green, yellow, and red colors represent high, medium, and low-level target variables, respectively.
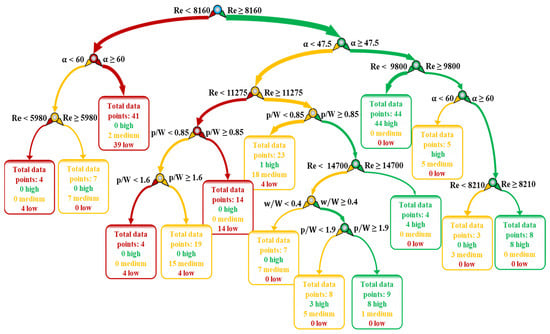
Figure 5.
Decision tree classification of Nusselt number (training error 8.0%, testing error 11.0%).
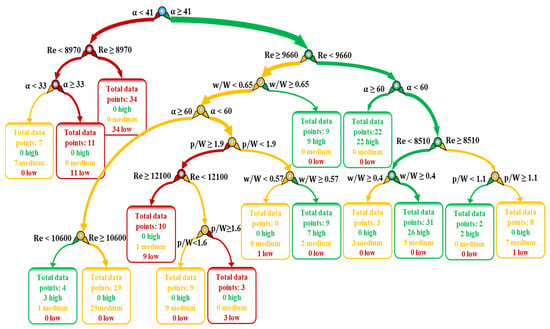
Figure 6.
Decision tree classification of friction factor (training error 7.0%, testing error 11.0%).
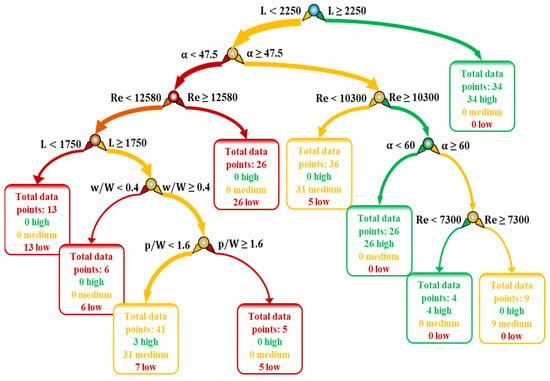
Figure 7.
Decision tree classification of PEC (training error 9.5%, testing error 12.0%).
Figure 5 shows the decision tree built for the Nusselt number based on the computational details explained in Section 2.2. In this tree, the Reynolds number is detected as the most impactful feature on tree growth, supporting the results obtained from the SHAP analysis. First of all, right-hand-side paths with Reynolds numbers greater than or equal to 8160 produce high-level output variables. Among the many pathways, Reynolds numbers between 8160 and 9800 and attack angles greater than or equal to 47.5° lead to a high Nusselt number with perfect accuracy (44 out of 44). Following the right-hand-side path, a Reynolds number greater than or equal to 8210 and an attack angle greater than or equal to 60° leads to another pure leaf node with eight data points. On the other hand, when the Reynolds number is greater than or equal to 8160, and the attack angle is below 47.5°, a relative pitch ratio greater than or equal to 0.85 in combination with a Reynolds number greater than or equal to 14,700 results in four high-level data points with 100% accuracy. The last high-level path in this decision tree is achieved when the Reynolds number is lower than 14,700, the wing-to-width ratio is equal to or greater than 0.4, and the relative pitch ratio is equal to or greater than 1.9, with eight high-level data points out of nine demonstrating high accuracy.
In accordance with the present results, a previous study conducted by Wijayanta et al. [42] demonstrated that vortices cannot effectively sweep the inner space at a higher pitch; hence, increasing the relative pitch ratio resulted in a decrease in the Nusselt number. A reduced rate of heat transfer results from the improper interaction of vortices with one another.
Finally, the overall accuracy of the decision tree is provided with the confusion matrix in Table 3. Low-, medium-, and high-level Nusselt numbers are classified correctly, with accuracy of 94%, 95%, and 76%, respectively. In addition, F1 scores of the three different-level data classifications are 0.91, 0.94, and 0.80, respectively, corresponding to low-, medium-, and high-level entries, showing remarkable accuracy of the decision tree model.

Table 3.
Confusion matrix for the decision tree classification of Nusselt numbers (split criterion: deviance, maximum number of splits: 189, minimum leaf size: 1).
The highest Nusselt number must be achieved by preserving a desired value of the PEC greater than or equal to 1. Therefore, high- or medium-level target variables of friction factors must be the target since they are more likely to contain a high Nusselt number with adequate PEC value. The optimal decision tree structure for friction factor analysis is shown in Figure 6, which starts with the attack angle (α) of DWVG. Following the path with the rule of attack angle greater than or equal to 41°, there are 13 possible paths in total. Among these, six lead to high friction factor (f) levels. The following split along the branch is provided by the Reynolds number. Continuing with Reynolds numbers lower than 9660, five paths are created, and three out of five lead to a high friction factor level. The next decision node satisfying the attack angle greater than or equal to 60° yields a leaf node containing 22 high-level friction factor data points, indicating pure classification. Following the other path, which has an attack angle of less than 60°, the Reynolds number provides the next cut. The combination of a Reynolds number lower than 8510 and a wing-to-width ratio higher than 0.4 leads to a high-level friction factor with considerably high accuracy, including 26 high data points out of 31, which is the path with the most generalized rules. The green and thicker branches in Figure 6 lead to a high-level friction factor. The other path with rules of Reynolds number greater than or equal to 8510 and relative pitch ratio of less than 1:1 results in a higher friction factor with 100% accuracy prediction, although with few data points (two samples). When the Reynolds number is greater than or equal to 9660 with the combination of an attack angle of greater than or equal to 41° and a wing-to-width ratio of greater than or equal to 0.65, this results in a high-level friction factor with an accuracy of 100%, which includes nine data points. If the wing-to-width ratio is less than 0.65 and the Reynolds number is limited between 9660 and 10,600 while keeping the attack angle greater than or equal to 60°, a high level of friction factor can be achieved with an accuracy of 75% containing three high-level target variables out of four data points. The last high-level target reaching the path satisfies the requisites of attack angle between 41° and 60°, Reynolds number greater than or equal to 9660, wing-to-width ratio less than 0.65, relative pitch ratio less than 1.9, and wing-to-width ratio greater than or equal to 0.57. The seven out of nine data points in this path represent high-level friction factors. The observed relationships are in accordance with previous findings in studies that highlighted friction factor enhancement due to an increase in attack angle [43,70] or a decrease in relative pitch ratio [42].
As shown in Figure 6, the general condition in order to yield high friction factors is to keep the Reynolds number lower than 8510, attack angle in the range of 41–60°, and wing-to-width ratio greater than or equal to 0.4. Through numerical study, Gonul et al. [65] also supported this configuration by finding the optimum attack angle to be 55°. The configuration of Reynolds number lower than 9660 and attack angle greater than or equal to 60° must be highlighted as an alternative path leading to a high friction factor.
The overall accuracy of the decision tree model was analyzed with the confusion matrix, as shown in Table 4. According to Table 4, low and medium levels of the target variable of friction factor are classified with approximately 97% accuracy for testing data. Low- and medium-level data points are also accurately classified. Moreover, F1 scores were added to Table 4 to provide a balanced assessment of the decision tree model performance using harmonic means by combining precision and recall into one metric. F1 scores of all level classes are very high for test sections: 0.88, 0.97, and 0.81 for low-, medium-, and high-level data points, respectively.

Table 4.
Confusion matrix for the decision tree classification of the friction factor (split criterion: deviance, maximum number of splits: 47, minimum leaf size: 3).
The final decision tree in this study was built for the PEC, as shown in Figure 7. Where length values are greater than or equal to 2250, a considerable number of high-level data points are classified correctly with 100% accuracy, as shown in the right-hand-side leaf node, including 34 data points, achieved by only one split from the root node. If the length values are less than 2250, the branch bifurcates by attack angle such that only if the data entries are greater than or equal to 47.5° can pure levels containing only high-level PEC values be reached. The second-most generalized path can be drawn by following this sequence and proceeding with the Reynolds number being greater or equal to 10,300 and the attack angle being lower than 60°, ultimately categorizing the data inputs exclusive to a high-level PEC. It should be noted that when the attack angle is greater than or equal to 60°, the Reynolds number is within the limits of 7300 and 10,300, the length is less than 2250, and it is also possible to reach a high-level leaf node containing four data entries.
As with previous cases, the general accuracy of the decision tree was evaluated by using the confusion matrix, as shown in Table 5. Looking at the confusion matrix, the right column of the testing data indicates recall (accuracy) values for all three-level data points. Considering the testing results, the recall value, precision, and F1 scores for high-level PEC values are 0.90, 0.75, and 0.82, respectively. Thus, this decision tree is highly reliable in terms of determining the general rule combination to obtain high PEC values, which is the overall thermo-hydraulic performance indicator among the three target variables.

Table 5.
Confusion matrix for the decision tree classification of PEC (split criterion: deviance, maximum number of splits: 122, minimum leaf size: 1).
3.3. Limitations
The results presented in this study are subject to at least three limitations. First, the data used were gathered from only seven related experimental studies, resulting in a limited number of data points (300), as previously stated. Second, five descriptor variables were included in the analysis that were found to be common and available in the literature, and other features that possibly affected the target variables were excluded due to the lack of data. Third, the models were trained for the given ranges of the features, as shown in Table 1; thereby, they can only provide reliable results in these ranges.
The current study proved that SHAP and decision tree analysis are useful tools for understanding how design variables affect target variables at different levels. However, the results can be assumed to be accurate only within the studied data range. For instance, if a unique feature is added as a descriptor variable or a value of a variable falls outside the range in our database, the target values may differ from the actual results. It is also recommended that further studies should include new features and a wider range of existing features to observe presently unknown effects on output variables.
4. Conclusions
In this work, decision tree classification and the SHAP method were employed to analyze the thermo-hydraulic performance of heat exchangers based on the design features (Reynolds number, attack angle, length, wing-to-width ratio, and relative pitch ratio) of delta wing vortex generators. Three different target variables (Nusselt number, friction factor, and performance evaluation criterion) were chosen as target variables, and they were evaluated separately.
Decision trees were used to find the optimum ranges of design features to achieve the highest thermal and hydraulic performance. For instance, a high Nusselt number can be obtained when the Reynolds number is between 8160 and 9800 and the attack angle is greater than or equal to 47.5°. On the other hand, a high friction factor can be achieved if the attack angle is between 41° and 60° while keeping the Reynolds number lower than 8510 and the wing-to-width ratio greater than or equal to 0.4. Finally, to achieve a high-performance evaluation criterion, the length should be kept higher than 2250 mm, and the attack angle value should be set in the range of 47.5° to 60°.
The SHAP interpretable machine learning method was applied to discover the importance of design features and their positive and negative effects on the target variables. For the Nusselt number, the most significant design feature was the Reynolds number, followed by the attack angle and the relative pitch ratio. It was also found that higher Reynolds numbers and attack angles and medium relative pitch ratios positively affect the Nusselt number. It was revealed that a higher attack angle and relative pitch ratio may positively influence the friction factor. Finally, the length and the attack angle were found to be the most significant variables affecting the performance evaluation criterion.
As a final remark, the present study has extended our knowledge of the impact of the design features of DWVGs on the thermo-hydraulic performance of heat exchangers. Hence, the configurations provided here can be used for further related studies, which can potentially enhance energy efficiency and optimize performance.
Author Contributions
Conceptualization, M.E.G. and K.M.M.T.; methodology, Z.Y.A. and M.E.G.; software, Z.Y.A.; validation, Z.Y.A. and M.A.; formal analysis, Z.Y.A. and M.A.; investigation, Z.Y.A. and M.A.; resources, M.A.; data curation, Z.Y.A.; writing—original draft preparation, Z.Y.A. and M.A.; writing—review and editing, Z.Y.A., M.E.G., K.M.M.T. and M.A.; visualization, Z.Y.A.; supervision, M.E.G., K.M.M.T. and M.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data are available upon request.
Conflicts of Interest
The authors declare no conflicts of interest.
Nomenclature
| Parameters | |
| ANN | artificial neural network |
| BR | blockage ratio (-) |
| DT | decision tree |
| DWVG | delta wing vortex generator |
| f | friction factor (-) |
| h | convective heat transfer coefficient (W/m2·K) |
| L | tube length (m) |
| MAE | mean absolute error |
| Nu | Nusselt number |
| p | pitch distance (m) |
| p/W | relative pitch ratio (-) |
| PEC | performance evaluation criteria |
| Re | Reynolds number (-) |
| SHAP | SHapley Additive exPlanations |
| VG | vortex generator |
| w | width of delta wing (m) |
| W | width of the aluminum strip (m) |
| Greek Letters | |
| α | attack angle (°) |
References
- IEA. Electricity 2024—Analysis. Available online: https://www.iea.org/reports/electricity-2024 (accessed on 29 February 2024).
- Helbling, M.; Meierrieks, D. Global Warming and Urbanization. J. Popul. Econ. 2023, 36, 1187–1223. [Google Scholar] [CrossRef]
- IEA. World Energy Outlook 2023—Analysis. Available online: https://www.iea.org/reports/world-energy-outlook-2023 (accessed on 29 February 2024).
- Mahmoudinezhad, S.; Sadi, M.; Ghiasirad, H.; Arabkoohsar, A. A Comprehensive Review on the Current Technologies and Recent Developments in High-Temperature Heat Exchangers. Renew. Sustain. Energy Rev. 2023, 183, 113467. [Google Scholar] [CrossRef]
- Li, K.; Wen, J.; Wang, S.; Li, Y. Multi-Parameter Optimization of Serrated Fins in Plate-Fin Heat Exchanger Based on Fluid-Structure Interaction. Appl. Therm. Eng. 2020, 176, 115357. [Google Scholar] [CrossRef]
- Yang, Q.; He, Y.; Song, K.; Hou, Q.; Zhang, Q.; Wu, X. Thermal Performance Improvement of a Circular Tube-and-Fin Heat Exchanger by Ellipsoidal Protrusions on Fin Surfaces. Int. J. Therm. Sci. 2024, 196, 108746. [Google Scholar] [CrossRef]
- Fazeli, K.; Vafai, K. Analysis of Optimized Combined Microchannel and Heat Pipes for Electronics Cooling. Int. J. Heat Mass Transf. 2024, 219, 124842. [Google Scholar] [CrossRef]
- Azizi, Y.; Bahramkhoo, M.; Kazemi, A. Influence of Non-Uniform Magnetic Field on the Thermal Efficiency Hydrodynamic Characteristics of Nanofluid in Double Pipe Heat Exchanger. Sci. Rep. 2023, 13, 407. [Google Scholar] [CrossRef] [PubMed]
- Ul Atas Khan, A.; Cheema, T.A.; Muhammad Rizwan, H.; Ullah, R.; Tayyab, M.; Park, C.W. Shell and Tube Heat Exchange Comparison with Gravitational Water Vortex Flow Configuration. Appl. Therm. Eng. 2024, 238, 122000. [Google Scholar] [CrossRef]
- Kareem, Z.S.; Mohd Jaafar, M.N.; Lazim, T.M.; Abdullah, S.; Abdulwahid, A.F. Passive Heat Transfer Enhancement Review in Corrugation. Exp. Therm. Fluid Sci. 2015, 68, 22–38. [Google Scholar] [CrossRef]
- Liu, S.; Sakr, M. A Comprehensive Review on Passive Heat Transfer Enhancements in Pipe Exchangers. Renew. Sustain. Energy Rev. 2013, 19, 64–81. [Google Scholar] [CrossRef]
- Bezaatpour, M.; Goharkhah, M. Convective Heat Transfer Enhancement in a Double Pipe Mini Heat Exchanger by Magnetic Field Induced Swirling Flow. Appl. Therm. Eng. 2020, 167, 114801. [Google Scholar] [CrossRef]
- Diao, Y.H.; Guo, L.; Liu, Y.; Zhao, Y.H.; Wang, S. Electric Field Effect on the Bubble Behavior and Enhanced Heat-Transfer Characteristic of a Surface with Rectangular Microgrooves. Int. J. Heat Mass Transf. 2014, 78, 371–379. [Google Scholar] [CrossRef]
- Dhanalakshmi, N.P.; Nagarajan, R.; Sivagaminathan, N.; Prasad, B.V.S.S.S. Acoustic Enhancement of Heat Transfer in Furnace Tubes. Chem. Eng. Process. Process Intensif. 2012, 59, 36–42. [Google Scholar] [CrossRef]
- Izadpanah, E.; Babaie Rabiee, M.; Sadeghi, H.; Talebi, S. Effect of Rotating and Oscillating Blade on the Heat Transfer Enhancement of Non-Newtonian Fluid Flow in a Channel. Appl. Therm. Eng. 2017, 113, 1277–1282. [Google Scholar] [CrossRef]
- Mashayekhi, R.; Arasteh, H.; Talebizadehsardari, P.; Kumar, A.; Hangi, M.; Rahbari, A. Heat Transfer Enhancement of Nanofluid Flow in a Tube Equipped with Rotating Twisted Tape Inserts: A Two-Phase Approach. Heat Transf. Eng. 2022, 43, 608–622. [Google Scholar] [CrossRef]
- Sadeghianjahromi, A.; Kheradmand, S.; Nemati, H.; Liaw, J.-S.; Wang, C.-C. Compound Heat Transfer Enhancement of Wavy Fin-and-Tube Heat Exchangers through Boundary Layer Restarting and Swirled Flow. Energies 2018, 11, 1959. [Google Scholar] [CrossRef]
- Välikangas, T.; Singh, S.; Sørensen, K.; Condra, T. Fin-and-Tube Heat Exchanger Enhancement with a Combined Herringbone and Vortex Generator Design. Int. J. Heat Mass Transf. 2018, 118, 602–616. [Google Scholar] [CrossRef]
- Awais, M.; Bhuiyan, A.A. Heat Transfer Enhancement Using Different Types of Vortex Generators (VGs): A Review on Experimental and Numerical Activities. Therm. Sci. Eng. Prog. 2018, 5, 524–545. [Google Scholar] [CrossRef]
- Joardar, A.; Jacobi, A.M. Heat Transfer Enhancement by Winglet-Type Vortex Generator Arrays in Compact Plain-Fin-and-Tube Heat Exchangers. Int. J. Refrig. 2008, 31, 87–97. [Google Scholar] [CrossRef]
- Samadifar, M.; Toghraie, D. Numerical Simulation of Heat Transfer Enhancement in a Plate-Fin Heat Exchanger Using a New Type of Vortex Generators. Appl. Therm. Eng. 2018, 133, 671–681. [Google Scholar] [CrossRef]
- Abdollahi, A.; Shams, M. Optimization of Shape and Angle of Attack of Winglet Vortex Generator in a Rectangular Channel for Heat Transfer Enhancement. Appl. Therm. Eng. 2015, 81, 376–387. [Google Scholar] [CrossRef]
- Gentry, M.C.; Jacobi, A.M. Heat Transfer Enhancement by Delta-Wing Vortex Generators on a Flat Plate: Vortex Interactions with the Boundary Layer. Exp. Therm. Fluid Sci. 1997, 14, 231–242. [Google Scholar] [CrossRef]
- Gentry, M.C.; Jacobi, A.M. Heat Transfer Enhancement by Delta-Wing-Generated Tip Vortices in Flat-Plate and Developing Channel Flows. J. Heat Transf. 2002, 124, 1158–1168. [Google Scholar] [CrossRef]
- Zhao, Z.; Luo, L.; Qiu, D.; Wang, S.; Wang, Z.; Sundén, B. On the Topology of Vortex Structures and Heat Transfer of a Gas Turbine Blade Internal Tip with Different Arrangement of Delta-Winglet Vortex Generators. Int. J. Therm. Sci. 2021, 160, 106676. [Google Scholar] [CrossRef]
- Sawhney, J.S.; Maithani, R.; Chamoli, S. Experimental Investigation of Heat Transfer and Friction Factor Characteristics of Solar Air Heater Using Wavy Delta Winglets. Appl. Therm. Eng. 2017, 117, 740–751. [Google Scholar] [CrossRef]
- Huisseune, H.; T’Joen, C.; Jaeger, P.D.; Ameel, B.; Schampheleire, S.D.; Paepe, M.D. Performance Enhancement of a Louvered Fin Heat Exchanger by Using Delta Winglet Vortex Generators. Int. J. Heat Mass Transf. 2013, 56, 475–487. [Google Scholar] [CrossRef]
- Alpaydin, E. Introduction to Machine Learning, 4th ed.; The MIT Press: Cambridge, MA, USA, 2020. [Google Scholar]
- Larose, D.T.; Larose, C.D. Discovering Knowledge in Data: An Introduction to Data Mining; John Wiley & Sons: Hoboken, NJ, USA, 2014; ISBN 978-0-470-90874-7. [Google Scholar]
- Tan, P.-N.; Steinbach, M.; Kumar, V. Introduction to Data Mining; Pearson Education: Noida, India, 2016. [Google Scholar]
- Liao, T.; Zhao, C.Y.; Wang, H.; Ju, S. Data-Driven Design of Multilayer Hyperbolic Metamaterials for near-Field Thermal Radiative Modulator with High Modulation Contrast. Int. J. Heat Mass Transf. 2024, 219, 124831. [Google Scholar] [CrossRef]
- Ren, F.; Zhang, F.; Zhu, Y.; Wang, Z.; Zhao, F. Enhancing Heat Transfer from a Circular Cylinder Undergoing Vortex Induced Vibration Based on Reinforcement Learning. Appl. Therm. Eng. 2024, 236, 121919. [Google Scholar] [CrossRef]
- Wang, C.; Vafai, K. Heat Transfer Enhancement for 3D Chip Thermal Simulation and Prediction. Appl. Therm. Eng. 2024, 236, 121499. [Google Scholar] [CrossRef]
- Seal, M.K.; Noori Rahim Abadi, S.M.A.; Mehrabi, M.; Meyer, J.P. Machine Learning Classification of In-Tube Condensation Flow Patterns Using Visualization. Int. J. Multiph. Flow 2021, 143, 103755. [Google Scholar] [CrossRef]
- Farahani, S.D.; Mamoei, A.J.; Alizadeh, A. Thermal Performance of Microchannel Heat Sink Integrated with Porous Medium, Slip Coefficient and Phase Change Material and Machine Learning Approach. J. Energy Storage 2023, 74, 109357. [Google Scholar] [CrossRef]
- Zhou, L.; Garg, D.; Qiu, Y.; Kim, S.-M.; Mudawar, I.; Kharangate, C.R. Machine Learning Algorithms to Predict Flow Condensation Heat Transfer Coefficient in Mini/Micro-Channel Utilizing Universal Data. Int. J. Heat Mass Transf. 2020, 162, 120351. [Google Scholar] [CrossRef]
- Berber, A.; Gürdal, M. Estimation of Forced Heat Convection in a Rectangular Channel with Curved-Winglet Vortex Generator: A Machine Learning Approach. Therm. Sci. Eng. Prog. 2023, 37, 101563. [Google Scholar] [CrossRef]
- Longo, G.A.; Mancin, S.; Righetti, G.; Zilio, C.; Ceccato, R.; Salmaso, L. Machine Learning Approach for Predicting Refrigerant Two-Phase Pressure Drop inside Brazed Plate Heat Exchangers (BPHE). Int. J. Heat Mass Transf. 2020, 163, 120450. [Google Scholar] [CrossRef]
- Khan, M.Z.A.; Khan, H.A.; Aziz, M. Performance Optimization of Heat-Exchanger with Delta-Wing Tape Inserts Using Machine Learning. Appl. Therm. Eng. 2022, 216, 119135. [Google Scholar] [CrossRef]
- Wijayanta, A.T.; Yaningsih, I.; Aziz, M.; Miyazaki, T.; Koyama, S. Double-Sided Delta-Wing Tape Inserts to Enhance Convective Heat Transfer and Fluid Flow Characteristics of a Double-Pipe Heat Exchanger. Appl. Therm. Eng. 2018, 145, 27–37. [Google Scholar] [CrossRef]
- Eiamsa-ard, S.; Promvonge, P. Influence of Double-Sided Delta-Wing Tape Insert with Alternate-Axes on Flow and Heat Transfer Characteristics in a Heat Exchanger Tube. Chin. J. Chem. Eng. 2011, 19, 410–423. [Google Scholar] [CrossRef]
- Wijayanta, A.T.; Yaningsih, I.; Juwana, W.E.; Aziz, M.; Miyazaki, T. Effect of Wing-Pitch Ratio of Double-Sided Delta-Wing Tape Insert on the Improvement of Convective Heat Transfer. Int. J. Therm. Sci. 2020, 151, 106261. [Google Scholar] [CrossRef]
- Wijayanta, A.; Aziz, M.; Kariya, K.; Miyara, A. Numerical Study of Heat Transfer Enhancement of Internal Flow Using Double-Sided Delta-Winglet Tape Insert. Energies 2018, 11, 3170. [Google Scholar] [CrossRef]
- Yaningsih, I.; Wijayanta, A.T.; Miyazaki, T.; Koyama, S. V-Cut Twisted Tape Insert Effect on Heat Transfer Enhancement of Single Phase Turbulent Flow Heat Exchanger; AIP Publishing: Jatinangor, Indonesia, 2018; p. 030038. [Google Scholar]
- Yaningsih, I.; Wijayanta, A.; Miyazaki, T.; Koyama, S. Impact of Blockage Ratio on Thermal Performance of Delta-Winglet Vortex Generators. Appl. Sci. 2018, 8, 181. [Google Scholar] [CrossRef]
- Wijayanta, A.T.; Istanto, T.; Kariya, K.; Miyara, A. Heat Transfer Enhancement of Internal Flow by Inserting Punched Delta Winglet Vortex Generators with Various Attack Angles. Exp. Therm. Fluid Sci. 2017, 87, 141–148. [Google Scholar] [CrossRef]
- Günay, M.E.; Tapan, N.A. Evaluation of Polymer Electrolyte Membrane Electrolysis by Explainable Machine Learning, Optimum Classification Model, and Active Learning. J. Appl. Electrochem. 2023, 53, 415–433. [Google Scholar] [CrossRef]
- Cohen, S.; Ruppin, E.; Dror, G. Feature Selection Based on the Shapley Value. In Proceedings of the International Joint Conference on Artificial Intelligence, Scotland, UK, 30 July–5 August 2005. [Google Scholar]
- Molnar, C. Interpretable Machine Learning: A Guide for Making Black Box Models Explainable, 2nd ed.; Independently published; 2022. [Google Scholar]
- Rokach, L.; Maimon, O. Data Mining with Decision Trees: Theory and Applications; Series in Machine Perception and Artificial Intelligence; World Scientific: Singapore, 2007; Volume 69, ISBN 978-981-277-171-1. [Google Scholar]
- Sharifi, S.; Pakdel, A.; Ebrahimi, M.; Reecy, J.M.; Fazeli Farsani, S.; Ebrahimie, E. Integration of Machine Learning and Meta-Analysis Identifies the Transcriptomic Bio-Signature of Mastitis Disease in Cattle. PLoS ONE 2018, 13, e0191227. [Google Scholar] [CrossRef] [PubMed]
- Günay, M.E.; Tapan, N.A.; Akkoç, G. Analysis and Modeling of High-Performance Polymer Electrolyte Membrane Electrolyzers by Machine Learning. Int. J. Hydrogen Energy 2022, 47, 2134–2151. [Google Scholar] [CrossRef]
- El Habib Daho, M.; Settouti, N.; El Amine Lazouni, M.; El Amine Chikh, M. Weighted Vote for Trees Aggregation in Random Forest. In Proceedings of the 2014 International Conference on Multimedia Computing and Systems (ICMCS), Marrakech, Morocco, 14–16 April 2014; pp. 438–443. [Google Scholar]
- Behfard, M.; Sohankar, A. Numerical Investigation for Finding the Appropriate Design Parameters of a Fin-and-Tube Heat Exchanger with Delta-Winglet Vortex Generators. Heat Mass Transf. 2016, 52, 21–37. [Google Scholar] [CrossRef]
- Da Silva, F.A.S.; Dezan, D.J.; Pantaleão, A.V.; Salviano, L.O. Longitudinal Vortex Generator Applied to Heat Transfer Enhancement of a Flat Plate Solar Water Heater. Appl. Therm. Eng. 2019, 158, 113790. [Google Scholar] [CrossRef]
- Darbari, B.; Rashidi, S.; Keshmiri, A. Nanofluid Heat Transfer and Entropy Generation inside a Triangular Duct Equipped with Delta Winglet Vortex Generators. J. Therm. Anal. Calorim. 2020, 140, 1045–1055. [Google Scholar] [CrossRef]
- Dezan, D.J.; Salviano, L.O.; Yanagihara, J.I. Heat Transfer Enhancement and Optimization of Flat-Tube Multilouvered Fin Compact Heat Exchangers with Delta-Winglet Vortex Generators. Appl. Therm. Eng. 2016, 101, 576–591. [Google Scholar] [CrossRef]
- Dezan, D.J.; Rocha, A.D.; Ferreira, W.G. Parametric Sensitivity Analysis and Optimisation of a Solar Air Heater with Multiple Rows of Longitudinal Vortex Generators. Appl. Energy 2020, 263, 114556. [Google Scholar] [CrossRef]
- Li, H.-Y.; Liao, W.-R.; Li, T.-Y.; Chang, Y.-Z. Application of Vortex Generators to Heat Transfer Enhancement of a Pin-Fin Heat Sink. Int. J. Heat Mass Transf. 2017, 112, 940–949. [Google Scholar] [CrossRef]
- Li, L.; Du, X.; Zhang, Y.; Yang, L.; Yang, Y. Numerical Simulation on Flow and Heat Transfer of Fin-and-Tube Heat Exchanger with Longitudinal Vortex Generators. Int. J. Therm. Sci. 2015, 92, 85–96. [Google Scholar] [CrossRef]
- Song, K.; Tagawa, T.; Chen, Z.; Zhang, Q. Heat Transfer Characteristics of Concave and Convex Curved Vortex Generators in the Channel of Plate Heat Exchanger under Laminar Flow. Int. J. Therm. Sci. 2019, 137, 215–228. [Google Scholar] [CrossRef]
- Wang, C.; Wang, L.; Sundén, B. A Novel Control of Jet Impingement Heat Transfer in Cross-Flow by a Vortex Generator Pair. Int. J. Heat Mass Transf. 2015, 88, 82–90. [Google Scholar] [CrossRef]
- Promvonge, P.; Promthaisong, P.; Skullong, S. Numerical Heat Transfer in a Solar Air Heater Duct with Punched Delta-Winglet Vortex Generators. Case Stud. Therm. Eng. 2021, 26, 101088. [Google Scholar] [CrossRef]
- Deshmukh, P.W.; Prabhu, S.V.; Vedula, R.P. Heat Transfer Enhancement for Laminar Flow in Tubes Using Curved Delta Wing Vortex Generator Inserts. Appl. Therm. Eng. 2016, 106, 1415–1426. [Google Scholar] [CrossRef]
- Gönül, A.; Okbaz, A.; Kayaci, N.; Selim Dalkilic, A. Flow Optimization in a Microchannel with Vortex Generators Using Genetic Algorithm. Appl. Therm. Eng. 2022, 201, 117738. [Google Scholar] [CrossRef]
- Xu, Y.; Islam, M.D.; Kharoua, N. Experimental Study of Thermal Performance and Flow Behaviour with Winglet Vortex Generators in a Circular Tube. Appl. Therm. Eng. 2018, 135, 257–268. [Google Scholar] [CrossRef]
- Lei, Y.; Zheng, F.; Song, C.; Lyu, Y. Improving the Thermal Hydraulic Performance of a Circular Tube by Using Punched Delta-Winglet Vortex Generators. Int. J. Heat Mass Transf. 2017, 111, 299–311. [Google Scholar] [CrossRef]
- Carpio, J.; Valencia, A. Heat Transfer Enhancement through Longitudinal Vortex Generators in Compact Heat Exchangers with Flat Tubes. Int. Commun. Heat Mass Transf. 2021, 120, 105035. [Google Scholar] [CrossRef]
- Zhai, C.; Islam, M.D.; Simmons, R.; Barsoum, I. Heat Transfer Augmentation in a Circular Tube with Delta Winglet Vortex Generator Pairs. Int. J. Therm. Sci. 2019, 140, 480–490. [Google Scholar] [CrossRef]
- Ekrani, S.M.; Ganjehzadeh, S.; Esfahani, J.A. Multi-Objective Optimization of a Tubular Heat Exchanger Enhanced with Delta Winglet Vortex Generator and Nanofluid Using a Hybrid CFD-SVR Method. Int. J. Therm. Sci. 2023, 186, 108141. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).