A Review of Artificial Intelligence Methods in Predicting Thermophysical Properties of Nanofluids for Heat Transfer Applications
Abstract
1. Introduction
2. Thermophysical Properties of Nanofluids
2.1. Thermal Conductivity
2.2. Viscosity
2.3. Specific Heat Capacity
3. Algorithms
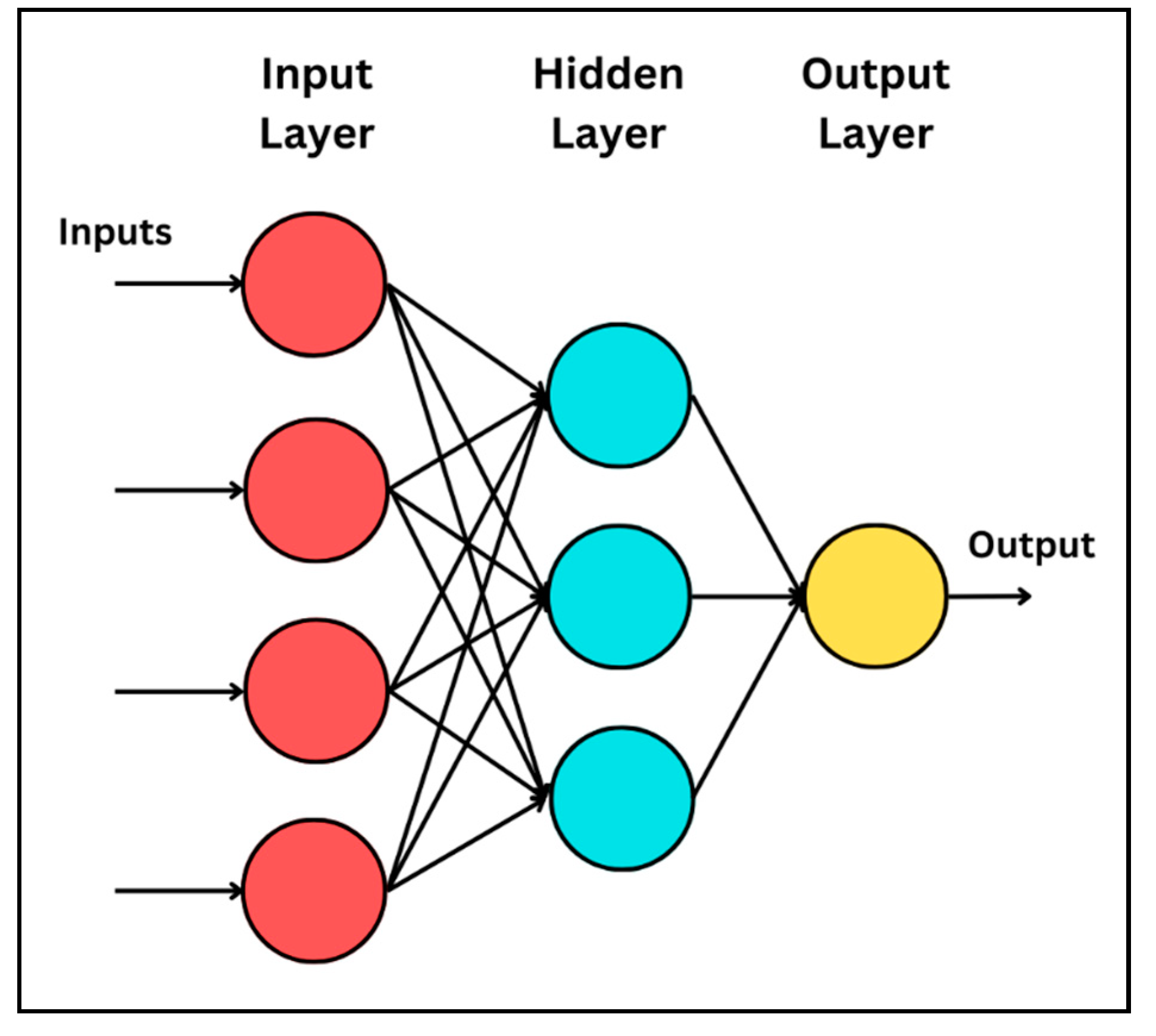
3.1. Artificial Neural Network
3.1.1. RBF Neural Network
3.1.2. GMDH-Type Neural Network
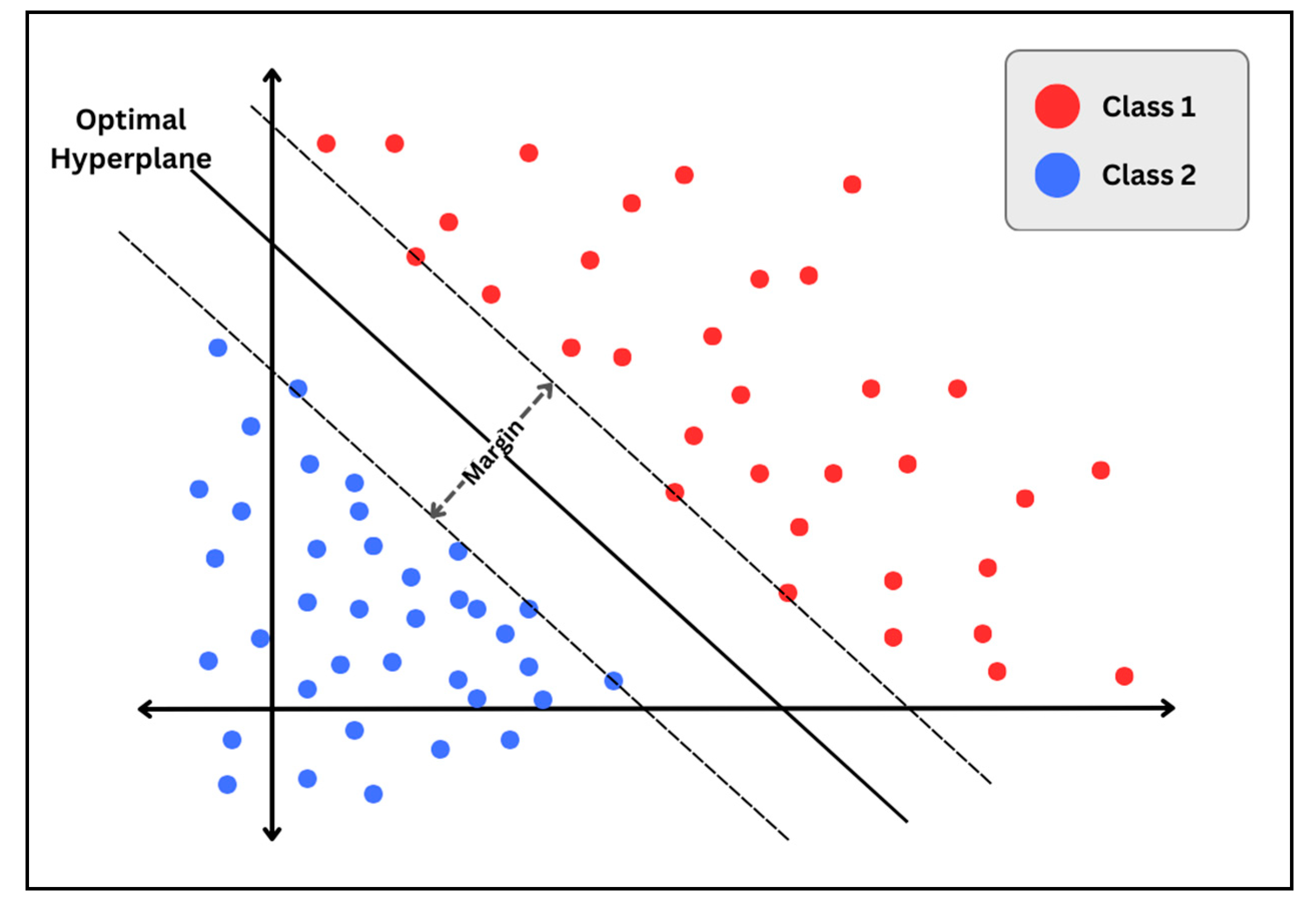
3.2. Support Vector Machine
3.3. Decision Tree
3.3.1. Decision Tree Regression
3.3.2. Alternating Decision Tree
3.3.3. M5 Tree
3.3.4. Random Forest
3.3.5. Extra Tree Regression
3.3.6. AdaBoost
3.3.7. Boosted Regression Tree
3.3.8. Gradient Boosting Machine
3.3.9. XG Boost
3.4. Genetic Algorithm
3.5. Adaptive Neuro Fuzzy Interface
3.6. Regression
3.6.1. Non-Linear Regression
3.6.2. Multivariate Adaptive Regression Splines
3.6.3. Multivariate Polynomial Regression
3.6.4. Gaussian Process Regression
4. Application of AI for Predicting Thermophysical Properties of Nanofluids
4.1. Applications of AI for Predicting Thermal Conductivity of Nanofluids
4.2. Applications of AI for Predicting Viscosity of Nanofluids
4.3. Applications of AI for Predicting Specific Heat Capacity of Nanofluids
5. Conclusions and Future Scope
- i.
- One of the noteworthy findings of our review is the consistent superiority of AI-based models over traditional theoretical and correlation-based approaches in predicting the thermophysical properties of nanofluids. These theoretical models often exhibit uncertainties and fail to predict experimental results precisely, limiting their practical applications [91,176,177]. As outlined in the previous sections, the utilization of machine learning algorithms has yielded a more accurate estimation of the properties of NFs due to their ability to effectively map non-linear relationships between input and output variables [126]. Not only do these models offer higher accuracy, but they also present a more accessible and cost-effective alternative to experimental methods.
- ii.
- Furthermore, our review underscores the vast potential of nanofluids to revolutionize heat transfer fluids and coolants in various applications. However, nanofluid thermophysical properties exhibit non-linear relationships and are challenging to model using traditional theoretical models, while conducting experimental measurements is time-consuming, labour-intensive, and costly. In this scenario, AI techniques like ML become useful. ML extracts patterns and knowledge from given data without first principles, introducing a new paradigm: ‘use data to discover, rather than validate, new hypotheses and models’ [178]. Integrating big data and machine learning is transforming various industries, including multiphysics research, leveraging high-quality data from improved experimental and simulation studies and archival data. By harnessing AI techniques to predict the complex relation governing nanofluid thermophysical properties, researchers are paving the way for innovative thermal and energy systems solutions for industrial applications like solar collectors, heat exchangers, and PV/T systems [176].
- iii.
- However, data availability is a specific challenge related to applying AI methods in nanofluid thermophysical property prediction. For instance, the ML models are specific to the dataset they are trained on. For example, an ML model trained on the prediction of SHC of CuO/EG nanofluid in a plate heat exchanger would only be able to predict the SHC of CuO/ethylene glycol nanofluids and not of other nanofluids. It would also work only for plate heat exchangers rather than other configurations. This limits the applicability of ML models. If one desires a model that can predict the SHC of different nanofluids, the nanofluid/nanoparticle type should also be used as an additional input to the model. Among the papers reviewed, only the work by Esfani et al. [88] used nanoparticle type as an input parameter. This aspect highlights the substantial scope of research in this domain. However, incorporating nanoparticle type and other parameters in the input may increase the complexity of the dataset. As the complexity of the dataset increases, it becomes necessary to include more and more data points to obtain a good fit and avoid over-fitting, which is often not feasible due to the limitations of data availability and constraints of computational resources, which are necessary to run complex AI models. In such situations, dimensionality reduction techniques such as the Principal Component Analysis and the Linear Discriminant Analysis may be employed to reduce the dimensionality of the dataset.In addition, it must be borne in mind that the prediction models may not fully consider external factors such as impurities, contaminants, or changes in operational conditions. Moreover, the sensitivity of specific algorithms to hyperparameter settings may also impact the robustness and reliability of predictions.
- iv.
- Data availability is another issue that could hinder the progress of nanofluid research using AI. AI techniques such as ML require large amounts of data, and the absence of such data can seriously affect the models. Most of the reviewed work in this study has used relatively small datasets. Applying complex algorithms like the ANN on small datasets can result in overfitting, significantly reducing the predictions’ reliability. For this reason, a large amount of quality data is necessary. Experimental methods and computer-based simulations can generate these datasets. However, such exercises are liable to be expensive and time-consuming for individual research groups. However, once sufficient data are generated and made available globally in the public domain by researchers, these can be used to develop robust and powerful AI models to charter futuristic applications in efficient thermal management.
- v.
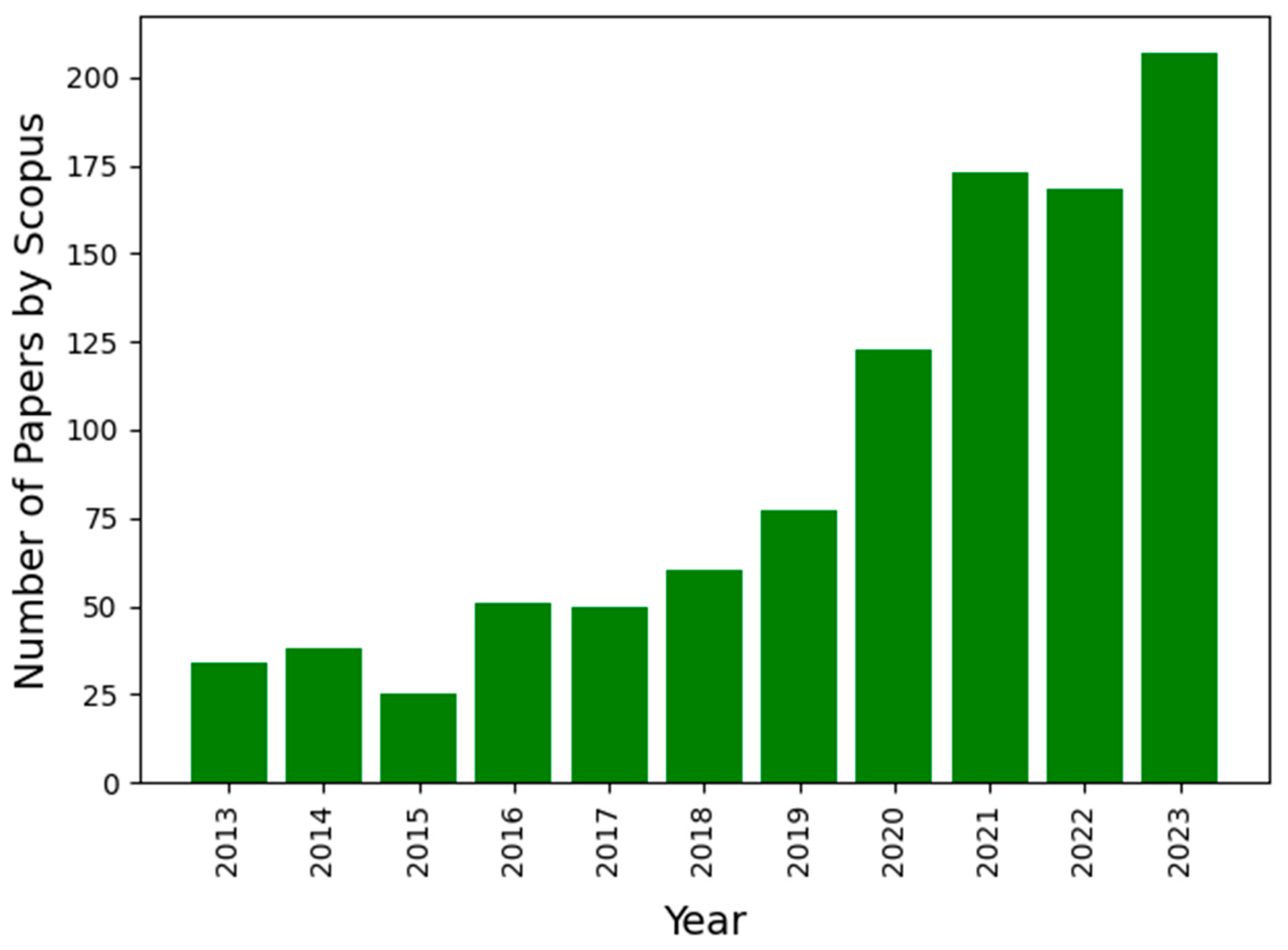
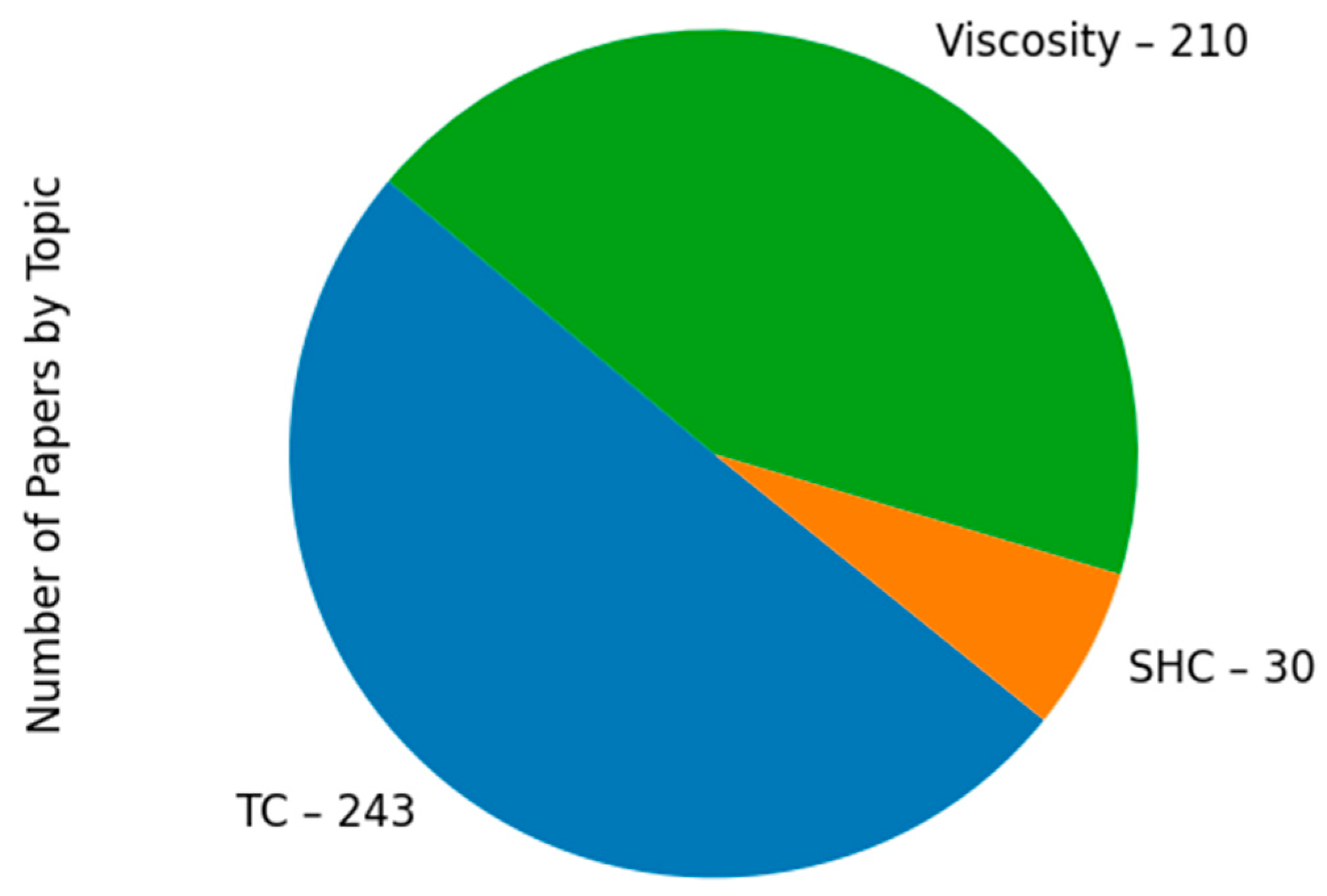
- It is worth noting that while thermal conductivity and viscosity have been extensively studied, the SHC of nanofluids still needs to be explored. Figure 4 presents the number of publications on nanofluid thermophysical property research with AI techniques such as ML and GA acquired from the Scopus database (as of 25 February 2024).Research on nanofluid TC with AI techniques has resulted in 243 publications; on viscosity, it has yielded 210 publications. However, just 30 published articles are devoted to applying AI techniques to the SHC of nanofluids. This trend may be attributed to the fact that, while TC and viscosity are primary thermophysical properties of any heat transfer medium, SHC considerations are relatively unimportant in applications where phase changes can be neglected. However, several researchers have pointed out the importance of SHC in enhancing the heat transfer properties of nanofluids [129,179]. Based on the preceding statistics, paying more attention to the SHC of nanofluids becomes imperative. This presents an exciting avenue for future research endeavours.
- vi.
- Applying AI, ML, and GA techniques in nanofluid research is still a relatively nascent field with steady academic and research interest growth. Several researchers [45,90,93] have demonstrated innovative approaches by combining metaheuristic techniques like GA with traditional ML models such as ANN and SVM, creating more robust models. This field of study is expected to grow even more in the coming years, with more and more researchers contributing to this field.
Funding
Conflicts of Interest
Abbreviations
| AdaBoost | adaptive boosting |
| ADTree | alternating decision tree |
| AI | artificial intelligence |
| ANFIS | adaptive neuro-fuzzy interface system |
| ANN | artificial neural network |
| BRT | boosted regression tree |
| BSVR | Bayesian support vector regression |
| CNT | Carbon nanotube |
| DI | diamond |
| DSC | differential scanning calorimeter |
| DTR | decision tree regression |
| EG | ethylene glycol |
| ETR | extra tree regression |
| GA | genetic algorithm |
| GBM | gradient boosting machine |
| GMDH | group method of data handling |
| GPR | Gaussian process regression |
| IL | ionic liquid |
| LSSVM | least square support vector machine |
| MAE | mean absolute error |
| MARS | multivariate adaptive regression splines |
| MDSC | modulated differential scanning calorimeter |
| MGGP | multi-gene genetic programming |
| ML | machine learning |
| MLP | multi-layer perceptron |
| MO | mineral oil |
| MPR | multivariable polynomial regression |
| MWCNT | multi-walled carbon nanotube |
| NLR | non-linear regression |
| NN | neural network |
| PV/T | photovoltaic/thermal |
| RBF-NN | radial basis function neural network |
| RBF | radial basis function |
| RF | random forest |
| RMS | root mean square |
| RMSE | root mean square error |
| RSM | response surface methodology |
| SGB | stochastic gradient boosting |
| SHC | specific heat capacity |
| SVM | support vector machine |
| SVR | support vector regression |
| TC | thermal conductivity |
| XGBoost | extreme gradient boosting |
References
- Rosenzweig, R. Ferrohydrodynamics; Cambridge: New York, NY, USA, 1985; pp. 57–59. Available online: https://books.google.co.in/books?id=Vv-1QgAACAAJ (accessed on 31 December 2023).
- Akoh, H.; Tsukasaki, Y.; Yatsuya, S.; Tasaki, A. Magnetic properties of ferromagnetic ultrafine particles prepared by vacuum evaporation on running oil substrate. J. Cryst. Growth 1978, 45, 495–500. [Google Scholar] [CrossRef]
- Choi, S.U.; Eastman, J.A. Enhanced Heat Transfer Using Nanofluids; Technical Report; Argonne National Lab. (ANL): Argonne, IL, USA, 2001. Available online: https://www.osti.gov/servlets/purl/196525 (accessed on 31 December 2023).
- Lee, S.W.; Park, S.D.; Bang, I.C. Critical heat flux for CuO nanofluid fabricated by pulsed laser ablation differentiating deposition characteristics. Int. J. Heat Mass Transf. 2012, 55, 6908–6915. [Google Scholar] [CrossRef]
- Kim, H.J.; Bang, I.C.; Onoe, J. Characteristic stability of bare Au-water nanofluids fabricated by pulsed laser ablation in liquids. Opt. Lasers Eng. 2009, 47, 532–538. [Google Scholar] [CrossRef]
- Lo, C.-H.; Tsung, T.-T.; Lin, H.-M. Preparation of silver nanofluid by the submerged arc nanoparticle synthesis system (sanss). J. Alloys Compd. 2007, 434–435, 659–662. [Google Scholar] [CrossRef]
- Lo, C.-H.; Tsung, T.-T.; Chen, L.-C. Shape-controlled synthesis of Cu-based nanofluid using submerged arc nanoparticle synthesis system (sanss). J. Cryst. Growth 2005, 277, 636–642. [Google Scholar] [CrossRef]
- Prasher, R.; Phelan, P.E.; Bhattacharya, P. Effect of aggregation kinetics on the thermal conductivity of nanoscale colloidal solutions (nanofluid). Nano Lett. 2006, 6, 1529–1534. [Google Scholar] [CrossRef] [PubMed]
- Muthukumaran, T.; Gnanaprakash, G.; Philip, J. Synthesis of stable magnetic nanofluids of different particle sizes. J. Nanofluids 2012, 1, 85–92. [Google Scholar] [CrossRef]
- Zhu, H.; Zhang, C.; Tang, Y.; Wang, J.; Ren, B.; Yin, Y. Preparation and thermal conductivity of suspensions of graphite nanoparticles. Carbon 2007, 45, 226–228. [Google Scholar] [CrossRef]
- Kao, M.; Lo, C.; Tsung, T.; Wu, Y.; Jwo, C.; Lin, H. Copper-oxide brake nanofluid manufactured using arc-submerged nanoparticle synthesis system. J. Alloys Compd. 2007, 434–435, 672–674. [Google Scholar] [CrossRef]
- Philip, J.; Shima, P.D.; Raj, B. Nanofluid with tunable thermal properties. Appl. Phys. Lett. 2008, 92, 043108. [Google Scholar] [CrossRef]
- Yu, W.; Xie, H. A Review on nanofluids: Preparation, stability mechanisms, and applications. J. Nanomater. 2012, 2012, 435873. [Google Scholar] [CrossRef]
- Hernandez, R. Polymer gels with magnetic nanoparticles. applications in magnetic hyperthermia. polysolvat-9. In Proceedings of the 9th International IUPAC Conference on Polymer-Solvent Complexes & Intercalates, Kiev, Ukraine, 11–14 September 2012. [Google Scholar]
- Yang, D.; Yang, F.; Hu, J.; Long, J.; Wang, C.; Fu, D.; Ni, Q. Hydrophilic multi-walled carbon nanotubes decorated with magnetite nanoparticles as lymphatic targeted drug delivery vehicles. Chem. Commun. 2009, 29, 4447–4449. [Google Scholar] [CrossRef] [PubMed]
- Taylor, R.A.; Otanicar, T.; Rosengarten, G. Nanofluid-based optical filter optimization for PV/T systems. Light Sci. Appl. 2012, 1, e34. [Google Scholar] [CrossRef]
- Mahendran, V.; Philip, J. Naked eye visualization of defects in ferromagnetic materials and components. NDT E Int. 2013, 60, 100–109. [Google Scholar] [CrossRef]
- Dudda, B.; Shin, D. Effect of nanoparticle dispersion on specific heat capacity of a binary nitrate salt eutectic for concentrated solar power applications. Int. J. Therm. Sci. 2013, 69, 37–42. [Google Scholar] [CrossRef]
- Mahian, O.; Kianifar, A.; Kalogirou, S.A.; Pop, I.; Wongwises, S. A review of the applications of nanofluids in solar energy. Int. J. Heat Mass Transf. 2013, 57, 582–594. [Google Scholar] [CrossRef]
- Wang, Z.; Wu, Z.; Han, F.; Wadsö, L.; Sundén, B. Experimental comparative evaluation of a graphene nanofluid coolant in miniature plate heat exchanger. Int. J. Therm. Sci. 2018, 130, 148–156. [Google Scholar] [CrossRef]
- Bigdeli, M.B.; Fasano, M.; Cardellini, A.; Chiavazzo, E.; Asinari, P. A review on the heat and mass transfer phenomena in nanofluid coolants with special focus on automotive applications. Renew. Sustain. Energy Rev. 2016, 60, 1615–1633. [Google Scholar] [CrossRef]
- Ijam, A.; Saidur, R. Nanofluid as a coolant for electronic devices (cooling of electronic devices). Appl. Therm. Eng. 2012, 32, 76–82. [Google Scholar] [CrossRef]
- Leong, K.; Saidur, R.; Kazi, S.; Mamun, A. Performance investigation of an automotive car radiator operated with nanofluid-based coolants (nanofluid as a coolant in a radiator). Appl. Therm. Eng. 2010, 30, 2685–2692. [Google Scholar] [CrossRef]
- Raj, C.P.C.; Surendran, S.A.; Amjathkhan, B.; Metilda, J.B.; Devaraj, S.; Aristotle, E. Nano fluids for improving efficiency in wind turbine cooling system. Adv. Mater. Res. 2014, 984, 784–791. [Google Scholar] [CrossRef]
- Goel, N.; Taylor, R.A.; Otanicar, T. A review of nanofluid-based direct absorption solar collectors: Design considerations and experiments with hybrid pv/thermal and direct steam generation collectors. Renew. Energy 2020, 145, 903–913. [Google Scholar] [CrossRef]
- de Risi, A.; Milanese, M.; Colangelo, G.; Laforgia, D. High efficiency nanofluid cooling system for wind turbines. Therm. Sci. 2014, 18, 543–554. [Google Scholar] [CrossRef]
- Rostamzadeh, H.; Rostami, S. Performance enhancement of waste heat extraction from generator of a wind turbine for freshwater production via employing various nanofluids. Desalination 2019, 478, 114244. [Google Scholar] [CrossRef]
- Narei, H.; Ghasempour, R.; Noorollahi, Y. The effect of employing nanofluid on reducing the bore length of a vertical ground-source heat pump. Energy Convers. Manag. 2016, 123, 581–591. [Google Scholar] [CrossRef]
- Diglio, G.; Roselli, C.; Sasso, M.; Channabasappa, U.J. Borehole heat exchanger with nanofluids as heat carrier. Geothermics 2018, 72, 112–123. [Google Scholar] [CrossRef]
- Daneshipour, M.; Rafee, R. Nanofluids as the circuit fluids of the geothermal borehole heat exchangers. Int. Commun. Heat Mass Transf. 2017, 81, 34–41. [Google Scholar] [CrossRef]
- Karami, M.; Akhavan-Bahabadi, M.; Delfani, S.; Raisee, M. Experimental investigation of CuO nanofluid-based direct absorption solar collector for residential applications. Renew. Sustain. Energy Rev. 2015, 52, 793–801. [Google Scholar] [CrossRef]
- Menbari, A.; Alemrajabi, A.A.; Rezaei, A. Heat transfer analysis and the effect of cuo/water nanofluid on direct absorption concentrating solar collector. Appl. Therm. Eng. 2016, 104, 176–183. [Google Scholar] [CrossRef]
- Hatami, M.; Mosayebidorcheh, S.; Jing, D. Thermal performance evaluation of alumina-water nanofluid in an inclined direct absorption solar collector (idasc) using numerical method. J. Mol. Liq. 2017, 231, 632–639. [Google Scholar] [CrossRef]
- Colangelo, G.; Favale, E.; Miglietta, P.; de Risi, A.; Milanese, M.; Laforgia, D. Experimental test of an innovative high concentration nanofluid solar collector. Appl. Energy 2015, 154, 874–881. [Google Scholar] [CrossRef]
- Li, Q.; Zheng, C.; Shirazi, A.; Mousa, O.B.; Moscia, F.; Scott, J.A.; Taylor, R.A. Design and analysis of a medium-temperature, concentrated solar thermal collector for air-conditioning applications. Appl. Energy 2017, 190, 1159–1173. [Google Scholar] [CrossRef]
- Mahesh, A. Solar collectors and adsorption materials aspects of cooling system. Renew. Sustain. Energy Rev. 2017, 73, 1300–1312. [Google Scholar] [CrossRef]
- Sardarabadi, M.; Passandideh-Fard, M.; Heris, S.Z. Experimental investigation of the effects of silica/water nanofluid on pv/t (photovoltaic thermal units). Energy 2014, 66, 264–272. [Google Scholar] [CrossRef]
- Sarsam, W.S.; Amiri, A.; Kazi, S.; Badarudin, A. Stability and thermophysical properties of non-covalently functionalized graphene nanoplatelets nanofluids. Energy Convers. Manag. 2016, 116, 101–111. [Google Scholar] [CrossRef]
- Moldoveanu, G.M.; Huminic, G.; Minea, A.A.; Huminic, A. Experimental study on thermal conductivity of stabilized Al2O3 and SiO2 nanofluids and their hybrid. Int. J. Heat Mass Transf. 2018, 127, 450–457. [Google Scholar] [CrossRef]
- Khodadadi, H.; Toghraie, D.; Karimipour, A. Effects of nanoparticles to present a statistical model for the viscosity of mgo-water nanofluid. Powder Technol. 2019, 342, 166–180. [Google Scholar] [CrossRef]
- Akilu, S.; Baheta, A.T.; Kadirgama, K.; Padmanabhan, E.; Sharma, K. Viscosity, electrical and thermal conductivities of ethylene and propylene glycol-based β-sic nanofluids. J. Mol. Liq. 2019, 284, 780–792. [Google Scholar] [CrossRef]
- Cai, Y.; Nan, Y.; Guo, Z. Enhanced absorption of solar energy in a daylighting louver with Ni-water nanofluid. Int. J. Heat Mass Transf. 2020, 158, 119921. [Google Scholar] [CrossRef]
- Esfe, M.H.; Raki, H.R.; Emami, M.R.S.; Afrand, M. Viscosity and rheological properties of antifreeze based nanofluid containing hybrid nano-powders of mwcnts and TiO2 under different temperature conditions. Powder Technol. 2019, 342, 808–816. [Google Scholar] [CrossRef]
- Li, F.; Li, L.; Zhong, G.; Zhai, Y.; Li, Z. Effects of ultrasonic time, size of aggregates and temperature on the stability and viscosity of Cu-ethylene glycol (eg) nanofluids. Int. J. Heat Mass Transf. 2019, 129, 278–286. [Google Scholar] [CrossRef]
- Esfe, M.H.; Bahiraei, M.; Mahian, O. Experimental study for developing an accurate model to predict viscosity of cuo–ethylene glycol nanofluid using genetic algorithm based neural network. Powder Technol. 2018, 338, 383–390. [Google Scholar] [CrossRef]
- Doganay, S.; Turgut, A.; Cetin, L. Magnetic field dependent thermal conductivity measurements of magnetic nanofluids by 3ω method. J. Magn. Magn. Mater. 2019, 474, 199–206. [Google Scholar] [CrossRef]
- Sidik, N.A.C.; Yazid, M.N.A.W.M.; Samion, S. A review on the use of carbon nanotubes nanofluid for energy harvesting system. Int. J. Heat Mass Transf. 2017, 111, 782–794. [Google Scholar] [CrossRef]
- Aparna, Z.; Michael, M.; Pabi, S.; Ghosh, S. Thermal conductivity of aqueous Al2O3/Ag hybrid nanofluid at different temperatures and volume concentrations: An experimental investigation and development of new correlation function. Powder Technol. 2019, 343, 714–722. [Google Scholar] [CrossRef]
- Xu, G.; Fu, J.; Dong, B.; Quan, Y.; Song, G. A novel method to measure thermal conductivity of nanofluids. Int. J. Heat Mass Transf. 2019, 130, 978–988. [Google Scholar] [CrossRef]
- Keyvani, M.; Afrand, M.; Toghraie, D.; Reiszadeh, M. An experimental study on the thermal conductivity of cerium oxide/ethylene glycol nanofluid: Developing a new correlation. J. Mol. Liq. 2018, 266, 211–217. [Google Scholar] [CrossRef]
- Bahiraei, M.; Rahmani, R.; Yaghoobi, A.; Khodabandeh, E.; Mashayekhi, R.; Amani, M. Recent research contributions concerning use of nanofluids in heat exchangers: A critical review. Appl. Therm. Eng. 2018, 133, 137–159. [Google Scholar] [CrossRef]
- Nazarzade, S.; Ghorbani, H.R.; Jafarpourgolroudbary, H. Synthesis, preparation and the experimental study of silver/water nanofluid to optimize convective heat transfer in a shell and tube heat exchanger. Inorg. Nano-Metal Chem. 2019, 49, 173–176. [Google Scholar] [CrossRef]
- Ullah, R.; Ishtiaq, T.M.; Mamun, A.H. Heat transfer enhancement in shell and tube heat exchanger by using Al2O3/water and TiO2/water nanofluid. AIP Conf. Proc. 2019, 2121, 070018. [Google Scholar] [CrossRef]
- Said, Z.; Rahman, S.; Assad, M.E.H.; Alami, A.H. Heat transfer enhancement and life cycle analysis of a shell-and-tube heat exchanger using stable CuO/water nanofluid. Sustain. Energy Technol. Assess. 2019, 31, 306–317. [Google Scholar] [CrossRef]
- Somasekhar, K.; Rao, K.M.; Sankararao, V.; Mohammed, R.; Veerendra, M.; Venkateswararao, T. A CFD Investigation of Heat Transfer Enhancement of Shell and Tube Heat Exchanger Using Al2O3-Water Nanofluid. Mater. Today Proc. 2018, 5, 1057–1062. [Google Scholar] [CrossRef]
- Esfahani, M.R.; Languri, E.M. Exergy analysis of a shell-and-tube heat exchanger using graphene oxide nanofluids. Exp. Therm. Fluid Sci. 2017, 83, 100–106. [Google Scholar] [CrossRef]
- Bahmani, M.H.; Sheikhzadeh, G.; Zarringhalam, M.; Akbari, O.A.; Alrashed, A.A.; Shabani, G.A.S.; Goodarzi, M. Investigation of turbulent heat transfer and nanofluid flow in a double pipe heat exchanger. Adv. Powder Technol. 2018, 29, 273–282. [Google Scholar] [CrossRef]
- Bahiraei, M.; Naghibzadeh, S.M.; Jamshidmofid, M. Efficacy of an eco-friendly nanofluid in a miniature heat exchanger regarding to arrangement of silver nanoparticles. Energy Convers. Manag. 2017, 144, 224–234. [Google Scholar] [CrossRef]
- Sarafraz, M.; Hormozi, F. Intensification of forced convection heat transfer using biological nanofluid in a double-pipe heat exchanger. Exp. Therm. Fluid Sci. 2015, 66, 279–289. [Google Scholar] [CrossRef]
- Sözen, A.; Variyenli, H.I.; Özdemir, M.B.; Gürü, M.; Aytaç, I. Heat transfer enhancement using alumina and fly ash nanofluids in parallel and cross-flow concentric tube heat exchangers. J. Energy Inst. 2016, 89, 414–424. [Google Scholar] [CrossRef]
- Saeedan, M.; Nazar, A.R.S.; Abbasi, Y.; Karimi, R. Cfd investigation and neutral network modeling of heat transfer and pressure drop of nanofluids in double pipe helically baffled heat exchanger with a 3-d fined tube. Appl. Therm. Eng. 2016, 100, 721–729. [Google Scholar] [CrossRef]
- Shakiba, A.; Vahedi, K. Numerical analysis of magnetic field effects on hydro-thermal behaviour of a magnetic nanofluid in a double pipe heat exchanger. J. Magn. Magn. Mater. 2016, 402, 131–142. [Google Scholar] [CrossRef]
- Kumar, N.R.; Bhramara, P.; Addis, B.M.; Sundar, L.S.; Singh, M.K.; Sousa, A.C. Heat transfer, friction factor and effectiveness analysis of Fe3O4/water nanofluid flow in a double pipe heat exchanger with return bend. Int. Commun. Heat Mass Transf. 2017, 81, 155–163. [Google Scholar] [CrossRef]
- Ali, A.Y.M.; El-Shazly, A.H.; El-Kady, M.; Fathi, H.I.; El-Marghany, M.R. Effect of using MgO-Oil nanofluid on the performance of a counter-flow double pipe heat exchanger. Key Eng. Mater. 2019, 801, 193–198. [Google Scholar] [CrossRef]
- Sun, B.; Peng, C.; Zuo, R.; Yang, D.; Li, H. Investigation on the flow and convective heat transfer characteristics of nanofluids in the plate heat exchanger. Exp. Therm. Fluid Sci. 2016, 76, 75–86. [Google Scholar] [CrossRef]
- Elias, M.M.; Saidur, R.; Ben-Mansour, R.; Hepbasli, A.; Rahim, N.A.; Jesbains, K. Heat transfer and pressure drop characteristics of a plate heat exchanger using water based Al2O3 nanofluid for 30° and 60° chevron angles. Heat Mass Transf. 2018, 54, 2907–2916. [Google Scholar] [CrossRef]
- Attalla, M.; Maghrabie, H.M. An experimental study on heat transfer and fluid flow of rough plate heat exchanger using Al2O3/water nanofluid. Exp. Heat Transf. 2020, 33, 261–281. [Google Scholar] [CrossRef]
- Sarafraz, M.; Nikkhah, V.; Madani, S.; Jafarian, M.; Hormozi, F. Low-frequency vibration for fouling mitigation and intensification of thermal performance of a plate heat exchanger working with CuO/water nanofluid. Appl. Therm. Eng. 2017, 121, 388–399. [Google Scholar] [CrossRef]
- Taghizadeh-Tabari, Z.; Heris, S.Z.; Moradi, M.; Kahani, M. The study on application of TiO2/water nanofluid in plate heat exchanger of milk pasteurization industries. Renew. Sustain. Energy Rev. 2016, 58, 1318–1326. [Google Scholar] [CrossRef]
- Pourhoseini, S.; Naghizadeh, N. An experimental study on optimum concentration of silver-water microfluid for enhancing heat transfer performance of a plate heat exchanger. J. Taiwan Inst. Chem. Eng. 2017, 75, 220–227. [Google Scholar] [CrossRef]
- Behrangzade, A.; Heyhat, M.M. The effect of using nano-silver dispersed water based nanofluid as a passive method for energy efficiency enhancement in a plate heat exchanger. Appl. Therm. Eng. 2016, 102, 311–317. [Google Scholar] [CrossRef]
- Pourhoseini, S.; Naghizadeh, N.; Hoseinzadeh, H. Effect of silver-water nanofluid on heat transfer performance of a plate heat exchanger: An experimental and theoretical study. Powder Technol. 2018, 332, 279–286. [Google Scholar] [CrossRef]
- Anoop, K.; Sadr, R.; Yu, J.; Kang, S.; Jeon, S.; Banerjee, D. Experimental study of forced convective heat transfer of nanofluids in a microchannel. Int. Commun. Heat Mass Transf. 2012, 39, 1325–1330. [Google Scholar] [CrossRef]
- Anoop, K.; Cox, J.; Sadr, R. Thermal evaluation of nanofluids in heat exchangers. Int. Commun. Heat Mass Transf. 2013, 49, 5–9. [Google Scholar] [CrossRef]
- Sarafraz, M.; Hormozi, F. Heat transfer, pressure drop and fouling studies of multi-walled carbon nanotube nano-fluids inside a plate heat exchanger. Exp. Therm. Fluid Sci. 2016, 72, 1–11. [Google Scholar] [CrossRef]
- Goodarzi, M.; Amiri, A.; Goodarzi, M.S.; Safaei, M.R.; Karimipour, A.; Languri, E.M.; Dahari, M. Investigation of heat transfer and pressure drop of a counter flow corrugated plate heat exchanger using MWCNT based nanofluids. Int. Commun. Heat Mass Transf. 2015, 66, 172–179. [Google Scholar] [CrossRef]
- Kumar, V.; Tiwari, A.K.; Ghosh, S.K. Effect of chevron angle on heat transfer performance in plate heat exchanger using ZnO/water nanofluid. Energy Convers. Manag. 2016, 118, 142–154. [Google Scholar] [CrossRef]
- Ramezanizadeh, M.; Ahmadi, M.H.; Nazari, M.A.; Sadeghzadeh, M.; Chen, L. A review on the utilized machine learning approaches for modeling the dynamic viscosity of nanofluids. Renew. Sustain. Energy Rev. 2019, 114, 109345. [Google Scholar] [CrossRef]
- Elsheikh, A.H.; Sharshir, S.W.; Abd Elaziz, M.; Kabeel, A.E.; Guilan, W.; Haiou, Z. Modeling of solar energy systems using artificial neural network: A comprehensive review. Sol. Energy 2019, 180, 622–639. [Google Scholar] [CrossRef]
- Yan, S.; Wang, F.; Shi, Z.; Tian, R. Heat transfer property of SiO2/water nanofluid flow inside solar collector vacuum tubes. Appl. Therm. Eng. 2017, 118, 385–391. [Google Scholar] [CrossRef]
- Moldoveanu, G.M.; Minea, A.A.; Huminic, G.; Huminic, A. Al2O3/TiO2 hybrid nanofluids thermal conductivity. J. Therm. Anal. Calorim. 2019, 137, 583–592. [Google Scholar] [CrossRef]
- Esfe, M.H.; Saedodin, S.; Yan, W.-M.; Afrand, M.; Sina, N. Study on thermal conductivity of water-based nanofluids with hybrid suspensions of CNTs/Al2O3 nanoparticles. J. Therm. Anal. Calorim. 2016, 124, 455–460. [Google Scholar] [CrossRef]
- Moldoveanu, G.M.; Ibanescu, C.; Danu, M.; Minea, A.A. Viscosity estimation of Al2O3, SiO2 nanofluids and their hybrid: An experimental study. J. Mol. Liq. 2018, 253, 188–196. [Google Scholar] [CrossRef]
- Maxwell, J.C. A Treatise on Electricity and Magnetism: Pt. III. Magnetism. pt. IV. Electromagnetism; Clarendon Press: Oxford, UK, 1881; Volume 2, Available online: https://www.aproged.pt/biblioteca/MaxwellII.pdf (accessed on 31 December 2023).
- Hamilton, R.L.; Crosser, O.K. Thermal conductivity of heterogeneous two component systems. Ind. Eng. Chem. Fundam. 1962, 1, 187–191. [Google Scholar] [CrossRef]
- Koo, J.; Kleinstreuer, C. A new thermal conductivity model for nanofluids. J. Nanoparticle Res. 2004, 6, 577–588. [Google Scholar] [CrossRef]
- Sundar, L.S.; Mesfin, S.; Ramana, E.V.; Said, Z.; Sousa, A.C. Experimental investigation of thermo-physical properties, heat transfer, pumping power, entropy generation, and exergy efficiency of nanodiamond + Fe3O4/60:40% water-ethylene glycol hybrid nanofluid flow in a tube. Therm. Sci. Eng. Prog. 2021, 21, 100799. [Google Scholar] [CrossRef]
- Esfahani, J.; Safaei, M.R.; Goharimanesh, M.; de Oliveira, L.R.; Goodarzi, M.; Shamshirband, S.; Filho, E.P.B. Comparison of experimental data, modelling and non-linear regression on transport properties of mineral oil based nanofluids. Powder Technol. 2017, 317, 458–470. [Google Scholar] [CrossRef]
- Rostamian, S.H.; Biglari, M.; Saedodin, S.; Esfe, M.H. An inspection of thermal conductivity of CuO-SWCNTS hybrid nanofluid versus temperature and concentration using experimental data, ANN modelling and new correlation. J. Mol. Liq. 2017, 231, 364–369. [Google Scholar] [CrossRef]
- Ahmadi, M.H.; Nazari, M.A.; Ghasempour, R.; Madah, H.; Shafii, M.B.; Ahmadi, M.A. Thermal conductivity ratio prediction of Al2O3/water nanofluid by applying connectionist methods. Colloids Surf. A Physicochem. Eng. Asp. 2018, 541, 154–164. [Google Scholar] [CrossRef]
- Alade, I.O.; Oyehan, T.A.; Popoola, I.K.; Olatunji, S.O.; Bagudu, A. Modeling thermal conductivity enhancement of metal and metallic oxide nanofluids using support vector regression. Adv. Powder Technol. 2018, 29, 157–167. [Google Scholar] [CrossRef]
- Esfe, M.H.; Esfandeh, S.; Afrand, M.; Rejvani, M.; Rostamian, S.H. Experimental evaluation, new correlation proposing and ANN modeling of thermal properties of EG based hybrid nanofluid containing zno-dwcnt nanoparticles for internal combustion engines applications. Appl. Therm. Eng. 2018, 133, 452–463. [Google Scholar] [CrossRef]
- Ahmadi, M.H.; Nazari, M.A.; Mahian, O.; Ghasempour, R. A proposed model to predict thermal conductivity ratio of Al2O3/EG nanofluid by applying least squares support vector machine (LSSVM) and genetic algorithm as a connectionist approach. J. Therm. Anal. Calorim. 2019, 135, 271–281. [Google Scholar] [CrossRef]
- Akhgar, A.; Toghraie, D.; Sina, N.; Afrand, M. Developing dissimilar artificial neural networks (ANNs) to prediction the thermal conductivity of MWCNT-TiO2/water-ethylene glycol hybrid nanofluid. Powder Technol. 2019, 355, 602–610. [Google Scholar] [CrossRef]
- Shahsavar, A.; Khanmohammadi, S.; Karimipour, A.; Goodarzi, M. A novel comprehensive experimental study concerned synthesizes and prepare liquid paraffin-Fe3O4 mixture to develop models for both thermal conductivity & viscosity: A new approach of GMDH type of neural network. Int. J. Heat Mass Transf. 2019, 131, 432–441. [Google Scholar] [CrossRef]
- Rostami, S.; Kalbasi, R.; Sina, N.; Goldanlou, A.S. Forecasting the thermal conductivity of a nanofluid using artificial neural networks. J. Therm. Anal. Calorim. 2021, 145, 2095–2104. [Google Scholar] [CrossRef]
- Sharma, P.; Ramesh, K.; Parameshwaran, R.; Deshmukh, S.S. Thermal conductivity prediction of titania-water nanofluid: A case study using different machine learning algorithms. Case Stud. Therm. Eng. 2022, 30, 101658. [Google Scholar] [CrossRef]
- Sahin, F.; Genc, O.; Gökcek, M.; Çolak, A.B. An experimental and new study on thermal conductivity and zeta potential of Fe3O4/water nanofluid: Machine learning modeling and proposing a new correlation. Powder Technol. 2023, 420, 118388. [Google Scholar] [CrossRef]
- Martyr, A.; Plint, M. Engine Testing: The Design, Building, Modification and Use of Powertrain Test Facilities; Elsevier: Amsterdam, The Netherlands, 2012. [Google Scholar] [CrossRef]
- Phuoc, T.X.; Massoudi, M. Experimental observations of the effects of shear rates and particle concentration on the viscosity of Fe2O3–deionized water nanofluids. Int. J. Therm. Sci. 2009, 48, 1294–1301. [Google Scholar] [CrossRef]
- Einstein, A. A new determination of molecular dimensions. Ann. Phys. 1906, 19, 289–306. [Google Scholar] [CrossRef]
- Andrade, E.N.D.C. The viscosity of liquids. Nature 1930, 125, 309–310. [Google Scholar] [CrossRef]
- Batchelor, G.K. The effect of brownian motion on the bulk stress in a suspension of spherical particles. J. Fluid Mech. 1977, 83, 97–117. [Google Scholar] [CrossRef]
- Bicerano, J.; Douglas, J.F.; Brune, D.A. Model for the viscosity of particle dispersions. J. Macromol. Sci. Part C Polym. Rev. 1999, 39, 561–642. [Google Scholar] [CrossRef]
- Vajjha, R.S. Measurements of Thermophysical Properties of Nanofluids and Computation of Heat Transfer Characteristics. Ph.D. Thesis, University of Alaska Fairbanks, Fairbanks, AK, USA, 2008. [Google Scholar]
- Alrashed, A.A.; Gharibdousti, M.S.; Goodarzi, M.; de Oliveira, L.R.; Safaei, M.R.; Filho, E.P.B. Effects on thermophysical properties of carbon based nanofluids: Experimental data, modelling using regression, ANFIS and ANN. Int. J. Heat Mass Transf. 2018, 125, 920–932. [Google Scholar] [CrossRef]
- Hemmat Esfe, M.; Rostamian, H.; Esfandeh, S.; Afrand, M. Modeling and prediction of rheological behavior of Al2O3-mwcnt/5w50 hybrid nano-lubricant by artificial neural network using experimental data. Phys. A Stat. Mech. Its Appl. 2018, 510, 625–634. [Google Scholar] [CrossRef]
- Demirpolat, A.B.; Das, M. Prediction of viscosity values of nanofluids at different pH values by alternating decision tree and multilayer perceptron methods. Appl. Sci. 2019, 9, 1288. [Google Scholar] [CrossRef]
- Ghaffarkhah, A.; Bazzi, A.; Dijvejin, Z.A.; Talebkeikhah, M.; Moraveji, M.K.; Agin, F. Experimental and numerical analysis of rheological characterization of hybrid nano-lubricants containing COOH-Functionalized MWCNTs and oxide nanoparticles. Int. Commun. Heat Mass Transf. 2019, 101, 103–115. [Google Scholar] [CrossRef]
- Toghraie, D.; Sina, N.; Jolfaei, N.A.; Hajian, M.; Afrand, M. Designing an artificial neural network (ANN) to predict the viscosity of silver/ethylene glycol nanofluid at different temperatures and volume fraction of nanoparticles. Phys. A Stat. Mech. Its Appl. 2019, 534, 122142. [Google Scholar] [CrossRef]
- Ahmadi, M.H.; Mohseni-Gharyehsafa, B.; Ghazvini, M.; Goodarzi, M.; Jilte, R.D.; Kumar, R. Comparing various machine learning approaches in modeling the dynamic viscosity of CuO/water nanofluid. J. Therm. Anal. Calorim. 2020, 139, 2585–2599. [Google Scholar] [CrossRef]
- Gholizadeh, M.; Jamei, M.; Ahmadianfar, I.; Pourrajab, R. Prediction of nanofluids viscosity using random forest (RF) approach. Chemom. Intell. Lab. Syst. 2020, 201, 104010. [Google Scholar] [CrossRef]
- Kanti, P.; Sharma, K.V.; Yashawantha, K.M.; Dmk, S. Experimental determination for viscosity of fly ash nanofluid and fly ash-Cu hybrid nanofluid: Prediction and optimization using artificial intelligent techniques. Energy Sources Part A Recover. Util. Environ. Eff. 2021, 1–20. [Google Scholar] [CrossRef]
- Dai, X.; Andani, H.T.; Alizadeh, A.; Abed, A.M.; Smaisim, G.F.; Hadrawi, S.K.; Karimi, M.; Shamsborhan, M.; Toghraie, D. Using gaussian process regression (GPR) models with the matern covariance function to predict the dynamic viscosity and torque of SiO2/ethylene glycol nanofluid: A machine learning approach. Eng. Appl. Artif. Intell. 2023, 122, 106107. [Google Scholar] [CrossRef]
- Freire, E. Differential Scanning Calorimetry; Humana Press: Totowa, NJ, USA, 1995; pp. 191–218. [Google Scholar] [CrossRef]
- Higano, M.; Miyagawa, A.; Saigou, K.; Masuda, H.; Miyashita, H. Measuring the specific heat capacity of magnetic fluids using a differential scanning calorimeter. Int. J. Thermophys. 1999, 20, 207–215. [Google Scholar] [CrossRef]
- Tiznobaik, H.; Shin, D. Enhanced specific heat capacity of high-temperature molten salt-based nanofluids. Int. J. Heat Mass Transf. 2013, 57, 542–548. [Google Scholar] [CrossRef]
- Shahrul, I.; Mahbubul, I.; Khaleduzzaman, S.; Saidur, R.; Sabri, M. A comparative review on the specific heat of nanofluids for energy perspective. Renew. Sustain. Energy Rev. 2014, 38, 88–98. [Google Scholar] [CrossRef]
- Pak, B.C.; Cho, Y.I. Hydrodynamic and heat transfer study of dispersed fluids with submicron metallic oxide particles. Exp. Heat Transf. 1998, 11, 151–170. [Google Scholar] [CrossRef]
- Xuan, Y.; Roetzel, W. Conceptions for heat transfer correlation of nanofluids. Int. J. Heat Mass Transf. 2000, 43, 3701–3707. [Google Scholar] [CrossRef]
- Sundar, L.S.; Singh, M.K.; Sousa, A.C. Turbulent heat transfer and friction factor of nanodiamond-nickel hybrid nanofluids flow in a tube: An experimental study. Int. J. Heat Mass Transf. 2018, 117, 223–234. [Google Scholar] [CrossRef]
- Alade, I.O.; Rahman, M.A.A.; Saleh, T.A. Predicting the specific heat capacity of alumina/ethylene glycol nanofluids using support vector regression model optimized with bayesian algorithm. Sol. Energy 2019, 183, 74–82. [Google Scholar] [CrossRef]
- Hassan, M.A.; Banerjee, D. A soft computing approach for estimating the specific heat capacity of molten salt-based nanofluids. J. Mol. Liq. 2019, 281, 365–375. [Google Scholar] [CrossRef]
- Alade, I.O.; Rahman, M.A.A.; Abbas, Z.; Yaakob, Y.; Saleh, T.A. Application of support vector regression and artificial neural network for prediction of specific heat capacity of aqueous nanofluids of copper oxide. Sol. Energy 2020, 197, 485–490. [Google Scholar] [CrossRef]
- Daneshfar, R.; Bemani, A.; Hadipoor, M.; Sharifpur, M.; Ali, H.M.; Mahariq, I.; Abdeljawad, T. Estimating the heat capacity of non-newtonian ionanofluid systems using ann, anfis, and sgb tree algorithms. Appl. Sci. 2020, 10, 6432. [Google Scholar] [CrossRef]
- Adun, H.; Kavaz, D.; Wole-Osho, I.; Dagbasi, M. Synthesis of Fe3O4-Al2O3-ZnO/water ternary hybrid nanofluid: Investigating the effects of temperature, volume concentration and mixture ratio on specific heat capacity, and development of hybrid machine learning for prediction. J. Energy Storage 2021, 41, 102947. [Google Scholar] [CrossRef]
- Jamei, M.; Karbasi, M.; Olumegbon, I.A.; Mosharaf-Dehkordi, M.; Ahmadianfar, I.; Asadi, A. Specific heat capacity of molten salt-based nanofluids in solar thermal applications: A paradigm of two modern ensemble machine learning methods. J. Mol. Liq. 2021, 335, 116434. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, X. Machine learning specific heat capacities of nanofluids containing CuO and Al2O3. AIChE J. 2021, 67, e17289. [Google Scholar] [CrossRef]
- Said, Z.; Sharma, P.; Elavarasan, R.M.; Tiwari, A.K.; Rathod, M.K. Exploring the specific heat capacity of water-based hybrid nanofluids for solar energy applications: A comparative evaluation of modern ensemble machine learning techniques. J. Energy Storage 2022, 54, 105230. [Google Scholar] [CrossRef]
- Mcculloch, W.S.; Pitts, W.H. A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biophys. 1943, 5, 115–133. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Ruder, S. An overview of gradient descent optimization algorithms. arXiv 2016, arXiv:1609.04747. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Adv. Neural Inf. Process. Syst. 2012, 25, 84–90. Available online: https://proceedings.neurips.cc/paper_files/paper/2012/file/c399862d3b9d6b76c8436e924a68c45b-Paper.pdf (accessed on 31 December 2023). [CrossRef]
- Jordan, M.I.; Mitchell, T.M. Machine learning: Trends, perspectives, and prospects. Science 2015, 349, 255–260. [Google Scholar] [CrossRef]
- Chen, S.; Cowan, C.; Grant, P. Orthogonal least squares learning algorithm for radial basis function networks. IEEE Trans. Neural Netw. 1991, 2, 302–309. [Google Scholar] [CrossRef]
- Broomhead, D.; Lowe, D. Multivariable functional interpolation and adaptive networks. Complex Syst. 1988, 2, 321–355. Available online: https://sci2s.ugr.es/keel/pdf/algorithm/articulo/1988-Broomhead-CS.pdf (accessed on 31 December 2023).
- Ivakhnenko, A.G. The group method of data handling, a rival of the method of stochastic approximation. Sov. Autom. Control 1968, 13, 43–55. [Google Scholar]
- Vapnik, V.N. A note on one class of perceptrons. Automat. Rem. Control. 1964, 25, 821–837. Available online: https://classes.engr.oregonstate.edu/eecs/fall2023/ai534-400/extra/vapnik-1964.pdf (accessed on 31 December 2023).
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Boser, B.E.; Guyon, I.M.; Vapnik, V.N. A training algorithm for optimal margin classifiers. In Proceedings of the Fifth Annual Workshop on Computational Learning Theory, Pittsburgh, PA, USA, 27–29 July 1992; pp. 144–152. [Google Scholar] [CrossRef]
- Cohn, T.; Preotiuc-Pietro, D.; Lawrence, N. Gaussian Processes for Natural Language Processing. In Proceedings of the 52nd Annual Meeting of the Association for Computational Linguistics: Tutorials, Association for Computational Linguistics, Baltimore, MD, USA, 22 June 2014; pp. 1–3. [Google Scholar] [CrossRef]
- Wistuba, M.; Rawat, A. Scalable multi-class bayesian support vector machines for structured and unstructured data. arXiv 2018, arXiv:1806.02659. [Google Scholar] [CrossRef]
- Law, T.; Shawe-Taylor, J. Practical bayesian support vector regression for financial time series prediction and market condition change detection. Quant. Financ. 2017, 17, 1403–1416. [Google Scholar] [CrossRef]
- Xu, H.; Song, S.; Li, J.; Guo, T. Hybrid model for daily runoff interval predictions based on bayesian inference. Hydrol. Sci. J. 2023, 68, 62–75. [Google Scholar] [CrossRef]
- Nurwaha, D. Comparison of kernel functions of support vector machines: A case study for the solar cell output power prediction. Int. J. Energy Appl. Technol. 2020, 7, 1–6. [Google Scholar] [CrossRef]
- Wirasati, I.; Rustam, Z.; Aurelia, J.E.; Hartini, S.; Saragih, G.S. Comparison some of kernel functions with support vector machines classifier for thalassemia dataset. IAES Int. J. Artif. Intell. 2021, 10, 430. [Google Scholar] [CrossRef]
- Thorstan, J. Text categorization with support vector machines: Learning with many relevant features. In Proceedings of the European Conference on Machine Learning, Chemnitz, Germany, 21–23 April 1998; Springer: Berlin/Heidelberg, Germany, 1998; pp. 137–142. [Google Scholar] [CrossRef]
- Burges, C.J.C. A tutorial on support vector machines for pattern recognition. Data Min. Knowl. Discov. 1998, 2, 121–167. [Google Scholar] [CrossRef]
- Scholkopf, B.; Smola, A.J.; Williamson, R.C.; Bartlett, P.L. New Support Vector Algorithms. Neural Comput. 2000, 12, 1207–1245. [Google Scholar] [CrossRef]
- Breiman, L. Classification and Regression Trees; Routledge: Boca Raton, FL, USA, 1984. [Google Scholar] [CrossRef]
- Quinlan, J.R. Induction of decision trees. Mach. Learn. 1986, 1, 81–106. [Google Scholar] [CrossRef]
- Halalsheh, N.; Alshboul, O.; Shehadeh, A.; Al Mamlook, R.E.; Al-Othman, A.; Tawalbeh, M.; Almuflih, A.S.; Papelis, C. Breakthrough curves prediction of selenite adsorption on chemically modified zeolite using boosted decision tree algorithms for water treatment applications. Water 2022, 14, 2519. [Google Scholar] [CrossRef]
- Freund, Y.; Mason, L. The alternating decision tree learning algorithm. In Proceedings of the 16th International Conference on Machine Learning, San Francisco, CA, USA, 27–30 June 1999; Available online: https://cseweb.ucsd.edu/~yfreund/papers/atrees.pdf (accessed on 4 March 2024).
- Nepomuceno-Chamorro, I.A.; Aguilar-Ruiz, J.S.; Riquelme, J.C. Inferring gene regression networks with model trees. BMC Bioinform. 2010, 11, 517. [Google Scholar] [CrossRef] [PubMed]
- Prasetyaningrum, P.T.; Pratama, I.; Chandra, A.Y. Implementation of Machine Learning to Determine the Best Employees Using Random Forest Method. Int. J. Comput. Netw. Secur. Inf. Syst. 2021, 2, 53–59. [Google Scholar] [CrossRef]
- Padmaja, B.; Prasa, V.; Sunitha, K. A novel random split point procedure using extremely randomized (extra) trees ensemble method for human activity recognition. EAI Endorsed Trans. Pervasive Heal. Technol. 2020, 6, e5. [Google Scholar] [CrossRef]
- Chen, S.; Shen, B.; Wang, X.; Yoo, S.-J. A strong machine learning classifier and decision stumps based hybrid adaboost classification algorithm for cognitive radios. Sensors 2019, 19, 5077. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd Acm Sigkdd International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar] [CrossRef]
- Holland, J.H. Genetic Algorithms. Sci. Am. 1992, 267, 66–73. [Google Scholar] [CrossRef]
- Goldberg, D.E. Genetic algorithms in search, Optimization. Mach. Learn. 1988, 3, 95–99. [Google Scholar] [CrossRef]
- Mitchell, M. An Introduction to Genetic Algorithms; MIT Press: Cambridge, MA, USA, 1998. [Google Scholar] [CrossRef]
- Gandomi, A.H.; Alavi, A.H. Multi-stage genetic programming: A new strategy to nonlinear system modeling. Inf. Sci. 2011, 181, 5227–5239. [Google Scholar] [CrossRef]
- Garg, A.; Garg, A.; Tai, K.; Sreedeep, S. An integrated srm-multi-gene genetic programming approach for prediction of factor of safety of 3-d soil nailed slopes. Eng. Appl. Artif. Intell. 2014, 30, 30–40. [Google Scholar] [CrossRef]
- Jang, J.-S.R. Anfis: Adaptive-network-based fuzzy inference system. IEEE Trans. Syst. Man Cybern. 1993, 23, 665–685. [Google Scholar] [CrossRef]
- Jang, J.-S.R.; Sun, C.-T.; Mizutani, E. Neuro-fuzzy and soft computing a computational approach to learning and machine intelligence [book review]. IEEE Trans. Autom. Control 1997, 42, 1482–1484. [Google Scholar] [CrossRef]
- Amemiya, T. Non-Linear Regression Models. In Handbook of Econometrics; Elsevier: Amsterdam, The Netherlands, 1983; Volume 1, Chapter 6; pp. 333–389. [Google Scholar] [CrossRef]
- Friedman, J.H. Multivariate Adaptive Regression Splines. Ann. Stat. 1991, 19, 1–67. [Google Scholar] [CrossRef]
- Wilson, A.G.; Knowles, D.A.; Ghahramani, Z. Gaussian process regression networks. arXiv 2011, arXiv:1110.4411. Available online: https://arxiv.org/pdf/1110.4411.pdf (accessed on 31 December 2023).
- Yu, W.; Choi, S. The Role of Interfacial Layers in the Enhanced Thermal Conductivity of Nanofluids: A Renovated Maxwell Model. J. Nanoparticle Res. 2003, 5, 167–171. [Google Scholar] [CrossRef]
- Jeffrey, D.J. Conduction through a random suspension of spheres. Proc. R. Soc. Lond. A Math. Phys. Sci. 1973, 1602, 355–367. [Google Scholar] [CrossRef]
- Maïga, S.E.B.; Nguyen, C.T.; Galanis, N.; Roy, G. Heat transfer behaviours of nanofluids in a uniformly heated tube. Superlattices Microstruct. 2004, 35, 543–557. [Google Scholar] [CrossRef]
- Esfe, M.H.; Afrand, M.; Yan, W.-M.; Yarmand, H.; Toghraie, D.; Dahari, M. Effects of temperature and concentration on rheological behavior of MWCNTs/SiO2(20–80)-SAE40 hybrid nano-lubricant. Int. Commun. Heat Mass Transf. 2016, 76, 133–138. [Google Scholar] [CrossRef]
- Wang, X.; Xu, X.; Choi, S.U.S. Thermal conductivity of nanoparticle—Fluid mixture. J. Thermophys. Heat Transf. 1999, 13, 474–480. [Google Scholar] [CrossRef]
- Ma, T.; Guo, Z.; Lin, M.; Wang, Q. Recent trends on nanofluid heat transfer machine learning research applied to renewable energy. Renew. Sustain. Energy Rev. 2021, 138, 110494. [Google Scholar] [CrossRef]
- Zhou, S.-Q.; Ni, R. Measurement of the specific heat capacity of water-based Al2O3 nanofluid. Appl. Phys. Lett. 2008, 92, 093123. [Google Scholar] [CrossRef]
- Mendez, M.; Ianiro, A.; Noack, B.; Brunton, S. (Eds.) Data-Driven Fluid Mechanics: Combining First Principles and Machine Learning; Cambridge University Press: Cambridge, UK, 2023. [Google Scholar] [CrossRef]
- Adun, H.; Wole-Osho, I.; Okonkwo, E.C.; Kavaz, D.; Dagbasi, M. A critical review of specific heat capacity of hybrid nanofluids for thermal energy applications. J. Mol. Liq. 2021, 340, 116890. [Google Scholar] [CrossRef]
| Authors | Formula |
|---|---|
| Maxwell, 1881 [84] | |
| Hamilton and Crosser, 1962 [85] | |
| Koo and Kleinstreuer, 2004 [86] | |
| Sundar et al., 2021 [87] |
| Authors | Equation |
|---|---|
| Einstein, 1906 [101] | |
| Andrade, 1930 [102] | |
| Batchelor, 1977 [103] | |
| Bicerano et al., 1999 [104] | |
| Vajjha and Das, 2008 [105] |
| Authors | Formula |
|---|---|
| Pak et al. [119] | |
| Xuan et al. [120] | |
| Sundar et al. [121] |
| Algorithm | Advantages | Disadvantages | Applicability |
|---|---|---|---|
| ANN |
|
| Works well with large amounts of sample data for image and speech recognition, time series prediction, and natural language processing. |
| SVM |
|
| Effective for text and hypertext categorization, image classification, and bioinformatics, especially with a clear margin of separation. |
| DT |
|
| Suitable for classification and regression tasks, customer segmentation, and feature selection where data can be split into clear decisions. |
| GA |
|
| Ideal for optimization problems, scheduling and planning, and machine learning parameter tuning where traditional approaches are inefficient. |
| ANFIS |
|
| Applicable in control systems, time series prediction, and pattern and sequence recognition where fuzzy logic can enhance model interpretability. |
| Regression |
|
| Works well in predicting sales and market trends, risk assessment in finance, and evaluating trends in data with linear relationships. |
| Authors | Method | Nanofluid | Input Variables | MSE | R2 |
|---|---|---|---|---|---|
| Esfahani et al., 2017 [88] | ANFIS | Ag/MO | volume concentration and type of nanoparticles | 3.79 × 10−4 | 0.989 |
| Esfahani et al., 2017 [88] | ANFIS | Cu/MO | ‘do’ | 2.88 × 10−4 | 0.979 |
| Esfahani et al., 2017 [88] | ANFIS | TiO2/MO | ‘do’ | 2.03 × 10−4 | 0.986 |
| Rostamian et al., 2017 [89] | ANN | CuO-SWCNTs/EG water | temperature and solid volume fraction | - | - |
| Ahmadi et al., 2018 [90] | SVM with GA | Al2O3/Water | temperature, size of nanoparticles, volume concentration | 5.5 × 10−4 | 0.783 |
| Alade et al., 2018 [91] | SVM | (Al and Cu) with water, EG, and Transformer Oil | suspension temperature, thermal conductivities of the base fluid and nanoparticles, particle size, and volume fraction | 1.23 | 0.993 |
| Alade et al., 2018 [91] | SVM | (Al2O3 and CuO) with water, EG, and Transformer Oil | ‘do’ | 1.79 | 0.961 |
| Esfe et al., 2018 [92] | ANN | ZnO–DWCNT in EG | nanoparticle concentration, temperature, nanoparticle composition | 5.35 × 10−5 | 0.99 |
| Ahmadi et al., 2019 [93] | SVM with GA | Al2O3/EG | temperature, concentration of nanoparticles, and particle size | 4.59 × 10−5 | 0.99 |
| Akhgar et al., 2019 [94] | ANN | MWCNT–TiO2/Water–EG Hybrid Nanofluid | temperature and volume fraction | 1.02 × 10−5 | - |
| Shahsavar et al., 2019 [95] | GMDH type NN | Fe3O4/paraffin | volume concentration and temperature | 3.2 × 10−4 | 0.96 |
| Rostami et al., 2020 [96] | ANN | MWCNT–Paraffin | mass fraction and temperature | 7.53 × 10−5 | 0.993 |
| Sharma et al., 2022 [97] | GBR | TiO2/Water | temperature, volume fraction, shape, and size of nanoparticles | 0.2 × 10−3 | 0.99 |
| Sharma et al., 2022 [97] | SVR | TiO2/Water | ‘do’ | 0.2× 10−1 | 0.69 |
| Sharma et al., 2022 [97] | DTR | TiO2/Water | ‘do’ | 1.1 × 10−3 | 0.98 |
| Sahin et al., 2023 [98] | ANN | Fe3O4/Water | temperature and concentration | 1.47 × 10−5 | 0.997 |
| Authors | Method | Nanofluid | Input Variables | MSE | R2 |
|---|---|---|---|---|---|
| Esfahani et al., 2017 [88] | ANFIS | Ag/MO | volume concentration of nanoparticles and the type of nanoparticles | 2.21 × 10−5 | 0.977 |
| Esfahani et al., 2017 [88] | ANFIS | Cu/MO | ‘do’ | 3.84 × 10−5 | 0.999 |
| Esfahani et al., 2017 [88] | ANFIS | TiO2/MO | ‘do’ | 1.02 × 10−5 | 0.998 |
| Alrashed et al., 2018 [106] | NLR | MWCNT–COOH/water | temperature and volume fraction | 7.36 × 10−5 | - |
| Alrashed et al., 2018 [106] | NLR | Diamond–COOH/water | ‘do’ | 8.24 × 10−4 | - |
| Alrashed et al., 2018 [106] | ANN | MWCNT–COOH/water | ‘do’ | 3.89 × 10−5 | - |
| Alrashed et al., 2018 [106] | ANN | Diamond–COOH/water | ‘do’ | 8.5 × 10−4 | - |
| Alrashed et al., 2018 [106] | ANFIS | MWCNT–COOH/water | ‘do’ | 1.84 × 10−8 | - |
| Alrashed et al., 2018 [106] | ANFIS | Diamond–COOH/water | ‘do’ | 7.47 × 10−4 | - |
| Esfe et al., 2018 [45] | GA-ANN | CuO/EG | volume concentration and temperature | - | 0.999 |
| Esfe et al., 2018 [107] | ANN | Al2O3– MWCNT/5W50 | temperature, volume fraction, and shear rate | 0.7 × 10−6 | 0.999 |
| Demirpolat and Das, 2019 [108] | ADTree | CuO/(water + ethanol + EG) | Reynolds number, pH, nanoparticle percentage, nanofluid temperature, nanofluid density, and average speed of nanofluids | 5.6 × 10−2 | - |
| Demirpolat and Das, 2019 [108] | MLP | ‘do’ | ‘do’ | 2.3 × 10−2 | - |
| Shahsavar et al., 2019 [95] | GMDH-NN | Fe3O4/liquid paraffin | nanoparticle concentration, temperature, and shear rate | 3.24 × 10−6 | 0.96 |
| Ghaffarkhah et al., 2019 [109] | DT | 80 Vol% (SiO2, Al2O3, MgO, and ZnO) + 20 Vol% COOH-functionalized MWCNTs/SAE 40 Engine oil | temperature and solid volume fraction | - | - |
| Ghaffarkhah et al., 2019 [109] | RBF-ANN | ‘do’ | ‘do’ | - | - |
| Ghaffarkhah et al., 2019 [109] | RF | ‘do’ | ‘do’ | - | - |
| Ghaffarkhah et al., 2019 [109] | SVM | ‘do’ | ‘do’ | - | - |
| Toghraie et al., 2019 [110] | ANN | Ag/EG | temperature and volume fraction of nanoparticles | 6.96 × 10−5 | - |
| Ahmadi et al., 2020 [111] | ANN | CuO/water | size, temperature, and concentration of the nanoparticles | 5.6 × 10−4 | 0.999 |
| Ahmadi et al., 2020 [111] | GMDH | CuO/water | ‘do’ | 6.5 × 10−4 | 0.999 |
| Ahmadi et al., 2020 [111] | MARS | CuO/water | ‘do’ | 1.4 × 10−3 | 0.999 |
| Ahmadi et al., 2020 [111] | M5-Tree | CuO/water | ‘do’ | 1.22 × 10−2 | 0.995 |
| Ahmadi et al., 2020 [111] | MPR | CuO/water | ‘do’ | 1.63 × 10−2 | 0.994 |
| Gholizadeh et al., 2020 [112] | RF | Various nanofluids 1 | temperature, solid volume fraction, viscosity of the base fluid, nanoparticle size, and density of nanoparticles | 1.92 × 10−2 | 0.978 |
| Gholizadeh et al., 2020 [112] | MLP | Various nanofluids 1 | ‘do’ | 1.42 × 10−1 | 0.837 |
| Gholizadeh et al., 2020 [112] | SVR | Various nanofluids 1 | ‘do’ | 9.2 × 10−2 | 0.885 |
| Kanti et al., 2021 [113] | MGGP | (Fly ash)/water | concentration range and temperature range of nanofluids | 3.61 × 10−6 | 0.999 |
| Kanti et al., 2021 [113] | MGGP | (Fly-ash–Cu)/water | ‘do’ | 3.97 × 10−5 | 0.995 |
| Kanti et al., 2021 [113] | ANN | (Fly ash)/water | ‘do’ | 3.17 × 10−6 | 0.999 |
| Kanti et al., 2021 [113] | ANN | (Fly-ash–Cu)/water | ‘do’ | 1.16 × 10−5 | 0.999 |
| Dai et al., 2023 [114] | GPR | SiO2/EG | volume fraction, shear rate, and temperature | 5.76 × 10−2 | 0.996 |
| Authors | Method | Nanofluid | Input Variables | MSE | R2 |
|---|---|---|---|---|---|
| Alade et al., 2019 [122] | BSVR | Al2O3/EG | volume fraction, temperature, SHC of nanoparticles and SHC of EG | 2.2 × 10−5 | 0.999 |
| Hassan and Banerjee, 2019 [123] | ANN | (Al2O3, SiO2, TiO2)/Molten Salt (KNO3 + NaNO3) | temperature and mass fraction | 6.593× 10−2 | 0.999 |
| Alade et al., 2020 [124] | BSVR | CuO/water | SHC of nanoparticles, fluid temperature, volume fraction | 5.29 × 10−6 | 0.999 |
| Alade et al., 2020 [124] | ANN | CuO/water | ‘do’ | 6.25 × 10−6 | 0.999 |
| Daneshfar et al., 2020 [125] | MLP–ANN | Al2O3/IL | nanoparticle concentration, critical temperature, operational temperature, acentric factor, and molecular weight of pure ionic liquids | 1.32 × 10−2 | 0.943 |
| Daneshfar et al., 2020 [125] | ANFIS | Al2O3/IL | ‘do’ | 3.2 × 10−2 | 0.875 |
| Daneshfar et al., 2020 [125] | RBF–ANN | Al2O3/IL | ‘do’ | 2.01 × 10−2 | 0.92 |
| Daneshfar et al., 2020 [125] | SGB tree | Al2O3/IL | ‘do’ | 2.49 × 10−3 | 0.987 |
| Adun et al., 2021 [126] | ANN | Fe3O4–Al2O3–ZnO/water | temperature, volume concentration, and mixture ratio | 480.4338 | 0.942 |
| Adun et al., 2021 [126] | GA-SVR | ‘do’ | ‘do’ | 89.69037 | 0.997 |
| Jamei et al., 2021 [127] | ETR | Molten salt (nitrate)-based nanofluids | solid mass fraction, temperature, SHC of base fluid, mean diameter, and density of nanoparticles | 2.42 × 10−2 | 0.993 |
| Jamei et al., 2021 [127] | ABR | ‘do’ | ‘do’ | 3.44 × 10−2 | 0.990 |
| Jamei et al., 2021 [127] | RF | ‘do’ | ‘do’ | 5.41 × 10−2 | 0.984 |
| Jamei et al., 2021 [127] | BRT | ‘do’ | ‘do’ | 6.29 × 10−2 | 0.981 |
| Zhang and Xu, 2021 [128] | GPR | (Al2O3,CuO)/(water EG) | temperature, SHCs of nanoparticles and base liquids, and nanoparticle volume concentrations | 3.61 × 10−6 | 0.999 |
| Said et al., 2022 [129] | GPR | (metal oxide + MWCNT)/water | volume concentration, temperature range, SHC of base fluid, nanofluid density, base fluid density, and average nanoparticle diameter | 54.06 | 0.995 |
| Said et al., 2022 [129] | XGBoost | (metal oxide + MWCNT)/water | ‘do’ | 98.13 | 0.995 |
| Said et al., 2022 [129] | SVM | (metal oxide + MWCNT)/water | ‘do’ | 97.97 | 0.990 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Basu, A.; Saha, A.; Banerjee, S.; Roy, P.C.; Kundu, B. A Review of Artificial Intelligence Methods in Predicting Thermophysical Properties of Nanofluids for Heat Transfer Applications. Energies 2024, 17, 1351. https://doi.org/10.3390/en17061351
Basu A, Saha A, Banerjee S, Roy PC, Kundu B. A Review of Artificial Intelligence Methods in Predicting Thermophysical Properties of Nanofluids for Heat Transfer Applications. Energies. 2024; 17(6):1351. https://doi.org/10.3390/en17061351
Chicago/Turabian StyleBasu, Ankan, Aritra Saha, Sumanta Banerjee, Prokash C. Roy, and Balaram Kundu. 2024. "A Review of Artificial Intelligence Methods in Predicting Thermophysical Properties of Nanofluids for Heat Transfer Applications" Energies 17, no. 6: 1351. https://doi.org/10.3390/en17061351
APA StyleBasu, A., Saha, A., Banerjee, S., Roy, P. C., & Kundu, B. (2024). A Review of Artificial Intelligence Methods in Predicting Thermophysical Properties of Nanofluids for Heat Transfer Applications. Energies, 17(6), 1351. https://doi.org/10.3390/en17061351







