Numerical Simulation on Two-Phase Ejector with Non-Condensable Gas
Abstract
1. Introduction
2. Numerical Simulation Model
2.1. Governing Equation
2.2. Interfacial Heat and Mass Transfer Model
2.3. Interfacial Momentum Transfer Model
2.4. Turbulence Model
2.5. Geometric Structure and Mesh
2.6. Boundary Conditions and Solution Settings
2.7. Mesh Independence Test and Model Validation
3. Results and Discussion
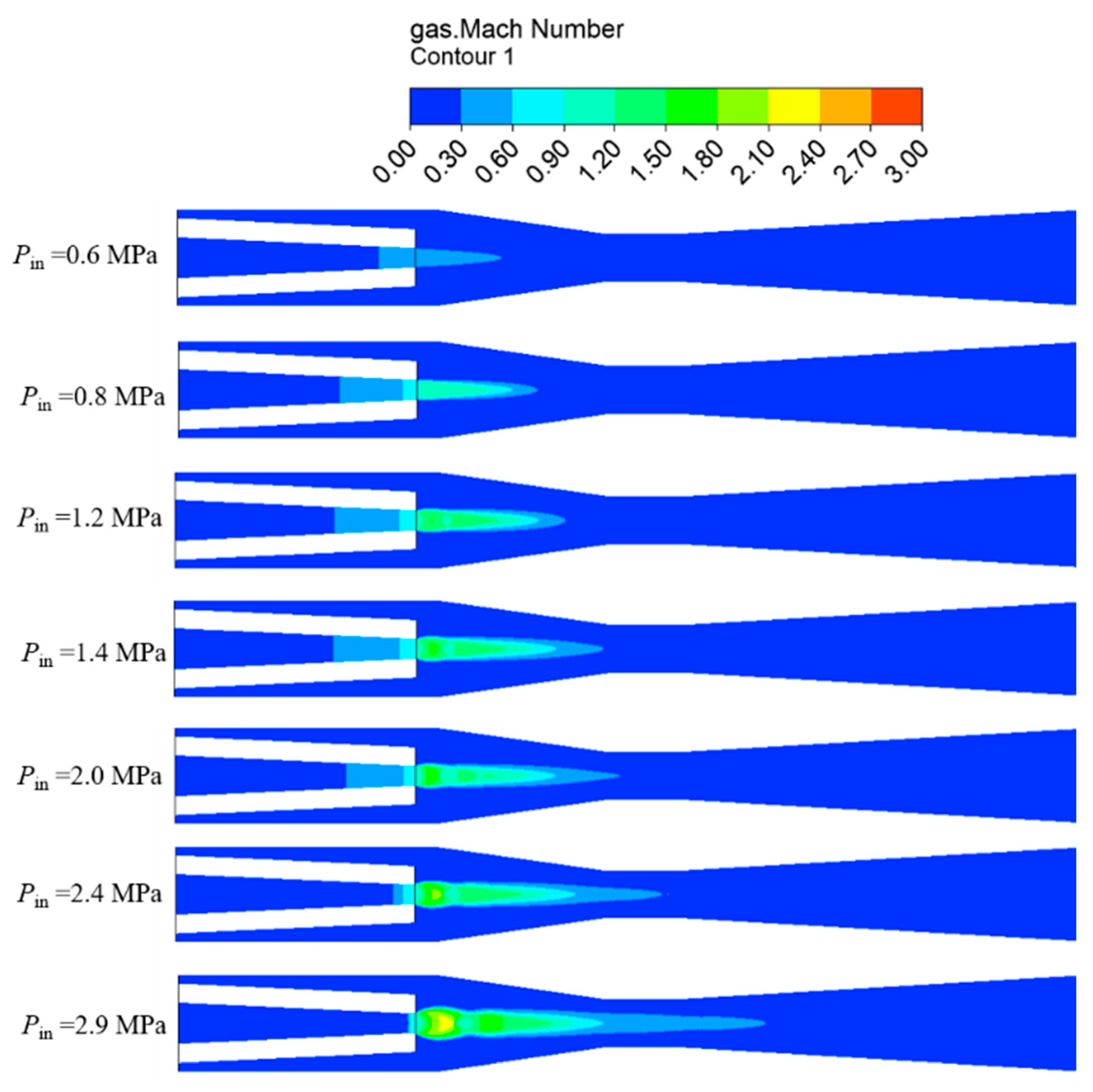
3.1. Analysis of Flow Filed Parameters at Different Steam Inlet Pressures
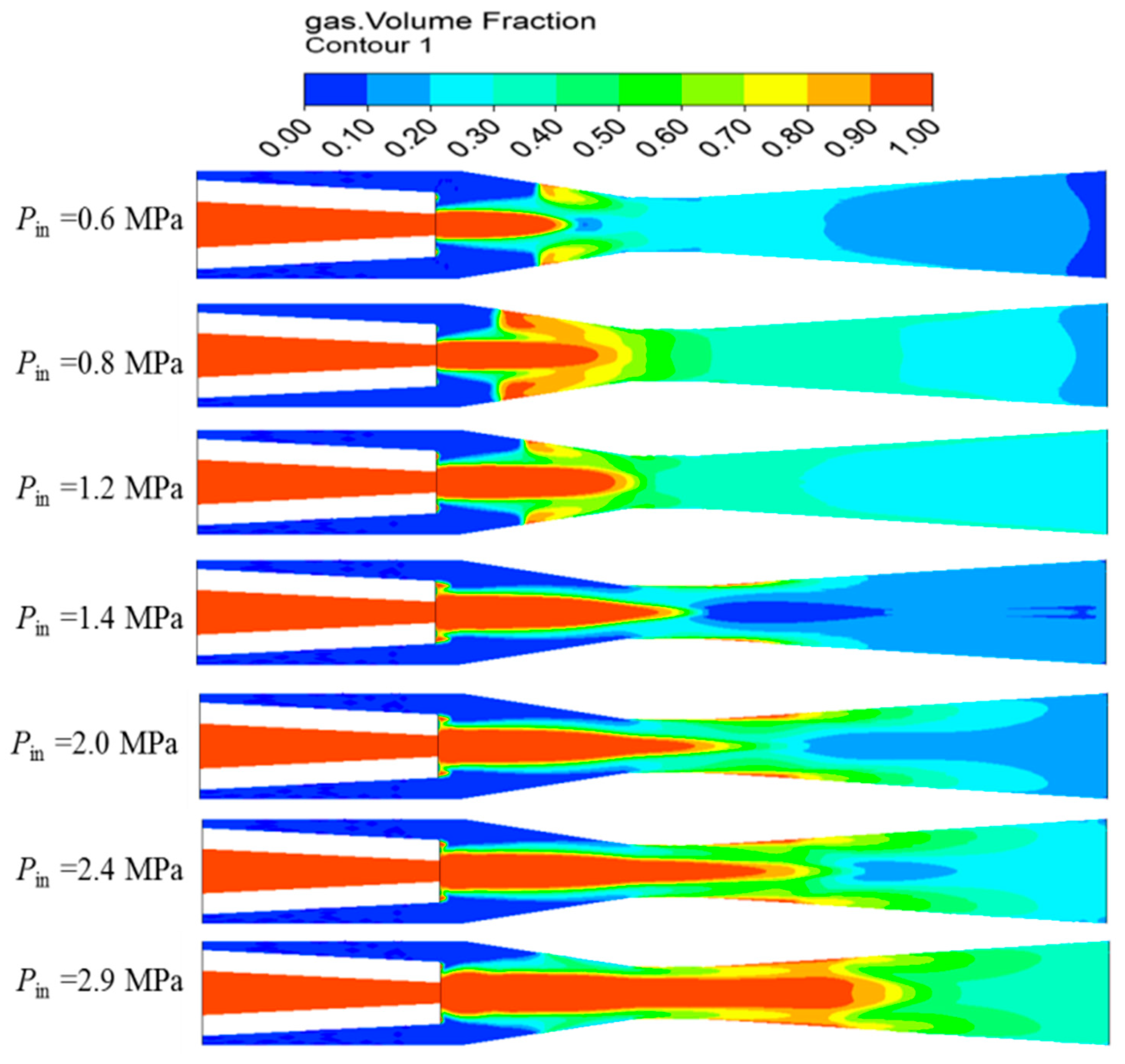
3.1.1. Void Fraction Distribution
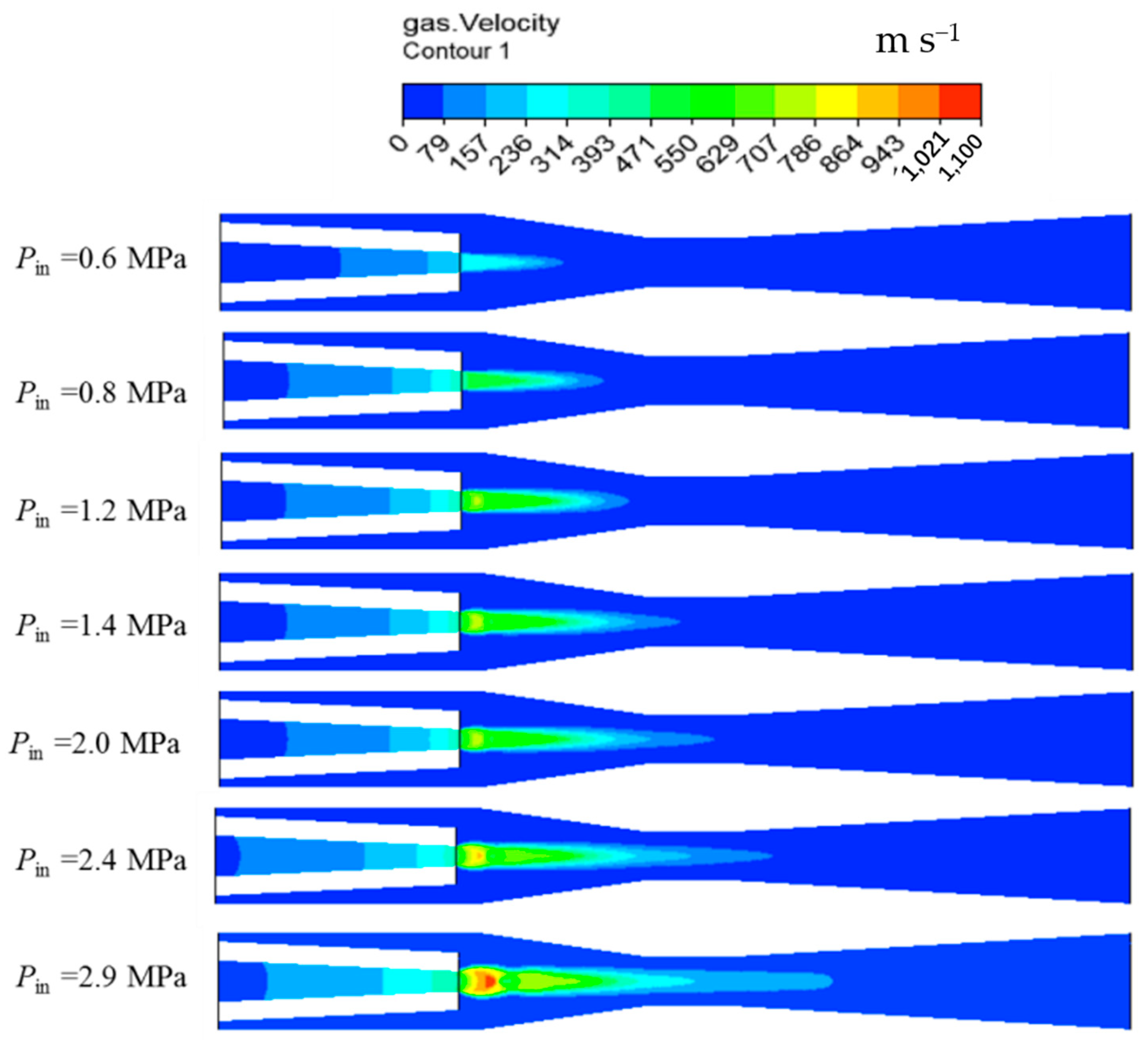
3.1.2. Distribution of Vapor-Liquid Two-Phase at Different Velocity
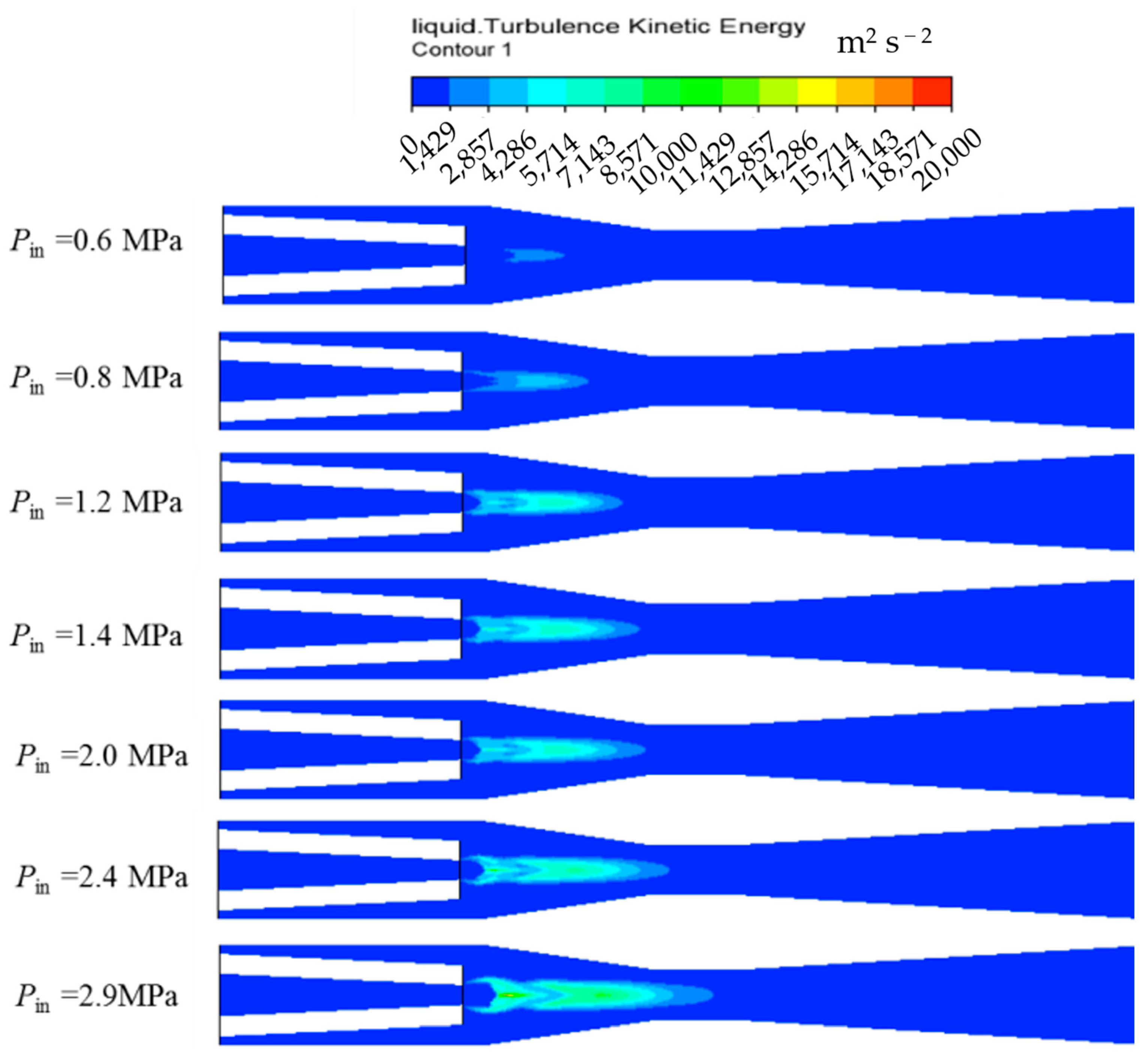
3.1.3. Contours of Turbulent Kinetic Energy
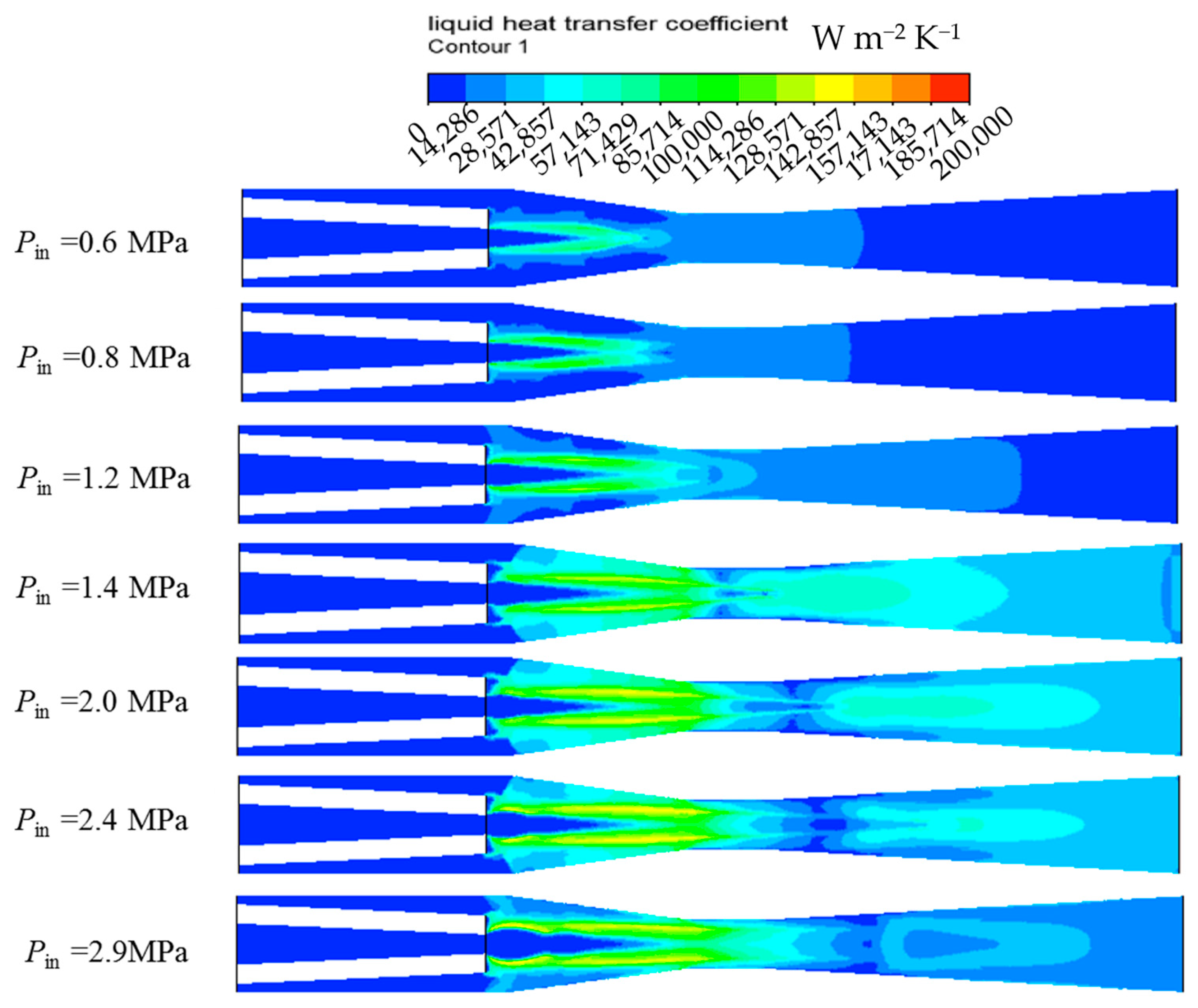
3.2. Analysis of Heat and Mass Transfer Characteristics at Different Steam Inlet Pressures
3.2.1. Heat Transfer Characteristics
3.2.2. Mass Transfer Coefficient
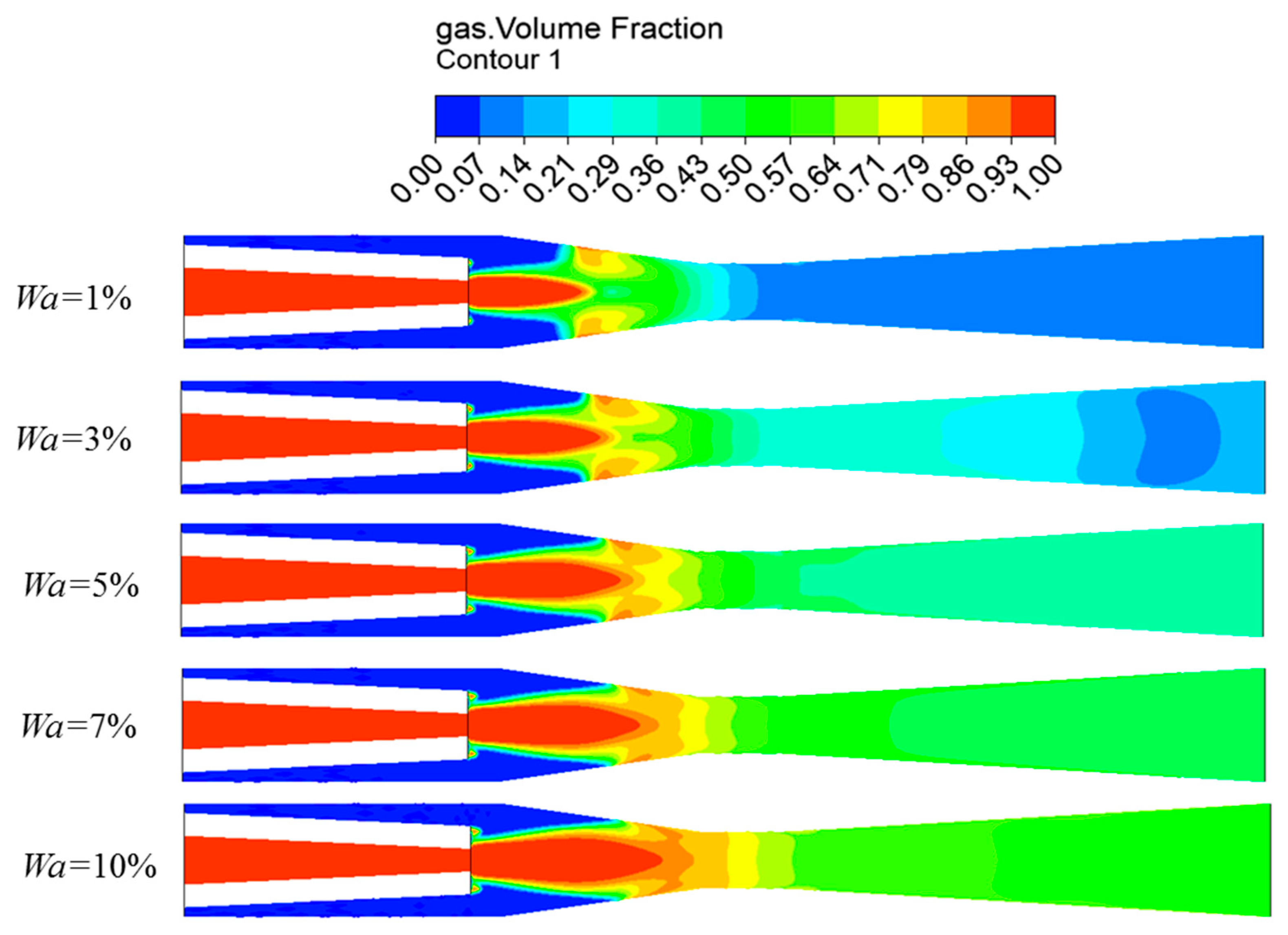
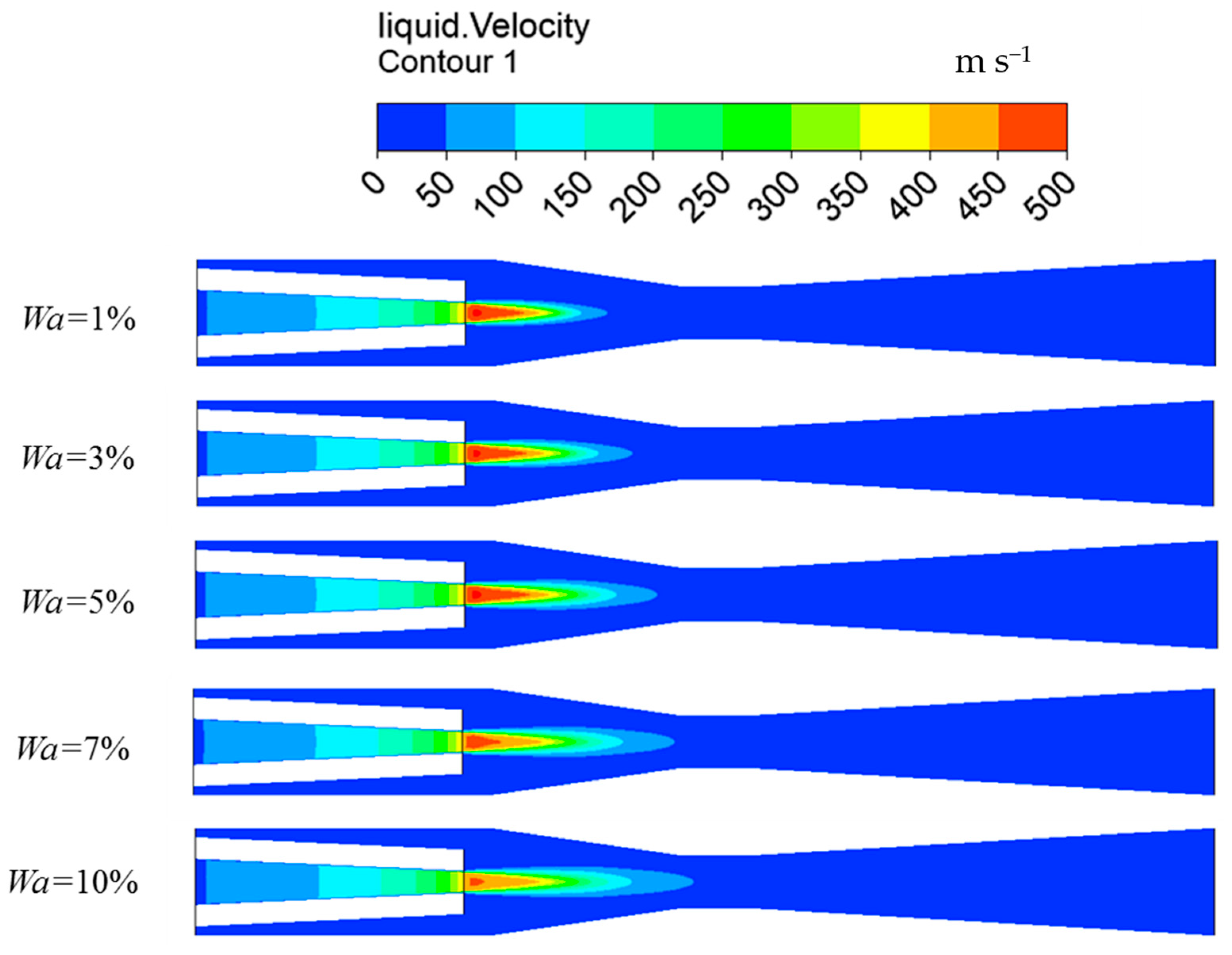
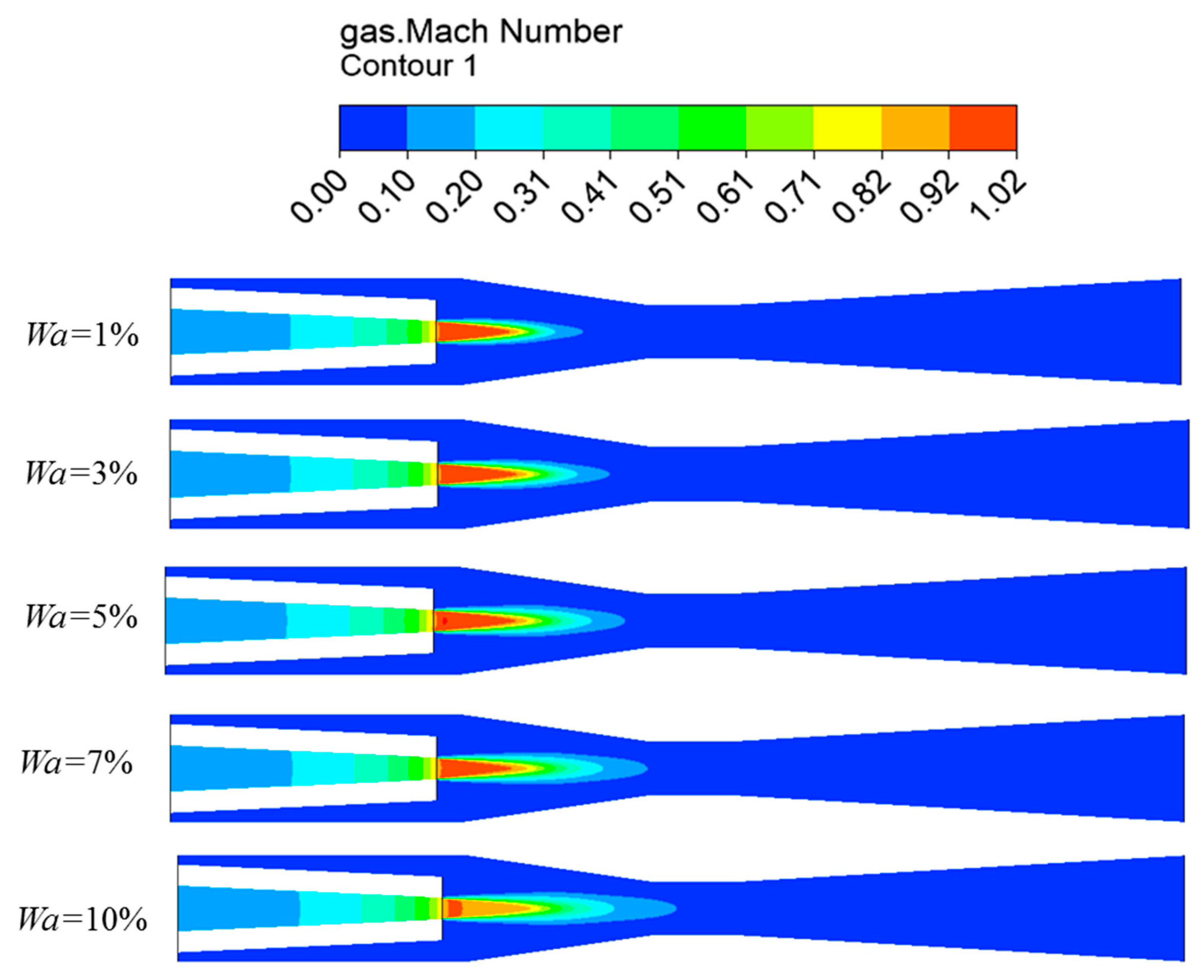
3.3. Analysis of Flow Filed Parameters with Different Non-Condensable Gas Mass Fractions
3.3.1. Void Fraction Distributions
3.3.2. Distribution of Vapor-Liquid Two-Phase at Different Velocities
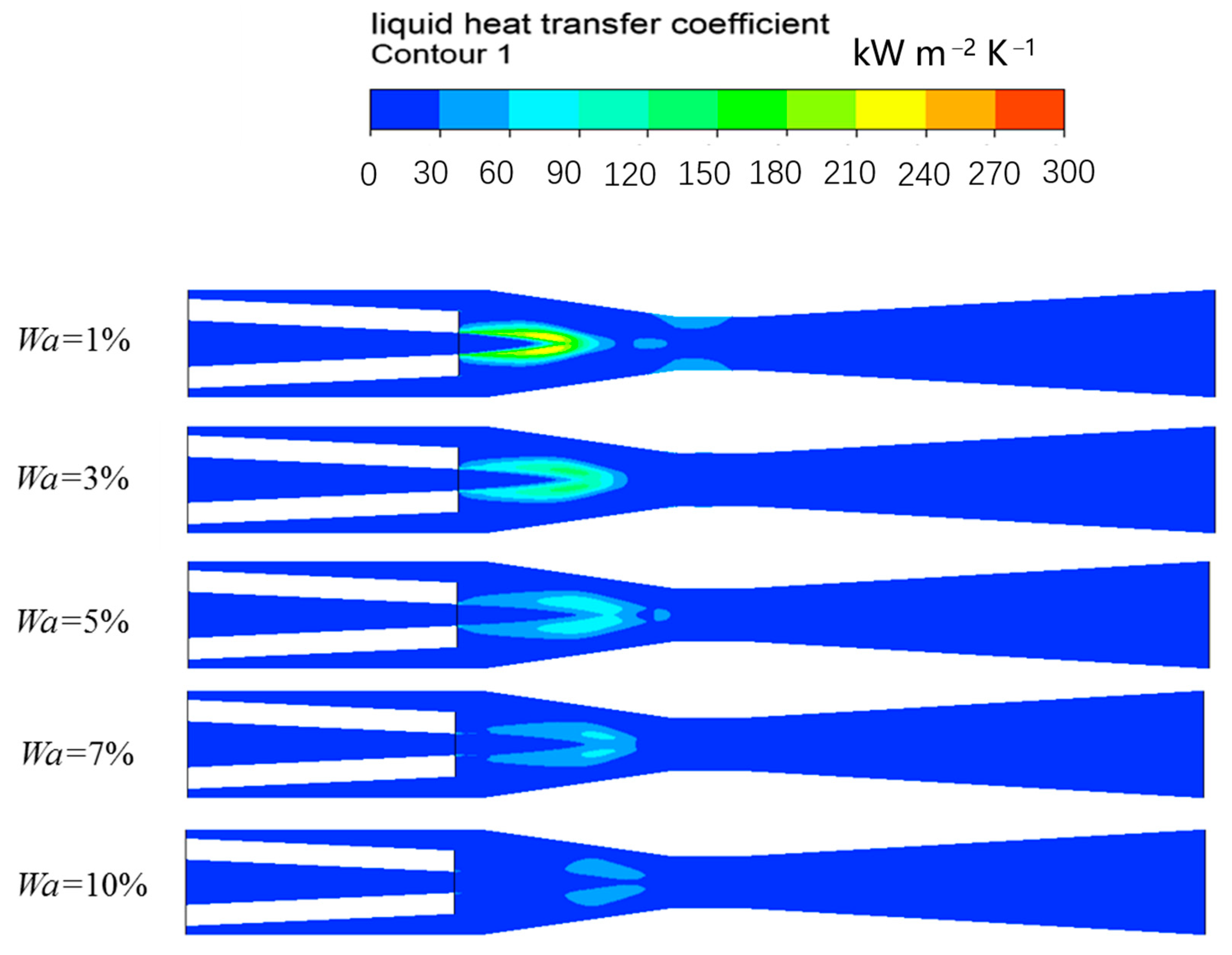
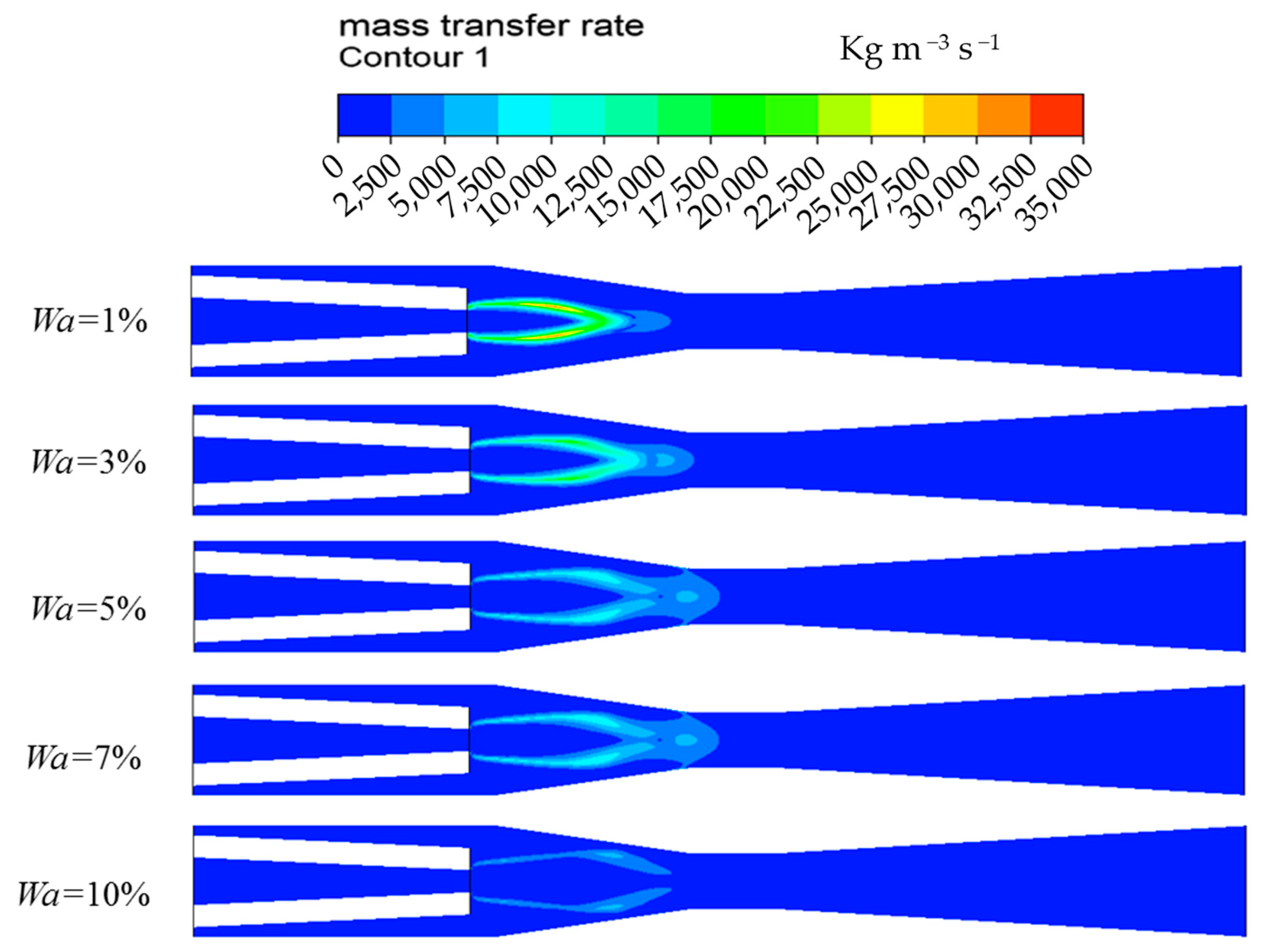
3.4. Analysis of Heat and Mass Transfer Characteristics at Different Non-Condensable Gas Mass Fractions
3.4.1. Heat Transfer Characteristics
3.4.2. Mass Transfer Characteristics
4. Conclusions
- (1)
- The steam plume penetration length increases with the inlet steam pressure. The steam mass flow rate increases with the inlet steam pressure, and a greater interfacial area is needed to condensate the steam. Therefore, the steam plume penetration length also increases.
- (2)
- The maximum velocity of the vapor and liquid phases increases with the inlet steam pressure, resulting in a higher relative Reynolds number, which leads to a higher local heat transfer coefficient. The steam condensation process would be enhanced and the saturation temperature would increase due to higher local pressure.
- (3)
- Non-condensable gas hinders the steam–water direct contact condensation. Increasing the non-condensable gas mass fraction, the interfacial heat transfer would be prevented, and the steam condensation rate and maximum velocity of the vapor and liquid phases decrease, while the penetration length of the steam plume increases.
- (4)
- With the non-condensable gas mass fraction rising from 1% to 10%, the viscosity, density, and thermal conductivity of the mixture of water and air all decrease significantly. The Prandtl number also decreases, which leads to a lower heat transfer coefficient and Nusselt number on the liquid side.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Volume fraction | |
| Density | |
| m | Mass flow rate |
| μeffw | Viscosity of water |
| ew | Internal energy of water |
| Stress tensor | |
| w | Mass fraction |
| Pin | Steam inlet pressure |
| Ss | Source term due to the condensation |
| Hw | Enthalpy of saturated water |
| hw | Heat transfer coefficient on liquid side |
| Asw | Phase interface area |
| Tsat | Saturation temperature under local partial pressure. |
| Prwa | Prandtl number |
| Rer | Relative Reynolds number between two-phase |
| Mass-weighted average velocity of water and air | |
| Latent heat of saturated steam | |
| Turbulent kinetic viscosity | |
| Turbulent energy dissipation rate | |
| kw | Turbulent kinetic energy |
| Subscript | |
| w | Water |
| s | Steam |
| a | Air |
References
- Liang, K.S.; Griffith, P. Experimental and Analytical Study of Direct Contact Condensation of Steam in Water. Nucl. Eng. Des. 1994, 147, 425–435. [Google Scholar] [CrossRef]
- Yang, X.P.; Chong, D.T.; Liu, J.P.; Zong, X.; Yan, J.J. Experimental Study on the Direct Contact Condensation of the Steam-Air Mixture in Sub-Cooled Water Flow in a Rectangular Channel. Int. J. Heat Mass Transf. 2015, 88, 424–432. [Google Scholar] [CrossRef]
- Qu, X.H.; Tian, M.C. Acoustic and Visual Study on Condensation of Steam-Air Mixture Jet Plume in Subcooled Water. Chem. Eng. Sci. 2016, 144, 216–223. [Google Scholar] [CrossRef]
- Zhou, Y.; Yang, X.P.; Fu, P.F.; Liu, J.P.; Yan, J.J. Numerical Investigation on Submerged Steam Jet Condensation in Subcooled Water Flow in a Restricted Channel with the Presence of Non-condensable Gas. Int. J. Therm. Sci. 2021, 170, 107122. [Google Scholar] [CrossRef]
- Lewis, M.T.; Hickey, J.P. Conjugate Heat Transfer in High-Speed External Flows: A Review. J. Thermophys. Heat Transf. 2023, 37, 697–712. [Google Scholar] [CrossRef]
- Jia, B.; Xian, C.G.; Tsau, J.S.; Zuo, X.; Jia, W.F. Status and outlook of oil field chemistry-assisted analysis during the energy transition period. Energy Fuels 2022, 36, 12917–12945. [Google Scholar] [CrossRef]
- Chun, M.H.; Kim, Y.S.; Park, J.W. An Investigation of Direct Condensation of Steam Jet in Subcooled Water. Int. Commun. Heat Mass Transf. 1996, 23, 947–958. [Google Scholar] [CrossRef]
- Liu, G.Y.; Yan, J.J.; Pan, D.D.; Li, W.J.; Wu, X.Z.; Xing, T.A. Research on the Steam Plume Shape and Pressure Fields of Supersonic Steam Jet in Subcooled Water. J. Eng. Thermophys. 2010, 31, 781–784. [Google Scholar]
- Xu, Q.; Guo, L.J.; Zou, S.F.; Chen, J.W.; Zhang, X.M. Experimental Study on Direct Contact Condensation of Stable Steam Jet in Water Flow in a Vertical Pipe. Int. J. Heat Mass Transf. 2013, 66, 808–817. [Google Scholar] [CrossRef]
- Liu, J.Q.; Liu, X.X.; Sun, Z.N.; Ming, Z.M. Experimental Investigation on Pressure Oscillation of Submerged Steam Jet Condensation with Non-condensable Gas. At. Energy Sci. Technol. 2019, 53, 312–318. [Google Scholar]
- Cong, Y.L.; Wang, Y.C.; Chen, W.X.; Chong, D.T.; Yan, J.J. Effect of Non-condensable Gas on Pressure Oscillation of Submerged Steam Jet. J. Univ. Chin. Acad. Sci. 2017, 34, 135–140. [Google Scholar]
- Cong, Y.L.; Chong, D.T.; Yan, J.J. Effect of Non-condensable Gas on Pressure Oscillation Intensity of Submerged Steam Jet. At. Energy Sci. Technol. 2019, 53, 2389–2397. [Google Scholar]
- Ma, X.; Xiao, X.; Jia, H.; Li, J.; Ji, Y.L.; Lian, Z.H.; Guo, Y. Experimental Research on Steam Condensation in Presence of Non- condensable Gas under High Pressure. Ann. Nucl. Energy 2021, 158, 108282. [Google Scholar] [CrossRef]
- Qu, X.H.; Tian, M.C.; Zhang, G.M.; Leng, X.L. Effect of Non-condensable Gas on Steam Jet Condensation Characteristics. CIESC J. 2015, 66, 3841–3848. [Google Scholar]
- Zhou, L.; Chong, D.T.; Liu, J.P.; Yan, J.J. Numerical Study on Fow Pattern of Sonic Steam Jet Condensed into Subcooled Water. Ann. Nucl. Energy 2016, 99, 206–215. [Google Scholar] [CrossRef]
- Zhou, L.; Chen, W.X.; Chong, D.T.; Liu, J.P.; Yan, J.J. Numerical Investigation on Flow Characteristic of Supersonic Steam Jet Condensed into a Water Pool. Int. J. Heat Mass Transf. 2017, 108, 351–361. [Google Scholar] [CrossRef]
- Zhou, L.; Wang, L.; Chong, D.T.; Yan, J.J.; Liu, J.P. CFD Analysis to Study the Effect of Non-condensable Gas on Stable Condensation Jet. Prog. Nucl. Energy 2017, 98, 143–152. [Google Scholar] [CrossRef]
- Tan, B.; Cai, J.J.; Liu, R.; Chang, J. Research on Condensation Heat Transfer Model with Non-condensable Gas under High Pressure. At. Energy Sci. Technol. 2021, 55, 1047–1053. [Google Scholar]
- Geng, S.H.; Dang, J.J.; Zhao, J.; Zhang, J.N.; Sun, J.L.; Qin, K. Numerical Simulation of Convective Condensation of Steam with Large Proportion of Non-Condensable Gas under High Pressure. J. Unmanned Undersea Syst. 2021, 29, 88–96. [Google Scholar]
- Cravero, C.; De Domenico, D.; Marsano, D. Uncertainty Quantification Analysis of Exhaust Gas Plume in a Crosswind. Energies 2023, 16, 3549. [Google Scholar] [CrossRef]
- Xia, L.; Zou, Z.J.; Wang, Z.H.; Zou, L.; Gao, H. Surrogate model based uncertainty quantification of CFD simulations of the viscous flow around a ship advancing in shallow water. Ocean Eng. 2021, 234, 109206. [Google Scholar] [CrossRef]
- Norman, T.L.; Revankar, S.T. Jet-Plume Condensation of Steam-Air Mixtures in Subcooled Water, Part 1: Experiments. Nucl. Eng. Des. 2010, 240, 524–532. [Google Scholar] [CrossRef]
- Qu, X.H. Investigation on the Direct Contact Condensation of Steam with Non-Condensable Gas and Its Application in Steam-Water Ejector. Ph.D. Thesis, Shandong University, Qingdao, China, 27 November 2017. [Google Scholar]
- Shah, A. Thermal Hydraulic Analysis of Steam Jet Pump. Ph.D. Thesis, Pakistan Institute of Engineering and Applied Sciences, Islamabad, Pakistan, 2012. [Google Scholar]
- Chen, X.B.; Tian, M.C.; Zhang, G.M.; Liu, H.K. Numerical simulation on interfacial characteristics in supersonic steam–water injector using particle model method. Energies 2019, 12, 1108. [Google Scholar] [CrossRef]
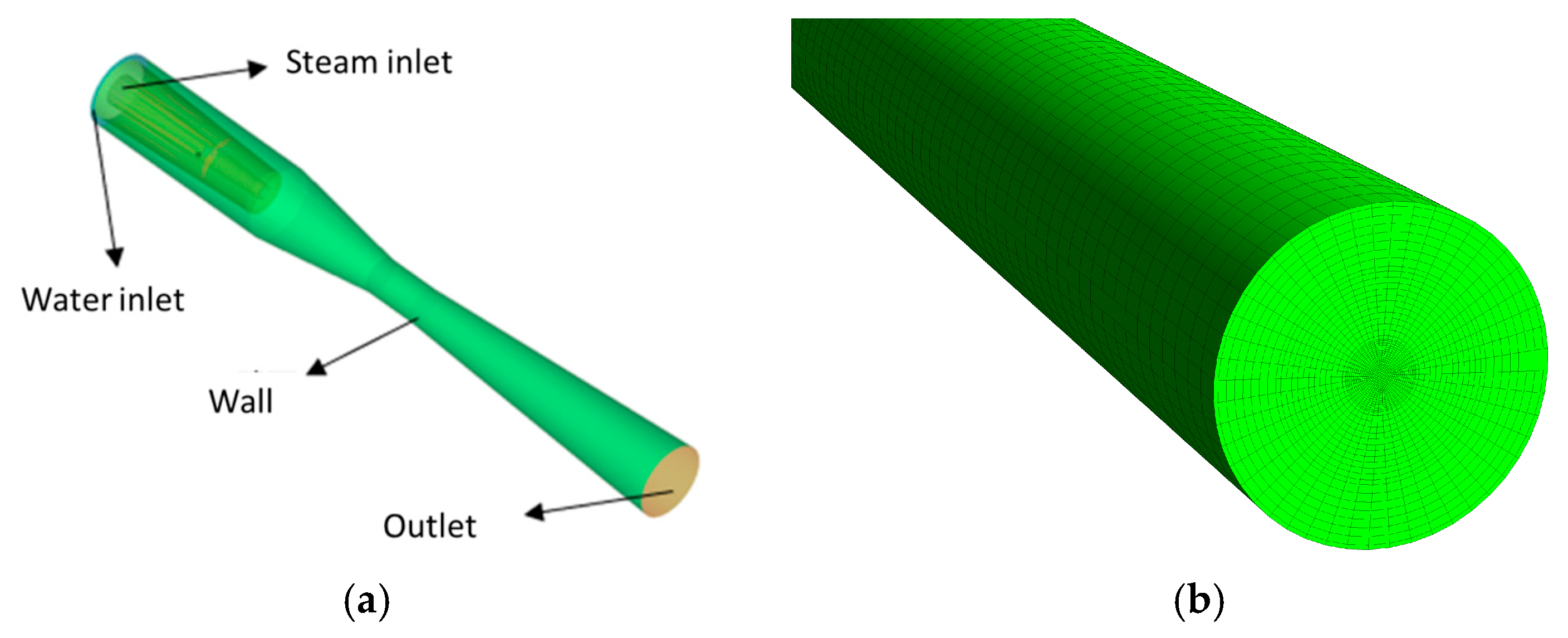
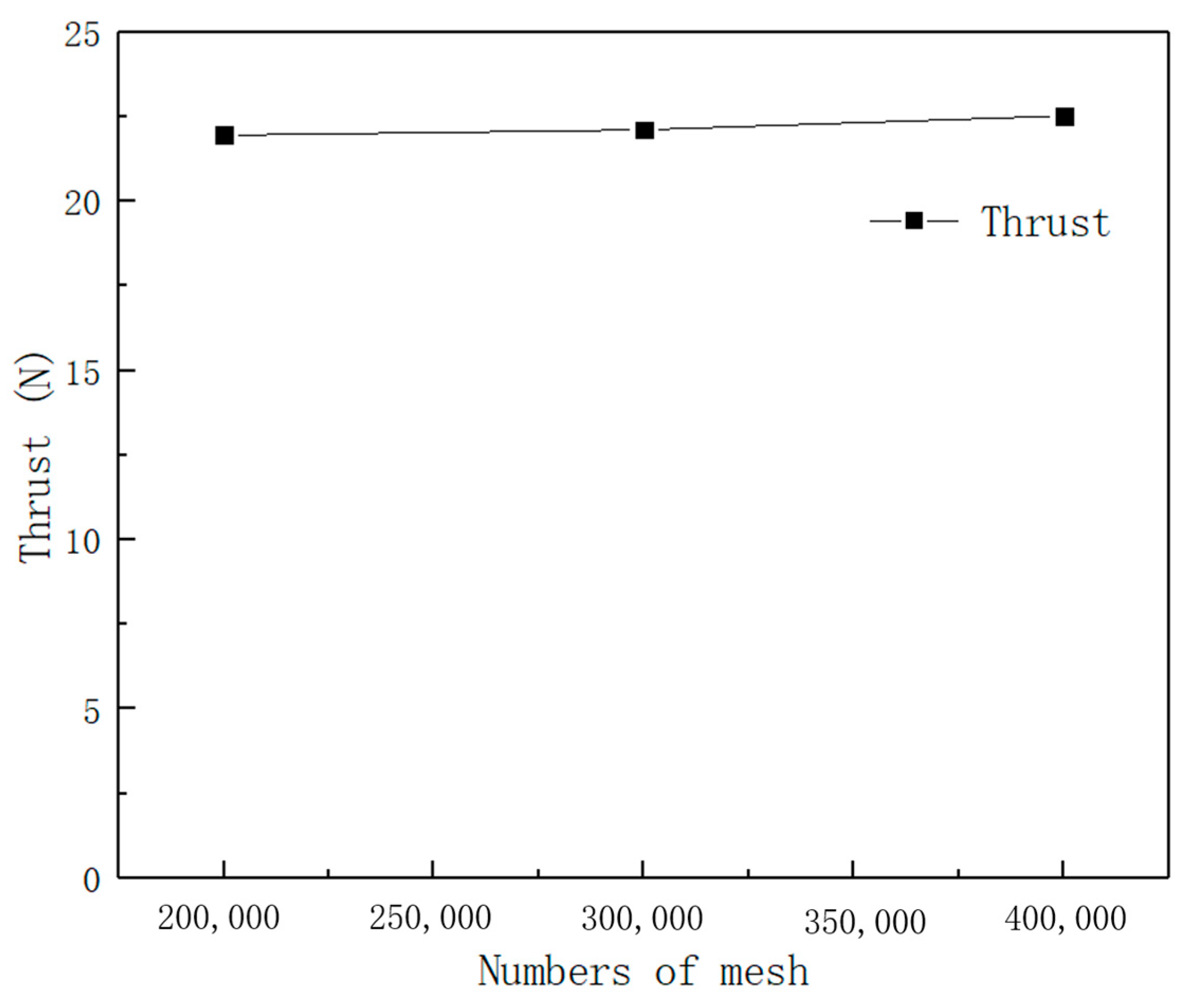




| Parameters | Units | Value |
|---|---|---|
| Steam nozzle throat diameter | mm | 10 |
| Steam nozzle outlet diameter | mm | 4 |
| Throat nozzle distance | mm | 40 |
| Outlet diameter | mm | 20 |
| Steam inlet pressure | MPa | 0.6–2.9 |
| Outlet pressure | kPa | 500 |
| Mass fraction of non-condensable gas | / | 0–0.1 |
| Experiment Result (kPa) | Simulation Result (kPa) | Relative Error (%) |
|---|---|---|
| 103.04 | 109.36 | 6.1% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chai, Y.; Lin, Y.; Xiao, Q.; Huang, C.; Ke, H.; Li, B. Numerical Simulation on Two-Phase Ejector with Non-Condensable Gas. Energies 2024, 17, 1341. https://doi.org/10.3390/en17061341
Chai Y, Lin Y, Xiao Q, Huang C, Ke H, Li B. Numerical Simulation on Two-Phase Ejector with Non-Condensable Gas. Energies. 2024; 17(6):1341. https://doi.org/10.3390/en17061341
Chicago/Turabian StyleChai, Yinghua, Yuansheng Lin, Qi Xiao, Chonghai Huang, Hanbing Ke, and Bangming Li. 2024. "Numerical Simulation on Two-Phase Ejector with Non-Condensable Gas" Energies 17, no. 6: 1341. https://doi.org/10.3390/en17061341
APA StyleChai, Y., Lin, Y., Xiao, Q., Huang, C., Ke, H., & Li, B. (2024). Numerical Simulation on Two-Phase Ejector with Non-Condensable Gas. Energies, 17(6), 1341. https://doi.org/10.3390/en17061341





