Prediction of ORF for Optimized CO2 Flooding in Fractured Tight Oil Reservoirs via Machine Learning
Abstract
1. Introduction
2. Methodology
2.1. Data Preparation
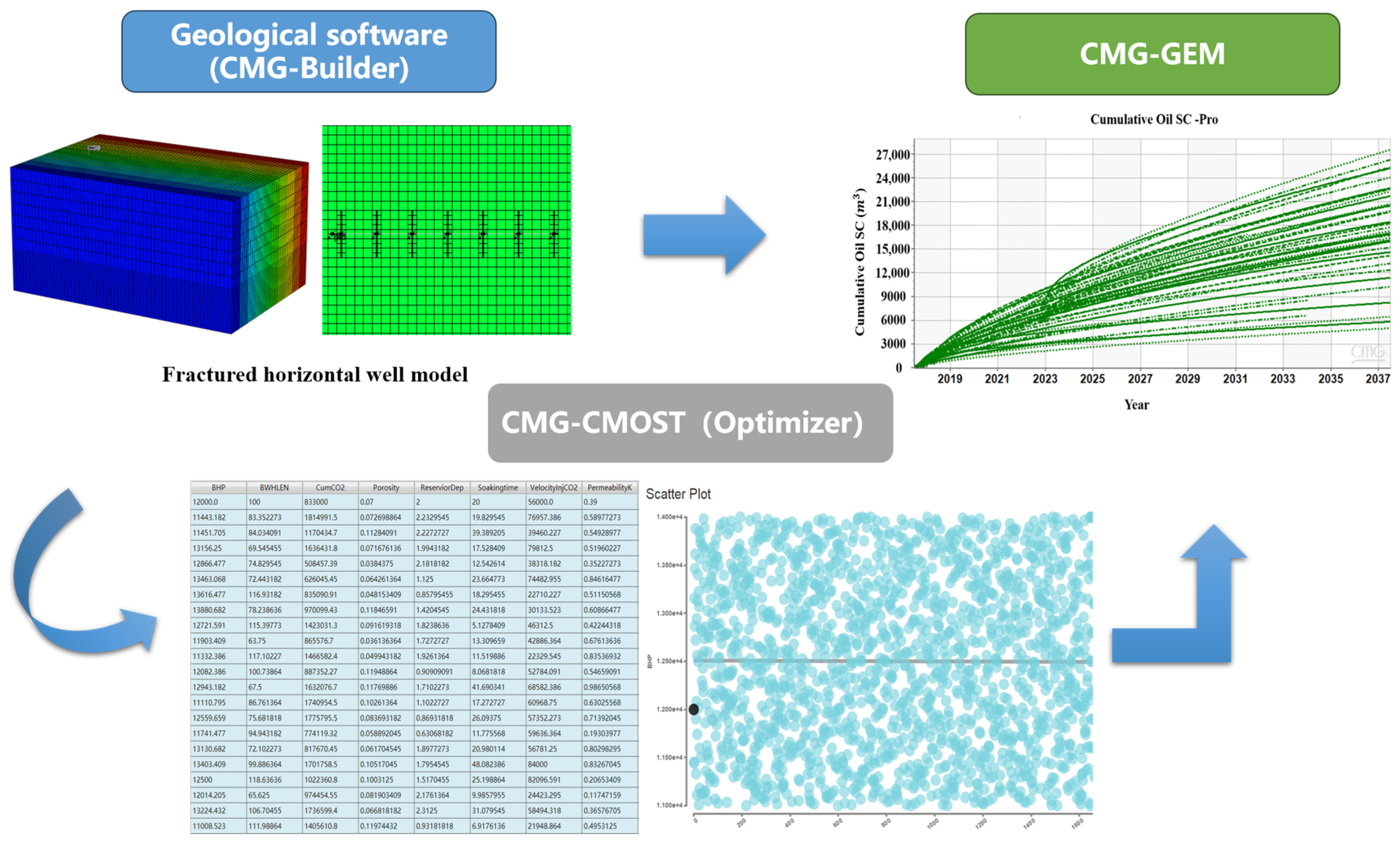
2.1.1. Reservoir Model Description
2.1.2. Obtaining Numerical Simulation Data
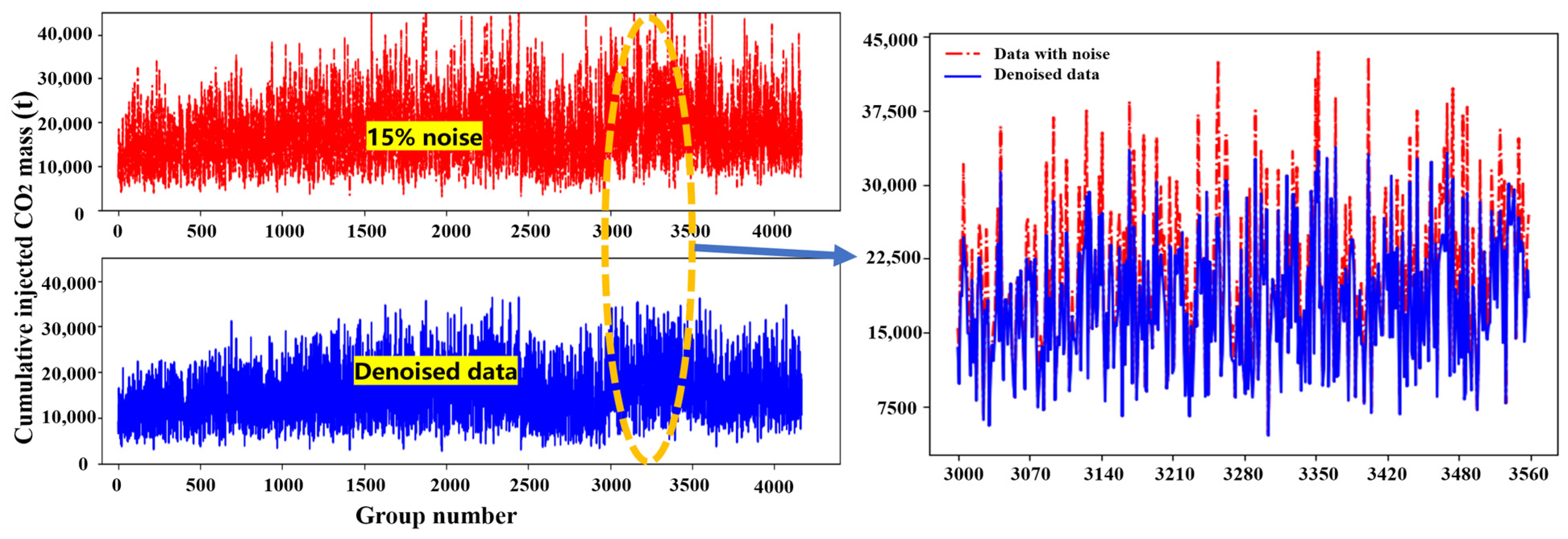
2.1.3. Data Preprocessing
Obtaining Data with Noise
Obtaining Denoised Data
Data Normalization
2.2. Theory of Machine Learning Techniques
2.2.1. Random Forest
2.2.2. XGBoost
2.2.3. Light Gradient Boosting Machine (LightGBM)
2.3. Workflow
2.3.1. Dataset Partitioning
2.3.2. ML Model Development
2.3.3. Model Performance Evaluation
3. Results and Discussion
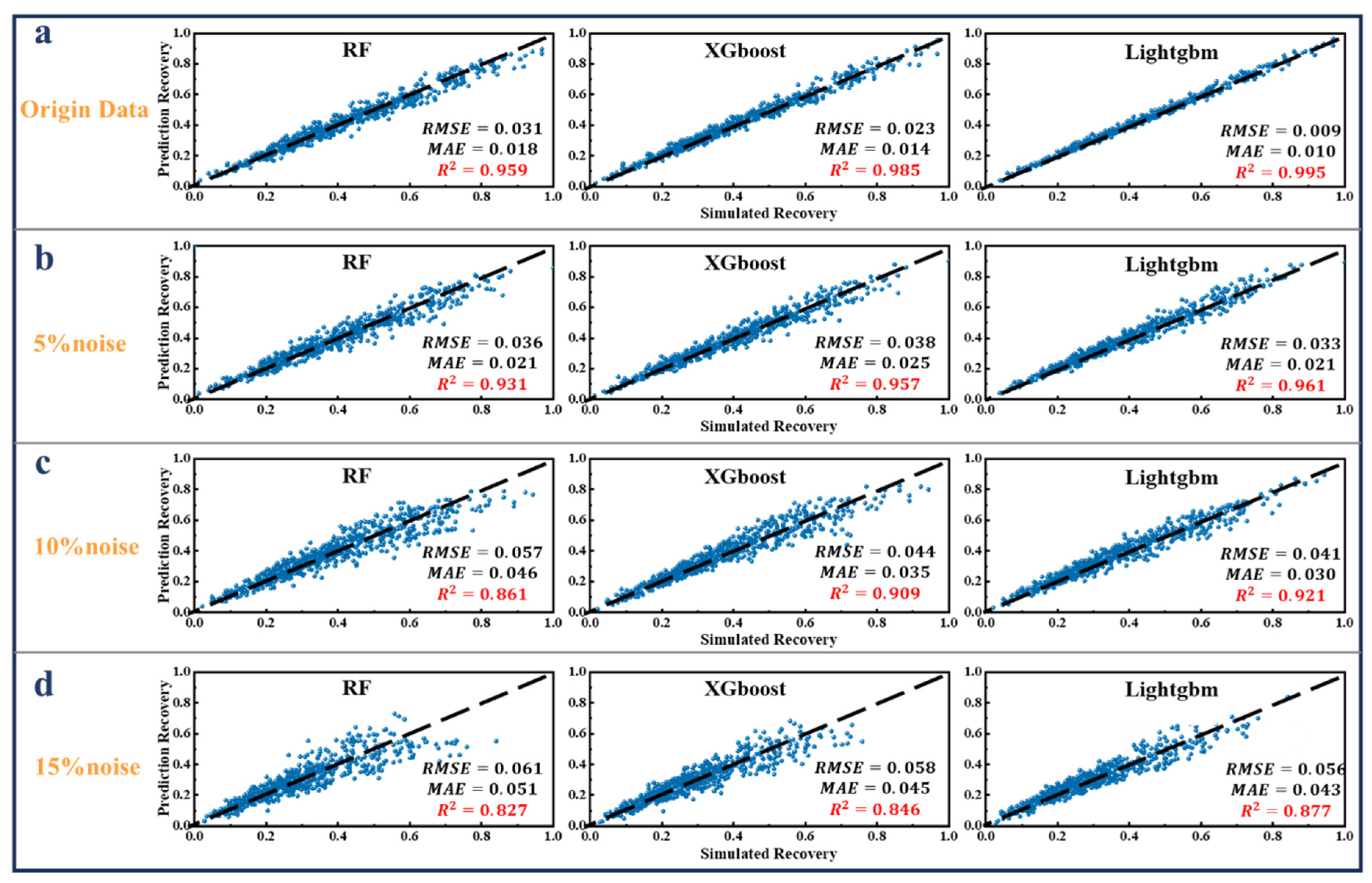
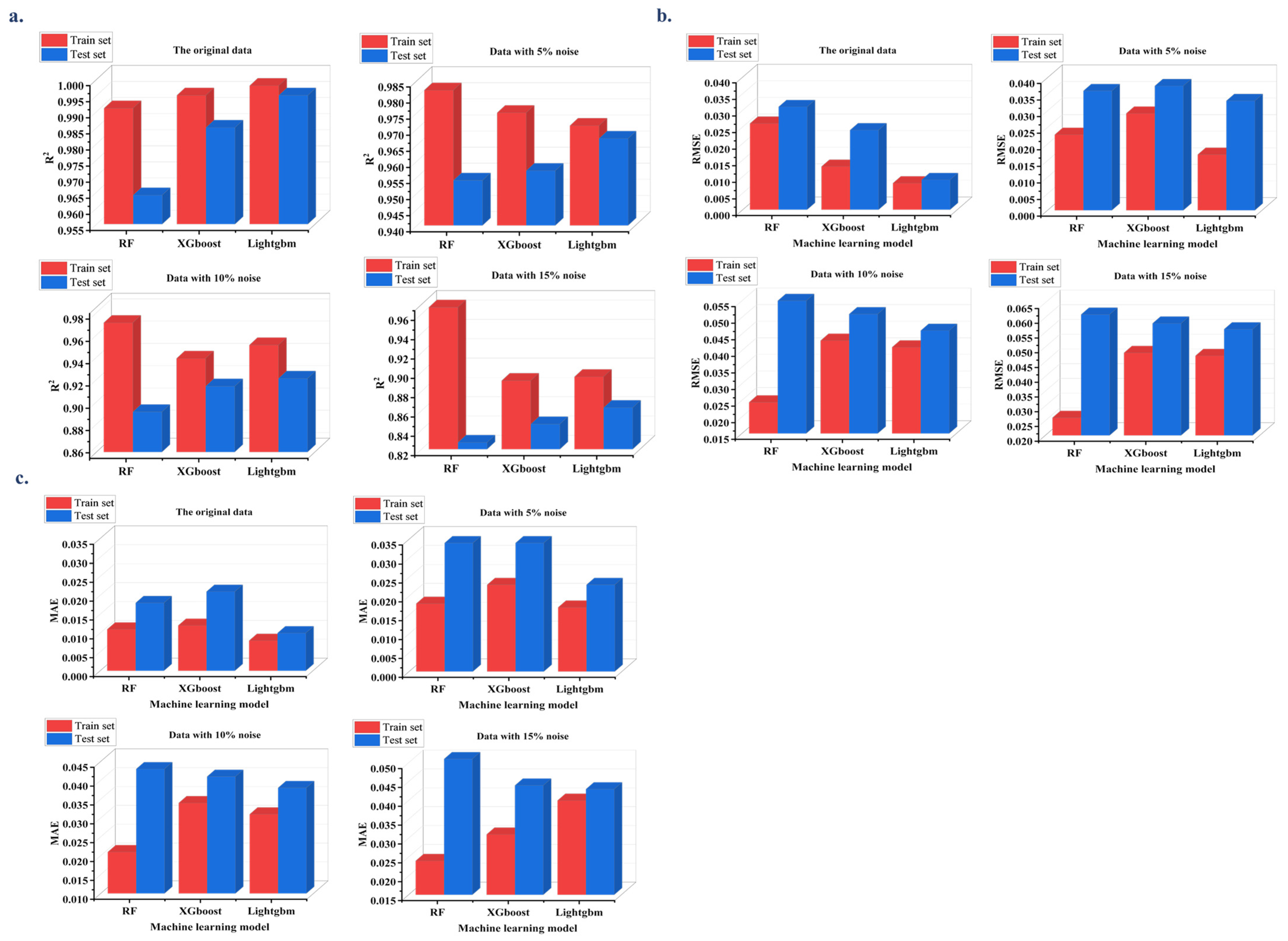
3.1. Evaluation of Model Performance
3.2. Effect of Noise on the ML Model Oil Recovery Factor Predictions
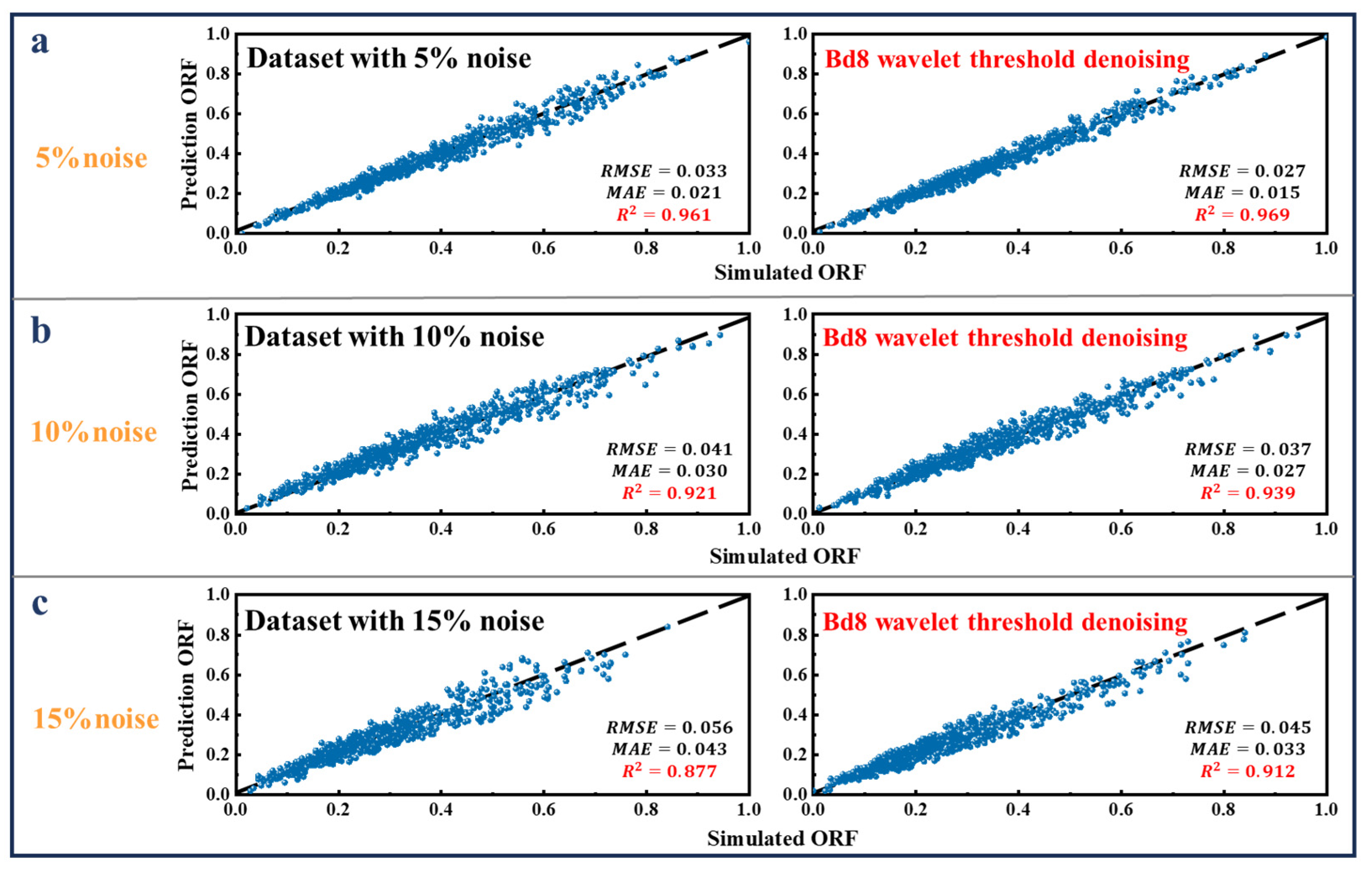
3.3. Model Analysis after Data Denoising
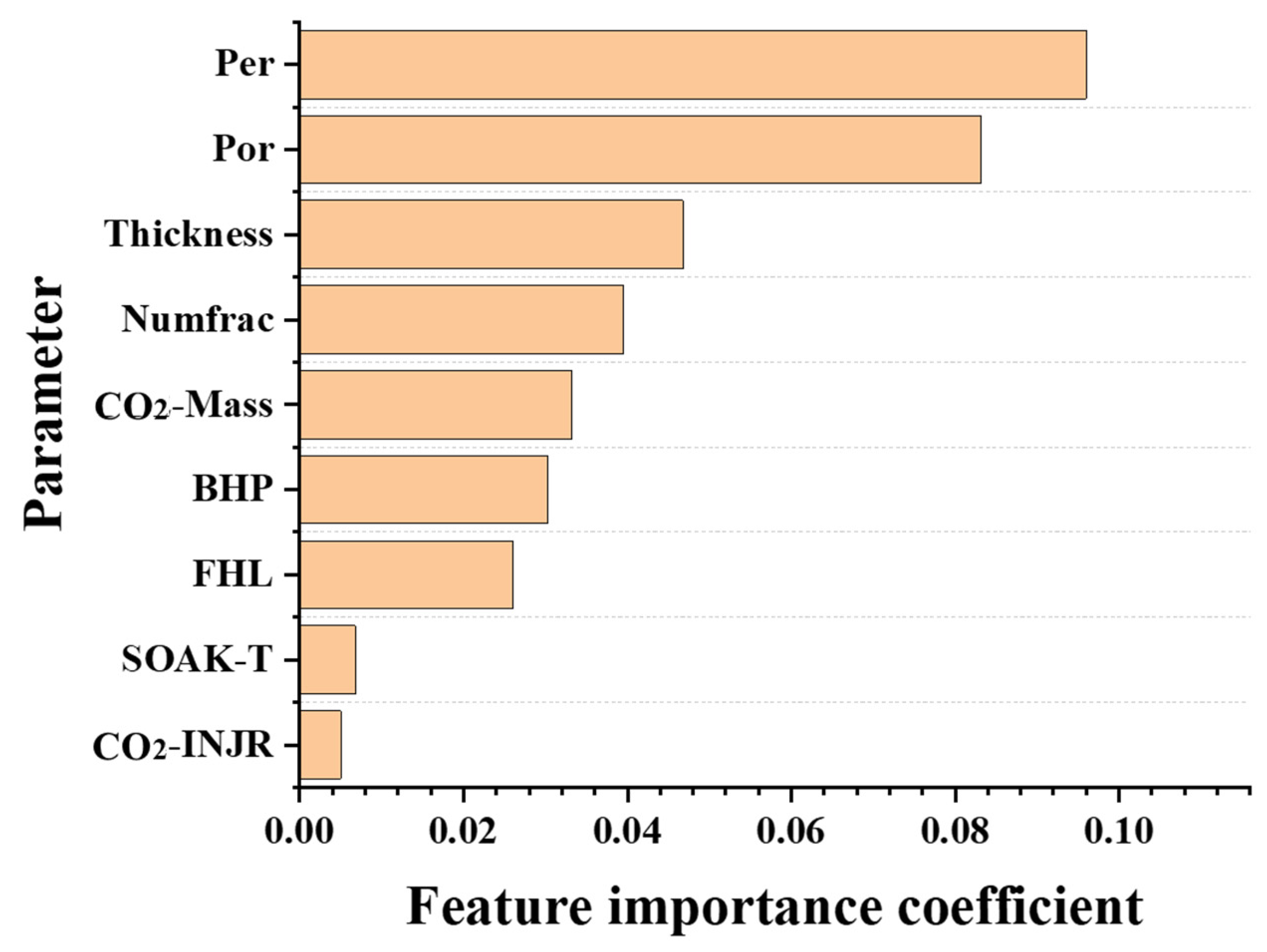
3.4. Screening and Evaluation of Main Control Factors
4. Conclusions
- (1)
- By considering actual blocks as examples, a numerical simulation model for CO2 flooding in low-permeability tight oil reservoirs has been developed. Utilizing the Latin hypercube design method, a comprehensive dataset comprising 4090 numerical simulations is generated, providing a robust foundation for the ML model to analyze ORF.
- (2)
- The study examines the impact of introducing varying levels of noise (5%, 10%, and 15%) to the simulation data on the predictive accuracy of LightGBM, XGBoost, and RF models regarding ORF. Findings reveal that the LightGBM model outperforms the others, demonstrating superior predictive capabilities for CO2 flooding recovery efficiency in tight oil reservoirs, with R2 values of 0.995, 0.961, 0.921, and 0.877 for the original, 5% noise, 10% noise, and 15% noise datasets, respectively.
- (3)
- This research identifies the primary factors influencing CO2-enhanced oil recovery, ranked as follows: permeability, porosity, reservoir thickness, number of fracturing fractures, CO2 mass, BHP, fracture half-length, soak time, and CO2 injection rate.
- (4)
- The method proposed here stands as a promising alternative to conventional CO2-ORF prediction techniques. Embracing ML for supplementary decision making offers a more adaptable and accurate framework for evaluations, reducing the risk of misjudgments associated with static indicator ranges.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| EOR | enhancing oil recovery |
| ORF | oil recovery factor |
| R2 | correlation factor |
| RMSE | root mean square error |
| MAE | mean absolute percentage error |
| ML | machine learning |
| RF | random forest |
| XGBoost | extreme gradient boosting |
| LightGBM | light gradient boosting machine |
| ANN | artificial neural network |
| Por | porosity |
| Perm | permeability |
| Thickness | reservoir thickness |
| FHL | fracture half-length |
| BHP | bottom hole flowing pressure |
| CO2-INJ | injection rate of CO2 |
| CO2-CMASS | cumulative injected CO2 mass |
| SOAK-T | soaking time |
| Numfrac | number of fractures |
| original numerical simulation data | |
| noise level | |
| random number | |
| truth data | |
| noise data | |
| corresponding wavelet coefficient | |
| wavelet function | |
| fundamental wavelet | |
| a | scaling factor |
| b | translation factor |
| Fourier transform of | |
| normalized data | |
| minimum value of this type of data | |
| maximum value of this type of data | |
| the first derivatives of the objective function for each sample within a leaf-node area | |
| the second derivatives of the objective function for each sample within a leaf-node area | |
| J | the total count of leaf nodes |
| the optimal value assigned to the Jth leaf node of each decision tree | |
| γ | user-defined values |
| λ | user-defined values |
References
- Vo Thanh, H.; Sheini Dashtgoli, D.; Zhang, H.; Min, B. Machine-learning-based prediction of oil recovery factor for experimental CO2-Foam chemical EOR: Implications for carbon utilization projects. Energy 2023, 278, 127860. [Google Scholar] [CrossRef]
- Farajzadeh, R.; Eftekhari, A.A.; Dafnomilis, G.; Lake, L.W.; Bruining, J. On the sustainability of CO2 storage through CO2—Enhanced oil recovery. Appl. Energy 2020, 261, 114467. [Google Scholar] [CrossRef]
- Zuloaga-Molero, P.; Yu, W.; Xu, Y.; Sepehrnoori, K.; Li, B. Simulation Study of CO2-EOR in Tight Oil Reservoirs with Complex Fracture Geometries. Sci. Rep. 2016, 6, 33445. [Google Scholar] [CrossRef] [PubMed]
- Chen, T.; Song, L.; Zhang, X.; Yang, Y.; Fan, H.; Pan, B. A Review of Mineral and Rock Wettability Changes Induced by Reaction: Implications for CO2 Storage in Saline Reservoirs. Energies 2023, 16, 3484. [Google Scholar] [CrossRef]
- Bello, A.; Ivanova, A.; Cheremisin, A. A Comprehensive Review of the Role of CO2 Foam EOR in the Reduction of Carbon Footprint in the Petroleum Industry. Energies 2023, 16, 1167. [Google Scholar] [CrossRef]
- Zhang, J.; Tian, L. Tight oil recovery prediction based on extreme gradient boosting algorithm and support vector regression algorithm variable weight combination model. Sci. Technol. Eng. 2022, 22, 4778–4787. [Google Scholar]
- Sun, R.; Pu, H.; Yu, W.; Miao, J.; Zhao, J.X. Simulation-based enhanced oil recovery predictions from wettability alteration in the Middle Bakken tight reservoir with hydraulic fractures. Fuel 2019, 253, 229–237. [Google Scholar] [CrossRef]
- Miura, K.; Wang, J. An Analytical Model to Predict Cumulative Steam Oil Ratio (CSOR) in Thermal Recovery SAGD Process. In Proceedings of the Canadian Unconventional Resources and International Petroleum Conference, Calgary, AB, Canada, 19–21 October 2010; p. 137604. [Google Scholar]
- Teng, L.; Zhang, D.; Li, Y.; Wang, W.; Wang, L.; Hu, Q.; Ye, X.; Bian, J.; Teng, W. Multiphase mixture model to predict temperature drop in highly choked conditions in CO2 enhanced oil recovery. Appl. Therm. Eng. 2016, 108, 670–679. [Google Scholar] [CrossRef]
- Guo, C.; Li, H.; Tao, Y.; Lang, L.; Niu, Z. Water invasion and remaining gas distribution in carbonate gas reservoirs using core displacement and NMR. J. Cent. South Univ. 2020, 27, 531–541. [Google Scholar] [CrossRef]
- Al-Jifri, M.; Al-Attar, H.; Boukadi, F. New proxy models for predicting oil recovery factor in waterflooded heterogeneous reservoirs. J. Pet. Explor. Prod. 2021, 11, 1443–1459. [Google Scholar] [CrossRef]
- Fathaddin, M.T.; Thomas, M.M.; Pasarai, U. Predicting oil recovery through CO2 flooding simulation using methods of continuous and water alternating gas. J. Phys. Conf. Ser. 2019, 1402, 55015. [Google Scholar] [CrossRef]
- Yuan, Z.; Wang, J.; Li, S.; Ren, J.; Zhou, M. A new approach to estimating recovery factor for extra-low permeability water-flooding sandstone reservoirs. Pet. Explor. Dev. 2014, 41, 377–386. [Google Scholar] [CrossRef]
- Yue, M.; Song, T.; Chen, Q.; Yu, M.; Wang, Y.; Wang, J.; Du, S.; Song, H. Prediction of effective stimulated reservoir volume after hydraulic fracturing utilizing deep learning. Pet. Sci. Technol. 2023, 41, 1934–1956. [Google Scholar] [CrossRef]
- Huang, J.; Wang, H. Pore-Scale Simulation of Confined Phase Behavior with Pore Size Distribution and Its Effects on Shale Oil Production. Energies 2021, 14, 1315. [Google Scholar] [CrossRef]
- Sun, H.; Wang, H.; Zhu, S.; Nie, H.; Liu, Y.; Li, Y.; Li, S.; Cao, W.; Chang, B. Reserve evaluation of high pressure and ultra-high-pressure reservoirs with power function material balance method. Nat. Gas Ind. B 2019, 6, 509–516. [Google Scholar] [CrossRef]
- Cheng, M.; Lei, G.; Gao, J.; Xia, T.; Wang, H. Laboratory Experiment, Production Performance Prediction Model, and Field Application of Multi-slug Microbial Enhanced Oil Recovery. Energy Fuels 2014, 28, 6655–6665. [Google Scholar] [CrossRef]
- Hadia, N.; Chaudhari, L.; Aggarwal, A.; Mitra, S.K.; Vinjamur, M.; Singh, R. Experimental and numerical investigation of one-dimensional waterflood in porous reservoir. Exp. Therm. Fluid Sci. 2007, 32, 355–361. [Google Scholar] [CrossRef]
- Zhong, Q.; Shi, Y.; Liu, P.; Peng, B.; Zhuang, Y. Study on injecting time of CO2 flooding in low permeability reservoir. Fault-Block Oil Gas Field 2012, 19, 346–349. [Google Scholar]
- Al-qaness, M.A.A.; Ewees, A.A.; Thanh, H.V.; AlRassas, A.M.; Dahou, A.; Elaziz, M.A. Predicting CO2 trapping in deep saline aquifers using optimized long short-term memory. Environ. Sci. Pollut. Res. 2023, 30, 33780–33794. [Google Scholar] [CrossRef]
- Esmaili, S.; Mohaghegh, S.D. Full field reservoir modeling of shale assets using advanced data-driven analytics. Geosci. Front. 2016, 7, 11–20. [Google Scholar] [CrossRef]
- Miah, M.I.; Ahmed, S.; Zendehboudi, S. Connectionist and mutual information tools to determine water saturation and rank input log variables. J. Pet. Sci. Eng. 2020, 190, 106741. [Google Scholar] [CrossRef]
- Yasin, Q.; Sohail, G.M.; Ding, Y.; Ismail, A.; Du, Q. Estimation of Petrophysical Parameters from Seismic Inversion by Combining Particle Swarm Optimization and Multilayer Linear Calculator. Nat. Resour. Res. 2020, 29, 3291–3317. [Google Scholar] [CrossRef]
- Muojeke, S.; Venkatesan, R.; Khan, F. Supervised data-driven approach to early kick detection during drilling operation. J. Pet. Sci. Eng. 2020, 192, 107324. [Google Scholar] [CrossRef]
- Hegde, C.; Pyrcz, M.; Millwater, H.; Daigle, H.; Gray, K. Fully coupled end-to-end drilling optimization model using machine learning. J. Pet. Sci. Eng. 2020, 186, 106681. [Google Scholar] [CrossRef]
- Gurina, E.; Klyuchnikov, N.; Zaytsev, A.; Romanenkova, E.; Antipova, K.; Simon, I.; Makarov, V.; Koroteev, D. Application of machine learning to accidents detection at directional drilling. J. Pet. Sci. Eng. 2020, 184, 106519. [Google Scholar] [CrossRef]
- Zhu, W.; Song, T.; Wang, M.; Jin, W.; Song, H.; Yue, M. Stratigraphic subdivision-based logging curves generation using neural random forests. J. Pet. Sci. Eng. 2022, 219, 111086. [Google Scholar] [CrossRef]
- Gupta, S.; Fuehrer, F.; Jeyachandra, B.C. In Production Forecasting in Unconventional Resources using Data Mining and Time Series Analysis. In Proceedings of the SPE/CSUR Unconventional Resources Conference, Calgary, AB, Canada, 30 September–2 October 2014. [Google Scholar]
- Lala, A.M.S.; Lala, H.M.S. Study on the improving method for gas production prediction in tight clastic reservoir. Arab. J. Geosci. 2017, 10, 70. [Google Scholar] [CrossRef]
- Lin, B.; Guo, J.; Liu, X.; Xiang, J.; Zhong, H. Prediction of flowback ratio and production in Sichuan shale gas reservoirs and their relationships with stimulated reservoir volume. J. Pet. Sci. Eng. 2020, 184, 106529. [Google Scholar] [CrossRef]
- Liu, W.; Yang, Y.; Qiao, C.; Liu, C.; Lian, B.; Yuan, Q. Progress of Seepage Law and Development Technologies for Shale Condensate Gas Reservoirs. Energies 2023, 16, 2446. [Google Scholar] [CrossRef]
- Al-Mudhafar, W.J. Integrating lithofacies and well logging data into smooth generalized additive model for improved permeability estimation: Zubair formation, South Rumaila oil field. Mar. Geophys. Res. 2019, 40, 315–332. [Google Scholar] [CrossRef]
- Al-Mudhafar, W.J. Integrating machine learning and data analytics for geostatistical characterization of clastic reservoirs. J. Pet. Sci. Eng. 2020, 195, 107837. [Google Scholar] [CrossRef]
- Pan, B.; Song, T.; Yue, M.; Chen, S.; Zhang, L.; Edlmann, K.; Neil, C.W.; Zhu, W.; Iglauer, S. Machine learning–based shale wettability prediction: Implications for H2, CH4 and CO2 geo-storage. Int. J. Hydrogen Energy 2024, 56, 1384–1390. [Google Scholar] [CrossRef]
- Van, S.L.; Chon, B.H. Effective Prediction and Management of a CO2 Flooding Process for Enhancing Oil Recovery Using Artificial Neural Networks. J. Energy Resour. Technol. 2017, 140, 032906. [Google Scholar] [CrossRef]
- Cheraghi, Y.; Kord, S.; Mashayekhizadeh, V. Application of machine learning techniques for selecting the most suitable enhanced oil recovery method; challenges and opportunities. J. Pet. Sci. Eng. 2021, 205, 108761. [Google Scholar] [CrossRef]
- Esene, C.; Zendehboudi, S.; Shiri, H.; Aborig, A. Deterministic tools to predict recovery performance of carbonated water injection. J. Mol. Liq. 2020, 301, 111911. [Google Scholar] [CrossRef]
- Pan, S.; Zheng, Z.; Guo, Z.; Luo, H. An optimized XGBoost method for predicting reservoir porosity using petrophysical logs. J. Pet. Sci. Eng. 2022, 208, 109520. [Google Scholar] [CrossRef]
- Huang, Z.; Chen, Z. Comparison of different machine learning algorithms for predicting the SAGD production performance. J. Pet. Sci. Eng. 2021, 202, 108559. [Google Scholar] [CrossRef]
- Shen, B.; Yang, S.; Gao, X.; Li, S.; Ren, S.; Chen, H. A novel CO2-EOR potential evaluation method based on BO-LightGBM algorithms using hybrid feature mining. Geoenergy Sci. Eng. 2023, 222, 211427. [Google Scholar] [CrossRef]
- Taber, J.J.; Martin, F.D.; Seright, R.S. EOR Screening Criteria Revisited—Part 1: Introduction to Screening Criteria and Enhanced Recovery Field Projects. Spe Reserv. Eng. 1997, 12, 189–198. [Google Scholar] [CrossRef]
- Lee, J.H.; Park, Y.C.; Sung, W.M.; Lee, Y.S. A Simulation of a Trap Mechanism for the Sequestration of CO2 into Gorae V Aquifer, Korea. Energy Sources Part A Recovery Util. Environ. Eff. 2010, 32, 796–808. [Google Scholar]
- Liu, B.; Zhang, Y. CO2 Modeling in a Deep Saline Aquifer: A Predictive Uncertainty Analysis Using Design of Experiment. Environ. Sci. Technol. 2011, 45, 3504–3510. [Google Scholar] [CrossRef] [PubMed]
- Abbaszadeh, M.; Shariatipour, S.M. Investigating the Impact of Reservoir Properties and Injection Parameters on Carbon Dioxide Dissolution in Saline Aquifers. Fluids 2018, 3, 76. [Google Scholar] [CrossRef]
- Gao, M.; Liu, Z.; Qian, S.; Liu, W.; Li, W.; Yin, H.; Cao, J. Machine-Learning-Based Approach to Optimize CO2-WAG Flooding in Low Permeability Oil Reservoirs. Energies 2023, 16, 6149. [Google Scholar] [CrossRef]
- Li, S.; Wang, Z.; Kang, Y.; Hou, J. Noise reduction of a safety valve pressure relief signal based on an improved wavelet threshold function. J. Vib. Shock. 2021, 40, 143–150. [Google Scholar]
- Li, W.; Xu, W.; Zhang, T. Improvement of Threshold Denoising Method Based on Wavelet Transform. Comput. Simul. 2021, 38, 348–351. [Google Scholar]
- Song, T.; Zhu, W.; Chen, Z.; Jin, W.; Song, H.; Fan, L.; Yue, M. A novel well-logging data generation model integrated with random forests and adaptive domain clustering algorithms. Geoenergy Sci. Eng. 2023, 231, 212381. [Google Scholar] [CrossRef]
- Liaw, A.; Wiener, M. Classification and regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- Vo Thanh, H.; Lee, K. Application of machine learning to predict CO2 trapping performance in deep saline aquifers. Energy 2022, 239, 122457. [Google Scholar] [CrossRef]
- Vo Thanh, H.; Yasin, Q.; Al-Mudhafar, W.J.; Lee, K. Knowledge-based machine learning techniques for accurate prediction of CO2 storage performance in underground saline aquifers. Appl. Energy 2022, 314, 118985. [Google Scholar] [CrossRef]
- Meng, M.; Zhong, R.; Wei, Z. Prediction of methane adsorption in shale: Classical models and machine learning based models. Fuel 2020, 278, 118358. [Google Scholar] [CrossRef]
- Gholami, H.; Mohamadifar, A.; Collins, A.L. Spatial mapping of the provenance of storm dust: Application of data mining and ensemble modelling. Atmos. Res. 2020, 233, 104716. [Google Scholar] [CrossRef]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.Y. Lightgbm: A highly efficient gradient boosting decision tree. Adv. Neural Inf. Process. Syst. 2017, 30, 1–2. [Google Scholar]
- Stazio, A.; Victores, J.G.; Estevez, D.; Balaguer, C. A Study on Machine Vision Techniques for the Inspection of Health Personnels’ Protective Suits for the Treatment of Patients in Extreme Isolation. Electronics 2019, 8, 743. [Google Scholar] [CrossRef]




| Parameters | Value | Units |
|---|---|---|
| Reservoir depth | 2126 | m |
| Reservoir pressure | 20.9 | MPa |
| Saturation pressure | 10.18 | MPa |
| Reservoir temperature | 84 | °C |
| Rock Compressibility | 1 × 10−8 | 1/kPa |
| Permeability | 0.39 | mD |
| Porosity | 0.071 | - |
| Fracture conductivity | 30 | mD·m |
| Horizontal well length | 1020 | m |
| Fracture half-length | 120 | m |
| The maximum CO2 injection volume | 1500 | t |
| Injection rate of CO2 | 50 | t/day |
| Minimum bottomhole flow pressure | 11 | MPa |
| Maximum surface oil rate | 50 | m3/d |
| Soaking time | 20 | d |
| Parameter | Symbol | Minimum | Maximum | Base Case | Units |
|---|---|---|---|---|---|
| Porosity | Por | 0.03 | 0.12 | 0.071 | - |
| Permeability | Per | 0.05 | 1.05 | 0.39 | mD |
| Reservior thickness | Thickness | 6.5 | 35 | 26 | m |
| Fracture half-length | FHL | 60 | 120 | 100 | m |
| Bottom hole flowing pressure | BHP | 11 | 14 | 12 | MPa |
| Injection rate of CO2 | CO2-INJR | 30 | 150 | 100 | t/day |
| Accumulated injection mass of CO2 | CO2-Mass | 750 | 3500 | 1500 | t |
| Soaking time | SOAK-T | 5 | 50 | 20 | day |
| Number of fractures | Numfrac | 5 | 10 | 7 | - |
| Model | Hyperparameter | Range |
|---|---|---|
| RF | n_estimators | 10, 50, 100, 300, 500 |
| max_depth | 10, 20, 40, 70, 100 | |
| min_samples_leaf | 1, 2, 4, 6, 8 | |
| max_features | 0.2, 0.4, 0.7, 0.8, 1 | |
| learning_rate | 0.001, 0.01, 0.05, 0.1, 1 | |
| min_samples_split | 1, 2, 4, 6, 8 | |
| XGboost | n_estimators | 10, 50, 80, 100, 200 |
| max_depth | 1, 2, 4, 6, 8 | |
| num_leaves | 8, 16, 32, 64, 128 | |
| learning_rate | 0.001, 0.01, 0.05, 0.1, 1 | |
| randam_state | 0, 6, 12, 20, 30 | |
| min_child_weight | 0.1, 0.2, 0.4, 0.6, 0.8 | |
| subsample | 0.5, 0.6, 0.7, 0.8, 1 | |
| colsample_bytree | 0.5, 0.6, 0.7, 0.8, 1 | |
| LightGBM | n_estimators | 50, 100, 300, 500, 800 |
| max_depth | 3, 4, 5, 6, 7 | |
| num_leaves | 8, 16, 32, 64, 128 | |
| learning_rate | 0.01, 0.05, 0.1, 0.5, 1 | |
| max_bin | 10, 30, 50, 60, 70 | |
| bagging_fraction | 0, 0.1, 0.4, 0.7, 1 | |
| bagging_freg | 10, 40, 50, 60, 80 | |
| bagging_seed | 10, 20, 40, 60, 80 | |
| Feature_fraction | 0.5, 0.6, 0.7, 0.8, 0.9 |
| Model | Hyperparameter | Optimal Value (Original Data) | Optimal Value (5% Noise) | Optimal Value (10% Noise) | Optimal Value (15% Noise) |
|---|---|---|---|---|---|
| RF | n_estimators | 100 | 200 | 200 | 100 |
| max_depth | 70 | 70 | 70 | 20 | |
| min_samples_leaf | 2 | 2 | 2 | 1 | |
| max_features | 0.7 | 0.7 | 0.8 | 0.8 | |
| learning_rate | 0.1 | 0.1 | 0.1 | 0.05 | |
| min_samples_split | 4 | 4 | 2 | 5 | |
| XGboost | n_estimators | 80 | 80 | 100 | 100 |
| max_depth | 4 | 4 | 6 | 6 | |
| num_leaves | 16 | 32 | 32 | 16 | |
| learning_rate | 0.1 | 0.1 | 0.1 | 0.05 | |
| randam_state | 9 | 12 | 20 | 20 | |
| min_child_weight | 0.6 | 0.8 | 0.8 | 0.8 | |
| subsample | 1 | 1 | 1 | 0.8 | |
| colsample_bytree | 1 | 1 | 1 | 0.8 | |
| Lightbgm | n_estimators | 300 | 300 | 500 | 300 |
| max_depth | 5 | 5 | 5 | 5 | |
| num_leaves | 32 | 32 | 32 | 32 | |
| learning_rate | 0.05 | 0.01 | 0.01 | 0.05 | |
| max_bin | 50 | 50 | 60 | 60 | |
| bagging_fraction | 0.6 | 0.7 | 0.6 | 0.4 | |
| bagging_freg | 40 | 40 | 50 | 80 | |
| bagging_seed | 40 | 40 | 60 | 60 | |
| Feature_fraction | 0.8 | 0.8 | 0.8 | 0.8 |
| Data | Indicator | RF | XGboost | LightGBM |
|---|---|---|---|---|
| Training | R2 | 0.992 | 0.995 | 0.996 |
| RMSE | 0.017 | 0.013 | 0.008 | |
| MAE | 0.011 | 0.010 | 0.009 | |
| Testing | R2 | 0.959 | 0.985 | 0.995 |
| RMSE | 0.031 | 0.023 | 0.009 | |
| MAE | 0.018 | 0.014 | 0.010 |
| Type of Wavelet Bases | Level | 5% Noise | 10% Noise | 15% Noise | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| RMSE | MAE | R2 | RMSE | MAE | R2 | RMSE | MAE | R2 | ||
| Bd6 | J = 1 | 0.032 | 0.019 | 0.966 | 0.044 | 0.032 | 0.921 | 0.055 | 0.046 | 0.864 |
| J = 2 | 0.069 | 0.054 | 0.787 | 0.076 | 0.062 | 0.725 | 0.083 | 0.068 | 0.682 | |
| J = 3 | 0.104 | 0.077 | 0.570 | 0.106 | 0.084 | 0.529 | 0.109 | 0.091 | 0.500 | |
| Sym10 | J = 1 | 0.039 | 0.029 | 0.924 | 0.049 | 0.039 | 0.904 | 0.063 | 0.051 | 0.827 |
| J = 2 | 0.072 | 0.056 | 0.771 | 0.079 | 0.064 | 0.712 | 0.086 | 0.068 | 0.698 | |
| J = 3 | 0.102 | 0.078 | 0.512 | 0.107 | 0.086 | 0.493 | 0.110 | 0.092 | 0.461 | |
| Type of Wavelet Bases | 5% Noise | 10% Noise | 15% Noise | ||||||
|---|---|---|---|---|---|---|---|---|---|
| RMSE | MAE | R2 | RMSE | MAE | R2 | RMSE | MAE | R2 | |
| Haar | 0.054 | 0.043 | 0.891 | 0.059 | 0.045 | 0.865 | 0.077 | 0.064 | 0.783 |
| Bd4 | 0.49 | 0.038 | 0.905 | 0.056 | 0.046 | 0.848 | 0.068 | 0.057 | 0.791 |
| Bd6 | 0.032 | 0.019 | 0.956 | 0.044 | 0.032 | 0.921 | 0.055 | 0.046 | 0.864 |
| Bd8 | 0.027 | 0.015 | 0.969 | 0.037 | 0.027 | 0.939 | 0.045 | 0.033 | 0.912 |
| Bd9 | 0.033 | 0.021 | 0.955 | 0.050 | 0.041 | 0.896 | 0.064 | 0.051 | 0.831 |
| Sym7 | 0.059 | 0.045 | 0.855 | 0.063 | 0.051 | 0.827 | 0.069 | 0.060 | 0.797 |
| Sym8 | 0.044 | 0.033 | 0.915 | 0.058 | 0.046 | 0.853 | 0.065 | 0.052 | 0.836 |
| Sym9 | 0.037 | 0.028 | 0.931 | 0.045 | 0.33 | 0.911 | 0.061 | 0.050 | 0.843 |
| Sym10 | 0.039 | 0.029 | 0.924 | 0.049 | 0.039 | 0.904 | 0.063 | 0.051 | 0.827 |
| Coif1 | 0.108 | 0.081 | 0.471 | 0.117 | 0.095 | 0.431 | 0.124 | 0.101 | 0.327 |
| Coif2 | 0.087 | 0.069 | 0.685 | 0.101 | 0.085 | 0.507 | 0.108 | 0.088 | 0.513 |
| Coif3 | 0.072 | 0.061 | 0.803 | 0.077 | 0.065 | 0.765 | 0.083 | 0.069 | 0.692 |
| Coif4 | 0.069 | 0.058 | 0.793 | 0.073 | 0.064 | 0.727 | 0.079 | 0.068 | 0.688 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yue, M.; Dai, Q.; Liao, H.; Liu, Y.; Fan, L.; Song, T. Prediction of ORF for Optimized CO2 Flooding in Fractured Tight Oil Reservoirs via Machine Learning. Energies 2024, 17, 1303. https://doi.org/10.3390/en17061303
Yue M, Dai Q, Liao H, Liu Y, Fan L, Song T. Prediction of ORF for Optimized CO2 Flooding in Fractured Tight Oil Reservoirs via Machine Learning. Energies. 2024; 17(6):1303. https://doi.org/10.3390/en17061303
Chicago/Turabian StyleYue, Ming, Quanqi Dai, Haiying Liao, Yunfeng Liu, Lin Fan, and Tianru Song. 2024. "Prediction of ORF for Optimized CO2 Flooding in Fractured Tight Oil Reservoirs via Machine Learning" Energies 17, no. 6: 1303. https://doi.org/10.3390/en17061303
APA StyleYue, M., Dai, Q., Liao, H., Liu, Y., Fan, L., & Song, T. (2024). Prediction of ORF for Optimized CO2 Flooding in Fractured Tight Oil Reservoirs via Machine Learning. Energies, 17(6), 1303. https://doi.org/10.3390/en17061303






