Assessment of CO2 Sequestration Capacity in a Low-Permeability Oil Reservoir Using Machine Learning Methods
Abstract
1. Introduction
2. The Establishment of a Numerical Model of CO2 Flooding and Burial
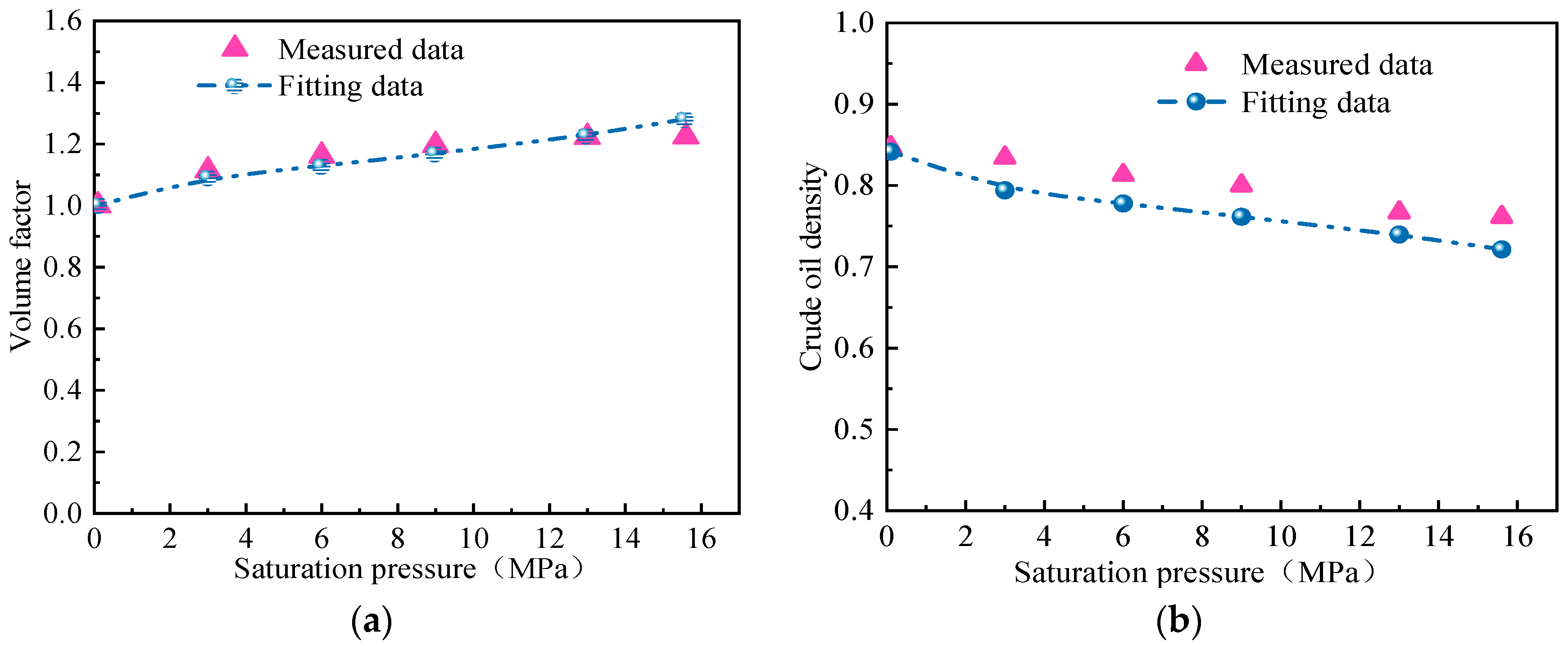
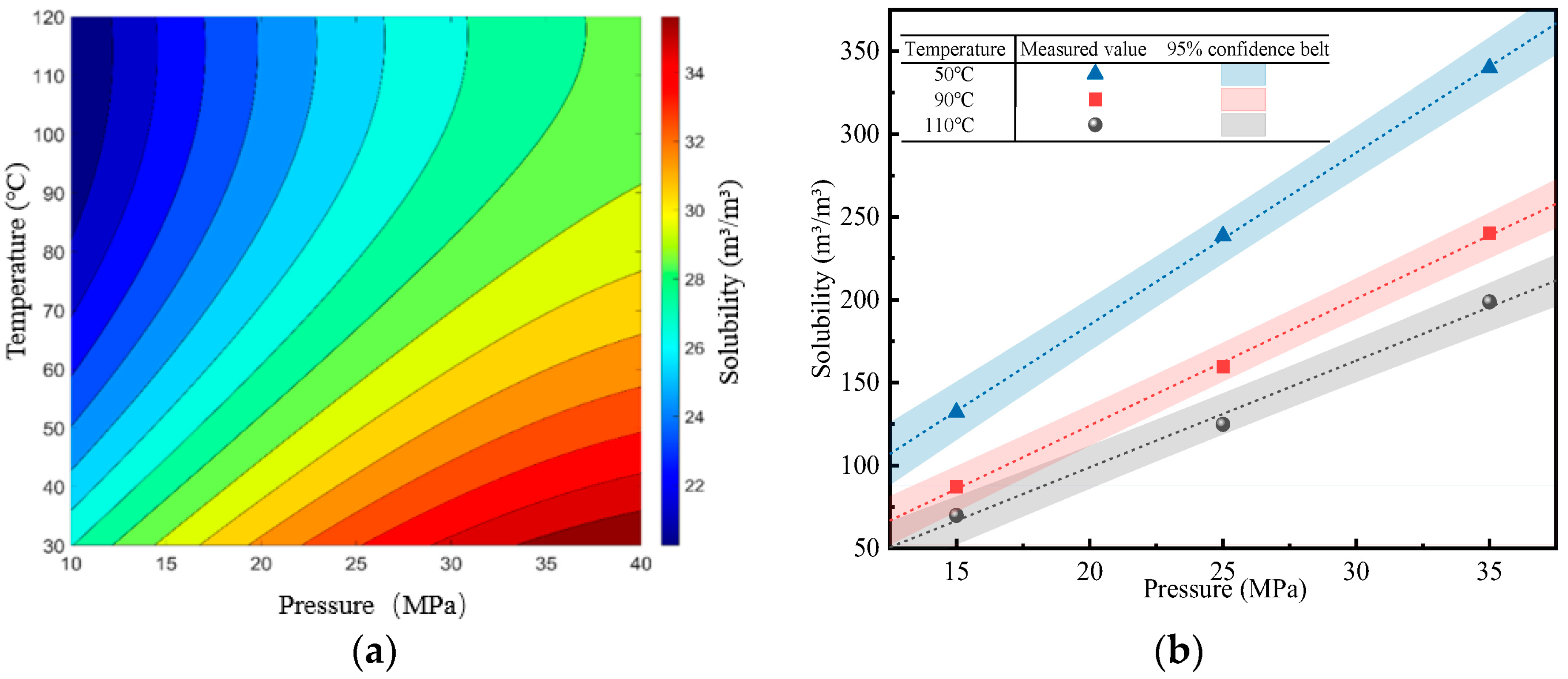
2.1. The Fitting of the Phase of Fluids
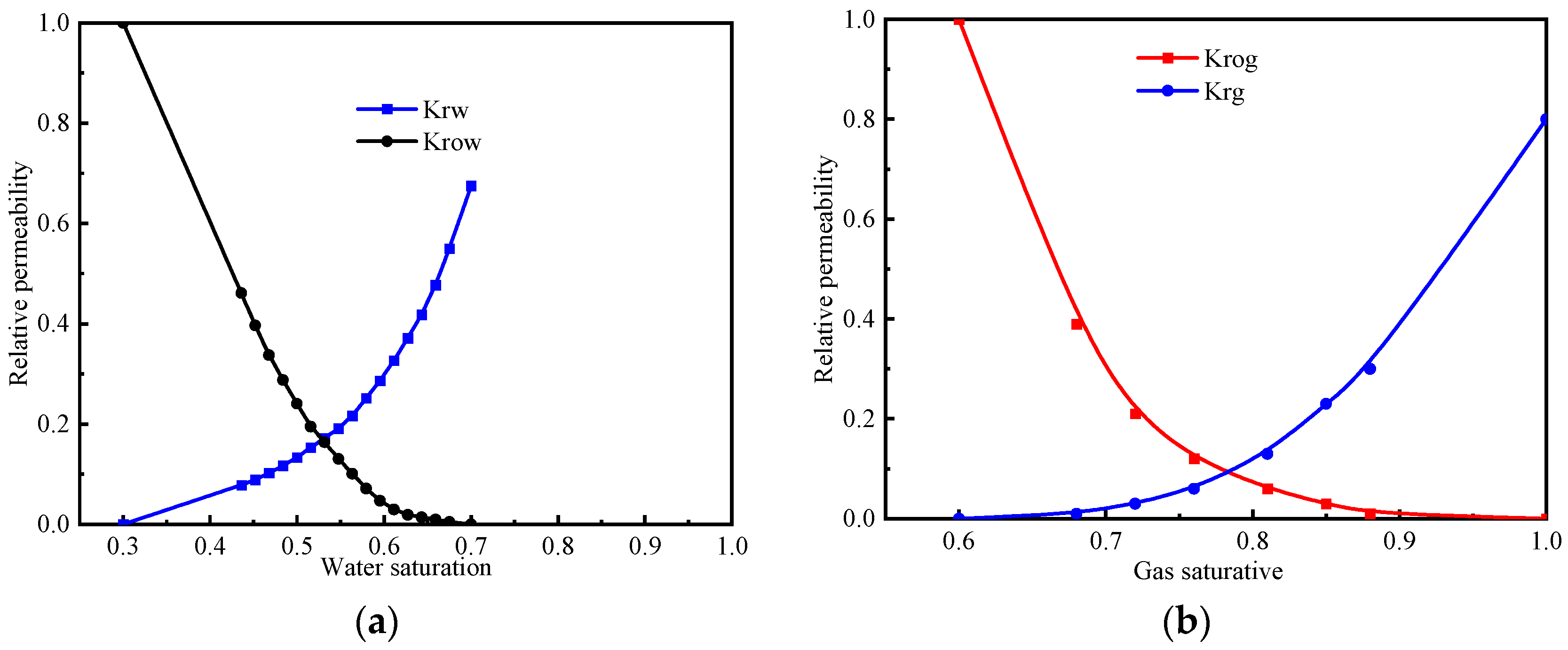
2.2. The Establishment of the Low-Permeability Reservoir Model
2.3. The Solution of Effective Buried Storage Coefficient
3. Numerical Simulation Study of CO2 Flooding and Storage
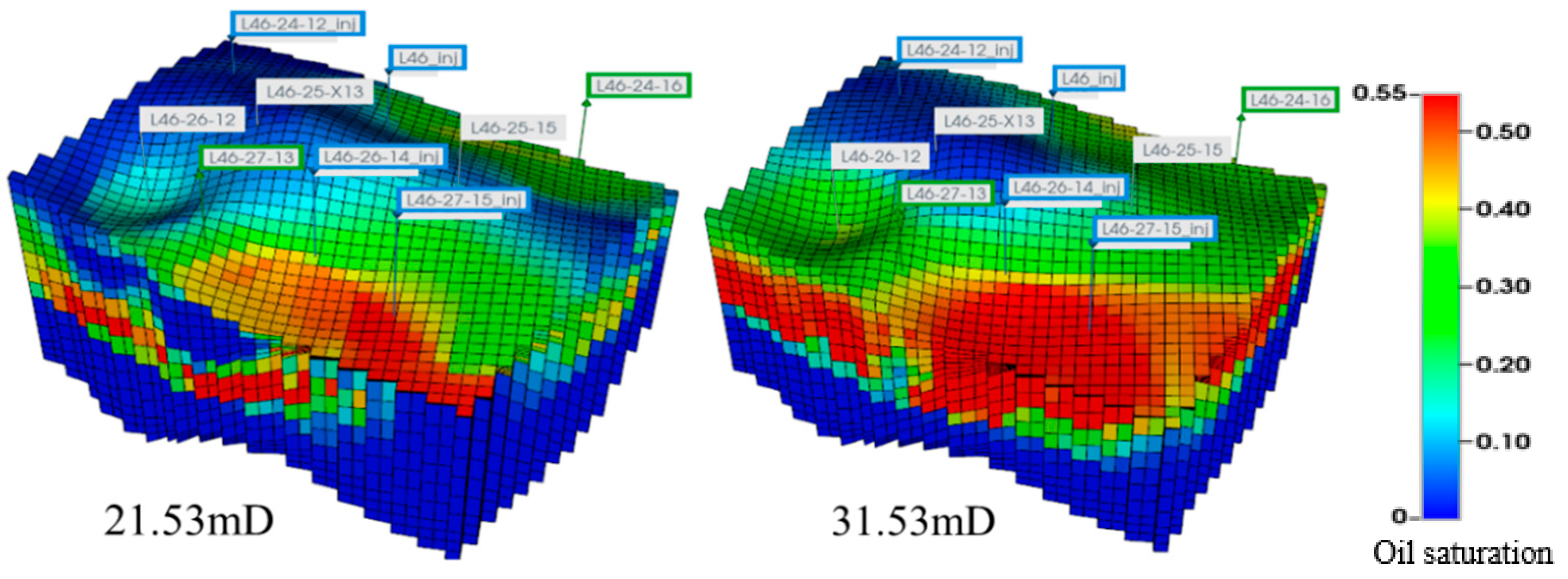
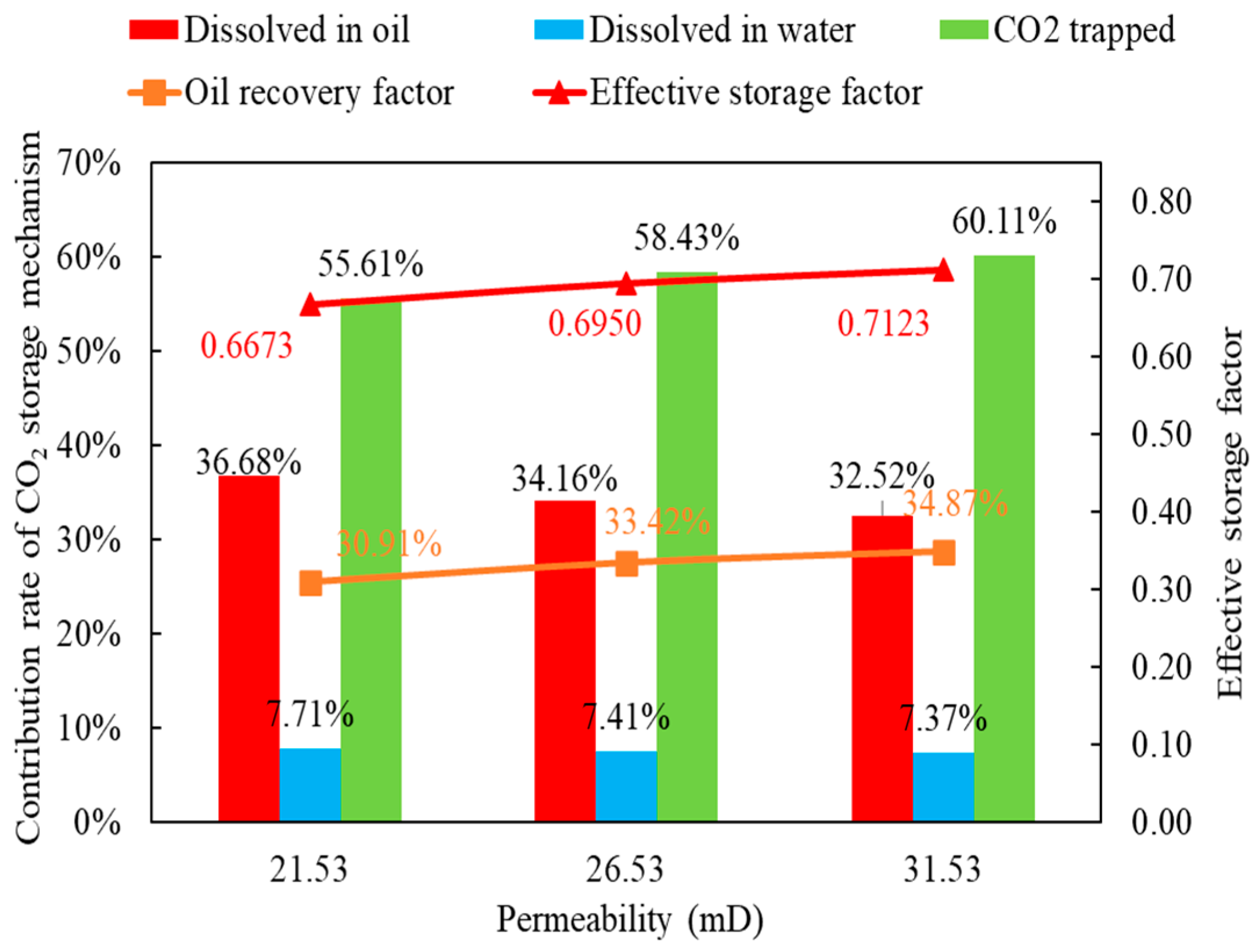
3.1. Effect of Permeability on CO2 Flooding and Storage
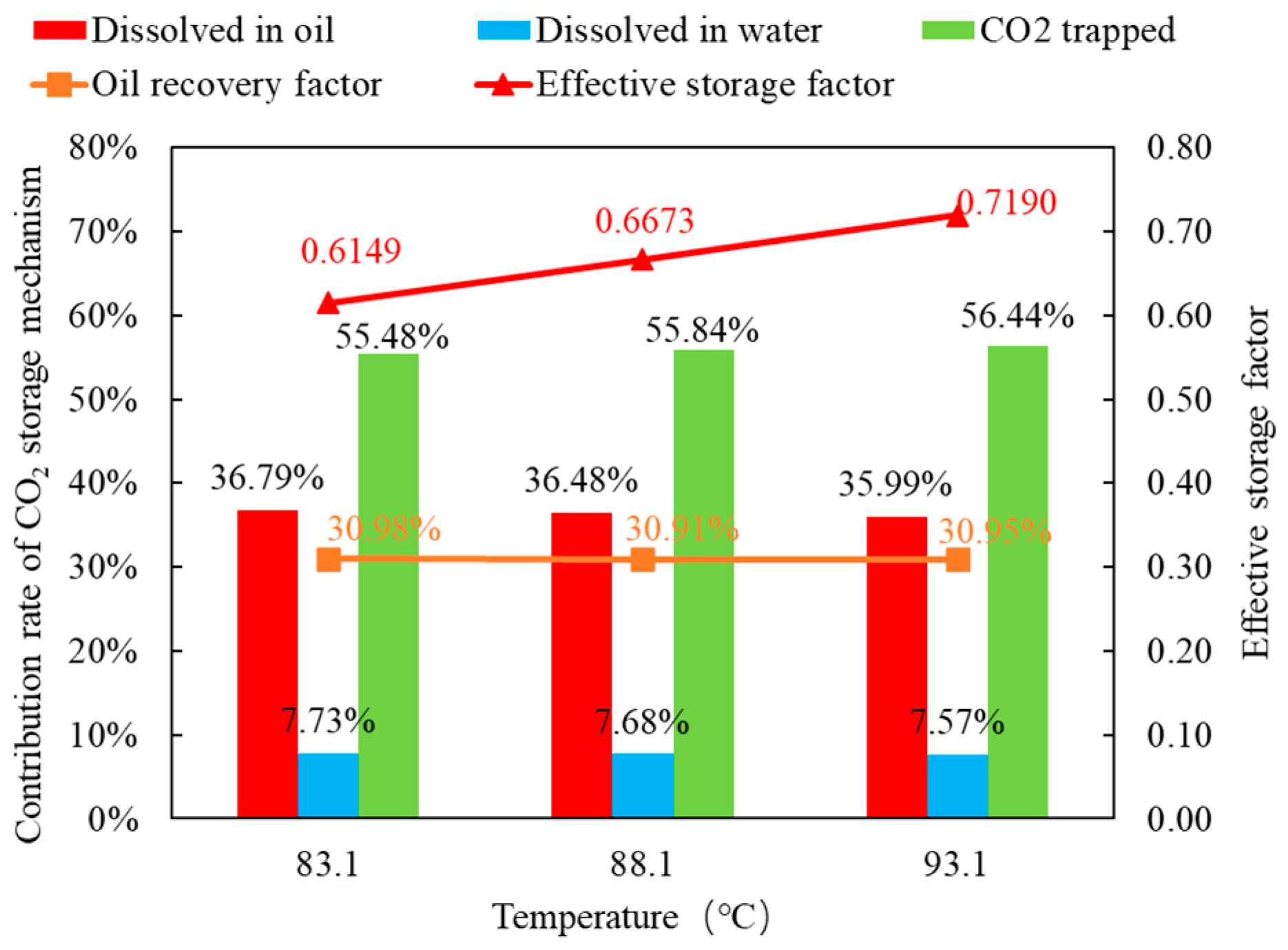
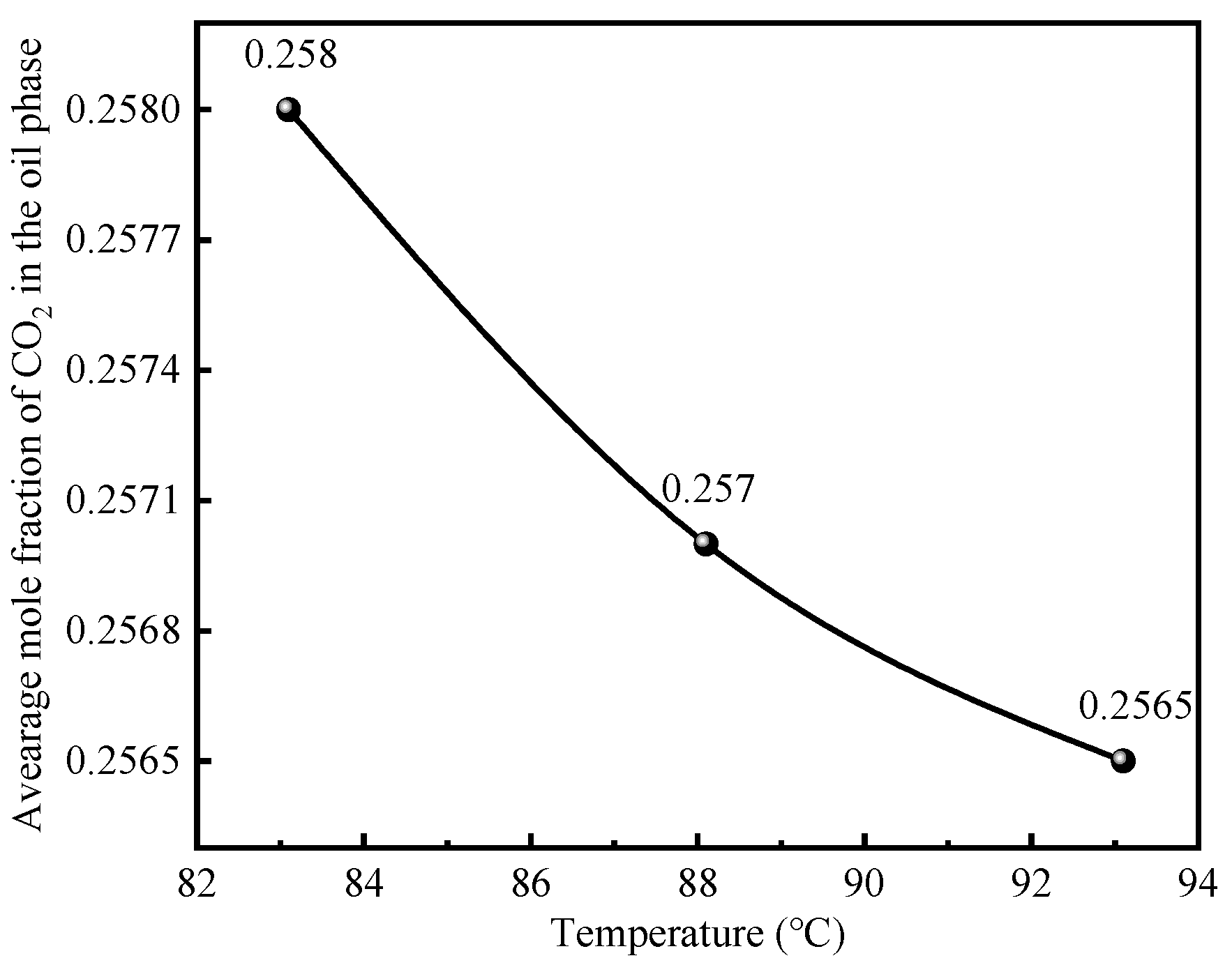
3.2. Effect of Reservoir Temperature on CO2 Flooding and Storage
3.3. Effect of Original Reservoir Pressure on CO2 Flooding and Storage
4. Prediction Model for the Effective Storage Coefficient Using Artificial Intelligence
4.1. Prediction Model for Effective Burial Coefficient
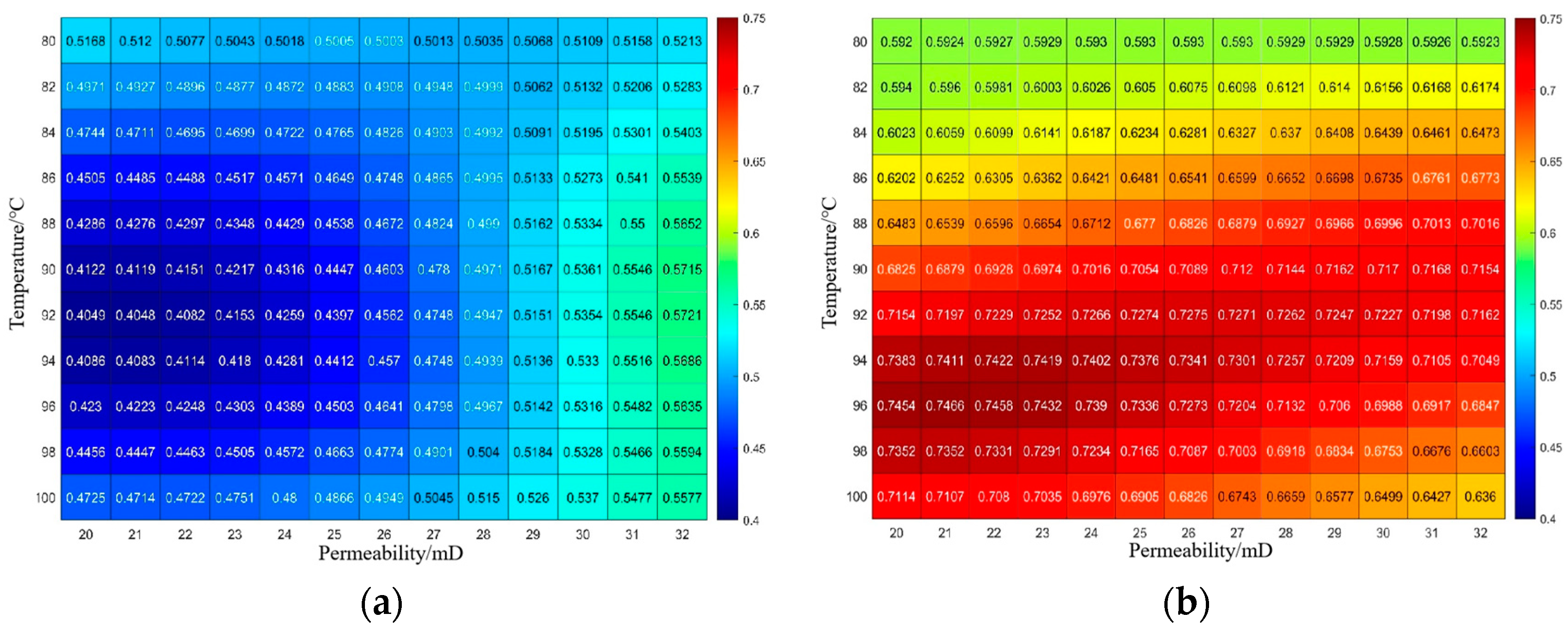
4.2. Establishment and Application of Effective Storage Coefficient Plates
5. Conclusions
- (1)
- In low-permeability oil reservoirs, an increase in permeability results in a decrease in the contribution rate of CO2 dissolution and sequestration in oil and water, while the proportion of structurally bound sequestration increases from 55% to 60%.
- (2)
- Temperature has little impact on the contribution rate of different CO2 sequestration mechanisms. The proportion of CO2 sequestration through dissolution in oil and water decreases slightly due to the reduced solubility coefficient of CO2 in oil and water at higher temperatures.
- (3)
- Higher initial reservoir pressure improves the effectiveness of CO2 enhanced oil recovery. However, when the pressure surpasses a certain threshold, gas channeling may occur during the later stages of injection, which can lead to decreased recovery and storage efficiency. During field implementation, it is crucial to ensure that the reservoir pressure exceeds the minimum miscibility pressure of CO2 and crude oil, while also maintaining it below the maximum allowable pressure of the injection equipment and pipelines.
- (4)
- A method was established using supervised machine learning to train regression models—with permeability, reservoir temperature, and initial reservoir pressure as the input variables, and the effective storage coefficient as the target function—to determine CO2 effective sequestration coefficients through artificial intelligence training models. Charts depicting effective sequestration coefficients under various conditions (permeability, reservoir pressure, temperature) enable accurate and rapid calculation of effective sequestration volumes and identification of favorable sequestration areas.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, Z.; Fan, Z.; Chen, X.; Fan, Z.; Wei, Q.; Wang, X.; Yue, W.; Liu, B.; Wu, Y. Global Oil and Gas Development in 2022: Situation, Trends, and Enlightenment. Pet. Explor. Dev. 2023, 50, 1167–1186. [Google Scholar] [CrossRef]
- Wang, Q.; Li, S.; Li, R. China’s Dependency on Foreign Oil Will Exceed 80% by 2030: Developing a Novel NMGM-ARIMA to Forecast China’s Foreign Oil Dependence from Two Dimensions. Energy 2018, 163, 151–167. [Google Scholar] [CrossRef]
- Tang, X.; Li, Y.; Cao, J.; Liu, Z.Y.; Chen, X.; Liu, L.; Zhang, Y.Q. Adaptability and enhanced oil recovery performance of surfactant polymer flooding in inverted seven-spot well pattern. Phys. Fluids 2023, 35, 053116. [Google Scholar] [CrossRef]
- Wei, B.; Song, T.; Zhao, J.Z.; Valeriy, K.; Pu, W.F. Improving the Recovery Efficiency and Sensitivity of Tight Oil Reservoirs by Dissolved Gas Reinjection. J. Southwest Pet. Univ. Sci. Technol. Ed. 2019, 41, 85–95. [Google Scholar]
- Wang, R.; Zhang, Y.; Lyu, C.; Lun, Z.M.; Cui, M.L.; Lang, D.J. Displacement characteristics of CO2 flooding in extra-high water-cut reservoirs. Energy Geosci. 2024, 5, 100115. [Google Scholar] [CrossRef]
- Wei, B.; Song, T.; Gao, Y.; Xiang, H.; Xu, X.G.; Valeriy, K.; Bai, J.L.; Zhai, Z.W. Effectiveness and sensitivity analysis of solution gas re-injection in Baikouquan tight formation, Mahu sag for enhanced oil recovery. Petroleum 2020, 6, 253–263. [Google Scholar] [CrossRef]
- Zou, C.; Lin, M.; Ma, F. Development, challenges and strategies of natural gas industry under carbon neutral target in China. Pet. Explor. Dev. 2024, 51, 476–497. [Google Scholar] [CrossRef]
- Davoodi, S.; Al-Shargabi, M.; Wood, D.A.; Mehrad, M.; Rukavishnikov, S. Carbon dioxide sequestration through enhanced oil recovery: A review of storage mechanisms and technological applications. Fuel 2024, 366, 131313. [Google Scholar] [CrossRef]
- Shi, C.; Zhi, J.; Yao, X.; Zhang, H.; Yu, Y.; Zeng, Q.S.; Li, L.J.; Zhang, Y.X. How can China achieve the 2030 carbon peak goal—A crossover analysis based on low-carbon economics and deep learning. Energy 2023, 269, 126776. [Google Scholar] [CrossRef]
- Zhong, Z.; Chen, Y.; Fu, M.; Li, M.Z.; Yang, K.S.; Zeng, L.P.; Liang, J.; Ma, R.P.; Xie, Q. Role of CO2 geological storage in China’s pledge to carbon peak by 2030 and carbon neutrality by 2060. Energy 2023, 272, 127165. [Google Scholar] [CrossRef]
- Tang, X.-C.; Li, Y.-Q.; Liu, Z.-Y.; Zhang, N. Nanoparticle-reinforced foam system for enhanced oil recovery (EOR): Mechanistic review and perspective. Pet. Sci. 2023, 20, 2282–2304. [Google Scholar] [CrossRef]
- Dou, L.; Sun, L.; Lyu, W.; Wang, M.Y.; Gao, F.; Gao, M.; Jiang, H. Trend of global carbon dioxide capture, utilization and storage industry and challenges and countermeasures in China. Pet. Explor. Dev. 2023, 50, 1246–1260. [Google Scholar] [CrossRef]
- Tang, X.; Li, Y.; Han, X.; Zhou, Y.B.; Zhan, J.F.; Xu, M.M.; Zhou, R.; Cui, K.; Chen, X.L.; Wang, L. Dynamic characteristics and influencing factors of CO2 huff and puff in tight oil reservoirs. Pet. Explor. Dev. 2021, 48, 946–955. [Google Scholar] [CrossRef]
- Zhang, Z.H.; Yang, Z.M.; Liu, X.G.; Xiong, W.; Wang, X.W. A grading evaluation method for low-permeability reservoirs and its application. Acta Pet. Sin. 2012, 33, 437–441. [Google Scholar]
- Mahdaviara, M.; Sharifi, M.; Ahmadi, M. Toward evaluation and screening of the enhanced oil recovery scenarios for low permeability reservoirs using statistical and machine learning techniques. Fuel 2022, 325, 124795. [Google Scholar] [CrossRef]
- Wei, B.; Zhang, X.; Wu, R.; Zou, P.; Gao, K.; Xu, X.G.; Pu, W.F.; Wood, C. Pore-scale monitoring of CO2 and N2 flooding processes in a tight formation under reservoir conditions using nuclear magnetic resonance (NMR): A case study. Fuel 2019, 246, 34–41. [Google Scholar] [CrossRef]
- Hill, L.B.; Li, X.; Wei, N. CO2-EOR in China: A comparative review. Int. J. Greenh. Gas Control 2020, 103, 103173. [Google Scholar] [CrossRef]
- Wang, L.; Wei, B.; You, J.; Pu, W.F.; Tang, J.Y.; Lu, J. Performance of a tight reservoir horizontal well induced by gas huff–n–puff integrating fracture geometry, rock stress-sensitivity and molecular diffusion: A case study using CO2, N2 and produced gas. Energy 2023, 263, 125696. [Google Scholar] [CrossRef]
- Lu, L.; Liu, B. A Feasibility Research Method and Project Design on CO2 Miscible Flooding for a Small Complex Fault Block Field. In Proceedings of the SPE International Oil and Gas Conference and Exhibition in China, Beijing, China, 2–6 November 1998; pp. SPE-50930-MS, 501–515. [Google Scholar]
- Xu, S.; Ren, G.; Younis, R.M.; Feng, Q. Revisiting field estimates for carbon dioxide storage in depleted shale gas reservoirs: The role of geomechanics. Int. J. Greenh. Gas Control 2021, 105, 103222. [Google Scholar] [CrossRef]
- Haishui, H.A.N.; Shiyi, Y.U.A.N.; Shi, L.I.; Xiaolei, L.; Xinglong, C. Dissolving capacity and volume expansion of carbon dioxide in chain n-alkanes. Pet. Explor. Dev. 2015, 42, 97–103. [Google Scholar]
- He, Y.; Liu, M.; Tang, Y.; Jia, C.Q.; Wang, Y.; Rui, Z.H. CO2 storage capacity estimation by considering CO2 Dissolution: A case study in a depleted gas Reservoir, China. J. Hydrol. 2024, 630, 130715. [Google Scholar] [CrossRef]
- Kutsienyo, E.J.; Ampomah, W.; Sun, Q.; Balch, R.S.; You, J.; Aggrey, W.N.; Cather, M. Evaluation of CO2-EOR Performance and Storage Mechanisms in an Active Partially Depleted Oil Reservoir. In Proceedings of the SPE Europec featured at 81st EAGE Conference and Exhibition, London, UK, 3–6 June 2019; p. SPE-195534-MS. [Google Scholar]
- Sedaghatinasab, R.; Kord, S.; Moghadasi, J.; Soleymanzaden, A. Relative Permeability Hysteresis and Capillary Trapping during CO2 EOR and Sequestration. Int. J. Greenh. Gas Control 2021, 106, 103262. [Google Scholar] [CrossRef]
- Wang, Y.Z.; Cao, R.Y.; Jia, Z.H.; Wang, B.Y.; Ma, M.; Cheng, L.S. A multi-mechanism numerical simulation model for CO2-EOR and storage in fractured shale oil reservoirs. Pet. Sci. 2024, 21, 1814–1828. [Google Scholar] [CrossRef]
- Zhang, R.H.; Wu, J.F.; Zhao, Y.L.; He, X.; Wang, R.H. Numerical simulation of the feasibility of supercritical CO2 storage and enhanced shale gas recovery considering complex fracture networks. J. Pet. Sci. Eng. 2021, 204, 108671. [Google Scholar] [CrossRef]
- Yamaguchi, A.J.; Sato, T.; Tobase, T.; Wei, X.; Huang, L.; Zhang, J.; Bian, J.; Liu, T. Multiscale numerical simulation of CO2 hydrate storage using machine learning. Fuel 2023, 334, 126678. [Google Scholar] [CrossRef]
- Liu, D.; Li, Y.; Agarwal, R.K. Numerical simulation of long-term storage of CO2 in Yanchang shale reservoir of the Ordos basin in China. Chem. Geol. 2016, 440, 288–305. [Google Scholar] [CrossRef]
- Andrić, I.; Pinaa, A.; Ferrão, P.; Fournier, J.; Lacarrière, B.; Le Corre, O. Assessing the feasibility of using the heat demand-outdoor temperature function for a long-term district heat demand forecast. Energy Procedia 2017, 158, 6079–6086. [Google Scholar] [CrossRef]
- Thibeau, S.; Bachu, S.; Birkholzer, J.; Holloway, S.; Neele, F.; Zhou, Q. Using Pressure and Volumetric Approaches to Estimate CO2 Storage Capacity in Deep Saline Aquifers. Energy Procedia 2014, 63, 5294–5304. [Google Scholar] [CrossRef]
- Shen, P.P.; Liao, X.W.; Liu, Q.J. Methodology for estimation of CO2 storage capacity in reservoirs. Pet. Explor. Dev. 2009, 36, 216–220. [Google Scholar] [CrossRef]
- Zhao, X.; Liao, X.; Wang, W.; Chen, C.Z.; Rui, Z.H.; Wang, H. The CO2 storage capacity evaluation: Methodology and determination of key factors. J. Energy Inst. 2014, 87, 297–305. [Google Scholar] [CrossRef]
- Abdulwarith, A.; Ammar, M.; Dindoruk, B. Prediction/Assessment of CO2 EOR and Storage Efficiency in Residual Oil Zones Using Machine Learning Techniques. In Proceedings of the SPE/AAPG/SEG Carbon, Capture, Utilization, and Storage Conference and Exhibition, Houston, TX, USA, 11–13 March 2024; p. SPE-CCUS-2024-4011705. [Google Scholar]
- Ren, D.; Wang, X.; Kou, Z.; Wang, S.C.; Wang, H.; Wang, X.G.; Tang, Y.; Jiao, Z.S.; Zhou, D.S.; Zhang, R.J. Feasibility evaluation of CO2 EOR and storage in tight oil reservoirs: A demonstration project in the Ordos Basin. Fuel 2023, 331, 125652. [Google Scholar] [CrossRef]
- Gao, R.; Lv, C.Y.; Zhou, K.; Lun, Z.M.; Zhou, B. A CO2 flooding dynamic storage potential calculation method based on compositional flash calculation. Oil Drill. Prod. Technol. 2021, 43, 70–75. [Google Scholar]
- Li, S.Y.; Qiao, C.Y.; Li, Z.M.; Hui, Y.T. The effect of permeability on supercritical CO2 diffusion coefficient and determination of diffusive tortuosity of porous media under reservoir conditions. J. CO2 Util. 2018, 28, 1–14. [Google Scholar] [CrossRef]



| Component | Molar Composition/% | Component | Molar Composition/% |
|---|---|---|---|
| N2 | 0.02 | C6–C12 | 10.46 |
| CO2 | 0.36 | C13–C21 | 15.07 |
| CH4 | 48.67 | C22–C29 | 12.47 |
| C2-C5 | 9.58 | C30–C38 | 3.37 |
| Saturation Pressure/MPa | Viscosity/(mPa·s) | Gas–Oil Ratio/(m3/m3) | ||||||
|---|---|---|---|---|---|---|---|---|
| Experimental Value | Simulation Value | Error/% | Experimental Value | Simulation Value | Error/% | Experimental Value | Simulation Value | Error/% |
| 15.6 | 16.2 | 3.84% | 3.2 | 3.1 | 3.2% | 91.5 | 89.2 | 2.5% |
| Component | Critical Pressure/MPa | Critical Temperature/K | Critical Volume/(L·mol−1) | Acentric Factor | Molecular Weight/(g·mol−1) | Ωa | Ωb |
|---|---|---|---|---|---|---|---|
| N2 | 3.39 | 126.2 | 0.09 | 0.04 | 28.01 | 0.46 | 0.08 |
| CO2 | 7.38 | 304.2 | 0.094 | 0.23 | 44.01 | 0.46 | 0.08 |
| CH4 | 4.6 | 190.6 | 0.099 | 0.01 | 16.04 | 0.46 | 0.08 |
| C2–C5 | 3.76 | 422.54 | 0.257 | 0.19 | 59.37 | 0.46 | 0.08 |
| C6–C12 | 2.32 | 562.96 | 0.422 | 0.35 | 129.25 | 0.46 | 0.09 |
| C13–C21 | 2.26 | 800 | 0.875 | 0.72 | 300.62 | 0.55 | 0.09 |
| C22–C29 | 0.79 | 778.85 | 1.215 | 0.97 | 430.22 | 0.41 | 0.07 |
| C30–C38 | 0.66 | 680.06 | 1.482 | 1.12 | 499.32 | 0.37 | 0.06 |
| Model | Fine Model | RMSE | MSE | R2 | MAE |
|---|---|---|---|---|---|
| Gaussian process regression model | Quadratic rational GPR | 0.032237 | 0.001039 | 0.919931 | 0.023666 |
| Square exponential GPR | 0.036601 | 0.00134 | 0.844762 | 0.027608 | |
| Matern 5/2 | 0.051279 | 0.00263 | 0.521953 | 0.039756 | |
| Exponent GPR | 0.032237 | 0.001039 | 0.919934 | 0.023666 |
| Initial Formation Pressure/MPa | Average Permeability/mD | Reservoir Temperature/°C | Bound Water Saturation | Pore Volume/m3 | Recovery Rate/% | |
|---|---|---|---|---|---|---|
| Before CO2 Breakout | After CO2 Breakout | |||||
| 31 | 22 | 88 | 0.3 | 6,108,620 | 2.54 | 20.01 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, Z.; Tian, M.; Li, M.; Mi, Y.; Jiang, Y.; Song, T.; Cao, J.; Liu, Z. Assessment of CO2 Sequestration Capacity in a Low-Permeability Oil Reservoir Using Machine Learning Methods. Energies 2024, 17, 3979. https://doi.org/10.3390/en17163979
Fan Z, Tian M, Li M, Mi Y, Jiang Y, Song T, Cao J, Liu Z. Assessment of CO2 Sequestration Capacity in a Low-Permeability Oil Reservoir Using Machine Learning Methods. Energies. 2024; 17(16):3979. https://doi.org/10.3390/en17163979
Chicago/Turabian StyleFan, Zuochun, Mei Tian, Man Li, Yidi Mi, Yue Jiang, Tao Song, Jinxin Cao, and Zheyu Liu. 2024. "Assessment of CO2 Sequestration Capacity in a Low-Permeability Oil Reservoir Using Machine Learning Methods" Energies 17, no. 16: 3979. https://doi.org/10.3390/en17163979
APA StyleFan, Z., Tian, M., Li, M., Mi, Y., Jiang, Y., Song, T., Cao, J., & Liu, Z. (2024). Assessment of CO2 Sequestration Capacity in a Low-Permeability Oil Reservoir Using Machine Learning Methods. Energies, 17(16), 3979. https://doi.org/10.3390/en17163979








