Preliminary Insight into Ice Melting, Surface Subsidence, and Wellhead Instability during Oil and Gas Extraction in Permafrost Region
Abstract
1. Introduction
- (1)
- The factors affecting the mechanical properties of permafrost in an ultra-low temperature environment (below −20 °C) were studied.
- (2)
- The influence mechanism of various factors on the mechanical properties of permafrost was explored.
- (3)
- Wellhead stability during oil and gas development in permafrost was analyzed.
2. Experiments and Methods
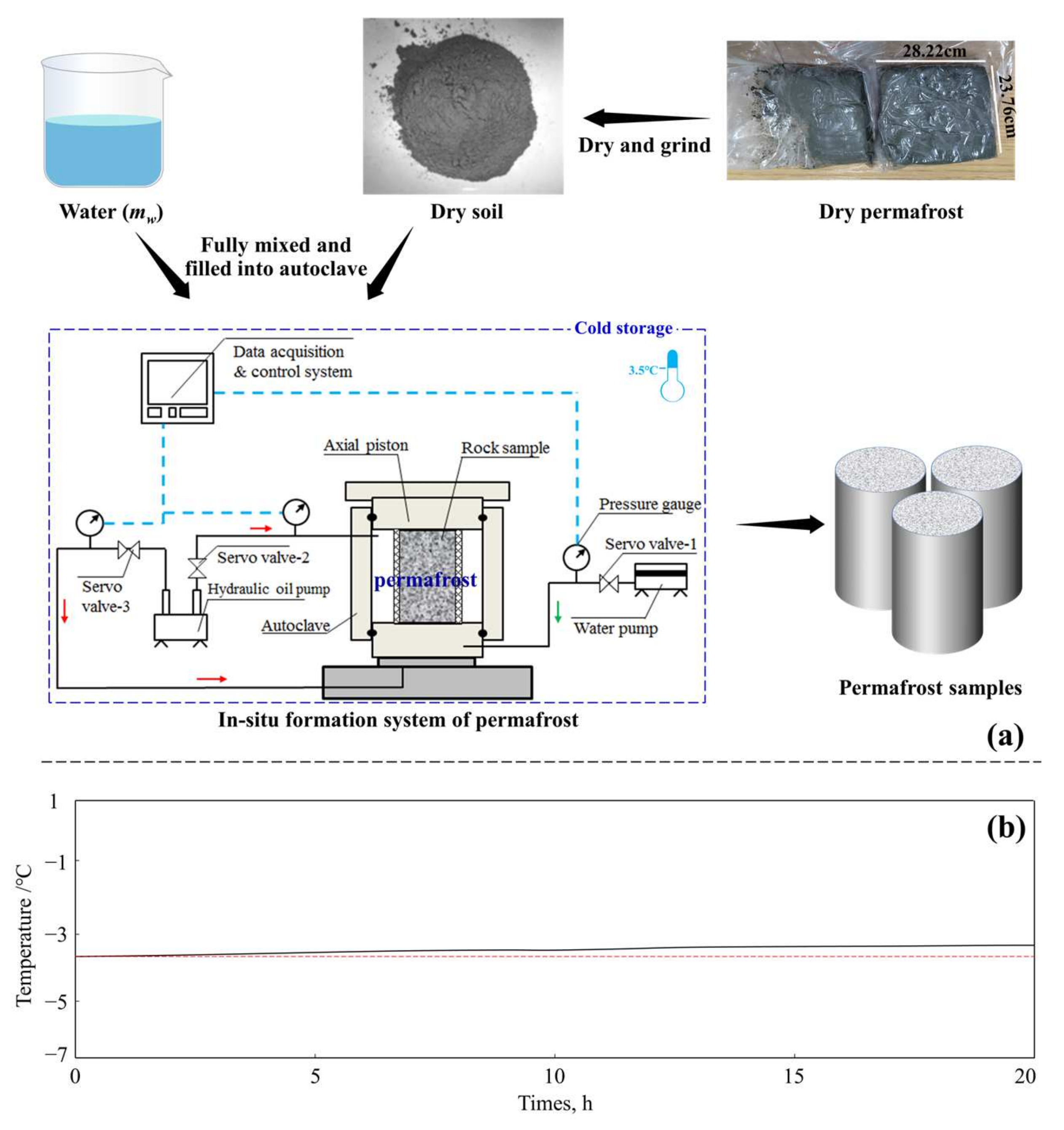
2.1. Experimental System
2.2. Experimental Methodology and Materials
- (1)
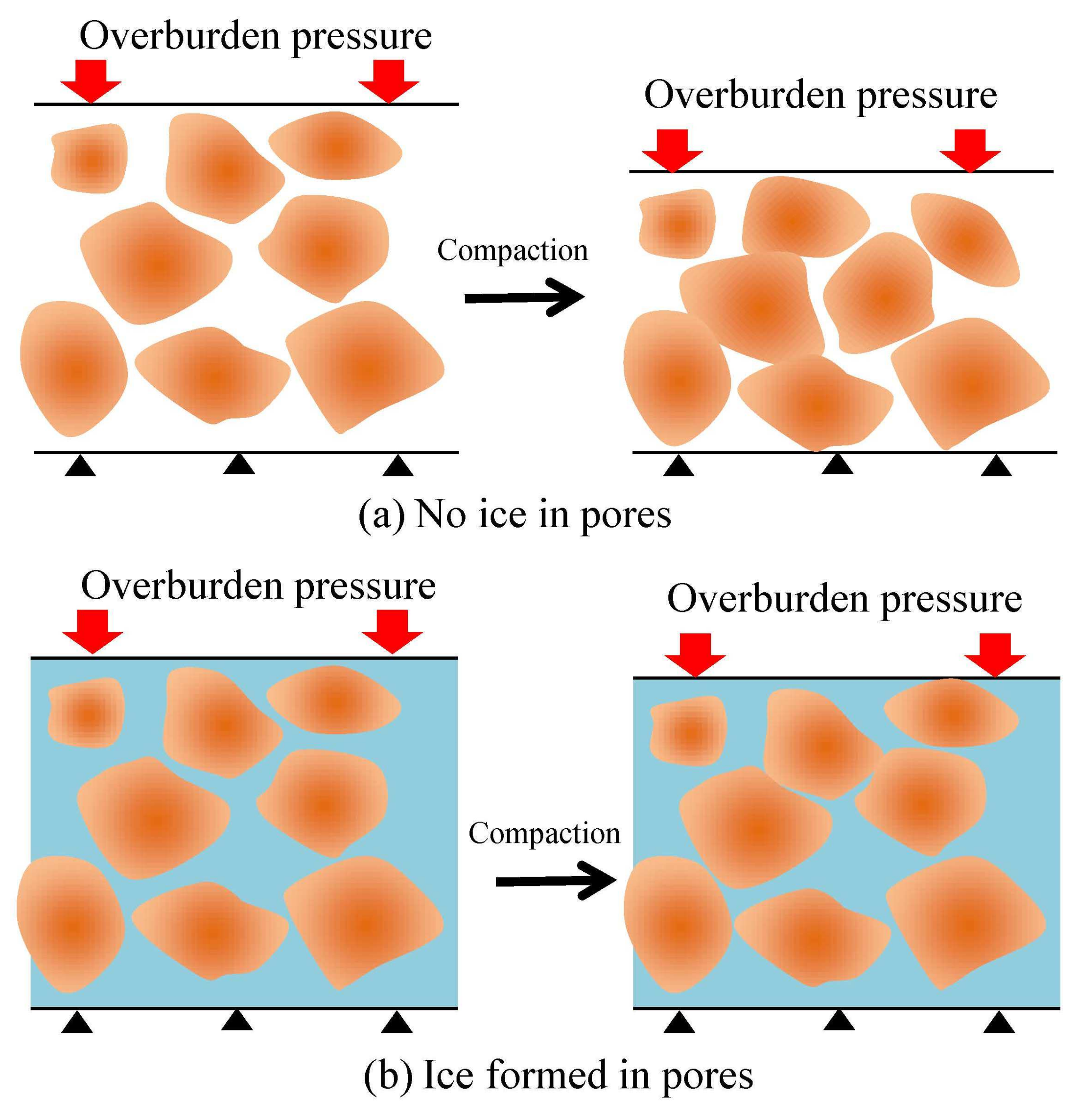
- Remolding of soil samples. As mentioned above, permafrost is difficult and expensive to preserve. In the present work, all permafrost rock samples used for mechanical experiments were artificially prepared. The process of preparing permafrost rock samples is shown in Figure 3. As observed in Figure 3a, samples obtained from the Arctic region need to be fully dried before preparation. The purpose is to ensure that water saturation in prepared permafrost samples meets the design value. Then, crushed permafrost samples need to be fully mixed with distilled water in the preparation tool. At this time, the temperature in the cold storage unit is adjusted to the required value. Importantly, this temperature should be below the freezing point. Samples were prepared by placing the preparation tool on the triaxial experimental machine. The load applied to the rock sample during the preparation process is determined by in situ stress testing, and it should be equal to the overlying pressure (σv). As shown in Figure 3b, when the temperature in the preparation tool remains stable, it indicates that the operation has been completed.
- (2)
- Measurement of mechanical properties. Confining pressure (corresponding to the horizontal stress at a specific depth) was applied to the outside surface of the sample by a hydraulic oil pump. In this study, the effective confining pressure was set at values of 0, 1.5, 3.0, and 4.5 MPa. Importantly, the confining pressure should be maintained for 6 h until all water in the sample is frozen. After that, the sample is axially loaded at a rate of 0.25 mm/min until shear failure occurs. Stress and strain are recorded in real time through the experimental data acquisition and control system in the experiment. Based on the stress–strain curve, the mechanical parameters of the permafrost samples can be obtained.
3. Results
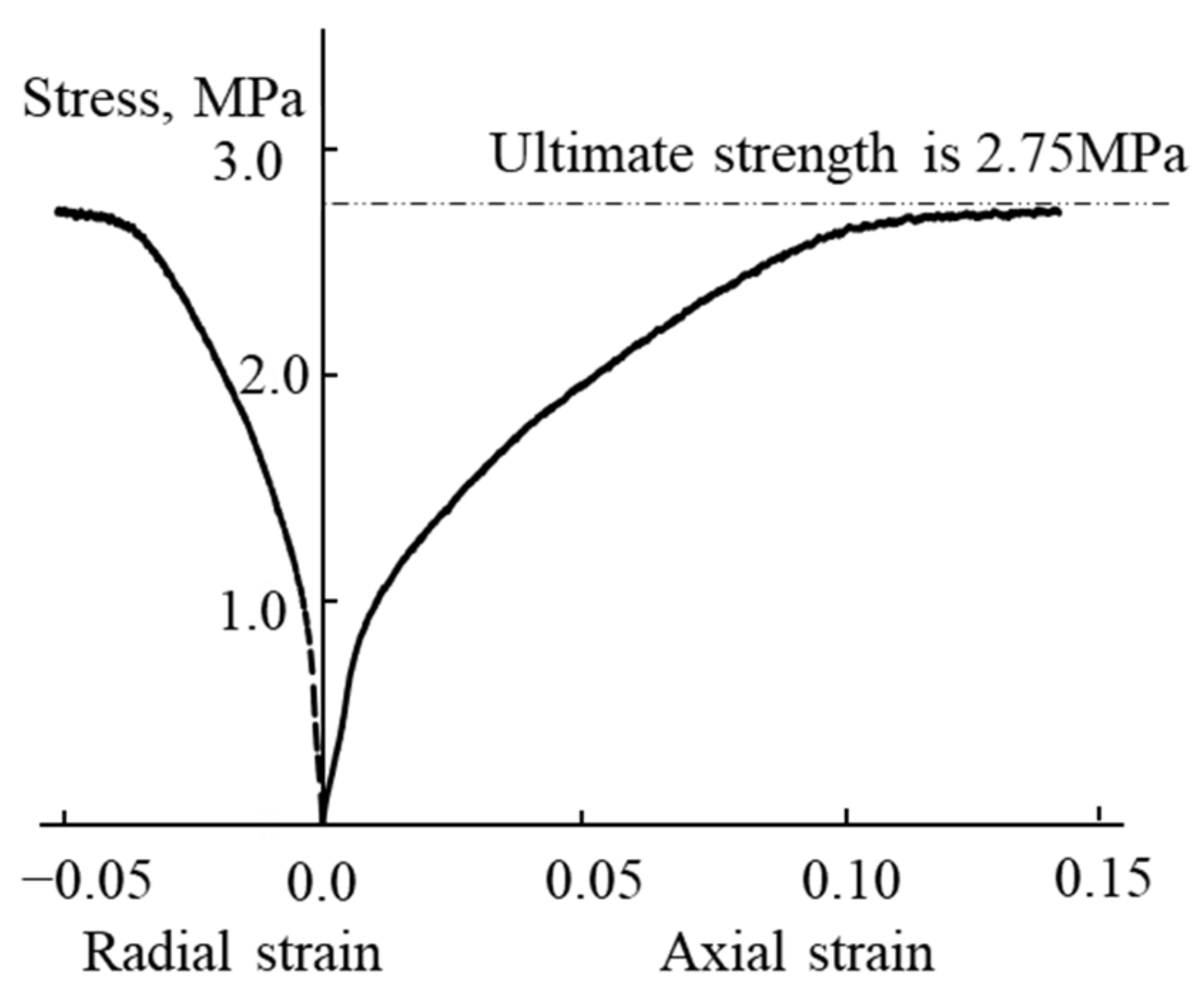
3.1. Ultimate Strength
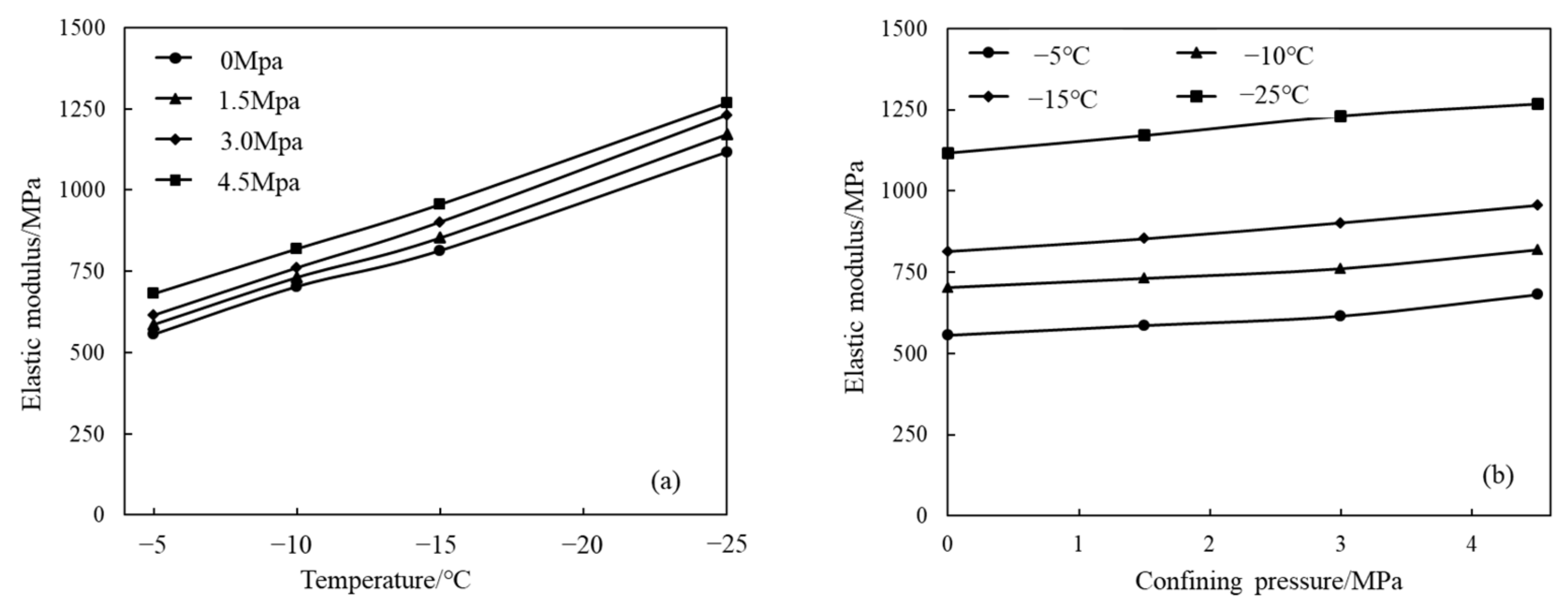
3.2. Elastic Modulus and Poisson’s Ratio
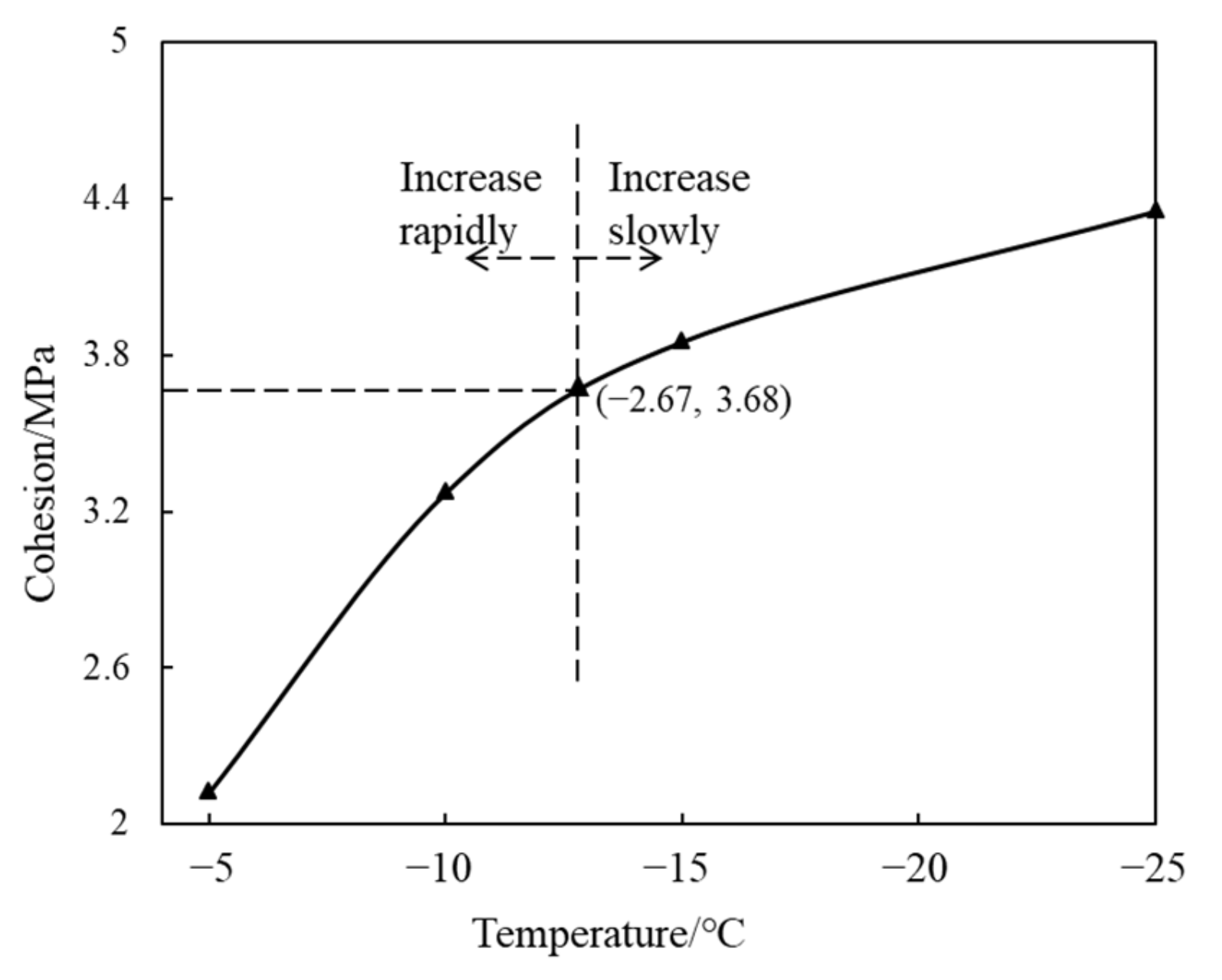
3.3. Cohesion and Internal Friction Angle
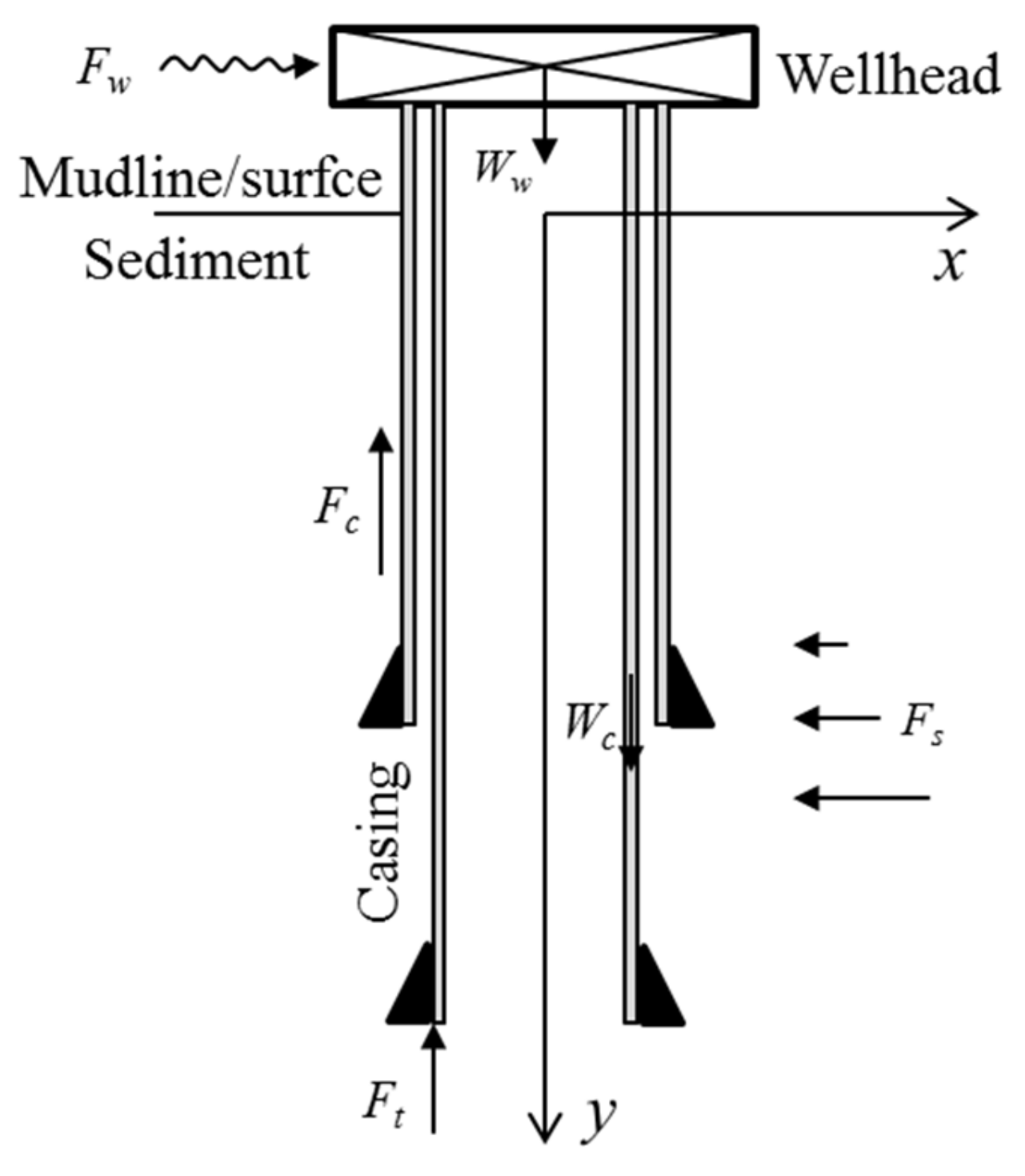
4. Numerical Simulation of Ice Melting, Surface Subsidence, and Wellhead Stability
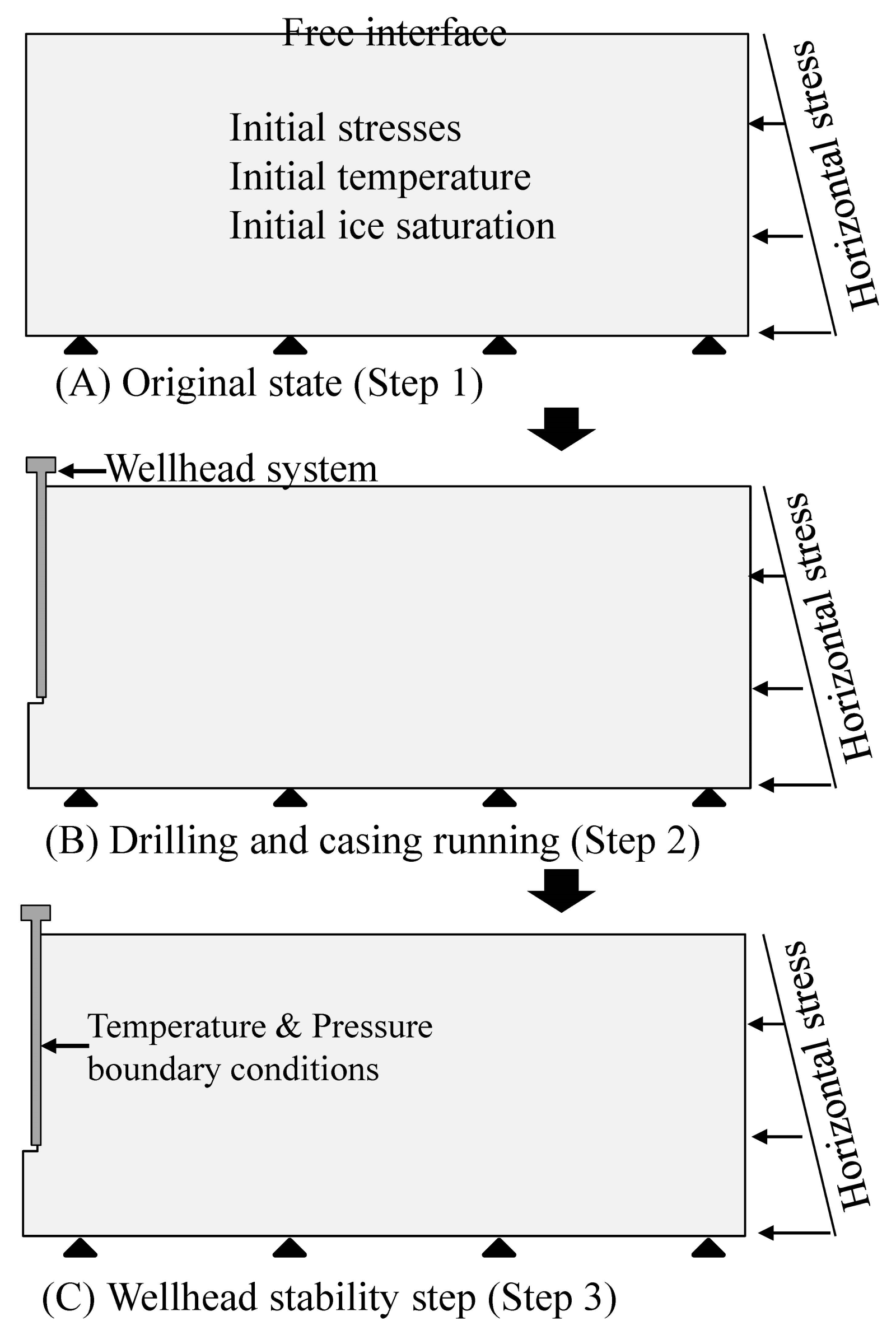
4.1. Numerical Model
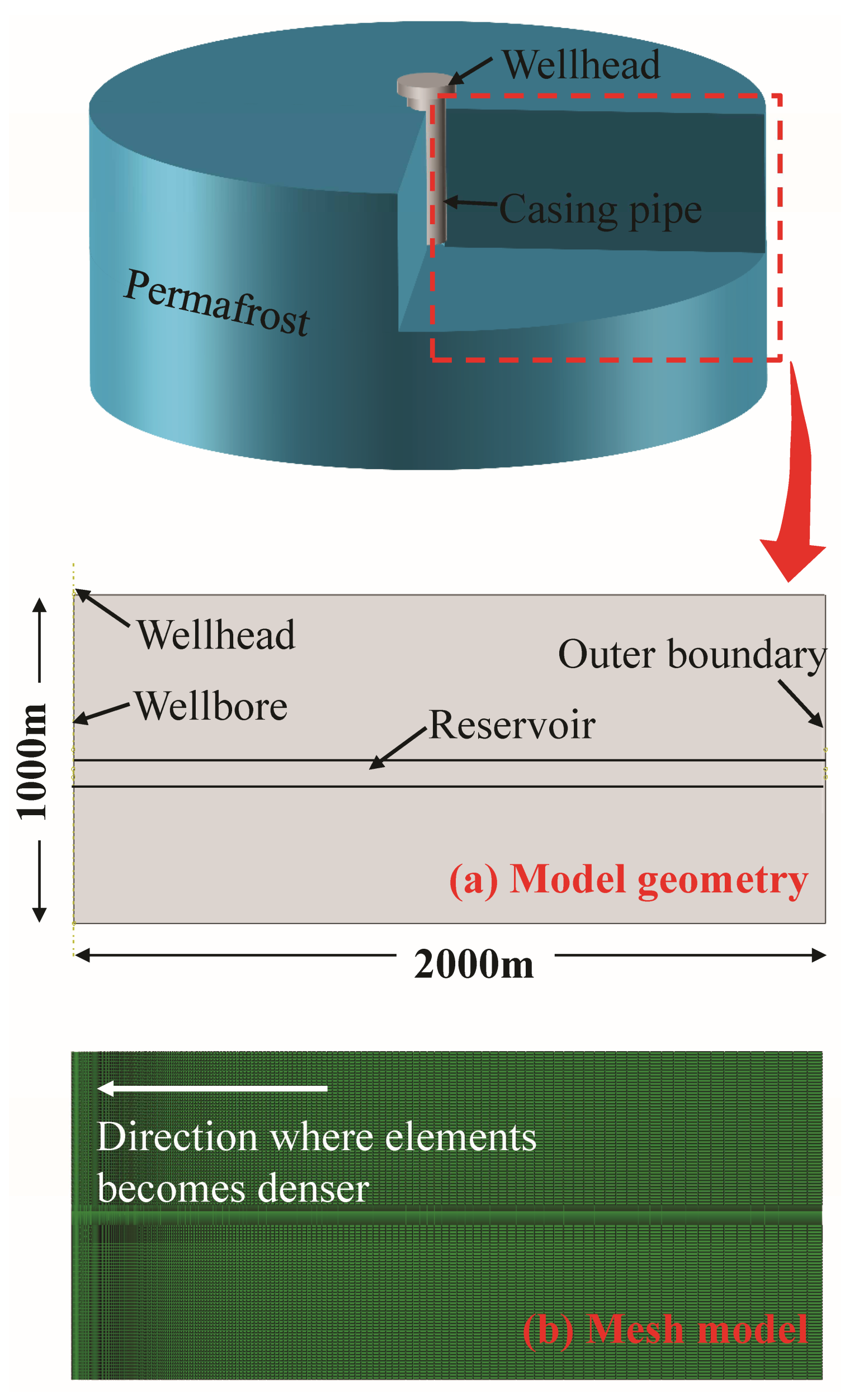
4.1.1. Model Geometry
4.1.2. Simulation Methodology
4.2. Basic Parameters for Investigation
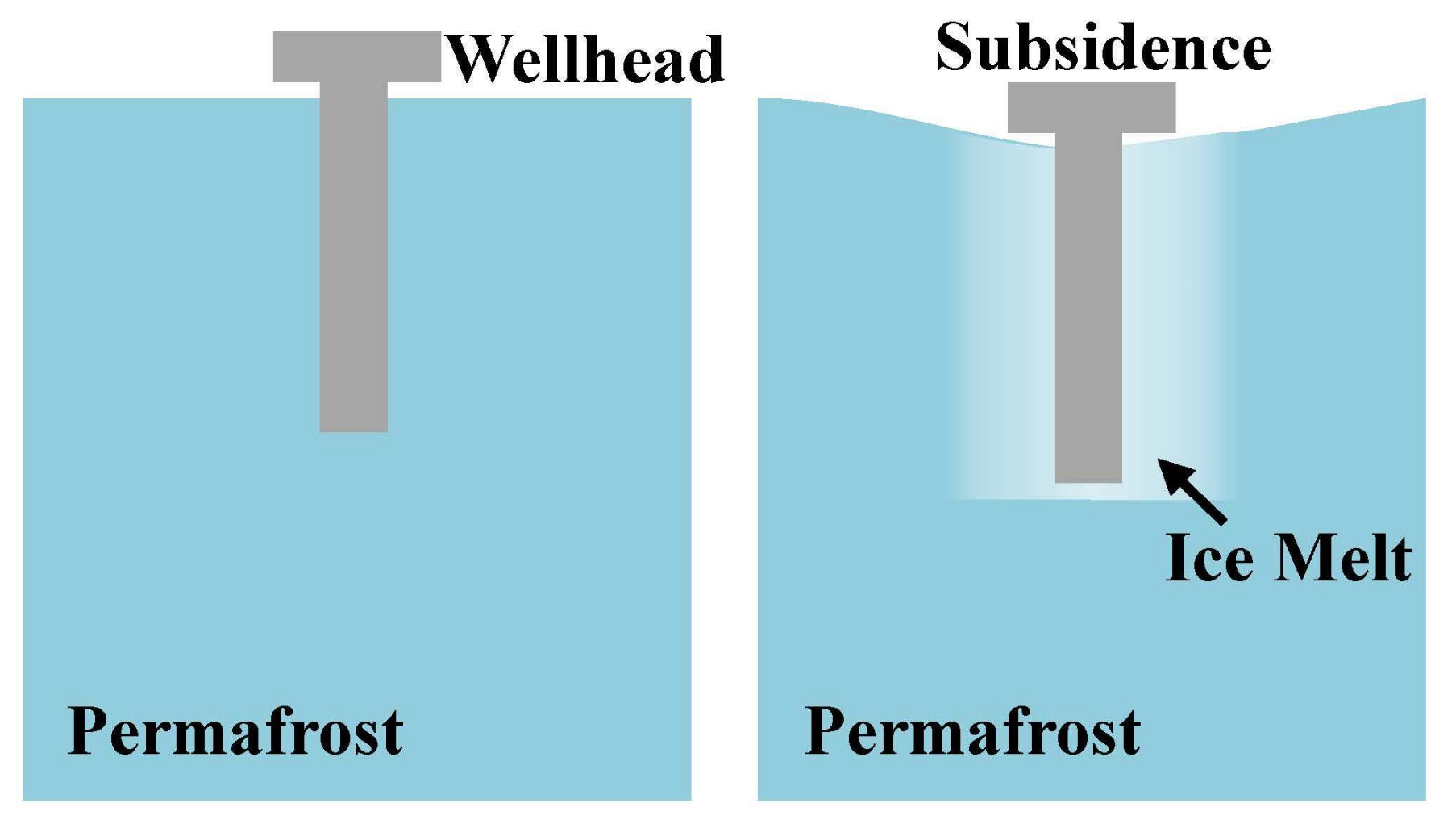
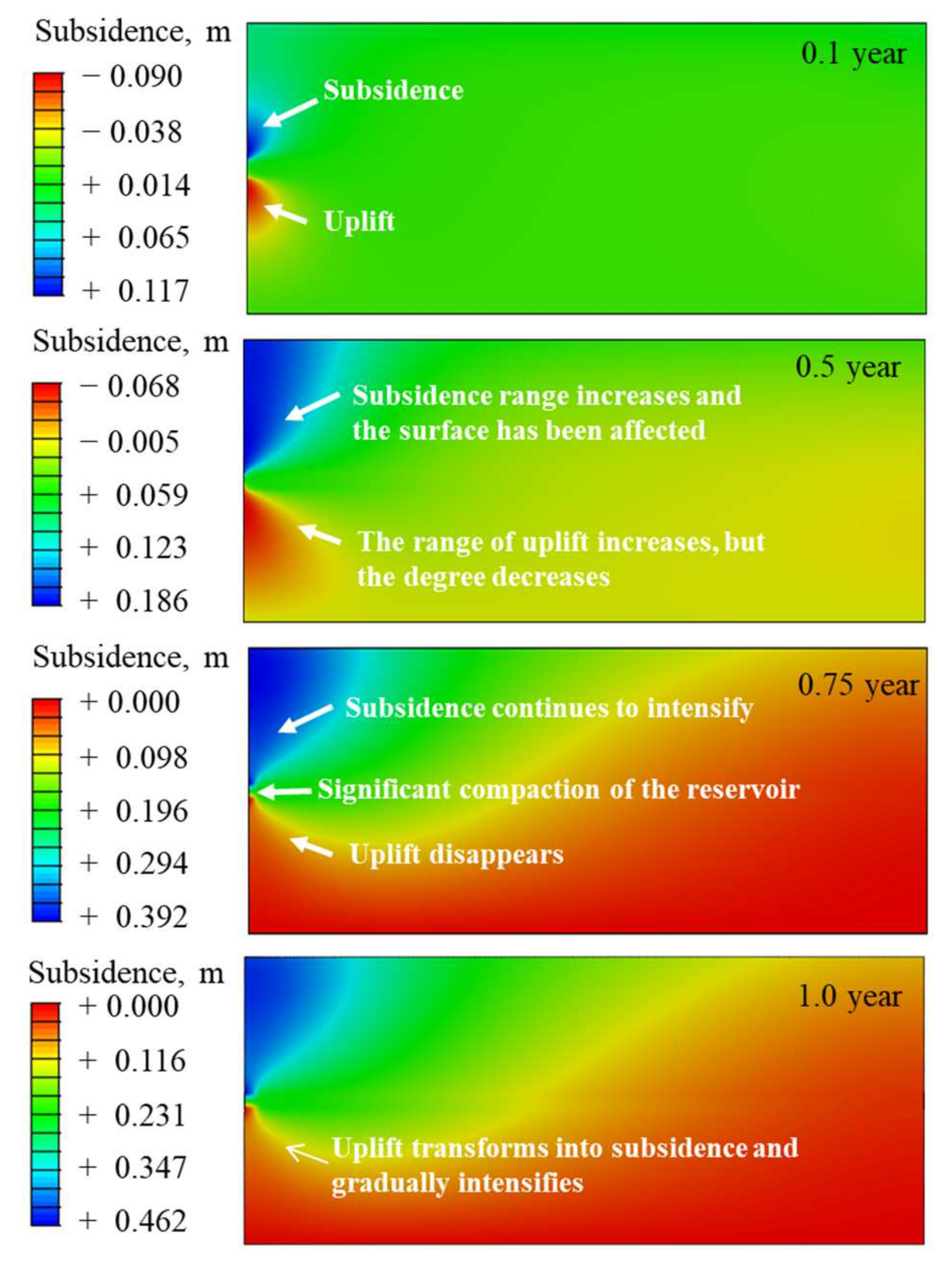
4.3. Ice Melting and Permafrost Subsidence
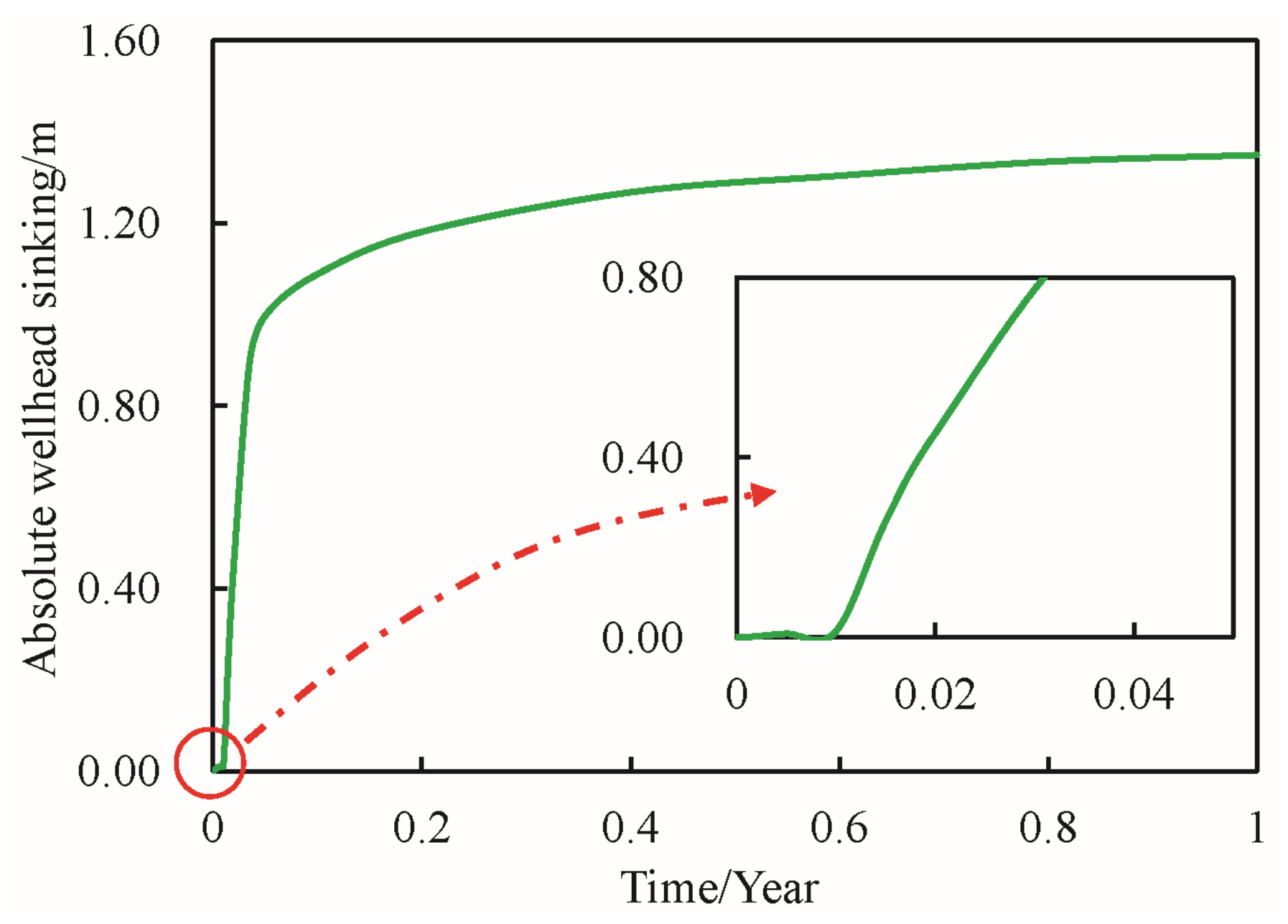
4.4. Instability Behavior of a Wellhead in Permafrost
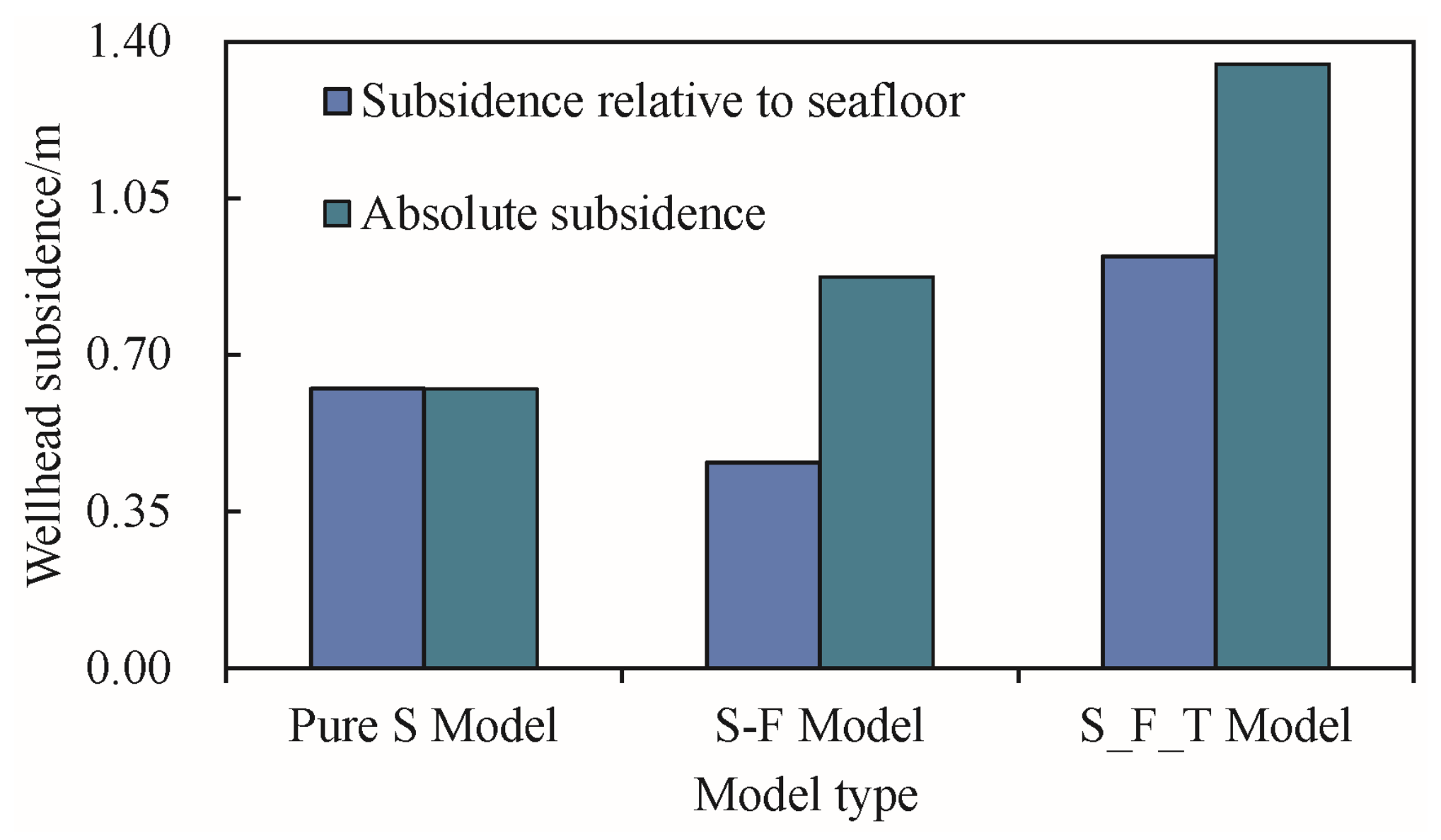
4.5. Effect of Model Type on Wellhead Stability
4.6. Prevention of Ice Melting and Wellhead Instability in Permafrost
5. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A


References
- Wang, X.; Wang, Z.; Deng, X.; Sun, B.; Zhao, Y.; Fu, W. Coupled thermal model of wellbore and permafrost in Arctic regions. Appl. Therm. Eng. 2017, 123, 1291–1299. [Google Scholar] [CrossRef]
- Yakushev, V. Environmental and Technological Problems for Natural Gas Production in Permafrost Regions. Energies 2023, 16, 4522. [Google Scholar] [CrossRef]
- Misyurkeeva, N.; Buddo, I.; Kraev, G.; Smirnov, A.; Nezhdanov, A.; Shelokhov, I.; Belonosov, A. Periglacial Landforms and Fluid Dynamics in the Permafrost Domain: A Case from the Taz Peninsula, West Siberia. Energies 2022, 15, 2794. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, F.; Yang, Z.; Yang, P. Experimental investigation on the mechanical properties of thawed deep permafrost from the Kuparuk River Delta of the North Slope of Alaska. Cold Reg. Sci. Technol. 2022, 195, 103482. [Google Scholar] [CrossRef]
- Chen, P.; Li, R.; Jia, G.; Lan, H.; Fu, K.; Liu, X. A Decade Review of the Art of Inspection and Monitoring Technologies for Long-Distance Oil and Gas Pipelines in Permafrost Areas. Energies 2023, 16, 1751. [Google Scholar] [CrossRef]
- Deng, X.; Pan, S.; Wang, Z.; Ke, K.; Zhang, J. Application of the Darcy-Stefan model to investigate the thawing subsidence around the wellbore in the permafrost region. Appl. Therm. Eng. 2019, 156, 392–401. [Google Scholar] [CrossRef]
- Kutasov, I.; Eppelbaum, L. The effect of thermal properties changing (at ice-water transition) on the radius of permafrost thawing. Cold Reg. Sci. Technol. 2018, 151, 156–158. [Google Scholar] [CrossRef]
- Li, Y.; Cheng, Y.; Yan, C.; Xue, M.; Niu, C.; Gao, Y.; Wang, T. Simulating the effect of frozen soil thaw on wellhead stability during oil and gas drilling operations in arctic waters. J. Cold Reg. Eng. 2020, 34, 04020026. [Google Scholar] [CrossRef]
- Cheng, Y.; Xue, M.; Shi, J.; Li, Y.; Yan, C.; Han, Z.; Yang, J. Numerical simulating the influences of hydrate decomposition on wellhead stability. Processes 2023, 11, 1586. [Google Scholar] [CrossRef]
- Wan, Y.; Wu, N.; Hu, G.; Xin, X.; Jin, G.; Liu, C.; Chen, Q. Reservoir stability in the process of natural gas hydrate production by depressurization in the shenhu area of the south China sea. Nat. Gas. Ind. B 2018, 5, 631–643. [Google Scholar] [CrossRef]
- Sun, J.; Zhang, L.; Ning, F.; Lei, H.; Liu, T.; Hu, G.; Lu, H.; Lu, J.; Liu, C.; Jiang, G.; et al. Production potential and stability of hydrate-bearing sediments at the site GMGS3-W19 in the South China Sea: A preliminary feasibility study. Mar. Pet. Geol. 2017, 86, 447–473. [Google Scholar] [CrossRef]
- Wang, Y.; Gao, D.; Wang, J.; Ning, B. Investigation on influence of temperature and pressure on fatigue damage of subsea wellhead in deepwater drilling. J. Pet. Sci. Eng. 2022, 212, 110328. [Google Scholar] [CrossRef]
- Wang, Y.; Gao, D. On the static mechanics of the tubular system during installation of the surface casing in deepwater drilling. Appl. Ocean. Res. 2021, 110, 102599. [Google Scholar] [CrossRef]
- Xu, Y.; Guan, Z.; Jin, Y.; Liu, Y.; Sun, Y.; Zhang, B.; Sheng, Y. Risk Assessment Method of Subsea Wellhead Instability in Consideration of Uncertain Factors in Deepwater Drilling. Arab. J. Sci. Eng. 2018, 43, 2659–2672. [Google Scholar] [CrossRef]
- Li, Q.; Cheng, Y.; Zhang, H.; Yan, C.; Liu, Y. Simulating the effect of hydrate dissociation on wellhead stability during oil and gas development in deepwater. J. Ocean. U China 2018, 17, 35–45. [Google Scholar] [CrossRef]
- Yang, Z.; Still, B.; Ge, X. Mechanical properties of seasonally frozen and permafrost soils at high strain rate. Cold Reg. Sci. Technol. 2015, 113, 12–19. [Google Scholar] [CrossRef]
- Bilodeau, J.; Verreault, J.; Doré, G. Assessment of the physical and mechanical properties of permafrost in Nunavik, Quebec, Canada. In Proceedings of the 18th International Conference on Cold Regions Engineering and 8th Canadian Permafrost Conference, Quebec City, Canada, 18–22 August 2019; pp. 17–25. [Google Scholar]
- Zhang, H.; Cheng, Y.; Li, Q.; Yan, C.; Han, X. Numerical analysis of wellbore instability in gas hydrate formation during deep-water drilling. J. Ocean. U China 2018, 17, 8–16. [Google Scholar] [CrossRef]
- Arenson, L.; Johansen, M.; Springman, S. Effects of volumetric ice content and strain rate on shear strength under triaxial conditions for frozen soil samples. Permafr. Periglac. 2004, 15, 261–271. [Google Scholar] [CrossRef]
- Romanovsky, V.; Smith, S.; Christiansen, H. Permafrost thermal state in the polar Northern Hemisphere during the international polar year 2007–2009: A synthesis. Permafr. Periglac 2010, 21, 106–116. [Google Scholar] [CrossRef]
- Lu, J.; Zhang, M.; Zhang, X.; Pei, W.; Bi, J. Experimental study on the freezing–thawing deformation of a silty clay. Cold Reg. Sci. Technol. 2018, 151, 19–27. [Google Scholar] [CrossRef]
- Wang, F.; Liu, X.; Jiang, B.; Zhuo, H.; Chen, W.; Chen, Y.; Li, X. Low-loading Pt nanoparticles combined with the atomically dispersed FeN4 sites supported by FeSA-NC for improved activity and stability towards oxygen reduction reaction/hydrogen evolution reaction in acid and alkaline media. J. Colloid. Interf. Sci. 2023, 635, 514–523. [Google Scholar] [CrossRef]
- Yamamoto, Y.; Springman, S. Axial compression stress path tests on artificial frozen soil samples in a triaxial device at temperatures just below 0 °C. Can. Geotech. J. 2014, 51, 1178–1195. [Google Scholar] [CrossRef]
- Li, Z.; Spangenberg, E.; Schicks, J.; Kempka, T. Numerical simulation of coastal sub-permafrost gas hydrate formation in the Mackenzie Delta, Canadian Arctic. Energies 2022, 15, 4986. [Google Scholar] [CrossRef]
- Melnikov, V.P.; Osipov, V.I.; Brouchkov, A.V.; Badina, S.V.; Sadurtdinov, M.R.; Drozdov, D.S.; Malkova, G.V.; Zheleznyak, M.N.; Zhdaneev, O.V.; Ostarkov, N.A.; et al. Past and future of permafrost monitoring: Stability of Russian energetic infrastructure. Energies 2022, 15, 3190. [Google Scholar] [CrossRef]
- Nassr, A.; Esmaeili-Falak, M.; Katebi, H.; Javadi, A. A new approach to modeling the behavior of frozen soils. Eng. Geol. 2018, 246, 82–90. [Google Scholar] [CrossRef]
- Guan, J.; Zhang, X.; Chen, X.; Ding, M.; Wang, W.; Yu, S. Influence of seasonal freezing-thawing soils on seismic performance of high-rise cap pile foundation in permafrost regions. Cold Reg. Sci. Technol. 2022, 199, 103581. [Google Scholar] [CrossRef]
- Wei, B.; Huang, H.; Hou, J.; Sukop, M. Study on the meniscus-induced motion of droplets and bubbles by a three-phase Lattice Boltzmann model. Chem. Eng. Sci. 2018, 176, 35–49. [Google Scholar] [CrossRef]
- Ji, Y.; Kneafsey, T.; Hou, J.; Zhao, J.; Liu, C.; Guo, T.; Wei, B.; Zhao, E.; Bai, Y. Relative permeability of gas and water flow in hydrate-bearing porous media: A micro-scale study by lattice Boltzmann simulation. Fuel 2022, 321, 124013. [Google Scholar] [CrossRef]
- Wei, B.; Hou, J.; Sukop, M.; Du, Q.; Wang, H. Flow behaviors of emulsions in constricted capillaries: A lattice Boltzmann simulation study. Chem. Eng. Sci. 2020, 227, 115925. [Google Scholar] [CrossRef]
- Blunt, M. Flow in porous media--pore-network models and multiphase flow. Curr. Opin. Colloid. 2001, 6, 197–207. [Google Scholar] [CrossRef]
- Li, C.; Brouchkov, A.; Cheverev, V.; Sokolov, A.; Li, K. Emission of Methane and Carbon Dioxide during Soil Freezing without Permafrost. Energies 2022, 15, 2693. [Google Scholar] [CrossRef]
- Li, Q.; Liu, J.; Wang, S.; Guo, Y.; Han, X.; Li, Q.; Cheng, Y.; Dong, Z.; Li, X.; Zhang, X. Numerical Insights into Factors Affecting Collapse Behavior of Horizontal Wellbore in Clayey Silt Hydrate-Bearing Sediments and the Accompanying Control Strategy. Ocean. Eng. 2024, 297, 117029. [Google Scholar] [CrossRef]
- Etzelmüller, B.; Hagen, J.; Vatne, G.; Ødegård, R.; Sollid, J. Glacier debris accumulation and sediment deformation influenced by permafrost: Examples from Svalbard. Ann. Glaciol. 1996, 22, 53–62. [Google Scholar] [CrossRef]
- Mamot, P.; Weber, S.; Schröder, T.; Krautblatter, M. A temperature- and stress-controlled failure criterion for ice-filled permafrost rock joints. Cryosphere 2018, 12, 3333–3353. [Google Scholar] [CrossRef]
- Jiao, C.; Niu, F.; He, P.; Ren, L.; Luo, J.; Shan, Y. Deformation and Volumetric Change in a Typical Retrogressive Thaw Slump in Permafrost Regions of the Central Tibetan Plateau, China. Remote Sens. 2022, 14, 5592. [Google Scholar] [CrossRef]





| No. | T, °C | Pc, MPa | D, cm | H, cm |
|---|---|---|---|---|
| 1 | −5 | 0 | 24.32 | 51.04 |
| 2 | −10 | 25.07 | 51.43 | |
| 3 | −15 | 24.38 | 52.57 | |
| 4 | −25 | 25.37 | 53.17 | |
| 5 | −5 | 1.5 | 24.65 | 48.92 |
| 6 | −10 | 24.82 | 52.34 | |
| 7 | −15 | 25.31 | 51.67 | |
| 8 | −25 | 25.16 | 50.91 | |
| 9 | −5 | 3.0 | 24.42 | 51.37 |
| 10 | −10 | 24.89 | 53.14 | |
| 11 | −15 | 25.09 | 52.31 | |
| 12 | −25 | 25.17 | 49.88 | |
| 13 | −5 | 4.5 | 24.78 | 51.62 |
| 14 | −10 | 24.91 | 51.33 | |
| 15 | −15 | 25.22 | 50.61 | |
| 16 | −25 | 24.93 | 49.93 |
| Parameters | Value |
|---|---|
| Elastic modulus/MPa | Refer to Figure 7 |
| Poisson’s ratio | Refer to Figure 8 |
| Cohesion/MPa | Refer to Figure 9 |
| Internal friction angle/° | Refer to Figure 10 |
| Permeability/mD | 2.0 |
| Initial temperature/°C | −10 + 3.0 De/100 |
| Pore pressure/MPa | ρfgDe/106 |
| Ice saturation/% | 50 |
| Vertical stress/MPa | ΡpgDe/106 |
| Horizontal stress/MPa | ΡpgDe/106/B |
| Thermal conductivity/(W/(m·°C)) | 2.0 |
| Specific heat/(J/(kg·°C)) | 1650 |
| Fluid temperature/°C | 15 |
| Reservoir depth/m | 500 |
| Reservoir thickness/m | 50 |
| Production pressure difference/MPa | 2.0 |
| Fluid density/(kg/m3) | 900 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, X.; Su, Y.; Cheng, Y.; Li, Q. Preliminary Insight into Ice Melting, Surface Subsidence, and Wellhead Instability during Oil and Gas Extraction in Permafrost Region. Energies 2024, 17, 1292. https://doi.org/10.3390/en17061292
Zhou X, Su Y, Cheng Y, Li Q. Preliminary Insight into Ice Melting, Surface Subsidence, and Wellhead Instability during Oil and Gas Extraction in Permafrost Region. Energies. 2024; 17(6):1292. https://doi.org/10.3390/en17061292
Chicago/Turabian StyleZhou, Xiaohui, Yinao Su, Yuanfang Cheng, and Qingchao Li. 2024. "Preliminary Insight into Ice Melting, Surface Subsidence, and Wellhead Instability during Oil and Gas Extraction in Permafrost Region" Energies 17, no. 6: 1292. https://doi.org/10.3390/en17061292
APA StyleZhou, X., Su, Y., Cheng, Y., & Li, Q. (2024). Preliminary Insight into Ice Melting, Surface Subsidence, and Wellhead Instability during Oil and Gas Extraction in Permafrost Region. Energies, 17(6), 1292. https://doi.org/10.3390/en17061292







