Development of 1D Model of Constant-Volume Combustor and Numerical Analysis of the Exhaust Nozzle
Abstract
1. Introduction
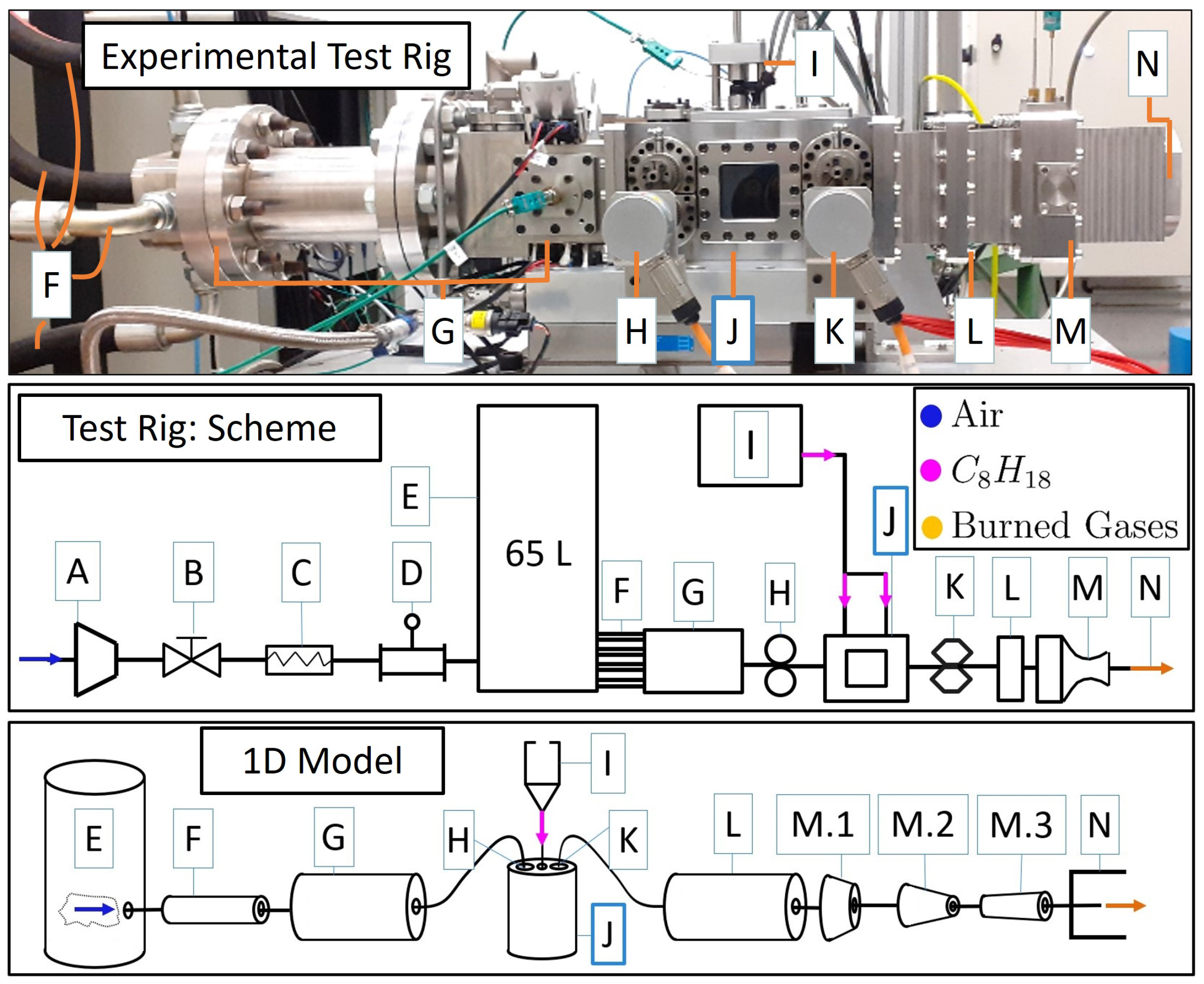
2. 1D Model of the Constant-Volume Combustion Test Rig
2.1. Model Setup
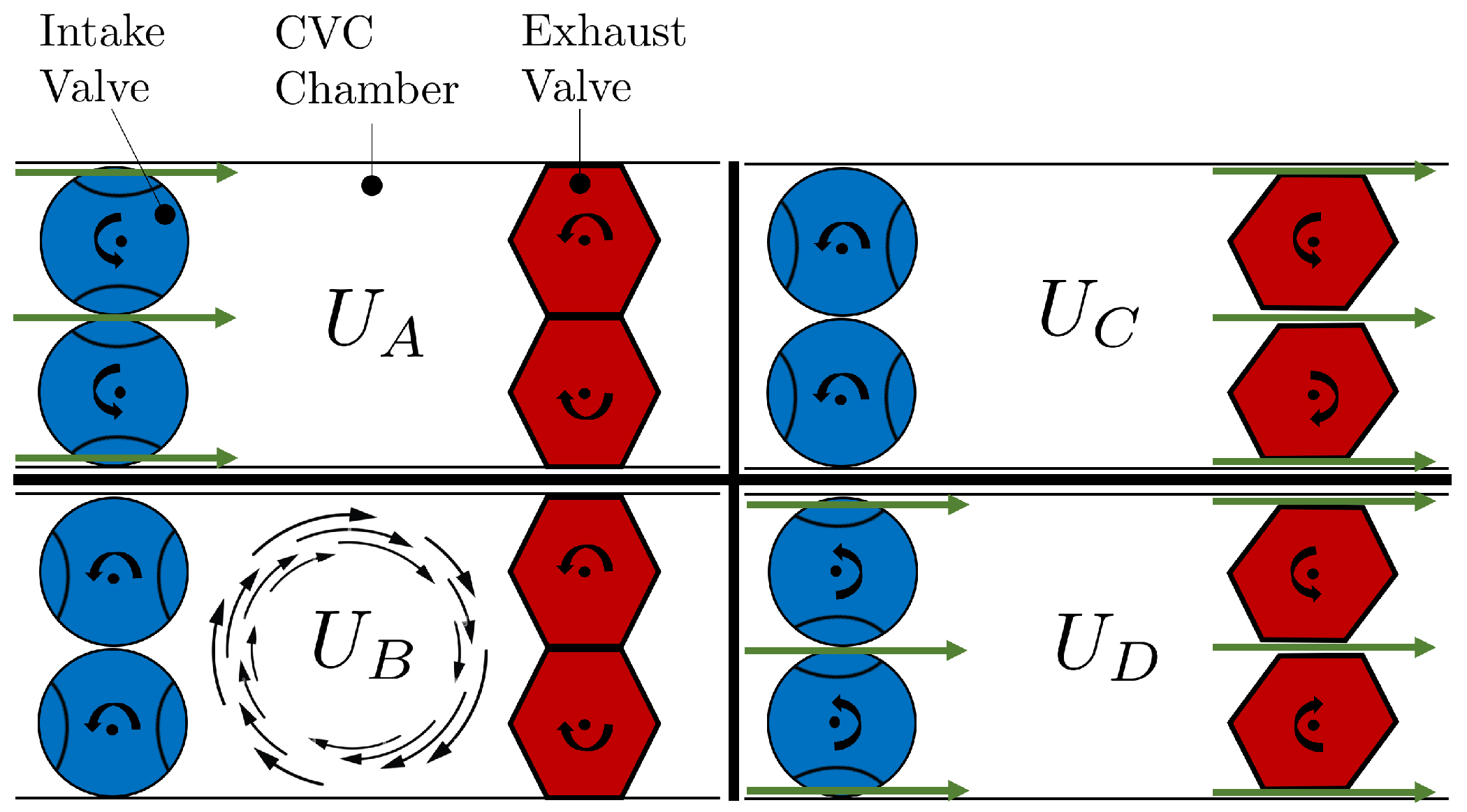
2.1.1. CVC Configuration
2.1.2. Numerical Setup
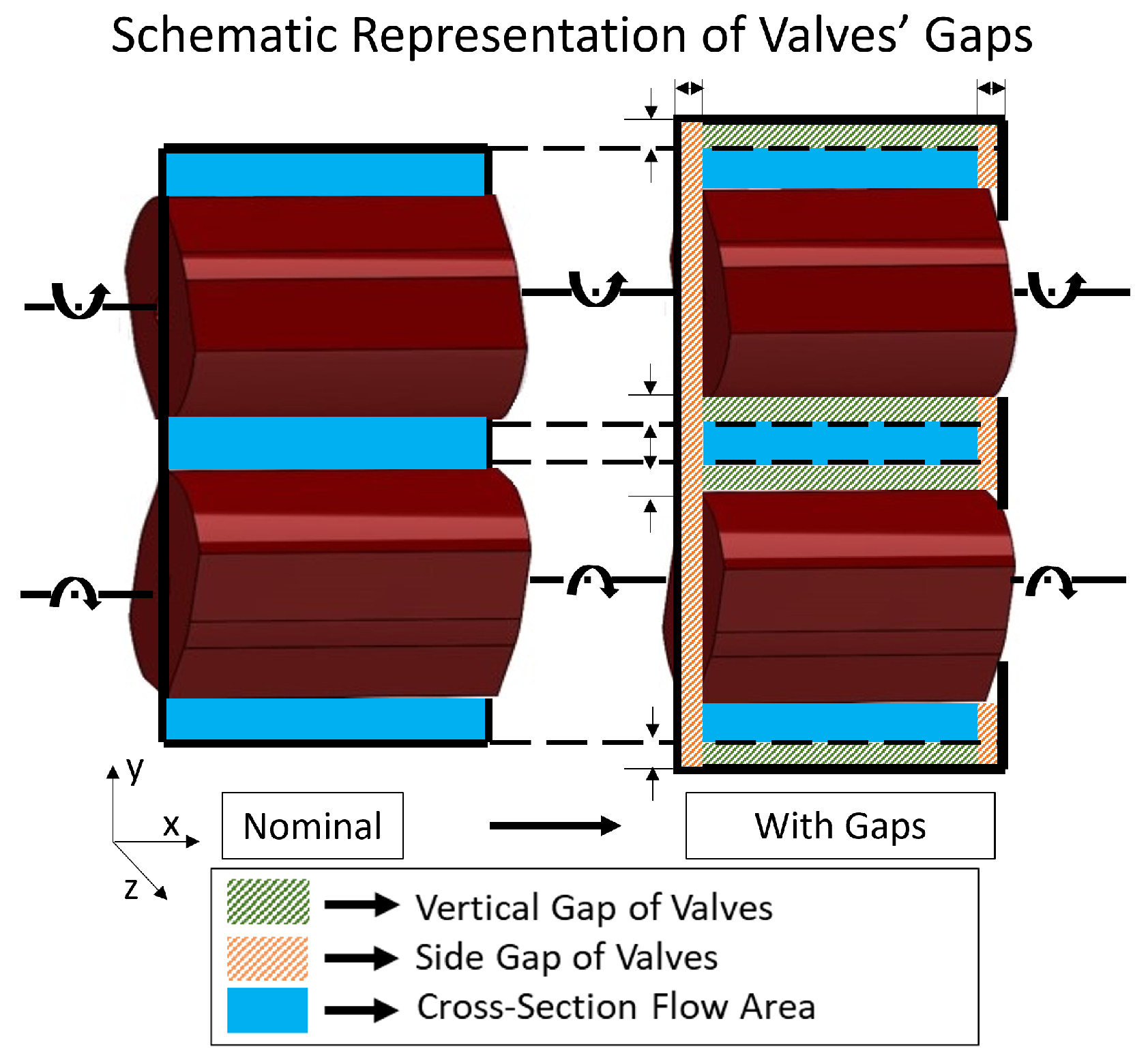
2.1.3. Parametrization of Valves
2.1.4. Burning Rate
2.1.5. Heat Loss Model
2.2. Results of Model
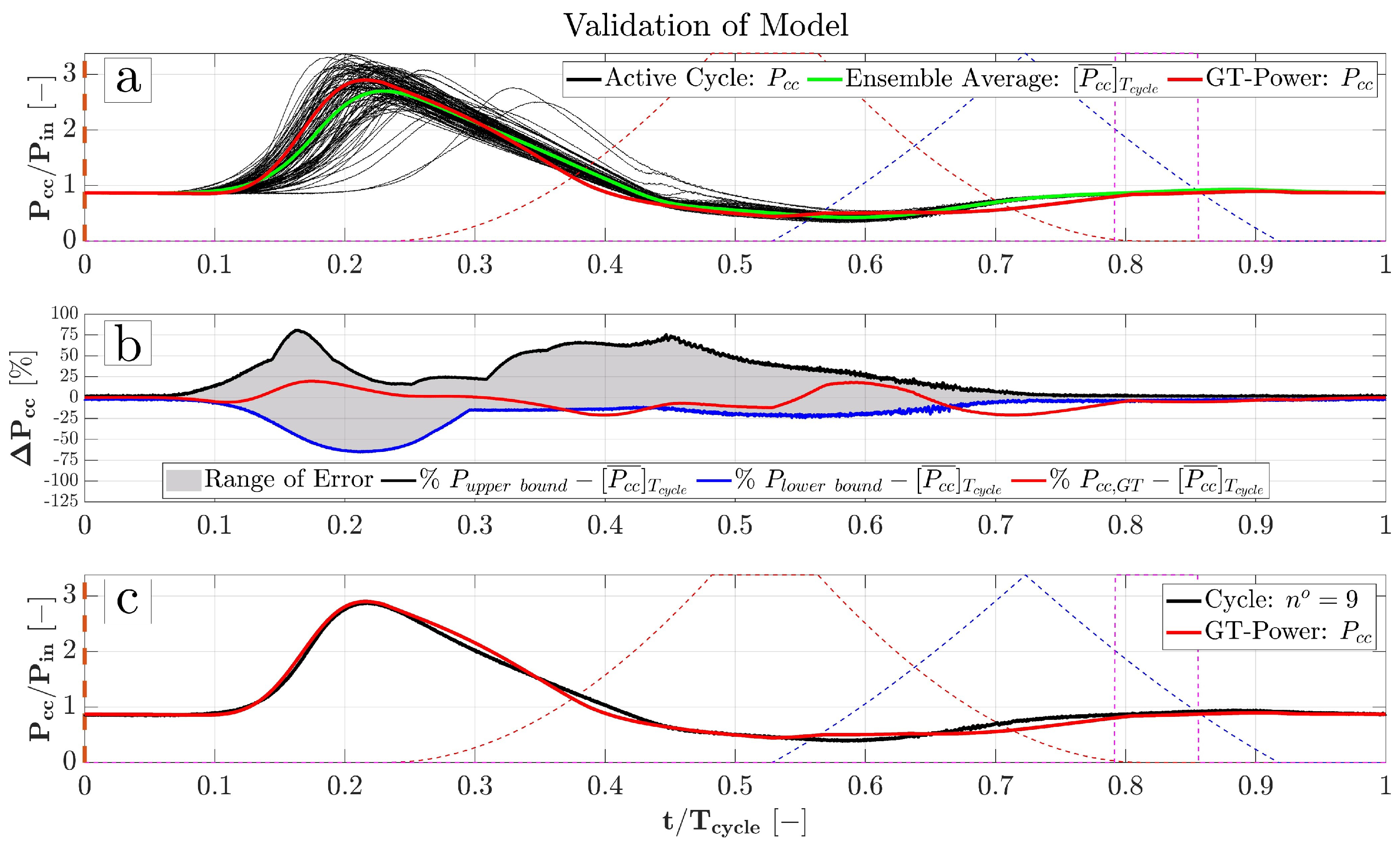
2.2.1. Validation of Model
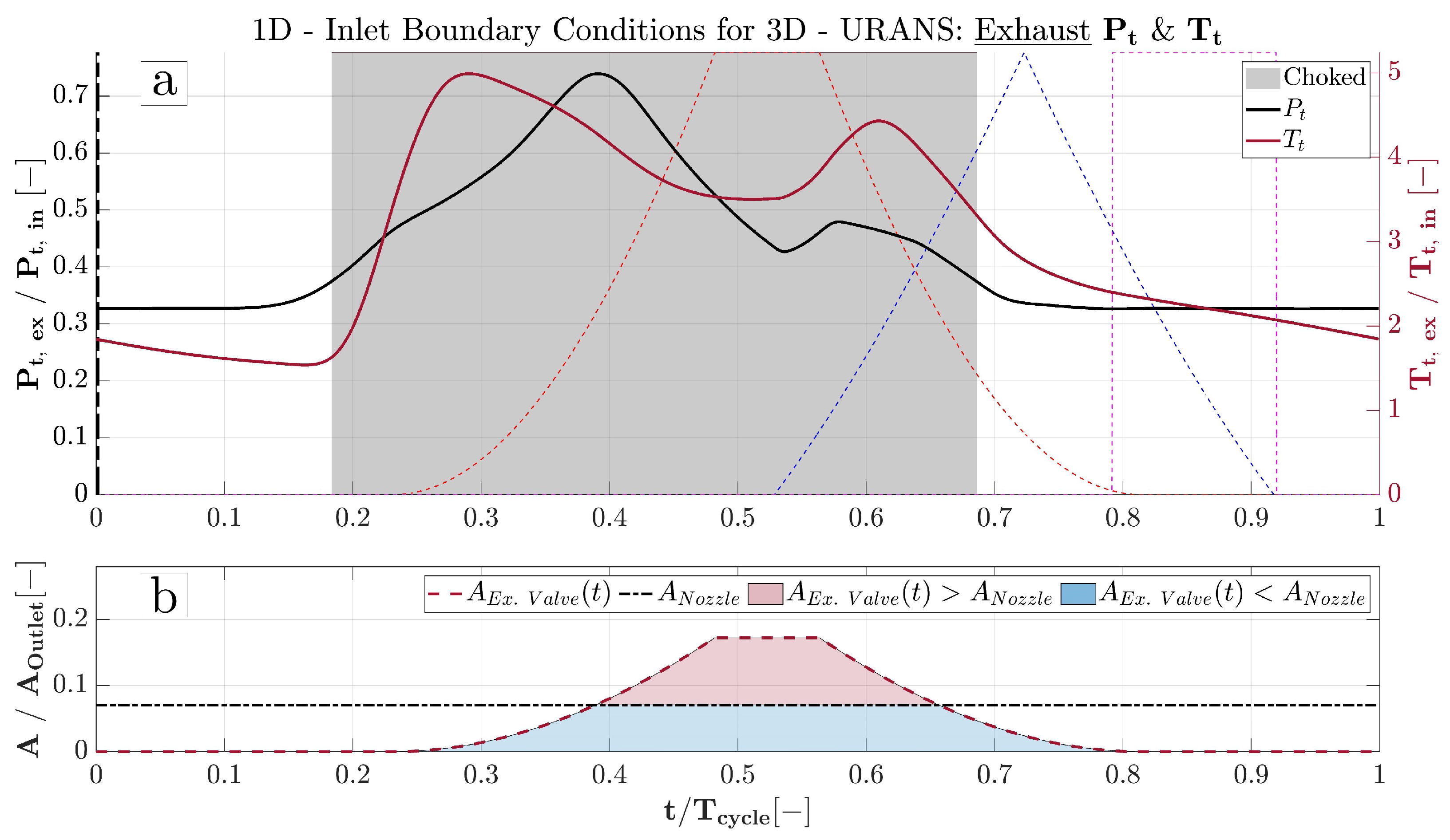
2.2.2. Transient Conditions of Exhaust System
3. 3D Transient Analysis of Exhaust System
3.1. Governing Equations
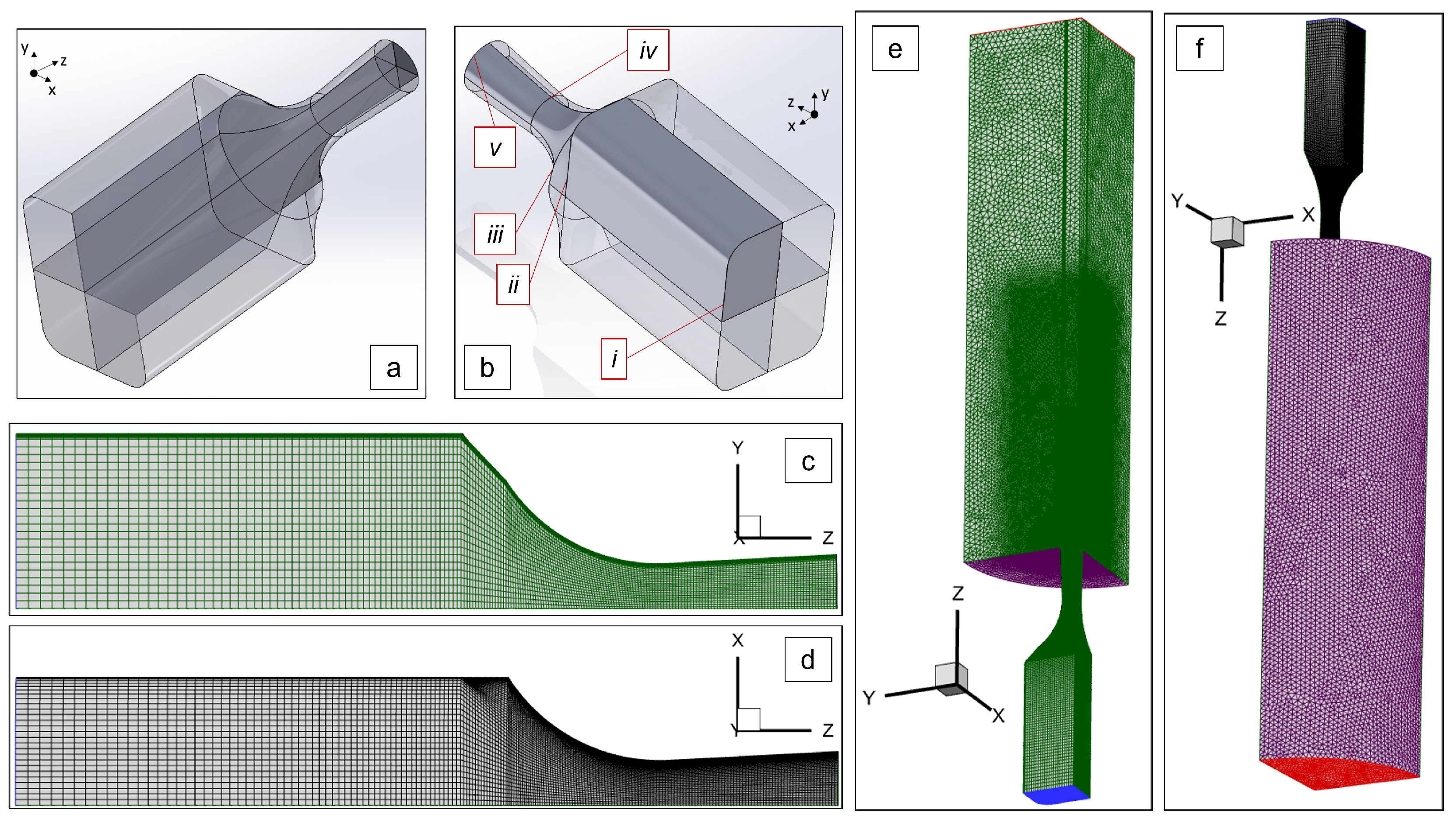
3.2. Numerical Setup
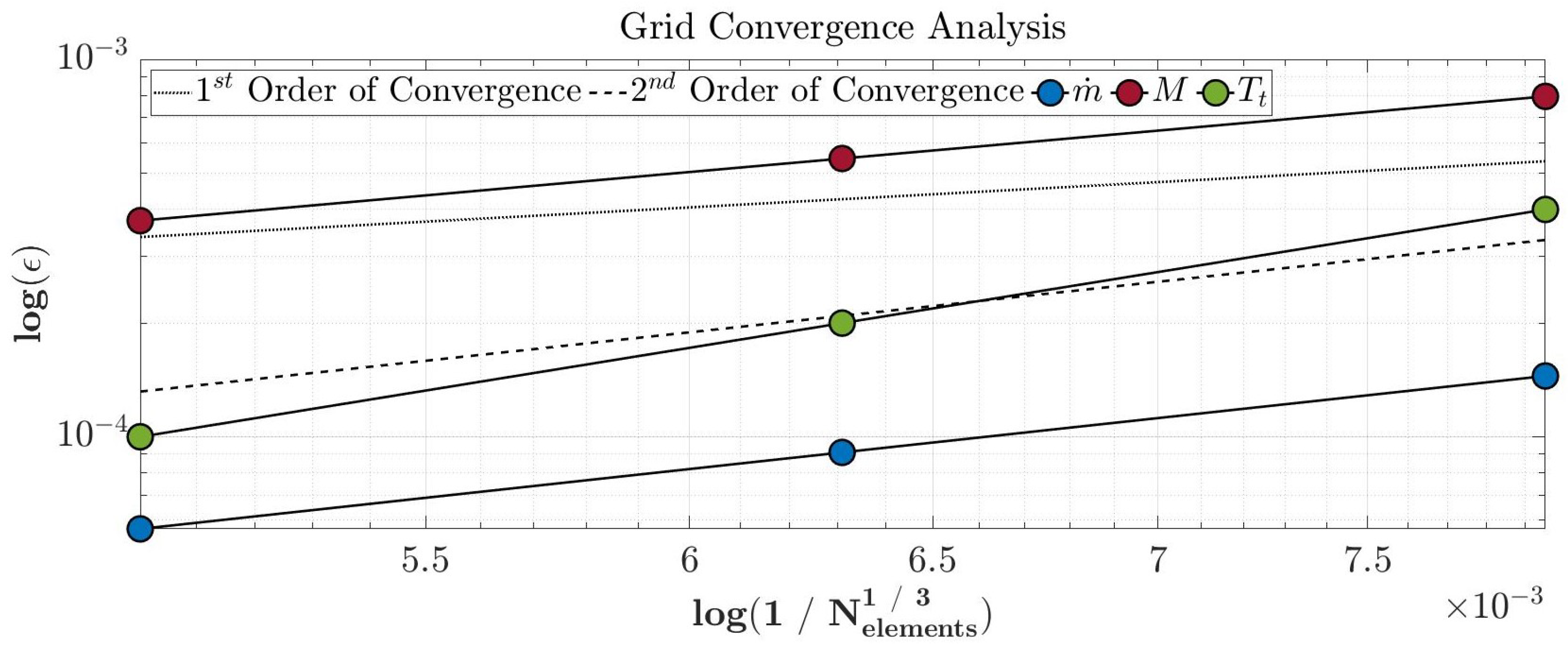
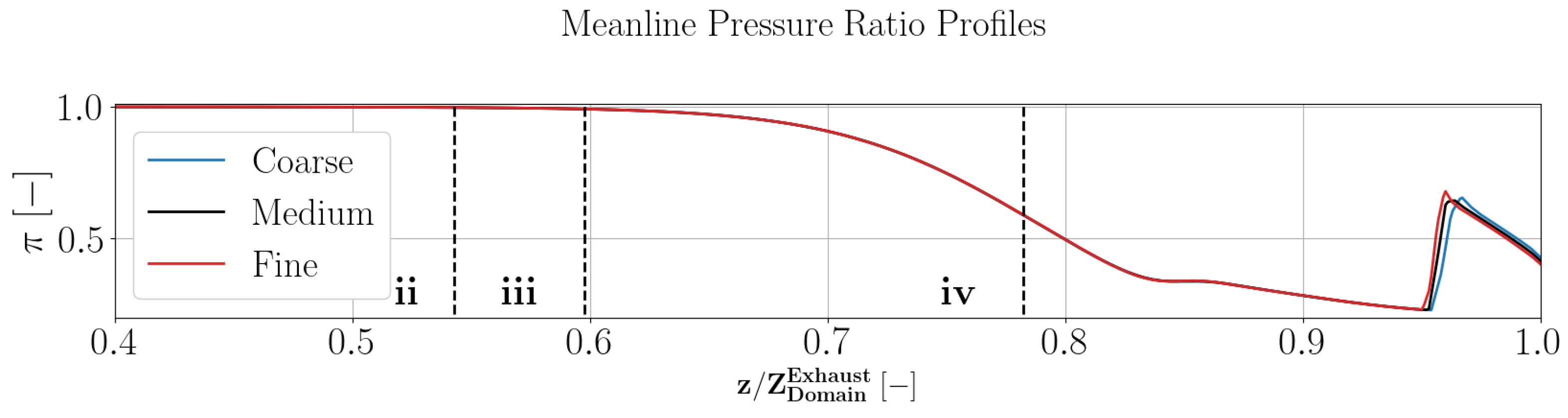
3.3. Periodic Convergence Criteria
3.4. Results of URANS CFD
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Greek Symbols | |
| Corrective Coefficient of viscosity | |
| Pressure Difference | |
| Kronecker Delta | |
| Relative Error | |
| Damping Efficiency | |
| Effective Diffusivity for Specific Dissipation Rate | |
| Effective Diffusivity for Turbulence Kinetic Energy | |
| Thermal Conductivity | |
| Dynamic Viscosity | |
| Reference Dynamic Viscosity | |
| Eddy Viscosity | |
| Specific Rate of Dissipation | |
| Stagnation Pressure Losses | |
| Equivalence Ratio | |
| Pressure Ratio | |
| Density | |
| Molecular Stress Tensor | |
| Characteristic Time | |
| Roman Symbols | |
| Mass Flow Rate | |
| Normalised Cross-Correlation | |
| Reduced Range | |
| A | Area |
| a | Specific Heat Capacity Coefficient |
| Specific Heat Capacity | |
| Coefficient of Velocity Chamber | |
| Discharge Coefficient | |
| D | Diameter |
| Damping Factor | |
| Time Step | |
| e | Specific Energy |
| F | Force |
| f | Frequency |
| g | Acceleration of Gravity |
| Generation of Specific Dissipation Rate | |
| Generation of Turbulence Kinetic Energy | |
| H | Total Specific Enthalpy |
| h | Specific Enthalpy |
| Heat Transfer Coefficient | |
| k | Turbulence Kinetic Energy |
| L | Lift |
| l | Length |
| Valve’s Clearance | |
| M | Mach Number |
| m | Mass |
| Molecular Weight | |
| Nusselt Number | |
| Pressure | |
| Stagnation Pressure | |
| Prandtl Number | |
| Reynolds Stress | |
| Reynolds Number | |
| Rotating Factor | |
| Temperature Term | |
| Shear Stress Term | |
| Energy Transfer Rate per Volume Term | |
| T | Temperature |
| t | Time |
| Reference Temperature | |
| Period of Cycle | |
| Stagnation Temperature | |
| Velocity | |
| V | Volume |
| x | Length |
| Non-Dimensional Burning Rate | |
| Dissipation of Specific Rate of Dissipation | |
| Dissipation of Turbulent Kinetic Energy | |
| Subscripts | |
| 0 | Closing of Intake Valves Moment |
| Average Time Moment | |
| Bends and Taps Contribution | |
| Combustion Chamber | |
| Additional Source Term | |
| Loss Source Term | |
| Exhaust | |
| f | Fuel |
| Friction Contribution | |
| i | Average Time Moment |
| Intake | |
| K | Middle Cross-Section of Chamber |
| Valve’s Clearance | |
| Operation | |
| t | Total |
| Abbreviations | |
| PDC | Pulse Detonation Combustor |
| RDC | Rotating Detonation Combustor |
| HPT | High-Pressure Turbine |
| IGV | Inlet Guide Vane |
| PGC | Pressure Gain Combustion |
| CVC | Constant Volume Combustor |
| GCI | Grid Convergence Index |
| RANS | Reynolds-Averaged Navier–Stokes |
| URANS | Unsteady Reynolds-Averaged Navier–Stokes |
References
- Stefanizzi, M.; Capurso, T.; Filomeno, G.; Torresi, M.; Pascazio, G. Recent Combustion Strategies in Gas Turbines for Propulsion and Power Generation toward a Zero-Emissions Future: Fuels, Burners, and Combustion Techniques. Energies 2021, 14, 6694. [Google Scholar] [CrossRef]
- Perkins, H.D.; Paxson, D.E. Summary of Pressure Gain Combustion Research at NASA; Technical Report, NASA TM-2018-219874; NASA: Washington, DC, USA, 2018.
- Holzwarth, H. Rotary Combustion Engine. U.S. Patent 783,434, 28 February 1905. [Google Scholar]
- Glassman, I.; Yetter, R.A.; Glumac, N.G. Flame phenomena in premixed combustible gases. In Combustion, 5th ed.; Academic Press: Waltham, MA, USA, 2015; Chapter 4; pp. 147–254. [Google Scholar] [CrossRef]
- Ciccarelli, G.; Dorofeev, S. Flame Acceleration and Transition to Detonation in Ducts. Prog. Energy Combust. Sci. 2008, 34, 499–550. [Google Scholar] [CrossRef]
- Wolański, P. Detonative Propulsion. Proc. Combust. Inst. 2013, 34, 125–158. [Google Scholar] [CrossRef]
- Nordeen, C.A. Concepts and Definitions: Efficiency of detonation. In Thermodynamics of a Rotating Detonation Engine; University of Connecticut: Storrs, CT, USA, 2013; Chapter 1; pp. 10–15. [Google Scholar]
- Heiser, W.H.; Pratt, D.T. Thermodynamic Cycle Analysis of Pulse Detonation Engines. J. Propuls. Power 2002, 18, 68–76. [Google Scholar] [CrossRef]
- Stathopoulos, P.; Vinkeloe, J.; Paschereit, C.O. Thermodynamic Evaluation of Constant Volume Combustion for Gas Turbine Power Cycles. In Proceedings of the Numerical Set Updings of the 11th International Gas Turbine Congress, Tokyo, Japan, 15–20 November 2015; pp. 15–20. [Google Scholar]
- Sousa, J.; Paniagua, G.; Collado Morata, E. Thermodynamic Analysis of a Gas Turbine Engine with a Rotating Detonation Combustor. Appl. Energy 2017, 195, 247–256. [Google Scholar] [CrossRef]
- Neumann, N.; Peitsch, D. Potentials for Pressure Gain Combustion in Advanced Gas Turbine Cycles. Appl. Sci. 2019, 9, 3211. [Google Scholar] [CrossRef]
- Anand, V.; Gutmark, E. A Review of Pollutants Emissions in Various Pressure Gain Combustors. Int. J. Spray Combust. Dyn. 2019, 11, 175682771987072. [Google Scholar] [CrossRef]
- Akbari, P.; Nalim, R.; Mueller, N. A Review of Wave Rotor Technology and Its Applications. J. Eng. Gas Turbines Power 2006, 128, 717–735. [Google Scholar] [CrossRef]
- Roy, G.; Frolov, S.; Borisov, A.; Netzer, D. Pulse Detonation Propulsion: Challenges, Current Status, and Future Perspective. Prog. Energy Combust. Sci. 2004, 30, 545–672. [Google Scholar] [CrossRef]
- Bobusch, B.C.; Berndt, P.; Paschereit, C.O.; Klein, R. Shockless Explosion Combustion: An Innovative Way of Efficient Constant Volume Combustion in Gas Turbines. Combust. Sci. Technol. 2014, 186, 1680–1689. [Google Scholar] [CrossRef]
- Ma, J.Z.; Luan, M.Y.; Xia, Z.J.; Wang, J.P.; Zhang, S.j.; Yao, S.b.; Wang, B. Recent Progress, Development Trends, and Consideration of Continuous Detonation Engines. AIAA J. 2020, 58, 4976–5035. [Google Scholar] [CrossRef]
- Lu, F.K.; Braun, E.M. Rotating Detonation Wave Propulsion: Experimental Challenges, Modeling, and Engine Concepts. J. Propuls. Power 2014, 30, 1125–1142. [Google Scholar] [CrossRef]
- Hishida, M.; Fujiwara, T.; Wolanski, P. Fundamentals of Rotating Detonations. Shock Waves 2009, 19, 1–10. [Google Scholar] [CrossRef]
- Lee, J.H.S. Introduction: The detonation Structure. In The Detonation Phenomenon, 1st ed.; Cambridge University Press: New York, NY, USA, 2008; Chapter 1; pp. 11–12. [Google Scholar] [CrossRef]
- Fernelius, M.; Gorrell, S.E.; Hoke, J.; Schauer, F. Effect of Periodic Pressure Pulses on Axial Turbine Performance. In Proceedings of the 49th AIAA/ASME/SAE/ASEE Joint Propulsion Conference, San Jose, CA, USA, 15–17 July 2013; p. 3687. [Google Scholar] [CrossRef]
- Fernelius, M.H.; Gorrell, S.E. Predicting Efficiency of a Turbine Driven by Pulsing Flow. In Proceedings of the Volume 2A: Turbomachinery, Charlotte, NC, USA, 26–30 June 2017; p. V02AT40A008. [Google Scholar] [CrossRef]
- Fernelius, M.H.; Gorrell, S.E. Mapping Efficiency of a Pulsing Flow-Driven Turbine. J. Fluids Eng. 2020, 142, 061202. [Google Scholar] [CrossRef]
- Fernelius, M.H.; Gorrell, S.E. Design of a Pulsing Flow Driven Turbine. J. Fluids Eng. 2021, 143, 041501. [Google Scholar] [CrossRef]
- Paniagua, G.; Iorio, M.; Vinha, N.; Sousa, J. Design and Analysis of Pioneering High Supersonic Axial Turbines. Int. J. Mech. Sci. 2014, 89, 65–77. [Google Scholar] [CrossRef]
- Liu, Z.; Braun, J.; Paniagua, G. Performance of Axial Turbines Exposed to Large Fluctuations. In Proceedings of the 53rd AIAA/SAE/ASEE Joint Propulsion Conference, Atlanta, GA, USA, 10–12 July 2017; p. 4817. [Google Scholar] [CrossRef]
- Liu, Z.; Braun, J.; Paniagua, G. Integration of a Transonic High-Pressure Turbine with a Rotating Detonation Combustor and a Diffuser. Int. J. Turbo Jet-Engines 2023, 40, 1–10. [Google Scholar] [CrossRef]
- Liu, Z.; Braun, J.; Paniagua, G. Thermal Power Plant Upgrade via a Rotating Detonation Combustor and Retrofitted Turbine with Optimized Endwalls. Int. J. Mech. Sci. 2020, 188, 105918. [Google Scholar] [CrossRef]
- Ni, R.H.; Humber, W.; Ni, M.; Sondergaard, R.; Ooten, M. Performance Estimation of a Turbine Under Partial-Admission and Flow Pulsation Conditions at Inlet. In Proceedings of the Volume 6C: Turbomachinery, San Antonio, TX, USA, 3–7 June 2013; p. V06CT42A019. [Google Scholar] [CrossRef]
- Xisto, C.; Petit, O.; Grönstedt, T.; Rolt, A.; Lundbladh, A.; Paniagua, G. The Efficiency of a Pulsed Detonation Combustor–Axial Turbine Integration. Aerosp. Sci. Technol. 2018, 82–83, 80–91. [Google Scholar] [CrossRef]
- Naples, A.; Hoke, J.; Battelle, R.; Schauer, F. T63 Turbine Response to Rotating Detonation Combustor Exhaust Flow. J. Eng. Gas Turbines Power 2019, 141, 021029. [Google Scholar] [CrossRef]
- Boust, B.; Michalski, Q.; Bellenoue, M. Experimental Investigation of Ignition and Combustion Processes in a Constant-Volume Combustion Chamber for Air-Breathing Propulsion. In Proceedings of the 52nd AIAA/SAE/ASEE Joint Propulsion Conference, Salt Lake City, UT, USA, 25–27 July 2016; p. 4699. [Google Scholar] [CrossRef]
- DS/EN ISO 9300; Measurement of Gas Flow by Means of Critical Flow Venturi Nozzles. Dansk Standard; American National Standards Institute: New York, NY, USA, 1987.
- Labarrere, L.; Poinsot, T.; Dauptain, A.; Duchaine, F.; Bellenoue, M.; Boust, B. Experimental and Numerical Study of Cyclic Variations in a Constant Volume Combustion Chamber. Combust. Flame 2016, 172, 49–61. [Google Scholar] [CrossRef]
- Boust, B.; Bellenoue, M.; Michalski, Q. Pressure Gain and Specific Impulse Measurements in a Constant-Volume Combustor Coupled to an Exhaust Plenum. In Proceedings of the Active Flow and Combustion Control 2021, Berlin, Germany, 28–29 September 2021; pp. 3–15. [Google Scholar] [CrossRef]
- Gallis, P.; Misul, D.A.; Salvadori, S.; Bellenoue, M.; Boust, B. Development and Validation of a 0-D/1-D Model to Evaluate Pulsating Conditions from a Constant Volume Combustor. In Proceedings of the Joint Meeting of International Workshop on Detonation for Propulsion (IWDP) and International Constant Volume and Detonation Combustion Workshop (ICVDCW), Berlin, Germany, 15–19 August 2022. [Google Scholar] [CrossRef]
- GT-SUITE Flow Theory Manual; GT-Power: Malvern, PA, USA, 2020.
- Courant, R.; Friedrichs, K.; Lewy, H. On the Partial Difference Equations of Mathematical Physics. Ibm J. Res. Dev. 1967, 11, 215–234. [Google Scholar] [CrossRef]
- Ghojel, J.I. Review of the Development and Applications of the Wiebe function: A Tribute to the Contribution of Ivan Wiebe to Engine Research. Int. J. Engine Res. 2010, 11, 297–312. [Google Scholar] [CrossRef]
- Labarrere, L. Un outil de simulation 0D pour la combustion isochore: CVC0D—Modélisation de la combustion. In Etude Théorique et Numérique de la Combustion à Volume Constant Appliquée à la Propulsion; Institut National Polytechnique de Toulouse: Toulouse, France, 2016; Chapter 3; p. 51. [Google Scholar]
- Ansys Fluent Theory Guide 2021 R1; ANSYS Inc.: Canonsburg, PA, USA, 2021.
- Wilcox, D.C. Formulation of the k-w Turbulence Model Revisited. AIAA J. 2008, 46, 2823–2838. [Google Scholar] [CrossRef]
- Roache, P.J. Verification of Codes and Calculations. AIAA J. 1998, 36, 696–702. [Google Scholar] [CrossRef]

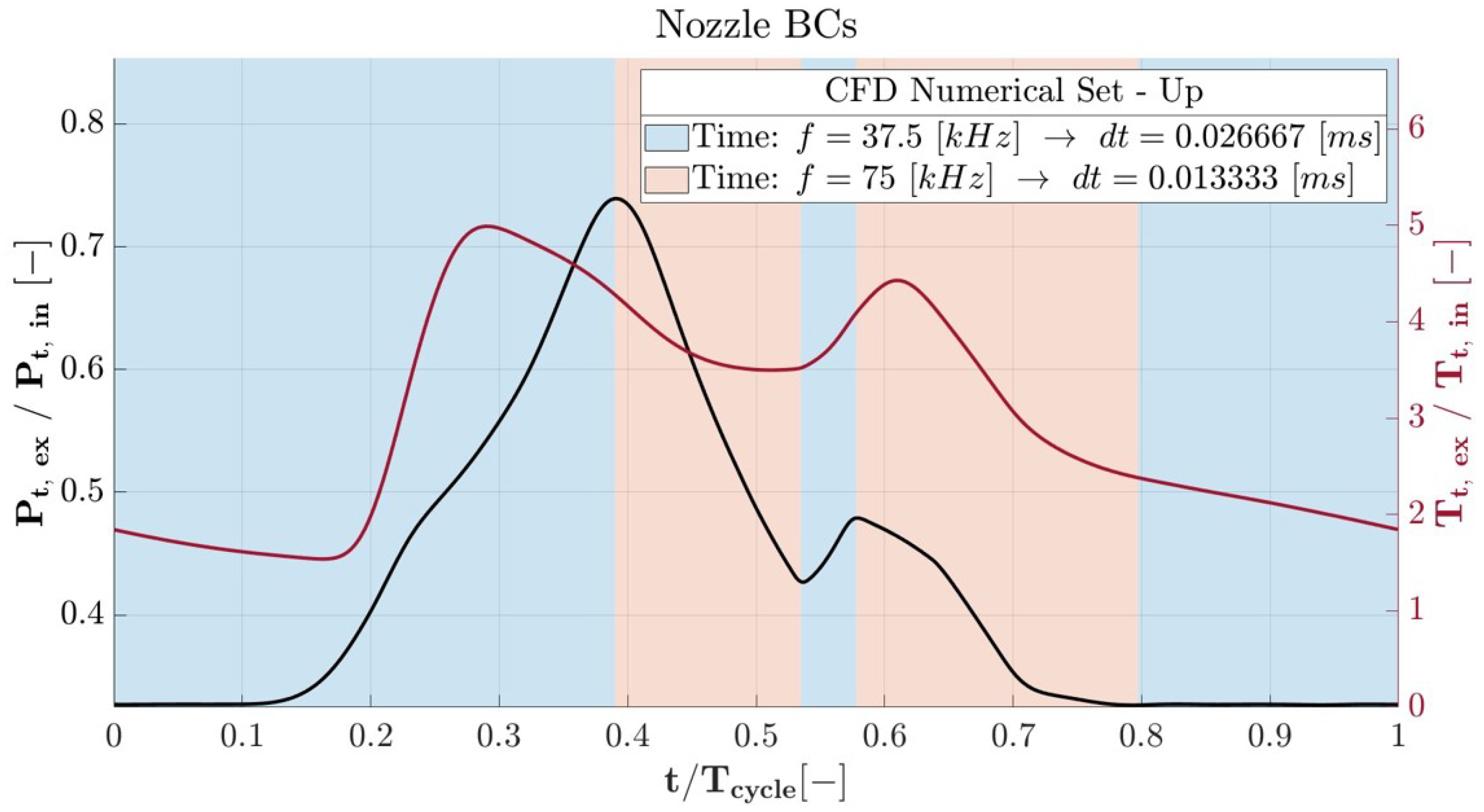

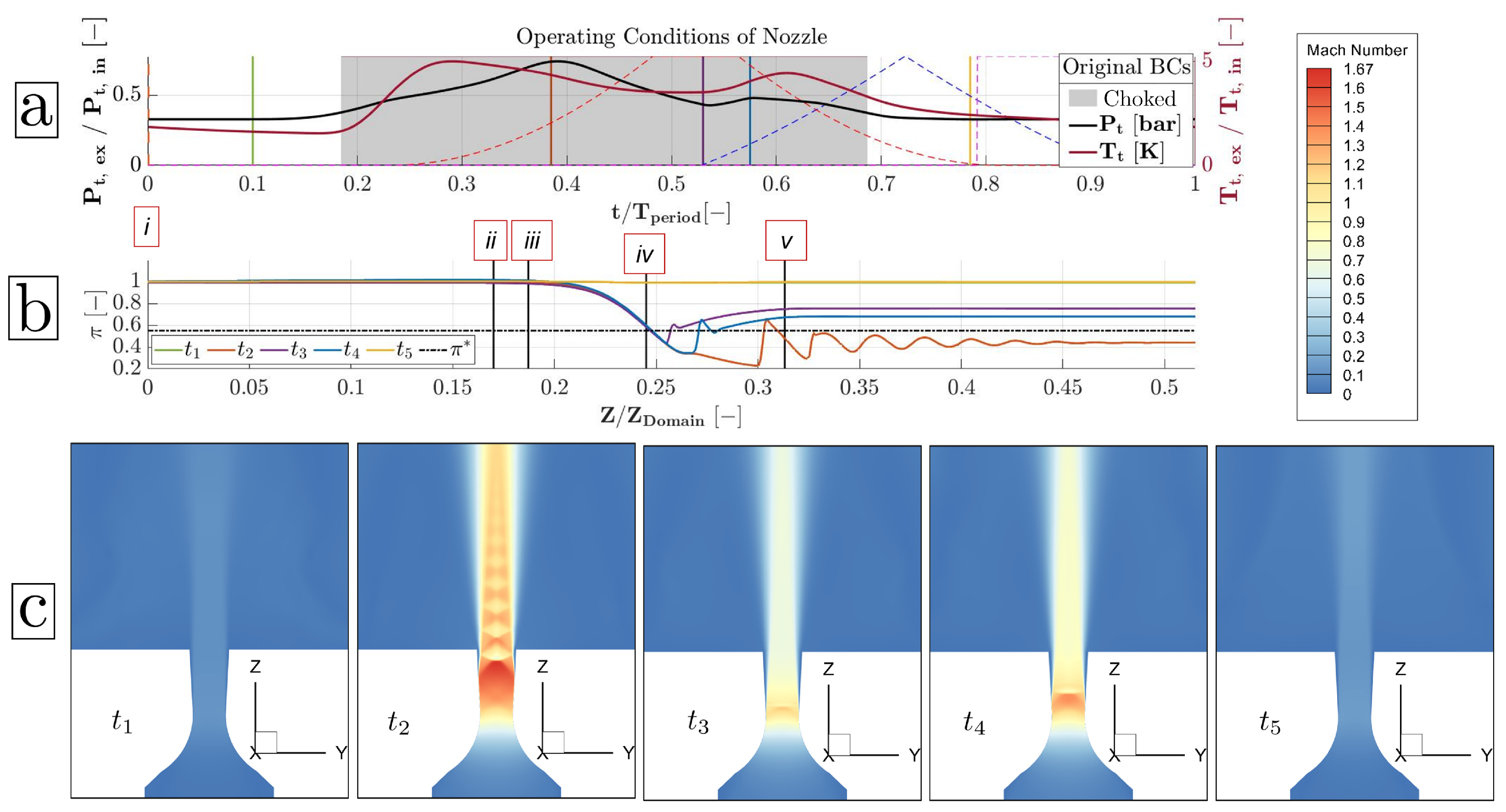
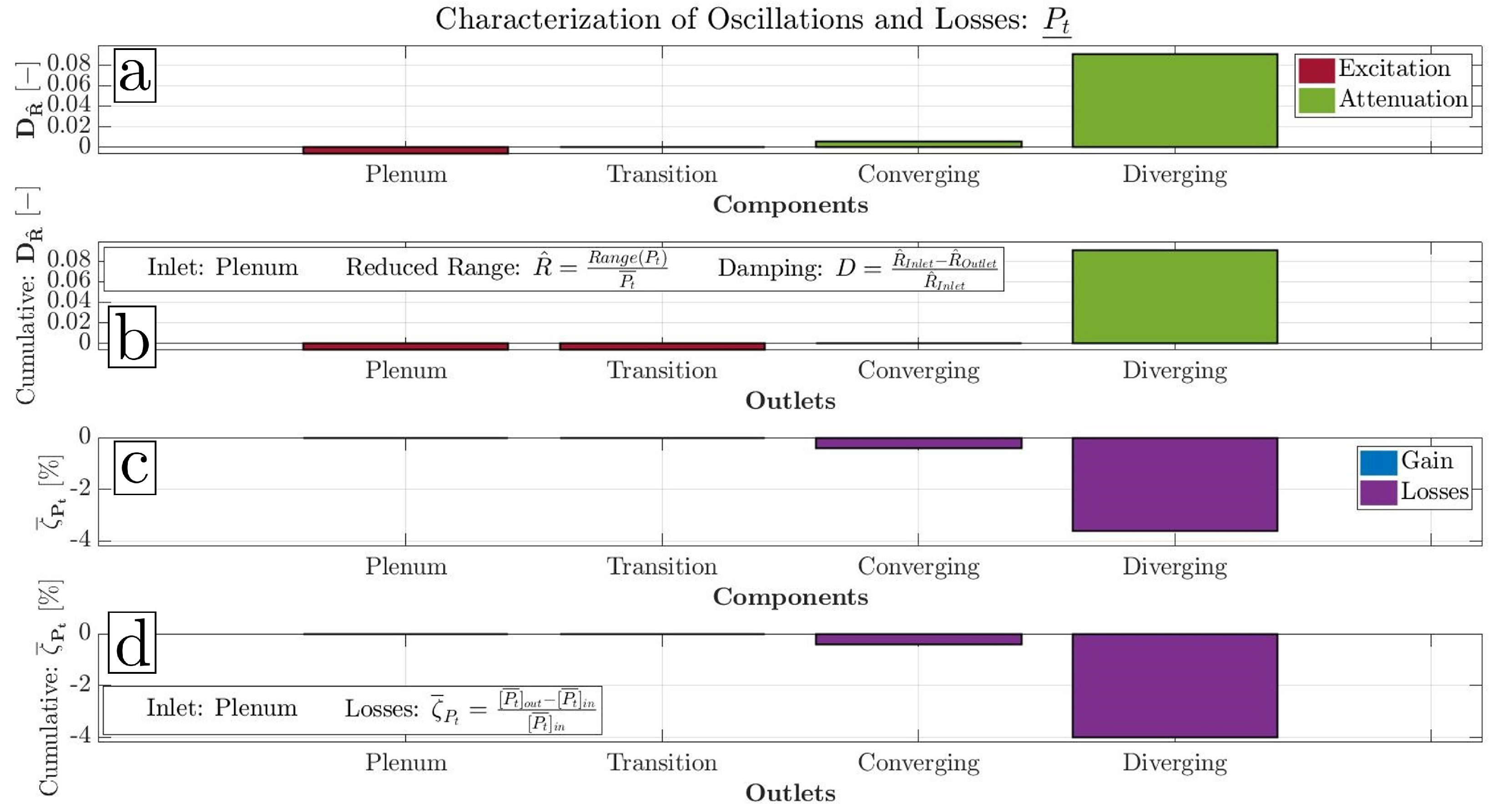
| Valve | n | ||
|---|---|---|---|
| Intake | 13% of | ||
| Exhaust | 1 | 6% of |
| 0 |
| vs. | |||
|---|---|---|---|
| −3.0564% −0.048936 [bar] | 21.1084% 1.232 [bar] | 10.1056% 0.37494 [bar] | |
| 0.90957% 0.020247 [bar] | 28.9296% 0.51703 [bar] | 9.392% 0.2258 [bar] |
| Boundary Conditions | |
|---|---|
| Type | Properties |
| Inlet | and |
| Outlet | |
| Symmetry | - |
| No - Slip Wall | Adiabatic |
| Free - Slip Wall | Adiabatic |
| Property | Grid | Refinement Ratio | GCI | Asymptotic Range of Convergence |
|---|---|---|---|---|
| Coarse–Medium Medium–Fine | ||||
| M | Coarse–Medium Medium–Fine | |||
| Coarse–Medium Medium–Fine | 1.2 × 6.2 × |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gallis, P.; Misul, D.A.; Boust, B.; Bellenoue, M.; Salvadori, S. Development of 1D Model of Constant-Volume Combustor and Numerical Analysis of the Exhaust Nozzle. Energies 2024, 17, 1191. https://doi.org/10.3390/en17051191
Gallis P, Misul DA, Boust B, Bellenoue M, Salvadori S. Development of 1D Model of Constant-Volume Combustor and Numerical Analysis of the Exhaust Nozzle. Energies. 2024; 17(5):1191. https://doi.org/10.3390/en17051191
Chicago/Turabian StyleGallis, Panagiotis, Daniela Anna Misul, Bastien Boust, Marc Bellenoue, and Simone Salvadori. 2024. "Development of 1D Model of Constant-Volume Combustor and Numerical Analysis of the Exhaust Nozzle" Energies 17, no. 5: 1191. https://doi.org/10.3390/en17051191
APA StyleGallis, P., Misul, D. A., Boust, B., Bellenoue, M., & Salvadori, S. (2024). Development of 1D Model of Constant-Volume Combustor and Numerical Analysis of the Exhaust Nozzle. Energies, 17(5), 1191. https://doi.org/10.3390/en17051191








