Mathematical Modeling and Numerical Approximation of Heat Conduction in Three-Phase-Lag Solid
Abstract
1. Introduction
2. A Mathematical Model for Heat Conduction in a Three-Phase-Lag Solid
3. Finite Difference Terminology and Preliminary Results
3.1. Discretization of the Domain and Notation
3.2. Finite Difference Notation for Discretization
4. Numerical Approximation of the System (10)–(15)
4.1. Discretization of the System (10)–(15) for and
4.2. Discretization of System (10)–(15) for
4.3. The Numerical Scheme and Properties
- Step 1.
- Define the input data provided in Table 1. Requirewhere Moreover, calculate , , and
- Step 2.
- Discretization of space and time. Using the relations provided in (16), calculate , , and Here, , and
- Step 3.
- Evaluation of functions of the mesh. Evaluate
- -
- the functions and on for and using relation (40) define the vectors and ;
- -
- the functions and on for and define the vectors and using the relations provided in (41);
- -
- the functions and on , using the relations provided in (9), for and define the vectors and
- -
- the function f on , using the relation provided in (9), for and define the matrix for
- Step 4.
- Step 5.
- Discretization of the equations. The equations are discretized as follows:
5. Numerical Examples
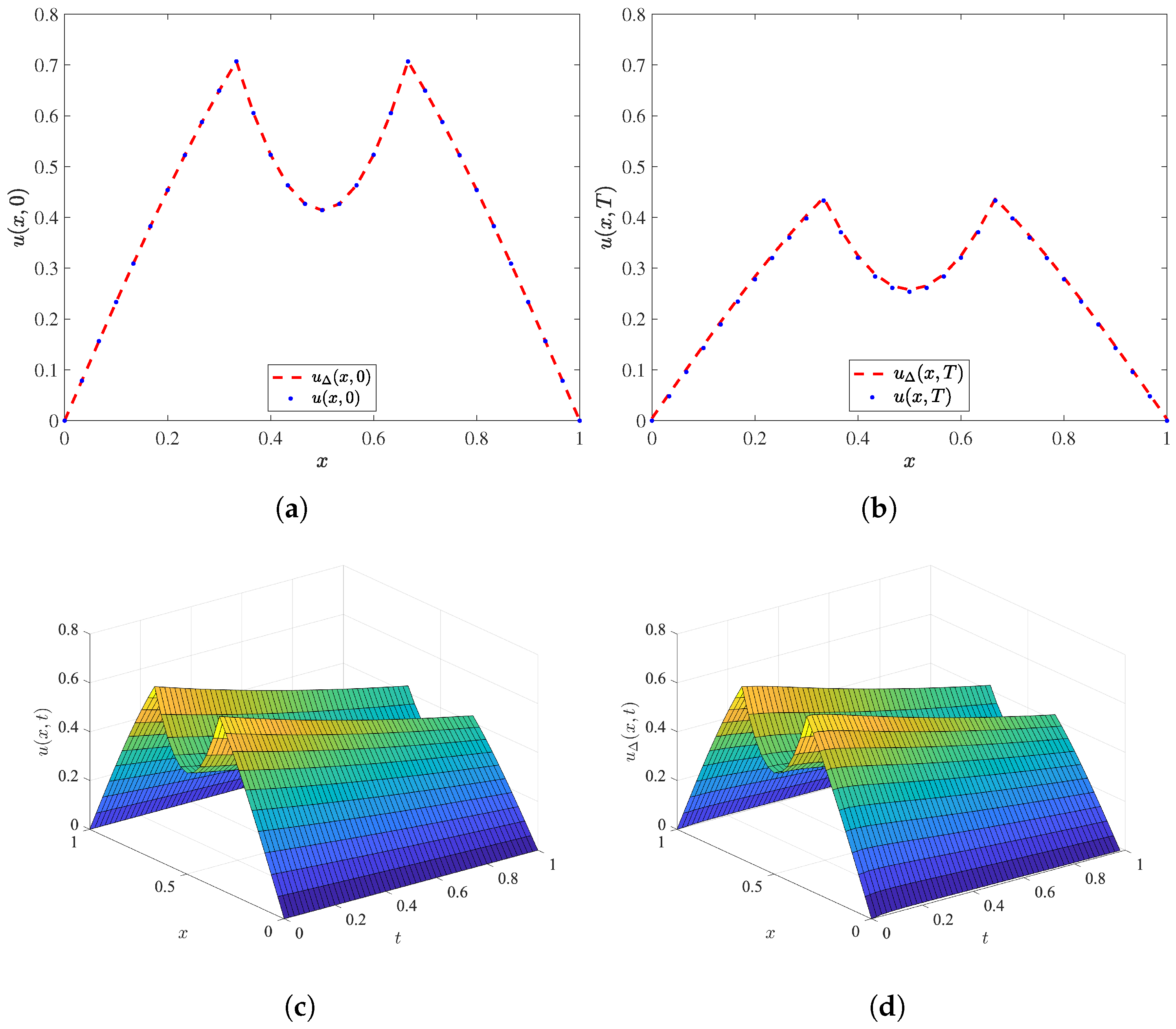
5.1. Example 1
| Example 1 | Example 2 | Example 3 | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Layer 1 | Layer 2 | Layer 3 | Layer 1 | Layer 2 | Layer 3 | Layer 1 | Layer 2 | Layer 3 | |
| 1/3 | 1/3 | 1/3 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 1 | 1 | 1 | 129 | 449 | 129 | 449 | 129 | 449 | |
| 1 | 1 | 1 | 8.5 | 0.136 | 8.5 | 0.136 | 8.5 | 0.136 | |
| 1 | 4 | 4/3 | 90 | 7.86 | 90 | 7.86 | 90 | 7.86 | |
| 4 | 1 | 6 | 317 | 94 | 317 | 317 | 94 | 317 | |
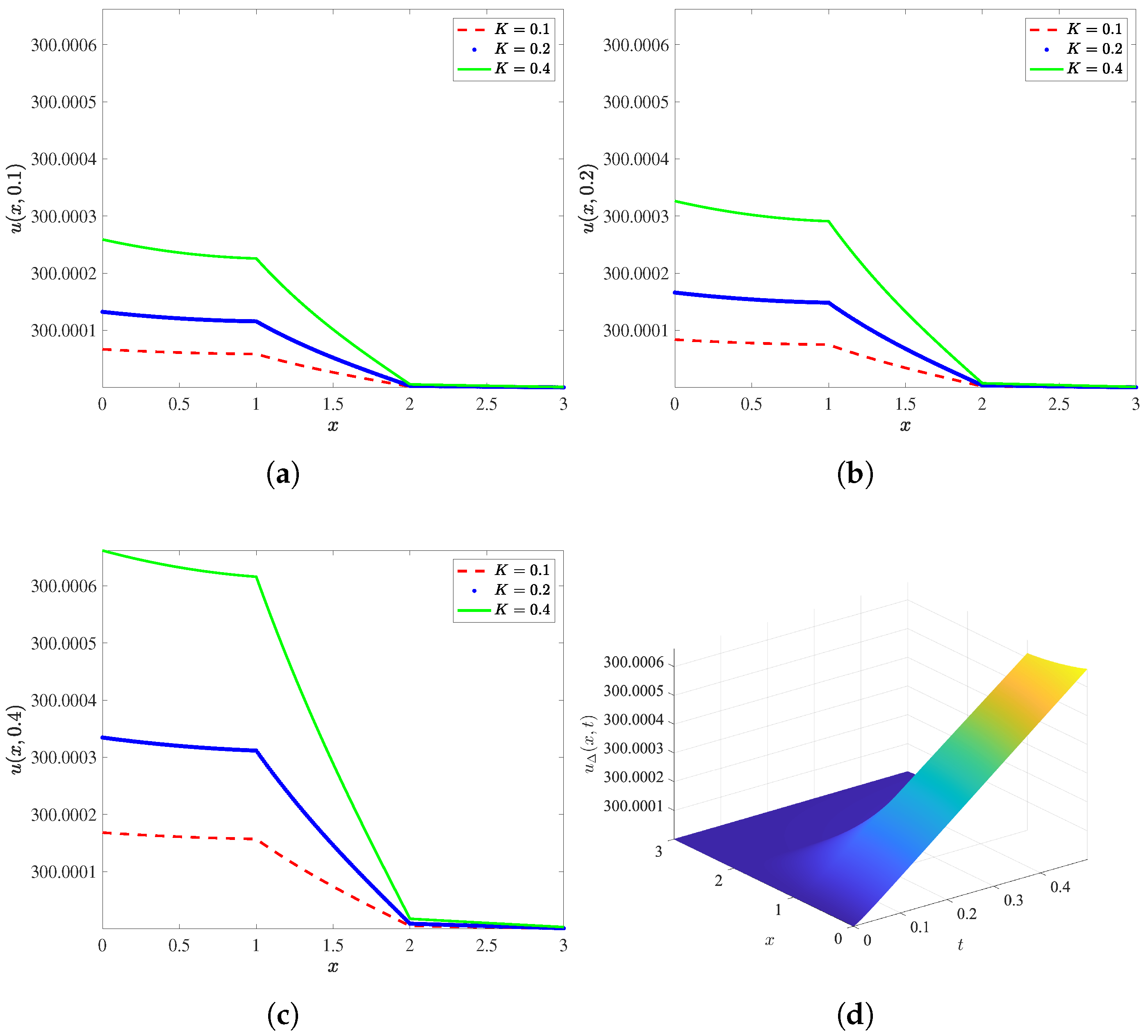
5.2. Example 2
5.3. Example 3
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Raimundo, A.M.; Oliveira, A.V.M. Assessing the Impact of Climate Changes, Building Characteristics, and HVAC Control on Energy Requirements under a Mediterranean Climate. Energies 2024, 17, 2362. [Google Scholar] [CrossRef]
- Jezierski, W.; Święcicki, A.; Werner-Juszczuk, A.J. Deterministic Mathematical Model of Energy Demand of Single-Family Building with Different Parameters and Orientation of Windows in Climatic Conditions of Poland. Energies 2024, 17, 2360. [Google Scholar] [CrossRef]
- Korkut, T.B.; Rachid, A. Numerical Investigation of Interventions to Mitigate Heat Stress: A Case Study in Dubai. Energies 2024, 17, 2242. [Google Scholar] [CrossRef]
- Tan, L.; Gao, D.; Liu, X. Can Environmental Information Disclosure Improve Energy Efficiency in Manufacturing? Evidence from Chinese Enterprises. Energies 2024, 17, 2342. [Google Scholar] [CrossRef]
- Walacik, M.; Chmielewska, A. Energy Performance in Residential Buildings as a Property Market Efficiency Driver. Energies 2024, 17, 2310. [Google Scholar] [CrossRef]
- Mohamed, M.; Zakuan, N.D.; Tengku Hassan, T.N.A.; Lock, S.S.M.; Mohd Shariff, A. Global Development and Readiness of Nuclear Fusion Technology as the Alternative Source for Clean Energy Supply. Sustainability 2024, 16, 4089. [Google Scholar] [CrossRef]
- Segura-Rodríguez, I.; Bhandari, R. Assessment of Bioenergy Potential from Biomass Waste to Improve Access to Clean Energy for Cooking in Mali. Sustainability 2024, 16, 455. [Google Scholar] [CrossRef]
- Aydın, O. Conjugate Heat Transfer Analysis of Double Pane Windows. Build. Environ. 2006, 41, 109–116. [Google Scholar] [CrossRef]
- Lee, J.-W. Workflow for Window Composition Detection to Aid Energy-Efficient Renovation in Low-Income Housing in Korea. Buildings 2024, 14, 966. [Google Scholar] [CrossRef]
- Koshlak, H.; Basok, B.; Davydenko, B. Heat Transfer Through Double-Chamber Glass Unit with Low-Emission Coating. Energies 2024, 17, 1100. [Google Scholar] [CrossRef]
- Jezierski, W.; Zukowski, M. Evaluation of the Impact of Window Parameters on Energy Demand and CO2 Emission Reduction for a Single-Family House. Energies 2023, 16, 4429. [Google Scholar] [CrossRef]
- Vercoulen, P.; Lee, S.; Han, X.; Zhang, W.; Cho, Y.; Pang, J. Carbon-Neutral Steel Production and Its Impact on the Economies of China, Japan, and Korea: A Simulation with E3ME-FTT:Steel. Energies 2023, 16, 4498. [Google Scholar] [CrossRef]
- Valentini, L.; Bittolo Bon, S.; Pugno, N.M. Combining Living Microorganisms with Regenerated Silk Provides Nanofibril-Based Thin Films with Heat-Responsive Wrinkled States for Smart Food Packaging. Nanomaterials 2018, 8, 518. [Google Scholar] [CrossRef]
- Oberländer, J.; Kirchner, P.; Keusgen, M.; Schöning, M.J. Strategies in Developing Thin-film Sensors for Monitoring Aseptic Food Processes: Theoretical Considerations and Investigations of Passivation Materials. Electrochim. Acta 2015, 183, 130–136. [Google Scholar] [CrossRef]
- Kant, K.; Shukla, A.; Sharma, A.; Biwole, P. Heat Transfer Studies of Photovoltaic Panel Coupled with Phase Change Material. Sol. Energy 2016, 140, 151–161. [Google Scholar] [CrossRef]
- De Mey, G.; Wyrzutowicz, J.; De Vos, A.; Maranda, W.; Napieralski, A. Influence of Lateral Heat Diffusion on the Thermal Impedance Measurement of Photovoltaic Panels. Sol. Energy Mater. Sol. Cells 2013, 112, 1–5. [Google Scholar] [CrossRef]
- Rahmatmand, A.; Harrison, S.; Oosthuizen, P. An Experimental Investigation of Snow Removal from Photovoltaic Solar Panels by Electrical Heating. Sol. Energy 2018, 171, 811–826. [Google Scholar] [CrossRef]
- Li, S.; Cao, B. Vortex Characteristics in Fourier and non-Fourier Heat Conduction Based on Heat Flux Rotation. Int. J. Heat Mass Transf. 2017, 108, 2403–2407. [Google Scholar] [CrossRef]
- Rosa, A.; Esquivel-Sirvent, R. Causality in non-Fourier Heat Conduction. J. Phys. Commun. 2022, 6, 105003. [Google Scholar] [CrossRef]
- Joseph, D.; Preziosi, L. Heat waves. Rev. Mod. Phys. 1989, 61, 41–73. [Google Scholar] [CrossRef]
- Dorfman, A.; Renner, Z. Conjugate Problems in Convective Heat Transfer: Review. Math. Probl. Eng. 2009, 2009, 927350. [Google Scholar] [CrossRef]
- Zudin, Y.B. Theory of Periodic Conjugate Heat Transfer, 3rd ed.; Springer: Berlin, Germany, 2011. [Google Scholar]
- Kazemi-Kamyab, V.; van Zuijlen, A.H.; Bijl, H. A High Order Time-accurate Loosely-coupled Solution Algorithm For Unsteady Conjugate Heat Transfer Problems. Comput. Methods Appl. Mech. Eng. 2013, 264, 205–217. [Google Scholar] [CrossRef]
- Ooi, E.H.; van Popov, V. An Efficient Hybrid BEM–RBIE Method For Solving Conjugate Heat Transfer Problems Comput. Math. Appl. 2014, 66, 2489–2503. [Google Scholar]
- Costa, R.; Nóbrega, J.M.; Clain, S.; Machado, G.J. Very High-order Accurate Polygonal Mesh Finite Volume Scheme for Conjugate Heat Transfer Problems With Curved Interfaces And Imperfect Contacts. Comput. Methods Appl. Mech. Eng. 2019, 357, 112560. [Google Scholar] [CrossRef]
- Pan, X.; Lee, C.; Choi, J.-I. Efficient Monolithic Projection Method For Time-dependent Conjugate Heat Transfer Problems. J. Comput. Phys. 2018, 369, 191–208. [Google Scholar] [CrossRef]
- Guo, S.; Feng, Y.; Tao, W.-Q. Deviation Analysis of Loosely Coupled Quasi-static Method for Fluid-thermal Interaction in Hypersonic Flows. Comput. Fluids 2017, 149, 194–204. [Google Scholar] [CrossRef]
- Errera, M.-P.; Duchaine, F. Comparative Study Of Coupling Coefficients In Dirichlet-robin Procedure For Fluid-structure Aerothermal Simulations J. Comput. Phys. 2016, 312, 218–234. [Google Scholar] [CrossRef]
- Kazemi-Kamyab, V.; van Zuijlen, A.H.; Bijl, H. Analysis And Application Of High Order Implicit Runge-kutta Schemes For Unsteady Conjugate Heat Transfer: A Strongly-coupled Approach. J. Comput. Phys. 2014, 272, 471–486. [Google Scholar] [CrossRef]
- Tzou, D.Y. Macro to Microscale Heat Transfer. The Lagging Behaviour, 2nd ed.; Taylor & Francis: Washington, DC, USA, 2014. [Google Scholar]
- Dai, W.; Han, F.; Sun, Z. Accurate Numerical Method For Solving Dual-phase-lagging Equation With Temperature Jump Boundary Condition In Nano Heat Conduction. Int. J. Heat Mass Transf. 2013, 64, 966–975. [Google Scholar] [CrossRef]
- Koshlak, H.; Basok, B.; Davydenko, B. Reduced Heat Loss Through Window Structures. Energy Technol. Resour. Sav. 2023, 76, 43–57. [Google Scholar]
- Basok, B.I.; Davydenko, B.V.; Pavlenko, A.M.; Kuzhel, L.M.; Novikov, V.H.; Goncharuk, S.M.; Ilienko, B.K.; Nikitin, Y.Y.; Veremiichuk, H.M. Reduced Heat Loss Through Window Structures. Energy Technol. Resour. Sav. 2023, 76, 43–57. [Google Scholar] [CrossRef]
- Ferraiuolo, M.; Manca, O. Heat transfer in a Multi-layered Thermal Protection System Under Aerodynamic Heating. Int. J. Therm. Sci. 2012, 53, 56–70. [Google Scholar] [CrossRef]
- Nassab, S.; Maramisaran, M. Transient Numerical Analysis of a Multi-layered Porous Heat Exchanger Including Gas Radiation Effects. Int. J. Therm. Sci. 2009, 48, 1586–1595. [Google Scholar] [CrossRef]
- Zhou, L.; Parhizi, M.; Jain, A. Temperature Distribution in a Multi-layer Cylinder with Circumferentially-varying Convective Heat Transfer Boundary Conditions. Int. J. Therm. Sci. 2021, 160, 106673. [Google Scholar] [CrossRef]
- Gao, Q.; Sun, W.; Zhang, J. Thermo-elasto-hydrodynamic Analysis of a Specific Multi-layer gas Foil Thrust Bearing Under Thermal-fluid-solid Coupling. Chin. J. Aeronaut. 2023, 36, 231–246. [Google Scholar] [CrossRef]
- Liang, Y.; Gao, X.; Xu, B.; Cui, M.; Zheng, B. A Reduced-order Modelling for Real-time Identification of Damages in Multi-layered Composite Materials. Inverse Probl. Sci. Eng. 2021, 29, 73–94. [Google Scholar] [CrossRef]
- Tzou, D.Y. A Unified Approach for Heat Conduction from Macro-to Micro-scale. ASME J. Heat Transf. 1995, 117, 8–16. [Google Scholar] [CrossRef]
- Sun, H.; Sun, Z.Z.; Dai, W. A Second-order Finite Difference Scheme for Solving the Dual-phase-lagging Equation In A Double-layered Nano-scale Thin Film. Numer. Methods Partial Differ. Equ. 2017, 33, 142–173. [Google Scholar] [CrossRef]
- Coronel, A.; Huancas, F.; Lozada, E.; Tello, A. A Numerical Method for a Heat Conduction Model in a Double-Pane Window. Axioms 2022, 11, 422. [Google Scholar] [CrossRef]
- Jou, D.; Casas-Vázquez, J.; Lebon, G. Extended Irreversible Thermodynamics Revisited (1988–1998). Rep. Prog. Phys. 1999, 62, 1035–1142. [Google Scholar] [CrossRef]
- Cattaneo, C. Sulla Conduzione Del Calore. Atti Sem. Mat. Fis. Univ. Modena 1948, 3, 83–101. [Google Scholar]
- Christov, C.I. On Frame Indifferent Formulation Of The Maxwell-catteneo Model of Finite-speed Heat Conduction. Mech. Res. Commun. 2009, 36, 481–486. [Google Scholar] [CrossRef]
- Ghazanfarian, J.; Abbassi, A. Effect Of Boundary Phonon Scattering On Dual-phase-lag Model To Simulate Micro- And Nano-scale Heat Conduction. Int. J. Heat Mass Transf. 2009, 52, 3706–3711. [Google Scholar] [CrossRef]
- Sun, Z.Z. Numerical Methods for Partial Differential Equations, 2nd ed.; Science Press: Beijing, China, 2012. [Google Scholar]
- Liao, H.L.; Sun, Z.Z. Maximum Norm Error Estimates Of Efficient Difference Schemes For Second-order Wave Equations. J. Comput. Appl. Math. 2011, 235, 2217–2233. [Google Scholar] [CrossRef]
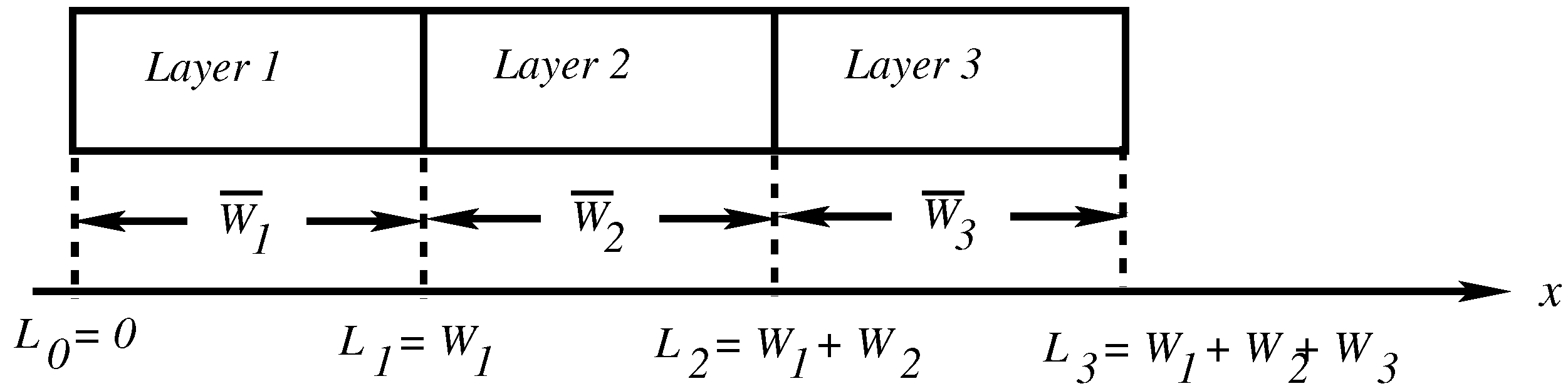

| Notation | Definition |
|---|---|
| Geometrical | |
| width of ℓth-layer | |
| left boundary | |
| interface 1 | |
| interface 2 | |
| right boundary | |
| interval denoting the ℓth-layer | |
| space domain | |
| time domain | |
| space–time domain | |
| Physical | |
| the heat capacitance of ℓth-layer | |
| heat flux phase lags of ℓth-layer | |
| temperature gradient phase lags of ℓth-layer | |
| thermal conductivity of ℓth-layer | |
| some proportionality constants | |
| Knudsen numbers | |
| heat source function of ℓth-layer | |
| initial distribution of the temperature | |
| initial distribution of the temporal derivative of temperature | |
| temperature flux at the left boundary of the solid | |
| temperature flux at the right boundary of the solid |
| under-diagonal | diagonal | upper-diagonal | |||||||
| (61) | |||||||||
| (49) | |||||||||
| (52) | |||||||||
| (62) | |||||||||
| under-diagonal | diagonal | upper-diagonal | |||||||
| (61) | |||||||||
| (49) | |||||||||
| (52) | |||||||||
| (62) | |||||||||
| (61) | |||||||||
| (49) | |||||||||
| (52) | |||||||||
| (62) | |||||||||
| under-diagonal | diagonal | upper-diagonal | |||||||
| (75) | |||||||||
| (73) | |||||||||
| (74) | |||||||||
| (76) | |||||||||
| under-diagonal | diagonal | upper-diagonal | |||||||
| (75) | |||||||||
| (73) | |||||||||
| (74) | |||||||||
| (76) | |||||||||
| under-diagonal | diagonal | upper-diagonal | |||||||
| (75) | |||||||||
| (73) | |||||||||
| (74) | |||||||||
| (76) | |||||||||
| (75) | |||||||||
| (73) | |||||||||
| (74) | |||||||||
| (76) | |||||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Coronel, A.; Lozada, E.; Berres, S.; Huancas, F.; Murúa, N. Mathematical Modeling and Numerical Approximation of Heat Conduction in Three-Phase-Lag Solid. Energies 2024, 17, 2497. https://doi.org/10.3390/en17112497
Coronel A, Lozada E, Berres S, Huancas F, Murúa N. Mathematical Modeling and Numerical Approximation of Heat Conduction in Three-Phase-Lag Solid. Energies. 2024; 17(11):2497. https://doi.org/10.3390/en17112497
Chicago/Turabian StyleCoronel, Anibal, Esperanza Lozada, Stefan Berres, Fernando Huancas, and Nicolás Murúa. 2024. "Mathematical Modeling and Numerical Approximation of Heat Conduction in Three-Phase-Lag Solid" Energies 17, no. 11: 2497. https://doi.org/10.3390/en17112497
APA StyleCoronel, A., Lozada, E., Berres, S., Huancas, F., & Murúa, N. (2024). Mathematical Modeling and Numerical Approximation of Heat Conduction in Three-Phase-Lag Solid. Energies, 17(11), 2497. https://doi.org/10.3390/en17112497








