ANN-LSTM-A Water Consumption Prediction Based on Attention Mechanism Enhancement
Abstract
1. Introduction
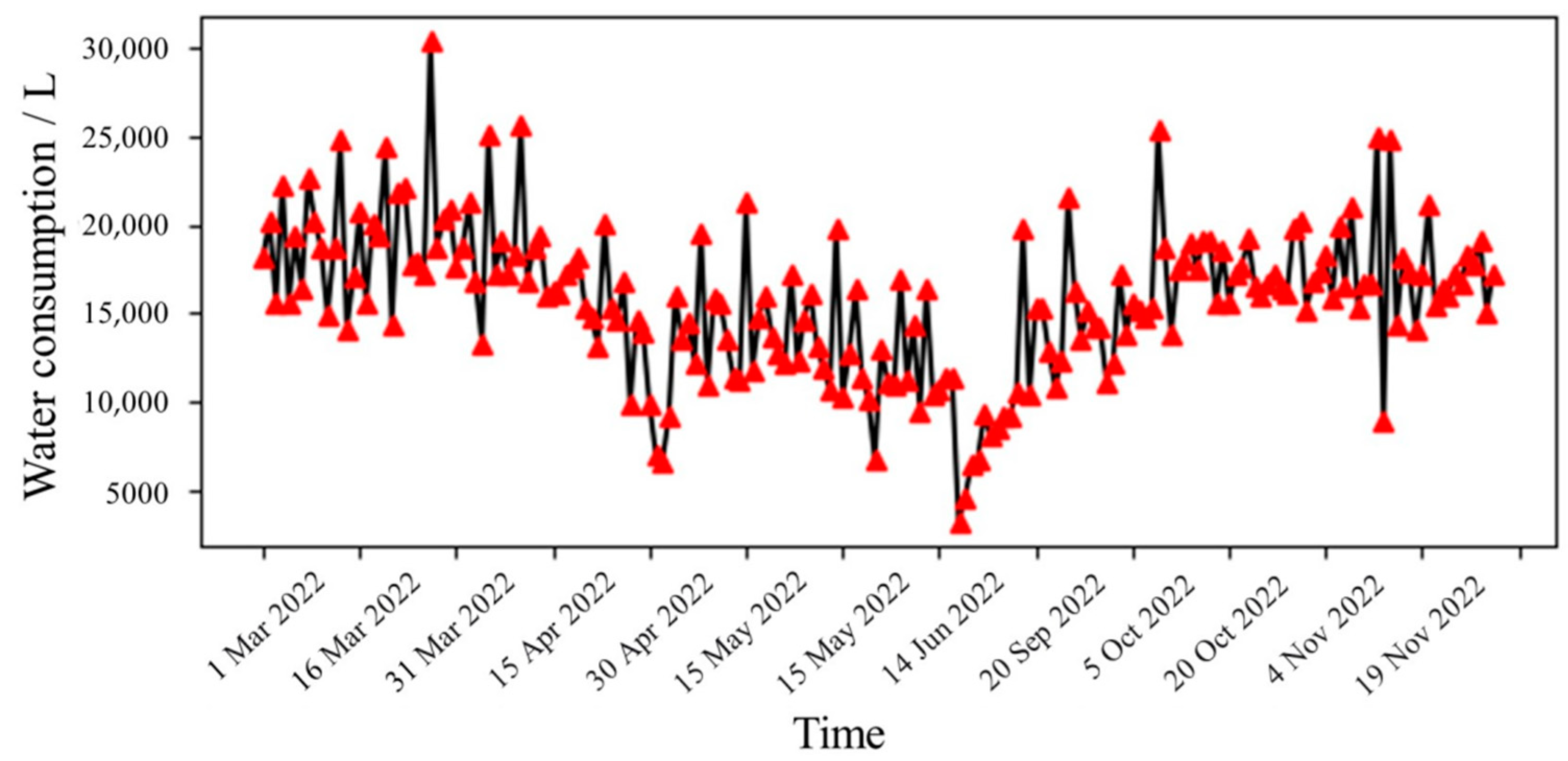
2. Data Analysis
2.1. Data Sources
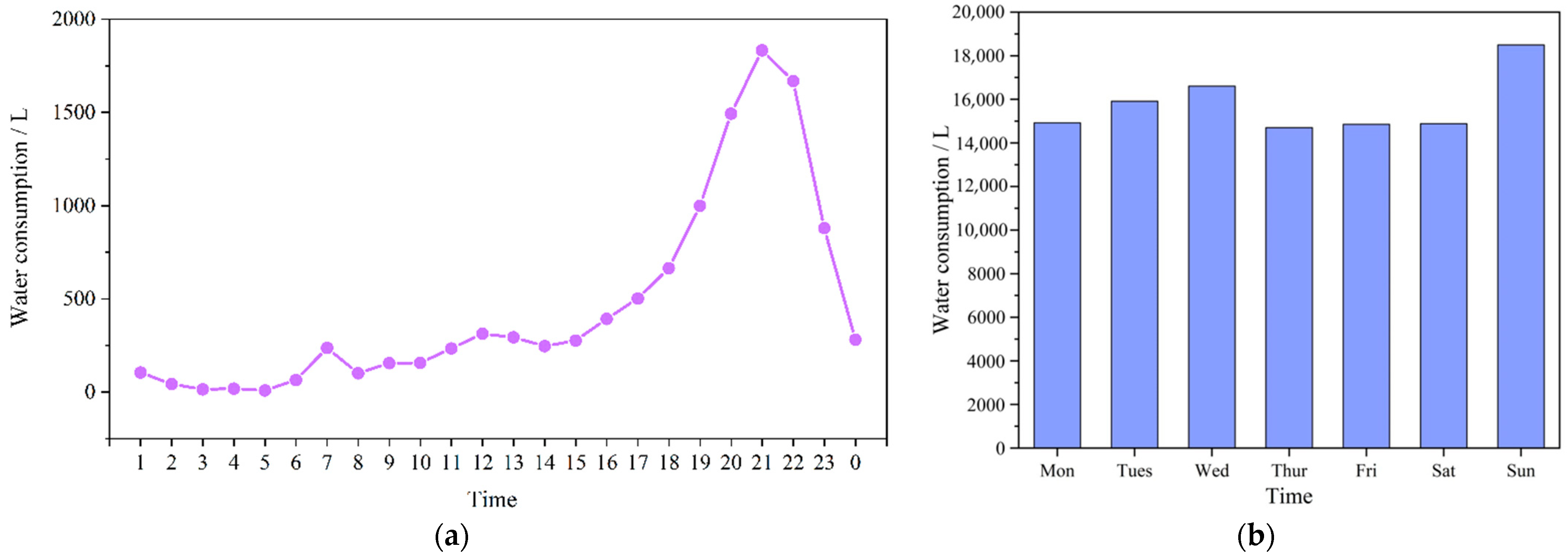
2.2. Analysis of Water Usage Habits
3. Methodology
3.1. Artificial Neural Network
3.2. Long Short-Term Memory
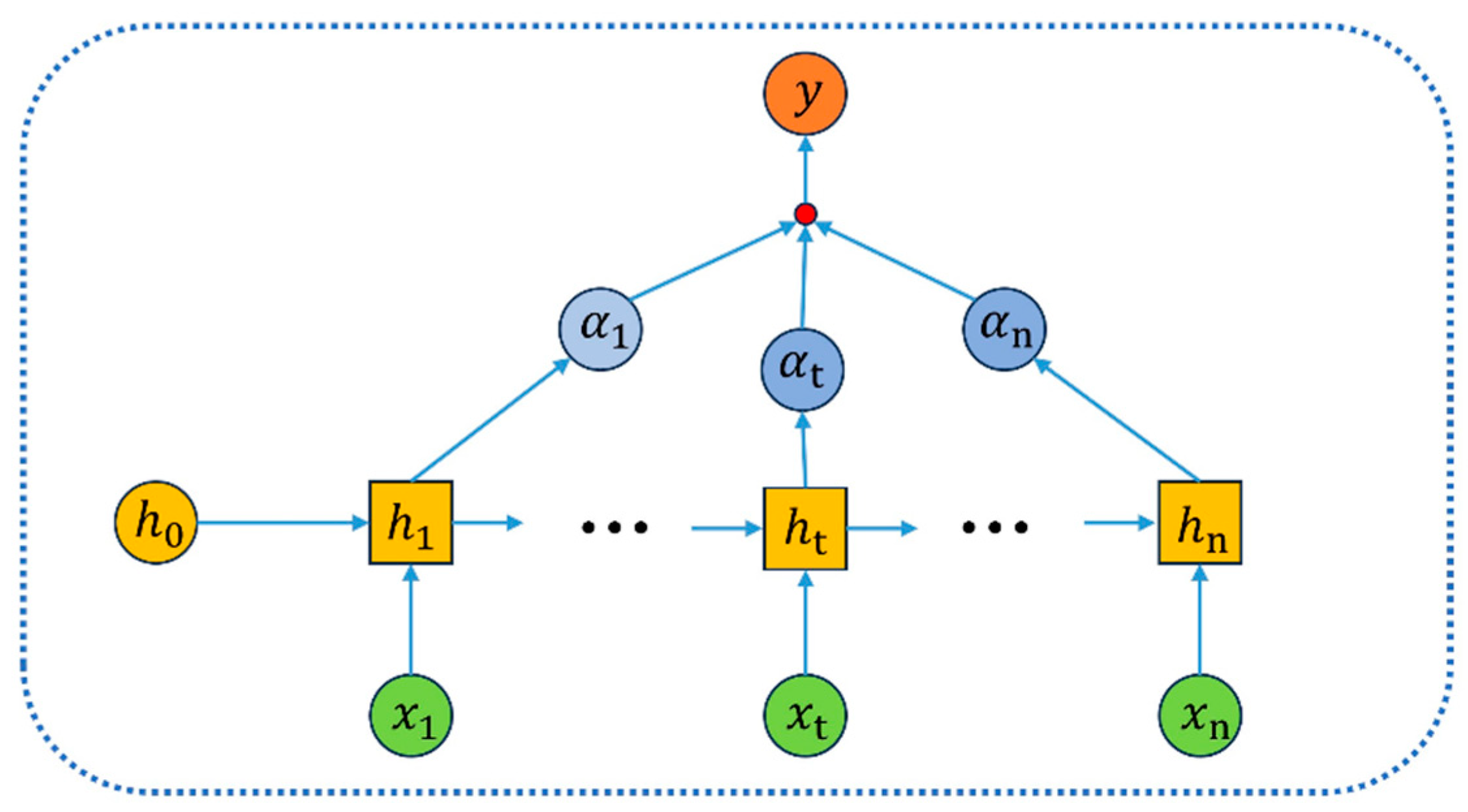
3.3. Attention Mechanism
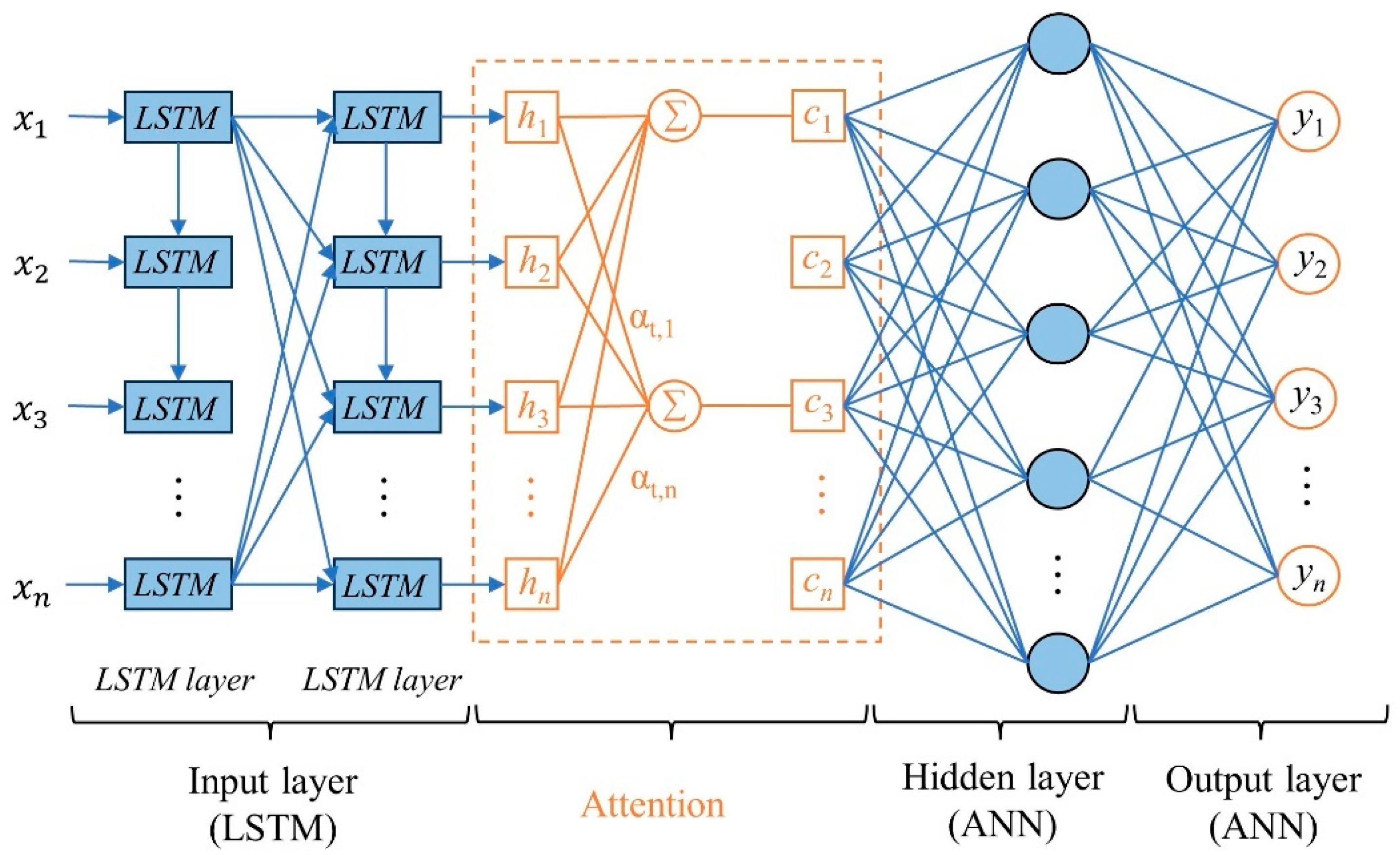
3.4. ANN-LSTM-A Model
4. Prediction and Analysis
4.1. Experimental Process
- (1)
- The DHW consumption data were normalized, 90% of the datasets were used for training, and the remaining 10% were used for testing.
- (2)
- The input and output of the ANN-LSTM-A model were determined, and the ANN-LSTM-A-based model for predicting DHW consumption was developed with the goal of determining the optimal number of iterations, batch size, and other relevant hyperparameters.
- (3)
- The ANN-LSTM-A model was trained, and the weights and bias values were optimized according to the output error of each iteration.
- (4)
- When the number of training iterations reached the maximum number, the training ended, and the ANN-LSTM-A model began to predict DHW consumption. If the number of training iterations did not reach the maximum number, the process returned to (3) to continue the iterations.
- (5)
- The test dataset was used to test the determined ANN-LSTM-A model, and the corresponding root mean square error (RMSE) and mean absolute error (MAE) values were calculated.
4.2. Evaluation Indicators
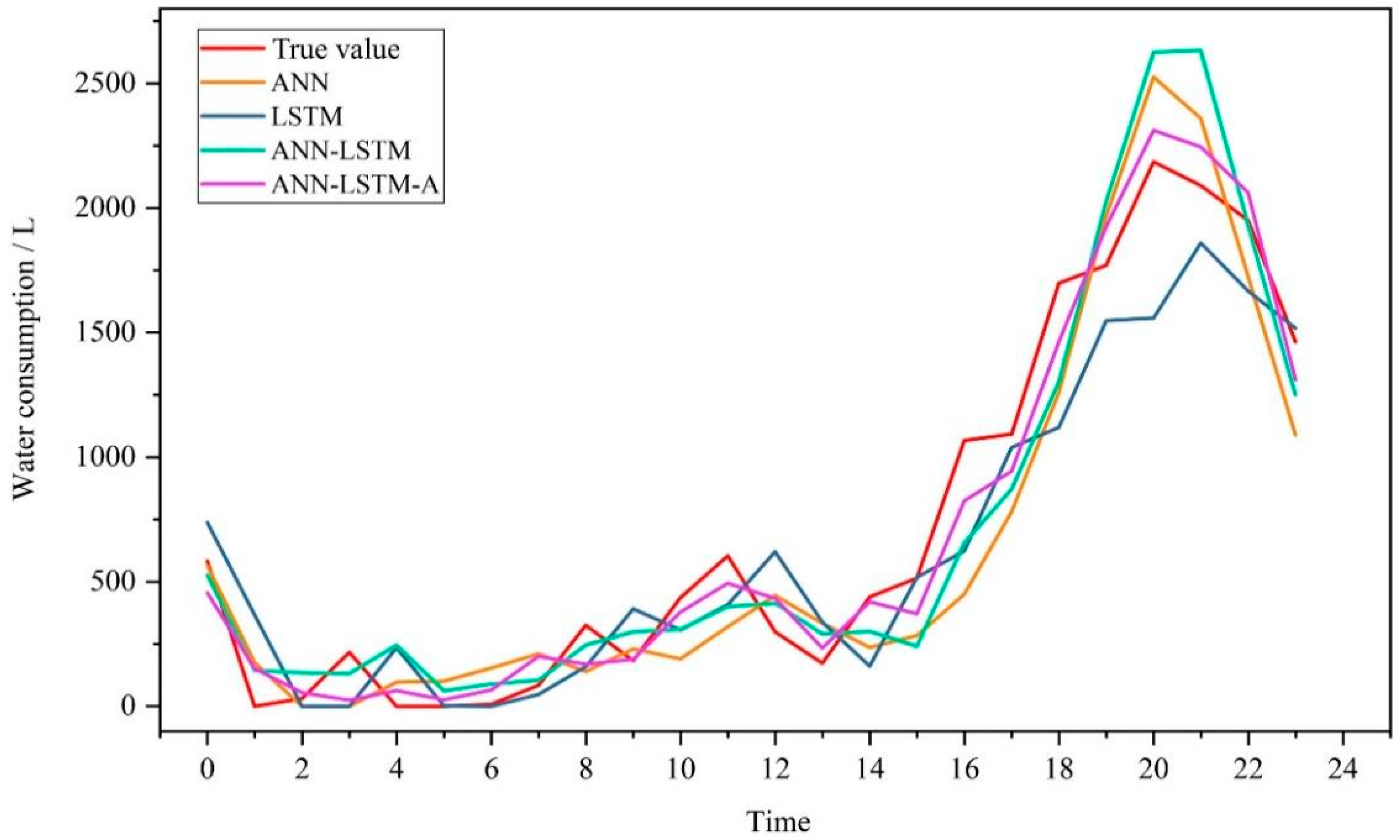
4.3. Comparison of Multi-Model Prediction Results
4.4. Learning Rate
5. Results and Discussion
6. Conclusions
- (1)
- Upon comparing the prediction results of the ANN, LSTM, ANN-LSTM, and ANN-LSTM-A models, it was observed that the ANN-LSTM-A model yielded a significantly improved performance. The RMSE and MAE values achieved by the ANN-LSTM-A model were found to be 15.4% and 17.9% lower than those obtained by the ANN model, 13.2% and 11.5% lower than the LSTM model, and 13.2% and 8% lower than the ANN-LSTM model, respectively. These results indicate that the ANN-LSTM-A model showcased superior predictive capabilities and demonstrated a higher degree of accuracy in forecasting water consumption. The utilization of the ANN-LSTM-A model can hence be deemed advantageous in enhancing the accuracy of water consumption prediction.
- (2)
- By comparing the ANN-LSTM and ANN-LSTM-A models, it was found that the ANN-LSTM-A model with an AM could better capture the key information in the time series data and automatically learn the weights and importance of different time points to adapt to various changes and trends in different time series. This effectively improved the accuracy of the model in the prediction of DHW consumption, and thus, this model is a reliable prediction tool.
- (3)
- When predicting the DHW consumption of student apartments, various conditions will inevitably have a certain influence on the prediction accuracy. For instance, changes in weather have a significant impact on water consumption. Hence, to enhance the predictive accuracy of the model, it is essential to incorporate meteorological conditions, seasons, and other related factors. Further analysis and exploration of these factors in future studies will help improve the accuracy of water consumption prediction.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lyu, Y.; Gao, H.; Yan, K.; Liu, Y.; Tian, J.; Chen, L.; Wan, M. Carbon peaking strategies for industrial parks: Model development and applications in China. Appl. Energy 2022, 322, 119442. [Google Scholar] [CrossRef]
- Liang, G. Research on the Evaluation System and Practice of Green Schools in the United States. Constr. Sci. Technol. 2013, 12, 35–38. [Google Scholar]
- Deng, L.; Chang, X.; Wang, P. Daily Water Demand Prediction Driven by Multi-source Data. Procedia Comput. Sci. 2022, 208, 128–135. [Google Scholar] [CrossRef]
- Yue, J.; Yang, H.; Feng, H.; Han, S.; Zhou, C.; Fu, Y.; Guo, W.; Ma, X.; Qiao, H.; Yang, G. Hyperspectral-to-image transform and CNN transfer learning enhancing soybean LCC estimation. Comput. Electron. Agric. 2023, 211, 108011. [Google Scholar] [CrossRef]
- Zhang, J.; Xin, X.; Shang, Y.; Wang, Y.; Zhang, L. Nonstationary significant wave height forecasting with a hybrid VMD-CNN model. Ocean Eng. 2023, 285, 115338. [Google Scholar] [CrossRef]
- Jing, Y.; Zhang, L.; Hao, W.; Huang, L. Numerical study of a CNN-based model for regional wave prediction. Ocean Eng. 2022, 255, 111400. [Google Scholar] [CrossRef]
- Cinar, Y.G.; Mirisaee, H.; Goswami, P.; Gaussier, E.; Aït-Bachir, A. Period-aware content attention RNNs for time series forecasting with missing values. Neurocomputing 2018, 312, 177–186. [Google Scholar] [CrossRef]
- Amalou, I.; Mouhni, N.; Abdali, A. Multivariate time series prediction by RNN architectures for energy consumption forecasting. Energy Rep. 2022, 8, 1084–1091. [Google Scholar] [CrossRef]
- Wang, Y.; Li, T.; Lu, W.; Cao, Q. Attention-inspired RNN Encoder-Decoder for Sensory Time Series Forecasting. Procedia Comput. Sci. 2022, 209, 103–111. [Google Scholar] [CrossRef]
- Chung, W.H.; Gu, Y.H.; Yoo, S.J. District heater load forecasting based on machine learning and parallel CNN-LSTM attention. Energy 2022, 246, 123350. [Google Scholar] [CrossRef]
- Yao, J.; Wu, W. Wave height forecast method with multi-step training set extension LSTM neural network. Ocean Eng. 2022, 263, 112432. [Google Scholar] [CrossRef]
- Fazlipour, Z.; Mashhour, E.; Joorabian, M. A deep model for short-term load forecasting applying a stacked autoencoder based on LSTM supported by a multi-stage attention mechanism. Appl. Energy 2022, 327, 120063. [Google Scholar] [CrossRef]
- Huang, R.; Ma, L.; He, J.; Chu, X. T-GAN: A deep learning framework for prediction of temporal complex networks with adaptive graph convolution and attention mechanism. Displays 2021, 68, 102023. [Google Scholar] [CrossRef]
- Yilmaz, B.; Korn, R. Synthetic demand data generation for individual electricity consumers: Generative Adversarial Networks (GANs). Energy AI 2022, 9, 100161. [Google Scholar] [CrossRef]
- Yuan, R.; Wang, B.; Mao, Z.; Watada, J. Multi-objective wind power scenario forecasting based on PG-GAN. Energy 2021, 226, 120379. [Google Scholar] [CrossRef]
- Singh, S.; Bansal, P.; Hosen, M.; Bansal, S.K. Forecasting annual natural gas consumption in USA: Application of machine learning techniques-ANN and SVM. Resour. Policy 2023, 80, 103159. [Google Scholar] [CrossRef]
- Ravikumar, K.S.; Chethan, Y.D.; Likith, C.; Chethan, S.P. Prediction of Wear Characteristics for Al-MnO2 Nanocomposites using Artificial Neural Network (ANN). In Materials Today: Proceedings; Elsevier: Amsterdam, The Netherlands, 2023. [Google Scholar]
- Nguyen, T.H.; Tran, N.L.; Phan, V.T.; Nguyen, D.D. Prediction of shear capacity of RC beams strengthened with FRCM composite using hybrid ANN-PSO model. Case Stud. Constr. Mater. 2023, 18, e02183. [Google Scholar] [CrossRef]
- Neudakhina, Y.; Trofimov, V. An ANN-based intelligent system for forecasting monthly electric energy consumption. In Proceedings of the 2021 3rd International Conference on Control Systems, Lipetsk, Russia, 10–12 November 2021. [Google Scholar]
- Afandi, A.; Lusi, N.; Catrawedarma, I.; Subono; Rudiyanto, B. Prediction of temperature in 2 meters temperature probe survey in Blawan geothermal field using artificial neural network (ANN) method. Case Stud. Therm. Eng. 2022, 38, 102309. [Google Scholar] [CrossRef]
- Rodrigues, F.; Cardeira, C.; Calado, J.M.F. The daily and hourly energy consumption and load forecasting using artificial neural network method: A case study using a set of 93 households in Portugal. Energy Procedia 2014, 62, 220–229. [Google Scholar] [CrossRef]
- Bennett, C.; Stewart, R.A.; Beal, C.D. ANN-based residential water end-use demand forecasting model. Expert Syst. Appl. 2013, 40, 1014–1023. [Google Scholar] [CrossRef]
- Walker, D.; Creaco, E.; Vamvakeridou-Lyroudia, L.; Farmani, R.; Kapelan, Z.; Savić, D. Forecasting domestic water consumption from smart meter readings using statistical methods and artificial neural networks. Procedia Eng. 2015, 119, 1419–1428. [Google Scholar] [CrossRef]
- Pascanu, R.; Mikolov, T.; Bengio, Y. On the difficulty of training recurrent neural networks. In Proceedings of the 30th International Conference on Machine Learning, Atlanta, GA, USA, 16–21 June 2013. [Google Scholar]
- Greff, K.; Srivastava, R.K.; Koutník, J.; Steunebrink, B.R.; Schmidhuber, J. LSTM: A search space odyssey. IEEE Trans. Neural Netw. Learn Syst. 2016, 28, 2222–2232. [Google Scholar] [CrossRef] [PubMed]
- Sherstinsky, A. Fundamentals of recurrent neural network (RNN) and long short-term memory (LSTM) network. Phys. D 2020, 404, 132306. [Google Scholar] [CrossRef]
- Niknam, A.; Zare, H.K.; Hosseininasab, H.; Mostafaeipour, A. Developing an LSTM model to forecast the monthly water consumption according to the effects of the climatic factors in Yazd, Iran. J. Eng. Res. 2023, 11, 100028. [Google Scholar] [CrossRef]
- Heidari, A.; Khovalyg, D. Short-term energy use prediction of solar-assisted water heating system: Application case of combined attention-based LSTM and time-series decomposition. Sol. Energy 2020, 207, 626–639. [Google Scholar] [CrossRef]
- Xu, Y.; Li, F.; Asgari, A. Prediction and optimization of heating and cooling loads in a residential building based on multi-layer perceptron neural network and different optimization algorithms. Energy 2022, 240, 122692. [Google Scholar] [CrossRef]
- Vijayalakshmi, K.; Vijayakumar, K.; Nandhakumar, K. Prediction of virtual energy storage capacity of the air-conditioner using a stochastic gradient descent based artificial neural network. Electr. Power Syst. Res. 2022, 208, 107879. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Niu, Z.; Zhong, G.; Yu, H. A review on the attention mechanism of deep learning. Neurocomputing 2021, 452, 48–62. [Google Scholar] [CrossRef]



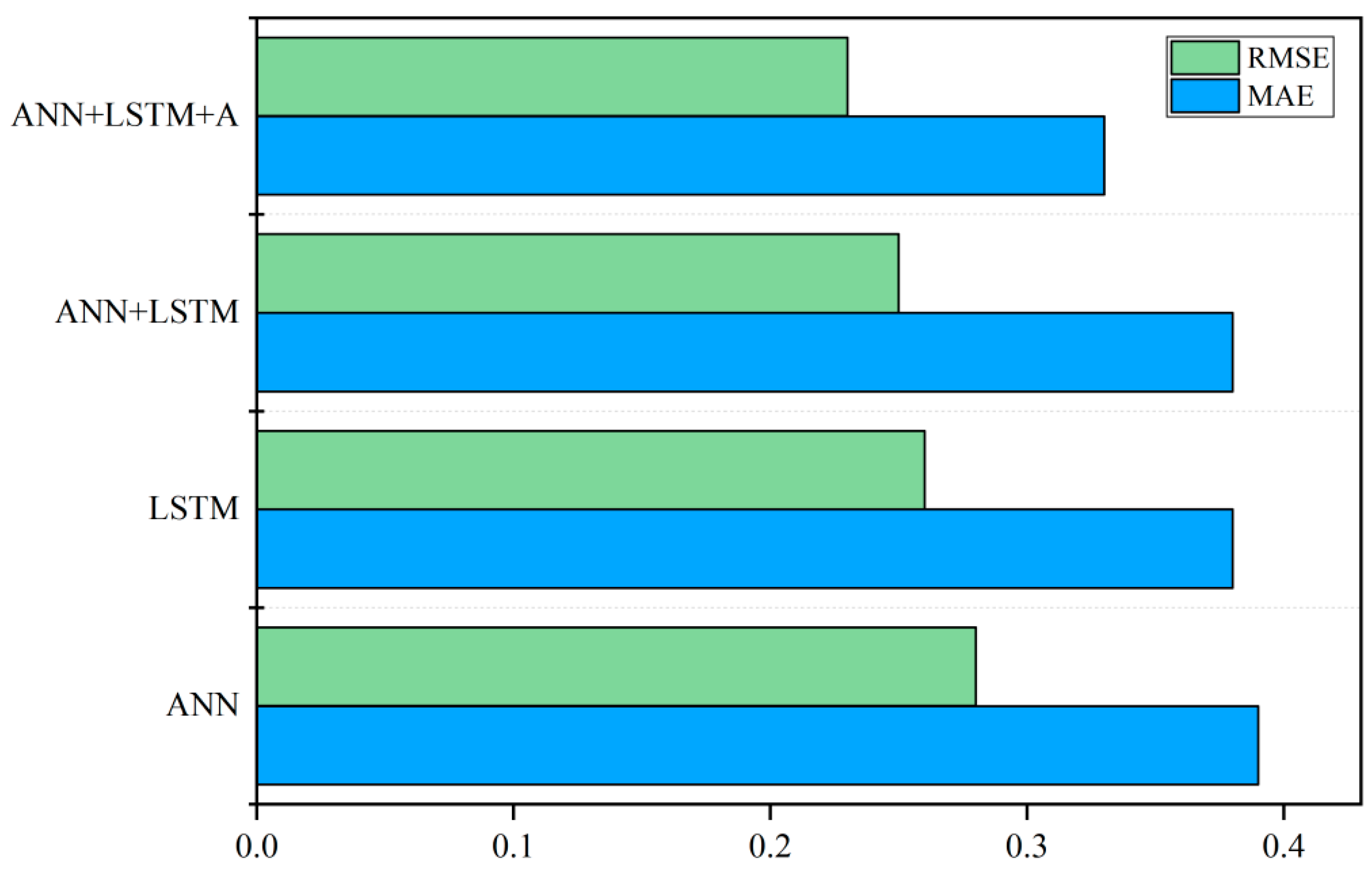


| Model | RMSE | MAE |
|---|---|---|
| ANN | 0.39 | 0.28 |
| LSTM | 0.38 | 0.26 |
| ANN-LSTM | 0.38 | 0.25 |
| ANN-LSTM-A | 0.33 | 0.23 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, X.; Meng, X.; Li, Z. ANN-LSTM-A Water Consumption Prediction Based on Attention Mechanism Enhancement. Energies 2024, 17, 1102. https://doi.org/10.3390/en17051102
Zhou X, Meng X, Li Z. ANN-LSTM-A Water Consumption Prediction Based on Attention Mechanism Enhancement. Energies. 2024; 17(5):1102. https://doi.org/10.3390/en17051102
Chicago/Turabian StyleZhou, Xin, Xin Meng, and Zhenyu Li. 2024. "ANN-LSTM-A Water Consumption Prediction Based on Attention Mechanism Enhancement" Energies 17, no. 5: 1102. https://doi.org/10.3390/en17051102
APA StyleZhou, X., Meng, X., & Li, Z. (2024). ANN-LSTM-A Water Consumption Prediction Based on Attention Mechanism Enhancement. Energies, 17(5), 1102. https://doi.org/10.3390/en17051102







