Stability Enhancement Method of Standalone Modular Multilevel Converters Based on Impedance Reshaping
Abstract
1. Introduction
2. An HSS-Based Approach to MMC Impedance Modeling
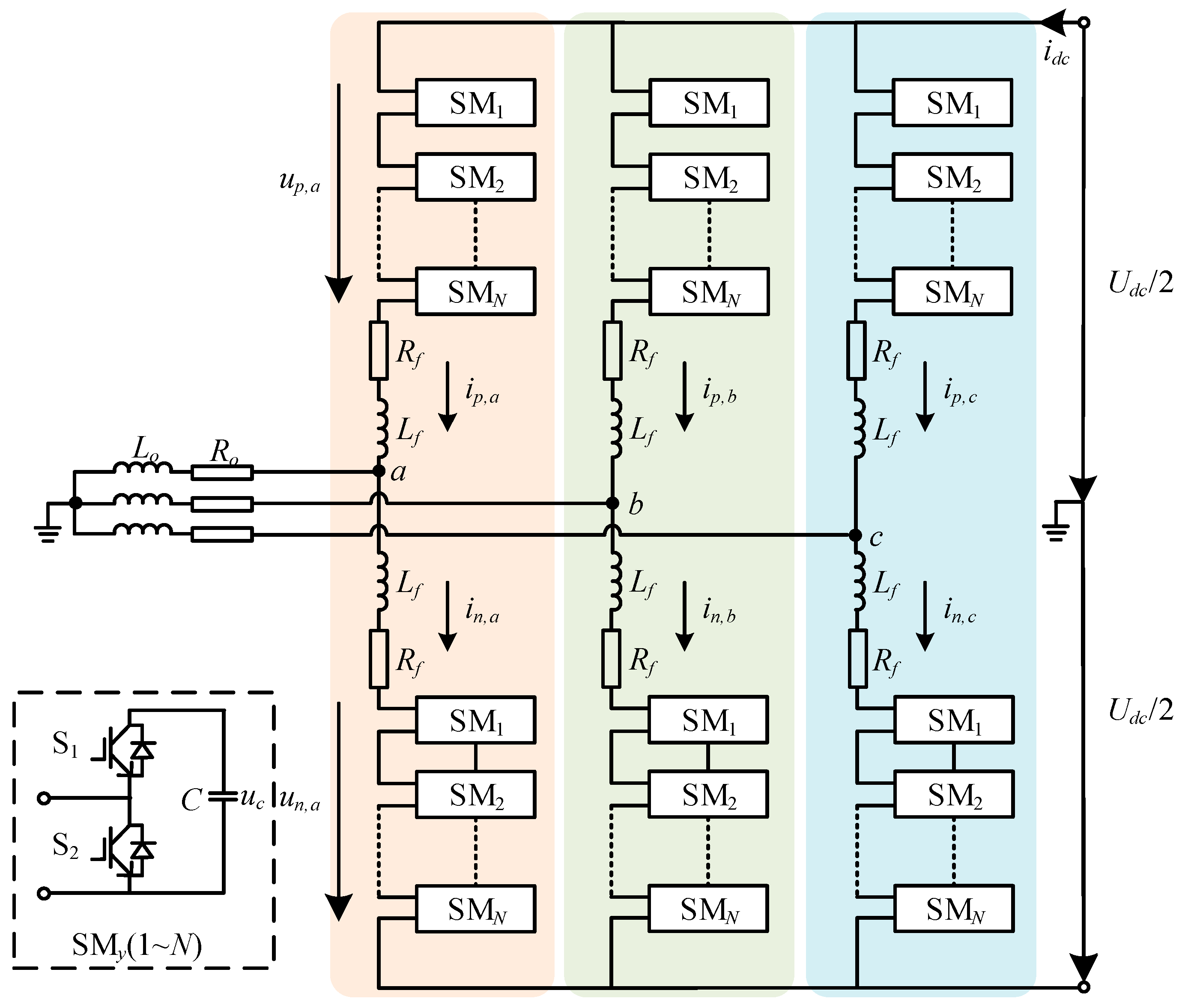
2.1. Average MMC Topology
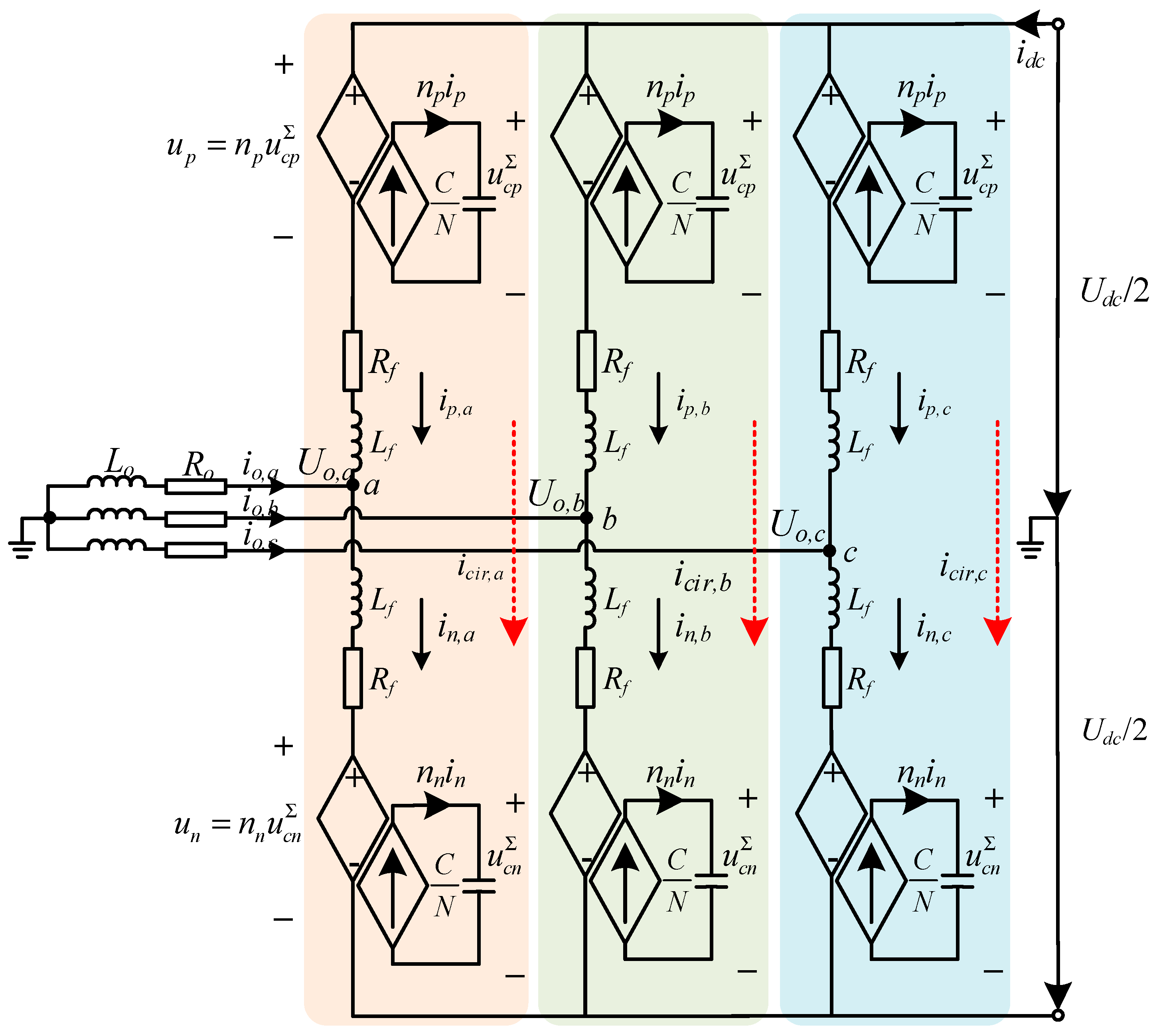
2.2. HSS Impedance Modeling of MMC
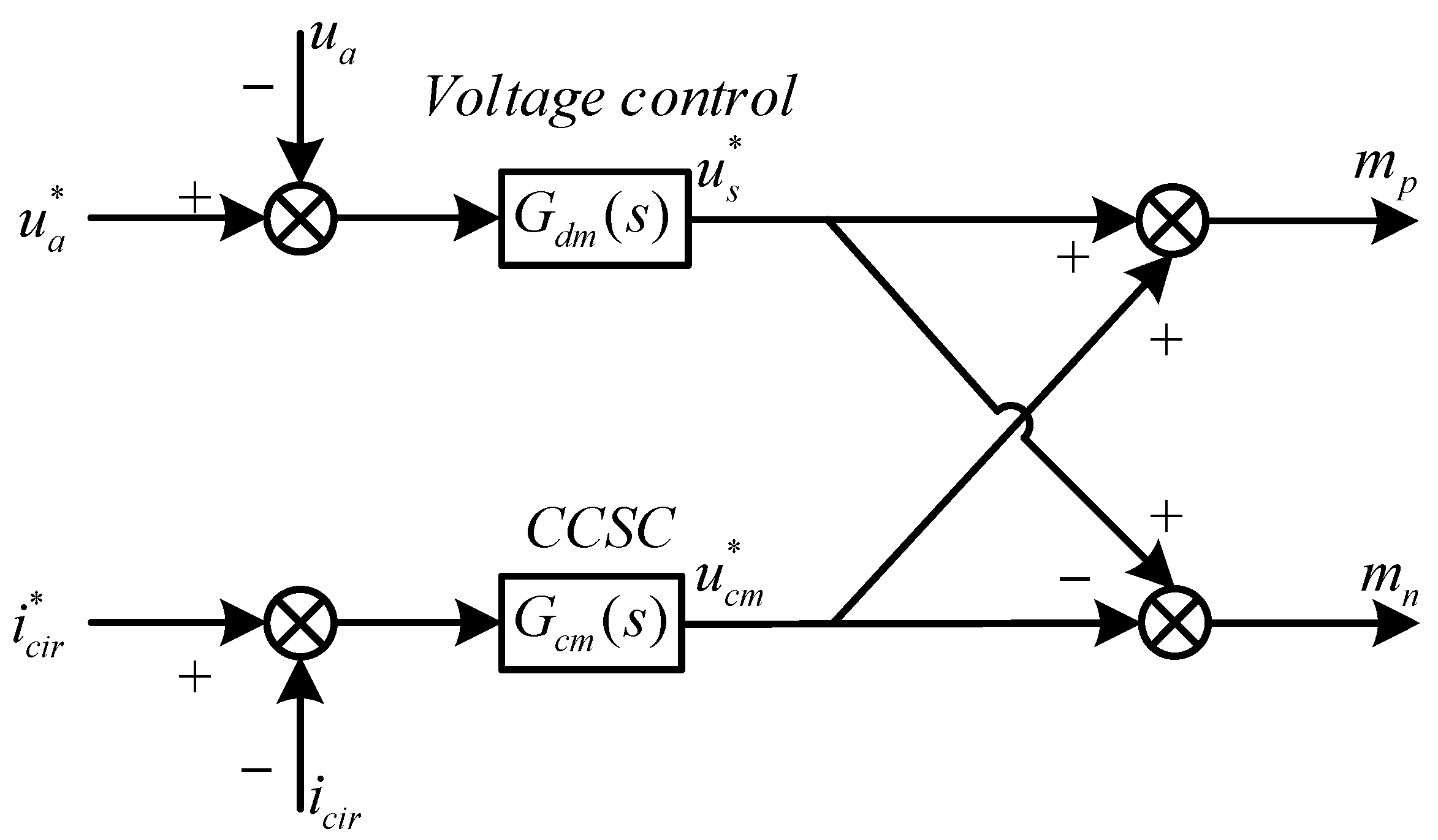
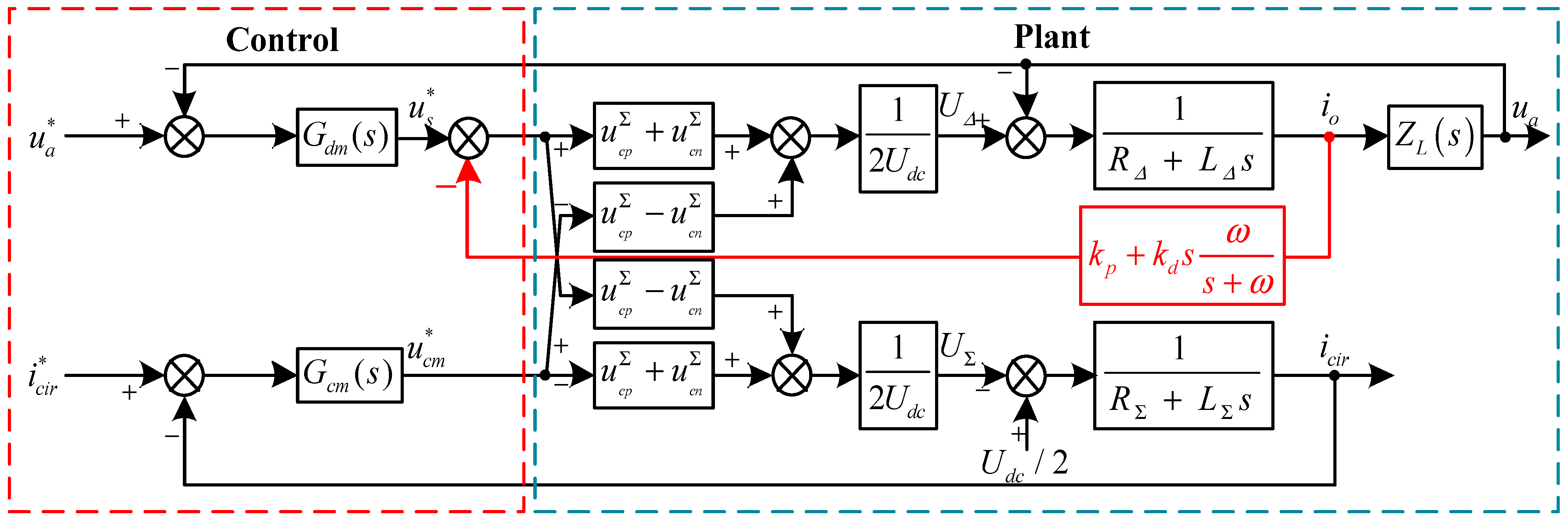
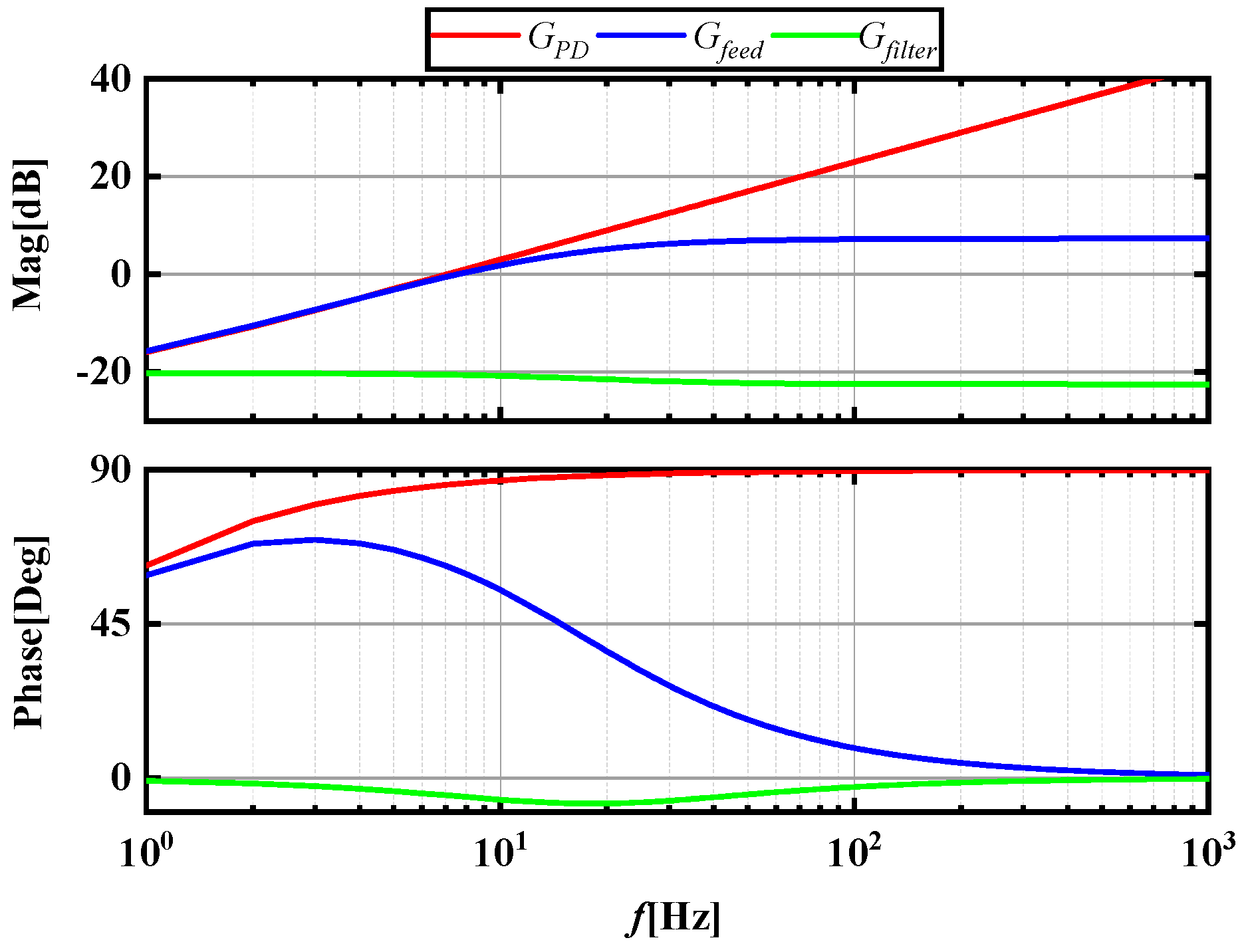
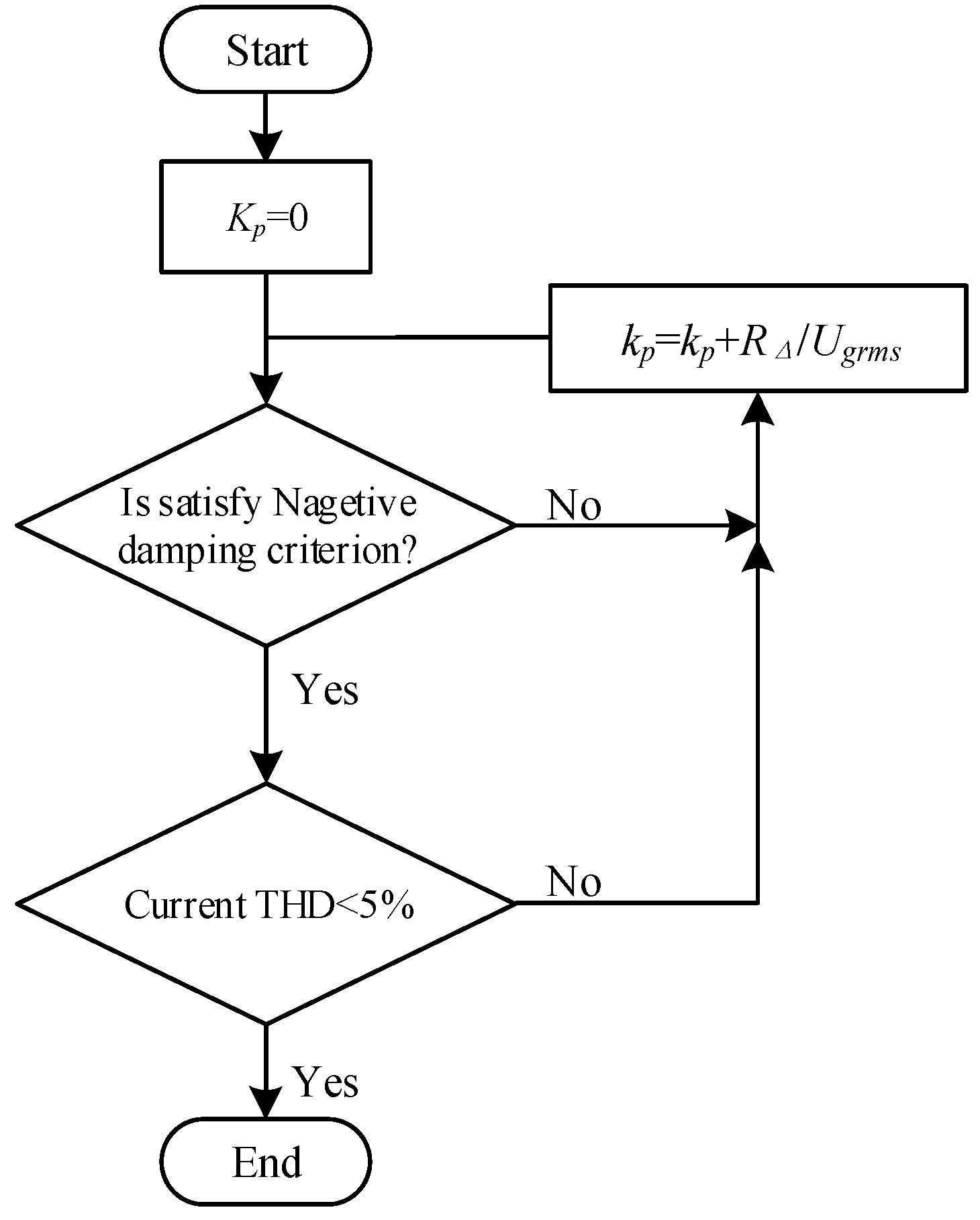
3. Proposed Method for Improving the Stability of MMCS Based on Impedance Reshaping
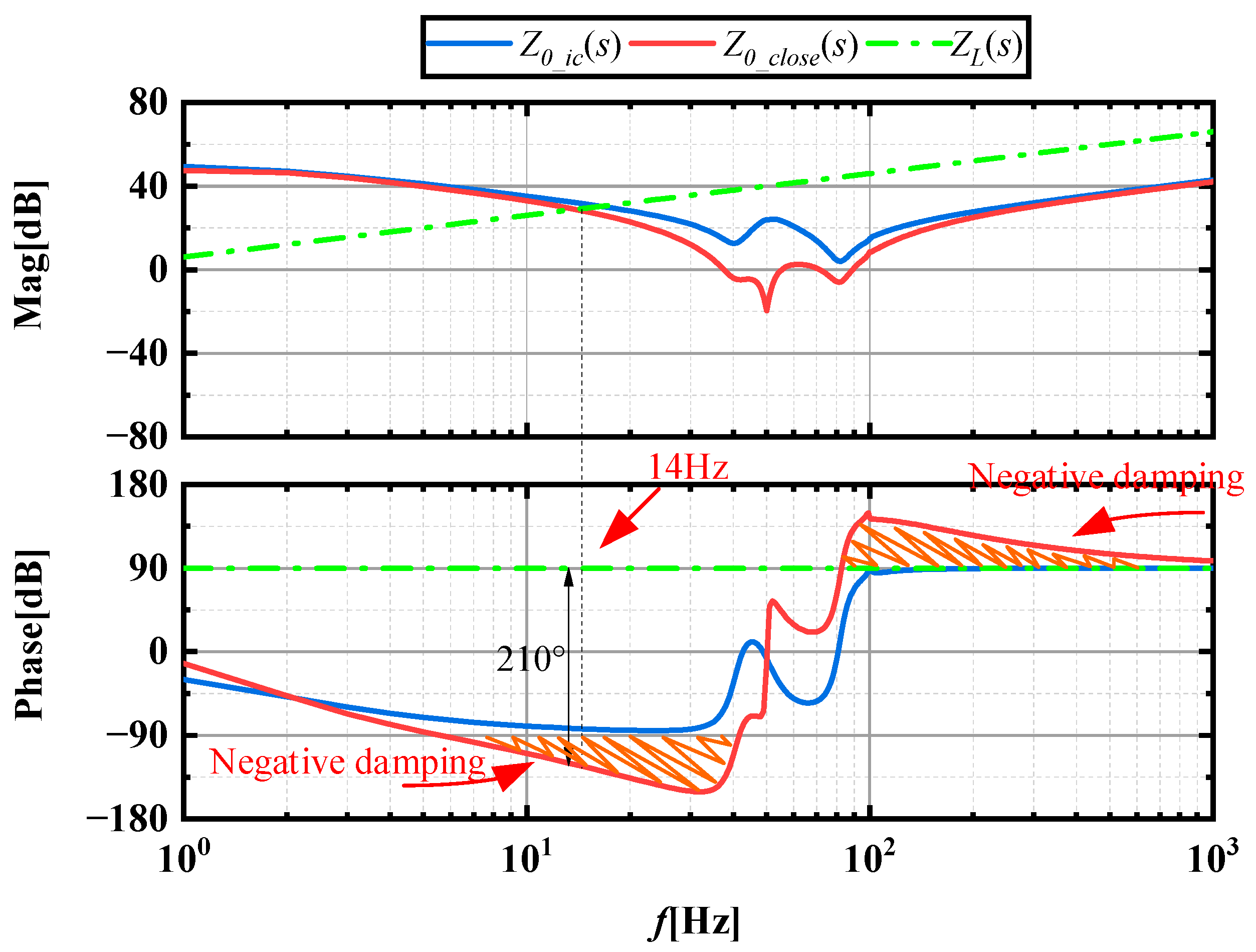
4. Case Study and Simulation Verifications
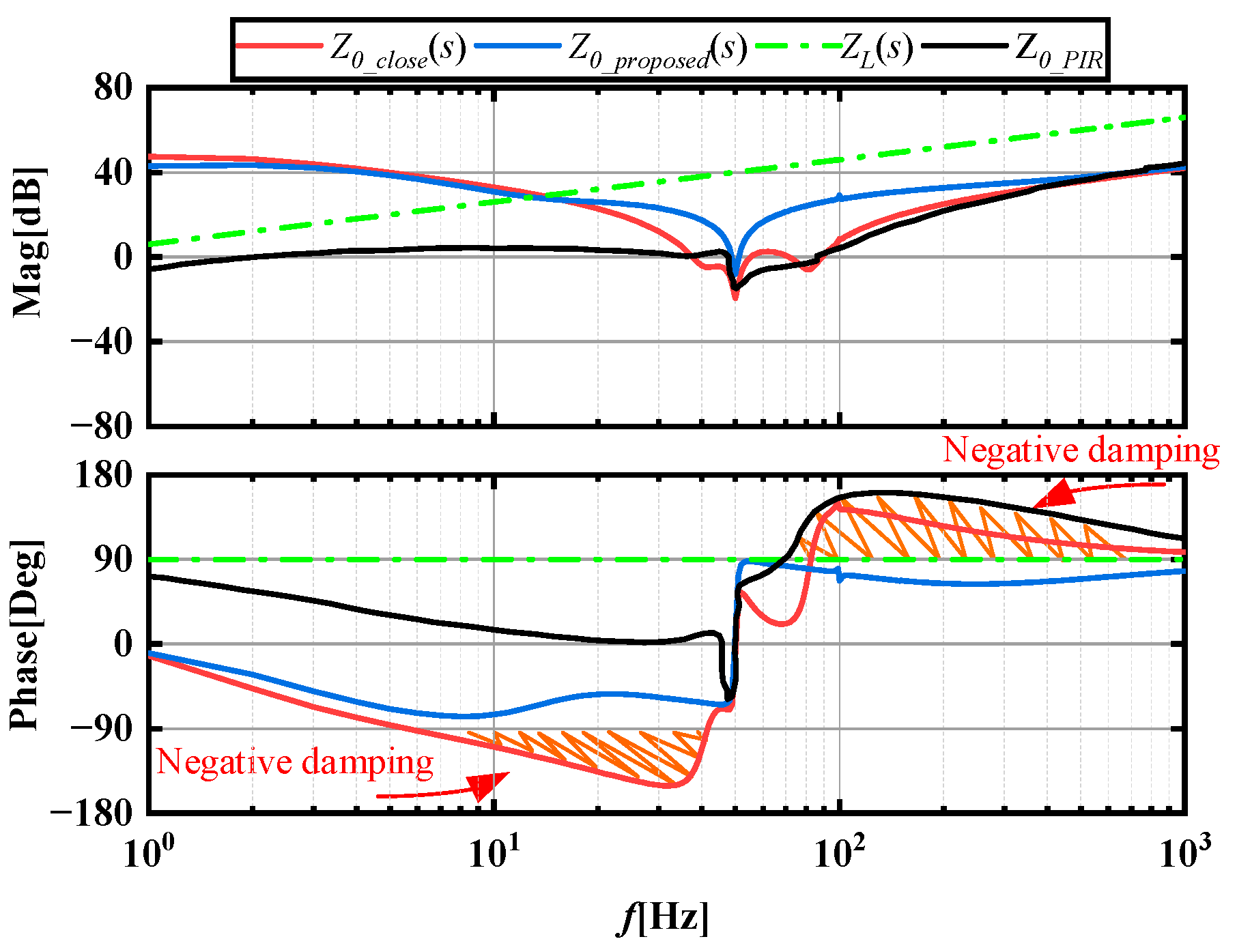
4.1. MMC Impedance Verification
4.2. Feed-Forward Current Compensation Control under the Control of Different Voltage Controller Parameters
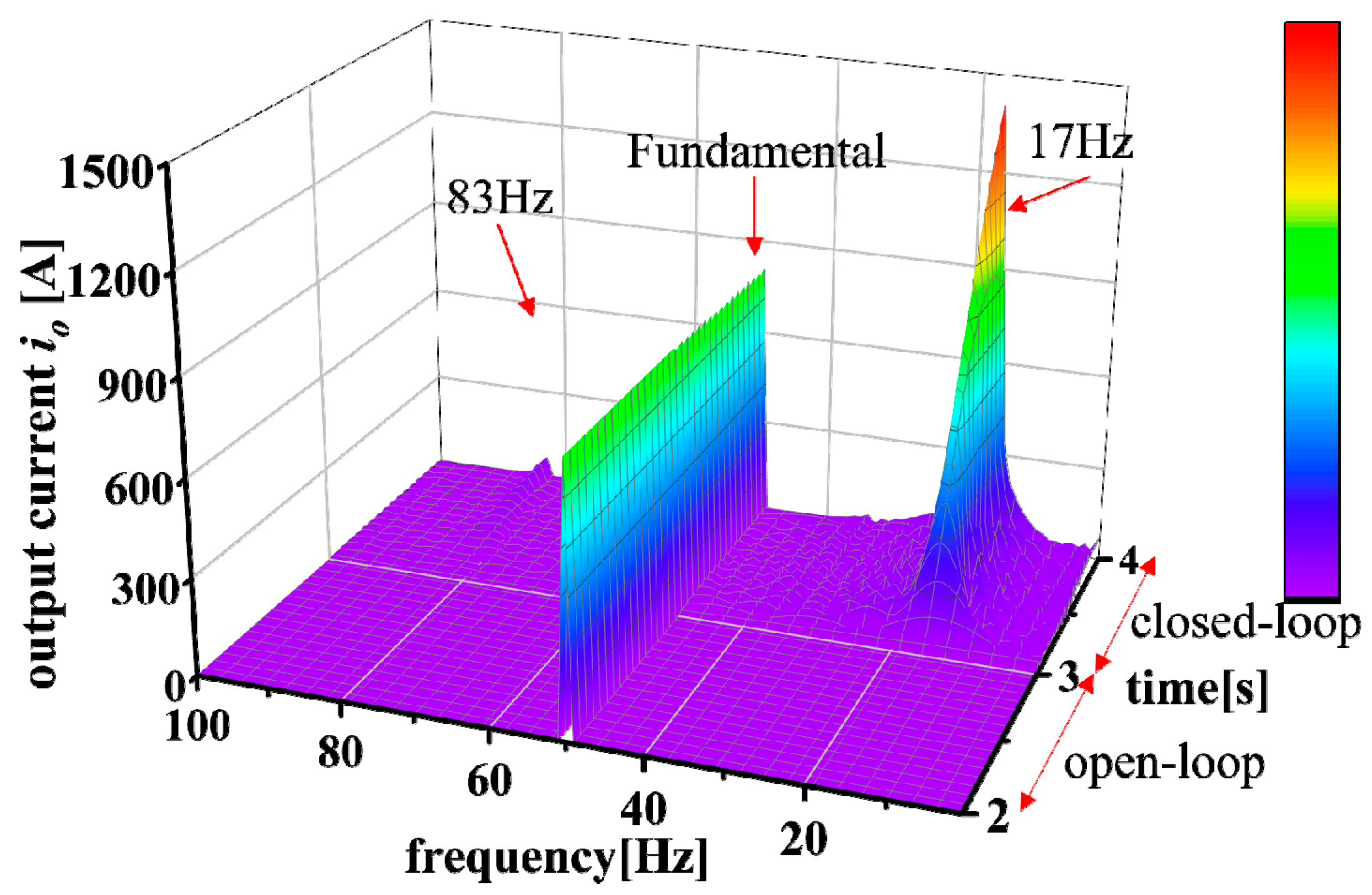
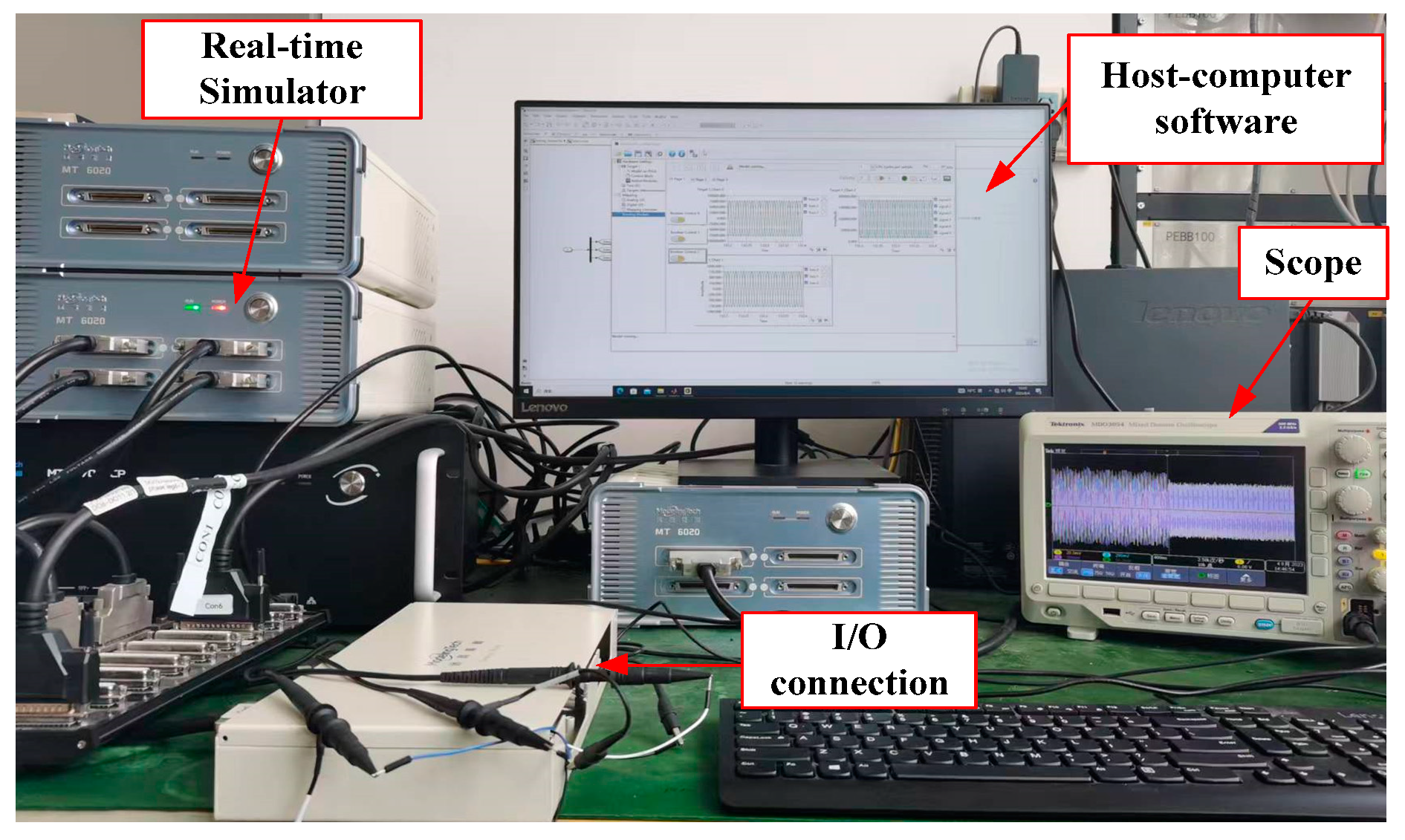
5. Experimental Verification
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Abbreviations | Full Name |
| MMC | modular multilevel converter |
| SSO | subsynchronous oscillation |
| HSS | harmonic state space |
| HVDC | high-voltage direct current |
| SM | submodule |
| DM | differential mode |
| CM | common mode |
| CCSC | circuit current suppression control |
| THD | total harmonic distortion |
Appendix A. HSS Modeling
Appendix B. MMC Parameters
| Symbol | Description | Value |
| Ugrms/kV | RMS value of the ac output voltage | 100 |
| Udc/kV | Dc side voltage | 200 |
| f0/Hz | Grid frequency | 50 |
| S0/kW | Rated output power | 100 |
| Lf/mH | Arm inductance | 45 |
| Rf/Ω | Arm resistance | 0.15 |
| C/mF | Capacitance of the submodule | 33 |
| N | Number of the submodule in each arm | 100 |
| L0/mH | Load impedance | 318 |
| KPdm | Proportional gains | 5 × 10−7 |
| KRdm | Resonance gains | 7.5 × 10−4 |
| ωv | Resonance bandwidths | π |
References
- Liu, Z.; Lv, X.; Wu, F.; Li, Z. Multi-Mode Active Inertia Support Strategy for MMC-HVDC Systems Considering the Constraint of DC Voltage Fluctuations. IEEE Trans. Power Deliv. 2023, 38, 2767–2781. [Google Scholar] [CrossRef]
- Guo, C.; Xu, L.; Yang, S.; Jiang, W. A Supplementary Damping Control for MMC-HVDC System to Mitigate the Low-Frequency Oscillation Under Low Inertia Condition. IEEE Trans. Power Deliv. 2023, 38, 287–298. [Google Scholar] [CrossRef]
- Pan, R.; Liu, D.; Liu, S.; Yang, J.; Kou, L.; Tang, G. Stability Comparison Between Grid-Forming and Grid-Following Based Wind Farms Integrated MMC-HVDC. J. Mod. Power Syst. Clean Energy 2023, 11, 1341–1355. [Google Scholar] [CrossRef]
- Lin, L.; Zeng, Q.; Zhu, J.; Shi, X.; Hu, J. High-Frequency Oscillation Mechanism Analysis and Suppression Strategy of Grid-Forming Control MMC-HVDC. IEEE Trans. Power Deliv. 2023, 38, 1588–1600. [Google Scholar] [CrossRef]
- Jia, K.; Dong, X.; Wen, Z.; Wu, W.; Bi, T. Harmonic Injection Based Fault Ride-through Control of MMC-HVDC Connected Offshore Wind Farms. IEEE Trans. Sustain. Energy 2023, 14, 1796–1806. [Google Scholar] [CrossRef]
- Yang, R.; Shi, G.; Zhang, C.; Li, G.; Cai, X. Internal Energy Based Grid-Forming Control for MMC-HVDC Systems with Wind Farm Integration. IEEE Trans. Ind. Appl. 2023, 59, 503–512. [Google Scholar] [CrossRef]
- Zhou, H.; Yao, W.; Zhou, M.; Ai, X.; Wen, J.; Cheng, S. Active Energy Control for Enhancing AC Fault Ride-Through Capability of MMC-HVDC Connected with Offshore Wind Farms. IEEE Trans. Power Syst. 2023, 38, 2705–2718. [Google Scholar] [CrossRef]
- Tang, G.; He, Z.; Pang, H.; Huang, X.; Zhang, X. Basic Topology and Key Devices of the Five-Terminal DC Grid. CSEE Power Energy Syst. 2015, 1, 22–35. [Google Scholar] [CrossRef]
- Paulo, M.S.; Almeida, A.D.O.; Almeida, P.M.D.; Barbosa, P.G. Control of an Offshore Wind Farm Considering Grid-Connected and Stand-Alone Operation of a High-Voltage Direct Current Transmission System Based on Multilevel Modular Converters. Energies 2023, 16, 5891. [Google Scholar] [CrossRef]
- Zou, C.; Rao, H.; Xu, S.; Li, Y.; Li, W.; Chen, J.; Zhao, X.; Yang, Y.; Lei, B. Analysis of Resonance Between a VSC-HVDC Converter and the AC Grid. IEEE Trans. Power Electron. 2018, 33, 10157–10168. [Google Scholar] [CrossRef]
- Yan, Z.; Xu, J.; Yu, G.; Bai, E.; Chen, W. Detailed Wideband Impedance Modeling and Resonance Analysis of Grid-Connected Modular Multilevel Converter. Energies 2023, 16, 4782. [Google Scholar] [CrossRef]
- Yan, Z.; Xu, J. Sequence Impedance Modeling and Analysis of Modular Multilevel Converter Considering DC Port Characteristics. Energies 2023, 16, 7770. [Google Scholar] [CrossRef]
- Guo, X.; Yuan, B.; Li, X.; Yin, C. Research on the High Frequency Oscillation of MMC-HVDC Integrated into Renewable Energy System. In Proceedings of the 2021 IEEE Southern Power Electronics Conference (SPEC), Kigali, Rwanda, 6 December 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1–6. [Google Scholar]
- Buchhagen, C.; Greve, M.; Menze, A.; Jung, J. Harmonic Stability-Practical Experience of a TSO. In Proceedings of the Wind Integration Workshop, Vienna, Austria, 14–17 November 2016; Volume 2016, pp. 1–6. [Google Scholar]
- Li, L.; Xu, C.; Enke, Y.U.; Xingwei, Y.U. Zhoushan Multi-Terminal VSC-HVDC Transmission Demonstration Project and Its Evaluation. South. Power Syst. Technol. 2019, 13, 10. [Google Scholar] [CrossRef]
- Lyu, J.; Cai, X.; Molinas, M. Optimal Design of Controller Parameters for Improving the Stability of MMC-HVDC for Wind Farm Integration. IEEE J. Emerg. Sel. Top. Power Electron. 2018, 6, 40–53. [Google Scholar] [CrossRef]
- Buchhagen, C.; Rauscher, C.; Menze, A.; Jung, D.J. BorWin1—First Experiences with Harmonic Interactions in Converter Dominated Grids. In Proceedings of the International ETG Congress, Bonn, Germany, 17–18 November 2015; Die Energiewende-Blueprints for the New Energy Age. VDE: Offenbach, Germany, 2015; pp. 1–7. [Google Scholar]
- Jamshidi Far, A.; Jovcic, D. Small-Signal Dynamic DQ Model of Modular Multilevel Converter for System Studies. IEEE Trans. Power Deliv. 2016, 31, 191–199. [Google Scholar] [CrossRef]
- Lyu, J.; Zhang, X.; Cai, X.; Molinas, M. Harmonic State-Space Based Small-Signal Impedance Modeling of a Modular Multilevel Converter With Consideration of Internal Harmonic Dynamics. IEEE Trans. Power Electron. 2019, 34, 2134–2148. [Google Scholar] [CrossRef]
- Ji, K.; Pang, H.; Yang, J.; Tang, G. DC Side Harmonic Resonance Analysis of MMC-HVDC Considering Wind Farm Integration. IEEE Trans. Power Deliv. 2021, 36, 254–266. [Google Scholar] [CrossRef]
- Cespedes, M.; Xing, L.; Sun, J. Constant-Power Load System Stabilization by Passive Damping. IEEE Trans. Power Electron. 2011, 26, 1832–1836. [Google Scholar] [CrossRef]
- Xue, Y.; Xu, Z.; Tang, G. Self-Start Control With Grouping Sequentially Precharge for the C-MMC-Based HVDC System. IEEE Trans. Power Deliv. 2014, 29, 187–198. [Google Scholar] [CrossRef]
- Zhu, Y.; Pou, J.; Konstantinou, G. Impedance Shaping Effects and Stability Assessment of Circulating Current Control Schemes in Modular Multilevel Converters. IEEE Trans. Power Deliv. 2023, 38, 666–676. [Google Scholar] [CrossRef]
- Li, Y.; An, T.; Zhang, D.; Pei, X.; Ji, K.; Tang, G. Analysis and Suppression Control of High Frequency Resonance for MMC-HVDC System. IEEE Trans. Power Deliv. 2021, 36, 3867–3881. [Google Scholar] [CrossRef]
- Li, Y.; Pang, H.; Kong, M.; Lu, J.; Ji, K.; Tang, G. Compensation Control and Parameters Design for High Frequency Resonance Suppression of MMC-HVDC System. CSEE JPES 2020, 7, 1161–1175. [Google Scholar] [CrossRef]
- Yang, S.; Liu, K.; Qin, L.; Zhu, S.; Xu, B.; Wang, Q. A Broadband Active Damping Method for High-Frequency Resonance Suppression in MMC-HVDC System. Int. J. Electr. Power Energy Syst. 2023, 146, 108791. [Google Scholar] [CrossRef]
- Dai, F.; Liu, S.; Wang, G.; Zeng, D. Coordinated Suppression Strategies for Passive and Active Resonances of the MMC-HVDC AC-side System on the Medium- and High-frequency Bands. IET Gener. Transm. Distrib. 2023, 17, 2963–2977. [Google Scholar] [CrossRef]
- Ludois, D.C.; Venkataramanan, G. Simplified Terminal Behavioral Model for a Modular Multilevel Converter. IEEE Trans. Power Electron. 2014, 29, 1622–1631. [Google Scholar] [CrossRef]
- Xiong, X.; Yang, Y.; Wu, C.; Zhao, C.; Blaabjerg, F. Improving the Stability of Standalone MMCs by Shaping the AC Side Impedance Using Insertion Index Compensation. IEEE J. Emerg. Sel. Top. Circuits Syst. 2022, 12, 81–89. [Google Scholar] [CrossRef]
- Zou, Z.; Liserre, M. Modeling Phase-Locked Loop-Based Synchronization in Grid-Interfaced Converters. IEEE Trans. Energy Convers. 2020, 35, 394–404. [Google Scholar] [CrossRef]
- Visioli, A. Practical PID Control; Advances in Industrial Control; Springer: London, UK, 2006; ISBN 978-1-84628-585-1. [Google Scholar]
- Langella, R.; Testa, A.; Alii, E. IEEE Recommended Practice and Requirements for Harmonic Control in Electric Power Systems. In IEEE Recommended Practice; IEEE: Piscataway, NJ, USA, 2014. [Google Scholar]
- Wu, H.; Wang, X.; Kocewiak, L.H. Impedance-Based Stability Analysis of Voltage-Controlled MMCs Feeding Linear AC Systems. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 4060–4074. [Google Scholar] [CrossRef]
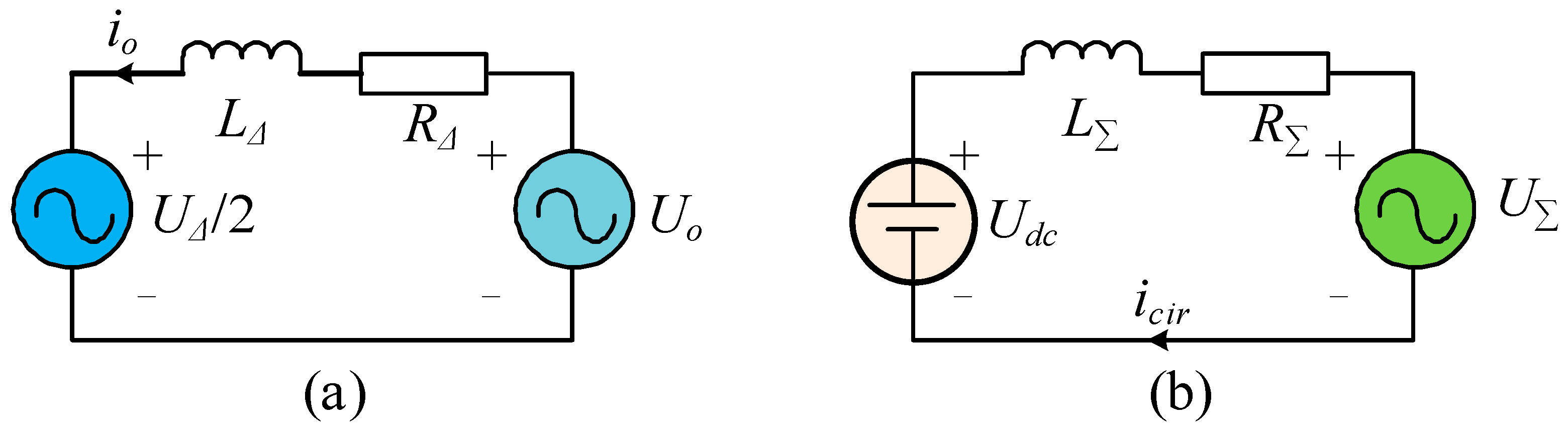

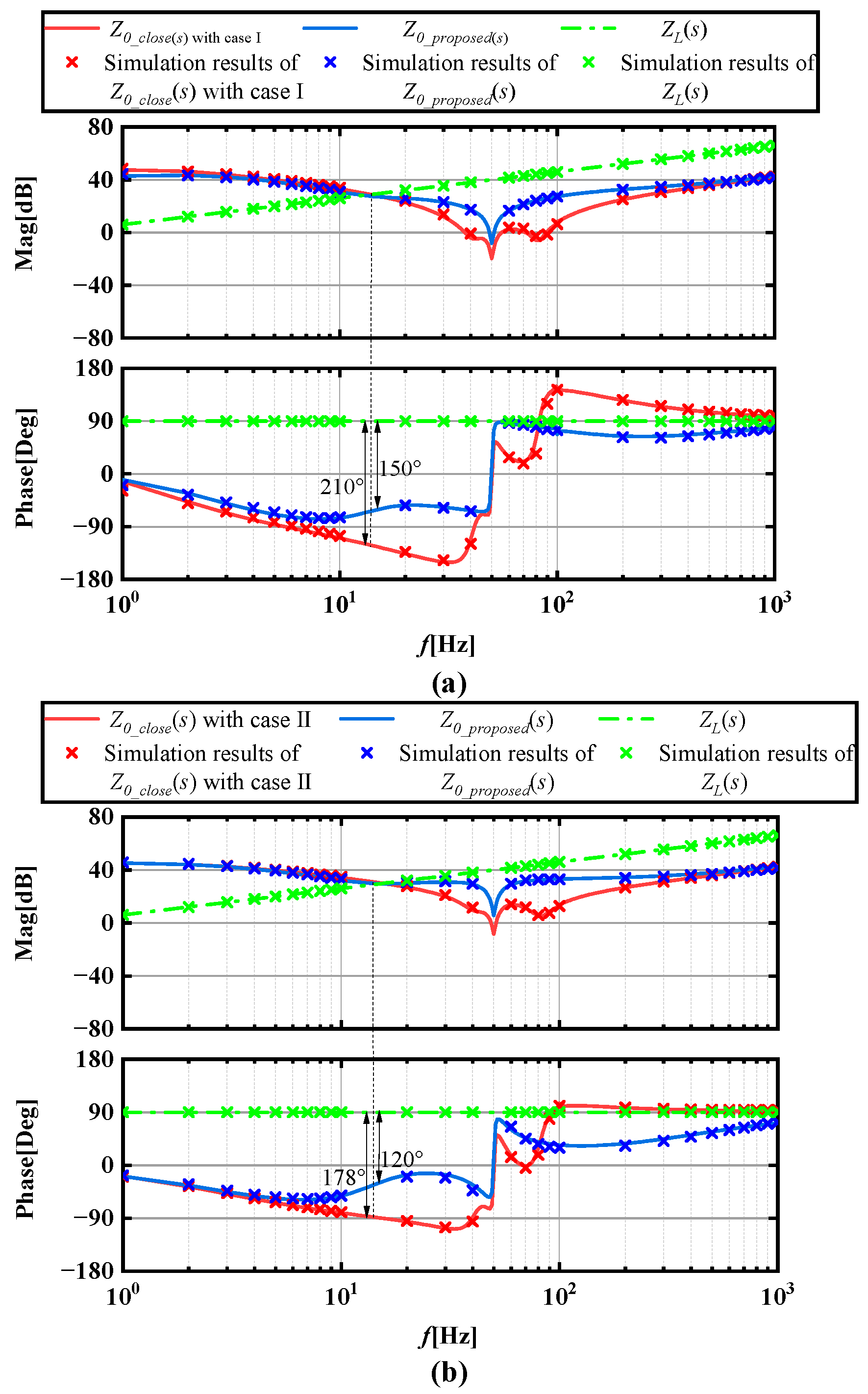


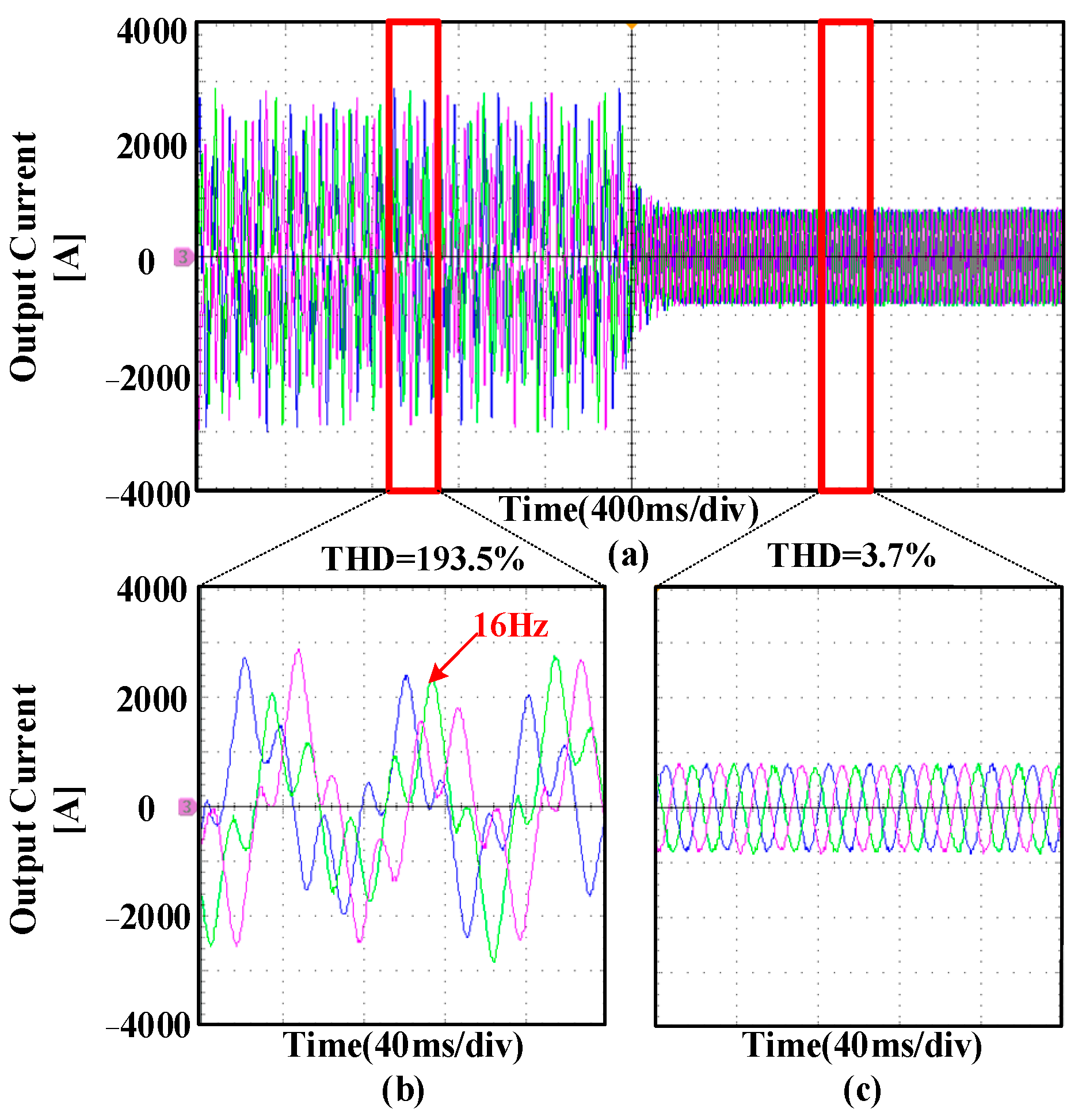
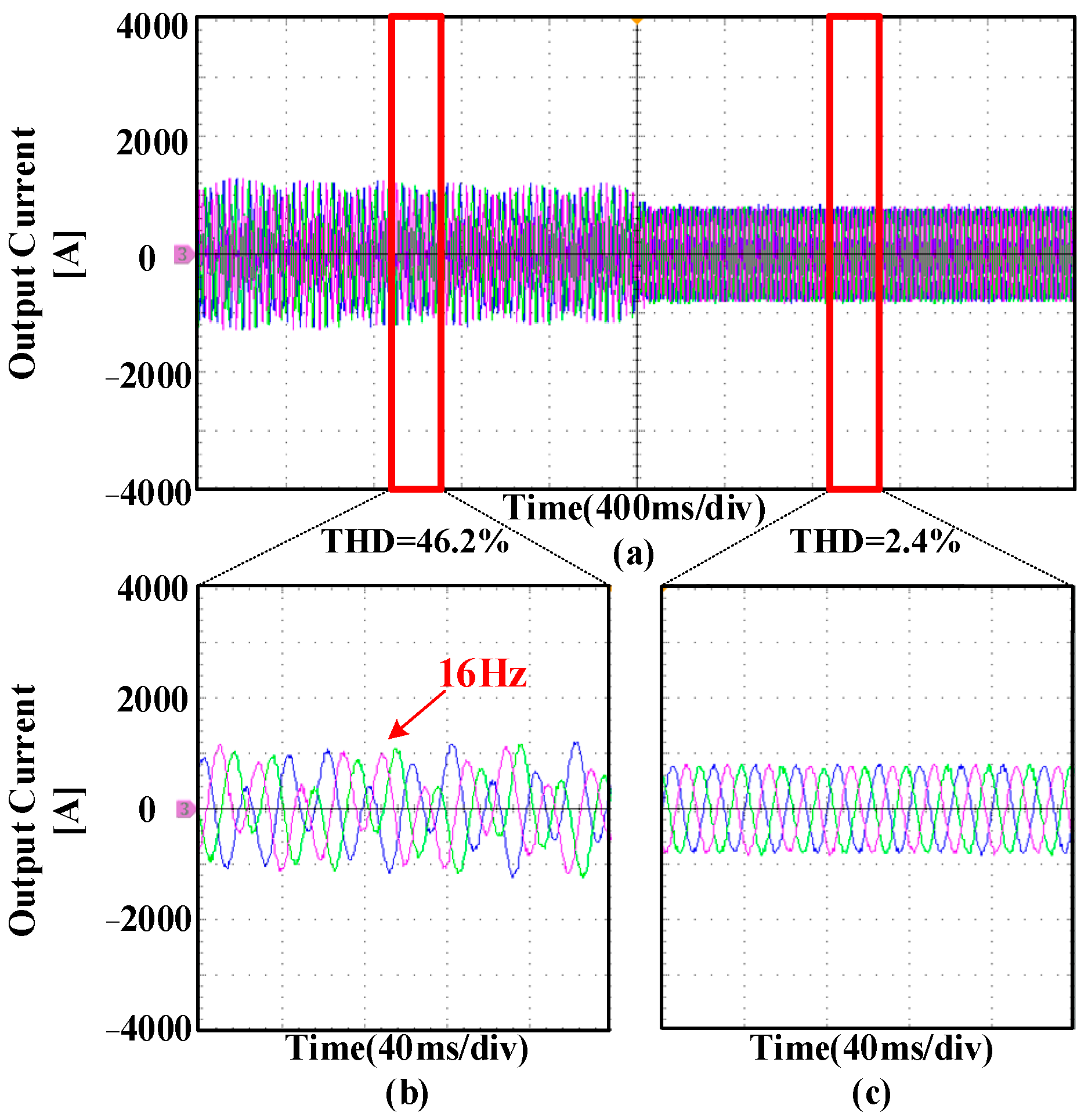
| Case Study | KPdm | KRdm |
|---|---|---|
| Case I | 5 × 10−7 | 7.5 × 10−4 |
| Case II | 5 × 10−7 | 1.5 × 10−4 |
| Refs. | Oscillation Frequency Type | Suppression Method | Feed-Forward Method |
|---|---|---|---|
| [24] | High Frequency | Second-order damping controller, round controller | Voltage feed-forward |
| [25] | High Frequency | First-order low pass filter, second-order, third-order band pass filter | Voltage feed-forward |
| [26] | High Frequency | Amplitude attenuation | / |
| [27] | Medium and high frequency | Combination of low-pass and high-pass filters | Voltage feed-forward |
| [33] | Low Frequency | PIR controller | / |
| Proposed | Low Frequency | Improved PD controller | Current feed-forward |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, Y.; Hua, L.; Yang, Y.; Li, C.; Luo, C.; Song, Z.; Yang, X.; Feng, H. Stability Enhancement Method of Standalone Modular Multilevel Converters Based on Impedance Reshaping. Energies 2024, 17, 895. https://doi.org/10.3390/en17040895
Zheng Y, Hua L, Yang Y, Li C, Luo C, Song Z, Yang X, Feng H. Stability Enhancement Method of Standalone Modular Multilevel Converters Based on Impedance Reshaping. Energies. 2024; 17(4):895. https://doi.org/10.3390/en17040895
Chicago/Turabian StyleZheng, Youzhuo, Long Hua, Yekui Yang, Chun Li, Chaoyi Luo, Zihong Song, Xingwu Yang, and Haibo Feng. 2024. "Stability Enhancement Method of Standalone Modular Multilevel Converters Based on Impedance Reshaping" Energies 17, no. 4: 895. https://doi.org/10.3390/en17040895
APA StyleZheng, Y., Hua, L., Yang, Y., Li, C., Luo, C., Song, Z., Yang, X., & Feng, H. (2024). Stability Enhancement Method of Standalone Modular Multilevel Converters Based on Impedance Reshaping. Energies, 17(4), 895. https://doi.org/10.3390/en17040895







