Abstract
To overcome the problem of current control effect being reduced by unideal factors in a motor control system, such as motor parameter variation, inverter dead time, nonlinearity of the system, etc., a sliding mode disturbance observer for an interior permanent magnet synchronous motor is proposed in this paper. The model of an interior permanent magnet synchronous motor with unideal factors is designed, and the unideal factors are unified into lumped disturbances of motor stator voltage. Then, the observer for lumped disturbance is designed. A recursive integral sliding surface is used to replace the terminal sliding surface to avoid the noise sensitivity and singularity problem of the traditional terminal sliding mode observer. The observer can estimate the lumped disturbance of the current loop without relying on the accurate system model in finite time. Moreover, the structure of the current loop does not need to be adjusted while using the observer to observe and compensate for disturbances. Experiments are carried out to verify the effectiveness of the proposed observer.
1. Introduction
The interior permanent magnet synchronous motor (IPMSM) has been widely utilized due to its simple structure, high efficiency, high power density, fast response and other excellent features [1,2]. Among the IPMSM control methods, the field-oriented control (FOC) is most widely applied due to the features of low torque ripple, fast response and high control precision. At the same time, the double-loop structure of FOC can control the torque and magnetic flux independently [3,4,5]. The inner current loop determines the dynamic and steady-state performance of stator currents [6,7]. However, IPMSM is a nonlinear and strong coupling system and contains unavoidable and unmeasured disturbances such as possible parameter variations in operating [8,9,10]. Moreover, the inverter includes nonlinearity such as dead time, voltage drop and other factors [11,12]. These unideal factors, which are usually ignored in motor control system modeling, will affect the current control accuracy and cause controller parameter mismatch. It is difficult to meet the high performance requirements of the IPMSM control system using traditional control methods.
With the development of power electronics and digital signal processing, many methods to improve current control accuracy have been proposed. In general, these methods can be divided into two groups. One is to improve the current control performance by introducing new control laws. Study [13] presents a method based on an adaptive linear neuron to suppress the current harmonics by a self-tuning voltage feedforward, which does not need to extract the current harmonics. Study [14] proposes a model predictive current control (MPCC) method with adaptive-adjusting timescales based on the motor operation conditions, which can improve the system dynamic response and the current prediction accuracy. Study [15] presents a fixed switching period sliding mode control (SMC) method which combines the advantages of FOC and direct torque control (DTC). This method can allow the control law to be transferred to the inverter directly by a novel decoupling algorithm to find a set of decoupled sliding surfaces. Study [16] analyzes the relationship between the low-pass filter in the feedback loop and the controller parameters, and proposes a modified model compensation active disturbance rejection control (ADRC) method, which can make the current response closer to that of the ideal closed-loop control system. Study [17] proposes a complex vector decoupling method considering the time delay caused by sampling, calculation and PWM modulation, which quantifies and compensates the phase delay to improve the dynamic performance.
Although the above methods improved the current control performance by introducing new control laws, the parameters’ perturbation and other unideal factors are ignored, and the system disturbances have not been eliminated yet.
The other methods obtained system information through sensors or observers and improve the controller [18,19,20,21,22,23,24,25,26]. Among them, disturbance observer (DO) gains the favor of many scholars and becomes a research hotspot because of its simple structure, lack of dependence on system model accuracy and lack of an additional hardware cost. At the same time, compensation based on the disturbance observer does not change the original structure of the controller. In [21], a multiple-models adaptive disturbance observer is proposed to solve the steady-state current error by estimating the lumped disturbances, which can improve the robustness to parameter perturbations and model mismatch. Study [22] proposes an adaptive observer based on the model reference adaptive system (MRAS), which improves the control performance, anti-interference ability and robustness of the control system. Study [23] presents a novel super-twisting algorithm associated with extended state observer (ESO) for FOC, which can estimate system disturbances, eliminate chattering, improve the system anti-interference ability, and obtain a fast dynamic response. Study [24] introduces an adaptive internal model observer (AIMO) to observe system disturbances quickly without static difference, which avoid disturbances caused by parameter variations. Study [25] proposes a sliding-mode observer based on adaptive super-twisting algorithm (ASTA-SMO) to improve the performance of deadbeat predictive current control (DPCC), which can predict future values of stator current and track system disturbance caused by parameter mismatch. Study [26] presents an adaptive stator current disturbance observer considering the discrete characteristics of the current prediction error, which structures a parallel strategy, observes the discrete disturbance related to each voltage vector separately, and then eliminates the prediction error.
The above disturbance observation methods can effectively estimate and compensate for system disturbances. Among them, the SMO has simple structure and is easy to implement. Other methods have disadvantages such as difficulty with observer parameter adjustment, a poor observation effect on nonlinear disturbances, etc. However, due to the discontinuous switching characteristics, the ordinary sliding mode method has a chattering problem [27]. The terminal sliding mode method introduces nonlinear terms into the sliding mode surface, which can make the observation error converge to zero in finite time, and its dynamic performance is better than the ordinary sliding mode method with state asymptotic convergence under linear sliding mode surface conditions [28]. And the terminal sliding mode method does not have switching items, which can effectively eliminate chattering. However, the introduction of nonlinear terms results in the existence of negative exponential term in the sliding mode control function which will bring about singularity problems [29].
In this research, a terminal sliding mode disturbance observer (SMDO) based on a recursive integral sliding mode surface for lumped disturbances of IPMSM is proposed. The observer can realize the lumped estimation of the electromagnetic parameter variation and external disturbances of the control system without relying on the accurate system model in finite time. At the same time, the noise sensitivity caused by the forward Euler derivative and the singularity problem of the traditional terminal sliding mode observer are avoided. In this paper, a novel IPMSM model is presented, and all the system disturbances as the lumped stator voltage variation are considered in Section 2. The recursive integral sliding mode disturbance observer is analyzed and designed in Section 3. The experimental results are given to verify the feasibility of the proposed observer in Section 4.
2. Modeling of IPMSM with Parameter Variation and Unknown Disturbance
According to study [2], the state equation of the IPMSM dynamic model in a synchronously rotating reference frame can be denoted as (1):
where ud, uq, id and iq are the stator voltage and current components in d- and q-axis, respectively; Rs is the nominal value of stator resistance; Ld and Lq are the nominal values of the inductance in the d- and q-axis, respectively; and ψf is the nominal value of permanent magnet flux linkage.
The system state variables are defined as x = [id iq]T, the input variables are defined as u = [ud uq]T, then (1) can be expressed as (2):
where
The motor parameters including stator resistance, stator inductance, and permanent magnet flux linkage vary with the varying operating condition, then the controller performance can be affected by the varying motor parameters. Meanwhile, the system nonlinearity, dead time and other factors of the inverter can also affect the motor voltage and current. After considering the above, the system state equation can be expressed as [2]:
where ΔR, ΔLd, ΔLq, Δψf are variations of Rs, Ld, Lq, and ψf, respectively; Δud and Δuq are the voltage variations caused by the other unideal factors. After considering the above issues, (2) can be obtained:
From (4), the variation in current response will induce additional errors, and cause parameter mismatch of the current controller, resulting in a decrease in the current control effect.
Considering the effects above, all the disturbances can be regarded as the lumped disturbance f = [fd fq]T in the d- and q-axis stator voltage.
Then (4) can be expressed as:
3. Design and Analysis of Recursive Integral Sliding Mode Disturbance Observer
Disturbance observer is an effective method to solve the current controller mismatch. After the lumped disturbance f is estimated by the disturbance observer, disturbance compensation controller can eliminate the disturbance influence efficaciously. The block diagram of the IPMSM control scheme with disturbance compensation is shown in Figure 1, where ωe* is the reference value of the rotating speed speed, x* is the reference value of current, is the estimated value of the lumped disturbances f, and fc is the disturbance compensation value obtained by .
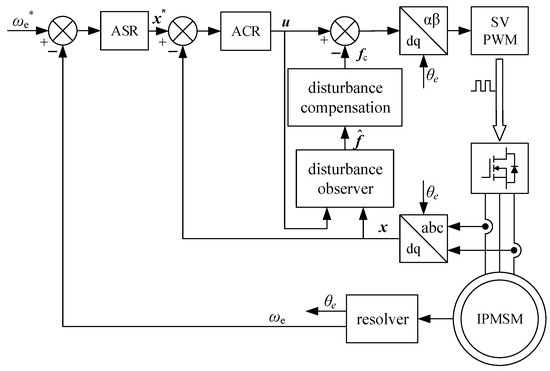
Figure 1.
Control scheme of IPMSM with disturbance compensation.
The controlled system with the disturbance observation and compensation can be equivalent to Figure 2, then the system state equation can be shown as (7):
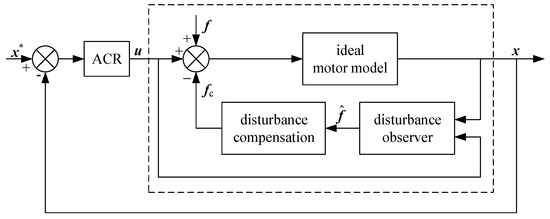
Figure 2.
Equivalent model of controlled system.
According to (7), when f − fc = 0, the effects of system disturbances can be compensated and the actual system state can be equivalent to the ideal state without disturbances. Then, the current loop parameters can be designed according to (2) under ideal conditions.
3.1. Design of Recursive Integral SMDO
The SMDO is constructed based on (6), and the observation equation is as follows:
where = []T, and are the observed values of id and iq, respectively; usmo = [usmod usmoq]T, usmod and usmoq are the d- and q-axis control functions, respectively.
The current observation error e = [eid eiq]T is defined as (9):
By substituting (6) and (8) into (9), the state equation of the current observation error is derived as:
To ensure the observation error can converge to 0 in finite time, and the observer control functions usmod and usmoq are non-singular, an integral fast terminal sliding mode surface is selected as [27]:
where αid, αiq, βid, βiq, γid, and γiq are sliding mode observer coefficients; in general, αid > 0, αiq > 0, βid > 0, βiq > 0, 0 < γid < 1, and 0 < γiq < 1.
When the control functions usmo satisfy the SMDO reachability condition and the observer is in sliding mode, the first-order derivative of the sliding mode surface is 0:
The equivalent observer control function ueq can be obtained according to (10) and (12):
Since there are nonlinear and unmeasurable factors in the lumped disturbances f, and the observer cannot obtain the estimated values directly by only using the equivalent control functions ueq, it is necessary to design the disturbance tracking functions uf = [ufd ufq]T to estimate the lumped disturbances. According to (6) and (10), (14) can be obtained as follows:
The state equation of error e is rewritten as:
On the basis of an integral fast terminal sliding mode surface si, the recursive sliding mode surface sf is adopted to realize the estimation of lumped disturbances f, and the SMDO based on the recursive terminal sliding mode surface is obtained. The sf is as (16):
where αfd, αfq, βfd, βfq, γfd, and γfq are sliding mode observer coefficients of sf; in general, αfd > 0, αfq > 0, βfd > 0, βfq > 0, 0 < γfd < 1, and 0 < γfq < 1.
The first-order derivative of sf is given in (17):
In order to solve the disturbance tracking function uf in SMDO, (15) is substituted into (11) to obtain the first and second order derivative of si:
The disturbance tracking function uf is selected as (20):
According to Equations (13), (14) and (20), the observer control function usmo can be obtained as (21):
When the observer is in the balance state e = 0, the equivalent observer control function ueq in (21) is equal to zero and the disturbance tracking function uf in (21) is equal to the lumped disturbance f, so uf is the observed value of the lumped disturbance.
The block diagrams of the disturbance observer are shown in Figure 3.
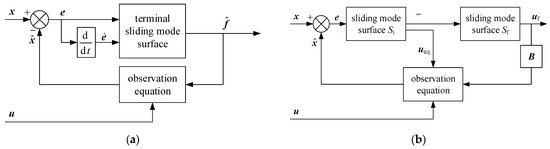
Figure 3.
Block diagrams of SMDO (a) traditional terminal SMDO (b) recursive integral SMDO.
While using the traditional terminal sliding mode method to observe the system states, the system state equation is usually in the form of an integral chain [28]. At this time, the system state equation as follows:
where ef = f − = [efd efq]T, and usmoT is the sliding mode control function and is also the observed value of .
The sliding mode surface is selected as (23) according to study [29], and the recursive sliding mode surfaces is selected as (24):
where αij > 0, βij > 0, and 0 < γij < 1 (i =1, 2; j = d, q) are sliding mode coefficients.
According to (22)–(24), the control function usmoT is selected as:
According to (25), the control function usmoT contains the current observation error e and the disturbance observation error ef. e can be obtained directly based on the actual current of the system and observed current of the observer, but ef needs to be obtained by derivation of e. In common, ef is calculated as , which is sensitive to noise. Tc is the control period of the current loop. At the same time, since γ1d − 1 < 0 and γ1q − 1 < 0, the observer has a singular problem, while e = 0 and ef ≠ 0.
Compared with traditional terminal SMDO, the proposed recursive integral SMDO considers lumped disturbance as a motor stator voltage variation. The state equation of observer is the first-order differential equation shown in (10). The observer control function usmo as shown in (21) only requires the current observation error e and does not contain the derivative si or e. And the observer control function usmo does not contain the negative exponential term, there is no singular problem when the observer is in sliding mode. Therefore, the proposed recursive integral SMDO can avoid the noise sensitivity and singularity problem while tracking the system lumped disturbance in finite time.
The SMDO only demands the input and output information of a system, and the lumped disturbance can be eliminated by disturbance observation and compensation.
3.2. Stability Analysis
The Lyapunov function Vi is defined as (26), and its first-order differential is given as (27):
When the control period of the current loop is short enough, and can be considered as zero. < 0 is drawn while the observer parameter ranges are αfd > 0, αfq > 0, βfd > 0, βfq > 0, 1 > γfd > 0, and 1 > γfq > 0. It can be derived that is asymptotically stable at itsorigin, which implies that the current observation error e can converge to 0 in finite time with the control function usmo.
Define the disturbance observation error ef = f − uf, and define the Lyapunov function Vf as follows:
According to (18) and (19), the first-order derivative of Vf is given as:
It can be derived that ef is also asymptotically stable at its origin. Thus, the current observation results of SMDO can converge to the actual currents, and the disturbance tracking functions uf converge to the lumped disturbance f in finite time.
The trajectory of the observation error e is denoted as (30):
When the current observation error is close to the balance state e = 0, the convergence speed is mainly determined by (31):
When the current observation error is far from its origin, the convergence speed is mainly determined by (32):
By solving (30), the time to arrive at e = 0 can be derived as:
4. Experimental Results
An experimental setup was built to validate the proposed algorithm, as shown in Figure 4. An IPMSM, an asynchronous induction motor (ACIM) and a torque sensor are connected via diaphragm couplings, where the IPMSM is used to test the algorithm proposed in this paper, and the ACIM is used to provide the load torque. The parameters of IPMSM are listed in Table 1.
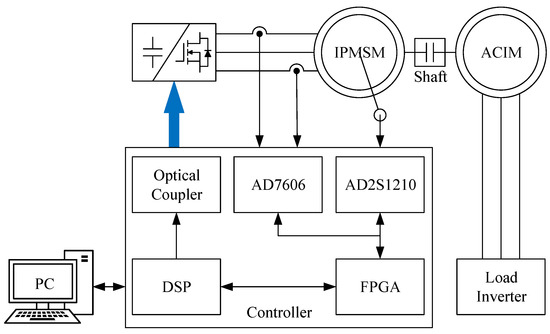
Figure 4.
Block diagram of test platform.

Table 1.
Parameters of IPMSM.
The control algorithm of IPMSM is implemented through DSP TI TMS320F28377D. The CPU1 of DSP communicates with the PC while running the basic motor control algorithm. The CPU2 is responsible for realizing the disturbance observer. The interfaces of multiple peripherals including resolver-to-digital converter (R/D Converter), analog–digital converter (ADC), and digital–analog converter (DAC), the external I/O interface, and the hardware protection logic are implemented in FPGA Xilinx XC6SLX16. Hall sensors are used to obtain voltage and current information of IPMSM. A rotating transformer is used to measure the speed and position of IPMSM. The pulse width modulation (PWM) switching frequency is 20 kHz, and the DC bus voltage is 200 V. An oscilloscope (DLM5054), a recorder (DL850) and a power analyzer (WT5000) manufactured by Yokogawa were used to record the system data during the experiments. The experimental setup is shown in Figure 5.

Figure 5.
Experimental setup.
Experiments are carried out to validate the proposed recursive integral SMDO. During the experiments, the same parameters are applied to the speed loop and current loop. After IPMSM reaches 1400 rpm, the load torque increases from 0 N·m to 20 N·m, then decreases to 0 N·m.
Figure 6 shows the experimental results of currents without disturbance compensation. In Figure 6a,b, the top waveforms in each figure are the currents idn and iqn, calculated by DSP based on the current motor currents id and iq and the voltage given values ud and uq of the current loop through the state Equation (1) under ideal conditions. The middle waveforms in each figure are the actual id and iq obtained by park transformation of the measured phase currents. The waveforms at the bottom of each figure are the current observation values and of the observer. id varies between −1.4 A and −5.7 A, and iq varies between 34.2 A and 38.2 A when speed is 1400 rpm and torque is 20 N·m.
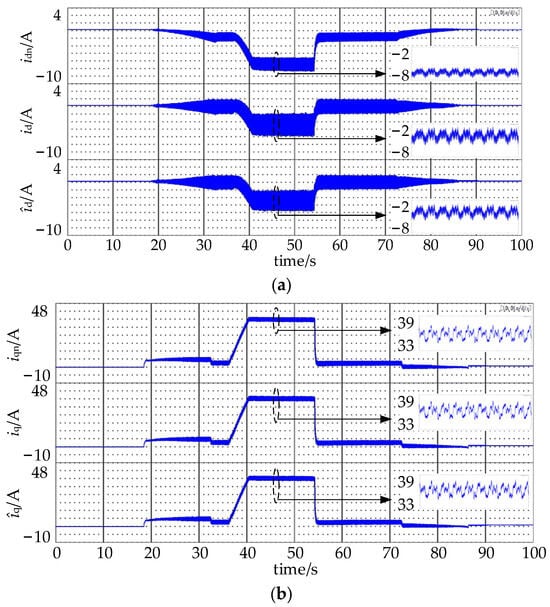
Figure 6.
Waveforms of currents without disturbance compensation. (a) d-axis currents (b) q-axis currents.
Due to the disturbances shown in (3), the actual currents id and iq are not equal to the theoretical currents idn and iqn calculated by DSP. The difference between the actual currents and the theoretical currents errorid= idn − id and erroriq = iqn − iq are shown in Figure 7. The absolute values of errorid and erroriq increase with speed and load increasing. The errorid varies between −3.8 A and −1.8 A, and the erroriq varies between −0.2 A and −0.9 A when speed is 1400 rpm and torque is 20 N·m.
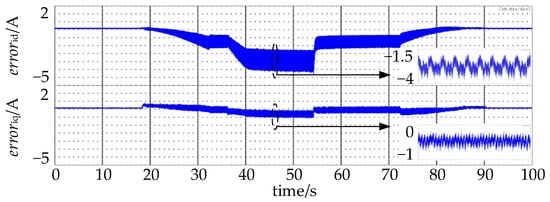
Figure 7.
errorid and erroriq without disturbance compensation.
Figure 8 shows the difference between the observed currents and the actual currents, that is, the current observation error e in (9). Although the fluctuation range of observation error increases with the increase in speed and load, it still remains within a small range. Both eid and eiq fluctuate between −0.2 and 0.2.
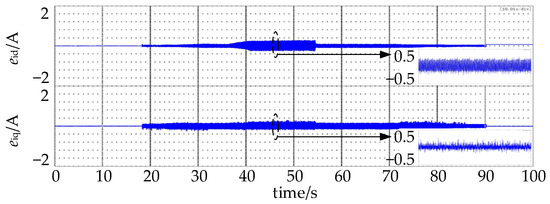
Figure 8.
Current observation error without disturbance compensation.
Figure 9 shows the derivative of the current observation error calculated by DSP based on the formula . The derivation based on the backward Euler method will amplify the quantization errors and noise in the error e, and also bring about truncation error. These factors will affect the accuracy of disturbance observation while using the traditional terminal SMDO.
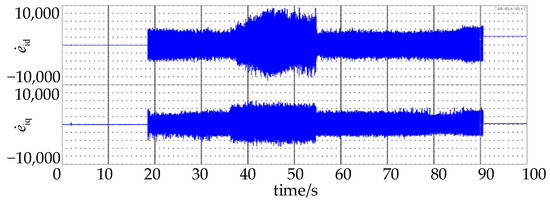
Figure 9.
Derivative of current observation error.
The observed lumped disturbance is shown in Figure 10. The absolute values of observed disturbance values also increase with speed and load increasing. varies between 8.1 V and 13.4 V, and varies between 2.2 V and 5.5 V when speed is 1400 rpm and torque is 20 N·m.
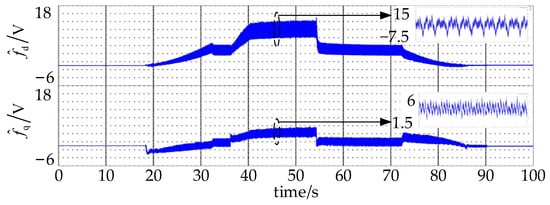
Figure 10.
Observation values of lumped disturbance.
Figure 11, Figure 12, Figure 13, Figure 14 and Figure 15 show the experimental results when the observed lumped disturbance is utilized in the system.
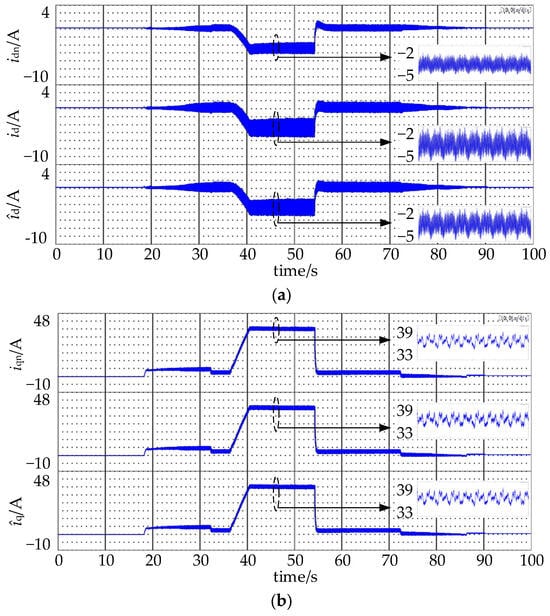
Figure 11.
Waveforms of currents with disturbance compensation. (a) d-axis currents (b) q-axis currents.
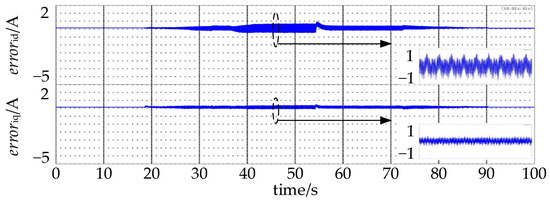
Figure 12.
errorid and erroriq with disturbance compensation.
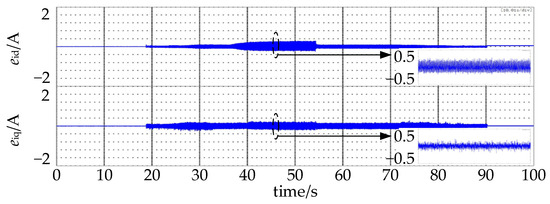
Figure 13.
Current observation error with disturbance compensation.
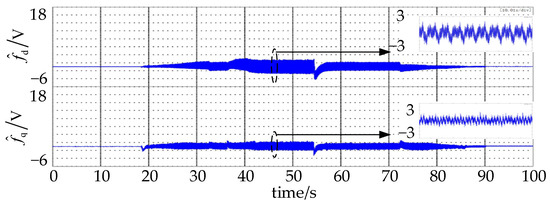
Figure 14.
Observation values of remaining lumped disturbances.
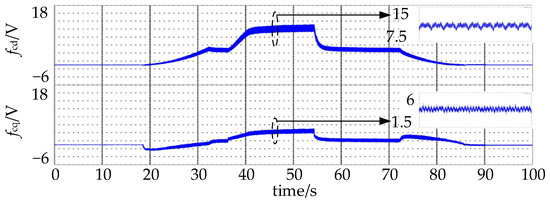
Figure 15.
Disturbance compensation values.
Figure 11 shows the currents with the disturbance compensation. id varies between −1.8 A and −5.2 A, and iq varies between −34.6 A and 38.1 A under 1400 rpm and 20 N·m. Compared with the current waveforms in Figure 6, the fluctuations in the motor currents id and iq become smaller.
errorid and erroriq after adding the disturbance compensation are shown in Figure 12, which indicates that the absolute values of steady-state differences no longer increase with the increase in speed and load, but remain close to zero. The errorid varies between −0.9 A and 0.8 A, and the erroriq varies between −0.3 A and −0.3 A under 1400 rpm and 20 N·m.
Figure 13 shows the current observation error e. eid and eiq still fluctuate between −0.2 and 0.2. The introduction of the disturbance compensation does not affect the accuracy of current observation.
The observed lumped disturbance value with the disturbance compensation is shown in Figure 14. At this time, is no longer the observed values of f, but f − fc in (7), that is, the remaining disturbances after compensation. The steady-state of also become close to zero. varies between −2.2 V and 2.1 V, and varies between −1.2 V and 1.2 V when speed is 1400 rpm and torque is 20 N·m.
Figure 15 shows the compensation value fc of the lumped disturbance. The absolute value of fc also increases with the increase in speed and load torque. fcd varies between 9.8 V and 12.0 V, and fcd varies between 3.1 V and 4.5 V when speed is 1400 rpm and torque is 20 N·m. Compared with Figure 10, fc is close to the observed value when the system is not compensated.
Table 2 shows the comparison of the peak-to-peak values of system states when the lumped disturbances are compensated and uncompensated under 1400 rpm and 20 N·m where the current fluctuation and control error are at the maximum. It can be seen from Table 2 that the fluctuation in the system state becomes smaller after compensation, which means that the current loop control precision is higher and the motor output torque is more stable.

Table 2.
Comparison of system states.
5. Conclusions and Future Studies
This article proposed a sliding mode disturbance observer for IPMSM. An IPMSM model which unifies the unideal factors in the current loop into the lumped disturbance of the motor stator voltage is considered. Furthermore, a terminal SMDO based on the recursive integral sliding mode surface is used to observe the lumped disturbances of the system. The integral sliding mode surface avoids the noise sensitivity and singularity problems of the traditional terminal sliding mode surface, and the introduction of the recursive sliding mode surface enables the estimation of lumped disturbances. The stability analysis shows that the recursive integral SMDO proposed in this article can realize the estimated values of currents and lumped disturbances to converge to the real values in finite time. Compensation based on observation values of lumped disturbance can improve current control accuracy and eliminate controller current loop parameter mismatch without changing the structure of the current loop. The experimental results are presented to validate the proposed observer. With the introduction of disturbance observation and compensation, the accuracy current control is improved, the current control errors are maintained near 0, and the fluctuations in error are reduced by about 15%. At the same time, the fluctuation in current in the d-axis is reduced by 20.9%, and the fluctuation in current in the q-axis is reduced by 12.5%. The proposed terminal sliding mode SMDO only considers the voltage equation of IPMSM to observe lumped disturbance of the current loop, and considers the motor speed to be a constant rather than a variable. Future work will combine the IPMSM torque equation to estimate the disturbance of speed loop disturbance while observing the lumped disturbance of the current loop, and improve the performance of the IPMSM control system by compensating for disturbances in the current loop and speed loop.
Author Contributions
Methodology, Y.T.; Software, X.C.; Resources, Q.G.; Supervision, D.X. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wu, G.; Huang, S.; Wu, Q.; Rong, F.; Zhang, C.; Liao, W. Robust Predictive Torque Control of N*3-Phase PMSM for High-Power Traction Application. IEEE Trans. Power Electron. 2020, 35, 10799–10809. [Google Scholar] [CrossRef]
- Yang, J.; Chen, W.-H.; Li, S.; Guo, L.; Yan, Y. Disturbance/Uncertainty Estimation and Attenuation Techniques in PMSM Drives—A Survey. IEEE Trans. Ind. Electron. 2017, 64, 3273–3285. [Google Scholar] [CrossRef]
- Rauth, S.S.; Samanta, B. Comparative Analysis of IM/BLDC/PMSM Drives for Electric Vehicle Traction Applications Using ANN-Based FOC. In Proceedings of the 2020 IEEE 17th India Council International Conference (INDICON), New Delhi, India, 10–13 December 2020; pp. 1–8. [Google Scholar]
- Gupta, S.; George, S.; Awate, V. PI Controller Design and Application for SVPWM Switching Technique Based FOC of PMSM. In Proceedings of the 2023 Second International Conference on Trends in Electrical, Electronics, and Computer Engineering (TEECCON), Bangalore, India, 26–27 August 2023; pp. 172–177. [Google Scholar]
- Zhang, Y.; Shen, W.; Yang, H. An Improved Deadbeat Predictive Current Control of PMSM Drives Based on the Ultra-Local Model. Chin. J. Electr. Eng. 2023, 9, 27–37. [Google Scholar] [CrossRef]
- Xu, C.; Han, Z.; Lu, S. Deadbeat Predictive Current Control for Permanent Magnet Synchronous Machines with Closed-Form Error Compensation. IEEE Trans. Power Electron. 2020, 35, 5018–5030. [Google Scholar] [CrossRef]
- Yang, R.; Sun, T.; Feng, W.; He, S.; Zhu, S.; Chen, X. Accurate Online MTPA Control of IPMSM Considering Derivative Terms. Chin. J. Electr. Eng. 2021, 7, 100–110. [Google Scholar] [CrossRef]
- Agoro, S.; Husain, I. High-Fidelity Nonlinear Modeling of an Asymmetrical Dual Three-Phase PMSM. In Proceedings of the 2023 IEEE International Electric Machines & Drives Conference (IEMDC), San Francisco, CA, USA, 15–18 May 2023; pp. 1–7. [Google Scholar]
- Li, Z.; Li, H. MTPA Control of PMSM System Considering Saturation and Cross-Coupling. In Proceedings of the 2012 15th International Conference on Electrical Machines and Systems (ICEMS), Sapporo, Japan, 21–24 October 2012; pp. 1–5. [Google Scholar]
- Xia, J.; Li, Z.; Yu, D.; Guo, Y.; Zhang, X. Robust Speed and Current Control with Parametric Adaptation for Surface-Mounted PMSM Considering System Perturbations. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 2807–2817. [Google Scholar] [CrossRef]
- Zhou, G.; Wang, B.; Xu, K.; Liu, Q. An Inverter Nonlinearity Compensation Method for PMSM Drives Based on Dead-Time Elimination. In Proceedings of the 2023 26th International Conference on Electrical Machines and Systems (ICEMS), Zhuhai, China, 5–8 November 2023; pp. 662–667. [Google Scholar]
- Zhu, S.; Huang, W.; Yan, Y. A Simple Inverter Nonlinearity Compensation Method Using On-Line Voltage Error Observer. In Proceedings of the 2019 22nd International Conference on Electrical Machines and Systems (ICEMS), Harbin, China, 11 August 2019; pp. 1–6. [Google Scholar]
- Wang, L.; Zhu, Z.Q.; Bin, H.; Gong, L.M. Current Harmonics Suppression Strategy for PMSM with Nonsinusoidal Back-EMF Based on Adaptive Linear Neuron Method. IEEE Trans. Ind. Electron. 2020, 67, 9164–9173. [Google Scholar] [CrossRef]
- Niu, F.; Chen, X.; Huang, S.; Huang, X.; Wu, L.; Li, K.; Fang, Y. Model Predictive Current Control with Adaptive-Adjusting Timescales for PMSMs. CES Trans. Electr. Mach. Syst. 2021, 5, 108–117. [Google Scholar] [CrossRef]
- Repecho, V.; Biel, D.; Arias, A. Fixed Switching Period Discrete-Time Sliding Mode Current Control of a PMSM. IEEE Trans. Ind. Electron. 2018, 65, 2039–2048. [Google Scholar] [CrossRef]
- Gao, Y.; Zhao, H.; Ma, K.; Huo, X. Control Design for Current Loop of PMSM Using A Modified Model-Compensation ADRC Controller. In Proceedings of the 2020 39th Chinese Control Conference (CCC), Shenyang, China, 27–29 July 2020; pp. 2545–2550. [Google Scholar]
- Ding, Y.; Sun, L. Complex Vector Decoupling and Delay Compensation for PMSM at Low Carrier Ratio. In Proceedings of the 2023 IEEE 6th International Electrical and Energy Conference (CIEEC), Hefei, China, 12–14 May 2023; pp. 1025–1031. [Google Scholar]
- Ma, X.; Bi, C. A Technology for Online Parameter Identification of Permanent Magnet Synchronous Motor. CES Trans. Electr. Mach. Syst. 2020, 4, 237–242. [Google Scholar] [CrossRef]
- Liang, G.; Huang, S.; Li, M.; Wu, X. A high-order fast terminal sliding-mode disturbance observer based on mechanical parameter identification for PMSM. Trans. China Electrotech. Soc. 2020, 35, 395–403. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, X.; Zhou, K. Current deviation decoupling control with a sliding mode observer for permanent magnet synchronous motor. Trans. China Electrotech. Soc. 2020, 35, 1642–1652. [Google Scholar] [CrossRef]
- Bai, C.; Yin, Z.; Zhang, Y.; Liu, J. Multiple-Models Adaptive Disturbance Observer-Based Predictive Control for Linear Permanent-Magnet Synchronous Motor Vector Drive. IEEE Trans. Power Electron. 2022, 37, 9596–9611. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, Z.; Feng, S.; Wang, J.; Guo, X.; Sun, H. Design of Model-Free Speed Regulation System for Permanent Magnet Synchronous Linear Motor Based on Adaptive Observer. IEEE Access 2022, 10, 68545–68556. [Google Scholar] [CrossRef]
- Le, T.-L.; Hsieh, M.-F.; Nguyen, M.-T. Robust Speed Control with Disturbance Rejection for Surface-Mounted Permanent Magnet Synchronous Motor. In Proceedings of the 2022 6th International Conference on Green Technology and Sustainable Development (GTSD), Hefei, China, 12–14 July 2022; pp. 459–463. [Google Scholar]
- Chen, M.; Wang, F.; He, L.; Ke, D.; Zuo, K.; Rodriguez, J. Predictive Current Control of Permanent Magnet Synchronous Motor Based on An Adaptive Internal Model Observer. In Proceedings of the 2020 IEEE 9th International Power Electronics and Motion Control Conference (IPEMC2020-ECCE Asia), Nanjing, China, 29 November–2 December 2020; pp. 2567–2571. [Google Scholar]
- Zhao, F.; Lian, G.; Ban, F.; Hou, Z. Improved Deadbeat Predictive Current Control Combined Adaptive Super-Twisting Algorithm Based Sliding-Mode Observer for Permanent-Magnet Synchronous Motors Drives. In Proceedings of the 2020 IEEE 5th Information Technology and Mechatronics Engineering Conference (ITOEC), Chongqing, China, 12–14 June 2020; pp. 1749–1754. [Google Scholar]
- Wang, F.; Zuo, K.; Lin, G.; He, L.; Rodriguez, J.; Garcia, C. Adaptive Stator Current Disturbance Observer Based on the Predictive Current Control for PMSM. In Proceedings of the IECON 2020 The 46th Annual Conference of the IEEE Industrial Electronics Society, Singapore, 18–21 October 2020; pp. 4612–4618. [Google Scholar]
- Jie, Y.; Qing-Lin, W.; Yuan, L. Sliding Mode Variable Structure Control Theory: A Survey. In Proceedings of the 31st Chinese Control Conference, Hefei, China, 25–27 July 2012; pp. 3197–3202. [Google Scholar]
- Du, X.; Fang, X.; Liu, F. Continuous Full-Order Nonsingular Terminal Sliding Mode Control for Systems with Matched and Mismatched Disturbances. IEEE Access 2019, 7, 130970–130976. [Google Scholar] [CrossRef]
- Zhao, Y. A Novel Piece-Wise Non-Singular Fast Terminal Sliding Mode Control for Second-Order Nonlinear System. In Proceedings of the 2022 World Automation Congress (WAC), San Antonio, TX, USA, 11–15 October 2022; pp. 18–22. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).