A Low-Complexity Double Vector Model Predictive Current Control for Permanent Magnet Synchronous Motors
Abstract
:1. Introduction
2. Math Model and Cost Function
3. Conventional Double Vectors MPCC Based on the Deadbeat of q-Axis Current
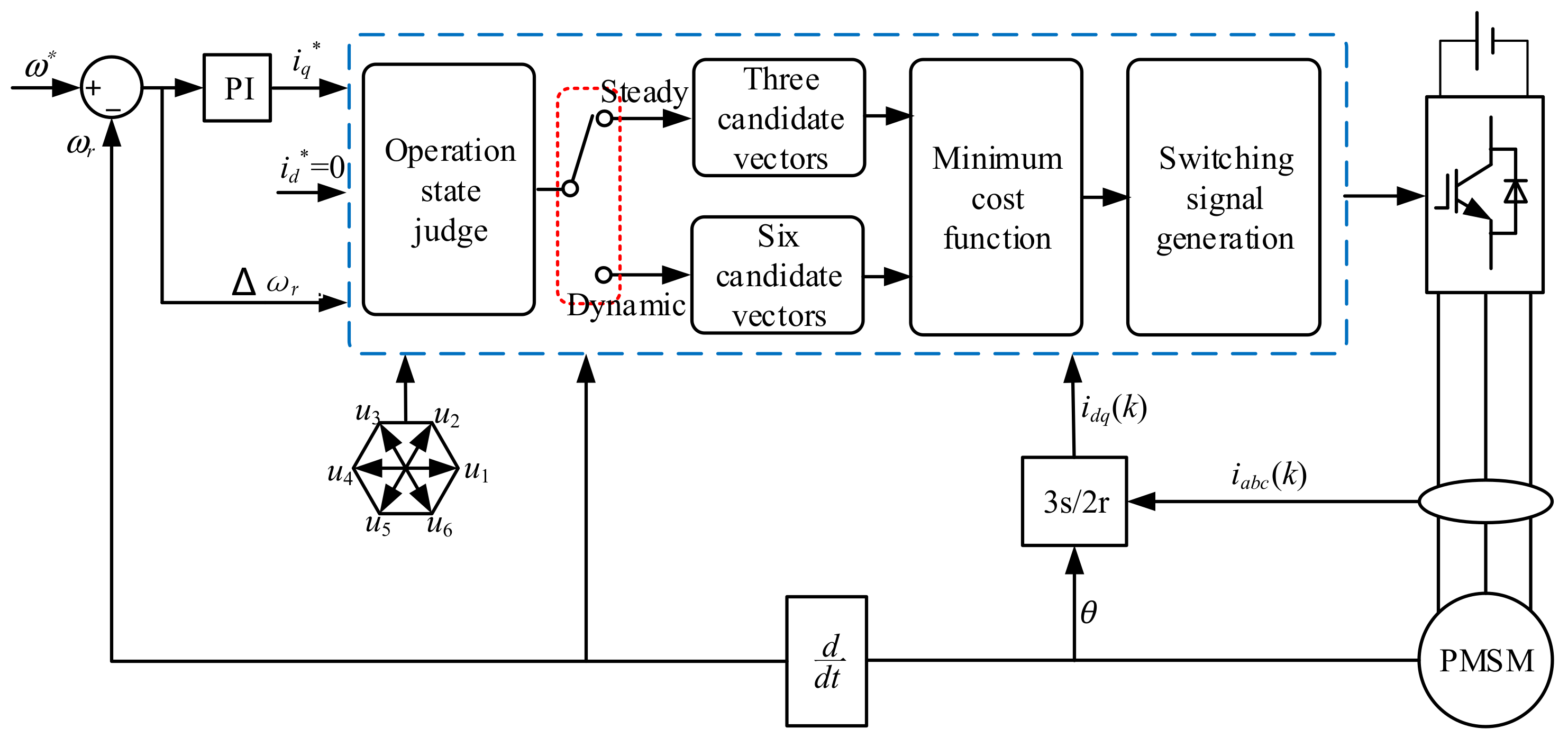
4. Low-Complexity Double Vector Model Predictive Current Control
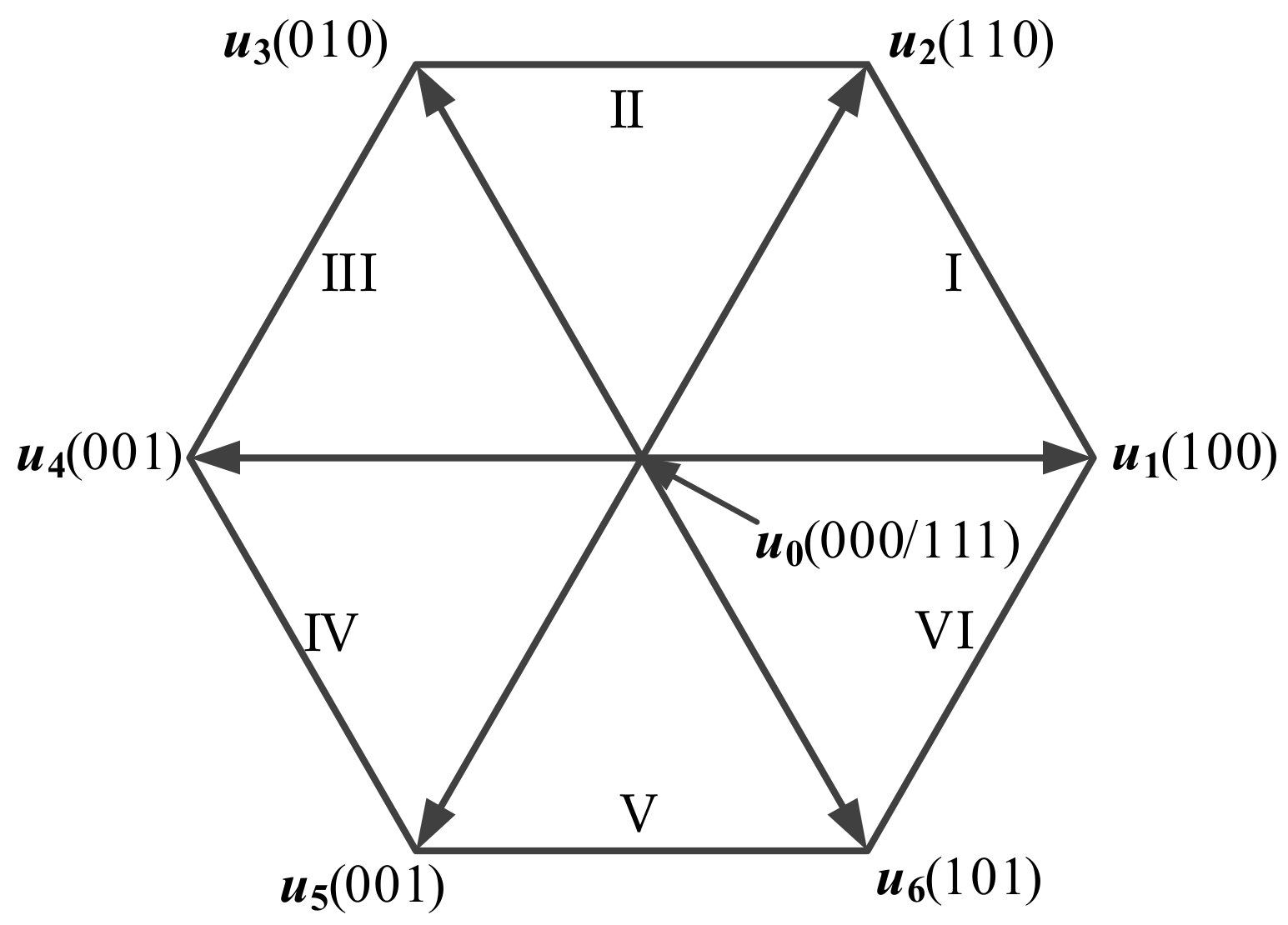
4.1. Low-Complexity Determined Method for the First Active Vector
| uold | Candidate Vectors |
|---|---|
| u1 | u6(101), u1(100), u2(110) |
| u2 | u1(100), u2(110), u3(010) |
| u3 | u2(110), u3(010), u4(011) |
| u4 | u3(010), u4(011), u5(001) |
| u5 | u4(011), u5(001), u6(101) |
| u6 | u5(001), u6(101), u1(100) |
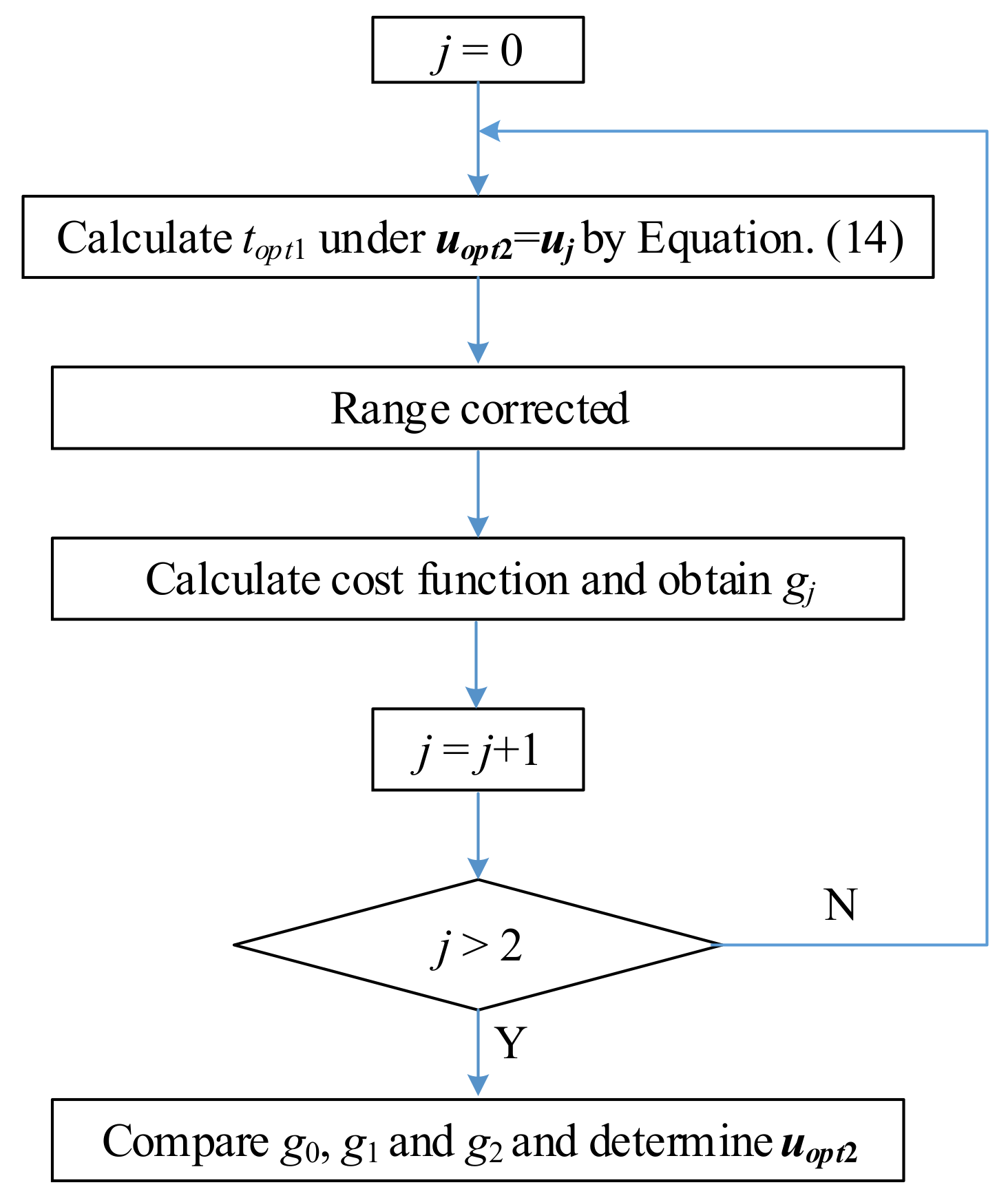
4.2. The Principle of Determining the Second Vector
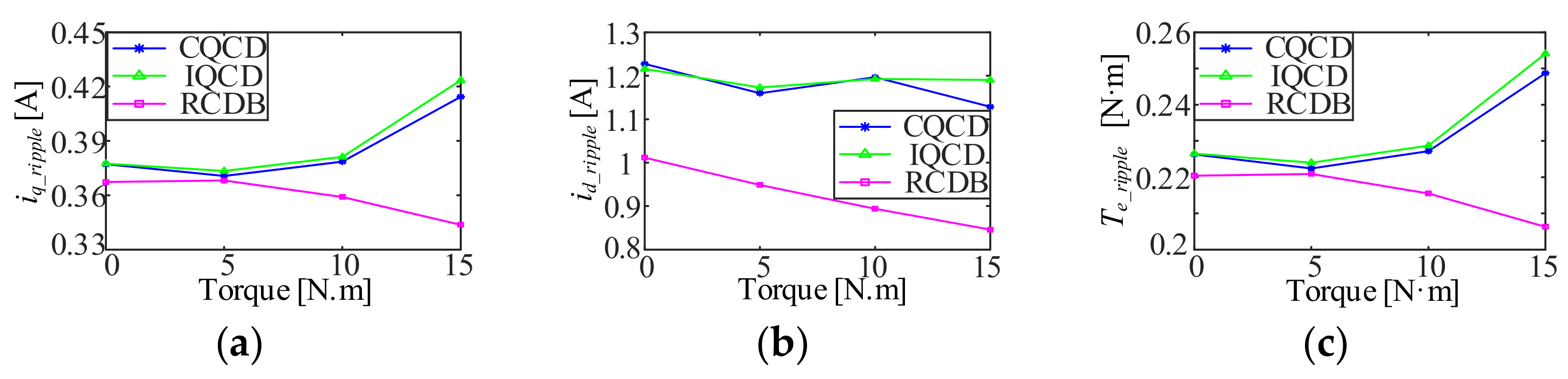
5. Simulation Results
- (1)
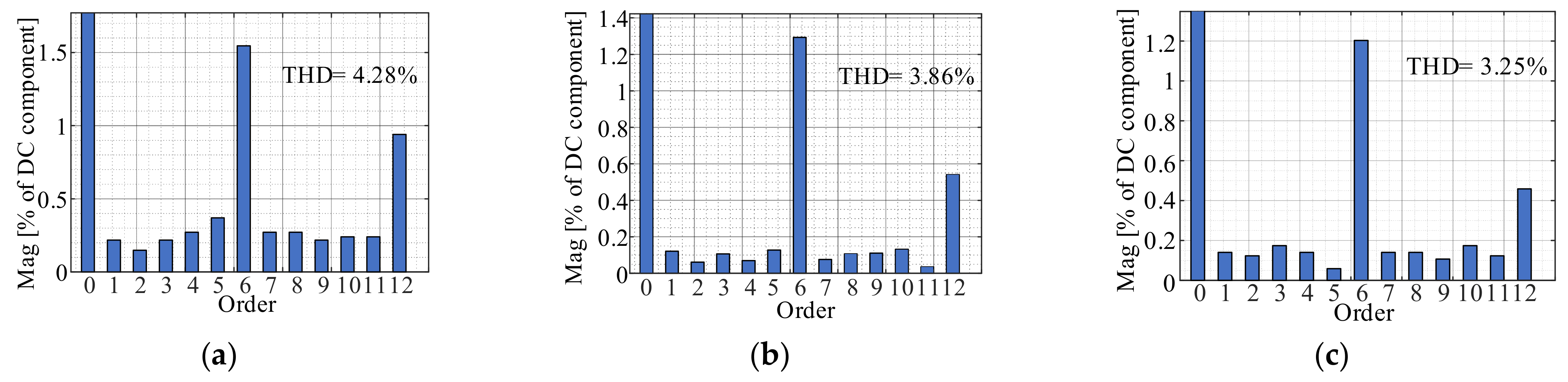
- Conventional q-axis current deadbeat double vectors model predictive current control (CQCD-MPCC): As introduced in Section 3, the first optimal vector with the duty cycle is determined according to the deadbeat condition of the q-axis current, and the second optimal vector is restricted to the zero vector.
- (2)
- Improved q-axis current deadbeat double vectors model predictive current control (IQCD-MPCC): Compared to CQCD-MPCC, the second optimal vector is expanded to the six basic active vectors from the only zero vector.
- (3)
- Proposed low-complexity double vectors model predictive current control (LCDVMPCC): When the PMSM operates in the steady-state, the first optimal vector is determined from three candidate vectors, and the second optimal vector with the duty cycle is determined according to the deadbeat condition of the q-axis current and minimization of the cost function.
Simulation Results for the Steady-State
6. Experimental Results
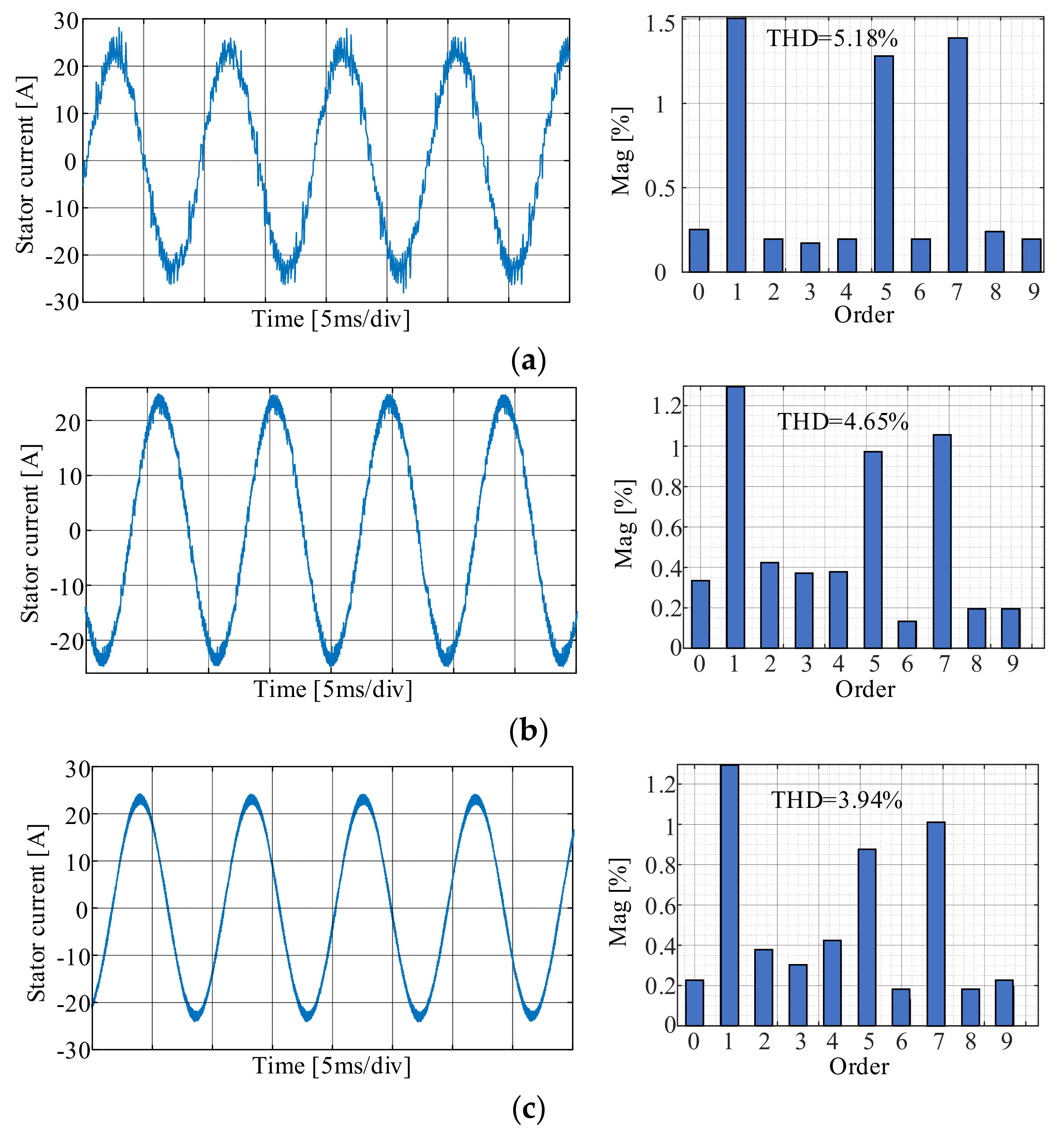
6.1. Experimental Results for the Steady-State
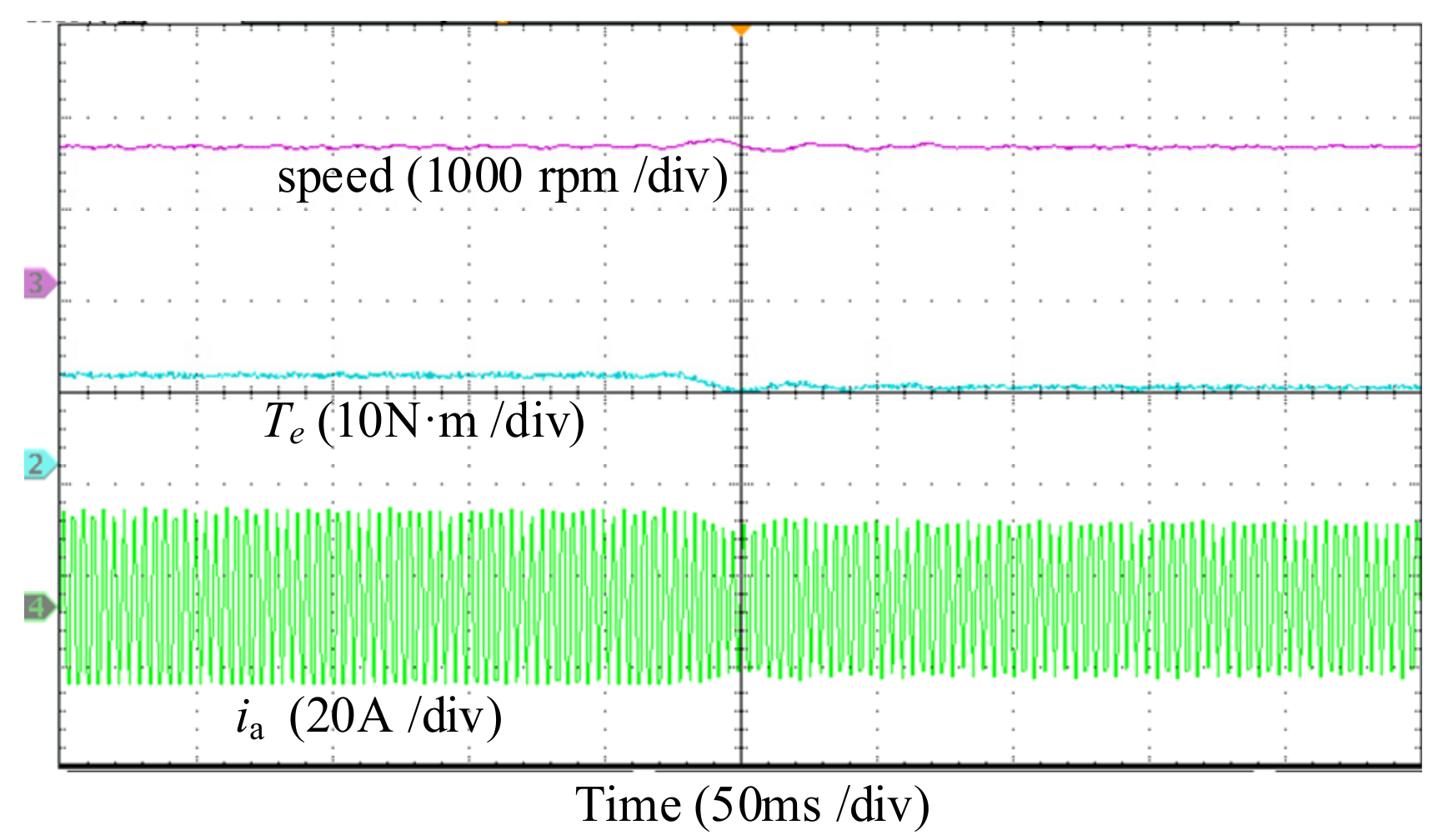
6.2. Experimental Results for the Dynamic-State
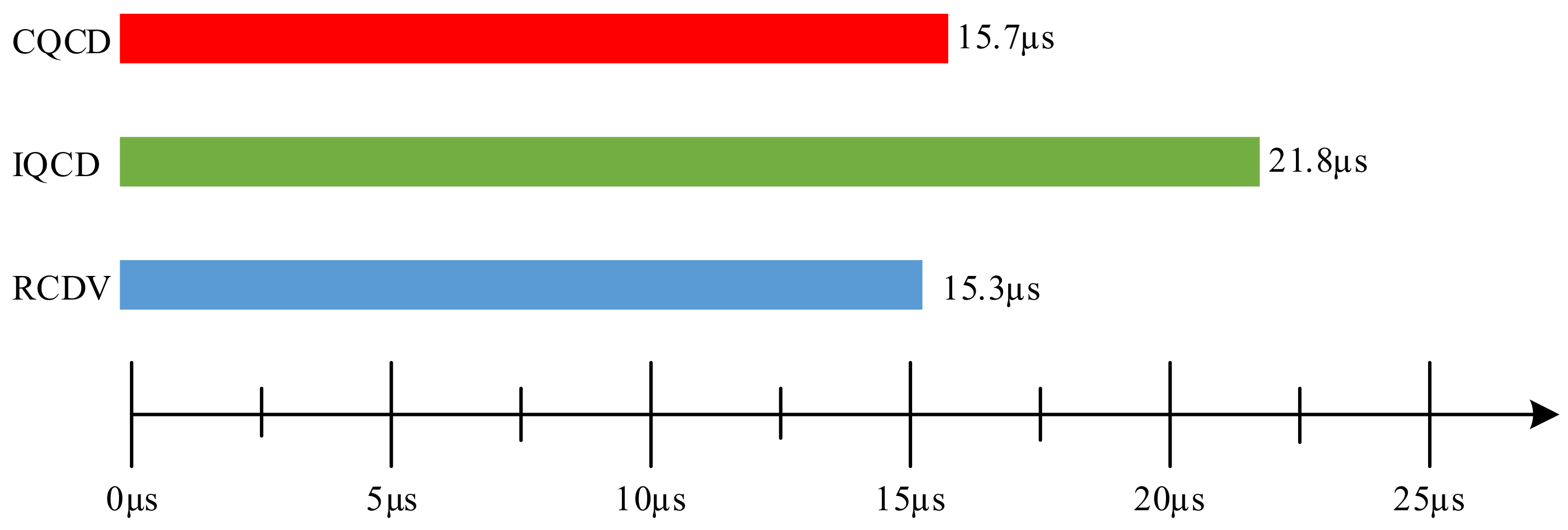
6.3. Execution Time of the Three MPCC Methods
6.4. Performance Comparisons between the Proposed Control and the Controls Mentioned in This Paper
7. Conclusions
- (1)
- During steady-state operation, the number of candidate vectors is reduced from six to three, so the computational complexity can be reduced.
- (2)
- Compared to other double vectors MPCCs, the proposed method can expand the range of vector selection, and optimal vectors with the duty cycle are determined according to the deadbeat of q-axis current and minimization of the cost function so that a better steady-state performance can be obtained.
- (3)
- In the practical use of the PMSM drive system, parameter variations in inductance and resistance may occur, generating errors in vector selection and the duty cycle calculation. Therefore, parameter identification algorithms will be introduced in future research.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| ud/uq | Stator voltages in d-q axis (V) |
| id/iq | Stator currents in d-q axis (A) |
| Ld/Lq | Inductances in d-q axis (H) |
| Rs | Stator resistance (Ω) |
| Ts | Control period (s) |
| Ψf | Flux linkage (Wb) |
| idref/iqref | References of the stator current in d-q axis (A) |
| ωe/ωr | Electric and mechanical angular frequencies (rad/s) |
| ∆ωr | The error of the speed (rad/s) |
| ui | The i-th active vector (V) |
| sdi / sqi | The current rates of change of id and iq caused by ui (V/s) |
| di | Duty cycle of ui (%) |
| uold | First optimal active vector applied in the previous control period (V) |
| uopt1/uopt2 | The first and second optimal voltage vectors (V) |
| topt1 | Dwell time of uopt1 (s) |
| sqopt1 | The current rate of change of iq caused by uopt1 (V/s) |
| ia | Stator current of phase a (A) |
| id_ripple/iq_ripple | The ripples of id and iq (A) |
| Te | Electromagnetic torque (N·m) |
| Te_ripple | The ripple of Te (N·m) |
References
- Miao, Y.; Liao, W.; Huang, S.; Liu, P.; Wu, X.; Song, P.; Li, G. DC-Link Current Minimization Scheme for IM Drive System Fed by Bidirectional DC Chopper-Based CSI. IEEE Trans. Transp. Electrif. 2023, 9, 2839–2850. [Google Scholar] [CrossRef]
- Song, P.; Liu, Y.; Liu, C. Research on Parameter Design and Control Method for Current Source Inverter–Fed IM Drive Systems. Machines 2022, 10, 922. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, T.; Miao, Y. Research on the Modulation and Control Strategy for a Novel Single-Phase Current Source Inverter. Energies 2023, 16, 6729. [Google Scholar] [CrossRef]
- Wu, X.; Wu, T.; Huang, S.; Pan, W.; Lyu, M.; He, Y.; Cui, H. Hybrid Position Estimation Strategy with a Smooth Transition for IPMSM Sensorless Drives in the Wide Speed Range. IEEE Trans. Power Electron. 2022, 37, 7916–7927. [Google Scholar] [CrossRef]
- Dong, Z.; Chen, Y.; Feng, K.; Liu, C. Multivector-Based Model Predictive Current Control with Zero-Sequence Current Suppression for Three-Phase Series-End Winding Permanent Magnet Synchronous Motor Drives. IEEE Trans. Transp. Electrif. 2023, 9, 3282–3294. [Google Scholar] [CrossRef]
- Chen, W.; Zeng, S.; Zhang, G.; Shi, T.; Xia, C. A Modified Double Vectors Model Predictive Torque Control of Permanent Magnet Synchronous Motor. IEEE Trans. Power Electron. 2019, 34, 11419–11428. [Google Scholar] [CrossRef]
- Carlet, P.G.; Tinazzi, F.; Bolognani, S.; Zigliotto, M. An Effective Model-Free Predictive Current Control for Synchronous Reluctance Motor Drives. IEEE Trans. Ind. Appl. 2019, 55, 3781–3790. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, H. Model Predictive Torque Control of Induction Motor Drives with Optimal Duty Cycle Control. IEEE Trans. Power Electron. 2014, 29, 6593–6603. [Google Scholar] [CrossRef]
- Miao, Y.; Song, P.; Lyu, M.; Liu, X.; Huang, S. Design of Cost Function without Weighting Factor for Predictive Torque Control of Surface-Mounted Permanent Magnet Synchronous Motor. Trans. China Electrotech. Soc. 2023, 38, 3141–3150. [Google Scholar]
- Dong, Z.; Song, Z.; Wang, W.; Liu, C. Improved Zero-Sequence Current Hysteresis Control-Based Space Vector Modulation for Open-End Winding PMSM Drives with Common DC Bus. IEEE Trans. Ind. Electron. 2023, 70, 10755–10760. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, H. Two-Vector-Based Model Predictive Torque Control without Weighting Factors for Induction Motor Drives. IEEE Trans. Power Electron. 2016, 31, 1381–1390. [Google Scholar] [CrossRef]
- Morel, F.; Lin-Shi, X.; Retif, J.-M.; Allard, B.; Buttay, C. A Comparative Study of Predictive Current Control Schemes for a Permanent-Magnet Synchronous Machine Drive. IEEE Trans. Ind. Electron. 2009, 56, 2715–2728. [Google Scholar] [CrossRef]
- Xu, Y.; Ren, J.; Fan, L.; Yin, Z. Multidisturbance Suppressed Model Predictive Direct Speed Control with Low Pulsation for PMSM Drives. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 6135–6147. [Google Scholar] [CrossRef]
- Zhang, X.; Hou, B. Double Vectors Model Predictive Torque Control Without Weighting Factor Based on Voltage Tracking Error. IEEE Trans. Power Electron. 2018, 33, 2368–2380. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, L.; Hou, B. Improved Model Predictive Torque Control of Permanent Magnet Synchronous Motor. Proc. CSEE 2017, 37, 4800–4809. [Google Scholar]
- Xu, Y.; Li, Y.; Zhou, Q.; Li, Z. A Double Vectors Selection Direct Torque Control Strategy of Permanent Magnet Synchronous Motor. Proc. CSEE 2018, 38, 5211–5288. [Google Scholar]
- Khalilzadeh, M.; Vaez-Zadeh, S. A Robust Predictive Torque and Flux Control for IPM Motor Drives without a Cost Function. IEEE Trans. Power Electron. 2021, 36, 8067–8075. [Google Scholar] [CrossRef]
- Nasr, A.; Gu, C.; Buticchi, G.; Bozhko, S.; Gerada, C. A Low-Complexity Modulated Model Predictive Torque and Flux Control Strategy for PMSM Drives without Weighting Factor. IEEE J. Emerg. Sel. Top. Power Electron. 2023, 11, 1305–1316. [Google Scholar] [CrossRef]
- Song, P.; Wang, H.; Zhang, J.; Liu, Y.; Deng, T. Research on Phase Current Reconstruction for DPWM2 of Induction Motor Drive System Based on DC-Link Current Sampling. Machines 2022, 10, 1104. [Google Scholar] [CrossRef]







| Parameters | Value |
|---|---|
| Rated voltage | 300 V |
| Rated power | 4 kW |
| Rated speed | 3000 rpm |
| Rated torque | 10 N·m |
| Rated current | 18 A |
| Pole pairs | 4 |
| Stator resistance | 0.15 Ω |
| Stator inductance | 1.625 mH |
| Device | Type and Parameters | Manufacture |
|---|---|---|
| DC bus | DS1020 | eTOMMENS/Dongguan, China |
| PMSM | 180ST-M, 4.5 kW | Customed |
| Encoder | OIH, 2500 C/T | Tamagawa/Japan |
| Torque sensor | YH502, 0–50 N·m | ALIPO/Guangzhou, China |
| Magnetic powder brake | TS-PB-A, 0–50 N·m | YOUYAN/Wuxi, China |
| RTU-BOX | RTU-BOX204 | Rtunit/Nanjing, China |
| Comparative Items | CQCD-MPCC | IQCD-MPCC | LCDV-MPCC |
|---|---|---|---|
| Calculation number for the 1st vector | 6 | 6 | 3 |
| Calculation number for the 2nd vector | 0 | 6 | 3 |
| Calculation complexity | Low | High | Low |
| Steady-state performance | Low | Moderate | High |
| Dynamic performance | Moderate | Moderate | Moderate |
| Range of candidate vectors | Small | Wide | Wide |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, H.; Zhang, Y. A Low-Complexity Double Vector Model Predictive Current Control for Permanent Magnet Synchronous Motors. Energies 2024, 17, 147. https://doi.org/10.3390/en17010147
Dong H, Zhang Y. A Low-Complexity Double Vector Model Predictive Current Control for Permanent Magnet Synchronous Motors. Energies. 2024; 17(1):147. https://doi.org/10.3390/en17010147
Chicago/Turabian StyleDong, Hongliang, and Yi Zhang. 2024. "A Low-Complexity Double Vector Model Predictive Current Control for Permanent Magnet Synchronous Motors" Energies 17, no. 1: 147. https://doi.org/10.3390/en17010147
APA StyleDong, H., & Zhang, Y. (2024). A Low-Complexity Double Vector Model Predictive Current Control for Permanent Magnet Synchronous Motors. Energies, 17(1), 147. https://doi.org/10.3390/en17010147





