Research on the Dispatching of Electric Vehicles Participating in Vehicle-to-Grid Interaction: Considering Grid Stability and User Benefits
Abstract
1. Introduction
- (1)
- Based on the changes in speed and acceleration of electric vehicles during driving, a dynamic microscopic energy consumption model of electric vehicles is established, and the energy consumption of electric vehicles under four scenarios of acceleration, deceleration, constant speed and idle speed is analyzed, which improves the accuracy of energy consumption calculations for electric vehicles.
- (2)
- Considering the TOU price and the state of remaining power, hierarchical decision making and analysis of electric vehicle users’ charging willingness are carried out based on the fuzzy reasoning system.
- (3)
- The theory of social behavior is introduced to analyze the willingness of EV users to participate in V2G response based on the expected utility model, which improves the subjective initiative of users.
- (4)
- Subsidies for electric vehicles to participate in V2G are in line with the policies being implemented in the relevant regions in China and are more in line with reality.
2. EV-Charging and -Discharging-Demand Model
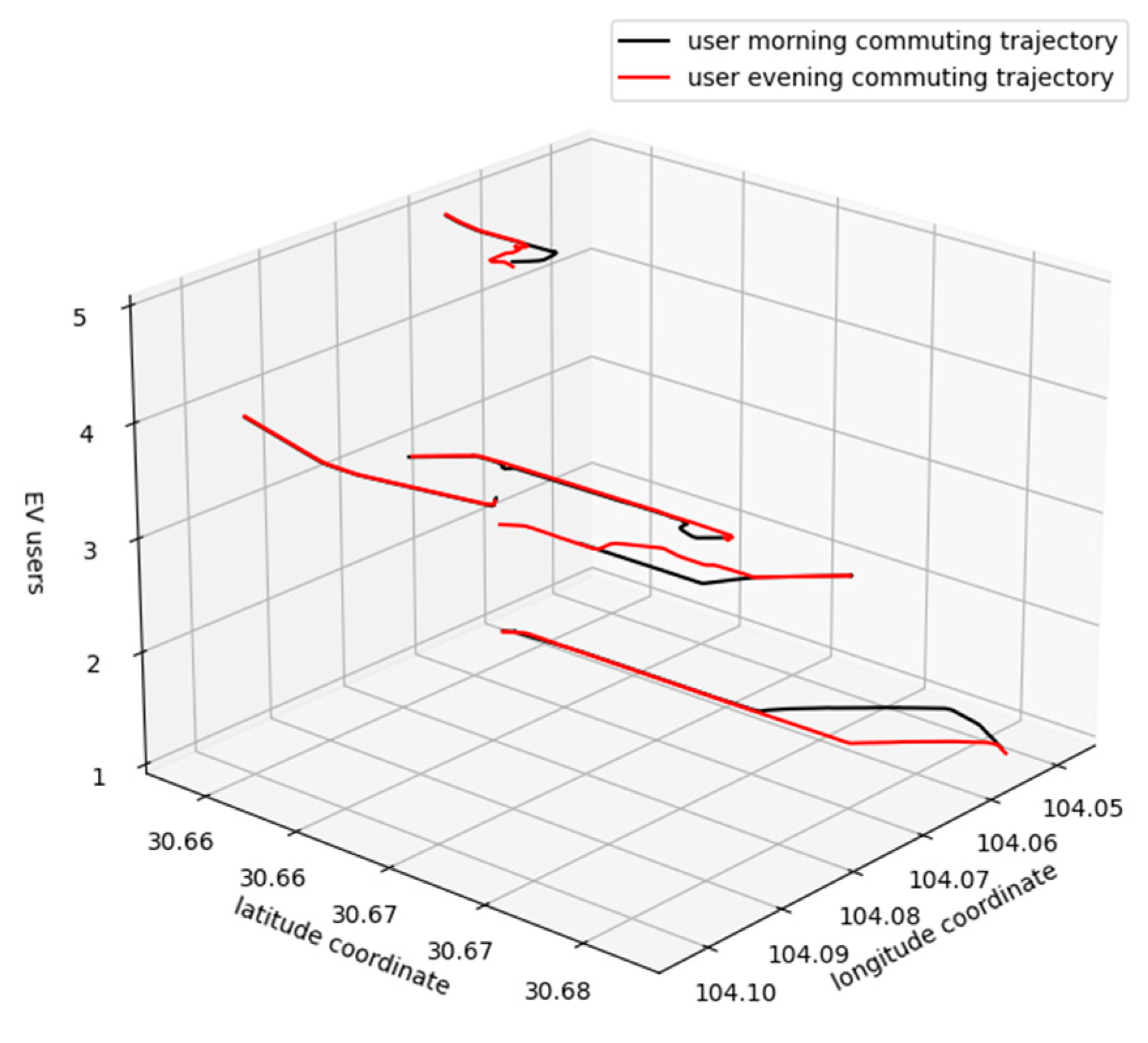
2.1. GPS Data Pre-Processing
2.2. Travel Chain Construction
- (1)
- Construct the matching relationship between the early travel chain Cm(i) and the late travel chain :where , , are the real-time longitudinal and latitudinal coordinates and time stamps corresponding to the i-th message in the m-th morning-commute-trajectory data, respectively, where , n is the total length of the trip chain; ,, are the real-time longitudinal and latitudinal coordinates and timestamps corresponding to the j-th message in the e-th evening-commute-trajectory data, respectively, where , l is the total length of the trip chain.
- (2)
- Match the early and late trajectory data obtained through mining in the spatial position:where , are the set of travel chain trajectories obtained by matching the beginning and end longitudinal and latitudinal coordinates, respectively; , are the minimum value of distance error allowed in the matching process; is the set of successfully matched travel chain data ensemble; and z is the number of successful matches, .
2.3. EV-Driving Characteristics
2.3.1. Battery Initial State of Charge
2.3.2. EV Dynamic Energy Consumption Model
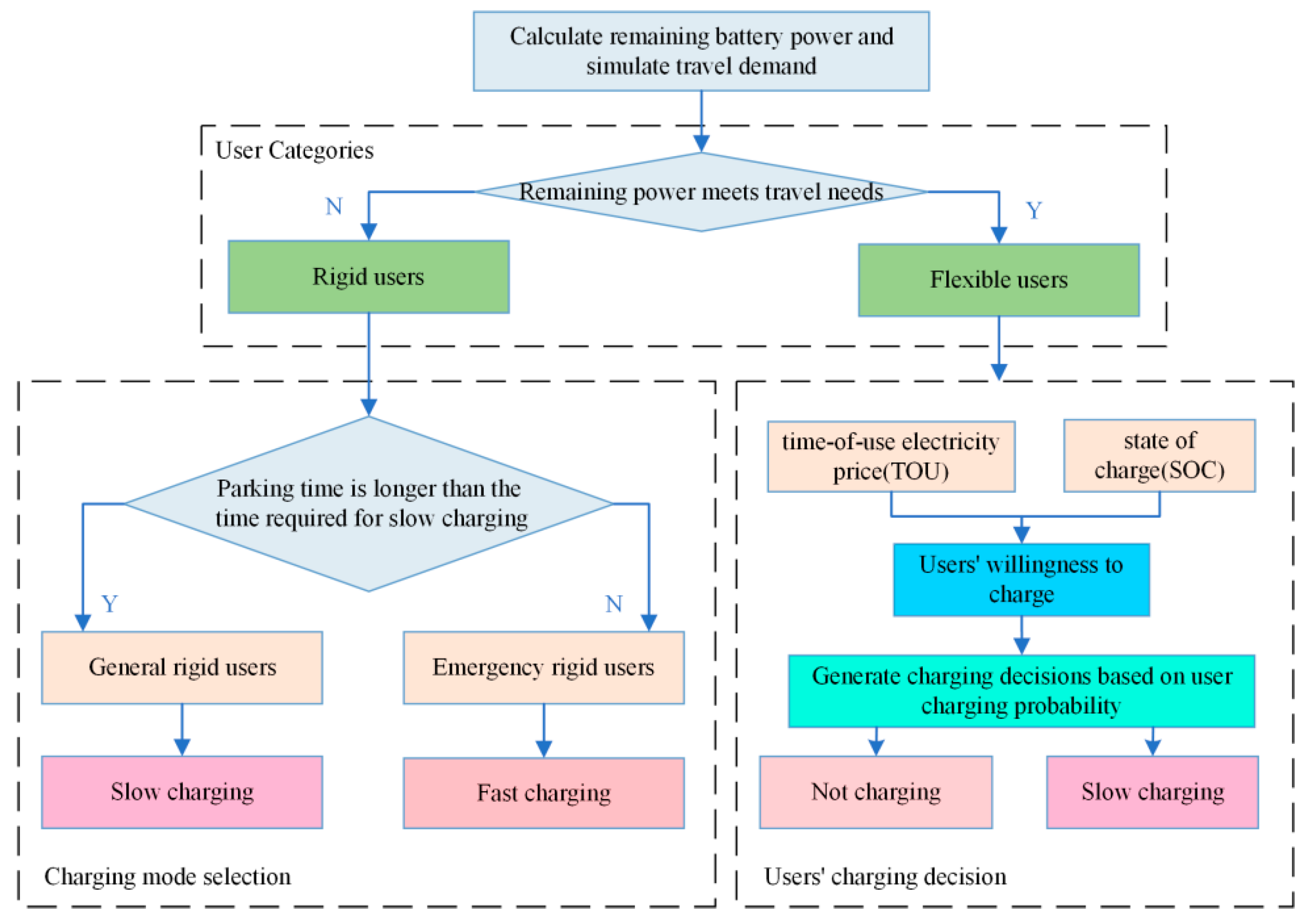
2.4. Hierarchical Charging Decision Model for EV Users
2.4.1. Classification of Users Based on Travel Needs
2.4.2. Charging Mode Selection for Rigid Users
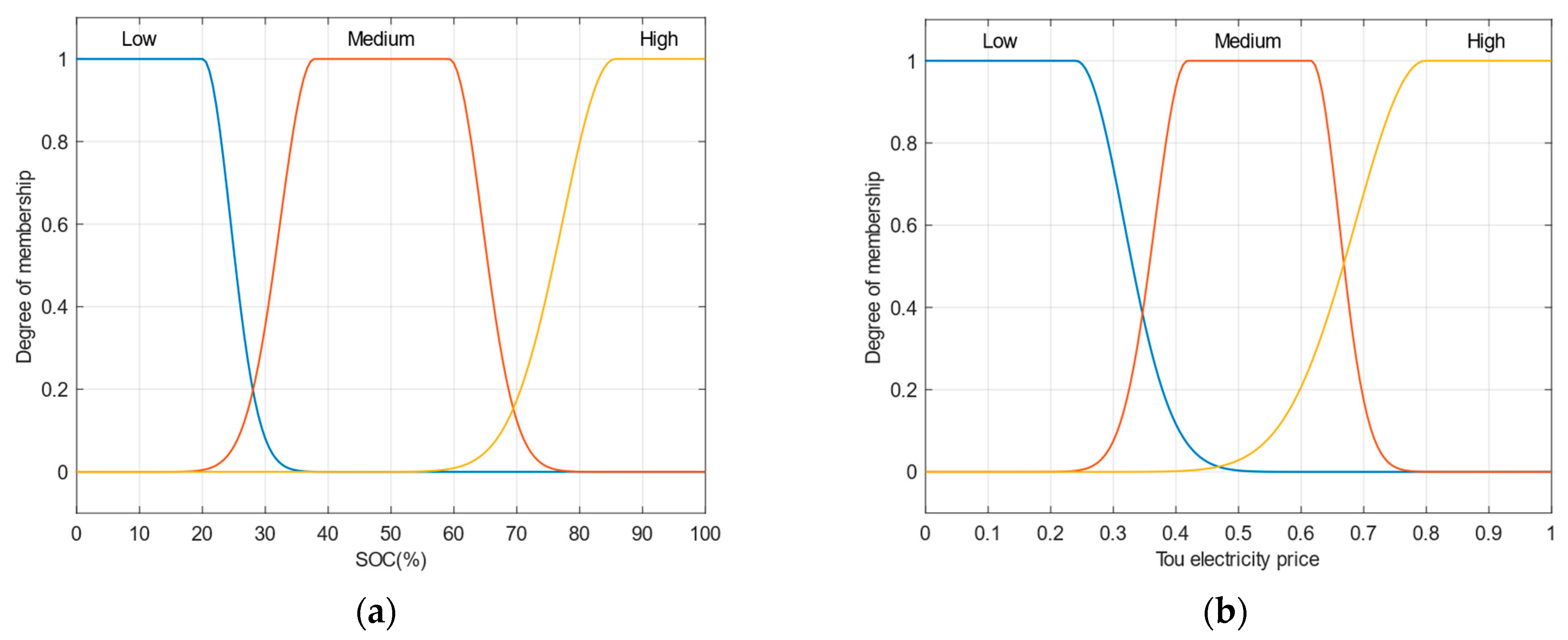
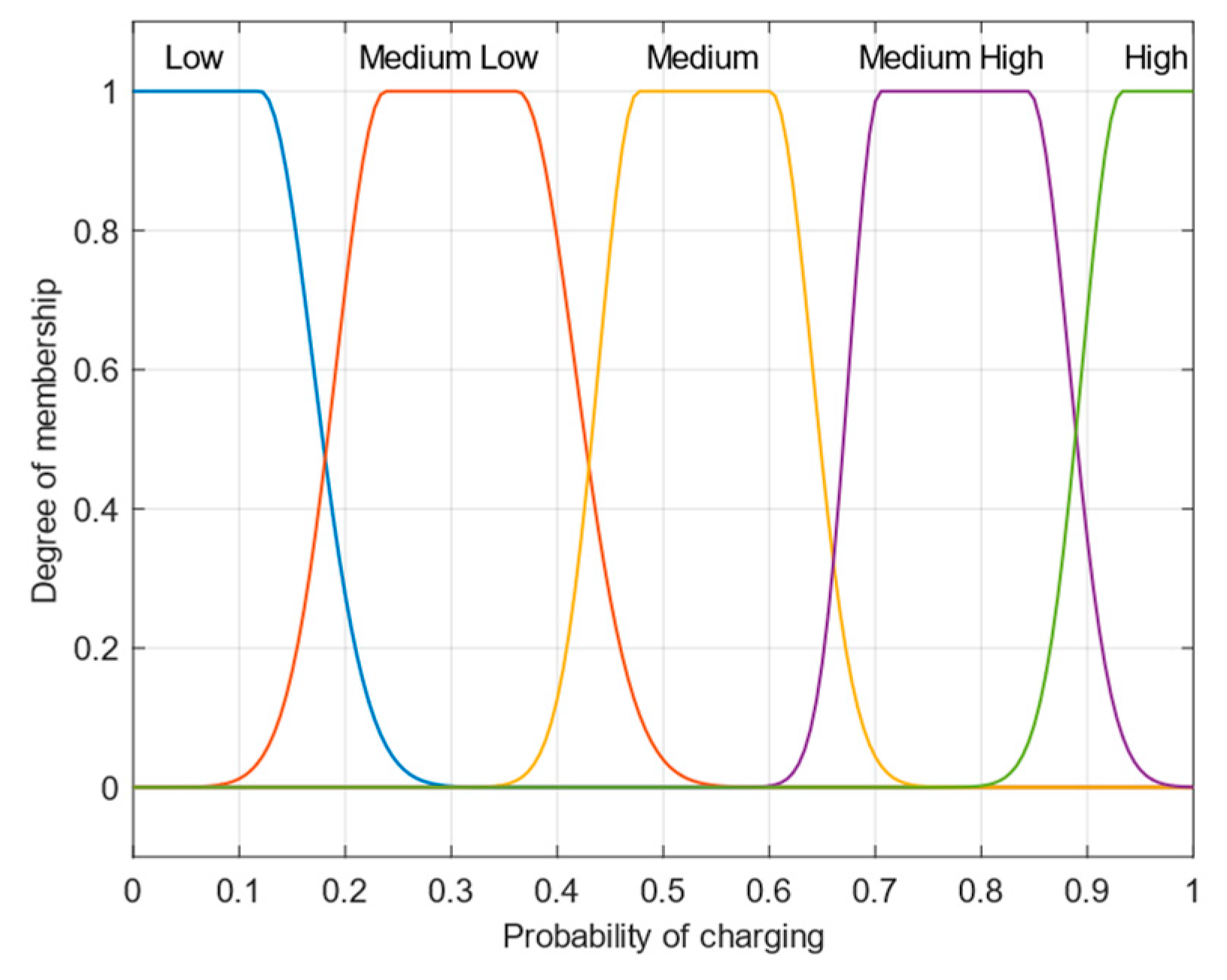
2.4.3. Charging-Probability Analysis for Flexible Users
- (1)
- Battery-charging status
- (2)
- Time-of-use electricity price
- (1)
- Calculate the remaining power of the EV and judge whether its charge status can satisfy the next trip; based on this the users are classified into rigid users and flexible users.
- (2)
- For rigid users, if their parking time is sufficient, they are defined as ordinary rigid users and choose the slow-charging method; if slow charging cannot meet the demand of the next trip within the parking time, they are defined as emergency rigid users and choose fast-charging method.
- (3)
- For flexible users, the charging tariff and the state of charge are considered to judge whether they are charged or not. Considering the battery life, the flexible users who choose to charge will give priority to the slow-charging method.
2.5. Charging-Demand Load Calculation
- (1)
- Mine and fuse the GPS track data, analyze the characteristics of the trip chain, and simulate the spatiotemporal characteristics of users in different trips;
- (2)
- When a journey ends, update the status;
- (3)
- Simulate the user’s next trip, and calculate the user’s power demand in advance;
- (4)
- Classify users according to the satisfaction degree of travel power demand, and make charging decisions and judgments on charging modes for different users;
- (5)
- Determine the charging time distribution of electric-vehicle-charging demand in the current area, and superimpose the charging demand generated in different areas to obtain the temporal and spatial distribution of the overall charging demand.
2.6. V2G-Demand-Response Decision Model
2.6.1. V2G Penetration Threshold Model
2.6.2. Expected Utility Model
2.6.3. Selection Probability Model for EV Users
- (1)
- Based on the trip chain obtained through matching, parameters such as vehicle price and psychological threshold of EV users are randomly selected and generated.
- (2)
- The aggregators in the study area judge the EV users’ decision to participate in V2G according to the probabilistic selection model, including three stages: charging demand confirmation, scheme evaluation, and participation decision. Firstly, it judges whether it can satisfy the next trip based on the remaining battery power, and collects information that affects the user’s participation decision, including car price, battery capacity and loss, social behavior, etc.; then, if both the charge state and the psychological threshold do not meet the requirements, the user abandons their participation in V2G, otherwise the utility value of the user’s participation in V2G and its selection probability are calculated according to the expected utility model; and finally, we use the discrete choice model to obtain their decision results, and the participation results are disseminated through social networks.
- (3)
- Count the number of EVs participating in V2G-demand response in the study area, determine whether traversal is completed for all EV users, and if traversal is completed, terminate the procedure and save the obtained number of EV-user participants for response scheduling in subsequent sections.
3. V2G-Demand-Response Scheduling Model
3.1. Response Capacity and Response Time of EV Users
3.2. Objective Function
- (1)
- Minimization of grid load fluctuations. In this paper, the daily load mean squared difference is introduced to characterize the system load volatility:where is the mean square difference of system load; is the conventional load; is the charging power of EV at time t; is the charging power of energy storage at time t; is the PV output; is the discharging power of EVA at time t; is the discharging power of energy storage at time t; is the daily average load of the region; and the dispatching period set in the paper is one day, divided into 96 dispatching periods.
- (2)
- Minimal cost of electricity for customers.where Ci,t,ch, Ci,t,disch are the charging cost and discharging benefit of EV users, respectively; denotes the EV-charging state at moment t, 1 for charging and 0 for not charging; zi,t denotes the EV-discharging state at moment t, 1 for discharging and 0 for not discharging.
3.3. Constraints
- (1)
- Power balance constraintwhere is photovoltaic output; is the discharge power of EVA at time t; is the discharge efficiency; is the charging efficiency; is the energy storage discharge power at time t; pbat,t is the energy storage charging power at time t; is the energy storage charging efficiency; is the energy storage discharge efficiency; and is the base load.
- (2)
- PV-output constraintwhere is the upper limit of PV output in the time period t.
- (3)
- EVA discharge power constraintAccording to the rules, the single EV user is only allowed to participate in one response on that day, the discharge power of EVA can be controlled using Equations (35) and (36).
- (4)
- Battery state-of-charge constraintwhere , indicates the upper and lower limits of the battery-charging state, with values of 0.9 and 0.2, respectively.
- (5)
- Charging and discharging mutual exclusion constraintIn order to prevent the mutually exclusive state of charging and discharging of energy storage in the scheduling process, state constraints are introduced.where denotes the storage charging state at moment t; denotes the storage discharging state at moment t. Both are binary variables.
3.4. Solution Method
4. Case Study
4.1. Parameter Analysis
4.1.1. Regional EV Data
4.1.2. Charging Power and Efficiency
4.1.3. POI Data Analysis
4.2. Result Analysis
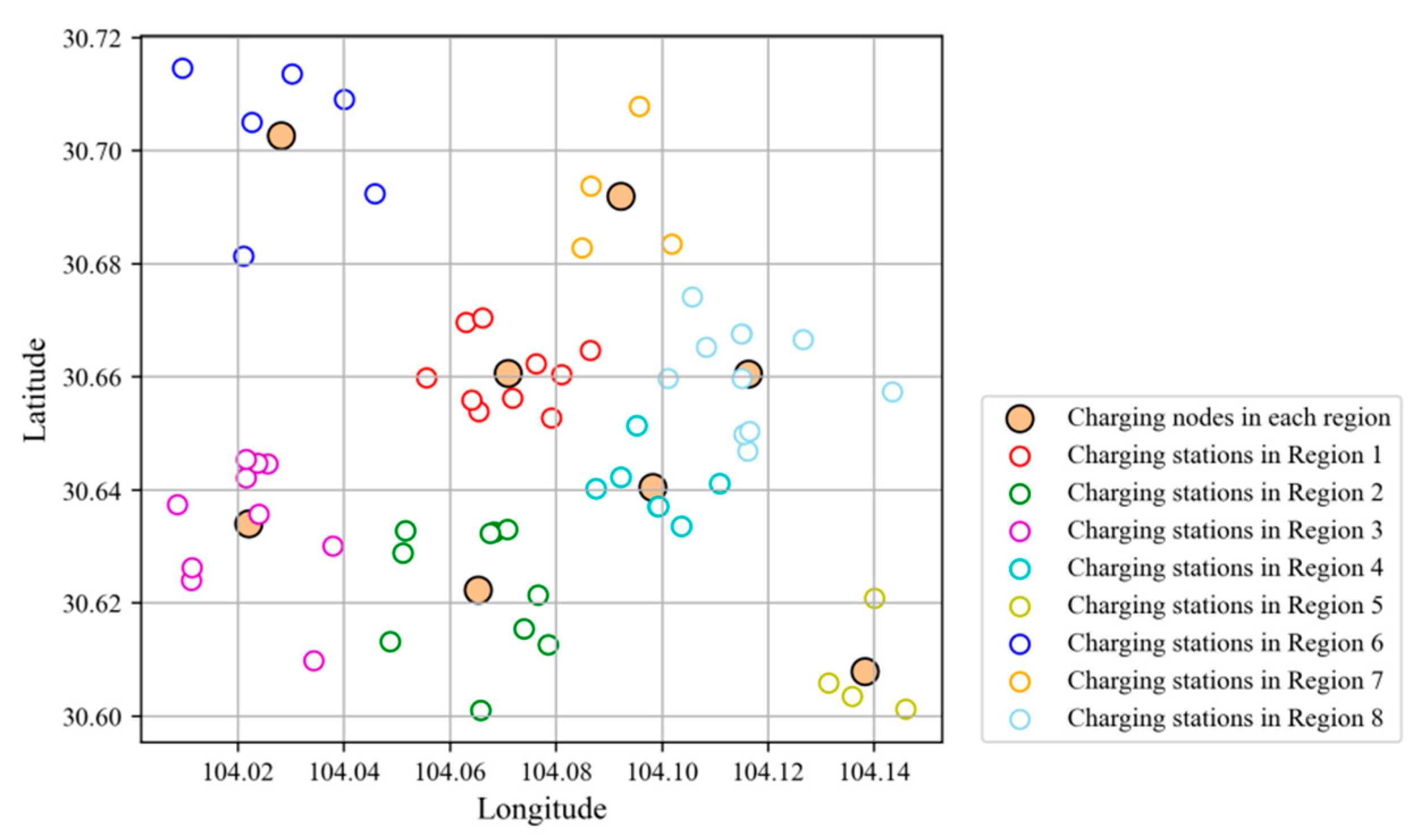
4.2.1. Zoning of Charging Stations
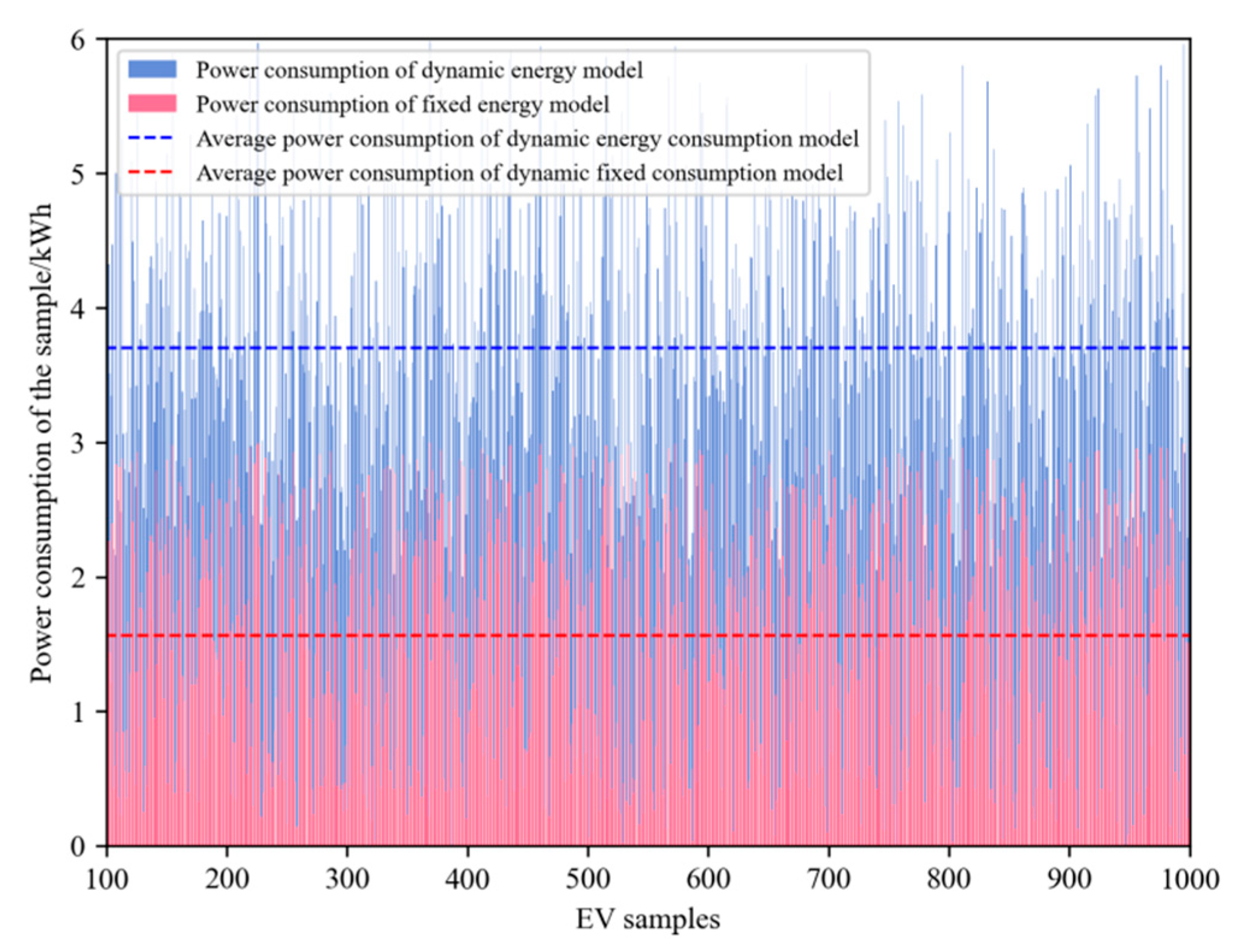
4.2.2. Comparison of Micro Dynamic Energy Consumption and Fixed Mileage Energy Consumption
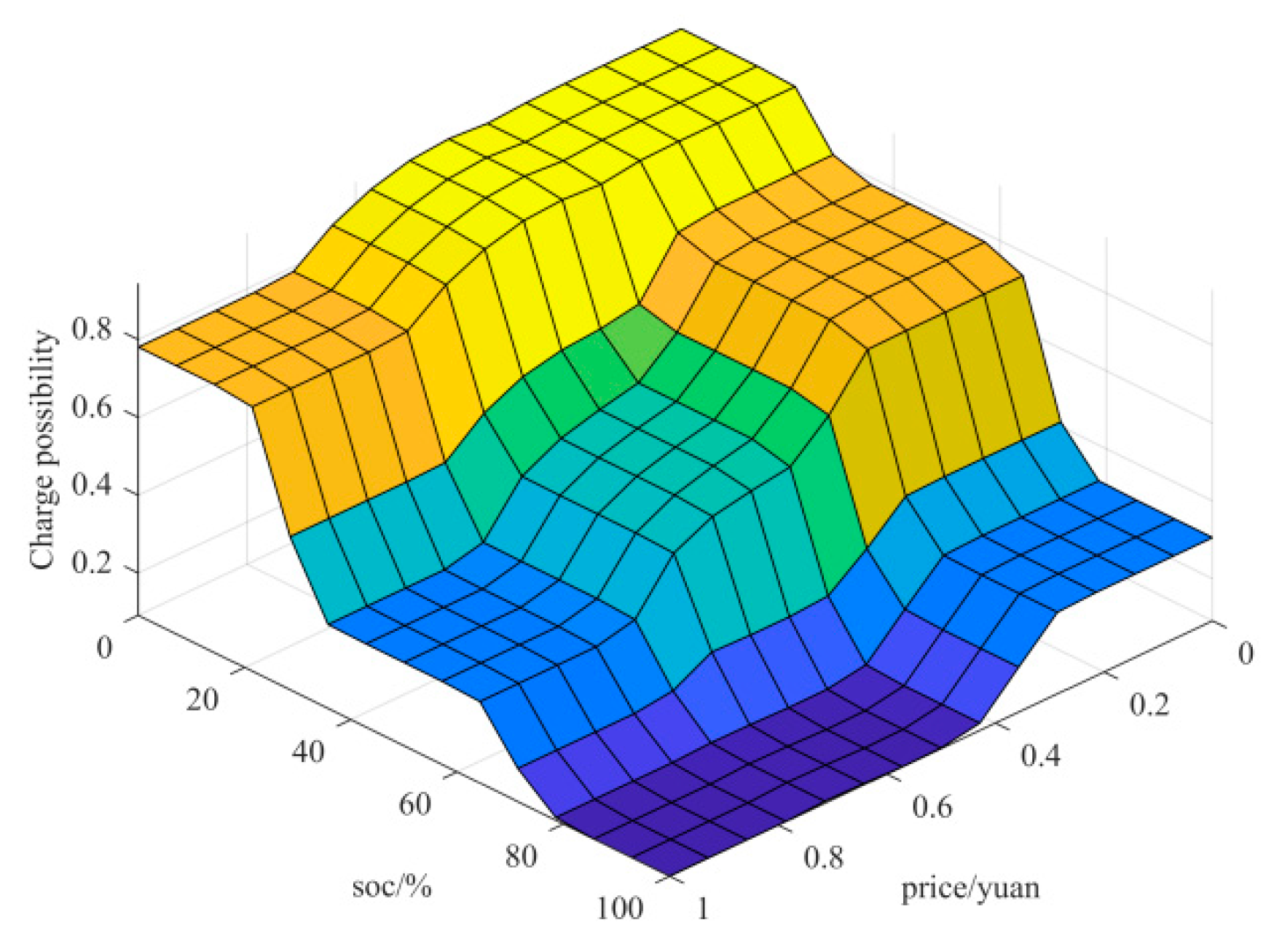
4.2.3. Fuzzy Reasoning System Evaluation
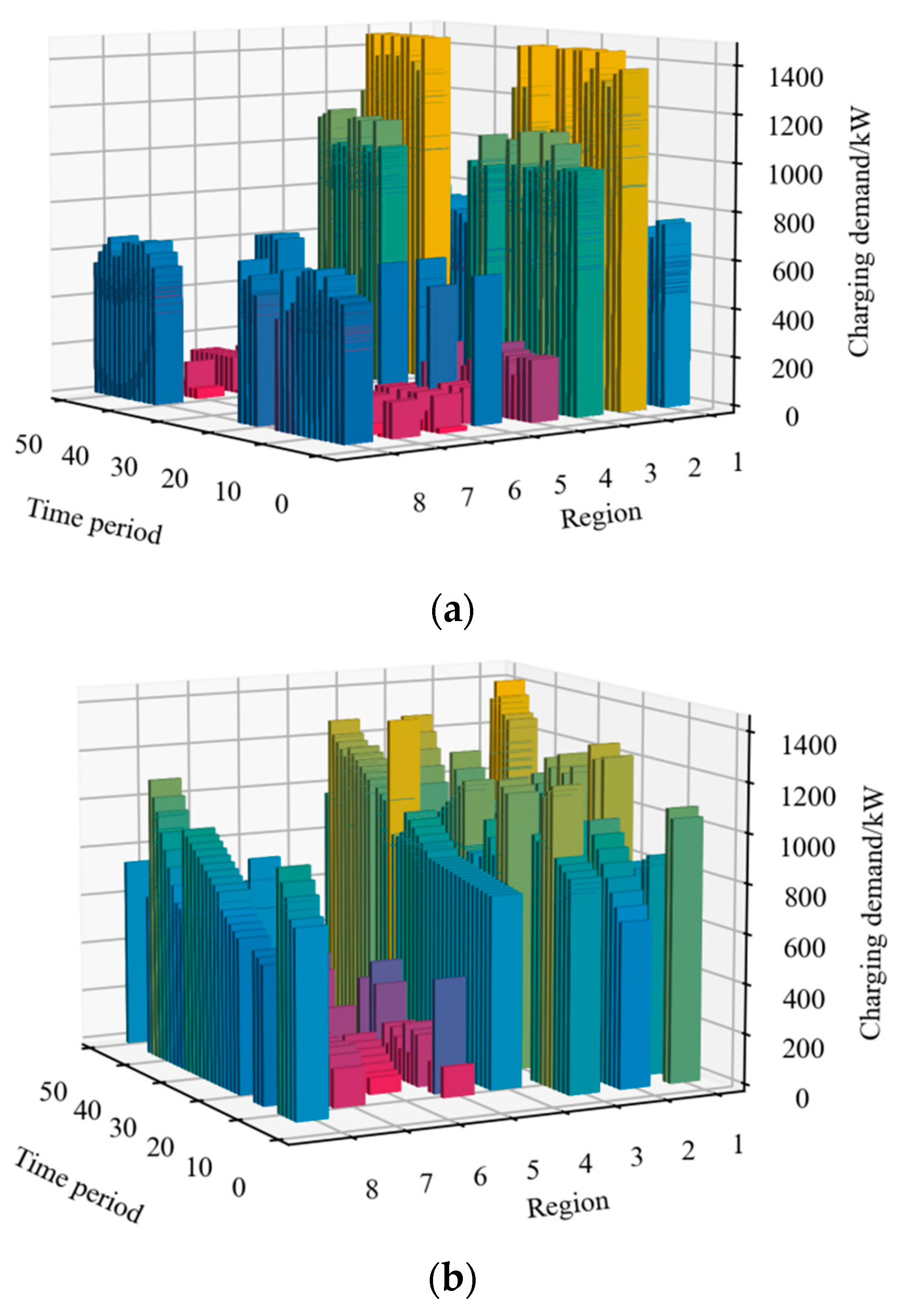
4.2.4. Regional-Charging-Demand Estimation
4.2.5. EV Users Participate in V2G Decision-Making Behavior
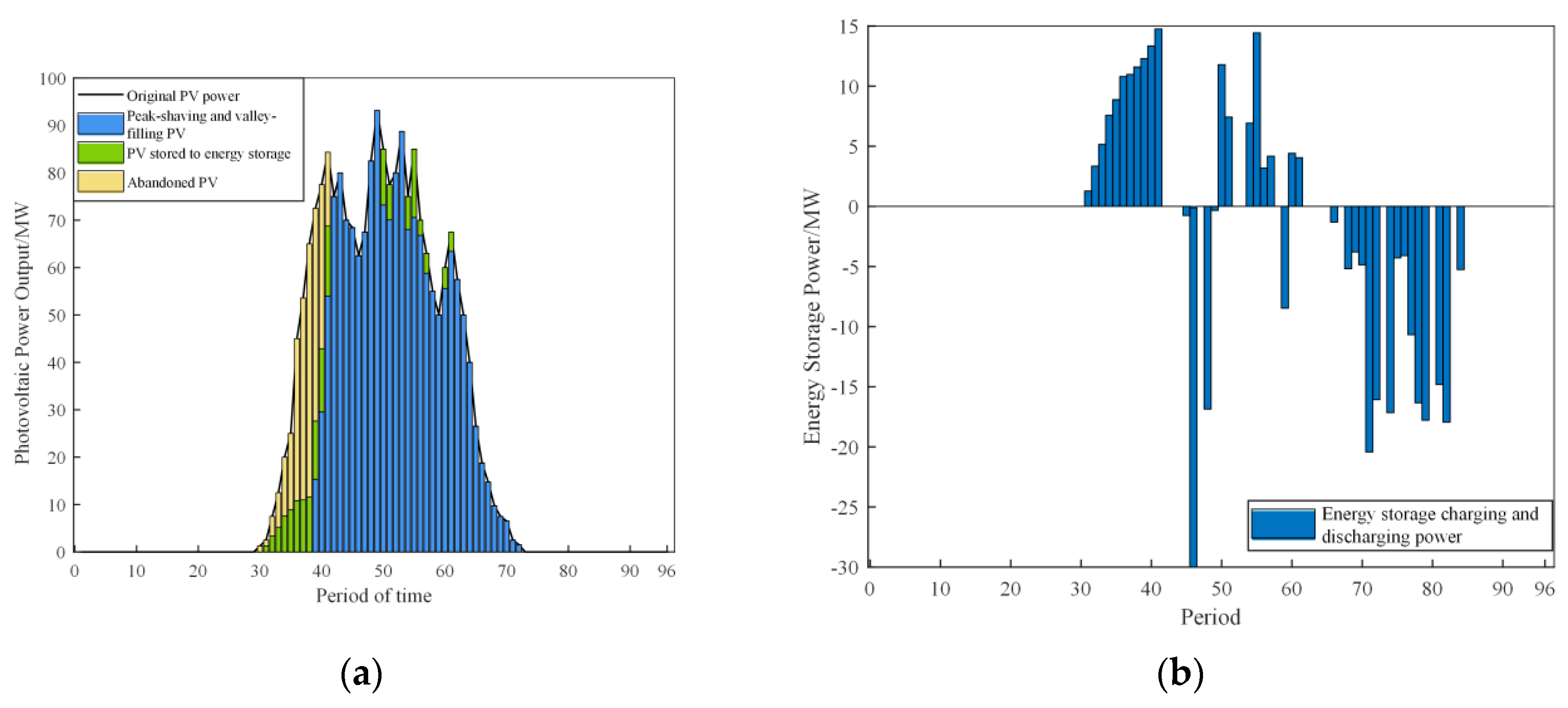
4.2.6. Analysis of Optimization-Scheduling Results
- (1)
- The discharge compensation rules adopted in this paper limit the time and number of EV users participating in V2G response, resulting in a low total EV response;
- (2)
- Considering factors such as electric vehicle discharge safety and the idle proportion of slow pile filling during the day, this paper assumes that electric vehicles participate in the V2G-discharge process using slow-power filling, resulting in a low discharge power in this process;
- (3)
- Due to the low EV permeability in the study area, the EV-charging demand accounts for a low proportion of the load demand in the region, resulting in a small number of EVs that can participate in the demand response.
5. Conclusions
- (1)
- The EV-charging-demand load obtained using GPS trajectory data is more consistent with the actual charging situation of domestic EV, which not only improves the accuracy of charging demand estimation at different periods, but also obtains the spatiotemporal distribution of charging demand.
- (2)
- The charging and discharging behavior of EV users is very random, and the charging probability generated using the fuzzy reasoning system is the most important factor affecting the charging state. In the probabilistic choice model of V2G-demand response, the enthusiasm of EV users to participate in the response is mainly affected by the EV battery capacity and cost benefit.
- (3)
- The adjustment effect of V2G on the power grid is very small, and the cooperation of EV charging and discharging with the output of other new energy units in the region can improve the consumption level of new energy and also play a good role in the stable regulation of the power grid. In addition, the potential of EV participation in V2G regulation is affected by many aspects, such as discharge compensation rules, discharge power size, EV price changes, etc., which can provide policy guidance for relevant departments in the region.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Desensitized Information for Drivers | Desensitized Information for Orders | Timestamp | Longitude | Latitude |
|---|---|---|---|---|
| 7bb6f**********48f84 | de247**********3d97b | 1478504981 | 104.09886 | 30.65442 |
| 7bb6f**********48f84 | de247**********3d97b | 1478504984 | 104.09898 | 30.65462 |
| 7bb6f**********48f84 | de247**********3d97b | 1478504987 | 104.09917 | 30.65492 |
| 7bb6f**********48f84 | de247**********3d97b | 1478504990 | 104.09936 | 30.65523 |
- (1)
- The trajectory data are arranged in time series by order, and the single-day data are divided into several sets.
- (2)
- The range of selected research areas is 104.0081~104.1504, 30.6010~30.7212.
- (3)
- Delete orders with a travel time less than 300 s [27], and delete multiple duplicates within a short distance in the same order.
- (4)
- Delete the trajectory data whose instantaneous speed is greater than 120 km/h. The calculation formula of the instantaneous speed is as follows:
| Period of Time | Electricity Price/CNY (kWh)−1 |
|---|---|
| Peak time period (11:00–12:00, 14:00–21:00) | 0.22 |
| Normal time period (7:00–11:00, 12:00–14:00, 21:00–23:00) | 0.55 |
| Low time period (23:00–23:45, 00:00–7:00 the next day) | 0.88 |
| Type | Proportion/% | Psychological Threshold |
|---|---|---|
| innovator | 2.50 | 0 |
| early adopter | 13.5 | 0.05 |
| early/late follower | 68.0 | 0.15 |
| laggard | 16.0 | 0.35 |
References
- Zang, J.; Li, C. Adjustment and Interpretation of New Energy Automobile Industry Development Plan (2021–2035). Automot. Tech. 2021, Z1, 32–34. [Google Scholar]
- Chen, L.; Zhang, Y.; Figueiredo, A. Overview of charging and discharging load forcasting for electric vehicles. Autom. Electr. Power Syst. 2019, 43, 177–197. [Google Scholar]
- Zhang, M.; Cai, Y.; Yang, X.; Li, L. Analysis method of charging demand Distribution for household electric vehicles considering user charging differences. Electr. Power Autom. Equip. 2020, 40, 154–163. [Google Scholar]
- Huang, N.; Liu, D.; Cai, G.; Pan, X.; Zhang, L. Charging Load Interval Prediction for electric Vehicles Based on Multi-Correlated Daily Scenarios. Proc. CSEE 2021, 41, 7980–7990. [Google Scholar]
- Xing, Q.; Chen, Z.; Zhang, Z.; Huang, X.; Leng, Z.; Sun, K.; Chen, Y.; Wang, H. Charging Demand Forecasting Model for Electric Vehicles Based on Online Ride-Hailing Trip Data. IEEE Access 2019, 7, 137390–137409. [Google Scholar] [CrossRef]
- Zhang, Y.; Guo, L.; Liu, Y.; Li, X.; Yin, C. Numerical modeling method of charging load Probability Distribution for electric vehicles. Autom. Electr. Power Syst. 2021, 45, 61–70. [Google Scholar]
- Zhang, Q.; Wang, Z.; Tan, W.; Liu, H.; Li, C. Spatial-temporal Distribution Prediction of electric vehicle Charging load Based on MDP Random Path Simulation. Autom. Electr. Power Syst. 2018, 42, 59–66. [Google Scholar]
- Li, H.; Song, Y.; Li, S.; Zhu, Y.; Kang, Y.; Dong, H. Charging load forecasting method for electric vehicles based on ArcGIS network structure and traffic congestion analysis. Grid Technol. 2024, 1–14. [Google Scholar] [CrossRef]
- Shi, R.; Li, S.; Zhang, P.; Lee, K.Y. Integration of renewable energy sources and electric vehicles in V2G network with adjustable robust optimization. Renew. Energy 2020, 153, 1067–1080. [Google Scholar] [CrossRef]
- Shang, Y.; Shang, Y.; Yu, H.; Shao, Z.; Jian, L. Achieving efficient and adaptable dispatching for vehicle-to-grid using distributed edge computing and attention-based LSTM. IEEE Trans. Ind. Inform. 2021, 18, 6915–6926. [Google Scholar] [CrossRef]
- Gamil, M.M.; Senjyu, T.; Masrur, H.; Takahashi, H.; Lotfy, M.E. Controlled V2Gs and battery integration into residential microgrids: Economic and environmental impacts. Energy Convers. Manag. 2022, 253, 115171. [Google Scholar] [CrossRef]
- Kandpal, B.; Pareek, P.; Verma, A. A robust day-ahead scheduling strategy for EV charging stations in unbalanced distribution grid. Energy 2022, 249, 123737. [Google Scholar] [CrossRef]
- Liu, D.; Sun, Y.; Qu, Y.; Li, B.; Xu, Y. Analysis and accurate prediction of user’s response behavior in incentive-based demand response. IEEE Access 2018, 7, 3170–3180. [Google Scholar] [CrossRef]
- Jiang, J.; Kou, Y.; Bie, Z.; Li, G. Optimal real-time pricing of electricity based on demand response. Energy Procedia 2019, 159, 304–308. [Google Scholar] [CrossRef]
- Liu, X. Research on flexibility evaluation method of distribution system based on renewable energy and electric vehicles. IEEE Access 2020, 8, 109249–109265. [Google Scholar] [CrossRef]
- Wu, W.; Lin, B. Benefits of electric vehicles integrating into power grid. Energy 2021, 224, 120108. [Google Scholar] [CrossRef]
- Zhang, Q.; Tan, W.; Cai, J.; Wang, Z.; Li, C. Electric vehicle Discharge Price Negotiation Strategy based on Fuzzy Bayes Learning. Proc. CSEE 2018, 38, 61–71+343. [Google Scholar]
- Mu, Y.; Wu, J.; Jenkins, N.; Jia, H.; Wang, C. A Spatial–Temporal model for grid impact analysis of plug-in electric vehicles. Appl. Energy 2014, 114, 456–465. [Google Scholar] [CrossRef]
- Wen, J.; Tao, S.; Xiao, X.; Luo, C.; Liao, K. Electric Vehicle Charging Demand Analysis based on Stochastic Travel Chain Simulation. Power Grid Technol. 2015, 39, 1477–1484. [Google Scholar]
- Fiori, C.; Montanino, M.; Nielsen, S.; Seredynski, M.; Viti, F. Microscopic energy consumption modelling of electric buses: Model development, calibration, and validation. Transp. Res. Part D Transp. Environ. 2021, 98, 102978. [Google Scholar] [CrossRef]
- Huber, J.; Dann, D.; Weinhardt, C. Probabilistic forecasts of time and energy flexibility in battery electric vehicle charging. Appl. Energy 2020, 262, 114525. [Google Scholar] [CrossRef]
- Zhang, H.; Hu, Z.; Song, Y.; Xu, Z.; Jia, L. Electric vehicle charging load Forecasting Method considering Spatiotemporal Distribution. Autom. Electr. Power Syst. 2014, 38, 13–20. [Google Scholar]
- Arias, M.B.; Kim, M.; Bae, S. Prediction of electric vehicle charging-power demand in realistic urban traffic networks. Appl. Energy 2017, 195, 738–753. [Google Scholar] [CrossRef]
- Yang, W.; Xiang, Y.; Liu, J.; Gu, C. Electric vehicle scale evolution Model based on Multi-agent Technology. Power Grid Technol. 2017, 41, 2146–2154. [Google Scholar]
- Yang, W.; Xiang, Y.; Liu, J.; Gu, C. Agent-Based Modeling for Scale Evolution of Plug-In Electric Vehicles and Charging Demand. IEEE Trans. Power Syst. 2018, 33, 1915–1925. [Google Scholar] [CrossRef]
- Gong, S.; Cheng, V.H.S.; Ardeshiri, A.; Rashidi, T.H. Incentives and concerns on vehicle-to-grid technology expressed by Australian employees and employers. Transp. Res. Part D Transp. Environ. 2021, 98, 102986. [Google Scholar] [CrossRef]
- Zhou, C.; Xiang, Y.; Tong, H.; Rao, P.; Qing, Y.; Liu, Y. Estimation of electric vehicle charging demand and V2G adjustable capacity driven by trajectory data. Autom. Electr. Power Syst. 2022, 46, 46–55. [Google Scholar]




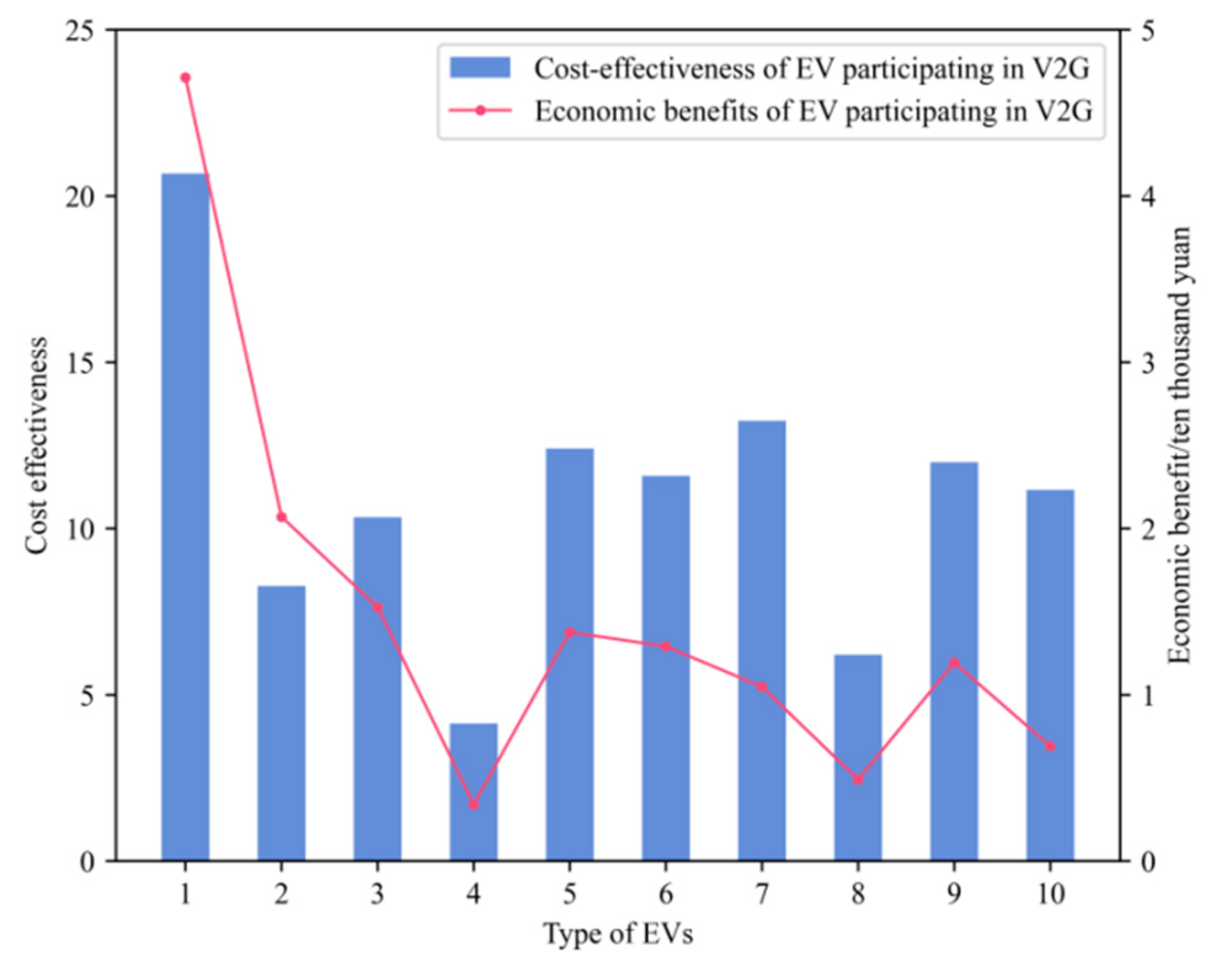


| EV Type | Inventory/Vehicle | Battery Capacity/(kW·h) | Endurance Mileage/km | Price Bracket |
|---|---|---|---|---|
| Geely-Emgrand | 6099 | 52 | 500 | Low-grade |
| Mustang EC70 | 4358 | 49 | 304 | Mid-grade |
| Tesla modelX | 3467 | 100 | 605 | High-grade |
| BMW-520PHEV | 2534 | 18 (Hybrid) | 95 | High-grade |
| BYD-Yuan | 1971 | 50 | 401 | Low-grade |
| Denza | 1703 | 70 | 451 | Mid-grade |
| Dongfeng-Junfeng | 1650 | 31 | 255 | Low-grade |
| BYD-Tang | 1656 | 18 (Hybrid) | 90 | Mid-grade |
| BAIC EU | 1431 | 45 | 300 | Low-grade |
| Chery Q1 | 1385 | 20 | 200 | Low-grade |
| Scenarios | Load Variance/kW2 | Electricity Cost/CNY |
|---|---|---|
| Scenario 1 | 1,187,500 | 29,878.30 |
| Scenario 2 | 750,630 | 13,398.71 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, G.; Liu, H.; Xie, T.; Li, H.; Zhang, K.; Wang, R. Research on the Dispatching of Electric Vehicles Participating in Vehicle-to-Grid Interaction: Considering Grid Stability and User Benefits. Energies 2024, 17, 812. https://doi.org/10.3390/en17040812
Zhang G, Liu H, Xie T, Li H, Zhang K, Wang R. Research on the Dispatching of Electric Vehicles Participating in Vehicle-to-Grid Interaction: Considering Grid Stability and User Benefits. Energies. 2024; 17(4):812. https://doi.org/10.3390/en17040812
Chicago/Turabian StyleZhang, Gang, Hong Liu, Tuo Xie, Hua Li, Kaoshe Zhang, and Ruogu Wang. 2024. "Research on the Dispatching of Electric Vehicles Participating in Vehicle-to-Grid Interaction: Considering Grid Stability and User Benefits" Energies 17, no. 4: 812. https://doi.org/10.3390/en17040812
APA StyleZhang, G., Liu, H., Xie, T., Li, H., Zhang, K., & Wang, R. (2024). Research on the Dispatching of Electric Vehicles Participating in Vehicle-to-Grid Interaction: Considering Grid Stability and User Benefits. Energies, 17(4), 812. https://doi.org/10.3390/en17040812







