Efficiency Improvement of Permanent Magnet Synchronous Motors Using Model Predictive Control Considering Core Loss
Abstract
1. Introduction
- (1)
- Reliability and robustness;
- (2)
- Torque and power density;
- (3)
- Dynamic performance;
- (4)
- Very wide speed range;
- (5)
- The energy efficiency of high-speed cruising.
1.1. Gap and Motivation
1.2. Literature Review
1.3. Research Method
1.3.1. Concept
1.3.2. Assumptions
1.3.3. Description of the Tool
1.3.4. Analysis Theme
1.3.5. Research Results
2. Application of Core Loss ECM in MPC and LMA Development
2.1. Equivalent Circuit Model with Core Loss
2.1.1. Conventional ECM of PMSM
| Motor Characteristics | Symbol | Value |
|---|---|---|
| Number of pole pairs | 4 | |
| Stator winding resistance | 0.0974 Ω | |
| d-axis inductance | 83.955 μH | |
| q-axis inductance | 328.365 μH | |
| PM flux linkage | 0.0479 Wb | |
| Rated speed | 3600 r/min | |
| Rated current | 180 A | |
| Rated power | 20 kW | |
| Rated torque | 53 Nm | |
| No-load equivalent core loss resistance | Ω (n represents the motor speed) | |
| Load equivalent core loss resistance | 21 Ω |
2.1.2. Core Loss Equivalent Circuit Model of PMSM
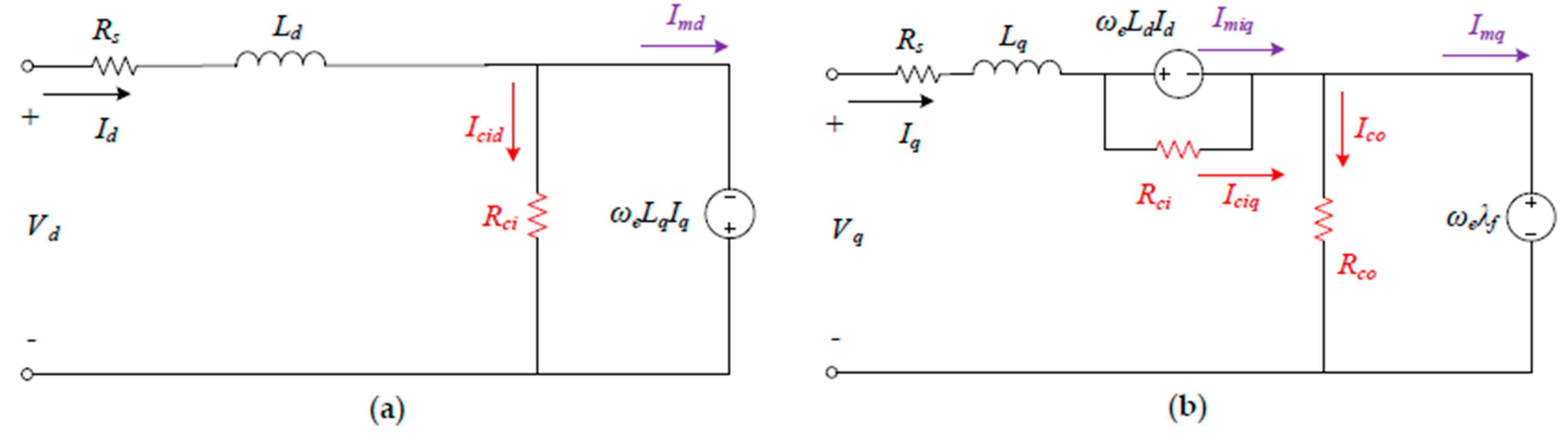
2.1.3. Determination of Core Loss Resistances
- Simulation and calculation based on the finite element method and professional software. It constructs the relationships between the core power loss and the flux densities and the load currents to construct separate curves. And then evaluate the load equivalent core loss resistances as constants or variables concerning some parameters like speed [33,34].
2.2. Model Predictive Direct Torque Control (MPDTC)
2.3. Loss Minimization Algorithm (LMA)
2.3.1. Conventional ECM
2.3.2. Conventional ECM
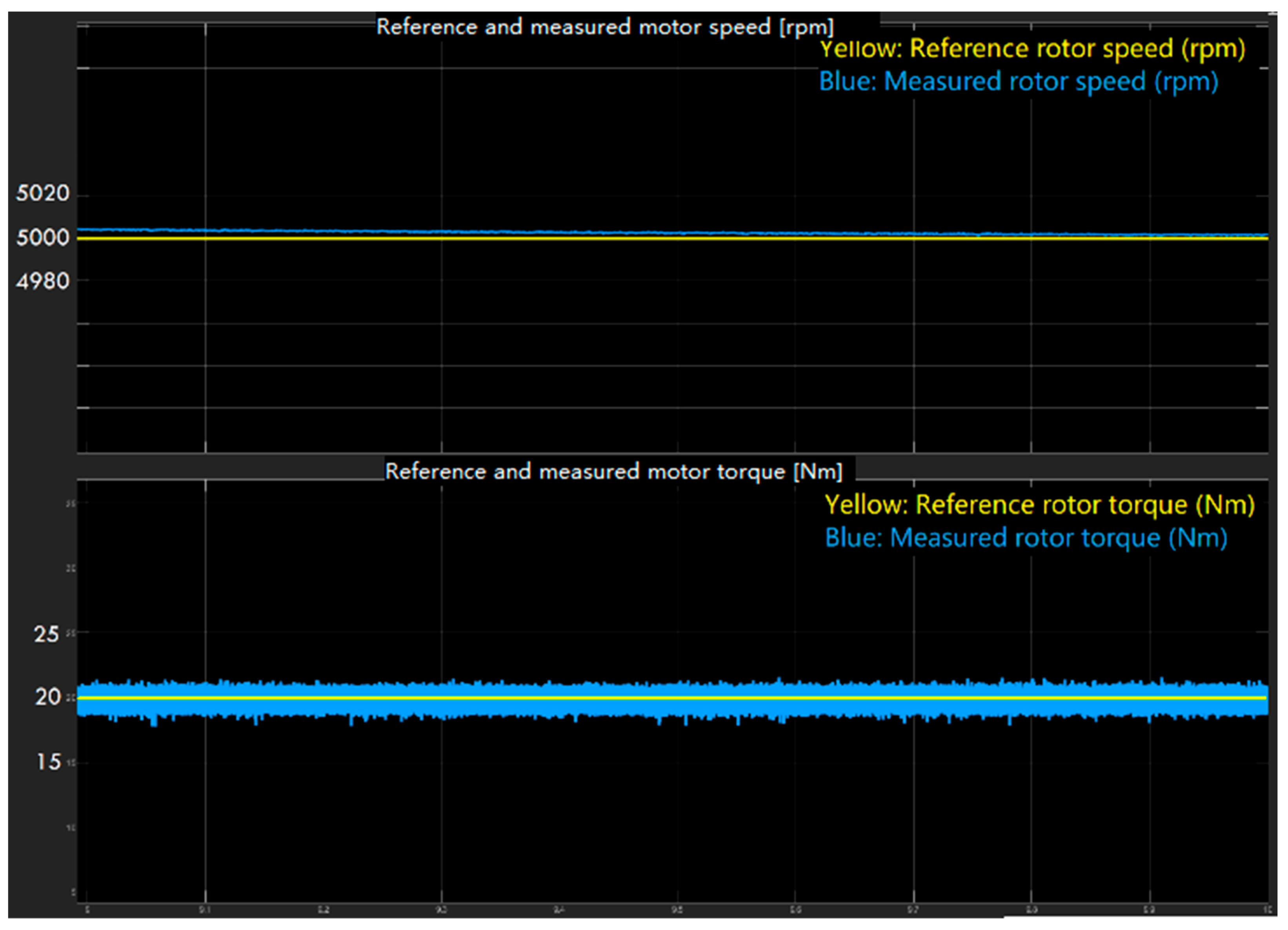
3. Simulation Results
3.1. Comparison Scheme
3.2. Simulation Results
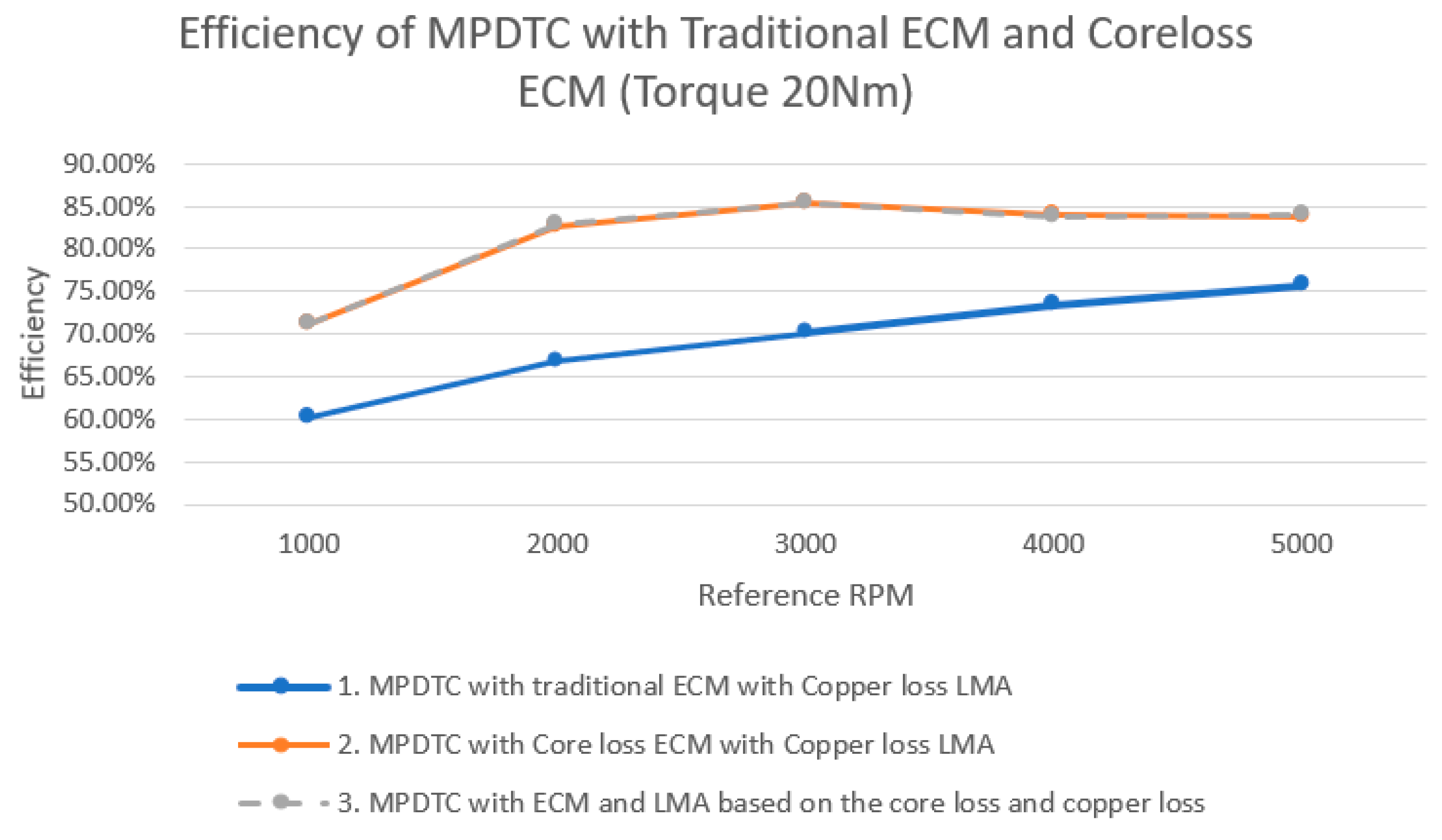
3.2.1. Under Load
| MPDTC with Conventional Loss ECM with Copper Loss LMA | |||||
|---|---|---|---|---|---|
| Ref Speed (rpm) | Torque (Nm) | Shaft Output Power (W) | Copper Loss (W) | DC Power (W) | Efficiency (%) |
| 1000 | 20 | 2093 | 632.6 | 3473 | 60.26% |
| 2000 | 20 | 4189 | 641.9 | 6272 | 66.79% |
| 3000 | 20 | 6284 | 661 | 8960 | 70.13% |
| 4000 | 20 | 8378 | 679.1 | 11,420 | 73.36% |
| 5000 | 20 | 10,470 | 695.7 | 13,820 | 75.76% |
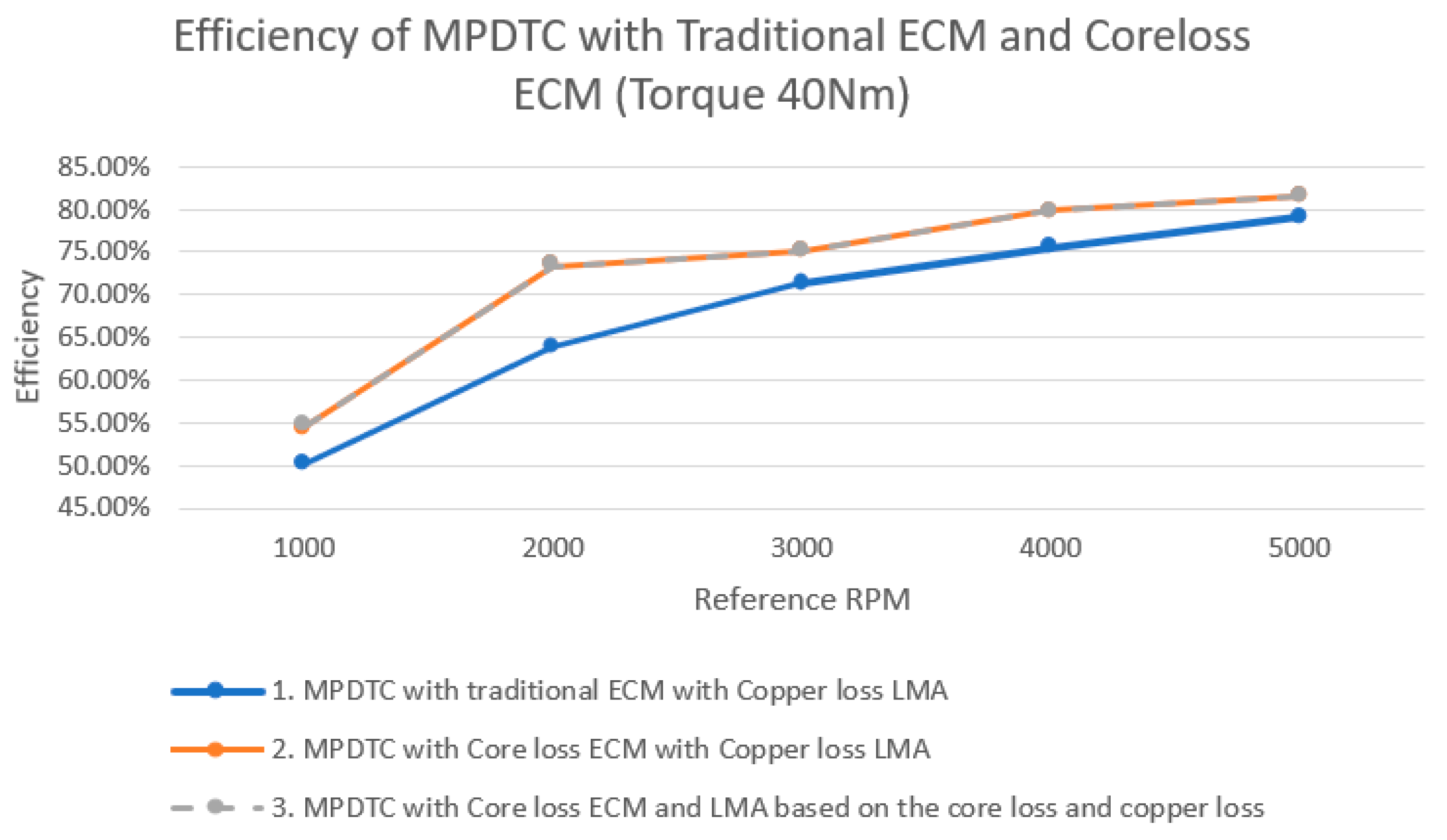
| 1000 | 40 | 4182 | 3764 | 8340 | 50.14% |
| 2000 | 40 | 8377 | 3835 | 13,130 | 63.80% |
| 3000 | 40 | 12,570 | 3914 | 17,620 | 71.34% |
| 4000 | 40 | 16,760 | 3998 | 22,180 | 75.56% |
| 5000 | 40 | 20,950 | 4038 | 26,490 | 79.09% |
| MPDTC with Core Loss ECM with Copper Loss LMA | Improvement Compared to MPDTC with Conventional ECM (%) | ||||||
|---|---|---|---|---|---|---|---|
| Ref Speed (rpm) | Torque (Nm) | Shaft Output Power (W) | Copper Loss (W) | Core Loss (W) | DC Power (W) | Efficiency (%) | |
| 1000 | 20 | 2093 | 425.6 | 138.4 | 2939 | 71.21% | 18.17% |
| 2000 | 20 | 4190 | 420.7 | 322.6 | 5072 | 82.61% | 23.69% |
| 3000 | 20 | 6285 | 426 | 569.3 | 7370 | 85.28% | 21.59% |
| 4000 | 20 | 8380 | 411.5 | 904.5 | 9965 | 84.09% | 14.63% |
| 5000 | 20 | 10,480 | 392.9 | 1383 | 12,510 | 83.77% | 10.58% |
| 1000 | 40 | 4183 | 1445 | 149.2 | 7679 | 54.47% | 8.63% |
| 2000 | 40 | 8378 | 1467 | 367 | 11,420 | 73.36% | 14.99% |
| 3000 | 40 | 12,570 | 1457 | 667 | 16,710 | 75.22% | 5.45% |
| 4000 | 40 | 16,760 | 1438 | 1076 | 20,970 | 79.92% | 5.77% |
| 5000 | 40 | 20,950 | 1416 | 1645 | 25,700 | 81.52% | 3.07% |
| MPDTC with Core Loss ECM and LMA Based on the Core Loss and Copper Loss | Improvement Compared to MPDTC with Conventional ECM (%) | ||||||
|---|---|---|---|---|---|---|---|
| Ref Speed (rpm) | Torque (Nm) | Shaft Output Power (W) | Copper Loss (W) | Core Loss (W) | DC Power (W) | Efficiency (%) | |
| 1000 | 20 | 2093 | 425.7 | 138.4 | 2942 | 71.14% | 18.05% |
| 2000 | 20 | 4190 | 420.9 | 322.5 | 5058 | 82.84% | 24.03% |
| 3000 | 20 | 6285 | 426.4 | 568.8 | 7367 | 85.31% | 21.64% |
| 4000 | 20 | 8380 | 411.5 | 903 | 10,010 | 83.72% | 14.11% |
| 5000 | 20 | 10,480 | 394.6 | 1380 | 12,480 | 83.97% | 10.84% |
| 1000 | 40 | 4183 | 1445 | 149.2 | 7661 | 54.60% | 8.89% |
| 2000 | 40 | 8378 | 1467 | 366.3 | 11,420 | 73.36% | 14.99% |
| 3000 | 40 | 12,570 | 1459 | 663.7 | 16,710 | 75.22% | 5.45% |
| 4000 | 40 | 16,760 | 1443 | 1066 | 20,970 | 79.92% | 5.77% |
| 5000 | 40 | 20,950 | 1426 | 1624 | 25,710 | 81.49% | 3.03% |
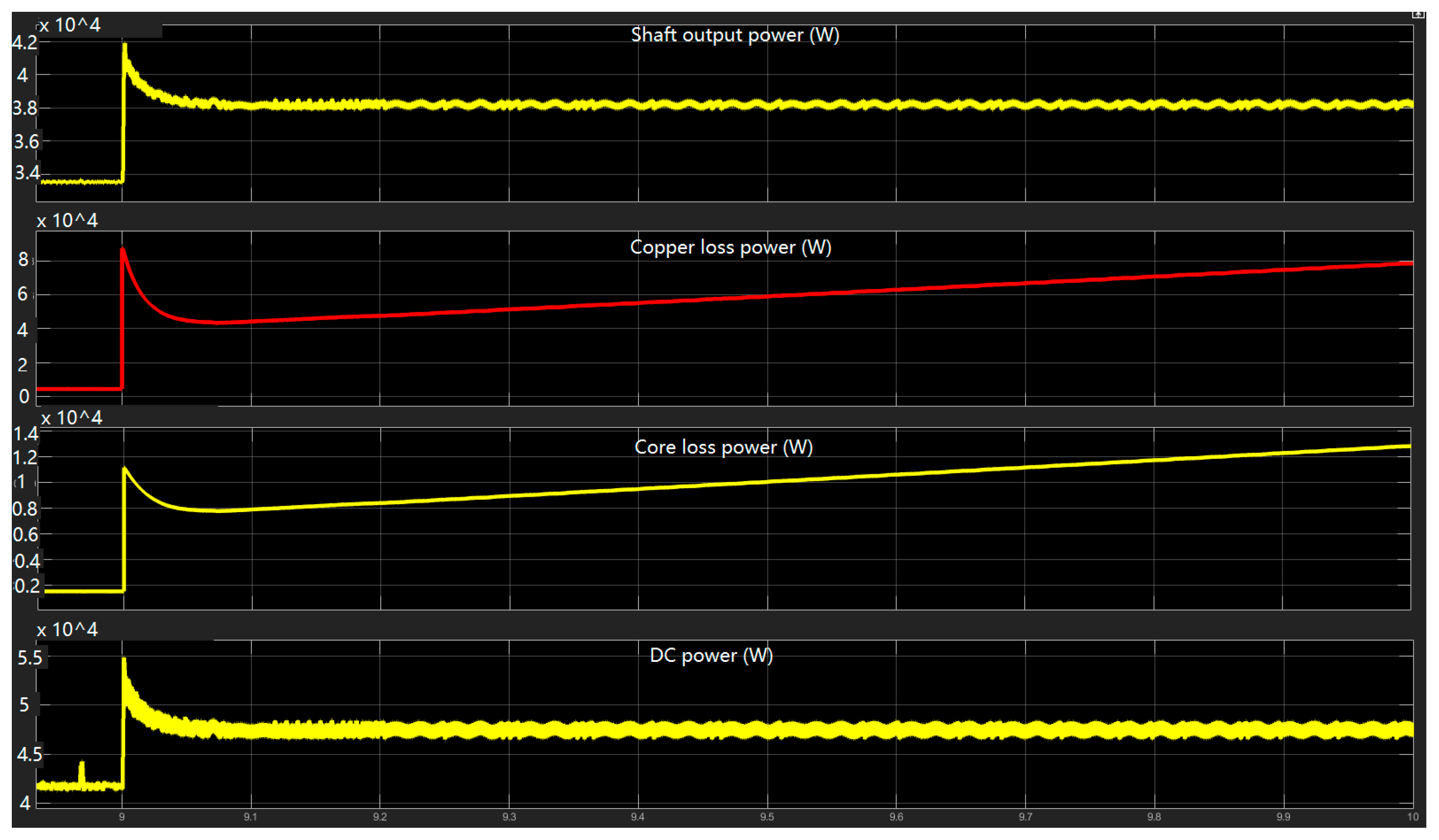
3.2.2. Nominal Load
| Ref Speed (rpm) | Torque (Nm) | Shaft Output Power (W) | Copper Loss (W) | Core Loss (W) | DC Power (W) | Efficiency (%) | Improvement Compared to MPDTC with Conventional ECM (%) |
|---|---|---|---|---|---|---|---|
| MPDTC with conventional loss ECM with copper loss LMA | |||||||
| 3600 | 53 | 20,070 | 2398 | 26,790 | 74.92 | ||
| MPDTC with core loss ECM and LMA based on the core loss and copper loss | |||||||
| 3600 | 53 | 19,990 | 2311 | 993.5 | 25,630 | 77.99 | 4.1 |
3.2.3. Overload
4. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chau, K.T.; Chan, C.C.; Liu, C. Overview of Permanent-Magnet Brushless Drives for Electric and Hybrid Electric Vehicles. IEEE Trans. Ind. Electron. 2008, 55, 2246–2257. [Google Scholar] [CrossRef]
- Kiyota, K.; Chiba, A. Design of Switched Reluctance Motor Competitive to 60 kW IPMSM in Third Generation Hybrid Electric Vehicle. IEEE Trans. Ind. Appl. 2012, 48, 2303–2309. [Google Scholar] [CrossRef]
- Gu, W.; Zhu, X.; Quan, L.; Du, Y. Design and Optimization of Permanent Magnet Brushless Machines for Electric Vehicle Applications. Energies 2015, 8, 13996–14008. [Google Scholar] [CrossRef]
- Jang, H.; Kim, H.; Liu, H.; Lee, H.; Lee, J. Investigation on the Torque Ripple Reduction Method of a Hybrid Electric Vehicle Motor. Energies 2021, 14, 1413. [Google Scholar] [CrossRef]
- Gundogdu, T.; Zhu, Z.Q.; Chan, C.C. Comparative Study of Permanent Magnet, Conventional, and Advanced Induction Machines for Traction Applications. World Electr. Veh. J. 2022, 13, 137. [Google Scholar] [CrossRef]
- Schwarzer, V.; Ghorbani, R. Drive Cycle Generation for design optimization of Electric Vehicles. IEEE Trans. Veh. Technol. 2012, 62, 89–97. [Google Scholar] [CrossRef]
- Fodorean, D.; Idoumghar, L. Improved performances of a PMSM with reduced torque ripples, optimized based on hybrid algorithm, dedicated for light EV. IEEE Trans. Ind. Electron. 2017, 64, 9824–9833. [Google Scholar] [CrossRef]
- Ba, X.; Gong, Z.; Guo, Y.; Zhang, C.; Zhu, J. Development of Equivalent Circuit Models of Permanent Magnet Synchronous Motors Considering Core Loss. Energies 2022, 15, 1995. [Google Scholar] [CrossRef]
- Adamopoulos, N.K.; Karamountzou, F.A.; Sarigiannidis, A.G.; Kladas, A.G. Comparison of field oriented versus model predictive torque control techniques for monitoring interior PM traction motor over wide Speed Range. In Proceedings of the 2017 IEEE 11th International Symposium on Diagnostics for Electrical Machines, Power Electronics and Drives (SDEMPED), Tinos, Greece, 29 August–1 September 2017. [Google Scholar] [CrossRef]
- Kim, S.K.; Kim, J.S.; Lee, Y.I. Model Predictive Control (MPC) based direct torque control (DTC) of Permanent Magnet Synchronous Motors (PMSMs). In Proceedings of the 2013 IEEE International Symposium on Industrial Electronics, Taipei, Taiwan, 28–31 May 2013. [Google Scholar] [CrossRef]
- Farah, N.; Lei, G.; Zhu, J.; Guo, Y. Two-Vector Dimensionless Model Predictive Control of PMSM Drives Based on Fuzzy Decision Making. CES Trans. Electr. Mach. Syst. 2022, 6, 393–403. [Google Scholar] [CrossRef]
- Nishio, Y.; Sanada, M.; Morimoto, S.; Inoue, Y. Loss Evaluation Based on Experiment on Compact and High-Speed IPMSM Using Strong Magnet and Low-Iron-Loss Material. In Proceedings of the 2020 23rd International Conference on Electrical Machines and Systems (ICEMS), Hamamatsu, Japan, 24–27 November 2020; pp. 839–844. [Google Scholar]
- Liu, L.; Guo, Y.; Lei, G.; Zhu, J. Iron Loss Calculation for High-Speed Permanent Magnet Machines Considering Rotating Magnetic Field and Thermal Effects. IEEE Trans. Appl. Supercond. 2021, 31, 5205105. [Google Scholar] [CrossRef]
- Guo, Y.; Liu, L.; Ba, X.; Lu, H.; Lei, G.; Yin, W.; Zhu, J. Designing High-Power-Density Electric Motors for Electric Vehicles with Advanced Magnetic Materials. World Electr. Veh. J. 2023, 14, 114. [Google Scholar] [CrossRef]
- Yamazaki, K.; Fukushima, Y.; Sato, M. Loss Analysis of Permanent-Magnet Motors with Concentrated Windings—Variation of Magnet Eddy-Current Loss due to Stator and Rotor Shapes. IEEE Trans. Ind. Appl. 2009, 45, 1334–1342. [Google Scholar] [CrossRef]
- Karamanakos, P.; Geyer, T.; Kennel, R. On the Choice of Norm in Finite Control Set Model Predictive Control. IEEE Trans. Power Electron. 2017, 33, 7105–7117. [Google Scholar] [CrossRef]
- Li, T.; Sun, X.; Lei, G.; Yang, Z.; Guo, Y.; Zhu, J. Finite-Control-Set Model Predictive Control of Permanent Magnet Synchronous Motor Drive Systems—An Overview. IEEE/CAA J. Autom. Sin. 2022, 9, 2087–2105. [Google Scholar] [CrossRef]
- Tian, K.; Wang, J.; Wu, B.; Cheng, Z.; Zargari, N.R. A virtual space vector modulation technique for the reduction of common-mode voltages in both magnitude and third-order component. IEEE Trans. Power Electron. 2015, 31, 839–848. [Google Scholar] [CrossRef]
- Xie, W.; Wang, X.; Wang, F.; Xu, W.; Kennel, R.; Gerling, D. Dynamic Loss Minimization of Finite Control Set-Model Predictive Torque Control for Electric Drive System. IEEE Trans. Power Electron. 2016, 31, 849–860. [Google Scholar] [CrossRef]
- Eftekhari, S.R.; Davari, S.A.; Naderi, P.; Garcia, C.; Rodriguez, J. Robust Loss Minimization for Predictive Direct Torque and Flux Control of an Induction Motor with Electrical Circuit Model. IEEE Trans. Power Electron. 2020, 35, 5417–5426. [Google Scholar] [CrossRef]
- Zhu, Z.; Ng, K.; Schofield, N.; Howe, D. Analytical Prediction of Rotor Eddy Current Loss in Brushless Machines Equipped with Surface-Mounted Permanent Magnets. II. Accounting for Eddy Current Reaction Field. In Proceedings of the Fifth International Conference on Electrical Machines and Systems (ICEMS), Shenyang, China, 18–20 August 2001. [Google Scholar] [CrossRef]
- Roshen, W. Iron Loss Model for Permanent-Magnet Synchronous Motors. IEEE Trans. Magn. 2007, 43, 3428–3434. [Google Scholar] [CrossRef]
- Okamoto, S.; Denis, N.; Kato, Y.; Ieki, M.; Fujisaki, K. Core loss reduction of an interior permanent-magnet synchronous motor using amorphous stator core. IEEE Trans. Ind. Appl. 2016, 52, 2261–2268. [Google Scholar] [CrossRef]
- Li, L.; Huang, X.; Kao, B.; Yan, B. Research of Core Loss of Permanent Magnet Synchronous Motor (PMSM) in AC servo system. In Proceedings of the 2008 International Conference on Electrical Machines and Systems (ICEMS), Wuhan, China, 17–20 October 2008; pp. 602–607. [Google Scholar]
- Appino, C.; Bottauscio, O.; Barriere, O.; Fiorillo, F.; Manzin, A.; Ragusa, C. Computation of eddy current losses in Soft Magnetic Composites. IEEE Trans. Magn. 2012, 48, 3470–3473. [Google Scholar] [CrossRef]
- Yoshida, Y.; Nakamura, K.; Ichinokura, O. Calculation of Eddy Current Loss in Permanent Magnet Motor Caused by Carrier Harmonics Based on Reluctance Network Analysis. In Proceedings of the 15th European Conference on Power Electronics and Applications (EPE), Lille, France, 2–6 September 2013. [Google Scholar] [CrossRef]
- Consoli, A.; Raciti, A. Analysis of Permanent Magnet Synchronous Motors. IEEE Trans. Ind. Appl. 1991, 27, 350–354. [Google Scholar] [CrossRef]
- Hur, J. Characteristic Analysis of Interior Permanent-Magnet Synchronous Motor in Electrohydraulic Power Steering Systems. IEEE Trans. Ind. Electron. 2008, 55, 2316–2323. [Google Scholar] [CrossRef]
- Lee, B.; Kwon, S.; Sun, T.; Hong, J.; Lee, G.; Hur, J. Modeling of Core Loss Resistance for d-q Equivalent Circuit Analysis of IPMSM Considering Harmonic Linkage Flux. IEEE Trans. Magn. 2011, 47, 1066–1069. [Google Scholar] [CrossRef]
- Guo, Y.; Ba, X.; Liu, L.; Hou, L.; Lei, G.; Zhu, J.G. Performance Enhancement of Permanent Magnet Synchronous Motors Based on Improved Circuit Models. In Proceedings of the 25th International Conference on Electrical Machines and Systems (ICEMS), Chiang Mai, Thailand, 29 November–2 December 2022; pp. 1–6. [Google Scholar]
- Ba, X.; Sun, X.; Gong, Z.; Guo, Y.; Zhang, C.N.; Zhu, J.G. A Generalized Per-Phase Equivalent Circuit Model of the PMSM with Predicted Core Loss. IEEE/ASME Trans. Mechatron. 2023, 28, 1512–1521. [Google Scholar] [CrossRef]
- Cavallaro, C.; Di Tommaso, A.O.; Miceli, R.; Raciti, A.; Galluzzo, G.R.; Trapanese, M. Efficiency Enhancement of Permanent-Magnet Synchronous Motor Drives by Online Loss Minimization Approaches. IEEE Trans. Ind. Electron. 2005, 52, 1153–1160. [Google Scholar] [CrossRef]
- Guo, Y.; Zhu, J.; Lin, Z.; Zhong, J. Measurement and Modeling of Core Losses of Soft Magnetic Composites under 3-D Magnetic Excitations in Rotating Motors. IEEE Trans. Magn. 2005, 41, 3925–3927. [Google Scholar] [CrossRef]
- Guo, Y.; Zhu, J.; Lu, H.; Lin, Z.; Li, Y. Core Loss Calculation for Soft Magnetic Composite Electrical Machines. IEEE Trans. Magn. 2012, 48, 3112–3115. [Google Scholar] [CrossRef]
- Zhang, Y.; Alatawneh, N.; Cheng, M.; Pillay, P. Magnetic Core Losses Measurement Instrumentations and a Dynamic Hysteresis Loss Model. In Proceedings of the 2009 IEEE Electrical Power & Energy Conference (EPEC), Montreal, QC, Canada, 22–23 October 2009. [Google Scholar] [CrossRef]
- Boubaker, N.; Matt, D.; Enrici, P.; Nierlich, F.; Durand, G. Measurements of Iron Loss in PMSM Stator Cores Based on CoFe and SiFe Lamination Sheets and Stemmed from Different Manufacturing Processes. IEEE Trans. Magn. 2018, 55, 8100309. [Google Scholar] [CrossRef]
- Rodríguez Pérez, J.; Estay, P. Predictive Control of Power Converters and Electrical Drives; IEEE: Chichester, UK, 2012; pp. 133–144. [Google Scholar]
- Cheng, L.; Zeng, Z.; Chang-Chien, L.; Tsai, M.; Ling, K.; Wu, I. Model Predictive Direct Torque Control of Permanent Magnet Synchronous Motor for Torque Ripple Reduction. In Proceedings of the 2019 IEEE 4th International Future Energy Electronics Conference (IFEEC), Singapore, 25–28 November 2019. [Google Scholar] [CrossRef]
- Sun, X.; Cao, J.; Lei, G.; Guo, Y.; Zhu, J. A Robust Deadbeat Predictive Controller with Delay Compensation Based on Composite Sliding-Mode Observer for PMSMs. IEEE Trans. Power Electron. 2021, 36, 10742–10752. [Google Scholar] [CrossRef]

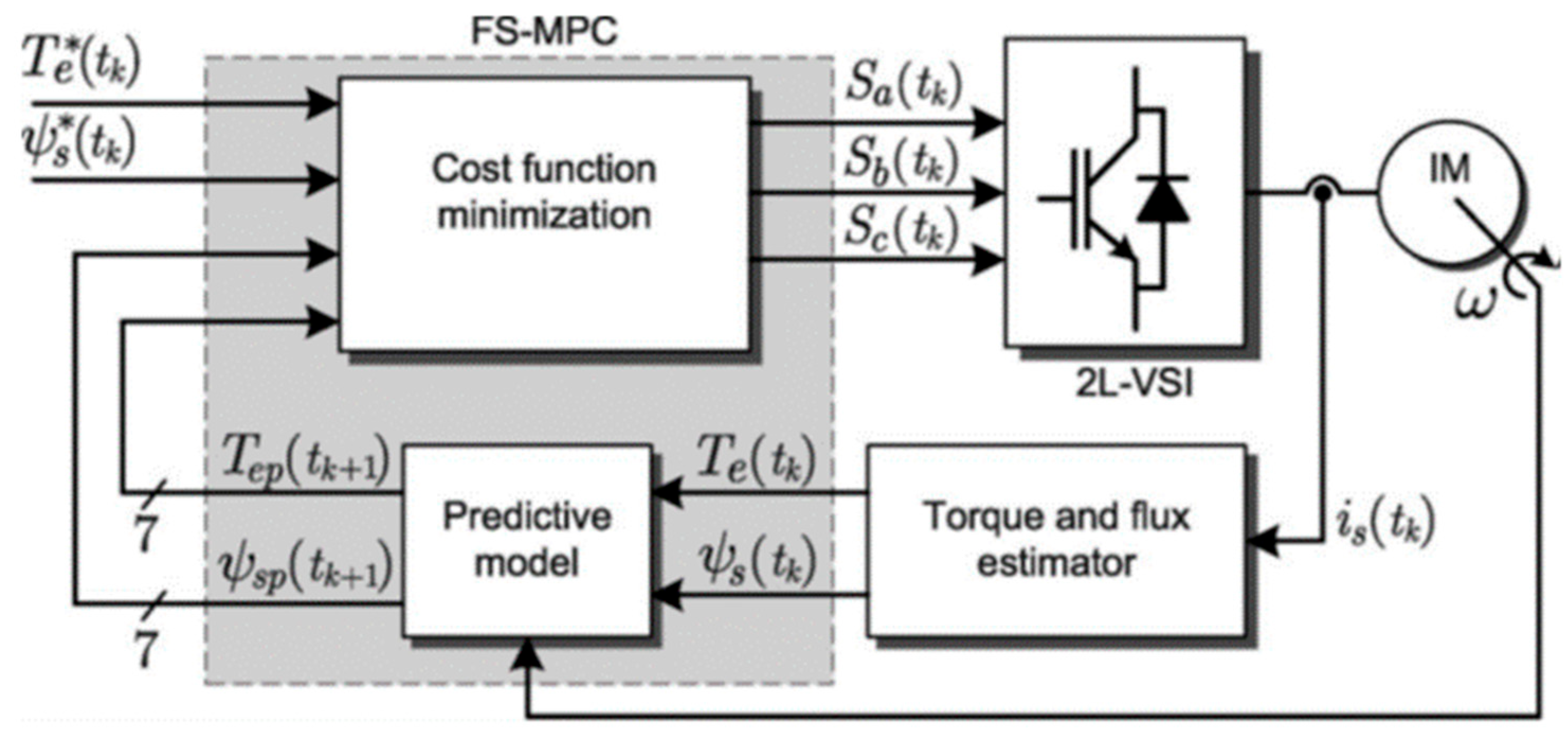


| Voltage Vector V | |||
|---|---|---|---|
| 0 | 0 | 0 | |
| 1 | 0 | 0 | |
| 1 | 1 | 0 | |
| 0 | 1 | 0 | |
| 0 | 1 | 1 | |
| 0 | 0 | 1 | |
| 1 | 0 | 1 | |
| 1 | 1 | 1 |
| Constant Parameters | Value |
|---|---|
| Speed loop proportional gain | 0.5 |
| Speed loop integral gain | 0.5 |
| ) | 1 |
| Strategy | Simulation Strategies |
|---|---|
| 1 | MPDTC with conventional ECM with copper loss LMA |
| 2 | MPDTC with core loss ECM with copper loss LMA |
| 3 | MPDTC with core loss ECM and LMA based on the core loss and copper loss |
| MPDTC with Conventional ECM with Copper Loss LMA | |||||
|---|---|---|---|---|---|
| Ref Speed (rpm) | Torque (Nm) | Shaft Output Power (W) | Copper Loss (W) | DC Power (W) | Efficiency (%) |
| 1000 | 60 | 6027 | 2800 | 12,570 | 47.95 |
| 2000 | 60 | 12,480 | 2842 | 19,600 | 63.67 |
| 3000 | 60 | 18,820 | 2871 | 26,180 | 71.89 |
| 4000 | 60 | 25,120 | 2894 | 32,760 | 76.68 |
| 5000 | 60 | 31,420 | 2915 | 39,060 | 80.44 |
| 1000 | 80 | 8261 | 4349 | 18,560 | 44.51 |
| 2000 | 80 | 16,720 | 4387 | 26,360 | 63.43 |
| 3000 | 80 | 25,120 | 4432 | 34,890 | 72.00 |
| 4000 | 80 | 33,510 | 4434 | 43,180 | 77.61 |
| 5000 | 80 | 38,920 | No measurable value | 48,530 | 80.20 |
| MPDTC with Core Loss ECM and LMA Based on the Core Loss and Copper Loss | Improvement Compared to MPDTC with Conventional ECM (%) | ||||||
|---|---|---|---|---|---|---|---|
| Ref Speed (rpm) | Torque (Nm) | Shaft Output Power (W) | Copper Loss (W) | Core Loss (W) | DC Power (W) | Efficiency (%) | |
| 1000 | 60 | 6033 | 2809 | 154.6 | 11,480 | 52.55 | 9.60 |
| 2000 | 60 | 12,480 | 2833 | 414.6 | 18,830 | 66.28 | 4.09 |
| 3000 | 60 | 18,830 | 2831 | 777.3 | 25,180 | 74.78 | 4.03 |
| 4000 | 60 | 25,140 | 2816 | 1263 | 31,880 | 78.86 | 2.84 |
| 5000 | 60 | 31,450 | 2882 | 1939 | 38,200 | 82.33 | 2.35 |
| 1000 | 80 | 8238 | 4341 | 173.2 | 17,440 | 47.24 | 6.13 |
| 2000 | 80 | 16,710 | 4393 | 473.9 | 26,300 | 63.54 | 0.17 |
| 3000 | 80 | 25,130 | 4376 | 901.8 | 34,250 | 73.37 | 1.91 |
| 4000 | 80 | 33,530 | 4436 | 1485 | 41,800 | 80.22 | 3.36 |
| 5000 | 80 | 38,190 | No steady state measurable | No steady state measurable | 47,320 | 80.71 | 0.63 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hou, L.; Guo, Y.; Ba, X.; Lei, G.; Zhu, J. Efficiency Improvement of Permanent Magnet Synchronous Motors Using Model Predictive Control Considering Core Loss. Energies 2024, 17, 773. https://doi.org/10.3390/en17040773
Hou L, Guo Y, Ba X, Lei G, Zhu J. Efficiency Improvement of Permanent Magnet Synchronous Motors Using Model Predictive Control Considering Core Loss. Energies. 2024; 17(4):773. https://doi.org/10.3390/en17040773
Chicago/Turabian StyleHou, Lian, Youguang Guo, Xin Ba, Gang Lei, and Jianguo Zhu. 2024. "Efficiency Improvement of Permanent Magnet Synchronous Motors Using Model Predictive Control Considering Core Loss" Energies 17, no. 4: 773. https://doi.org/10.3390/en17040773
APA StyleHou, L., Guo, Y., Ba, X., Lei, G., & Zhu, J. (2024). Efficiency Improvement of Permanent Magnet Synchronous Motors Using Model Predictive Control Considering Core Loss. Energies, 17(4), 773. https://doi.org/10.3390/en17040773









