Abstract
Floating offshore wind turbines (FOWTs) may experience six degree of freedom (DoF) movements under the influence of environmental conditions. Different combinations of platform movements with the same amplitude and frequency may have distinct influences on the aerodynamic characteristics of the wind turbine. In this study, a detailed, full-scale CFD model of NREL 5 MW wind turbine is developed to investigate the specific aerodynamic and near wake characteristics under the influence of surge, pitch, and coupled surge–pitch platform motion based on the OpenFOAM tool box. It is clearly noted that different platform movements led to varying relative velocities of the blade, which affected the aerodynamic performance of wind turbines such as thrust, torque, and angle of attack (AOA). On the other hand, when the wind turbine was subjected to combined surge–pitch motion with the same phase, the wake velocity field fluctuated greatly, and the velocity at the center of the wake even exceeded the free flow velocity. Moreover, the platform movement affected the gap between the shed vortices. When the wind turbine moved forward, the gap between the vortices increased, while when the wind turbine moved backward, the gap between the vortices decreased or even converged, resulting in vortex–vortex interaction.
1. Introduction
According to the 2022 Global Wind Energy Report [1], a new installed capacity of nearly 94 GW was added globally in 2021. Despite its significant potential, offshore wind power remains largely untapped as a global renewable energy resource. Globally, the total installed capacity is 837 GW, of which only 35 GW is contributed by offshore wind turbines. The floating offshore wind turbines represent a highly promising form of renewable energy technology with the potential to provide clean and sustainable electricity worldwide, which can reduce dependence on traditional fossil fuels. However, compared with fixed offshore wind turbines, floating offshore wind turbines (FOWTs) are influenced by the motion of the floating platform, leading to variations in aerodynamic loads and power output of the turbines [2,3,4,5]. Moreover, the wind turbines are subjected to vibrations and stress induced by the platform’s motion, which may result in structural fatigue and reduced lifespan of the turbines.
FOWTs are typically affected by the influence of wind, waves, and current, causing the floating platforms to undergo six degrees of freedom (DoFs) motion (surge, sway, heave, roll, pitch, and yaw), affecting the relative velocity of the wind turbine blades and thereby resulting in complex changes in aerodynamic characteristics, including an unsteady state of the rotor, variations in wake, dynamic stall, and wind turbine–wake interaction. Experimental and numerical methods can be used to study the aerodynamic characteristics of wind turbines. For the experimental method, Hand et al. [6] conducted wind tunnel tests using the National Renewable Energy Laboratory (NREL) Phase VI wind turbine to measure aerodynamic parameters such as thrust, power, and pressure coefficients of the wind turbine at various operating conditions. Bartl et al. [7] used laser Doppler anemometry to study the wake characteristics of wind turbines under different yawed inflow conditions. The study revealed that the wake flow is asymmetric with respect to positive and negative yaw angles, and a pair of counter-rotating vortices was observed creating a kidney-shaped velocity deficit in all inflow conditions. Schottler et al. [8] conducted experimental research to compare the wake characteristics of two different model wind turbines by considering the effect of yaw misalignment. They found that the shape and width of the wake varied under different conditions, which had a significant impact on wind turbine layout and control strategies. Wang et al. [9] conducted wind tunnel experiments to investigate the unsteady aerodynamic performance of blunt wind turbine airfoils influenced by boundary layer separation and wake eddies. The results indicated that the aerodynamic performance and boundary layer instability are influenced by various factors, including wake characteristics, vortex shedding, and airfoil trailing edge thickness. Fontanella et al. [10] conducted wind tunnel experiments to study the unsteady aerodynamic response of floating wind turbines under surge motion, and the results showed that experimental data aligned with quasi-steady theory predictions at low frequencies, but may exhibit unsteady effects at higher frequencies.
The numerical simulation methods for floating offshore wind turbines typically include the blade element moment (BEM) method, actuator disk method (ADM), actuator line method (ALM), free vortex method (FVM), and blade-resolved computational fluid dynamic (CFD) method. The BEM is a fundamental theory adopted to analyze wind turbine performance. It is based on the principle of dividing the wind turbine blades into small sections and then analyzing the aerodynamic forces and changes in momentum on each blade section. Using this method, the overall performance of the wind turbine, including power extraction and disturbance to the flow, can be calculated. Dai et al. [11] proposed an effective method for calculating aerodynamic loads on large wind turbine blades based on the BEM theory and found that aerodynamic loads are influenced by multiple factors, but appropriate control methods can reduce load fluctuations. Zhong et al. [12] proposed a new tip loss correction model based on the BEM method, separately correcting the lift coefficient and drag coefficient, thereby improving accuracy and robustness.
The FVM is based on the free vortex theory to describe the complexity of the interaction between flow and blades in wind turbines. In the FVM, the trailing and vortices are modeled by shed straight-line vortex filaments to simulate the interaction between the flow and the turbine blades. It assumes that vortices are structures that conserve energy and continuously transport and release kinetic energy in the flow. By tracking the motion and changes of vortices, performance parameters of wind turbines, such as torque, extracted power, and flow disturbances, can be calculated. Rodriguez and Jaworski [13] established an aeroelastic simulation framework for wind turbines using the FVM method, successfully simulating the performance of floating offshore wind turbines under various wave-induced conditions, revealing significant aeroelastic interactions between blade deformation and the rotor near-wake, particularly under rated and super-rated wave-induced motions. Jeon et al. [14] studied the unsteady aerodynamic characteristics of FOWTs in pitch motion based on FVM, and found that FVM can effectively predict the turbulence wake state (TWS) and vortex ring state (VRS) of a wind turbine. Farrugia et al. [15] investigated the complex wake characteristics under extreme wave conditions based on the FVM and found that the average power and thrust under platform surge motion depend on the motion frequency, amplitude of the platform, and rotor operating conditions.
The ADM and ALM treat the rotating blade region of a wind turbine as a virtual “actuator disk” and “actuator line”, which can generate aerodynamic forces, simulating the effect of actual blades on the flow. Réthoré et al. [16] reassigned the blade loads to body forces in the computational domain based on the ADM and studied the aerodynamic and wake characteristics of wind turbines. Micallef et al. [17] found that the ADM performed well in predicting wake expansion in the outboard regions close to the tip, but had poor predictive capability over the inboard and mid-board regions, and the tip correction had almost no effect on wake expansion prediction. Ravensbergen et al. [18] introduced a multi-fidelity framework (ALM-VMS) for wind turbine flow modeling, which effectively replicated the wake structure of a wind turbine and showed good agreement with experimental data, making it suitable for analyzing an entire wind farm in complex terrain. Arabgolarcheh et al. [19] conducted a study using the ALM method to investigate the vortex trajectories in the wake of wind turbines during surge motion, as well as blade–vortex interactions, and they discovered periodic variations in vortex strength.
With the improvement of computational power and the continuous development of CFD technology, more complex wind turbine simulations can be conducted. Wu et al. [20] developed a simulation model based on the CFD method and investigated the aerodynamic characteristics of rotors under the influence of pitch motion. Tran et al. [21] conducted a study on the unsteady aerodynamic characteristics of FWOT under pitch motion based on CFD and overset grid techniques. Kyle et al. [22] investigated the propeller state and vortex ring state of the wind turbine under surge motion and analyzed the aerodynamics under a different state. Cai et al. [23] studied the changes in the aerodynamic characteristics of the wind turbine in yawed inflow and observed that the interaction between the blades and the tower could not be ignored. In addition, many fully coupled models based on CFD methods are also widely used to analyze FOWTs’ aerodynamics, hydrodynamics, and mooring dynamics. Tran et al. [24] established a fully coupled model to investigate the unsteady aerodynamics, hydrodynamics, and fully coupled aero-hydrodynamics including mooring line loads, and achieved good agreement compared to the simulation results from FAST. Liu et al. [25] developed FOWT mesh motion technology based on OpenFOAM, established a fully coupled model of FOWT simulation, and studied the aerodynamic characteristics and motion response under different wind and wave conditions. Zhou et al. [26] further studied the effects of different inflow conditions on aerodynamic load and platform motion response based on the fully coupled model.
The FOWT may experience six DoF motion with different amplitudes and frequencies under complicated environmental conditions [27,28]. More importantly, due to the different type of wind turbine platform and the mooring system, a combination of different platform movements of the FOWT may be induced, for example, the spar FOWT is more likely to experience the combined in-phase surge–pitch motion, which will enlarge the relative motion of the rotor caused by the platform’s movement [29,30]. Semi-submersible platforms are more likely to experience the combined motion of half a cycle of difference between the surge and pitch motion, which will weaken the relative motion of the rotor [31,32]. Under the influence of complex platform movement, the wind turbine rotor may experience complex changes in aerodynamic characteristics. Guo et al. [33] studied the influence of different platform movements on the aerodynamic characteristics of the wind turbine and found that the relative wind speed of the rotor is the key factor affecting the thrust and output power. Arabgolarcheh et al. investigated the changes in the near-field wake [19] and far-field wake [34] of FOWTs under the influence of different platform movements based on ALM, but they did not consider the coupled case of different movement combinations.
Following the above statement, it is worth investigating the changes in aerodynamic characteristics and wake influenced by complex platform motion based on the blade-resolved CFD method. In this study, a wind turbine simulation model was set up based on the CFD method to study the influences of different platform movements on the wind turbine’s aerodynamic characteristics and analyze the velocity distribution in the near wake and the changes in the vortices in order to analyze the unsteady effects caused by the platform movements.
2. Methodology
In this investigation, the computational fluid dynamics (CFD) simulation was conducted using OpenFOAM-v2012 [35] software. The Reynolds-averaged N-S equations are shown below:
where is the Reynolds stress tensor.
The mean strain rate tensor is given as:
The inclusion of the Reynolds stress term introduces additional variables, resulting in an equation with unknowns. To maintain a closed equation, the Boussinesq eddy-viscosity approximation establishes a relationship between the Reynolds stress and the mean motion field as follows:
where is the turbulence kinetic energy and represents the eddy viscosity.
The SST turbulence model [36] was employed to achieve equation closure, which combined the and models to approximate the eddy viscosity. The SST model was transformed into a model near the wall and a model away from the wall.
3. Model Description
3.1. Description of Wind Turbine Model
The NREL 5 MW baseline offshore wind turbine was utilized in this research to study the load and wake characteristics. Figure 1 demonstrates the properties of the NREL 5 MW baseline wind turbine. Parameters are presented in Table 1.
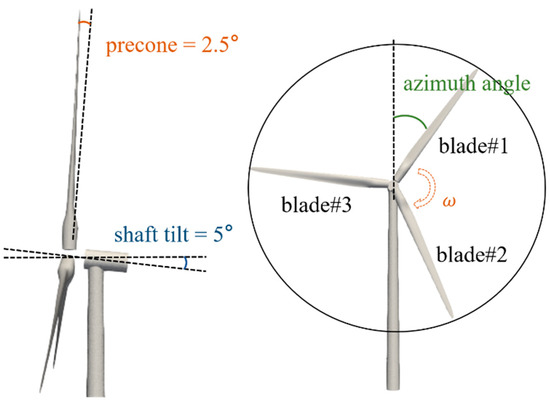
Figure 1.
Schematic diagram of NREL 5 MW wind turbine model.

Table 1.
Properties of NREL 5 MW baseline wind turbine.
3.2. Description of Wind Turbine Motion
The motion of the wind turbine platform is typically expressed through a sine or cosine function when subjected to regular wave loads. The surge and pitch motion of the platform can induce additional relative velocity of the FOWT rotor. The coupling of surge and pitch motion in distinct phases can introduce more complex aerodynamic behaviors of the rotor.
This study focuses on analyzing the aerodynamic characteristics of the wind turbine in a specific motion state. Acknowledging the impracticality of accounting for all the complex motions of the platform, it is crucial to select a platform movement that is authentic and representative. Philippe et al. [37] conducted a study on the 6-DoF response of a 5 MW wind turbine on a floating platform under varying wind and wave conditions. Their findings revealed that the response amplitude operators (RAO) of the wind turbine in surge and pitch could attain values of 5 and 3.5, respectively, at a wave period of 8.1 s. In order to achieve the maximum possible RAO, this study employed the same wave period of 8.1 s as utilized by Philippe et al. [37]. Additionally, the wave distributions for locations around the British Isles [38] were referenced in this study to ensure the authenticity of surge and pitch motion. And the significant wave height (Hsig) of 4 m, from the wave monitoring data of reference [38], was adopted as the basis for calculating the platform response.
Wave amplitude, Awave, is defined as
Surge and pitch motion amplitudes at of 4 m are calculated as 7.07 m and 4.95°, respectively.
3.2.1. Description of Wind Turbine Surge Motion
In this study, platform surge and pitch motion are considered as types of periodic sinusoidal motion. The surge displacement, , is described as
where is the surge amplitude and is the surge frequency.
The surge velocity, , can be calculated by
The relative velocity of rotor can be described as
where is the wind speed.
3.2.2. Description of Wind Turbine Pitch Motion
The pitch displacement, , can be described as
where , are the amplitude and frequency of platform pitch motion, respectively.
The angular velocity of the platform pitch motion can be calculated by
The linear velocity at the rotor’s center can be described as
where is the distance between the rotor center and pitch rotation center.
3.2.3. Description of Wind Turbine Coupled Surge-Pitch Motion
To precisely describe the coupled surge–pitch motion of the wind turbine within a consistent coordinate system, it is imperative to project the velocity associated with the surge motion onto the axial direction of the rotor. Furthermore, it is essential to acknowledge the potential existence of a phase difference between the surge and pitch motions, which can be attributed to variances in platform type or wave load. Building upon the previous descriptions of the surge and pitch motion in Section 3.2.1 and Section 3.2.2, the velocity of rotor movement under the coupled surge–pitch motion can be expressed as follows:
where denotes the phase difference between surge and pitch motion. In order to study the influence of different platform motions on the aerodynamic characteristics of the rotor in detail, a total of five cases are presented in Table 2.

Table 2.
Case design of platform motion.
4. Description and Validation of Modeling Method
4.1. Description of Modeling Method
To account for the rotation of the rotor and the pitch motion of the platform, the arbitrary mesh interface (AMI) sliding mesh technique was implemented in OpenFOAM. In Figure 2, two cylindrical surfaces are defined as AMI sliding surfaces, allowing for rotational movement. Moreover, a method of moving the total grid was adopted to achieve the surge motion of FOWT in this study. The inlet and outlet velocity boundary conditions were “fixedValue” and “inletOutlet”, respectively. The inlet pressure boundary condition was “zeroGradient”, and the outlet pressure boundary condition was “fixedValue”, with a zero value.
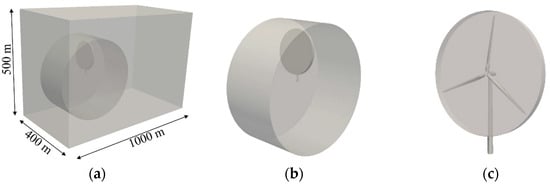
Figure 2.
AMI sliding surfaces of pitch motion and blade rotation: (a) computation domain; (b) pitch motion; (c) rotor rotation.
For the purpose of mesh quality enhancement and computational resource optimization, a poly-hexcore mesh was generated using Fluent meshing in this study. The polyhedral mesh optimizes the mesh quality near the wall, and the hexahedral mesh in the region away from the wall enhances the orthogonality of the mesh, thereby increasing the mesh quality. The computational domain dimensions were defined as 1000 m, 400 m, and 500 m in the x-, y-, and z-directions, respectively, corresponding to the incoming flow direction, horizontal direction, and gravity direction. Grid diagrams for these directions are presented in Figure 3. A total of 3.43 million grids were created in this simulation. Six boundary layers were generated near the blade, and the minimum boundary layer size was 0.004 m. A refined mesh was used behind the rotor to accurately simulate the vortices, with a minimum refinement size of 0.5 m.
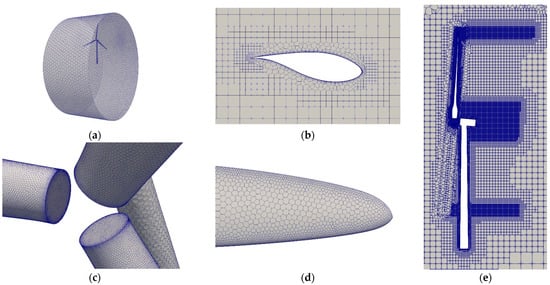
Figure 3.
Mesh for the simulation: (a) mesh of pitch AMI; (b) mesh of boundary layer; (c) mesh of blade root; (d) mesh of blade tip; (e) refinement zone.
4.2. Validation of Modelling Method
In this study, the stability of the simulation was limited by the Courant number, which refers to the relation between the time step and the space step.
where is the control volume velocity at the face cell, is the time step, and is the vector that represents the distance between its cell center and its neighboring center. In this study, the time step was set to 0.001 s to ensure that the Courant number near the blade in the simulation was basically less than 1, and the maximum Courant number was less than 8. The simulation was conducted using a pimple Foam solver and performed using an AMD 7532 CPU with 64 cores, which takes 120 h for a 50 s simulation. In order to ensure the accuracy of our calculations and analysis, a mesh convergence test was conducted to assess the wind turbine’s thrust and power at a wind speed of 11.4 m/s. This test involved three different mesh densities: a coarse grid, the previously described medium grid, and a fine grid. The results of the convergence test are illustrated in Figure 4, displaying the average thrust and power data recorded from 20 to 30 s of simulation time. Relative errors for each mesh density are detailed in Table 3. Analysis revealed a 2.10% relative error in thrust between the coarse and fine meshes, whereas the difference between the medium and fine meshes was only 0.22%. Correspondingly, the power discrepancy between the coarse and fine meshes was 2.34%, while the difference between the medium and fine meshes was a mere 0.12%. Although the fine grid can obtain more accurate simulation results, it required a longer simulation time. These results emphasize that the medium grid attains the desired calculation accuracy while optimizing computational efficiency. Thus, the medium grid was selected for the optimal balance between accuracy and computational resources for subsequent calculations and analysis.
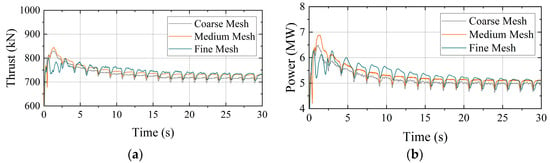
Figure 4.
Mesh convergence analysis of (a) thrust and (b) power.

Table 3.
Analysis of grid convergence of CFD models.
5. Results and Discussion
5.1. Aerodynamic Characteristics of Rotor under Different Platform Movement
The six-DoF motion of the FOWT platform may exert a significant influence on various aerodynamic parameters, particularly impacting rotor thrust and power. Among the various platform motions, it was observed that the surge and pitch motions had the most pronounced effects on aerodynamic characteristics. The alterations in aerodynamic characteristics of the wind turbine, as influenced by different platform motions within a single motion period, are presented in Figure 5. Specifically, Figure 5a,b illustrate the fluctuations in aerodynamic thrust and torque corresponding to distinct platform movements, while Figure 5c–e provide visual representations of variations in AOA, and Figure 5f shows the motion velocity of the rotor center specifically in the rotor’s normal direction. The trends in rotor thrust variations remained notably consistent when influenced by individual surge and pitch motions. When subjected to surge motion, the highest and lowest thrust values were recorded as 1124.71 kN and 264.87 kN, respectively. When subjected to the influence of pitch motion, the maximum and minimum thrust values were found to be 1133.77 kN and 156.29 kN, respectively. In the case of in-phase coupled surge–pitch motion, a reduction in the minimum aerodynamic thrust was observed, accompanied by significant fluctuations in the maximum thrust. These phenomena can be attributed to dynamic stall induced by the excessive rotor motion velocity, resulting in high AOA. During the in-phase coupled motion, the maximum and minimum thrust values were registered at 944.96 kN and −244.87 kN, respectively. Furthermore, when dynamic stall occurred, there was a rapid thrust reduction of approximately 220 kN within a 2/8T interval. As the surge motion lagged, the amplitude of thrust variation exhibited a gradual reduction. Specifically, when the surge motion lagged by T/4, maximum and minimum thrust values of 1205.36 kN and 17.67 kN were observed, respectively. In contrast, when the surge motion exhibited a T/2 phase lag, the maximum and minimum thrust values were recorded as 831.74 kN and 634.27 kN, respectively.
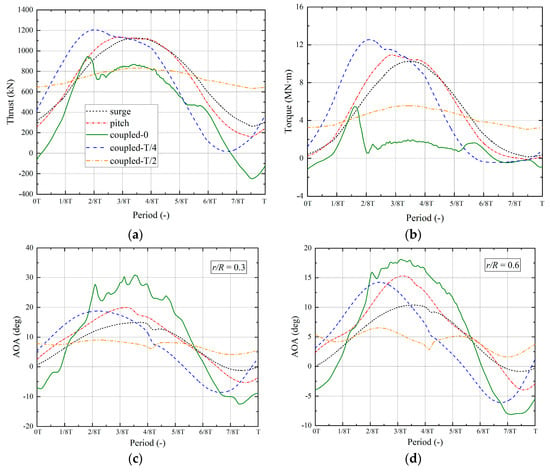
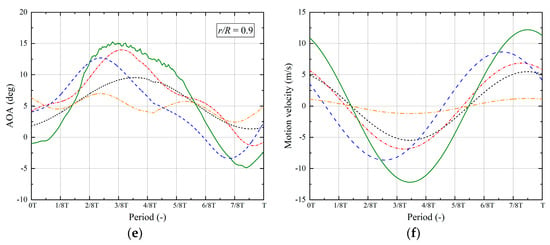
Figure 5.
Aerodynamic characteristics of rotors in different cases: (a) variations in thrust; (b) variations in power; (c) variations in AOA at blade span of 0.3 R; (d) variations in AOA at 0.6 R; (e) variations in AOA at 0.9 R; (f) motion velocity of the rotor center.
Rotor torque exhibited a parallel pattern to that of thrust. When influenced by surge and pitch motions, the maximum and minimum rotor torque values were 10.22 MN·m and 0.16 MN·m and 10.92 MN·m and −0.18 MN·m, respectively. In the context of in-phase coupled surge–pitch motion, the maximum torque was observed at 5.45 MN·m, with the minimum torque at −0.93 MN·m. Notably, dynamic stall prompted a rapid decrease of approximately 4.9 MN·m at around 2/8 T. When the surge motion lagged by T/4, maximum and minimum torque values of 12.53 MN·m and −0.39 MN·m were observed, respectively. In cases where the surge motion lagged by T/2, the maximum and minimum torque values were found to be 5.56 MN·m and 3.08 MN·m, respectively.
AOA variations at different blade cross-sections displayed consistent trends across various operational conditions. It is noteworthy that, with increasing blade radius, the amplitude of AOA variation gradually diminished. At the blade radius of 0.3 r, when subjected to surge motion, the maximum and minimum AOA values were measured at 14.86° and −1.23°, respectively. In the case of pitch motion alone, the maximum and minimum AOA values were observed to be 19.94° and −5.29°, respectively. In the context of in-phase coupled surge–pitch motion, the maximum and minimum AOA values reached 30.85° and −12.46°, respectively. As the surge motion lagged by T/4, the maximum and minimum AOA values were registered as 18.76° and −8.43°, respectively. When surge motion lagged by T/2, the maximum and minimum AOA values were found to be 9.06° and 4.09°, respectively.
It is noteworthy to emphasize that there exist notable disparities in rotor motion velocity concerning distinct platform movements. The highest amplitude of rotor motion velocity was observed when it is in phase-coupled surge–pitch motion, whereas the lowest amplitude occurred when the surge motion exhibited a phase lag of T/2. Notably, even when the surge motion lagged by T/4, the amplitude of rotor motion velocity surpassed that of surge and pitch motions when considered individually. These fluctuations in rotor motion velocity bear considerable consequences for aerodynamic loads and alterations in AOA. The patterns observed in the curves depicted in Figure 5a–e exhibit a striking contrast with the trends evident in the velocity changes illustrated in Figure 5f, underscoring the direct impact of motion velocity on the aerodynamic characteristics of the rotor. As the wind turbine moved upwind, there was a concurrent rise in the relative velocity of the rotor, resulting in an increase in thrust, torque, and AOA. In contrast, these parameters experienced a decline when the wind turbine underwent downwind motion. On the whole, wind turbine aerodynamic parameter variations differ significantly under different platform motion forms. In the cases where the wind turbine experiences in-phase coupled surge–pitch motion, it enlarged the rotor movement velocity, consequently amplifying the amplitude of rotor thrust, torque, and AOA. In contrast, when the surge motion lagged by T/2, the motions induced by platform surge and pitch tended to counterbalance one another, resulting in a reduction in the amplitude of associated aerodynamic parameter fluctuations. Thus, in addition to considering the amplitude and frequency of platform motion, different platform motions also exert a noteworthy influence on aerodynamic characteristics. The superimposition of smaller platform motions can engender substantial aerodynamic variations.
5.2. Velocity Distribution under Different Platform Motion
The near wake field of a wind turbine may manifest diverse characteristics in response to different platform motions. The velocity field within this wake is a pivotal aspect that is indispensable for investigating variations in the wake itself. The presence of complex platform motions can give rise to intricate alterations in the wake field, potentially amplifying turbulence intensity and exerting an influence on wake recovery. Figure 6 illustrates modifications in the velocity field of the rotor wake at the 1 R position, situated behind the rotor, during various moments influenced by different platform motions. “r” represents the distance from the rotor center to the velocity measurement point, “R” denotes the rotor radius, and “U0” signifies the free-stream velocity maintained at 11.4 m/s. Typically, the velocity deficit within the wake field remains around 0.6 at any specific moment, with the wake center exhibiting a minimal velocity deficit. Exclusively influenced by surge motion, the velocity deficit at the center of the wake demonstrates noteworthy variations at the 1/8T moment. The minimum velocity deficit recorded is 0.24, while the maximum velocity deficit reaches 1.14. This observation implies that, during this specific moment, the velocity at the wake center exceeds the free stream velocity. Under the exclusive influence of pitch motion, the minimum velocity deficit at the wake center is 0.43, and the maximum velocity deficit is 0.98. When subjected to in-phase coupled surge–pitch motion, the velocity deficit undergoes substantial variations within the wake center region, featuring slightly elevated deficits on the upper half of the curve compared to other conditions. Notably, as surge motion lags, the fluctuations in velocity deficit across the entire wake region gradually diminish. During the 4/8T–6/8T moments, the wake velocity distribution remains relatively consistent across all conditions; however, at the 7/8T–1T moment, significant disparities in wake velocity distribution emerge among different conditions. As a conclusion, the wind turbine wake sustains a velocity deficit of approximately 0.6 under the influence of relatively minor platform motions. In the wake center region, the velocity deficit is maintained at approximately 0.9–1.0. Nevertheless, as wind turbine platform motions become more intricate, the wake undergoes intricate changes, characterized by pronounced fluctuations in wake center velocity during specific moments. This phenomenon can result in substantial velocity deficits, or even velocities surpassing the free-stream velocity.
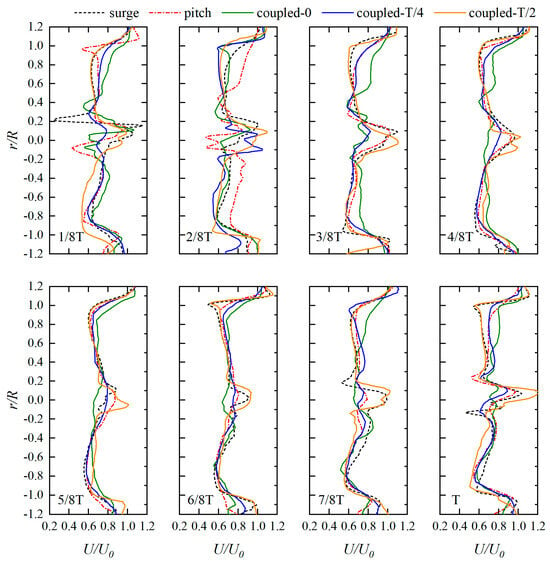
Figure 6.
Wake velocity deficit of different cases.
5.3. Vortex Characteristics behind Rotor
Figure 7 illustrates the unsteady flow field behind the wind turbine rotor and tower during various platform movements. It is noteworthy that there were distinct tip vortices present behind the blade tip, while a multitude of intricate vortices congregated behind the nacelle. The continuity of the tip vortex is easily disrupted due to vortex shedding from the tower, leading to the fragmentation of the tip vortex behind the tower. The vortex within the wind turbine wake appears to be similar under the influence of either surge motion or pitch motion alone. During forward motion of the wind turbine, the separation between blade tip vortices widens, whereas backward motion results in a reduction in this gap, with the possibility of vortices intersecting. Under the influence of pitch motion at 4/8T, the interaction between the two tip vortices became apparent. When the wind turbine underwent in-phase coupled surge–pitch motion, the wake state exhibited pronounced instability, manifesting in the formation of a multitude of intricate vortices at the center of the rotor and behind the tower. During forward motion, a substantial gap existed between the two blade tip vortices, while backward motion led to a heightened interaction between the new blade tip vortex and the preceding one. Additionally, there were vortices with lower strength dispersed in other regions behind the rotor. As the platform’s surge motion lagged, there was a gradual reduction in wake intensity, accompanied by a gradual clarification of the tip vortex structure.

Figure 7.
Visualization of instantaneous unsteady vorticity contours in different cases.
To delve deeper into the impacts of various platform motions on wind turbine wake characteristics, Figure 8 depicts the near wake vortex structure under five distinct simulation conditions. Generally, as the complexity of platform motion increases, the vortex structure becomes more intricate. Specifically, when subjected to either surge motion or pitch motion alone, the blade tip vortex largely retains its initial form. It is worth noting that, as the wind turbine moves forward, the gap between tip vortices widens. Conversely, when the wind turbine moves backward, the gap between tip vortices narrows or even converges, leading to interaction between these vortices. When the wind turbine is subject to in-phase coupled surge–pitch motion, it undergoes dynamic stall during forward motion, leading to the emergence of numerous shedding vortices along the entire blade. Furthermore, a significant accumulation of vortices behind the nacelle is observed, potentially contributing to the pronounced alteration in wake center velocity depicted in Figure 6. As the surge motion lags, the blade tip vortices behind the rotor gradually become more distinct, and the number of vortices behind the nacelle decreases.
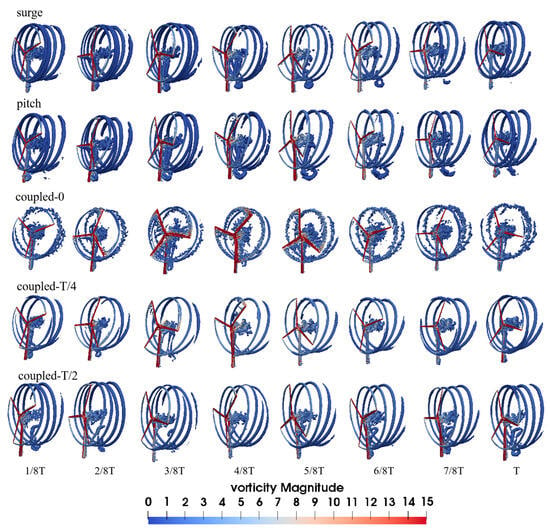
Figure 8.
Vortex variations in difference cases.
6. Conclusions
In this study, a CFD simulation model of the FOWT was established to study the aerodynamic and near wake characteristics under the influence of different platform movements. The following conclusions were obtained:
- (1)
- Different platform movements cause different rotor motion velocities, which affect the aerodynamic characteristics of the wind turbine, such as thrust, torque, and AOA. When the wind turbine is affected by the in-phase surge–pitch motion, the rotor load fluctuation amplitude is the largest, even resulting in negative thrust and torque. The amplitude of the wind turbine load change also decreases with the lag of the surge motion. When the surge motion lags by T/2, the amplitude of wind turbine load change is the smallest due to the counteracting effect between the surge and the pitch motion.
- (2)
- The wake velocity field changes dramatically under the influence of complex platform motion. When the amplitude of the platform motion is small, the velocity of the wake center is larger, and the velocity deficit in other regions is about 0.6. When the platform experiences the same phase-coupled surge–pitch motion, the wake center velocity fluctuates sharply, and the maximum velocity even exceeds the free flow velocity.
- (3)
- When the platform moves forward, the gap between blade tip vortices increases, and it decreases when it moves backward. When the forward motion speed of the wind turbine is high, the blade may experience dynamic stall and a large amount of vorticity shed along the whole blade. When the wind turbine moves backward with a higher velocity, the distance between blade tip vortices decreases and vortices even cross, resulting in interactions between vortexes. Moreover, when the wind turbine is undergoing the same phase-coupled surge–pitch motion, a large number of vortices gather behind the nacelle and gradually decrease with the lag of the surge motion.
Author Contributions
Conceptualization, S.L., Y.C. and H.Z.; Methodology, S.L. and Y.C.; Software, S.L. and Y.C.; Validation, S.L. and Y.C.; Formal analysis, S.L. and Y.C.; Investigation, S.L. and Y.C.; Writing—original draft, S.L. and Y.C.; Writing—review & editing, H.Z. and J.Z.; Supervision, H.Z. and X.L.; Project administration, X.L.; Funding acquisition, X.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research work was financially supported by the National Natural Science Foundation of China, Grant No. is 51939002. Their financial supports are gratefully acknowledged.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- GWEC. Global Wind Report 2022; GWEC: Brussels, Belgium, 2022. [Google Scholar]
- Bossuyt, J.; Scott, R.; Ali, N.; Cal, R.B. Quantification of wake shape modulation and deflection for tilt and yaw misaligned wind turbines. J. Fluid Mech. 2021, 917, A3. [Google Scholar] [CrossRef]
- Fercak, O.; Bossuyt, J.; Ali, N.; Cal, R.B. Decoupling wind-wave-wake interactions in a fixed-bottom offshore wind turbine. Appl. Energy 2022, 309, 118358. [Google Scholar] [CrossRef]
- Kadum, H.; Rockel, S.; Hoelling, M.; Peinke, J.; Cal, R.B. Wind turbine wake intermittency dependence on turbulence intensity and pitch motion. J. Renew. Sustain. Energy 2019, 11, 053302. [Google Scholar] [CrossRef]
- Zhao, H.; Hu, Y.; Bi, C.; Li, X. Numerical study on hydrodynamic behaviors of and flow field around UHMWPE plane nets. Aquac. Eng. 2024, 106, 102397. [Google Scholar] [CrossRef]
- Hand, M.M.; Simms, D.A.; Fingersh, L.J.; Jager, D.W.; Cotrell, J.R.; Schreck, S.; Larwood, S.M. Unsteady Aerodynamics Experiment Phase VI: Wind Tunnel Test Configurations and Available Data Campaigns; Technical Report NREL/TP-500-29955; National Renewable Energy Lab.: Golden, CO, USA, 2001. [Google Scholar]
- Bartl, J.; Mühle, F.; Schottler, J.; Sætran, L.; Peinke, J.; Adaramola, M.; Hölling, M. Wind tunnel experiments on wind turbine wakes in yaw: Effects of inflow turbulence and shear. Wind Energy Sci. 2018, 3, 329–343. [Google Scholar] [CrossRef]
- Schottler, J.; Bartl, J.; Mühle, F.; Sætran, L.; Peinke, J.; Hölling, M. Wind tunnel experiments on wind turbine wakes in yaw: Redefining the wake width. Wind Energy Sci. 2018, 3, 257–273. [Google Scholar] [CrossRef]
- Wang, G.; Zhang, L.; Shen, W.Z. LES simulation and experimental validation of the unsteady aerodynamics of blunt wind turbine airfoils. Energy 2018, 158, 911–923. [Google Scholar] [CrossRef]
- Fontanella, A.; Bayati, I.; Mikkelsen, R.; Belloli, M.; Zasso, A. UNAFLOW: A holistic wind tunnel experiment about the aerodynamic response of floating wind turbines under imposed surge motion. Wind Energy Sci. 2021, 6, 1169–1190. [Google Scholar] [CrossRef]
- Dai, J.C.; Hu, Y.P.; Liu, D.S.; Long, X. Aerodynamic loads calculation and analysis for large scale wind turbine based on combining BEM modified theory with dynamic stall model. Renew. Energy 2011, 36, 1095–1104. [Google Scholar] [CrossRef]
- Zhong, W.; Shen, W.Z.; Wang, T.; Li, Y. A tip loss correction model for wind turbine aerodynamic performance prediction. Renew. Energy 2020, 147, 223–238. [Google Scholar] [CrossRef]
- Rodriguez, S.N.; Jaworski, J.W. Strongly-coupled aeroelastic free-vortex wake framework for floating offshore wind turbine rotors. Part 2: Application. Renew. Energy 2020, 149, 1018–1031. [Google Scholar] [CrossRef]
- Jeon, M.; Lee, S.; Lee, S. Unsteady aerodynamics of offshore floating wind turbines in platform pitching motion using vortex lattice method. Renew. Energy 2014, 65, 207–212. [Google Scholar] [CrossRef]
- Farrugia, R.; Sant, T.; Micallef, D. A study on the aerodynamics of a floating wind turbine rotor. Renew. Energy 2016, 86, 770–784. [Google Scholar] [CrossRef]
- Réthoré, P.; van der Laan, P.; Troldborg, N.; Zahle, F.; Sørensen, N.N. Verification and validation of an actuator disc model. Wind Energy 2014, 17, 919–937. [Google Scholar] [CrossRef]
- Micallef, D.; Ferreira, C.; Herráez, I.; Höning, L.; Yu, W.; Capdevila, H. Assessment of actuator disc models in predicting radial flow and wake expansion. J. Wind Eng. Ind. Aerodyn. 2020, 207, 104396. [Google Scholar] [CrossRef]
- Ravensbergen, M.; Bayram Mohamed, A.; Korobenko, A. The actuator line method for wind turbine modelling applied in a variational multiscale framework. Comput. Fluids 2020, 201, 104465. [Google Scholar] [CrossRef]
- Arabgolarcheh, A.; Jannesarahmadi, S.; Benini, E. Modeling of near wake characteristics in floating offshore wind turbines using an actuator line method. Renew. Energy 2022, 185, 871–887. [Google Scholar] [CrossRef]
- Wu, C.K.; Nguyen, V. Aerodynamic simulations of offshore floating wind turbine in platform-induced pitching motion. Wind Energy 2017, 20, 835–858. [Google Scholar] [CrossRef]
- Tran, T.; Kim, D.; Song, J. Computational Fluid Dynamic Analysis of a Floating Offshore Wind Turbine Experiencing Platform Pitching Motion. Energies 2014, 7, 5011–5026. [Google Scholar] [CrossRef]
- Kyle, R.; Lee, Y.C.; Früh, W. Propeller and vortex ring state for floating offshore wind turbines during surge. Renew. Energy 2020, 155, 645–657. [Google Scholar] [CrossRef]
- Cai, Y.; Zhao, H.; Li, X.; Liu, Y. Effects of yawed inflow and blade-tower interaction on the aerodynamic and wake characteristics of a horizontal-axis wind turbine. Energy 2023, 264, 126246. [Google Scholar] [CrossRef]
- Tran, T.T.; Kim, D. Fully coupled aero-hydrodynamic analysis of a semi-submersible FOWT using a dynamic fluid body interaction approach. Renew. Energy 2016, 92, 244–261. [Google Scholar] [CrossRef]
- Liu, Y.; Xiao, Q.; Ackermann, K.; Peyrard, C.; Wan, D. Establishing a fully coupled CFD analysis tool for floating offshore wind turbines. Renew. Energy 2017, 112, 280–301. [Google Scholar] [CrossRef]
- Zhou, Y.; Xiao, Q.; Liu, Y.; Incecik, A.; Ackermann, K.; Wan, D.; Pan, G.; Li, S. Exploring inflow wind condition on floating offshore wind turbine aerodynamic characterisation and platform motion prediction using blade resolved CFD simulation. Renew. Energy 2022, 182, 1060–1079. [Google Scholar] [CrossRef]
- Cai, Y.; Zhao, H.; Li, X.; Liu, Y. Aerodynamic analysis for different operating states of floating offshore wind turbine induced by pitching movement. Energy 2023, 285, 129538. [Google Scholar] [CrossRef]
- Ren, N.; Li, Y.; Ou, J. Coupled wind-wave time domain analysis of floating offshore wind turbine based on Computational Fluid Dynamics method. J. Renew. Sustain. Energy 2014, 6, 023106. [Google Scholar] [CrossRef]
- Huang, Y.; Wan, D. Investigation of Interference Effects Between Wind Turbine and Spar-Type Floating Platform Under Combined Wind-Wave Excitation. Sustainability 2020, 12, 246. [Google Scholar] [CrossRef]
- Aliyar, S.; Ducrozet, G.; Bouscasse, B.; Bonnefoy, F.; Sriram, V.; Ferrant, P. Numerical coupling strategy using HOS-OpenFOAM-MoorDyn for OC3 Hywind SPAR type platform. Ocean Eng. 2022, 263, 112206. [Google Scholar] [CrossRef]
- Cheng, P.; Huang, Y.; Wan, D. A numerical model for fully coupled aero-hydrodynamic analysis of floating offshore wind turbine. Ocean Eng. 2019, 173, 183–196. [Google Scholar] [CrossRef]
- Tran, T.T.; Kim, D. The coupled dynamic response computation for a semi-submersible platform of floating offshore wind turbine. J. Wind Eng. Ind. Aerodyn. 2015, 147, 104–119. [Google Scholar] [CrossRef]
- Guo, Y.; Wang, X.; Mei, Y.; Ye, Z.; Guo, X. Effect of coupled platform pitch-surge motions on the aerodynamic characters of a horizontal floating offshore wind turbine. Renew. Energy 2022, 196, 278–297. [Google Scholar] [CrossRef]
- Arabgolarcheh, A.; Rouhollahi, A.; Benini, E. Analysis of middle-to-far wake behind floating offshore wind turbines in the presence of multiple platform motions. Renew. Energy 2023, 208, 546–560. [Google Scholar] [CrossRef]
- Jasak, H. Error Analysis and Estimation for the Finite Volume Method with Applications to Fluid Flows. Ph.D. Thesis, Imperial College London, University of London, London, UK, 1996. [Google Scholar]
- Menter, F.R. Review of the shear-stress transport turbulence model experience from an industrial perspective. Int. J. Comput. Fluid D 2009, 23, 305–316. [Google Scholar] [CrossRef]
- Philippe, M.; Babarit, A.; Ferrant, P. Modes of response of an offshore wind turbine with directional wind and waves. Renew. Energy 2013, 49, 151–155. [Google Scholar] [CrossRef]
- Fugro GEOS. Wind and Wave Frequency Distributions for Sites Around the British Isles; OTO Report 01030; HSE Books: Norwich, UK, 2001. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).