A Method to Design an Efficient Airfoil for Small Wind Turbines in Low Wind Speed Conditions Using XFLR5 and CFD Simulations
Abstract
1. Introduction
2. Methodology
- Step 1: Selection of airfoil models.The initial step involved selecting suitable airfoil models that have been proven to perform effectively in low wind speed conditions, typically ranging from 4 m/s to 6 m/s. This selection was based on a thorough review of the existing literature and previous studies that identified the airfoil models capable of stable operation under such conditions. The data on the original airfoil samples were sourced from website [36]. The blade models were selected from the original blade models that operate stably in low wind speed conditions from 4 m/s to 6 m/s.
- Step 2: Modify the airfoil model using XFLR5 software.Once the airfoil model was selected, the next step was to import the original airfoil data into the XFLR5 software. This software is adapt at analyzing the aerodynamic properties of airfoils, particularly at low Reynolds numbers. The process of data importation was followed by reverse engineering to adjust the key geometric parameters. Specifically, the parameters of maximum thickness and the position of maximum thickness were modified. These adjustments aimed to enhance the lift-to-drag ratio (CL/CD), thereby improving the overall aerodynamic efficiency of the airfoil. This step was critical in tailoring the airfoil geometry to better suit the operational requirements of low wind speed conditions.The XFLR5 software was used to analyze the wind turbine blade at a low Re number. The lift coefficient, drag coefficient, and lift/thrust coefficient ratio were evaluated with different angles of attacks at a low Re number.When the number of panels had been determined, XFLR5 calculated the velocity and the AoA values on the surface of each panel, thereby determining the values of vortex strength (), lift force (L), and drag force (D) over the entire surface of the airfoil. The characteristic values, such as the pressure coefficient (Cp), lift coefficient (CL), and drag coefficient (CD), of the airfoil were determined as in Equations (2)–(5):where: c is the chord of the airfoil [m]; ρ is the density of air [kg/m3].The formula for calculating the Reynolds number to the flow velocity at any position in the model is given as follows:
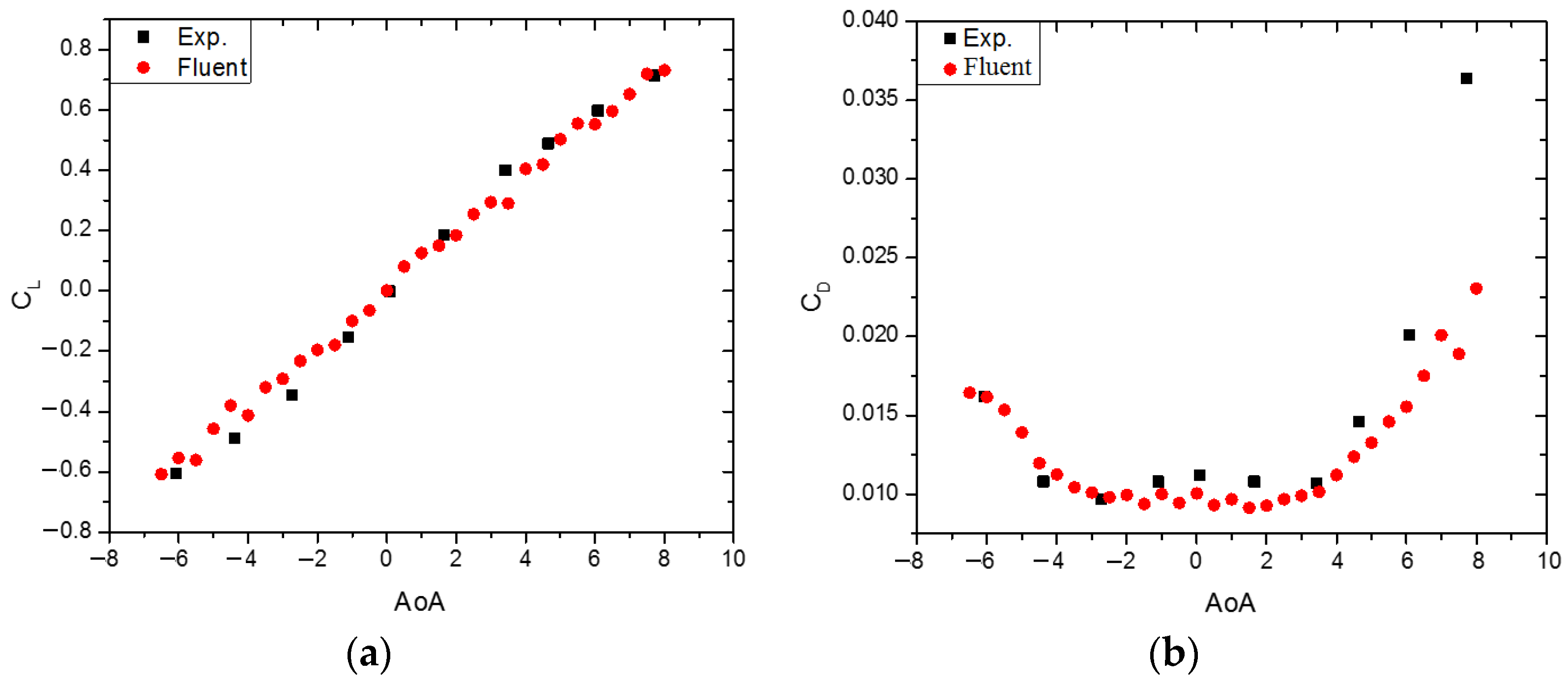
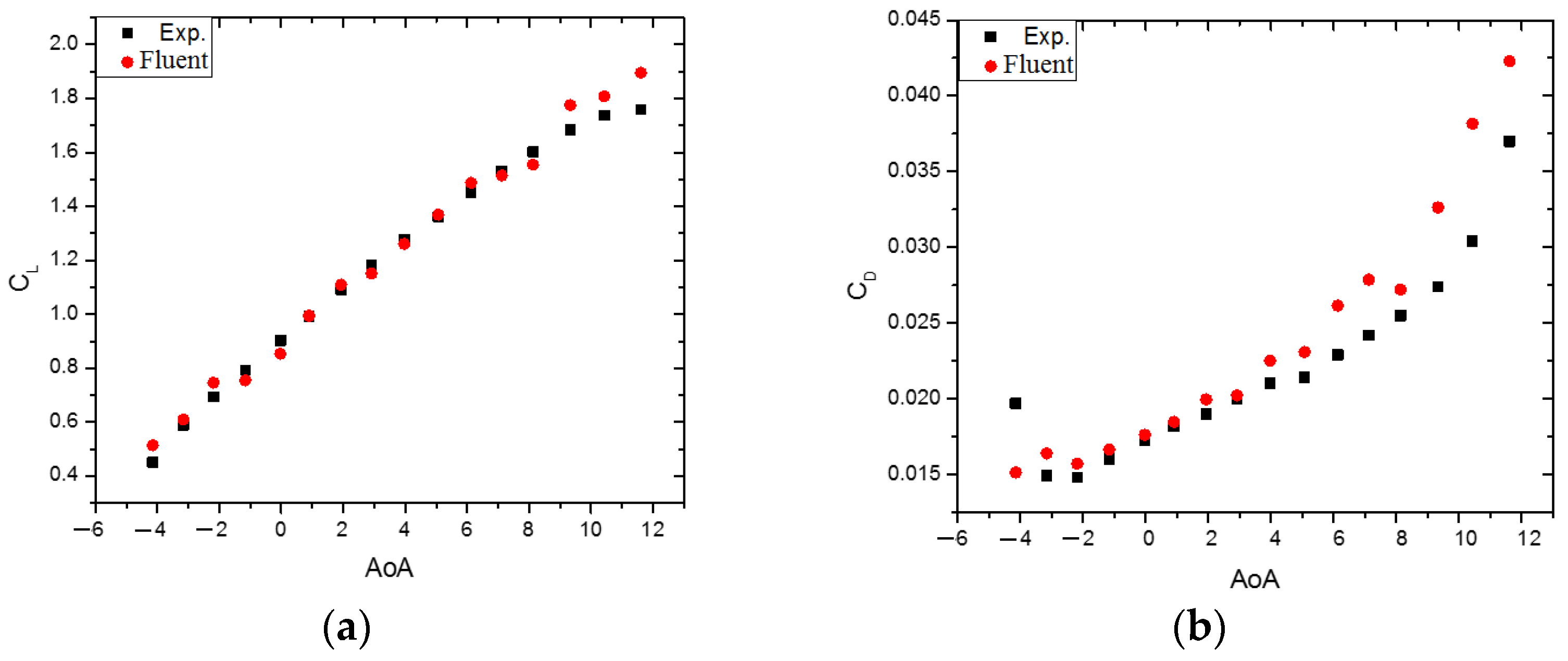
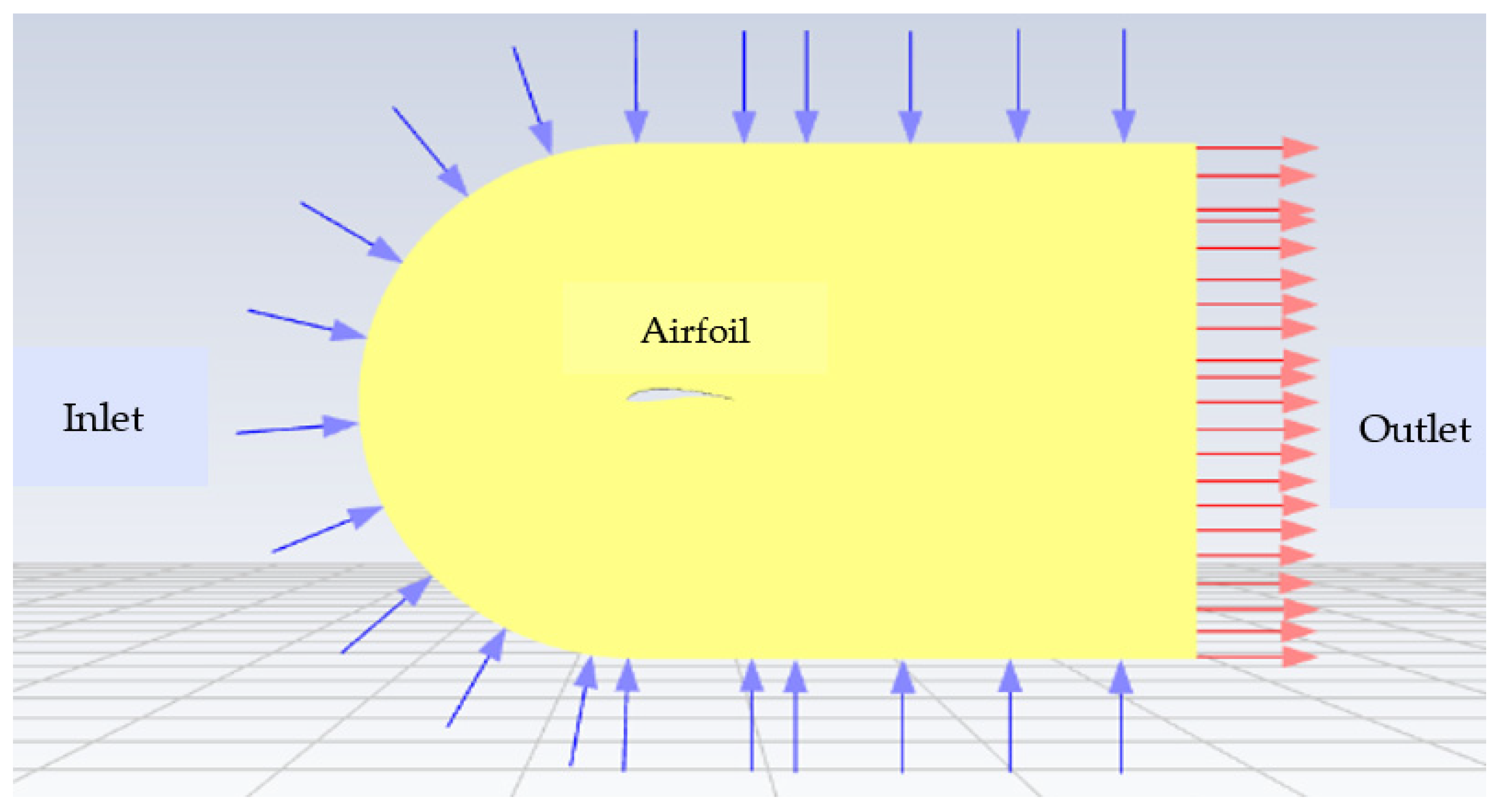
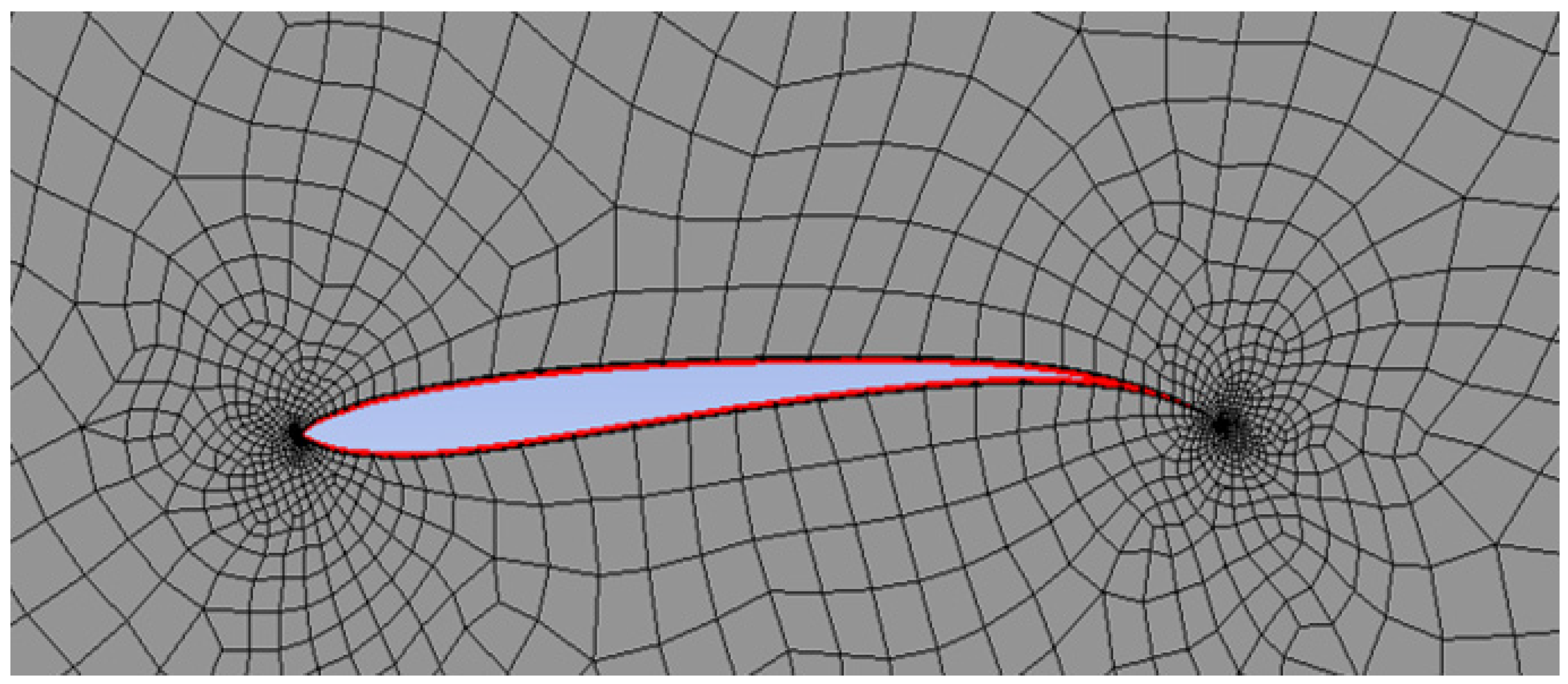
- Step 3: Model selection and evaluation using computational fluid dynamics (CFD).The modified airfoil model was then built and analyzed using a CFD simulation. Initially, the new airfoil models were created by changing the MT and MC (MT is the maximum thickness and MC is the maximum camber of the airfoil) characteristics based on the S1010 model. Then, all the samples were analyzed based on the CFD model. This model helps determine the interaction processes of the incoming flow with each position on the surface of the blade samples. This entire calculation process was based on equations such as the conservation of mass, conservation of energy, and conservation of momentum. This system of equations is commonly known as the Navier–Stokes system of equations. Solving these conservation equations is based on the Reynolds-Averaged Navier–Stokes (RANS) method. The accuracy and convergence of this method depends largely on the selection of the model parameters such as the mesh size, the thickness of the first mesh layer in contact with the airfoil surface, the number of mesh layers, and the size of the space surrounding the airfoil pattern. The RANS equations for the wind velocity variable are defined in Cartesian coordinates as in the following equation system (6):where: is the density of the air, kg/m3; is the dynamic viscosity of the air, Pa.s; and is the Reynolds stresses. Once the wind speed at each point was determined according to the system of Equation (6), the lift forces L and drag forces D of the corresponding airfoil model were also calculated. From there, the values of the lift coefficient CL and drag coefficient CD of the airfoil model were also found based on Formulas (1) and (2). The k-ε turbulence model was employed to simulate the airflow around the airfoil. The turbulence model used in this study was the Realizable k-ε Turbulence Model, as shown in Equation (7):where: andS is the scalar measure of the deformation.The values σk, σε, C1ε, C3ε, C1, and C2 are constants.The simulation results, including the lift coefficient (CL), drag coefficient (CD), and the lift-to-drag ratio (CL/CD), were compared with those of the original airfoil to evaluate the improvements in low wind speed conditions from 4 m/s to 6m/s.
- Step 4: Final model selection.The final step in the methodology was the detailed design of the airfoil, incorporating the dimensions that would optimize its aerodynamic performance. These dimensions were selected based on the simulation results and aimed at maximizing the efficiency of the wind turbine blade. The design specifications were meticulously chosen to ensure that the blade could harness low wind speeds effectively, thereby enhancing the overall performance of the wind turbine.
3. Application and Results
4. Comparison Results and Discussion
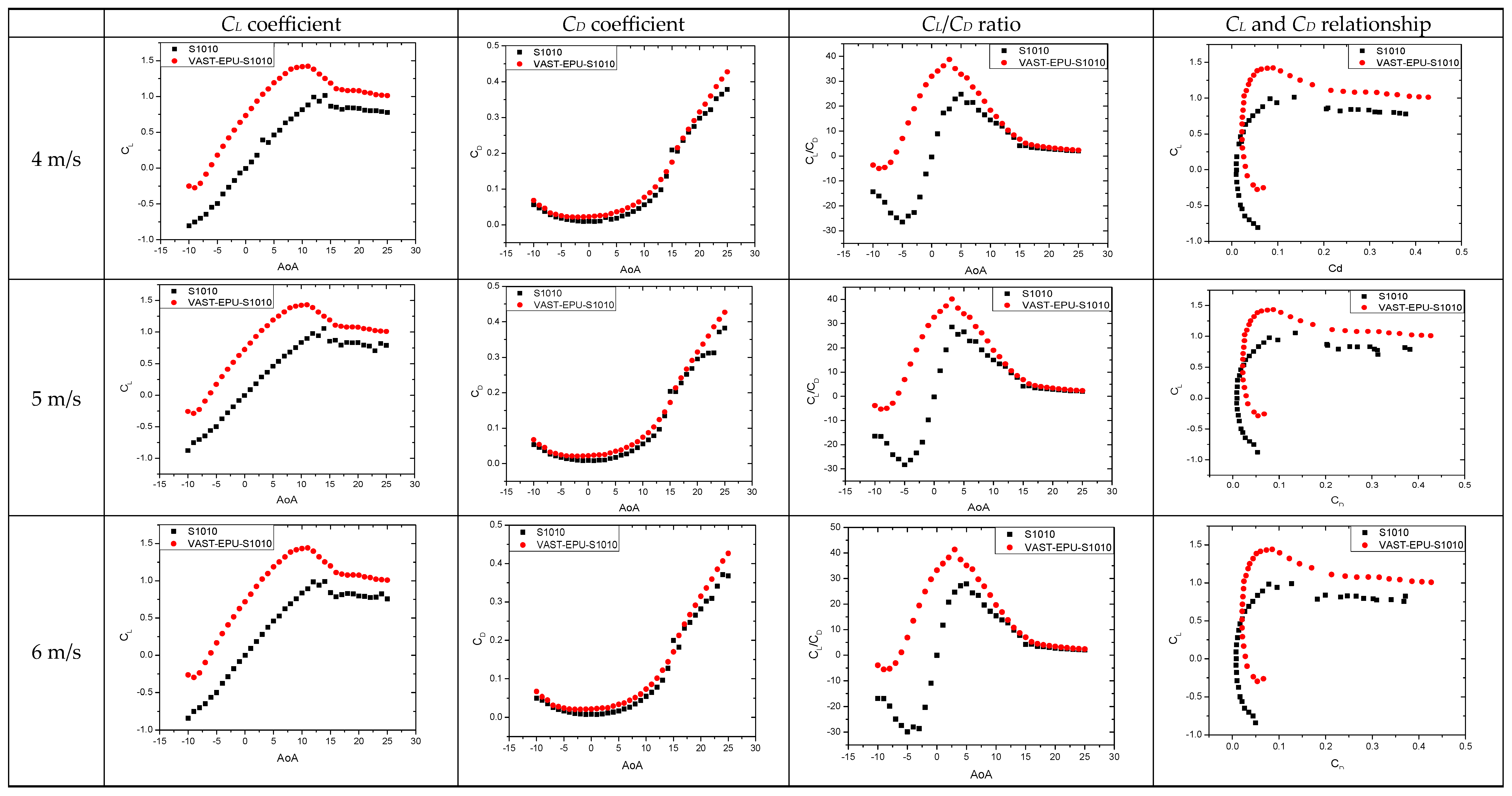
4.1. Airfoil Performance in Low Wind Speed Regions
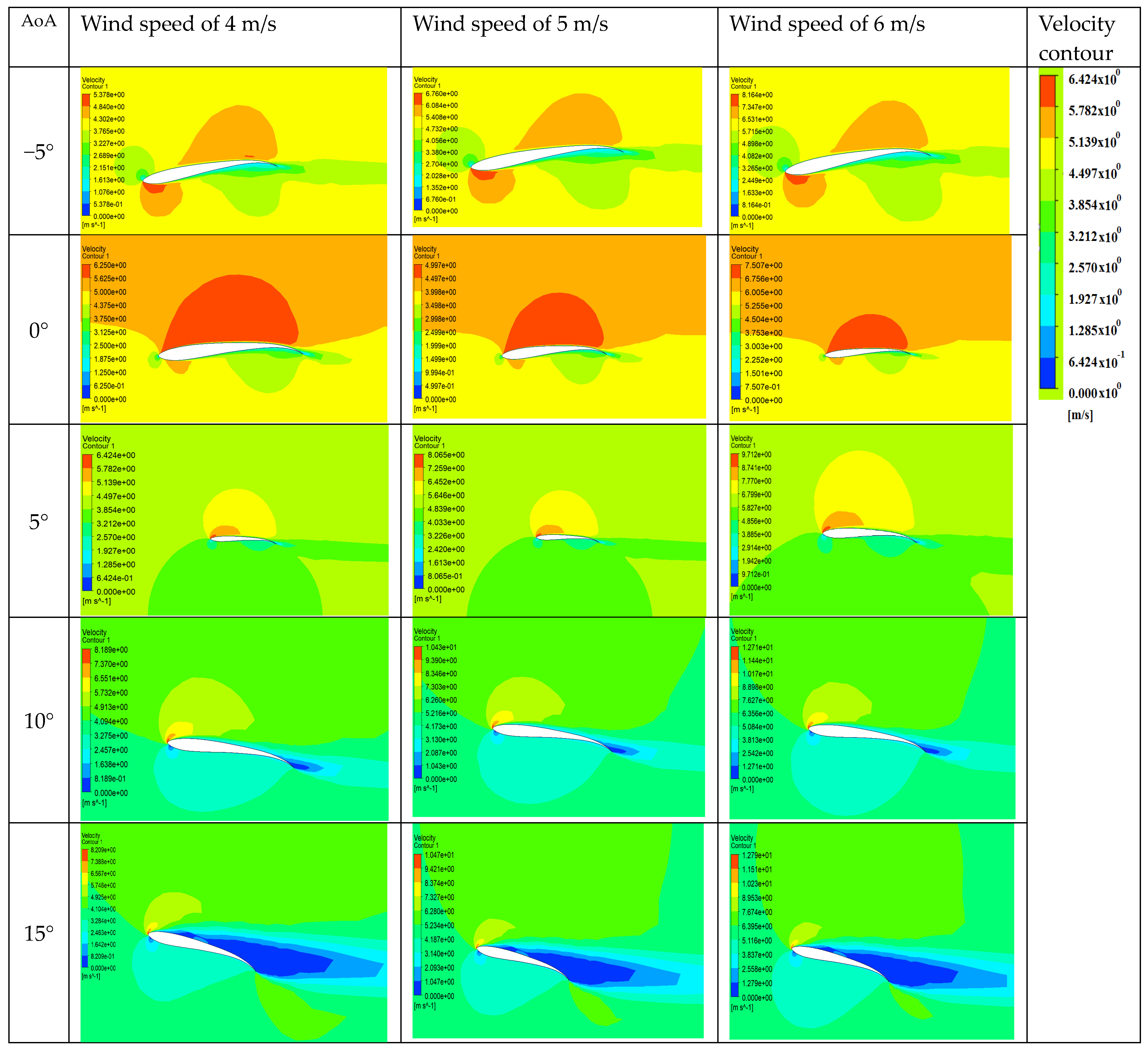
4.2. Effect of Angle of Attack on the Airfoil Performance
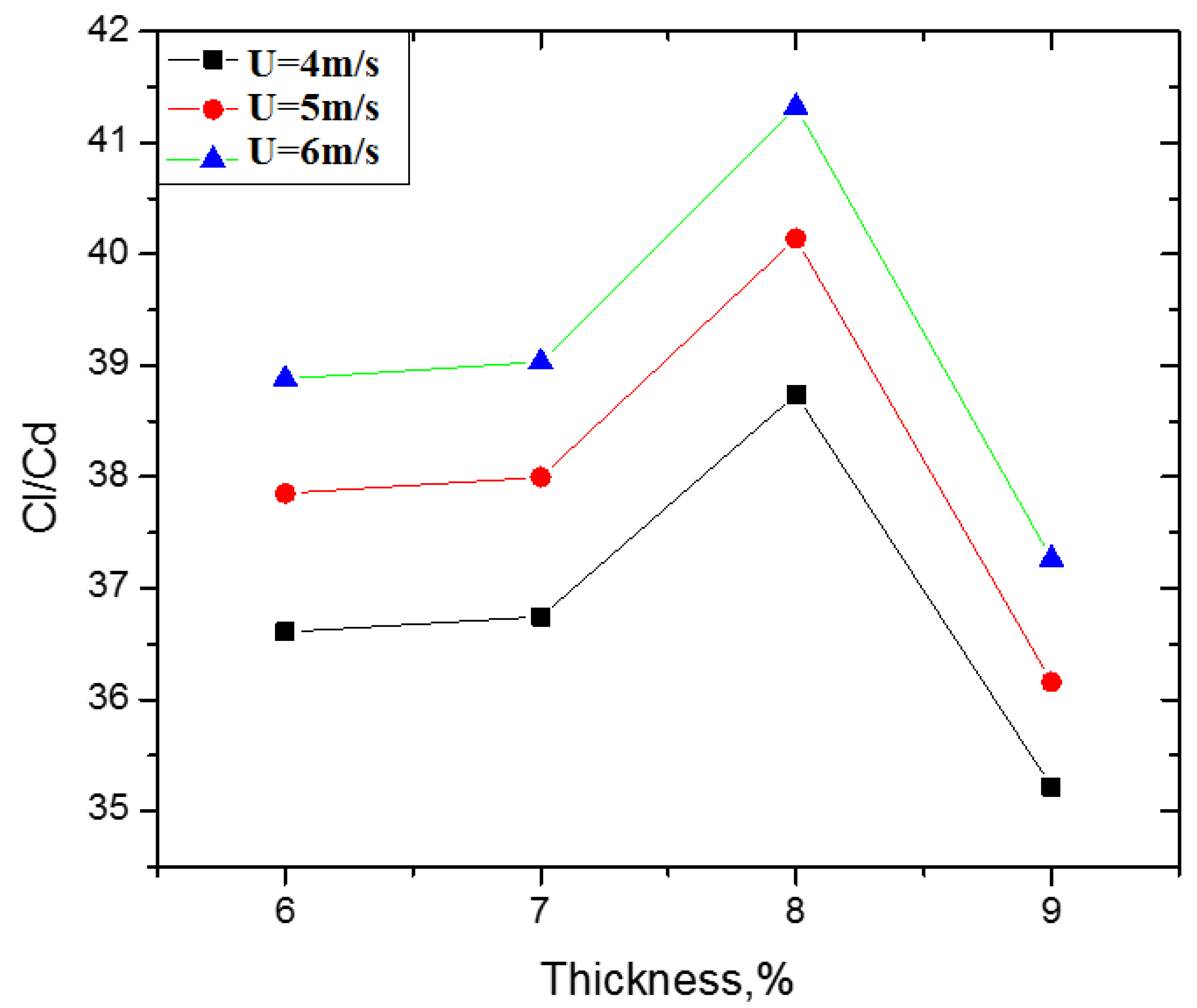
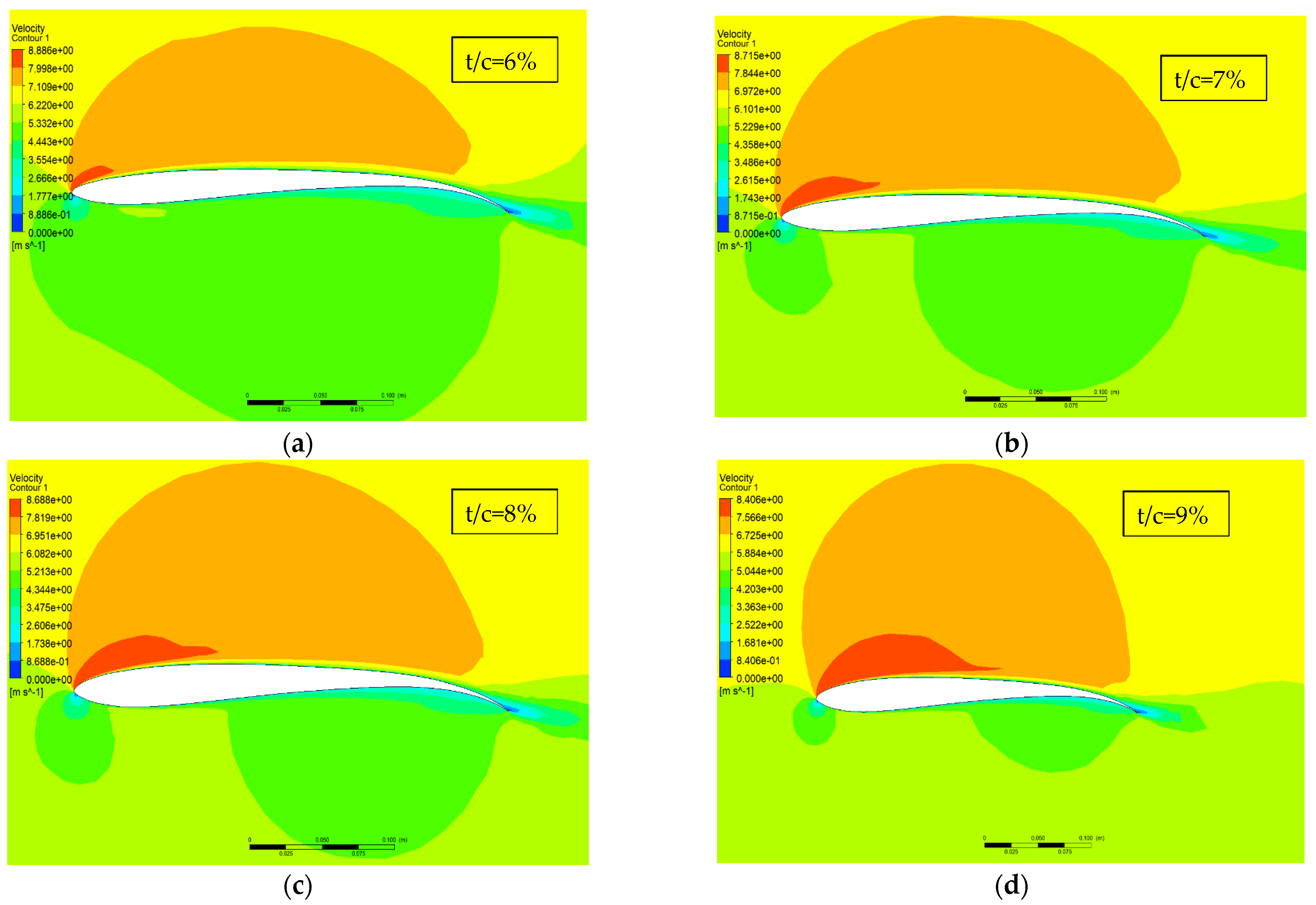
4.3. Effect of Thickness on the Airfoil Performance
5. Conclusions
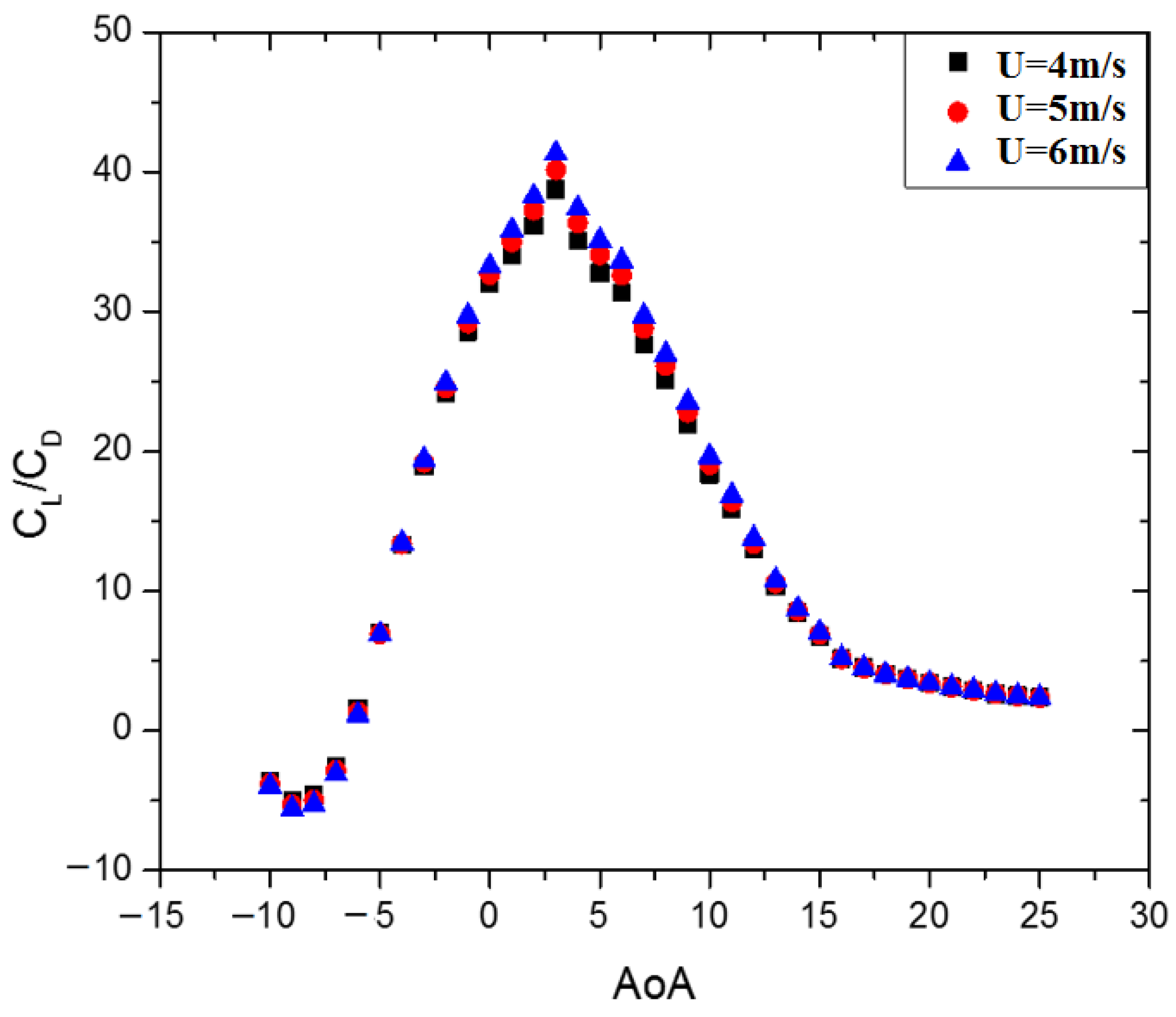
- The new VAST-EPU-S1010 airfoil was redesigned and simulated in low wind speed conditions of 4–6 m/s. The maximum value of the lift/drag ratio of the new airfoil increased from 35.7% to 45.5% compared to the original airfoil model. The maximum value of CL/CD was 41.32 at a wind speed of 6 m/s. Furthermore, the wind speed also affected the CL/CD ratio, with the maximum value of CL/CD at 6 m/s being higher than at 4 m/s by about 6.25%.
- At a low wind speed, the influence of the angle of attack from −5°–15° was also simulated and evaluated. The results show that the airfoil efficiency around the optimal angle of attack of 3° was the highest and that the airfoil efficiency decreased as the angle of attack increased. From an angle of attack of 10° or more, the tail of the airfoil appeared as a separate layer and the velocity vector moved in different directions. The higher the angle of attack, the earlier the separation layer appeared and occupied a larger surface area of the airfoil.
- Thickness also affects the aerodynamic performance of the airfoil. The new VAST-EPU-S1010 airfoil model was optimized at a maximum thickness of 8% and a maximum thickness position of 20.32%.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- GWEC. Global Wind Report 2023; GWEC: Brussels, Belgium, 2023; 120p. [Google Scholar]
- IEC 61400-1; International Standard. Wind Turbines—Part 1: Design Requirements. Version 3. IEC: Geneva, Switzerland, 2005.
- Singh Ronit, K.; Rafiuddin Ahmed, M. Blade design and performance testing of a small wind turbine rotor for low wind speed applications. Renew. Energy 2013, 50, 812–819. [Google Scholar] [CrossRef]
- Clifton-Smith, M.; Wood, D.; Wright, A. Optimising wind turbine design for operation in low wind speed environments. Wind Energy Syst. 2011, 13, 366–387. [Google Scholar]
- Wright, A.K.; Wood, D.H. The starting and low wind speed behavior of a small horizontal axis wind turbine. J. Wind Eng. Ind. Aerodyn. 2004, 92, 1265–1279. [Google Scholar] [CrossRef]
- Cohen, J.; Schweizer, T.; Laxson, A.; Butterfield, S.; Schreck, S.; Fingersh, L.; Veers, P.; Ashwill, T. Technology Improvement Opportunities for Low Wind Speed Turbines and Implications for Cost of Energy Reduction; Technical Report NREL/TP-500-41036; National Renewable Energy Laboratory: Golden, CO, USA, 2008. [Google Scholar]
- Manwell, J.; McGowan, J.; Rogers, A. Wind Energy Explained: Theory, Design, and Application, 2nd ed.; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 2009; ISBN 978-0-470-01500-1. [Google Scholar]
- Xudong, W.; Shen, W.-Z.; Zhu, W.-J.; Sørensen, J.-N.; Jin, C. Shape optimization of wind turbine blades. Wind Energy 2009, 12, 781–803. [Google Scholar] [CrossRef]
- Maalawi, K.Y.; Negm, H.M. Optimal frequency design of wind turbine blades. J. Wind Eng. Ind. Aerodyn. 2002, 90, 961–986. [Google Scholar] [CrossRef]
- National Renewable Energy Laboratory. 2023. OpenFAST Documentation. Available online: https://openfast.readthedocs.io/en/main/ (accessed on 15 August 2023).
- Marten, D. The QBlade Software. 2023. Available online: https://qblade.org/ (accessed on 15 August 2023).
- Liao, C.C.; Zhao, X.L.; Xu, J.Z. Blade layers optimization of wind turbines using FAST and improved PSO. Renew. Energy 2012, 42, 227–233. [Google Scholar] [CrossRef]
- Zhu, J.; Cai, X.; Gu, R. Aerodynamic and structural integrated optimization design of horizontal-axis wind turbine blades. Energies 2016, 9, 66. [Google Scholar] [CrossRef]
- Yarusevych, S.; Sullivan, P.E.; Kawall, J.G. On vortex shedding from an airfoil in low-Reynolds-number flows. J. Fluid Mech. 2009, 632, 245–271. [Google Scholar] [CrossRef]
- Jones, G.; Santer, M.; Debiasi, M.; Papadakis, G. Control of flow separation around an airfoil at low Reynolds numbers using periodic surface morphing. J. Fluids Struct. 2018, 76, 536–557. [Google Scholar] [CrossRef]
- Healy, J. The influence of blade camber on the output of vertical-axis wind turbines. Wind Eng. 1978, 2, 146–155. [Google Scholar]
- Batista, N.; Melício, R.; Marias, J.; Catalão, J. Self-start evaluation in lift-type vertical axis wind turbines: Methodology and computational tool applied to asymmetrical airfoils. In Proceedings of the Power Engineering, Energy and Electrical Drives (POWERENG), 2011 International Conference, Malaga, Spain, 11–13 May 2011; pp. 1–6. [Google Scholar]
- Alam, M.; Iqbal, M. A low cut-in speed marine current turbine. J. Ocean Technol. 2010, 5, 49–61. [Google Scholar]
- Sogukpinar, H. The effects of NACA 0012 airfoil modification on aerodynamic performance improvement and obtaining high lift coefficient and post-stallairfoil. AIP Conf. Proc. 2018, 1935, 020001. [Google Scholar]
- Saxena, E.S.; Kumar, M.R. Design of NACA 2412 and its Analysis at Different Angle of Attacks, Reynolds Numbers, and a wind tunnel test. Int. J. Eng. Res. Gen. Sci. 2015, 3, 193–200. [Google Scholar]
- Lissaman, P.B.S. Low-Reynolds-number airfoils. Annu. Rev. Fluid Mech. 1983, 15, 223–239. [Google Scholar] [CrossRef]
- Clausen, P.D.; Wood, D.H. Research and development issues for small wind turbines. Renew. Energy 1999, 16, 922–927. [Google Scholar] [CrossRef]
- Giguere, P.; Selig, M.S. Low reynolds number airfoils for small horizontal axis wind turbines. Wind Eng. 1997, 21, 379. [Google Scholar]
- Tangler, J.L.; Somers, D.M. NREL Airfoil Families for HAWTs; National Renewable Energy Lab.: Golden, CO, USA, 1995. [Google Scholar]
- Timmer, W.A.; Van Rooij, R. Summary of the Delft University wind turbine dedicated airfoils. J. Sol. Energy Eng. 2003, 125, 488–496. [Google Scholar] [CrossRef]
- Fuglsang, P.; Bak, C.; Gaunaa, M.; Antoniou, I. Design and verification of the Risø-B1 airfoil family for wind turbines. J. Sol. Energy Eng. 2004, 126, 1002–1010. [Google Scholar] [CrossRef]
- Miley, S.J. A Catalog of Low Reynolds Number Airfoil Data for Wind Turbine Applications; Department of Aerospace Engineering Texas A&M University: College Station, TX, USA, 1982. [Google Scholar]
- Elizondo, J.; Martinez, J.; Probst, O. Experimental study of a small wind turbine for low- and medium-wind regimes. Int. J. Energy Res. 2009, 33, 309–326. [Google Scholar] [CrossRef]
- Giguere, P.; Selig, M.S. New airfoils for small horizontal axis wind turbines. ASME J. Sol. Energy Eng. 1998, 120, 108–114. [Google Scholar] [CrossRef]
- Anderson, J.D. Fundamentals of Aerodynamics, 3rd ed.; McGraw Hill: New York, NY, USA, 2001. [Google Scholar]
- McGranahan, B.D.; Selig, M.S. Aerodynamic Tests of Six Airfoils for Use on Small Wind Turbines; University of Illinois at Urbana-Champaign: Urbana, IL, USA, 2004. [Google Scholar]
- Henriques, J.C.C.; Silva, M.; Estanqueiro, A.I.; Gato, L.M.C. Design of a new urban wind turbine airfoil using a pressure-load inverse method. Renew. Energy 2009, 34, 2728–2734. [Google Scholar] [CrossRef]
- Ozgener, O.; Ozgener, L. Exergy and reliability analysis of wind turbine systems: A case study. Renew. Sustain. Energy Rev. 2007, 11, 1811–1826. [Google Scholar] [CrossRef]
- Venkatesan, S.P.; Kumar, V.P.; Kumar, M.S.; Kumar, S. Computational analysis of aerodynamic characteristics of dimple airfoil NACA 2412 at various angles of attack. Idea 2018, 46, 10. [Google Scholar]
- Dal Monte, A.; De Betta, S.; Castelli, M.R. Proposal for a coupled aerodynamic–structural wind turbine blade optimization. Compos. Struct. 2017, 159, 144–156. [Google Scholar] [CrossRef]
- Pourrajabian, A.; Ebrahimi, R.; Mirzaei, M. Applying micro scales of horizontal axis wind turbines for operation in low wind speed regions. J. Energy Convers. Manag. 2014, 87, 119–127. [Google Scholar] [CrossRef]
- Available online: http://airfoiltools.com/airfoil/details?airfoil=s1010-il (accessed on 15 August 2023).
- Grasso, F. ECN Airfoils for Large Offshore Wind Turbines Design and Wind Tunnel Testing. Wind Energy 2017, 2016, 2015. [Google Scholar]
- Li, X.; Yang, K.; Bai, J.; Xu, J. A method to evaluate the overall performance of the CAS-W1 airfoils for wind turbines. J. Renew. Sustain. Energy 2013, 5, 063118. [Google Scholar] [CrossRef]
- Selig, M.S.; Guglielmo, J.J.; Broeren, A.P.; Giguere, P. Summary of Low-Speed Airfoil Data; SoarTech Publications: Ann Arbor, MI, USA, 1995; Volume 1. [Google Scholar]
- Thin, D.V.; Duc, N.H.; Sang, L.Q. Aerodynamic Analysis of NACA64A010 Airfoil Using XFLR5 and ANSYS Fluent. GMSARN Int. J. 2024, 18, 258–266. [Google Scholar]
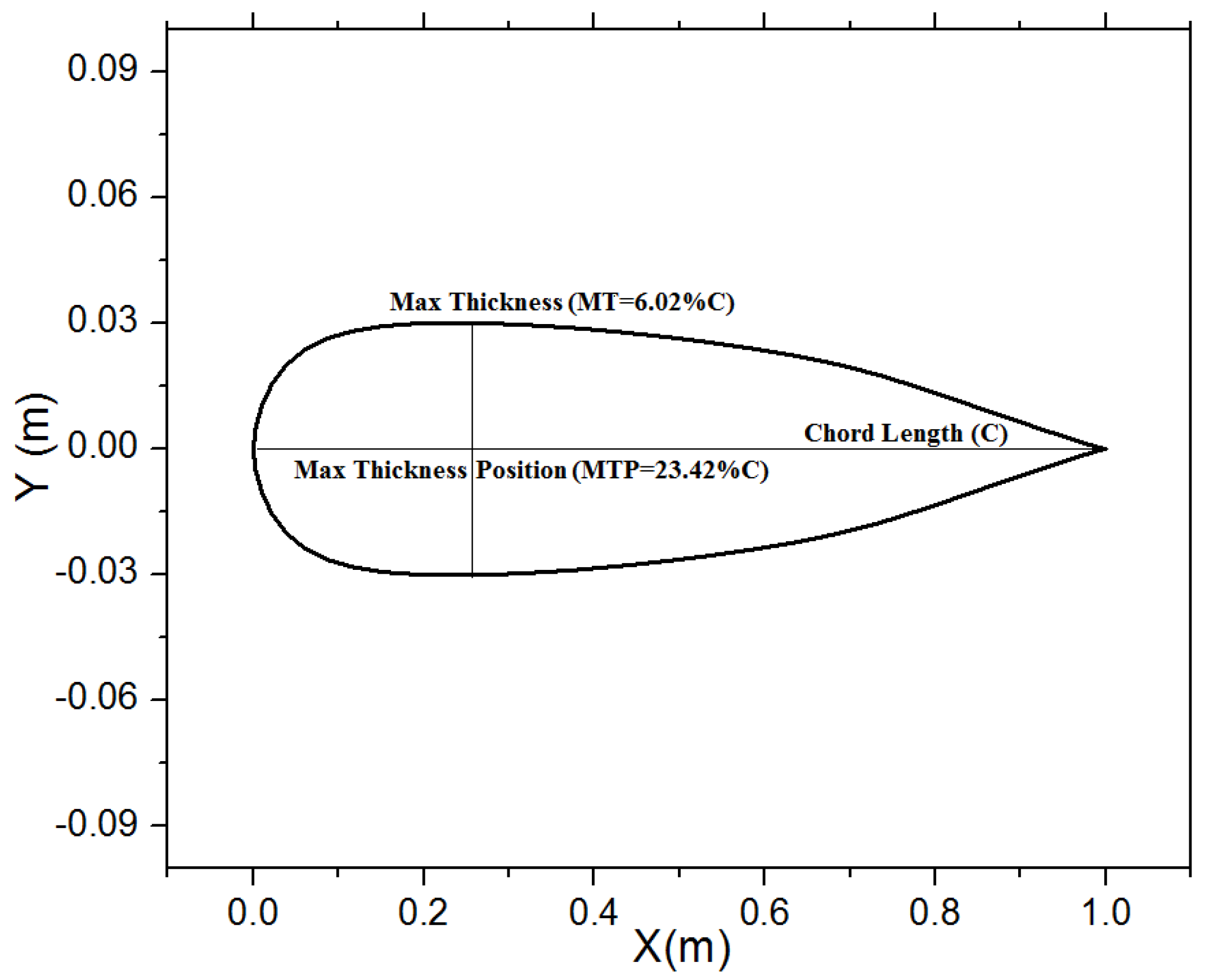


| S1010 | VAST-EPU-S1010 | |
|---|---|---|
| Thickness | 6.02% | 8.00% |
| Max. Thick. Pos. | 23.42% | 19.32% |
| Max. Camber | 0.00% | 6.4% |
| Max. Cam. Pos. | 0.00% | 59.56% |
| Thickness % | CL/CD Ratio 4 m/s | CL/CD Ratio 5 m/s | CL/CD Ratio 6 m/s |
|---|---|---|---|
| 6 | 36.608 | 37.852 | 38.882 |
| 7 | 36.746 | 37.998 | 39.035 |
| 8 | 38.739 | 40.141 | 41.323 |
| 9 | 35.219 | 36.159 | 37.266 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sang, L.Q.; Phengpom, T.; Thin, D.V.; Duc, N.H.; Hang, L.T.T.; Huyen, C.T.T.; Huong, N.T.T.; Tran, Q.T. A Method to Design an Efficient Airfoil for Small Wind Turbines in Low Wind Speed Conditions Using XFLR5 and CFD Simulations. Energies 2024, 17, 4113. https://doi.org/10.3390/en17164113
Sang LQ, Phengpom T, Thin DV, Duc NH, Hang LTT, Huyen CTT, Huong NTT, Tran QT. A Method to Design an Efficient Airfoil for Small Wind Turbines in Low Wind Speed Conditions Using XFLR5 and CFD Simulations. Energies. 2024; 17(16):4113. https://doi.org/10.3390/en17164113
Chicago/Turabian StyleSang, Le Quang, Tinnapob Phengpom, Dinh Van Thin, Nguyen Huu Duc, Le Thi Thuy Hang, Cu Thi Thanh Huyen, Nguyen Thi Thu Huong, and Quynh T. Tran. 2024. "A Method to Design an Efficient Airfoil for Small Wind Turbines in Low Wind Speed Conditions Using XFLR5 and CFD Simulations" Energies 17, no. 16: 4113. https://doi.org/10.3390/en17164113
APA StyleSang, L. Q., Phengpom, T., Thin, D. V., Duc, N. H., Hang, L. T. T., Huyen, C. T. T., Huong, N. T. T., & Tran, Q. T. (2024). A Method to Design an Efficient Airfoil for Small Wind Turbines in Low Wind Speed Conditions Using XFLR5 and CFD Simulations. Energies, 17(16), 4113. https://doi.org/10.3390/en17164113








