Dual-Stage Optimization Scheduling Model for a Grid-Connected Renewable Energy System with Hybrid Energy Storage

Abstract

To operate the grid-connected renewable energy system economically, this study presents a dual-stage optimization scheduling model for grid-connected systems with hybrid energy storage, including day-ahead and intra-days stages. In the day-ahead stage, an economically optimal scheduling model is developed, considering the price peak-to-valley difference. This model aims to enhance the economic efficiency of the system by utilizing hybrid energy storage. In the intra-day stage, more accurate renewable energy forecasts with a shorter time scale are considered. The objectives are to minimize the curtailment rate of renewable energy and to track the day-ahead scheduling outcomes. The NSGA-II algorithm is employed for multi-objective optimization, achieving equilibrium solutions considering multiple optimization objectives. Compared to other published works, the proposed model achieves a balance between different optimization objectives, enabling the system to operate economically and stably. It provides a comprehensive approach to optimize the scheduling of grid-connected systems with hybrid energy storage by considering both economic and operational aspects. Overall, this proposed dual-stage optimization model presents a viable approach to improve economic efficiency and mitigate renewable energy curtailment in grid-connected systems. By effectively integrating renewable energy sources and optimizing their utilization, this model contributes to enhancing the sustainability and optimal operation of the power grid.

1. Introduction

With the gradual depletion of fossil fuels and increasing calls for environmental protection, the substitution of renewable energy for fossil fuels as the source of the power grid has emerged as a solution to address energy and environmental issues [1]. However, due to the volatility and low inertia of renewable energy sources, their integration into the grid can lead to the source–load mismatch, necessitating the involvement of energy storage to achieve source–load balance and maintain the stability of the power grid [2].

Energy storage can be classified into power-based storage and energy-based storage, based on their characteristics [3]. Generally speaking, batteries are considered as power-type energy storage due to their high power density and short storage duration. On the other hand, energy-type storage methods, like hydrogen storage, have longer storage durations but cannot accommodate rapid power fluctuations. Hydrogen storage, as a form of energy-based storage, has gained increasing attention due to the rise of the hydrogen industry and hydrogen-powered vehicles as a means to balance the volatility of renewable energy [4].

The utilization of electrolyzers for electrochemical hydrogen generation represents an environmentally sustainable approach [5]. Electrolyzers encompass various types, including alkaline electrolyzers, proton exchange membrane electrolyzers, and solid oxide electrolyzers. Among these, alkaline electrolyzers have gained widespread application due to their well-established technology and cost-effectiveness [6]. In recent years, the integration of alkaline electrolyzers with lithium batteries for co-generation and energy storage has garnered considerable research interest. This stems from the complementary nature of hydrogen storage, offering high energy density, and lithium batteries, providing high power density [7]. Furthermore, the rapid reaction rates exhibited by lithium batteries can compensate for the slower response times of electrolyzers, enhancing overall system performance. Researchers have explored power allocation for hybrid energy storage systems (HESSs) from the perspectives of frequency decomposition, cost-effectiveness, and equipment characteristics to achieve optimal objectives. An optimal day-ahead optimization schedule for a gas-electric integrated energy system considering the bidirectional energy flow is proposed in [8]. Furthermore, Hong et al. [9] presented an optimization day-ahead scheduling model of wind-hydrogen systems considering hydrogen production efficiency.

Indeed, the studies mentioned above focus on day-ahead optimization. In day-ahead optimization, the time scale for source–load forecasting is typically one day, which often leads to lower prediction accuracy. This limitation can impact the effectiveness of implementing day-ahead optimization results. Due to the inherent variability and uncertainties associated with renewable energy sources and load patterns, accurately forecasting the source–load dynamics over a one-day horizon can be challenging. Factors such as weather conditions, demand fluctuations, and unforeseen events can introduce deviations between the predicted and actual source–load profiles. The lower prediction accuracy in day-ahead optimization can affect the realization of the intended outcomes, as the system may encounter unexpected variations in renewable energy availability or demand patterns [10]. Therefore, the dual-stage optimization model should be applied to the operation of renewable energy systems.

To date, several studies have addressed the dual-stage scheduling of day-ahead and intra-day operations. For example, Wang et al. [11] proposed a two-stage energy management model for the sustainable wind–PV–hydrogen–storage microgrid based on receding horizon optimization. Similarly, Yuan et al. [12] presented a two-time-scale microgrid energy management model for scheduling with low operational costs and high reliability against uncertainties. In [13], the authors proposed a novel multi-energy systems optimization model to maximize investment and operating synergy in the electricity, heating, and transport sectors.

However, these studies predominantly employed single-objective optimization approaches. In single-objective optimization, pursuing a specific target may lead to adverse effects on other objectives. In practice, the intra-day operational process involves numerous factors that require optimization, including wind and solar curtailment rates, grid power tracking, operational costs, and other relevant variables. In optimizing renewable energy power systems, reducing the curtailment rate of wind and solar energy may increase the demand for energy storage, thus raising operational costs [6]. Treating these factors as components of a multi-objective optimization problem is a more appropriate approach. By incorporating multiple objectives, the optimization framework can better capture the complex trade-offs and interdependencies among different operational aspects, leading to more comprehensive and effective decision-making strategies [14].

Multiple multi-objective optimization algorithms, such as the non-dominated sorting genetic algorithm (NSGA-II), moth–flame optimization (MFO), and multi-objective particle swarm optimization (MOPSO), have been proposed in recent years, providing effective tools for solving complex multi-objective problems and offering a range of optimal solutions based on different preferences [15,16]. The MOPSO is employed to optimize the operation of microgrids in [17]. The MFO algorithm is utilized for wind farm layout optimization in [18]. Anosri et al. [19] compared different classes of multi-objective optimization algorithms in the context of reliability design optimization. Among the multi-objective optimization algorithms, one representative is the non-dominated sorting genetic algorithm II (NSGA-II). NSGA-II, an advanced algorithm capable of handling multi-objective optimization, has been utilized by researchers for economic optimization in power systems-related studies. Rejeb et al. [20] applied NSGA-II to estimate the optimal results of the proposed multi-generation system. In [21], a suggested system producing electricity and hydrogen was planned in a daily triple-periodic framework and solved by NSGA-II. With NSGA-II, Maheri et al. [22] designed reproduction operators for robust exploration and exploitation at both size and configuration levels. Since NSGA-2 has a wide range of applications, it is used in this paper to solve the multi-objective problem in the intra-day stage.

This paper aims to apply HESS for the power balance and economic efficiency of renewable energy systems. The main contributions of this work include the following:

• We propose a dual-stage optimization scheduling model for grid-connected systems with HESS to balance renewable energy, with day-ahead and intra-day stages.
• In the day-ahead stage, we propose a scheduling model that utilizes the price peak-to-valley difference and HESS to enhance the system’s efficiency. In the intra-day stage, we introduce a multi-objective model, and NSGA-II is applied as a solution algorithm to achieve the optimization of multiple objectives simultaneously.
• Case studies show that for a real renewable energy system with HESS, the proposed scheduling model reduces its daily costs by around 6% compared with the rule-based operation. Model comparisons are conducted to compare the proposed model and other existing models.

The remainder of this paper is organized as follows. In Section 2, the system modeling and equipment characteristics are described. Section 3 presents the source–load forecasting method. The dual-stage optimization scheduling model is proposed in Section 4. Case studies are presented in Section 5. Finally, Section 6 concludes the paper.

2. System Modeling

2.1. System Description

Figure 1 depicts the structure of a renewable energy system augmented with HESS. In this system, renewable energy sources include wind and solar energy. The majority of the load is supplied by the output of renewable energy sources, which consists of both electrical load and hydrogen load. The energy balance of the system is maintained by a HESS composed of batteries and electrolyzers. The HESS plays a crucial role in two aspects:

• Participating in the day-ahead optimal system scheduling, utilizing the price difference in the electricity grid to achieve economic optimization.
• Balancing the source–load imbalance that may occur during the day-ahead scheduling.

Unlike the transient power characteristics of the source load, the state and actions of energy storage devices, such as battery charging and discharging, and power adjustment of electrolyzers, are time-dependent. Therefore, a comprehensive understanding and optimal utilization of the HESS is essential [23].

This approach assists in resolving the intra-day supply-demand mismatch caused by the prediction errors in source–load forecasting, as the energy exchange between the system and the grid needs to align with the results of the day-ahead scheduling.

2.2. Wind Turbine

The output power of a wind turbine can be expressed as (1) [24].

$$p_{wind}\left(v_w\right)=\left\{\begin{array}{c}0,0\le v_w<v_{in}\hfill \\ \frac{v_w-v_{in}}{v_{rated}-v_{in}}\times p_{wind}^{rated},v_{in}\le v_w<v_{rated}\hfill \\ p_{wind}^{rated},v_{rated}\le v_w<v_{out}\hfill \\ 0,v_w\ge v_{out}\hfill \end{array}\right.$$

(1)

where $v_{in}$ and $v_{out}$ are the cut-in and cut-out wind velocities, respectively. $v_{rated}$ and $p_{wind}^{rated}$ represent the rated wind velocity and power.

2.3. Photovoltaic

The output power of a photovoltaic power generation device is related to the solar irradiation intensity and the ambient temperature, which can be calculated as (2) [25]:

$$p_{pv}(G_{pv},T_e)=p_{pv}^{rated}{f}_{pv}\frac{G_{pv}}{G_{STC}}(1-{\alpha }_p(T_e-T_{ref}))$$

(2)

where $p_{pv}^{rated}$ represents the rated power output (kW) of the PV under standard test condition (STC), $G_{STC}$ and $T_{ref}$ are the STC irradiation and temperature, $G_{pv}$ represents the real-time solar irradiation intensity, $f_{pv}$ is the discount factor of the power output, ${\alpha }_p$ is the temperature coefficient, and $T_e$ denotes the real-time panel temperature.

$$T_e\left(G_{pv}\right)=T_a+G_{pv}·\frac{T_{c,NOCT}-T_{a,NOCT}}{G_{NOCT}}$$

(3)

The panel temperature $T_e$ can be determined by (3), where $T_a$ is the actual ambient temperature, $T_{c,NOCT}$ and $T_{a,NOCT}$ are the nominal operating cell temperature (NOCT) of the PV panels and the NOCT of the ambient temperature, and $G_{NOCT}$ is the NOCT of irradiation intensity [25].

2.4. Hybrid Energy Storage System

In a hybrid energy storage system, the storage state of the battery is determined by the previous moment’s storage state and the actions taken at the current moment. This paper takes into account the energy dissipation in the battery and expresses its storage state according to (4).

$$SoC\left(t\right)=SoC(t-\delta t)·(1-{\gamma }_b)+({\eta }_{b-ch}·p_{b-ch}\left(t\right)-\frac{p_{b-dis}\left(t\right)}{{\eta }_{b-dis}})·\delta t/Q_b^{Rated}$$

(4)

where $SoC\left(t\right)$ is the state of charge at time t, ${\gamma }_b$ is the dissipation rate of the battery, $p_{b-ch}\left(t\right)$ and $p_{b-dis}\left(t\right)$ are the charge and discharge power of the battery at time t, and $Q_{Rated}^b$ is the rated storage capacity of the battery, which is one of the variables to be optimized.

Compared to the direct energy storage process of batteries, hydrogen storage systems involve the conversion of electrical energy into hydrogen energy through electrolyzers before storage. This process is slower and less efficient than battery charging and discharging. However, hydrogen storage systems have lower unit energy storage construction costs than batteries and offer excellent environmental benefits. Additionally, they can meet users’ hydrogen energy demands, like fuel cell vehicles or industrial processes [2]. Equations (5) and (6) illustrate the chemical process of electrolysis, converting electricity to hydrogen.

$H_2$ evolution reaction in the negative pole:

$$H_2+2O{H}^{-}-2H_{2}O=2e^{-}$$

(5)

$O_2$ evolution reaction in the positive pole:

$$2O{H}^{-}-\frac{1}{2}{O}_2-H_{2}O=2e^{-}$$

(6)

Equation (7) explains the mathematical model for the electrolyzer [6].

$$m_{elz-out}=\frac{{\eta }_{elz}{p}_{elz}}{LH{V}_{H_2}}$$

(7)

where $m_{elz-out}$ represents the hydrogen generated from the electrolyzer, $p_{elz}$ represents the electricity consumed by the electrolyzer, and $LH{V}_{H_2}$ denotes the low heating value of hydrogen gas.

The hydrogen gas produced by the electrolyzer is compressed by a compressor to the appropriate pressure and then input into the hydrogen storage tank. The storage state of the hydrogen tank is also dependent on the previous moment’s state and the production/output at the current moment, as indicated by (8) [24].

$$LoH\left(t\right)=LoH(t-\delta t)·(1-{\gamma }_h)+({\eta }_{h-in}{m}_{elz-out}\left(t\right)-\frac{m_{h-out}\left(t\right)}{{\eta }_{h-out}})·\delta t/Q_h^{Rated}$$

(8)

where $LoH\left(t\right)$ is the state of hydrogen of a storage tank at time t, ${\gamma }_h$ is the hydrogen dissipation rate of the tank, $m_{h-out}\left(t\right)$ is the hydrogen output rate of the tank, $\delta t$ is the time step of optimization, and $Q_h^{Rated}$ is the rated storage capacity of the tank.

3. Source–Load Forecasting Method

The electrical load and renewable energy generation, such as wind and solar power, often exhibit complex temporal characteristics, and a single network structure may not achieve satisfactory predictive performance. This paper proposes the use of a convolutional neural network-long short-term memory (CNN-LSTM) network for source–load forecasting. The CNN network is commonly used to process raw data, automatically extracting internal features and reducing algorithm complexity. The LSTM network, with its memory units, is effective in handling long-term sequential data [26].

In the CNN-LSTM network, historical source–load data and meteorological data are used as inputs. The CNN layer extracts features, followed by pooling operations to reduce dimensionality. The fully connected layer then transforms the features into a one-dimensional structure, extracting the feature vector. The LSTM layer learns the internal patterns of load variations from the extracted features to achieve the forecasting function. Finally, the output layer provides the prediction results, corresponding to the predicted source–load sequence [27].

The proposed forecasting method starts with a four-layer one-dimensional convolutional network for feature extraction from the input source–load sequence. The convolutional network uses larger kernel sizes to extract coarse-grained temporal features initially and gradually reduces the kernel size to extract fine-grained temporal features. The number of channels is increased as the network deepens. The kernel sizes for the 4 convolutional layers are 24, 12, 8, and 2, and the corresponding channel numbers are 132, 232, 332, and 432. Batch normalization is applied after each convolutional layer to stabilize data distribution and accelerate convergence. Additionally, a dropout layer with a dropout rate of 0.25 is added after each convolutional layer to prevent overfitting.

The data extracted by the convolutional layers are then fed into the LSTM network for model training. The LSTM network consists of 2 LSTM layers, with each layer having 256 neurons. After training, the model’s predictions are obtained by passing the results through a fully connected layer.

In this paper, the input for day-ahead source–load forecasting consists of the source–load data and weather data from the previous week, as well as the weather forecast for the target day. The output is the hourly source–load data for the target day.

For intra-day forecasting, the input includes the source–load data and weather data for the next 48 h, along with the weather forecast for the next hour. The output is the minute-level source–load data for the next hour.

4. Dual-Stage Optimization Scheduling Model

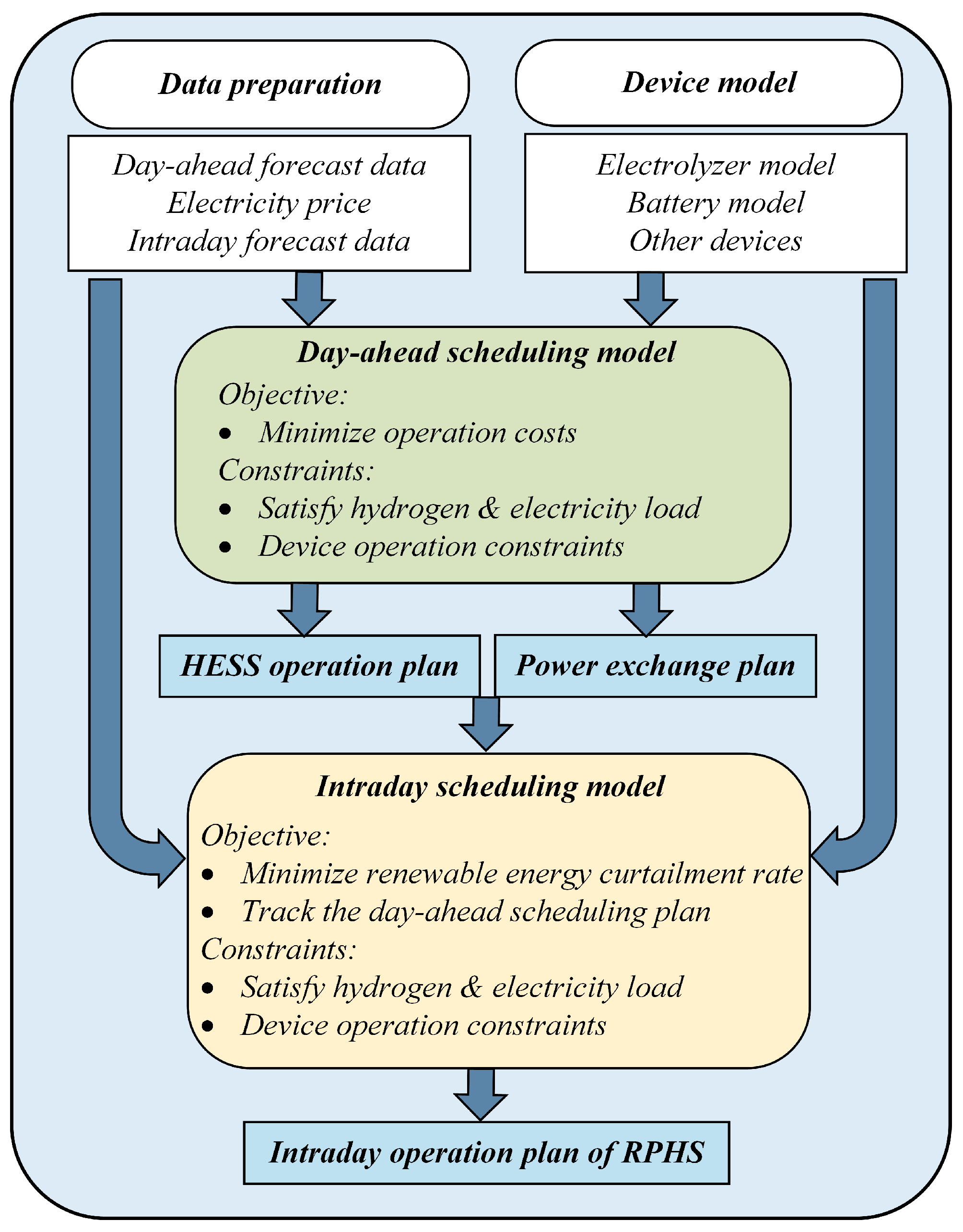
The flowchart of the proposed dual-stage optimization scheduling model is presented in Figure 2. The white blocks denote the preparation of the model, including data acquisition, forecasting, and device modeling. The green blocks illustrate the day-ahead scheduling model, while the yellow blocks are the intraday scheduling model. Blue blocks denote the scheduling results. 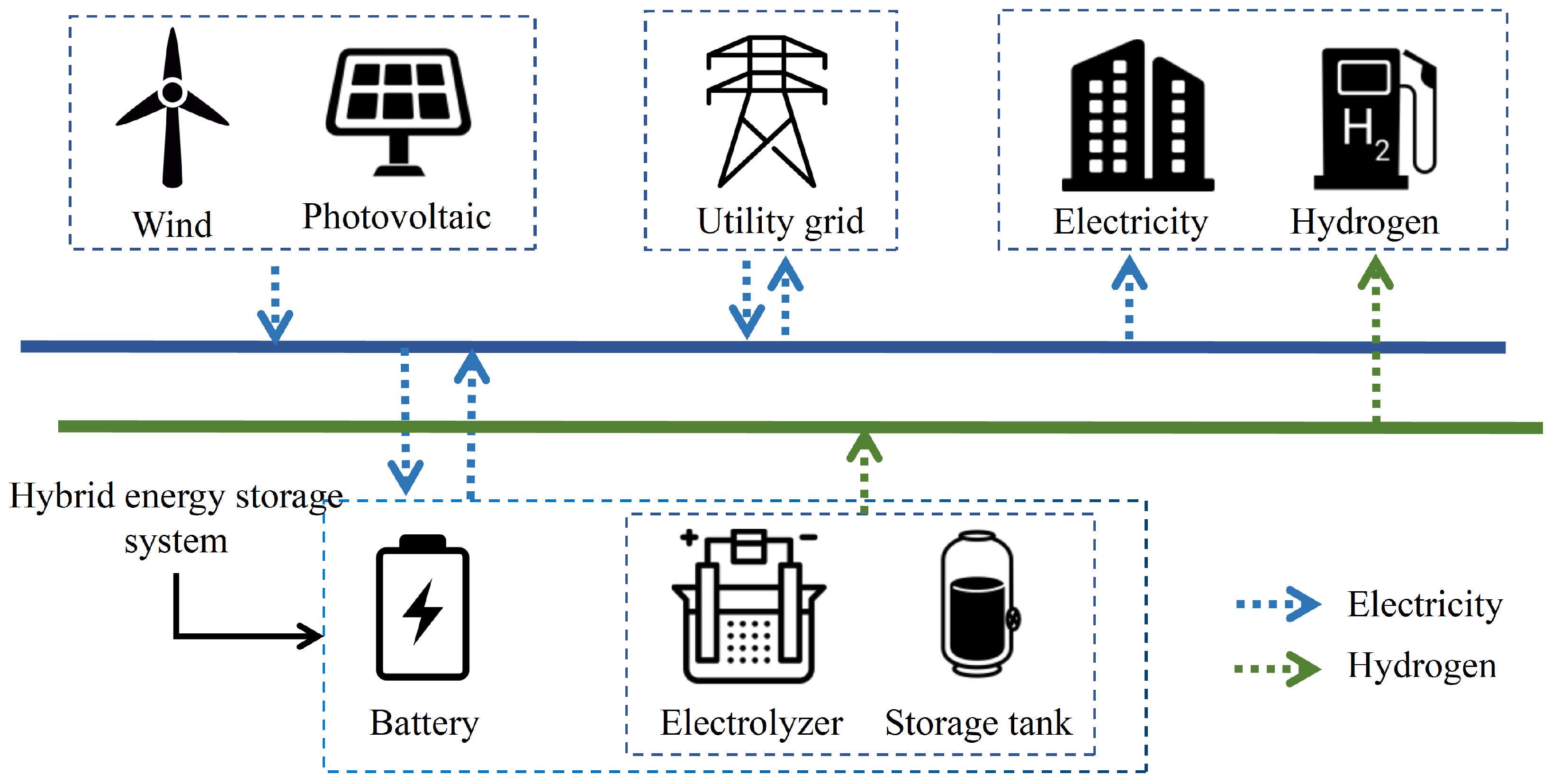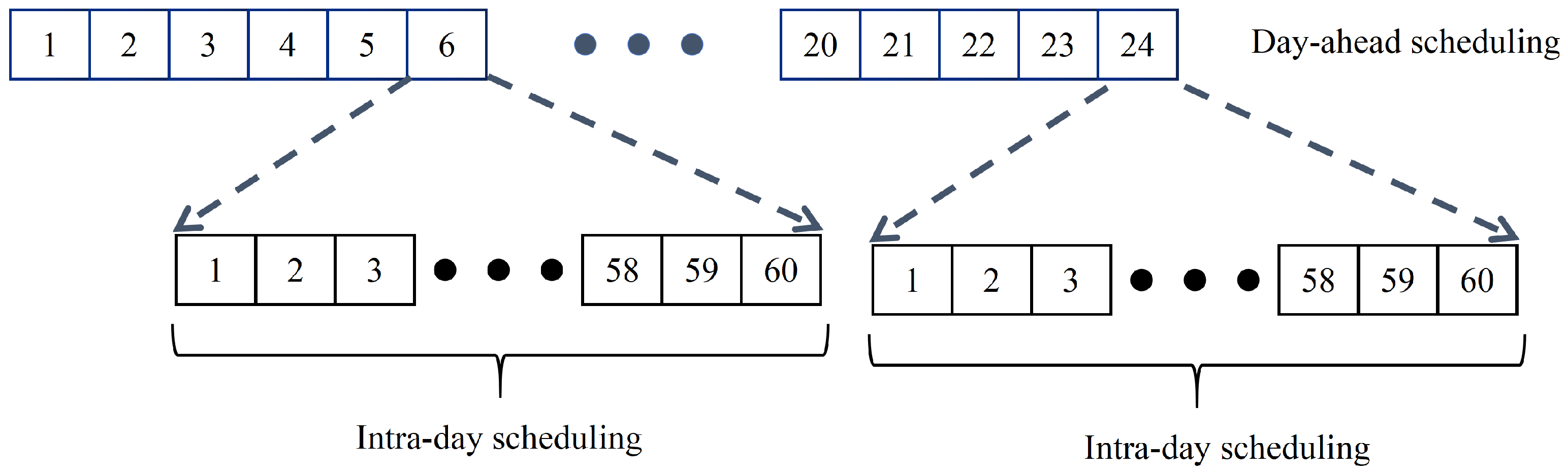The architecture diagram of the proposed two-stage optimization scheduling model is shown in Figure 3. The model consists of two stages: day-ahead and intra-day optimization. In the day-ahead stage, the time scale is one day with a resolution of one hour and the optimization goal is to minimize the daily operation costs. In the intra-day stage, the time scale is one hour, and it utilizes the day-ahead optimization results as a reference. The intra-day optimization stage aims to compensate for power deviations caused by inaccurate source–load forecasting using HESS balancing. The resolution of the intra-day optimization is one minute. The optimization variables of the proposed model are the power of the electrolyzer, the charging or discharging power of the battery, and the power exchange with the utility grid.

4.1. Day-Ahead Optimal Scheduling Model

4.1.1. Optimization Goal

The objective of the day-ahead optimization stage is to minimize the daily operating costs. In the proposed renewable energy system, the proposed renewable energy system, these costs primarily include electricity price costs, equipment operation and maintenance costs, battery degradation costs, and penalty costs incurred due to wind and solar power curtailment. The operating revenue mainly consists of income from selling electricity to the grid and hydrogen sales. The daily costs can be expressed as (9).

$$Ob{j}_{d-h}=C_{e-pur}+C_{o-m}+C_{b-de}+C_{re-pal}-B_{e-sell}-B_{h-sell}$$

(9)

The electricity cost benefits can be expressed as (10). The impact of electricity prices on costs is significant. This paper aims to optimize the economic efficiency of the system by utilizing the price difference between peak and off-peak hours through day-ahead power scheduling.

$$C_{e-pur}=\sum _{t=1}^T{c}_{e-pur}\left(t\right)p_{e-pur}\left(t\right)$$

(10)

The equipment operation and maintenance costs can be expressed as (11). The battery degradation costs are related to the battery’s charging and discharging power, which can be expressed as (12).

$$C_{o-m}=\sum _{t=1}^T\left[o_{elz}{p}_{elz}\left(t\right)+o_{cmp}{p}_{cmp}\left(t\right)+o_{pv}{p}_{pv}\left(t\right)+o_{wind}{p}_{wind}\left(t\right)\right]$$

(11)

$$C_{b-de}=\sum _{t=1}^T\left[d_b{p}_{b-ch}\left(t\right)+d_b{p}_{b-dis}\left(t\right)\right]$$

(12)

Equation (13) illustrates the penalty costs incurred due to wind and solar power curtailment.

$$C_{re-pal}=\sum _{t=1}^T\left[c_{re-pal}{p}_{re-pal}\left(t\right)\right]$$

(13)

Given the interconnected nature of the system, it is imperative to account for the revenue generated by exporting electricity to the grid, as expressed in (14). Nonetheless, it should be noted that the selling price of electricity to the grid is typically subject to temporal variations and tends to be significantly lower than the purchasing price. This discrepancy arises due to the inherent risk associated with integrating electricity from the renewable energy system into the power grid, as it may potentially impact grid stability.

$$B_{e-sell}=\sum _{t=1}^T{c}_{e-sell}\left(t\right)p_{e-sell}\left(t\right)$$

(14)

Furthermore, the system can also generate revenue by selling hydrogen energy, as shown in (15).

$$B_{h-sell}=\sum _{t=1}^T{c}_{h-sell}{m}_{h-sell}\left(t\right)$$

(15)

4.1.2. Constraints

Power and hydrogen balances should be satisfied during the operation, as expressed in (16) and (17).

$$p_{pv}\left(t\right)+p_{wind}\left(t\right)=p_{load}\left(t\right)+p_{elz}\left(t\right)+p_{cmp}\left(t\right)+p_{b-ch}\left(t\right)-p_{b-dis}\left(t\right)+p_{g-ex}\left(t\right)+p_{re-pal}\left(t\right)$$

(16)

$$m_{h-sell}\left(t\right)=m_{h-out}\left(t\right)$$

(17)

The operational power of the compressor is indeed related to factors such as the hydrogen production rate of the electrolyzer and the pressure of the hydrogen storage tank. In this paper, it is assumed that the operational power of the compressor is directly proportional to the hydrogen production rate, as expressed in (18).

$$p_{cmp}\left(t\right)=\beta m_{elz-out}\left(t\right)$$

(18)

In the day-ahead optimization, it is necessary to ensure the safe and stable operation of the equipment. This necessitates operating the devices within certain power ranges.

$$p_{elz}^{min}\le p_{elz}\left(t\right)\le p_{elz}^{max}$$

(19)

$$p_{cmp}^{min}\le p_{cmp}\left(t\right)\le p_{cmp}^{max}$$

(20)

$$p_{b-ch}^{min}\le p_{b-ch}\left(t\right)\le p_{b-ch}^{max}$$

(21)

$$p_{b-dis}^{min}\le p_{b-dis}\left(t\right)\le p_{b-dis}^{max}$$

(22)

$$p_{g-ex}^{min}\le p_{g-ex}\left(t\right)\le p_{g-ex}^{max}$$

(23)

The states for both the battery and hydrogen storage tanks also need to be constrained. Overcharging or over-discharging can lead to a decrease in battery lifespan. Additionally, a portion of the storage capacity needs to be reserved for intra-day optimization during day-ahead scheduling. Therefore, the lower and upper limits for the storage state are set at 0.2 and 0.8, respectively [28].

$$0.2\le SoC\left(t\right)\le 0.8$$

(24)

$$0.2\le LoH\left(t\right)\le 0.8$$

(25)

In order to maximize the energy utilization efficiency of the system, the battery is not allowed to charge and discharge simultaneously.

$$p_{b-ch}\left(t\right)·p_{b-dis}\left(t\right)=0$$

(26)

Ultimately, in order to ensure optimal energy utilization, it is necessary to limit the curtailment rate of wind and solar power within a certain range, as indicated in (27).

$$\left[\sum _t^{t=T}{p}_{re-pal}\left(t\right)\right]/\left[\sum _t^{t=T}{p}_{wind}\left(t\right)+p_{pv}\left(t\right)\right]\le {\epsilon }_{re-cul}$$

(27)

4.2. Intra-Day Optimal Scheduling Model

4.2.1. Optimization Goal

The main objective of the intra-day optimization stage is to align the energy exchange between the system, the energy flow of EHSS, and the grid with the day-ahead scheduling results while minimizing the curtailment rate of wind and solar power. As a result, the intra-day optimization model becomes a multi-objective model with the objective functions represented by (28).

$$\begin{array}{c}Ob{j}_{i-d}=\left\{E_{grd},E_{cul},E_{hess}\right\}\hfill \\ E_{grd}={\displaystyle \sum _{\tau }^{\tau =\lambda }}|p_{g-ex}-{\tilde{p}}_{g-ex}\left(\tau \right)|/\left(\lambda p_{g-ex}\right)\hfill \\ E_{cul}={\displaystyle \sum _{\tau }^{\tau =\lambda }}\left|{\tilde{p}}_{re-pal}\left(\tau \right)\right|/(\lambda p_{pv}+\lambda p_{wind})\hfill \\ E_{hess}={\displaystyle \sum _{\tau }^{\tau =\lambda }}(|p_b-{\tilde{p}}_b|+|p_{elz}-{\tilde{p}}_{elz}|)/(\lambda p_b+\lambda p_{elz})\hfill \end{array}$$

(28)

where $\tau$ represents the optimization time interval of intra-day operation, while $\lambda$ represents the optimization time period.

4.2.2. Constraints

Similar to the day-ahead operation, during the intra-day operation of the system, several constraints also need to be considered, including the power and hydrogen energy balance constraint, as specified in (16) and (17), the compressor’s power constraint, as specified in (18), the equipment operating range constraint, as specified in (19)–(23), storage constraints for lithium batteries and hydrogen tanks, as specified in (24) and (25), as well as the constraint that prevents simultaneous charging and discharging of the batteries, as specified in (26).

4.3. Solution Method

The day-ahead optimization scheduling model can be formulated as a mixed-integer linear programming (MILP) problem and is solved directly by applying Matlab R2022a with Gurobi 10.0. However, the intra-day scheduling is a multi-objective optimization problem. In this study, the non-dominated sorting genetic algorithm II (NSGA-II) method is employed to solve the intra-day optimization problem.

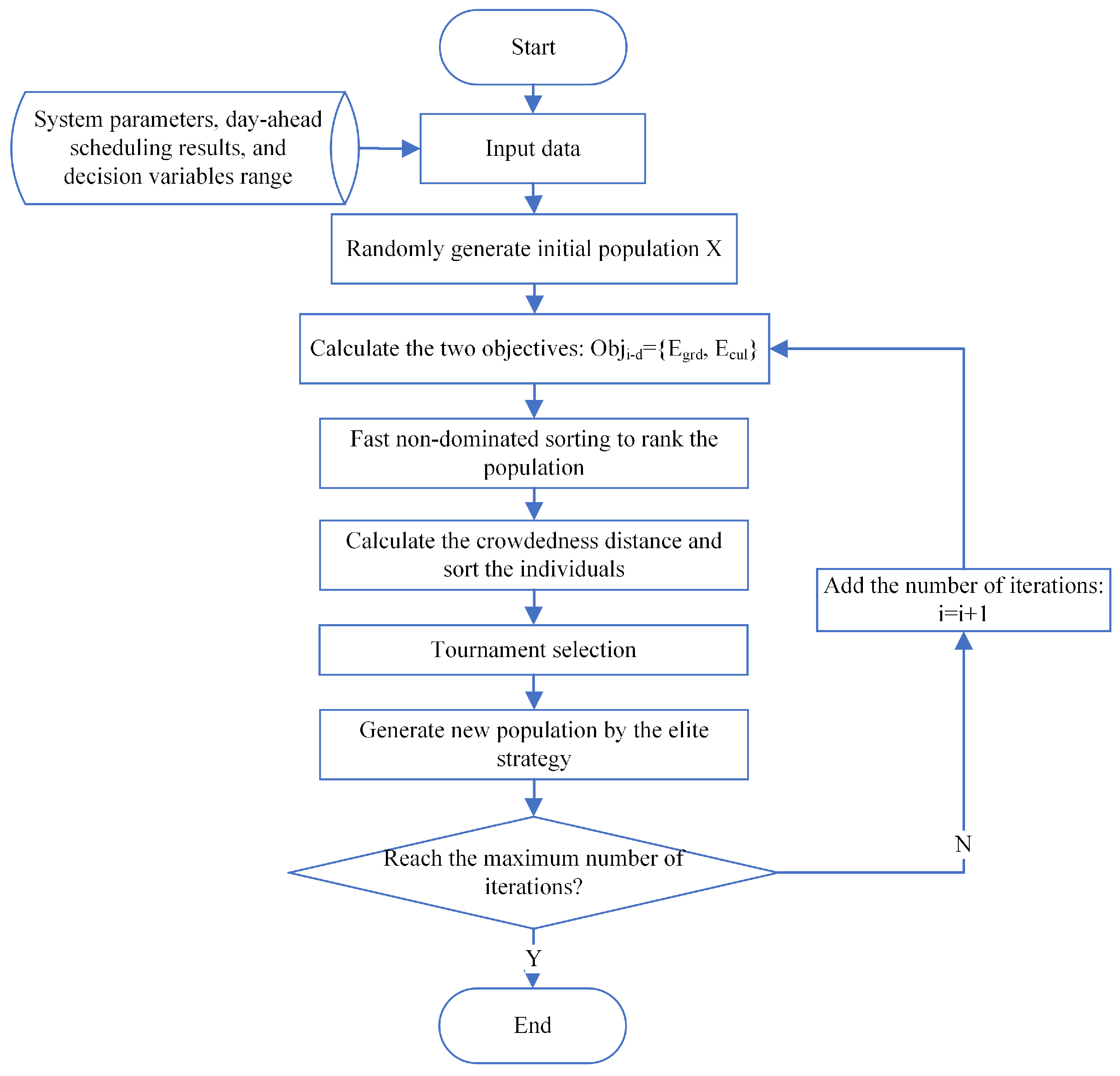
The NSGA-II algorithm, originally proposed by Deb et al. [29], is a well-structured optimization algorithm widely utilized for solving complex engineering problems. It incorporates several key components such as fast-non-dominated sorting, a smart maintenance approach, and effective crowding distance assessment, which collectively contribute to improving the convergence rate and maintaining population diversity. The solving process of intra-day multi-objective optimization problems based on NSGA-II is shown in Figure 4. During the initialization stage, careful consideration is given to the limitations of decision variables for optimization. If an original population is available, the algorithm proceeds to the generation of the second population; otherwise, it performs the non-dominated selection, followed by selection, crossover, and mutation steps to create the original population. A merging technique is employed to combine the initial and offspring populations. If a new parent population is generated, the algorithm continues with selection, crossover, and mutation steps. Otherwise, it reverts back to the fast-non-dominated sorting, crowding distance assignment, and selection of suitable individuals before proceeding to the selection, crossover, and mutation steps. This iterative process continues for a specified number of generations. Finally, when the maximum number of generations is reached, the algorithm plots the Pareto frontier and employs an optimal point selection method to determine the final optimal solution [21].

Non-dominated sorting and the elitism preservation strategy contribute to the improved performance of the NSGA-II algorithm in terms of computational efficiency, preservation of good solutions, and maintaining population diversity, thereby enhancing its effectiveness in solving multi-objective optimization problems. With the NSGA-II, a three-dimensional Pareto front can effectively showcase the results of multi-objective optimization. It provides a clear visualization of the trade-off relationship between the three objectives and allows for a comprehensive understanding of the optimal solutions in the problem domain.

5. Case Studies

5.1. Parameters and Data Curation

This study validates the proposed scheduling method in a laboratory’s practical experimental system, of which, the electrolyzer is presented in Figure 5. Due to the limitations of the laboratory environment, the capacity of the equipment in the system is relatively small, within 100 kW. It should be noted that the optimized operation method proposed in this paper has little relationship with the equipment capacity level, and can also be applied to large-scale renewable energy systems. The rated power of the wind turbine, PV, electrolyzer, and compressor are 12 kW, 60 kW, 20 kW, and 5 kW, respectively. The storage capacity of the battery and hydrogen tank are 15 kWh and 5 kg. The cut-in wind speed of the wind turbine is 2.5 m/s, the cut-out wind speed is 25 m/s, and the rated wind speed is 12 m/s. The equipment parameters for the PV and wind system of this study are presented in

Table 1. Parameters of the PV and wind turbines.

Parameters	Values	Parameters	Values
$p_{wind}^{rated}$	12 kW	$p_{pv}^{rated}$	60 kW
$v_{in}$	2.5 m/s	$v_{out}$	25 m/s
$v_{rated}$	12 m/s	$G_{STC}$	1 kW/${\mathrm{m}}^2$
$T_{c,NOCT}$	20 °C	$T_{ref}$	25 °C
$G_{NOCT}$	0.8 kW/${\mathrm{m}}^2$	${\alpha }_p$	0.005 °C−1
$T_{a,NOCT}$	25 °C	$f_{PV}$	80%

. The other critical operation parameters, including unit operation and maintenance costs, are presented in

Table 2. Other operation parameters of the system.

Parameters	Values	Parameters	Values
$p_{elz}^{max}$ (kW)	20	$o_{pv}/o_{wind}$ ($/kW)	0.033
${\eta }_{b-in}/{\eta }_{b-out}$	0.975	$o_{elz}$	0.29
$p_{elz}^{min}$ (kW)	5	$c_{re-pal}$ ($/kW)	0.05
$p_{cmp}^{max}$ (kW)	5	$o^{Hs}$ ($/kg)	0.017
$p_{b-ch}^{max}$ (kW)	30	$d^b$ ($/kW)	0.020
$LH{V}_{H_2}$ kJ/mol	242	$o_{Cmp}$ ($/kW)	0.012
$\beta$	2	${\gamma }_b/{\gamma }_h$	0.0006%
${\eta }_{elz}$	0.65	$Q_b^{Rated}$ (kWh)	15
$Q_h^{Rated}$ (kg)	5	${\eta }_{h-in}/{\eta }_{h-out}$	0.975

, where the parameter values related to the equipment are derived from the real settings in the laboratory, and the parameter values related to the price are derived from [5].

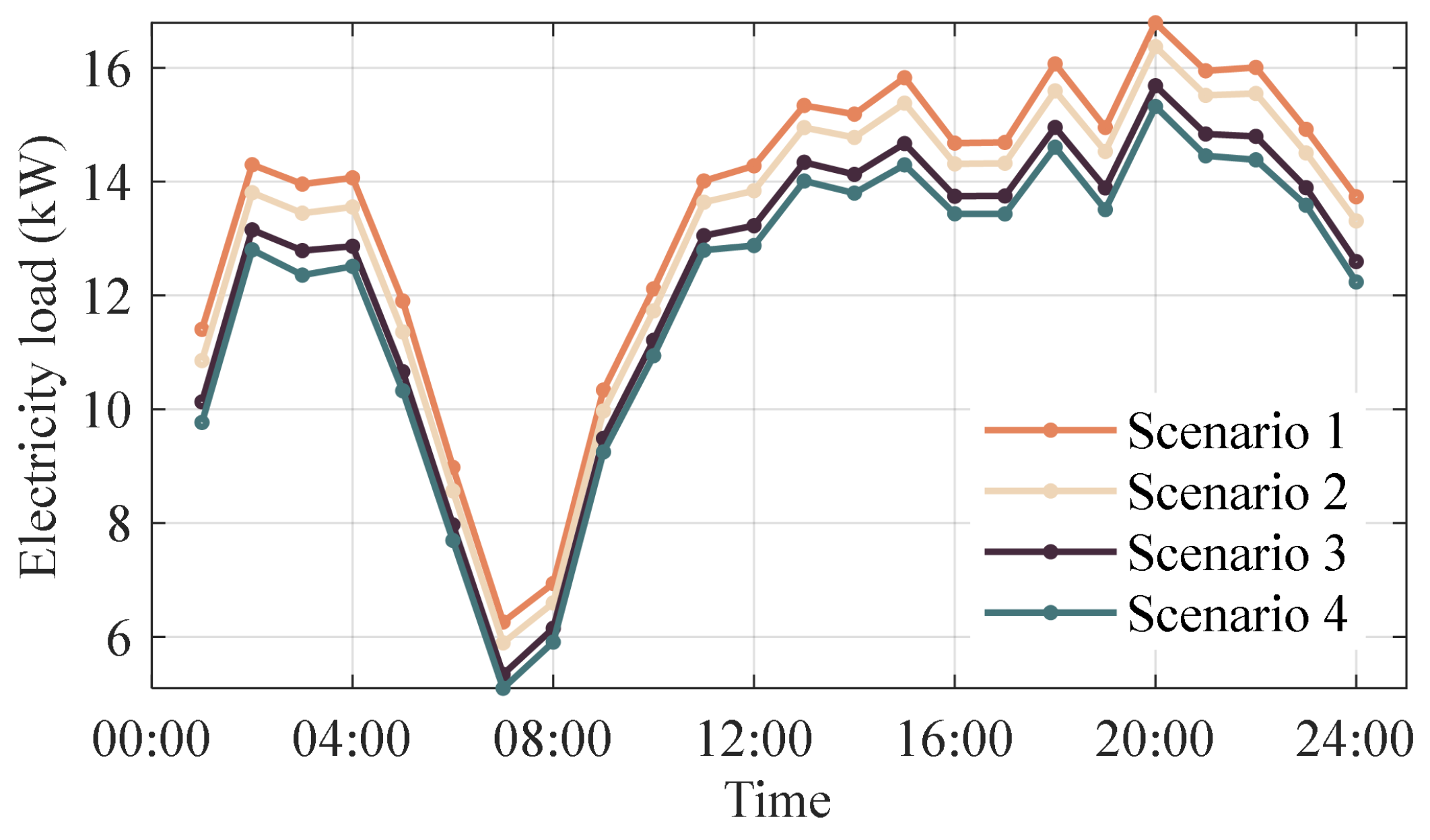
Case studies were conducted in four scenarios, of which, the day-ahead source–load forecasts are shown in Figure 6, Figure 7 and Figure 8. As can be seen, the PV energy in Scenarios 1 and 2 is sufficient, while the wind power in Scenario 1 is much less than the others. In Scenarios 3 and 4, the PV energy is lacking, and there are non-steamed bun-shaped PV curves in Scenario 4, which are caused by the gloomy weather. The energy demand of the system performs basically the same in the four scenarios. Additionally, Figure 9a illustrates the electricity price for energy exchange between the system and the grid, while Figure 9b represents the hydrogen energy demand. In this study, it is assumed that the hydrogen energy output of the system is connected to an industrial park, resulting in a relatively stable hydrogen energy load.

5.2. Day-Ahead Optimization Results

The comparison between the proposed method and the conventional operational results is presented in

Table 3. Day-ahead optimization results of four typical days and the comparison with the conventional operation.

		Scenario 1	Scenario 2	Scenario 3	Scenario 4
Daily costs ($)	Conventional operation	71.34	46.73	74.52	60.78
	Optimized operation	66.82	44.10	70.10	56.46
Costs reduction rate (%)		6.34	5.63	5.93	7.11

. The operational strategy of the conventional method is as follows: When the power output from renewable energy sources exceeds the electricity demand, the excess power is primarily utilized by the electrolyzer to produce hydrogen. Once the hydrogen storage tank is full or the remaining power is insufficient to meet the minimum operating power of the electrolyzer, the remaining electricity is absorbed by the battery for storage and later use. It can be observed that—for the four selected typical days—the economic performance of the day-ahead optimization scheduling method proposed in this paper surpasses that of the non-optimized system, with around a 6% cost reduction rate.

These observations highlight the system’s adaptive strategies in response to electricity prices and renewable energy availability. Such strategies involve optimizing hydrogen production based on price differentials and leveraging energy storage capabilities to maximize system efficiency and cost-effectiveness.

The system operation results for the four scenarios are shown in Figure 10a–d. In the figure, “$ELZ$” refers to the electrolyzer power, “$GR{D}_P$” represents the power purchased from the grid, “$GR{D}_S$” represents the power sold to the grid, and “$SOC$” and “$LOH$” indicate the energy storage levels of the battery and hydrogen tank, respectively.

By examining the power exchange between the system and the grid, it can be observed that the system’s power purchase from the grid is considered as the power input (negative value), while the power sold to the grid is considered as the power output (positive value). Comparing the four scenarios, it is evident that almost all the power sold to the grid is concentrated between 11:00 and 15:00, as indicated by the red box in the figure. This is because the electricity selling price to the grid is the highest during this time period, and the PV power generation is also high, resulting in concentrated power selling during this timeframe.

The power sold to the grid is closely related to the system’s source–load balance. When renewable energy generation is low, as shown in Scenario 3, the system only purchases power from the grid and does not sell power to the grid. It is worth noting that the optimization model proposed in this paper takes into account the varying electricity prices. Therefore, the system attempts to avoid purchasing power from the grid during high-priced periods, such as 11:00–15:00 and 18:00–20:00 in Scenario 3. In these two time periods, the system compensates for the low input from the source and the high output from the load in two different ways. In the former time period, the system reduces the electrolyzer’s power and releases hydrogen from the storage tank to minimize energy consumption. In the latter time period, the system achieves energy balance by discharging the battery. These operational strategies contribute to the economic benefits of the system. Similar time periods can be observed in Scenarios 2 and 4, as indicated by the black box in the figure. Furthermore, it can be observed that the variation trend of the hydrogen storage level is generally opposite to the trend of electricity prices. This confirms that the optimization method proposed in this paper can effectively allocate renewable energy power by producing hydrogen during periods of low electricity prices and prioritizing meeting the electricity demand during periods of high electricity prices, thereby reducing system costs.

Finally, it can be seen that the variation rate of the battery’s SOC is relatively small. This also indicates that adopting the HESS can effectively reduce the required battery capacity, which is beneficial for reducing the system’s construction costs. If only a battery energy storage system is used, a significant increase in battery capacity would be required to achieve source–load balance.

5.3. Intra-Day Optimization Results

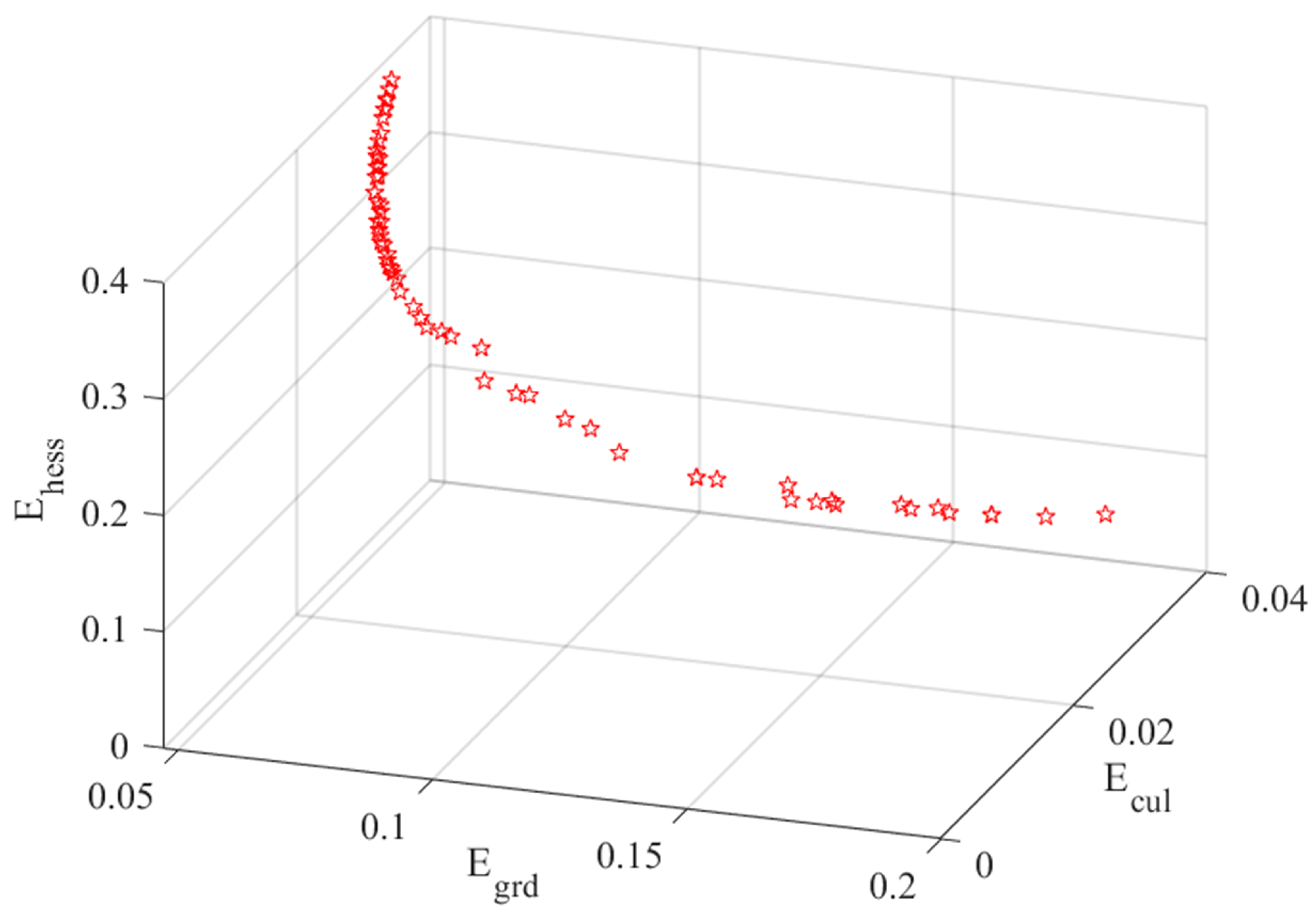
Figure 11 illustrates the intra-day optimization Pareto frontier for the first hour of a typical day in Scenario 1. The points on the Pareto frontier represent the optimal solution set of the multi-objective optimization model for day-ahead planning. At each point along this boundary, one objective cannot be further improved without sacrificing another objective. In other words, it represents the best trade-off or balance achieved among multiple objectives. The Pareto frontier showcases the range of feasible solutions that offer different trade-offs between objectives, allowing decision-makers to choose the most suitable solution based on their preferences and priorities.

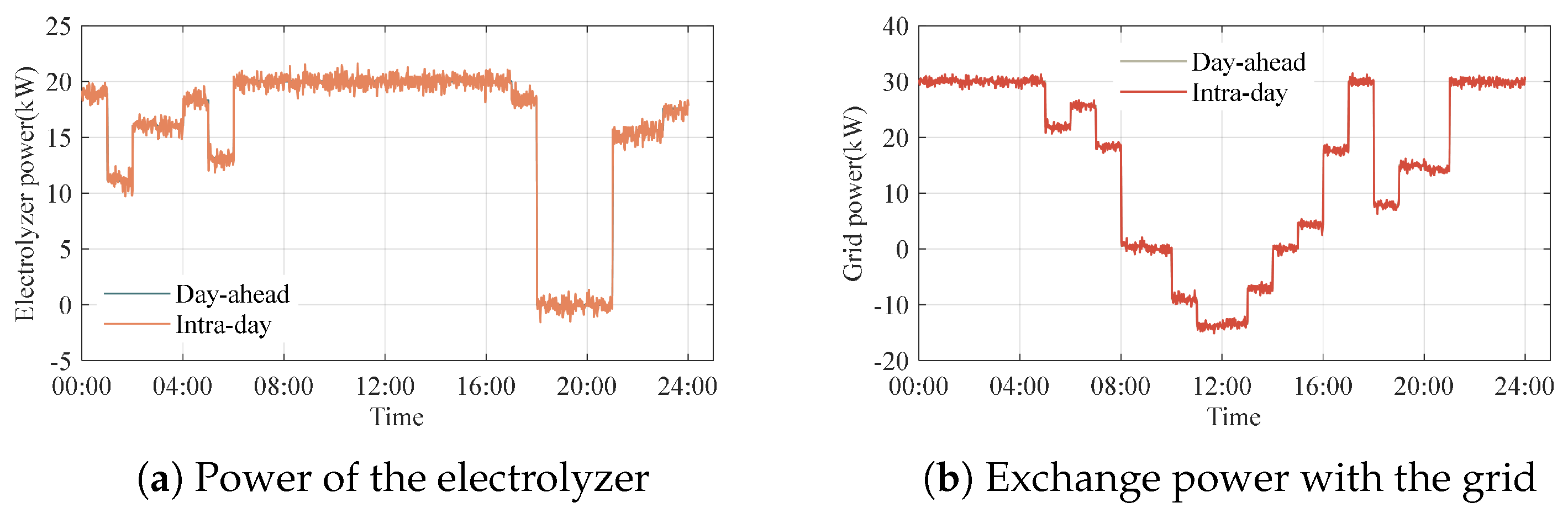
The intra-day operation results of Scenario 1 are presented in Figure 12a. It is evident that the operation of the electrolyzer during the intra-day period closely follows the day-ahead scheduling plan. Furthermore, Figure 12b depicts the power exchange between the system and the grid, demonstrating good tracking performance.

5.4. Model Comparison

We compare the proposed dual-stage optimization model with the other existing models, of which, the optimization goals and solution methods are shown in

Table 4. Optimization goals and solution methods of the four models.

	Optimization Goals		Solution Methods
	Day-Ahead	Intra-Day	Day-Ahead	Intra-Day
Model A [7]	Daily operation costs	/	Particle swarm algorithm	/
Model B [30]	/	Costs & Power abandonment rate	/	NSGA-II
Model C [31]	Daily operation costs	Trace the day-ahead operation schemes	Particle swarm algorithm	Particle swarm algorithm
Model D (Proposed model)	Daily operation costs	Trace the day-ahead operation schemes & Power abandonment rate	MILP	NSGA-II

. Model A represents a day-ahead model designed to minimize day-ahead costs as its optimization objective. The particle swarm optimization (PSO) algorithm is employed to solve this model. Meanwhile, Model B incorporates minute-level intra-day optimization and encompasses two objectives: operational profit and curtailment rate of renewable energy. Given its multi-objective nature, the study employs NSGA-II to tackle this optimization problem. In Model B, the original optimization objective was operational profit. However, in this paper, the consideration of revenue generated from hydrogen energy is omitted. As a result, the objective is transformed into the operational cost as a substitute measure to facilitate model comparison. Model C shares similarities with the proposed model in this paper, as both are dual-stage optimization models. In the day-ahead optimization, Model C focuses on minimizing operational costs but diverges in the intra-day optimization, where the objective is to achieve a tracking rate based on the day-ahead dispatch results, without explicitly considering the curtailment rate of renewable energy. Notably, the literature does not emphasize the two-stage solving approach for Model C, and this paper replaces it with the PSO algorithm.

Table 5. Optimization results of the four models.

	Model A	Model B	Model C	Model D
Daily operating costs ($)	45.2	46.1	45.3	44.1
Deviation of exchanged electricity (%)	5.3	/	1.4	2.1
Renewable energy curtailment rate (%)	6.4	1.7	7.6	1.3

illustrates the daily operating costs, the deviation of exchanged electricity with the grid compared to the day-ahead schedule, and the actual renewable energy curtailment rate for four models, using Scenario 2 as an example.

From the optimization results of the four models, it can be observed that there is minimal difference in the daily operating results. This is because the daily operation is consistently considered by all the models. However, in terms of tracking the day-ahead operation results and managing renewable energy curtailment, Model D exhibits a more balanced and outstanding performance. This can be attributed to the fact that Model A focuses solely on day-ahead optimization and cannot handle the uncertainties arising from wind and solar forecasts. On the other hand, Model C’s intra-day optimization stage is a single-objective optimization that only considers tracking the day-ahead dispatch results, overlooking the issue of renewable energy curtailment. In contrast, both Model B and Model D adopt multi-objective optimization, providing a more balanced consideration of renewable energy curtailment. However, Model B is an intra-day optimization model and cannot provide operational guidance for the day-ahead operation. Therefore, Model D can be considered a more balanced and effective system operation optimization model among them.

By comparing the solution methods of the four models, it is evident that NSGA-II achieves good results for multi-objective optimization, while PSO is more favored for single-objective optimization due to its powerful search capabilities. The day-ahead optimization in this paper is formulated as a MILP model, which can be solved directly using solvers, resulting in faster computation. However, this approach sacrifices modeling accuracy, such as not considering the variability of electrolyzer efficiency with power. It is important to note that the proposed intra-day optimization stage in this paper helps alleviate the potential issues arising from the lower modeling accuracy to some extent.

6. Conclusions

This paper proposes a dual-stage optimization scheduling method for grid-connected systems with hybrid energy storage to balance renewable energy. The model consists of an economically optimal day-ahead scheduling model and an intra-day stage that uses accurate renewable energy forecasting to minimize curtailment. The proposed model offers several advantages, including enhanced economic efficiency in the day-ahead stage and multi-objective optimization in the intra-day stage. It provides a comprehensive approach to optimize the scheduling of grid-connected systems with hybrid energy storage, achieving a balance between different optimization objectives. Compared with other works, the proposed model balances economic and operational considerations, enabling the system to operate economically and stably. However, the faster solution speed of the day-ahead stage sacrifices some modeling accuracy, making it suitable for scenarios where high modeling accuracy is not critical.

Overall, the proposed dual-stage optimization model offers a promising solution for achieving economic efficiency and minimizing curtailment in grid-connected systems with renewable energy sources, contributing to the effective integration of renewable energy and the sustainable operation of the power grid.

Refining electrolyzer modeling and exploring faster and more effective optimization algorithms are promising directions for future research. Improving electrolyzer modeling accuracy will better capture system dynamics, while advanced algorithms will enhance the efficiency and effectiveness of the optimization process, enabling more comprehensive and optimal system operations. These advancements will contribute to the development of sophisticated and efficient energy management strategies in the future.