Variable-Angle Random High-Frequency Voltage Injection Strategy with Cross-Saturation Effect Compensation for Sensorless Synchronous Reluctance Motor Drives
Abstract
1. Introduction
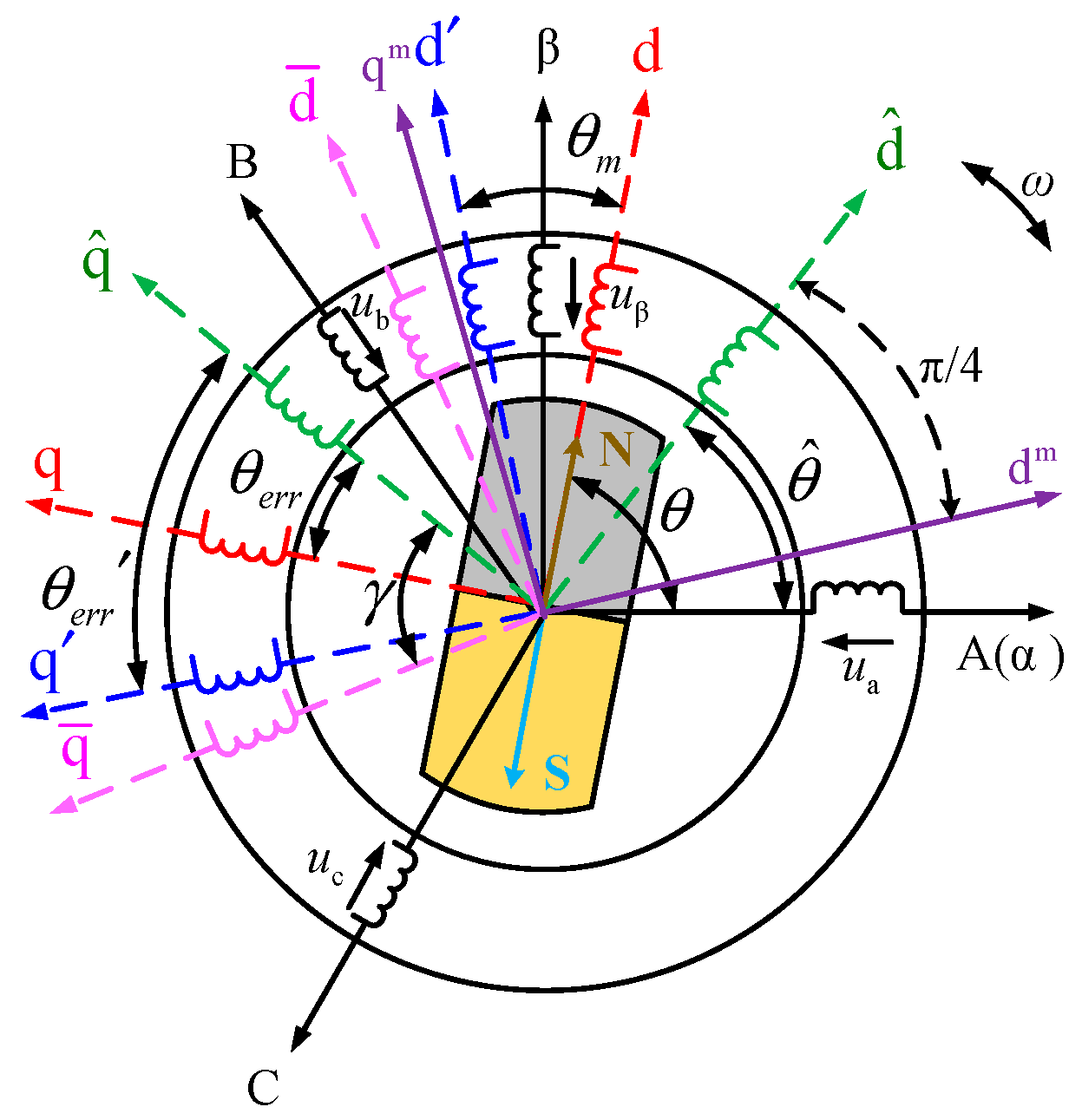
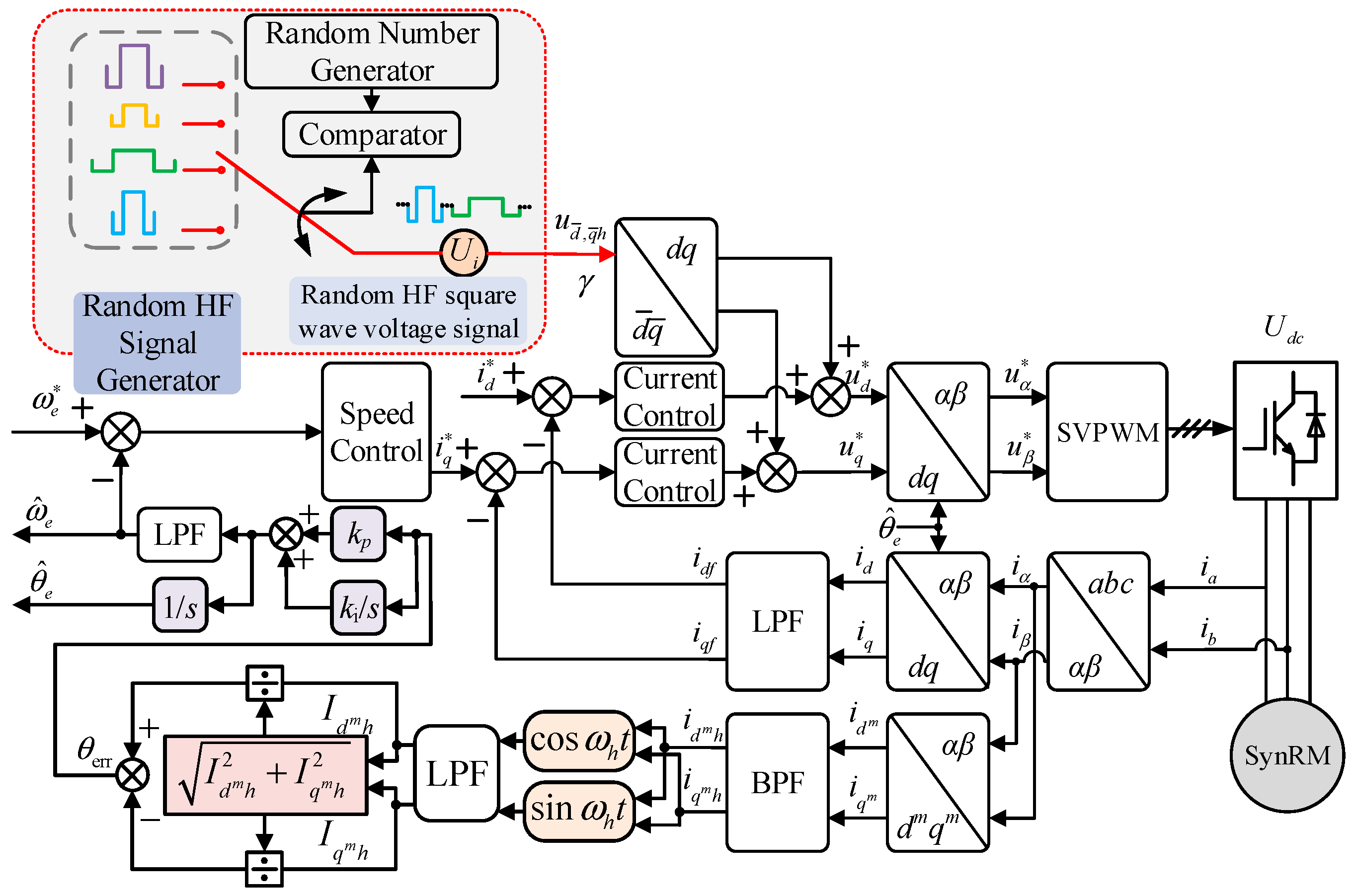
2. Proposed Random High-Frequency Square-Wave Voltage Injection-Based Sensorless Control Strategy
2.1. Proposed Random Injection Scheme
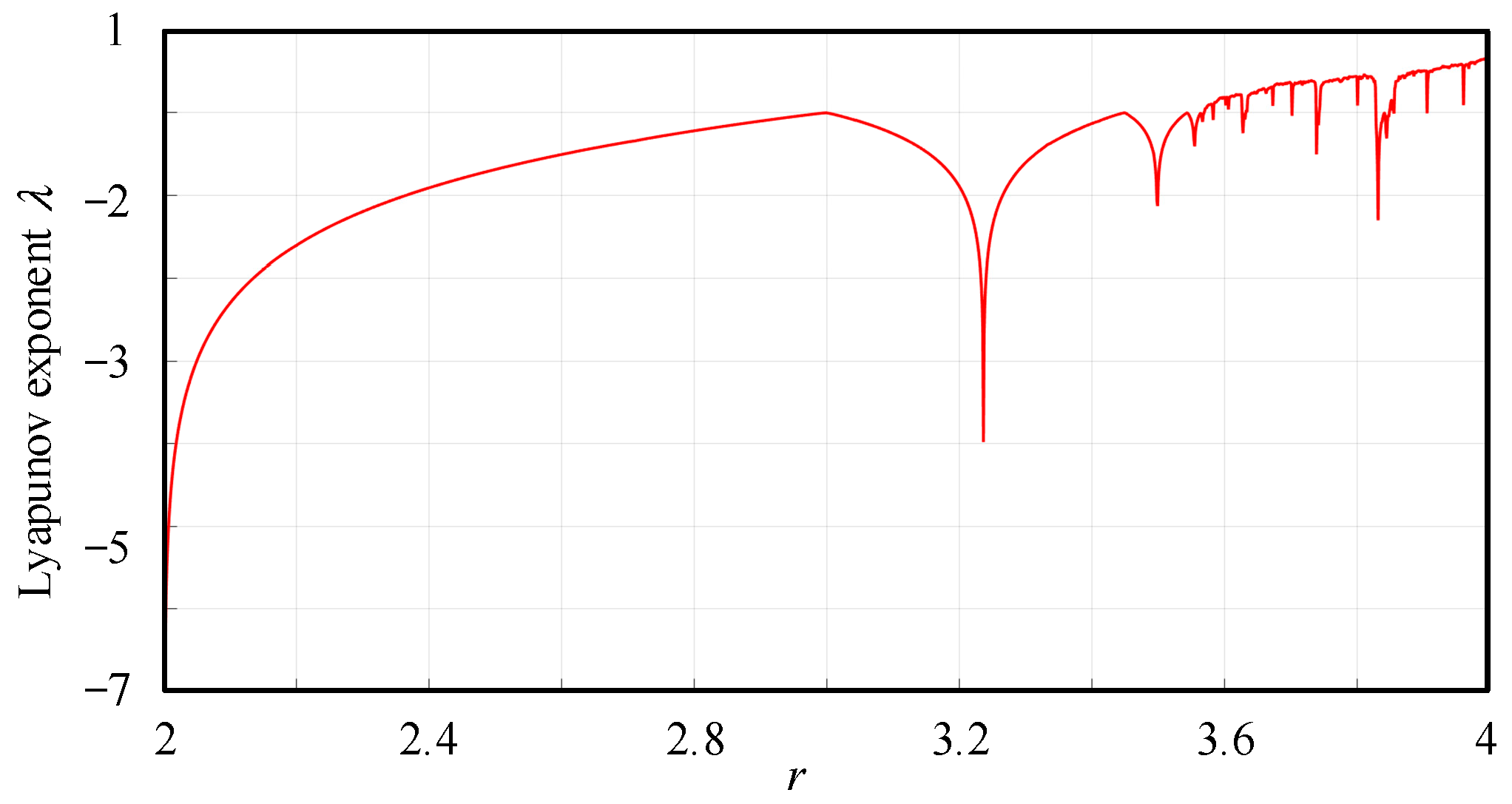
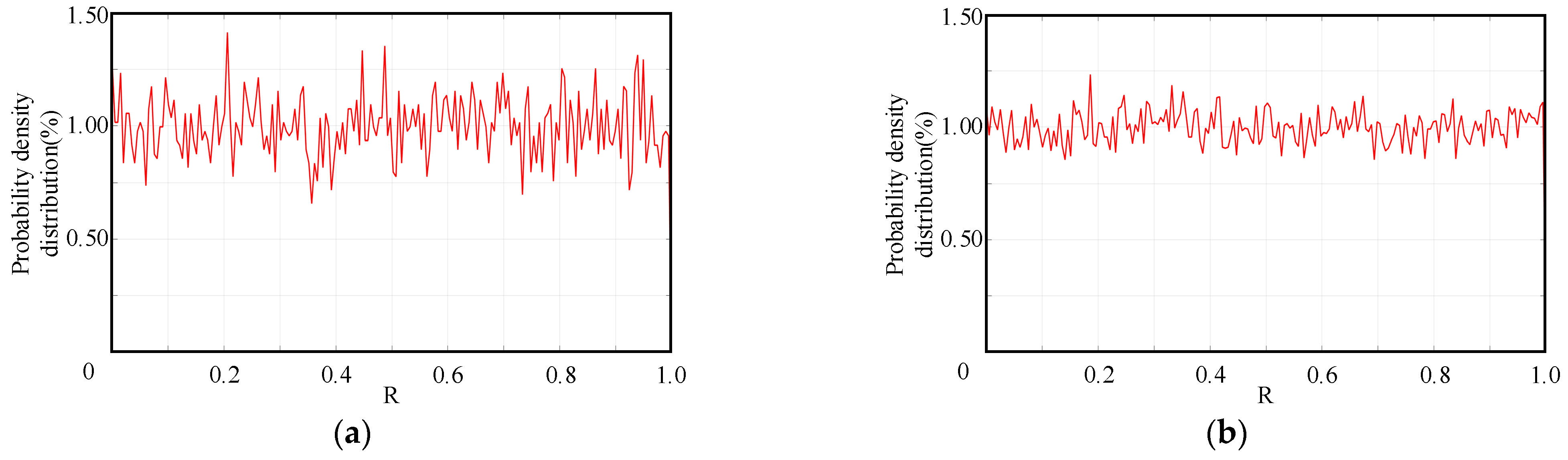
2.2. Chaotic Mapping Method-Based Random Number Generation Principle
3. SynRM Cross-Saturation Effect Suppression Algorithm Based on Variable-Angle Injection
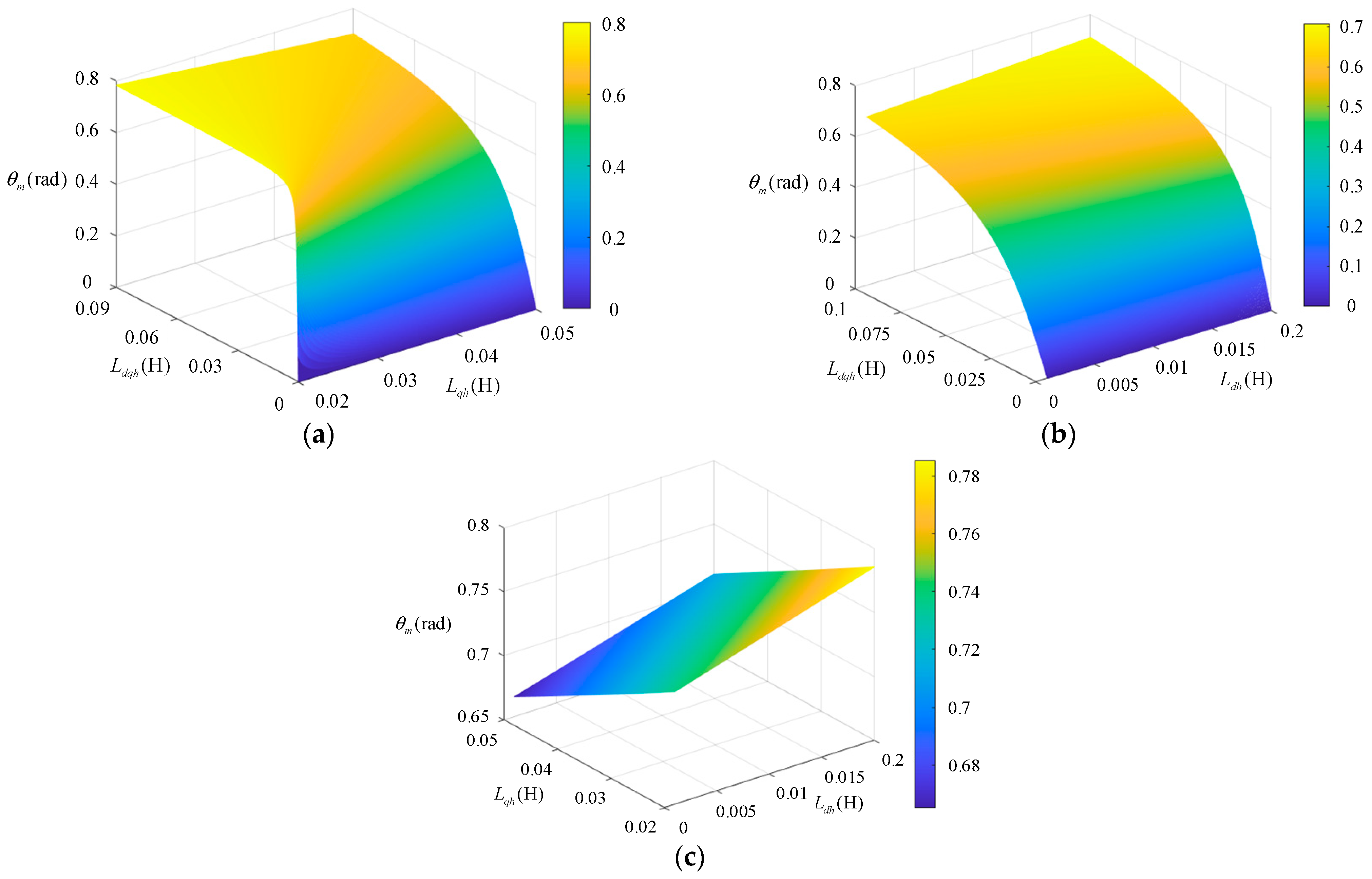
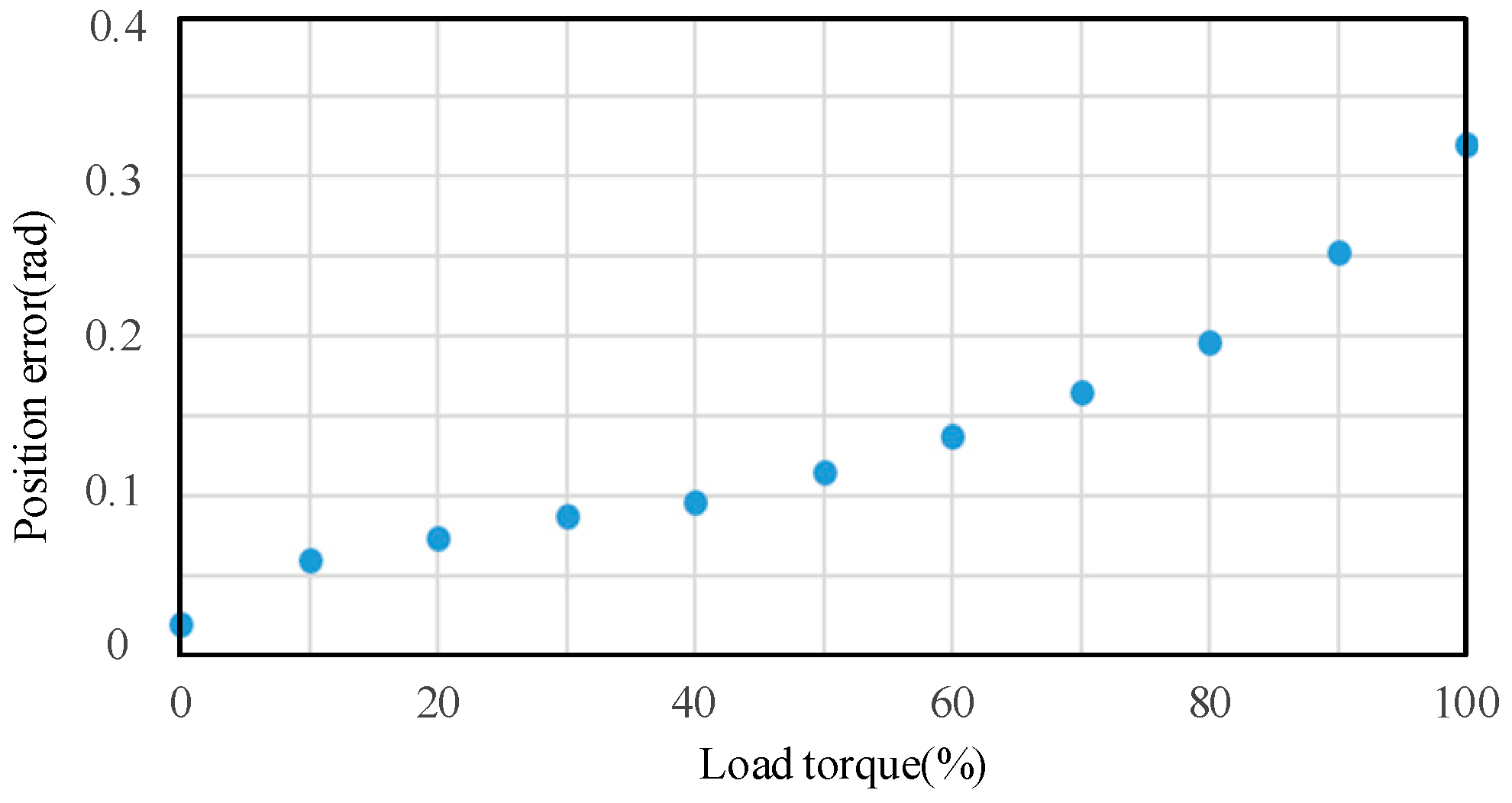
3.1. Analysis of Position Error Caused by Cross-Saturation
- (1)
- When Ldh is fixed, θm increases with the increase in Ldqh and decreases with the increase in Lqh. θm changes significantly when Ldqh is small and tends to be stable when Ldqh is large.
- (2)
- When Lqh is fixed, θm increases with the increase in Ldqh and increases with the increase in Ldh.
- (3)
- When Ldqh is fixed, the change in θm is less obvious. θm increases with the increase in Ldh and decreases with the increase in Lqh.
3.2. Variable-Angle Square-Wave Injection with Cross-Saturation Effect Compensation
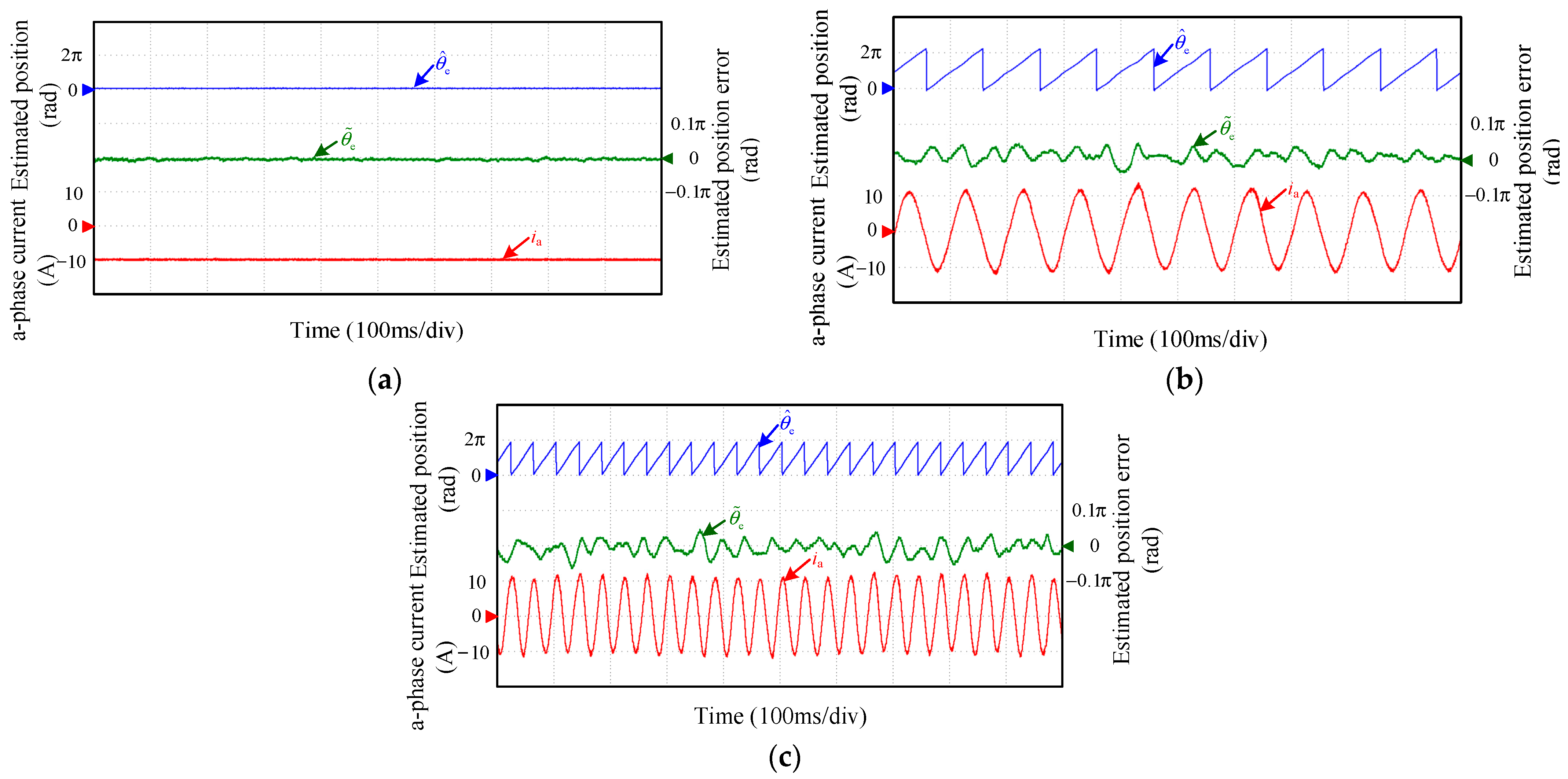
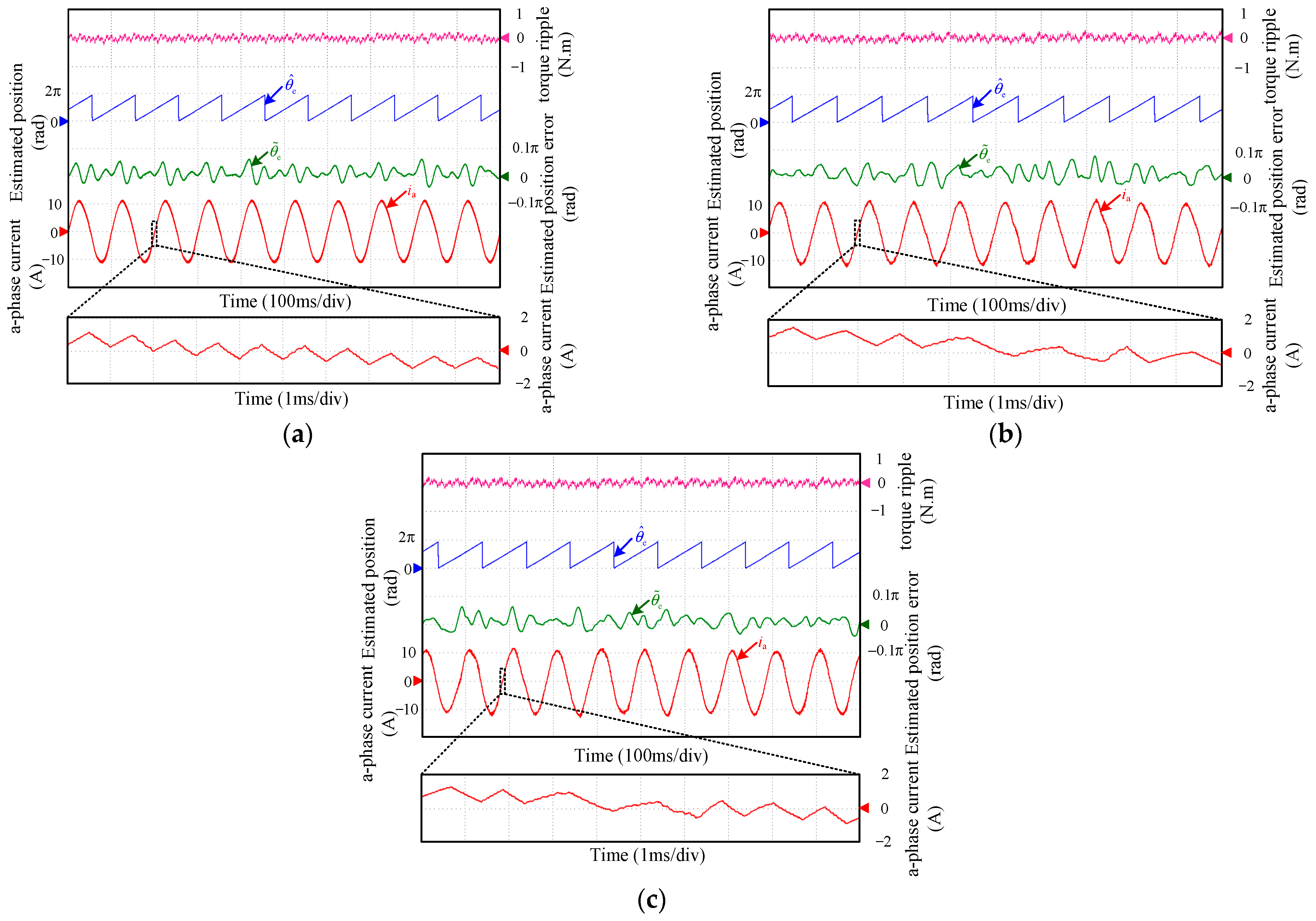
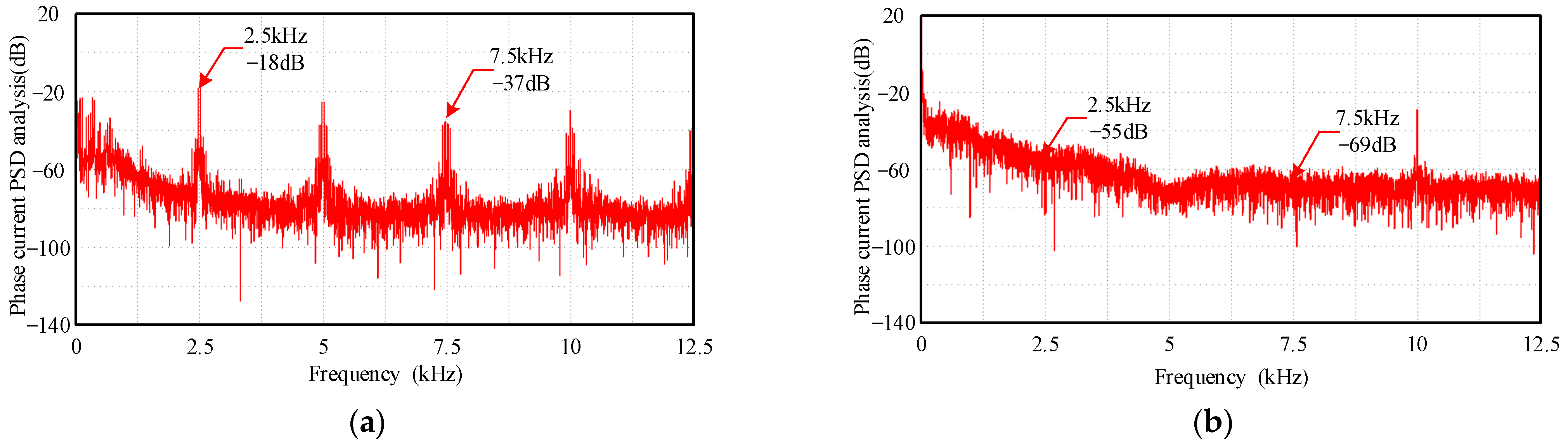
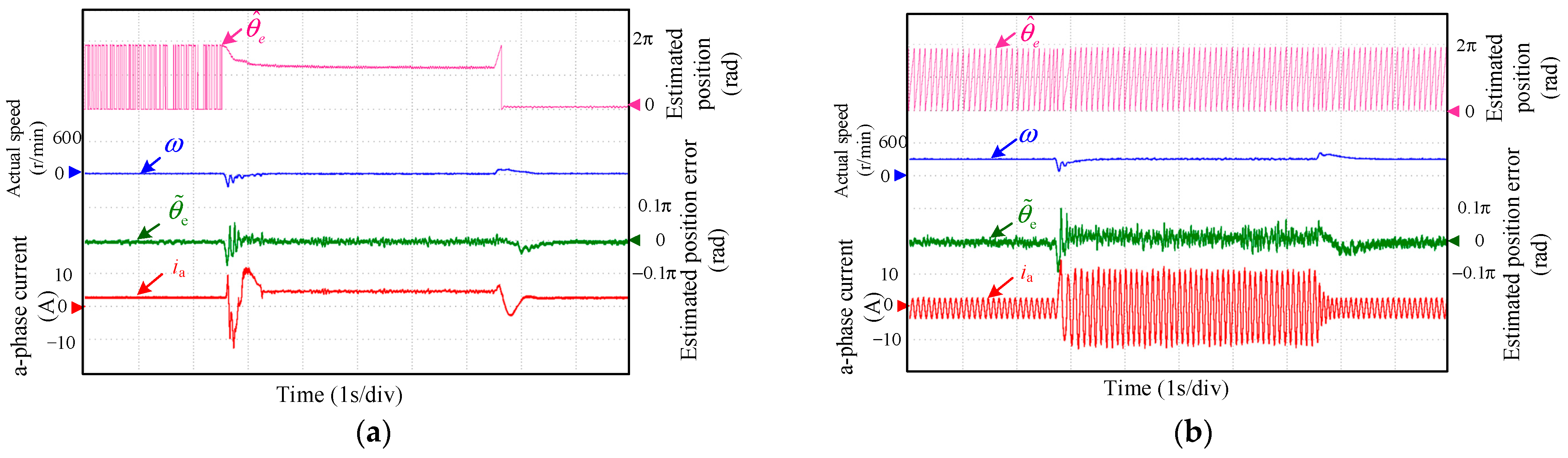
4. Experimental Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Foti, S.; De Caro, S.; Scimone, T.; Testa, A.; Tornello, L.D.; Scelba, G.; Cacciato, M. Rotor Position Error Compensation in Sensorless Synchronous Reluctance Motor Drives. IEEE Trans. Power Electron. 2022, 37, 4442–4452. [Google Scholar] [CrossRef]
- Kim, H.; Park, Y.; Oh, S.-T.; Jeong, G.; Seo, U.-J.; Won, S.-H.; Lee, J. Study on Analysis and Design of Line-Start Synchronous Reluctance Motor Considering Rotor Slot Opening and Bridges. IEEE Trans. Magn. 2022, 58, 1–6. [Google Scholar] [CrossRef]
- Farhan, A.; Abdelrahem, M.; Saleh, A.; Shaltout, A.; Kennel, R. Robust Sensorless Direct Speed Predictive Control of Synchronous Reluctance Motor. In Proceedings of the 2020 IEEE 29th International Symposium on Industrial Electronics (ISIE), Delft, The Netherlands, 17–19 June 2020; pp. 1541–1546. [Google Scholar]
- Deng, W.; Tang, J.; Cheng, W. An Enhanced Rotating Vector-Based Direct Torque Control for Matrix Converter-Fed PMSM Drives Using Virtual Pulsating Vectors. CPSS Trans. Power Electron. Appl. 2023, 8, 65–73. [Google Scholar] [CrossRef]
- Yang, X.; Wang, Y.; Shen, J. MRAS sensorless control for synchronous reluctance motors. Electr. Mach. Control. 2019, 23, 1–9. [Google Scholar]
- Guo, L.; Ma, J.; Qi, J. Model-free Predictive Current Control Strategy for Synchronous Reluctance Motor. Electr. Drive 2020, 50, 8–14. [Google Scholar]
- Farhan, A.; Abdelrahem, M.; Shaltout, A.; Kennel, R.; Saleh, A. Encoderless Current Predictive Control of Synchronous Reluctance Motor by Extended Kalman Filter based State Estimation. In Proceedings of the PCIM Europe Digital Days 2020, International Exhibition and Conference for Power Electronics, Intelligent Motion, Renewable Energy and Energy Management, Nuremburg, Germany, 7–8 July 2020. [Google Scholar]
- Mirazim, M.S.; Kiyoumars, A. Magnetic Field Analysis of SynRel and PMASynRel Machines with Hyperbolic Flux Barriers Using Conformal Mapping. IEEE Trans. Transp. Electrif. 2020, 6, 52–61. [Google Scholar] [CrossRef]
- Pasqualotto, D.; Rigon, S.; Zigliotto, M. Sensorless Speed Control of Synchronous Reluctance Motor Drives Based on Extended Kalman Filter and Neural Magnetic Model. IEEE Trans. Ind. Electron. 2023, 70, 1321–1330. [Google Scholar] [CrossRef]
- Wu, X.; Huang, S.; Liu, K.; Lu, K.; Hu, Y.; Pan, W.; Peng, X. Enhanced Position Sensorless Control Using Bilinear Recursive Least Squares Adaptive Filter for Interior Permanent Magnet Synchronous Motor. IEEE Trans. Power Electron. 2020, 35, 681–698. [Google Scholar] [CrossRef]
- Teng, Q.; Yang, H.; Tian, J. Nonlinear Function Integral Sliding Mode-Based Model Predictive Current Control for PMSM Drives With DC-Bus Voltage Observer. CPSS Trans. Power Electron. Appl. 2022, 7, 399–408. [Google Scholar] [CrossRef]
- Yoon, Y.-D.; Sul, S.-K.; Morimoto, S.; Ide, K. High bandwidth sensorless algorithm for AC machines based on square-wave type voltage injection. In Proceedings of the 2009 IEEE Energy Conversion Congress and Exposition, San Jose, CA, USA, 20–24 September 2009. [Google Scholar]
- Agarlita, S.C.; Boldea, I.; Blaabjerg, F. High-Frequency-Injection-Assisted “Active-Flux”-Based Sensorless Vector Control of Reluctance Synchronous Motors, With Experiments from Zero Speed. IEEE Trans. Ind. Appl. 2012, 48, 1931–1939. [Google Scholar] [CrossRef]
- Yousefi-Talouki, A.; Pescetto, P.; Pellegrino, G.; Boldea, I. Combined Active Flux and High-Frequency Injection Methods for Sensorless Direct-Flux Vector Control of Synchronous Reluctance Machines. IEEE Trans. Power Electron. 2018, 33, 2447–2457. [Google Scholar] [CrossRef]
- Huang, Y.; Yang, K.; Luo, C.; Li, R.; Luo, Y. Sensorless Model Predictive Current Control for SynRM Based on Alternate High-Frequency Square-wave Voltage Injection. In Proceedings of the 2023 IEEE International Conference on Predictive Control of Electrical Drives and Power Electronics (PRECEDE), Wuhan, China, 16–19 June 2023. [Google Scholar]
- Yu, K.; Wang, Z. Online Decoupled Multi-parameter Identification of Dual Three-Phase IPMSM Under Position-Offset and HF Signal Injection. IEEE Trans. Ind. Electron. 2023, 71, 3429–3440. [Google Scholar] [CrossRef]
- Lee, H.J.; Joo, J.E.; Lee, H.J.; Yoon, Y.D. A Torque Reference Limiter to Avoid Unstable Region of High-Frequency Signal Injection-Based Sensorless Control. In Proceedings of the 2022 IEEE Transportation Electrification Conference & Expo (ITEC), Anaheim, CA, USA, 15–17 June 2022; pp. 692–696. [Google Scholar]
- Wang, G.; Xiao, D.; Zhao, N.; Zhang, X.; Wang, W.; Xu, D. Low-Frequency Pulse Voltage Injection Scheme-Based Sensorless Control of IPMSM Drives for Audible Noise Reduction. IEEE Trans. Ind. Electron. 2017, 64, 8415–8426. [Google Scholar] [CrossRef]
- Tang, Q.P.; Shen, A.; Luo, X.; Xu, J. IPMSM Sensorless Control by Injecting Bi-directional Rotating HF Carrier Signals. IEEE Trans. Power Electron. 2018, 33, 10698–10707. [Google Scholar] [CrossRef]
- Lara, J.; Chandra, A. Performance Investigation of Two Novel HSFSI Demodulation Algorithms for Encoderless FOC of PMSMs Intended for EV Propulsion. IEEE Trans. Ind. Electron. 2018, 65, 1074–1083. [Google Scholar] [CrossRef]
- Almarhoon, A.H.; Zhu, Z.Q.; Xu, P. Improved Rotor Position Estimation Accuracy by Rotating Carrier Signal Injection Utilizing Zero-Sequence Carrier Voltage for Dual Three-Phase PMSM. IEEE Trans. Ind. Electron. 2017, 64, 4454–4462. [Google Scholar] [CrossRef]
- Weber, B.; Wiedmann, K.; Mertens, A. Increased signal-to-noise ratio of sensorless control using current oversampling. In Proceedings of the 2015 9th International Conference on Power Electronics and ECCE Asia (ICPE-ECCE Asia), Seoul, Republic of Korea, 1–5 June 2015. [Google Scholar]
- Medjmadj, S.; Diallo, D.; Mostefai, M.; Delpha, C.; Arias, A. PMSM Drive Position Estimation: Contribution to the High-Frequency Injection Voltage Selection Issue. IEEE Trans. Energy Convers. 2015, 30, 349–358. [Google Scholar] [CrossRef]
- Wang, G.; Yang, L.; Zhang, G.; Zhang, X.; Xu, D. Comparative Investigation of Pseudorandom High-Frequency Signal Injection Schemes for Sensorless IPMSM drives. IEEE Trans. Power Electron. 2017, 32, 2123–2132. [Google Scholar] [CrossRef]
- Stumberger, G.; Dolinar, D.; Hamler, A. Cross Magnetization Effect on Inductances of Linear Synchronous Reluctance Motor Under Load Conditions. IEEE Trans. Magn. 2001, 37, 3658–3662. [Google Scholar] [CrossRef]
- Im, J.-B.; Kim, W.; Kim, K.; Jin, C.-S.; Choi, J.-H.; Lee, J. Inductance Calculation Method of Synchronous Reluctance Motor Including Iron Loss and Cross Magnetic Saturation. IEEE Trans. Magn. 2009, 45, 2803–2806. [Google Scholar]
- Liu, J.M.; Zhu, Z.Q. Novel sensorless control strategy with injection of high-frequency pulsating carrier signal into stationary reference frame. IEEE Trans. Ind. Appl. 2014, 50, 2574–2583. [Google Scholar] [CrossRef]
- Wang, M.; Sun, D.; Ke, W.; Nian, H. A Universal Lookup Table-Based Direct Torque Control for OW-PMSM Drives. IEEE Trans. Power Electron. 2021, 36, 6188–6191. [Google Scholar] [CrossRef]
- Jang, J.-H.; Sul, S.-K.; Ha, J.-I.; Ide, K.; Sawamura, M. Sensorless Drive of Surface-Mounted Permanent-Magnet Motor by High-Frequency Signal Injection Based on Magnetic Saliency. IEEE Trans. Ind. Appl. 2003, 39, 1031–1039. [Google Scholar] [CrossRef]
- Bi, G.; Wang, G.; Zhang, G.; Xu, D. A Novel Demodulation Method Based High-Frequency Signal Injection for Sensorless SPMSM Control Considering Cross-Saturation Effect. In Proceedings of the 2018 IEEE 27th International Symposium on Industrial Electronics (ISIE), Cairns, Australia, 12–15 June 2018; pp. 95–100. [Google Scholar]
- Sujitha, A.; Lakshmi, L.; Mathan, N.; Narmadha, R. Analysis of an Efficient Linear Congruential Generator Architecture for Digital Applications. In Proceedings of the 2023 Fifth International Conference on Electrical, Computer and Communication Technologies (ICECCT), Erode, India, 22–24 February 2023; pp. 1–4. [Google Scholar]
- Li, C.; Wang, G.; Zhang, G.; Xu, D.; Xiao, D. Saliency-Based Sensorless Control for SynRM Drives with Suppression of Position Estimation Error. IEEE Trans. Ind. Electron. 2019, 66, 5839–5849. [Google Scholar] [CrossRef]





| Electric Machine Parameter | Value |
|---|---|
| Rated power (kW) | 3 |
| Rated current (A) | 7.6 |
| Rated voltage (V) | 360 |
| Rated speed (r/min) | 3000 |
| Phase resistance (Ω) | 0.524 |
| d-axis inductance (mH) | 51 |
| q-axis inductance (mH) | 19 |
| Pairs of poles | 2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lv, L.; Hu, Z.; Li, S.; Guo, R.; Wang, J.; Wang, G.; Li, S. Variable-Angle Random High-Frequency Voltage Injection Strategy with Cross-Saturation Effect Compensation for Sensorless Synchronous Reluctance Motor Drives. Energies 2024, 17, 725. https://doi.org/10.3390/en17030725
Lv L, Hu Z, Li S, Guo R, Wang J, Wang G, Li S. Variable-Angle Random High-Frequency Voltage Injection Strategy with Cross-Saturation Effect Compensation for Sensorless Synchronous Reluctance Motor Drives. Energies. 2024; 17(3):725. https://doi.org/10.3390/en17030725
Chicago/Turabian StyleLv, Liangnian, Ziming Hu, Sisi Li, Rui Guo, Jinpeng Wang, Gaolin Wang, and Shulin Li. 2024. "Variable-Angle Random High-Frequency Voltage Injection Strategy with Cross-Saturation Effect Compensation for Sensorless Synchronous Reluctance Motor Drives" Energies 17, no. 3: 725. https://doi.org/10.3390/en17030725
APA StyleLv, L., Hu, Z., Li, S., Guo, R., Wang, J., Wang, G., & Li, S. (2024). Variable-Angle Random High-Frequency Voltage Injection Strategy with Cross-Saturation Effect Compensation for Sensorless Synchronous Reluctance Motor Drives. Energies, 17(3), 725. https://doi.org/10.3390/en17030725





