Abstract
Aiming at the problem of ultra-low-frequency oscillation (ULFO) caused by an irrational setting of governor parameters of high-head hydraulic turbine units, this paper proposes a method to optimize the additional damping control parameters of the governor to suppress ULFO. Firstly, the mechanism of ULFO is elaborated and the effect of system damping torque on ULFO is analyzed. Secondly, Hamilton’s theory is used to rank the magnitude of each unit’s contribution to the ULFO. Then, the parameters of the damping controller are optimized using the variational modal decomposition–Hilbert transform method and the Grey Wolf Optimization algorithm. It realizes the phase compensation of the hydroelectric unit governor and suppresses the ultra-low-frequency oscillation. Finally, the proposed method is validated using the simulation conducted in CloudPSS. The test results indicate that the proposed method can effectively suppress the ULFO caused by the high-head hydroelectric unit.
1. Introduction
Traditional low-frequency oscillation refers to the oscillation frequency in the range of 0.1 Hz to 2.5 Hz. It occurs due to the insufficient damping of the system triggered by the relative oscillation between the generator rotor, which can be investigated using the small disturbance stability analysis method [1]. In recent years, there has been a recurrent observation of the phenomenon of ultra-low-frequency oscillation (ULFO) with a frequency below 0.1 Hz in systems with a relatively high total capacity of hydropower units. A few ultra-low-frequency oscillation accidents have occurred in the power system [2,3,4]. In March 2016, frequency oscillations with a duration of 25 min and a period of 20 s occurred in the Southern Power Grid during an asynchronous networking test in Yunnan, China [5]. When the ULFO occurs, all generators in the system change their speeds in synchronization, and none of the existing analysis methods can accurately assess the unit’s contribution to the ULFO. In addition, with the increasing scale of hydropower development, many high-head and large-capacity hydropower units are put into use, which brings new challenges to the suppression of ULFO in hydropower systems. Thus, it is imperative to conduct research on ULFO suppression methods of high-head, large-capacity units.
Reference [6] calculated the participation factor of the individual state variable in the ULFO mode, unveiling the contribution of the individual variable to the ULFO. Reference [7] investigated the main factors affecting the damping level of the system, including the water hammer effect and the unit operation level. It pointed out that a smaller time constant of the water hammer effect could enhance the damping torque and facilitate frequency stabilization. Meanwhile, the reduction in unit power generation in the rated power range further deteriorates the frequency stability of the system [8]. Reference [9] revealed the mechanism that generators in ULFO always oscillate at the same pace. References [10,11] provide a new means of PID parameter optimization by comparing the damping characteristics of different control modes of the governor to select the governor control mode. Meanwhile, a practical PID parameter tuning strategy for the hydraulic turbine governor is proposed to suppress the ULFO. Reference [12] designed a full-feedback robust stabilization controller to suppress the oscillations, and the method can effectively improve the speed performance of a black start. Reference [13] used a QSS model to efficiently coordinate the design of PSS4B type stabilizers to improve frequency dynamics. Reference [14] proposed a governor parameter optimization model based on the characteristics of frequency oscillation. Reference [15] proposed a particle swarm optimization algorithm based hydraulic turbine governor parameter optimization to improve the stability of the system. Reference [16] compared the effect of PSS and GPSS to improve the damping ratio, and the results show that GPSS control has higher involvement and controllability. Reference [17] designed an additional stabilizer that effectively suppresses damped, low-frequency, inter-area oscillations. Reference [18] designed an additional damper for the hydraulic turbine governor suitable for ultra-low-frequency oscillations to improve the safety of the system.
This paper analyzes the mechanism of ULFO generation in high-head and large-capacity units. Then, it calculates the amount of energy change in the generator injection system based on the Hamiltonian energy function and ranks the contribution of the ULFO of the unit. At the same time, this paper proposes a ULFO suppression method. The method is based on the governor additional damping control. The phase compensation of the hydraulic turbine governor is realized by optimizing the parameters of the additional damping controller through the variational mode decomposition algorithm and the Gray Wolf Optimization (GWO) algorithm. The simulation results indicate that the contribution of the hydropower unit to the ULFO can be evaluated using the proposed method and the suppression of the ULFO can be realized. The parameters and their implications are shown in Table 1.

Table 1.
Description of symbols in this paper.
The main contributions of the paper are threefold: (1) The mechanism of ULFO generation in high-head and large-capacity is analyzed in this paper, which considers the elastic water strike model of the diversion pipes. (2) A Hamiltonian function-based method for calculating the amount of energy change in the generator injection system is proposed to rank the contribution of the ULFO of the unit. (3) An ULFO suppression method based on the governor additional damping control and GWO is proposed. It can realize the phase compensation of the turbine governor and suppress the ULFO of the high-head, large-capacity units.
2. Ultra-Low-Frequency Oscillation Mechanism
When the ULFO occurs, there is no relative oscillation between the units. Therefore, the synchronization network can be equated to a single system and the frequency changes of each node in the system at the same time are the same. A single-machine infinite-bus system is employed to investigate the mechanism of ULFO generation, which is shown in Figure 1.
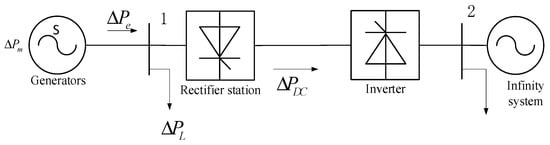
Figure 1.
Single-machine infinite-bus system, where
is the change in generator mechanical power, is the change in generator electromagnetic power, is the change in local load power, and is the change in DC delivered power.
The equations of motion of the generator rotor in Figure 1 can be written as follows:
where denotes the time constant of inertia, denotes the generator mechanical torque, and denotes the generator electromagnetic torque. Both electromagnetic and mechanical torque can be written in the form of the vector sum of torque-damping components and torque-synchronizing components:
where represents the mechanical torque-damping component, represents the mechanical torque-synchronizing component, represents the electromagnetic torque-damping component, and represents the electromagnetic torque-synchronizing component. The result of bringing Equation (2) into Equation (1) can be represented by the following equation:
ULFO is a small disturbance stability problem, which occurs when the generator damping torque is negative, i.e., .
The generator damping factor always provides positive damping since . When the network losses are neglected, the electromagnetic torque can be considered to be supplied by both the local load and the DC in the system of Figure 1. The mechanical torque of the generator is provided by the governor. The effect of the governor on the damping component of the mechanical torque is investigated by taking a high-head hydro generator as an example in the following.
The schematic diagram of the high-head hydraulic turbine governor is illustrated in Figure 2, where is the frequency variation and is the mechanical torque of the hydraulic turbine. The transfer function of the PID governor used in this paper is given by Equation (4). Furthermore, due to the long water diversion pipe of the high-head turbine, the traditional rigid turbine model is not suitable. Therefore, this paper uses the elastic water hammer model to represent the transfer of the high-head turbine generator, which is denoted by in Equation (5):
where is the differential coefficient, is the proportionality coefficient, is the integration coefficient, is the modulation coefficient, is the time constant of the mechanical system, is the time constant of the water hammer effect, and is the time of reflection of the pipeline. Assuming that the ULFO corner frequency is , is brought into Equation (6) to obtain Equation (7), is the mechanical torque damping component, and is the total damping coefficient of the governor and the hydraulic turbine.
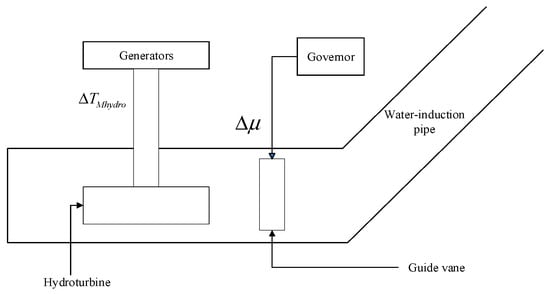
Figure 2.
Hydraulic turbine governor model.
The positive or negative of is determined by the cosine of the sum of the governor phase displacement and the turbine phase displacement. When , the governor provides positive damping to the system. and are in the same direction. When , and the generator damping coefficient D are not the same number. Then, governor provides negative damping for the system and and are reversed.
The principle of negative damping generated by governor is shown in Figure 3. When is in the second quadrant, the projection on the coordinate axis is reversed with . Therefore, the mechanical torque-damping component is negative and the governor provides negative damping to the system. When the negative damping torque provided by the governor is greater than the positive damping torque provided by the other devices, the total system damping torque will be negative and ULFO will occur. When is in the second quadrant, the damping capability of the generator is improved if an additional mechanical torque is provided in the third quadrant. And, the larger the amplitude, the smaller the phase angle difference of with , the larger the positive damping component provided by , and the more obvious the effect on the system damping enhancement. In Figure 3, has a larger amplitude and smaller phase angle difference of compared to . Thus, is more effective for system damping enhancement.
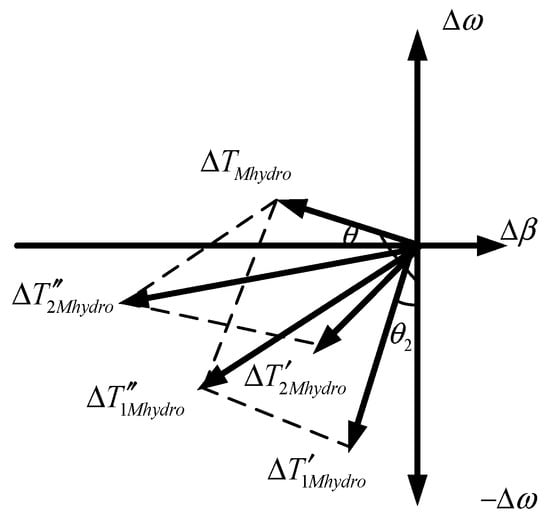
Figure 3.
Principle of negative damping generated by the governor.
3. Assessment of the Contribution of Ultra-Low-Frequency Oscillations in High-Head Units Based on Hamilton’s Theory
The Hamiltonian system describes an open system that can exchange energy with the outside world and has energy dissipation and generation. There are strict definitions and mathematical expressions for the energy exchanges between the system and the outside world as well as for the inner energy structure of the system. The calculation of the amount of energy change in the generator injection network based on Hamilton’s theory allows for an assessment of the unit’s contribution to the ultra-low-frequency oscillations.
A system is considered:
where M is an n-dimensional manifold and is an arbitrary vector field. If there is a Hamiltonian function , the system (8) be expressed as follows:
Then, it can be argued that there exists a generalized Hamiltonian realization of the system (8), where is the structure matrix. can be further decomposed to obtain the following:
where is an antisymmetric matrix, is a symmetric matrix, and and are symmetric, semi-positive definite matrices.
Figure 4 shows the energy transfer structure between the hydraulic turbine and the power grid. is the change in the mechanical power of the governor; is the change in output power of the hydraulic turbine.

Figure 4.
Energy transfer structure of hydraulic turbine machine.
A Hamiltonian realization of Equation (10) is performed and the Hamiltonian function is shown in Equation (11).
The Hamilton function represents the total energy of the generator (kinetic energy + potential energy), and the derivative of the rotor equation of motion with respect to the state variable x is as follows:
The Hamilton realization of Equation (11) can then be expressed in Equation (13).
Among them,
Simultaneous multiplication of both sides of Equation (13) by the Hamiltonian operator yields the energy flow equation for the generator system as shown in Equation (15):
where denotes the rate of change of energy injected into the power system by the generator; is the rate of change of kinetic energy stored in the generator; denotes the rate of change of energy dissipated by the generator; denotes the rate of change of the energy produced by the generator, which is zero; and denotes the rate of change of energy input into the generator by the prime mover. , , , and can be expressed as Equation (16):
Equation (15) can also be rewritten as Equation (17):
From Equation (17), the rate of change of energy injected into the power system by the generator is equal to the rate of change of energy injected into the generator by the prime mover minus the rate of change of the energy dissipated by the generator and the rate of change of the stored energy (kinetic energy) of the generator. The increment of energy injected into the network by the generator can be obtained by integrating over time, which is defined as the Hamiltonian energy of the unit . It can be expressed using Equation (18):
When continues to decrease and the slope of the characteristic curve is less than 0, it indicates that the energy injected by the generator into the network gradually decreases, which is conducive to the stability of the system and indicates that the unit’s contribution to the ULFO is small. When continues to increase and the slope of the characteristic curve is greater than 0, it shows that the energy injected into the network by the generator continues to increase, which is not conducive to system stabilization and indicates that the unit has a large contribution to the ULFO. In addition, the larger the , the larger the contribution of the unit to the ULFO.
4. Identification of System Modal Parameters Based on Variational Modal Decomposition–Hilbert Transform Method
Variational Mode Decomposition (VMD) is an adaptive, fully non-recursive approach to modal variation and signal processing. This method can determine the number of modal decompositions and realize the effective separation of Intrinsic Mode Functions (IMF). It is reliable to obtain the optimal solution when dealing with the variational problem. Compared with other methods, it has a more solid mathematical theoretical foundation, which is suitable for the processing of non-smooth signals.
For the signal , its constrained variational model expression is as follows:
where denotes the unit pulse function, means convolution operation, , , and denotes the center frequency of each mode.
To find the optimal solution, the augmented generalized Lagrange function is constructed as follows:
where is the quadratic penalty factor and is the Lagrange operator.
The decomposed components of the response signal can be obtained using the alternating multiplier algorithm to solve Equation (20). The modal component and the center frequency are expressed as follow:
where is the Wiener filter of the current signal, is the center frequency of the power spectrum of the current modal function, and denotes the Fourier inverse transform. The real part is removed to obtain the time domain modal component.
The Hilbert transform is an important mathematical tool in the field of signal processing, which can estimate the instantaneous frequency and amplitude of the signal. However, the Hilbert transform can only identify narrowband signals. Therefore, the Hilbert transform is combined with the VMD method in this paper.
The HT transformation is applied to each IMF component obtained via VMD:
The parsing signals are constructed as follows:
Then, the instantaneous amplitude and instantaneous phase of the IMF component are as follows:
The instantaneous frequency is as follows:
The instantaneous amplitude–frequency characteristics of the signal can be further computed to obtain the time–domain expression of the system under step perturbation. Furthermore, the low-order linearized model of the system that contains the most dominant modes of the system is obtained.
5. Research on ULFO Suppression Method Based on Additional Damping Controller
5.1. Analysis of the Principle of Suppressing ULFO Oscillation via Additional Damping Control of Hydraulic Turbine Governor
When the hydroelectric unit provides negative damping torque to the system, the projection of on the coordinate axis is reversed with and the unit contributes to the ULFOs. When the hydropower unit provides positive damping torque to the system, the projection of on the coordinate axis is in the same direction as and the unit’s contribution to the ULFO is small.
If an additional mechanical torque located in the third quadrant is provided so that the projection of the synthesized mechanical torque on the axes of is in the same direction as , the mechanical torque damping coefficient is of the same sign as the generator damping coefficient D. And, the generator damping characteristics are improved. The larger the amplitude of , the smaller the phase angle difference of with and the more obvious the effect on system damping enhancement.
5.2. Design of Additional Damping Controller for Hydraulic Turbine Governor
To improve the damping characteristics of the hydroelectric unit governor, an additional damping controller link is added to the high-head hydroelectric unit governor model [18,19]. The hydroelectric unit governor model with the additional damping controller is shown in Figure 5.
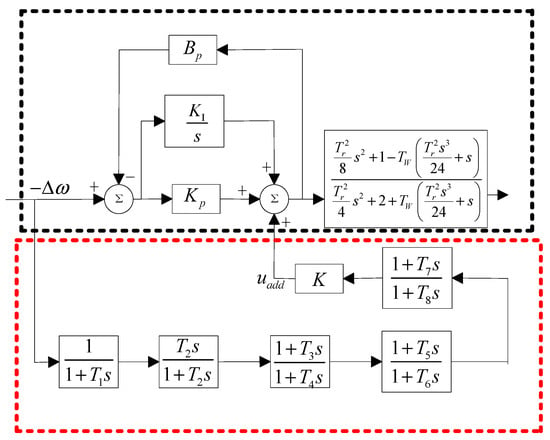
Figure 5.
Modified hydroelectric unit governor model considering the additional damping control.
An additional damping controller is shown within the red dashed line in Figure 5. Its input signal is the system frequency deviation signal and its output signal is the additional opening reference signal , which is accessed before the mechanical system link of the governor. The phase adjustment of the original mechanical torque can be realized by adding to the output signal vector of the PID regulator.
The first link of the additional damping controller is the low-pass filter and the second link is the isolation link. The others are the phase compensation links. The ULFO frequency range is 0.01~0.1 Hz. Therefore, the low-pass filter link is designed with a cutoff frequency of 0.1 Hz to filter out the high-frequency component. It can also prevent the additional damping controller from operating incorrectly in cases of low-frequency oscillations, sub-synchronous oscillations, and other stability problems. The cutoff frequency of the isolation link is 0.01 Hz, which is used to filter out the DC component. The phase compensation link adopts first-order phase compensation. is the gain link for adjusting the size of the output signal of the additional damping controller.
The amplitude and phase angle of the additional mechanical torque are greatly affected by the time constant and gain coefficient of the phase compensation link. These parameters can be optimized by using the improved GWO algorithm.
5.3. The Grey Wolf Optimization Algorithm
To realize the optimization of the parameters of the additional damping controller, the modal parameters of the unit’s ultra-low-frequency oscillations are first identified based on the VMD–Hilbert transform method. Then, the minimum damping ratio calculated using the algorithmic identification is used as the adaptive value, which is used to optimize the time constant and the gain coefficient in the additional damping controller combined with the improved GWO algorithm.
5.3.1. Basic Grey Wolf Optimization Algorithm
The GWO algorithm draws inspiration from the hunting mechanism of grey wolves. It has many advantages, such as having a simple principle, fewer parameters to adjust, easy implementation, a strong global search capability, etc. In the optimization process, the possible solutions are regarded as wolves, and the optimal solution among all the solutions is regarded as the prey [20]. The solutions are graded and searched until the optimal solution is found by considering the hierarchical ordering of the wolves and the hunting technique; each solution is categorized and searched until finding the best solution.
In the structure of the GWO algorithm, individuals in a wolf pack are categorized into four classes based on factors related to physical strength, intelligence, leadership, and age, from top to bottom: , , and . One of the wolves, wolf, is the leader of the pack, the optimal individual in the pack, and has the right to make important decisions, such as hunting, bedtime, and wake-up time. The wolf belongs to the second rank, and is second only to the . The second is the wolf, and the remaining are the wolves. The hunting process is decided and guided by , , and wolves, with wolves at the bottom of the hierarchy following the instructions of high-level wolves to hunt.
In the GWO algorithm, the best three solutions obtained in each iteration are given to , , and wolves, and the other grey wolves change their positions according to , , and wolves. They are expressed using the following equations:
where , , and are the distances of the th individual from , , and at generation q, respectively. , , and are the locations of , , and at generation , respectively. ; represents the random numbers between 0 and 1.
Subsequently, other individuals in the pack use the positions between , and to determine the location of the prey and encircle it, which can be expressed as follows:
where is the updated position of the th individual, , , is the current number of iterations, and is the maximum number of iterations; , , and are the moving orientation of each wolf after being influenced by , , and wolf, respectively. The moving direction of the prey can be judged using Equation (33) and the global optimal solution can be found through a continuous iterative search.
5.3.2. Improved Grey Wolf Optimization Algorithm
- (1)
- Tent-mapping-based population initialization
Employing a uniformly distribuSted initial population in the search space is favorable to improve the efficiency of the GWO algorithm. The initial grey wolf population of the traditional GWO algorithm is randomly generated, which may result in a local optimum. Chaotic sequences are characterized by better regularity and ergodicity. Tent mapping yields a more evenly balanced sequence distribution compared to other mappings. Therefore, it is employed to initialize the gray wolf population in this paper. Tent mapping is given by the following:
A highly uniform distribution sequence is generated when u = 0.5. In this case, Equation (34) is changed to the following:
Then, the population X is denoted as follows:
where and are the upper and lower bounds of the search, respectively.
- (2)
- Adaptive Adjustment Weighting Factor
To meet the requirements of the GWO algorithm at different times, adaptive weight is introduced in the position update:
where and are the upper and lower limits of the weight, respectively; is the number of iterations. In this paper, and .
The is larger at the beginning of the algorithm iteration, which facilitates the global search of the algorithm. gradually decreases at the end of the iteration, which enables the gray wolf to better search for the better solution around the prey.
The improved positional equations are shown in Equations (38)–(40).
5.3.3. Optimization Conditions and Constraints
To optimize the additional damping controller parameters to enhance the damping of the system’s ULFOs, the fitness function is defined as follows:
where denotes the damping ratio of the ULFO mode. It can be recognized using the VMD–Hilbert algorithm. The objective function and constraints of the improved gray wolf optimization algorithm are described using Equation (42):
The objective function max indicates that the optimization direction is to select the value with a large adaptation value as the optimal solution. The larger the adaptation value , the larger the damping ratio of the corresponding ULFO mode, which is conducive to improving the suppression ability of ULFO. Due to the low ULFO frequency, the typical range of the time constant is between 1 and 6 and the typical range of the gain coefficient is between 0.1 and 1.
6. Ultra-Low-Frequency Oscillation Suppression Method
The ULFO suppression method based on the additional damping controller of the hydroelectric unit governor is shown in Figure 6 with the following steps:
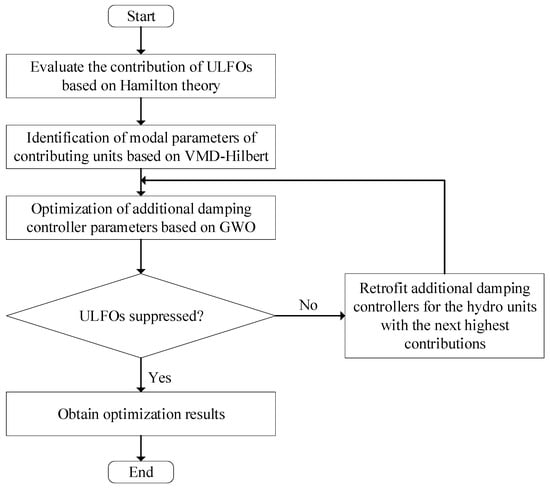
Figure 6.
Flowchart of the ultra-low-frequency oscillation suppression method.
- (1)
- Construct the Hamiltonian energy function: calculate the Hamiltonian energy of the hydropower unit and evaluate it, and rank the contribution of the ULFO of the hydropower unit.
- (2)
- Use the VMD–Hilbert algorithm to identify the low-order linearized model of the hydroelectric units with a high contribution degree, which can describe the relationship from the opening degree to the frequency.
- (3)
- According to the order of contribution from high to low, additional damping controllers are installed for the hydropower units with large contributions. The controller parameters are optimized using the Grey Wolf Optimization algorithm.
- (4)
- Verify whether the ULFOs are suppressed by simulations and output the final optimization results.
7. Case Studies
To validate the effectiveness of the proposed method for the suppression of ULFOs of high-head and large-capacity hydropower units, an improved 4M2A system model and an AC/DC grid model are constructed in CloudPSS.
7.1. Simulation Validation in Improved 4M2A System
- (1)
- Simulation model and load step perturbation
The simulation test system shown in Figure 7 is obtained based on the standard 4M2A model.
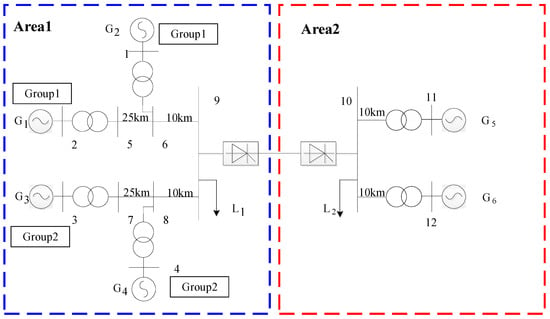
Figure 7.
Improved 4M2A system.
The DC sender side is area 1 and the receiver side is area 2. Area 1 contains four hydro generators and area 2 contains two hydro generators. All hydro generators are high-capacity hydro units with high head. The rated capacity is 900 MV·A. The DC system is rated to deliver power of 400 MW. The load L1 in the area 1 is 2188 MW and the load L2 in area 2 is 1854 MW. The DC delivery power is 400 MW. The generator governor model of area 1 is shown in Figure 5 and the governor parameters are shown in Table 2.

Table 2.
G1–G4 hydroelectric unit governor parameters.
The load disturbance is simulated using a loss of 100 MW load power in area 1 at . The frequency of area 1 is shown in Figure 8.
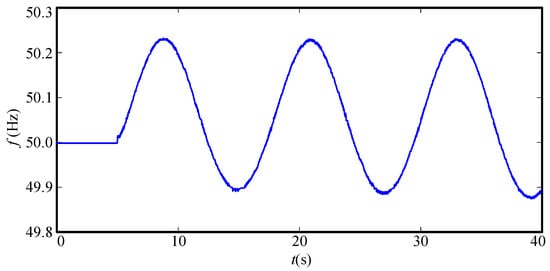
Figure 8.
Frequency of area 1.
After the load disturbance, the ULFO occurs, whose frequency is 0.064 Hz and damping ratio is −0.003. To inhibit the ULFO, it is necessary to rank the contribution degree of the ULFO of the unit. Then, the additional damping controllers need to be installed on the units with large contribution degrees and the parameters of the controllers need to be optimized.
- (2)
- Hamilton energy-based ranking of unit ULO contributions
The energy increments injected into the network by generators G1–G4 are calculated and shown in Figure 9. It is obvious that the of G1 and G2 gradually increases with time, which indicates a continuous increase in the energy injected into the system. In contrast, the of G3 and G4 gradually decreases with time, which indicates a continuous decrease in the energy injected into the system. By comparing the Hamiltonian energy of the units, the ordering of the contribution of the hydroelectric units to the ULFO is assessed as G1 = G2 > G3 = G4.
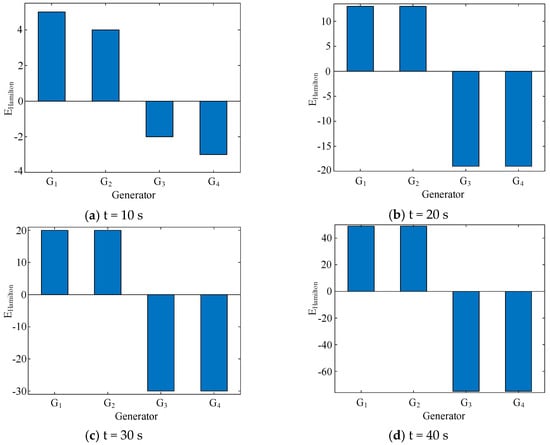
Figure 9.
of generators G1–G4 at different moments.
- (3)
- Additional damping controller parameter optimization
To suppress the ULFOs, additional damping controllers are installed on the governors of G1 and G2. G1 is taken as an example to explain the optimization process of additional damping controller parameters.
Since the frequency of the ULFO is 0.01 Hz to 0.1 Hz, the time constant of the filter is set to 1.59 and is set to 15.9.
The step perturbation of the opening degree of G1 is simulated to identify the system model. At , 2% opening degree step perturbation occurs at the outlet of the G1 governor. The system frequency change is selected as the identification signal to obtain the system model based on the VMD–Hilbert identification algorithm:
A closed-loop simulation system is built in CloudPSS considering the G1 generator governor, the additional damping controller, and the linearized model of the grid-connected system of the high-head, large-capacity unit. The structural diagram of the closed-loop model is illustrated in Figure 10. The parameters of the additional damping controller are optimized using the improved GWO algorithm. The population size is set to 50 and is 100. G2 additional damping controller time constants and gain coefficients are optimized as above. The optimized G1 and G2 additional damping controller parameters are shown in Table 3.
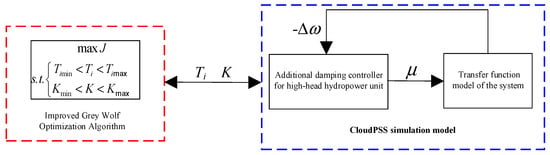
Figure 10.
The structural diagram of the closed-loop model.

Table 3.
G1/G2 additional damping controller parameters.
G1 is taken as an example to analyze the effect of the additional damping controller on the phase angle difference θ between the mechanical torque ΔTMhydro and system frequency −Δω. It can be found that when the G1 generator is equipped with the additional damping controller the phase angle difference θ decreases by 52° under the ULFO mode 0.064 Hz. At this time, the G1 hydroelectric unit provides positive damping.
When the G1 and G2 generator governors are equipped with additional damping controllers, the same load step disturbance is simulated and the system frequency of different optimization methods is shown in Figure 11. It can be seen that when the G1 and G2 generator is equipped with additional damping controller the main vibration mode of the system frequency is almost unchanged. The damping ratio is increased from −0.003 to 0.325 and the ULFO is effectively suppressed. Furthermore, it can be seen that GWO has a better performance than PSO in optimizing the parameters of the additional damping controller, which shows the effectiveness of the proposed method.
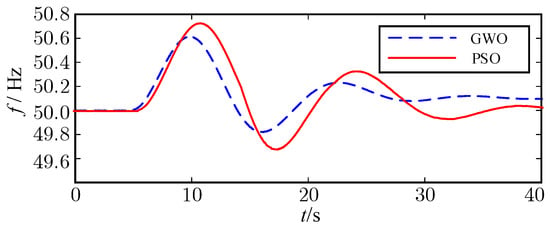
Figure 11.
Frequency response of load disturbance with additional damping controller.
7.2. Analysis and Verification of ULFO Suppression in Large-Scale AC and DC Power Grids
To validate the effectiveness of the proposed method on AC and DC networks, a simulation model as shown in Figure 12 is built in the CloudPSS platform. The model includes a total of 197 nodes, among which the 500 kV main grid is 85 nodes. The hydroturbine model of the high-head, large-capacity unit is accessed on Gen1A-1, Gen1A-3, and Gen1B-2, respectively. The N-1 fault between the bus1A-17 and the bus1A-13 line is set up at 25 s, at which time the system generates ULFOs. The frequency response of the system after the fault is shown in Figure 13.
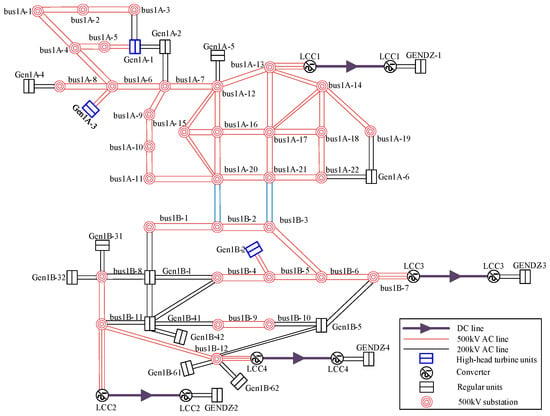
Figure 12.
Large-scale AC/DC grid with high-capacity turbine units with high head.
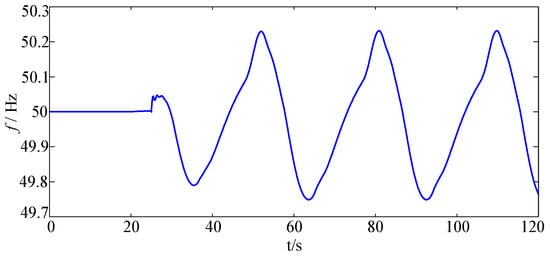
Figure 13.
Frequency response of the system after the fault.
After the fault, the ULFO occurs and the frequency of the ULFO is 0.0345 Hz. To suppress the ULFO of the AC/DC power grid, the damping controller is added and the parameter optimization is carried out using the method described above. The frequency waveform with damping control is finally obtained and illustrated in Figure 14. It can be seen that the proposed method can effectively suppress the ULFO phenomenon of high-capacity hydraulic turbine units with high head in large-scale AC/DC power grid, which is conducive to the frequency stability of the system. In addition, it also shows that GWO has better optimization compared with PSO.
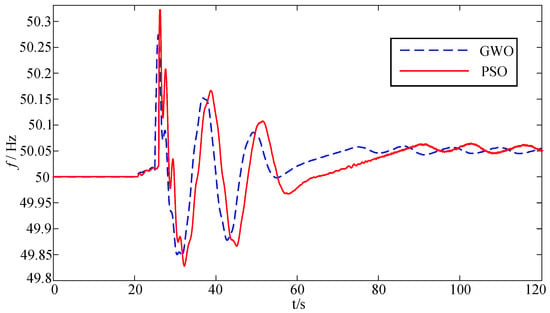
Figure 14.
Frequency response of the system with additional damping controller.
8. Conclusions
In this paper, an analytical model of ULFO is established. Then, the damping characteristics of the hydraulic turbine governor with high head are explored based on the frequency domain analysis, which points out that the negative damping provided by the hydraulic turbine governor is the fundamental reason for the generation of the ULFO. Based on the Hamiltonian energy function calculation, the change in the amount of energy injected into the network by the generator is obtained and the ordering of the contribution of the hydropower unit to the ULFO is realized. To suppress the ULFOs and improve the damping characteristics of the hydraulic turbine governor, this paper proposes a ULFO suppression method. Specifically, an additional damping controller for the governor of the hydropower unit is designed. Then, the improved GWO algorithm and the VMD–Hilbert identification algorithm are applied in the optimal design of the parameters of the additional damping controller. The results show that the contribution of the hydroelectric unit to the ULFO can be evaluated and the ULFO can be effectively suppressed.
Author Contributions
Conceptualization, S.Z. and S.G.; methodology, L.L. and W.L.; software, W.L. and D.L.; validation, S.Z. and L.L.; formal analysis, S.Z. and W.L.; investigation, D.L.; resources, W.L.; data curation, P.Z. and B.Z.; writing—original draft preparation, B.Z. and H.H.; writing—review and editing, S.Z. and B.Z.; visualization, D.L.; supervision, S.G. and Y.W.; project administration, S.Z. and Y.W.; funding acquisition, S.Z. and Y.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the Scientific Research Project of China Three Gorges Construction Engineering Corporation (JGJD0323002).
Data Availability Statement
All data are contained within the article.
Conflicts of Interest
Authors Sixiang Zhang, Weijun Liu and Daijun Luo were employed by China Three Gorges Construction Engineering Corporation. Authors Longyuan Li and Peng Zou were employed by Southwest Electric Power Design Institute Co., Ltd. of China Power Engineering Consulting Group. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Kundur, P. Power System Stability and Control; McGraw-Hill: New York, NY, USA, 1994. [Google Scholar]
- Seppänen, J.; Lehtonen, M.; Kuivaniemi, M.; Haarla, L. Long Term Characteristics of Ultra Low Frequency Oscillations in the Nordic Power System. In Proceedings of the 2022 IEEE PES Innovative Smart Grid Technologies Conference Europe (ISGT-Europe), Novi Sad, Serbia, 10–12 October 2022; pp. 1–5. [Google Scholar] [CrossRef]
- Pico, H.V.; McCalley, J.D.; Angel, A.; Leon, R.; Castrillon, N.J. Analysis of Very Low Frequency Oscillations in Hydro-Dominant Power Systems Using Multi-Unit Modeling. IEEE Trans. Power Syst. 2012, 27, 1906–1915. [Google Scholar] [CrossRef]
- Chen, Y.; Liu, Y.; Tang, Z.; Hou, J.; Zhang, Y.; Mo, W.; Chen, H. Analysis of ultra-low frequency oscillation in yunnan asynchronous sending system. In Proceedings of the 2017 IEEE Power & Energy Society General Meeting, Chicago, IL, USA, 16–20 July 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Liu, C.X.; Zhang, J.F.; Chen, Y.P. Mechanism analysis and simulation on ultra low frequency oscillation of Yunnan power grid in asynchronous interconnection mode. Southern Power Syst. Technol. 2016, 10, 29–34. [Google Scholar]
- Teng, Y.; Zhang, P.; Han, R.; Fan, C.; Wang, X.; Jiang, Z.; Zhang, C.; Sun, Y.; Gong, Y.; Yi, J. Mechanism and Characteristics analysis of Ultra-low Frequency Oscillation phenomenon in a Power Grid with a High Proportion of Hydropower. In Proceedings of the 2018 International Conference on Power System Technology (POWERCON), Guangzhou, China, 6–8 November 2018; pp. 575–584. [Google Scholar] [CrossRef]
- Han, X.; Jiang, Q.; Liu, T.; Li, B.; Ding, L.; Chen, G. Research on Ultra-Low Frequency Oscillation Caused by Hydro Power in Hydro-Dominant Power System. In Proceedings of the 2018 International Conference on Power System Technology (POWERCON), Guangzhou, China, 6–8 November 2018; pp. 1909–1914. [Google Scholar] [CrossRef]
- Mo, W.; Chen, Y.; Chen, H.; Liu, Y.; Zhang, Y.; Hou, J.; Gao, Q.; Li, C. Analysis and Measures of Ultralow-Frequency Oscillations in a Large-Scale Hydropower Transmission System. IEEE J. Emerg. Sel. Top. Power Electron. 2018, 6, 1077–1085. [Google Scholar] [CrossRef]
- Wang, P.; Li, B.; Zhao, J.; Liu, T.; Jiang, Q.; Chen, G. The Mechanism of Ultra-Low Frequency Oscillations With the Same Mode Shapes. IEEE Access 2020, 8, 198047–198057. [Google Scholar] [CrossRef]
- Chen, G.; Tang, F.; Shi, H.; Yu, R.; Wang, G.; Ding, L.; Liu, B.; Lu, X. Optimization Strategy of Hydrogovernors for Eliminating Ultralow-Frequency Oscillations in Hydrodominant Power Systems. IEEE J. Emerg. Sel. Top. Power Electron. 2018, 6, 1086–1094. [Google Scholar] [CrossRef]
- Chen, G.; Han, X.; Wang, G.; Zhang, Y.; Zhang, H.; Ai, D.; Tang, F.; Wang, L.; Shi, H. Practical Strategy for Adjusting Parameters of Hydro-Governors in Hydro-Dominant Power Systems Accommodating Asynchronous Interconnection. In Proceedings of the 2018 International Conference on Power System Technology (POWERCON), Guangzhou, China, 6–9 November 2018; pp. 585–590. [Google Scholar] [CrossRef]
- Pico, H.N.V.; Aliprantis, D.C.; McCalley, J.D.; Elia, N.; Castrillon, N.J. Analysis of Hydro-Coupled Power Plants and Design of Robust Control to Damp Oscillatory Modes. IEEE Trans. Power Syst. 2015, 30, 632–643. [Google Scholar] [CrossRef]
- Rimorov, D.; Kamwa, I.; Joós, G. Quasi-Steady-State Approach for Analysis of Frequency Oscillations and Damping Controller Design. IEEE Trans. Power Syst. 2016, 31, 3212–3220. [Google Scholar] [CrossRef]
- Chen, L.; Lu, X.; Min, Y.; Zhang, Y.; Chen, Q.; Zhao, Y.; Ben, C. Optimization of Governor Parameters to Prevent Frequency Oscillations in Power Systems. IEEE Trans. Power Syst. 2018, 33, 4466–4474. [Google Scholar] [CrossRef]
- Liu, C.; Shi, H.; Chen, G.; Zhang, H.; Han, X.; Ding, L.; Fan, C. Governor Parameters Optimization Strategy and Support System for Hydro-dominant Power Systems. In Proceedings of the 2018 International Conference on Power System Technology (POWERCON), Guangzhou, China, 6–8 November 2018; pp. 254–259. [Google Scholar] [CrossRef]
- Shi, X.; Cai, W.; Shi, H.; Ron, H.; Liang, T.; Wang, Y.; Zhang, M. Analysis of Ultra-Low Frequency Oscillation in Hydro-Dominant Power System and Suppression Strategy by GPSS. IEEE Trans. Ind. Appl. 2023, 59, 2796–2806. [Google Scholar] [CrossRef]
- Mantzaris, J.C.; Metsiou, A.; Vournas, C.D. Analysis of Interarea Oscillations Including Governor Effects and Stabilizer Design in South-Eastern Europe. IEEE Trans. Power Syst. 2013, 28, 4948–4956. [Google Scholar] [CrossRef]
- Wang, G.; Tang, Y.; Li, Y.; Ai, D.; Chen, G.; Wei, W. Control Method for Additional Damper in Hydro-turbine Speed Governor of Hydro-dominant Power Systems. CSEE J. Power Energy Syst. 2020, 9, 589–598. [Google Scholar] [CrossRef]
- Yunhao, W.; Wei, L.; Bo, F.; Yong, J. An Additional Damping Strategy Base on Central Filter for Ultra-low Frequency Oscillation Suppression. In Proceedings of the 2022 4th International Conference on Power and Energy Technology (ICPET), Beijing, China, 28–31 July 2022; pp. 1232–1236. [Google Scholar]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).