Research on a Two-Layer Optimal Dispatching Method Considering the Mutual Aid of Peak Regulating Resources among Regional Power Grids
Abstract
1. Introduction
2. System Peak Regulating Resource Analysis
2.1. Analysis of Different Power Supplies
2.2. Analysis of Coal-Fired Thermal Units’ Energy Consumption Costs
2.3. Analysis of Pumped Storage Units’ Peak Regulating Costs
3. Two-Layer Optimization Dispatching Model of the Regional Power Grid
3.1. Introduction of the Model
3.2. Units’ Optimization Dispatching Model in Each Province
3.2.1. Objective Function
3.2.2. Constraints
System Power Balance Constraints
Thermal Power Unit Climbing Constraints
Pumped Storage Operation Constraints
Upper and Lower Limits of Thermal Power Units
3.3. Analysis of Peak Regulation Amplitude and Gap between Provinces in the Regional Power Grid
3.4. Optimization Scheduling Model of Inter-Provincial Transmission Curves
3.4.1. Objective Function
3.4.2. Constraints
Transmission Limit Constraints
Constraints of Transmission Power Limitation
4. Case Study
4.1. Example System Analysis Based on IEEE RTS-96
4.1.1. Overview of the Example System
4.1.2. Analytical Calculation
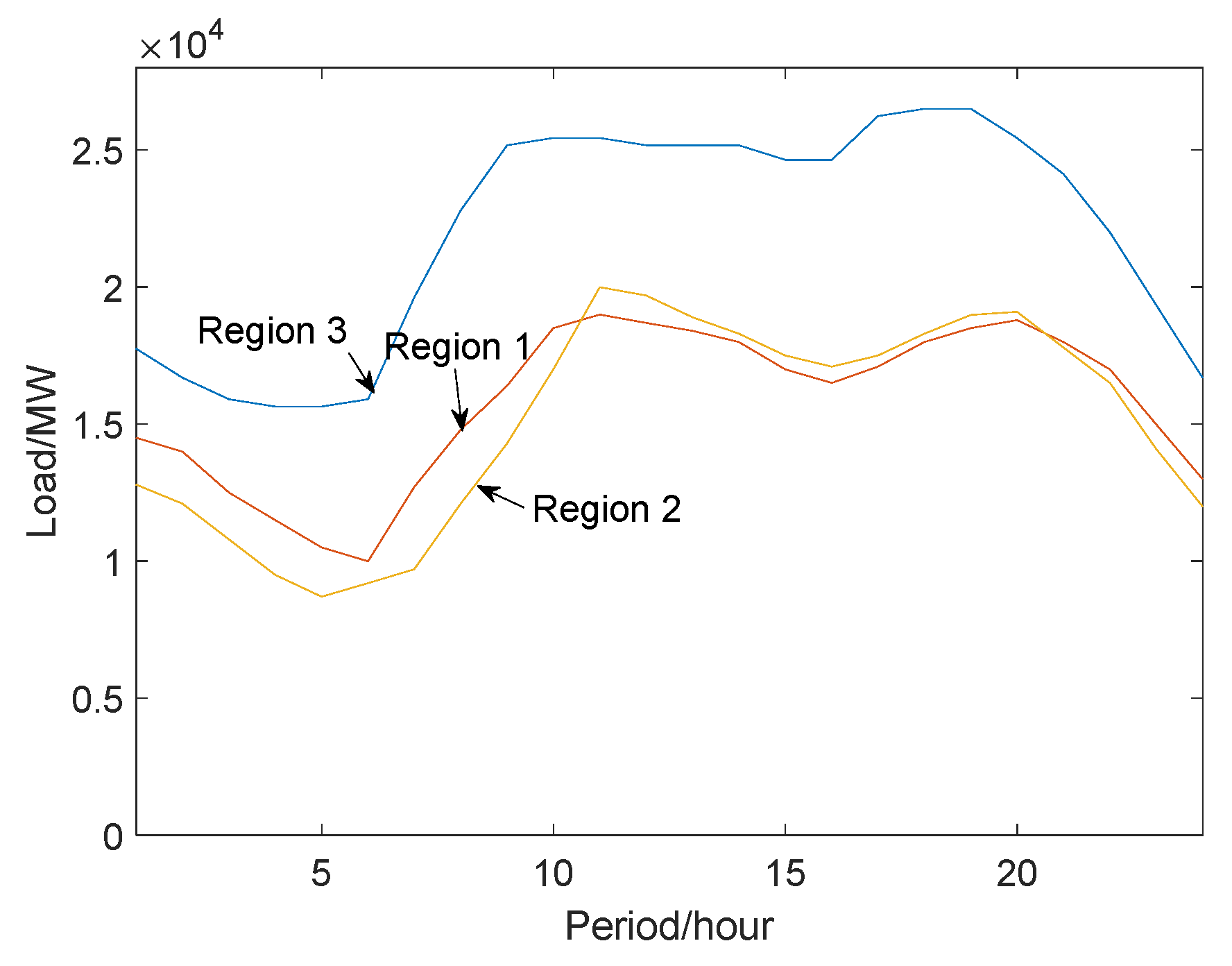
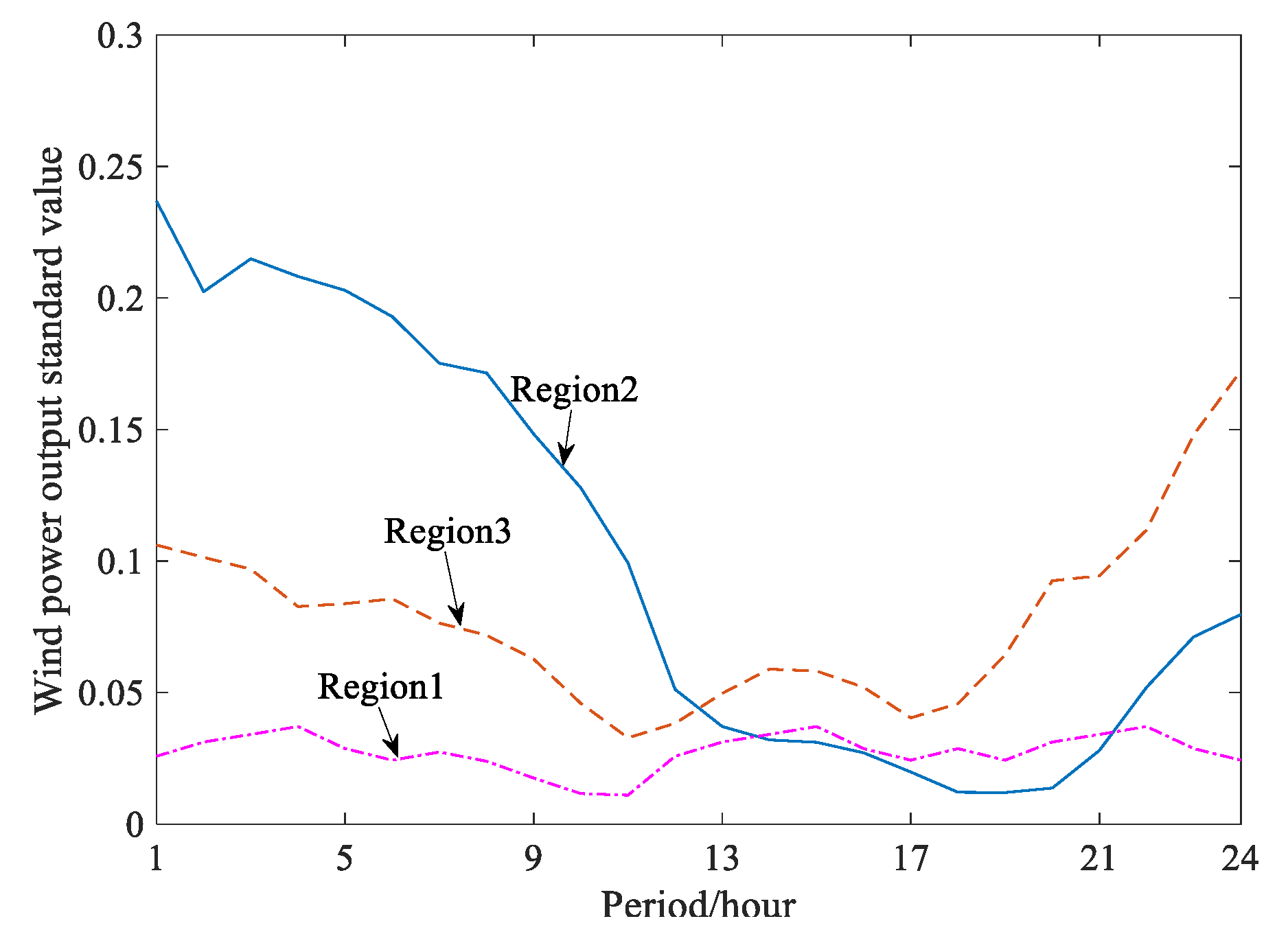
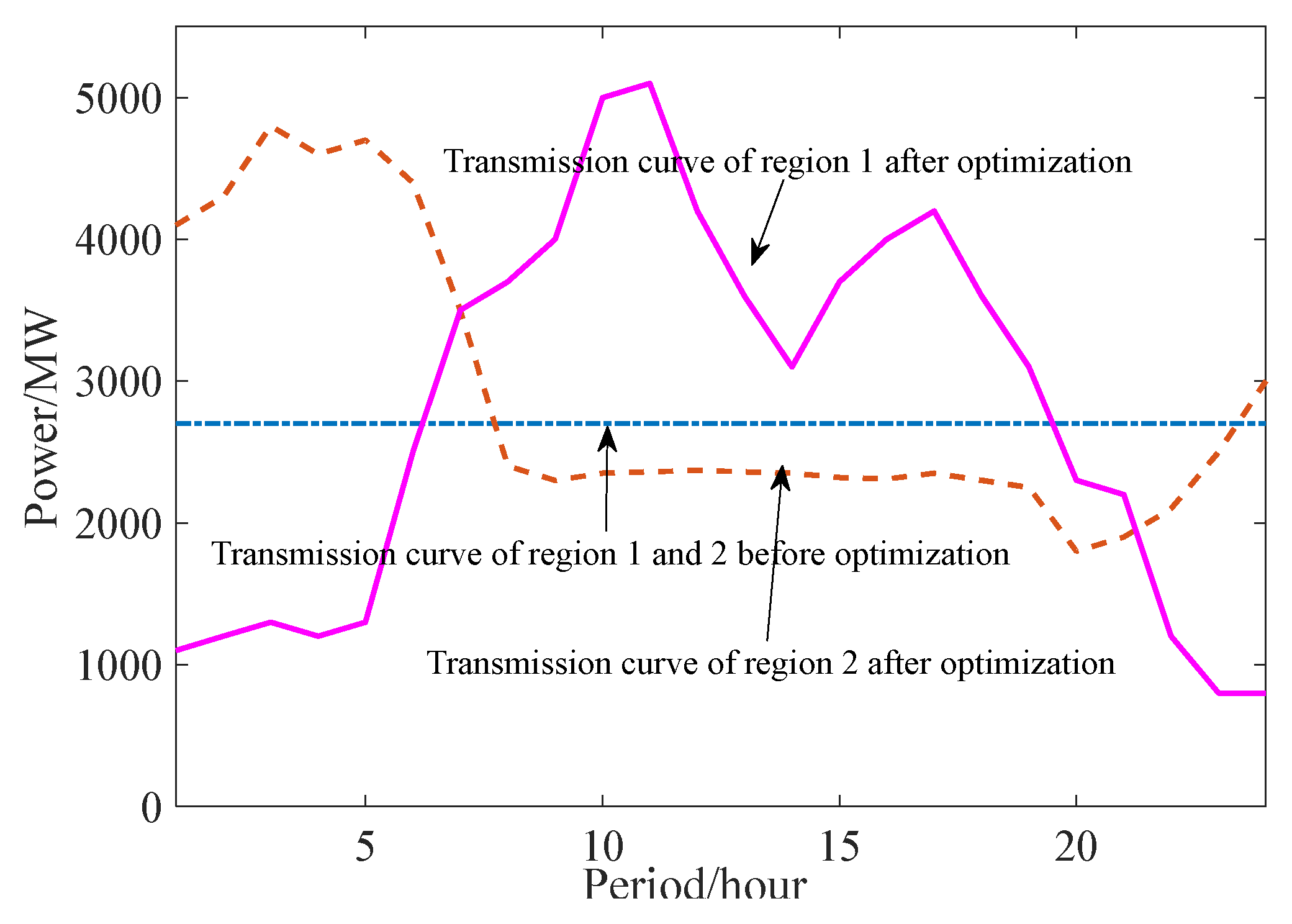
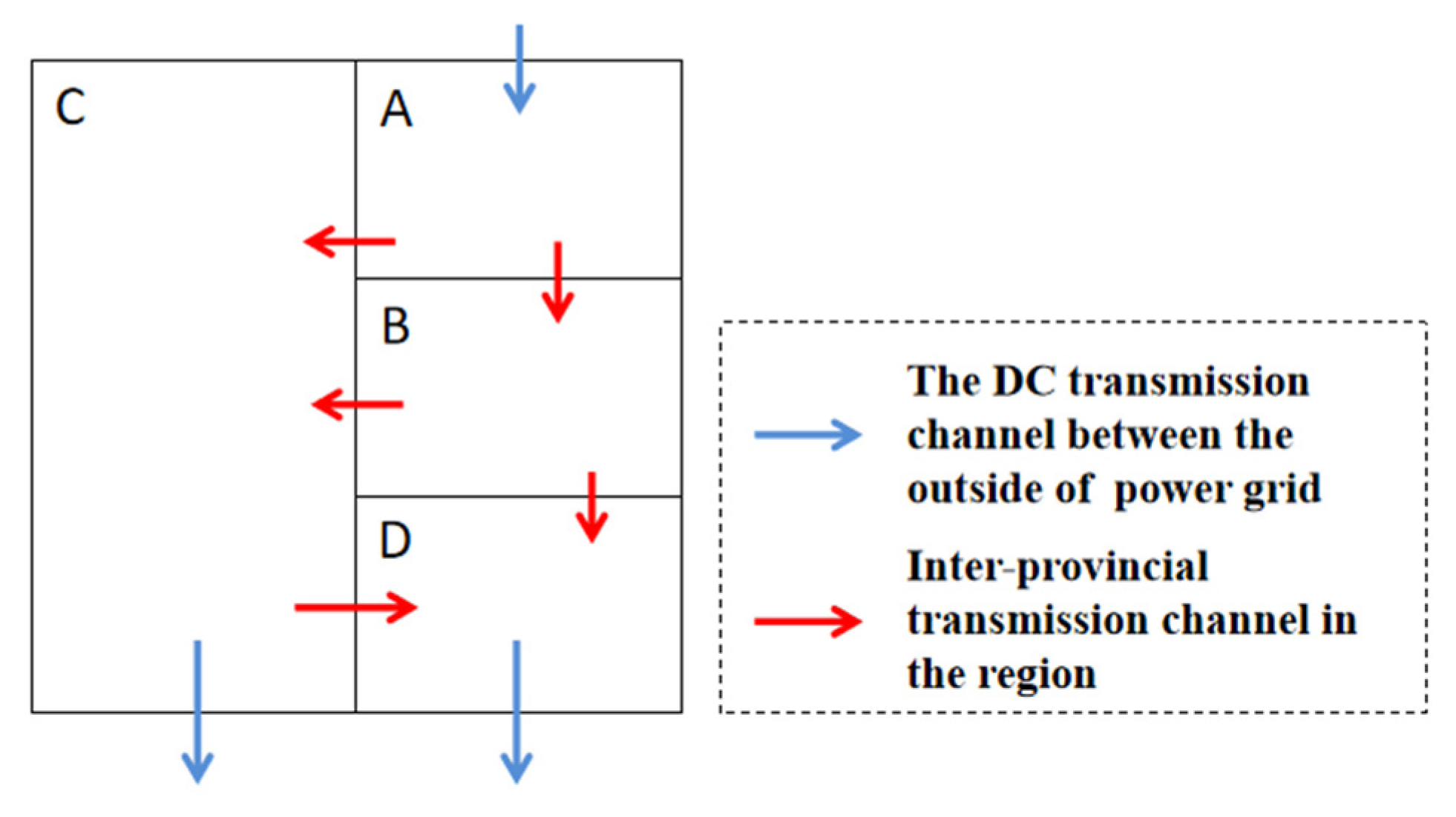
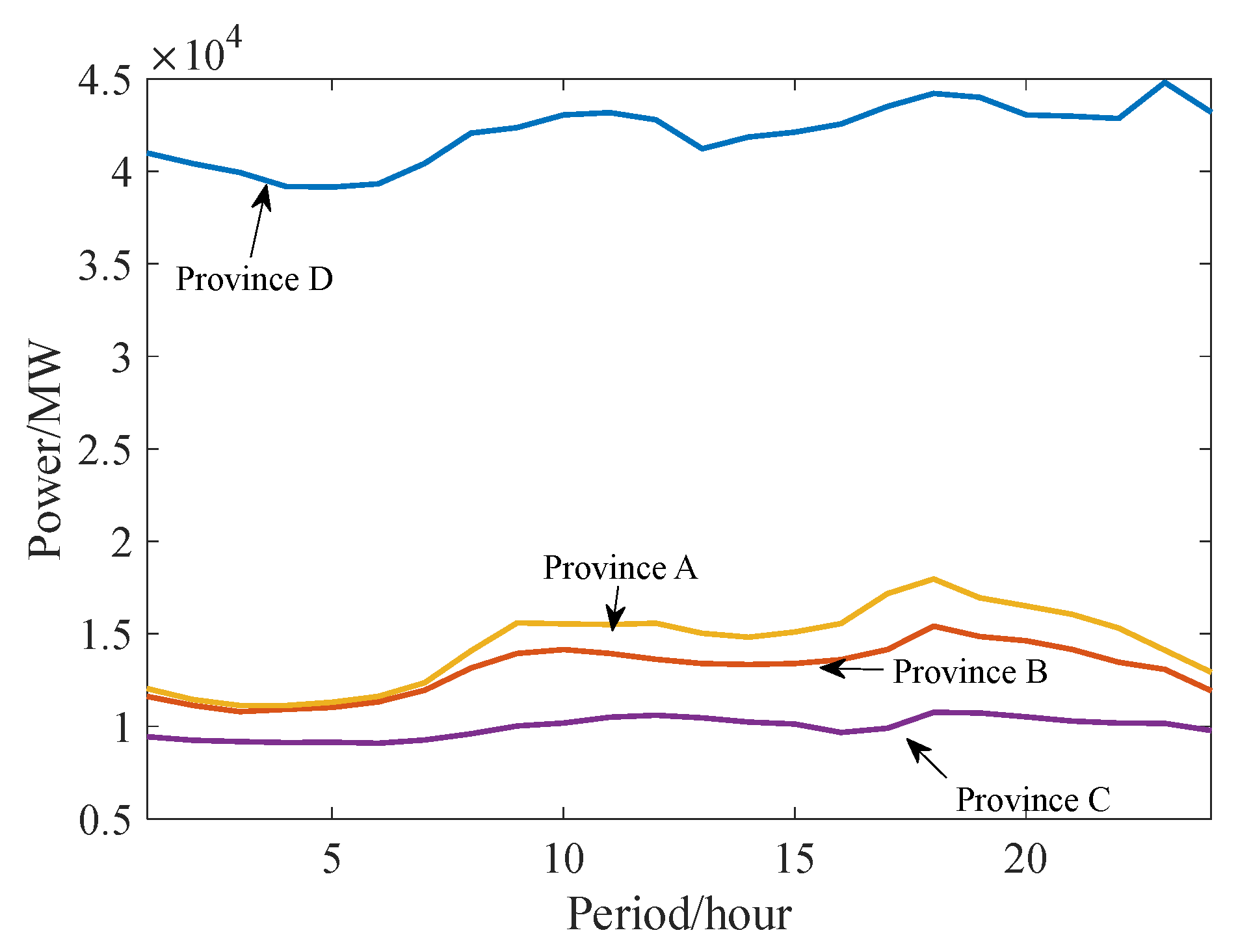
4.2. Example System Analysis Based on an Actual Regional Power Grid
4.2.1. Overview of the Regional System
4.2.2. Analytical Calculation
4.3. Comparison and Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, N.; Zhou, T.; Duan, C. Impact of large-scale wind farm connecting with power grid on peak load regulation demand. Power Syst. Technol. 2010, 34, 152–158. [Google Scholar]
- Zhang, Z.; Zhou, L.; Sun, Y.; Gao, X.; Liu, J.; Dong, Y. Joint Optimal Dispatching Strategy of Pumped Storage and Thermal Power Units with Large-Scale Wind Power Integration. In Proceedings of the 2021 IEEE 5th Conference on Energy Internet and Energy System Integration, Taiyuan, China, 22–24 October 2021. [Google Scholar]
- Zhang, Y.; Le, J.; Liao, X.; Zheng, F.; Liu, K.; An, X. Multi-objective hydro-thermal-wind coordination scheduling integrated with large-scale electric vehicles using imopso. Renew. Energy 2018, 128, 91–107. [Google Scholar] [CrossRef]
- Cheng, D.; Xu, B.; Li, W.; Wu, Q.; Cheng, L.; Zhang, Y.; Zhao, W.; Ma, W.; Zhao, J. Optimal Economic Dispatch Strategy of a Hybrid Energy Storage Microgrid Based on Genetic Algorithm. In Proceedings of the 2023 IEEE 18th Conference on Industrial Electronics and Applications, Ningbo, China, 18–22 August 2023. [Google Scholar]
- Yang, D.; Yang, Z.; He, G.; Geng, J.; Ligao, J. Wind Power Accommodation Method for Regional Integrated Heat-Power System Considering Generation and Load Uncertainties. Access 2021, 9, 2169–2180. [Google Scholar] [CrossRef]
- Zhu, L.; Chen, N.; Han, H. Key problems and solutions of wind power accommodation. Autom. Electr. Power Syst. 2011, 35, 29–34. [Google Scholar]
- Jiang, P.; Yang, S.; Huo, Y. Static security analysis of power systems considering randomness of wind farm output. Autom. Electr. Power Syst. 2013, 37, 35–40. [Google Scholar]
- Zhang, H.; Yin, Y.; Shen, H. Peak-load regulating adequacy evaluation associated with large-scale wind power integration. Proc. CSEE 2011, 31, 26–31. [Google Scholar]
- Kabouris, J.; Kanellos, F.D. Impacts of large-scale wind penetration on designing and operation of electric power systems. IEEE Trans. Sustain. Energy 2010, 1, 107–114. [Google Scholar] [CrossRef]
- Lin, Z.; Chen, H.; Chen, J.; Huang, J.; Li, M.; Wu, Q. Risk-averse robust interval economic dispatch for power systems with large-scale wind power integration. CSEE J. Power Energy Syst. 2021, 12, 2096–2106. [Google Scholar]
- Ying, Y.; Wang, Z.; Wu, X. Multi-objective strategy for deep peak shaving of power grid considering uncertainty of new energy. Power Syst. Prot. Control 2020, 48, 34–42. [Google Scholar]
- Yang, L.; Liang, X.; Wang, X. Combined heat and power economic dispatching considering peak regulation right trading to improve secondary accommodation capability of wind power. Power Syst. Technol. 2020, 44, 1872–1880. [Google Scholar]
- Tan, Q.; Ding, Y.; Zhang, Y. Optimization model of an efficient collaborative power dispatching system for carbon emissions trading in China. Energies 2017, 10, 1405. [Google Scholar] [CrossRef]
- Lin, L.; Zou, L.; Zhou, P. Multi-angle economic analysis on deep peak regulation of thermal power units with large-scale wind power integration. Autom. Electr. Power Syst. 2017, 41, 21–27. [Google Scholar]
- Yang, B.; Cao, X.; Cai, Z.; Yang, T.; Chen, D.; Gao, X.; Zhang, J. Unit Commitment Comprehensive Optimal Model Considering the Cost of Wind Power Curtailment and Deep Peak Regulation of Thermal Unit. Access 2020, 8, 505–512. [Google Scholar] [CrossRef]
- Lin, L.; Tian, X. Analysis of deep peak regulation and its benefit of thermal units in power system with large scale wind power integrated. Power Syst. Technol. 2017, 41, 2255–2263. [Google Scholar]
- Tian, L.; Xie, Y.; Hu, B.; Liu, X.; Li, F. A deep peak regulation auxiliary service bidding strategy for CHP units based on a risk-averse model and district heating network energy storage. Energies 2019, 12, 3314. [Google Scholar] [CrossRef]
- Huang, H.; Xiong, H.; Jiang, B. Design of day-ahead trading mechanism for trans-province peak-shaving auxiliary service of regional power grid. Smart Power 2020, 48, 119–124. [Google Scholar]
- Lu, S.; Zhang, X.; Xu, Y. Two-stage iterative method to optimize tie-line exchange power based on marginal power generation cost. Power Syst. Prot. Control 2021, 49, 77–88. [Google Scholar]
- Zhang, Y.; Hou, Y.; Hu, T. Regional power network environment/economic power dispatching considering balance of power between provinces. Eng. J. Wuhan Univ. 2017, 50, 548–555. [Google Scholar]
- Ohtake, H.; Uno, F.; Oozeki, T.; Yamada, Y.; Takenaka, H.; Nakajima, T. Outlier events of solar forecasts for regional power grid in Japan using jma mesoscale model. Energies 2018, 11, 2714. [Google Scholar] [CrossRef]
- Fang, B.; Xiao, L.; Sun, C.; Chen, Y.; Xue, Y.; Zhang, D. An optimization dispatch method for regional power grid considering peaking resource mutual support. Electr. Drive 2022, 52, 54–60. [Google Scholar]
- Li, J. An improved quantum-behaved particle swarm optimization method for economic dispatch problems with multiple fuel options and valve-points effects. Energies 2012, 5, 240–250. [Google Scholar]
- Liu, D.; Huang, Y.; Wang, W. Analysis on provincial system available capability of accommodating wind power considering peak load dispatch and transmission constraints. Autom. Electr. Power Syst. 2011, 35, 77–81. [Google Scholar]
- Zhuo, Z.; Zhang, N.; Xie, X. Key technologies and developing challenges of power system with high proportion of renewable energy. Autom. Electr. Power Syst. 2021, 45, 171–191. [Google Scholar]
- Chen, J.; Wu, W.; Zhang, B.; Wang, B.; Guo, Q. A spinning reserve allocation method for power generation dispatch accommodating large-scale wind power integration. Energies 2013, 6, 5357–5381. [Google Scholar] [CrossRef]




| Power Supply | Peak Regulating Ability |
|---|---|
| Coal-fired units | Conventional thermal units: 40~50% After flexibility transformation: 55~70% |
| Gas units | Have shutdown ability, peak regulation ability: 100% |
| Cascade hydro-power unit (non-runoff) | Have shutdown ability, peak regulation ability: 100% |
| Pump storage units | 160% |
| Other energy storage units | 160% |
| Small hydro-power stations (radial flow) | 0% |
| Wind | 0% |
| Photovoltaic | 0% |
| Region | Units Capacities/MW | Wind Power Capacities/MW | Peak Regulating Capacities | Peak Regulating Capacities without Oil | Peak Regulating Capacities with Oil |
|---|---|---|---|---|---|
| Region 1 | 29,410 | 1300 | 50% | 40% | 35% |
| Region 2 | 29,410 | 1300 | 50% | 45% | 40% |
| Region 3 | 21,100 | 1300 | 50% | 43% | 38% |
| Before Optimization | After Optimization | |||||
|---|---|---|---|---|---|---|
| Region | Total Costs/USD 100 Million | Operation Costs/USD 100 Million | Abandon Punishment Costs/USD 100 Million | Total Costs/USD 100 Million | Operation Costs/USD 100 Million | Abandon Punishment Costs/USD 100 Million |
| 1 | 0.28 | 0.23 | 0.05 | 0.24 | 0.22 | 0.02 |
| 2 | 0.27 | 0.23 | 0.04 | 0.25 | 0.23 | 0.02 |
| 3 | 0.25 | 0.2 | 0.05 | 0.22 | 0.19 | 0.03 |
| Total | 0.8 | 0.66 | 0.14 | 0.71 | 0.64 | 0.07 |
| Before Optimization | After Optimization | |||||||
|---|---|---|---|---|---|---|---|---|
| Province | Total Costs/USD 100 Million | Operation Costs/USD 100 Million | Abandon Punishment Costs/USD 100 Million | New Energy Utilization Rate% | Total Costs/USD 100 Million | Operation Costs/USD 100 Million | Abandon Punishment Costs/USD 100 Million | New Energy Utilization Rate% |
| A | 0.46 | 0.396 | 0.064 | 87.9 | 0.419 | 0.377 | 0.042 | 89.9 |
| B | 0.545 | 0.452 | 0.092 | 84.8 | 0.495 | 0.433 | 0.061 | 88.3 |
| C | 0.455 | 0.335 | 0.121 | 89.6 | 0.423 | 0.315 | 0.108 | 90.7 |
| D | 0.653 | 0.599 | 0.053 | 93.3 | 0.617 | 0.565 | 0.052 | 93.5 |
| Total | 2.113 | 1.782 | 0.33 | 87.7 | 1.954 | 1.69 | 0.263 | 90.9 |
| Model | Optimization Results | |
|---|---|---|
| Total Costs/USD 100 Million | New Energy Utilization Rate% | |
| 1 | 1.953 | 90.9 |
| 2 | 2.116 | 87.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, T.; Lou, S.; Zhang, M.; Li, Y.; Feng, W.; Liu, J. Research on a Two-Layer Optimal Dispatching Method Considering the Mutual Aid of Peak Regulating Resources among Regional Power Grids. Energies 2024, 17, 667. https://doi.org/10.3390/en17030667
Yang T, Lou S, Zhang M, Li Y, Feng W, Liu J. Research on a Two-Layer Optimal Dispatching Method Considering the Mutual Aid of Peak Regulating Resources among Regional Power Grids. Energies. 2024; 17(3):667. https://doi.org/10.3390/en17030667
Chicago/Turabian StyleYang, Tianmeng, Suhua Lou, Meng Zhang, Yanchun Li, Wei Feng, and Jicheng Liu. 2024. "Research on a Two-Layer Optimal Dispatching Method Considering the Mutual Aid of Peak Regulating Resources among Regional Power Grids" Energies 17, no. 3: 667. https://doi.org/10.3390/en17030667
APA StyleYang, T., Lou, S., Zhang, M., Li, Y., Feng, W., & Liu, J. (2024). Research on a Two-Layer Optimal Dispatching Method Considering the Mutual Aid of Peak Regulating Resources among Regional Power Grids. Energies, 17(3), 667. https://doi.org/10.3390/en17030667





