A Two-Layer Control Strategy for the Participation of Energy Storage Battery Systems in Grid Frequency Regulation
Abstract
1. Introduction
2. Regional Grid Frequency Regulation Model with Multiple BESSs
3. Distribution Model Based on ACE and ARR Signals
- When ΔA(s) < 0
- When ΔA(s) > 0
4. Two-Layer Control Strategy Based on FM Duty Assignment
4.1. Two-Tier Control Structure
4.2. Frequency Dynamic Correction Layer
4.2.1. Model Predictions
4.2.2. Rolling Optimization
4.2.3. Rolling Optimization
4.2.4. MPC Implementation Frequency Dynamic Correction Process
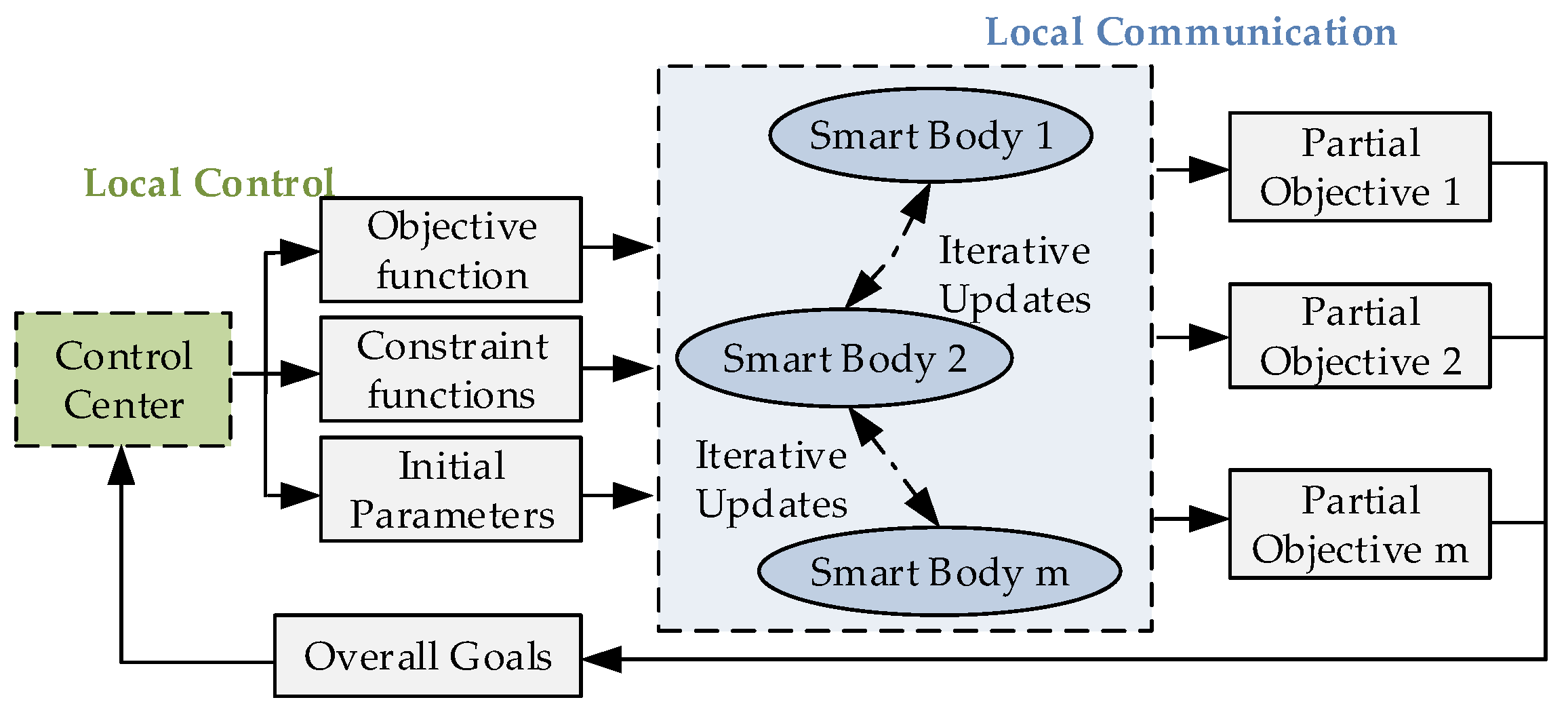
4.3. Power Balancing Control Layer
4.3.1. Objective Function and Constraint Function
4.3.2. Parameter Initialization
4.3.3. Iterative Update
4.3.4. Power Balancing Control Process
5. Simulation Analysis
5.1. Simulation Parameters
5.2. Step Perturbation
5.3. Continuous Perturbation
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, W.; Sun, N.; Ma, Z.C.; Liu, W.F.; Dong, H.Y. A Two-Layer Optimization Strategy for Battery Energy Storage Systems to Achieve Primary Frequency Regulation of Power Grid. Energies 2023, 16, 2811. [Google Scholar] [CrossRef]
- Wu, Z.; Gao, D.W.; Zhang, H.; Yan, S.; Wang, X. Coordinated Control Strategy of Battery Energy Storage System and PMSG-WTG to Enhance System Frequency Regulation Capability. IEEE Trans. Sustain. Energy 2017, 8, 1330–1343. [Google Scholar] [CrossRef]
- Tang, R.; Yang, J.; Yang, W. Stability of Frequency Regulation of Pumped-Storage Plants with Multiple Units Sharing Common Penstock and Busbar. IOP Conf. Ser. Earth Environ. Sci. 2018, 163, 012094. [Google Scholar] [CrossRef]
- Nema, S.; Prakash, V.; Pandžić, H. Adaptive Synthetic Inertia Control Framework for Distributed Energy Resources in Low-Inertia Microgrid. IEEE Access 2022, 10, 54969–54979. [Google Scholar] [CrossRef]
- Nema, S.; Prakash, V.; Pandžić, H. Coordinated Synthetic Inertia Control Provision from Distributed Energy Resources and Energy Storage Systems. In Proceedings of the 2022 International Conference on Intelligent Controller and Computing for Smart Power (ICICCSP), Hyderabad, India, 21–23 July 2022; pp. 1–5. [Google Scholar]
- Lee, J.; Kim, J.M.; Yi, J.; Won, C.Y. Battery Management System Algorithm for Energy Storage Systems Considering Battery Efficiency. Electronics 2021, 10, 1859. [Google Scholar] [CrossRef]
- Wang, K.; Qiao, Y.; Xie, L.; Li, J.; Lu, Z.; Yang, H. A Fuzzy Hierarchical Strategy for Improving Frequency Regulation of Battery Energy Storage System. J. Mod. Power Syst. Clean Energy 2021, 9, 689–698. [Google Scholar] [CrossRef]
- You, J.; Jiang, T. Power Regulation Strategy of Virtual Pumped Storage Power Station Based on Compressed Air Energy Storage. IOP Conf. Ser. Mater. Sci. Eng. 2019, 677, 032030. [Google Scholar] [CrossRef]
- Hollinger, R.; Diazgranados, L.M.; Wittwer, C.; Engel, B. Optimal Provision of Primary Frequency Control with Battery Systems by Exploiting All Degrees of Freedom within Regulation. Energy Procedia 2016, 99, 204–214. [Google Scholar] [CrossRef]
- Subroto, R.K.; Lian, K.L.; Chu, C.-C.; Liao, C.-J. A fast frequency control based on model predictive control taking into account of optimal allocation of power from the energy storage system. IEEE Trans. Power Del. 2021, 36, 2467–2478. [Google Scholar] [CrossRef]
- Xia, W.; Liming, Y.; Kerui, W.; Shaoping, L. Bi-level non-convex joint optimization model of energy storage in energy and primary frequency regulation markets. Int. J. Electr. Power Energy Syst. 2021, 134, 107408. [Google Scholar]
- Tang, Y.; Yang, C.; Yan, Z.; Xue, Y.; He, Y. Coordinated Control of a Wind Turbine and Battery Storage System in Providing Fast-Frequency Regulation and Extending the Cycle Life of Battery. Front. Energy Res. 2022, 10, 927453. [Google Scholar] [CrossRef]
- Li, C.; Li, P.; Yu, H.; Li, H.; Zhao, J.; Li, S.; Wang, C. Optimal Planning of Community Integrated Energy Station Considering Frequency Regulation Service. J. Mod. Power Syst. Clean Energy 2021, 9, 264–273. [Google Scholar] [CrossRef]
- Jin, C.; Lu, N.; Lu, S.; Makarov, Y.V.; Dougal, R.A. A Coordinating Algorithm for Dispatching Regulation Services between Slow and Fast Power Regulating Resources. IEEE Trans. Smart Grid. 2014, 5, 1043–1050. [Google Scholar]
- Punyakaew, S.; Parnichkun, M. Vibration Energy Harvesting for Low Frequency Using Auto-Tuning Parametric Rolling Pendulum under Exogenous Multi-Frequency Excitations. Theor. Appl. Mech. Lett. 2020, 10, 448–455. [Google Scholar] [CrossRef]
- Cheng, Y.; Tabrizi, M.; Sahni, M.; Povedano, A.; Nichols, D. Dynamic Available AGC Based Approach for Enhancing Utility Scale Energy Storage Performance. IEEE Trans. Smart Grid 2014, 5, 1070–1078. [Google Scholar] [CrossRef]
- Lv, L.X.; Chen, S.H.; Zhang, X.B.; Pang, T.; Huang, C.X. A secondary frequency control strategy for power system considering the consistency of scaled battery energy storage. Thermoelectr. Power Gener. 2021, 50, 108–117. [Google Scholar]
- Zhou, W.Z. Research on State Estimation-Based Frequency Control Strategy for Energy Storage Battery-Assisted Power Grid. Master’s Thesis, Changsha University of Science and Technology, Changsha, China, 2021. [Google Scholar]
- Li, X.R.; Huang, J.Y.; Chen, Y.Y.; Li, S.J.; Ouyang, L.L. Sensitivity analysis-based control strategy for energy storage battery participation in secondary frequency regulation. J. Electr. Eng. Technol. 2017, 32, 224–233. [Google Scholar]
- Cao, X.; Zhao, N. A Cooperative Management Strategy for Battery Energy Storage System Providing Enhanced Frequency Response. Energy Rep. 2022, 8, 120–128. [Google Scholar] [CrossRef]
- Liao, X.B.; Liu, K.P.; Le, J.; Ran, X.H.; Wang, N.B.; Zhou, Z.H.; Wei, Q. Cooperative control strategy for cross-region AGC units based on two-layer model prediction structure. Chin. J. Electr. Eng. 2019, 39, 4674–4685+4970. [Google Scholar]
- Zhang, S.P.; Dong, S.F.; Xu, C.S.; Han, R.J.; Shou, T.; Li, J.B. A two-layer control strategy for large-scale energy storage participation in grid frequency regulation. Power Syst. Autom. 2020, 44, 55–62. [Google Scholar]
- Zhang, S.Q.; Liu, H.Y.; Wang, F.; Guo, H.; Shi, T.L. Distributed equilibrium control strategy of “PXP” energy storage cluster for secondary frequency regulation demand of power grid. Chin. J. Electr. Eng. 2022, 42, 886–900. [Google Scholar]
- Machowski, J.; Bialek, J.; Bumby, J. Power System Dynamics: Stability and Control, 2nd ed.; John Wiley & Sons: New York, NY, USA, 2008; pp. 342–343. [Google Scholar]
- Cohen, J.E. Cooperation and self-interest: Pareto-inefficiency of Nash equilibria in finite random games. Proc. Natl. Acad. Sci. USA 1998, 95, 9724–9731. [Google Scholar] [CrossRef] [PubMed]
- Oneal, A. R A simple method for improving control area performance: Area control error(ACE) diversity interchange ADI. IEEE Trans. Power Syst. 1995, 10, 1071–1076. [Google Scholar] [CrossRef]
- Zhou, N.; Etingov, P.V.; Makarov, Y.V.; Guttromson, R.T.; McManus, B. Improving area control error diversity interchange (ADI) program by incorporating congestion constraints. In Proceedings of the 2010 PES Transmission & Distribution, New Orleans, LA, USA, 19–22 April 2010; pp. 1–8. [Google Scholar]
- Apostolopoulou, D.; Sauer, P.W.; Domínguez-García, A. D Balancing authority area coordination with limited exchange of information. In Proceedings of the IEEE Power & Energy Society General Meeting, Denver, CO, USA, 26–30 July 2015; pp. 1–5. [Google Scholar]
- Andreasson, M.; Dimarogonas, D.V.; Johansson, K.H.; Sandberg, H. Distributed vs centralized power systems frequency control. In Proceedings of the European Control Conference (ECC), Zurich, Switzerland, 17–19 July 2013; pp. 3524–3529. [Google Scholar]
- Zhang, X.; Papachristodoulou, A. A real-time control framework for smart power networks with star topology. In Proceedings of the 2013 American Control Conference, Washington, DC, USA, 17–19 June 2013; pp. 5062–5067. [Google Scholar]
- Li, N.; Zhao, C.; Chen, L. Connecting automatic generation control and economic dispatch from an optimization view. In Proceedings of the American Control Conference (ACC), Portland, OR, USA, 4–6 June 2014; pp. 735–743. [Google Scholar]
- Wang, Z.; Liu, F.; Chen, L.; Mei, S. Distributed economic automatic generation control: A game theoretic perspective. In Proceedings of the IEEE Power & Energy Society General Meeting, Denver, CO, USA, 26–30 July 2015; pp. 1–5. [Google Scholar]
- Andreasson, M. Control of Multi-Agent Systems with Applications to Distributed Frequency Control Power Systems; KTH School of Electrical Engineering: Stockholm, Sweden, 2013. [Google Scholar]
- Andreasson, M.; Wiget, R.; Dimarogonas, D.V.; Johansson, K.H.; Andersson, G. Distributed secondary frequency control through MTDC transmission systems. In Proceedings of the 54th IEEE Conference on Decision and Control (CDC), Osaka, Japan, 15–18 December 2015; pp. 2627–2634. [Google Scholar]
- Venkat, A.N.; Hiskens, I.A.; Rawlings, J.B.; Wright, S.J. Distributed MPC strategies with application to power system automatic generation control. IEEE Trans. Control. Syst. Technol. 2008, 16, 1192–1206. [Google Scholar] [CrossRef]
- Chan, M.L.; Dunlop, R.D.; Schweppe, F. Dynamic equivalents for average system frequency behavior following major distribances. IEEE Trans. Power Appar. Syst. 1972, PAS-91, 1637–1642. [Google Scholar]
- Anderson, P.M.; Mirheydar, M. A low-order system frequency response model. IEEE Trans. Power Syst. 1990, 5, 720–729. [Google Scholar] [CrossRef]
- Cherukuri, A.; Cortés, J. Asymptotic stability of saddle points under the saddle-point dynamics. In Proceedings of the American Control Conference (ACC), Chicago, IL, USA, 1–3 July 2015; pp. 2020–2025. [Google Scholar]
- Boyd, S.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004; pp. 233–239. [Google Scholar]
- Zhang, Y.M.; Xu, C.L.; Qi, Q.; Zhang, B.; Li, J. Modeling study on secondary frequency regulation of energy storage battery-assisted thermal power generating units. Energy Sav. Technol. 2022, 40, 180–185. [Google Scholar]
- Zhang, S.Q.; Yuan, B.; Xu, Q.S.; Zhao, J.F. Optimal control strategy of grid secondary frequency regulation with the participation of scaled energy storage. Power Autom. Equip. 2019, 39, 82–88+95. [Google Scholar]
- Li, R.; Li, X.R.; Tan, Z.X.; Huang, J.Y.; Ma, W. An integrated control strategy considering energy storage battery participation in secondary frequency regulation. Power Syst. Autom. 2018, 42, 74–82. [Google Scholar]
- Chang, K.; Zhou, T.; Zhang, H.N.; Liu, S.F. Energy storage battery participation in grid secondary frequency regulation parameter optimization. Electron. Des. Eng. 2022, 30, 64–68. [Google Scholar]
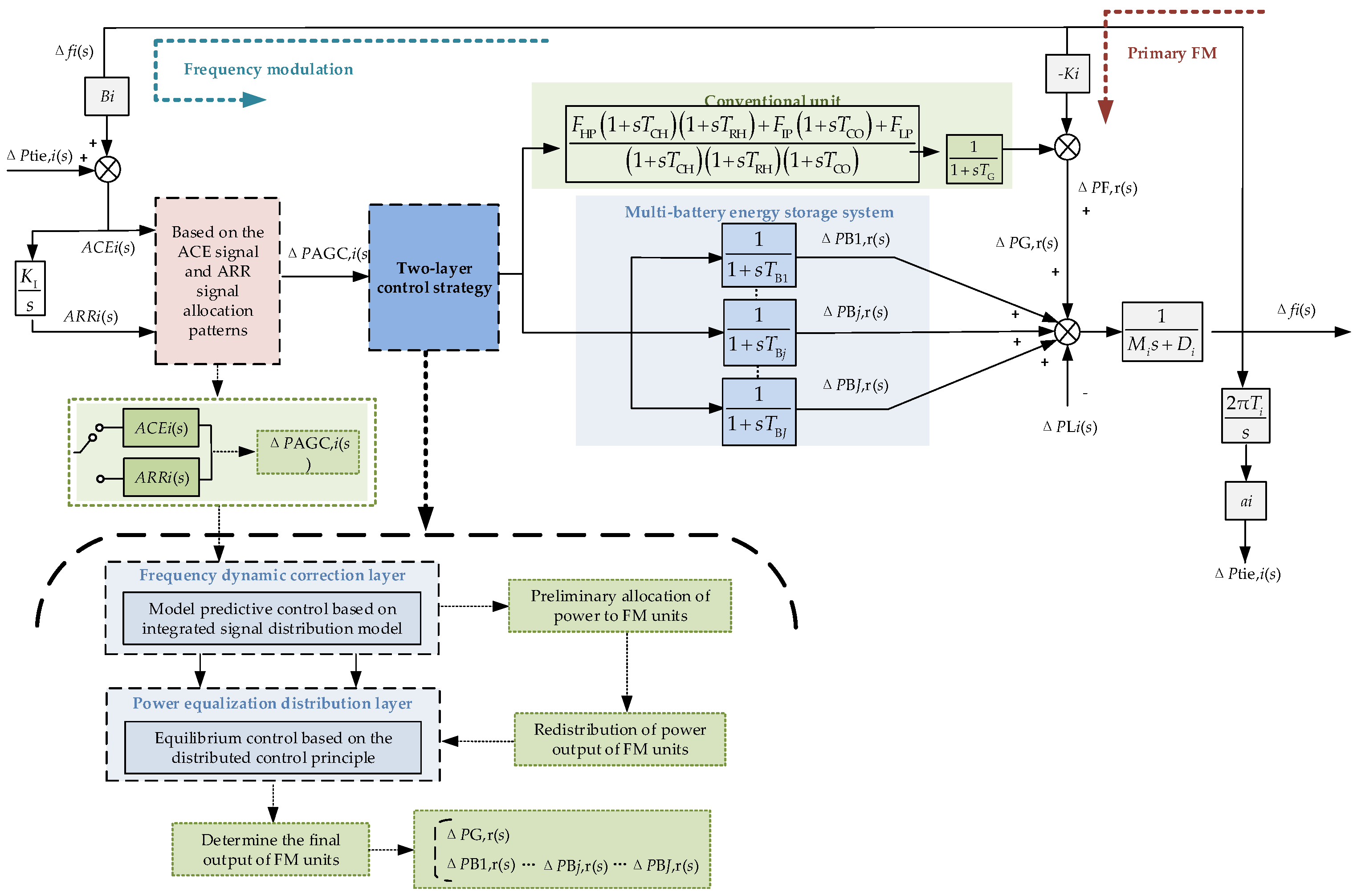









| Parameters | Definition | Unit (p.u.) |
|---|---|---|
| ΔPtie,i(s) | System contact line power deviation | MW |
| Δfi(s) | Frequency deviation | Hz |
| ΔPAGC,i(s) | Secondary FM demand out of force | MW |
| ΔPF,r(s) | Actual power output of conventional unit with primary frequency regulation | MW |
| ΔPG,r(s) | Actual power output of conventional unit with secondary frequency regulation | MW |
| ΔPBj,r(s) | Energy storage battery secondary FM actual power output | MW |
| Ki | Primary FM factor | -- |
| Bi | Power system deviation factor | -- |
| KI | PI controller parameters | -- |
| GBj(s) | Battery storage model | -- |
| Gg(s) | Conventional unit model | -- |
| ΔPLi(s) | Load disturbance | -- |
| Mi | System rotational inertia | -- |
| Di | System damping factor | -- |
| Ti | Capacity delay factor for adjacent areas | -- |
| ai | Capacity conversion factor for adjacent areas | -- |
| ACEi(s) | Area control deviation signal | -- |
| ARRi(s) | Regional control demand signals | -- |
| Conventional Units | BESS 1 | BESS 2 | BESS 3 | BESS 4 | Unit | |
|---|---|---|---|---|---|---|
| Power Backup | −750~750 | −60~60 | −50~50 | −40~40 | −30~30 | MW |
| Climbing rate | −800~800 | −104~104 | −104~104 | −104~104 | −104~104 | MW·h |
| Battery Capacity | -- | 50 | 40 | 20 | 10 | MW·h |
| Charging and discharging efficiency | -- | 0.9 | 0.9 | 0.9 | 0.9 | -- |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, P.; Xin, S.; Wang, Y.; Xu, Q.; Chen, C.; Chen, W.; Dong, H. A Two-Layer Control Strategy for the Participation of Energy Storage Battery Systems in Grid Frequency Regulation. Energies 2024, 17, 664. https://doi.org/10.3390/en17030664
Zhang P, Xin S, Wang Y, Xu Q, Chen C, Chen W, Dong H. A Two-Layer Control Strategy for the Participation of Energy Storage Battery Systems in Grid Frequency Regulation. Energies. 2024; 17(3):664. https://doi.org/10.3390/en17030664
Chicago/Turabian StyleZhang, Pan, Shijin Xin, Yunwen Wang, Qing Xu, Chunsheng Chen, Wei Chen, and Haiying Dong. 2024. "A Two-Layer Control Strategy for the Participation of Energy Storage Battery Systems in Grid Frequency Regulation" Energies 17, no. 3: 664. https://doi.org/10.3390/en17030664
APA StyleZhang, P., Xin, S., Wang, Y., Xu, Q., Chen, C., Chen, W., & Dong, H. (2024). A Two-Layer Control Strategy for the Participation of Energy Storage Battery Systems in Grid Frequency Regulation. Energies, 17(3), 664. https://doi.org/10.3390/en17030664





