Distributed Coordinated Operation of Active Distribution Networks with Electric Heating Loads Based on Dynamic Step Correction ADMM
Abstract
1. Introduction
- (1)
- Considering the thermal delay effect and heat loss of the thermal system, the centralized optimization operation model of active distribution networks containing EHLs is formulated as a standard sharing problem, and a distributed optimization operation model of EHLs active distribution networks based on ADMM solution is established.
- (2)
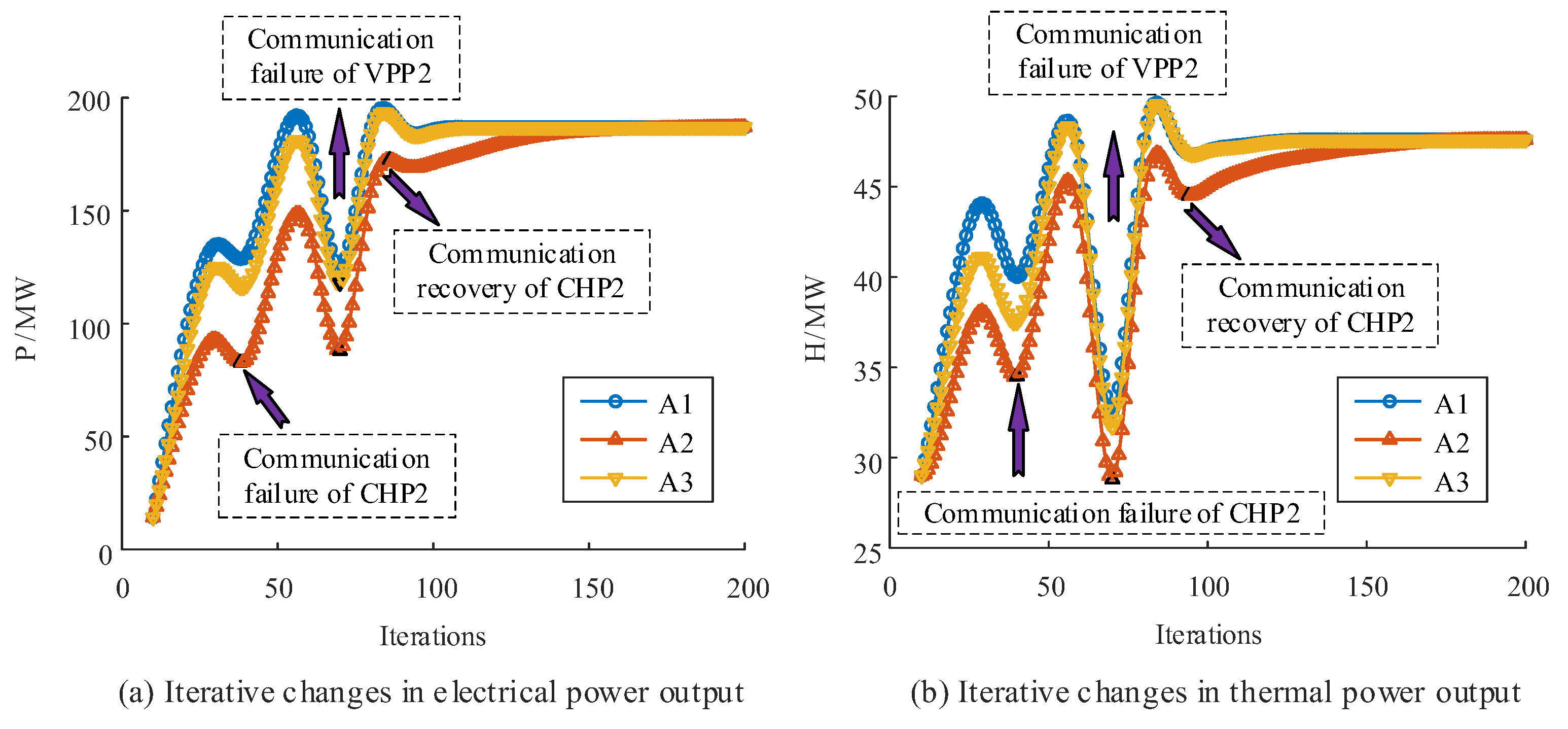
- The iterative process is improved by dynamically updating the step, which results in fewer iterations and better convergence performance compared to the original ADMM. In addition, this method can not only obtain the optimal solution with the minimum number of iterations under normal operation but also obtain the optimal solution with the minimum number of iterations in the case of communication failures.
- (3)
- The effectiveness of the distributed coordinated operation method proposed in this paper was simulated and verified by constructing an IEEE33 distribution system. The results showed that the proposed distributed coordinated operation method has strong robustness to the randomness of the number of distributed units and parameters. Moreover, EHLs participating in coordinated operation can expand the consumption space of wind power and photovoltaic power, and improve the economic efficiency of system operation.
2. Centralized Optimal Operation Model for Active Distribution Networks with EHLs
2.1. Objective Function
2.2. Constraints
2.2.1. Power Balance Constraints
2.2.2. Thermal Power Balance Constraints Considering Thermal Loss and Thermal Delay Effects
2.2.3. Conventional Unit Operation Constraints
2.2.4. Operation Constraints of Cogeneration Units
2.2.5. Operational Constraints for Wind and Photovoltaic Power Generation
2.2.6. EHLs Operational Constraints
2.2.7. Energy Sharing Constraints
3. Distributed Optimal Operation Model for Active Distribution Networks with EHLs
4. Distributed Solution Based on Dynamic Step Correction ADMM
4.1. Implementation of ADMM
| Algorithm 1. ADMM-based distributed optimization |
| Input: Forecast electric load , forecast thermal load , wind power forecast output , photovoltaic forecast output , Lagrange multiplier and , penalty coefficient and , tolerance parameter and , energy price and equipment operation parameter Output: Minimum operating cost of active distribution network with EHLs |
| Step 1: Initialize , , , , , iteration number k = 1. Step 2: Establish an optimization operation model for active distribution networks with EHLs, including optimization objective functions and constraint conditions. Step 3: Parallel optimization and solution of various variables in the model. Step 4: According to Equations (37)–(39), iteratively update variables and , auxiliary variables and , and dual variables and . Step 5: Update iteration number k = k + 1. Step 6: According to Equation (41), determine whether the stop condition is met. If the stop condition is met, the iteration stops. Otherwise, return to Step3 for repeated calculations. |
4.2. Dynamic Step Correction of ADMM
| Algorithm 2. ADMM based on dynamic step size correction |
| Step 1: Set residual variation value ; Step 2: for k Calculate and according to Equation (42) if min else Update according to Equation (43) end is sent to Algorithm 1 for step3 update Step 3: end |
5. Simulation and Analysis
5.1. Example Setting
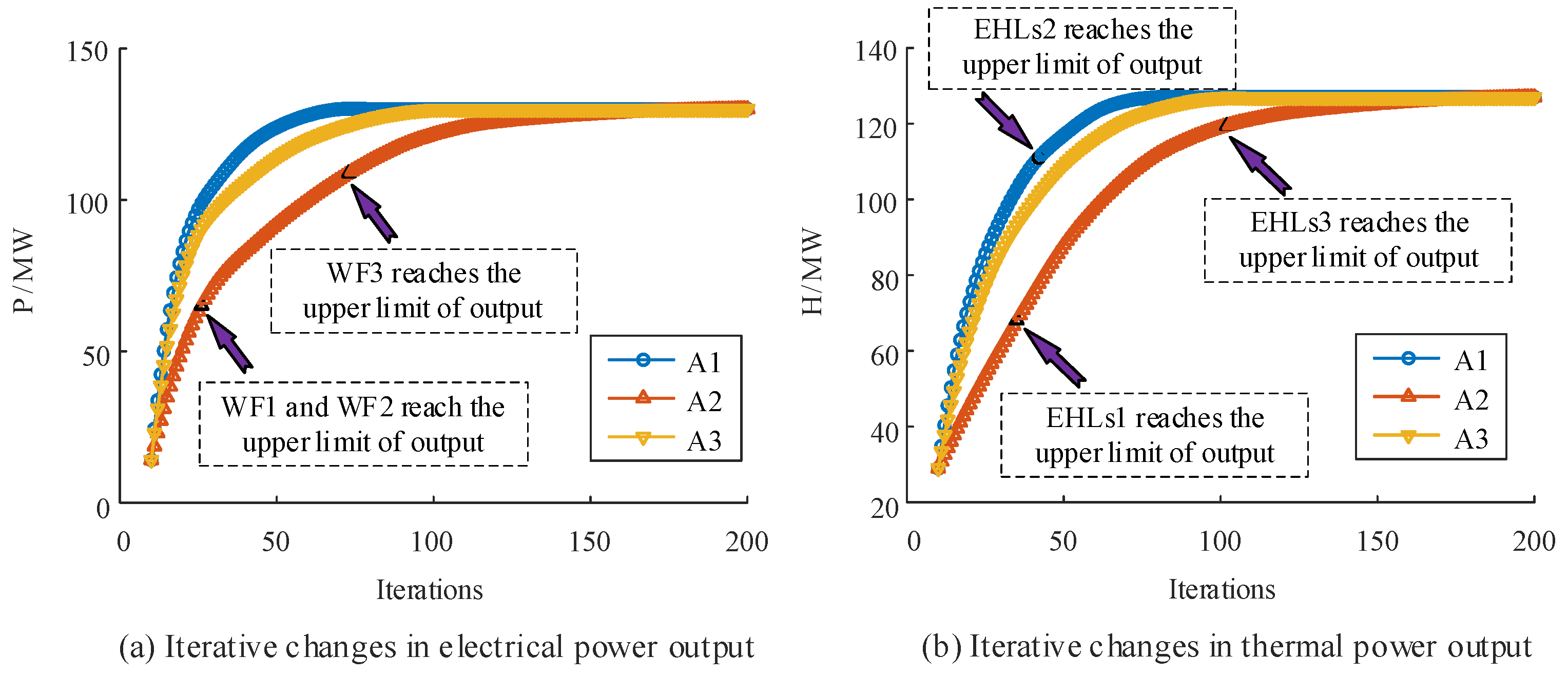
5.2. Algorithm Performance Analysis
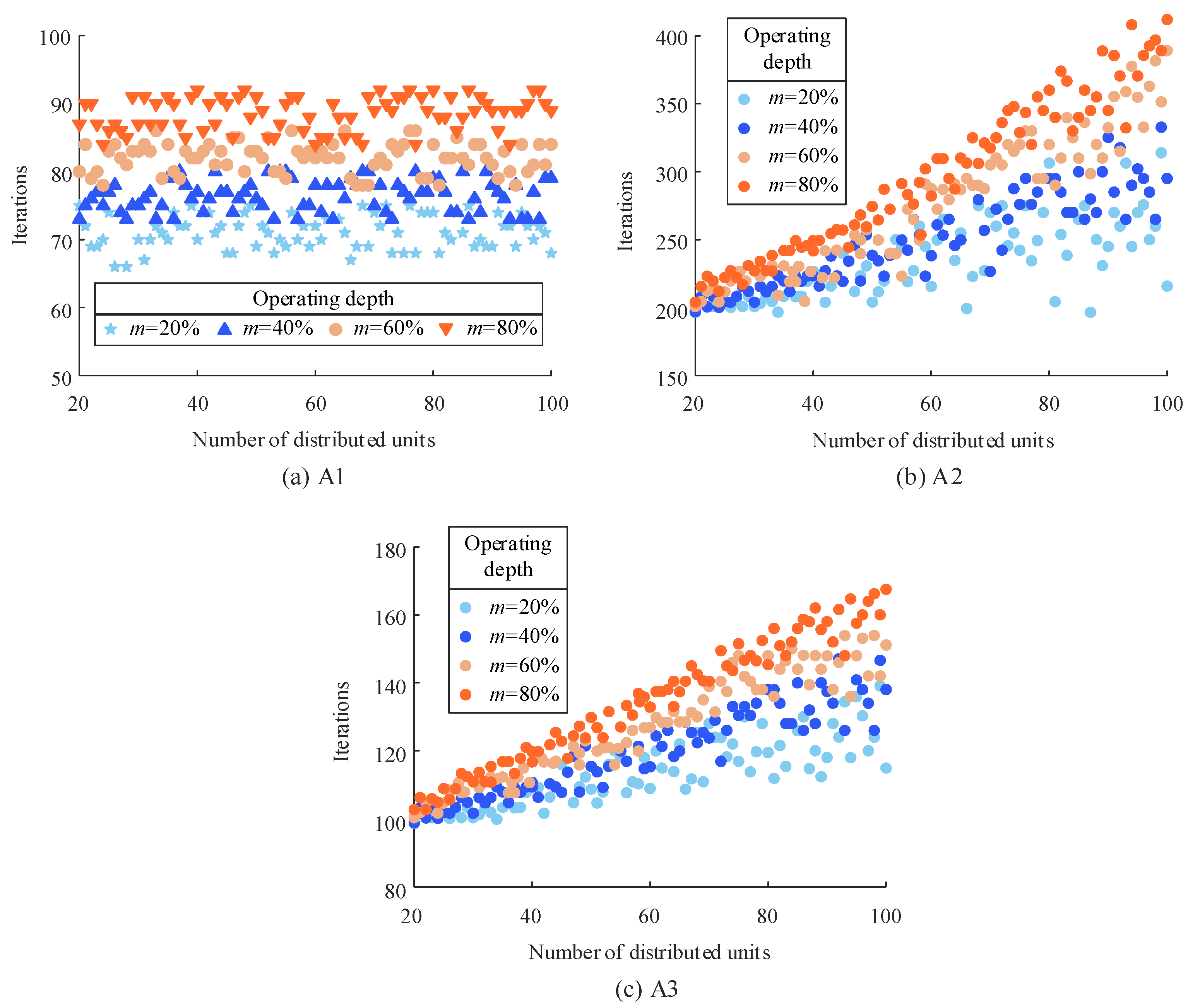
5.3. The Impact of Distributed Unit Randomness
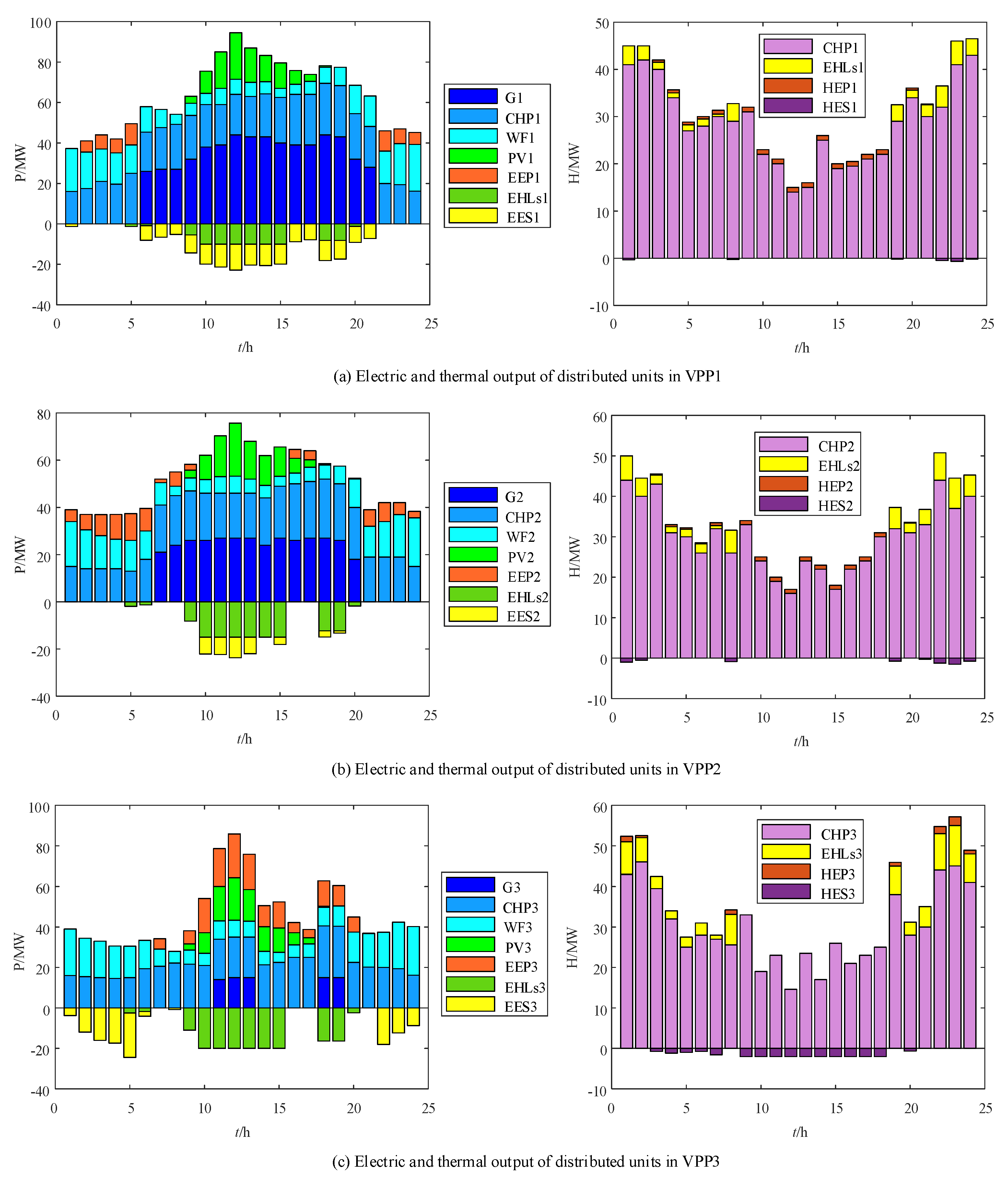
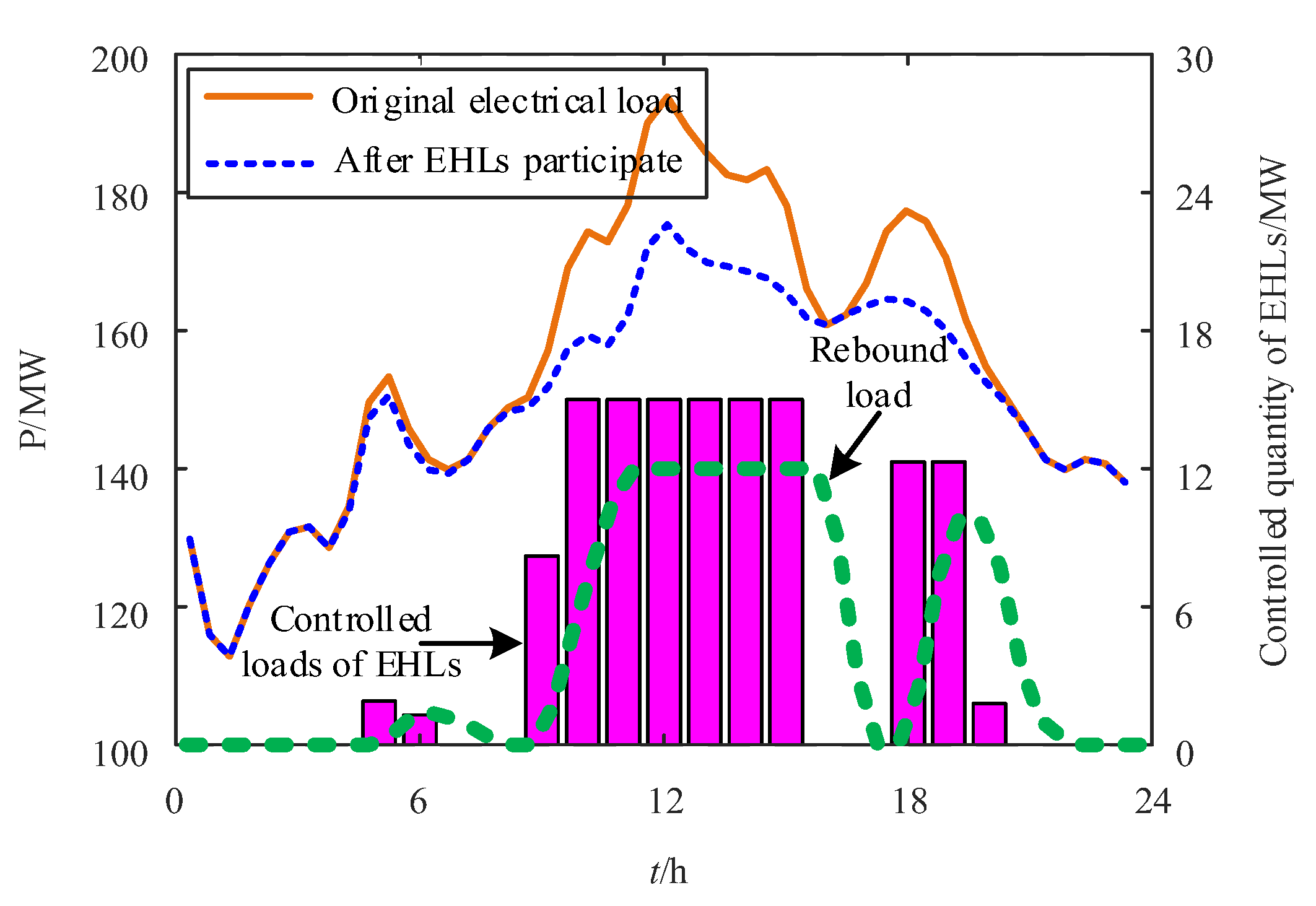
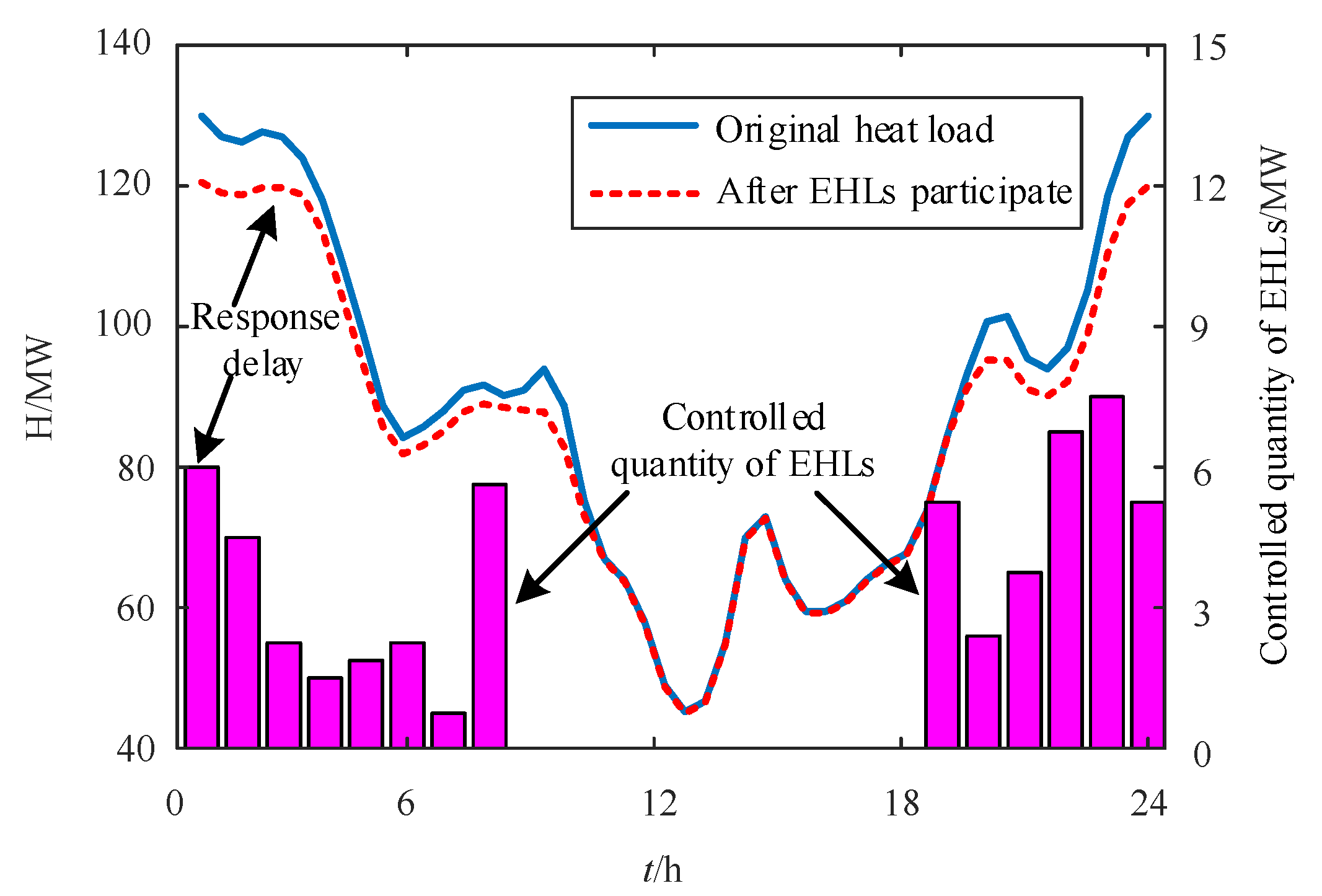
5.4. Distributed Coordinated Operation Results of the Active Distribution Network with EHLs
6. Conclusions
- (1)
- In the process of solving ADMM, considering dynamic step correction can reduce the number of iterations and improve the convergence and computational efficiency of ADMM.
- (2)
- The proposed distributed coordinated operation method has strong robustness to the randomness of the number of distributed units and parameters.
- (3)
- After EHLs participate in coordinated operation, they can expand the consumption space of wind and photovoltaic power, improve the economic efficiency of system operation, and during the controlled period of EHLs, the peak values of electricity and heat loads significantly decrease, reflecting the energy-saving and emission reduction effect of EHLs on the system.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dehnavi, G.; Ginn, H.L. Distributed load sharing among converters in an autonomous microgrid including PV and wind power units. IEEE Trans. Smart Grid 2019, 10, 4289–4298. [Google Scholar] [CrossRef]
- Liu, J.; Cheng, H.Z.; Zeng, P.L.; Yao, L.Z. Rapid assessment of maximum distributed generation output based on security distance for interconnected distribution networks. Int. J. Electr. Power Energy Syst. 2018, 101, 13–24. [Google Scholar] [CrossRef]
- Wu, D.; Lian, J.; Sun, Y.; Yang, T.; Hansen, J. Hierarchical control framework for integrated coordination between distributed energy resources and demand response. Electr. Power Syst. Res. 2017, 150, 45–54. [Google Scholar] [CrossRef]
- Albadi, M.H.; El-Saadany, E.F. A summary of demand response in electricity markets. Electr. Power Syst. Res. 2008, 78, 1989–1996. [Google Scholar] [CrossRef]
- Yang, J.; Yuan, W.B.; Sun, Y.; Han, H.; Hou, X.C.; Guerrero, J.M. A novel quasi-master–slave control frame for PV-storage independent microgrid. Int. J. Electr. Power Energy Syst. 2018, 97, 262–274. [Google Scholar] [CrossRef]
- Li, P.; Wang, Z.X.; Wang, N.; Yang, W.H.; Li, M.Z.; Zhou, X.C. Stochastic robust optimal operation of community integrated energy system based on integrated demand response. Int. J. Electr. Power Energy Syst. 2021, 128, 106735. [Google Scholar] [CrossRef]
- Huang, W.J.; Zhang, X.; Li, K.P.; Zhang, N.; Strbac, G.; Kang, C.Q. Resilience oriented planning of urban multi-energy systems with generalized energy storage sources. IEEE Trans. Power Syst. 2022, 37, 2906–2918. [Google Scholar] [CrossRef]
- Masrur, H.; Shafie-Khah, M.; Hossain, M.J.; Senjyu, T. Multi-energy microgrids incorporating EV integration: Optimal design and resilient operation. IEEE Trans. Smart Grid 2022, 13, 3508–3518. [Google Scholar] [CrossRef]
- Seyedyazdi, M.; Mohammadi, M.; Farjah, E. A combined driver-station interactive algorithm for a maximum mutual interest in charging market. IEEE Trans. Intell. Transp. Syst. 2020, 21, 2534–2544. [Google Scholar] [CrossRef]
- Huang, X.Z.; Xu, Z.F.; Sun, Y.; Xue, Y.L.; Wang, Z.; Liu, Z.J. Heat and power load dispatching considering energy storage of district heating system and electric boilers. J. Mod. Power Syst. Clean Energy 2018, 5, 992–1003. [Google Scholar] [CrossRef]
- Wang, J.D.; Liu, J.X.; Li, C.H.; Zhou, Y.; Wu, J.Z. Optimal scheduling of gas and electricity consumption in a smart home with a hybrid gas boiler and electric heating system. Energy 2020, 204, 17951. [Google Scholar] [CrossRef]
- Zheng, X.Y.; Wei, C.; Qin, P.; Guo, J.; Yu, Y.H.; Song, F. Characteristics of residential energy consumption in China: Findings from a household survey. Energy Policy 2014, 75, 126–135. [Google Scholar] [CrossRef]
- International Energy Agency (IEA). Energy Balances of OECD Countries 2014; International Energy Agency: Paris, France, 2014. [Google Scholar]
- Chen, X.Y.; Kang, C.Q.; O’Malley, M.; Xia, Q.; Bai, J.H.; Liu, C. Increasing the flexibility of combined heat and power for wind power integration in China: Modeling and implications. IEEE Trans. Power Syst. 2015, 30, 1848–1857. [Google Scholar] [CrossRef]
- Chen, C.Y.; Chen, Y.; Zhao, J.B.; Zhang, K.F.; Ni, M.; Ren, B. Data-driven resilient automatic generation control against false data injection attacks. IEEE Trans. Industr. Inform. 2021, 17, 8092–8101. [Google Scholar] [CrossRef]
- Yu, X.; Xue, Y. Smart grids: A cyber–physical systems perspective. Proc. IEEE 2016, 104, 1058–1070. [Google Scholar] [CrossRef]
- Wen, Y.; Qu, X.; Li, W.; Liu, X.; Ye, X. Synergistic operation of electricity and natural gas networks via ADMM. IEEE Trans. Smart Grid 2018, 9, 4555–4565. [Google Scholar] [CrossRef]
- Shi, W.; Ling, Q.; Yuan, K.; Wu, G.; Yin, W. On the linear convergence of the ADMM in decentralized consensus optimization. IEEE Trans. Signal Process 2014, 62, 1750–1761. [Google Scholar] [CrossRef]
- Du, Y.; Zhang, W.; Zhang, T. ADMM-based distributed state estimation for integrated energy system. CSEE J. Power Energy 2019, 5, 275–283. [Google Scholar] [CrossRef]
- He, C.; Wu, L.; Liu, T.; Shahidehpour, M. Robust co-optimization scheduling of electricity and natural gas system via ADMM. IEEE Trans. Sustain. Energy 2017, 8, 658–670. [Google Scholar] [CrossRef]
- He, Y.; Yan, M.; Shahidehpour, M.; Li, Z.; Guo, C.; Wu, L. Decentralized optimization of multi-area electricity-natural gas flows based on cone reformulation. IEEE Trans. Power Syst. 2018, 33, 4531–4542. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, W.; Zhang, Y.; Bao, G. Day-ahead scheduling of distribution level integrated electricity and natural gas system based on fast-ADMM with restart algorithm. IEEE Access 2018, 6, 17557–17569. [Google Scholar] [CrossRef]
- Farivar, M.; Low, S.H. Branch flow model: Relaxations and convexification–Part I. IEEE Trans. Power Syst. 2013, 28, 2554–2564. [Google Scholar] [CrossRef]
- Boyd, S.; Parikh, N.; Chu, E.; Peleato, B.; Eckstein, J. Distributed optimization and statistical learning via the alternating direction method of multipliers. Found. Trends Mach. Learn. 2011, 3, 1–122. [Google Scholar] [CrossRef]
- Ratanakuakangwan, S.; Morita, H. Hybrid stochastic robust optimization and robust optimization for energy planning—A social impact-constrained case study. Appl. Energy 2021, 298, 117258. [Google Scholar] [CrossRef]


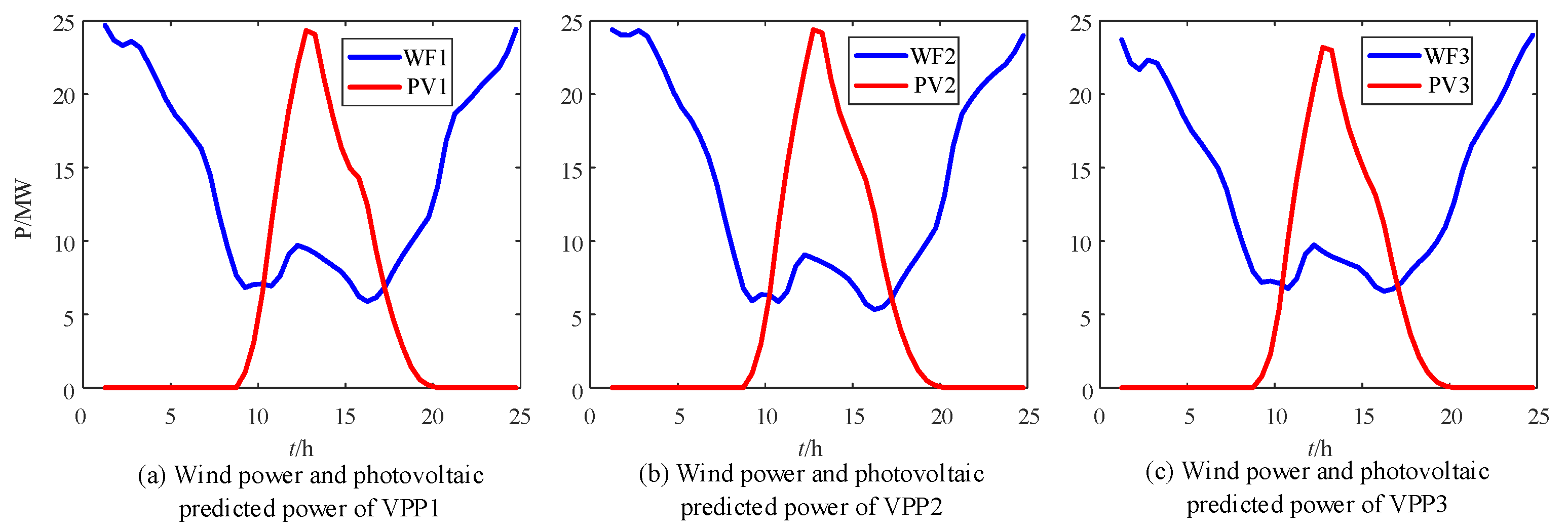

| Parameters | VPP1 | VPP2 | VPP3 |
|---|---|---|---|
| ($/MW2) | 0.0018 | 0.0019 | 0.0021 |
| ($/MW) | 18.39 | 20.51 | 22.67 |
| ($/h) | 298 | 249 | 228 |
| (MW) | 20 | 15 | 10 |
| (MW) | 60 | 40 | 20 |
| /h | 5 | 4 | 2 |
| /h | 5 | 4 | 2 |
| S/$ | 891 | 540 | 377 |
| CHP Output Range | VPP1 | VPP2 | VPP3 |
|---|---|---|---|
| A (P/MW, H/MW) | (17.0, 0.0) | (16.0, 0.0) | (17.0, 0.0) |
| B (P/MW, H/MW) | (12.0, 12.0) | (11.0, 11.0) | (12.0, 12.0) |
| C (P/MW, H/MW) | (30.0, 61.2) | (28.0, 58.2) | (30.0, 61.2) |
| D (P/MW, H/MW) | (34.0, 61.2) | (33.0, 58.2) | (34.0, 61.2) |
| E (P/MW, H/MW) | (44.0, 0.0) | (42.0, 0.0) | (44.0, 0.0) |
| CHP Unit Parameters | VPP1 | VPP2 | VPP3 |
|---|---|---|---|
| 4.07102 | 4.03102 | 4.07102 | |
| 2.23101 | 2.26101 | 2.23101 | |
| 5.60 | 5.61 | 5.60 | |
| 9.9010−4 | 9.8810−4 | 9.9010−4 | |
| 3.3610−5 | 3.3610−5 | 3.3610−5 | |
| 3.9310−4 | 3.9410−4 | 3.9310−4 |
| Parameters | VPP1 | VPP2 | VPP3 |
|---|---|---|---|
| 0.0011 | 0.0011 | 0.0011 | |
| 0.0012 | 0.0012 | 0.0012 |
| Parameters | VPP1 | VPP2 | VPP3 |
|---|---|---|---|
| 0 | 0 | 0 | |
| 10 | 15 | 20 | |
| 2 | 2 | 2 | |
| 5 | 5 | 5 | |
| 0.4 | 0.4 | 0.4 | |
| 0.3 | 0.3 | 0.3 | |
| 0.1 | 0.1 | 0.1 |
| Method | Convergence Accuracy | Error | Iterations | Operating Cost ($) |
|---|---|---|---|---|
| A1 | 10−5 | 1.31 10−6 | 69 | 2.3071 105 |
| A2 | 9.88 10−6 | 196 | 2.3080 105 | |
| A3 | −2.37 10−6 | 93 | 2.3074 105 | |
| A1 | 10−4 | 1.31 10−6 | 57 | 2.3071 105 |
| A2 | 9.94 10−5 | 162 | 2.3097 105 | |
| A3 | 2.12 10−5 | 79 | 2.3084 105 | |
| A1 | 10−3 | 1.31 10−6 | 42 | 2.3071 105 |
| A2 | 9.36 10−4 | 121 | 2.3113 105 | |
| A3 | 2.43 10−5 | 66 | 2.3096 105 | |
| A1 | 10−2 | 1.31 10−6 | 28 | 2.3073 105 |
| A2 | 2.41 10−3 | 72 | 2.3133 105 | |
| A3 | 2.96 10−5 | 45 | 2.3114 105 |
| Strategies | Thermal Delay and Heat Loss | EHLs Operation | Operating Cost/ ($) |
|---|---|---|---|
| A | × | × | 2.3283 105 |
| B | √ | × | 2.3213 105 |
| C | × | √ | 2.3191 105 |
| D | √ | √ | 2.3071 105 |
| Strategies | ) | Wind Power Abandonment Rate/% |
|---|---|---|
| A | 270.18 | 27.6 |
| B | 184.03 | 18.8 |
| C | 141.94 | 14.5 |
| D | 65.59 | 6.7 |
| Strategies | ) | Photovoltaic Abandonment Rate/% |
|---|---|---|
| A | 70.63 | 19.4 |
| B | 52.06 | 14.3 |
| C | 42.23 | 11.6 |
| D | 18.57 | 5.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, S.; Bao, G.; Hu, Y. Distributed Coordinated Operation of Active Distribution Networks with Electric Heating Loads Based on Dynamic Step Correction ADMM. Energies 2024, 17, 533. https://doi.org/10.3390/en17020533
Li S, Bao G, Hu Y. Distributed Coordinated Operation of Active Distribution Networks with Electric Heating Loads Based on Dynamic Step Correction ADMM. Energies. 2024; 17(2):533. https://doi.org/10.3390/en17020533
Chicago/Turabian StyleLi, Shoudong, Guangqing Bao, and Yanwen Hu. 2024. "Distributed Coordinated Operation of Active Distribution Networks with Electric Heating Loads Based on Dynamic Step Correction ADMM" Energies 17, no. 2: 533. https://doi.org/10.3390/en17020533
APA StyleLi, S., Bao, G., & Hu, Y. (2024). Distributed Coordinated Operation of Active Distribution Networks with Electric Heating Loads Based on Dynamic Step Correction ADMM. Energies, 17(2), 533. https://doi.org/10.3390/en17020533





