Abstract
The inconsistency in state-of-charge (SOC) for electric vehicle batteries will cause component damage and lifespan reduction of batteries. Meanwhile, the consistency in the state-of-health (SOH) also negatively influences the consensus of SOC. To ensure the consensuses of SOC and SOH simultaneously, this paper introduces an innovative distributed optimal Kalman consensus filter (KCF) approach to battery management systems. In addition, at the stage where sensors transmit information to each other, a new event-triggering mechanism (ETM) based on dynamic information is proposed to reduce communication overhead effectively. Theoretical analysis verifies the optimality of the algorithm. By numerical simulations, the proposed event-triggered distributed optimal KCF (ET-DOKCF) method can improve the performance of SOC-SOH estimation and save communication resources.
1. Introduction
Due to the serious environmental pollution problems caused by the exhaust emissions emitted by diesel and gasoline vehicles, electric vehicles (EVs) have attracted more and more attention in recent years and have become a new research focus [1]. The researchers in [2] provide an efficient strategy for the optimal scheduling of large-scale EVs connected to a predictable wind power grid. In contrast, the optimal scheduling of a predictable wind power grid provides an effective solution. In [3], a novel, innovative environmental mathematical formulation and corresponding deep reinforcement learning algorithm applied to EVs are proposed to improve the self-consumption of photovoltaic power generation and the charging state of EVs during charging. It is proved through experiments that it can maximize the SOCial benefits of the transportation system and is significant to the sustainable development of urban transportation [4]. Nowadays, EVs are powered by a battery pack consisting of multiple battery units, and users can access real-time information about each battery, such as state-of-charge (SOC) and state-of-health (SOH), by the BMS [5]. These parameters are the key performance indicators of each battery unit in the EV battery pack.
SOC consistency refers to the degree of consistency of the state of charge of each battery in a battery pack consisting of multiple batteries. Due to the manufacturing process of battery cells, age, charge and discharge times, environmental conditions, and other factors, the capacity and performance of each battery cell will gradually appear different, resulting in some battery cells in the battery pack than other battery cells earlier than the entire state of charge or discharge state. Therefore, it is necessary to ensure the consistency of the SOC of each cell in the battery pack to improve the efficiency and reliability of the battery pack. Researchers in [6] have proposed an active balancing method based on two flyback converters for series-connected battery packs. The balancing energy can be transferred between the whole battery and any individual cell. In [7], authors propose a novel lossless two-stage equalization circuit topology based on a conventional buck-boost circuit to achieve equalization of series-connected lithium-ion battery packs with higher efficiency and lower cost—the proposed topology efficiently consensus lithium-ion battery packs without adding additional devices. The experiment in [8] showed that 24 lithium-iron-phosphate battery packs composed of series-connected batteries were tested for cycling performance. After 300 cycles, significant differences were shown in the SOC level of individual batteries, and some batteries significantly deviated from the average SOC, exhibiting severe “sweep broom” effects. To prevent over-discharging of low SOC batteries, the battery pack must be prematurely terminated, resulting in a decrease in the actual usable capacity of the battery packs. Furthermore, based on the data from China’s Zhangbei Reserve Power Station, the station’s battery packs consist of lithium-ion batteries of the same batch and type, divided into six battery packs, each of which has been in operation for two years [9]. The issue of varying battery capacities within the group is becoming more pronounced. In one group, the battery with the highest SOH had its capacity reduced by , while the battery with the lowest SOH had its capacity reduced by . The inconsistencies in SOH lead to significantly decreased battery capacity, performances, and lifespans, which indirectly impact the consistency of SOC. As a result, a consensus of SOC and SOH must be considered simultaneously.
The first problem to be solved is how to accurately estimate SOC and SOH. In [10], authors constructed a distributed control-oriented electro-thermal coupled model and used an improved parameter identification method to construct an offline model parameter database. Recursive least squares and particle swarm optimization methods with variable forgetting factors were used to identify the electrical and thermal parameters. A SOC-corrected core temperature estimation technique finally moves forward. In [11], the authors proposed a fully distributed state estimation method for power systems based on weighted least squares and graph theory. In addition, unlike the existing methods, the method proposed in this paper is a bus-level DSE method, which does not require the power system to be divided into multiple regions. The fully distributed approach of the method is enlightening for SOC estimation of multiple batteries. In [12], the researchers employ the open-circuit voltage (OCV) to estimate SOC accurately. In [13], the authors utilize a combination of BP neural networks and PSO algorithms for SOC estimation. In [14], a novel SOC closed-loop estimation algorithm is introduced, based upon the fusion of the ESP model and ampere-hour integration, which combines the merits of both methods and enhances the accuracy of SOC estimation. Regarding SOH estimation, the study by [15] proposes a method based upon an improved ant lion optimization algorithm and support vector regression (IALO-SVR), providing more precise estimations than conventional methods. In [16], the author suggests using an extended Kalman filter-recursive least squares parameter identification method based on the second-order RC equivalent circuit model. In [17], a new deep learning network framework is proposed to achieve SOH estimation. To improve the accuracy of the estimates, the researchers in [18] proposed a method based on a hybrid neural network called Gate Recursive Unit-Convolutional Neural Network, which can learn the shared information and time dependence of charging profiles through deep learning techniques, and can utilize the newly observed charging profiles (e.g., voltages, currents, and temperatures) to estimate SOH. In [19], proposed as a means of estimating SOC and SOH, an adaptive segmented equivalent circuit model based on the extended Kalman filter is illustrated in the degradation study and the model validation procedure. The findings demonstrate the applicability of the segmented parameter adaptation described in this study to various battery chemistries and aging conditions. In [20], the authors propose an improved Remora optimization algorithm. After detecting the optimal values of the parameters, the SOC will be evaluated by a dual adaptive Kalman filtering algorithm. Then, the SOH is estimated based on the predicted cell SOC. In [21], in order to improve the accuracy of real-time estimation of battery state, a novel back-propagation neural network-double extended Kalman filter based on finite-element memory recursive least squares is proposed for the synergistic estimation of SOC and SOH in lithium-ion batteries by creating a second-order equivalent circuit model. The researchers in [22] proposed an adaptive double square root Kalman filter with a resting region to accomplish the estimation while accounting for aging effects. The first filter estimates the SOC and SOH, and the second adaptively updates the drift model parameters based on the dormant region. However, these algorithms have two drawbacks: they can only estimate either SOC or SOH, or they estimate both but need to be simplified.
Then, the consensus between SOC and SOH should be considered. In [23], the authors compare the SOC consensus problems under continuous systems, discrete systems, self-triggering, and event-triggering mechanisms (ETM). In [24], a distributed model predictive control approach is proposed to achieve dynamic response to load perturbations and maintain SOC consistency for heterogeneous energy storage systems. The authors suggest an adaptive power management plan for standalone microgrids to address these issues based on the battery’s available SOC. Distributed energy resources can be smoothly transitioned from maximum power point tracking mode to adaptive sag mode and vice versa, using the suggested battery SOC-based adaptive power management sag control method [25]. In [26], this article proposes a further multi-layer SOH consensus scheme to consensus SOH across all batteries through a comprehensive portfolio of SOH’s large-scale BESS balancing strategy and commercial battery balancing technology. In [27], this paper presents a battery management approach for monitoring and controlling temperature, SOC, SOH, etc., enhancing the efficiency of rechargeable batteries. This approach provides some insights into our work. However, these algorithms can only perform observation processing on one parameter at a time, which cannot meet the multi-parameter situation in the actual situation. Therefore, it needs to be improved.
It is well known that network systems are always limited by energy and bandwidth, which is why the ETM was introduced. In [28,29], the authors proposed an ETM with fixed thresholds. In [30], the authors considered the SOC consensus under the ETM and added the power supply and demand consensus in the context of energy storage systems. In [31,32], two different ETMs were proposed, and satisfactory results were achieved. However, these ETMs usually adopt fixed thresholds, which do not consider the change in information during operation and cause the waste of this information. Based on these works, this study aims to propose a new design for the ETM. During the information-gathering phase, the trigger condition is established by the value of the battery itself. In the information transmission stage, the trigger condition is determined by the transmitted information and the collected information, thereby enhancing the flexibility of the overall mechanism and eliminating the drawback of information waste caused by fixed thresholds of the existing mechanism.
The novelties of this work are summarized as follows:
- (1)
- To achieve accurate estimation of SOC and SOH of EV batteries, a novel distributed optimal Kalman consensus filter is proposed for a battery management system; it reduces the estimated error.
- (2)
- A new event-triggered approach based on dynamic information is introduced to use information from the sensor and its neighbors entirely to save communication resources.
- (3)
- To eliminate the impact of SOH on SOC, state estimation and consensus control are performed on both SOC and SOH simultaneously. This joint-consensus concept is proposed as more conducive to realistic battery management.
The remaining parts of this article are as follows: In Section 2, the ET-DOKCF and two different ETMs are introduced. Section 3 introduces some definitions of the ET-DOKCF, and a brief analysis of the system’s stability is provided. Section 4 provides a filtering comparison of the three algorithms, a comparison of ETMs, anti-interference performances of the proposed algorithm under different real noises, and the display of consistency results. Section 5 concludes this paper, and the derivation of ET-DOKCF is given in the Appendix A.
2. Problem Statement
2.1. SOC Consensus
SOC represents the state-of-charge of a battery, reflecting the remaining power of the battery, and is one of the core parameters of a battery. As defined by the Advanced Battery Consortium of America, SOC is the ratio of the battery’s remaining charge to its calibrated capacity under the same operating conditions at a specific discharge multiplier, expressed in the following formula:
where and are the remaining capacity and rated charge, respectively. The battery pack of an EV consists of many batteries, which can have differences when they leave the factory, which is known as the inconsistency of SOC. Each battery undergoes multiple charges and discharges in the usage process, increasing this difference. Some of these batteries may be fully charged during the charging process, and in order to ensure that they do not overcharge, the battery pack will stop charging in advance, resulting in the battery pack not reaching a full state. In contrast, some batteries discharge quickly during the discharge process, reaching an empty state before other batteries. To prevent over-discharging, the battery pack also stops discharging. This inconsistency can decrease the battery’s service life, and serious cases can lead to dangers such as explosions. Therefore, it is necessary to control the consensus of SOC to reduce inconsistencies between battery cells and improve the service life and safety of EVs [33].
2.2. SOH Consensus
Battery SOH refers to a battery’s state of health, which measures its performance and longevity. Battery SOH is usually expressed as a percentage and reflects the ratio between the maximum capacity of the battery and its original rated capacity. As battery usage time increases due to chemical reactions, material aging, and cycling fatigue, the battery’s usable capacity will gradually decline, and the SOH value will decrease accordingly. When the SOH value drops to a certain level, the battery’s performance will be significantly reduced, and it is necessary to consider replacement or rehabilitation. Battery SOH monitoring is critical to ensuring the reliability and safety of battery systems, especially in EVs, energy storage systems, and portable electronic devices. The following formula can represent SOH:
where and are the remaining capacity and nominal capacity, respectively. Similarly, as the usage time increases, the inconsistency of SOH among the individual batteries in a battery pack will gradually worsen, thereby aggravating the inconsistency of SOC and deepening the differences in charging level and discharge depth among the battery units, forming a vicious cycle that can damage the battery. Therefore, the coordinated consensus control of SOC and SOH is crucial.
2.3. BMS with SOC and SOH
The BMS (Battery Management System)’s organizational structure is displayed in Figure 1. It is an electrical system designed to monitor and manage battery performance. Usually, it comprises hardware and software that continuously tracks the battery’s vital indicators, including temperature, voltage, current, and other essential factors. It guarantees the battery’s safe and dependable operation. Additionally, by maintaining the battery’s health and extending the battery pack’s service life through equalization activities, the BMS forecasts the battery’s life. BMSs are a critical component in EVs, energy storage systems, and other devices that require battery power, improving energy efficiency and reducing the risk of potential failures by accurately managing the battery charging and discharging process. It estimates the SOC and SOH of a battery by collecting real-time battery voltage, current, temperature, and other data. SOC is usually measured by the Ah integral method, which calculates the battery’s remaining charge based on the battery’s discharge curve and actual discharge current. Measuring SOH, on the other hand, requires long-term monitoring of the charge/discharge cycles of the battery, which is combined with the rated and actual capacity of the battery to calculate the battery’s SOH. In order to improve the accuracy of measurement, the BMS will periodically use calibration algorithms to correct the SOC and SOH to compensate for errors caused by battery aging and other factors. The BMS can effectively monitor battery performance, predict battery life, and ensure that the battery operates within a safe range. There are many reasons for errors in this process. Therefore, achieving accurate estimates of SOC and SOH is the basis for consensus issues.
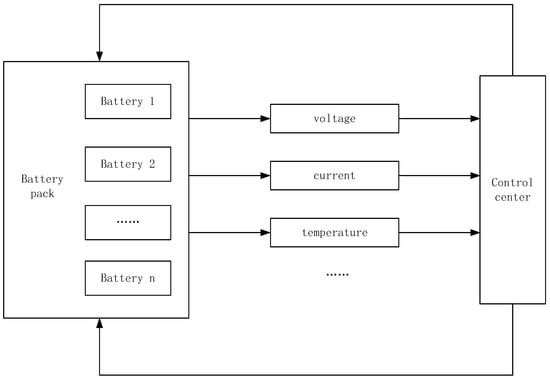
Figure 1.
Architecture of BMS.
The main methods used by BMS to regulate SOC and SOH are:
- (1)
- Equalize Charging: Ensure that each cell in the battery pack is charged at the same rate to avoid over-charging or under-charging specific cells to keep their SOC and SOH consistent.
- (2)
- Equalize discharge: Make sure each cell in the battery pack is discharged at the same rate to avoid over-discharge, which will cause the SOC and SOH of some cells to decrease.
- (3)
- Regular testing: Regularly test the SOC and SOH of each cell in the battery pack to detect and resolve inconsistencies.
- (4)
- Temperature control: Keep the working temperature of the battery pack in a suitable range to avoid temperature differences that cause changes in the SOC and SOH of the battery cells.
- (5)
- Avoid overcharging and overdischarging: Avoid overcharging and overdischarging battery packs to minimize wear and tear on the battery cells.
2.4. Problem Formulation
The state of a battery in BMS is modeled as:
where , and the and represent the SOC and SOH of the battery at k instant, respectively. and are known real-time-varying matrices with proper dimensions, is the process noise.
The state of each battery is observed by a sensor network consisting of N sensors, and the measurement model for sensor i is:
where is the measurement of sensor i for the battery and is observation noise of sensor i with the following statistics:
where if , and otherwise.
The algorithm in this paper is applied to the control center of the BMS in Figure 1. First, the ET-DOKCF, relying on the sensor network, estimates the SOC and SOH of each battery pack. When inconsistencies are found, a balancing algorithm is used to adjust the SOC and SOH to be consistent so that each cell in the whole battery pack has the same SOC and SOH and to mitigate or even eliminate the negative impacts of the inconsistencies of the SOC and SOH on the EVs.
First of all, we introduce the ET-DOKCF. In this work, we use sensors in BMS to detect and estimate the SOC and SOH and then make their consensus. Each sensor collects, processes, and transmits information to its neighbors. Let denote a graph, where is the set of nodes and is the set of edges in which an ordered pair i to j means that there exists a directed edge from i to j. Especially, for undirected topology, is equal to . The neighbour set of node i is denoted by . An undirected communication graph is said to be connected if there exists one node j such that there exists a path from i to j for any j. We assumed that the undirected graph G is connected in this paper.
The introduction of ETMs has reduced the waste of communication resources and the burden of communication. In the ETM of the communication transmission stage proposed in this paper, the sensor and the sensor information of its neighbor nodes determine the triggering threshold. So, compared with traditional ETM, which does not consider the fixed threshold of this information, it avoids the waste of information and is more flexible. Specifically, at each time k, the sensor i collects information from the battery when the following conditions are met:
where , and denotes the latest triggered time of sensor i, and is the threshold parameter of sensor i. When the condition in the above formula is satisfied, the event is triggered while the information observed by this sensor is corrected to .
Sensor i transfers information to its neighbors if and only if the following conditions are met:
where , , denotes the latest triggered time, and and posteriori and a priori state estimate of the of , respectively. is a small normal number. The left side of the above formula is the variation of the sensor’s information, and the threshold on the right side consists of information from its neighboring sensors. Hence, it results in less wasted information compared to a fixed threshold the user sets.
The last transition times and are updated as:
Relying on the increasingly intelligent wireless sensor networks, the Kalman consensus filter (KCF) has been widely researched and applied. KCF is a target-tracking algorithm based on the Kalman filtering algorithm, where each sensor in a sensor network can be viewed as an individual KCF and multiple KCFs communicate and collaborate to achieve accurate target tracking. The KCF algorithm is derived from the Kalman filter, a recursive filter that estimates the system state through prediction and updating. It uses a dynamic model of the system and an observation model to predict future system state values. It uses the observations to update these predictions to minimize the prediction error. KCF introduces the concept of consistency based on the traditional Kalman filter algorithm. Consistency means that the estimated error of each node decreases during the iteration process and finally converges to a stable value. The estimates of all KCFs achieve consistency and reach an identical value. This algorithm can improve the accuracy and robustness of target tracking. The KCF is formulated as follows:
As shown in (10), the Kalman filter partially filters the information observed by itself and determines the filtering effect by the size of the value. The component consensus is different in that it incorporates information from other nodes, and the results from these nodes together form the basis of the KCF’s estimation of the target. Through an iterative process, the values of all the filters will eventually reach a consistent value, resulting in a relatively accurate estimate. It should be noted that the choice of value and the filter settings need to be decided according to the specific situation. In practical applications, it is necessary to choose the appropriate parameter settings according to the characteristics of the specific scene and target to achieve the best filtering effect. Evaluating and optimizing the filter’s performance is also necessary to ensure it performs well in various situations.
According to the above description, based on the traditional KCF structure, we combine the ETMs in (8) and (9) to form a new SOC and SOH estimation method to predict SOC and SOH more accurately. When the variation of a critical parameter reaches a certain threshold, we trigger the execution of the KCF algorithm and make corrections based on the new observation information. This process is iterated consistently until the values of all filters reach consistency, resulting in a relatively accurate SOC and SOH estimate.
Figure 2 shows the architecture of the ET-DOKCF in BMS. Each sensor obtains the observed value from its observed battery, and the transmitted by the sensor of its neighbor node is processed by the consensus component and sent to the Kalman filter to obtain , and send its own to the sensor of the neighbor node. Of course, the observation and transmission of information need to be constrained by the ETM.
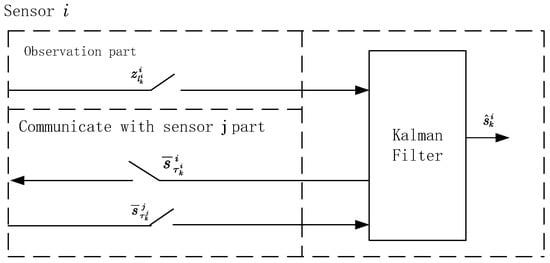
Figure 2.
Architecture of the ET-DOKCF of sensor i.
The problem now is to obtain an optimal set of Kalman gains to minimize the mean square error (MSE) that is, each sensor has a minimum error in estimating the corresponding battery state. Moreover, setting the appropriate consensus gains to achieve consensus in all battery states while ensuring system stability.
3. Event-Triggered Distributed Optimal Kalman Consensus Filter and Balance Algorithm
For a smooth derivation, we first need some definitions. The priori estimated error and the posterior estimated error for the battery at time instant k as:
Moreover, denoting the errors related to the event-triggered schedules as:
Then, the asSOCiated error covariance matrices can be given by:
For convenience, we identify the notations that can define the matrices , , , , , by , , , , , , respectively.
Substituting (12) and (13) to (11), we have:
and similarly for sensor j:
Based on the above definition, the ET-DOKCF algorithm is formulated as (20)–(24):
where
The above completes the accurate estimates of SOC and SOH. After obtaining the exact estimates of SOC and SOH for each cell, equalization is required in case of inconsistency. The algorithm originates from the study of multi-agent consistency, is based on algebraic graph theory, and can be realized using concise formulas. Let the number of batteries in the BMS be M, and the estimated values of SOC and SOH for ith battery are and . Denote the and , then the balance algorithm is:
where I is the unit matrix, and and are constant parameters, T is the sampling period, and L is the Laplace matrix for the topological diagram between batteries. This balance algorithm possesses the distinct advantage that it enables the SOC and SOH of the system to be consistent at all times in a simple yet effective manner, thus avoiding the need to introduce cumbersome and complex steps and formulas to achieve this goal. In addition, the algorithm requires a relatively small number of parameters and formulas, further simplifying the implementation process. With this feasible approach, the consistency of SOC and SOH can be efficiently maintained without burdening the implementer.
The above is a complete algorithm for estimating and balancing battery SOC and SOH based on ET-DOKCF, and the whole process can be described by Algorithm 1 as follows:
Algorithm 1 Estimation and Balance of SOC and SOH Based on ET-DOKCF |
|
Remark 1.
The research on can be categorized into numerical and matrix forms. Among numerous findings, selecting the appropriate to maintain system stability without compromising algorithm efficiency remains a pending issue. In the context of this article, with prolonged usage and frequent charging and discharging, the BMS performance degrades, and unstable factors arise in the presence of complex computing systems. Consequently, we adopt the former approach where is assumed as a small constant, such as 0.1. The value can be adjusted according to usage scenarios, ensuring system stability while reducing computational complexity. Furthermore, the ETMs in this paper eliminate the possibility of the Zeno phenomenon based on discrete time.
4. Numerical Simulation
Figure 3 depicts a network structure containing five batteries that, together, form a whole. Among them, we have chosen one of the batteries as a representative and made it the focus of our study, exploring it in detail in parts 4.1, 4.2, and 4.3. However, in Part 4.4, we focus on the whole network by including all the batteries in our study. Thus, we have conducted a comprehensive study of each battery in this network.
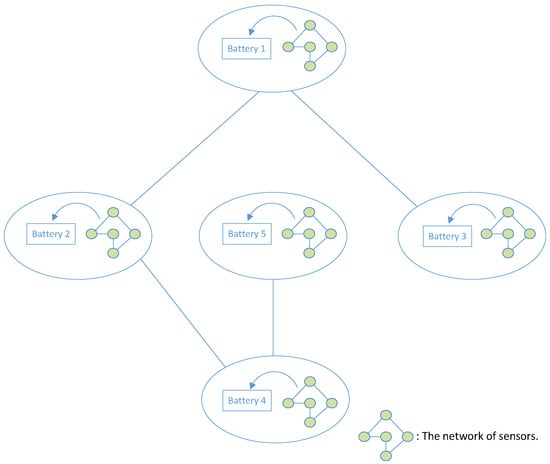
Figure 3.
Topology diagram of batteries.
4.1. Comparison of Estimated Errors of Three Different KCFs
The state model and corresponding observation model for the battery are as follows:
where sampling time , the initial moment the state of each battery is . The above SOC and SOH values are from [34,35], and more detailed data can be found in the CALCE Battery Group of the University of Maryland and the NASA battery data set.
In order to measure the estimation ability of the algorithm intuitively and effectively, we use the following formula to represent the estimated error of the battery SOC and SOH: the smaller their values represented, the smaller the estimated error of SOC and SOH, the stronger the estimation ability of the algorithm.
where K is the number of experiments, and in this article.
Figure 4 illustrates the estimated error of the two existing filters and the filter used in this paper for the same set of SOC data, which is calculated as (29). The comparison shows that the estimated error of the traditional KCF algorithm is between 0.8 and 1, and the estimated error of the suboptimal KCF algorithm is between 0.4 and 0.6, which is improved but still relatively large. Moreover, the estimated error of the ET-DOKCF algorithm proposed in this paper is minimized between 0.2 and 0.4, reducing the estimated error. This indicates that the algorithm proposed in this paper has a significant advantage in filtering effects. Therefore, by comparing the estimated errors of the three algorithms in Figure 4, the ET-DOKCF algorithm proposed in this paper has the best filtering effect and can provide a more accurate and reliable SOC estimation when dealing with actual vehicle operation data. This will help to improve vehicle efficiency, reduce costs, and improve the safety and reliability of vehicles.
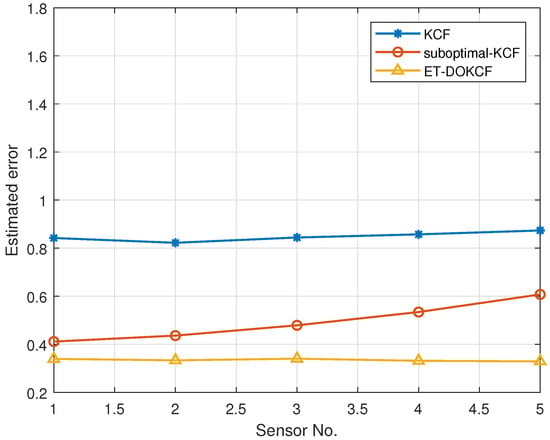
Figure 4.
Comparison of the estimated errors of the three different KCFs.
In order to validate the noise immunity of the proposed algorithm, we use various accurate white noise data from the actual noise database noiseX92 for simulation experiments, thus ensuring the authenticity and reliability of the test results. We obtain the presentation results in Figure 5a,b by carefully analyzing these data. From the figures, the algorithm proposed in this paper exhibits a relatively stable estimated error under different natural noise environments. This error always stays around 0.3 and does not fluctuate drastically due to the enhancement or weakening of the noise. The algorithm in this paper not only excels in error control but, more importantly, exhibits solid anti-interference ability. No matter how the noise changes, the algorithm can quickly adapt and maintain a stable performance output. This finding provides us with strong technical support in practical applications and proves the practical value of our proposed algorithm.
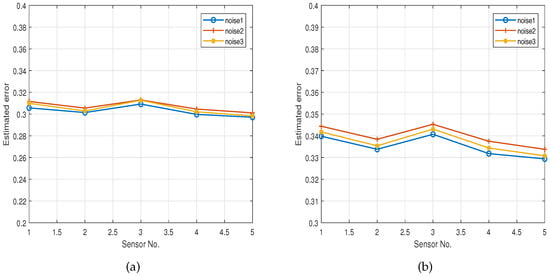
Figure 5.
(a) Estimated errors of SOC; (b) estimated error of SOH.
4.2. Comparison of AITRs of Two Different ETMs
In order to compare the ETM proposed in this paper with the existing ETM with a threshold fixed, we introduce the average information transfer rate (AITR):
where K is the iteration step, and the is:
On this basis, the two different ETMs can be compared by the AITR of each sensor. The final results in Figure 6 show that the AITR under the mechanism of this paper is more significant than under the fixed threshold. This shows that the ETMs mentioned in this paper can fully utilize the real-time information and avoid wasting the information compared to the fixed threshold, which strongly supports the introduction and Section 2.4 on ETM.
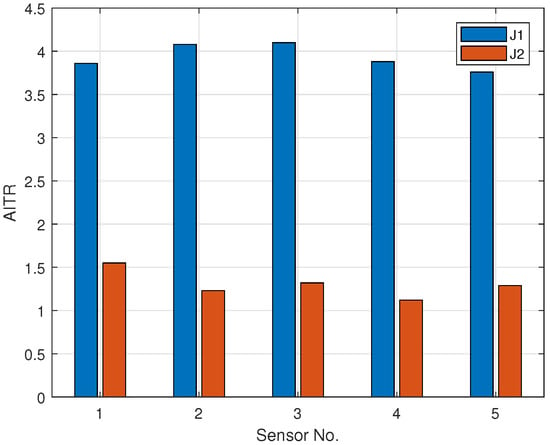
Figure 6.
AITR and .
Figure 7 compares the SOC and SOH estimated errors for cells with and without SOH consensus. It is evident that when the SOH is inconsistent, the SOC and SOH estimated errors are relatively high in the range of 0.3–0.4. On the other hand, when the SOH is consistent, the estimated errors are significantly reduced to the range of 0.1–0.2. This indicates that SOH’s consistency directly affects the estimation’s accuracy. In addition, the results show that the estimated error is further reduced when SOH consistency is taken into account, which emphasizes the importance of SOH consistency in improving the accuracy of SOC and SOH estimation and strongly supports the contents of [8,9] in the introduction.
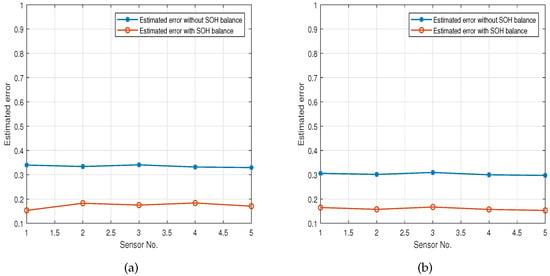
Figure 7.
(a) Estimated errors of SOC; (b) estimated error of SOH.
4.3. Consistency Results
Figure 8 shows the SOC and SOH alignment process after the estimation calculations. In this process, the BMS regulates the state of each battery to match the process. The BMS will use various algorithms and techniques, including the ET-DOKCF algorithm, to monitor and analyze the battery’s voltage, current, and other relevant parameters and adjust the battery’s temperature, discharge rate, and charging strategy in real-time to bring the battery’s SOC and SOH into consistency. This consistency adjustment improves the battery’s overall performance, extends the battery’s service life, and reduces the risk of battery failure. This process is continuous, and the BMS will constantly adjust and optimize the battery state to achieve the best battery management results. Ultimately, this will help improve electric vehicles’ driving performance and reliability while reducing maintenance costs and energy consumption.
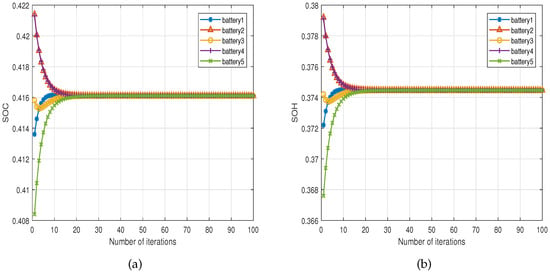
Figure 8.
(a) SOC consensus; (b) SOH consensus.
The following five Table 1, Table 2, Table 3, Table 4 and Table 5 show the number of event triggers for each battery sensor network. Stage 1 is where the sensor collects information, and stage 2 is where sensor information is transmitted. According to the data in the table, the number of triggers in stage 1 resides between 40 and 70. In contrast, the number of triggers in stage 2 resides between 20 and 30, proving that the ETMs in this paper can effectively reduce the number of communications, save resources, and simultaneously alleviate the burden on the communication network.

Table 1.
The numbers of event triggering of sensors of battery 1.

Table 2.
The numbers of event triggering of sensors of battery 2.

Table 3.
The numbers of event triggering of sensors of battery 3.

Table 4.
The numbers of event triggering of sensors of battery 4.

Table 5.
The numbers of event triggering of sensors of battery 5.
5. Conclusions
This paper proposes an ET-DOKCF algorithm combined with BMS to simultaneously realize the estimation and consensus of SOC and SOH. Meanwhile, a new ETM based on dynamic information is introduced, which fully uses the process information transmitted between sensors, effectively reducing the number of communications, saving resources, and reducing the communication burden. In addition, the simulation results show that the estimated error of the proposed algorithm is minimized compared with other algorithms. It is proven that SOH inconsistency negatively affects the estimation of SOC and SOH, making their estimated errors larger. After simulation tests under accurate noise data, the anti-noise performance of the algorithm in this paper is good. The subsequent consensus algorithm makes SOC and SOH consistent simultaneously, realizing the purpose of consensus control. In the future, we will continue to study the algorithm’s performance in actual tests, realize more accurate estimation by improving the algorithm, and reduce the estimated error. Moreover, based on the development of the BMS as a background and taking into account user demand and the direction of intelligence, we will work on optimizing the algorithm and implementing more intelligent control strategies to further the development of electric vehicles towards more innovative and more convenient services. Through such improvements, we aim to reduce the consumption of traditional energy sources, mitigate the negative impact on the climate, and positively contribute to the realization of climate mitigation.
Author Contributions
Conceptualization and formal analysis, X.F.; Investigation, Y.F.; Resources, Y.F; Writing—review and editing, M.X. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China (62203008, 61973002, 62203352), the Natural Science Research Project of Universities in Anhui Province (KJ2021A0012), Opening Foundation of Key Laboratory of Intelligent Computing and Signal Processing (Anhui University), Ministry of Education (2020B002).
Data Availability Statement
The authors confirm that the data supporting the findings of this study are available within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations and Nomenclature
The following abbreviations and nomenclature are used in this manuscript:
| Abbreviations | |
| SOC | State-of-charge |
| SOH | State-of-health |
| EV | Electric vehicle |
| KCF | Kalman consensus filter |
| BMS | Battery Management System |
| ETM | Event triggering mechanism |
| OCV | Open-circuit voltage |
| PSO | Particle Swarm Optimization |
| IALO-SVR | Improved ant lion optimization algorithm and support vector regression |
| RC | Resistance-Capacitance Circuits |
| BESS | Battery Energy Storage System |
| AITR | Average information transfer rate |
| ET-DOKCF | Event-triggered distributed optimal KCF |
| Nomenclature | |
| Covariance matrix | |
| The trace of a matrix | |
| Euclidean vector norm | |
| The transpose of a matrix | |
| State of battery unit | |
| Observations of sensor i at time k | |
| Euclidean vector norm | |
| Rated capacity | |
| Remaining charge | |
| Remaining capacity | |
| Nominal capacity | |
| The state transition matrix at time k | |
| System noise input matrix at time k | |
| Process noise at time k | |
| M | Number of batteries in BMS |
| Observation matrix of sensor i | |
| Observation noise of sensor i at time k | |
| SOC of battery at time k | |
| SOH of battery at time k | |
| Observation error of sensor i at time k | |
| Error threshold constant of sensor i | |
| Ante estimated error of sensor i for at time k | |
| The sum of the errors between sensor i and its neighbors | |
| The set of neighbors for sensor i | |
| The event trigger moment in the information collection phase of sensor i for | |
| The event trigger moment for information transmission phase of sensor i at time k | |
| Priori state estimate of sensor i | |
| Posteriori state estimate of sensor i | |
| Kalman gain of sensor i at time k | |
| Kalman consensus gain of sensor i at time k | |
| MSE of sensor i for at time k | |
| Priori estimated error of sensor i at time k | |
| Posteriori estimated error of sensor i at time k | |
| State error of sensor i at time k | |
| Priori estimated error of sensor i time k | |
| Covariance matrix of and for nth battery at time k | |
| Covariance matrix of and | |
| Covariance matrix of and | |
| Covariance matrix of and | |
| Covariance matrix of and | |
| Covariance matrix of and | |
| Covariance matrix of and | |
| Covariance matrix of and at time k | |
| Partial derivative symbol | |
| Noise matrix of sensor i at time k | |
| T | Sampling time |
| The estimated value of SOC for ith battery at time k | |
| The estimated value of SOH for ith battery at time k | |
| Input of SOC of ith battery at time k | |
| Input of SOH of ith battery at time k | |
| Constant parameter | |
| Constant parameter | |
| Vector of SOC of all the batteries at time k | |
| Vector of SOH of all the batteries at time k | |
| L | Laplace matrix |
| Average information transfer rate of sensor i | |
| Number of information transmission of sensor i |
Appendix A
Based on the above definition, the following is the derivation of ET-DOKCF.
In (23), when the MSE covariance of sensor i is in form of:
Since the total MSE for all sensors in the network of nth battery is:
the optimal Kalman gains can be obtained by setting derivative of the trace of with respect to zero:
From matrix calculus, for any two matrices X and Y, the following properties hold:
Therefore, the following properties hold:
then we get the optimal Kalman gain as:
We define the information of battery received by sensor i at time k as set , so the information set collected by sensor i till time k is:
As the definition in (13):
and let , we have:
This finishes the derivation and proof of ET-DOKCF.
References
- Ehsani, M.; Singh, K.V.; Bansal, H.O.; Mehrjardi, R.T. State of the art and trends in electric and hybrid electric vehicles. Proc. IEEE 2021, 109, 967–984. Available online: https://ieeexplore.ieee.org/document/9422914 (accessed on 13 June 2023). [CrossRef]
- Liu, S.; Liu, Y.; Zhang, B.; Liu, C. Full-Speed Region Predictive Current Control Method of Symmetrical Series-Winding PMSM With Higher DC-Link Utilization. IEEE Trans. Ind. Electron. 2023, 1–12. [Google Scholar] [CrossRef]
- Zhang, C.; Yin, W.; Wen, T. An advanced multi-objective collaborative scheduling strategy for large scale EV charging and discharging connected to the predictable wind power grid. Energy 2024, 287, 129495. [Google Scholar] [CrossRef]
- Dorokhova, M.; Martinson, Y.; Ballif, C.; Wyrsch, N. Deep reinforcement learning control of electric vehicle charging in the presence of photovoltaic generation. Appl. Energy 2021, 301, 117504. [Google Scholar] [CrossRef]
- Mei, Z.; Que, Z.; Qiu, H.; Zhu, Z.; Cai, Z. Optimizing the configuration of electric vehicle charging piles in public parking lots based on a multi-agent model. Phys. A Stat. Mech. Appl. 2023, 632, 129329. [Google Scholar] [CrossRef]
- Ding, X.; Zhang, D.; Cheng, J.; Wang, B.; Chai, Y.; Zhao, Z.; Xiong, R.; Luk, P.C.K. A novel active equalization topology for series-connected lithium-ion battery packs. IEEE Trans. Ind. Appl. 2020, 56, 6892–6903. [Google Scholar] [CrossRef]
- Xiong, R.; Pan, Y.; Shen, W.; Li, H.; Sun, F. Lithium-ion battery aging mechanisms and diagnosis method for automotive applications: Recent advances and perspectives. Renew. Sustain. Energy Rev. 2020, 131, 110048. [Google Scholar] [CrossRef]
- Baumhöfer, T.; Brühl, M.; Rothgang, S.; Sauer, D.U. Production caused variation in capacity aging trend and correlation to initial cell performance. J. Power Sources 2014, 247, 332–338. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, Y.; Chen, Z. SOC-Modified Core Temperature Estimation of Lithium-Ion Battery Based on Control-Oriented Electro-Thermal Model. IEEE Trans. Power Electron. 2023, 38, 11642–11651. [Google Scholar] [CrossRef]
- Li, Q.; Cheng, L.; Gao, W.; Gao, D.W. Fully distributed state estimation for power system with information propagation algorithm. J. Mod. Power Syst. Clean Energy 2020, 8, 627–635. [Google Scholar] [CrossRef]
- Yuan, L.; Gu, J.; Wen, H.; Jin, Z. Improved particle filter for non-gaussian forecasting-aided state estimation. J. Mod. Power Syst. Clean Energy. 2022. Available online: https://ieeexplore.ieee.org/document/9808354 (accessed on 13 June 2023).
- Susanna, S.; Dewangga, B.R.; Wahyungoro, O.; Cahyadi, A.I. Comparison of simple battery model and thevenin battery model for SOC estimation based on OCV method. In Proceedings of the 2019 International Conference on Information and Communications Technology (ICOIACT), Yogyakarta, Indonesia, 24–25 July 2019; pp. 738–743. [Google Scholar]
- Lipu, H.; Hannan, M.; Hussain, A.; Saad, M. Optimal BP neural network algorithm for state of charge estimation of lithium-ion battery using PSO with PCA feature selection. J. Renew. Sustain. Energy 2017, 9, 064102. [Google Scholar] [CrossRef]
- Ren, L.; Zhu, G.; Kang, J.; Wang, J.V.; Luo, B.; Chen, C.; Xiang, K. An algorithm for state of charge estimation based on a single-particle model. J. Energy Storage 2021, 39, 102644. [Google Scholar] [CrossRef]
- Li, Q.; Li, D.; Zhao, K.; Wang, L.; Wang, K. State of health estimation of lithium-ion battery based on improved ant lion optimization and support vector regression. J. Energy Storage 2022, 50, 104215. [Google Scholar] [CrossRef]
- Tan, X.; Zhan, D.; Lyu, P.; Rao, J.; Fan, Y. Online state-of-health estimation of lithium-ion battery based on dynamic parameter identification at multi timescale and support vector regression. J. Power Sources 2021, 484, 229233. [Google Scholar] [CrossRef]
- Fan, Y.; Xiao, F.; Li, C.; Yang, G.; Tang, X. A novel deep learning framework for state of health estimation of lithium-ion battery. J. Energy Storage 2020, 32, 101741. [Google Scholar] [CrossRef]
- Huang, Z.; Best, M.; Knowles, J.; Fly, A. Adaptive Piecewise Equivalent Circuit Model with SOC/SOH Estimation Based on Extended Kalman Filter. 2022. Available online: https://ieeexplore.ieee.org/document/9935824 (accessed on 2 June 2023).
- Reshma, P.; Manohar, V.J. Collaborative evaluation of SOC, SoP and SOH of lithium-ion battery in an electric bus through improved remora optimization algorithm and dual adaptive Kalman filtering algorithm. J. Energy Storage 2023, 68, 107573. [Google Scholar] [CrossRef]
- Wang, C.; Wang, S.; Zhou, J.; Qiao, J.; Yang, X.; Xie, Y. A novel back propagation neural network-dual extended Kalman filter method for state-of-charge and state-of-health co-estimation of lithium-ion batteries based on limited memory least square algorithm. J. Energy Storage 2023, 59, 106563. [Google Scholar] [CrossRef]
- Li, Z.; Shen, S.; Zhou, Z.; Cai, Z.; Gu, W.; Zhang, F. Novel method for modelling and adaptive estimation for SOC and SOH of lithium-ion batteries. J. Energy Storage 2023, 62, 106927. [Google Scholar] [CrossRef]
- Ma, L.; Xu, Y.; Zhang, H.; Yang, F.; Wang, X.; Li, C. Co-estimation of state of charge and state of health for lithium-ion batteries based on fractional-order model with multi-innovations unscented Kalman filter method. J. Energy Storage 2022, 52, 104904. [Google Scholar] [CrossRef]
- Huang, C.; Yang, M.; Ge, H.; Deng, S.; Chen, C. DMPC-based load frequency control of multi-area power systems with heterogeneous energy storage system considering SOC consensus. Electr. Power Syst. Res. 2024, 228, 110064. [Google Scholar] [CrossRef]
- Kandari, R.; Gupta, P.; Kumar, A. Battery state of charge based improved adaptive droop control for power management of a microgrid having large scale renewable generation. Sustain. Energy Technol. Assessments 2023, 57, 103146. [Google Scholar] [CrossRef]
- Meng, T.; Lin, Z.; Shamash, Y.A. A Comparison Study of Different State-of-Charge Balancing Strategies for Smart Battery Systems. In Proceedings of the 2020 IEEE 16th International Conference on Control & Automation (ICCA), Singapore, 9–11 October 2020; pp. 1434–1439. [Google Scholar]
- Ma, Z.; Gao, F.; Gu, X.; Li, N.; Wang, X. Multilayer SOH Equalization Scheme for MMC Battery Energy Storage System. 2020. Available online: https://ieeexplore.ieee.org/document/9084234 (accessed on 12 July 2023).
- Ren, H.; Zhao, Y.; Chen, S.; Wang, T. Design and implementation of a battery management system with active charge balance based on the SOC and SOH online estimation. Energy 2019, 166, 908–917. Available online: https://www.sciencedirect.com/science/article/abs/pii/S2352152X22009112 (accessed on 16 May 2023). [CrossRef]
- Liu, C.; Sun, S. Event-triggered optimal and suboptimal distributed Kalman consensus filters for sensor networks. J. Frankl. Inst. 2021, 358, 5163–5183. [Google Scholar] [CrossRef]
- Zhang, C.; Jia, Y. Distributed Kalman consensus filter with event-triggered communication: Formulation and stability analysis. J. Frankl. Inst. 2017, 354, 5486–5502. [Google Scholar] [CrossRef]
- Caballero-Águila, R.; Hermoso-Carazo, A.; Linares-Pérez, J. Networked distributed fusion estimation under uncertain outputs with random transmission delays, packet losses and multi-packet processing. Signal Process. 2019, 156, 71–83. [Google Scholar] [CrossRef]
- Muehlebach, M.; Trimpe, S. Distributed event-based state estimation for networked systems: An LMI approach. IEEE Trans. Autom. Control 2017, 63, 269–276. [Google Scholar] [CrossRef]
- Battistelli, G.; Chisci, L.; Selvi, D. A distributed Kalman filter with event-triggered communication and guaranteed stability. Automatica 2018, 93, 75–82. [Google Scholar] [CrossRef]
- Sun, W.; Li, Y.; Liu, L.; Mai, R. A switched-capacitor battery equalization method for improving balancing speed. IET Electr. Power Appl. 2021, 15, 555–569. [Google Scholar] [CrossRef]
- Braco, E.; San Martin, I.; Sanchis, P.; Ursúa, A.; Stroe, D.I. Health indicator selection for state of health estimation of second-life lithium-ion batteries under extended ageing. J. Energy Storage 2022, 55, 105366. [Google Scholar] [CrossRef]
- Kumar, B.; Khare, N.; Chaturvedi, P. FPGA-based design of advanced BMS implementing SOC/SOH estimators. Microelectron. Reliab. 2018, 84, 66–74. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).