Abstract
Energy management systems (EMSs) play a central role in improving the performance of microgrids by ensuring their efficient operation while minimizing operational costs and environmental impacts. This paper presents a comprehensive study of mixed integer linear programming (MILP) based EMSs developed and implemented in MATLAB 2021a using YALMIP software for the energy management of a new positive energy district in the city of Savona, Italy, as part of the Interreg Alpine Space Project ALPGRIDS. The main objective of this research is to optimize the functioning of the microgrid, focusing on cost efficiency and environmental sustainability. In pursuit of this objective, the EMS undergoes comprehensive testing and analysis, replicating actual conditions and addressing the diverse demands of end-users across typical days throughout the year, considering real electricity selling and purchase prices. The EMS also accounts for the reactive power capabilities of the various technologies integrated into the microgrid. The levelized cost of electricity (LCOE) serves as a metric for assessing curtailment costs, while penalties related to reactive power absorption from the distribution network are appraised in alignment with prevailing regulatory guidelines. The case study provides valuable insights into the practical implementation of EMS technology in microgrids and demonstrates its potential for sustainable energy management in complex urban energy districts. In all scenarios, the battery energy storage system (BESS) and combined heat and power (CHP) are pivotal for load satisfaction and microgrid resilience. BESSs balance supply and demand, which are crucial in periods of low renewable energy availability, while the versatile CHP efficiently addresses energy demands, contributing significantly to overall microgrid effectiveness. Their synergy ensures reliable load satisfaction, showcasing the dynamic and adaptive nature of microgrid energy management across diverse scenarios.
Keywords:
microgrids; optimization; EMS; E-mobility; V2G; smart grid; MILP; positive energy district 1. Introduction
In the dynamic landscape of 2021, renewable energy faced several complex challenges due to the ongoing impact of the COVID-19 pandemic, economic volatility, and geopolitical tensions. The impact of the pandemic and the rise in commodity prices have disrupted renewable energy supply chains and led to delays in projects. However, amidst these challenges, the discussion on the role of renewables in improving energy security gained momentum, fuelled by a sharp rise in energy prices. Despite these hurdles, the renewable energy sector exhibited robust growth, reaching record highs in power capacity. Investment in renewable power and fuels saw a fourth consecutive year of increase, resulting in solar and wind power jointly contributing over 10% to the world’s electricity generation for the first time [1]. In 2021, the International Energy Agency’s Net Zero by 2050 scenario set ambitious targets, influencing 17 countries’ pledges for net-zero emissions by COP26. The Glasgow Climate Pact emphasized reducing fossil fuel usage, with 140 countries committing to “phasing down” coal power. Notable exceptions like Australia, China, India, and the U.S. did not join in stopping financing for new coal plants. The renewable energy sector progressed, with a 17% surge in capacity additions in 2021, reaching 314 GW. Global renewable capacity rose to 3146 GW, but urgent deployment is needed to meet IEA and IRENA benchmarks, requiring 825 GW annually until 2050. With increasing energy demand, microgrids play a pivotal role in the future energy landscape. They offer decentralized and resilient solutions, aligning with global sustainability goals. To address energy wastage, optimize existing microgrids, and transform grids into smart grids, “Smart Microgrids” link users to production systems, balancing supply and consumption in real-time. Collaborating with energy communities, microgrids create virtuous urban districts using renewable self-production. Microgrids usually consist of low-voltage distribution networks with distributed energy resources, operating in islanded mode or connected to the main grid [1,2,3,4,5,6,7,8]. Intelligent microgrids enable the minimization of energy exchange with the external grid. It is important to mention that districts, where annual self-production surpasses consumption on a global scale, are referred to as “Positive Energy Districts” (PEDs) [9]. Microgrids (MGs) face several challenges, including the high investment costs associated with RESs, the need for optimal energy source utilization, control complexities, a lack of system protection and regulatory standards, and concerns related to customer privacy. Given the prevalent deployment of inherently intermittent RESs and the growing integration of probabilistic controllable loads into MGs, researchers have concentrated on addressing energy management issues.
Fundamentals, Evolution, and Classification of Energy Management Systems
The International Electrotechnical Commission, through its standard [10], which pertains to the EMS application program interface in power systems management, defines an energy management system (EMS) as “a computer system that comprises a software platform providing fundamental support services and a suite of applications delivering the necessary functionality for the effective operation of electrical generation and transmission facilities, ensuring sufficient security of energy supply at minimal cost” [11]. Similarly, an MG EMS, encompassing these attributes, typically consists of modules designed to execute decision-making strategies. Modules such as DERs/load forecasting, human–machine interfaces (HMIs), and supervisory control and data acquisition (SCADA), among others, play a crucial role in ensuring the efficient implementation of EMS decision-making strategies by transmitting optimal decisions to each generation, storage, and load unit [12].
Leveraging energy from RESs has become standard for enhancing grid resilience and achieving emission reduction goals. As energy demand rises, ensuring a reliable supply is crucial. However, integrating RESs presents challenges, necessitating the storage of excess energy, notably in grid-connected battery energy storage systems (BESSs). The sustainability and reliability of grids face hurdles with RES integration, emphasizing the pivotal role of grid-connected BESSs in managing surplus energy. In microgrids, whether grid-connected or islanded, effective power flow management is critical. This is particularly crucial given the unpredictable nature of RESs, characterized by intermittency and varying availability. To enhance the reliability of microgrids, the integration of the BESS is crucial. However, this integration introduces complexity, prompting the need for an EMS to orchestrate and optimize the whole energy system. The EMS acts as the operational brain, ensuring the efficient and effective functioning of microgrids in the face of dynamic and unpredictable energy inputs from renewable sources.
In recent times [13], there has been a substantial upswing in the adoption of large-scale energy storage systems. This surge is propelled by advancements in both the cost-efficiency and performance of energy storage technologies. Furthermore, the necessity to integrate distributed generation, alongside government incentives and mandates, has significantly contributed to this growth. To harness the full potential of energy storage as a flexible grid asset capable of delivering multiple grid services, the implementation of EMSs and optimization methods is imperative. These systems must exhibit adaptability to a spectrum of use cases and regulatory landscapes, ensuring their efficacy and safe utilization in diverse energy storage scenarios.
An energy management strategy can be applied to either grid-connected or islanded microgrids comprising RESs and BESSs. The optimization can be focused on either cost optimization or minimizing the cash flow of the system as well as the power exchange with the main grid in the grid-connected mode or the case of islanded mode to minimize the operation cost and to reduce emissions by scheduling DER [14]. The energy management system (EMS) of an MG encompasses both supply and demand-side management, aiming to satisfy system constraints and achieve economical, sustainable, and reliable MG operation [11]. The EMS offers numerous advantages, ranging from efficient generation dispatch and energy savings to reactive power support and frequency regulation. It contributes to enhancing reliability, reducing loss costs, maintaining energy balance, lowering greenhouse gas (GHG) emissions, and fostering customer participation while respecting customer privacy.
An EMS with a classical approach as described in [15] is one way to effectively model and manage the MG. The microgrid energy management system described here is formulated as a unit commitment problem, concerning the distribution network and its corresponding constraints. This leads to a mixed-integer non-linear programming (MINLP) formulation. To reduce computational time, the distribution power flow equations and nonlinear constraints are simplified by linearizing the MINLP formulation to MILP. MILP is a powerful tool in optimization and system analysis; it is particularly adept at addressing problems, featuring both integer and non-integer variables. This versatility renders MILP invaluable for tackling intricate and sizable problems [16,17,18]. In the realm of microgrids, where variables like power generation or grid exchange involve continuous values, and the states of microgrid components (such as grid-connected/islanded modes and energy storage system (ESS) charging/discharging states) can be expressed as binary or integer variables, MILP provides a flexible and robust solution.
This paper aims to describe the MILP-based EMS designed for the effective control of active and reactive power in a microgrid intended for integration into the SPEED2030 (Savona Positive Energy & Environment District). This district is envisioned as an extension of the existing University Savona Campus in Italy. The document is structured as follows: Section 2 accentuates the distinctive features of PEDs and provides an overview of the ALPGRIDS project. Section 3 outlines the proposed microgrid by detailing the employed technologies and the EMS model with its main constraints, the architecture of the optimization model, and the objective function related to it. The input data are briefly outlined in Section 4, presenting key inputs and assumptions. Section 5 presents the primary outcomes of the EMS and the results. Section 6 includes the discussion of results and Section 7 concludes the paper.
2. PED and ALPGRIDS Project
2.1. Positive Energy Districts (PEDs)
In the last decade, the concept of PEDs has garnered increasing attention as a typical approach to reducing carbon dioxide emissions globally. PEDs are recognized as effective tools for emission reduction in Europe and other parts of the world [19]. Scientific projects and regulatory bodies are actively investigating PEDs to encourage the use of renewable energy sources, reduce GHG emissions, enhance energy flexibility in buildings, and improve overall user comfort [20,21].
A PED is an energy-efficient urban district achieving zero net greenhouse gas emissions through active management of bidirectional energy flows and annual surplus energy generation [19,22]. PEDs, comprised of interconnected buildings linked to the power grid, employ various energy management techniques such as balancing, peak shaving, and demand response. These districts aim to create integrated environments, fostering sustainable production, consumption, and mobility, reducing primary energy use and greenhouse gas emissions while providing added value and incentives for consumers.
Aligned with the European Strategic Energy Technology Plan, the ’Positive Energy Districts and Neighborhoods for Sustainable Urban Development’ program, supported by 20 EU Member States and part of JPI Urban Europe [23], strives to establish 100 positive energy neighborhoods by 2025. In Italy, several PED projects are already in the planning and development stages across various cities, such as Parma, Milan, Bolzano, Florence, and Lecce [24]. These projects contribute to the broader European effort to advance sustainable urban development and exemplify Italy’s commitment to the goals outlined in the Positive Energy Districts program. As part of the Interreg Alpine Space ALPGRIDS project [25], an assessment was conducted to explore the potential of configuring the Savona pilot site as a PED.
2.2. ALPGRIDS Project
In the Legino district, situated approximately two kilometers from Savona, the ALPGRIDS initiative took root as an extension of the visionary Savona campus. Today, the Savona campus stands as a bustling center for educational institutions, university research laboratories, research centers, and small- to medium-sized enterprises [26]. The Savona campus has focused on the “Energy 2020” project [27], emphasizing sustainable energy principles. Key outcomes include the smart polygeneration microgrid (SPM) and smart energy building (SEB), designed for cost reduction, emissions control, and a comfortable environment [28].
Since 2019, the University of Genoa and IRE Liguria [29] have actively participated in the ALPGRIDS project across five Alpine arc countries. The initiative aims to establish smart microgrids for energy communities through seven pilot projects, including the creation of the urban PED SPEED2030 next to the Savona campus in Legino.
Aligned with PED guidelines [23,24], the Savona ALPGRIDS initiative emphasizes maximizing renewable energy production and optimizing resource utilization at a regional level. Utilizing microgrid configurations and promoting energy sharing through renewable energy communities (RECs), surplus energy benefits nearby areas, fostering the growth of existing PEDs and inspiring new ones. This approach attracts investments, modernizes infrastructure, and enhances public services [23,24,26]. The available areas for the new pilot project areas (SPEED2030) are highlighted in Figure 1. The district is conceptually divided into four zones devoted to different final uses:
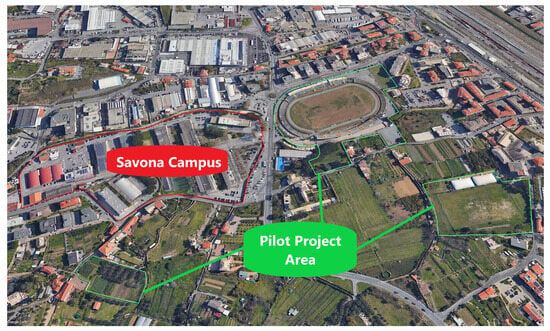
Figure 1.
Existing Savona campus and pilot project site.
- The main football stadium, an outdoor sports area, and the swimming pool;
- Commercial activity areas;
- University labs, research centers, and student accommodations;
- Social housing.
The pilot site study focused on meeting the stringent supply reliability needs of research laboratories while addressing diverse energy demands, including electricity, heating, and cooling for various buildings. The primary goal was to reduce primary energy consumption and environmental impact. This paper delves specifically into an in-depth analysis of the EMS applied to active and reactive power management within one of the two proposed microgrids for the SPEED2030 project. The microgrid is thoroughly investigated, exploring different scenarios that involve both the incorporation and exclusion of the electric mobility infrastructures. This comprehensive analysis extends to typical days during both winter and summer seasons. The study aims to assess the microgrid’s performance and resilience under diverse conditions, considering the specific challenges and opportunities posed by electric mobility integration across various seasonal contexts.
3. EMS: Application and Mathematical Model
3.1. Structure and Elements of the Microgrid
The design of the microgrid envisioned for the University’s upcoming structures in SPEED 2030 is illustrated in Figure 2. This AC microgrid incorporates a range of resources, including a combined heat and power (CHP) unit, rooftop-installed photovoltaic (PV) plants, a micro wind turbine, an absorption chiller, a heat pump, storage battery systems, and electric vehicle (EV) charging stations (comprising 2 AC, 2 DC, and 2 V2G types). The model utilized for this configuration is succinctly outlined in the following sections.
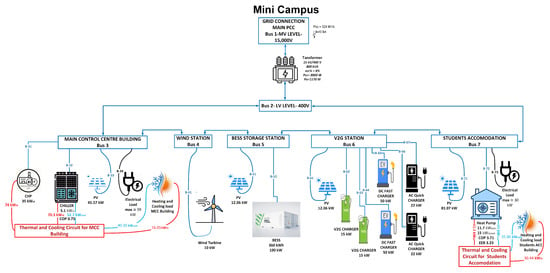
Figure 2.
The microgrid’s architecture with its components.
The microgrid comprises seven buses, each serving a specific role within the system. Bus 1 functions as the point of connection (POC) with the grid, facilitating external connectivity. Bus 2 serves as a coupling bus, completing the ring configuration and enhancing the overall stability of the microgrid. Bus 3 is dedicated to the microgrid control center (MCC) building, a centralized control hub housing the control room. This central control facility is intricately linked with the CHP unit, the chiller, and the rooftop PV installations. Bus 4 is designated as the wind station, managing the integration and utilization of power generated by the micro wind turbine. Bus 5 operates as a BESS station, featuring rooftop PV installations for energy generation. Bus 6 serves as a charging station equipped with PV installations positioned over a shed, emphasizing sustainable energy practices in electric vehicle charging. Finally, Bus 7 is associated with the students’ accommodation building. This building incorporates rooftop PV installations for power generation and employs a heat pump to address cooling or heating requirements. This diverse bus configuration illustrates the strategic allocation of roles and resources within the microgrid, showcasing a comprehensive and efficient design for meeting the energy needs of the university’s new buildings in the SPEED 2030 project.
3.2. Mathematical Model
The general flow diagram of the modeled EMS is represented in Figure 3.
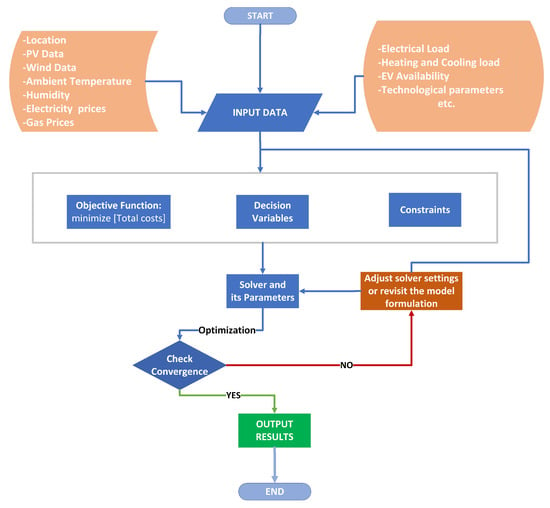
Figure 3.
EMS general flow chart.
3.2.1. Distributed Generation Models
The distributed generation units in the microgrid consist of three types: PV, wind turbine, and CHP. PV and wind are categorized as non-dispatchable distributed energy resources (DERs), implying their generation is dependent on environmental conditions and not controllable, apart from the possibility of implementing curtailment. On the other hand, CHP is considered a dispatchable DER, allowing for controlled and scheduled power generation to meet specific demand requirements.
- Renewable energy source (RES) model: In our model, we consider the contribution of the RES to the microgrid system. The active power output of the RES at different buses is denoted as in kilowatts [kW] as in (1), where b denotes the generic bus, r denotes the generic source, and t denotes the time interval. Additionally, the active power curtailment of the RES is represented by in [kW] as in (2), reflecting any reduction in the output due to operational or grid constraints. represents the available power of the RES as in (3). The Equation (4) limits the maximum power of the RES according to (CEI 0-16 page-117). The main constraints for RESs are as follows:For the reactive power, in (5) represents the inductive reactive power injected into the microgrid by the RES in [kvar], while in (6) represents the inductive reactive power absorbed by the RES in [kvar]. in (5) and (6) limits the inverter operating points, considering a rectangular capability curve. Binary variables in (7) and take the value of 1 when the RES injects or absorbs reactive power, respectively. The reactive power constraints are given as follows:These variables play a crucial role in capturing the dynamic behaviour and impact of the RES on the microgrid, enabling an analysis of active and reactive power interactions, as well as the ability to curtail active power output when necessary.
- CHP Model: The electric power produced is subject to the following constraints:These constraints in (8) and (9) limit the power between a lower threshold () and an upper one (). Specifically, represents the minimum technical part-load of the microturbine, typically advised by manufacturers to be above 30–50% of the nominal electrical power to maintain efficiency. Regarding the maximum power , it depends on the time instant t since the maximum electric power and efficiency are influenced by environmental (temperature, pressure, and humidity) and installation (altitude) conditions as in (A1) in Appendix A. The thermal power produced by the single unit at time t can either be positive or equal to zero and is correlated with the electric power through a linear function, as in (10), describing the partial load behaviour of the microturbine and was calculated as in (A2):The primary power of the microturbine at time t is linearly related to the electric power produced through Equation (11):where and are constant coefficients and is the maximum primary power which is calculated as in (A3). Finally, in Equation (12), thermal balance is defined as follows:where (thermal power used for heating purposes) and (thermal power provided to the absorption chiller) can assume positive values or be equal to zero.
3.2.2. BESS Model
The key variables related to the operation of the battery energy storage system (BESS) are as follows: In (18) the active power charged into the BESS is denoted as in kW, while the active power discharged from the BESS as in (21) is represented by in kilowatts. Binary variables in (24) are employed to indicate charging and discharging states, with equal to 1 when the BESS is charging, and equal to 1 when the BESS is discharging. The state of charge of the BESS at time t is denoted as as in (27). Additionally, the BESS’s reactive power output and absorption as in (29) and (30) are expressed as and in [kvar], respectively. The reference for the inverter operating limits is modified according to CEI standards. Binary variables and take the value of 1 when the BESS provides or absorbs reactive power, respectively, in (31). A rectangular capability curve is considered for the BESS unit. The constraints for the battery energy storage system (BESS) are as follows:
The following equation gives the state of charge of the BESS:
where is the self-discharging rate and is the rated capacity of the storage system in [kWh]. At the first time interval t = 1, SOC can be written as:
The reactive power constraints for the BESS are modeled as follows:
3.2.3. Grid Model
The exchange of electrical power with the national grid is characterized by several key parameters. In (32) and (33), the active power withdrawn from the national grid is denoted as in [kW], while the active power injected into the national grid is represented by in [kW]. The corresponding reactive power components in (35) and (36) include for reactive power withdrawn and for reactive power injected, both measured in [kvar]. In (34), binary variables and take the value of 1 when active power is withdrawn from or injected into the national grid, respectively. Similarly, in (37), binary variables and are assigned the value of 1 when inductive reactive power is withdrawn from or injected into the national grid, respectively. These variables are important in modeling the power exchange dynamics with the grid, enabling a comprehensive analysis of active and reactive power exchange. The introduced constraints for bought and sold power (exchange with the grid) are as follows:
The rectangular capability curve as in (36) and (37) is considered for the exchange with the grid depending upon the value of , which is the size of the transformer.
3.2.4. EV and Wall Box Model
In this model, the state of charge of electric vehicles (EVs) is denoted as , where v indicates the generic vehicle. Charger j is an AC-type, charger e is a DC-type, while charger f can exploit V2G. Charging power is categorized into different types, including for charging with respect to charger j, for charging with respect to charger e, for V2G charging, and for V2G discharging. The maximum power from the charger is defined as a piece-wise function harnessing the variable SOC of the vehicle as in (40), (42), (44), and (46). These constraints ensure the maximum power any charger can provide at time instant t is dependent on the SOC of the vehicle. The reactive power in V2G scenarios is captured by for absorbed inductive reactive power and for supplied inductive reactive power, both for the charger f and vehicle v at time t. Binary variables are introduced in (39), (41), and (43) to indicate charging and discharging states, with , , and taking the value of 1 when chargers j, e, and f are charging the vehicle v, respectively. Similarly, , , and are binary variables, as in (45), (54)–(56), indicating discharging, reactive power absorption, and reactive power supply, respectively, for the charger f and vehicle v at time t. The constraints are as follows:
To ensure the dedicated connection of each car to a specific charger at time t, binary variables are introduced and aggregated across chargers belonging to AC (designated as j), DC (e), and V2G (f), as in Equation (46). The summation has to be lower or equal to the binary variable , which represents the presence of the electric vehicle at the facility.
Below, in Equations (47)–(49), you will find binary variables designed to ensure that each charger can be exclusively connected to a single car at a given time instant, t.
Constraints (50)–(52) show the total power supplied to vehicles by AC, DC, and V2G chargers, respectively, and (53) represents the total discharging power supplied by V2G chargers to the grid.
Constraints (54) and (55) define the reactive power capability of the V2G chargers, and Equation (56) uses binary variables to make sure either the reactive power is absorbed or supplied at time t. It is assumed that AC and DC chargers cannot exchange reactive power.
The constraints for the SOC of EVs are given by Equations (57)–(59).
The state of charge of each vehicle is given by the following Equation (60):
where is the vehicle energy consumption in [kWh/km] and is the vehicle transportation demand in [km].
3.2.5. Heating and Cooling System Modeling
The fulfillment of heating and cooling requirements for specific buildings, such as student accommodations and the MCC building, is achieved through dedicated systems. In the student accommodation, a heat pump serves dual purposes by fulfilling both heating and cooling requests. Conversely, in the MCC building, an absorption chiller is installed. This chiller utilizes the CHP system to provide cooling, while the heating requirements are directly supplied by the CHP system.
- Heat Pump Model: The thermal power produced by the HP is denoted as , while the corresponding electrical power consumed to generate the required thermal power is represented as as in (61). Additionally, the cooling power (63) produced by the HP is captured by , with the associated electrical power consumption denoted as . Constraints (62) and (64) denote the cooling and heating power of the heat pump. Binary variables and in (65) take the value of 1 if the HP is in the heating or cooling mode, respectively. These variables play a crucial role in modeling the operational states of the HP system, allowing for a comprehensive analysis of its thermal and electrical performance. The key constraints for the heat pump are as follows:
- Absorption Chiller Model: As shown in (66), the thermal power required by the chiller is denoted as . The corresponding electrical power consumed by the chiller, as in (68), generates the necessary cooling power, and is represented by . Additionally, the cooling power produced by the chiller in (69) is denoted by . These variables are essential in characterizing the operational dynamics of the chiller system, providing insights into the interplay between thermal and electrical components. The main constraints for the chiller system are as follows:Equation (69) defines the relation between the heating power required by the chiller and the produced cooling power; the relation is properly linearized.
- Thermal balance:Equation (70) expresses the thermal balance, ensuring that the sum of the thermal power produced by the CHP system for heating () and the thermal power produced by the heat pump (HP) () is used to satisfy the thermal load () in bus b at time t. The parameter is a factor used to consider heating loss.
- Cooling Balance:Equation (71) represents the cooling balance, ensuring that the sum of cooling power produced by the chiller () and the cooling power produced by the heat pump (HP) () allows satisfying the cooling load () in bus b at time t. The parameter is a factor that is used to consider cooling losses.
- Trigeneration Balance:Equation (72) represents the trigeneration balance, linking the thermal power produced by the CHP and sent to the chiller () and the thermal power consumed by the chiller () in bus b at time t. The parameter is introduced to consider the losses of the chiller in trigeneration, considering the heat being supplied by CHP through the pipes.
3.2.6. Active and Reactive Power Balance
- Active power balance
- Reactive power balance
3.2.7. Load Flow Constraints
Linearized load flow equations: The following equations represent the linearized versions of the full-load flow equations for connected nodes b and k at time t:
Here, in Equations (75) and (76), b and k represent two connected nodes. Variables and denote the active power and reactive power in [p.u.] flowing from bus b to bus k at time t, respectively. The quantities and represent the per unit resistance and reactance of the link between nodes b and k, respectively. Variables and represent the per unit voltage magnitudes, while and represent the voltage phase angles at nodes b and k at time t, respectively.
3.2.8. Objective Function: Minimization of Operating Costs
- The net cost associated with buying and selling active power at each time interval.
- The net cost related to absorbing and injecting reactive power at each time interval.
- The cost of fuel consumption for CHP.
- The costs associated with curtailing power from PV and wind sources at each time interval.
- The revenue from selling power to EVs by charging them with different charging points, including AC, DC, and V2G systems.
- The cost associated with remunerating the discharging of V2G technology.
4. Input Data: Acquisition and Processing
The development of the EMS for the Speed 2030 Minicampus microgrid is grounded in meticulous attention to location-specific data. To ensure the reliability of our EMS modeling, we sourced data from reputable platforms, such as PV-gis [30], an online database maintained by the European Union that provides comprehensive information on irradiance, temperature, and humidity for photovoltaic systems. Additionally, wind data were procured from the Region Liguria’s official website, where there is a database containing essential information like wind speed, temperature, and humidity for Savona city, where our microgrid is situated. For electrical load profiles, we conducted a detailed analysis of the real-time data from the existing microgrid of the Savona campus and manipulated them to align with the specific requirements of the new microgrid. In determining the thermal and cooling loads of the buildings, we referred to ASHRAE’s building standards manual and adhered to EU norms for A-grade sustainable buildings within PED as per the United Nations’ sustainability goals. Before the modeling of the EMS, continuous validation and calibration of data were performed to further enhance the accuracy and reliability of the EMS model.
4.1. Electric Mobility
In the electric mobility segment of the EMS for the microgrid, a diverse selection of 14 vehicles was chosen. These vehicles represent various models available in the market, each with unique charging capabilities that support AC and DC charging, and some with V2G capabilities. The technical specifications of these vehicles, encompassing power consumption, range capacity, battery type, and charging and discharging powers for V2G-enabled cars, are detailed in Table 1. The chosen usage types for these vehicles are deliberately diverse, reflecting the microgrid’s dynamic nature. Some vehicles are designated for university use, others are allocated for professors, while additional units serve technicians and students alike. The demand profiles for various cars are meticulously chosen, aligning with the daily habits of campus residents, employees, and university-assigned EVs. The selection of these demand profiles is grounded in a justifiable consideration of the everyday travel requirements of the respective owners. Figure 4 illustrates the typical demand profiles tailored to different usage types, offering a visual representation of the nuanced energy needs associated with the diverse activities and travel patterns within the campus.

Table 1.
Selected cars and their specifications.
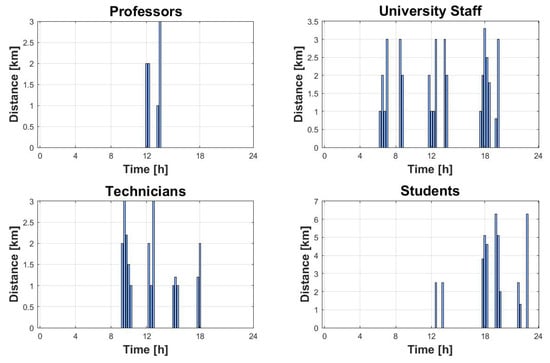
Figure 4.
Car demand profile graphs.
4.2. Specifications of Charging Stations
The charging infrastructure, as in Table 2, consists of six types of chargers available, consisting of two each for AC, DC, and V2G. The maximum power outputs for these chargers are 22 kW for AC, 50 kW for DC, and 15 kW for V2G.

Table 2.
Charging station data.
The Level 2 or Type 2 chargers, commonly found in homes and garages, are associated with AC chargers. On the other hand, DC chargers, known as Level 3 or DC fast chargers (DCFCs), represent the quickest way to charge a vehicle. It is important to note that not every electric vehicle can charge at a Level 3 charger, highlighting the need for diverse charging infrastructures to cater to different EV models and charging capabilities. For bidirectional charging (V2G), the cars are equipped with CCS connection ports. As of now, only a handful of models are available in the market for V2G [31]. The charger’s maximum power delivery to the electric vehicle battery is determined through a piecewise function depending upon the state of charge (SOC) of the battery. This dynamic function is used, adapting to variations in SOC and distinctively accommodating the charging process for both AC and DC types.
4.3. Different Technologies Size Estimation
The optimal size of the different technologies installed in the microgrid was determined, as suggested by the study described in [9]. The analysis of results from this paper played a pivotal role in guiding the selection of technology sizes. The chosen sizes of different technologies are systematically presented in Table 3, reflecting a careful consideration of factors to achieve an efficient and effective microgrid configuration. This approach aims to strike a balance between meeting the energy needs of the mini campus and optimizing the microgrid’s capability.

Table 3.
Sizes of different technologies.
Tailoring the microgrid components to meet specific requirements and calculate the thermal and cooling needs of the buildings, the sizes of the CHP system, chiller, and heat pump were carefully selected. The chosen sizes are presented in Table 4, in precise alignment with the thermal and cooling demands of the buildings.

Table 4.
Technology Data.
4.4. Load Profile Estimation
The estimation of electrical, thermal, and cooling loads in Table 5 for the campus buildings was carefully conducted, taking into account the A-grade classification in building standards. The calculations for thermal and cooling loads are referenced from ASHRAE’s manual. Specifically, the guidelines outlined in ASHRAE Standard 169 and the ASHRAE Handbook of Fundamentals.

Table 5.
Building data.
5. Results
The microgrid designed for the mini campus was specifically optimized to cater to typical conditions throughout the year, including summer, winter, and off-season days. The findings of this study, detailed in this paper, provide valuable insights into the effective management of the microgrid, particularly in response to seasonal variations. This comprehensive optimization approach enhances our understanding of how the microgrid adapts and performs under different climatic conditions, allowing for more informed and efficient operational strategies.
Table 6 illustrates various scenarios analyzed concerning E-mobility, comparing instances where it is considered and those where it is not. This comparison is conducted for typical days throughout the year, aiming to assess the impact of E-mobility on the operational dynamics of the EMS within the microgrid.

Table 6.
Different cases examined.
5.1. Analysis of Different Cases (Typical Days)
5.1.1. Typical Summer Day
- Case considering E-mobility: Active and reactive power flowing across different busses in the microgrid are considered here with E-mobility. On a typical summer day, the microgrid exhibits a dynamic and adaptive energy distribution pattern, as illustrated by Figure 5. During daylight hours, the availability of sunlight allows the PV system to significantly contribute to the power supply, covering a substantial portion of the energy demand. The CHP unit efficiently operates during the day due to the request from the grid to satisfy the load and at night when solar power is unavailable. As the sun sets, the graph reveals a shift in energy sources, with a notable presence of the CHP unit and an increasing contribution from the grid. Interestingly, the demand for electric mobility charging emerges, either directly from the grid or supplied by the CHP unit at night. An interesting trend can be seen for the reactive power request: photovoltaics are supplying reactive power services even at night, with significant contributions from CHP and some from the wind turbine for the reactive power request.
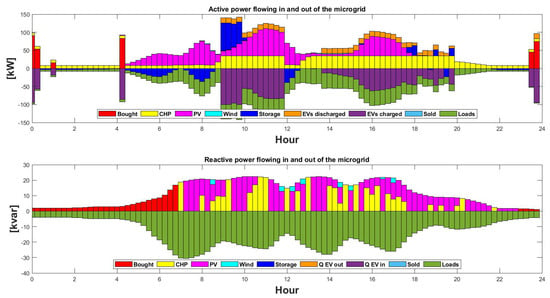
Figure 5.
Active and reactive power flow on a typical summer day with E-mobility.
Voltage profiles in Figure 6 for all 7 buses are coherent with the above Figure 5 as we can see the drop in the voltage when the request suddenly shoots, giving rise to the voltage drop. Instead, a drop in the power request or an increase in power production contributes to a voltage rise. Notably, the EMS adeptly maintains the voltage within the desired range of 0.9 to 1.1 [p.u.], effectively mitigating any adverse effects from the observed drops or rises in voltage.
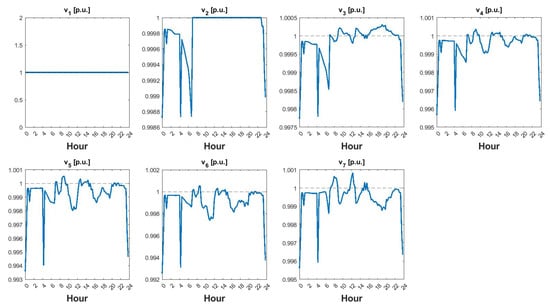
Figure 6.
Voltage profile of different buses on a typical summer day with E-mobility.
The PV inverter’s semi-circular capability curve is shown in Figure 7 with the real operating points. The figure does not show points in the second quadrant as there is no absorption of inductive reactive power by RES plants in the presented case study:
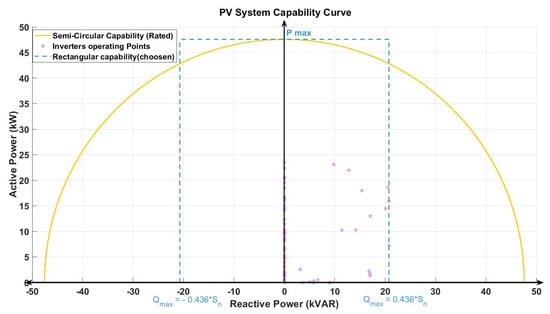
Figure 7.
PV inverter capability curve. Pink stars represent the hourly operating points of the inverter. The yellow semi-circular line represents the non-linearized capability curve of the inverter. The blue dashed line represents the rectangular capability curve chosen for the PV technology.
Active and reactive power flowing across different buses in the microgrid on a typical summer day with E-mobility are shown in Figure 8 (a) and (b), respectively. Among the seven buses, it can be seen that bus 2 practically acts as a transition bus, completing the ring topology. The other two buses, 3 and 7, correspond to the MCC building and student accommodation, respectively.
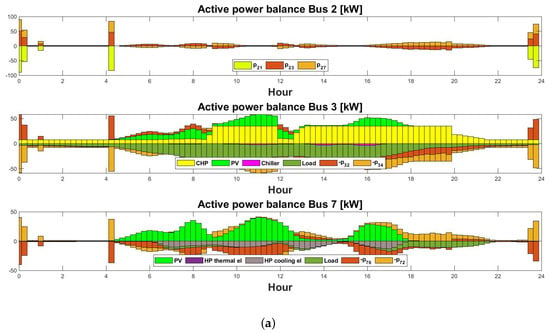
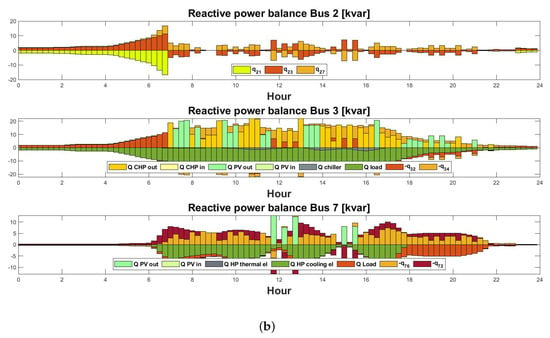
Figure 8.
(a) Active power flows across different buses in [kW] on a typical summer day with E-mobility. (b) Reactive power flows across different buses in [kvar] on a typical summer day with E-mobility.
The profiles of the cars used by the professors and technicians are shown in Figure 9. The cars used by professors are typically present only in the daytime when the university is open and can be charged only at that time at the campus. Instead, the other car is owned by the university and used by technicians for office work; this car is V2G enabled.
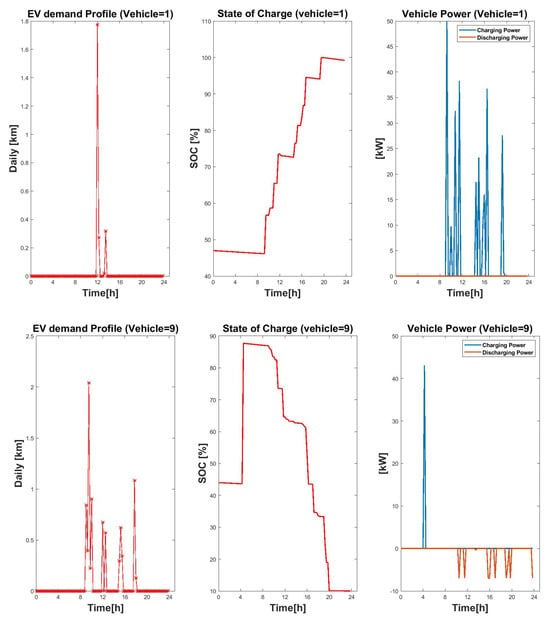
Figure 9.
EV’s demand, SOC and EV charging and discharging power.
- Case without considering E-mobility: Active and reactive power flowing in and out of the microgrid across different buses on a typical summer day, excluding E-mobility considerations, are shown in Figure 10 (a) and (b) respectively. On a typical summer day, excluding the EV scenario, it is evident that the majority of the load demand is met by PV generation. In certain instances, there is even surplus energy available for sale to the external grid. Additionally, a portion of the load demand is fulfilled by CHP, contributing to a scenario where minimal energy is procured from the external grid.
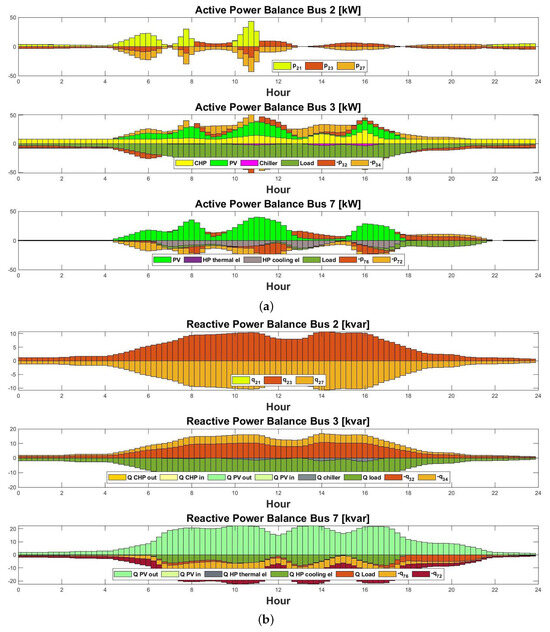 Figure 10. (a) Active power flows across different buses in [kW] on a typical summer day without E-mobility. (b) Reactive power flows across different buses in [kvar] on a typical summer day without E-mobility.
Figure 10. (a) Active power flows across different buses in [kW] on a typical summer day without E-mobility. (b) Reactive power flows across different buses in [kvar] on a typical summer day without E-mobility.
5.1.2. Typical Winter Day
- Case considering E-mobility: Active and reactive power flowing across different buses in the microgrid on a typical winter day with E-mobility is shown in Figure 11. During the winter season, when sunlight availability is diminished, the load requirements are diversely addressed by alternative technologies. The CHP system, wind turbine, and occasionally, V2G interactions, play pivotal roles in satisfying the load demand. Additionally, the BESS is employed in certain instances when necessary, due to the shortfall from other sources, energy is bought from the external grid. This dynamic mix effectively addresses the challenges posed by reduced solar availability.
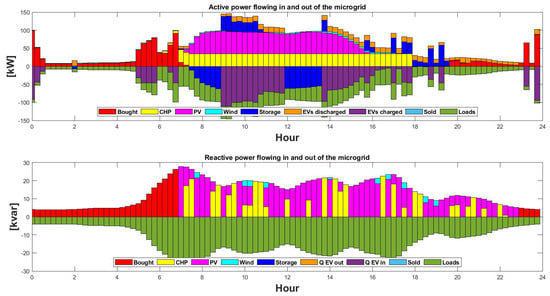
Figure 11.
Active and reactive power balance of the microgrid on a typical winter day with E-mobility.
The voltage profile showing different buses on a typical summer day when considering E-mobility is shown in Figure 12. The voltage variations indicate drops during periods of heightened power requests and rises when production surpasses the demand. Remarkably, the EMS successfully kept the voltage within the specified range of 0.9 to 1.1 [p.u.], effectively mitigating any impacts from the observed fluctuations.
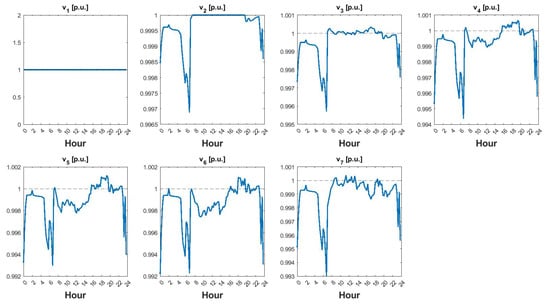
Figure 12.
Voltage profile of different buses on a typical winter day with E-mobility.
The active and reactive power flow across different buses in the microgrid during the winter case with E-mobility is shown in Figure 13 (a) and (b) respectively. The bar graph analysis reveals that during winter when the availability of PV power is limited, the majority of the power demand is fulfilled by the CHP system in bus 3. Conversely, in bus 7, the load request is predominantly met by the on-site PV system. This is attributed to the substantial capacity of the roof-top PV installation in that building, allowing it to independently satisfy the load request.
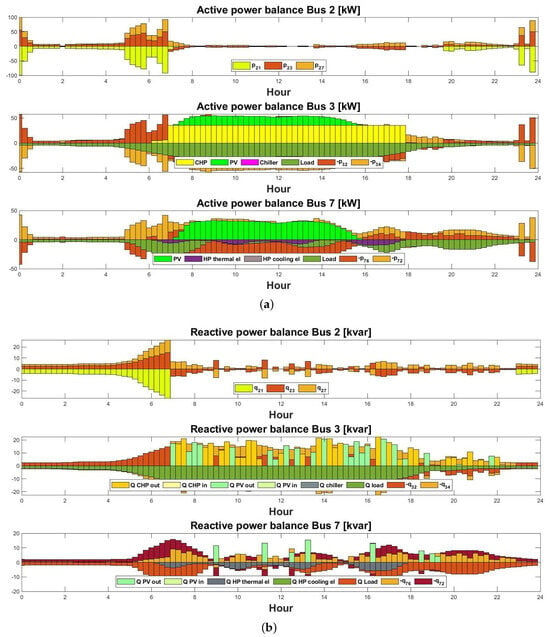
Figure 13.
(a) Active power flows across different buses in [kW] on a typical winter day with E-mobility. (b) Reactive power flows across different buses in [kvar] on a typical winter day with E-mobility.
The vehicle profiles for professors and technicians, as illustrated in Figure 14, represent the daily usage patterns of these vehicles. These are day-request vehicles, owned by individuals who reside off-campus. As a result, the charging of these vehicles is confined to daytime hours when the owners are present on campus.
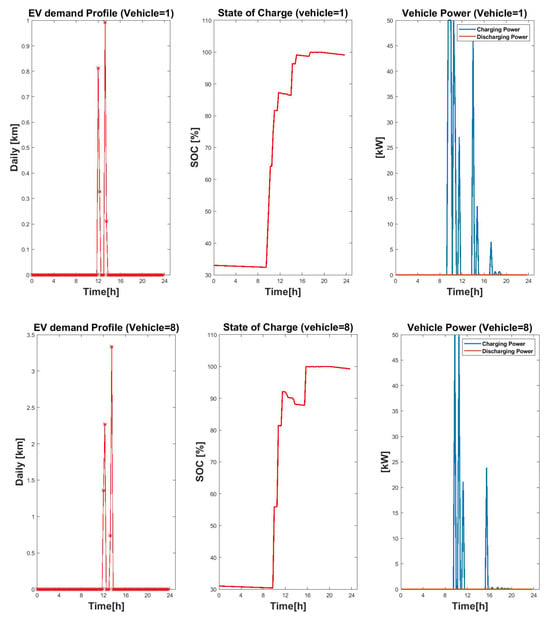
Figure 14.
EV’s demand profile, SOC and EV charging and discharging power.
- Case without considering E-mobility: In the scenario of a typical winter day without E-mobility, the load request experiences a reduction, and predominantly, the active power demand is met solely by the RES. During periods of RES unavailability, the deficient portion is bought either from the external grid or generated by the CHP system. On the other hand, the provision of reactive power is managed by on-site RESs or other technologies present in different buses. Active and reactive power flowing in different buses are shown in Figure 15 (a) and (b) respectively.
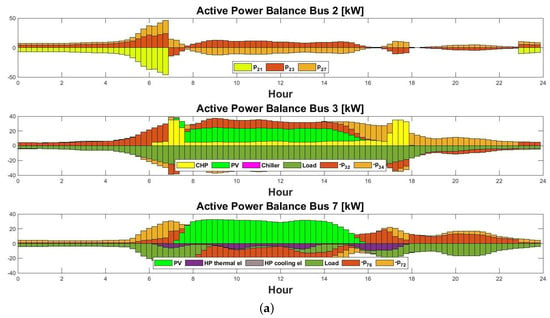
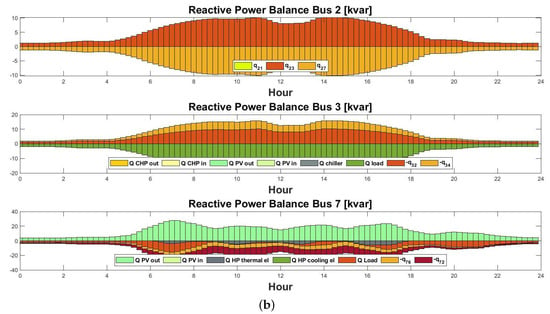 Figure 15. (a) Active power flows across different buses in [kW] on a typical winter day without E-mobility. (b) Reactive power flows across different buses in [kvar] on typical a winter day without E-mobility.
Figure 15. (a) Active power flows across different buses in [kW] on a typical winter day without E-mobility. (b) Reactive power flows across different buses in [kvar] on typical a winter day without E-mobility.
5.1.3. Off-Season Day
Off-season days, such as during the spring or autumn, are characterized by minimal demand for heating and cooling in buildings. In this evaluation, we examined how the absence of heating and cooling requests during these transitional periods impacts the EMS operation.
- Case considering E-mobility: In the off-season case, active and reactive power flows across different buses in the microgrid for a typical off-season day with E-mobility are depicted in Figure 16. This scenario explores the integration of E-mobility within microgrids. The bar graph visually demonstrates the significant impact of E-mobility on the power flow within the microgrid and its buses. When the microgrid is unable to meet the power demand internally, it absorbs the required power from the external grid. Additionally, there are instances where a portion of the power demand is fulfilled through V2G technology.
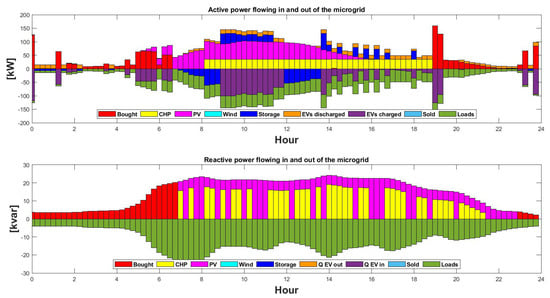
Figure 16.
Active and reactive power balance of the microgrid on a typical off-season day with E-mobility.
The voltage profiles for various buses during a typical off-season day with E-mobility are illustrated in Figure 17. The fluctuations in voltage depict voltage drops during increased power requests and voltage rises when the production exceeds the demand.
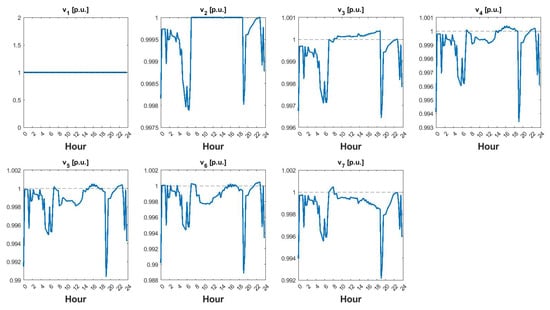
Figure 17.
Voltage profile of different buses for a typical off-season day with E-mobility.
The behaviour of EVs used by a technician for university purposes and a student who does not live on campus are shown in Figure 18. The first car shown can exploit V2G while the second one is a normal EV without V2G technology. In this figure, one can see the demand, the SOC of a vehicle, charging, and discharging profile.
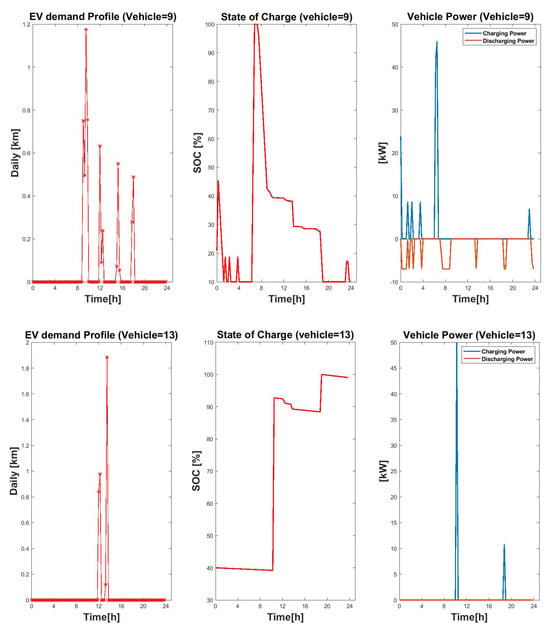
Figure 18.
EV’s demand profile, SOC, and charging and discharging power.
- Case without considering E-mobility: Active and reactive power flows across different buses in the microgrid on a typical off-season day without E-mobility are shown in Figure 19a,b. With the detailed analysis of the bus-wise power flow, we can see that in the absence of RES production, the CHP is turned on to satisfy the load request, and part of the request is satisfied from the external grid.
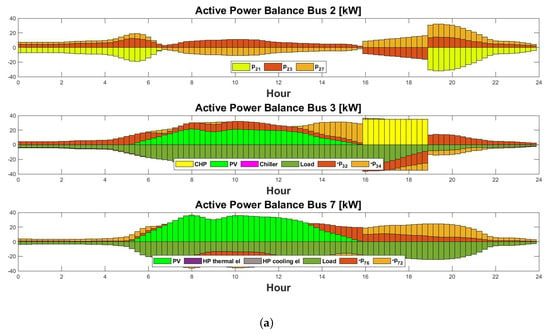
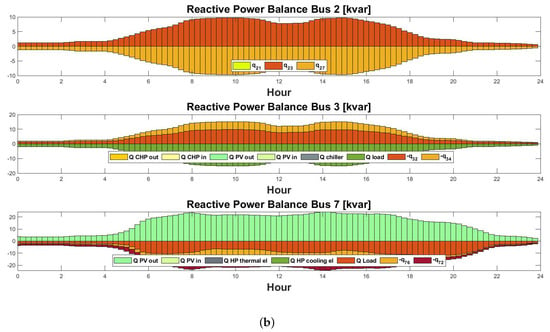 Figure 19. (a) Active power flows across different buses in [kW] on an off-season day. (b) Reactive power flows across different buses in [kvar] on an off-season day.
Figure 19. (a) Active power flows across different buses in [kW] on an off-season day. (b) Reactive power flows across different buses in [kvar] on an off-season day.
6. Discussion
In the context of the diverse scenarios examined, as detailed in Table 6, the summer case emerges prominently, showcasing substantial renewable energy source (RES) production attributed to the ample availability of sunlight. Notably, the excess energy generated during this period is judiciously stored in battery energy storage systems (BESSs). This stored energy serves a pivotal role in meeting subsequent demands during periods when solar availability diminishes, such as during nighttime hours.
Table 7 provides a detailed overview of the EMS with or without E-mobility on typical summer, winter, and off-season days, respectively. This includes costs, revenues, electricity bought and sold, renewable energy production, energy storage, loads, CHP generation, heating and cooling energy produced, etc.

Table 7.
EMS results.
The inclusion of E-mobility introduces significant variations in energy-related parameters, costs, and revenues. The impact of electric vehicle operations is evident in the fluctuations of renewable energy production, energy storage, and loads, showcasing the interconnectedness of these elements with e-mobility activities. The financial aspects, as reflected in costs and revenues, exhibit differences in magnitude between the two scenarios, emphasizing the distinct economic implications associated with integrating electric mobility. Additionally, the comparison showcases the role of CHP generation, which remains consistent across both scenarios but exhibits seasonal variability. This analysis illuminates the influence of E-mobility on EMS performance and shows the intricate interplay between renewable energy systems, energy storage, and electric vehicle integration. The strategic utilization of excess energy from the summer case significantly contributes to a reduction in the net exchange of power with the external grid. In instances where there is heightened demand due to E-mobility, a proportionate amount of energy is procured. Conversely, in scenarios without EVs, surplus energy is sold to the external grid. In the winter case, where solar energy availability is constrained, the CHP system emerges as a crucial asset in meeting load requirements. This holds for both scenarios, with and without E-mobility.
The effective utilization of the CHP system is obtained to satisfy energy demands in the absence of significant thermal or cooling requests during the off-season. In this specific scenario, where the CHP’s thermal output is not immediately required, the EMS strategically opts to minimize the CHP operation. Instead, the system opts to buy energy directly from the grid, a decision driven by cost-effectiveness and operational efficiency.
7. Conclusions
The proposed EMS allows for precise control over both active and reactive power generated from diverse sources within the microgrid. It intricately examines power flow, with a focus on controllable inverters for RESs and storage systems. This integration offers the potential to optimize the management of both active and reactive power, leading to improved voltage profiles and enhanced efficiency in power exchange with the external network.
The introduction of electric mobility into the microgrid infrastructure introduces potential challenges, including voltage drops and overloaded branches, especially in unregulated EV charging scenarios. The EMS steps in as a solution by implementing intelligent charging strategies and harnessing V2G technology. Through the EMS, the microgrid gains the ability to utilize electric vehicles strategically, mitigating the variability associated with the RES and elevating overall grid reliability. In all scenarios examined, the BESS and CHP play pivotal roles in achieving load satisfaction and ensuring effective microgrid management. The BESS intelligently stores excess energy, serving as a linchpin in balancing supply and demand; it is especially crucial during periods of reduced renewable energy availability like in the winter case. Simultaneously, the versatile CHP efficiently addresses energy demands, particularly in seasons with limited solar energy, contributing significantly to overall microgrid effectiveness. Efficiently coupling RESs, BESSs, and electric mobility within the microgrid has the potential to render it quasi-independent from the external network, leading to reduced operating costs and emissions. As a prospect for future research, a sensitivity analysis will be conducted to evaluate the impact of different technologies and variable electricity prices on the microgrid functionality.
Author Contributions
Conceptualization, A.S., S.B. and B.B.; methodology, A.S., S.B. and B.B.; software, A.S.; data curation, A.S.; writing—original draft preparation, A.S.; writing—review and editing, A.S.; visualization, A.S.; supervision, F.D. and S.B.; project administration, F.D.; funding acquisition, F.D. and S.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the ALPGRIDS project, contract agreement no. 843 (www.alpine-space.eu/alpgrids, accessed on 21 July 2023).
Data Availability Statement
Data presented in this study cannot be disclosed due to confidentiality and privacy reasons but could be made available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AC | Alternating Current |
| BESS | Battery Energy Storage System |
| CEI | Comitato Elettrotecnico Italiano |
| CHP | Combined Heat and Power |
| COP | Coefficient of Performance |
| DC | Direct Current |
| DCFC | DC Fast Charger |
| DER | Distributed Energy Source |
| EER | Energy Efficiency Ratio |
| EMS | Energy Management System |
| ESS | Energy Storage System |
| EV | Electric Vehicle |
| GHG | Green House Gas |
| HP | Heat Pump |
| IEA | International Energy Agency |
| IRENA | International Renewable Energy Agency |
| LF | Load Flow |
| MCC | Microgrid Control Center |
| MG | Microgrid |
| MILP | Mixed Integer Linear Programming |
| MINLP | Mixed Integer Non-Linear Programming |
| PED | Positive Energy District |
| PV | Photo Voltaic |
| REC | Renewable Energy Community |
| RES | Renewable Energy Source |
| SEB | Smart Energy Building |
| SET | Strategic Energy Technology Plan |
| SOC | State of Charge |
| V2G | Vehicle To Grid |
Appendix A
Appendix A.1. Mathematical Formulas and Definitions
The following section presents the supplementary data and formulas essential for the MILP model.
Renewable energy sources (RESs)
- : Available power from the RES [kW]
- : Nominal apparent power of the RES inverter [kVA]
Combined Heat and Power (CHP)
- : Nominal apparent power of the CHP inverter [kVA]
- : Electrical power correction factor (altitude dependent)
- : Electrical power correction factor (temperature dependent)
- and : Constant coefficients (experimentally evaluated)
- and : Constant coefficients related to partial load behavior
- : Cost of Fuel for CHP [€/kWh]
It was decided to relate the maximum power to the nominal electrical power as follows:
where and are two correction factors: depends on the altitude of the installation site, while depends on the ambient temperature . represents the maximum thermal power, which can be produced by the unit and is calculated as a function of the temperature () of the water coming back from the users:
is the maximum primary power that can be absorbed, calculated as follows:
where represents the electrical efficiency of the CHP when it works at the maximum power. It depends on the altitude of the site and environmental conditions:
where and are two reduction factors. Specifically, considers the altitude of the site, while deals with the influence of ambient temperature . indicates the nominal electrical efficiency of the CHP, evaluated at a 15 °C ambient temperature, 101,325 Pa ambient pressure, and 60% ambient relative humidity.
Electrical Load (non-manageable)
- : Active power electrical demand [kW]
- : Reactive power electrical demand [kvar]
- : Maximum power bought from the national grid [kW]
- : Maximum power sold to the national grid [kW]
- : Price of electricity bought [€/kWh]. The dynamic electricity pricing depends on the time slots based on the F1, F2, and F3 slots, as shown below in Figure A1:
- : Revenue for electricity sold [€/kWh]
- : Price of reactive power withdrawn [€/kvar h]
- : Revenue for reactive power injected [€/kvar h]
- : Cost of curtailment for the RES [€/kWh]Curtailment costs for the RESs are considered equal to the LCOE for the respective technology and the price of the fuel is at par with the market price:, ,
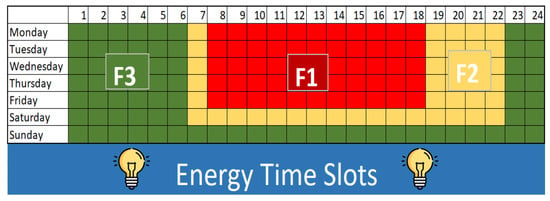
Figure A1.
Reference for the dynamic pricing for active power bought, where F1 = 0.35 [€/kWh], F2 = 0.25 [€/kWh], F3 = 0.15 [€/kWh].
Transformer
- : Nominal apparent power of the transformer [kVA]
- : Nominal voltage (line to line) primary side [kV]
- : Nominal voltage (line to line) secondary side [kV]
- : On Load loss of the transformer [W]
- : Short circuit voltage of the transformer [-]The parameters for the transformer system are as follows: , , , , and .
Storage Batteries
- , : Charging and discharging efficiencies
- , : Max charging and discharging power [kW]
- , : Min charging and discharging power [kW]
- : Nominal apparent power of the electrical storage inverter [kVA]
- : Rated capacity of the storage system [kWh]
- : Number of batteries
- , : Min and max states of charge
- : Ideal self-discharging rate
- : Time interval, where = 0.25
Electrical Vehicle (EV)
- , , : Max charging powers [kW]
- : Max discharging power V2G [kW]
- : EV availability
- , : Min and max states of charge [%]
- : Initial state of charge
- , : State of charge at arrival and departure [%]
- : Capacity of EV battery [kWh]
- , : Charging efficiencies for AC and DC chargers
- , : Charging and discharging efficiencies for V2G chargers
- : Vehicle energy consumption [kWh/km]
- : Vehicle transportation demand [km]
- : Factor for calculating self-discharging
Heat Pump
- , , : Constants from product data sheets
- : Ambient temperature
- : Constant from product data sheets
- : COP of Heat pump
- : EER of Heat pump
- : Max thermal power by heat pump (temperature dependent)
- : Max cooling power by heat pump (temperature dependent)
- , , , and .
Chiller
- : Min thermal power of chiller
- : Max thermal power of chiller (temperature dependent)
- : Factor for determining electrical power absorbed
- Additional data: , , , ,
- . The efficiencies for heating, cooling, and the chiller are , , and , respectively.
References
- GSR2022-Full Report. Renewables 2022 Global Status Report. Available online: https://www.ren21.net/wp-content/uploads/2019/05/GSR2022_Full_Report.pdf (accessed on 20 January 2022).
- Net Zero Tracker. Post-COP26 Snapshot. Available online: https://zerotracker.net/analysis/post-cop26-snapshot (accessed on 19 January 2022).
- Energy Information Administration (EIA). Wholesale Electricity Prices Trended Higher in 2021 Due to Increasing Natural Gas Prices, Today in Energy. Available online: https://www.eia.gov/todayinenergy/detail.php?id=50798 (accessed on 7 January 2022).
- Carbon Brief. COP26: Key Outcomes Agreed at the UN Climate Talks in Glasgow. Available online: https://www.carbonbrief.org/cop26-key-outcomes-agreed-at-the-un-climate-talks-in-glasgow (accessed on 15 November 2021).
- COP26. COP26 Presidency Outcomes: The Climate Pact. Available online: https://ukcop26.org/wp-content/uploads/2021/11/COP26-Presidency-Outcomes-The-Climate-Pact.pdf (accessed on 15 November 2021).
- Global Energy Monitor. Global Ownership of Coal Plants, Global Coal Plant Tracker. Available online: https://globalenergymonitor.org/projects/global-coal-plant-tracker/summary-tables (accessed on 18 February 2022).
- IEA. op. cit. Note 41; IRENA, World Energy Transitions Outlook 2021. Available online: https://irena.org/publications/2021/Jun/World-EnergyTransitions-Outlook (accessed on 2 November 2021).
- Katiraei, F.; Iravani, R.; Hatziargyriou, N.; Dimeas, A. Microgrids management. IEEE Power Energy Mag. 2008, 6, 54–65. [Google Scholar] [CrossRef]
- Sawhney, A.; Bracco, S.; Delfino, F.; Bonvini, B. Optimal planning and operation of a small size Microgrid within a Positive Energy District. In Proceedings of the 2022 AEIT International Annual Conference (AEIT), Rome, Italy, 3–5 October 2022; pp. 1–6. [Google Scholar] [CrossRef]
- IEC 61970; Energy Management System Application Program Interface (EMS-API)-ALL PARTS. International Electrotechnical Commission: Geneva, Switzerland, 2005.
- Zia, M.F.; Elbouchikhi, E.; Benbouzid, M. Microgrids energy management systems: A critical review on methods, solutions, and prospects. Appl. Energy 2018, 222, 1033–1055. [Google Scholar] [CrossRef]
- Chen, C.; Duan, S.; Cai, T.; Liu, B.; Hu, G. Smart energy management system for optimal microgrid economic operation. IET Renew Power Gener. 2011, 5, 258–267. [Google Scholar] [CrossRef]
- Byrne, R.H.; Nguyen, T.A.; Copp, D.A.; Chalamala, B.R.; Gyuk, I. Energy Management and Optimization Methods for Grid Energy Storage Systems. IEEE Access 2018, 6, 13231–13260. [Google Scholar] [CrossRef]
- An, L.N.; Lam, N.T.; Tuan, T.Q. Optimal energy management strategies of microgrids. In Proceedings of the 2016 IEEE Symposium Series on Computational Intelligence (SSCI), Athens, Greece, 6–9 December 2016. [Google Scholar]
- Zaree, N.; Vahidinasab, V. An MILP formulation for centralized energy management strategy of microgrids. In Proceedings of the 2016 Smart Grids Conference (SGC), Kerman, Iran, 20–21 December 2016; pp. 1–8. [Google Scholar] [CrossRef]
- Kantor, I.; Robineau, J.-L.; Butun, H.; Maréchal, F. A mixed-integer linear programming formulation for optimizing multi-scale material and energy integration. Front. Energy Res. 2020, 8, 49. [Google Scholar] [CrossRef]
- Shafiullah, M.; Abido, M.; Hossain, M.; Mantawy, A. An improved OPP problem formulation for distribution grid observability. Energies 2018, 11, 3069. [Google Scholar] [CrossRef]
- Shafiullah, M.; Hossain, M.I.; Abido, M.A.; Abdel-Fattah, T.; Mantawy, A.H. A modified optimal PMU placement problem formulation considering channel limits under various contingencies. Measurement 2019, 135, 875–885. [Google Scholar] [CrossRef]
- Derkenbaeva, E.; Vega, S.H.; Hofstede, G.J.; van Leeuwen, E. Positive energy districts: Mainstreaming energy transition in urban areas. Renew. Sustain. Energy Rev. 2022, 153, 111782. [Google Scholar] [CrossRef]
- IEA EBC Annex 83. Positive Energy Districts. 2020. Available online: https://annex83.iea-ebc.org (accessed on 10 December 2022).
- Bossi, S.; Gollner, C.; Theierling, S. Towards 100 positive energy districts in europe: Preliminary data analysis of 61 european cases. Energies 2020, 13, 22. [Google Scholar] [CrossRef]
- Lindholm, O.; Rehman, H.u.; Reda, F. Positioning positive energy districts in european cities. Buildings 2021, 11, 19. [Google Scholar] [CrossRef]
- Urban Europe. Available online: https://jpi-urbaneurope.eu/ (accessed on 19 December 2022).
- Urban Europe. Europe towards Positive Energy Districts: A Compilation of Projects Towards Sustainable Urbanization and the Energy Transition; Urban Europe: Bruxelles, Belgium, 2020. [Google Scholar]
- Alpine Space EU. Available online: https://www.alpine-space.eu/projects/alpgrids/en/home (accessed on 15 December 2022).
- Savona Campus. Available online: https://campus-savona.unige.it/en/ (accessed on 29 September 2022).
- Energia 2020 Project. Available online: http://www.energia2020.unige.it/en/home/ (accessed on 23 December 2022).
- Bianco, G.; Bonvini, B.; Bracco, S.; Delfino, F.; Laiolo, P.; Piazza, G. Key Performance Indicators for an Energy Community based on sustainable technologies. Sustainability 2021, 13, 16. [Google Scholar] [CrossRef]
- IRE Liguria. Available online: http://www.ireliguria.it (accessed on 12 March 2023).
- Available online: https://re.jrc.ec.europa.eu/pvg_tools/en/ (accessed on 15 July 2023).
- European Alternative Fuels Observatory. Available online: https://alternative-fuels-observatory.ec.europa.eu/general-information/recharging-systems (accessed on 12 September 2023).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).