Fractional-Order Sliding-Mode Control and Radial Basis Function Neural Network Adaptive Damping Passivity-Based Control with Application to Modular Multilevel Converters

Abstract

This paper proposes a hybrid control scheme that combines fractional-order sliding-mode control (FOSMC) with radial basis function neural network adaptive damping passivity-based control (RBFPBC) for modular multilevel converters (MMC) under non-ideal operating conditions. According to the passive control theory, we establish the Euler–Lagrange (EL) models of positive and negative sequences based on the unbalanced grid. A passivity-based controller that satisfies the energy dissipation law is designed. To enable rapid convergence of the system energy storage function, a radial basis function neural network (RBFNN) is introduced to adjust the injection damping adaptively. Additionally, a fractional-order sliding-mode controller (FOSMC) is designed. The fractional-order sliding mode surface used can improve tracking performance, and effectively suppressed the undesirable chattering phenomenon compared to the traditional sliding-mode control (SMC). Finally, combining the two control methods can effectively solve the issue of passivity-based control (PBC) being too dependent on parameters. The proposed hybrid control scheme enhances the ability of the system to resist disturbances, and improves its overall robustness. Simulation results demonstrate the feasibility and effectiveness of this control method.

1. Introduction

The development of power electronic devices has led to the transformation of direct current transmission from the initial two-level converter to the three-level converter and finally to MMC. MMC has significant advantages in transmission efficiency and topology, compared to traditional converters, making it a popular choice for flexible direct current transmission [1]. However, the complex structure of MMC makes it difficult to control, and power quality and system reliability are still problematic in the event of a grid fault resulting in voltage imbalance or disturbances [2,3]. Therefore, further research is needed to improve the control under unbalanced grid conditions.

In the classical control theory, the proportional integral controller (PI) and proportional resonant controller (PR) can control the internal characteristics of the model well [4,5]. These controllers have the characteristics of simple structure, easy implementation, and a wide range of application. However, they have high sensitivity to changes in the environment. Thus, it is necessary to constantly adjust the quality of the data acquisition level with the environmental changes. Additionally, the tracking ability for time-varying alternating current (AC) signals is poor. As a result, many nonlinear control methods have been proposed to supplement traditional linear controllers. Compared with the traditional control, model predictive control (MPC), sliding-mode control (SMC), passivity-based control (PBC), etc. have been found to have better capability in dealing with non-ideal states. Reference [6] proposes the MPC strategy in the case of model mismatch and system parameter instability. A SMC strategy is designed for the inner loop in [7], which improves the transient characteristics of the system. It can make the system move according to a predetermined trajectory, and independent of the parameters of the system. However, chattering phenomena may occur, causing fluctuations as the system approaches the sliding mode surface. This can result in failure to converge, and eventually instability. To address this issue, fractional order sliding mode control (FOSMC) has been proposed as an improved nonlinear control method based on SMC. The sliding-mode surface designed by introducing the fractional order theory can effectively reduce the chattering phenomenon and obtain a better tracking performance compared with SMC, as demonstrated in [8,9,10].

In [11], a proposal for a passivity-based control (PBC) strategy of LCL converter is presented. PBC is a nonlinear control strategy that considers the energy point of view. By injecting damping into the system, the energy function and the error function of the system will asymptotically converge to the desired value. This control method offers the advantages of good stability, robustness and ease of implementation [12,13,14]. However, the PBC strategy has a disadvantage of relying on the control parameter too much, which can lead to shortcomings when facing the internal parameter changes or external disturbances, etc. [15,16]. Additionally, the size of the injection damping in PBC is closely related to the convergence speed of the energy storage function. If the injection damping is too small, it will slow down the response of the system. Theoretically, the larger the injection damping is, the faster the system convergence will be. However, in actual engineering, the system may become uncontrollable if the injection damping is too high. In order to ensure an appropriate value, several solutions have been proposed in [17,18,19,20].

In [17], the optimal damping parameter was obtained by observing the stability, amplitude and phase frequency characteristic curves of the system for different damping values. It should be noted that this method has a large human factor. Reference [18] derives the critical damping from the resonance relationship using a complex formula that is not applicable in practical engineering. The self-tuning of injection damping is achieved though the use of fuzzy control [19]. However, this method relies heavily on the rule table formed by experts’ experience, and lacks adaptive ability. Another approach is the use of the particle swarm optimization (PSO) algorithm to design the parameters of the PBC [20]. However, this method has a slow computational speed and requires offline tuning. The radial basis function neural network (RBFNN) is a feed-forward neural network that has a simple structure and excellent performance. It consists of three layers: topology-input layer, hidden layer and output layer. RBFNN solves the issues of high computation and slow learning speed that are present in most learning algorithms. Therefore, it is more suitable for online control. References [21,22,23] describe some applications in power electronics.

Motivated by the above studies, this paper proposes a hybrid control strategy, FOSMC-RBFPBC, which was used to control the MMC under unbalanced grids. Firstly, RBFNN is proposed for online adaptive control of injection damping in PBC, which solves the problem of injection damping size selection. It can make the system converge quickly by adjusting the injection damping size online. Secondly, FOSMC is used to obtain a better tracking performance. Finally, this research examines the advantages and disadvantages of the two control methods, FOSMC and RBFPBC, and proposes their combination to complement each other. The resulting system exhibits fast response speed and low sensitivity to parameter variations and external disturbances.

The manuscript is structured as follows: Section 2 presents the topology and control process of MMC. Section 3 details the design procedure for the FOSMC-PBC. Section 4 explains the use of RBFNN to adaptively adjust injection damping. Finally, Section 5 presents simulations for three different conditions to validate the proposed theoretical approach.

2. The Topology and Mathematical Modelling of MMC

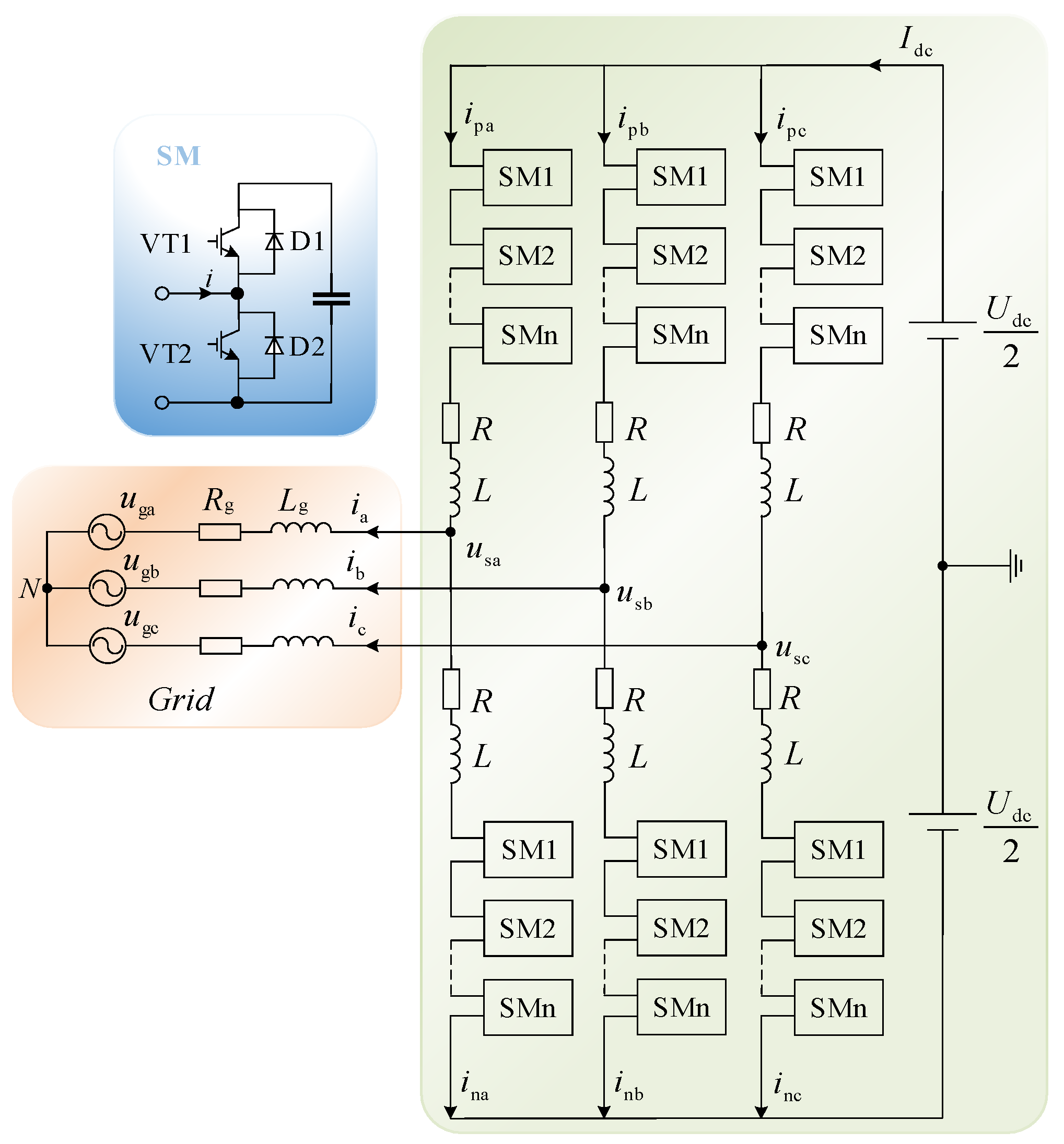
2.1. MMC Topology

The MMC topology is shown in Figure 1. The ABC three-phase and its upper and lower bridge arms are identical symmetrical structures, and each bridge arm consists of n sub-module, bridge arm inductance and bridge arm resistance connected in series, and the inverted AC current is connected to the power grid after passing through the filter inductance Lm and filter resistance Rm. The sub-module is a half-bridge structure. Controlling the output voltage magnitude of the MMC can be achieved by regulating the conduction and switching off of the switching devices within the sub-module.

2.2. MMC Mathematical Modelling

According to Kirchhoff’s law, the mathematical model for MMC can be obtained as

$$\{\begin{array}{l}{u}_{\mathrm{ga}}=u_{\mathrm{sa}}-(\frac{L}{2}+L_{\mathrm{g}})\frac{\mathrm{d}{i}_{\mathrm{a}}}{\mathrm{d}t}-(\frac{R}{2}+R_{\mathrm{g}})i_{\mathrm{a}}\\ u_{\mathrm{gb}}=u_{\mathrm{sb}}-(\frac{L}{2}+L_{\mathrm{g}})\frac{\mathrm{d}{i}_{\mathrm{b}}}{\mathrm{d}t}-(\frac{R}{2}+R_{\mathrm{g}})i_{\mathrm{b}}\\ u_{\mathrm{gc}}=u_{\mathrm{sc}}-(\frac{L}{2}+L_{\mathrm{g}})\frac{\mathrm{d}{i}_{\mathrm{c}}}{\mathrm{d}t}-(\frac{R}{2}+R_{\mathrm{g}})i_{\mathrm{c}}\end{array}$$

(1)

where, $u_{\mathrm{ga}}$, $u_{\mathrm{gb}}$ and $u_{\mathrm{gc}}$ are the three-phase AC voltages on the grid side; $u_{\mathrm{sa}}$, $u_{\mathrm{sb}}$ and $u_{\mathrm{sc}}$ are the three-phase AC voltages on the input side of the MMC; $i_{\mathrm{a}}$, $i_{\mathrm{b}}$ and $i_{\mathrm{c}}$ are the three-phase currents on the grid side.

A transformation of the above equation gives:

$$\{\begin{array}{l}{u}_{sd}=u_{gd}-R_{\mathrm{eq}}{i}_d-L_{\mathrm{eq}}\frac{\mathrm{d}{i}_d}{\mathrm{d}t}+\omega L_{\mathrm{eq}}{i}_q\\ u_{sq}=u_{\mathrm{g}q}-R_{\mathrm{eq}}{i}_q-L_{\mathrm{eq}}\frac{\mathrm{d}{i}_q}{\mathrm{d}t}-\omega L_{\mathrm{eq}}{i}_d\end{array}$$

(2)

where $R_{\mathrm{eq}}=R/2+R_{\mathrm{g}}$, $L_{\mathrm{eq}}=L/2+L_{\mathrm{g}}$; $\omega$ is the grid fundamental frequency corner frequency, $\omega =2\mathsf{\pi }f$.

Since there will be positive and negative sequence components when the grid is unbalanced, an expansion of (2) is performed:

$$\{\begin{array}{l}{u}_{sd}^{+}=u_{gd}^{+}-L_{\mathrm{eq}}\frac{\mathrm{d}{i}_d^{+}}{\mathrm{d}t}-R_{\mathrm{eq}}{i}_d^{+}+\omega L_{\mathrm{eq}}{i}_q^{+}\\ u_{sq}^{+}=u_{gq}^{+}-L_{\mathrm{eq}}\frac{\mathrm{d}{i}_q^{+}}{\mathrm{d}t}-R_{\mathrm{eq}}{i}_q^{+}-\omega L_{\mathrm{eq}}{i}_d^{+}\\ u_{sd}^{-}=u_{gd}^{-}-L_{\mathrm{eq}}\frac{\mathrm{d}{i}_d^{-}}{\mathrm{d}t}-R_{\mathrm{eq}}{i}_d^{-}-\omega L_{\mathrm{eq}}{i}_q^{-}\\ u_{sq}^{-}=u_{gq}^{-}-L_{\mathrm{eq}}\frac{\mathrm{d}{i}_q^{-}}{\mathrm{d}t}-R_{\mathrm{eq}}{i}_q^{-}+\omega L_{\mathrm{eq}}{i}_d^{-}\end{array}$$

(3)

Figure 2 displays the MMC control block diagram. The diagram illustrates the net side of the measured current after the separation of positive and negative sequences. The outer loop control of the current reference value is used to calculate the difference. The FOSMC-RBFPBC generates a given value of the voltage, which is then modulated to generate PWM waveforms. By controlling the MMC sub-modules of the power tube, overall system control is achieved.

3. Design of FOSMC-PBC Controller

3.1. Euler–Lagrange Model

Rewriting (3) into the EL-model form as

$$\{\begin{array}{l}{M}^{+}{\dot{x}}^{+}+J^{+}{x}^{+}+R^{+}{x}^{+}=u^{+}\\ M^{-}{\dot{x}}^{-}+J^{-}{x}^{-}+R^{-}{x}^{-}=u^{-}\end{array}$$

(4)

where

$$M^{+}=M^{-}=\left(\begin{array}{cc}{L}_{\mathrm{eq}}& 0\\ 0& L_{\mathrm{eq}}\end{array}\right),J^{+}=\left(\begin{array}{cc}\begin{array}{c}0\\ \omega L_{\mathrm{eq}}\end{array}& \begin{array}{c}-\omega L_{\mathrm{eq}}\\ 0\end{array}\end{array}\right),J^{-}=\left(\begin{array}{cc}\begin{array}{c}0\\ -\omega L_{\mathrm{eq}}\end{array}& \begin{array}{c}\omega L_{\mathrm{eq}}\\ 0\end{array}\end{array}\right)$$

$$R^{+}=R^{-}=\left(\begin{array}{cc}{R}_{\mathrm{eq}}& 0\\ 0& R_{\mathrm{eq}}\end{array}\right),u^{+}=\left(\begin{array}{c}{u}_{gd}^{+}-u_{sd}^{+}\\ u_{gq}^{+}-u_{sq}^{+}\end{array}\right),u^{-}=\left(\begin{array}{c}{u}_{gd}^{-}-u_{sd}^{-}\\ u_{gq}^{-}-u_{sq}^{-}\end{array}\right)$$

$$x^{+}=\left(\begin{array}{c}{i}_d^{+}\\ i_q^{+}\end{array}\right),x^{-}=\left(\begin{array}{c}{i}_d^{-}\\ i_q^{-}\end{array}\right)$$

The positive and negative superscripts represent the positive and negative sequence components. $u$ is the input vector; $x$ is the state variable; $J$ is the interconnection matrix; $R$ is the semipositive dissipation matrix; and $M$ is the positive definite energy storage matrix.

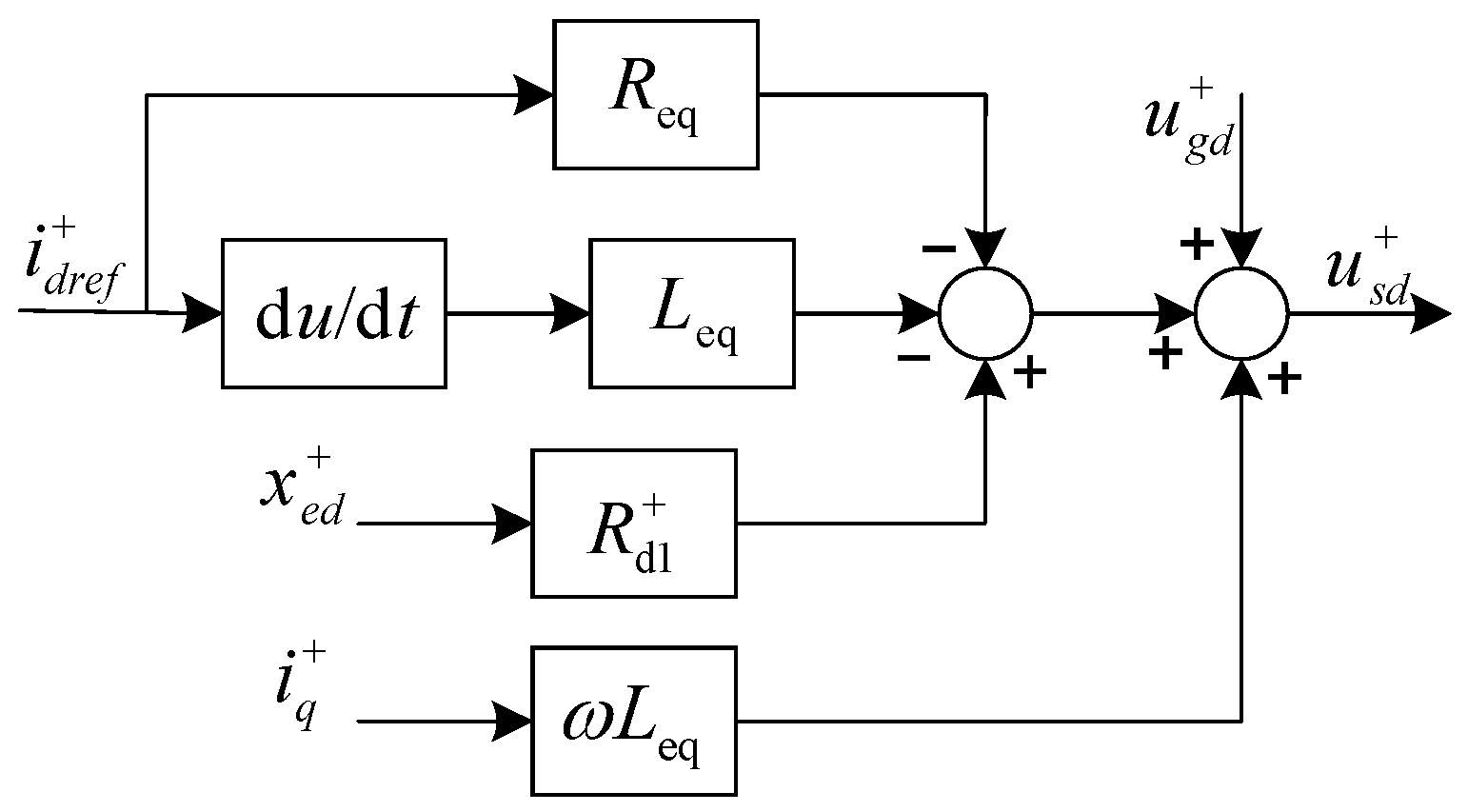
3.2. Passivity-Based Controller Design

For the system with n inputs and m outputs can given by:

$$\{\begin{array}{l}\dot{x}=f(x,u)\\ y=h(x)\end{array},x(0)=x_0\in R^n$$

(5)

where x, u, and y are state variables, input variables and output variables, respectively.

For the system (5), to prove that it is strictly passive, it is necessary to satisfy the following dissipation inequality for any t > 0:

$$H(x(t))-H(x(0))\le {\displaystyle {\int }_0^t{u}^{\mathrm{T}}\mathrm{yd}\tau -}{\displaystyle {\int }_0^{t}Q\left(\mathrm{x}\right)\mathrm{d}\tau }$$

(6)

Or:

$$\dot{H}(x)\le u^{\mathrm{T}}\mathrm{y}-Q(x)$$

(7)

The MMC energy storage functions for positive and negative order are chosen, respectively, as

$$\{\begin{array}{l}{V}^{+}=\frac{{(x^{+})}^{\mathrm{T}}{M}^{+}{x}^{+}}{2}\\ V^{-}=\frac{{(x^{-})}^{\mathrm{T}}{M}^{-}{x}^{-}}{2}\end{array}$$

(8)

Derivation of (8) gives:

$$\{\begin{array}{l}{\dot{V}}^{+}={(x^{+})}^{\mathrm{T}}{M}^{+}{\dot{x}}^{+}={(x^{+})}^{\mathrm{T}}{u}^{+}-{(x^{+})}^{\mathrm{T}}{J}^{+}{x}^{+}-{(x^{+})}^{\mathrm{T}}{R}^{+}{x}^{+}\\ {\dot{V}}^{-}={(x^{-})}^{\mathrm{T}}{M}^{-}{\dot{x}}^{-}={(x^{-})}^{\mathrm{T}}{u}^{-}-{(x^{-})}^{\mathrm{T}}{J}^{-}{x}^{-}-{(x^{-})}^{\mathrm{T}}{R}^{-}{x}^{-}\end{array}$$

(9)

According to (9), since it is an antisymmetric matrix, it can be obtained that ${(x^{+})}^{\mathrm{T}}{J}^{+}(x^{+})={(x^{-})}^{\mathrm{T}}{J}^{-}(x^{-})=0$. And then, making $y=x^{+}$, $Q\left(x\right)={(x^{+})}^{\mathrm{T}}{R}^{+}{x}^{+}$ and $y=x^{-}$, $Q\left(x\right)={(x^{-})}^{\mathrm{T}}{R}^{-}{x}^{-}$, respectively. The simplification of (9) can satisfy (7); it can be seen that the MMC system is strictly passive at all times. When the MMC is passively controlled, the system is stable and controllable.

Define the desired equilibrium points of the positive-sequence and negative-sequence inner-loop currents, respectively, as

$$x_{ref}^{+}=\left[\begin{array}{c}{i}_{dref}^{+}\\ i_{qref}^{+}\end{array}\right],x_{ref}^{-}=\left[\begin{array}{c}{i}_{dref}^{-}\\ i_{qref}^{-}\end{array}\right]$$

(10)

where $i_{dref}^{+}$, $i_{qref}^{+}$, $i_{dref}^{-}$ and $i_{qref}^{-}$ are the desired equilibrium points of the positive-sequence d-axis, positive-sequence q-axis, negative-sequence d-axis and negative-sequence q-axis currents, respectively, i.e., the reference values of the inner-loop currents.

The positive and negative order state variable errors are:

$$x_e^{+}=\left[\begin{array}{c}{x}_{ed}^{+}\\ x_{\mathrm{eq}}^{+}\end{array}\right]=\left[\begin{array}{c}{x}_d^{+}-x_{dref}^{+}\\ x_q^{+}-x_{qref}^{+}\end{array}\right],x_{\mathrm{e}}^{-}=\left[\begin{array}{c}{x}_{\mathrm{e}d}^{-}\\ x_{\mathrm{eq}}^{-}\end{array}\right]=\left[\begin{array}{c}{x}_d^{-}-x_{d\mathrm{ref}}^{-}\\ x_q^{-}-x_{q\mathrm{ref}}^{-}\end{array}\right]$$

(11)

Substituting (11) into (4), it can be obtained that

$$\{\begin{array}{l}{M}^{+}{\dot{x}}_e^{+}+J{x}_e^{+}+R^{+}{x}_e^{+}=u^{+}-M^{+}{\dot{x}}_{ref}^{+}-J{x}_{ref}^{+}-R{x}_{ref}^{+}\\ M^{-}{\dot{x}}_e^{-}+J{x}_e^{+}+R^{-}{x}_e^{-}=u^{-}-M^{-}{\dot{x}}_{ref}^{-}-J{x}_{ref}^{-}-R{x}_{ref}^{-}\end{array}$$

(12)

In order to speed up the convergence of the system, let the dissipation terms of the injected damping of the positive and negative sequences be

$$\{\begin{array}{l}{R}_{\mathrm{a}}^{+}{x}_e^{+}=(R^{+}+R_{\mathrm{d}}^{+})x_e^{+}\\ R_{\mathrm{a}}^{-}{x}_e^{-}=(R^{-}+R_{\mathrm{d}}^{-})x_e^{-}\end{array}$$

(13)

where $R_{\mathrm{a}}$ is the dissipation factor, and $R_{\mathrm{d}}$ is the injection damping.

$$R_{\mathrm{d}}^{+}=\left[\begin{array}{cc}{R}_{\mathrm{d}1}^{+}& 0\\ 0& R_{\mathrm{d}2}^{+}\end{array}\right],R_{\mathrm{d}}^{-}=\left[\begin{array}{cc}{R}_{\mathrm{d}1}^{-}& 0\\ 0& R_{\mathrm{d}2}^{-}\end{array}\right]$$

(14)

Combining (12) and (13) can give the following equation

$$\{\begin{array}{l}{M}^{+}{\dot{x}}_e^{+}+R_{\mathrm{a}}^{+}{x}_{\mathrm{e}}^{+}=u^{+}-M^{+}{\dot{x}}_{ref}^{+}-J^{+}{x}^{+}-R^{+}{x}_{ref}^{+}+R_{\mathrm{d}}^{+}{x}_e^{+}\\ M^{-}{\dot{x}}_e^{-}+R_{\mathrm{a}}^{-}{x}_e^{-}=u^{-}-M^{-}{\dot{x}}_{ref}^{-}-J^{-}{x}^{-}-R^{-}{x}_{ref}^{-}+R_{\mathrm{d}}^{-}{x}_e^{-}\end{array}$$

(15)

Let the right-hand side of (15) be 0. The control laws for the positive and negative sequences are selected as

$$\{\begin{array}{l}{u}^{+}=M^{+}{\dot{x}}_{ref}^{+}+J^{+}{x}^{+}+R^{+}{x}_{ref}^{+}-R_{\mathrm{d}}^{+}{x}_e^{+}\\ u^{-}=M^{-}{\dot{x}}_{ref}^{-}+J^{-}{x}^{-}+R^{-}{x}_{ref}^{-}-R_{\mathrm{d}}^{-}{x}_e^{-}\end{array}$$

(16)

The error energy storage function of the system can be defined as:

$$\{\begin{array}{l}{\dot{H}}^{+}=\partial {(x_e^{+})}^{\mathrm{T}}{M}^{+}{x}^{+}/\partial x^{+}={(x_e^{+})}^{\mathrm{T}}{M}^{+}{\dot{x}}_e^{+}\\ {\dot{H}}^{-}=\partial {(x_e^{-})}^{\mathrm{T}}{M}^{-}{x}^{-}/\partial x^{-}={(x_e^{-})}^{\mathrm{T}}{M}^{-}{\dot{x}}_e^{-}\end{array}$$

(17)

Substituting (16) into (17), it can be obtained that

$$\{\begin{array}{l}{\dot{H}}^{+}=-{(x_e^{+})}^{\mathrm{T}}(R^{+}+R_{\mathrm{d}}^{+})x_e^{+}<0\\ {\dot{H}}^{-}=-{(x_e^{-})}^{\mathrm{T}}(R^{-}+R_{\mathrm{d}}^{-})x_e^{-}<0\end{array}$$

(18)

According to (18), the chosen control law accelerates the convergence of the system. Substituting the corresponding matrices into (16), respectively, the passive control signals of the system under positive and negative sequences can be obtained as

$$\{\begin{array}{l}{u}_{sd}^{+}=u_{gd}^{+}-L_{\mathrm{eq}}\frac{\mathrm{d}{i}_{dref}^{+}}{\mathrm{d}t}+\omega L_{\mathrm{eq}}{i}_q^{+}-R_{\mathrm{eq}}{i}_{dref}^{+}+R_{\mathrm{d}1}^{+}{x}_{ed}^{+}\\ u_{sq}^{+}=u_{gq}^{+}-L_{\mathrm{eq}}\frac{\mathrm{d}{i}_{qref}^{+}}{\mathrm{d}t}-\omega L_{\mathrm{eq}}{i}_d^{+}-R_{\mathrm{eq}}{i}_{qref}^{+}+R_{\mathrm{d}2}^{+}{x}_{\mathrm{eq}}^{+}\\ u_{sd}^{-}=u_{gd}^{-}-L_{\mathrm{eq}}\frac{\mathrm{d}{i}_{dref}^{-}}{\mathrm{d}t}-\omega L_{\mathrm{eq}}{i}_q^{-}-R_{\mathrm{eq}}{i}_{dref}^{-}+R_{\mathrm{d}1}^{-}{x}_{ed}^{-}\\ u_{sq}^{-}=u_{gq}^{-}-L_{\mathrm{eq}}\frac{\mathrm{d}{i}_{qref}^{-}}{\mathrm{d}t}+\omega L_{\mathrm{eq}}{i}_d^{-}-R_{\mathrm{eq}}{i}_{qref}^{-}+R_{\mathrm{d}2}^{-}{x}_{\mathrm{eq}}^{-}\end{array}$$

(19)

The control block diagram of the d-axis passive control under positive sequence components is shown in Figure 3.

In practical engineering, the conversion between analog and digital signals requires a delay of one sampling period, so the control law of the discretized passive controller is as follows:

$$\{\begin{array}{l}{u}_{sd}^{+}(k)=u_{gd}^{+}(k+1)+\omega L_{\mathrm{eq}}{i}_q^{+}(k+1)-R_{\mathrm{eq}}{i}_{dref}^{+}(k+1)+R_{\mathrm{d}1}^{+}{x}_{ed}^{+}(k+1)\\ u_{sq}^{+}(k)=u_{gq}^{+}(k+1)-\omega L_{\mathrm{eq}}{i}_d^{+}(k+1)-R_{\mathrm{eq}}{i}_{qref}^{+}(k+1)+R_{\mathrm{d}2}^{+}{x}_{\mathrm{eq}}^{+}(k+1)\\ u_{sd}^{-}(k)=u_{gd}^{-}(k+1)-\omega L_{\mathrm{eq}}{i}_q^{-}(k+1)-R_{\mathrm{eq}}{i}_{dref}^{-}(k+1)+R_{\mathrm{d}1}^{-}{x}_{ed}^{-}(k+1)\\ u_{sq}^{-}(k)=u_{gq}^{-}(k+1)+\omega L_{\mathrm{eq}}{i}_d^{-}(k+1)-R_{\mathrm{eq}}{i}_{qref}^{-}(k+1)+R_{\mathrm{d}2}^{-}{x}_{\mathrm{eq}}^{-}(k+1)\end{array}$$

(20)

3.3. Fractional-Order Sliding-Mode Passivity-Based Controller Design

Fractional order calculus is an extension of calculus to a more general form, i.e., it can be differentiated or integrated to fractional order [24,25]. It can be defined as

$${}_{a}D_t^{\alpha }=\{\begin{array}{ll}\frac{{\mathrm{d}}^{\alpha }}{{\mathrm{d}\mathrm{t}}^{\alpha }}& \alpha >0\\ 1& \alpha =0\\ {\displaystyle {\int }_{\mathrm{a}}^t{(\mathrm{d}\tau )}^{\alpha }}& \alpha <0\end{array}$$

(21)

where ${}_{a}D_t^{\alpha }$ is the defining symbol of fractional-order calculus; $a$ and $t$ represent the upper and lower limits; and $\alpha$ is the number of integrations.

Common examples of fractional-order calculus are RL, GL, and Caputo. Caputo fractional-order differentiation is more widely used in practice; it is defined as

$$D^{\alpha }f(t)=\frac{1}{\Gamma (n-\alpha )}{\displaystyle {\int }_0^t\frac{f^{(n)}(\tau )}{{(t-\tau )}^{\alpha -n+1}}}d\tau ,n-1<\alpha <n$$

(22)

where $\Gamma (\cdot )$ is a gamma function, $\Gamma (\cdot )={\displaystyle {\int }_0^{\infty }{e}^{-t}}{t}^{\gamma -1}\mathrm{d}t$; n is a positive integer, n = 1.

Since the MMC system with sliding-mode controllers exhibits vibration during convergence, which tends to degrade the performance of the control system, the fractional-order theory is introduced into the sliding-mode surface to mitigate the vibration. For the positive and negative order systems, the following sliding-mode surface can be designed

$$\{\begin{array}{l}{s}_1=b_1{x}_{ed}^{+}+c_1{D}^{{\alpha }_1-1}{x}_{ed}^{+}+d_1{D}^{1-{\mu }_1}{x}_{ed}^{+}\\ s_2=b_2{x}_{\mathrm{eq}}^{+}+c_2{D}^{{\alpha }_2-1}{x}_{\mathrm{eq}}^{+}+d_2{D}^{1-{\mu }_2}{x}_{\mathrm{eq}}^{+}\\ s_3=b_3{x}_{ed}^{-}+c_3{D}^{{\alpha }_3-1}{x}_{ed}^{-}+d_3{D}^{1-{\mu }_3}{x}_{ed}^{-}\\ s_4=b_4{x}_{\mathrm{eq}}^{-}+c_4{D}^{{\alpha }_4-1}{x}_{\mathrm{eq}}^{-}+d_4{D}^{1-{\mu }_4}{x}_{\mathrm{eq}}^{-}\end{array}$$

(23)

where $b_i$, $c_i$, and $d_i$ are slip-mode surface coefficients, $i=1,2,3,4$; $D^{\alpha -1}{x}_{\mathrm{e}}$ is the $\alpha -1$ order integral over the deviation $x_{\mathrm{e}}$; $D^{1-\mu }{x}_{\mathrm{e}}$ is the $1-\mu$ order differentiation over the deviation $x_{\mathrm{e}}$. $0<\alpha$, $\mu <1$.

For ease of calculation, the fractional-order differential and fractional-order integral terms are each shifted forward by one sampling period, while the error $x_{\mathrm{e}}(k)$ is approximately changed to $x_{\mathrm{e}}(k)=i(k+1)-i_{\mathrm{ref}}(k-1)$. Combined with (22), the fractional-order sliding surface is given as follows:

$$\{\begin{array}{l}{s}_1(k)=b_1{x}_{ed}^{+}(k)+c_1{D}^{{\alpha }_1-1}{x}_{ed}^{+}(k-1)+d_1{D}^{1-{\mu }_1}{x}_{ed}^{+}(k-1)\\ s_2(k)=b_2{x}_{\mathrm{eq}}^{+}(k)+c_2{D}^{{\alpha }_2-1}{x}_{\mathrm{eq}}^{+}(k-1)+d_2{D}^{1-{\mu }_2}{x}_{\mathrm{eq}}^{+}(k-1)\\ s_3(k)=b_3{x}_{ed}^{-}(k)+c_3{D}^{{\alpha }_3-1}{x}_{ed}^{-}(k-1)+d_3{D}^{1-{\mu }_3}{x}_{ed}^{-}(k-1)\\ s_4(k)=b_4{x}_{\mathrm{eq}}^{-}(k)+c_4{D}^{{\alpha }_4-1}{x}_{\mathrm{eq}}^{-}(k-1)+d_4{D}^{1-{\mu }_4}{x}_{\mathrm{eq}}^{-}(k-1)\end{array}$$

(24)

Since the derivation process for the negative order is similar to that for the positive order, only the positive order will be analyzed next.

The MMC grid-side currents $i_d^{+}(k+1)$ and $i_q^{+}(k+1)$ need to be delayed by one sampling period due to the sampling delay of the digital controller, which cannot be obtained by instantaneous k-sampling. Therefore, with the help of the Euler discrete method [26], (3) can be discretized as

$$\{\begin{array}{l}{i}_d^{+}(k+1)=\frac{T_{\mathrm{s}}}{L_{\mathrm{eq}}}[u_{gd}^{+}(k)-u_{sd}^{+}(k)]+(1-\frac{T_s{R}_{\mathrm{eq}}}{L_{\mathrm{eq}}})i_d^{+}(k)+\omega T_s{i}_q^{+}(k)\\ i_q^{+}(k+1)=\frac{T_{\mathrm{s}}}{L_{\mathrm{eq}}}[u_{gq}^{+}(k)-u_{sq}^{+}(k)]+(1-\frac{T_s{R}_{\mathrm{eq}}}{L_{\mathrm{eq}}})i_q^{+}(k)-\omega T_s{i}_d^{+}(k)\end{array}$$

(25)

Substituting (24) into (23), it can be obtained that

$$\{\begin{array}{ll}{s}_1(k)& ={\mathrm{b}}_1[\frac{T_{\mathrm{s}}}{L_{\mathrm{eq}}}(u_{gd}^{+}(k)-u_{sd}^{+}(k))+(1-\frac{T_s{R}_{\mathrm{eq}}}{L_{\mathrm{eq}}})i_d^{+}(k)+\omega T_s{i}_q^{+}(k)-i_{dref}^{+}(k-1)]\\ & +c_1{D}^{\alpha -1}{x}_{ed}^{+}(k-1)+d_1{D}^{1-\mu }{x}_{ed}^{+}(k-1)\\ s_2(k)& =b_2[\frac{T_{\mathrm{s}}}{L_{\mathrm{eq}}}(u_{gq}^{+}(k)-u_{sq}^{+}(k))+(1-\frac{T_s{R}_{\mathrm{eq}}}{L_{\mathrm{eq}}})i_q^{+}(k)-\omega T_s{i}_d^{+}(k)-i_{qref}^{+}(k-1)]\\ & +c_2{D}^{\alpha -1}{x}_{\mathrm{eq}}^{+}(k-1)+d_2{D}^{1-\mu }{x}_{\mathrm{eq}}^{+}(k-1)\end{array}$$

(26)

In order to weaken the effect of uncertainty, the discrete exponential convergence law is given as

$$\{\begin{array}{c}{s}_1(k+1)-s_1(k)=-T_s{\epsilon }_1\mathrm{sgn}(s_1(k))-T_s{q}_1{s}_1(k)\\ s_2(k+1)-s_2(k)=-T_s{\epsilon }_2\mathrm{sgn}(s_2(k))-T_s{q}_2{s}_2(k)\end{array}$$

(27)

where ${\epsilon }_i$ and $q_i$ are convergence law coefficients and are positive integers, i = 1, 2.

To further improve the high-frequency chattering, $\mathrm{sgn}(\cdot )$ is replaced by the saturation function $\mathrm{sat}(\cdot )$.

$$\{\begin{array}{c}{s}_1(k+1)-s_1(k)=-T_s{\epsilon }_1\mathrm{sat}(s_1(k))-T_s{q}_1{s}_1(k)\\ s_2(k+1)-s_2(k)=-T_s{\epsilon }_2\mathrm{sat}(s_2(k))-T_s{q}_2{s}_2(k)\end{array}$$

(28)

where

$$\mathrm{sat}(s)=\{\begin{array}{l}1\begin{array}{ccc}& \begin{array}{cc}& \end{array}& \mathrm{s}>\Delta \end{array}\\ ks\begin{array}{cc}& \mathrm{s}\le \Delta ,k=\frac{1}{\Delta }\end{array}\\ -1\begin{array}{ccc}& & s<-\Delta \end{array}\end{array}$$

(29)

Combining (24) and (26), (28) can be written as

$$\{\begin{array}{ll}{s}_1(k+1)-s_1(k)& =b_1[x_{ed}^{+}(k+1)+i_{dref}^{+}(k-1)-\frac{T_{\mathrm{s}}}{L_{\mathrm{eq}}}{u}_{gd}^{+}(k)\\ & +\frac{T_{\mathrm{s}}}{L_{\mathrm{eq}}}{u}_{sd}^{+}(k)-(1-\frac{T_s{R}_{\mathrm{eq}}}{L_{\mathrm{eq}}})i_d^{+}(k)-\omega T_s{i}_q^{+}(k)]\\ & +c_1{D}^{\alpha -1}{x}_{ed}^{+}(k)-c_1{D}^{\alpha -1}{x}_{ed}^{+}(k-1)\\ & +d_1{D}^{1-\mu }{x}_{ed}^{+}(k)-d_1{D}^{1-\mu }{x}_{ed}^{+}(k-1)\\ s_2(k+1)-s_2(k)& =b_2[x_{\mathrm{eq}}^{+}(k+1)+i_{qref}^{+}(k-1)-\frac{T_{\mathrm{s}}}{L_{\mathrm{eq}}}{u}_{gq}^{+}(k)\\ & +\frac{T_{\mathrm{s}}}{L_{\mathrm{eq}}}{u}_{sq}^{+}(k)-(1-\frac{T_s{R}_{\mathrm{eq}}}{L_{\mathrm{eq}}})i_q^{+}(k)+\omega T_s{i}_d^{+}(k)]\\ & +c_2{D}^{\alpha -1}{x}_{\mathrm{eq}}^{+}(k)-c_2{D}^{\alpha -1}{x}_{\mathrm{eq}}^{+}(k-1)\\ & +d_2{D}^{1-\mu }{x}_{\mathrm{eq}}^{+}(k)-d_2{D}^{1-\mu }{x}_{\mathrm{eq}}^{+}(k-1)\end{array}$$

(30)

Combining (28) and (30), it can be obtained that

$$\{\begin{array}{ll}{x}_{ed}^{+}(k+1)& =-i_{dref}^{+}(k-1)+(1-\frac{T_s{R}_{\mathrm{eq}}}{L_{\mathrm{eq}}})i_d^{+}(k)+\frac{T_{\mathrm{s}}}{L_{\mathrm{eq}}}[u_{gd}^{+}(k)-u_{sd}^{+}(k)]+\omega T_s{i}_q^{+}(k)\\ & -\frac{c_1}{b_1}[D^{\alpha -1}{x}_{ed}^{+}(k)-D^{\alpha -1}{x}_{ed}^{+}(k-1)]-\frac{d_1}{b_1}[D^{1-\mu }{x}_{ed}^{+}(k)-D^{1-\mu }{x}_{ed}^{+}(k-1)]\\ & -\frac{1}{b_1}[T_s{\epsilon }_1\mathrm{sgn}(s_1(k))+T_s{q}_1{s}_1(k)]\\ x_{\mathrm{eq}}^{+}(k+1)& =-i_{qref}^{+}(k-1)+(1-\frac{T_s{R}_{\mathrm{eq}}}{L_{\mathrm{eq}}})i_q^{+}(k)+\frac{T_{\mathrm{s}}}{L_{\mathrm{eq}}}[u_{gq}^{+}(k)-u_{sq}^{+}(k)]-\omega T_s{i}_d^{+}(k)\\ & -\frac{c_2}{b_2}[D^{\alpha -1}{x}_{\mathrm{eq}}^{+}(k)-D^{\alpha -1}{x}_{\mathrm{eq}}^{+}(k-1)]+\frac{d_2}{b_2}[D^{1-\mu }{x}_{\mathrm{eq}}^{+}(k)-D^{1-\mu }{x}_{\mathrm{eq}}^{+}(k-1)]\\ & -\frac{1}{b_2}[T_s{\epsilon }_2\mathrm{sgn}(s_2(k))-T_s{q}_2{s}_2(k)]\end{array}$$

(31)

where $x_{ed}^{+}(k+1)$ and $x_{\mathrm{eq}}^{+}(k+1)$ can be considered as the inputs of the passive controller with fractional-order sliding-model nature, obtained from the original inputs $x_{ed}^{+}(k)$ and $x_{\mathrm{eq}}^{+}(k)$ of the PBC after passing through the fractional-order sliding-model controller, so that the two control methods of passive control and fractional-order sliding-model control can be efficiently combined, resulting in a new hybrid control strategy, i.e., fractional-order sliding-mode passive control (FOSMC-PBC).

Figure 4 illustrates the FOSMC-PBC control of the d-axis under positive order components, where the passive controller is the main part. The original input of the passive controller is controlled by a fractional-order sliding mode, thus obtaining a new state with sliding mode properties, which is used as the new input of the passive controller, during which the state will gradually converge to the equilibrium point along the fractional-order sliding mode surface, and the energy storage function of the system will gradually converge to 0. By combining the advantages of the two controllers, FOSMC and PBC, and letting them both “join hands”, the controller designed in this paper has both passive characteristics and strong anti-jamming ability, and at the same time can realize smaller jitter. Therefore, the proposed FOSMC-PBC control can obtain good dynamic response and strong robustness.

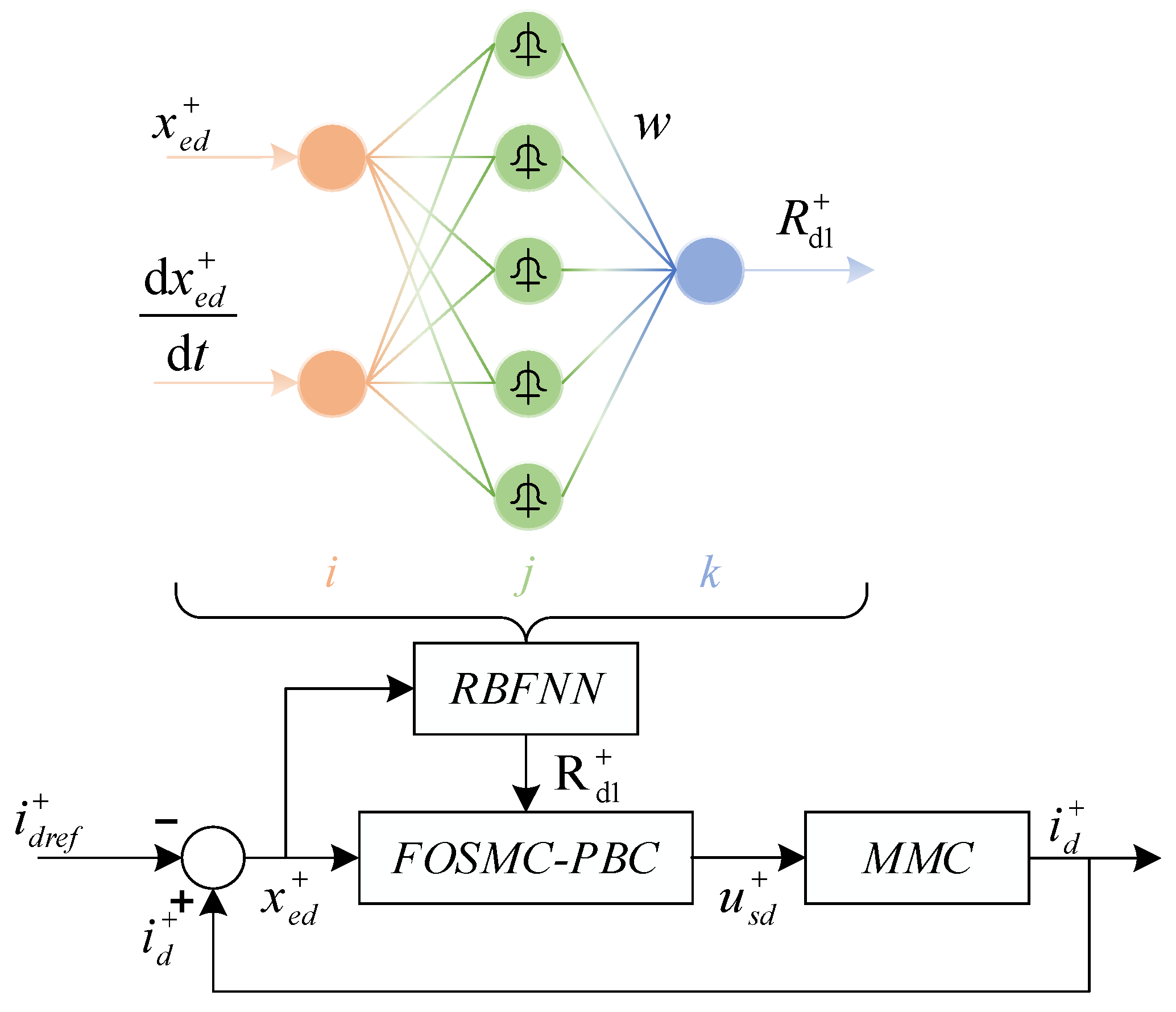
4. RBFNN-Based Injection Damping Adaptation Control

It can be seen that the size of the injection damping is closely related to the convergence speed of the energy storage function. If the injected damping is too small, it will slow down the response speed of the system. Theoretically, the larger the injection damping, the faster the system convergence speed, but when the injection damping is too large, the system will lose its stability, becoming an oscillation. Therefore, in order to ensure the stability of the system under the premise that the energy storage function can quickly converge to the desired equilibrium point, it is necessary to choose a suitable injection damping.

RBFNN is a kind of network that is widely used in online control nowadays. It has advantages such as excellent performance and simple structure. Therefore, in this paper, by constructing an RBFNN of 2-5-1, online adaptive injection damping is carried out, which further improves the ability of the system to resist parameter variations and external disturbances while making the system converge quickly.

As shown in Figure 5, the positive-order d-axis, for example, utilizes the error ${\mathrm{x}}_{\mathrm{e}d}^{+}$ and the rate of change $\mathrm{d}{x}_{\mathrm{e}d}^{+}/\mathrm{d}t$ of that error as inputs to the network.

The output of the input layer is

$$Ou{t}_{\mathrm{i}}^{\left(1\right)}=x(i),i=1,2$$

(32)

where $x(1)=i_d^{+}-i_{dref}^{+}$, $x(2)=\frac{\mathrm{d}(i_d^{+}-i_{dref}^{+})}{\mathrm{d}t}$.

The input of the hidden layer is

$$I{n}_j^{\left(2\right)}=\overrightarrow{x}$$

(33)

The output of the hidden layer is

$$Ou{t}_{{}_j}^2(m)=g(I{n}_j^{(2)}(m))$$

(34)

$$g(x)=\exp (\frac{{\Vert \overrightarrow{x}-{\stackrel{\rightharpoonup }{c}}_j\Vert }^2}{2b_j^2})$$

(35)

where $c_j$ is the center point of the Gaussian function; the closer it is to the input, the more sensitive the Gaussian function is; $b_j$ is the variance of the Gaussian function, which determines the mapping range of the Gaussian function, and the larger its value, the larger the mapping range.

The input of the NN output layer is

$$I{n}_k^{\left(3\right)}(m)={\displaystyle \sum _{m=1}^5{w}_{k}Ou{t}_j^{\left(2\right)}(m)}$$

(36)

The output of NN is as follows:

$$R_{\mathrm{d}1}^{+}=Ou{t}_k^{\left(3\right)}(m)=f(I{n}_k^{(3)}(m))$$

(37)

$$f(x)=\frac{a{e}^x}{e^x+e^{-x}}$$

(38)

where $w_k$ is the weight of the hidden layer to the output layer; a is the upper limit of the injected damping.

This NN’s performance function is as follows:

$$E(k)=\frac{1}{2}{(i_{{}_d}^{+}-i_{{}_{dref}}^{+})}^2$$

(39)

The network weight is adjusted using the gradient descent approach. An inertia term is included in the formula to improve convergence speed.

$$\mathsf{\Delta }{w}_{\mathrm{k}}(m)=-\alpha \frac{\partial E(m)}{\partial w_k}+\beta \mathsf{\Delta }{w}_k(m-1)$$

(40)

where α is the learning rate and β is the inertial coefficient.

5. Simulation Analysis

5.1. Simulation Setup

In order to verify the effectiveness and superiority of the FOSMC-RBFPBC controller designed in this paper, we built the MMC simulation model and its control system in MATLAB/SIMULINK, designed three kinds of non-ideal working conditions (sudden change of load on the network side, three-phase symmetrical faults, and asymmetrical faults), and compared and analyzed the fractional-order sliding mode passive control (FOSMC-PBC) strategy proposed in this paper with two kinds of control methods, namely, sliding-mode passive control (SMC-PBC) and proportional-integral (PI) control. The system simulation parameters are shown in

Table 1. Simulation parameters.

Parameters	Values
Grid voltage ugabc/kV	66
Grid-side inductors Lg/mH	1.2
Grid-side resistors Rg/Ω	0.4
Bridge arm resistors R/Ω	0.01
Bridge arm inductors Lf/mH	0.135
Submodule capacitance C/μF	12
Number of bridge arm submodules n	21
System frequency f/Hz	50
Switching frequency fs/kHz	20

, and the control parameters are shown in

Table 2. Control parameters.

Parameters	Values
PI	Kp = 5, Ki = 10
SMC-PBC	$R_{d1}^{+}$ = $R_{d1}^{-}$ = $R_{d2}^{+}$ = $R_{d2}^{-}$ = 80 ε1 = ε2 = ε3 = ε4 = 50, q1 = q2 = q3 = q4 = 100
FOPBC-RBFSMC	b1 = b2 = b3 = b4 = 8 c1 = c2 = c3 = c4 = 30 d1 = d2 = d3 = d4 = 3 ε1 = ε2 = ε3 = ε4 = 10 q1 = q2 = q3 = q4 = 23 α = 0.5, β = 0.3

.

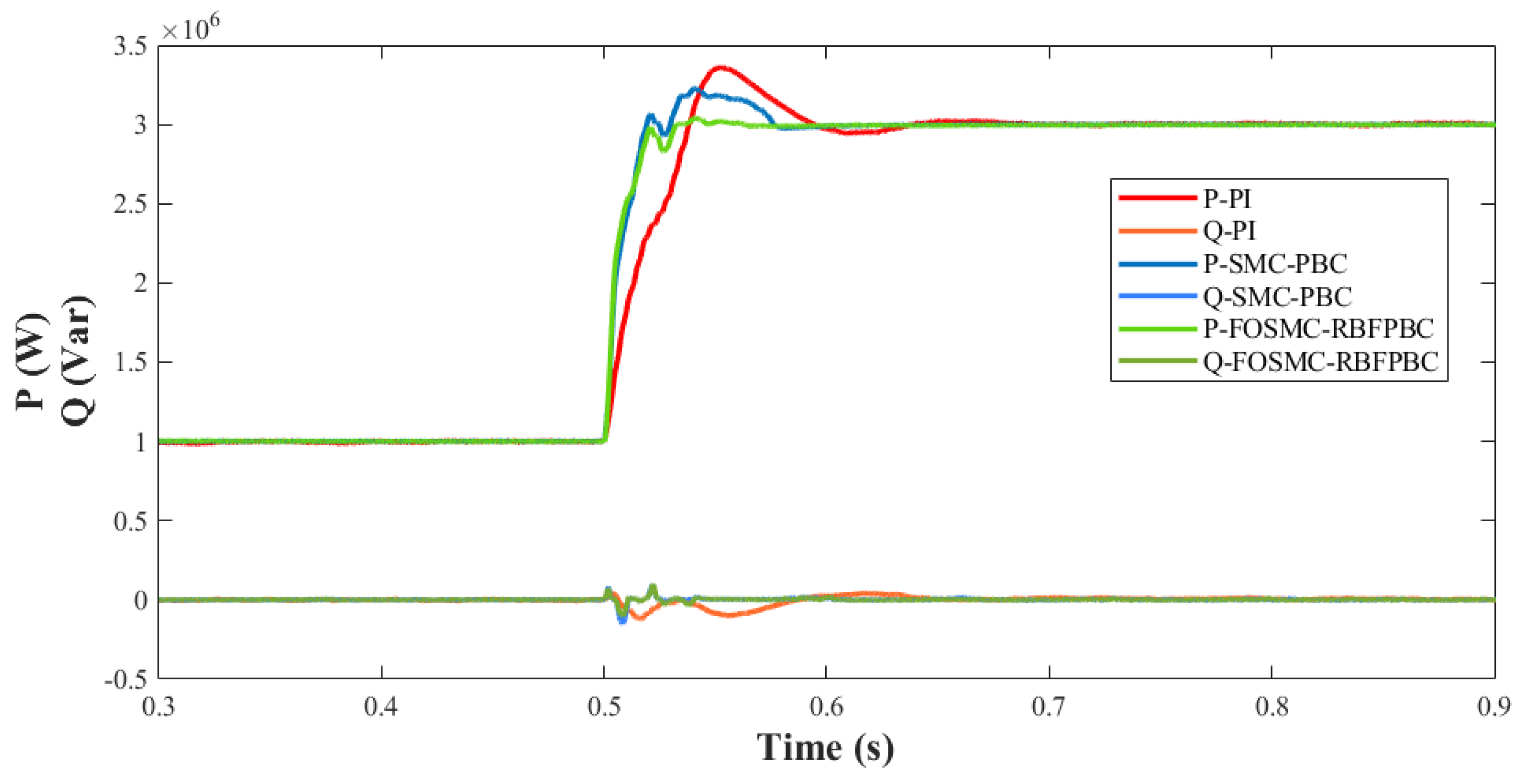
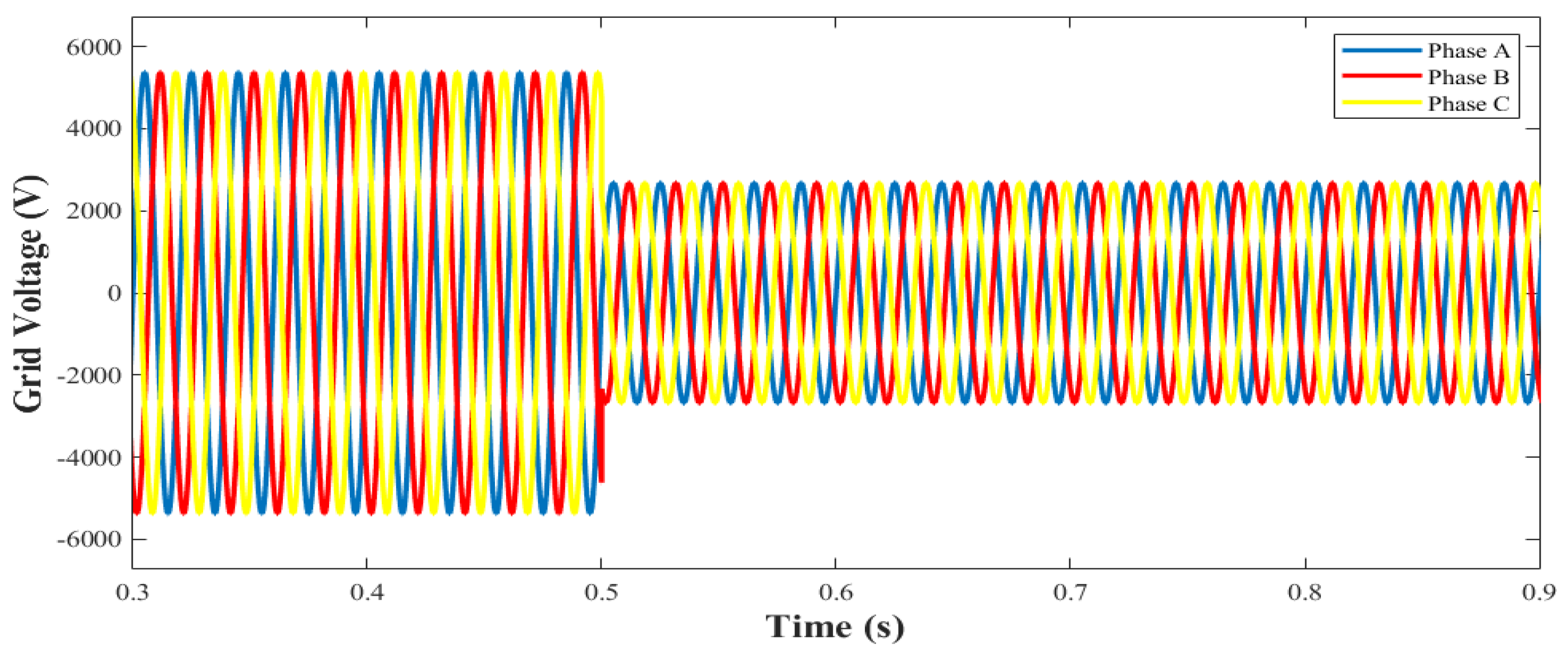
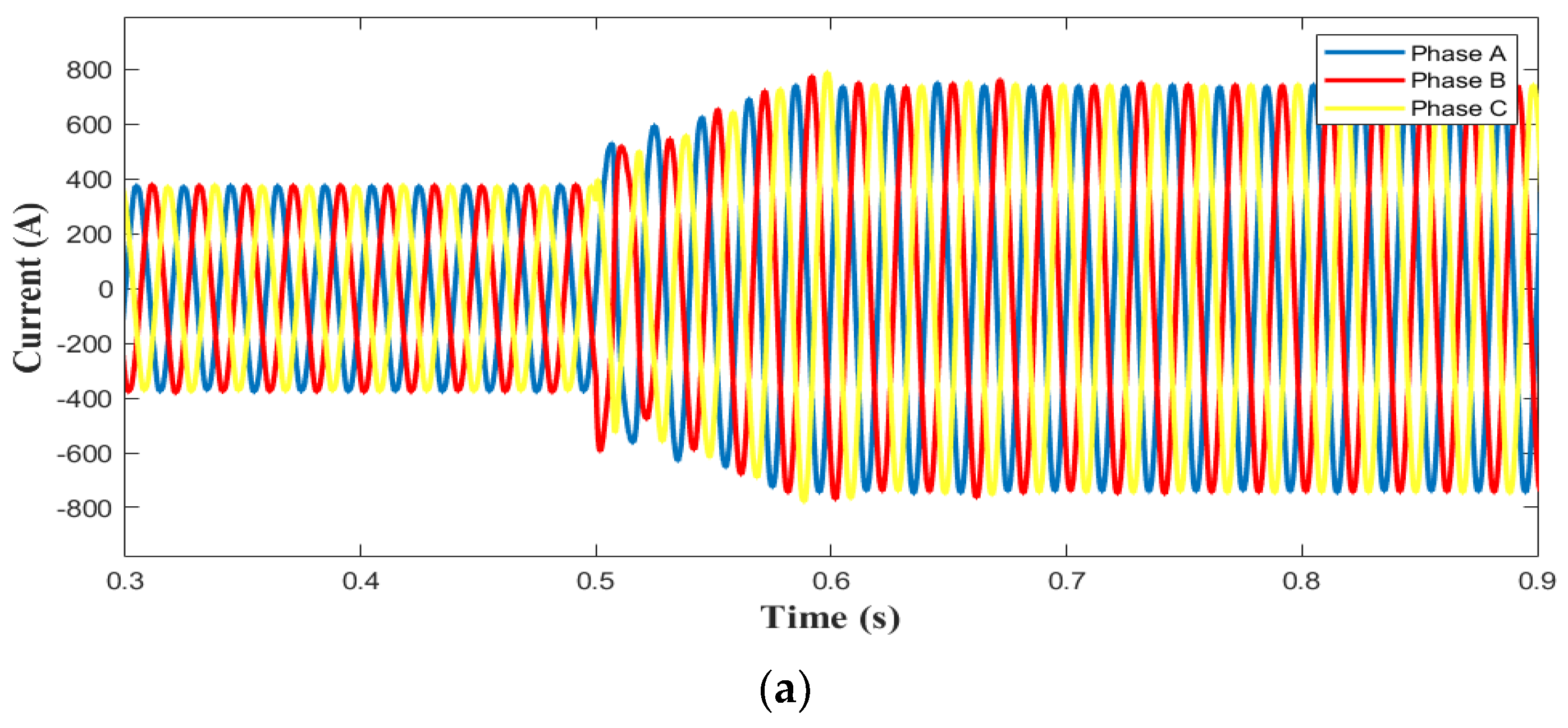
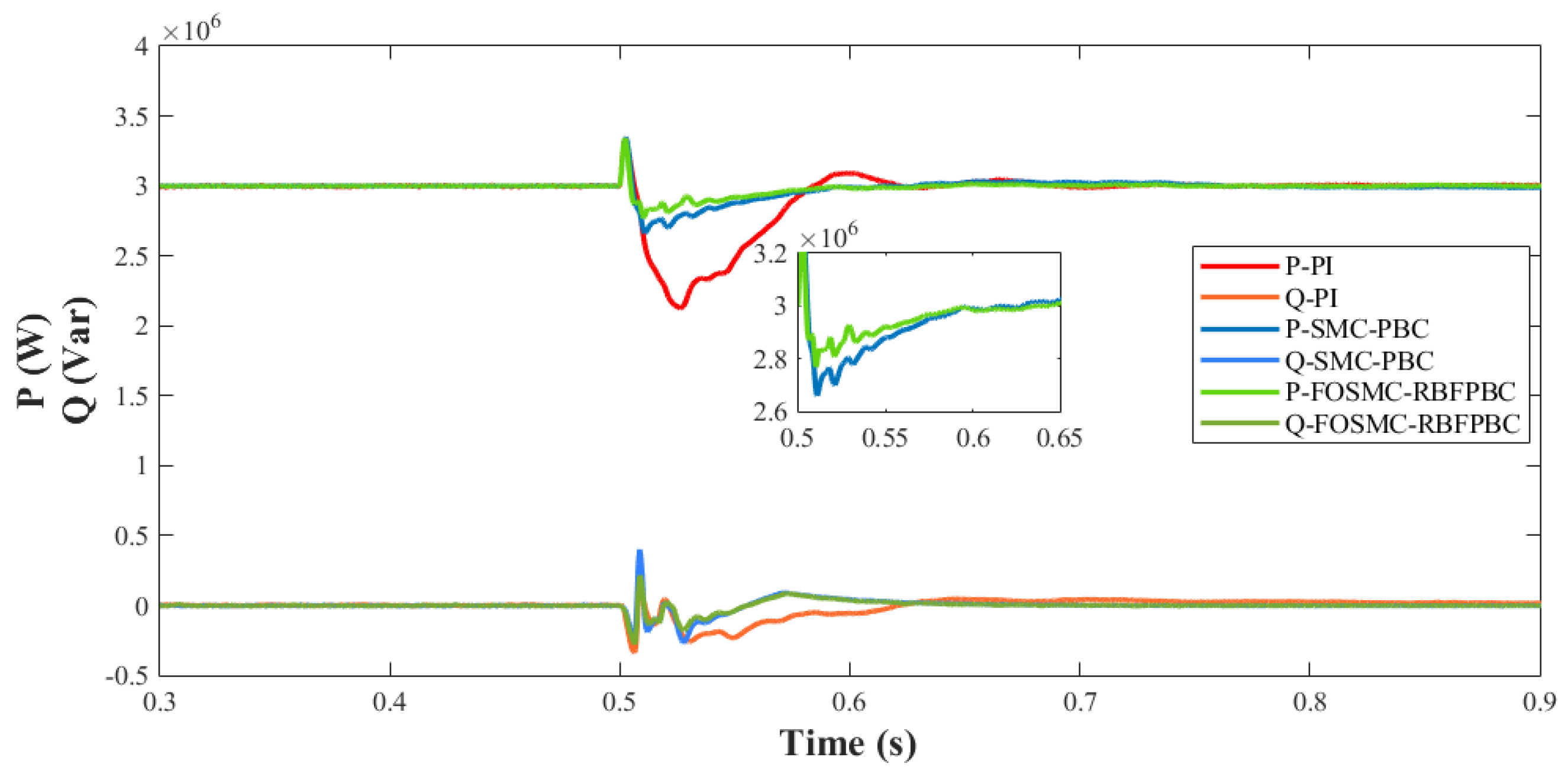
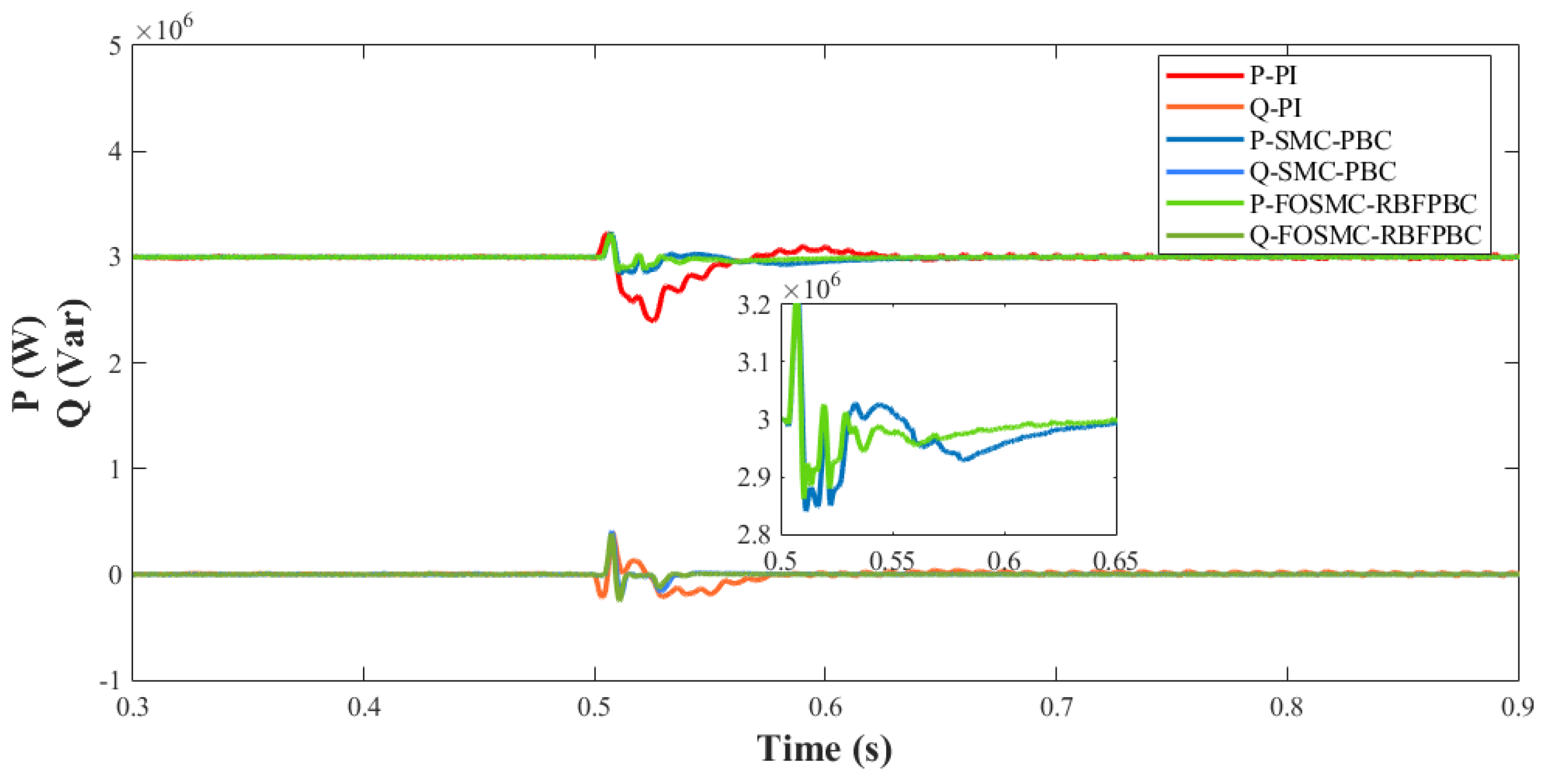
5.2. Grid-Side Disturbance

In the initial stage, the active power is set to 1 MW, and the reactive power is set to 0 MVar, with a increase of 2 MW of active load at 0.5 s suddenly.

Figure 6 shows the grid-side current waveforms, and Figure 6a–c use PI control, SMC-PBC control, and FOSMC-RBFPBC control, respectively. From Figure 6, it can be seen that the three control strategies can stabilize the system when coping with the sudden change in the load on the grid side, but it can be clearly seen that the PI control can cope with the lack of the ability to deal with the sudden change in the load, and its response speed is slow, and the regulation time is long; the SMC-PBC control, although it has been improved compared with the PI control, will make the current after smoothening the chattering due to the chattering problem that exists in the sliding mode, and FOSMC-RBFPBC control not only improves this chattering situation, but also has a smoother current, smaller overshoot, faster regulation time, and significantly better dynamic performance than the other two control strategies.

Figure 7 shows the output power waveform. From the figure, it can be seen that when the active load is put in at 0.5 s, it will lead to the fluctuation of the MMC output power as well. FOSMC-RBFPBC control has a clear advantage in dealing with the perturbation of the sudden change in the load, and it can reach the new stabilization point more quickly.

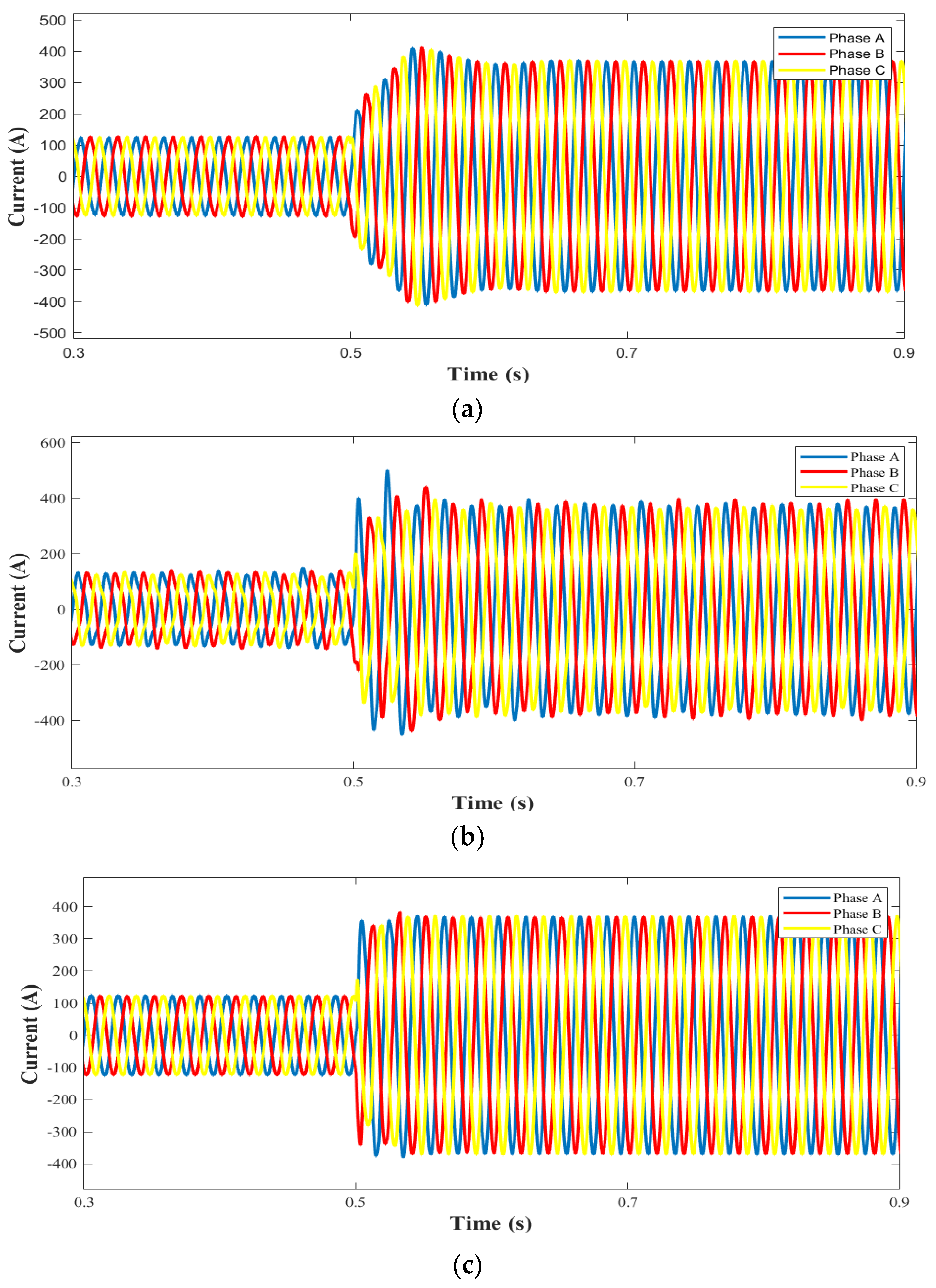
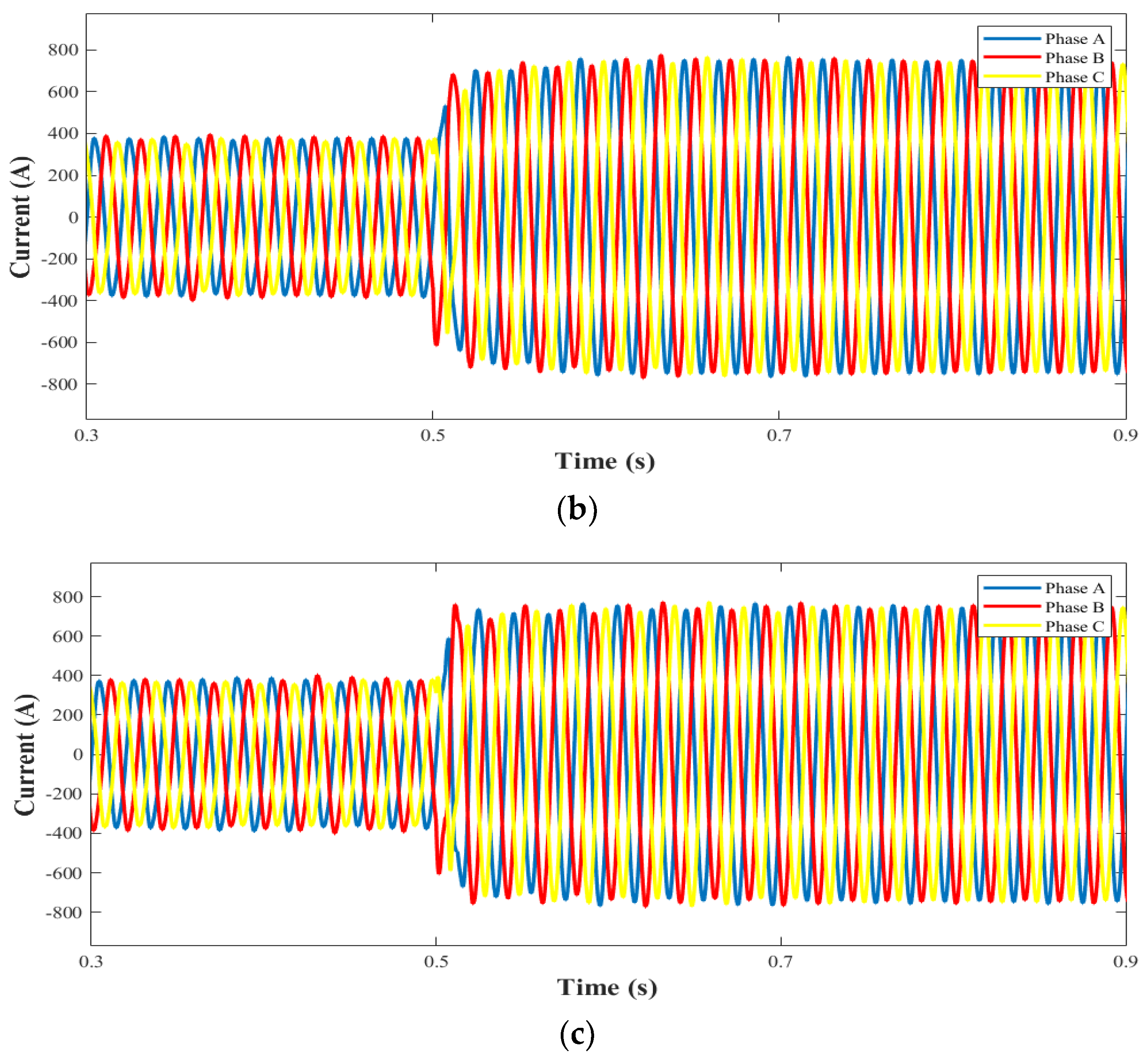
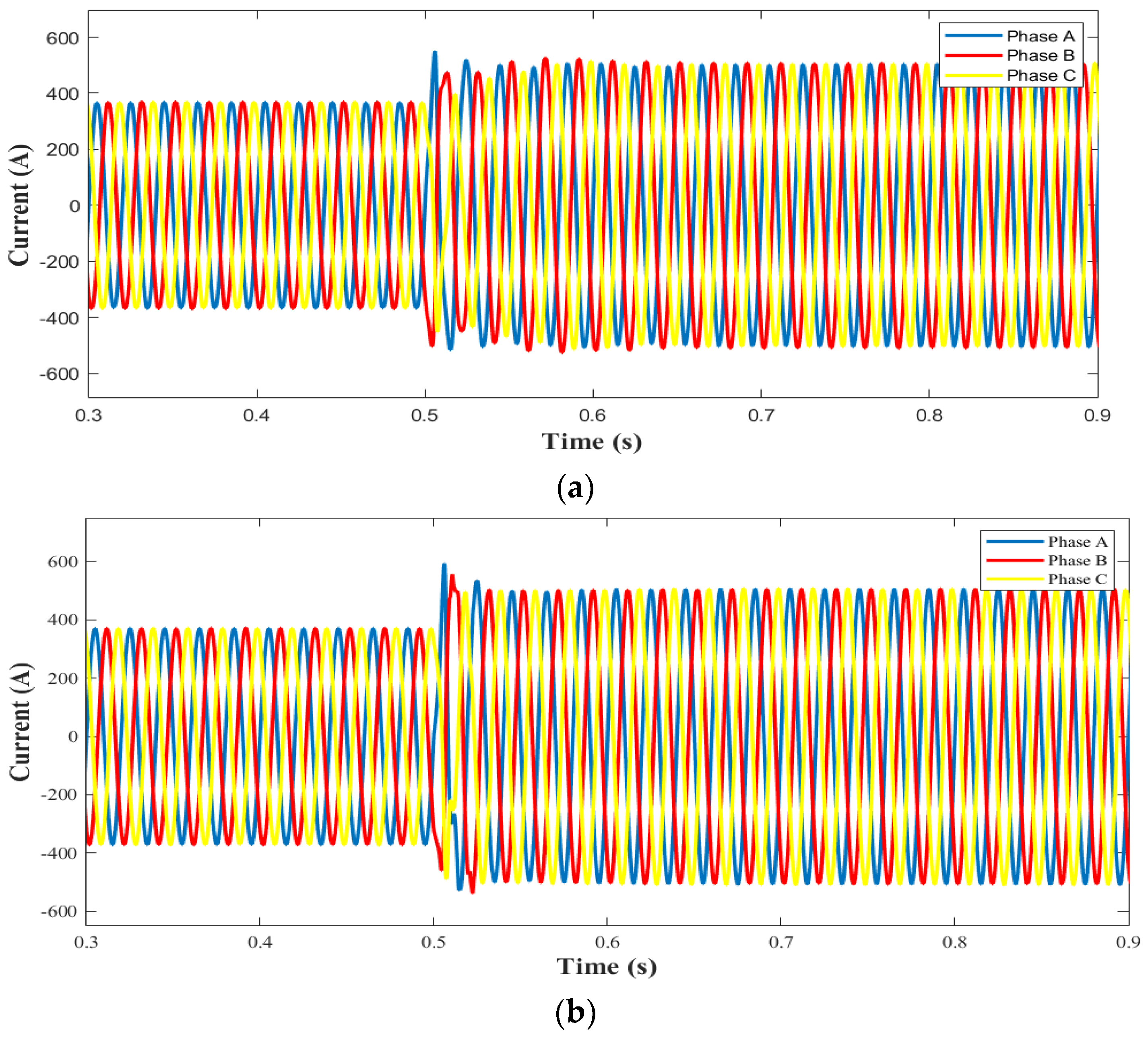
5.3. Three-Phase Symmetrical Failure

In the initial stage, the active power is set to 3 MW, the reactive power is set to 0 MVar, and a 0.5 p.u. three-phase symmetrical fault occurs at 1 s. The grid-side voltage waveform is shown in Figure 8.

Figure 9 shows the grid-side current waveforms. Due to the occurrence of a three-phase symmetry fault, the current increases rapidly, and after a period of time, balancing is restored. Under the FOSMC-RBFPBC control, the regulation time of the system is much shorter than that of the remaining two control strategies, and the quality of the current waveform is higher.

Figure 10 shows the output power waveforms, and it can be seen that the FOSMC-RBFPBC control not only has a faster regulation time but also has fewer power drops for dealing with the perturbation of the three-phase symmetry fault.

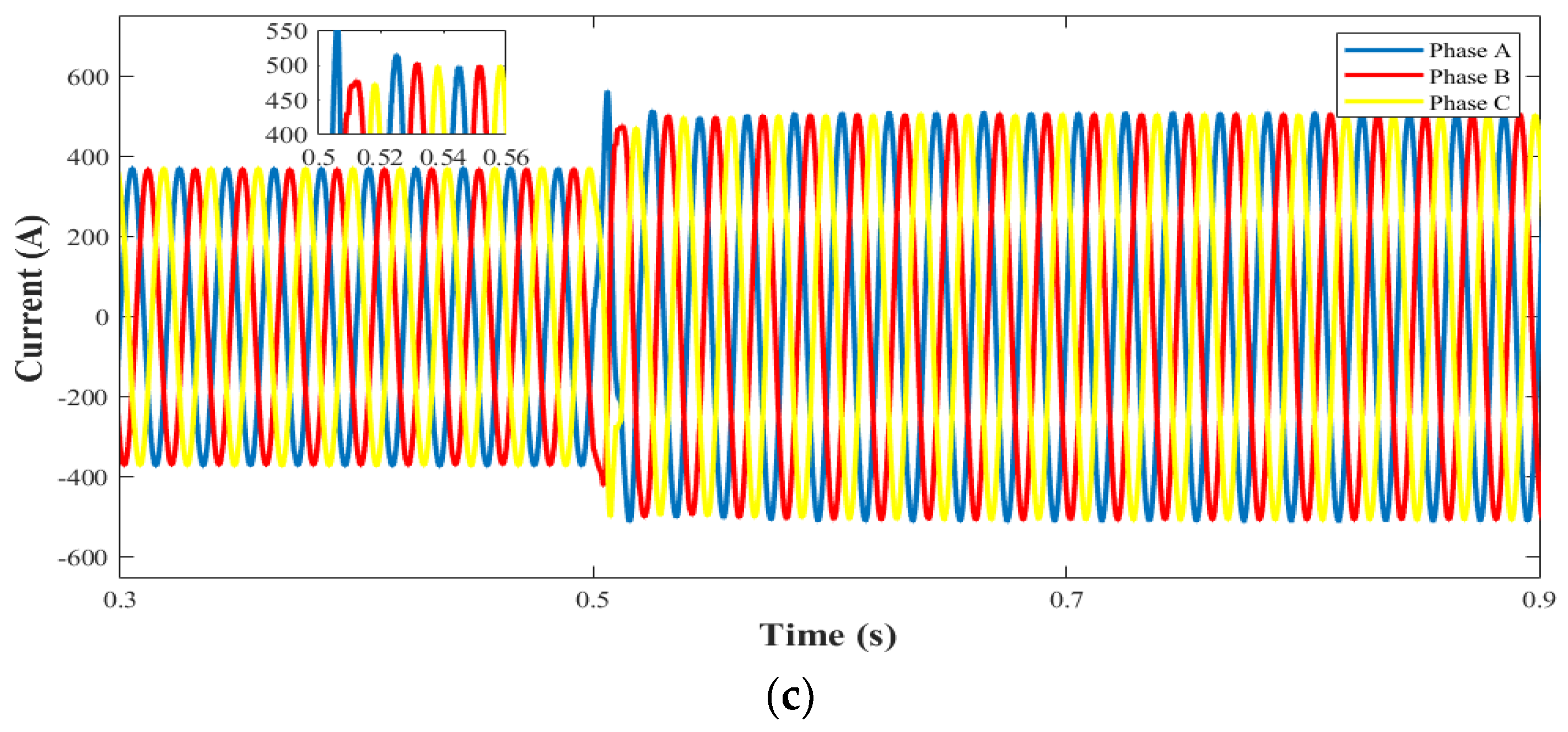
5.4. Asymmetrical Fault

In the initial stage, the active power is set to 3 MW, the reactive power is set to 0 MVar. and a 0.2 p.u. phase A asymmetrical fault occurs at 0.5 s. The network-side unbalanced voltage waveform is shown in Figure 11.

Figure 12 shows the waveforms of the grid-side current, and it can be seen that the overshooting of the net-side current is about the same for the three control methods, but the net-side current under the FOSMC-RBFPBC control takes only 25 ms to stabilize after a fault occurs, whereas the PI control takes 60 ms, and the SMC_PBC control takes 38 ms. So, the FOSMC-RBFPBC control has a much faster regulation time.

Figure 13 shows the output power waveform. As can be seen from the figure, the power under PI control has the largest drop and the longest regulation time; the FOSMC-RBFPBC control has the best effect, which is much better than PI control, and there is a slight improvement compared with the SMC-PBC control. Thus, the fractional-order sliding-mode passive control also has some advantages for dealing with the perturbation of unbalanced faults.

Table 3. FFT analysis of current of Phase A.

Current	FOSMC-RBFPBC	SMC-PBC	PI
FFT analysis	0.63%	0.95%	1.66%

shows the FFT analysis of the grid-side current during fault. From the table, it can be seen that the harmonic content of PI control is the highest; while the harmonic content under FOSMC-RBFPBC control is the lowest, which is 1.03% and 0.32% lower than that of PI control and SMC-PBC control, respectively. Thus, the FOSMC-RBFPBC control can have a good effect on harmonic suppression when unbalanced faults occur.

5.5. Analysis of Results

In this paper, we give the dynamic performance indicators (overshoot, setting time) of PI, SMC-PBC, and FOSMC-RBFPBC under three non-ideal states, as shown in

Table 4. Dynamic performance indicators.

Condition	Control Strategy	Overshoot/%	Setting Time/s
1	PI	12	0.25
	SMC-PBC	7.6	0.12
	FOSMC-RBFPBC	1.5	0.07
2	PI	29.08	0.14
	SMC-PBC	11.33	0.1
	FOSMC-RBFPBC	7.67	0.08
3	PI	20.13	0.18
	SMC-PBC	5.33	0.15
	FOSMC-RBFPBC	4.21	0.1

.

6. Conclusions

In this paper, a FOSMC-PBC control strategy is proposed for some challenges faced by the current MMC control technology in practice, and online self-tuning of the injected damping is performed using RBFNN. In this paper, by comparing and analyzing the PI control, SMC-PBC, and FOSMC-RBFPBC control under three kinds of non-ideal working conditions, and verifying them through simulation experiments, the following conclusions can be drawn:

(1)

Through the fractional-order theory and RBFNN injection damping adaptation, the passive control operation is freed from the shortcomings of being too dependent on the parameters, and the ability to resist perturbations is significantly improved. The system under FOSMC-RBFPBC control has better results in all three non-ideal operating conditions.

(2)

The FOSMC-RBFPBC control retains the original anti-disturbance performance of the sliding-mode control while having the passive characteristics of the system, and the introduction of the fractional-order sliding-mode surface improves the chattering phenomenon. The response speed, stability, overshooting, and robustness of the system are all improved significantly, and also, the FOSMC-RBFPBC control has a certain suppression effect on the harmonics.

(3)

In the future, RBFNN should be researched in greater depth, and more experiments should be conducted.