A Fault-Tolerant Control Strategy for Three-Level Grid-Connected NPC Inverters after Single-Arm Failure with Optimized SVPWM
Abstract
:1. Introduction
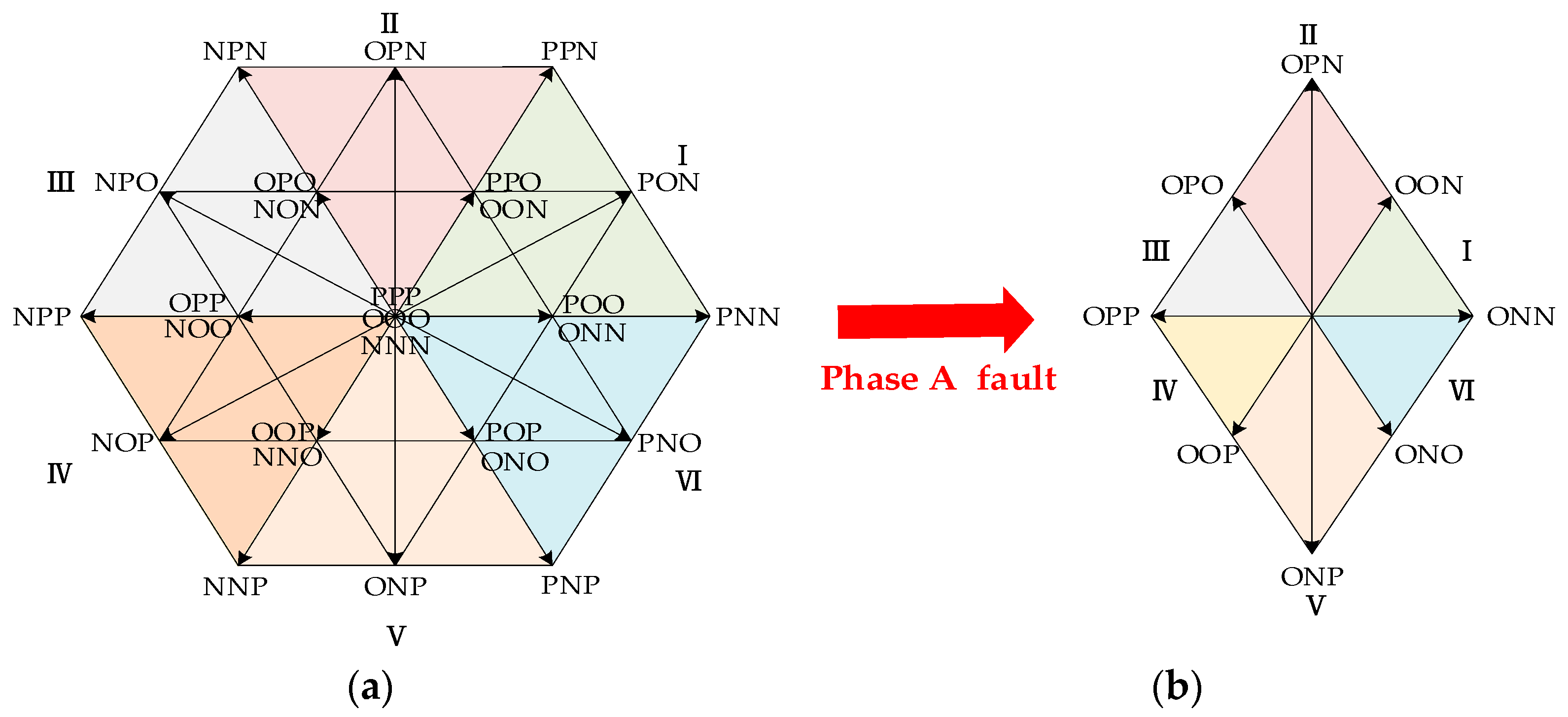
2. ESTPI Fault Topology and Mechanism of NPP Fluctuation
2.1. The Space Voltage Vector of ESTPI Topology
2.2. The NPP Fluctuant Mechanism of DC Bus
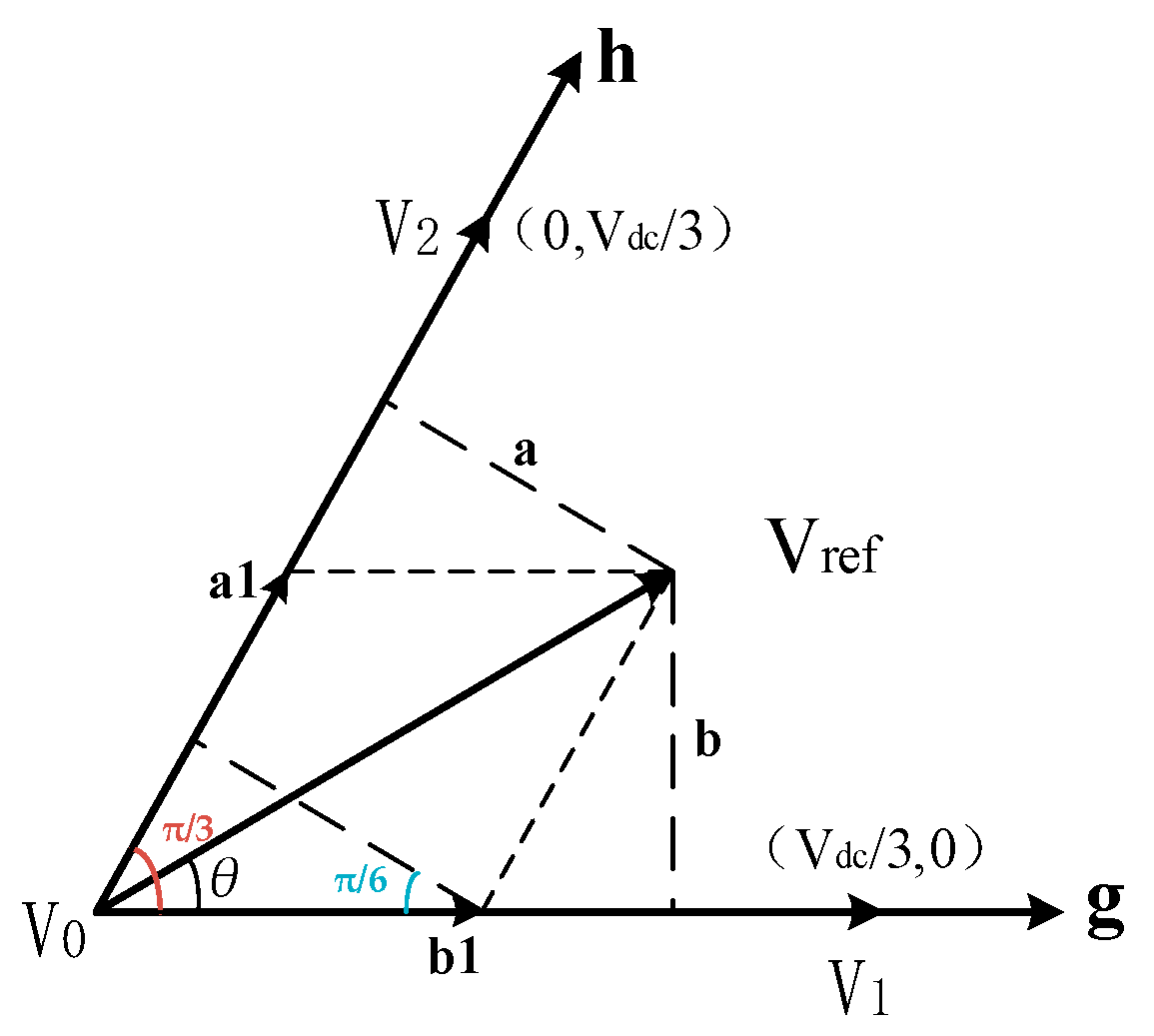
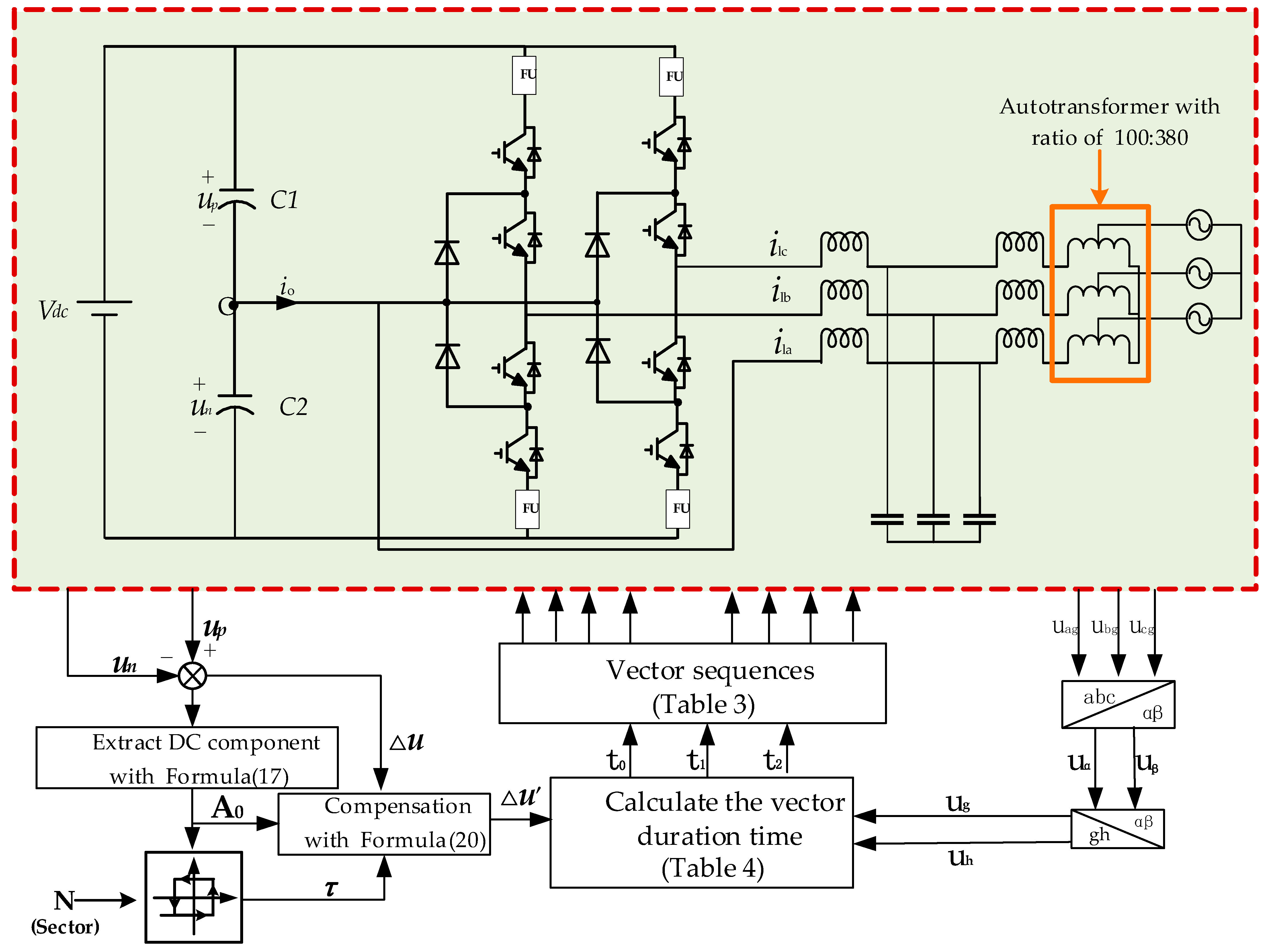
3. SVPWM Compensation and Optimization
3.1. SVPWM Compensation Strategy Considering NPP Fluctuation
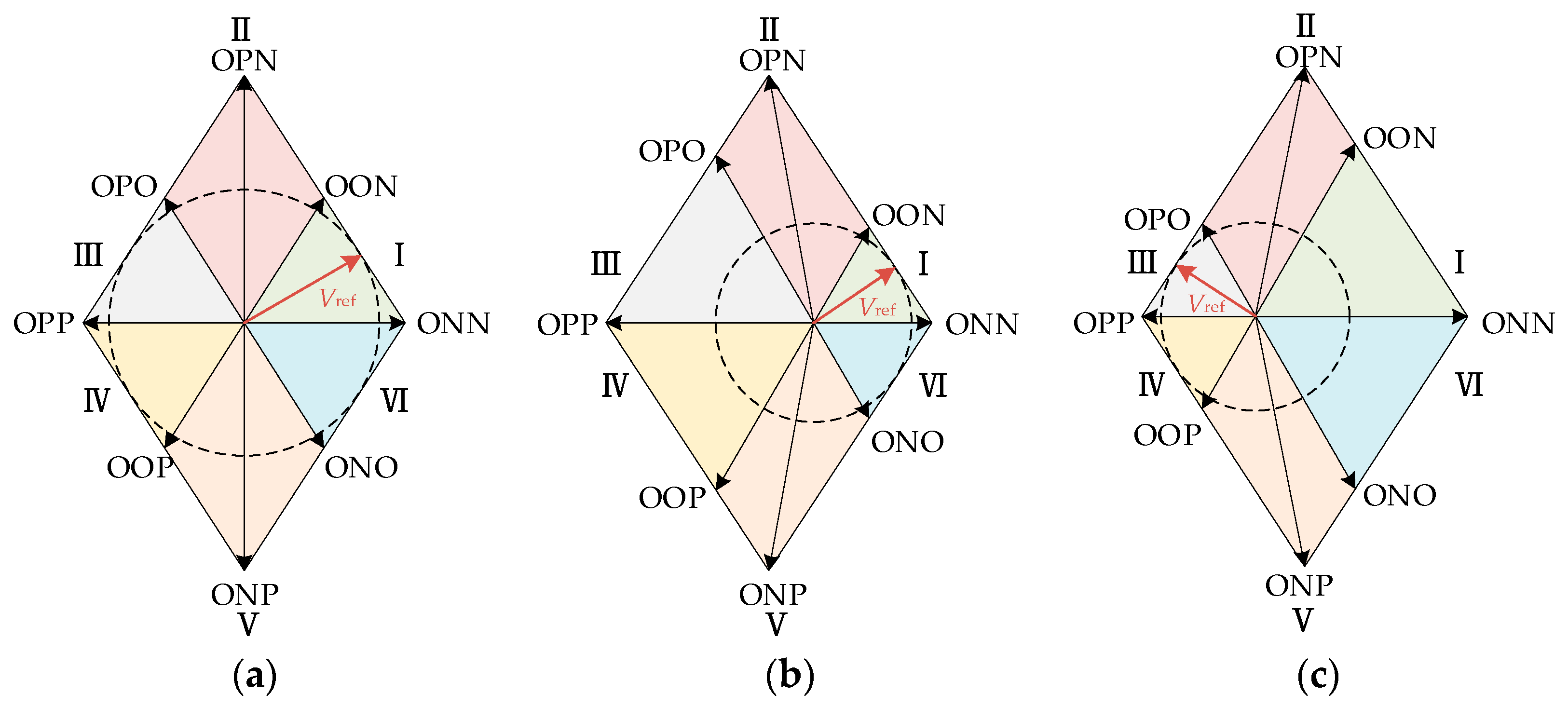
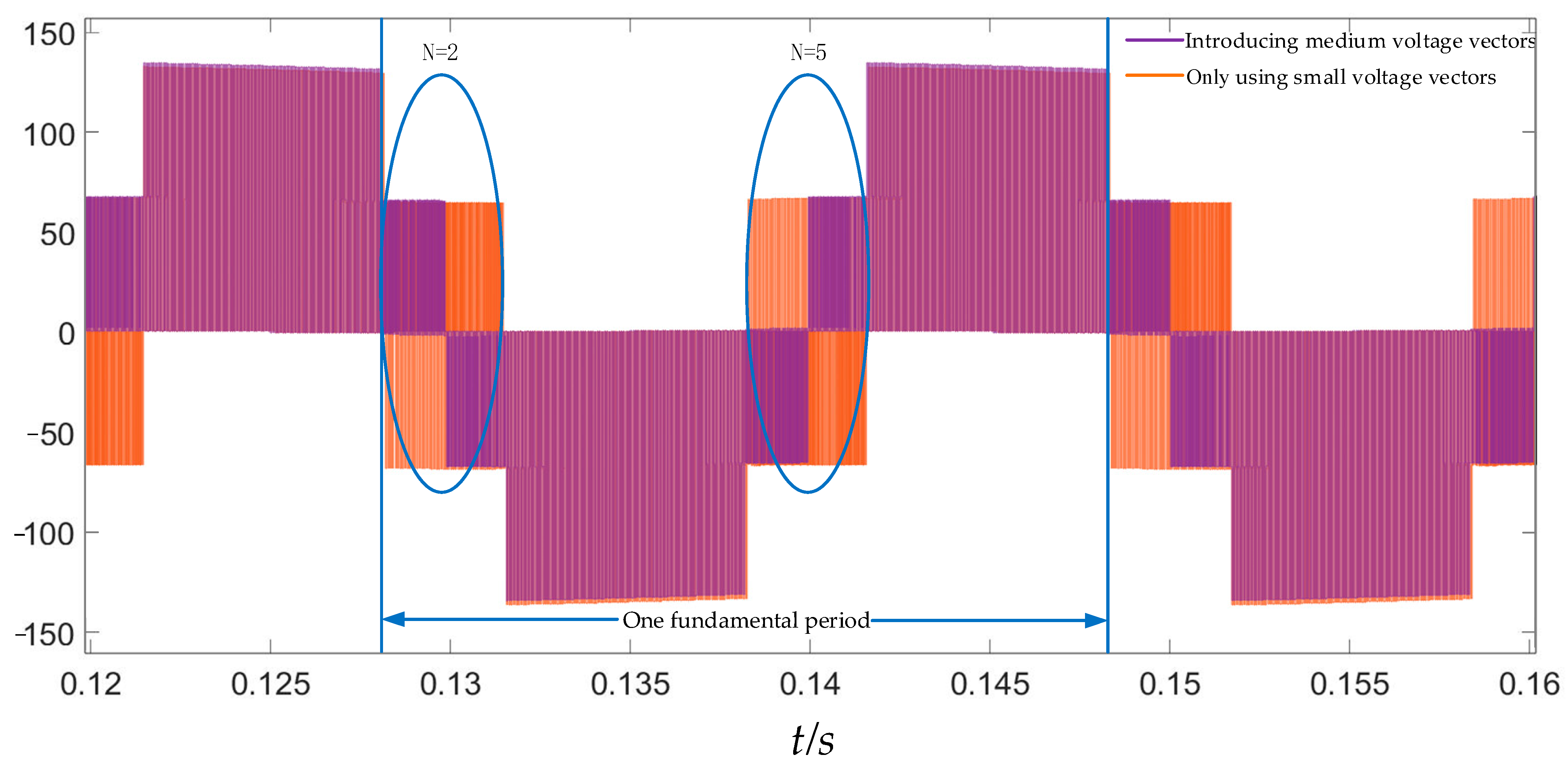
3.2. Optimization of SVPWM
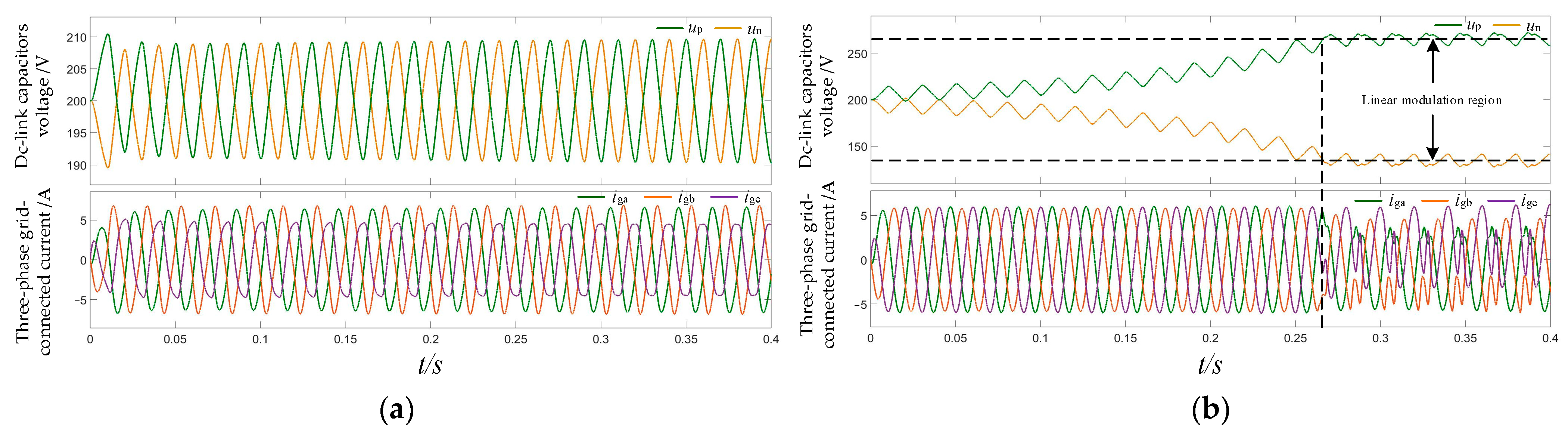
4. Simulation and Results Analysis
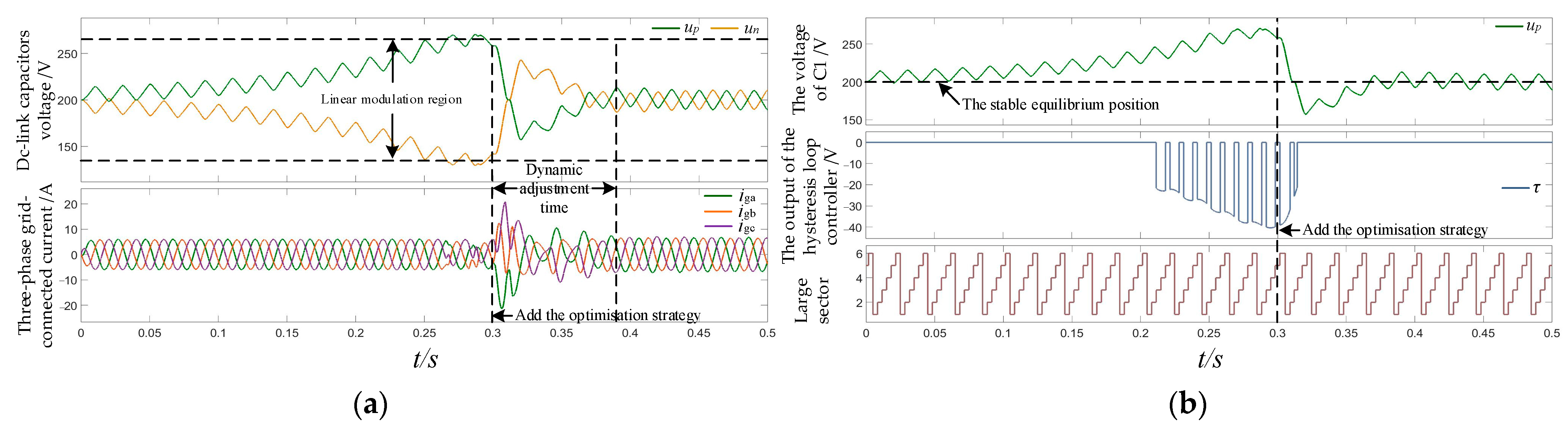
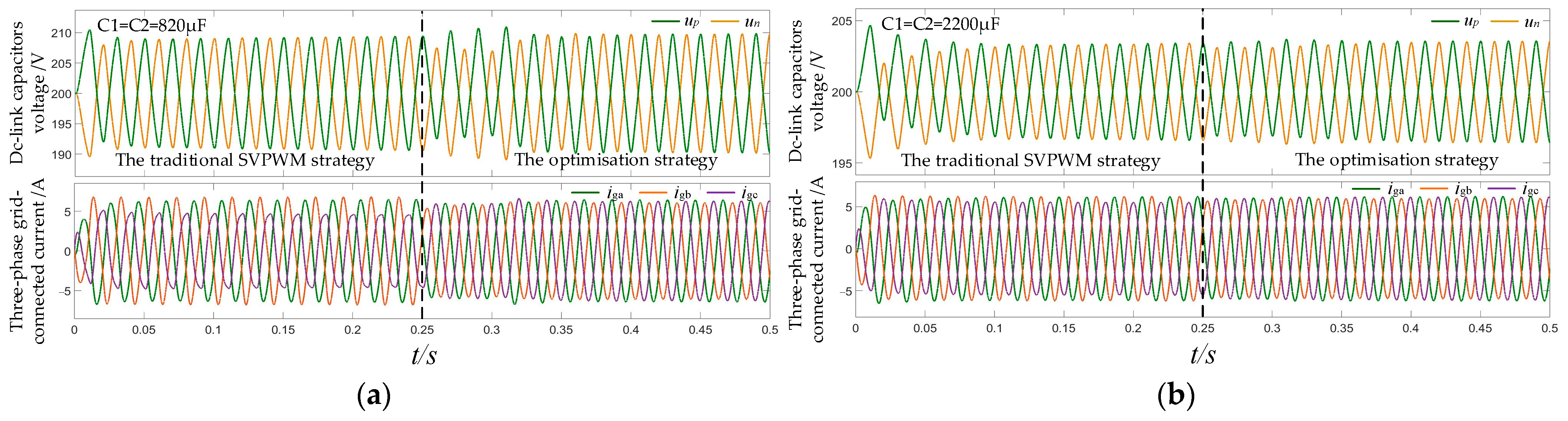
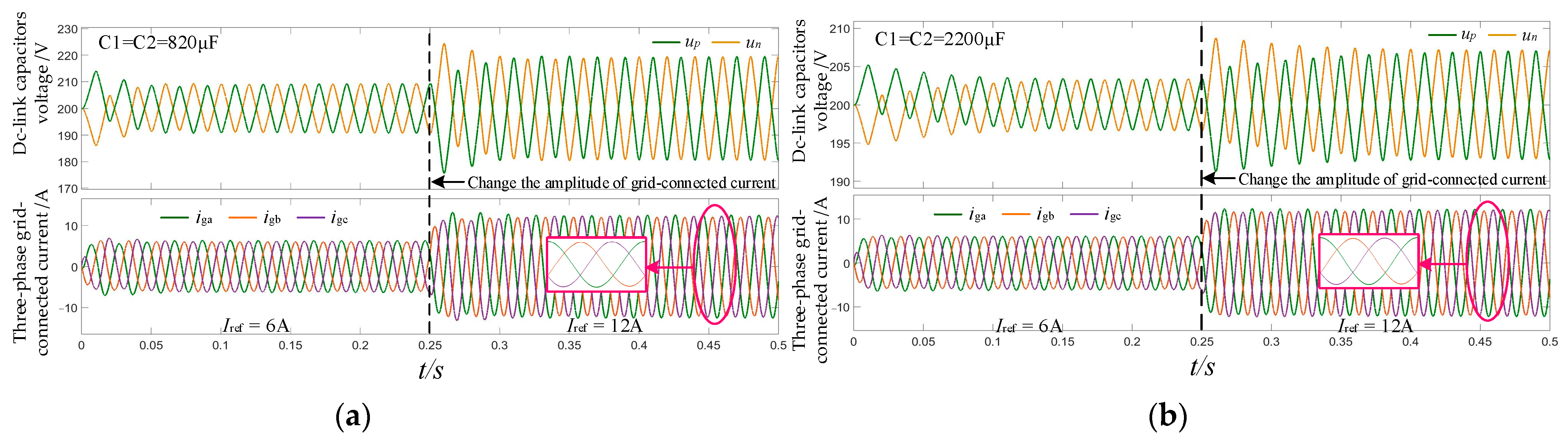
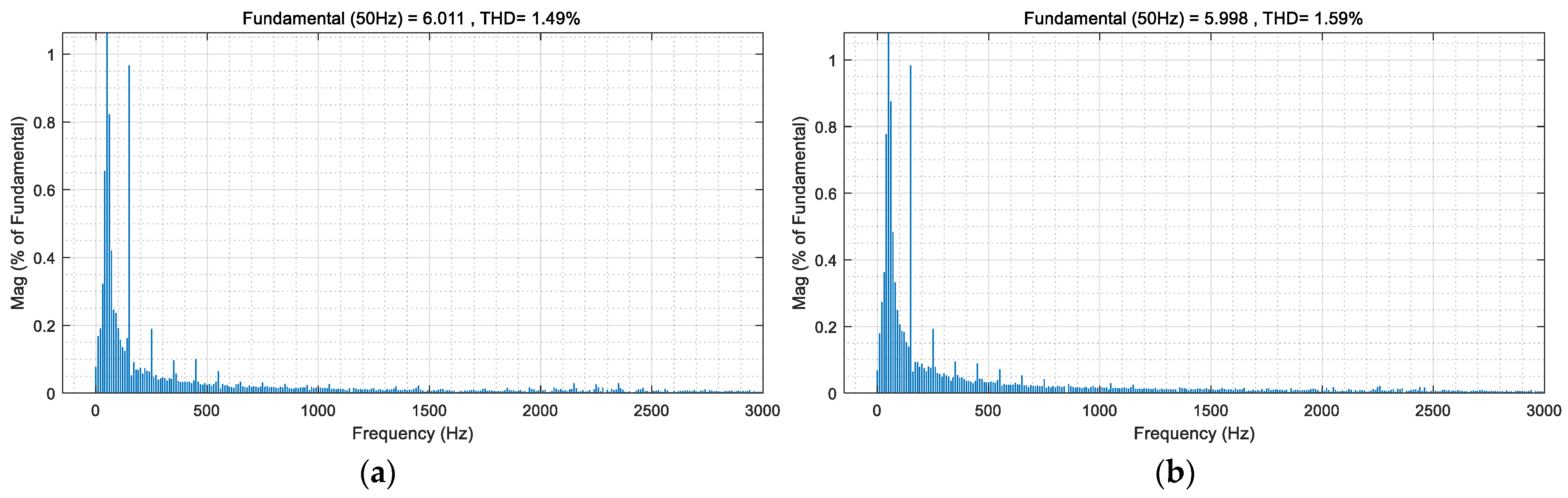
4.1. The Compensation Optimization Strategy Control Effect
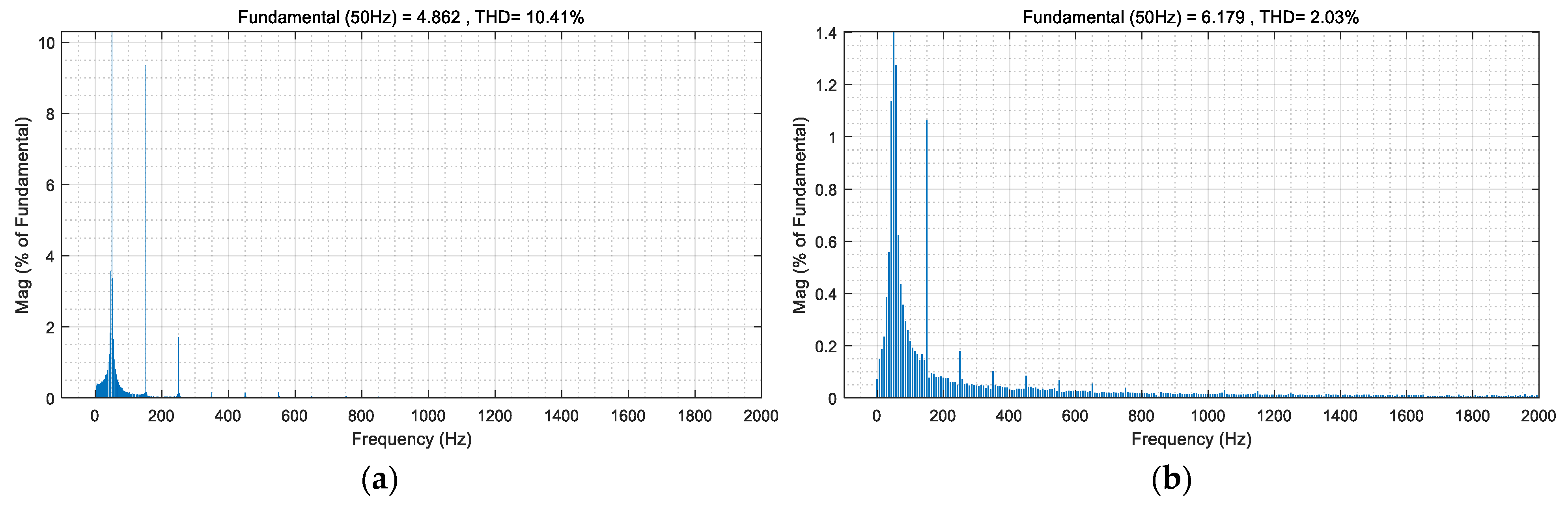
4.2. The Improvement of Common Mode Voltage
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Nabae, A.; Takahashi, I.; Akagi, H. A New Neutral-Point-Clamped PWM Inverter. IEEE Trans. Ind. Appl. 1981, IA-17, 518–523. [Google Scholar] [CrossRef]
- Rodriguez, J.; Bernet, S.; Steimer, P.K.; Lizama, I.E. A Survey on Neutral-Point-Clamped Inverters. IEEE Trans. Ind. Electron. 2010, 57, 2219–2230. [Google Scholar] [CrossRef]
- Choi, U.-M.; Lee, J.-S.; Blaabjerg, F.; Lee, K.-B. Open-Circuit Fault Diagnosis and Fault-Tolerant Control for a Grid-Connected NPC Inverter. IEEE Trans. Power Electron. 2015, 31, 7234–7247. [Google Scholar] [CrossRef]
- Chao, K.-H.; Ke, C.-H. Fault Diagnosis and Tolerant Control of Three-Level Neutral-Point Clamped Inverters in Motor Drives. Energies 2020, 13, 6302. [Google Scholar] [CrossRef]
- Yang, C.; Peng, T.; Yang, C.; Karimi, H.R.; Ding, X. Voltage Difference Residual-Based Open-Circuit Fault Diagnosis Approach for Three-Level Converters in Electric Traction Systems. IEEE Trans. Power Electron. 2020, 35, 3012–3028. [Google Scholar] [CrossRef]
- Fayyaz, M.M.; Syed, I.M.; Meng, Y.; Aman, M.N. Comprehensive Predictive Control Model for a Three-Phase Four-Legged Inverter. Energies 2023, 16, 2650. [Google Scholar] [CrossRef]
- Zhou, D.; Zhao, J.; Liu, Y. Finite-control-set model predictive control scheme of three-phase four-leg back-to-back converter-fed induction motor drive. IET Electr. Power Appl. 2017, 11, 761–767. [Google Scholar] [CrossRef]
- Zhang, W.; Xu, D. Fault Analysis and Fault-Tolerant Design for Parallel Redundant Inverter Systems in Case of IGBT Short-Circuit Failures. IEEE J. Emerg. Sel. Top. Power Electron. 2018, 6, 2031–2041. [Google Scholar] [CrossRef]
- Yu, Y.; Li, X.; Wei, L. Fault Tolerant Control of Five-Level Inverter Based on Redundancy Space Vector Optimization and Topology Reconfigruation. IEEE Access 2020, 8, 194342–194350. [Google Scholar] [CrossRef]
- Xu, S.Z.; Wang, C.J.; Wang, Y. An Improved Fault-Tolerant Control Strategy for High-Power ANPC Three-Level Inverter Under Short-Circuit Fault of Power Devices. IEEE Access 2019, 7, 55443–55457. [Google Scholar] [CrossRef]
- Azer, P.; Ouni, S.; Narimani, M. A Novel Fault-Tolerant Technique for Active-Neutral-Point-Clamped Inverter Using Carrier-Based PWM. IEEE Trans. Ind. Electron. 2020, 67, 1792–1803. [Google Scholar] [CrossRef]
- Liu, Y.C.; Ge, X.; Tang, Q. Relationship between Two Different Space-Vector Modulation Methods of Eight-Switch Three-Phase Inverters. In Proceedings of the 2016 IEEE 8th International Power Electronics and Motion Control Conference (IPEMC-ECCE Asia), Hefei, China, 22–26 May 2016; pp. 3206–3210. [Google Scholar] [CrossRef]
- Zhang, M.; Li, Z.; Guo, Y.; Zhang, X. Fault Tolerance and Overmodulation Algorithm for Three Level Neutral Point Clamped Inverters. In Proceedings of the 36th Chinese Control Conference (CCC), Dalian, China, 26–28 July 2017; pp. 7358–7363. [Google Scholar] [CrossRef]
- An, S.-W.; Kim, S.-M.; Lee, K.-B. Optimized Space-Vector Modulation to Reduce Neutral Point Current for Extending Capacitor Lifetime in Three-Level Inverters. IEEE Access 2020, 8, 97689–97697. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, W.; Li, C.; Wang, X.; Qin, H. Improved virtual SVPWM algorithm for CMV reduction and NPV oscillation elimination in Three-Level NPC inverter. Int. J. Electr. Power Energy Syst. 2023, 155, 109533. [Google Scholar] [CrossRef]
- Fan, B.; Fu, Z.; Fu, J.; Liu, L. Midpoint potential compensation balance control method based on virtual space vector pulse-width modulation for NPC three-level inverter. Int. Trans. Electr. Energy Syst. 2019, 29, e12044. [Google Scholar] [CrossRef]
- Xiang, C.; Zhang, X.; Ho-Ching, H.; Zhang, L.; Cheng, S. Duty VV-MPTC for Post-Fault Eight Switch Three-Phase Inverter Fed Induction Motor Drives with Reduced Neutral Point Voltage Fluctuation. IEEE Trans. Power Electron. 2021, 36, 11691–11700. [Google Scholar] [CrossRef]
- Yuan, Q.; Li, A.; Qian, J.; Xia, K. DC-link capacitor voltage control for the NPC three-level inverter with a newly MPC-based virtual vector modulation. IET Power Electron. 2020, 13, 1093–1102. [Google Scholar] [CrossRef]
- Lin, M.; Li, Y.; Li, N.; Wu, C.; Gao, J.-B. FCS-MPC Control Strategy for a New Fault Tolerant Three-Level Inverter. Automatika 2016, 57, 589–598. [Google Scholar] [CrossRef]
- Tang, Q.; Ge, X.; Liu, Y.-C. Performance Analysis of Two Different SVM-Based Field-Oriented Control Schemes for Eight-Switch Three-Phase Inverter-Fed Induction Motor Drives. In Proceedings of the 2016 IEEE 8th International Power Electronics and Motion Control Conference (IPEMC-ECCE Asia), Hefei, China, 22–26 May 2016; pp. 3374–3378. [Google Scholar] [CrossRef]
- Liu, Y.C.; Ge, X.; Tang, Q.; Gou, B. Two modified SVPWM algorithms for common-mode voltage reduction in eight-switch three-phase inverters. IET Power Electron. 2017, 53, 636–693. [Google Scholar] [CrossRef]
- Deng, Q.; Ge, X.; Lin, C.; Xie, D.; Gou, B.; Feng, X. An Optimized SVPWM Strategy for the Postfault Three-Level NPC Voltage Source Inverters. IEEE Trans. Ind. Appl. 2021, 57, 6182–6194. [Google Scholar] [CrossRef]


| Voltage Vector Type | Voltage Vector | Common-Mode Voltage |
|---|---|---|
| Zero voltage vector | OOO | 0 |
| Small voltage vectors | OPP | Vdc/3 |
| ONN | −Vdc/3 | |
| OPO, OOP | Vdc/6 | |
| OON, ONO | −Vdc/6 | |
| Medium voltage vectors | OPN, ONP | 0 |
| N | n | t1 (s) | Vector V1 | io1 (A) | t2 (s) | Vector V2 | io2 (A) |
|---|---|---|---|---|---|---|---|
| I | / | 2mTssin(π/3 − θ) | ONN | ila | 2mTssin(θ) | OON | −ilc |
| II | 1 | OON | −ilc | −2mTssin(π/3 − θ) | OPN | ila | |
| II | 2 | OPO | −ilb | 2mTssin(π/3 + θ) | OPN | ila | |
| III | / | 2mTssin(θ) | OPO | −ilb | −2mTssin(π/3 + θ) | OPP | ila |
| IV | / | −2mTssin(π/3 − θ) | OPP | ila | −2mTssin(θ) | OOP | −ilc |
| V | 1 | OOP | −ilc | 2mTssin(π/3 − θ) | ONP | ila | |
| V | 2 | ONO | −ilb | −2mTssin(π/3 + θ) | ONP | ila | |
| VI | / | −2mTssin(θ) | ONO | −ilb | 2mTssin(π/3 + θ) | ONN | ila |
| N | N | Vector Sequences | |
|---|---|---|---|
| Ⅰ | / | OOO-OON-ONN-OON-OOO | V0-V2-V1-V2-V0 |
| Ⅱ | 1 | OOO-OON-OPN-OON-OOO | V0-V1-V2-V1-V0 |
| Ⅱ | 2 | OOO-OPO-OPN-OPO-OOO | V0-V1-V2-V1-V0 |
| Ⅲ | / | OOO-OPO-OPP-OPO-OOO | V0-V1-V2-V1-V0 |
| Ⅳ | / | OOO-OOP-OPP-OOP-OOO | V0-V2-V1-V2-V0 |
| Ⅴ | 1 | OOO-OOP-ONP-OOP-OOO | V0-V1-V2-V1-V0 |
| Ⅴ | 2 | OOO-ONO-ONP-ONO-OOO | V0-V1-V2-V1-V0 |
| Ⅵ | / | OOO-ONO-ONN-ONO-OOO | V0-V1-V2-V1-V0 |
| Voltage Vector | Coordinate | Voltage Vector | Coordinate |
|---|---|---|---|
| VONN | VOPP | ||
| VOON | VOOP | ||
| VOPN | VONP | ||
| VOPO | VONO |
| N | n | t1 (s) | Vector V1 | io1 (A) | t2 (s) | Vector V2 | io2 (A) |
|---|---|---|---|---|---|---|---|
| Ⅰ | / | 2mTssin(π/3 − θ)/(1 − 2Δu/Vdc) | ONN | ila | 2mTssin(θ)/(1 − 2Δu/Vdc) | OON | −ilc |
| Ⅱ | 1 | 2mTssin(π/3 + θ)/(1 − 2Δu/Vdc) + 2mTssin(π/3 − θ)/(1 + 2Δu/Vdc) | OON | −ilc | −2mTssin(π/3 − θ)/(1 + 2Δu/Vdc) | OPN | ila |
| Ⅱ | 2 | −2mTssin(π/3 − θ)/(1 + 2Δu/Vdc) − 2mTssin(π/3 + θ)/(1 − 2Δu/Vdc) | OPO | −ilb | 2mTssin(π/3 + θ)/(1 − 2Δu/Vdc) | OPN | ila |
| Ⅲ | / | 2mTssin(θ)/(1 + 2Δu/Vdc) | OPO | −ilb | −2mTssin(π/3 + θ)/(1 + 2Δu/Vdc) | OPP | ila |
| Ⅳ | / | −2mTssin(π/3 − θ)/(1 + 2Δu/Vdc) | OPP | ila | −2mTssin(θ)/(1 − 2Δu/Vdc) | OOP | −ilc |
| Ⅴ | 1 | −2mTssin(π/3 + θ)/(1 + 2Δu/Vdc) − 2mTssin(π/3 − θ)/(1 − 2Δu/Vdc) | OOP | −ilc | 2mTssin(π/3-θ)/(1 − 2Δu/Vdc) | ONP | ila |
| Ⅴ | 2 | 2mTssin(π/3 − θ)/(1 − 2Δu/Vdc) + 2mTssin(π/3 + θ)/(1 + 2Δu/Vdc) | ONO | −ilb | −2mTssin(π/3 + θ)/(1 + 2Δu/Vdc) | ONP | ila |
| Ⅵ | / | −2mTssin(θ)/(1 − 2Δu/Vdc) | ONO | −ilb | 2mTssin(π/3 + θ)/(1 − 2Δu/Vdc) | ONN | ila |
| DC bus voltage (Vdc) | 400 V |
| Grid voltage (Ua,b,c) | 380 V |
| DC-link capacitance (C1, C2) | 820/2200 μF |
| Bridge arm side filter inductance (LC) | 2.4 mH |
| The capacitance of filter (C) | 10 μF |
| Grid-side filter inductance (Lg) | 0.6 mH |
| Frequency of sampling (f) | 15 kHz |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, J.; Bai, F.; Yang, Q.; Ren, S. A Fault-Tolerant Control Strategy for Three-Level Grid-Connected NPC Inverters after Single-Arm Failure with Optimized SVPWM. Energies 2023, 16, 7863. https://doi.org/10.3390/en16237863
Huang J, Bai F, Yang Q, Ren S. A Fault-Tolerant Control Strategy for Three-Level Grid-Connected NPC Inverters after Single-Arm Failure with Optimized SVPWM. Energies. 2023; 16(23):7863. https://doi.org/10.3390/en16237863
Chicago/Turabian StyleHuang, Jingtao, Feng Bai, Qing Yang, and Shiyi Ren. 2023. "A Fault-Tolerant Control Strategy for Three-Level Grid-Connected NPC Inverters after Single-Arm Failure with Optimized SVPWM" Energies 16, no. 23: 7863. https://doi.org/10.3390/en16237863
APA StyleHuang, J., Bai, F., Yang, Q., & Ren, S. (2023). A Fault-Tolerant Control Strategy for Three-Level Grid-Connected NPC Inverters after Single-Arm Failure with Optimized SVPWM. Energies, 16(23), 7863. https://doi.org/10.3390/en16237863






