1. Introduction
Transformers are among the most important components of transmission and distribution systems, and they are the key equipment used for power transmission. When an inter-turn short-circuit fault occurs inside a transformer, the arc releases energy, causing the temperature of the surrounding insulating oil to rise instantaneously such that it vaporizes, rapidly increasing the pressure inside the tank [
1]. Once the pressure exceeds the limit that can be borne by the tank structure, it cracks, and the combustible gas inside the tank comes into contact with oxygen. This can lead to ignition and an explosion that can damage the equipment, cause a fire at the substation, and lead to regional power failure. Serious accidents of this kind can cause casualties, significant economic loss, and power failure [
2]. Currently used electrical relay protection for large power transformers mainly includes current-break protection and zero-sequence current protection. However, although the internal fault current in case of inter-turn short-circuit faults is large, the reflected line current is not [
3]. Therefore, there is a “blind spot” in the protection provided for the transformer in case of inter-turn and inter-layer short-circuit faults. The development of non-electrical relay protection technology plays a critical role in fault protection in cases of inter-turn and inter-layer short-circuiting [
4]. The strong, local electric field formed by the short-circuiting of the winding and the layers of the transformer as well as the deterioration of the insulation oil often induce the breakdown of the insulation. This can lead to high-energy arc failure, and the arc discharge causes the insulation structure to generate a violent physical and chemical reaction. The high gas yield obtained by the high arc temperature causes the dissolved gas to escape in the form of bubbles and rapidly expand and accumulate in the transformer. The pressure-release valve cannot be used in this case to release the high pressure inside the transformer, which is at risk of an explosion that can cause a fire [
5,
6,
7,
8]. The expansion of bubbles caused by arc discharge and the rise in pressure caused by the accumulation of gas are the direct causes of the explosion of the transformer tank. A strong electric field arises before arc discharge, and the temperature and pressure inside the transformer continue to increase during arc development until an explosion occurs. The process of evolution of arc discharge in the transformer before it explodes involves the coupling of a strong electromagnetic field, a high-temperature field, and a strong stress field.
A considerable amount of research has been devoted to solving the above-mentioned problems. In the context of the mechanism of evolution of discharge in transformer oil, the IEEE’s Transformer Explosion and Prevention Group found that the arc voltage can be estimated based on the length of the discharge arc. The risk of explosion of the fuel tank of the transformer can then be evaluated based on the arc energy [
9]. However, the arc is only the initial stage as a source of energy generation, and there are still multiple processes to go through in the final evaluation of the risk of fuel tank explosion. Additionally, the accuracy of this assessment method is relatively poor. Researchers have also used optical images of the development of flow under AC voltages of different amplitudes to investigate the mechanisms of spatiotemporal evolution of the flow [
10]. The common morphology of stream discharge has been described, and such characteristic parameters as the stopping length of discharge and its cross-sectional have been compared and analyzed by studying the dynamic characteristics of the pre-breakdown discharge of the insulation oil under an impulse voltage [
11]. In the context of the production of arc gas in the insulation oil and the stress acting on the tank, researchers have investigated the mixed combustible gas generated by the action of arc discharge on the insulation oil under different conditions. They have characterized the risk of detonation owing to the mixed gas by calculating the limit of explosion [
12]. The above references focus on the study of the morphological characteristics and physical mechanisms of flow discharge, partial discharge, and arc development in oil, as well as the analysis of the characteristics of arc gas production. There is a lack of research on the law of pressure development, and no analysis of tank bursting.
A simple empirical equation has been formulated to express the rise in pressure in the transformer tank due to the arc failure of the transformer [
13]. Moreover, the dependence of the volume of bubbles, which influences the rise in pressure, on the arc energy has been examined to determine the volume of bubbles generated per unit energy [
14]. The references focus on the analysis of the composition of the gas generated after the combustion of transformer oil, as well as the study of stress on the tank, lacking an analysis of the process from pressure wave generation to transmission.
The performance of transformer tanks of varying shapes has also been assessed under the action of fault-induced pressure in the case of arc discharge [
15], but without considering the compressibility and viscosity of the insulation oil. This was combined with test data and an empirical formula to calculate the conditions of an increase in the voltage of transformer tanks of different sizes under different arc faults [
16,
17]. Additionally, the intensity of the measured pressure waves is the most critical characteristic [
18,
19,
20,
21,
22]. Although the above references have analyzed and calculated the energy of arc faults and the final force, they lack the connection between macroscopic fault characteristics such as inter-turn short circuits and inter-layer short circuits in the internal winding of transformers and microscopic arc discharge laws, and they also lack an analysis of the propagation mechanism of pressure waves inside.
The above shows that research in this area has explored the characteristics of abnormal discharge in transformer oil, including its form, the generation of degraded gas, and its spatiotemporal evolution. Researchers have derived the internal changes in pressure caused by arc discharge-induced fault in the fuel tank, and they have used it to examine the temperature, vibrations, and deformation of the tank and related characteristics.
In summary, prevalent research in this area has placed a greater emphasis on the physical mechanisms of the streamer and the partial discharge of the transformer oil. Although arc discharge is the main cause of transformer tank explosions, the currently available results do not organically link the action of the arc with the development of pressure in the tank. The law of pressure transfer in the transformer tank due to the presence of a large number of bubbles following arc discharge thus remains unclear.
This paper takes the temperature and stress fields of the arc discharge caused by short-circuiting of the turns of the winding in the transformer oil as the object of research. We theoretically analyze and deduce the characteristics of gas production caused by the short-circuiting of the turns based on the topology of the circuit, the AC system, and the properties of the insulation oil to establish a quantitative relationship between the short-circuiting of turns of the winding and the law of arc discharge at the macroscopic level. Moreover, we analyze and optimize the generation and action of the source of pressure on the wall of the tank and its internal components at the systemic level. We establish a model of the transfer of pressure in the transformer and use a finite element software to simulate the pressure and temperature fields in the tank under the action of the electric arc to verify the theoretical results. We seek to explain the law of generation of pressure by the gas in the tank as well as its transmission under an arc fault and propose an explosion-proof transformer tank to ensure the operational safety of the HVDC (high-voltage direct current) transmission system.
This paper is structured as follows:
Section 2 mainly discusses the arc discharge characteristics and gas generation mechanism in transformer insulation oil. In
Section 2.1, the calculation process of arc energy generated under a transformer inter-turn short circuit fault is derived, taking into account the arc energy and its influencing factors. Due to the influence of gas production on the initial pressure value, the relationship between the arc energy and gas production characteristics is analyzed in
Section 2.2, and the process of temperature and pressure transmission in oil inside the box under the action of arc is analyzed in
Section 2.3.
Section 3 mainly provides a detailed introduction to the process of establishing a finite element model using simulation models, while
Section 4 is divided into three sections to analyze the simulation results.
Section 4.1 presents the results and analysis of the pressure wave and the pressure on the tank, and
Section 4.2 analyzes the final effect of changing the position of the arc on the pressure value on the tank.
Section 4.3 introduces the relationship between the opening position of the pressure relief valve and the pressure bearing.
2. Characteristics of Arc Discharge and Gas Production in Transformer Oil
2.1. Arc Energy in the Case of Short-Circuiting between Turns of Winding
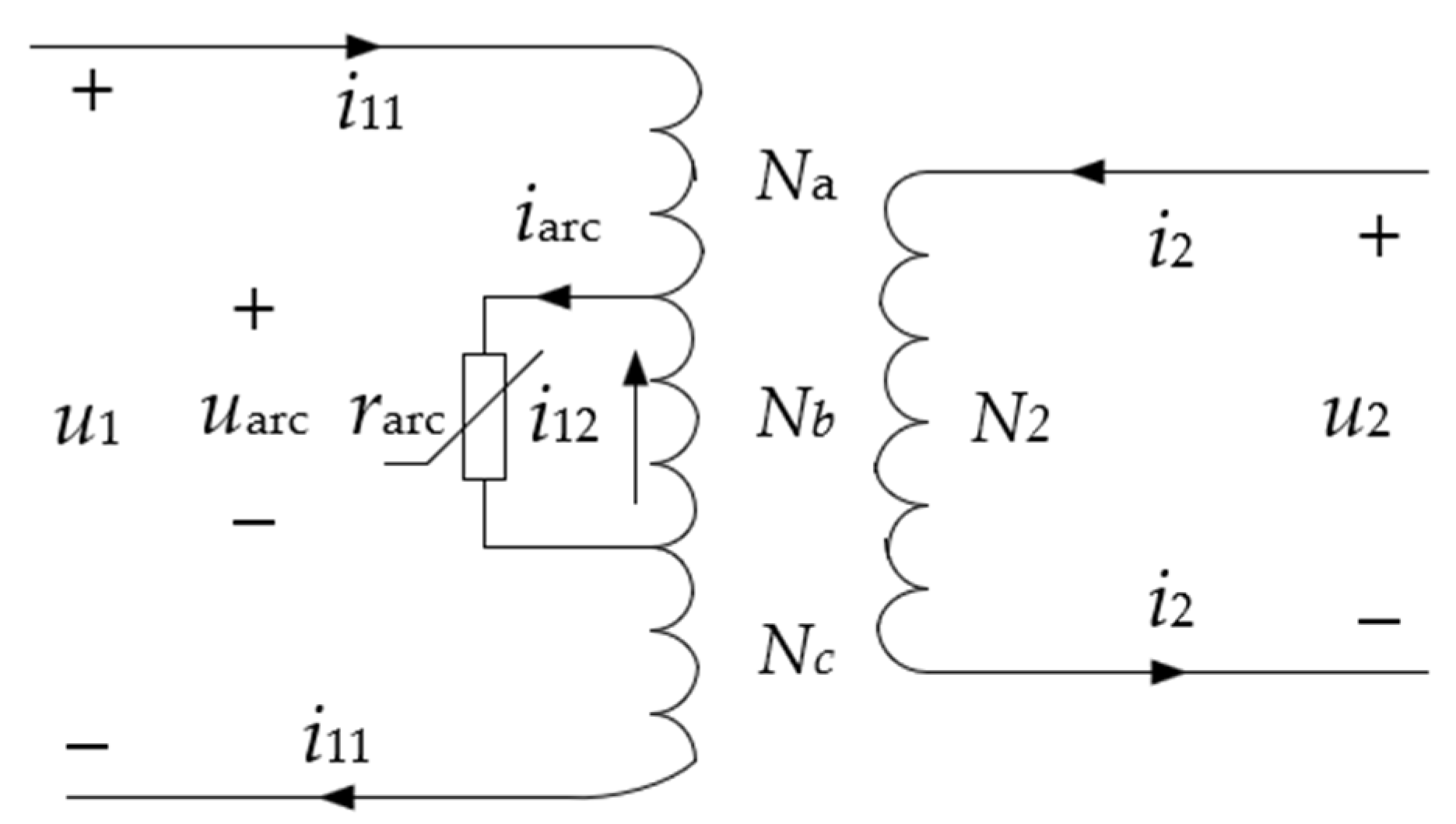
A small number of turns can usually lead to the breakdown of insulation oil and arc discharge in the case of a short-circuit fault in the transformer oil. When a fault occurs, insulation damage occurs in the part of the winding of the transformer where the turn-to-turn short circuit occurs. The damaged position of the winding and insulating oil are broken down under the action of a large electric field (voltage), and gas discharge in the insulating oil occurs. A short circuit between turns in the transformer generates an arc discharge in the oil. At this time, this part of the faulty winding is short-connected, and arc generation renders it a closed loop. This is equivalent to generating a new short-circuit transformer with a high ratio of turns of the coil, as shown in
Figure 1.
N1 in the figure represents the number of turns on the primary side of the transformer,
N2 is the number of turns on its secondary side, and
Nb is the number of turns between the occurrence of the inter-turn short-circuiting. Therefore, the winding of the original transformer becomes a winding composed of an inter-turn short-circuit winding and the remaining part in parallel.
We now analyze the equivalent arc resistance
rarc with respect to the flowing current
iarc from the point of view of the short-circuited turns. Given the saturation factor of the transformer, the magnetic flux in the core does not change significantly, even if a turn-to-turn short-circuit occurs. It is assumed in
Figure 1 that the potential induced on the primary side is
u1 and its impedance is
Z1. Then, the potential induced by the short-circuited turns
Nb is
uNb = (
Nb/
N1)
u1, its impedance,
Zb =
Z1(
Nb/
N1)
2, is very low, and this causes a large short-circuit current
i12 =
uNb/
Zb.
According to the empirical formula for its calculation, the arc energy
E(J) is an integral function of the arc current
iarc(
t), arc voltage
uarc(
t), and time
tarc(s):
It is necessary to know the functional relationship between the voltage and the current at both ends of the arc over time.
According to the analysis in
Figure 1, the arc current
iarc(
t) can be calculated as:
where
i11 is the current passing through the winding when an arc fault occurs. Assuming that the rated current passing through the coil of the transformer is
In,
i11 can be given as follows:
When
i12 =
uNb/Z
b, we can rewrite
i12 as follows when the rated voltage of the coil of the transformer is
Ue:
The magnitude of the current of the arc can then be expressed as:
The above magnitude of the arc current is derived by ignoring the changes in the impedance of the new short-circuit transformer generated by the short circuit. The impedance of the arc generated in the circuit is nonetheless dynamic. Once the arc resistance is considered, the magnitude of the arc current
i12′ is as follows:
At this time, the magnitude of the arc current is:
The arc current generated by the inter-turn short circuit obtained above in (7) is related not only to the rated voltage current of the operating transformer but also to the number of turns of the short-circuit point and the dynamic resistance of the arc.
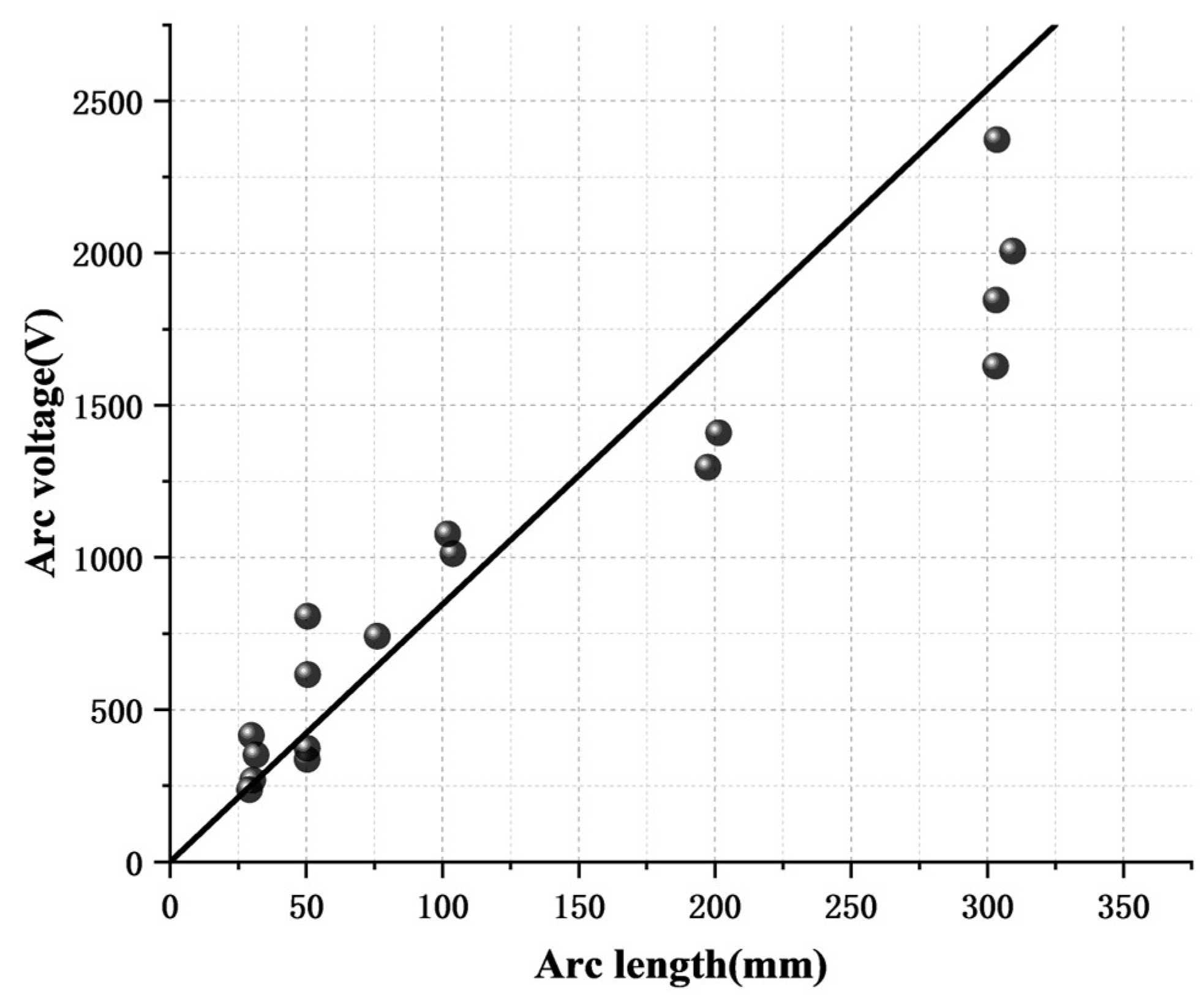
The energy produced by the arc can be obtained using (1) based on the current and voltage of the arc. The arc voltage is related to the arc length given in (8).
Figure 2 shows that the voltage of a 100 mm long arc was approximately 1000 V, and the curve fitted at each point was roughly a line representing direct proportionality [
23]:
The arc energy generated by the inter-turn short-circuiting can then be expressed as:
According to (9), the number of turns of the short-circuit point Nb, arc time tarc, arc length Larc, the transformer used, rated current In, and rated voltage Ue are the main variables influencing the arc energy.
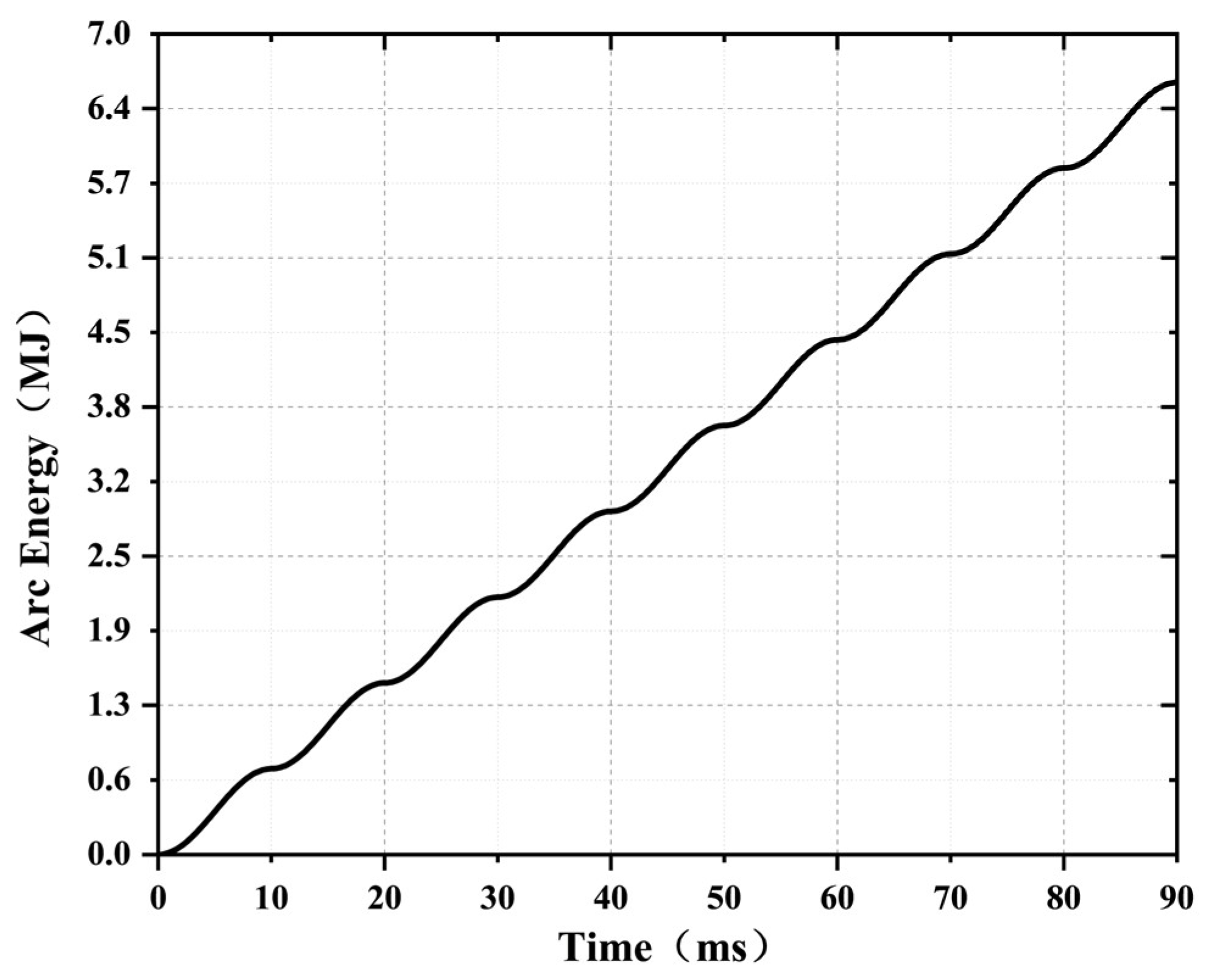
By taking the arc time
tarc as the independent variable, we plot the above parameters to explore the changing trend of arc energy with increasing arc time, as shown in
Figure 3.
The curve of the arc energy obtained in the case of 5% inter-turn short-circuiting in simulations of the single-phase high-voltage winding of the transformer shown in
Figure 3 demonstrates that the energy released by the arc is gradually accumulated over time.
2.2. Law of the Development of Arc Energy under the Action of Multiple Factors
In reference [
22], the approximate relationship between the internal arc fault energy of the transformer and the gas production is summarized by experiments performed using (10), where
β is the coefficient of conversion, which is generally set to 0.44:
We assumed that a 5% inter-turn short-circuiting fault occurred in the single-phase high-voltage winding of the transformer. The total number of turns of the high-voltage winding was 531 (N1 = 531), the number of turns of the short circuit was 27 (Nb = 27), the rated current of the high-voltage winding was 315 A (In = 315 A), and the rated voltage was 220 kV (Ue = 315 A). The high-voltage winding was 1750 mm high, which means that each turn of the winding was 3.3 mm high. The winding of the turns of the short circuit was 89 mm high, its impedance was 90.79 Ω, and the resistance of the arc was on the order of mΩ.
We used the type of fault and turns of the short circuit
Nb as independent variables to obtain (11):
Because the arc length
Larc is directly proportional to the number of turns of the short circuit,
Larc can be expressed as
kNb. Formula (11) can thus be approximated as (12):
It is evident from (12) that the relationship between the number of turns of the short circuit
Nb and the arc energy was a linear function. That is, the cumulative fault-induced arc energy increased approximately linearly with the number of short-circuit turns over time.
Figure 4 shows a plot generated using different numbers of turns of the short circuit in the formula. It is clear that the slope of the two curves was closely related to the severity of the fault; that is, the number of short-circuit turns.
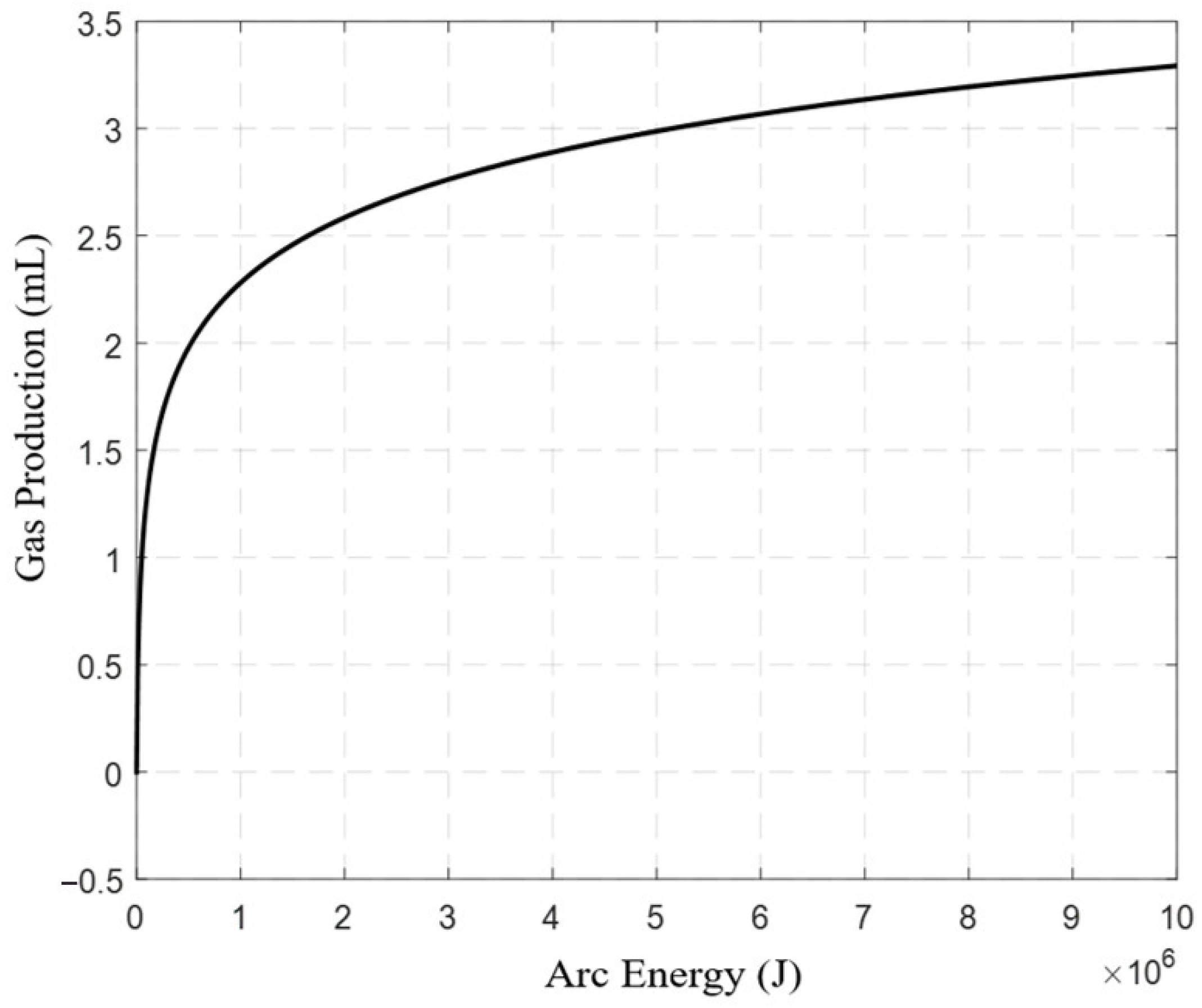
For gas production, (10) indicates that there is a logarithmic relationship between the gas production and arc energy. By substituting the arc energy Formula (12) into (10), the relationship between gas production and arc energy can be obtained, as shown in
Figure 5.
A logarithmic relationship was observed between the fault-induced arc energy and gas production. When the arc energy reached a certain value, the slope of the curve decreased rapidly and gradually tended toward saturation. This was caused by the saturation of the arc during the vaporization of the insulating oil.
2.3. Pressure Transfer under the Action of Arc Energy
The temperature of the arc is related to the medium environment, and the dissociation and de-dissociation speed of the arc combustion are different in different media. The temperature near the arc was approximately 4000~5000 K [
23,
24,
25], while the highest temperature at the center of the arc column was 10
4 K. The burning point of mineral oil that is generally used in the transformer is approximately 400 K. The insulating oil near the arc was instantly gasified and decomposed owing to the very high temperature. At this time, the energy released by the arc
Warc was mainly converted into energy absorbed by the decomposition of the insulation oil.
Warc radiated into the surrounding heat, and the energy absorbed by the evaporation of the oil led to the production of gas.
According [
26,
27,
28,
29,
30,
31,
32], the energy distribution mainly comes from
Wgas.
Under standard pressure, when the arc energy is 1 kJ, the corresponding gas production is approximately 5.8 × 10
−4 m
3/kJ. According to the above analysis, the transformer data in
Section 2.2 is input into Formulas (10) and (12) to calculate the amount of gas volume produced, which is approximately 10
−6 m
3 by 1 kJ of arc energy. This is much smaller than the gas produced under standard pressure and could thus be ignored when calculating the fluctuations in the temperature of oil. According to the law of heat conduction, the transfer of heat to and the rise in the temperature of the insulating oil according to the distance from the arc can be calculated using the following formula:
Tarc represents the temperature of the arc and the thermal conductivity, which is generally 0.15 W (m·K)
−1 in insulating oil [
33].
S represents the area of heat transfer between the insulating oil and the arc,
Toil represents the initial temperature of the insulating oil,
Toil’ represents its real-time temperature, and
L represents the distance between the insulating oil and the arc during heat conduction.
m is the unit mass of the insulating oil and
coil is its specific heat capacity. It is clear from (14) that heat transfer in the insulation oil was mainly influenced by the arc heat, and it gradually decreased with an increase in its distance to the arc.
The volume expansion of insulating oil has a hysteresis effect relative to the production of gas. The transient pressure of gas produced by the arc continues to drastically increase with the discharge time of the high-energy arc. Therefore, a high pressure was obtained at the interface of the gas and the insulating oil during the phase transition reaction, which spread around in the form of a pressure wave in the oil and acted on the wall of the tank. This caused the tank to bear the corresponding stress and deform once the pressure exceeded a certain limit, or to even accumulate too much elastic energy in a short time such that it burst. The change in the phase of the insulating oil from liquid to gas followed the law of the conservation of mass. The mass of the vaporized oil could then be obtained according to the mechanism of vaporization-induced evaporation of oil:
where
mog is the mass of the insulating oil undergoing a phase change,
Tgas represents the transient temperature of the generated gas, and Δ
Q* is the latent heat of vaporization of the insulating oil per unit mass (the heat absorbed by a certain liquid per unit mass during vaporization when the temperature is constant). We analyzed the components of the gases produced by the combustion of the arc in the insulation oil. They consisted of 7.85% ethylene, 13.96% methane, 14.87% methanol, 22.17% acetylene, and 30.77% propane [
34]. The molar mass of the gas generated in the insulation oil was approximately 28.99 g/mol. According to the ideal gas equation, its pressure can be calculated as follows:
In (15), n represents the amount of matter and R represents the molar gas constant, with a typical value of 8.31451 J/(mol·K).
The transient pressure of the generated gas can then be obtained by substituting (10) and (15) into (16):
Figure 5 shows that when the energy released by arc combustion over time accumulated to reach a certain value, the gas production approached saturation. We thus assumed that the volume of gas produced did not change when calculating the transient pressure and the transfer of internal pressure. The initial pressure of the generated gas was approximately proportional to the arc energy. The initial difference in pressure at the position of the arc in the insulation oil was as follows:
where
p0 is the atmospheric pressure, 1.01325 × 10
5 Pa;
ρoil is the density of the insulating oil;
g is the acceleration due to gravity; and
h is the depth with respect to the surface of the oil at which the arc discharge occurred. The derivation of some of the above equations is listed in the
Appendix A.
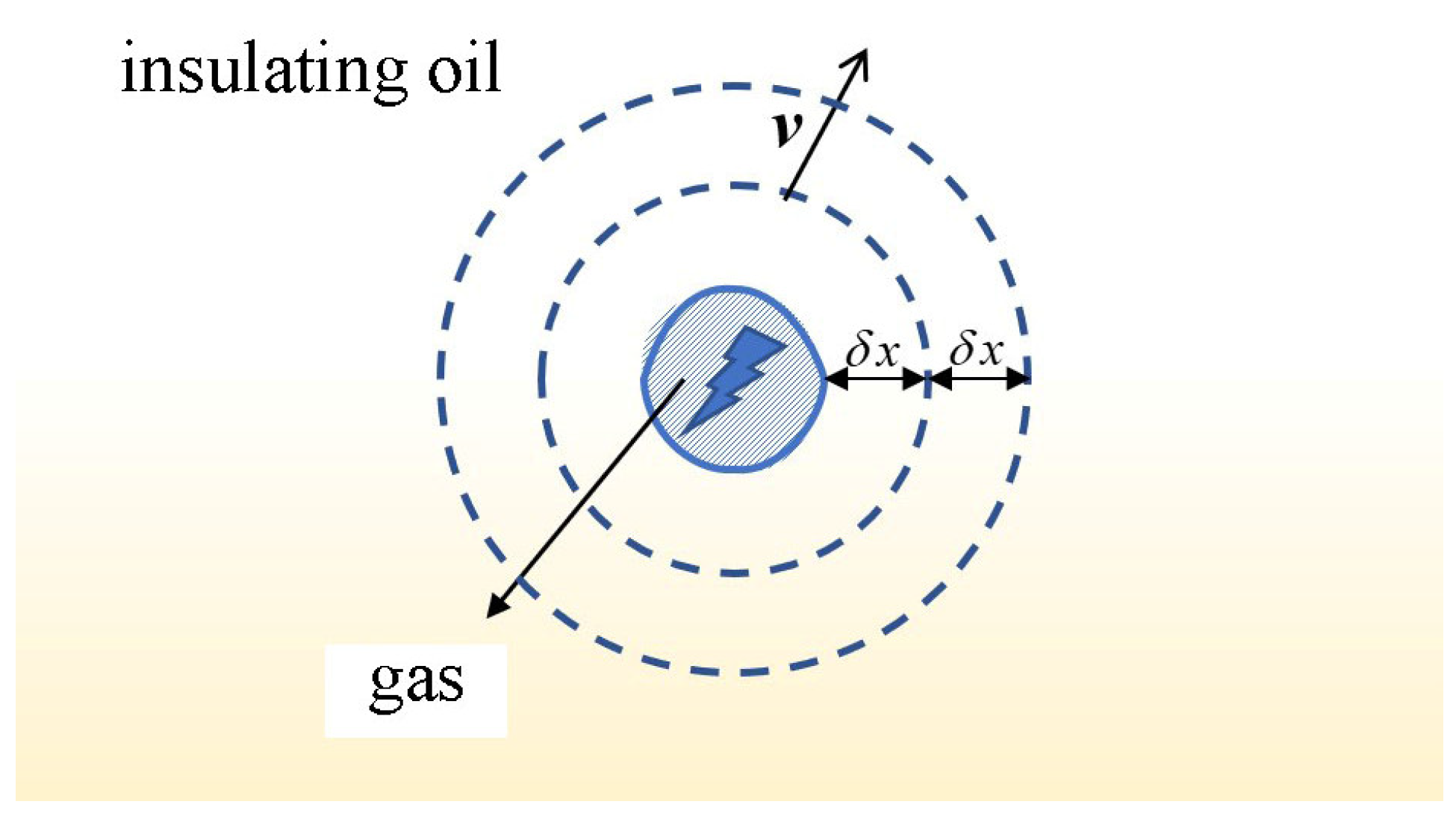
We analyzed the propagation of the pressure wave in the insulating oil. We regarded the generated gas pressure as a source of transient pressure that could provide initial shock-induced excitation in the oil tank Pv(t). The coupling of two-phase gas–liquid flow was calculated by using the volume function model (VOF). The shock induced by the source of transient pressure Pv(t) in the tank was transmitted to the insulating oil in the form of waves and acted on the wall of the tank, causing it to strain.
The insulating oil was compressible and viscous. The greater the viscosity of the fluid, the worse its fluidity; therefore, the viscosity of the oil weakened the transmission of the pressure wave.
Figure 6 shows that the compressibility of the oil caused the pressure wave to propagate with a velocity
v. When a difference in pressure was obtained between the gas and the surrounding insulating oil, the pressure at a distance of
δx from the gas increased instantaneously, Δ
p. The insulating oil at this distance was then transferred to its adjacent liquid surface
δx, causing its pressure to increase by Δ
p and its velocity to change from zero to
v. This process occurred in each layer to form an initial pressure wave with a magnitude Δ
p that propagated at a velocity
v toward the surrounding walls of the tank.
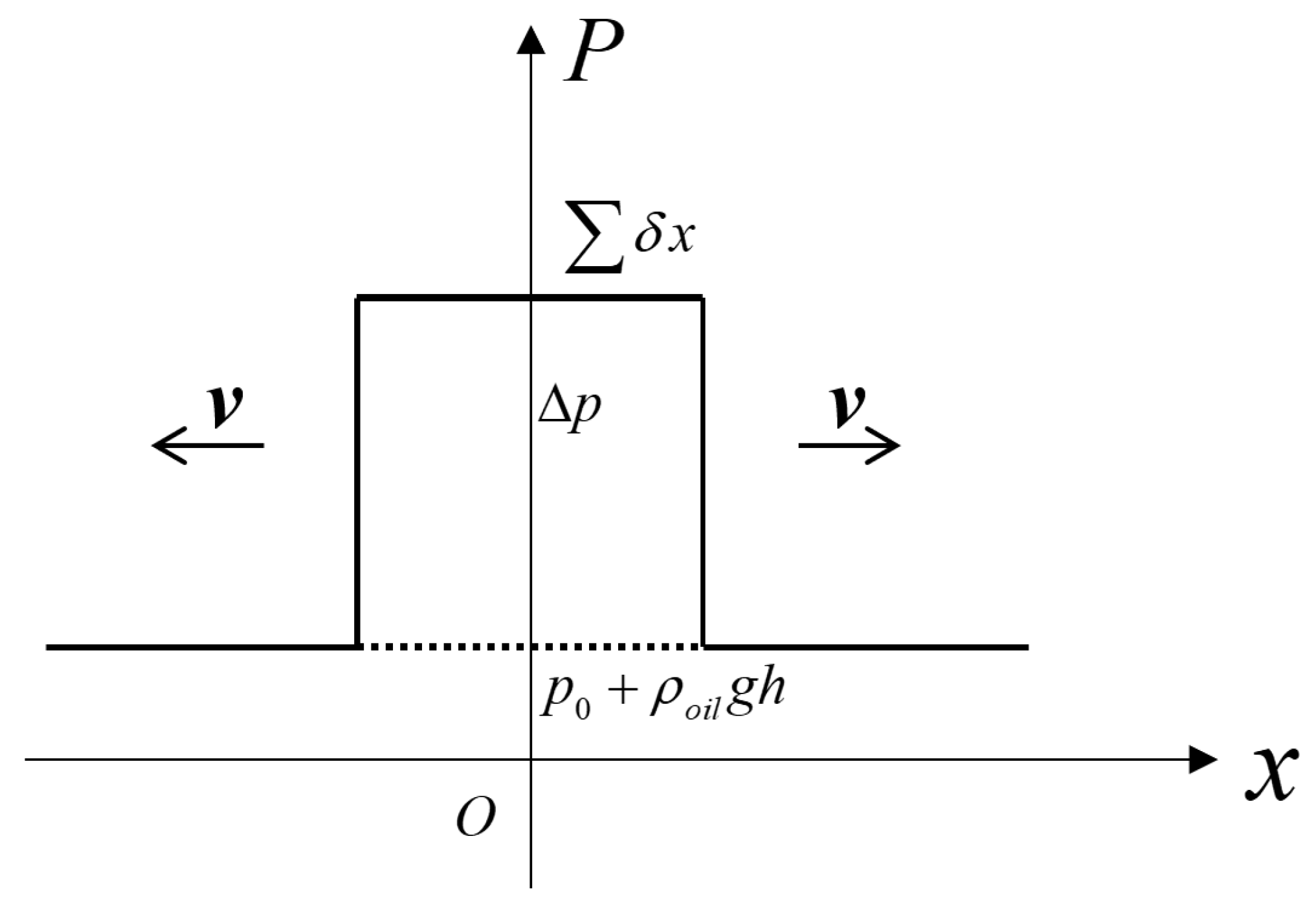
Figure 7 shows that the propagation of the pressure wave increased the pressure of the insulation oil by Δ
p. The pressure wave traveled over a distance of ∑
δx =
vΔ
t, causing the pressure of water to rise within this distance by Δ
p, while
p0 +
poilgh remained unchanged in the section in which the wave did not propagate. There is no reflection if a source of transient pressure
Pv(t) is generated in a frictionless and infinitely large container, and the pressure wave is indefinitely transmitted. However, the energy of the pressure wave continuously decreased during propagation in the actual transformer tank due to the influence of the viscous insulation oil and the elastic walls of the tank. Energy was thus transmitted to the walls of the tank.
3. Finite Element Simulation of Pressure in a Tank
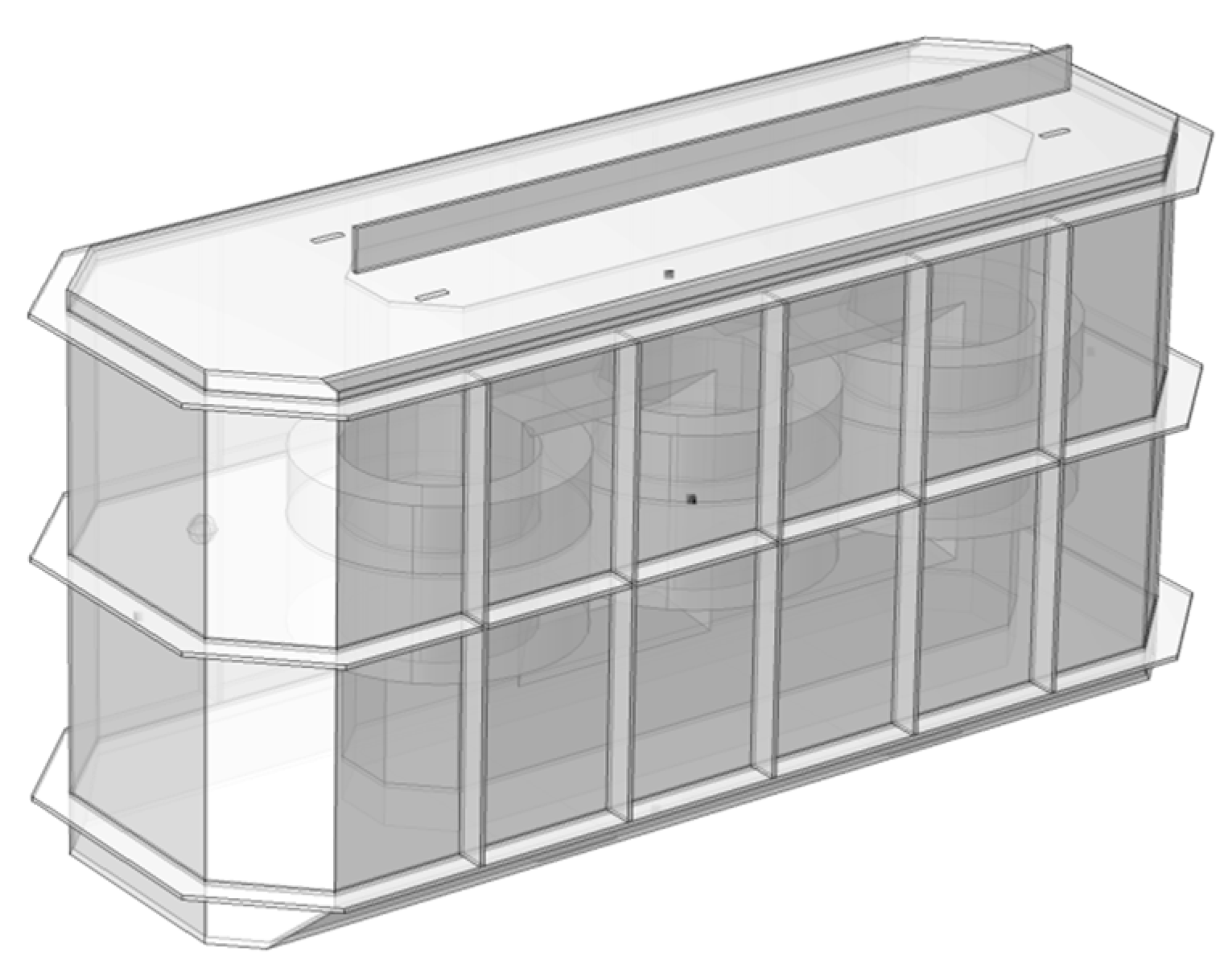
We used a finite element simulation software to represent the changes in the pressure in the transformer tank once an internal fault had occurred. We simulated a transformer tank by considering only three key components of the transformer. The overall geometric model of the tank is shown in
Figure 8. The length of the tank was 4 m, its width was 1.4 m, and its height was 2 m. A model of the core and the winding was provided inside the tank, and stiffeners were installed at suitable positions outside it.
The model of the tank can be divided into two parts: the tank itself and the winding with an iron core. The relevant models are shown in
Figure 9 and
Figure 10.
The thickness of the wall of the tank was set to 16 mm. The model was used to simulate the propagation of the pressure wave under the wall.
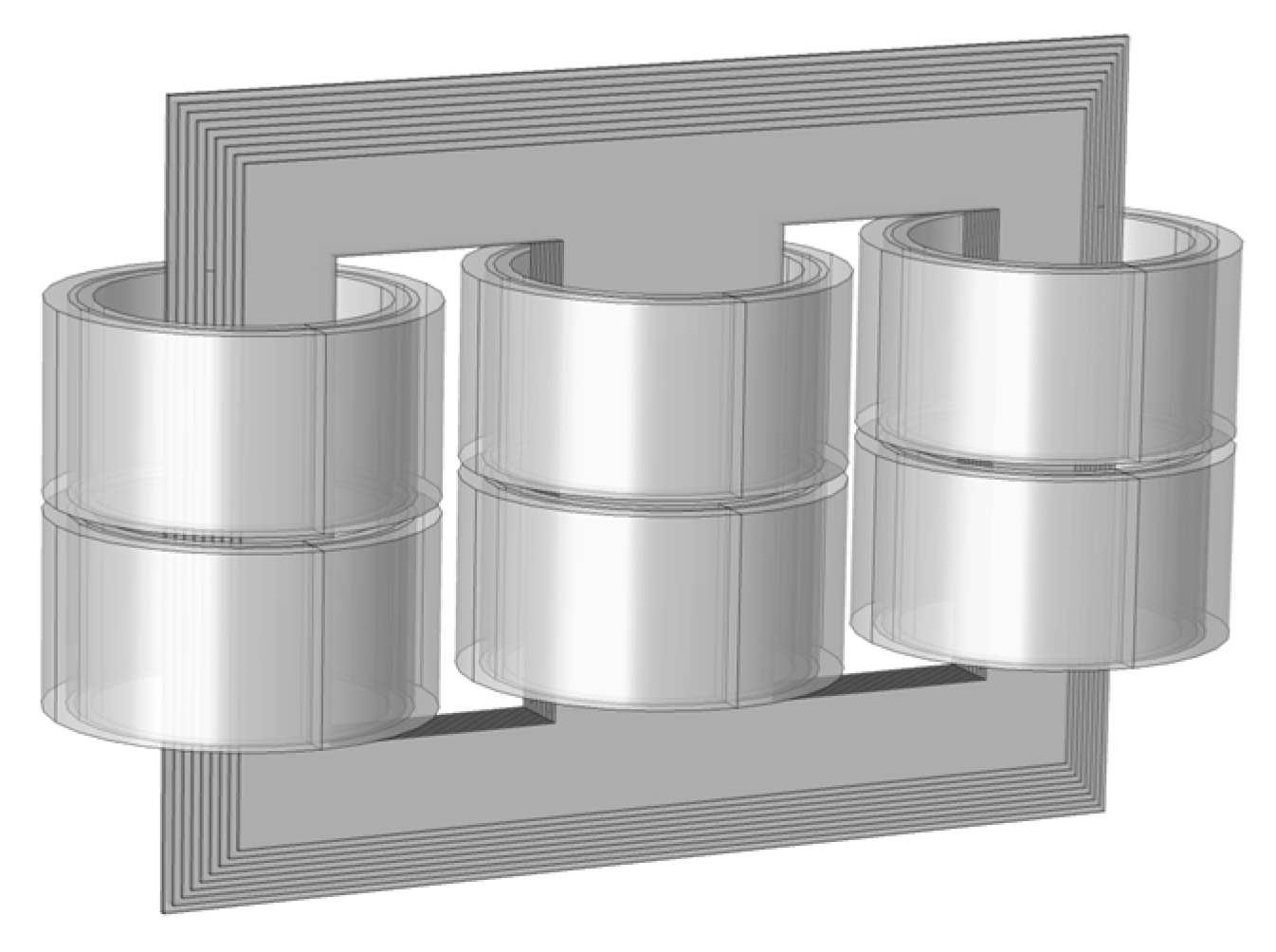
The model of the iron core shown in
Figure 10 was composed of multiple sheets of silicon and steel that were superimposed on each other, and the winding circuit was simulated by using the virtual circuit in the simulation software. The coil can be divided into primary and secondary coils. This model was used to simulate the distribution of force under the propagation of the pressure wave.
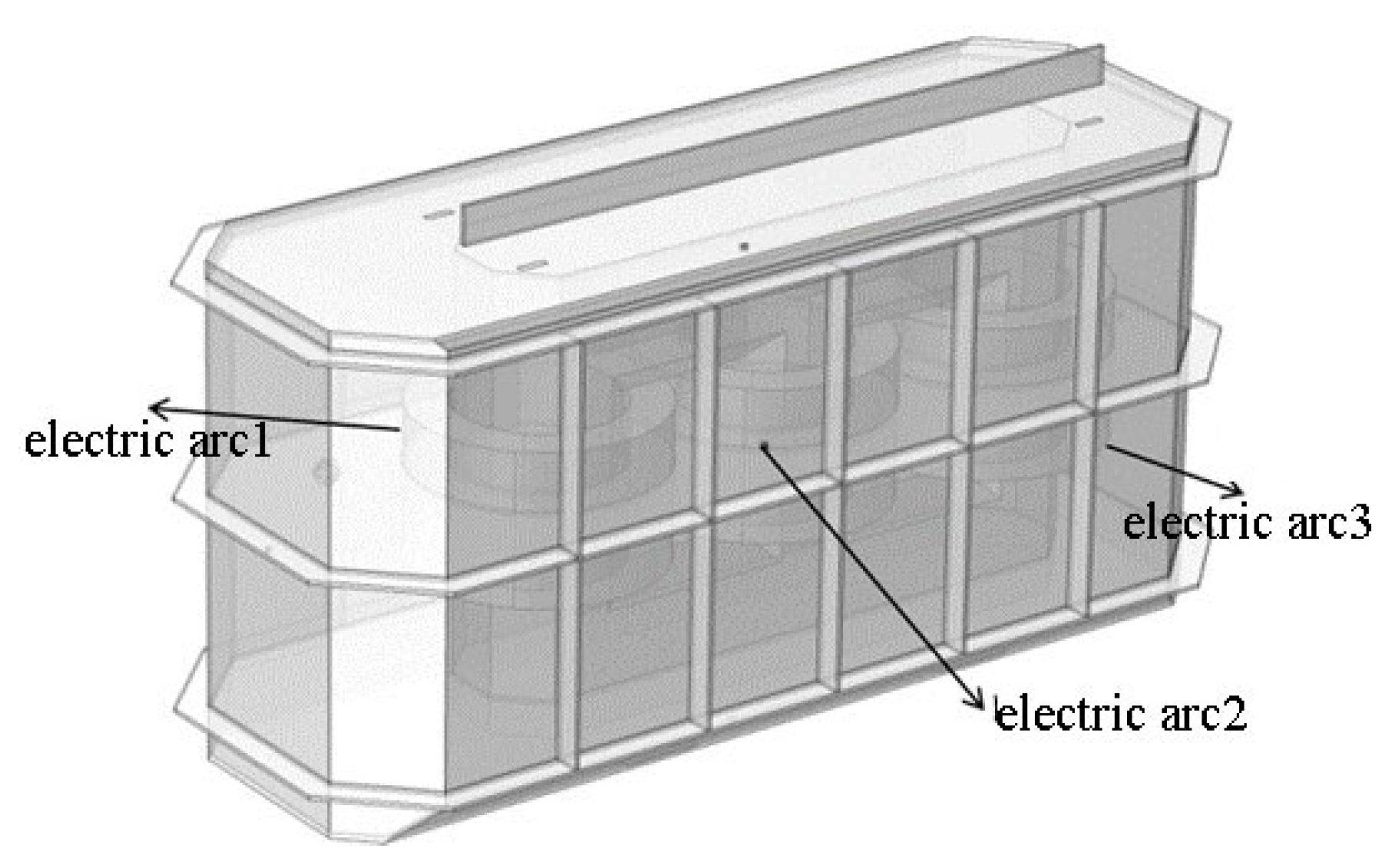
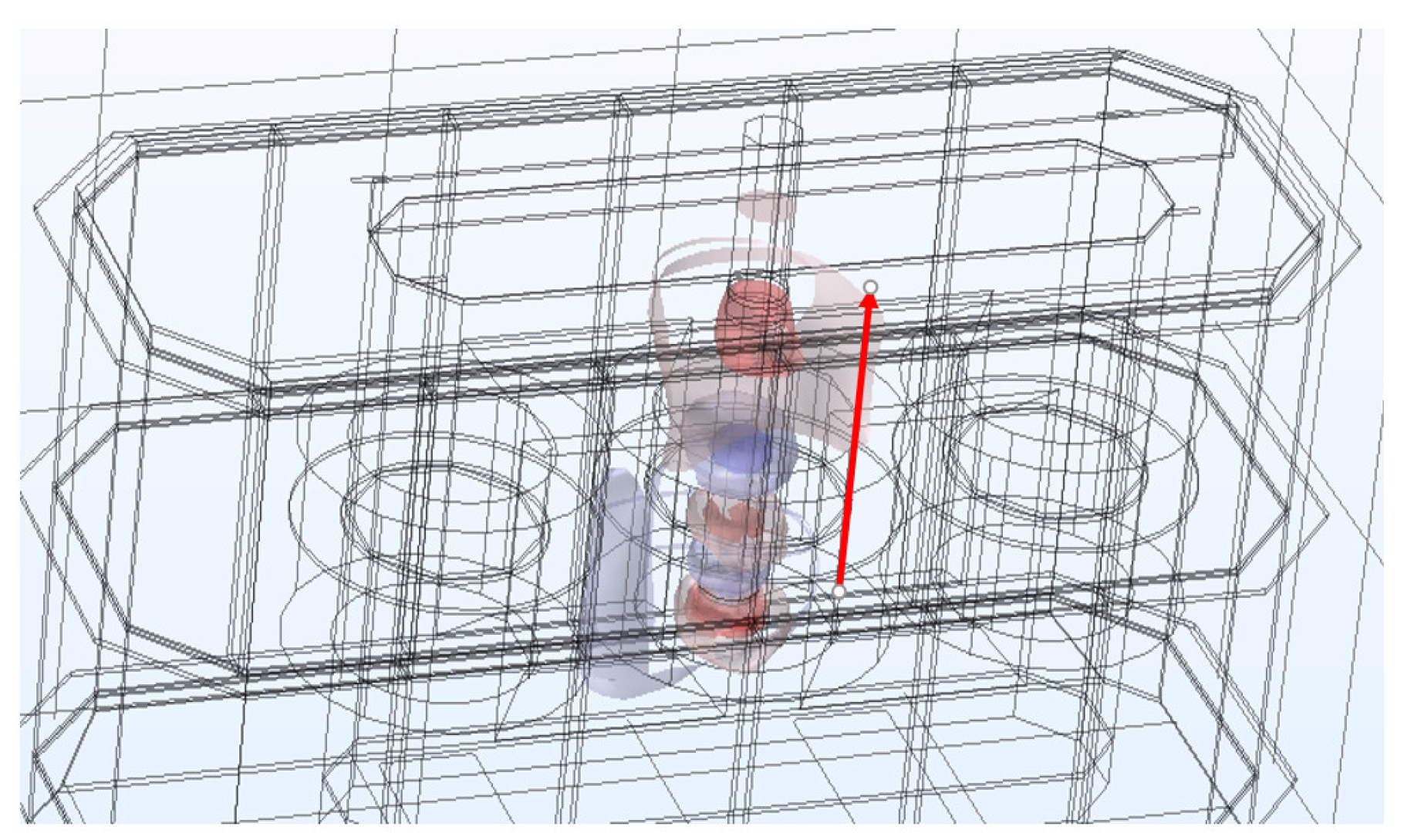
We varied the position of occurrence of the initial arc (that is, the initial position of generation of bubble-induced pressure) in the finite element simulations, and we set multiple probes at different positions in the tank and its wall for measurements, as shown in
Figure 11 and
Figure 12.
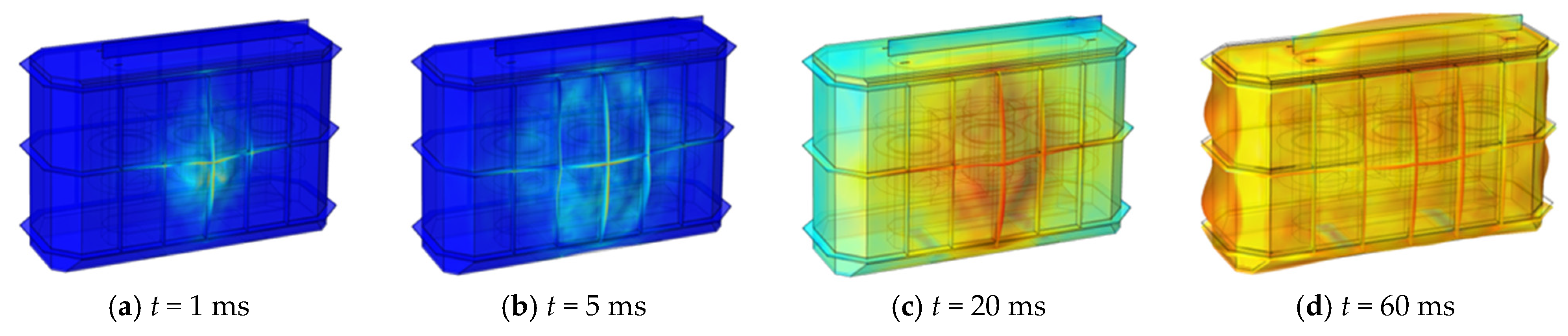
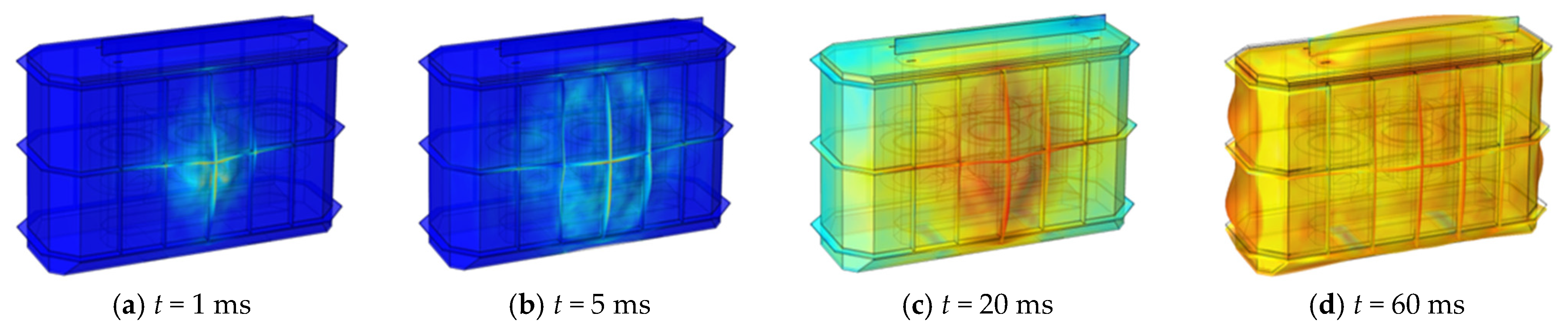
A finite-element mesh division was used, as shown in
Figure 13. We simulated the transfer of pressure inside the transformer tank under the action of the source of transient pressure and the distribution of pressure on the wall of the tank according to the initial position of the arc, and we analyzed the propagation of the pressure wave based on a diagram of the contours of the pressure distribution.