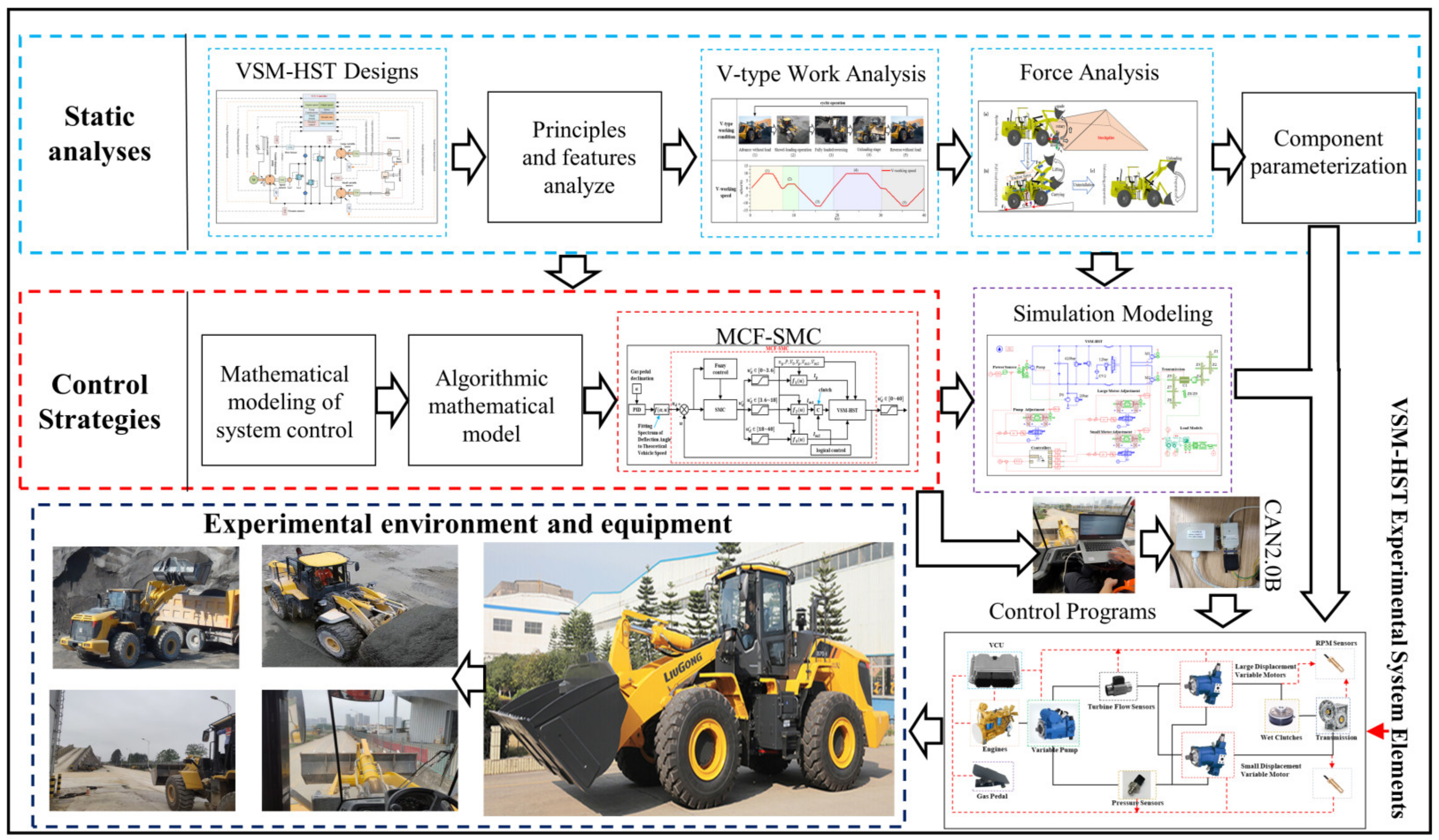
Research on the New Hydrostatic Transmission System of Wheel Loaders Based on Fuzzy Sliding Mode Control
Abstract
1. Introduction
- (a)
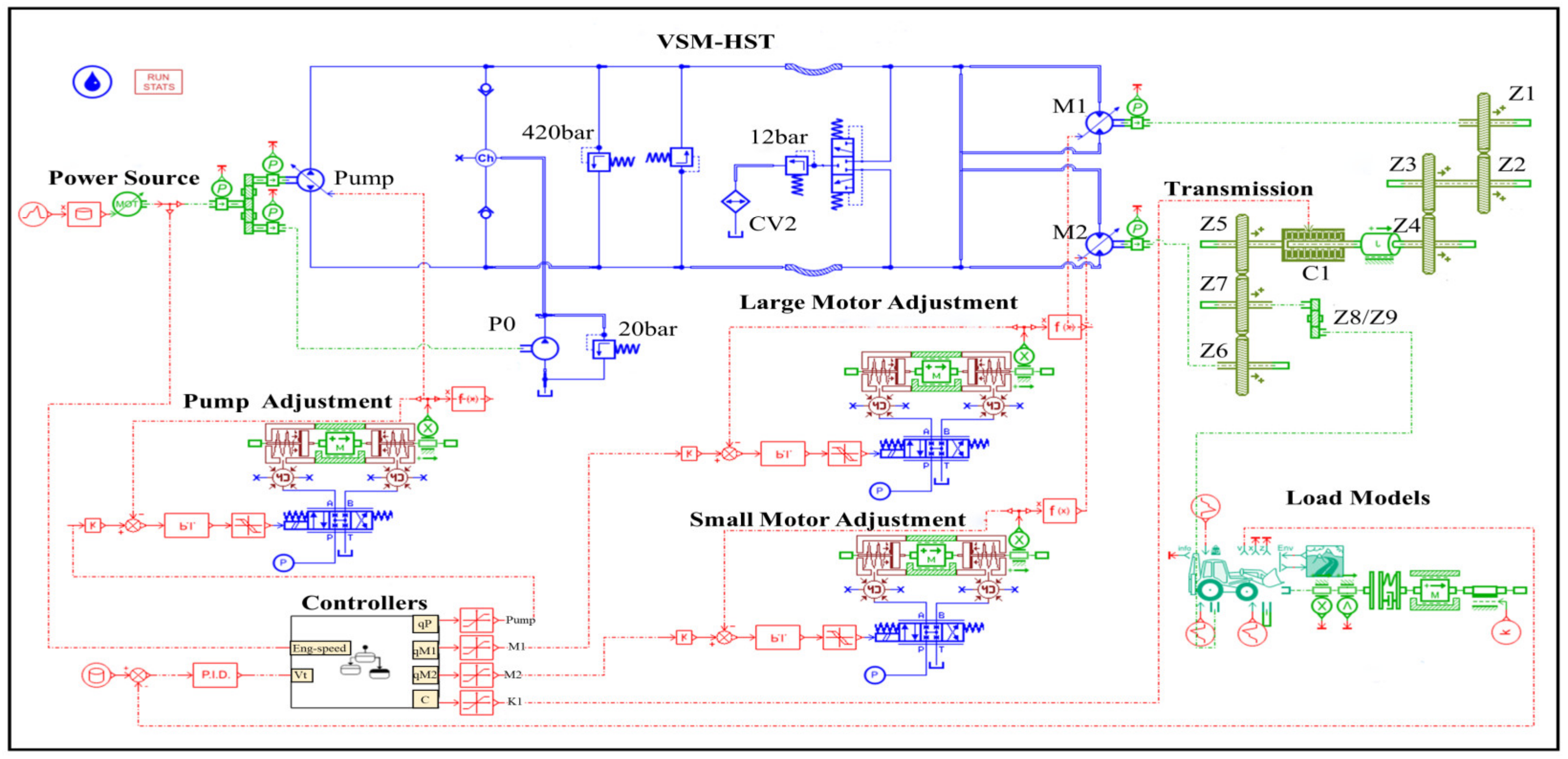
- A new hydrostatic transmission VSM-HST system is proposed, and its working principle, structural layout, and system characteristics are analyzed.
- (b)
- The speed and power requirements for the V-type operation of the VSM-HST loader system are discussed. The corresponding design parameters of the system are then determined.
- (c)
- The state equations of the VSM-HST system are developed, and a control strategy using MCF–SMC suitable for the system is formulated and evaluated. Simulation experiments are performed to compare the performance with several state-of-the-art strategies.
- (d)
- Together with the loader manufacturer, the initial prototype of a 7-ton loader, which features the VSM-HST system and its corresponding control strategy, was developed and successfully applied in actual engineering product production.
2. System Analysis
2.1. Working Principle
- (1)
- Realize automatic gear shifting throughout the entire V-shape operating scenario.
- (2)
- Realize integrated control of multiple variables in the system to match input power with output power, thereby reducing overflow losses and engine idling and improving total system efficiency.
- (3)
- Effectively track the target vehicle speed and reduce the impact of load changes on the vehicle speed.
2.2. System Features
2.3. Work Condition Analysis
3. Control Strategy
3.1. Mathematical
Models
3.2. MCF–SMC
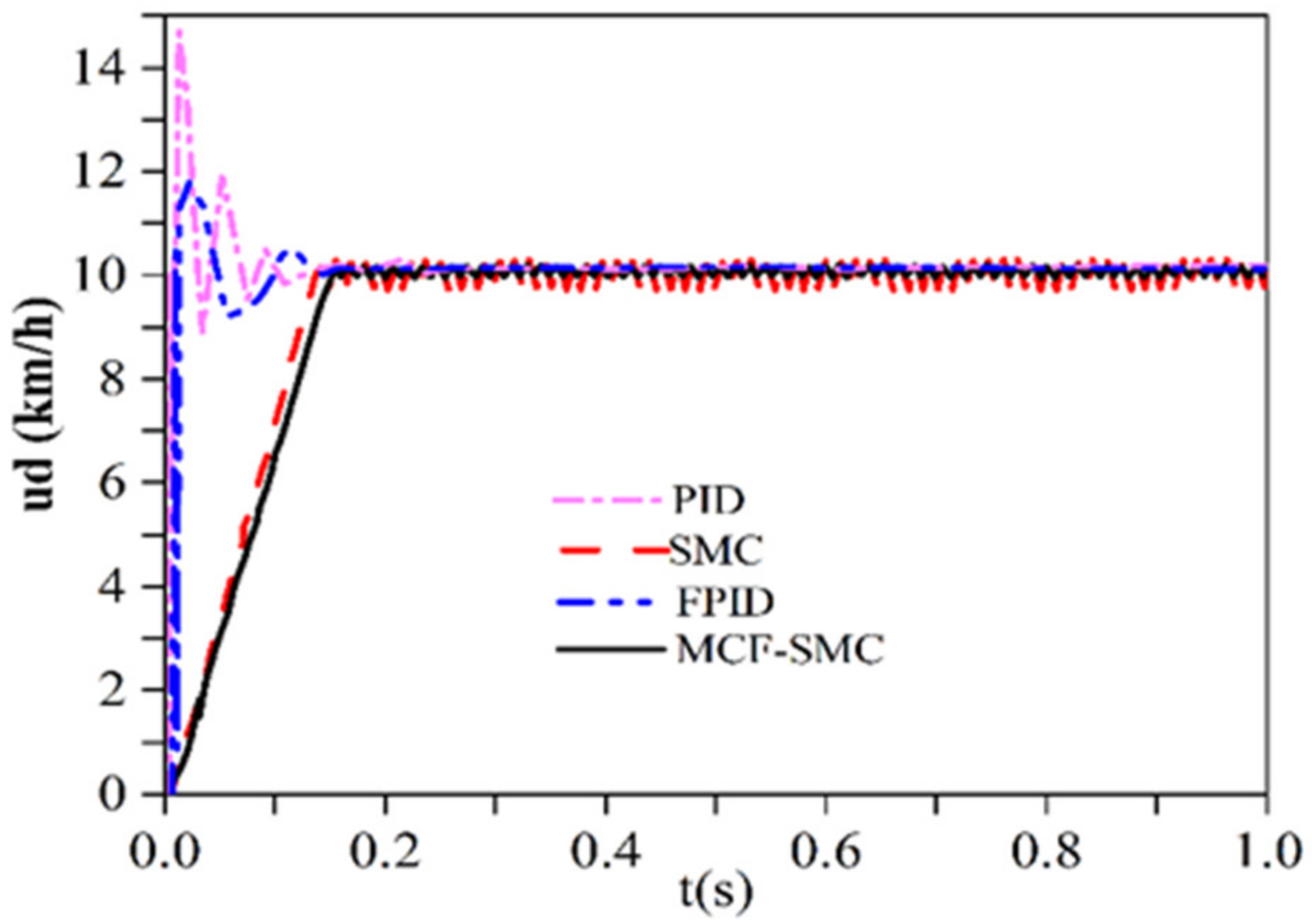
3.3. Simulation Results
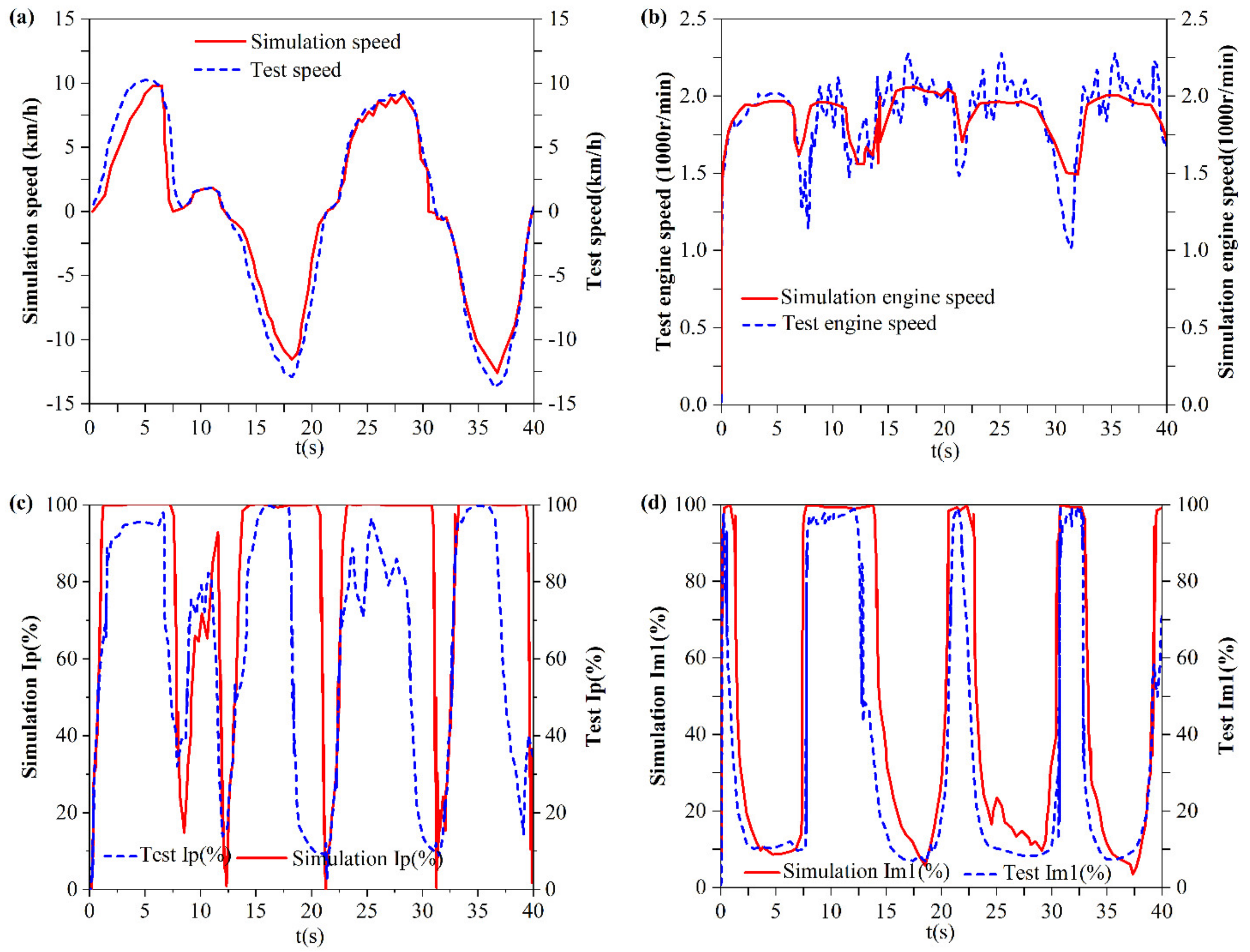
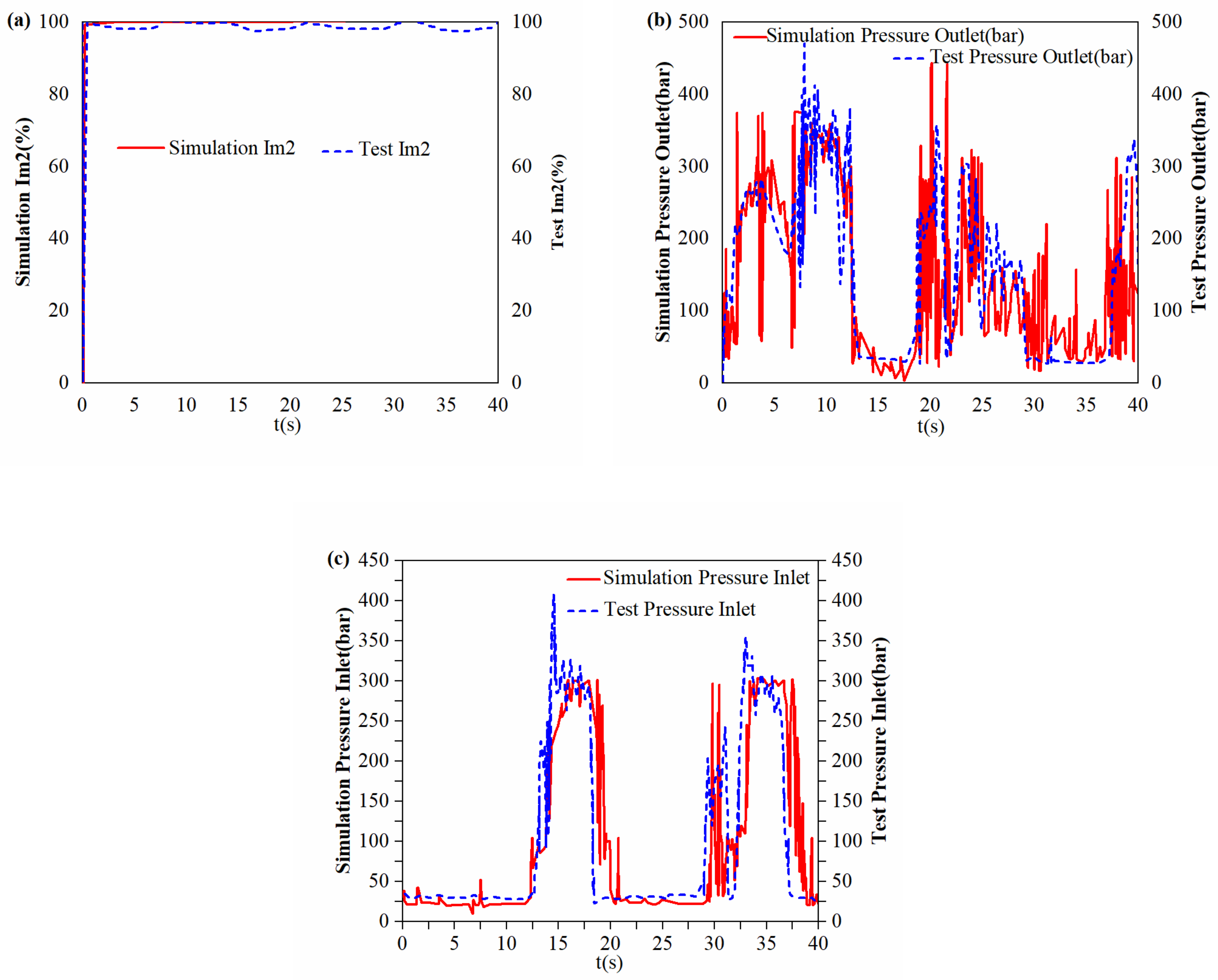
4. Experimental Verification
4.1. Experimental Design
- (1)
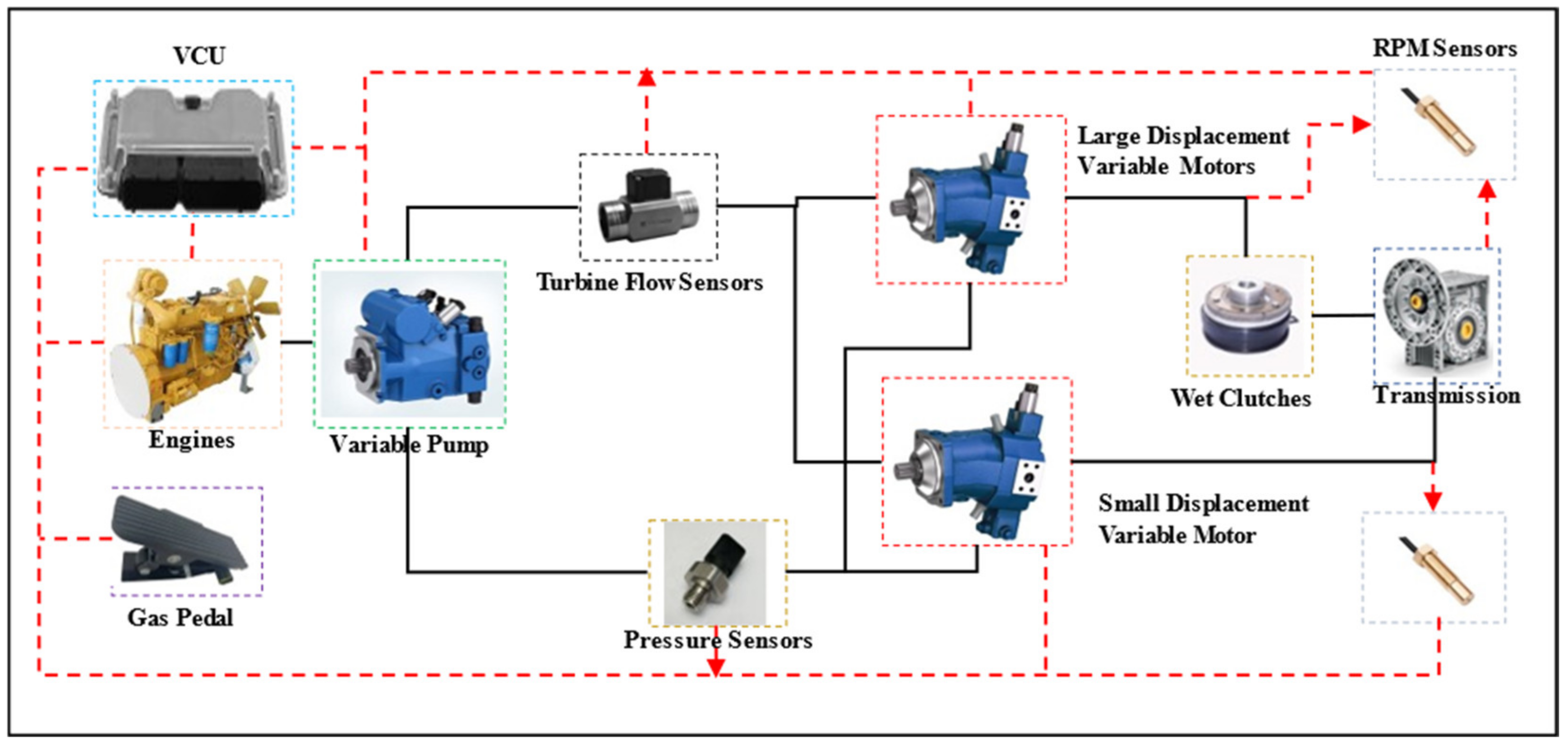
- The speed sensor was installed in the rear-wheel-drive shaft of the loader, and the variable pump input shaft was installed in two places. The pressure and flow sensors were installed in the hydraulic circuit, and the formulated control strategies and algorithms were written into the VCU controller. The sensors were connected to the controller, which was connected to the collector through the CAN2.0B bus. The controller was connected to the collector via the CAN2.0B bus.
- (2)
- The loader began from the initial position and accelerated by stepping on the accelerator pedal. It maintained a constant speed in the middle by controlling the accelerator pedal before releasing it near the pile. The loader stopped by using the resistance of the pile and then increased the accelerator pedal to shovel the load. Once the shoveling was complete, it drove in reverse by first accelerating and then reversing. After shoveling, the vehicle was reversed, first accelerating and then decelerating to the starting position, and then driving in the right direction to the loading truck, first accelerating and then decelerating to the loading truck for unloading. After unloading, the vehicle was reversed, first accelerating and then decelerating back to the home position. During this operation, the engine speed, wheel speed, system pressure, system flow, pump, and engine displacement of the loader were collected and recorded.
- (3)
- This procedure was repeated multiple times to ensure a consistent collection of experimental data.
4.2. Experimental Results
4.3. Experimental Discussion
- (a)
- The VSM-HST has the advantages of a more compact structure, a wider high-efficiency speed range, and higher total efficiency. It can directly transplant and replace the hydraulic traveling mechanism of traditional construction machinery and apply it to the whole product line.
- (b)
- MCF–SMC is specially designed for the VSM-HST system, which successfully realizes the overall control of multiple variables, effectively adapts to and controls the sudden change in speed caused by load change during the actual operation of wheel loader, and ensures the smoothness of the speed regulation process. It effectively overcomes the challenges posed by the time delay and nonlinearity of the hydraulic system and ensures the driving quality.
- (c)
- The VSM-HST and MCF–SMC solutions enable smooth, stepless automatic gear shifting over the entire speed range of the wheel loader, with free selection of high and low gears. The main components within the system are controllable, which greatly enhances the control potential of the system and facilitates intelligent retrofitting, especially for vehicle speed control of driverless construction machinery.
5. Conclusions
- (1)
- The proposed VSM-HST system can meet the speed requirements of different road conditions under the V-shaped working mode of the loader. The adjustment process is smooth, and the speed switching is smooth.
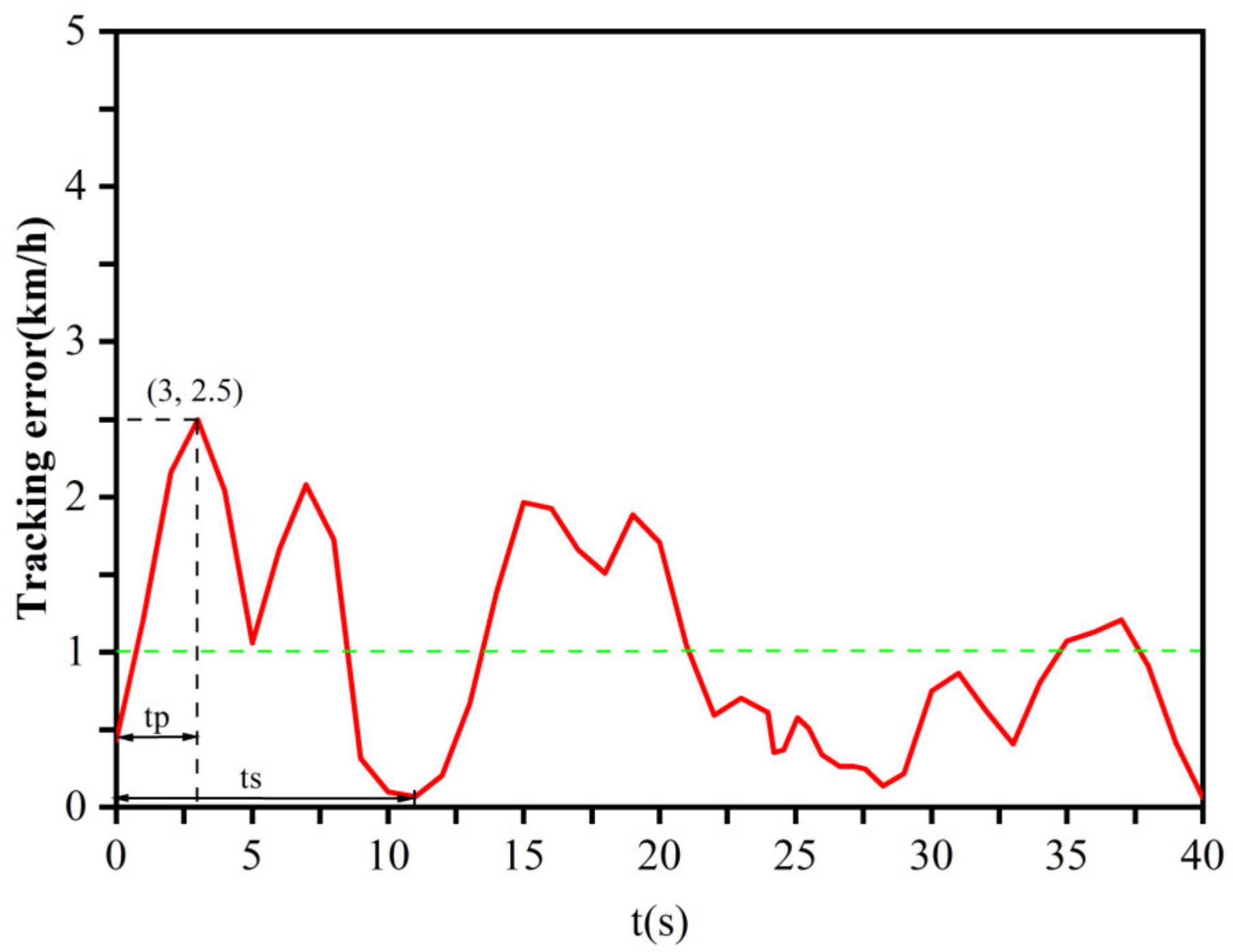
- (2)
- The proposed MCF–SMC control strategy can match the system well. The test proves that the maximum tracking error of the target speed is only 2.5 km/h under normal driving conditions, and the average deviation of the speed is 1 km/h when subjected to an external disturbance load not exceeding the rated load. A good control effect is achieved within the allowable error range.
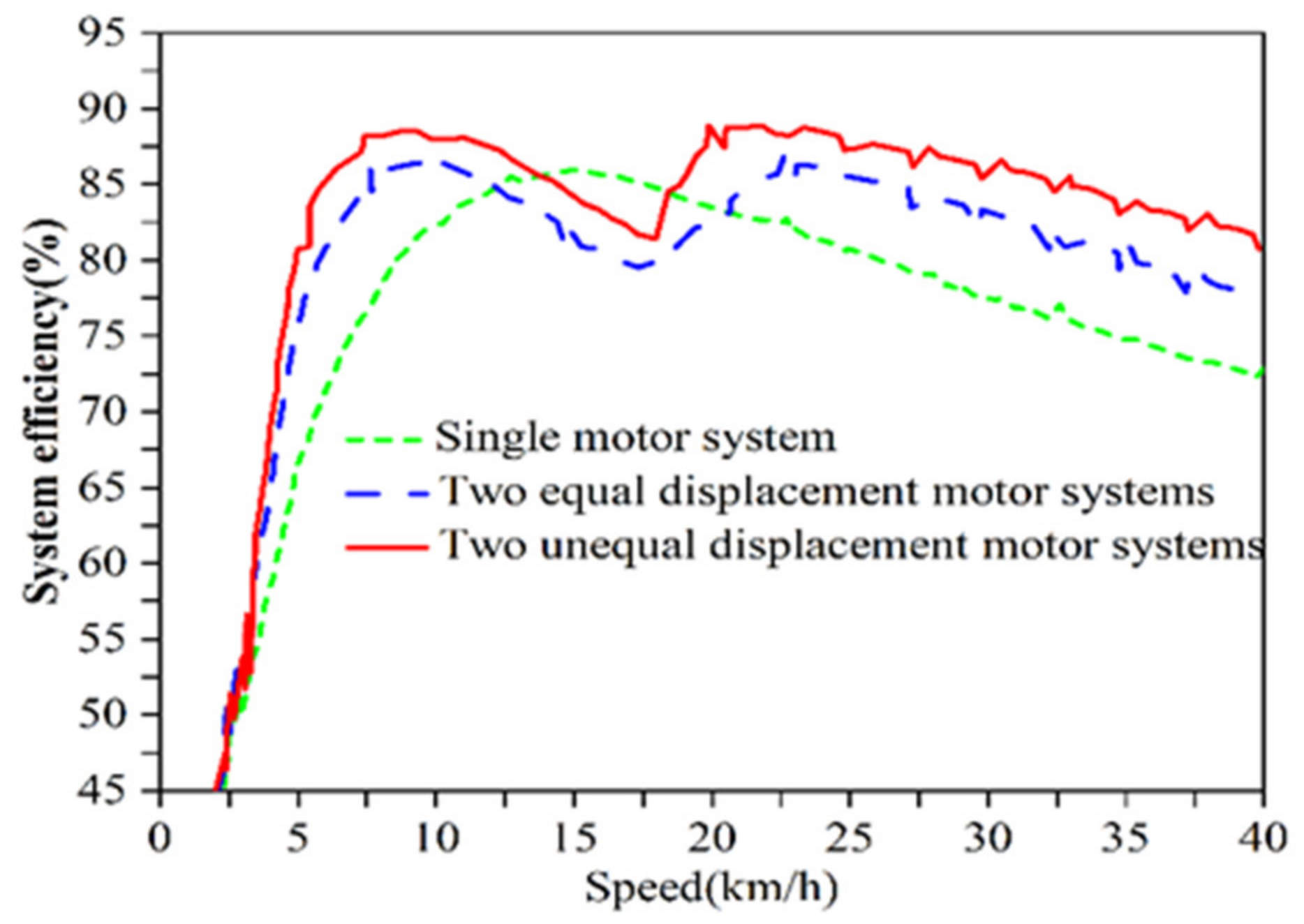
- (3)
- Compared with loaders using traditional hydrodynamic torque converter transmission systems, under the same initial conditions and operating conditions, the total efficiency of the VSM-HST system is increased by about 30%, and the total efficiency is increased by about 8% compared to other traditional HST schemes. This shows that this scheme can effectively improve transmission efficiency and reduce fuel consumption.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Frank, B.; Kleinert, J.; Filla, R. Optimal control of wheel loader actuators in gravel applications. Autom. Constr. 2018, 91, 1–14. [Google Scholar] [CrossRef]
- Nezhadali, V.; Frank, B.; Eriksson, L. Wheel loader operation—Optimal control compared to real drive experience. Control Eng. Pract. 2016, 48, 1–9. [Google Scholar] [CrossRef]
- Nilsson, T.; Fröberg, A.; Åslund, J. Development of look-ahead controller concepts for a wheel loader application. Oil Gas Sci. Technol. 2015, 70, 159–178. [Google Scholar] [CrossRef]
- You, Y.; Sun, D.; Qin, D. Shift strategy of a new continuously variable transmission based wheel loader. Mech. Mach. Theory 2018, 130, 313–329. [Google Scholar] [CrossRef]
- Lin, T.; Wang, Q.; Hu, B.; Gong, W. Development of hybrid powered hydraulic construction machinery. Autom. Constr. 2010, 19, 11–19. [Google Scholar] [CrossRef]
- Wang, F.; Chen, J.; Xu, B.; Stelson, K.A. Improving the reliability and energy production of large wind turbine with a digital hydrostatic drivetrain. Appl. Energy 2019, 251, 113309. [Google Scholar] [CrossRef]
- Xupeng, H.; Wenbin, S.; Hang, Z.; Yanni, Z.; Qiao, H.; Chaohui, W. Research of the hydrostatic transmission for deep-sea current energy converter. Energy Convers. Manag. 2020, 207, 112544. [Google Scholar] [CrossRef]
- Comellas, M.; Pijuan, J.; Nogués, M.; Roca, J. Efficiency analysis of a multiple axle vehicle with hydrostatic transmission overcoming obstacles. Veh. Syst. Dyn. 2018, 56, 55–77. [Google Scholar] [CrossRef]
- Rabbo, S.A.; Tutunji, T. Identification and analysis of hydrostatic transmission system. Int. J. Adv. Manuf. Technol. 2008, 37, 221–229. [Google Scholar] [CrossRef]
- Backas, J.; Ghabcheloo, R.; Huhtala, K. Gain scheduled state feedback velocity control of hydrostatic drive transmissions. Control Eng. Pract. 2017, 58, 214–224. [Google Scholar] [CrossRef]
- Do, H.T.; Park, H.G.; Ahn, K.K. Application of an adaptive fuzzy sliding mode controller in velocity control of a secondary controlled hydrostatic transmission system. Mechatronics 2014, 24, 1157–1165. [Google Scholar] [CrossRef]
- Schulte, H.; Gauterin, E. Fault-tolerant control of wind turbines with hydrostatic transmission using Takagi–Sugeno and sliding mode techniques. Annu. Rev. Control 2015, 40, 82–92. [Google Scholar] [CrossRef]
- Jiang, W.; Zhang, C.; Jia, P.; Yan, G.; Ma, R.; Chen, G.; Ai, C.; Zhang, T. A Study on the Electro-Hydraulic Coupling Characteristics of an Electro-Hydraulic Servo Pump Control System. Processes 2022, 10, 1539. [Google Scholar] [CrossRef]
- You, Y.; Sun, D.; Qin, D.; Wu, B.; Feng, J. A new continuously variable transmission system parameters matching and optimization based on wheel loader. Mech. Mach. Theory 2020, 150, 103876. [Google Scholar] [CrossRef]
- Cao, B.W.; Liu, C.Y.; Chen, W.; Tan, P.; Yang, J.W. Shovel-loading cooperative control of loader under typical working conditions. ISA Trans. 2023, 142, 702–715. [Google Scholar] [CrossRef] [PubMed]
- Wang, F.; Wen, Q.; Xu, X.; Xu, B.; Sun, Z. Site Operation Strategy for Wheel Loader/Truck Loading and Transportation Cycle. IEEE Trans. Veh. Technol. 2021, 70, 4129–4138. [Google Scholar] [CrossRef]
- Ur Rehman, A.; Awuah-Offei, K. Understanding How Speed, Tractive Effort, Digging Height, and Rake Angle Affect Bucket Penetration and Resistive Forces for Rubber Tire Loaders. Min. Metall. Explor. 2020, 37, 1423–1435. [Google Scholar] [CrossRef]
- Wu, B.; Hou, L.; Wang, S.; Yin, Y.; Yu, S. Predictive modeling of loader’s working resistance measurement based on multi-sourced parameter data. Autom. Constr. 2023, 149, 104805. [Google Scholar] [CrossRef]
- Takahashi, H.; Hasegawa, M.; Nakano, E. Analysis on the resistive forces acting on the bucket of a Load-Haul-Dump machine and a wheel loader in the scooping task. Adv. Robot. 1998, 13, 97–114. [Google Scholar] [CrossRef]
- Yuan, Z.; Lu, Y.; Hong, T.; Ma, H. Research on the load equivalent model of wheel loader based on pseudo-damage theory. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2022, 236, 1036–1048. [Google Scholar] [CrossRef]
- Gao, G.; Wang, J.; Ma, T.; Han, Y.; Yang, X. Optimisation strategy of torque distribution for the distributed drive electric wheel loader based on the estimated shovelling load. Veh. Syst. Dyn. 2022, 60, 2036–2054. [Google Scholar] [CrossRef]
- Tan, P.; Liu, X.-H.; Liu, C.-Y.; Zhang, C.; Chen, W.; Cao, B.-W.; Yang, K.; You, T. Investigating the matching characteristic of the full hydraulic braking system of the wheel loader. J. Braz. Soc. Mech. Sci. Eng. 2022, 44, 209. [Google Scholar] [CrossRef]
- Wu, H.W.; Lee, C.B. Influence of a relief valve on the performance of a pump/inverter controlled hydraulic motor system. Mechatronics 1996, 6, 1–19. [Google Scholar] [CrossRef]
- Huang, J.; Cheng, X.; Shen, Y.; Kong, D.; Wang, J. Deep Learning-Based Prediction of Throttle Value and State for Wheel Loaders. Energies 2021, 14, 7202. [Google Scholar] [CrossRef]
- Ma, W.; Zhang, Y.; Liu, C.; Wang, S. Prediction Method of the Fuel Consumption of Wheel Loaders in the V-Type Loading Cycle. Res. Artic. 2015, 2015, 538176. [Google Scholar] [CrossRef]
- Singh, V. A note on Routh’s criterion and Lyapunov’s direct method of stability. Proc. IEEE 1973, 61, 503. [Google Scholar] [CrossRef]
- Cerman, O.; Hušek, P. Adaptive fuzzy sliding mode control for electro-hydraulic servo mechanism. Expert Syst. Appl. 2012, 39, 10269–10277. [Google Scholar] [CrossRef]
- Chiang, M.-H.; Lee, L.-W.; Liu, H.-H. Adaptive Fuzzy Controller with Self-tuning Fuzzy Sliding-mode Compensation for Position Control of an Electro-hydraulic Displacement-controlled System. J. Intell. Fuzzy Syst. 2014, 26, 815–830. [Google Scholar] [CrossRef]
- Zhang, J.; Chen, D.; Shen, G.; Sun, Z.; Xia, Y. Corrigendum to “Disturbance observer based adaptive fuzzy sliding mode control: A dynamic sliding mode surface approach” [Automatic 129 (2021) 109606]. Automatic 2022, 142, 110413. [Google Scholar] [CrossRef]
- Lu, Y. Adaptive-Fuzzy Control Compensation Design for Direct Adaptive Fuzzy Control. IEEE Trans. Fuzzy Syst. 2018, 26, 3222–3231. [Google Scholar] [CrossRef]
- Abbasi, S.M.M.; Jalali, A. Fuzzy tracking control of fuzzy linear dynamical systems. ISA Transactions 2020, 97, 102–115. [Google Scholar] [CrossRef] [PubMed]
- Killian, M.; Mayer, B.; Schirrer, A.; Kozek, M. Cooperative Fuzzy Model-Predictive Control. IEEE Trans. Fuzzy Syst. 2016, 24, 471–482. [Google Scholar] [CrossRef]
- Mustafa, A.M.; Gong, Z.; Osman, M. Fuzzy Optimal Control Problem of Several Variables. Adv. Math. Phys. 2019, 2019, 2182640. [Google Scholar] [CrossRef]
- Phu, N.D.; Van Tri, P. The Fuzzy Dynamic Programming Problems. J. Intell. Fuzzy Syst. 2016, 30, 1663–1674. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhu, Y. Fuzzy optimal control of linear quadratic models. Comput. Math. Appl. 2010, 60, 67–73. [Google Scholar] [CrossRef]






| Operation Stage | Speed Interval | Unit |
|---|---|---|
| Priming stage | 0~8 | km/h |
| Heavy-Load stage | 8~16 | km/h |
| Pulling stage | 16~24 | km/h |
| Main Transportation stage | 24~32 | km/h |
| High-Speed stage | 32~40 | km/h |
| Name | Value | Unit |
|---|---|---|
| Overall vehicle mass | 21,650 | kg |
| Loading mass | 7000 | kg |
| Asphalt road resistance factor | 0.010–0.018 | |
| Pothole road resistance factor | 0.035–0.050 | |
| Gravel road resistance factor | 0.020–0.025 | |
| Compression road resistance factor | 0.050–0.150 | |
| Muddy road resistance factor | 0.100–0.250 | |
| Iced road resistance factor | 0.015–0.030 | |
| Dry sand road resistance factor | 0.100–0.300 | |
| Wheel radius | 0.75 | m |
| Windward area | 5 | m2 |
| Project | Highway | Dirt Road | Slope (30°) | Shovel |
|---|---|---|---|---|
| (kN) | 2.12 | 28.07 | 2.43 | 2.81 |
| (kN) | 0.00 | 0.00 | 140.38 | 0.00 |
| (N) | 185.00 | 11.57 | 2.89 | 0.50 |
| (kN) | 6.82 | 10.02 | 0.00 | 0.00 |
| (kN) | 0.00 | 0.00 | 0.00 | 84.50 |
| (kW) | 104.00 | 105.90 | 145.25 | 72.82 |
| Name | Value | Unit |
|---|---|---|
| Pump displacement | 175.4 | mL/r |
| Pump’s volumetric efficiency | 96 | % |
| Pump’s mechanical efficiency | 94 | % |
| Small-motor displacement | 164.2 | mL/r |
| Small-motor volumetric efficiency | 92 | % |
| Small-motor mechanical efficiency | 95 | % |
| Large-motor displacement | 170.6 | mL/r |
| Large-motor volumetric efficiency | 92 | % |
| Large-motor mechanical efficiency | 92 | % |
| Charge pump displacement | 24.5 | mL/r |
| Charge pump overflow pressure | 2.5 | MPa |
| Relief valve setting pressure | 42 | MPa |
| Flush valve setting pressure | 2 | MPa |
| Flush valve setting flow rate | 20 | L/min |
| Engine’s standard power | 180 | kW |
| Engine’s rated speed | 2000 | r/min |
| Maximum engine output torque | 1187 | Nm |
| Engine’s nominal fuel consumption | 235 | g/kWh |
| Lowest engine fuel consumption at full load | 230 | g/kWh |
| Drive axle’s transmission ratio (Z9/Z8) | 24.67 | |
| Larg-motor transmission ratio | 3.23 | |
| Small-motor transmission ratio (Z7/Z6) | 1.44 | |
| Transmission’s mechanical efficiency | 92 | % |
| NB | NM | NS | ZO | PS | PM | PB | |
|---|---|---|---|---|---|---|---|
| PB | ZO | PS | PM | PM | PM | PB | PB |
| PM | NS | ZO | PS | PM | PM | PM | PM |
| PS | NM | NS | ZO | PS | PM | PM | PM |
| ZO | NM | NM | NS | ZO | PS | PM | PM |
| NS | NM | NM | NM | NS | ZO | PS | PM |
| NM | NM | NM | NM | NM | NS | ZO | PS |
| NB | NB | NB | NM | NM | NM | NS | ZO |
| Items | Value | Unit |
|---|---|---|
| 175.4 | ||
| 164.2 | ||
| 170.6 | ||
| 352 | ||
| 64 | ||
| 9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Wang, Z.; Xie, L.; Wang, S.; Wang, Z.; Ma, W. Research on the New Hydrostatic Transmission System of Wheel Loaders Based on Fuzzy Sliding Mode Control. Energies 2024, 17, 565. https://doi.org/10.3390/en17030565
Wang X, Wang Z, Xie L, Wang S, Wang Z, Ma W. Research on the New Hydrostatic Transmission System of Wheel Loaders Based on Fuzzy Sliding Mode Control. Energies. 2024; 17(3):565. https://doi.org/10.3390/en17030565
Chicago/Turabian StyleWang, Xin, Zhongyu Wang, Lei Xie, Songlin Wang, Zhongshan Wang, and Wenxing Ma. 2024. "Research on the New Hydrostatic Transmission System of Wheel Loaders Based on Fuzzy Sliding Mode Control" Energies 17, no. 3: 565. https://doi.org/10.3390/en17030565
APA StyleWang, X., Wang, Z., Xie, L., Wang, S., Wang, Z., & Ma, W. (2024). Research on the New Hydrostatic Transmission System of Wheel Loaders Based on Fuzzy Sliding Mode Control. Energies, 17(3), 565. https://doi.org/10.3390/en17030565







