Occupant-Aware Energy Consumption Prediction in Smart Buildings Using a LSTM Model and Time Series Data

Abstract

Accurate energy consumption prediction in commercial buildings is a challenging research task. Energy prediction plays a crucial role in energy efficiency, management, planning, sustainability, risk management, diagnosis, and demand response. Although many studies have been conducted on building energy predictions, the impact of occupancy on energy prediction models for office-type commercial buildings remains insufficiently explored, despite its potential to improve energy efficiency by 20%. This study investigates energy prediction using a Long Short-Term Memory (LSTM) model that incorporates time-series power consumption data and considers occupancy. A real-world dataset containing the per-minute electricity consumption of various appliances in an office building in Houston, TX, USA, is utilized. The proposed machine learning models forecast future energy consumption based on hourly, 3-hourly, daily, and quarterly predictions for individual appliances and total energy usage. The model’s performance is evaluated using the following three metrics: Mean Absolute Percentage Error (MAPE), Mean Absolute Error (MAE), and Root Mean Square Error (RMSE). The results demonstrate the superiority of the proposed system.

1. Introduction

The intersection of industrialization, globalization, and urbanization has significantly escalated energy demand within the building sector, encompassing residential, commercial, and industrial structures. Therefore, the expansion in the size and number of buildings has intensified the strain on energy resources. The building sector as a whole consumes approximately 27.6% of the total energy in the United States. Commercial buildings alone account for a significant portion of this, representing about 18% of the total energy consumption in the country [1]. As depicted in Figure 1, the trend in energy consumption by commercial buildings from 2011 to 2020 demonstrates a consistent rise in power usage. This data highlight the urgent necessity to reevaluate and address the energy consumption patterns prevalent in the commercial building sector.

Commercial buildings offer substantial opportunities for enhancing energy efficiency. Irresponsible occupants might neglect to conserve and instead waste energy resources. Therefore, building managers face a double responsibility of maintaining user comfort and satisfaction while reducing energy use. This multifaceted problem indicates the immediate requirement for real-time solutions so that building managers can effectively utilize and monitor the energy consumed by commercial buildings.

The importance of occupancy in energy efficiency was demonstrated in our previous work, which utilized unsupervised machine learning techniques to identify inefficiencies [2]. Studies suggest that tailoring heating, ventilation, and air conditioning (HVAC) operations to consider occupant presence and behavior can result in substantial energy savings [3,4]. Supervised machine learning techniques applied to commercial buildings’ HVAC systems have been used to predict energy consumption, enabling the evaluation of energy-saving adjustments implemented by building managers [5]. By integrating unsupervised learning with occupant-aware supervised learning techniques, building managers can develop more effective energy-saving strategies and optimize Building Energy Management Systems (BEMS) to meet energy demands efficiently.

Addressing energy availability challenges requires proactive strategies, including the close monitoring and analysis of power consumption to enable accurate prediction and forecasting. By leveraging these approaches, building managers can efficiently manage energy demand and implement data-driven measures to optimize usage. Consequently, the ability to analyze and predict energy consumption in buildings has become an important component of energy management for the following reasons:

• Analyzing energy consumption patterns can help determine possibilities for energy optimization. In addition, building managers can make informed decisions to improve energy efficiency, minimize waste, and reduce operational costs. By accurately predicting energy consumption, energy managers can plan and allocate resources more effectively, which supports better future building designs.
• Various U.S. government programs aim to enhance the environmental sustainability of buildings. For example, the Department of Energy’s (DOE) Better Buildings Initiative encourages energy efficiency improvements by providing technical assistance and data sharing [6]. Furthermore, the ENERGY STAR program certifies energy-efficient buildings and products, supporting reductions in energy consumption and greenhouse gas emissions [7]. Such initiatives highlight the significance of leveraging advanced techniques, such as occupancy data-driven methods and machine learning models, for optimizing energy consumption and promoting sustainability in commercial and residential buildings.
• Predicting building energy consumption is important for reaching long-term sustainability goals. This process involves identifying opportunities to incorporate renewable energy sources and encouraging sustainable building practices.
• Identifying anomalies helps managers reduce costs and improve efficiency by understanding energy usage patterns. This supports sustainability goals and helps create a more reliable and effective energy management plan.
• Forecasting building load is crucial for demand response initiatives in the commercial sector. Building managers can use the forecast to anticipate peak demand periods and proactively adjust energy usage to meet grid requirements. Participation in demand response programs allows commercial buildings to contribute to grid stability, reduce pressure on energy infrastructure, and potentially receive lower energy costs.
• Occupancy information and energy forecasting are valuable for digital technologies such as Building Information Modeling (BIM) and Digital Twin (DT). BIM integrates building design and construction data into a digital model, enabling efficient planning and energy simulation and providing detailed building characteristics for precise input data in energy management tools [8,9]. DT extends this concept by creating real-time virtual replicas of physical systems, enabling advanced monitoring, optimization of energy consumption, and predictive analytics using real-world data. Their integration with these tools, like the open tool (OT) for renewable energy, can further enhance energy distribution strategies by leveraging Artificial Intelligence and Machine Learning (AI/ML) techniques such as LSTM networks for temporal energy forecasting [10,11]. The integration of BIM, DT, and data-driven models can significantly improve energy forecasting, management, and sustainability in smart buildings and urban systems.

Several studies employ ML techniques to predict energy consumption in buildings, including artificial neural networks (ANN’s) [12], the support vector machine (SVM), the decision tree (DT), and the adaptive neuro-fuzzy inferring system (ANFIS) [12,13,14]. The task learning-based approach is another technique that uses kernel-based learning to forecast electricity demand [15]. Sparse coding-based architecture is also used for medium-term load forecasting [16,17,18]. ARIMA-based time-series forecasting has generally succeeded in predicting short-term predictions, whereas LSTM, an improved version of RNN, was proven to be more useful in deducing longer-term predictions, especially in the time-series domain. The accuracy of these prediction models is impacted by human factors, such as occupancy and desired comfort level; building factors, such as building envelope parameters and the HVAC system; and weather factors, such as climate variability and seasonal differences [19]. However, previous work does not take into consideration occupancy in predicting building load. Therefore, in this study, we develop and analyze the performance of the LSTM model in an office-style commercial building in the Houston area.

This paper investigates whether occupancy significantly influences energy load prediction accuracy in the context of office buildings situated in hot and humid areas, such as Houston. The main contributions of this study are as follows:

• The paper uses a real-world dataset of a mid-size net-zero office building in the Houston area. The data contain occupancy information as well as time-series records of power consumption at 15 min intervals, covering the entire building’s power usage, as well as individual submeter data for HVAC, plug-ins, and lighting.
• The study is unique in that it includes occupancy in the prediction models and therefore provides an insight into the impact of occupancy in building energy predictions.

The rest of the paper is structured as follows. Section 2 introduces the literature review of energy consumption prediction. The LSTM prediction model is presented in Section 3. Section 4 contains the proposed methodology and the dataset details. Section 5 contains the prediction results and discusses the results obtained. We conclude and discuss the direction of our future work in Section 6.

2. Literature Review

Energy consumption estimation is considered a basic step for analyzing and estimating load management and future consumption in smart environments. However, due to temporal fluctuations and the existence of both linear and non-linear patterns in energy consumption data, researchers are exploring different statistical and AI techniques that can improve the accuracy of forecasting models. Various studies have been presented in the past that optimize the energy consumption estimation algorithms using different statistical and AI techniques.

Table 1. Forecasting energy consumption—a summary.

Approach	References	Key Contributions
Statistical Techniques	Dimitra Kouvara et al. [20], Durand et al. [21], Harveen et al. [22], Tianhe et al. [23], Meftah et al. [24], Allemar et al. [25]	The use of ARIMA or SARIMA leads to good forecasting of energy consumption at various scales.
Machine Learning Techniques	Zhenxiang Dong et al. [26], D. Mariano-Hernández et al. [27], Zhun et al. [28], Fu et al. [29], Valgaev et al. [30]	From decision trees and SVM to kNN, these techniques can predict energy demand accurately.
Deep Learning Techniques	Daniela Durand et al. [31], Syed et al. [32], Hao et al. [33], Zargham et al. [34], Rana et al. [35], Tan et al. [36], Almalaq et al. [37], Choi et al. [38]	Various techniques are adopted, including back-propagation neural networks, neuro-fuzzy networks using the power of artificial neural networks, AWNN, recurrent neural networks, and LSTMs. These techniques are ideal for sequential data prediction and fit for use in cases that require short- or long-term time-series predictions.
Ensemble Learning Techniques	AbdelKarim et al. [39], Diogo et al. [40], Fahmi et al. [41]	In comparison to statistical and machine learning techniques, ensemble learning showed significant improvements in forecasting energy consumption.

summarizes some of these studies.

AbdelKarim et al. [39] present a load forecast technique by decomposing the time-series data based on the historical evolution of each hour of the day. Researchers used the decomposed attributes to train different machine learning and deep learning algorithms, e.g., Multi-Layer Perceptron (MLP), Support Vector Machine (SVM), Radial Based Function (RBF), Reduced Error Pruning Tree (RepTree), and Gaussian Process (GP). They obtained satisfactory results and used MAPE, MAE, and RMSE as error metrics.

Hao et al. [33] investigated the methodologies used to collect electricity consumption-related information and multi-factor power consumption forecasting models. A comprehensive analysis and accurate power consumption data are required for robust and efficient power grid transformation. Researchers used a back-propagation neural network (BPNN) to forecast energy consumption using Pecan Street which considers multiple factors such as holidays, weekends, and weather conditions. Analysis proved that better forecasting accuracy is achieved when incorporating the factors into a high-sampling dataset (hourly, daily) compared to a low-sampling one (weekly, monthly).

Zargham et al. [34] proposed an intelligent technique for the forecasting load of a complicated electrical system located in the Fars province of Persia. They introduced a neuro-fuzzy technique for load prediction that uses the power of Artificial Neural Networks (ANN). The researchers used energy data for several years to train an effective and adaptive network. They found that ANN can effectively capture power consumption patterns whereas fuzzy logic can effectively identify signal trends. This model outperforms the traditional techniques for energy consumption estimation. Furthermore, researchers used the proposed intelligence network for the estimation of time-series behavior for several years. Zhun et al. [28] proposed a predictive model using a decision tree classifier. This method has a competitive advantage over other techniques such as ANN and regression because it generates an interpretable flowchart-like structure. Results highlighted significant factors with an accuracy of 93%. Users can utilize this technique without having too much computation knowledge.

The authors in [29] proposed an SVM-based machine-learning technique for predicting load at the building’s electric system level (power, lighting, air conditioning, and others). They trained 24 SVM models for the prediction of the hourly electricity load. The proposed model takes the hourly electricity loads and weather conditions of the past 2 days. A case study shows that the proposed technique outperforms other popular machine learning techniques, e.g., Decision Tree, ARIMAX, and ANN. The authors managed to predict the load with a mean bias error of 7.7% and a root mean square error of 15.2.

Valgaev et al. [30] proposed a k-Nearest Neighbor (k-NN) based technique for power demand forecasting as part of Smart City Demo Aspern (SCDA). Daily load curves and their successors were fed as input to the k-NN forecasting method. The proposed technique achieved significant results but was limited in forecasting future values. Furthermore, the proposed model parameterizes automatically and does not require any manual parameter setup. The proposed model predicts energy consumption for the next 24 h during weekdays, making this approach feasible in a low-voltage environment.

The authors in [35] proposed a new method for forecasting short-term load predictions, and it is known as the Advanced Wavelet Neural Network (AWNN). This method decomposes the load data into different components based on the frequencies and uses wavelet transform with cross-entropy to choose the best wavelet. The authors evaluated the performance of the proposed AWNN using Spanish and Australian electricity load data for multi-step ahead predictions and compared it with multiple benchmark algorithms. Using the AWNN led to good prediction accuracy and outperformed other forecasting techniques such as ARIMA and Model Tree Rule (MTR).

The work in [36] used LSTM to forecast a daily-day ahead energy consumption of a building using a 3-year dataset collected from a building in the Malacca campus. Analysis showed that including weather data such as temperature, wind speed, and rainfall duration positively impacts the model accuracy. To illustrate the power of the used model, it was compared to two other techniques, support vector regression (SVR) and GP regression. LSTM achieved the best root mean square error and mean absolute error scores.

Harveen et al. [22] worked on improving the ability of energy consumption predictions by using two statistical models named ARIMA and SARIMA that require stationary datasets. The dataset used was collected from a hospital over the last 11 years, and results proved that SARIMA outperformed the ARIMA model. The work done highlights the importance of using the two models for forecasting electricity consumption at various scales in different domains.

Tianhe et al. [23] proposed a technique based on seasonal, trend decomposition, X12, using the Loess decomposition methods for monthly forecasting. They decomposed the electricity consumption of each month following time-series decomposition individuation, which influences the factorization of processed data into trend, season, and random components. The researchers then selected an appropriate model for predicting the components for reconfiguring the monthly forecast. They developed the forecasting program using R V3.4 and Matlab V2019a and conducted a case study on university power consumption data. Results show that the proposed method led to effective forecasting outcomes.

Fahmi et al. [41] proposed a technique that estimates household electricity consumption using a combination of linear and non-linear models. They developed the Multiplicative SARIMA, Feed Forward Neural Network, Subset ARIMA, and hybrid model. Since the hybrid model combines linear and non-linear models, the hybrid Multiplicative SARIMA-FFNN and hybrid Subset ARIMA-FFNN were proposed. The results show that hybrid models perform better than traditional models.

Meftah et al. [24] adopted the ARIMA models to prove they can compete with different machine learning techniques used for electricity consumption forecasting. They identified the (p, d, q) values as well as stationarity of data by utilizing PACF and ACF plots. Despite the model’s simplicity, seasonal ARIMA led to satisfactory results with an error of 4.332%.

Allemar et al. [25] proposed a technique that uses the ARIMA (p, d, q) model for forecasting electric consumption. The researchers used the historical data generated from power statistics from 2003 to 2017. They identified the optical model after the selection of the lowest Akaike Information Criterion (AIC) value. The results show that the ARIMA model is an appropriate model for forecasting commercial, electrical and industrial electricity.

Diogo et al. [40] proposed a cost-effective solution for enhancing and improving energy consumption management techniques. The researchers proposed an evolutionary hybrid system (EvoHyS) that uses statistical and machine learning techniques. The proposed technique consists of teh following three steps: (i) predicting the linear and seasonal components using the SARIMA model, (ii) predicting the error series using a machine learning (ML) technique, and (iii) combining both non-linear and linear forecasts using a secondary ML model. The authors conducted experiments with energy data in the one-step scenario. The proposed approach improved significantly compared with the hybrid, statistical, and traditional ML techniques utilizing the Mean Squared Error (MSE) metric.

The researchers in [42] presented a pre-training technique for deep reinforcement learning (DRL) agents in thermal energy management using LSTM-based data-driven models. By using an EnergyPlus simulation environment and a recursive training approach, the DRL agent achieved an 80% reduction in indoor temperature violations compared to a rule-based controller (RBC) while maintaining the same energy consumption. The results showed the potential of data-driven models to enhance DRL scalability and reduce reliance on complex engineering simulations, with future work focusing on extending the approach to real-world deployment and integrating renewable energy systems. Moreover, the work in [43] developed a lightweight predictive model for NOx emissions in coal-fired boilers, targeting flexible power generation systems with fluctuating demands. The model used random forest for input selection, time-delay estimation for improved accuracy, and a novel Channel Equalization Block (CE-Block) to enhance CNN performance. Validated on a 600 MW boiler, the model reduced training time by 21.74%, improved RMSE by 20.97% and MAE by 22.11%, and increased $R^2$ by 3.48% compared to a baseline CNN, showing its effectiveness for dynamic NOx prediction.

The authors in [31] utilized LSTM neural networks for energy consumption prediction in smart buildings; in this work, they demonstrated its effectiveness in analyzing relationships between variables and determining the time window for generating prediction models. Specifically, they focused on predicting energy consumption using device and appliance data. It uses a feature engineering approach to analyze energy consumption variables and produce prediction models based on time-series data. The study used Pearson and Spearman correlations, multiple linear regression, and principal component analysis (PCA) to understand relationships between variables. It also explored autocorrelation and ARIMA models to define time windows for prediction. LSTM neural networks were employed to generate predictive models, evaluated using RMSE, MAPE, and $R^2$ metrics. The LSTM models were compared with other techniques across different datasets.

Recent studies have shown that Deep Neural Networks (DNN), particularly Recurrent Neural Networks (RNN), have been mainly used to predict sequential data. These methodologies have been used to predict both short- and long-term energy consumption [37,38]. The main drawback of RNN is the problem of vanishing and exploding gradients. However, this problem has been solved by using the LSTM model. This model works quite well for both long- and short-term time-series predictions along with the industry benchmark ARIMA model used for short-term forecasting.

While significant advancements have been made in energy consumption forecasting using various machine learning and deep learning techniques, occupancy data have been largely overlooked in these models. Occupants play a critical role in influencing energy consumption patterns, particularly in smart buildings where automation and adaptive systems respond to human presence. Incorporating occupancy data into forecasting models will bridge this gap, enabling more precise energy management strategies that reflect actual building usage, particularly in dynamic environments like office spaces. Therefore, there is a pressing need for further research to explore the integration of occupancy data in energy prediction models for smart buildings.

3. LSTM Prediction Models

In this study, we chose LSTM as our preferred technique. We thoroughly evaluated its performance compared to other methods, such as ARIMA and SVR. Our preliminary analysis showed that LSTM outperforms these alternative techniques, achieving a significantly lower error rate of 2.0463 (refer to

Table 2. RMSE of different machine learning architectures.

ML Architecture	RMSE
LSTM	2.0463
ARIMA	7.3890
SVR	3.1518

). This finding is consistent with the existing literature, highlighting LSTM’s superiority in various time-series forecasting tasks.

LSTM’s effectiveness can be attributed to its ability to capture temporal dependencies, manage nonlinear patterns, address the vanishing gradient problem, and adapt to varying time scales. In particular, power consumption data displays complex temporal relationships influenced by short-term and long-term dependencies, including hourly, daily, weekly, and seasonal cycles. LSTM’s recurrent architecture allows it to capture these dependencies by having information from past observations over extended periods.

Additionally, power consumption patterns often involve nonlinear relationships and complex dynamics affected by many factors, such as weather conditions, weekends, holidays, and occupancy levels. LSTM’s capability to model these nonlinear relationships allows it to learn and represent complex power consumption data patterns accurately. Furthermore, LSTM’s unique architecture effectively mitigates the vanishing gradient problem frequently encountered in traditional recurrent neural networks (RNNs). Including memory cells and gating mechanisms enables LSTM to propagate relevant information and capture dependencies across multiple time steps.

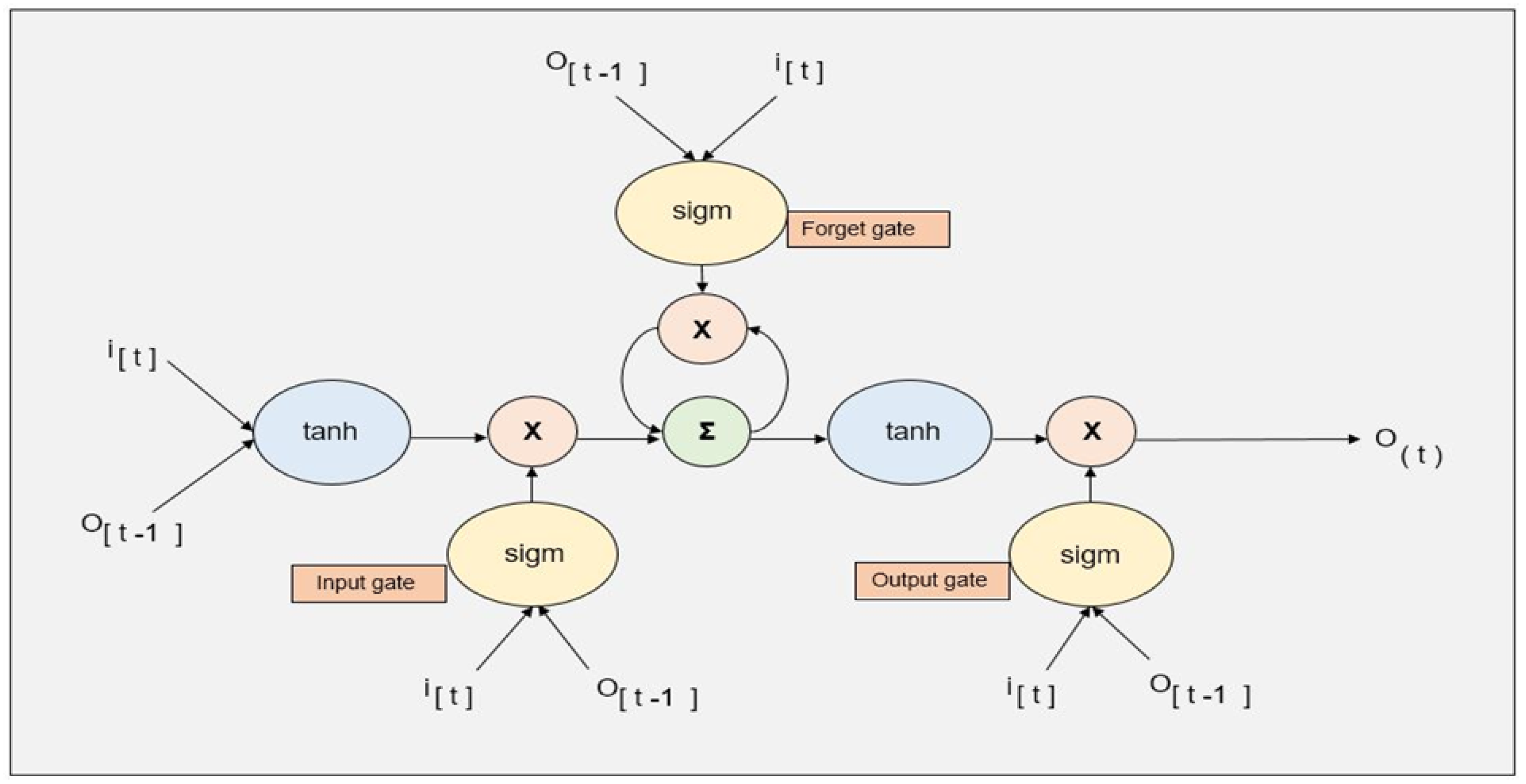
LSTM, categorized as a recurrent neural network (RNN) [44], was initially developed to address the challenge of vanishing gradients by introducing a model capable of retaining information over longer time periods. An LSTM network comprises memory cells, including self-loops, as shown in Figure 2. The self-loop permits saving the temporal data encrypted onto the cell’s state. The course of data along the network is operated through writing, erasing, and reading from the cell’s memory state [45].

The aforementioned operations are controlled by the following three gates in particular: (1) input gate, (2) forget gate, and (3) output gate. Equations (1)–(6) demonstrate one LSTM cell’s operations.

$$i_g=\sigma (i_t{W}_{ix}+o_{t-1}{W}_{im}+b_i)$$

(1)

$$f_g=\sigma (i_t{W}_{fx}+o_{t-1}{W}_{fm}+b_f)$$

(2)

$$o_g=\sigma (i_t{W}_{ox}+o_{t-1}{W}_{om}+b_o)$$

(3)

$$u=tanh(i_t{W}_{ux}+o_{t-1}{W}_{um}+b_u)$$

(4)

$$x_t=f_g^{\circ }{x}_{t-1}+i_g^{\circ }u$$

(5)

$$o_t=o_g^{\circ }tanh\left(u\right)$$

(6)

Here $i_g$ communicates to the input gate, $f_g$ corresponds to the forget gate, and $o_g$ corresponds to the output gate. Moreover, $x_{\left[t\right]}$ is the value of the state at time step t, $o_{\left[t\right]}$ is the output of the cell, and u is the update signal.

The input gate determines whether the update signal must alter the memory state or not. This is executed by employing a sigmoid function as a “soft switch”, whose on-state and off-state relies on the present input as well as the preceding output (Equation (1)). If the value of the input gate ($i_g$) is near zero, then, the update signal is multiplied by zero; hence, the state will not be affected by the update (Equation (5)). The forget gate and output gate work similarly.

LSTM cells could be stacked in a multi-layer architecture to establish a closer network. The architecture is mainly applied to estimate a result ${\widehat{y}}_{\left[t\right]}$ at time $t\in \mathbb{N}$, provided the set of all preceding inputs $\left\{i\right[0],i[1],\dots ,i[t\left]\right\}$.

4. Methodology

The methodology uses LSTM neural networks on a real-world dataset of a medium-sized office building in the Houston area. The sensors are implemented in different sectors of the building as part of the Building Management System (BMS) that tracks the electricity consumption of various equipment and appliances. Figure 3 describes the general structure of the model’s input and output. This section depicts the data utilized for the analysis and the preprocessing methods applied to ensure its quality and suitability for modeling. The LSTM model’s parameter configuration is discussed, detailing the choices made to optimize performance. The training process is described, highlighting the steps taken to effectively fit the model to the training data. Finally, the evaluation metrics employed to gauge the model’s performance include MAPE, MAE, RMSE, and the coefficient of determination (R-squared), which provide a comprehensive assessment of the model’s predictive accuracy.

4.1. Dataset

A real-world dataset has been used to develop and train the model. The attributes of the dataset are shown in

Table 3. Dataset attributes.

ID	ITEMS
1	Outdoor temperature
2	People counter
3	Lighting
4	HVAC
5	Plug loads
6	Elevator
7	Total consumption

. For the proposed model, we used data from the outdoor temperature, people counter, lighting, HVAC, plug loads, elevator, and total consumption. A sample of these data is given in

Table 4. Dataset sample.

Timestamp	Total (kWh)	Outdoor Temp	No. of Users	Elevator (kWh)	Plug (Load) kWh	Lighting (kWh)	AC (kWh)
13-10-18 0:00	5.72159	74	0	0.076933	2.556475	1.604462	1.483719
13-10-18 1:00	5.81373	73	0	0.076691	2.601041	1.605026	1.530972
13-10-18 2:00	6.635789	73	0	0.077806	2.507597	1.605784	2.444602
13-10-18 3:00	5.791026	74	0	0.077046	2.650629	1.605993	1.457357
13-10-18 4:00	6.422209	73	0	0.076961	2.612281	1.60525	2.127716
13-10-18 5:00	6.231321	73	0	0.076672	2.654008	1.606151	1.894491
13-10-18 6:00	5.858359	75	0	0.075979	2.672275	1.603844	1.506261
13-10-18 7:00	9.126334	77	0	0.076851	2.54318	0.69662	5.809684
13-10-18 8:00	8.885589	78	5	0.076296	2.569881	0.525307	5.714105
13-10-18 9:00	8.78415	82	5	0.075949	2.704809	0.525052	5.478341

.

4.2. Preprocessing

The dataset initially contained the energy consumed, which was recorded at every minute. We made four sets for the consumption of electricity out of the collected data as follows: hourly, 3-hourly, quarterly, and daily. Furthermore, the preprocessed sample of the dataset used for hourly consumption is presented in Table 4. The attributes of the dataset are explained below:

• The timestamp shows the date and time when the energy consumption was recorded.
• Total is the energy consumed by all appliances.
• Outdoor temperature is the average recorded outside temperature (in °F).
• No. of users is the recorded number of users in the building.
• Elevator is the energy consumption of elevators.
• Plug load is the energy consumption of the plugs.
• Lighting is the energy consumed by lighting appliances.
• AC is the energy consumption of the air conditioner.

4.3. LSTM Parameter Configuration

Theoretically, there is a huge number of combinations that can be made, even while utilizing grid search. A list of hyperparameters to optimize includes loss function, activation function, optimizer, dropout, batch size, number of hidden layers, and number of neurons. This can be reduced by fixing some hyperparameters, specifically, the activation function, optimizer, dropouts, and loss function. Tests were done to first figure out an optimal combination of these four hyperparameters for hourly, 3-hourly, quarterly, and daily datasets. Then, by fixing these hyperparameters, the remaining four were allowed to vary as grid search was used.

Table 5. Summary of the grid search experiment.

Parameters	Initial Hyperparameters	Final Hyperparameters
Loss function	MSE	MAE
Activation function	Sigmoid	selu
Optimizer	Adam	SGD (0.9 momentum)
Dropouts (input, hidden)	0.0, 0.0	0.0, 0.0
Batch size	24	24
Number of hidden layers	2	1
Number of neurons	10	10
Epochs	50	50
RMSE	0.86883	0.21977

summarizes multiple iterations of grid searching for the hourly dataset with 1-lag observation. The hyperparameters of the initial and final models are presented with RMSE as the error for comparison, in which there was a 75% improvement in error. As an experiment was concluded, the hyperparameter that yielded the lowest error was chosen, then, the next experiment was done until all hyperparameters that resulted in minimal errors were chosen, producing a model with the hyperparameters in the third column of Table 5.

Since less than 4 months’ worth of data are available, there is a high number of errors when trying to create models on the 3-hourly, quarterly, and daily datasets, as well as the inability to create models for a higher number of lag observations. Furthermore, it is not possible to predict an entire year’s worth of energy consumption due to the small data size.

5. Prediction Results and Analysis

We trained and evaluated our model on four different time frames to get more insights into the data and judge the proposed model’s performance. The train:test split was 78:22, or equivalently, 75 days of training data and 21 days of testing data. Four accuracy metrics were used to evaluate the performance of the LSTM-based prediction model, namely, the mean absolute precision error (MAPE), mean absolute error (MAE), root mean square error (RMSE), and coefficient of determination ($R^2$). Equations (7)–(10) demonstrate how each of the errors is calculated.

$$\mathrm{MAPE}={\displaystyle \frac{1}{n}}\sum _{i=1}^n\left|{\displaystyle \frac{y_i-y_i^{\prime }}{y_i}}\right|$$

(7)

$$\mathrm{MAE}={\displaystyle \frac{1}{n}}\sum _{i=1}^n|y_i-y_i^{\prime }|$$

(8)

$$\mathrm{RMSE}=\sqrt{{\displaystyle \frac{1}{n}}\sum _{i=1}^n{(y_i-y_i^{\prime })}^2}$$

(9)

$$R^2=1-{\displaystyle \frac{{\sum }_{i=1}^n{(y_i-y_i^{\prime })}^2}{{\sum }_{i=1}^n{(y_i-\overline{y})}^2}}$$

(10)

where $y_i^{\prime }$ and $y_i$ are the predicted and actual hourly energy consumption data, respectively.

Table 6. Optimal parameters for different lags and their respective testing errors.

Parameters	1-lag	24-lag	48-lag	168-lag
Loss function	MAE	MAE	MAE	MAE
Activation function	selu	Sigmoid	Sigmoid	Sigmoid
Optimizer	SGD	SGD	SGD	SGD
Dropouts (input, hidden)	0.0, 0.0	0.0, 0.0	0.0, 0.0	0.0, 0.0
Batch size	24	24	8	4
Number of hidden layers	1	1	1	1
Number of neurons	10	10	5	10
Epochs	50	20	50	30
Statistics
RMSE	0.21977	0.32031	0.22337	0.28790
R2	0.99641	0.99257	0.99649	0.99448
MAE	0.15549	0.21461	0.16086	0.21714
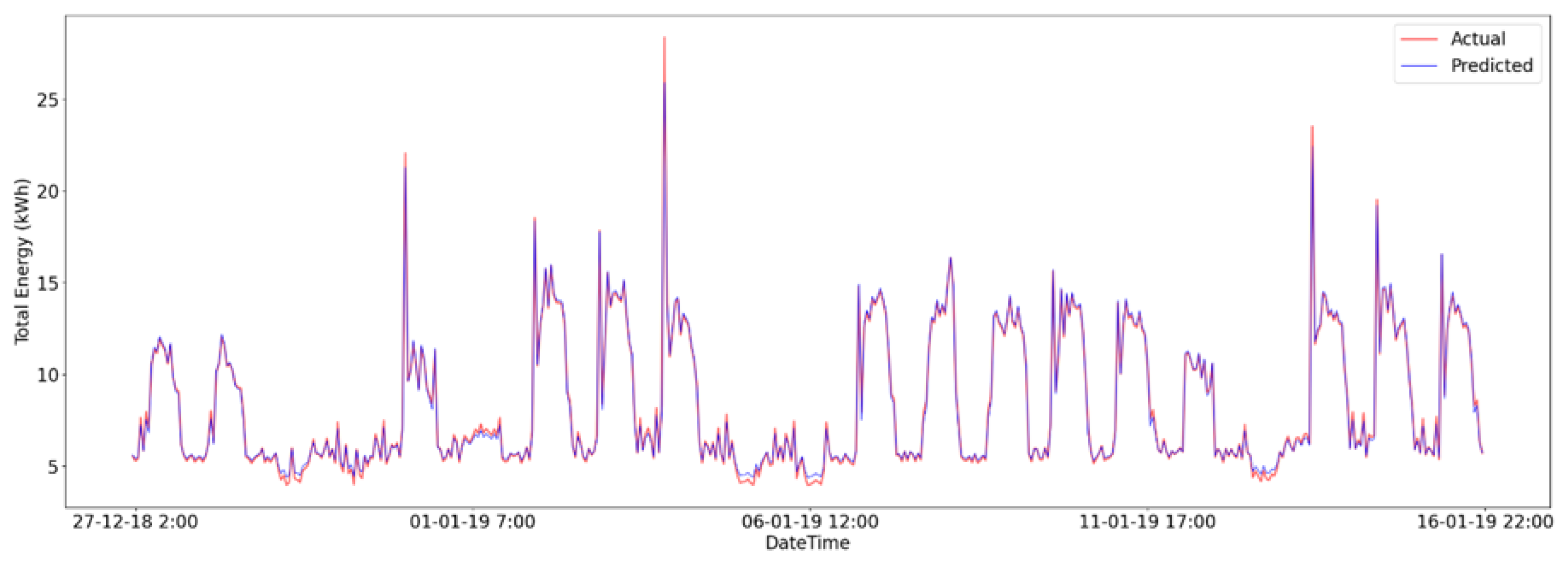
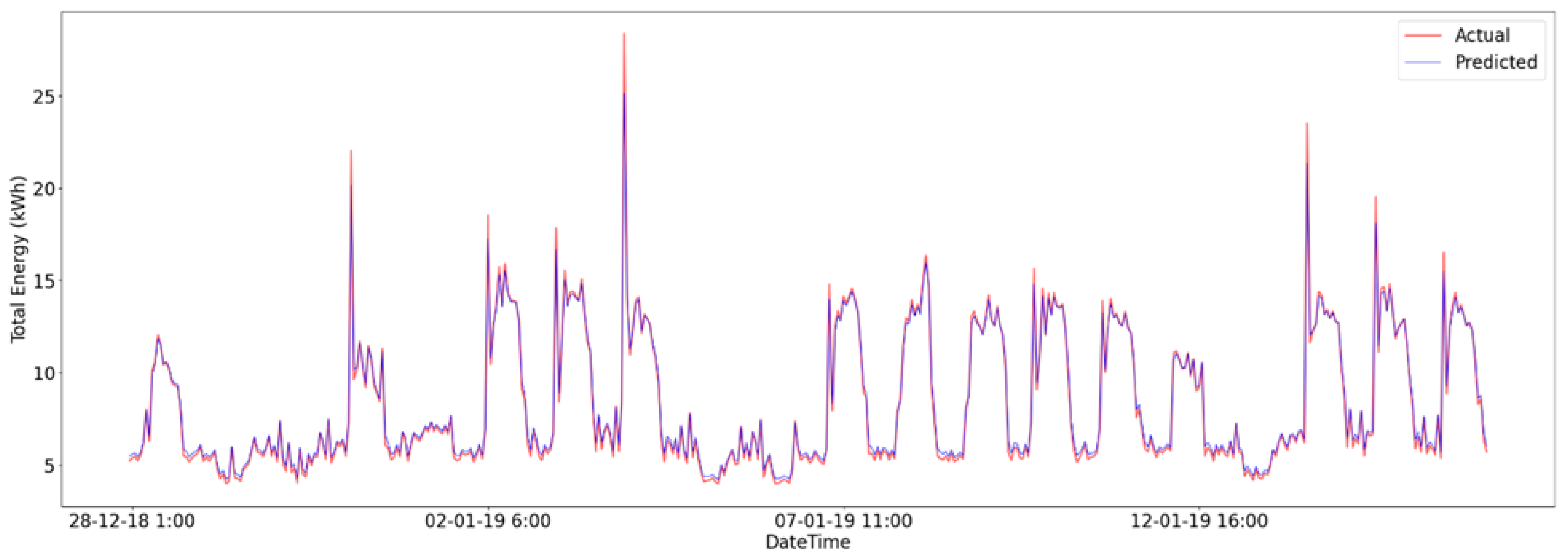
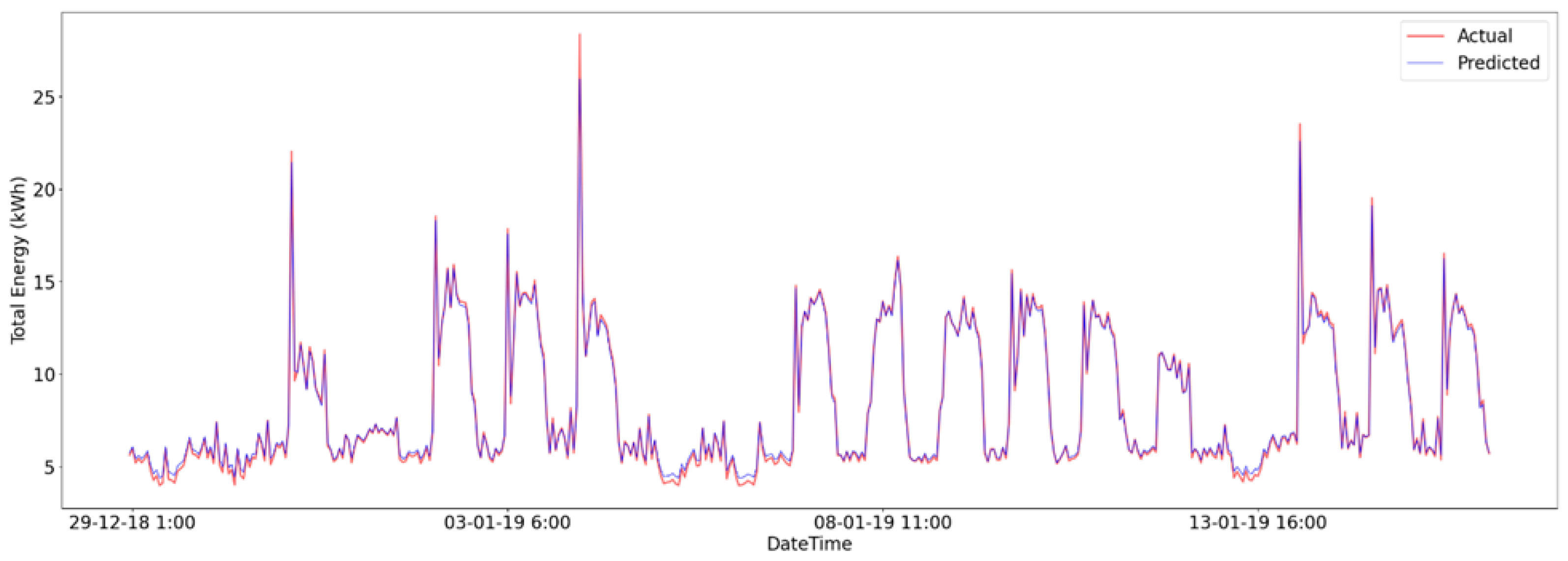
MAPE	0.02219%	0.02976%	0.02397%	0.02313%

provides a summary of all the models and their errors for different lag observations on the hourly dataset, namely, 1, 24, 48, and 168 lag, and Figure 4, Figure 5, Figure 6 and Figure 7 are plots of the predicted and actual energies with the y-axis representing the RMSE between the predictions produced by the model and the actual energy.

Effect of Occupancy on Prediction Accuracy

To assess the impact of occupancy on energy consumption prediction, we extended the LSTM model to include the number of users in the building as an additional feature. We trained and evaluated three models with different combinations of input features:

• Model A: outdoor temperature and number of users.
• Model B: number of users only.
• Model C: outdoor temperature only.

For consistency, all models were trained using the same architecture and hyperparameters.

Table 7. Hyperparameters used for the models incorporating occupancy data.

Hyperparameter	Value
Loss function	MAE
Activation function	selu
Optimizer	SGD (momentum = 0.9)
Dropout rates (input, hidden)	0.0, 0.0
Batch size	24
Number of hidden layers	1
Number of neurons	10
Epochs	30

summarizes the hyperparameters used for these models.

The models were evaluated using several metrics, including RMSE, MSE, $R^2$, adjusted $R^2$, MAE, and MAPE. The performance results on the test dataset are presented in

Table 8. Performance metrics for models with different input features.

Statistic	Model A	Model B	Model C
Input features	Temp + Users	Users Only	Temp Only
RMSE	0.25374	0.36216	0.29156
MSE	0.06438	0.13116	0.08501
$R^2$	0.98901	0.97762	0.98549
Adjusted $R^2$	0.98899	0.97757	0.98546
MAE	0.09306	0.21339	0.15018
MAPE	0.04135%	0.10975%	0.07802%

.

The results show that merging the outdoor temperature and occupancy data (Model A) results in the best performance across all evaluation metrics. Model A achieved an RMSE of 0.25374, which is lower than that of Model C (0.29156) and significantly lower than that of Model B (0.36216). Furthermore, the MAE and MAPE for Model A have the lowest values among the three models, with an MAE of 0.09306 and a MAPE of 0.04135%.

Comparing Models A and C, the addition of occupancy data with outdoor temperature improved the RMSE by approximately 13%. The MAE improved by approximately 38%, and the MAPE decreased from 0.07802% to 0.04135%. This demonstrates that occupancy data provides additional useful information that enhances the model’s ability to predict energy consumption accurately.

Model B, which uses only occupancy data as the input feature, achieved the worst among the three models. This indicates that while the number of users in the building does affect energy consumption, it is insufficient on its own to accurately predict energy usage. Environmental factors such as outdoor temperature play a significant role, likely due to the HVAC systems’ response to temperature variations.

The results show that incorporating occupancy data can enhance energy consumption predictions in smart buildings. Accurate occupancy sensing technologies, such as infrared sensors, Radio-Frequency Identification (RFID) systems, or Wi-Fi tracking, could provide more precise data and potentially lead to greater improvements in prediction accuracy.

In practical applications, even small improvements in prediction accuracy are valuable, as they can lead to better energy management strategies and increased overall energy efficiency. Therefore, building energy prediction models should consider including occupancy data when available.

6. Conclusions and Future Work

In a world marked by rapid industrialization and globalization, efficient energy management is playing a key role in smart energy management systems, necessitating the accurate prediction of future energy requirements. In this study, we comprehensively analyzed energy consumption forecasting in an office building in the Houston area, considering the individual consumptions of various categories inside the building (HVAC, plug-ins, etc.) and the overall energy demand. Our focus was on hourly, 3-hourly, quarterly, and daily consumption patterns. To achieve accurate predictions, we trained and evaluated LSTM using a real-world dataset of the building’s electricity consumption.

By employing evaluation metrics such as MAPE, MAE, and RMSE, we assessed the performance of our proposed models and obtained promising results. Our results indicate that the models accurately forecast energy usage across various time intervals, including hourly, 3-hourly, quarterly, and daily predictions for individual appliances and total energy consumption. In future work, we plan to expand the dataset size, which will enhance the robustness of our models. Additionally, we aim to explore different regularization techniques to improve the accuracy of predictions. Furthermore, we intend to investigate the effectiveness of deep learning algorithms in long-term energy consumption prediction. We also plan to include additional data, such as relative humidity, wind speed, specific household appliance consumption, and economic factors, to enhance our models’ predictive capability. By extending our research in these directions, we aim to contribute to the development of more effective and reliable methods for forecasting energy consumption in buildings. This will provide valuable insights for energy planning and management, facilitating the sustainable and efficient utilization of resources in the face of increasing energy demands.