Coordinated Volt-Var Control of Reconfigurable Microgrids with Power-to-Hydrogen Systems
Abstract
1. Introduction
- Developing comprehensive volt-var control by effectively managing various equipment, such as OLTC, SCBs, RESs, smart PV inverters (SPVIs), etc.;
- Incorporating the concepts of P2H and H2P into the volt-var control via an electrolyzer, hydrogen storage, and a fuel cell;
- Incorporating the concept of grid-to-vehicle and vehicle-to-grid EVA in the volt-var control of reconfigurable microgrids;
- Implementing the dynamic feeder reconfiguration in the presence of coordinating other equipment to increase the flexibility of the microgrids;
- Thoroughly considering the unpredictability and intermittency regarding loads, RESs, and EVAs via the UT method in order to evaluate the suggested volt-var control in a realistic manner;
- Developing volt-var control that can perform convex formulation, which results in finding the possible global solution in a finite time.
2. Problem Formulation
- SPVIs: Convert the direct current output from solar panels into alternating current and provide or absorb reactive power.
- OLTCs: Regulate voltage levels by adjusting the tap positions on transformers, which are generally installed after the slack bus.
- Electrolyzers: Generate hydrogen by converting electrical power into hydrogen through water electrolysis.
- Fuel cells: Convert stored hydrogen back into electricity.
- Hydrogen Storage: A tank located between the electrolyzer and the fuel cell that enhances flexibility by storing hydrogen generated from surplus renewable energy for use by the fuel cell.
- EVAs: Aggregations of EVs that are used as mobile energy storage systems.
- DGs: Diesel generators that are typically deployed to meet loads when renewable energy sources do not provide sufficient generation.
- Remote Switches: These switches enable microgrid operators to change the configuration of the microgrid in order to enhance its techno-economic efficiency.
2.1. Objective Function
2.2. List of Constraints
2.2.1. Smart PV Inverters
2.2.2. Electric Vehicles
2.2.3. Switchable Capacitor Banks
2.2.4. On-Load Tap Changer
2.2.5. Diesel Generator
2.2.6. Hydrogen-to-Power Conversion Technology
2.2.7. Power Flow
2.2.8. Radiality of Network
3. Unscented Transformation
- (1)
- Based on the input uncertain parameters, sample points are generated using the following expression:
- (2)
- For every generated sample point, the corresponding weighting factor is determined using the following equations:
- (3)
- The proposed problem is solved for the samples generated above to compute the fitness function for each sample point, as follows.
- (4)
- The mean, , and the covariance, , of the output variable are determined using the following formulas:
4. Simulation Results
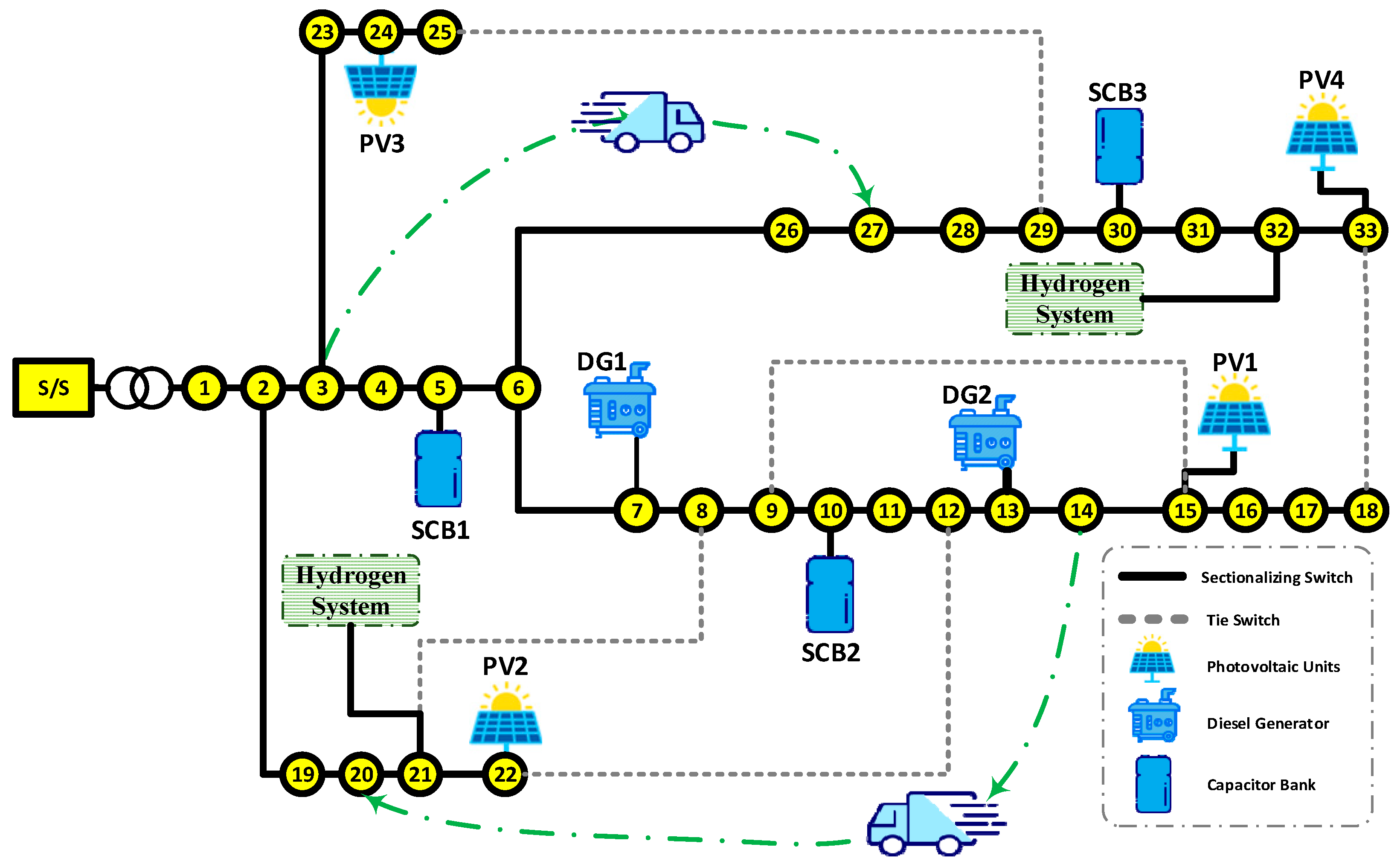
4.1. System Description
- Case 1: RESs (yes), DGs (yes), SCBs (yes), OLTC (yes), EVA (no), reconfiguration (no), electrolyzer (no), hydrogen storage (no), and fuel cell (no).
- Case 2: RESs (yes), DGs (yes), SCBs (yes), OLTC (yes), EVA (yes), reconfiguration (no), electrolyzer (no), hydrogen storage (no), and fuel cell (no).
- Case 3: RESs (yes), DGs (yes), SCBs (yes), OLTC (yes), EVA (yes), reconfiguration (yes), electrolyzer (no), hydrogen storage (no), and fuel cell (no).
- Case 4: RESs (yes), DGs (yes), SCBs (yes), OLTC (yes), EVA (yes), reconfiguration (yes), electrolyzer (yes), hydrogen storage (yes), and fuel cell (yes).
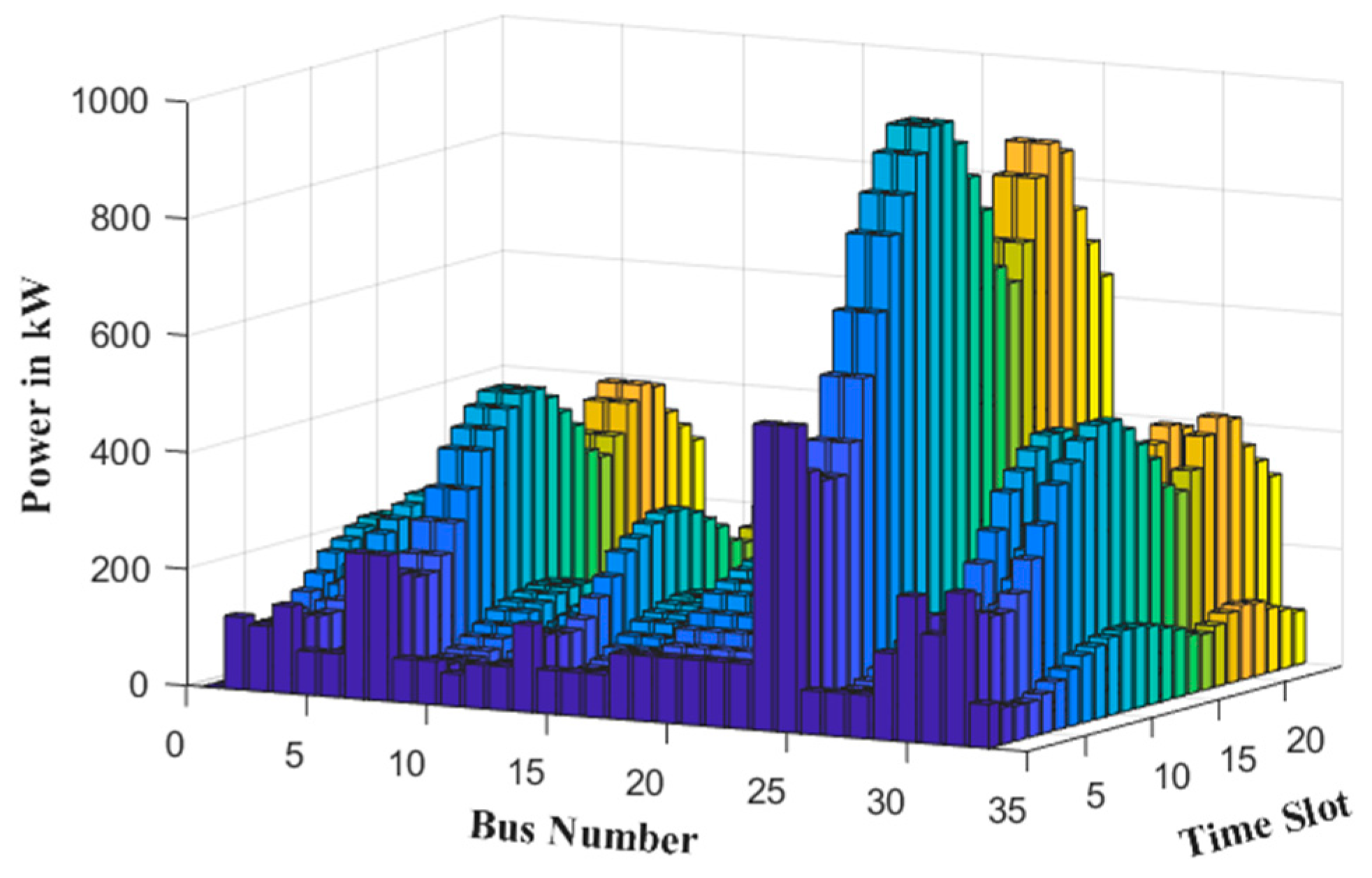
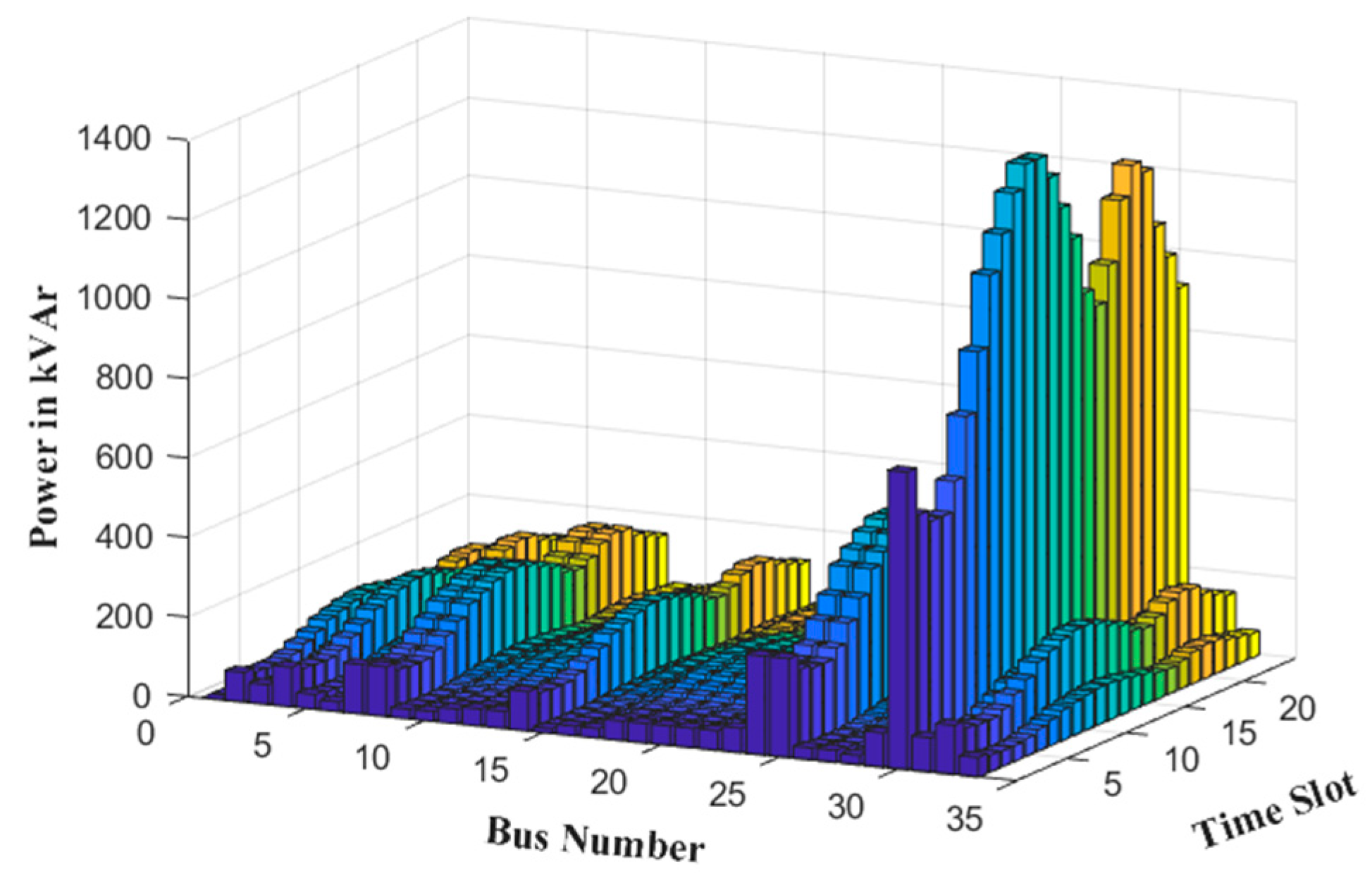
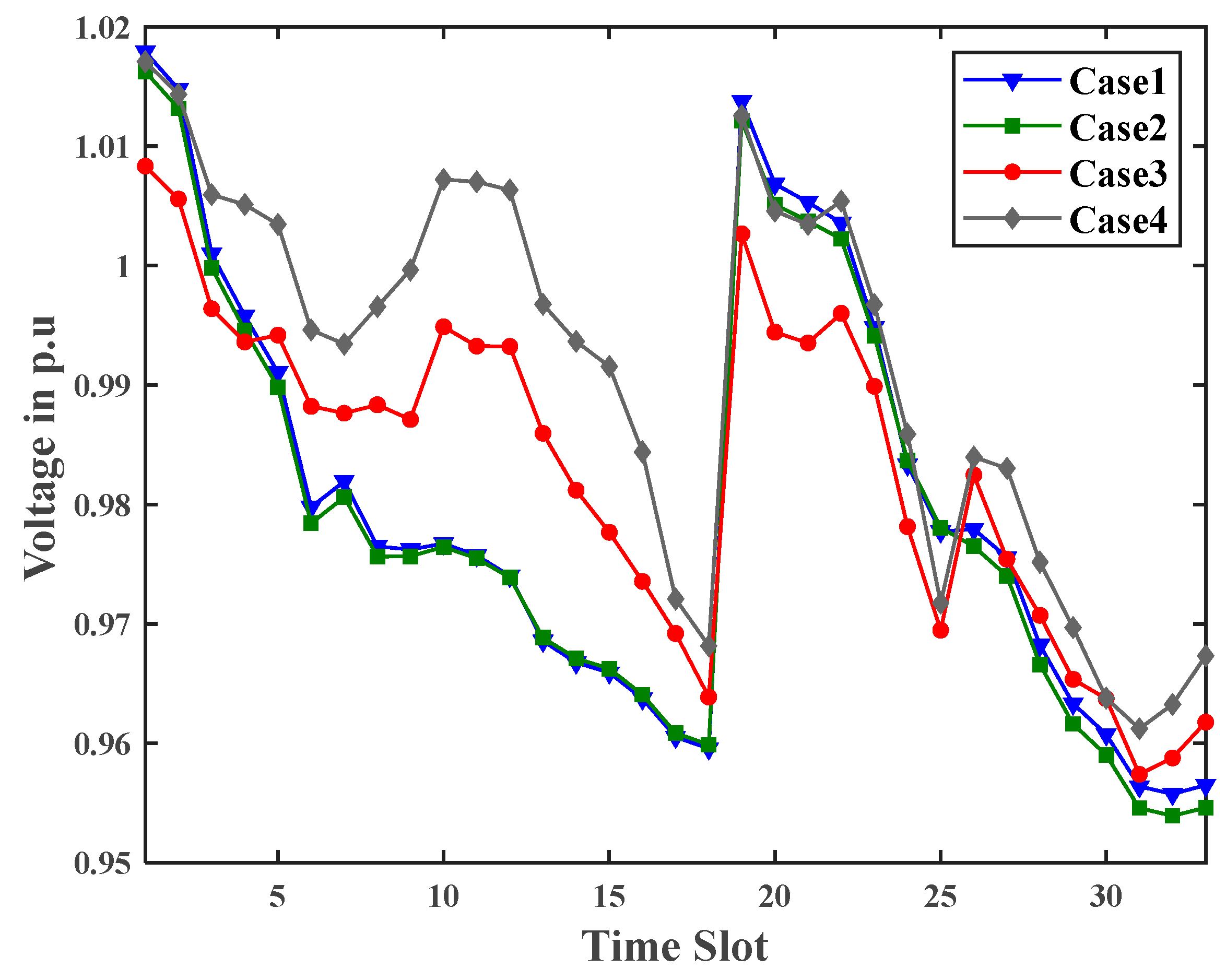
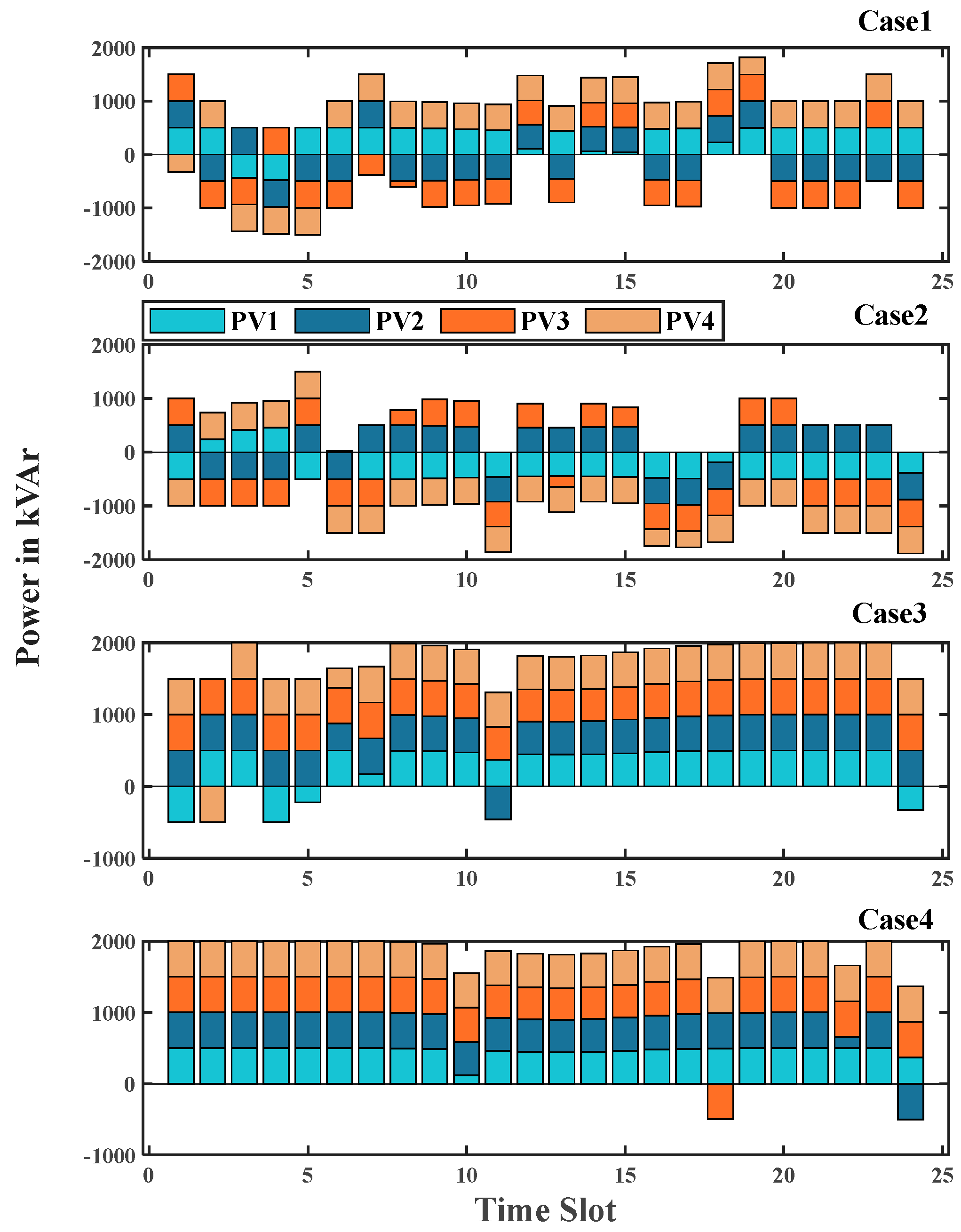
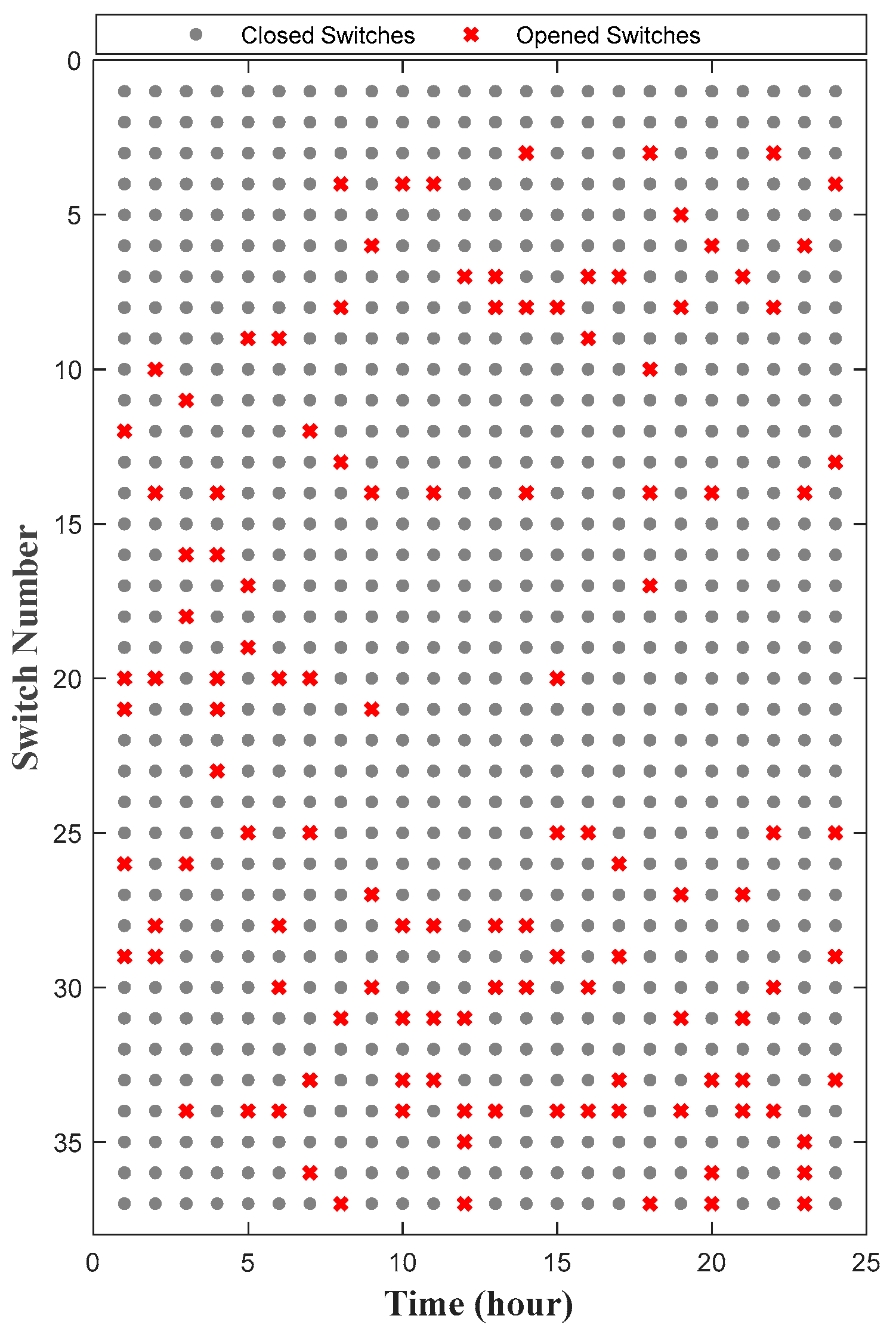
4.2. Numerical Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Sets, Indexes | |
| Set of parent buses | |
| Set of child buses | |
| Set of buses | |
| Set of branches | |
| Set of DGs | |
| Set of SPVIs | |
| Set of EVAs | |
| Set of time horizon | |
| Set of uncertain parameters | |
| Set of hydrogen system | |
| Set of capacitor banks | |
| Set of OLTC | |
| Cardinality of the set | |
| Set of buses connected to bus | |
| Index of buses | |
| Index of DGs | |
| Index of EVA | |
| Index of SPVIs | |
| Index of SCBs | |
| Index of time | |
| Index of OLTCs | |
| Indices of sample points | |
| Index of hydrogen system | |
| Parameters | |
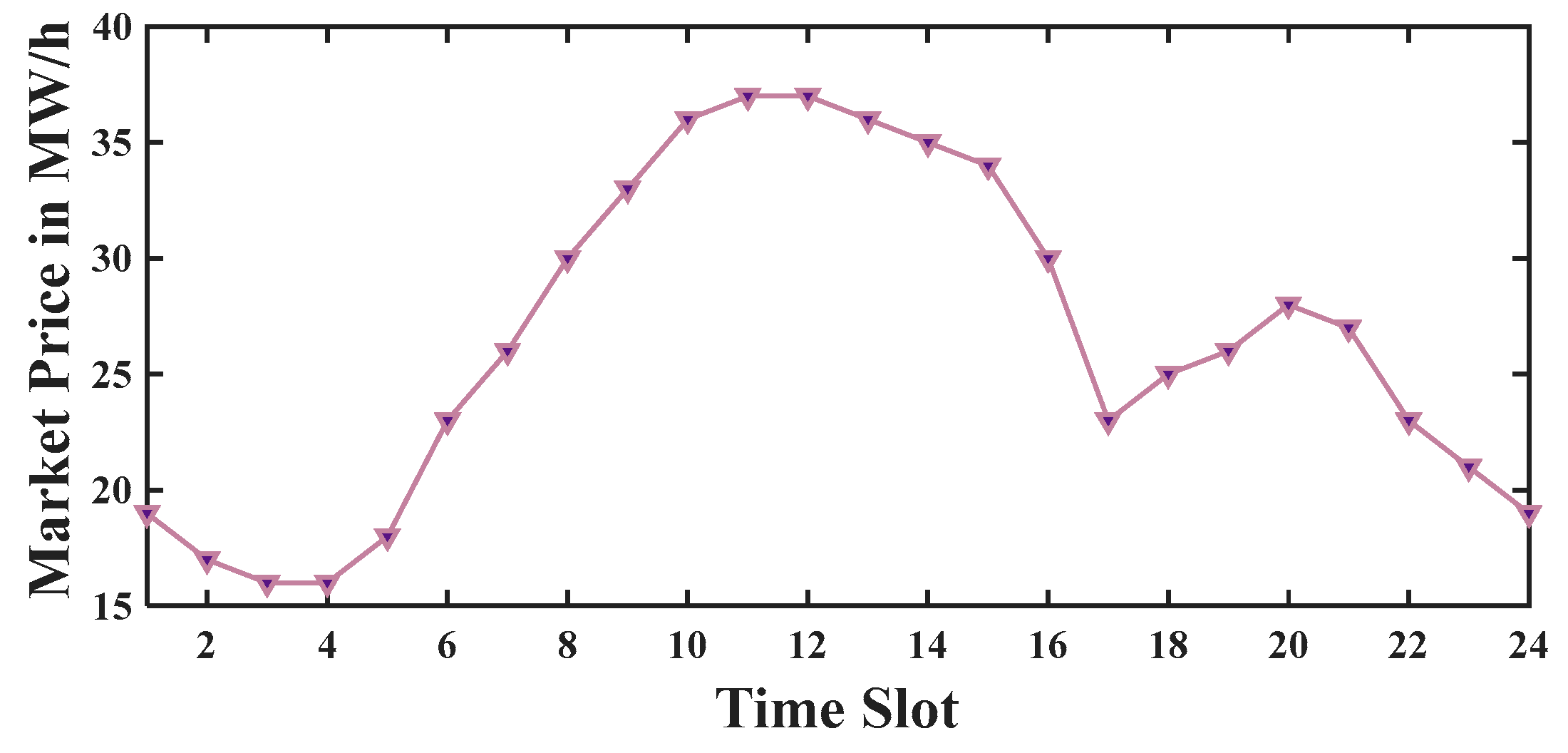
| Wholesale market price (upstream network) | |
| OLTC tap adjustment cost | |
| Switching cost of capacitor banks | |
| Operational cost per MWh of DG | |
| Minimum energy for | |
| Maximum energy for | |
| Initial energy for | |
| Ultimate energy for | |
| Amount of active power demand at -th bus | |
| Minimum output of DG | |
| Maximum output of DG | |
| Minimum charging of EVA | |
| Maximum charging of EVA | |
| Minimum discharging of EVA | |
| Maximum discharging of EVA | |
| Minimum generation limit of fuel cell | |
| Maximum generation limit of fuel cell | |
| Minimum consumption limit of electrolyzer | |
| Maximum consumption limit of electrolyzer | |
| Amount of reactive power demand at -th bus | |
| Quantity of reactive power via -th shunt capacitor bank at each step | |
| Ramp-up rate of -th DG | |
| Branch resistance to connect the bus to | |
| Ramp-up rate of -th DG | |
| Maximum capacity of branch to transmit the complex power | |
| Inverter rating to connect PV to network | |
| Minimum limit of state of hydrogen storage | |
| Maximum limit of state of hydrogen storage | |
| Final state of hydrogen ( | |
| Initial state of hydrogen ( | |
| Lower bound of OLTC taps | |
| Upper bound of OLTC taps | |
| Minimum acceptable voltage at -th bus | |
| Maximum acceptable voltage at -th bus | |
| Voltage of substation | |
| Weight of the mean value | |
| Weight of the -th sample point | |
| Branch reactance to connect the bus to | |
| Charging efficiency coefficient of EVA | |
| Discharging efficiency coefficient of EVA | |
| Electrolyzer efficiency coefficient | |
| Fuel cell efficiency coefficient | |
| Time interval | |
| Energy density of hydrogen, considered as 39 kWh/kg | |
| Maximum tap setting of the -th capacitor | |
| A big number | |
| Variables | |
| Covariance of input uncertain parameters | |
| Covariance of the output variable | |
| Energy of -th EVA | |
| The generated hydrogen by electrolyzer | |
| The consumed hydrogen by fuel cell | |
| Objective function | |
| Amount of active power which branch carries | |
| Amount of power injected into the microgrid via the upstream network | |
| Amount of active power which -th DG generates | |
| Charging rate of -th EVA | |
| Discharging rate of -th EVA | |
| Summation of active loads and generations at -th bus | |
| Amount of active power generated by -th PV resource | |
| Consumed power via -th electrolyzer | |
| Generated power via -th fuel cell | |
| Amount of reactive power that branch carries | |
| Amount of reactive power that -th DG generates | |
| Amount of reactive power generated by -th PV resource | |
| Summation of reactive loads and generations at -th bus | |
| Amount of reactive power that -th switchable capacitor bank provides | |
| State of charge of hydrogen storage | |
| Binary variables that indicate parent–child relationship indices | |
| Status of branch at time (open switches are represented as 0, while closed switches are represented as 1) | |
| -th sample observation of uncertain parameters | |
| Value of the fitness function at the -th sample observation | |
| Step of -th OLTC | |
| Voltage of bus | |
| Integer variable taking the steps of -th switchable capacitor bank | |
| Average value of input uncertain parameters | |
| Average value of the output variable | |
| Abbreviation | |
| P2H | Power-to-hydrogen |
| H2P | Hydrogen-to-power |
| DGs | Diesel generators |
| EVA | Electric vehicle aggregation |
| volt-var | Voltage and volt-ampere reactive |
| OLTC | Online tap changer transformer |
| PV | Photovoltaic array |
| RESs | Renewable energy sources |
| SCBs | Switchable capacitor banks |
| SPIs | Smart PV inverters |
| Volt-VAr | Voltage-volt ampere-reactive |
| VVC | Volt-VAr control |
| UT | Unscented transformation |
| Probability distribution function | |
References
- Hemmatpour, M.H.; Mohammadian, M.; Gharaveisi, A.A. Optimum Islanded Microgrid Reconfiguration Based on Maximization of System Loadability and Minimization of Power Losses. Int. J. Electr. Power Energy Syst. 2016, 78, 343–355. [Google Scholar] [CrossRef]
- Boland, J.; Filar, J.A.; Mohammadian, G.; Nazari, A. Australian Electricity Market and Price Volatility. Ann. Oper. Res. 2016, 241, 357–372. [Google Scholar] [CrossRef]
- Aryanezhad, M. Management and Coordination of LTC, SVR, Shunt Capacitor and Energy Storage with High PV Penetration in Power Distribution System for Voltage Regulation and Power Loss Minimization. Int. J. Electr. Power Energy Syst. 2018, 100, 178–192. [Google Scholar] [CrossRef]
- Liu, J.; Li, Y.; Rehtanz, C.; Cao, Y.; Qiao, X.; Lin, G.; Song, Y.; Sun, C. An OLTC-Inverter Coordinated Voltage Regulation Method for Distribution Network with High Penetration of PV Generations. Int. J. Electr. Power Energy Syst. 2019, 113, 991–1001. [Google Scholar] [CrossRef]
- Abbas, A.S.; El-Sehiemy, R.A.; Abou El-Ela, A.; Ali, E.S.; Mahmoud, K.; Lehtonen, M.; Darwish, M.M.F. Optimal Harmonic Mitigation in Distribution Systems with Inverter Based Distributed Generation. Appl. Sci. 2021, 11, 774. [Google Scholar] [CrossRef]
- Zafar, R.; Ravishankar, J.; Fletcher, J.E.; Pota, H.R. Multi-Timescale Voltage Stability-Constrained Volt/VAR Optimization with Battery Storage System in Distribution Grids. IEEE Trans. Sustain. Energy 2020, 11, 868–878. [Google Scholar] [CrossRef]
- Prabpal, P.; Kongjeen, Y.; Bhumkittipich, K. Optimal Battery Energy Storage System Based on VAR Control Strategies Using Particle Swarm Optimization for Power Distribution System. Symmetry 2021, 13, 1692. [Google Scholar] [CrossRef]
- Pamshetti, V.B.; Singh, S.; Thakur, A.K.; Singh, S.P. Multistage Coordination Volt/VAR Control with CVR in Active Distribution Network in Presence of Inverter-Based DG Units and Soft Open Points. IEEE Trans. Ind. Appl. 2021, 57, 2035–2047. [Google Scholar] [CrossRef]
- Gholami, K.; Azizivahed, A.; Arefi, A.; Li, L. Risk-Averse Volt-VAr Management Scheme to Coordinate Distributed Energy Resources with Demand Response Program. Int. J. Electr. Power Energy Syst. 2023, 146, 108761. [Google Scholar] [CrossRef]
- Sabillon-Antunez, C.; Melgar-Dominguez, O.D.; Franco, J.F.; Lavorato, M.; Rider, M.J. Volt-VAr Control and Energy Storage Device Operation to Improve the Electric Vehicle Charging Coordination in Unbalanced Distribution Networks. IEEE Trans. Sustain. Energy 2017, 8, 1560–1570. [Google Scholar] [CrossRef]
- Tushar, M.H.K.; Assi, C. Volt-VAR Optimization by Using Electric Vehicle, Renewable Energy and Residential Load-Shifting. In Proceedings of the 2016 IEEE International Conference on Smart Grid Communications, SmartGridComm 2016, Sydney, Australia, 6–9 November 2016; pp. 460–465. [Google Scholar] [CrossRef]
- Gholami, K.; Karimi, S.; Rastgou, A.; Nazari, A.; Moghaddam, V. Voltage Stability Improvement of Distribution Networks Using Reactive Power Capability of Electric Vehicle Charging Stations. Comput. Electr. Eng. 2024, 116, 109160. [Google Scholar] [CrossRef]
- Nandhakumar, S.K.; Muthukumar, R. Combined Reconfiguration and Capacitor Placement for Distribution System Volt/Var Control through Opposition Based Differential Evolution Algorithm. Automatika 2015, 56, 140–148. [Google Scholar] [CrossRef]
- Pamshetti, V.B.; Singh, S.; Singh, S.P. Combined Impact of Network Reconfiguration and Volt-VAR Control Devices on Energy Savings in the Presence of Distributed Generation. IEEE Syst. J. 2020, 14, 995–1006. [Google Scholar] [CrossRef]
- Microgrid, D. Volt—Var Optimization and Reconfiguration: Reducing Power Demand and Losses in a droop-based microgrid. IEEE Trans. Ind. Appl. 2021, 57, 2769–2781. [Google Scholar]
- Azizivahed, A.; Gholami, K.; Arefi, A.; Li, L.; Arif, M.T.; Haque, M.E. Stochastic Scheduling of Energy Sharing in Reconfigurable Multi-Microgrid Systems in the Presence of Vehicle-to-Grid Technology. Electr. Power Syst. Res. 2024, 231, 110285. [Google Scholar] [CrossRef]
- Guo, X.; Zhu, H.; Zhang, S. Overview of Electrolyser and Hydrogen Production Power Supply from Industrial Perspective. Int. J. Hydrogen Energy 2024, 49, 1048–1059. [Google Scholar] [CrossRef]
- Massaro, M.C.; Biga, R.; Kolisnichenko, A.; Marocco, P.; Monteverde, A.H.A.; Santarelli, M. Potential and Technical Challenges of On-Board Hydrogen Storage Technologies Coupled with Fuel Cell Systems for Aircraft Electrification. J. Power Sources 2023, 555, 232397. [Google Scholar] [CrossRef]
- Ghaithan, A.M.; Kondkari, M.; Mohammed, A.; Attia, A.M. Optimal Design of Concentrated Solar Power-Based Hydrogen Refueling Station: Mixed Integer Linear Programming Approach. Int. J. Hydrogen Energy 2024, 86, 703–718. [Google Scholar] [CrossRef]
- Shahbazbegian, V.; Shafie-khah, M.; Laaksonen, H.; Strbac, G.; Ameli, H. Resilience-Oriented Operation of Microgrids in the Presence of Power-to-Hydrogen Systems. Appl. Energy 2023, 348, 121429. [Google Scholar] [CrossRef]
- Yu, N.; Duan, W.; Fan, X. Hydrogen-Fueled Microgrid Energy Management: Novel EMS Approach for Efficiency and Reliability. Int. J. Hydrogen Energy 2024, 80, 1466–1476. [Google Scholar] [CrossRef]
- Zhang, W.; Gandhi, O.; Quan, H.; Rodríguez-Gallegos, C.D.; Srinivasan, D. A Multi-Agent Based Integrated Volt-Var Optimization Engine for Fast Vehicle-to-Grid Reactive Power Dispatch and Electric Vehicle Coordination. Appl. Energy 2018, 229, 96–110. [Google Scholar] [CrossRef]
- Malekpour, A.R.; Niknam, T. A Probabilistic Multi-Objective Daily Volt/Var Control at Distribution Networks Including Renewable Energy Sources. Energy 2011, 36, 3477–3488. [Google Scholar] [CrossRef]
- Baghaee, H.R.; Mirsalim, M.; Gharehpetian, G.B.; Talebi, H.A. Application of RBF Neural Networks and Unscented Transformation in Probabilistic Power-Flow of Microgrids Including Correlated Wind/PV Units and Plug-in Hybrid Electric Vehicles. Simul. Model. Pract. Theory 2017, 72, 51–68. [Google Scholar] [CrossRef]
- Dabbaghjamanesh, M.; Kavousi-Fard, A.; Mehraeen, S. Effective Scheduling of Reconfigurable Microgrids With Dynamic Thermal Line Rating. IEEE Trans. Ind. Electron. 2019, 66, 1552–1564. [Google Scholar] [CrossRef]
- Kavousi-Fard, A.; Niknam, T.; Fotuhi-Firuzabad, M. Stochastic Reconfiguration and Optimal Coordination of V2G Plug-in Electric Vehicles Considering Correlated Wind Power Generation. IEEE Trans. Sustain. Energy 2015, 6, 822–830. [Google Scholar] [CrossRef]
- Aien, M.; Fotuhi-Firuzabad, M.; Aminifar, F. Probabilistic Load Flow in Correlated Uncertain Environment Using Unscented Transformation. IEEE Trans. Power Syst. 2012, 27, 2233–2241. [Google Scholar] [CrossRef]
- Jashfar, S.; Esmaeili, S. Volt/Var/THD Control in Distribution Networks Considering Reactive Power Capability of Solar Energy Conversion. Int. J. Electr. Power Energy Syst. 2014, 60, 221–233. [Google Scholar] [CrossRef]
- Ameli, A.; Ahmadifar, A.; Shariatkhah, M.H.; Vakilian, M.; Haghifam, M.R. A Dynamic Method for Feeder Reconfiguration and Capacitor Switching in Smart Distribution Systems. Int. J. Electr. Power Energy Syst. 2017, 85, 200–211. [Google Scholar] [CrossRef]
- Emarati, M.; Barani, M.; Farahmand, H.; Aghaei, J.; del Granado, P.C. A Two-Level over-Voltage Control Strategy in Distribution Networks with High PV Penetration. Int. J. Electr. Power Energy Syst. 2021, 130, 106763. [Google Scholar] [CrossRef]
- Arunachalam, M.; Yoo, Y.; Al-Ghamdi, A.S.; Park, H.; Han, D.S. Integrating Green Hydrogen Production with Renewable Energy-Powered Desalination: An Analysis of CAPEX Implications and Operational Strategies. Int. J. Hydrogen Energy 2024, 84, 344–355. [Google Scholar] [CrossRef]
- Li, M.; Bai, Y.; Zhang, C.; Song, Y.; Jiang, S.; Grouset, D.; Zhang, M. Review on the Research of Hydrogen Storage System Fast Refueling in Fuel Cell Vehicle. Int. J. Hydrogen Energy 2019, 44, 10677–10693. [Google Scholar] [CrossRef]
- Mehrjerdi, H. Off-Grid Solar Powered Charging Station for Electric and Hydrogen Vehicles Including Fuel Cell and Hydrogen Storage. Int. J. Hydrogen Energy 2019, 44, 11574–11583. [Google Scholar] [CrossRef]
- Yuan, W.; Wang, J.; Qiu, F.; Chen, C.; Kang, C.; Zeng, B. Robust Optimization-Based Resilient Distribution Network Planning Against Natural Disasters. IEEE Trans. Smart Grid 2016, 7, 2817–2826. [Google Scholar] [CrossRef]
- Javadi, M.S.; Esmaeel Nezhad, A.; Jordehi, A.R.; Gough, M.; Santos, S.F.; Catalão, J.P.S. Transactive Energy Framework in Multi-Carrier Energy Hubs: A Fully Decentralized Model. Energy 2022, 238, 121717. [Google Scholar] [CrossRef]
- Dorostkar-Ghamsari, M.R.; Fotuhi-Firuzabad, M.; Lehtonen, M.; Safdarian, A. Value of Distribution Network Reconfiguration in Presence of Renewable Energy Resources. IEEE Trans. Power Syst. 2016, 31, 1879–1888. [Google Scholar] [CrossRef]
- Guo, Z.; Zhou, Z.; Zhou, Y. Impacts of Integrating Topology Reconfiguration and Vehicle-to-Grid Technologies on Distribution System Operation. IEEE Trans. Sustain. Energy 2020, 11, 1023–1032. [Google Scholar] [CrossRef]
- Mohseni, M.; Joorabian, M.; Lashkar Ara, A. Distribution System Reconfiguration in Presence of Internet of Things. IET Gener. Transm. Distrib. 2021, 15, 1290–1303. [Google Scholar] [CrossRef]
- Moghari, P.; Chabanloo, R.M.; Torkaman, H. Distribution System Reconfiguration Based on MILP Considering Voltage Stability. Electr. Power Syst. Res. 2023, 222, 109523. [Google Scholar] [CrossRef]
- Jabr, R.A.; Singh, R.; Pal, B.C. Minimum Loss Network Reconfiguration Using Mixed-Integer Convex Programming. IEEE Trans. Power Syst. 2012, 27, 1106–1115. [Google Scholar] [CrossRef]
- Aien, M.; Hajebrahimi, A.; Fotuhi-Firuzabad, M. A Comprehensive Review on Uncertainty Modeling Techniques in Power System Studies. Renew. Sustain. Energy Rev. 2016, 57, 1077–1089. [Google Scholar] [CrossRef]
- Aien, M.; Rashidinejad, M.; Fotuhi-Firuzabad, M. On Possibilistic and Probabilistic Uncertainty Assessment of Power Flow Problem: A Review and a New Approach. Renew. Sustain. Energy Rev. 2014, 37, 883–895. [Google Scholar] [CrossRef]
- Ramos, L.F.; Canha, L.N.; Do Prado, J.C.; de Menezes, L.R.A.X. A Novel Virtual Power Plant Uncertainty Modeling Framework Using Unscented Transform. Energies 2022, 15, 3716. [Google Scholar] [CrossRef]
- Chen, J.; Zhao, X.; Shi, K.; Ao, Z.; Zheng, X. Reliability Analysis of Transmission Tower Based on Unscented Transformation Under Ice and Wind Loads. Energies 2024, 17, 5604. [Google Scholar] [CrossRef]
- Parhoudeh, S.; Eguía López, P.; Kavousi Fard, A. Stochastic Scheduling of Grid-Connected Smart Energy Hubs Participating in the Day-Ahead Energy, Reactive Power and Reserve Markets. Smart Cities 2024, 7, 3587–3615. [Google Scholar] [CrossRef]
- Peres, W. A Probabilistic Load Flow for Unbalanced Three-Phase Islanded Microgrids Using Unscented Transformation. Int. J. Electr. Power Energy Syst. 2024, 155, 109554. [Google Scholar] [CrossRef]
- Gholami, K.; Jazebi, S. Multi-Objective Long-Term Reconfiguration of Autonomous Microgrids through Controlled Mutation Differential Evolution Algorithm. IET Smart Grid 2020, 3, 738–748. [Google Scholar] [CrossRef]






| EVA | Capacity (kWh) | Charge/Discharge (kW) | ||
|---|---|---|---|---|
| min | max | min | max | |
| 1 | 50 | 2000 | 200 | 200 |
| 2 | 50 | 2000 | 200 | 200 |
| EVA | Trip 1 | Trip 2 | ||||||
|---|---|---|---|---|---|---|---|---|
| Departure | Arrival | Departure | Arrival | |||||
| Time | Bus | Time | Bus | Time | Bus | Time | Bus | |
| 1 | 8 | 14 | 9 | 24 | 18 | 24 | 19 | 14 |
| 2 | 8 | 3 | 9 | 27 | 18 | 27 | 19 | 3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gholami, K.; Azizivahed, A.; Arefi, A.; Li, L.; Arif, M.T.; Haque, M.E. Coordinated Volt-Var Control of Reconfigurable Microgrids with Power-to-Hydrogen Systems. Energies 2024, 17, 6442. https://doi.org/10.3390/en17246442
Gholami K, Azizivahed A, Arefi A, Li L, Arif MT, Haque ME. Coordinated Volt-Var Control of Reconfigurable Microgrids with Power-to-Hydrogen Systems. Energies. 2024; 17(24):6442. https://doi.org/10.3390/en17246442
Chicago/Turabian StyleGholami, Khalil, Ali Azizivahed, Ali Arefi, Li Li, Mohammad Taufiqul Arif, and Md Enamul Haque. 2024. "Coordinated Volt-Var Control of Reconfigurable Microgrids with Power-to-Hydrogen Systems" Energies 17, no. 24: 6442. https://doi.org/10.3390/en17246442
APA StyleGholami, K., Azizivahed, A., Arefi, A., Li, L., Arif, M. T., & Haque, M. E. (2024). Coordinated Volt-Var Control of Reconfigurable Microgrids with Power-to-Hydrogen Systems. Energies, 17(24), 6442. https://doi.org/10.3390/en17246442








