Stability Boundary Characterization and Power Quality Improvement for Distribution Networks
Abstract
1. Introduction
- A D-Partition-based controller parameter design method is proposed for GFM converters, which can determine the Proportional Integral (PI) parameter stability domain that meets the requirements of phase margin, gain margin, and short circuit ratio.
- A current reference generation strategy is proposed to generate positive-sequence and negative-sequence reactive current commands considering the capacity limitations of the GFL converter and switch devices, which effectively achieves adaptive current limitations.
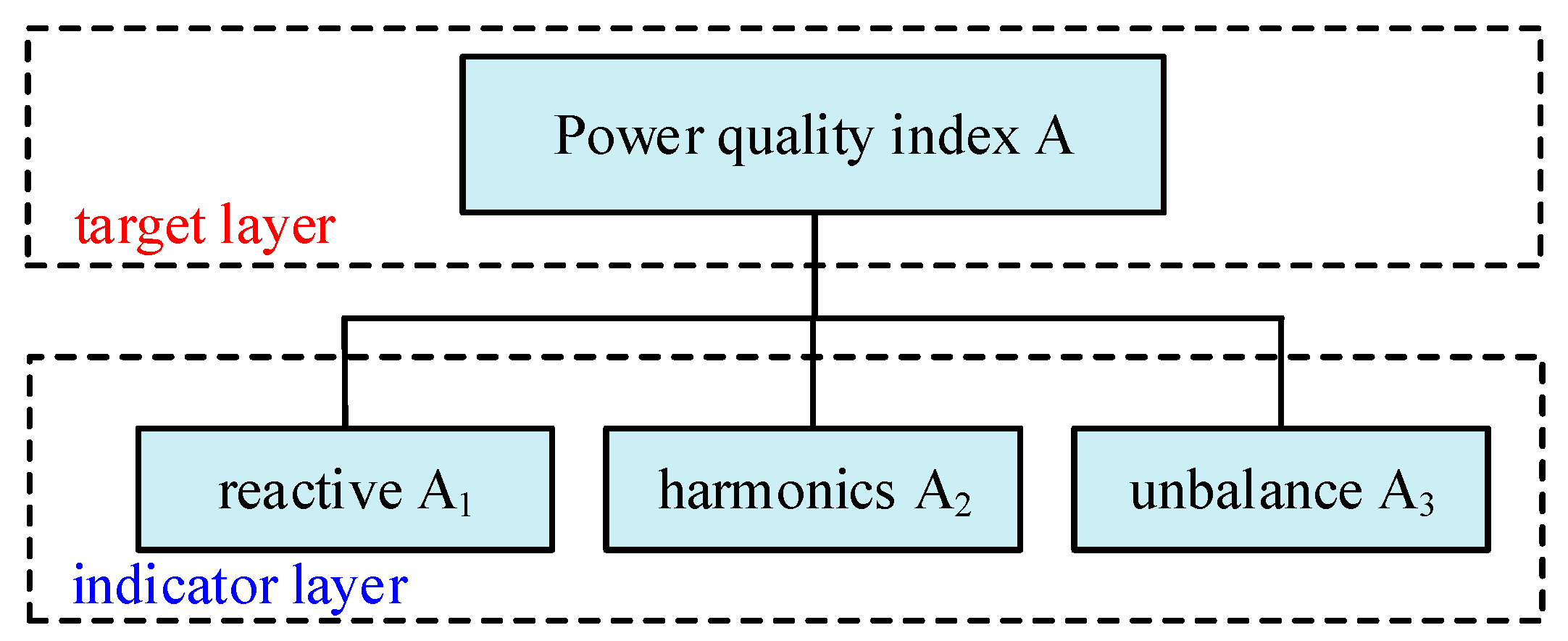
- In a multi-converter system, a compensation current control based on the analytic hierarchy process (AHP) and the coefficient of variation (CV) is proposed to achieve the balance between minimum capacity and optimal power quality.
2. System Description and Modeling
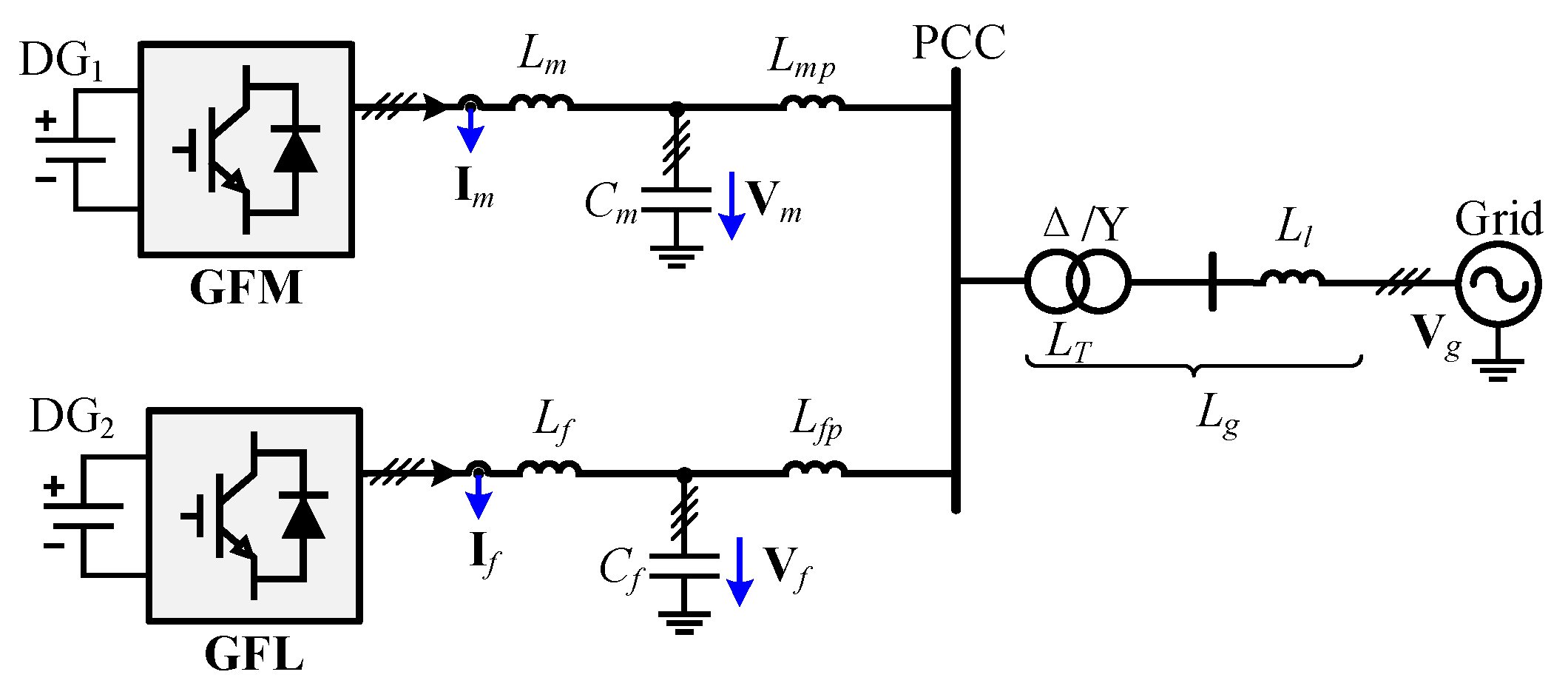
2.1. System Description
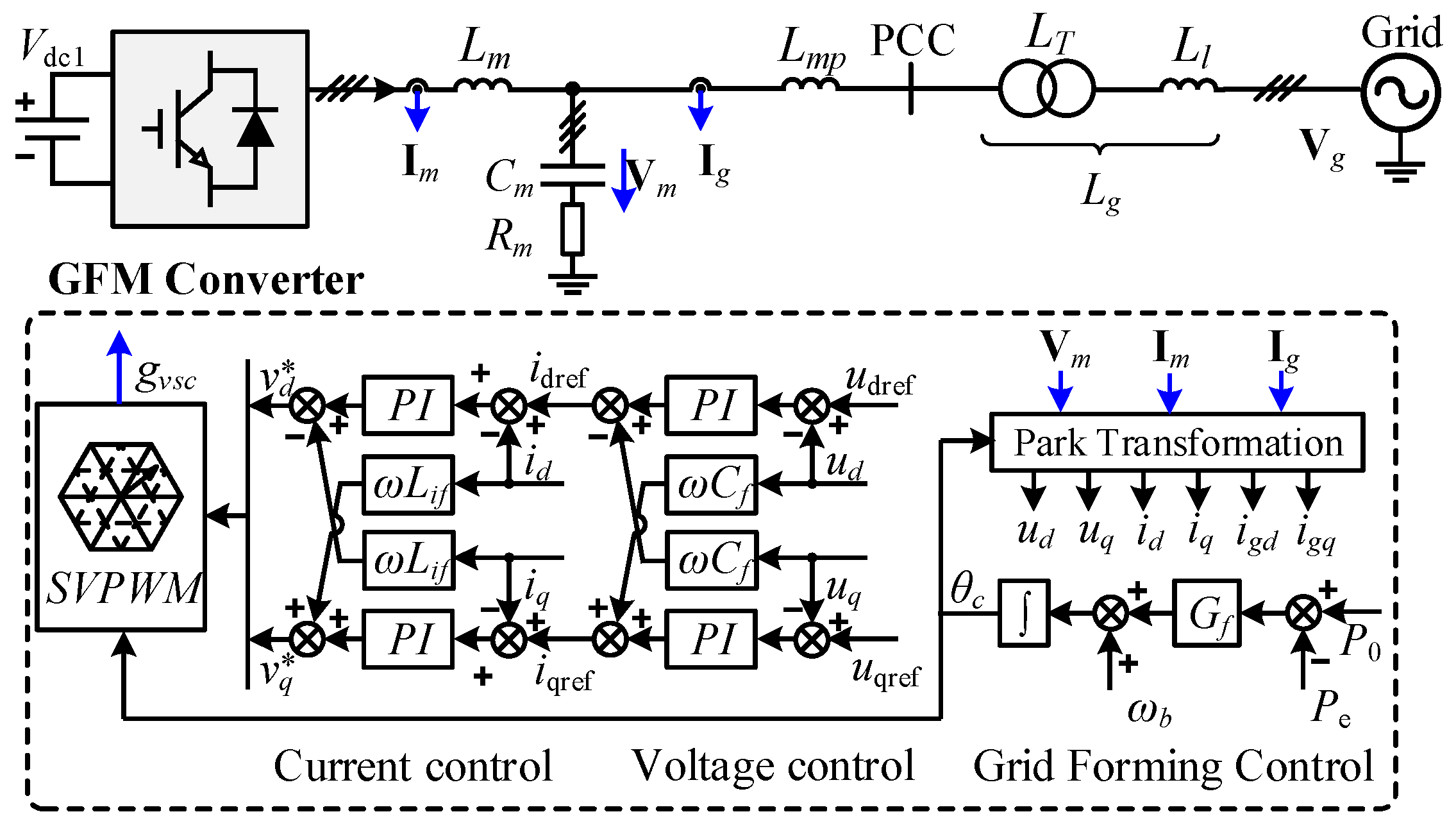
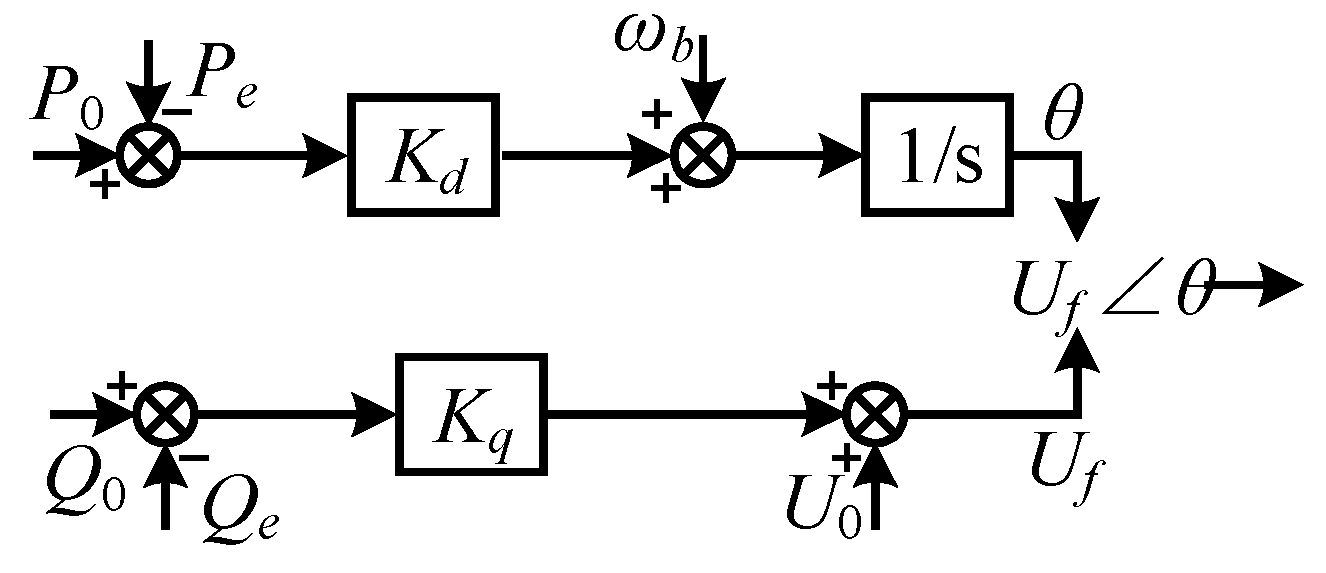
2.2. Modeling of GFM Converter
2.3. Modeling of GFL Converter
2.4. Comparison Between GFL and GFM Converter
3. Stability Boundary Characterization Based on D-Partition Method
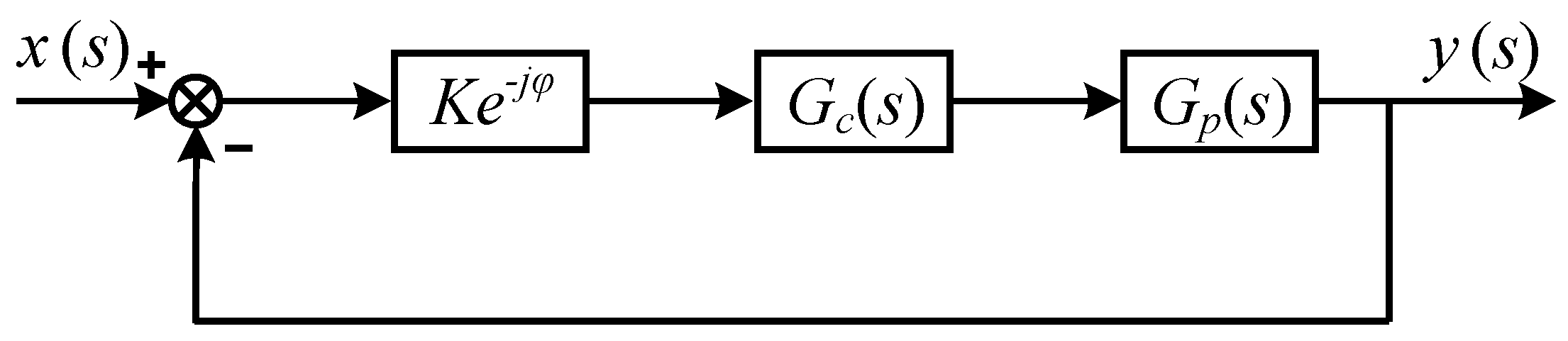
3.1. Principle of D-Partition Method
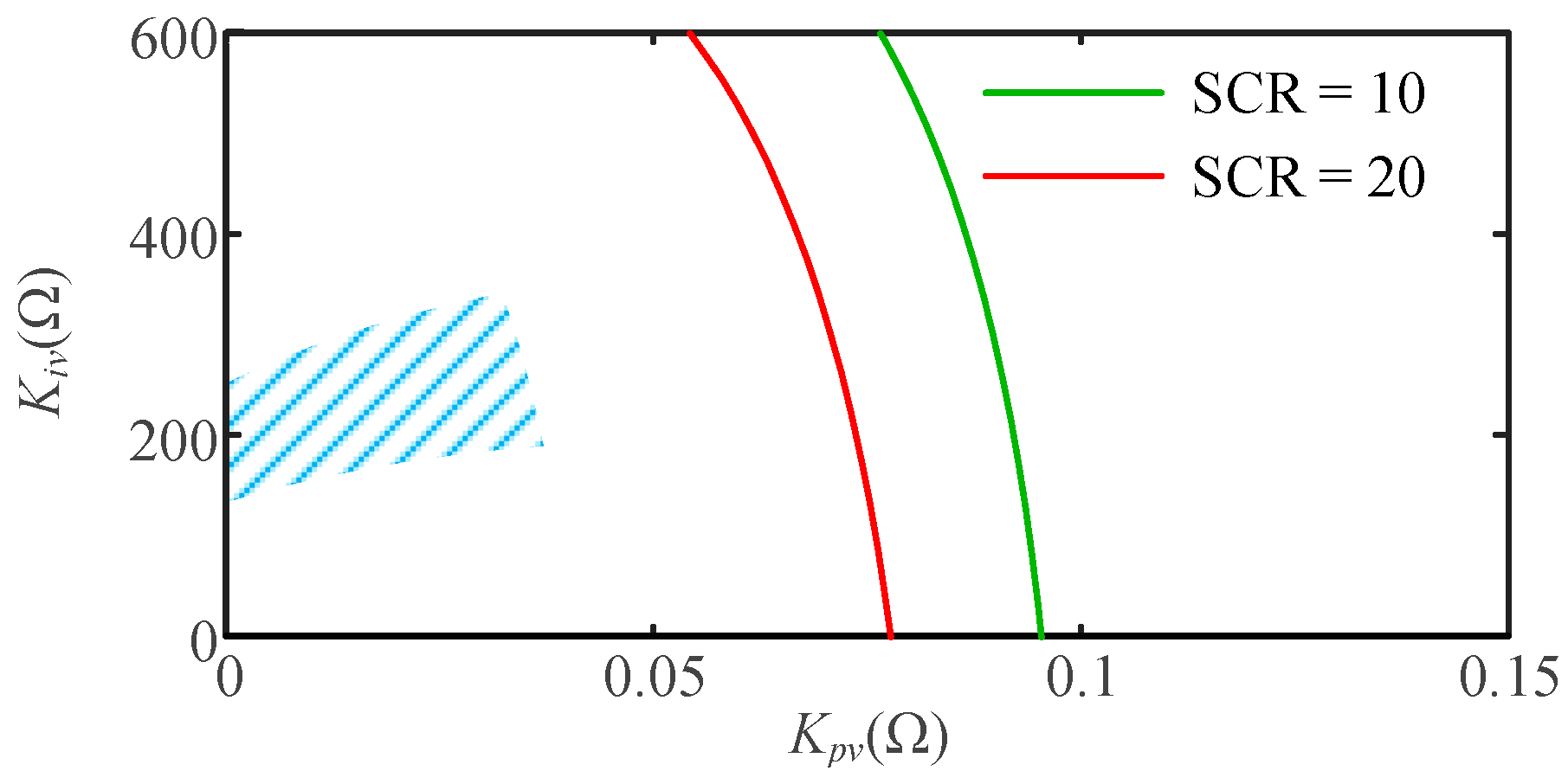
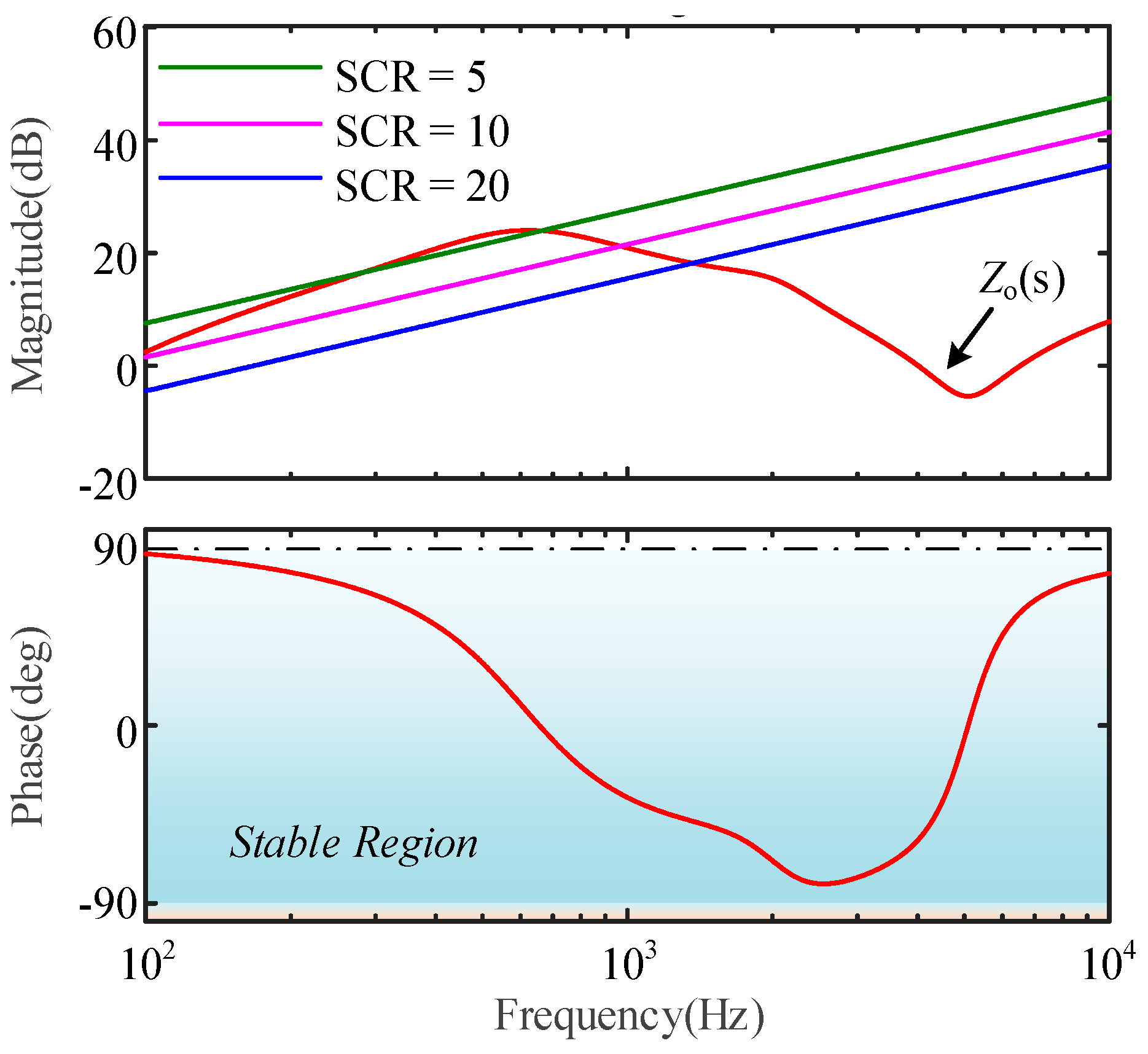
3.2. Stability Boundary Characteristics of GFM Converter
4. Positive and Negative Current Reference Generator
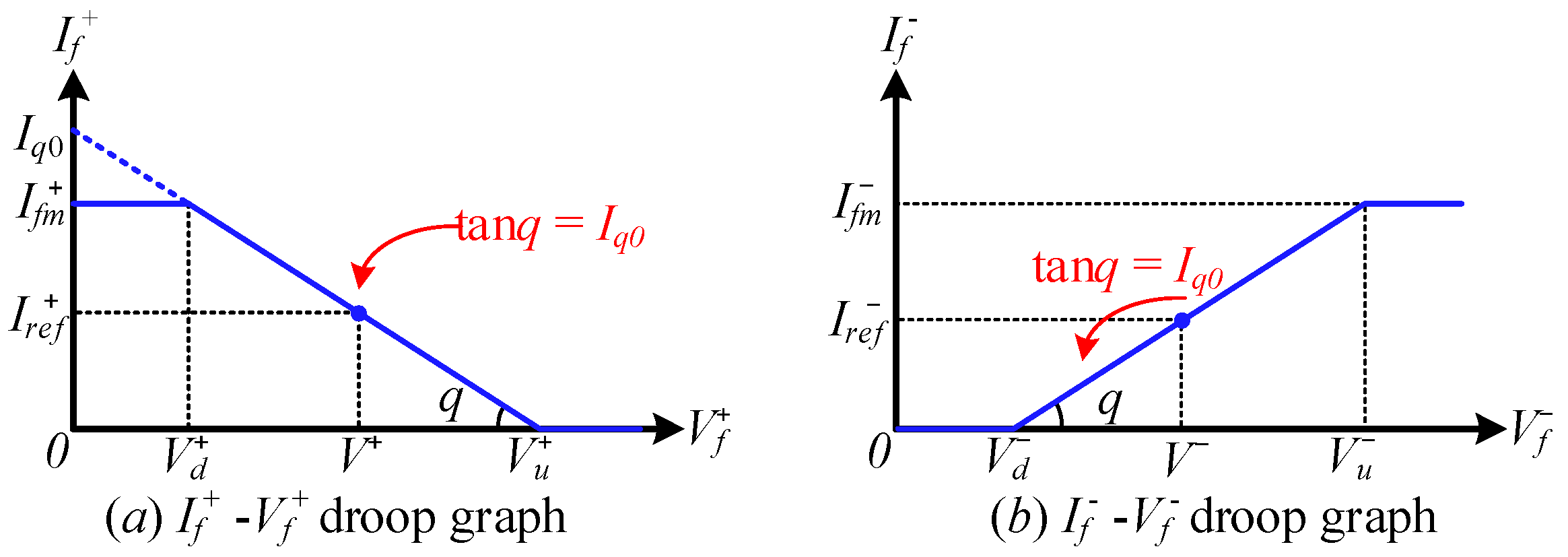
4.1. Current Generator Based on Voltage Droop Control
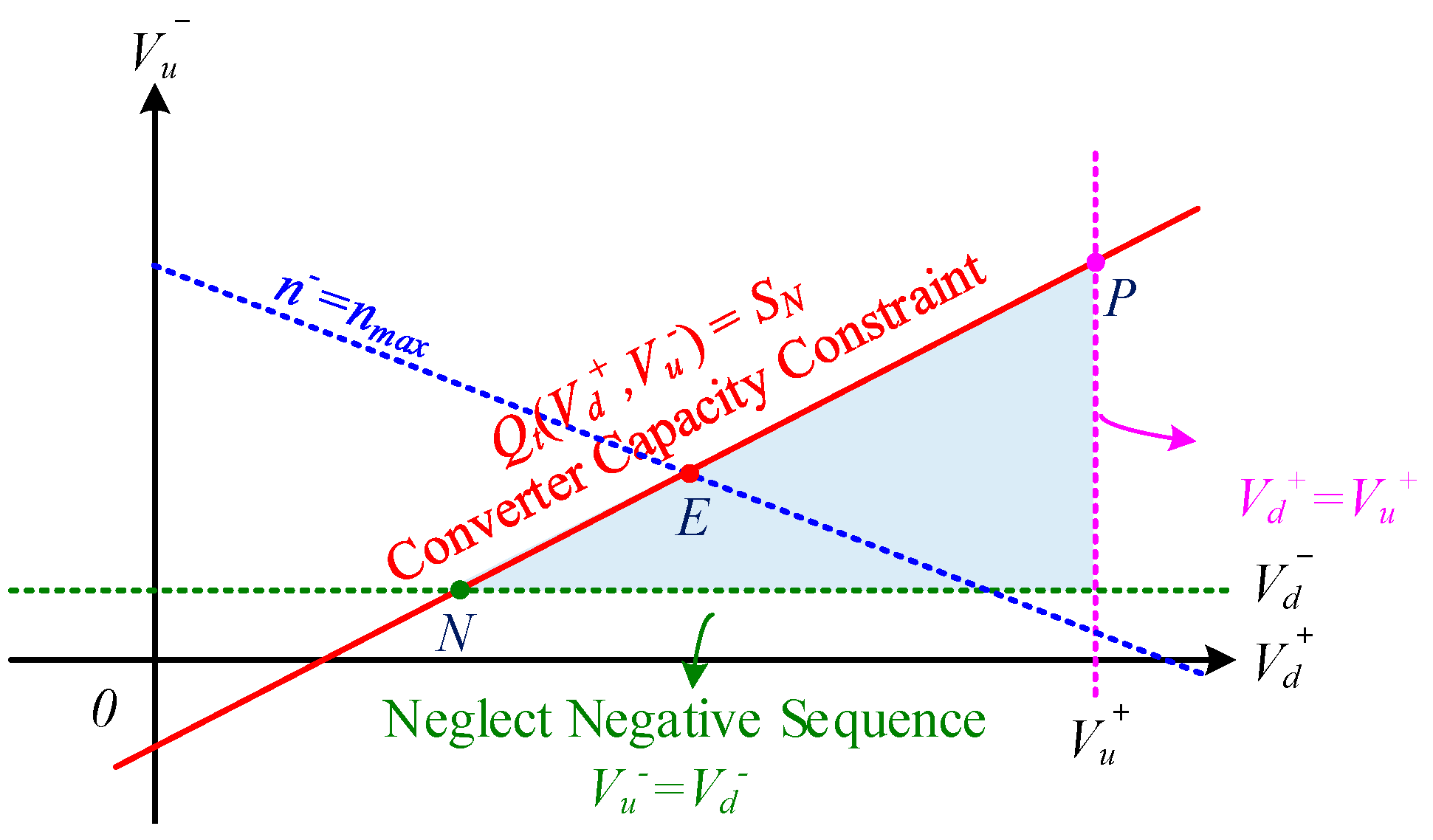
4.2. Limits of Converter Capacity
4.3. Limits of Switch Current
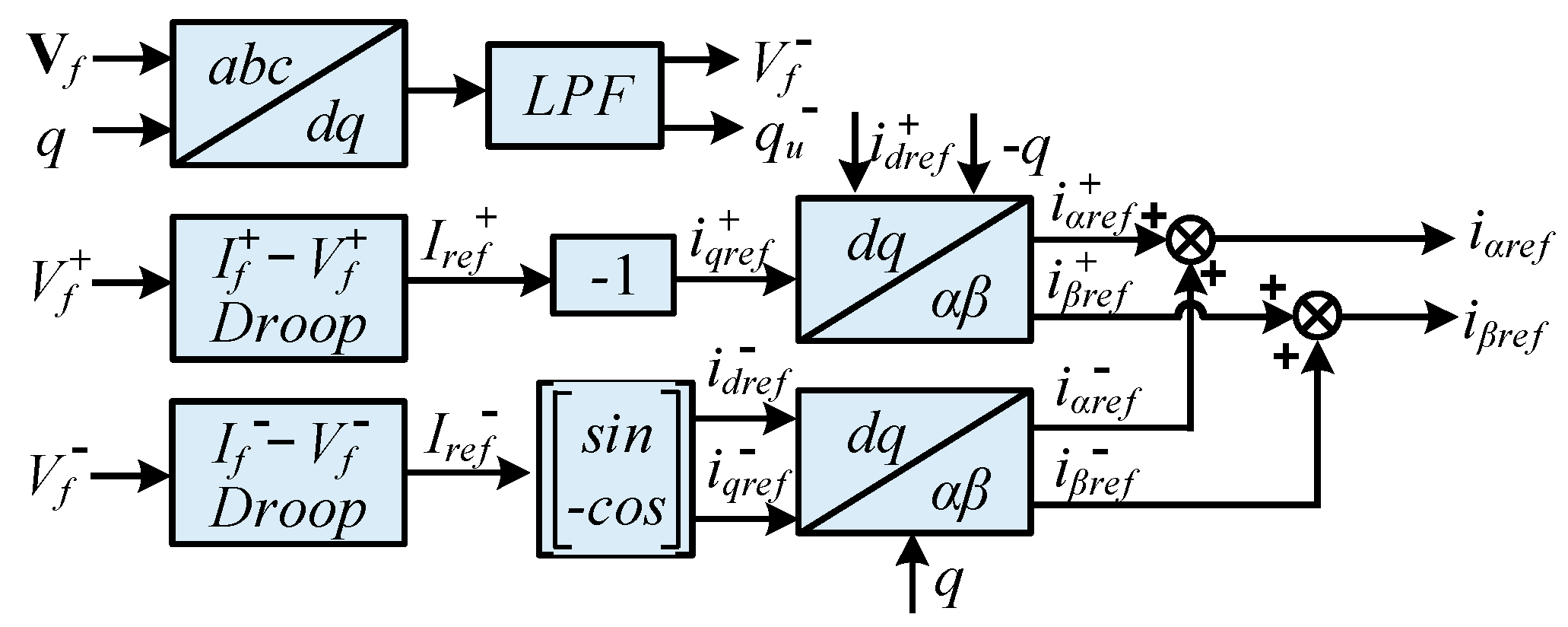
4.4. Structure of Current Reference Generator
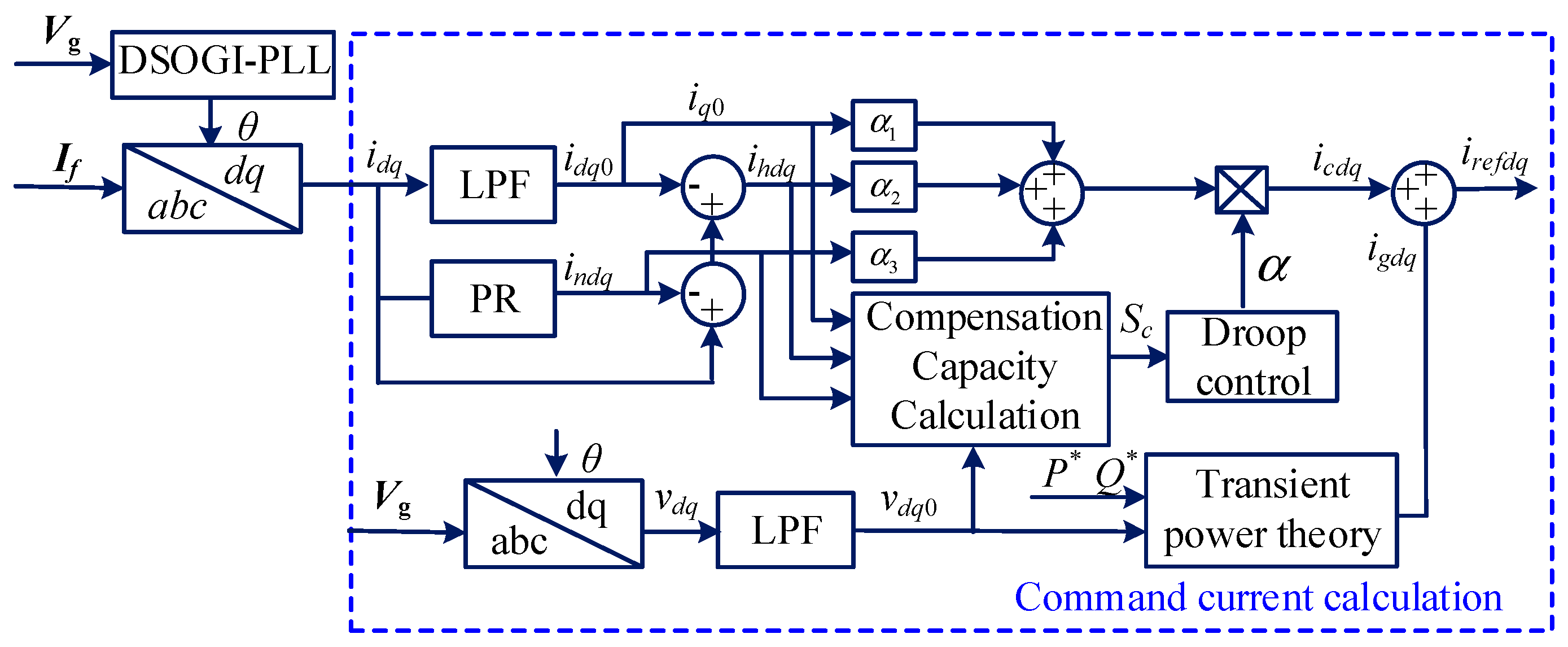
5. Enhanced Power Quality Control
5.1. Injected Current Calculation
5.2. Compensation Current Analysis
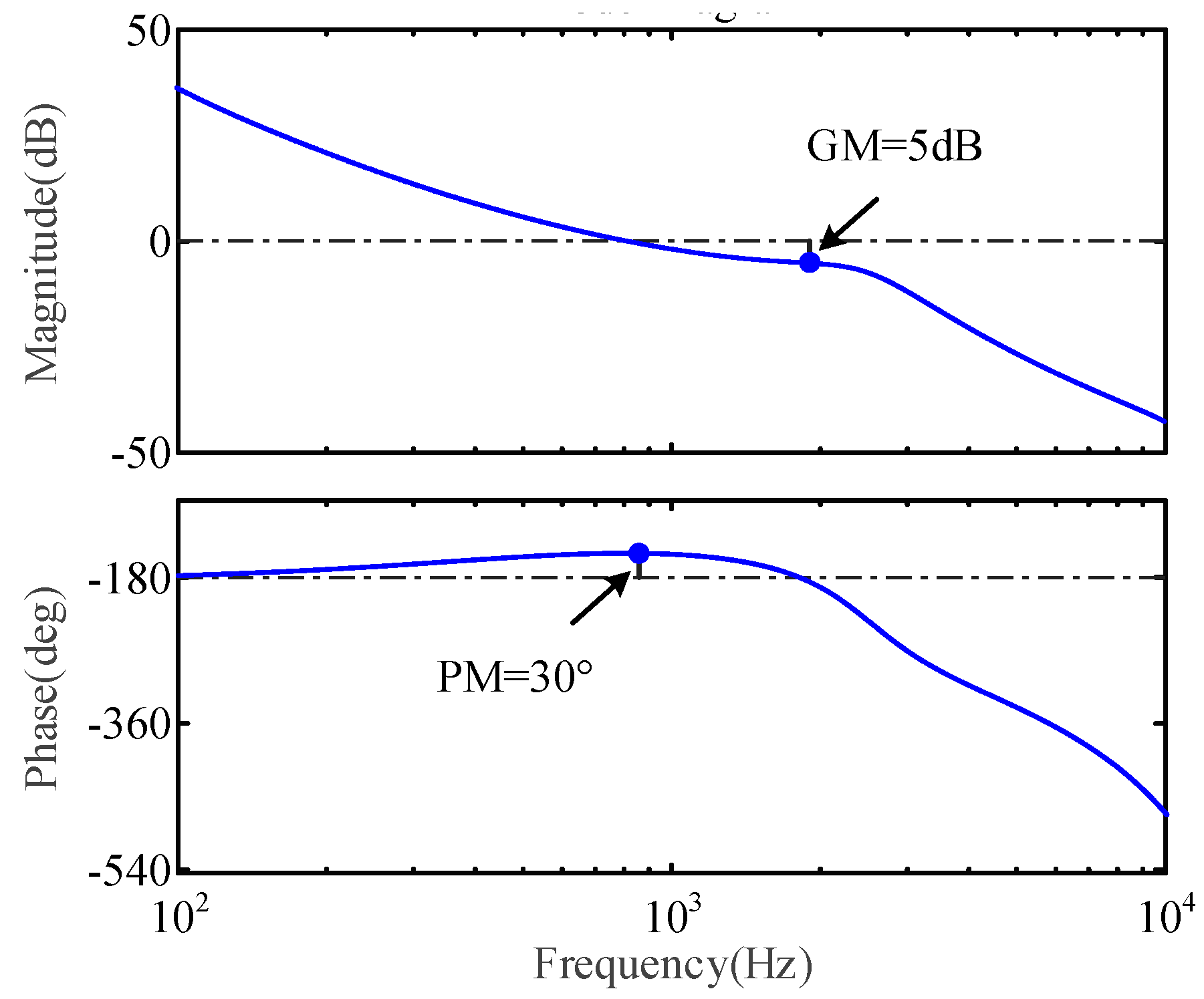
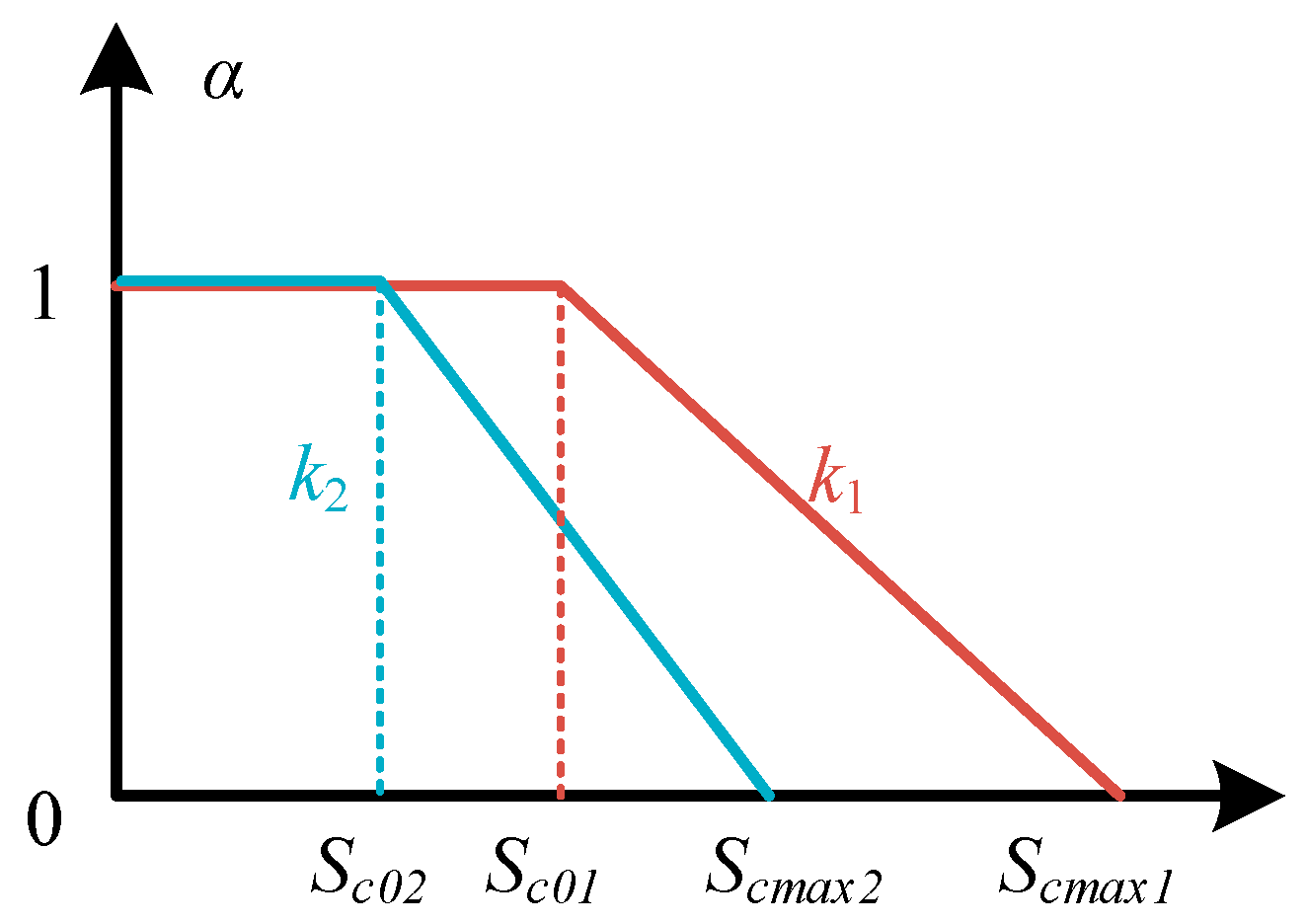
5.3. Controller Design
6. Simulation Validation
6.1. Stability Boundary Test of GFM Converter
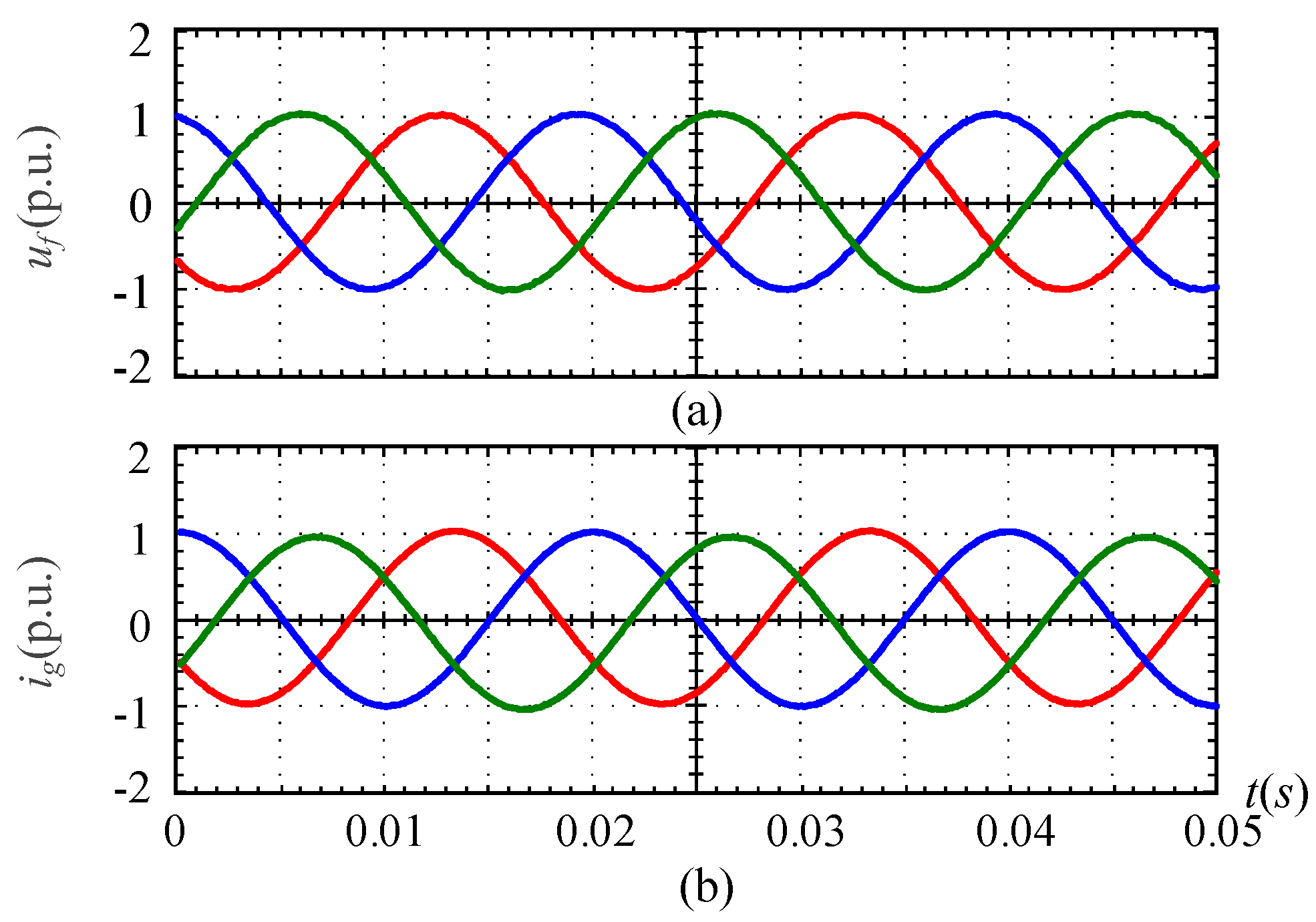
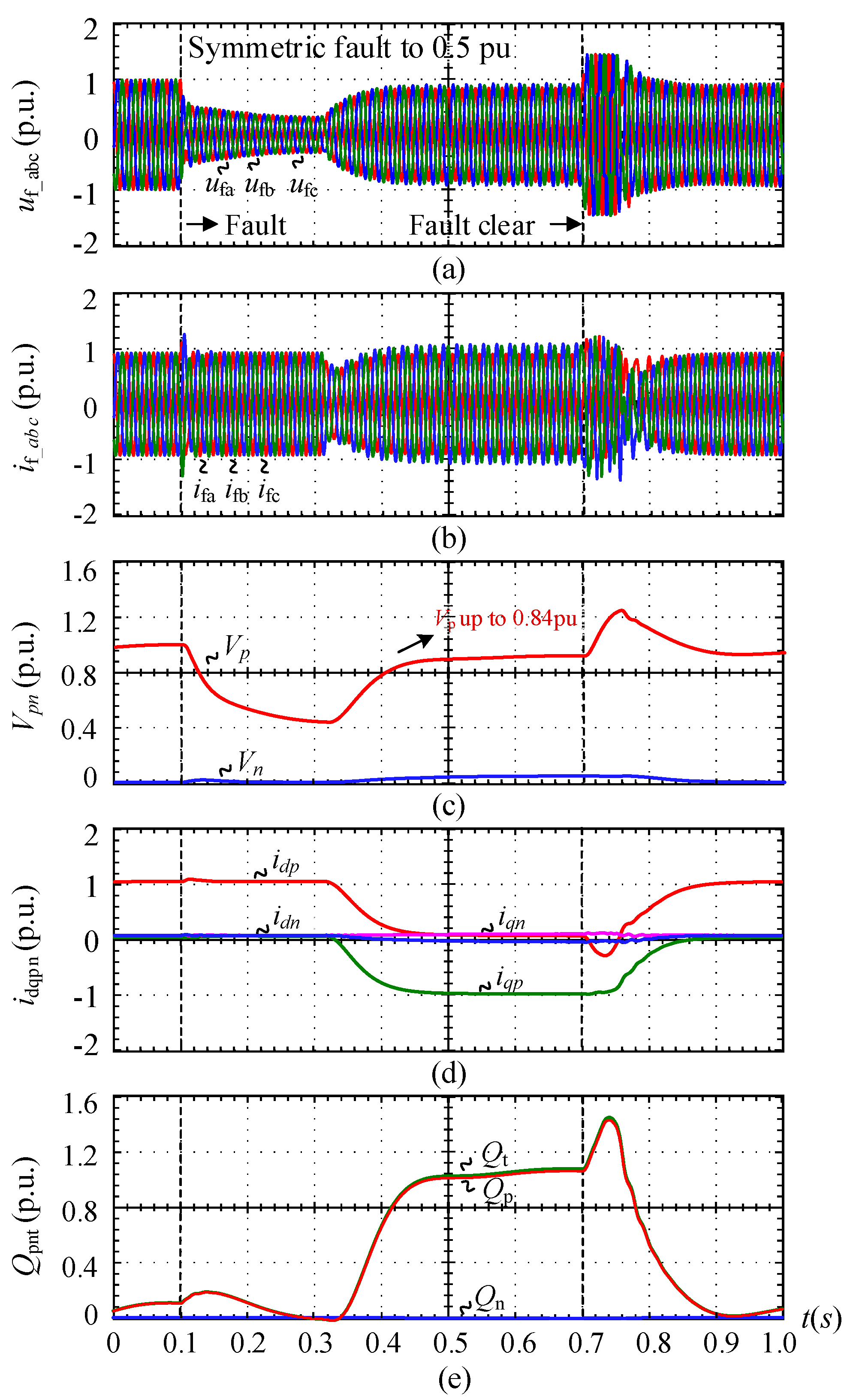
6.2. Symmetrical Grid Faults Test of GFL Converter
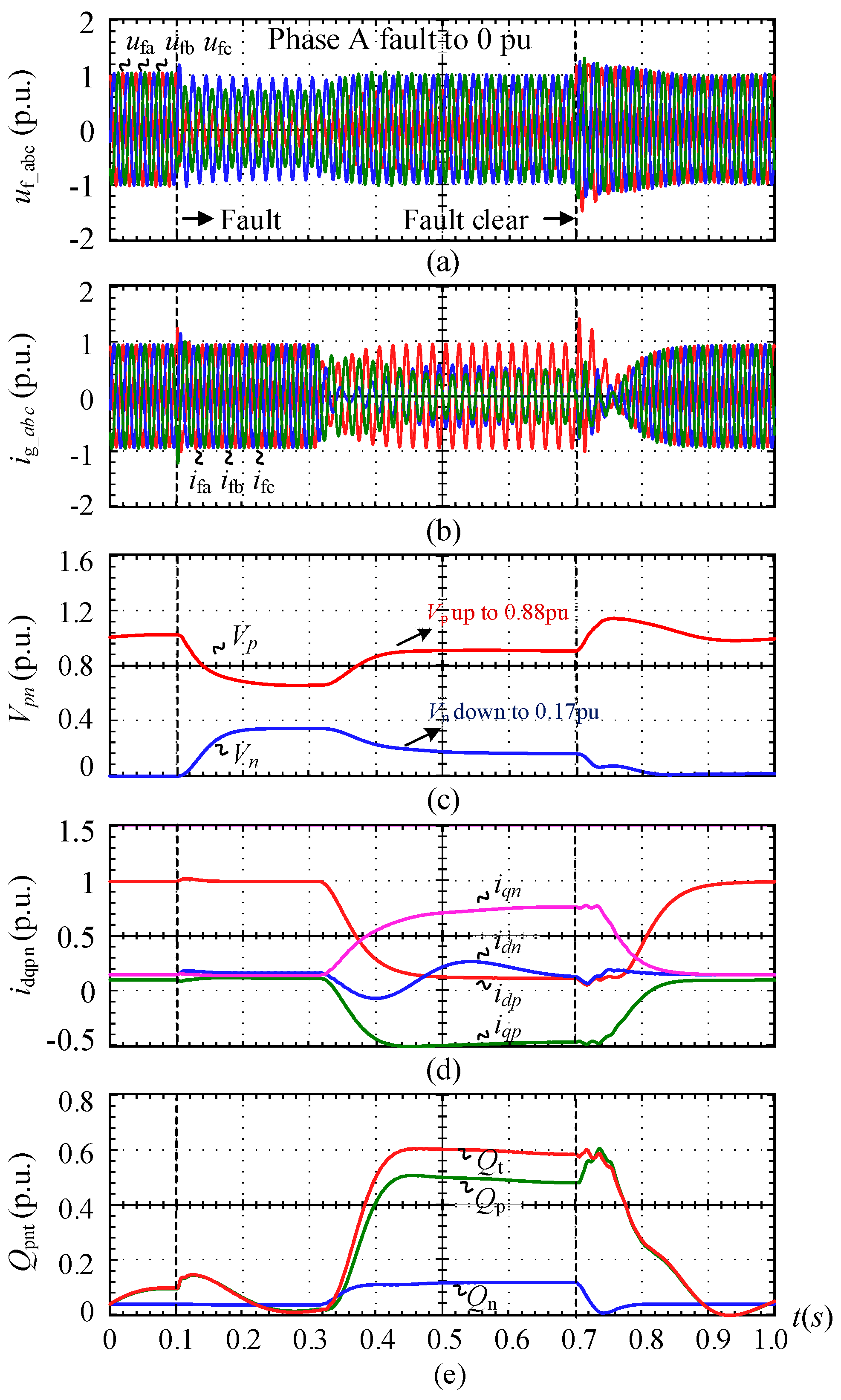
6.3. Asymmetrical Grid Faults Test of GFL Converter
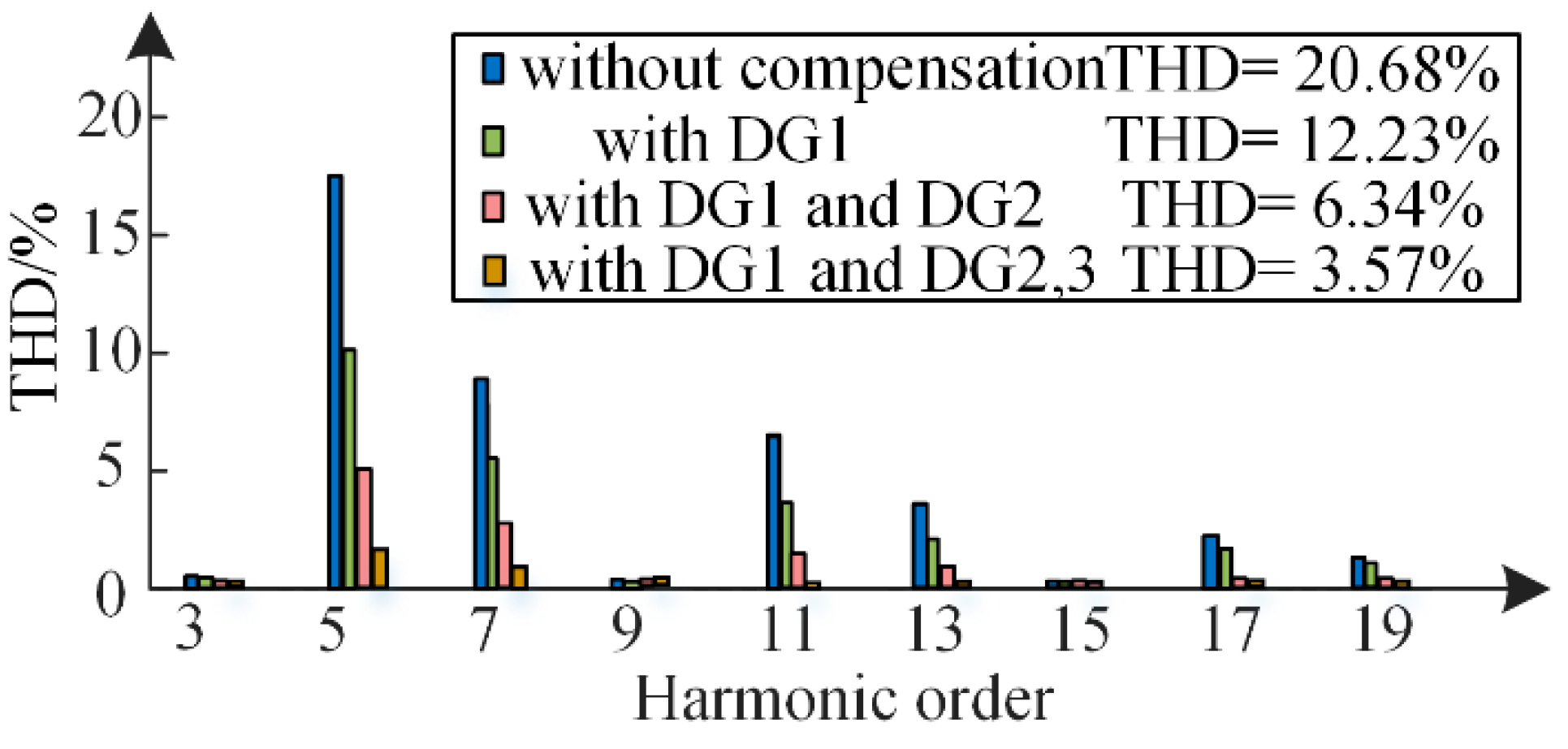
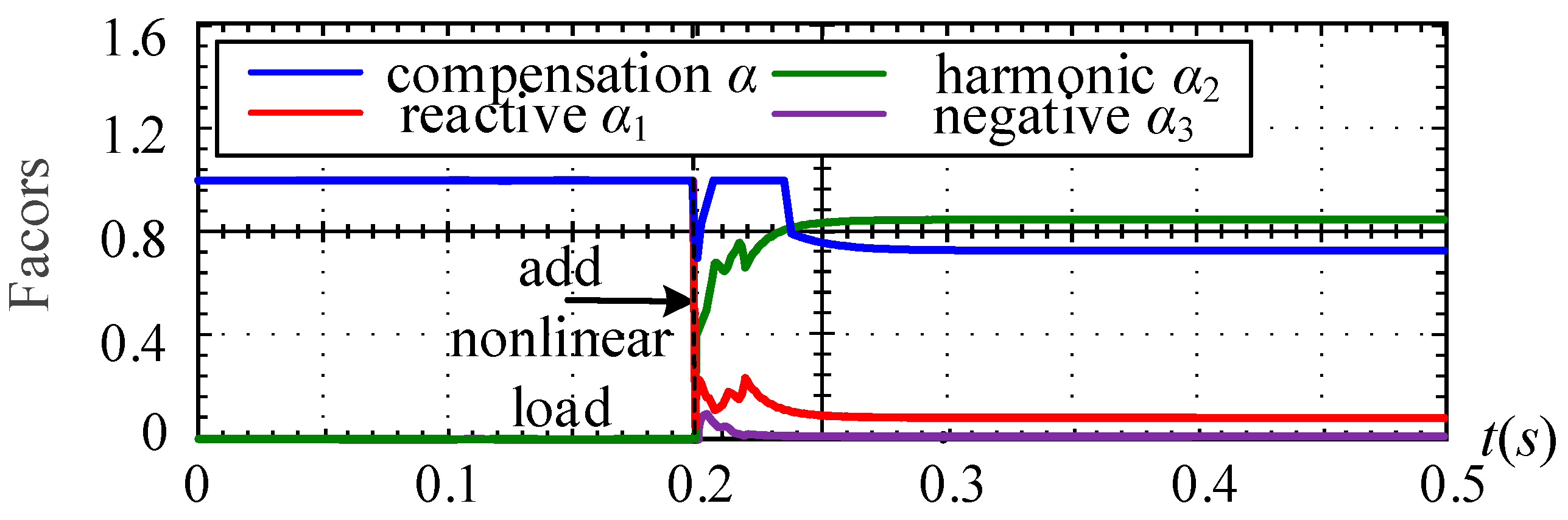
6.4. Cooperative Management of Multi-Converters
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, T.; Wang, X.; Liu, F.; Xin, K.; Liu, Y. A current limiting method for single-loop voltage-magnitude controlled grid-forming converters during symmetrical faults. IEEE Trans. Power Electron. 2022, 37, 4751–4763. [Google Scholar] [CrossRef]
- Shen, C.; Shuai, Z.; Shen, Y.; Peng, Y.; Liu, X.; Li, Z.; Shen, Z. Transient stability and current injection design of paralleled current-controlled vscs and virtual synchronous generators. IEEE Trans. Smart Grid 2021, 12, 1118–1134. [Google Scholar] [CrossRef]
- Rosso, R.; Wang, X.; Liserre, M.; Lu, X.; Engelken, S. Grid-forming converters: Control approaches, grid synchronization, and future trends–A review. IEEE Open J. Ind. Appl. 2021, 2, 93–109. [Google Scholar] [CrossRef]
- Afshari, A.; Davari, M.; Karrari, M.; Gao, W.; Blaabjerg, F. A multivariable, adaptive, robust, primary control enforcing predetermined dynamics of interest in islanded microgrids based on grid-forming inverter-based resources. IEEE Trans. Automat. Sci. Eng. 2024, 21, 2494–2506. [Google Scholar] [CrossRef]
- Brito, M.A.G.D.; Galotto, L., Jr.; Sampaio, L.P.; Melo, G.D.A.E.; Canesin, G.A. Evaluation of the main MPPT techniques for photovoltaic applications. IEEE Trans. Ind. Electron. 2013, 60, 1156–1167. [Google Scholar] [CrossRef]
- Zarei, S.F.; Mokhtari, H.; Ghasemi, M.A.; Peyghami, S.; Davari, P.; Blaabjerg, F. Control of grid-following inverters under unbalanced grid conditions. IEEE Trans. Energy Convers. 2020, 35, 184–192. [Google Scholar] [CrossRef]
- Tang, Y.; Loh, P.C.; Wang, P.; Choo, F.H.; Gao, F.; Blaabjerg, F. Generalized design of high-performance shunt active power filter with output LCL filter. IEEE Trans. Ind. Electron. 2012, 59, 1443–1452. [Google Scholar] [CrossRef]
- Zhang, S.; Qiao, W.; Qu, L.; Wang, J. Analysis and synchronization controller design of dual-port grid-forming voltage-source converters for different operation modes. iEnergy 2024, 3, 46–58. [Google Scholar] [CrossRef]
- Dannehl, J.; Wessels, C.; Fuchs, F.W. Limitations of voltage-oriented PI current control of grid-connected PWM rectifiers with LCL filters. IEEE Trans. Ind. Electron. 2009, 56, 380–388. [Google Scholar] [CrossRef]
- Twining, E.; Holmes, D.G. Grid current regulation of a three-phase voltage source inverter with an LCL input filter. IEEE Trans. Power Electron. 2003, 18, 888–895. [Google Scholar] [CrossRef]
- Zhang, X.; Yu, C.; Liu, F.; Li, F.; Xu, H. Overview on resonance characteristics and resonance suppression strategy of multi-parallel photovoltaic inverters. Chin. J. Elect. Eng. 2016, 2, 40–51. [Google Scholar]
- Hušek, P. Decentralized PI controller design based on phase margin specifications. IEEE Trans. Control Syst. Technol. 2014, 22, 346–351. [Google Scholar] [CrossRef]
- Hasan, S.; Agarwal, V. A voltage support scheme for distributed generation with minimal phase current under asymmetrical grid faults. IEEE Trans. Ind. Electron. 2023, 70, 10261–10270. [Google Scholar] [CrossRef]
- Zhao, C.; Sun, D.; Duan, X.; Nian, H. Current reference optimization for inverter-based resources to mitigate grid voltage vnbalance factor. IEEE Trans. Power Syst. 2024, 39, 6103–6106. [Google Scholar] [CrossRef]
- Lee, C.T.; Hsu, C.W.; Cheng, P.T. A low-voltage ride-through technique for grid-connected converters of distributed energy resources. IEEE Trans. Ind. Appl. 2011, 47, 1821–1832. [Google Scholar] [CrossRef]
- López, M.A.G.; de Vicuña, J.L.G.; Miret, J.; Castilla, M.; Guzmán, R. Control strategy for grid-connected three-phase inverters during voltage sags to meet grid codes and to maximize power delivery capability. IEEE Trans. Power Electron. 2018, 33, 9360–9374. [Google Scholar] [CrossRef]
- Pleshakova, E.; Osipov, A.; Gataullin, S.; Gataullin, T.; Vasilakos, A. Next gen cybersecurity paradigm towards artificial general intelligence: Russian market challenges and future global technological trends. J. Comput. Virol. Hack. Tech. 2024, 20, 429–440. [Google Scholar] [CrossRef]
- Zhao, X.; Bian, D. Currents’-physical-component-based reactive power compensation optimization in three-phase, four-wire systems. Appl. Sci. 2024, 14, 5043. [Google Scholar] [CrossRef]
- Zelenina, A.; Petrosov, D.; Pleshakova, E.; Osipov, A.; Ivanov, M.N.; Choporov, O.; Preobrazhenskiy, Y.; Petrsova, N.; Roga, S.; Lopatnuk, L.; et al. Modeling of management processes in distributed organizational systems. Proc. Comput. Sci. 2022, 213, 377–384. [Google Scholar] [CrossRef]
- Mousavi, S.Y.M.; Jalilian, A.; Savaghebi, M.; Guerrero, J.M. Coordinated control of multifunctional inverters for voltage support and harmonic compensation in a grid-connected microgrid. Electr. Power Syst. Res. 2018, 155, 254–264. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, D.; Wang, Y.; Wu, B.; Athab, H.S. Power and voltage balance control of a novel three-phase solid-state transformer using multilevel cascaded H-bridge inverters for microgrid applications. IEEE Trans. Power Electron. 2016, 31, 3289–3301. [Google Scholar] [CrossRef]
- Gataullin, T.M.; Gataullin, S.T. Best economic approaches under conditions of uncertainty. In Proceedings of the 2018 Eleventh International Conference on Management of Large-Scale System Development (MLSD), Moscow, Russia, 1–3 October 2018. [Google Scholar]
- Sharma, A.; Rajpurohit, B.S.; Singh, S.N. A review on economics of power quality: Impact, assessment and mitigation. Renew. Sustain. Energy Rev. 2018, 88, 363–372. [Google Scholar] [CrossRef]
- Sun, H.; Lin, X.; Chen, S.; Ji, X.; Liu, D.; Jiang, K. Transient stability analysis of the standalone solar-storage AC supply system based on grid-forming and grid-following converters during sudden load variation. IET Renew. Power Gener. 2022, 17, 1286–1302. [Google Scholar] [CrossRef]
- Shao, W.; Wu, R.; Ran, L.; Jiang, H.; Mawby, P.A.; Rogers, D.J.; Green, T.C.; Coombs, T.; Yardley, K.; Kastha, D.; et al. Apower module for grid inverter with in-built short-circuit fault current capability. IEEE Trans. Power Electron. 2020, 35, 10567–10579. [Google Scholar] [CrossRef]
- Qoria, T.; Gruson, F.; Colas, F.; Denis, G.; Prevost, T.; Guillaud, X. Critical clearing time determination and enhancement of grid-forming converters embedding virtual impedance as current limitation algorithm. IEEE J. Emerg. Sel. Topics Power Electron. 2020, 8, 1050–1061. [Google Scholar] [CrossRef]
- Lei, J.; Xiang, X.; Liu, B.; Li, W.; He, X. Transient stability analysis of grid forming converters based on damping energy visualization and geometry approximation. IEEE Trans. Ind. Electron. 2024, 71, 2510–2521. [Google Scholar] [CrossRef]
- Sun, J. Impedance-Based Stability Criterion for Grid-Connected Inverters. IEEE Trans. Power Electron. 2011, 26, 3075–3078. [Google Scholar] [CrossRef]
- Xie, Z.; Wu, W.; Chen, Y.; Gong, W. Admittance-based stability comparative analysis of grid-connected inverters with direct power control and closed-loop current control. IEEE Trans. Ind. Electron. 2021, 66, 8333–8344. [Google Scholar] [CrossRef]
- Zhou, L.; Wu, W.; Chen, Y.; He, Z.; Zhou, X.; Huang, X.; Yang, L.; Luo, A.; Guerrero, J.M. Virtual positive-damping reshaped impedance stability control method for the offshore MVDC system. IEEE Trans. Power Electron. 2019, 34, 4951–4966. [Google Scholar] [CrossRef]
- Zhang, X.; Zhong, Q.-C.; Ming, W. Stabilization of cascaded dc/dc converters via adaptive series-virtual-impedance control of the load converter. IEEE Trans. Power Electron. 2016, 31, 6057–6063. [Google Scholar] [CrossRef]
- Jalili, K.; Bernet, S. Design of LCL filters of active-front-end two-level voltage-source converters. IEEE Trans. Ind. Electron. 2009, 56, 1674–1689. [Google Scholar] [CrossRef]
- Qu, Z.; Peng, J.C.-H.; Yang, H.; Srinivasan, D. Modeling and analysis of inner controls effects on damping and synchronizing torque components in VSG-controlled converter. IEEE Trans. Energy Convers. 2021, 36, 488–499. [Google Scholar] [CrossRef]
- Lanzkron, R.; Higgins, T. D-decomposition analysis of automatic control systems. IRE Trans. Autom. Control 1959, 4, 150–171. [Google Scholar] [CrossRef]
- Li, M.; Zhang, X.; Guo, Z.; Pan, H.; Ma, M.; Zhao, W. Impedance adaptive dual-mode control of grid-connected inverters with large fluctuation of SCR and its stability analysis based on D-Partition method. IEEE Trans. Power Electron. 2021, 36, 14420–14435. [Google Scholar] [CrossRef]


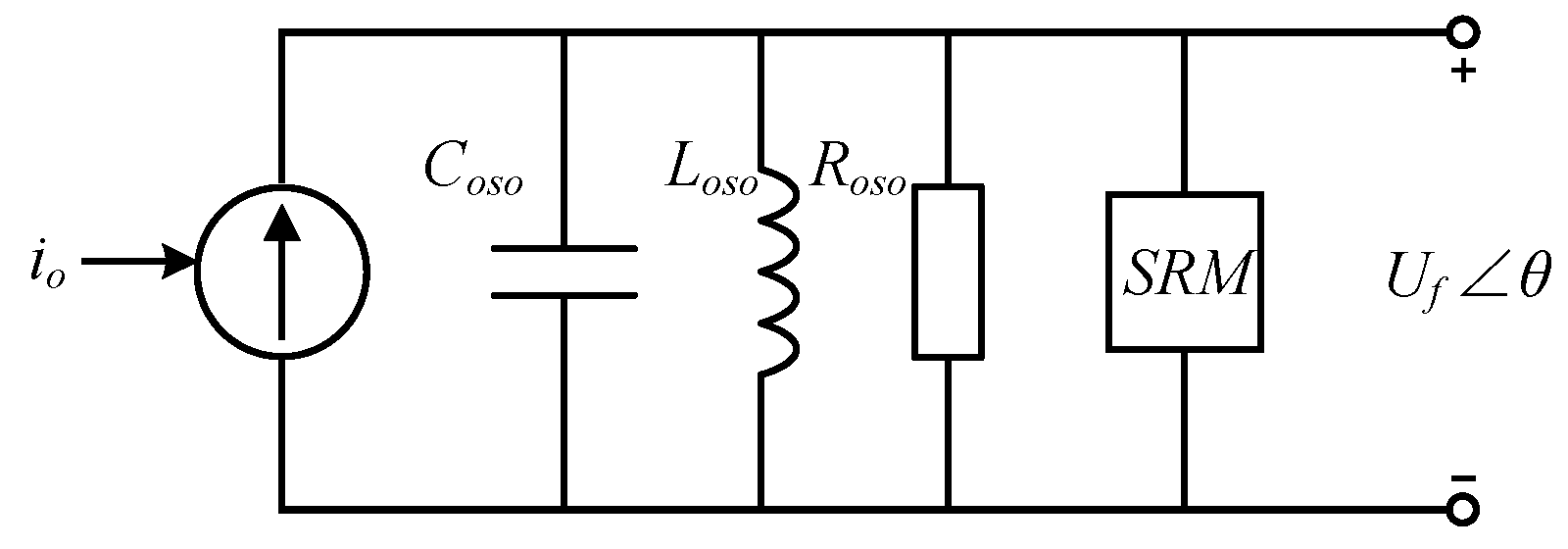


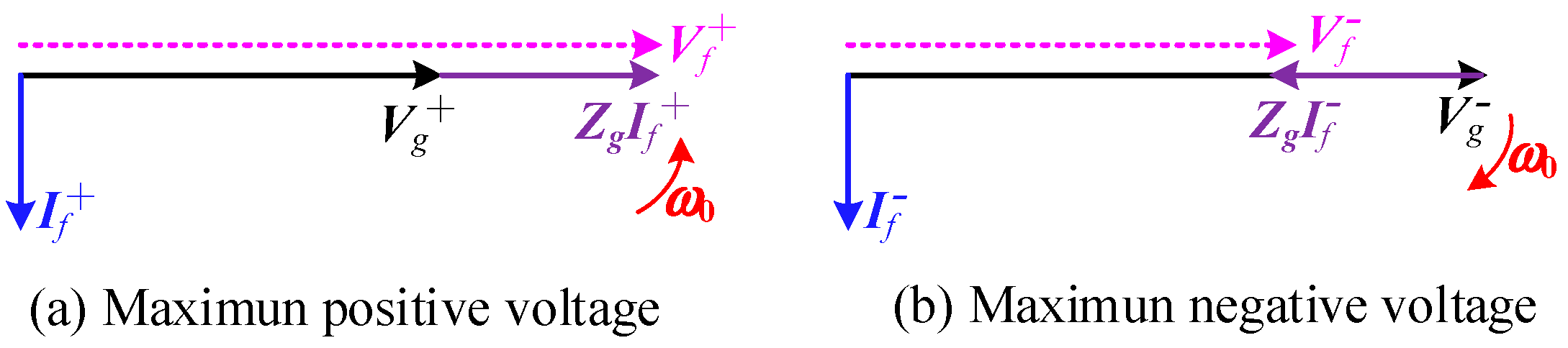









| Performance Area | Droop Control | VSG | VOC |
|---|---|---|---|
| Inertia Support | None | Present | Present |
| Response Speed | Fast | Slow | Fast |
| Current Sharing | Moderate | Moderate | Good |
| Output Oscillation | None | Present | Present |
| Power Regulation | Available | Available | Available |
| Parameters | Value | Parameters | Value |
|---|---|---|---|
| Grid voltage ugN | 380 V | Converter-side inductance Lm | 1.6 mH |
| Rated angular frequency ω0 | 50 Hz | Filter capacitance Cm | 20 μF |
| Switching frequency | 16 kHz | Passive damping resistance Rm | 0.5 Ω |
| Parameters | Value | Parameters | Value |
|---|---|---|---|
| Nominal Power | 150 kVA | DC-bus capacitor Cbus | 375 μF |
| AC frequency fac | 50 Hz | Switch frequency | 20 kHz |
| Filter inductance Lf | 100 μH | Line inductance Lg | 3 mH |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, M.; Long, Y.; Guo, S.; Xiao, Z.; Shi, T.; Xiang, X.; Fan, R. Stability Boundary Characterization and Power Quality Improvement for Distribution Networks. Energies 2024, 17, 6215. https://doi.org/10.3390/en17246215
Zhang M, Long Y, Guo S, Xiao Z, Shi T, Xiang X, Fan R. Stability Boundary Characterization and Power Quality Improvement for Distribution Networks. Energies. 2024; 17(24):6215. https://doi.org/10.3390/en17246215
Chicago/Turabian StyleZhang, Min, Yi Long, Shuai Guo, Zou Xiao, Tianling Shi, Xin Xiang, and Rui Fan. 2024. "Stability Boundary Characterization and Power Quality Improvement for Distribution Networks" Energies 17, no. 24: 6215. https://doi.org/10.3390/en17246215
APA StyleZhang, M., Long, Y., Guo, S., Xiao, Z., Shi, T., Xiang, X., & Fan, R. (2024). Stability Boundary Characterization and Power Quality Improvement for Distribution Networks. Energies, 17(24), 6215. https://doi.org/10.3390/en17246215





