Impact of Energy System Optimization Based on Different Ground Source Heat Pump Models
Abstract
1. Introduction
2. Modeling of Energy Systems
2.1. Buried Pipe Model
2.2. Heat Pump Model
2.3. Water Pump Model
2.4. Energy Storage Device Model
2.5. Demand and Electricity Price Profiles
3. Improved Particle Swarm Optimization Algorithm
3.1. Particle Swarm Algorithm Model
3.2. Improved Particle Swarm Optimization Algorithm Model
3.3. Objective Function
3.4. Constraint Condition
- (1)
- Power balance constraints
- (2)
- Hot and cold load constraints
- (3)
- Water pump unit flow constraint
- (1)
- Energy storage battery constraints
- (2)
- Cold storage device constraint
3.5. Other Descriptions
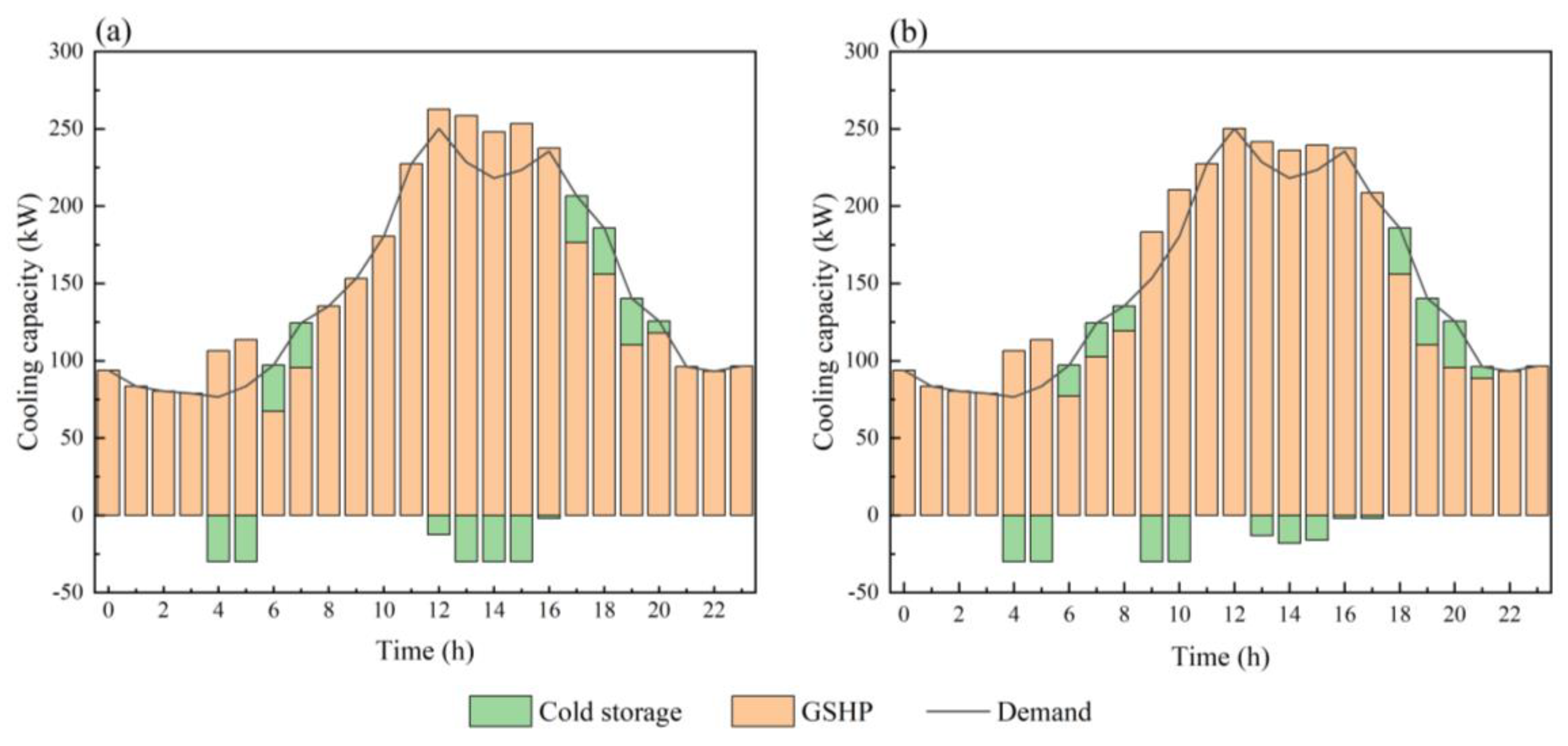
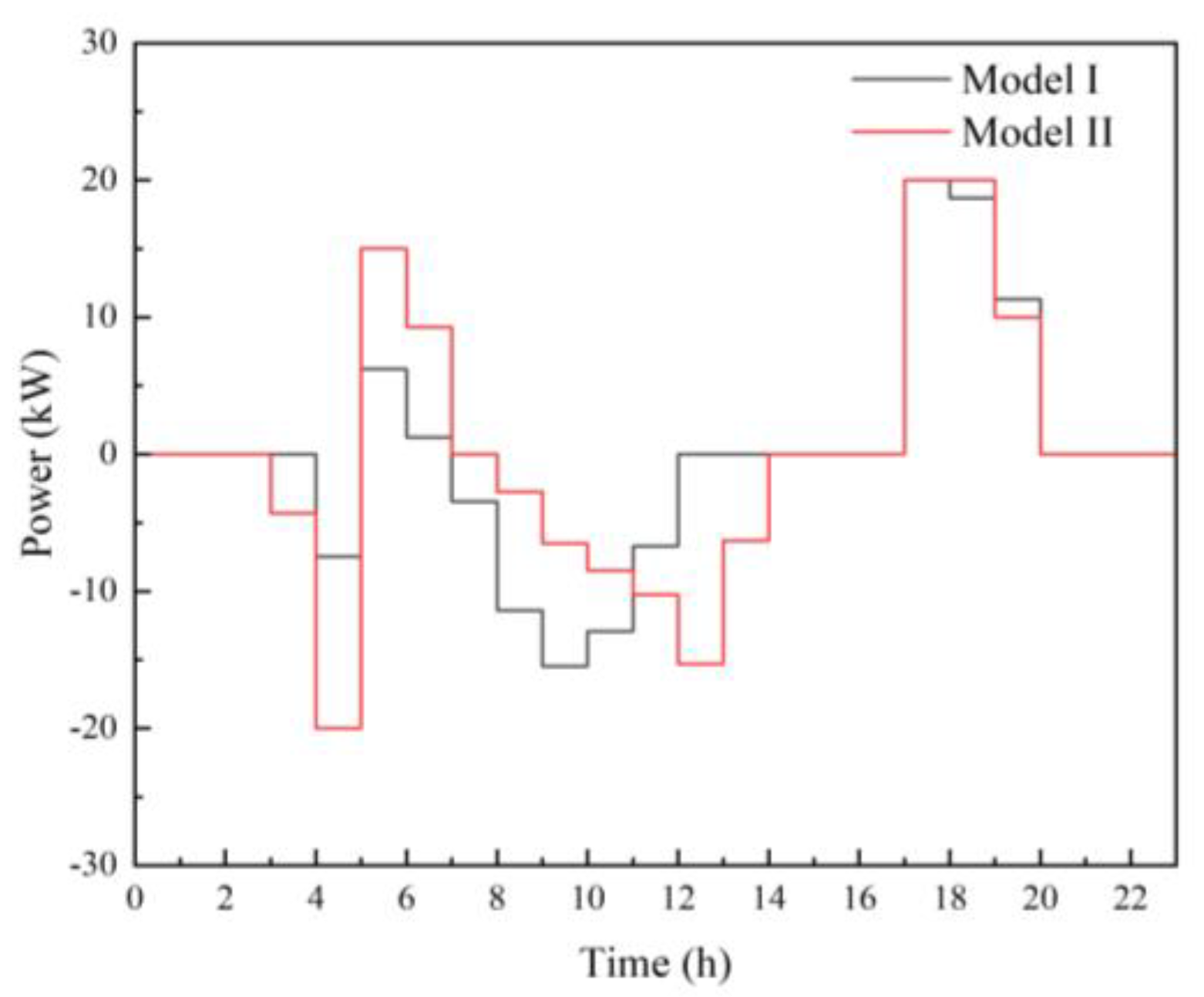
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, F.; Sun, B.; Zhang, C.; Zhang, L. Operation optimization for combined cooling, heating, and power system with condensation heat recovery. Appl. Energy 2018, 230, 305–316. [Google Scholar] [CrossRef]
- Chen, K.; Pan, M. Operation optimization of combined cooling, heating, and power superstructure system for satisfying demand fluctuation. Energy 2021, 237, 121599. [Google Scholar] [CrossRef]
- Li, Q.; Li, Q.; Wang, F.; Wu, J.; Wang, Y. The carrying behavior of water-based fracturing fluid in shale reservoir fractures and molecular dynamics of sand-carrying mechanism. Processes 2024, 12, 2051. [Google Scholar] [CrossRef]
- Li, L.L.; Liu, Z.F.; Tseng, M.L.; Zheng, S.J.; Lim, M.K. Improved tunicate swarm algorithm: Solving the dynamic economic emission dispatch problems. Appl. Soft Comput. 2021, 108, 107504. [Google Scholar] [CrossRef]
- De Luca, G.; Ballarini, I.; Lorenzati, A.; Corrado, V. Renovation of a social house into a NZEB: Use of renewable energy sources and economic implications. Renew Energy 2020, 159, 356–370. [Google Scholar] [CrossRef]
- Park, S.H.; Jang, Y.S.; Kim, E.J. Multi-objective optimization for sizing multi-source renewable energy systems in the community center of a residential apartment complex. Energy Convers. Manag. 2021, 244, 114446. [Google Scholar] [CrossRef]
- Jo, H.; Park, J.; Kim, I. Environmentally constrained optimal dispatch method for combined cooling, heating, and power systems using two-stage optimization. Energies 2021, 14, 4135. [Google Scholar] [CrossRef]
- Le, H.T.T.; Sanseverino, E.R.; Nguyen, D.Q.; Di Silvestre, M.L.; Favuzza, S.; Pham, M.H. Critical assessment of feed-in tariffs and solar photovoltaic development in Vietnam. Energies 2022, 15, 556. [Google Scholar] [CrossRef]
- Yang, C.; Tao, J.; Wuzhi, Z. Source-load coordination economic dispatch method for regional integrated energy system considering wind power accommodation. Power Syst. Technol. 2020, 44, 2474–2483. [Google Scholar]
- Gao, C.; Zhang, Z.; Wang, P. Day-Ahead Scheduling Strategy Optimization of Electric–Thermal Integrated Energy System to Improve the Proportion of New Energy. Energies 2023, 16, 3781. [Google Scholar] [CrossRef]
- Yang, Z.P.; Zhang, F.; Liang, J.; Han, X.S.; Xu, Z. Economic generation scheduling of CCHP microgrid with heat pump and energy storage. Power Syst. Technol. 2018, 42, 1735–1743. [Google Scholar]
- Zhang, Z.L.; Zhang, H.J.; Xie, B.; Zhang, X.T. Energy scheduling optimization of the integrated energy system with ground source heat pumps. J. Clean. Prod. 2022, 365, 132758. [Google Scholar] [CrossRef]
- Li, B.; Hu, P.; Zhu, N.; Lei, F.; Xing, L. Performance analysis and optimization of a CCHP-GSHP coupling system based on quantum genetic algorithm. Sustain. Cities Soc. 2019, 46, 101408. [Google Scholar] [CrossRef]
- Zeng, R.; Li, H.; Liu, L.; Zhang, X.; Zhang, G. A novel method based on multi-population genetic algorithm for CCHP–GSHP coupling system optimization. Energy Convers. Manag. 2015, 105, 1138–1148. [Google Scholar] [CrossRef]
- Ren, J.G.; Zhang, L.; Jin, L.; Tang, Y.; Tang, Q.; Liu, X. Day-ahead economic dispatch model of building integrated energy systems considering the renewable energy consumption. Eng. Sci. Technol. 2023, 55, 160–170. [Google Scholar]
- Tao, G.; Zhong, W.; Chen, X.; Zhou, G. Low carbon design optimization of integrated energy system with urban thermal power plant as core. Dongnan Daxue Xuebao (Ziran Kexue Ban)/J. Southeast Univ. (Nat. Sci. Ed.) 2022, 52, 631–640. [Google Scholar]
- Ikeda, S.; Choi, W.; Ooka, R. Optimization method for multiple heat source operation including ground source heat pump considering dynamic variation in ground temperature. Appl. Energy 2017, 193, 466–478. [Google Scholar] [CrossRef]
- Chen, C.; Chen, X.; Zhang, J.; Yu, K.; Gan, L. Stochastic operational optimal strategy for ground source heat pump system under TOU price. Power Syst. Prot. Control 2019, 47, 57–64. [Google Scholar]
- Yang, G.; Zhai, X.Q. Optimal design and performance analysis of solar hybrid CCHP system considering influence of building type and climate condition. Energy 2019, 174, 647–663. [Google Scholar] [CrossRef]
- Guan, X.; Zhang, H.; Xue, C. A method of selecting cold and heat sources for enterprises in an industrial park with combined cooling, heating, and power. J. Clean. Prod. 2018, 190, 608–617. [Google Scholar] [CrossRef]
- Li, L.L.; Liu, Y.W.; Tseng, M.L.; Lin, G.Q.; Ali, M.H. Reducing environmental pollution and fuel consumption using optimization algorithm to develop combined cooling heating and power system operation strategies. J. Clean. Prod. 2020, 247, 119082. [Google Scholar] [CrossRef]
- Sanaye, S.; Niroomand, B. Horizontal ground coupled heat pump: Thermal-economic modeling and optimization. Energy Convers. Manag. 2010, 51, 2600–2612. [Google Scholar] [CrossRef]
- De Ridder, F.; Diehl, M.; Mulder, G.; Desmedt, J.; Van Bael, J. An optimal controlalgorithm for borehole thermal energy storage systems. Energy Build 2011, 43, 2918–2925. [Google Scholar] [CrossRef]
- Neugebauer, M.; Sołowiej, P. Optimization with the use of genetic algorithms of thelocation depth of horizontal ground heat exchangers. Inżynieria Rol. 2012, 16, 89–97. [Google Scholar]
- Zeng, H.Y.; Diao, N.R.; Fang, Z.H. A finite line-source model for boreholes in geothermal heat exchangers. Heat Transf. Asian Res. 2002, 31, 558–567. [Google Scholar] [CrossRef]
- Chen, Y.; Pan, B.; Zhang, X.; Du, C. Thermal response factors for fast parameterized design and long-term performance simulation of vertical GCHP systems. Renew. Energy 2019, 136, 793–804. [Google Scholar] [CrossRef]
- Soltani, M.; Kashkooli, F.M.; Dehghani-Sanij, A.R.; Kazemi, A.R.; Bordbar, N.; Farshchi, M.J.; Elmi, M.; Gharali, K.; Dusseault, M.B. A comprehensive study of geothermal heating and cooling systems. Sustain. Cities Soc. 2019, 44, 793–818. [Google Scholar] [CrossRef]
- Hydeman, M.; Gillespie, K.L., Jr. Tools and techniques to calibrate electric chiller component models/discussion. ASHRAE Trans. 2002, 108, 733. [Google Scholar]
- Wen, Q.; Liu, G.; Wu, W.; Liao, S. Performance evaluation of distributed energy system integrating photovoltaic, ground source heat pump, and natural gas-based CCHP. Energy Convers. Manag. 2022, 252, 115039. [Google Scholar] [CrossRef]
- Li, X.; Zhang, J.; He, Y.; Zhang, Y.; Liu, Y.; Yan, K. Multi-objective Optimization Dispatching of Microgrid Based on Improved Particle Swarm Algorithm. Electr. Power Sci. Eng. 2021, 37, 1–7. [Google Scholar]
- Fu, X.; Huang, S.; Li, R.; Sun, H. Electric power output optimization for CCHP using PSO theory. Energy Procedia 2016, 103, 9–14. [Google Scholar] [CrossRef]
- Tharwat, A.; Elhoseny, M.; Hassanien, A.E.; Gabel, T.; Kumar, A. Intelligent Bézier curve-based path planning model using Chaotic Particle Swarm Optimization algorithm. Clust. Comput. 2019, 22, 4745–4766. [Google Scholar] [CrossRef]
- Zhang, B.; You, S.; Wang, S.; Ding, X.; Wang, C.; Gao, Y. From laboratory to on-site operation: Reevaluation of empirically based electric water chiller models. Build. Simul. 2022, 15, 213–232. [Google Scholar] [CrossRef]








| Parameter | Value |
|---|---|
| Initial soil temperature (°C) | 15 |
| depth (m) | 100 |
| Drilling diameter (m) | 0.08 |
| Number of boreholes | 49 |
| inside diameter (m) | 0.026 |
| Thermal conductivity of pipe [W/(m·K)] | 0.39 |
| U-shaped tube thickness (m) | 0.0024 |
| outside diameter (m) | 0.032 |
| Water Specific thermal capacity [J/(kg·K)] | 4181 |
| Convective heat transfer coefficient of tube [W/(m2·K)] | 3575 |
| Time (h) | Price [CNY·(kwh)−1] | |
|---|---|---|
| Peak period | 10:00–13:00 | 0.886 |
| 17:00–22:00 | ||
| Normal period | 07:00–10:00 | 0.667 |
| 13:00–17:00 | ||
| 22:00–23:00 | ||
| Low price period | 00:00–07:00 | 0.4513 |
| 23:00–24:00 | ||
| Consumption of Water Pump (kWh) | Consumption of Unit (kWh) | SystemCOP | Operating Costs (CNY) | PV Power Loss Rate | |
|---|---|---|---|---|---|
| Model I | 104 | 640.42 | 5.5 | 114.89 | 9.5% |
| Model II | 57.41 | 719.84 | 4.75 | 165.90 | 2.9% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lai, Y.; Gao, Y.; Gao, Y. Impact of Energy System Optimization Based on Different Ground Source Heat Pump Models. Energies 2024, 17, 6023. https://doi.org/10.3390/en17236023
Lai Y, Gao Y, Gao Y. Impact of Energy System Optimization Based on Different Ground Source Heat Pump Models. Energies. 2024; 17(23):6023. https://doi.org/10.3390/en17236023
Chicago/Turabian StyleLai, Yingjun, Yan Gao, and Yaping Gao. 2024. "Impact of Energy System Optimization Based on Different Ground Source Heat Pump Models" Energies 17, no. 23: 6023. https://doi.org/10.3390/en17236023
APA StyleLai, Y., Gao, Y., & Gao, Y. (2024). Impact of Energy System Optimization Based on Different Ground Source Heat Pump Models. Energies, 17(23), 6023. https://doi.org/10.3390/en17236023





