Co-Optimization of Speed Planning and Energy Management for Plug-In Hybrid Electric Trucks Passing Through Traffic Light Intersections
Abstract
1. Introduction
2. Plug-In Hybrid Electric Truck System Modeling
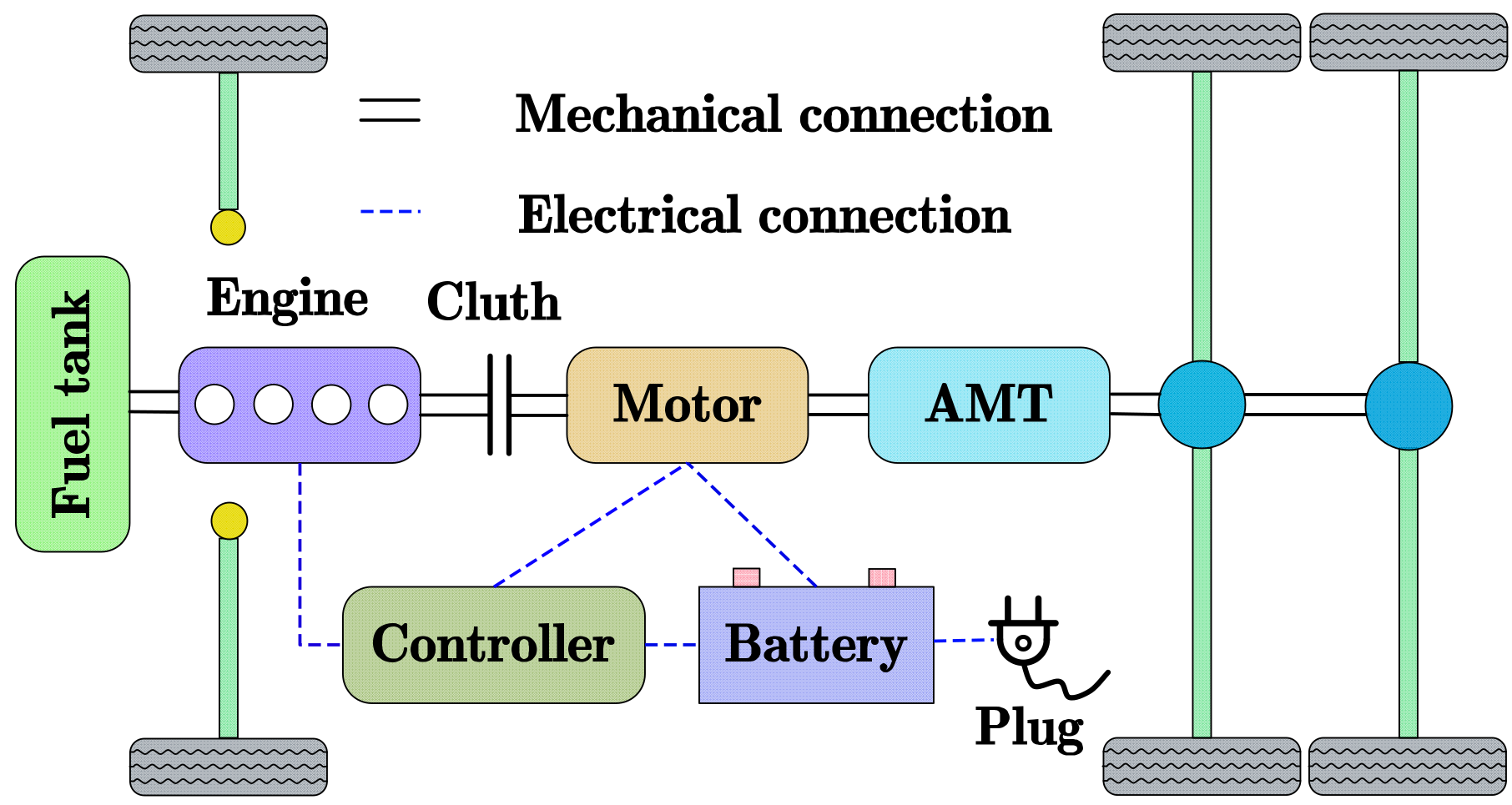
2.1. Plug-In Hybrid Electric Truck System
2.2. Vehicle Longitudinal Dynamics Model
2.3. Powertrain Component Model
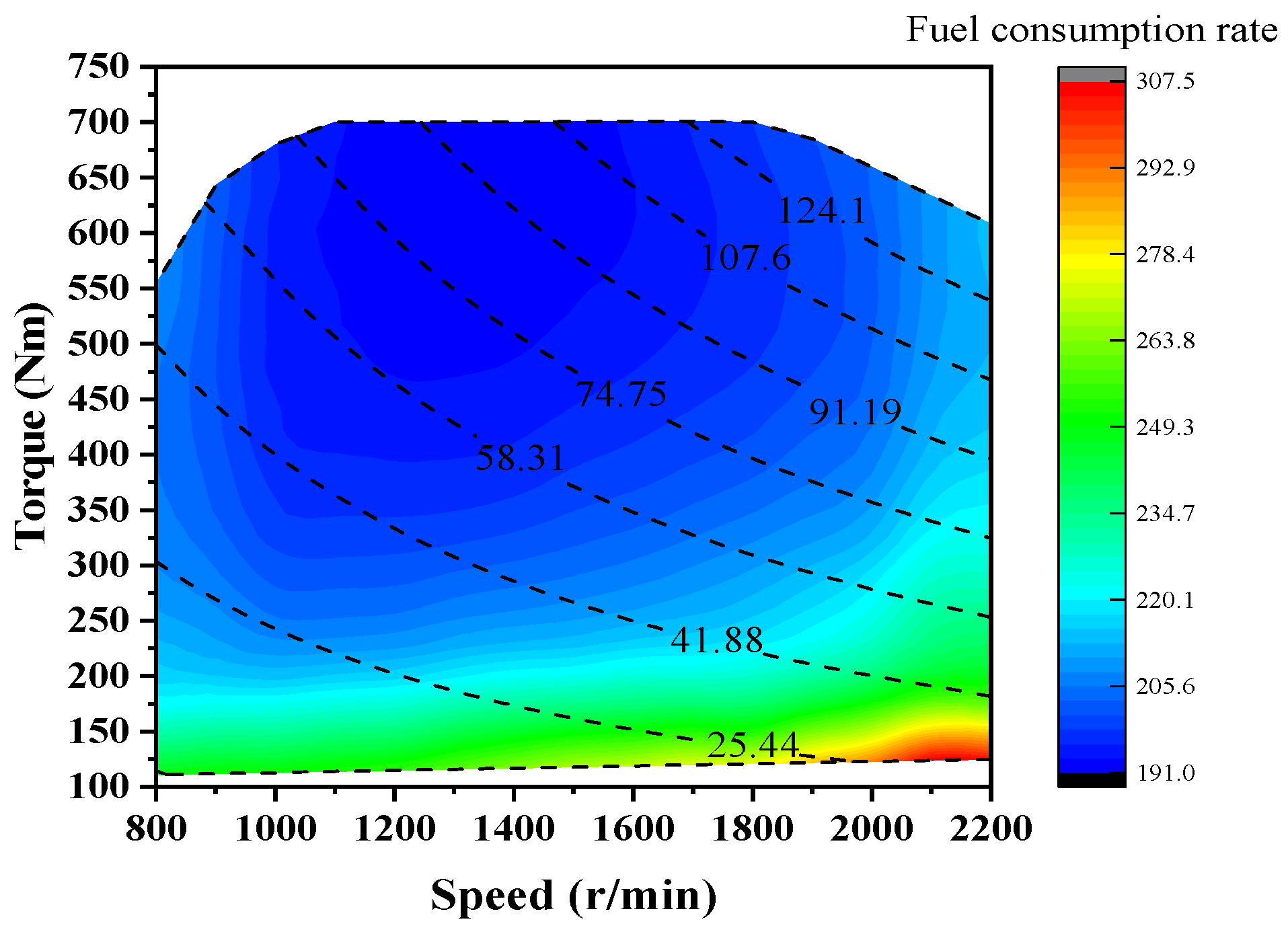
2.3.1. Engine Model
2.3.2. Motor Model
2.3.3. Battery Model
2.4. Traffic Signal Light Model
3. Energy Management Strategy Based on Dynamic Programming–Twin Delayed Deep Deterministic Policy Gradient Algorithm
3.1. Energy Management Strategy Framework
3.2. Upper-Level Speed-Planning Control
3.2.1. Speed-Planning Model
3.2.2. Speed-Planning Control Strategy Based on Dynamic Programming (DP) Algorithm
3.3. Lower-Level Energy Management Control
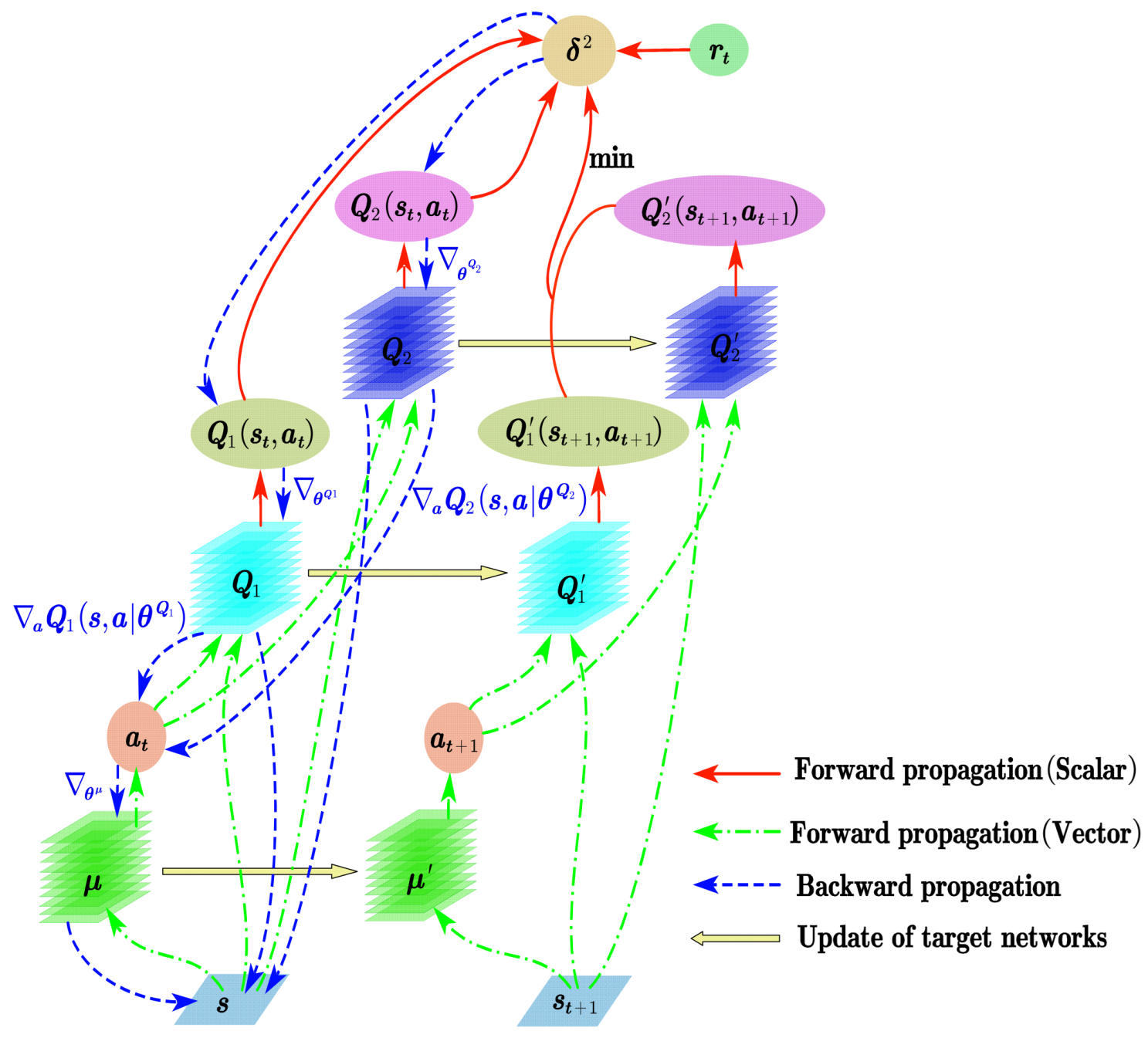
3.3.1. Twin Delayed Deep Deterministic Policy Gradient (TD3) Algorithm
| Algorithm 1: TD3 |
| Initialize critic networks, and , and actor network, , with parameters , , and Initialize target, networks , , Initialize replay buffer, Initialize learning rate, for t = 1:T do Initialize a random noise, Initialize state variables, According to states, , selection action, Get reward and new state Store transition tuple in replay buffer, Randomly sample mini batch of N transitions from , Update critic network parameters if t mod d, then Update by the deterministic policy gradient Update target network parameters end if end for |
3.3.2. Energy Management Strategy Based on TD3 Algorithm
4. Results and Discussion
4.1. Parameter Settings
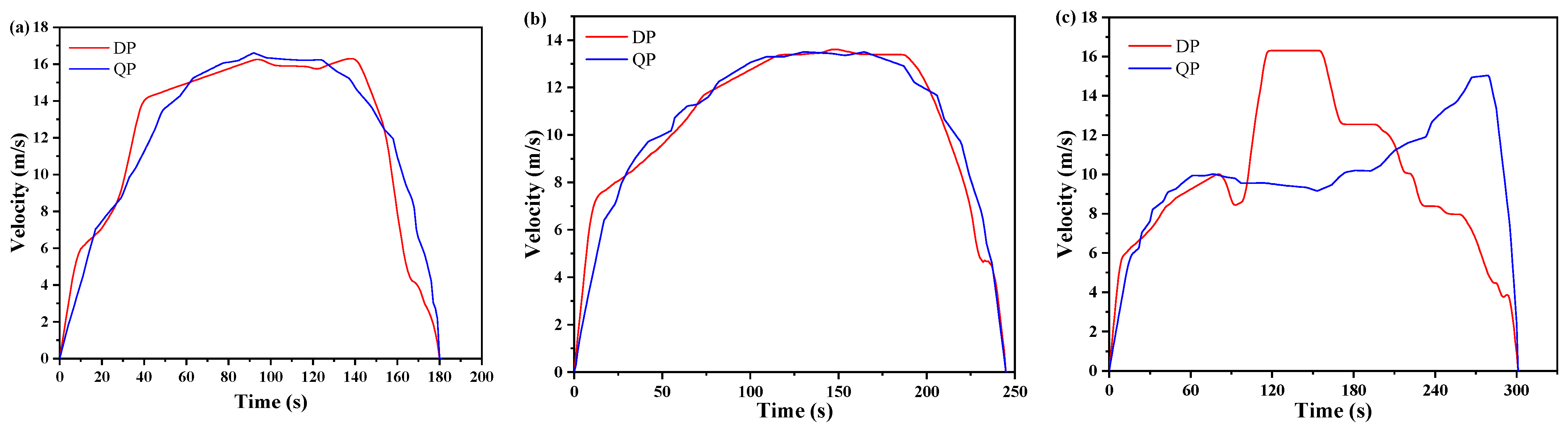
4.2. Analysis of Speed-Planning Results
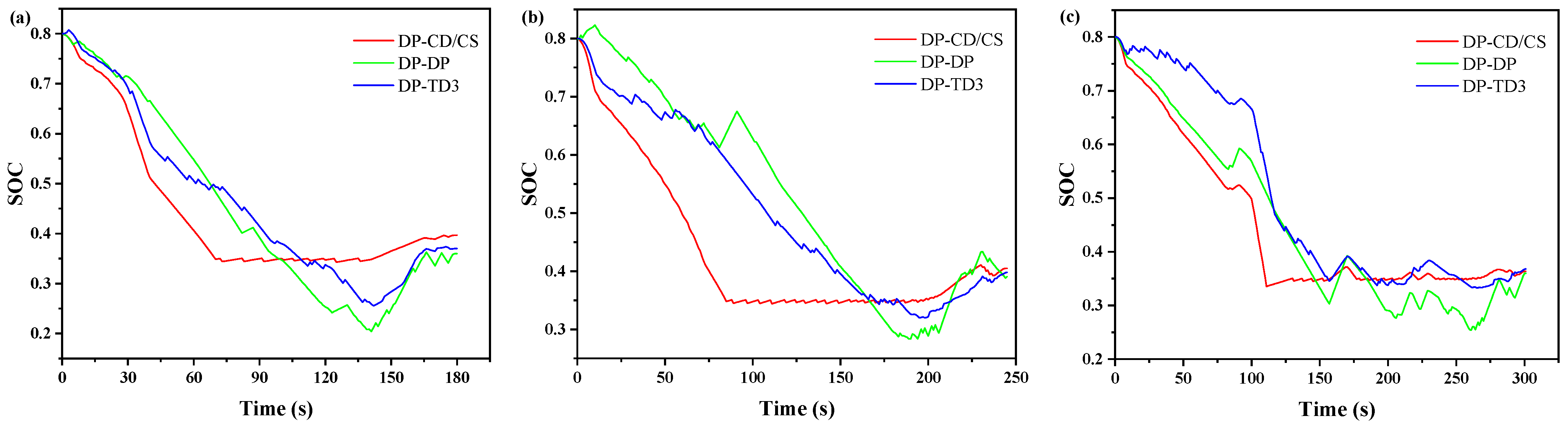
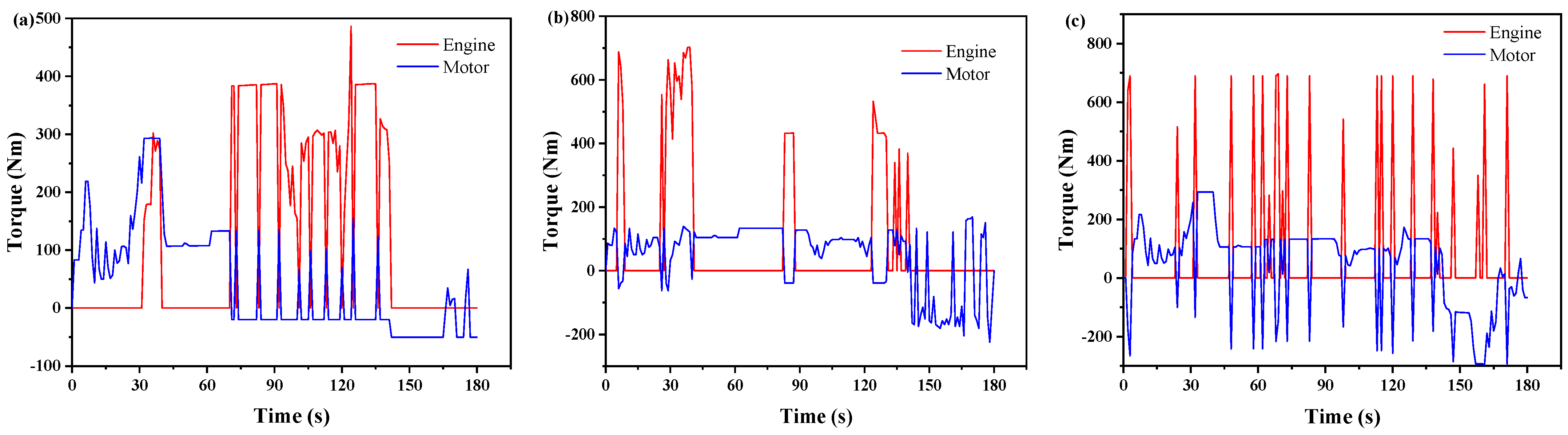
4.3. Analysis of Fuel Economy
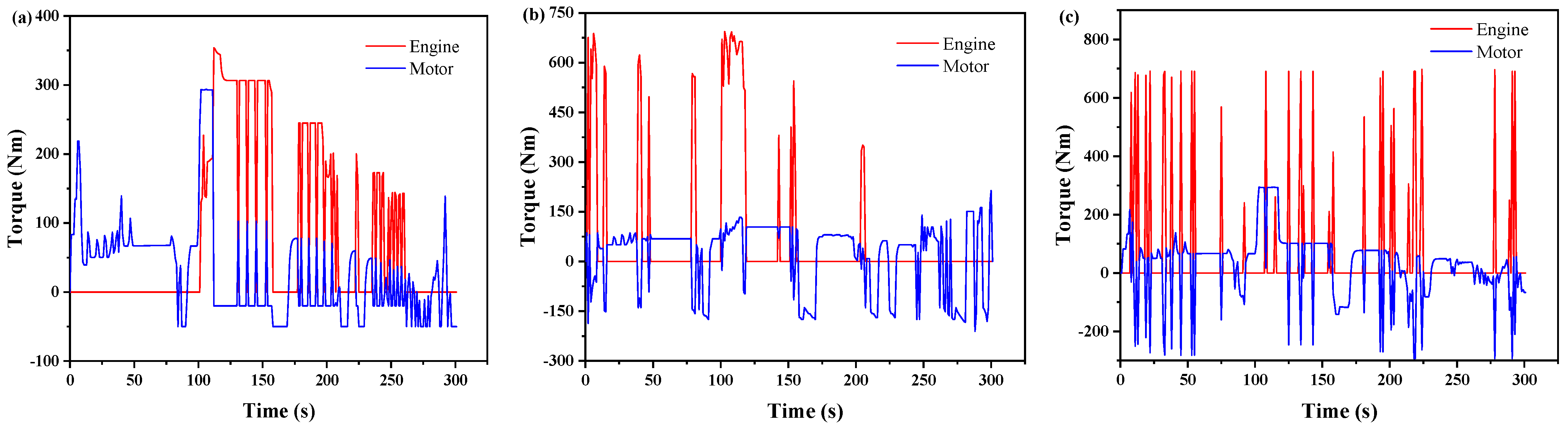
4.4. Hardware-in-the-Loop Experimental Verification
5. Conclusions
- (1)
- In the upper layer, a speed-planning model for the DP algorithm is constructed to plan the vehicle trajectory according to the position, phase, and timing of traffic signals in order to avoid stopping the vehicle due to red lights. The speed-planning model adeptly converts the nonlinear constraints associated with traffic signals into time-varying constraints. This strategic transformation effectively diminishes the model’s complexity while significantly enhancing computational efficiency.
- (2)
- In the lower layer, an energy management strategy is devised using the TD3 algorithm to efficiently allocate power for the plug-in hybrid electric truck. This strategy operates through the interaction between the TD3 agent and the environment.
- (3)
- The simulation results demonstrate that the DP-TD3 method significantly decreases the fuel consumption of plug-in hybrid electric trucks. In comparison to the DP-CD/CS method, there is a fuel saving of 17.05% in traffic scenario 1 and 12.35% in traffic scenario 2. The fuel saving in traffic scenario 3 is 14.42%, with an average of 14.61%.
- (4)
- The hardware-in-the-loop test results reveal that the fuel consumption of the DP-TD3 method is 9.97 L/100 km, a finding that aligns closely with the simulation results.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jia, C.C.; He, H.W.; Zhou, J.M.; Li, J.W.; Wei, Z.B.; Li, K.A. A novel health-aware deep reinforcement learning energy management for fuel cell bus incorporating offline high-quality experience. Energy 2023, 282, 12892. [Google Scholar] [CrossRef]
- Hu, J.; Shao, Y.L.; Sun, Z.X.; Wang, M.; Bared, J.; Huang, P. Integrated optimal eco-driving on rolling terrain for hybrid electric vehicle with vehicle-infrastructure communication. Transp. Res. Part C Emerg. Technol. 2016, 68, 228–244. [Google Scholar] [CrossRef]
- Liu, S.C.; Sun, H.W.; Yu, H.T.; Miao, J.; Zheng, C.; Zhang, X.W. A framework for battery temperature estimation based on fractional electro-thermal coupling model. J. Energy Storage 2023, 63, 107042. [Google Scholar] [CrossRef]
- Li, X.P.; Zhou, J.M.; Guan, W.; Jiang, F.; Xie, G.M.; Wang, C.F.; Zheng, W.G.; Fang, Z.J. Optimization of Brake Feedback Efficiency for Small Pure Electric Vehicles Based on Multiple Constraints. Energies 2023, 16, 6531. [Google Scholar] [CrossRef]
- Meng, X.Y.; Cassandras, C.G. Eco-Driving of Autonomous Vehicles for Nonstop Crossing of Signalized Intersections. IEEE Trans. Autom. Sci. Eng. 2022, 19, 320–331. [Google Scholar] [CrossRef]
- Li, J.; Liu, Y.G.; Zhang, Y.J.; Lei, Z.Z.; Chen, Z.; Li, G. Data-driven based eco-driving control for plug-in hybrid electric vehicles. J. Power Sources 2021, 498, 229916. [Google Scholar] [CrossRef]
- Xu, N.; Li, X.H.; Yue, F.L.; Jia, Y.F.; Liu, Q.; Zhao, D. An Eco-Driving Evaluation Method for Battery Electric Bus Drivers Using Low-Frequency Big Data. IEEE Trans. Intell. Transp. Syst. 2023, 24, 9296–9308. [Google Scholar] [CrossRef]
- Huang, Y.H.; Ng, E.C.Y.; Zhou, J.L.; Surawski, N.C.; Chan, E.F.C.; Hong, G. Eco-driving technology for sustainable road transport: A review. Renew. Sustain. Energy Rev. 2018, 93, 596–609. [Google Scholar] [CrossRef]
- Sankar, G.S.; Kim, M.; Han, K. Data-Driven Leading Vehicle Speed Forecast and Its Application to Ecological Predictive Cruise Control. IEEE Trans. Veh. Technol. 2022, 71, 11504–11514. [Google Scholar] [CrossRef]
- Huang, K.; Yang, X.F.; Lu, Y.; Mi, C.C.; Kondlapudi, P. Ecological Driving System for Connected/Automated Vehicles Using a Two-Stage Control Hierarchy. IEEE Trans. Intell. Transp. Syst. 2018, 19, 2373–2384. [Google Scholar] [CrossRef]
- Pan, C.; Li, Y.; Huang, A.; Wang, J.; Liang, J. Energy-optimized adaptive cruise control strategy design at intersection for electric vehicles based on speed planning. Sci. China-Technol. Sci. 2023, 66, 3504–3521. [Google Scholar] [CrossRef]
- Li, J.; Fotouhi, A.; Pan, W.J.; Liu, Y.G.; Zhang, Y.J.; Chen, Z. Deep reinforcement learning-based eco-driving control for connected electric vehicles at signalized intersections considering traffic uncertainties. Energy 2023, 279, 128139. [Google Scholar] [CrossRef]
- Sun, C.; Guanetti, J.; Borrelli, F.; Moura, S.J. Optimal Eco-Driving Control of Connected and Autonomous Vehicles Through Signalized Intersections. IEEE Internet Things J. 2020, 7, 3759–3773. [Google Scholar] [CrossRef]
- Guo, J.Q.; He, H.W.; Li, J.W.; Liu, Q.W. Real-time energy management of fuel cell hybrid electric buses: Fuel cell engines friendly intersection speed planning. Energy 2021, 226, 120440. [Google Scholar] [CrossRef]
- Wei, X.D.; Leng, J.H.; Sun, C.; Huo, W.W.; Ren, Q.; Sun, F.C. Co-optimization method of speed planning and energy management for fuel cell vehicles through signalized intersections. J. Power Sources 2022, 518, 230598. [Google Scholar] [CrossRef]
- Liu, X.; Yang, C.B.; Meng, Y.M.; Zhu, J.H.; Duan, Y.J.; Chen, Y.J. Hierarchical energy management of plug-in hybrid electric trucks based on state-of-charge optimization. J. Energy Storage 2023, 72, 107999. [Google Scholar] [CrossRef]
- Ibrahim, O.; Bakare, M.S.; Amosa, T.I.; Otuoze, A.O.; Owonikoko, W.O.; Ali, E.M.; Adesina, L.M.; Ogunbiyi, O. Development of fuzzy logic-based demand-side energy management system for hybrid energy sources. Energy Convers. Manag. X 2023, 18, 100354. [Google Scholar] [CrossRef]
- Fernandez, A.M.; Kandidayeni, M.; Boulon, L.; Chaoui, H. An Adaptive State Machine Based Energy Management Strategy for a Multi-Stack Fuel Cell Hybrid Electric Vehicle. IEEE Trans. Veh. Technol. 2020, 69, 220–234. [Google Scholar] [CrossRef]
- Qi, C.Y.; Song, C.X.; Xiao, F.; Song, S.X. Generalization ability of hybrid electric vehicle energy management strategy based on reinforcement learning method. Energy 2022, 250, 123826. [Google Scholar] [CrossRef]
- Wang, W.D.; Guo, X.H.; Yang, C.; Zhang, Y.B.; Zhao, Y.L.; Huang, D.G.; Xiang, C.L. A multi-objective optimization energy management strategy for power split HEV based on velocity prediction. Energy 2022, 238, 121714. [Google Scholar] [CrossRef]
- Pan, W.J.; Wu, Y.T.; Tong, Y.; Li, J.; Liu, Y.G. Optimal rule extraction-based real-time energy management strategy for series-parallel hybrid electric vehicles. Energy Convers. Manag. 2023, 293, 117474. [Google Scholar] [CrossRef]
- Chen, H.; Guo, G.; Tang, B.B.; Hu, G.; Tang, X.L.; Liu, T. Data-driven transferred energy management strategy for hybrid electric vehicles via deep reinforcement learning. Energy Rep. 2023, 10, 2680–2692. [Google Scholar] [CrossRef]
- Deng, K.; Liu, Y.X.; Hai, D.; Peng, H.J.; Löwenstein, L.; Pischinger, S.; Hameyer, K. Deep reinforcement learning based energy management strategy of fuel cell hybrid railway vehicles considering fuel cell aging. Energy Convers. Manag. 2022, 251, 115030. [Google Scholar] [CrossRef]
- Gissing, J.; Themann, P.; Baltzer, S.; Lichius, T.; Eckstein, L. Optimal Control of Series Plug-In Hybrid Electric Vehicles Considering the Cabin Heat Demand. IEEE Trans. Control Syst. Technol. 2016, 24, 1126–1133. [Google Scholar] [CrossRef]
- Peng, H.J.; Chen, Z.; Li, J.X.; Deng, K.; Dirkes, S.; Gottschalk, J.; Ünlübayir, C.; Thul, A.; Löwenstein, L.; Pischinger, S.; et al. Offline optimal energy management strategies considering high dynamics in batteries and constraints on fuel cell system power rate: From analytical derivation to validation on test bench. Appl. Energy 2021, 282, 116152. [Google Scholar] [CrossRef]
- Xiang, C.L.; Ding, F.; Wang, W.D.; He, W.; Qi, Y.L. MPC-based energy management with adaptive Markov-chain prediction for a dual-mode hybrid electric vehicle. Sci. China Technol. Sci. 2017, 60, 737–748. [Google Scholar] [CrossRef]
- Xu, F.G.; Shen, T.L. Look-Ahead Prediction-Based Real-Time Optimal Energy Management for Connected HEVs. IEEE Trans. Veh. Technol. 2020, 69, 2537–2551. [Google Scholar] [CrossRef]
- Deng, L.; Li, S.; Tang, X.L.; Yang, K.; Lin, X.K. Battery thermal- and cabin comfort-aware collaborative energy management for plug-in fuel cell electric vehicles based on the soft actor-critic algorithm. Energy Convers. Manag. 2023, 283, 116889. [Google Scholar] [CrossRef]
- Tang, X.L.; Zhou, H.T.; Wang, F.; Wang, W.D.; Lin, X.K. Longevity-conscious energy management strategy of fuel cell hybrid electric Vehicle Based on deep reinforcement learning. Energy 2022, 238, 121593. [Google Scholar] [CrossRef]
- Qi, C.Y.; Zhu, Y.W.; Song, C.A.X.; Yan, G.F.; Wang, D.; Xiao, F.; Zhang, X.; Cao, J.W.; Song, S.X. Hierarchical reinforcement learning based energy management strategy for hybrid electric vehicle. Energy 2022, 238, 121703. [Google Scholar] [CrossRef]
- Xiong, R.; Cao, J.Y.; Yu, Q.Q. Reinforcement learning-based real-time power management for hybrid energy storage system in the plug-in hybrid electric vehicle. Appl. Energy 2018, 211, 538–548. [Google Scholar] [CrossRef]
- Chang, C.C.; Zhao, W.Z.; Wang, C.Y.; Song, Y.D. A Novel Energy Management Strategy Integrating Deep Reinforcement Learning and Rule Based on Condition Identification. IEEE Trans. Veh. Technol. 2023, 72, 1674–1688. [Google Scholar] [CrossRef]
- Qi, X.W.; Luo, Y.D.; Wu, G.Y.; Boriboonsomsin, K.; Barth, M. Deep reinforcement learning enabled self-learning control for energy efficient driving. Transp. Res. Part C Emerg. Technol. 2019, 99, 67–81. [Google Scholar] [CrossRef]
- Huang, R.C.; He, H.W.; Zhao, X.Y.; Wang, Y.L.; Li, M.L. Battery health-aware and naturalistic data-driven energy management for hybrid electric bus based on TD3 deep reinforcement learning algorithm. Appl. Energy 2022, 321, 119353. [Google Scholar] [CrossRef]
- Zhang, Y.J.; Huang, Y.J.; Chen, Z.; Li, G.; Liu, Y.G. A Novel Learning-Based Model Predictive Control Strategy for Plug-In Hybrid Electric Vehicle. IEEE Trans. Transp. Electrif. 2022, 8, 23–35. [Google Scholar] [CrossRef]
- Fujimoto, S.; van Hoof, H.; Meger, D. Addressing Function Approximation Error in Actor-Critic Methods. In Proceedings of the 35th International Conference on Machine Learning (ICML), Stockholm, Sweden, 10–15 July 2018. [Google Scholar] [CrossRef]
- Zhou, L.Q.; Yang, D.P.; Zeng, X.H.; Zhang, X.M.; Song, D.F. Multi-objective real-time energy management for series-parallel hybrid electric vehicles considering battery life. Energy Convers. Manag. 2023, 290, 117234. [Google Scholar] [CrossRef]
- Xie, S.B.; Hu, X.S.; Qi, S.W.; Tang, X.L.; Lang, K.; Xin, Z.K.; Brighton, J. Model predictive energy management for plug-in hybrid electric vehicles considering optimal battery depth of discharge. Energy 2019, 173, 667–678. [Google Scholar] [CrossRef]










| Component | Parameters | Values |
|---|---|---|
| Vehicle | Gross vehicle weight | 18,000 kg |
| Frontal area | 5.1 m2 | |
| Coefficient of air resistance | 0.527 | |
| Motor transmission ratio | 5.48 | |
| Automatic mechanical transmission | 10.36, 6.48, 4.32, 3.47, 2.4, 1.5, 1, 0.8 | |
| Final drive ratio | 3.909 | |
| Motor | Maximum power | 158.3 kw |
| Maximum torque | 293 Nm | |
| Maximum speed | 12,000 r/min | |
| Engine | Maximum power | 169.1 kw |
| Maximum torque | 734 Nm | |
| Rated speed | 2200 r/min | |
| Battery | Rated voltage | 560.28 V |
| Capacity | 5 Ah | |
| Rated power | 78.4 kw |
| Hyperparameter | Value |
|---|---|
| Maximum episodes | 300 |
| Learning rate for actor network | 0.001 |
| Learning rate for critic network | 0.001 |
| Bath size | 64 |
| Soft replacement | 0.01 |
| Policy noise | 0.2 |
| Traffic Scenario | Scenario 1 | Scenario 2 | Scenario 2 |
|---|---|---|---|
| Number of traffic lights | 5 | 6 | 7 |
| Distance (m) | 2200 | 2600 | 3000 |
| Location of traffic lights (m) | 250, 900, 1300, 1650, 2200 | 300, 600, 1000, 1300, 2300, 2600 | 300, 700, 1000, 1700, 2100, 2500, 3000 |
| Duration of red light (s) | 15, 20, 30, 25, 35 | 25, 30, 25, 30, 20, 30 | 25, 30, 25, 30, 20, 30, 40 |
| Duration of green light (s) | 25, 40, 20, 30, 30 | 35, 20, 30, 40, 25, 30 | 35, 20, 30, 40, 25, 30, 20 |
| Duration of traffic signals (s) | 40, 60, 50, 55, 65 | 60, 50, 55, 70, 45, 60 | 60, 50, 55, 70, 45, 60, 60 |
| Initial times of traffic signals (s) | 5, 10, 10, 40, 30 | 25, 30, 25, 50, 0, 10 | 15, 30, 50, 20, 5, 45, 10 |
| Traffic Scenario | Scenario 1 | Scenario 2 | Scenario 3 | Average |
|---|---|---|---|---|
| DP computational time (s) | 17.83 | 18.67 | 19.51 | 18.67 |
| QP computational time (s) | 19.01 | 20.85 | 22.79 | 20.88 |
| Traffic Scenario | Method | Final Value of SOC | Fuel Consumption Value (L/100 km) | Fuel Saving-Rate Value (%) |
|---|---|---|---|---|
| Traffic scenario 1 | DP-CD/CS | 0.39 | 11.85 | 0 |
| DP-DP | 0.36 | 9.08 | 23.38 | |
| DP-TD3 | 0.37 | 9.83 | 17.05 | |
| Traffic scenario 2 | DP-CD/CS | 0.40 | 11.17 | 0 |
| DP-DP | 0.39 | 9.13 | 18.26 | |
| DP-TD3 | 0.40 | 9.79 | 12.35 | |
| Traffic scenario 3 | DP-CD/CS | 0.36 | 11.37 | 0 |
| DP-DP | 0.36 | 9.04 | 20.49 | |
| DP-TD3 | 0.37 | 9.73 | 14.42 |
| Hardware | Parameter |
|---|---|
| Processor | 3.8 GHz frequency, 16 GB RAM memory. |
| DS2680 board | 44-channel AI, 64-channel AO, 60-channel DI, 56-channel DO, 32-channel FI, 24-channel RO. |
| DS2690 board | 20-channel DI, 20-channel DO, 20-channel DI/DO. |
| DS2671 board | 4 CAN bus emulation channels. |
| Programmable power supply | Power, 1.5 KW; voltage, 0 V-52 V; current, 0 A-60 A. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Shi, G.; Yang, C.; Xu, E.; Meng, Y. Co-Optimization of Speed Planning and Energy Management for Plug-In Hybrid Electric Trucks Passing Through Traffic Light Intersections. Energies 2024, 17, 6022. https://doi.org/10.3390/en17236022
Liu X, Shi G, Yang C, Xu E, Meng Y. Co-Optimization of Speed Planning and Energy Management for Plug-In Hybrid Electric Trucks Passing Through Traffic Light Intersections. Energies. 2024; 17(23):6022. https://doi.org/10.3390/en17236022
Chicago/Turabian StyleLiu, Xin, Guojing Shi, Changbo Yang, Enyong Xu, and Yanmei Meng. 2024. "Co-Optimization of Speed Planning and Energy Management for Plug-In Hybrid Electric Trucks Passing Through Traffic Light Intersections" Energies 17, no. 23: 6022. https://doi.org/10.3390/en17236022
APA StyleLiu, X., Shi, G., Yang, C., Xu, E., & Meng, Y. (2024). Co-Optimization of Speed Planning and Energy Management for Plug-In Hybrid Electric Trucks Passing Through Traffic Light Intersections. Energies, 17(23), 6022. https://doi.org/10.3390/en17236022





