Correlating Sediment Erosion in Rotary–Stationary Gaps of Francis Turbines with Complex Flow Patterns
Abstract
1. Introduction
2. Erosion Wear in Francis Turbine Components
3. Numerical Study
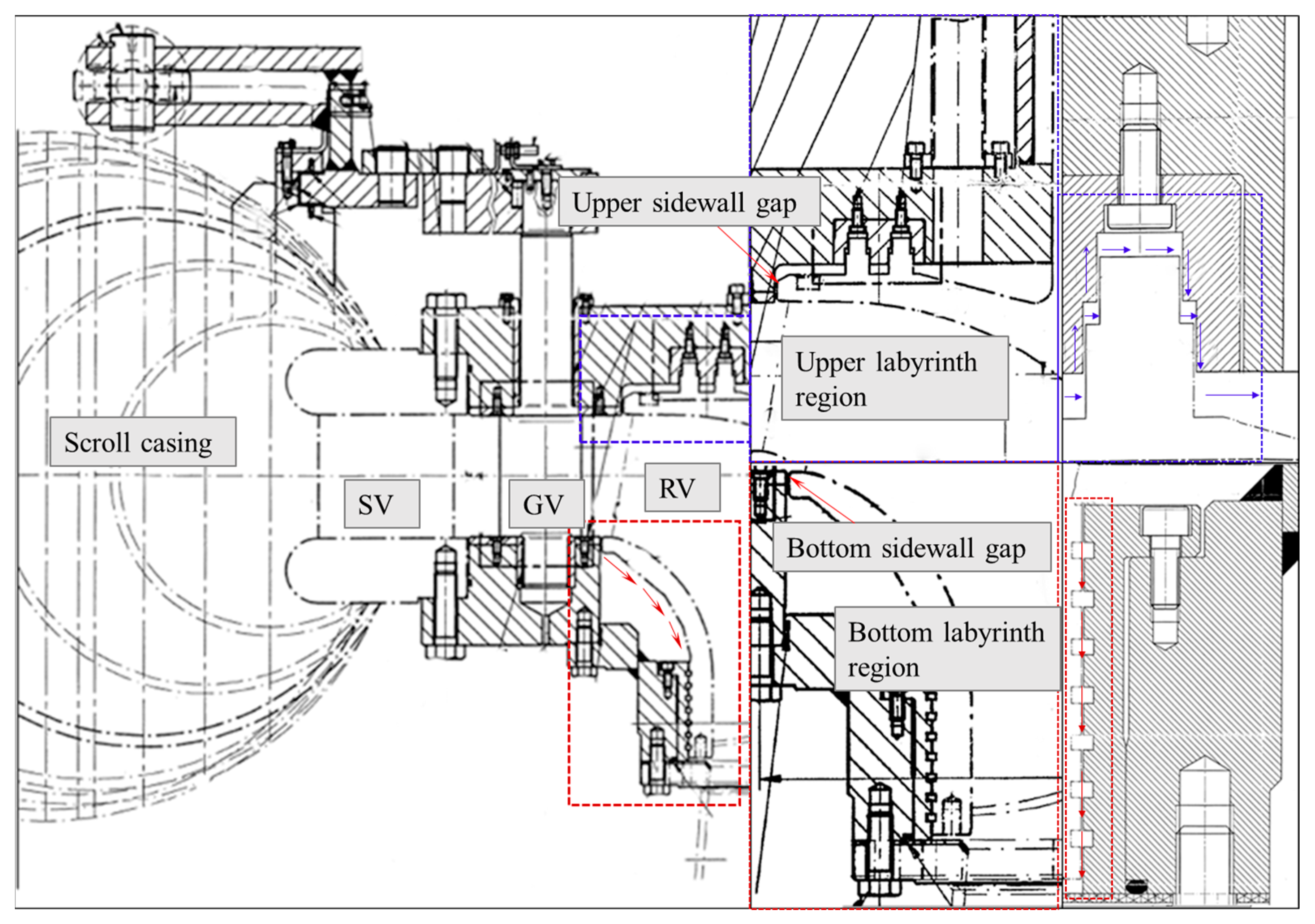
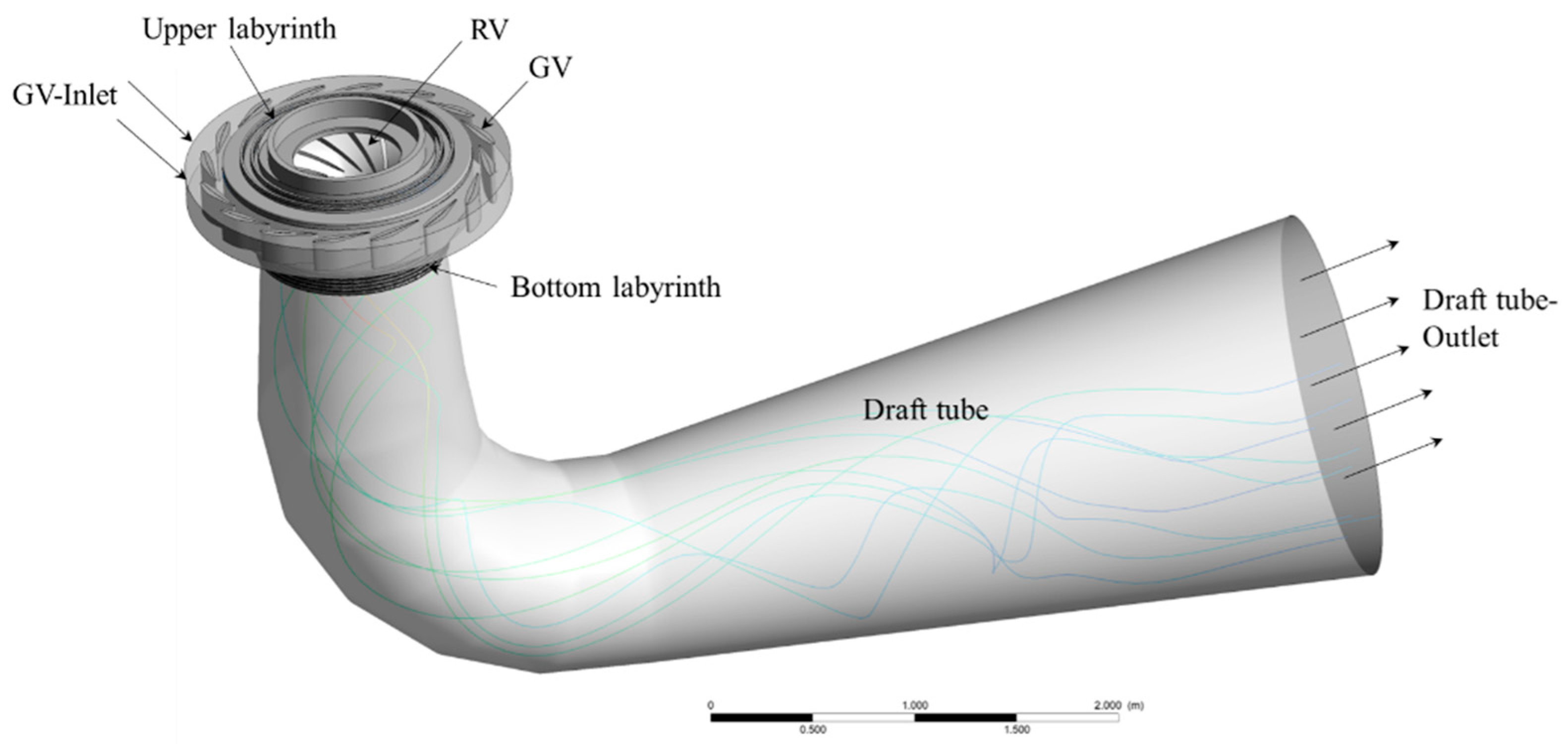
3.1. Development of Numerical Model
3.2. Boundary Conditions, Governing Equations, and Turbulence Model
3.3. Erosion Modeling
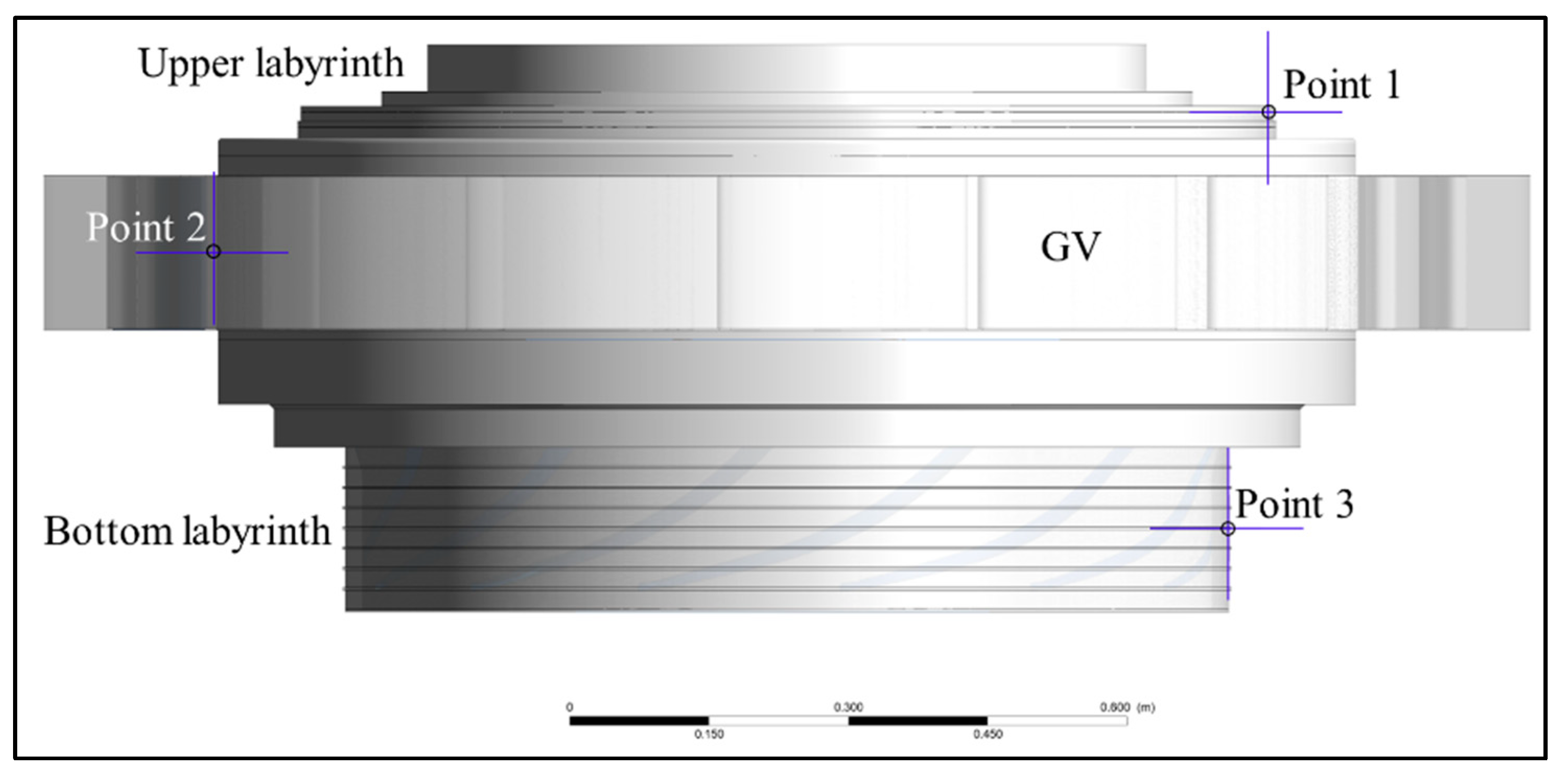
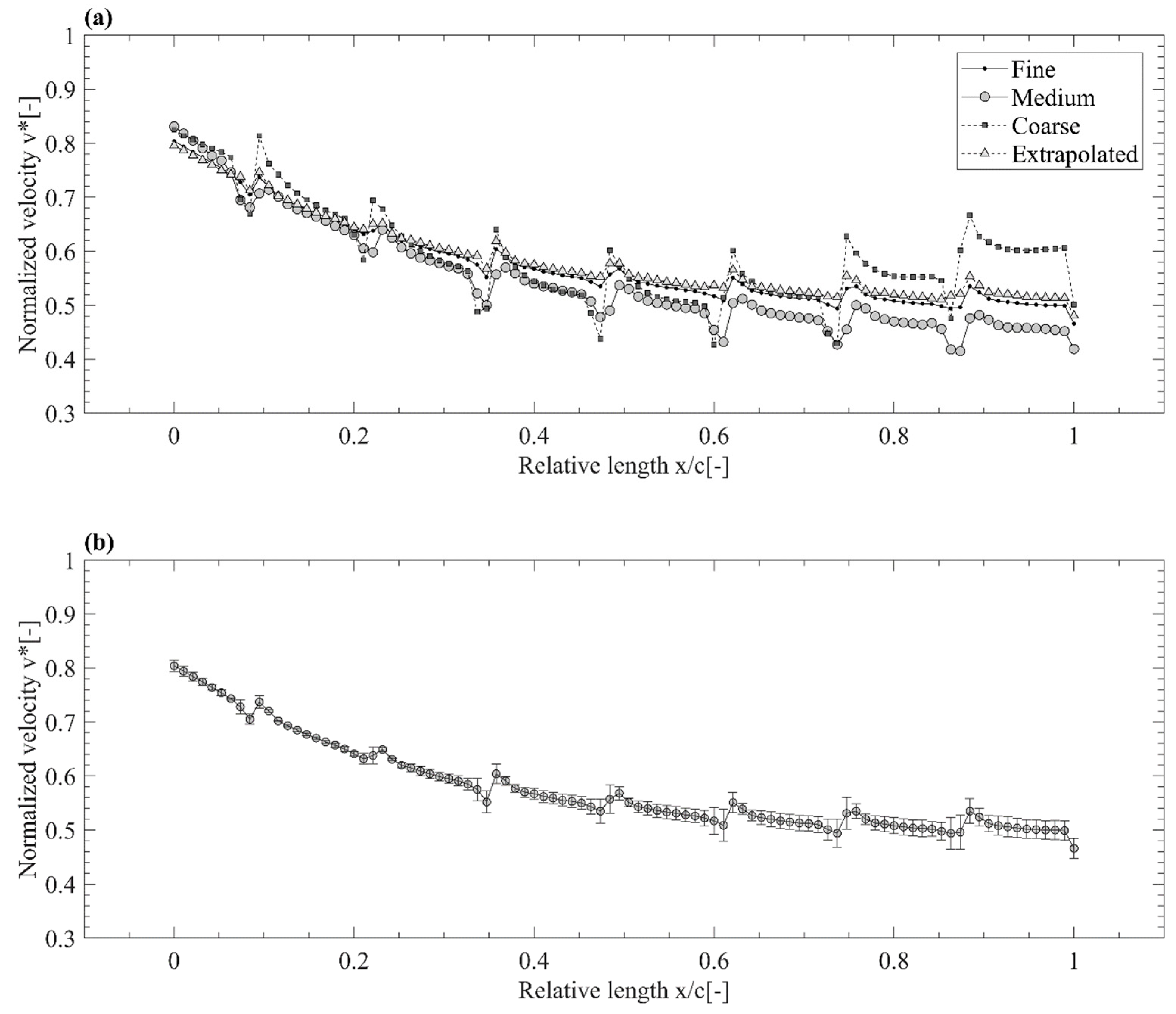
3.4. Grid Sensitivity Study
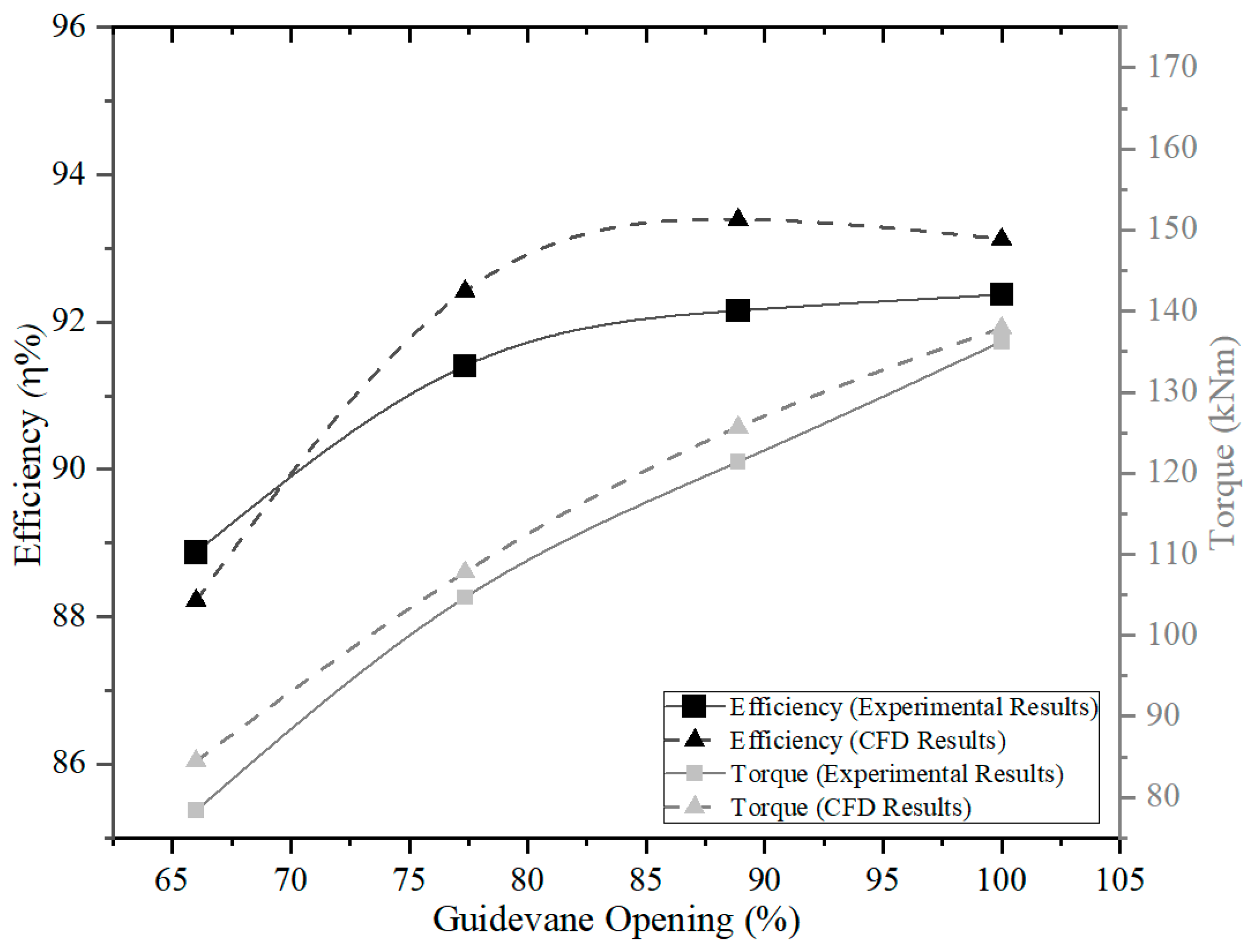
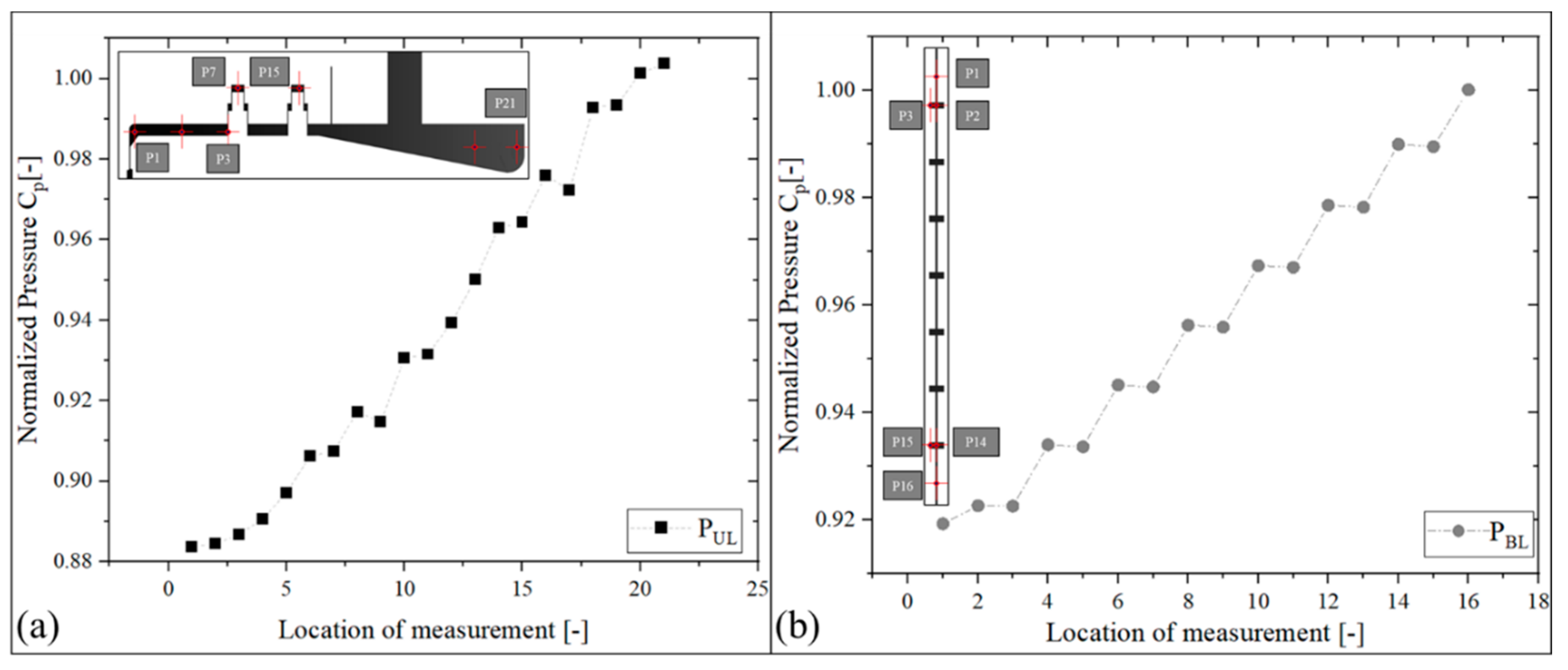
3.5. Validation of Numerical Model
4. Results and Discussion
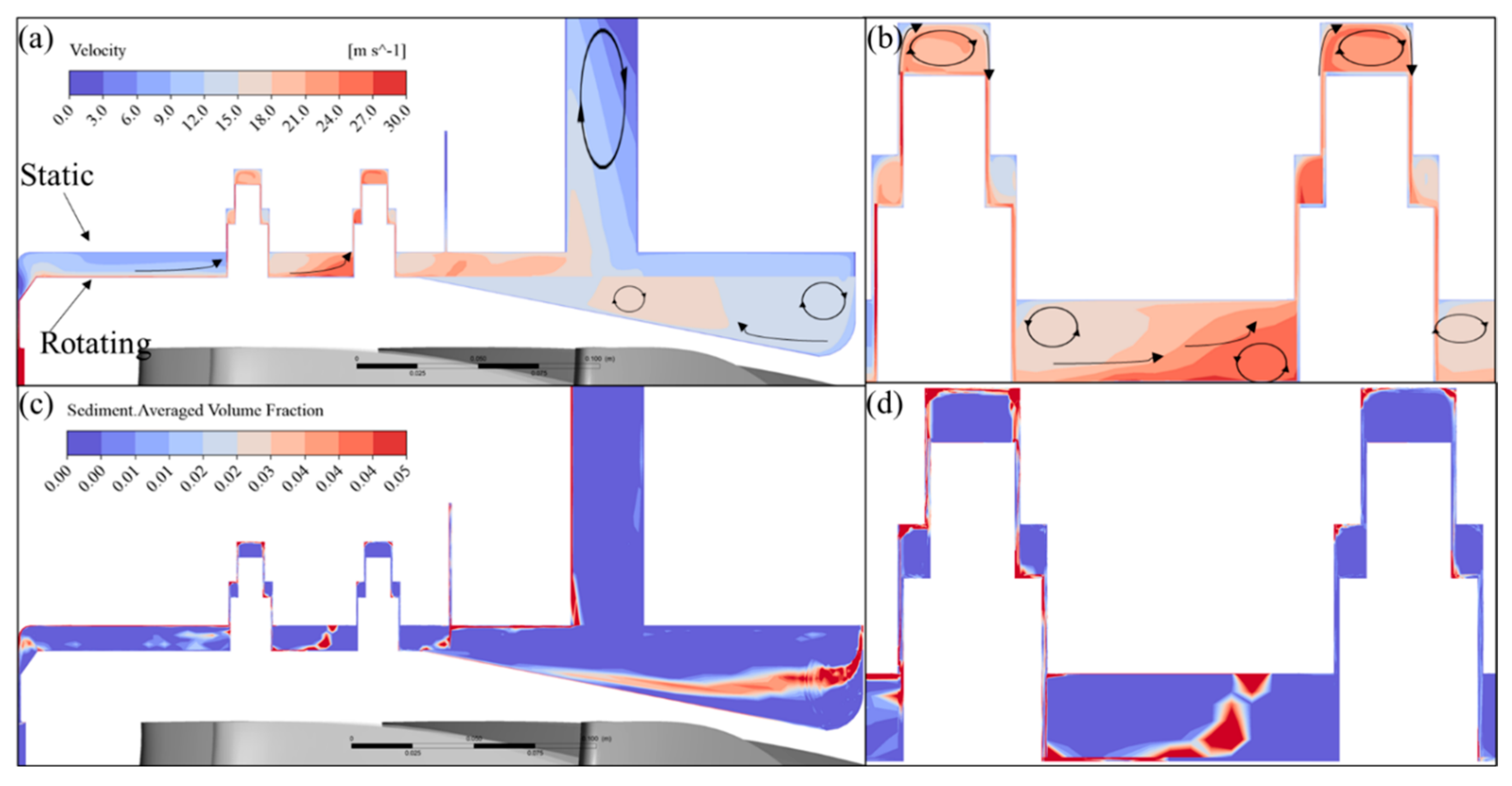
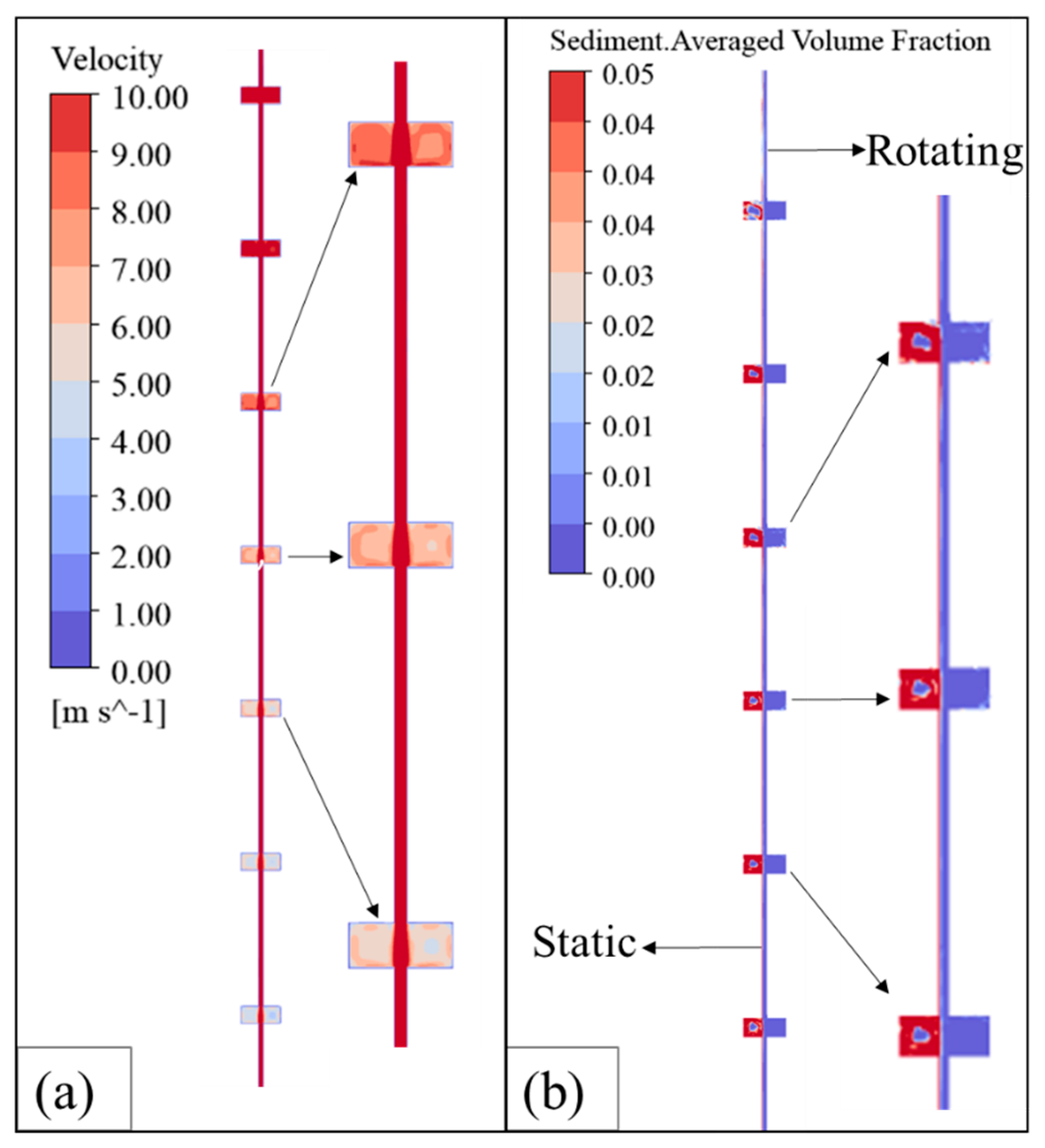
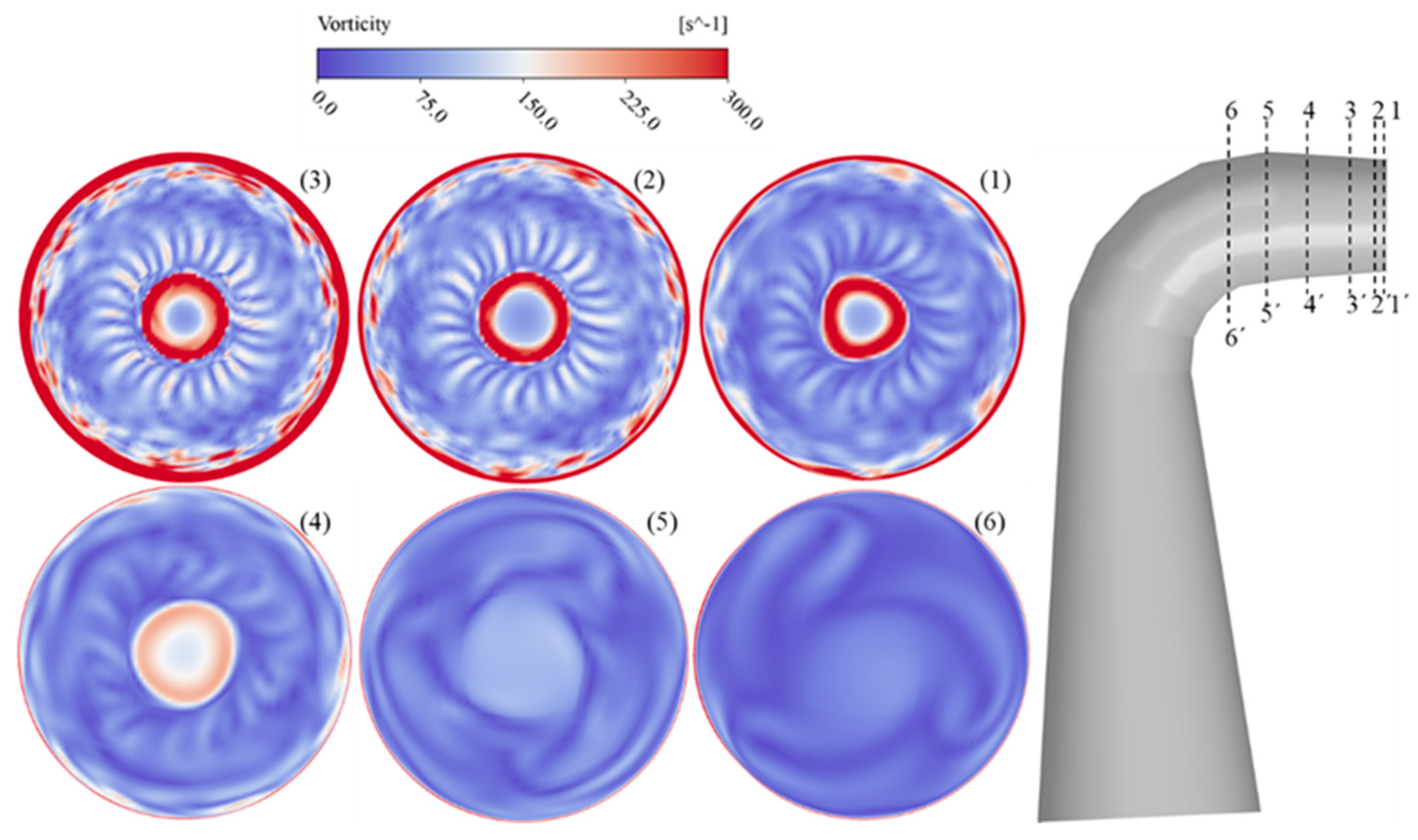
4.1. Flow in the Labyrinths
4.1.1. Upper Labyrinth Seal
4.1.2. Bottom Labyrinth Seal
4.2. Theoretical Implications and Overall Discussion
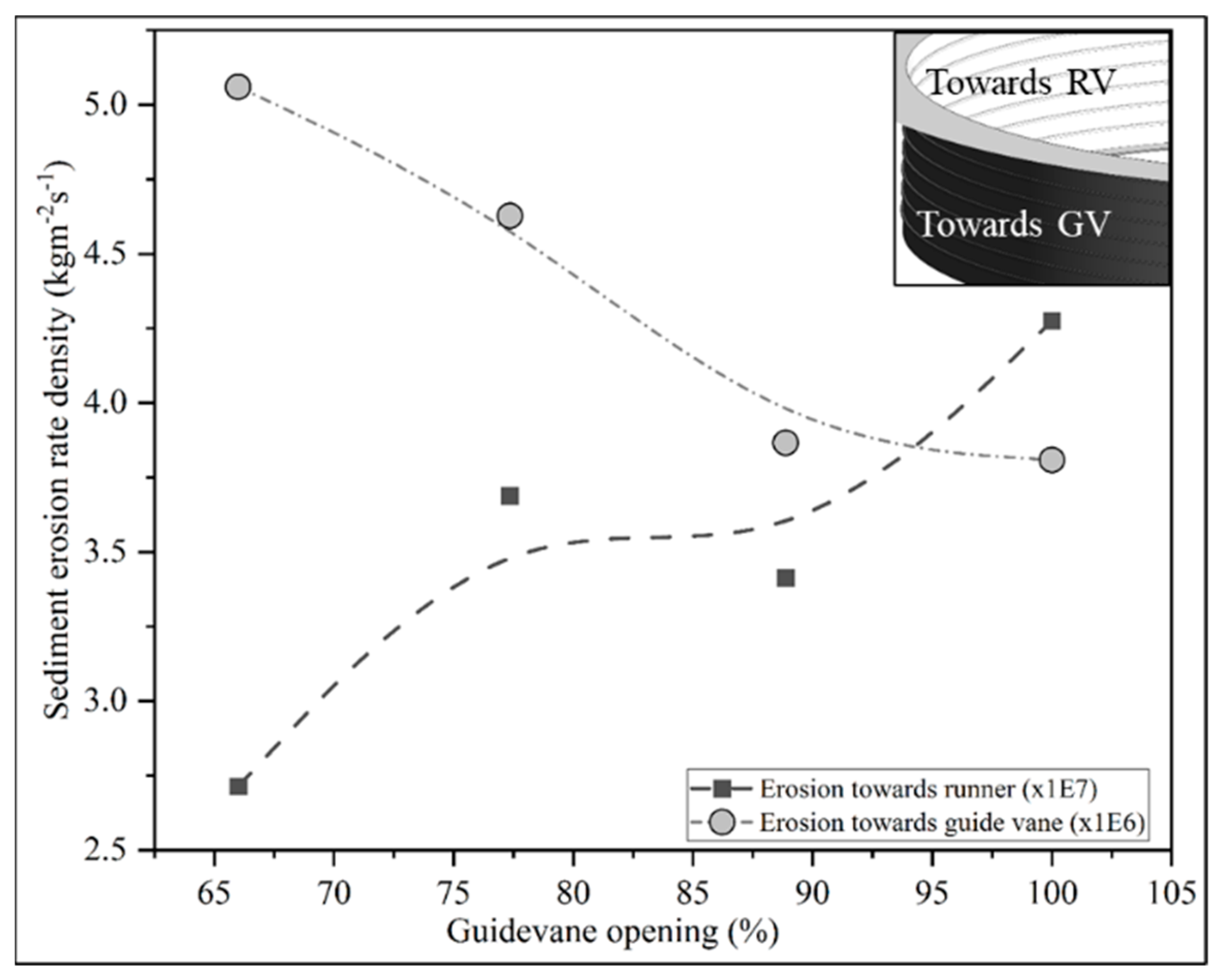
4.2.1. Guide Vane Clearance Gaps
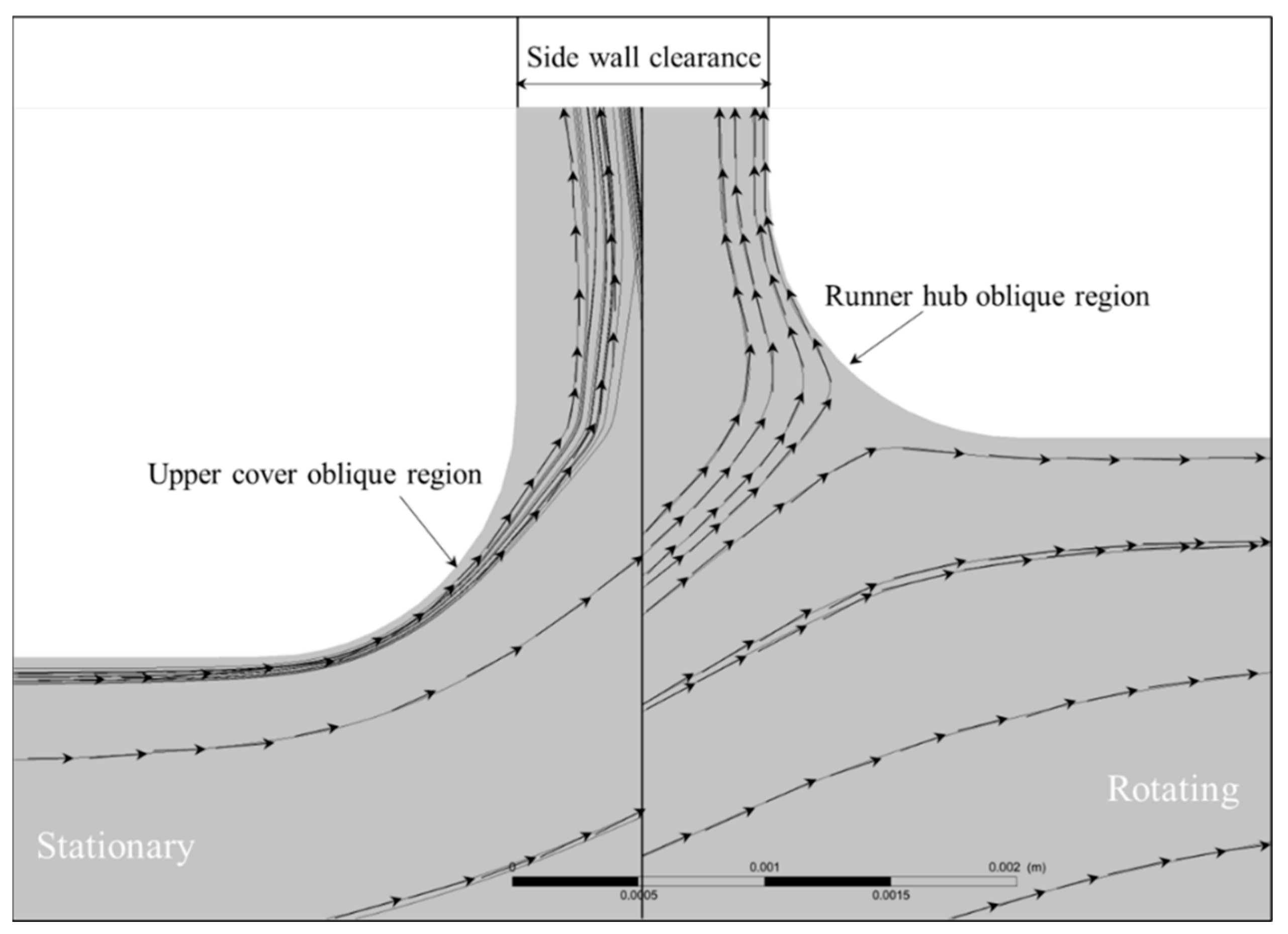
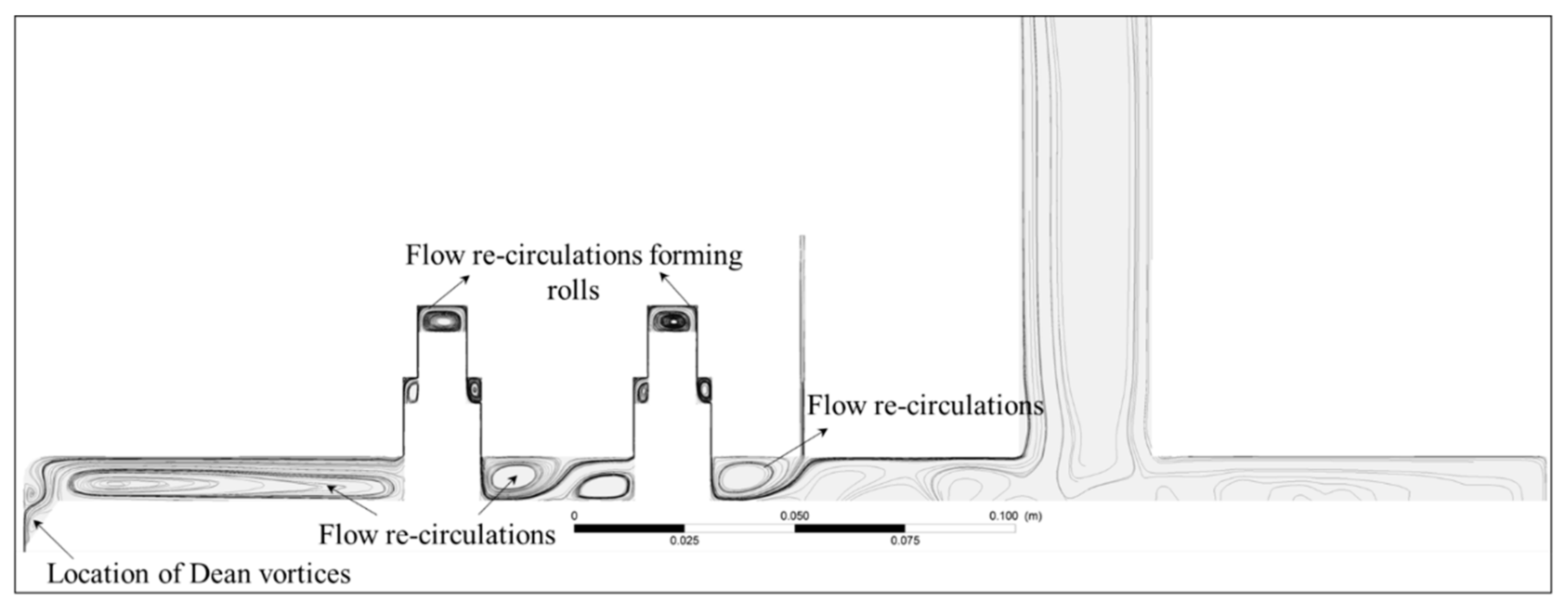
4.2.2. Runner Sidewall Gaps
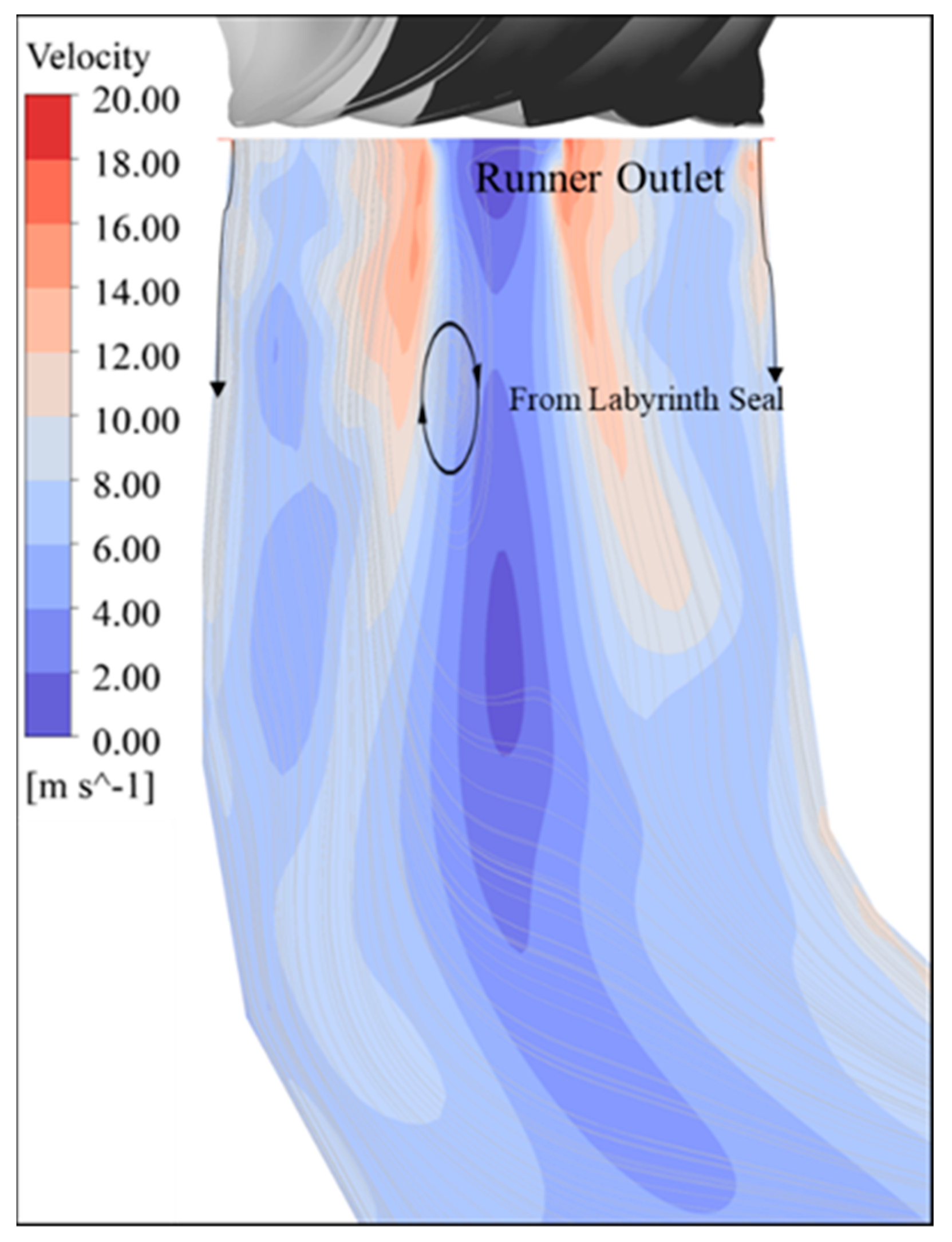
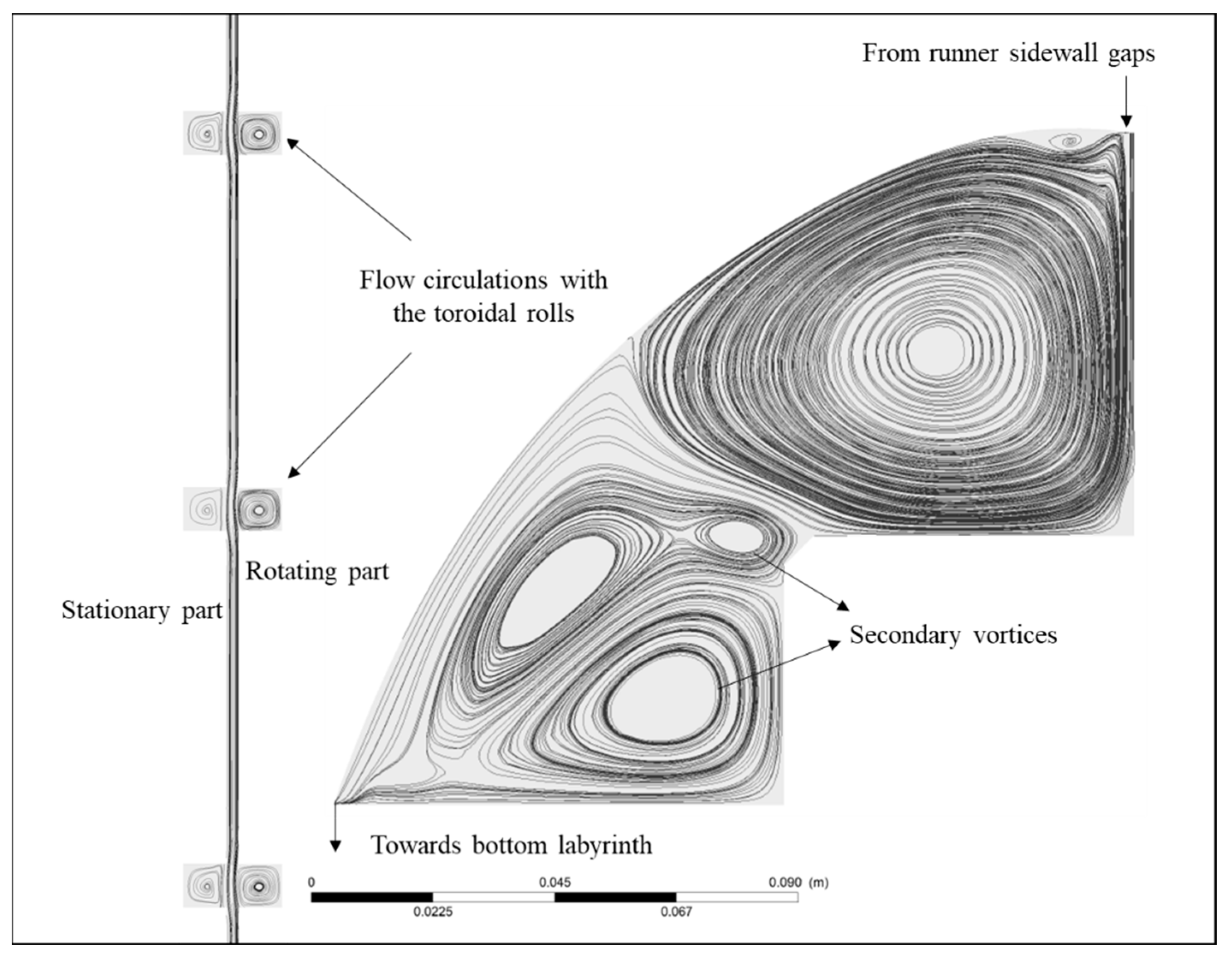
4.2.3. Upper and Lower Labyrinths
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| List of symbols | ||
| Cp | Normalized pressure | [-] |
| g | Acceleration due to gravity | m s−2 |
| GCIfine | Grid Convergence Index of fine mesh | [-] |
| h | Size of grid | m |
| H | Head | m |
| Ns | Specific speed | rpm |
| p | Apparent order for grid sensitivity study | [-] |
| Fluctuating pressure | Pa | |
| Mean pressure | Pa | |
| Q | Flow rate | m3 s−1 |
| Qed | Discharge factor | [-] |
| r | Grid refinement factor | [-] |
| y+ | Dimensionless wall space | [-] |
| Greek Symbols | ||
| ω | Angular velocity | rad-s−1 |
| δ | Uncertainty in measurement | % |
| Variable for GCI calculation | [-] | |
| ρ | Density | kg-m−3 |
| Torque | kN-m | |
| Efficiency | % | |
| Indices | ||
| 1, 2 | Position indication: fine and medium mesh indication | |
| c | Critical value | |
| List of Abbreviations | ||
| BEP | Best Efficiency Point | |
| CFD | Computational fluid dynamics | |
| GCI | Grid Convergence Index | |
| GV | Guide vane | |
| GV-CL | Guide vane clearance | |
| HPP | Hydropower Plant | |
| IEC | International Electro-Technical Commission | |
| LES | Large Eddy Simulation | |
| MW | Megawatt | |
| NLS | No-Load Speed | |
| RANS | Reynolds-Averaged Navier–Stokes | |
| RPM | Revolutions per Minute | |
| RSI | Rotor–stator interaction | |
| RV | Runner vane | |
| SAS | Scale-Adaptive Simulation | |
| SST | Shear Stress Transport | |
| 3-D | Three-dimensional | |
References
- IHA. Hydropower Status Report: Sector Trends and Insights; IHA: London, UK, 2018. [Google Scholar]
- Anup, K.C.; Thapa, B.; Lee, Y.H. Transient numerical analysis of rotor-stator interaction in a Francis turbine. Renew. Energy 2014, 65, 227–235. [Google Scholar] [CrossRef]
- Iliev, I.; Trivedi, C.; Dahlhaug, O.G. Variable-speed operation of Francis turbines: A review of the perspectives and challenges. Renew. Sustain. Energy Rev 2019, 103, 109–121. [Google Scholar] [CrossRef]
- Thapa, B.S.; Dahlhaug, O.G.; Thapa, B. Sediment erosion in hydro turbines and its effect on the flow around guide vanes of Francis turbine. Renew. Sustain. Energy Rev. 2015, 49, 1100–1113. [Google Scholar] [CrossRef]
- Gautam, S.; Neopane, H.P.; Acharya, N.; Chitrakar, S.; Thapa, B.S.; Zhu, B. Sediment erosion in low specific speed francis turbines: A case study on effects and causes. Wear 2020, 442, 203152. [Google Scholar] [CrossRef]
- Chitrakar, S.; Neopane, H.P.; Dahlhaug, O.G. Study of the simultaneous effects of secondary flow and sediment erosion in Francis turbines. Renew. Energy 2016, 97, 881–891. [Google Scholar] [CrossRef]
- Schiffer, J.; Benigni, H.; Jaberg, H. Analysis of the leakage behavior of Francis turbines and its impact on the hydraulic efficiency—A validation of an analytical model based on computational fluid dynamics results. J. Fluids Eng. Trans. ASME 2017, 139, 021106. [Google Scholar] [CrossRef]
- Standard No. IEC 60193: 1999-11; Hydraulic Turbines, Storage Pumps and Pump-Turbines—Model Acceptance Tests. IEC: Geneva, Switzerland, 1999.
- Iliev, I.; Trivedi, C.; Dahlhaug, O.G. Simplified hydrodynamic analysis on the general shape of the hill charts of Francis turbines using shroud-streamline modeling. J. Phys. Conf. Ser. 2018, 1042, 012003. [Google Scholar] [CrossRef]
- Zemanová, L.; Rudolf, P. Flow inside the sidewall gaps of hydraulic machines: A review. Energies 2020, 13, 6617. [Google Scholar] [CrossRef]
- Ayad, A.F.; Abdalla, H.M.; El-Azm, A.A. Study of the effect of impeller side clearance on the centrifugal pump performance using CFD. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition. American Society of Mechanical Engineers, Houston, TX, USA, 13–19 November 2015; Volume 7A, pp. 1–10. [Google Scholar] [CrossRef]
- Schiffer, J.; Benigni, H.; Jaberg, H.; Schneidhofer, T. Numerical simulation of the flow in a Francis turbine including the runner seals on crown and band side. In Proceedings of the HYDRD International Conference and Exhibition, National Harbor, MD, USA, 16–19 March 2015; pp. 3–10. [Google Scholar]
- Zhao, W. Investigation of Seal Technology for Francis Turbine; Norwegian University of Science and Technology: Trondheim, Norway, 2012. [Google Scholar]
- Yonezawa, K.; Watamura, T. Experimental and Numerical Investigations of Erosion on Runner Seal of a Francis Turbine. IOP Conf. Ser. Earth Environ. Sci. 2021, 774, 012034. [Google Scholar] [CrossRef]
- Hou, X.; Cheng, Y.; Yang, Z.; Liu, K.; Zhang, X.; Liu, D. Influence of clearance flow on dynamic hydraulic forces of pump-turbine during runaway transient process. Energies 2021, 14, 2830. [Google Scholar] [CrossRef]
- Koirala, R.; Thapa, B.; Neopane, H.P.; Zhu, B.; Chhetry, B. Sediment erosion in guide vanes of Francis turbine: A case study of Kaligandaki Hydropower Plant, Nepal. Wear 2016, 362–363, 53–60. [Google Scholar] [CrossRef]
- Acharya, N.; Gautam, S.; Chitrakar, S.; Trivedi, C.; Dahlhaug, O.G. Leakage Vortex Progression through a Guide Vane’s Clearance Gap and the Resulting Pressure Fluctuation in a Francis Turbine. Energies 2021, 14, 4244. [Google Scholar] [CrossRef]
- Acharya, N.; Trivedi, C.; Wahl, N.M.; Gautam, S.; Chitrakar, S.; Dahlhaug, O.G. Numerical study of sediment erosion in guide vanes of a high head Francis turbine. J. Phys. Conf. Ser. 2019, 1266, 012004. [Google Scholar] [CrossRef]
- Koirala, R.; Zhu, B.; Neopane, H.P. Effect of guide vane clearance gap on Francis turbine performance. Energies 2016, 9, 275. [Google Scholar] [CrossRef]
- Gautam, S.; Neopane, H.P.; Thapa, B.S.; Chitrakar, S.; Zhu, B. Numerical investigation of the effects of leakage flow from guide vanes of francis turbines using alternative clearance gap method. J. Appl. Fluid Mech. 2020, 13, 1407–1419. [Google Scholar] [CrossRef]
- Mack, R.; Drtina, P.; Lang, E. Numerical prediction of erosion on guide vanes and in labyrinth seals in hydraulic turbines. Wear 1999, 233–235, 685–691. [Google Scholar] [CrossRef]
- Song, X.; Zhou, X.; Song, H.; Deng, J.; Wang, Z. Study on the effect of the guide vane opening on the band clearance sediment erosion in a Francis turbine. J. Mar. Sci. Eng. 2022, 10, 1396. [Google Scholar] [CrossRef]
- Guo, X.; Yang, M.; Li, F.; Zhu, Z.; Cui, B. Investigation on cryogenic cavitation characteristics of an inducer considering thermodynamic effects. Energies 2024, 17, 3627. [Google Scholar] [CrossRef]
- Brekke, H. A review on oscillatory problems in Francis turbines. In New Trends in Technologies: Devices, Computer, Communication and Industrial Systems; Sciyo: Rijeka, Croatia, 2010; p. 217e232. [Google Scholar]
- Chitrakar, S.; Thapa, B.S.; Dahlhaug, O.G.; Neopane, H.P. Numerical and experimental study of the leakage flow in guide vanes with different hydrofoils. J. Comput. Des. Eng. 2017, 4, 218–230. [Google Scholar] [CrossRef]
- Brekke, H. Design of Hydraulic Machinery Working in Sand Laden Water. In Abrasive Erosion and Corrosion of Hydraulic Machinery; Imperial College Press: London, UK, 2002; pp. 155–181. [Google Scholar]
- Chitrakar, S.; Dahlhaug, O.G.; Neopane, H.P. Numerical investigation of the effect of leakage flow through erosion-induced clearance gaps of guide vanes on the performance of francis turbines. Eng. Appl. Comput. Fluid Mech. 2018, 12, 662–678. [Google Scholar] [CrossRef]
- Yan, J.; Zuo, Z.; Guo, W.; Hou, H.; Zhou, X.; Chen, H. Influences of wear-ring clearance leakage on performance of a small-scale pump-turbine. Proc. Inst. Mech. Eng. Part A J. Power Energy 2020, 234, 454–469. [Google Scholar] [CrossRef]
- Schröder, T.R.; Dohmen, H.J.; Brillert, D.; Benra, F.K. Impact of leakage inlet swirl angle in a rotor-stator cavity on flow pattern, radial pressure distribution and frictional torque in a wide circumferential reynolds number range. Int. J. Turbomach. Propuls. Power 2020, 5, 7. [Google Scholar] [CrossRef]
- Hu, B.; Brillert, D.; Dohmen, H.J.; Benra, F.K. Investigation on the flow in a rotor-stator cavity with centripetal through-flow. Int. J. Turbomach. Propuls. Power 2017, 2, 18. [Google Scholar] [CrossRef]
- Trivedi, C. Time-dependent inception of vortex rings in a Francis turbine during load variation: Large eddy simulation and experimental validation. J. Hydraul. Res. 2020, 58, 790–806. [Google Scholar] [CrossRef]
- Trivedi, C. Compressible large eddy simulation of a Francis turbine during speed-no-load: Rotor stator interaction and inception of a vortical flow. J. Eng. Gas Turbines Power 2018, 140, 112601. [Google Scholar] [CrossRef]
- Trivedi, C.; Cervantes, M.J.; Dahlhaug, O.G. Numerical Techniques Applied to Hydraulic Turbines: A Perspective Review. Appl. Mech. Rev. 2016, 68, 010802. [Google Scholar] [CrossRef]
- Menter, F.R.; Kuntz, M.; Langtry, R. Ten Years of Industrial Experience with the SST Turbulence Model. Turbul. Heat Mass Transf. 2003, 4, 625–632. [Google Scholar]
- Celik, I.B.; Ghia, U.; Roache, P.J.; Freitas, C.J.; Coleman, H.; Raad, P.E. Procedure for estimation and reporting of uncertainty due to discretization in CFD applications. J. Fluids Eng. Trans. ASME 2008, 130, 0780011–0780014. [Google Scholar] [CrossRef]
- Trivedi, C. A systematic validation of a Francis turbine under design and off-design loads. J. Verif. Valid. Uncertain. Quantif. 2019, 4, 011003. [Google Scholar] [CrossRef]
- Trivedi, C.; Cervantes, M.J. State of the art in numerical simulation of high head Francis turbines. Renew. Energy Environ. Sustain. 2016, 1, 20. [Google Scholar] [CrossRef]
- KC, A.; Lee, Y.H.; Thapa, B. CFD study on prediction of vortex shedding in draft tube of Francis turbine and vortex control techniques. Renew. Energy 2016, 86, 1406–1421. [Google Scholar] [CrossRef]
- Acharya, N. Erosion in Francis Turbines Due to Geometrical Positioning of Runner and Guide Vanes. Ph.D. Thesis, Norwegian University of Science and Technology, Trondheim, Norway, 2022. [Google Scholar]
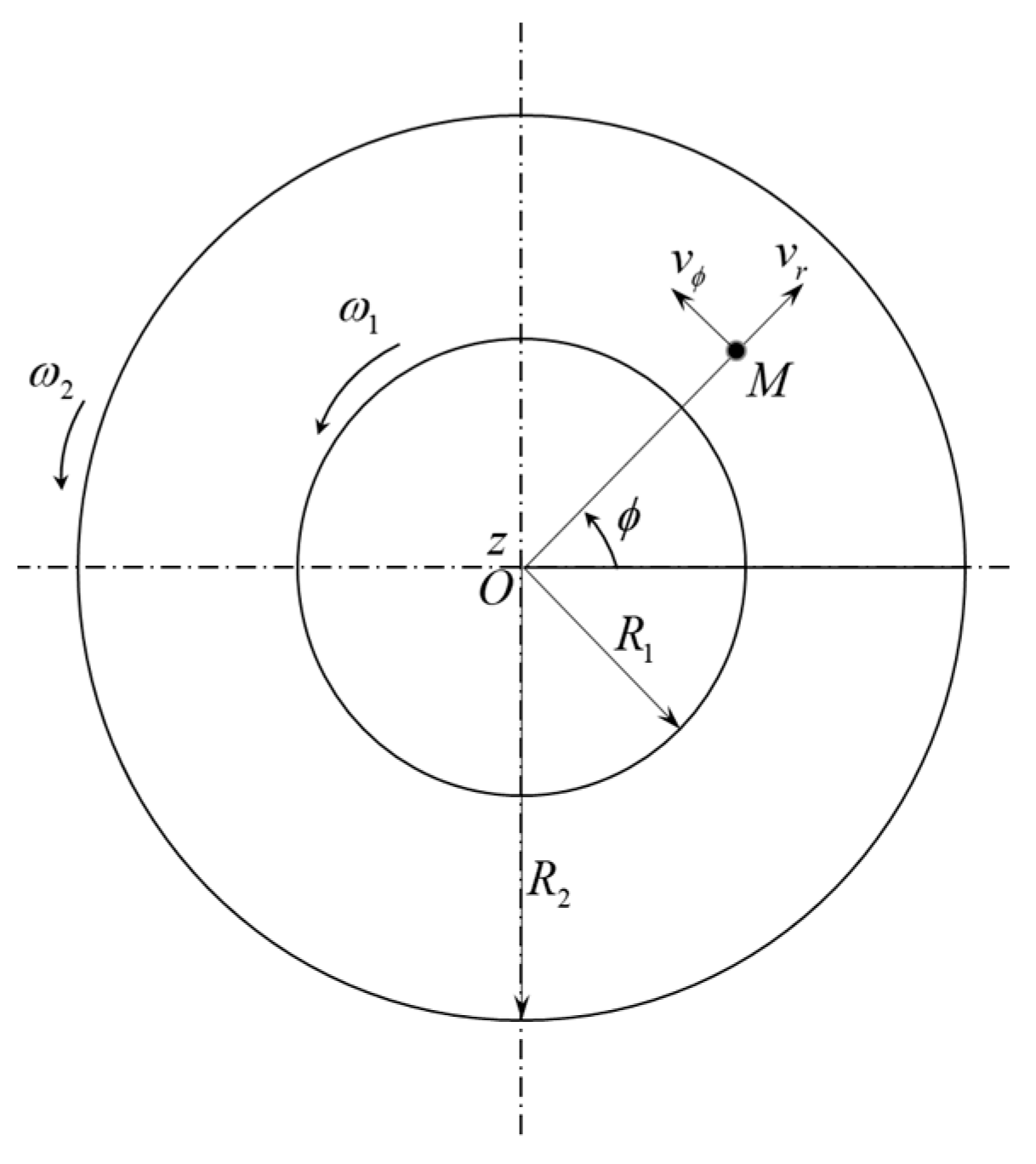
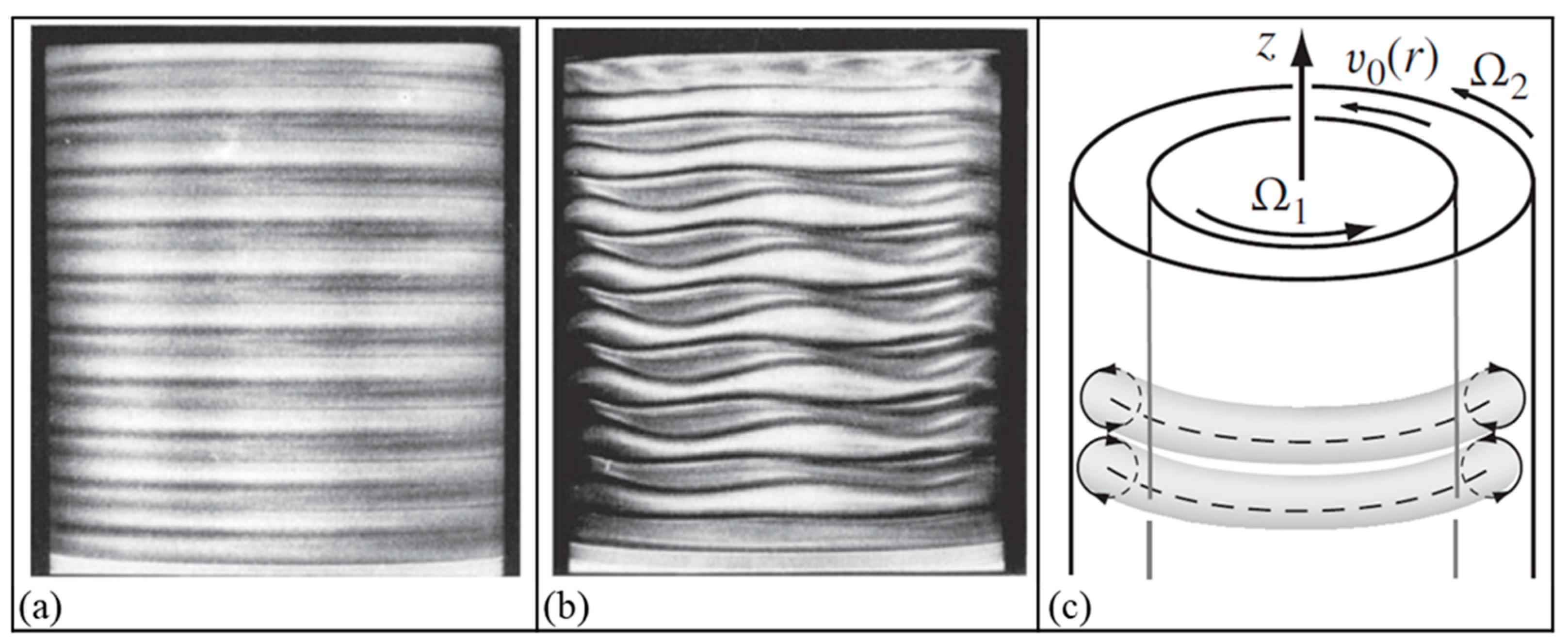
- Guyon, E.; Hulin, J.-P.; Petit, L.; Mitescu, C.D. Taylor–Couette instability. In Physical Hydrodynamics, 2nd ed.; Oxford University Press: Oxford, UK, 2001; pp. 126–127. [Google Scholar]






| Parameters | Description |
|---|---|
| Boundary condition | Inlet: mass flow rate for runner rotational speed of 750 rpm Outlet: 0 Pa relative pressure Wall: no slip |
| Turbulence intensity | 5% at the inlet |
| Fluid type | Incompressible, Newtonian fluid with density 1000 kg/m3 |
| Analysis type | Steady state Transient state: initialization from steady-state solution, time step size 1 deg runner rotation, total time 0.4 s |
| Turbulence model | SST |
| Discretization and solution control | High-resolution advection scheme Second-order backward Euler transient scheme |
| Convergence criteria | Single precision, 1 × 10−4 Transient solution: inner loop iterations 1–10 |
| Parameters | Description |
|---|---|
| Fluid flow with quartz | Homogenous, incompressible |
| Sediment flow | Particle transport fluid |
| Sediment properties | Size: 150 µm; shape factor: 0.7; and concentration: 5000 |
| Mass flow rate | 0.07 kg/s normal to the inlet |
| Turbulence dissipation force | Schiller–Naumann |
| Erosion model | Tabakoff erosion model |
| Variable | Coefficient | Value | Dimension |
|---|---|---|---|
| 3.52 | [-] | ||
| Velocity | 2375.14 | ms−1 | |
| 153.17 | ms−1 | ||
| 19.16 | ms−1 | ||
| Angle of maximum erosion | 45 | (deg) |
| Measurement Parameters (ɸ) | Coarse | Medium | Fine | ) | ) | (%) |
|---|---|---|---|---|---|---|
| Pressure at Point 1 (kPa) | 4634.02 | 4562.84 | 4566.34 | 4566.5 | 0.00076 | 0.004 |
| Pressure at Point 2 (kPa) | 5002.6 | 5561.3 | 5512.1 | 5508.1 | 0.0089 | 0.0902 |
| Pressure at Point 3 (kPa) | 4886.3 | 5119.6 | 5038.8 | 4999.5 | 0.0160 | 0.9747 |
| Torque (kNm) | 120.1 | 125.7 | 126.2 | 126.23 | 0.0048 | 0.0595 |
| Efficiency (%) | 90.12 | 93.40 | 93.46 | 93.46 | 0.00064 | 0.0011 |
| Erosion Rate (kg/m2/s) (×10−7) | 3.41 | 1.01 | 1.28 | 1.31 | 0.2151 | 2.98 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Acharya, N.; Gautam, S.; Chitrakar, S.; Iliev, I.; Dahlhaug, O.G. Correlating Sediment Erosion in Rotary–Stationary Gaps of Francis Turbines with Complex Flow Patterns. Energies 2024, 17, 5961. https://doi.org/10.3390/en17235961
Acharya N, Gautam S, Chitrakar S, Iliev I, Dahlhaug OG. Correlating Sediment Erosion in Rotary–Stationary Gaps of Francis Turbines with Complex Flow Patterns. Energies. 2024; 17(23):5961. https://doi.org/10.3390/en17235961
Chicago/Turabian StyleAcharya, Nirmal, Saroj Gautam, Sailesh Chitrakar, Igor Iliev, and Ole Gunnar Dahlhaug. 2024. "Correlating Sediment Erosion in Rotary–Stationary Gaps of Francis Turbines with Complex Flow Patterns" Energies 17, no. 23: 5961. https://doi.org/10.3390/en17235961
APA StyleAcharya, N., Gautam, S., Chitrakar, S., Iliev, I., & Dahlhaug, O. G. (2024). Correlating Sediment Erosion in Rotary–Stationary Gaps of Francis Turbines with Complex Flow Patterns. Energies, 17(23), 5961. https://doi.org/10.3390/en17235961






