Non-Condensation Turbulence Models with Different Near-Wall Treatments and Solvers Comparative Research for Three-Dimensional Steam Ejectors
Abstract
1. Introduction
2. Numerical Simulation Method
2.1. Mathematical Model
2.2. Solution Scheme and Boundary Conditions
- (1)
- All the residual terms’ convergence absolute criteria are <10−6 forever;
- (2)
- The difference in the mass flow rate between the inlet and the outlet is <1 × 10−7;
- (3)
- The calculated mass flow rate of two inlet sections and one outlet section is stable.
2.3. Mesh Creation
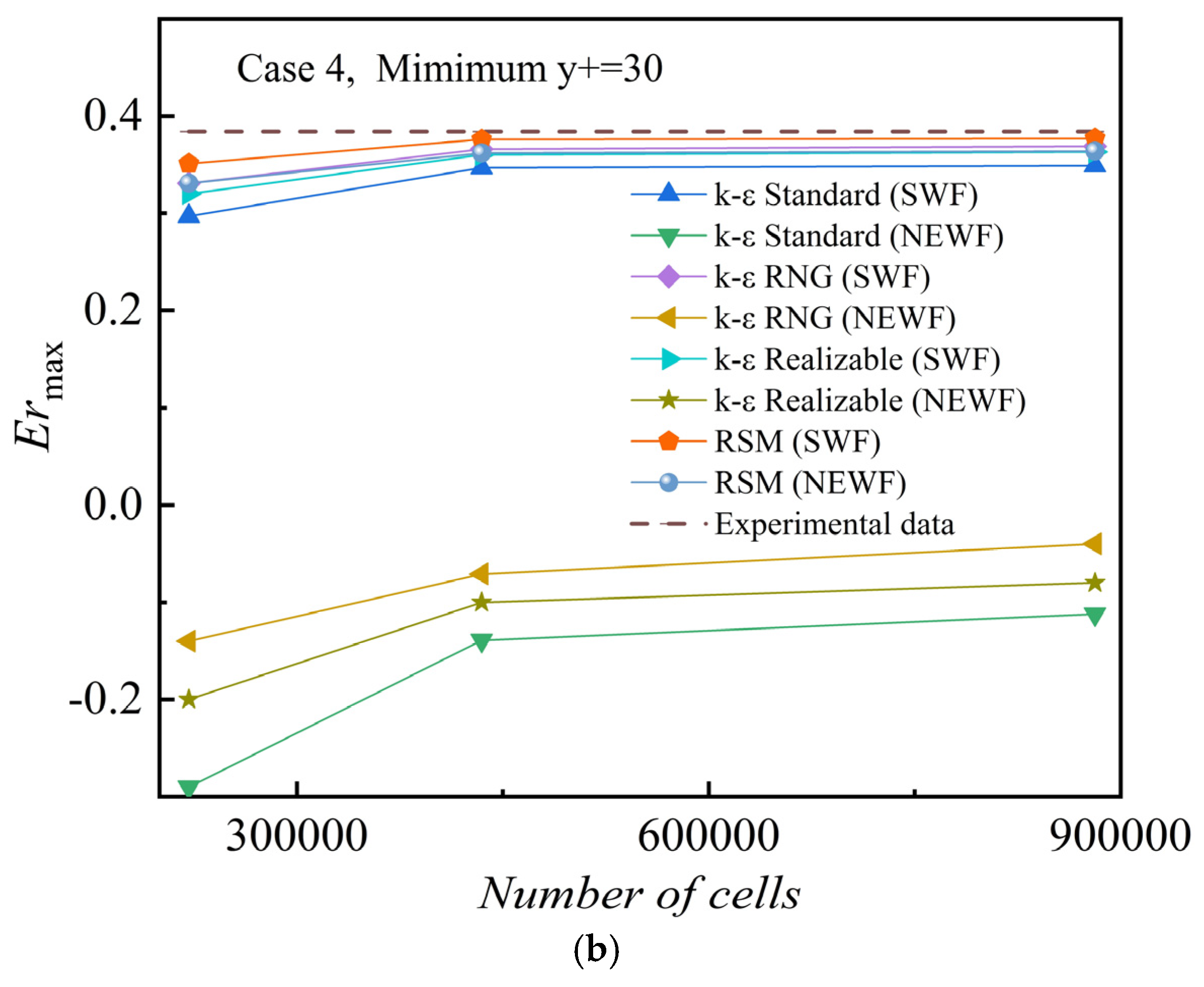
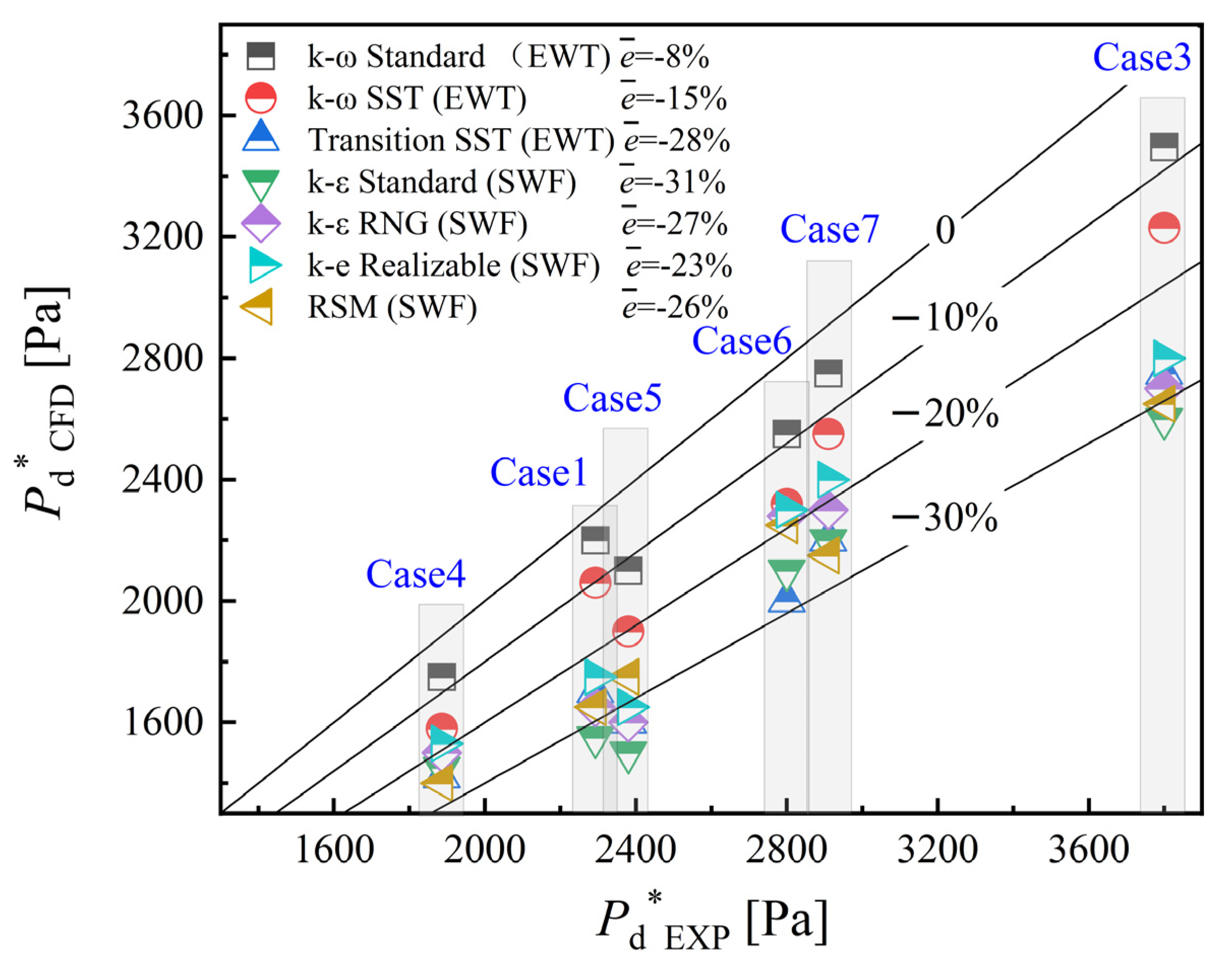
3. Results and Discussion
3.1. Validation, Comparison and Analysis of Different Near-Wall Treatments
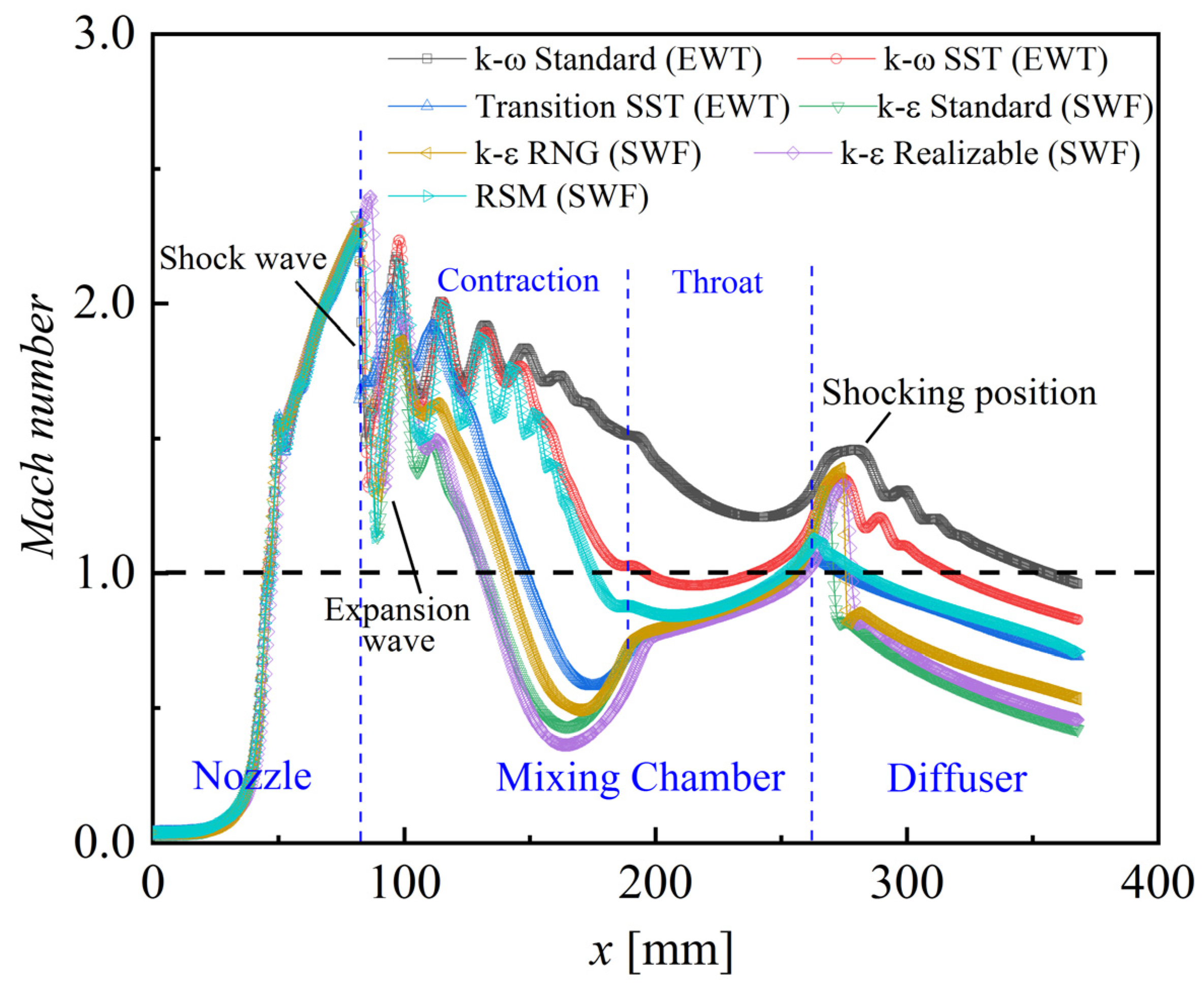
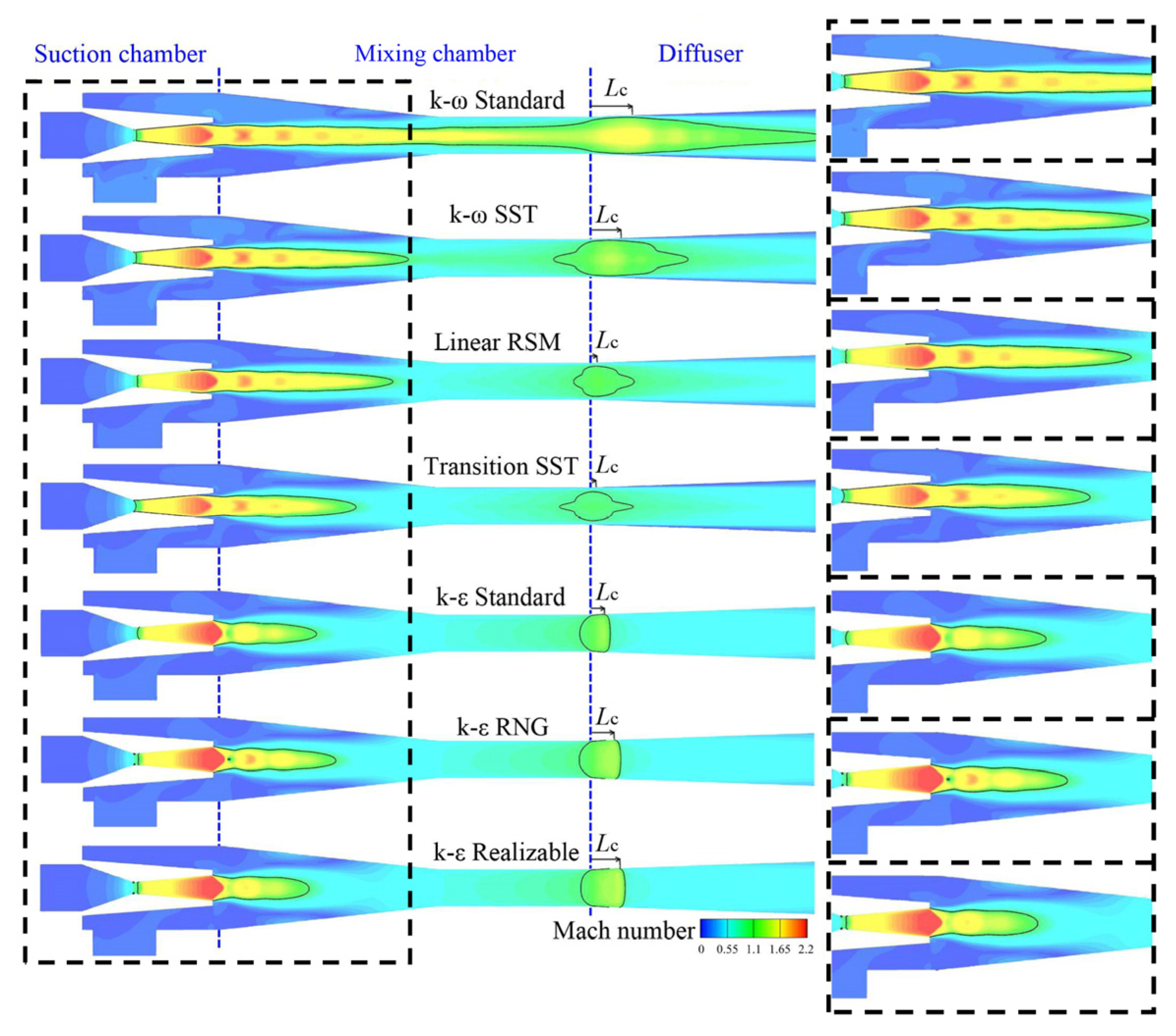
3.2. Validation, Comparison and Analysis of Different Turbulence Models
3.3. Comparison and Analysis of Density-Based Solver and Pressure-Based Solver
3.4. Validation, Comparison, and Analysis of 3-D and 2-D Models, Condensation Model, and Ideal-Gas Model
4. Conclusions
- (1)
- Considering non-equilibrium condensation and 3-D effects, the k-ω SST model with the low-Re boundary conditions has the most accurate prediction results globally and locally compared with the experiments: (a) The average relative error of Ermax and Pd* are 4% and −15%, (b) the shock wave type and the condensation position are well predicted. Moreover, it has the widest adaptability to working conditions and the best convergence of the seven turbulence models studied in this paper.
- (2)
- The difference in Ermax predicted by different models depends mainly on their mass flow rates of suction steam (Gs). The minimum difference in Gs predicted by different models is greater than 55%, while the maximum difference in Gm is less than 8%.
- (3)
- The number and types of shock waves, and the location of condensation phenomenon of different turbulence models, are various. The k-ε series models predict a normal shock in the diffuser while the other models predict a different number of oblique shock waves.
- (4)
- All other things being equal, the 3-D model can reduce the average relative error of Er by 78.4% compared to the 2-D model and the condensation model can reduce the average relative error of Er by 72.0% compared to the ideal-gas model.
- (5)
- A 3-D asymmetric condensation model with a density-based solver is recommended for simulating steam ejectors accurately.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| B | [m3/kg] | Virial coefficients |
| C | [m6/kg2] | Virial coefficients |
| CP | [J/(kg∙K)] | Isobaric heat capacity |
| E | [J] | Total energy |
| Er | [-] | Entrainment ratio |
| e | [%] | Relative error |
| F | [N/m3] | Source term |
| G | [kg/s] | Mass flow rate |
| h | [J/kg] | Specific enthalpy |
| hlv | [J/kg] | Latent heat of condensation |
| J | [1/s] | Nucleation rate |
| K | [W/(m2∙K)] | Heat transfer coefficient |
| k | [m2/s2] | Turbulent kinetic energy |
| kB | [-] | Boltzmann constant |
| Ma | [-] | Mach number |
| P | [Pa] | Pressure |
| R | [-] | Gas-law constant |
| r | [m] | Droplet radius |
| S | [-] | Super-saturation ratio |
| s | [J/(kg∙mol∙K)] | Specific entropy |
| ST | [kg∙K/ (m3∙s)] | Viscous dissipative term |
| T | [K] | Temperatures |
| Greek letters | ||
| β | [-] | Liquid mass fraction |
| Г | [kg/s] | Liquid mass generation rate |
| ρ | [kg/m3] | Density |
| γ | [-] | Specific heat capacities ratio |
| μ | [Pa/s] | Dynamic viscosity |
| σ | [N/m] | Liquid surface tension |
| η | [1/m3] | Droplet number density |
| θ | [-] | Non-isothermal correction factor |
| ν | [m2/s] | Kinematic viscosity |
| ε | [m2/s3] | Turbulent dissipation rate |
| τ | [N/m2] | Stress tensor |
| v | [m/s] | Velocity |
| Subscripts | ||
| sat | Saturation | |
| m | Motive steam | |
| s | Suction steam | |
| d | Discharge steam | |
| l | Liquid | |
| v | Vapor | |
| max | Maximum | |
| * | Critical | |
| - | Average | |
| eff | Effective | |
| i,j | Space components | |
| Abbreviations | ||
| D-B | Density-based solver | |
| P-B | Pressure-based solver | |
| RSM | Reynolds Stress Model | |
| SWF | Standard Wall Function | |
| NWF | Non-equilibrium Wall Function | |
| EWT | Enhanced Wall Treatment | |
| N-S | Navier-Stokes | |
| RANS | Reynolds-Averaged Navier–Stokes | |
References
- Li, Y.; Shen, S.; Niu, C.; Mu, X.; Zhang, L. The effect of variable motive pressures on the performance and shock waves in a supersonic steam ejector with non-equilibrium condensing. Int. J. Therm. Sci. 2023, 185, 108034. [Google Scholar] [CrossRef]
- Li, Y.; Shen, S.; Yang, Y. Three-dimensional characteristics of aerodynamic shockwave and condensation shockwave in steam ejectors. Desalination 2024, 581, 117606. [Google Scholar] [CrossRef]
- Wang, X.; Dong, J.; Zhang, G.; Fu, Q.; Li, H.; Han, Y.; Tu, J. The primary pseudo-shock pattern of steam ejector and its influence on pumping efficiency based on CFD approach. Energy 2019, 167, 224–234. [Google Scholar] [CrossRef]
- Han, Y.; Wang, X.; Yuen, A.C.Y.; Li, A.; Guo, L.; Yeoh, G.H.; Tu, J. Characterization of choking flow behaviors inside steam ejectors based on the ejector refrigeration system. Int. J. Refrig. 2020, 113, 296–307. [Google Scholar] [CrossRef]
- Wen, C.; Karvounis, N.; Walther, J.H.; Ding, H.; Yang, Y. Non-equilibrium condensation of water vapour in supersonic flows with shock waves. Int. J. Heat Mass Transf. 2020, 149, 119109. [Google Scholar] [CrossRef]
- Ansys, Inc. Ansys FLUENT 18.0—Theory Guide; Ansys Fluent: Canonsburg, PA, USA, 2019. [Google Scholar]
- Besagni, G.; Cristiani, N.; Croci, L.; Guédon, G.R.; Inzoli, F. Computational fluid-dynamics modelling of supersonic ejectors: Screening of modelling approaches, comprehensive validation and assessment of ejector component efficiencies. Appl. Therm. Eng. 2020, 186, 116431. [Google Scholar] [CrossRef]
- Besagni, G.; Inzoli, F. Computational fluid-dynamics modeling of supersonic ejectors: Screening of turbulence modeling approaches. Appl. Therm. Eng. 2017, 117, 122–144. [Google Scholar] [CrossRef]
- Hemidi, A.; Henry, F.; Leclaire, S.; Seynhaeve, J.M.; Bartosiewicz, Y. CFD analysis of a supersonic air ejector. Part II: Relation between global operation and local flow features. Appl. Therm. Eng. 2009, 29, 2990–2998. [Google Scholar] [CrossRef]
- Gagan, J.; Smierciew, K.; Butrymowicz, D.; Karwacki, J. Comparative study of turbulence models in application to gas ejectors. Int. J. Therm. Sci. 2014, 78, 9–15. [Google Scholar] [CrossRef]
- Zhu, Y.; Jiang, P. Experimental and numerical investigation of the effect of shock wave characteristics on the ejector performance. Int. J. Refrig. 2014, 40, 31–42. [Google Scholar] [CrossRef]
- Croquer, S.; Poncet, S.; Aidoun, Z. Turbulence modeling of a single-phase R134a supersonic ejector. Part 1: Numerical benchmark. Int. J. Refrig. 2016, 61, 140–152. [Google Scholar] [CrossRef]
- Ruangtrakoon, N.; Thongtip, T.; Aphornratana, S.; Sriveerakul, T. CFD simulation on the effect of primary nozzle geometries for a steam ejector in refrigeration cycle. Int. J. Therm. Sci. 2013, 63, 133–145. [Google Scholar] [CrossRef]
- Han, Y.; Wang, X.; Sun, H.; Zhang, G.; Guo, L.; Tu, J. CFD simulation on the boundary layer separation in the steam ejector and its influence on the pumping performance. Energy 2019, 167, 469–483. [Google Scholar] [CrossRef]
- Varga, S.; Soares, J.; Lima, R.; Oliveira, A.C. On the selection of a turbulence model for the simulation of steam ejectors using CFD. Int. J. Low-Carbon Technol. 2017, 12, 233–243. [Google Scholar] [CrossRef][Green Version]
- Wu, J.; Xu, P.; Li, L.; Li, Z.; Qi, H.; Wang, C.; Zhang, Y.; Xie, Y.; Tan, D. Multiphase dynamic interfaces and abrasive transport dynamics for abrasive flow machining in shear thickening transition states. Powder Technol. 2024, 446, 120150. [Google Scholar] [CrossRef]
- Tan, Y.; Ni, Y.; Xu, W.; Xie, Y.; Li, L.; Tan, D. Key technologies and development trends of the soft abrasive flow finishing method. J. Zhejiang Univ.-Sci. A 2023, 24, 1043–1064. [Google Scholar] [CrossRef]
- Aidoun, Z.; Ameur, K.; Falsafioon, M.; Badache, M. Current Advances in Ejector Modeling, Experimentation and Applications for Refrigeration and Heat Pumps. Part 1: Single-Phase Ejectors. Inventions 2019, 4, 15. [Google Scholar] [CrossRef]
- Li, C.; Li, Y.Z. Investigation of entrainment behavior and characteristics of gas-liquid ejectors based on CFD simulation. Chem. Eng. Sci. 2011, 66, 405–416. [Google Scholar] [CrossRef]
- Yazdani, M.; Alahyari, A.A.; Radcliff, T.D. Numerical modeling of two-phase supersonic ejectors for work-recovery applications. Int. J. Heat Mass Transf. 2012, 55, 5744–5753. [Google Scholar] [CrossRef]
- Sriveerakul, T.; Aphornratana, S.; Chunnanond, K. Performance prediction of steam ejector using computational fluid dynamics: Part 1. Validation of the CFD results. Int. J. Therm. Sci. 2007, 46, 812–822. [Google Scholar] [CrossRef]
- Tashtoush, B.M.; Moh’d A, A.N.; Khasawneh, M.A. A comprehensive review of ejector design, performance, and applications. Appl. Energy 2019, 240, 138–172. [Google Scholar] [CrossRef]
- Cai, L.; He, M.; Huang, K.Z.; Xiong, W. Computational fluid dynamics simulation of the supersonic steam ejector using different condensation model. Therm. Sci. 2019, 23, 236. [Google Scholar] [CrossRef]
- Mazzelli, F.; Little, A.B.; Garimella, S.; Bartosiewicz, Y. Computational and experimental analysis of supersonic air ejector: Turbulence modeling and assessment of 3D effects. Int. J. Heat Fluid Flow 2015, 56, 305–316. [Google Scholar] [CrossRef]
- Young, J.B. An equation of state for steam for turbomachinery and other flow calculations. J. Eng. Gas Turbines Power 1988, 110, 1–7. [Google Scholar] [CrossRef]
- Young, J.B. Spontaneous condensation of steam in supersonic nozzles. PCH Physicochem. Hydrodyn. 1982, 3, 57–82. [Google Scholar]
- Kong, N.; Qi, Z. Influence of speed of sound in two-phase region on 1-D ejector performance modelling. Appl. Therm. Eng. 2018, 139, 352–355. [Google Scholar] [CrossRef]
- Daiguji, H.; Ishazaki, K.; Ikohagi, T. A high-resolution numerical method for transonic non-equilibrium condensation flows through a steam turbine cascade. Proc. 6th Int. Symp. Comput. Fluid Dyn. 1995, 1, 479–484. [Google Scholar]
- Senoo, S.; Shikano, Y. Two-dimensional analysis for non-equilibrium homogeneously condensing flows through steam turbine cascade. JSME Int. J. Ser. B Fluids Therm. Eng. 2002, 45, 865–871. [Google Scholar] [CrossRef]
- Chen, Y.; Sun, C. Experimental study of the performance characteristics of a steam-ejector refrigeration system. Exp. Therm. Fluid Sci. 1997, 15, 384–394. [Google Scholar] [CrossRef]
- Zhang, G.; Zhang, X.; Wang, D.; Jin, Z.; Qin, X. Performance evaluation and operation optimization of the steam ejector based on modified model. Appl. Therm. Eng. 2019, 163, 114388. [Google Scholar] [CrossRef]
- Zhang, G.; Dykas, S.; Li, P.; Li, H.; Wang, J. Accurate condensing steam flow modeling in the ejector of the solar-driven refrigeration system. Energy 2020, 212, 118690. [Google Scholar] [CrossRef]
- Wang, X.; Dong, J.; Li, A.; Lei, H.; Tu, J. Numerical study of primary steam superheating effects on steam ejector flow and its pumping performance. Energy 2014, 78, 205–211. [Google Scholar] [CrossRef]
- Ariafar, K.; Buttsworth, D.; Al-Doori, G.; Malpress, R. Effect of mixing on the performance of wet steam ejectors. Energy 2015, 93, 2030–2041. [Google Scholar] [CrossRef]
- Mazzelli, F.; Giacomelli, F.; Milazzo, A. CFD modeling of condensing steam ejectors: Comparison with an experimental test-case. Int. J. Therm. Sci. 2018, 127, 7–18. [Google Scholar] [CrossRef]
- Zhang, G.; Wang, X.; Pourranjbar, D.; Dykas, S.; Li, H.; Chen, J. The comprehensive analysis of the relationship between the latent heat, entrainment ratio, and ejector performance under different superheating degree conditions considering the non-equilibrium condensation. Appl. Therm. Eng. 2022, 200, 117701. [Google Scholar] [CrossRef]
- Li, Y.; Niu, C.; Shen, S.; Mu, X.; Zhang, L. Double choking characteristics of three-dimensional steam ejector with non-equilibrium condensing. Appl. Therm. Eng. 2022, 211, 118446. [Google Scholar] [CrossRef]
- Moore, M.J.; Walters, P.T.; Crane, R.I.; Davidson, B.J. Predicting the fog-drop size in wet-steam turbines. In Proceedings of the IMechE Conference on Heat and Fluid Flow in Steam and Gas Turbine Plant, Coventry, UK, 3–5 April 1973; pp. C37–C73. [Google Scholar]
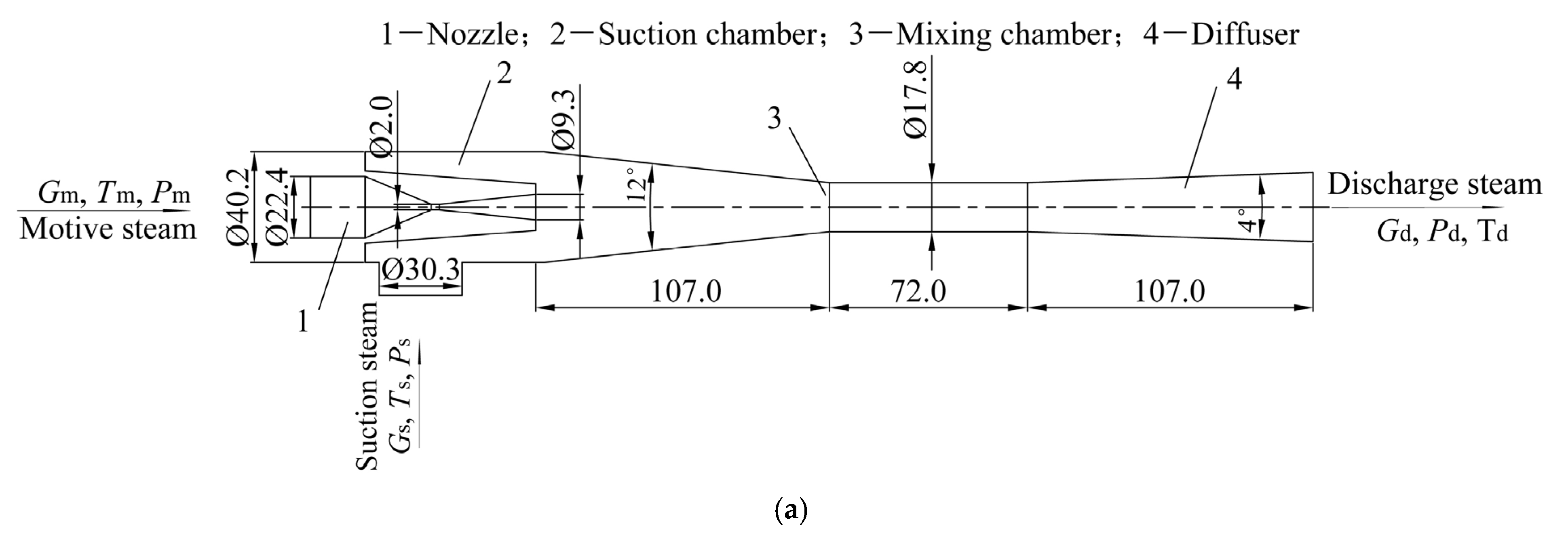

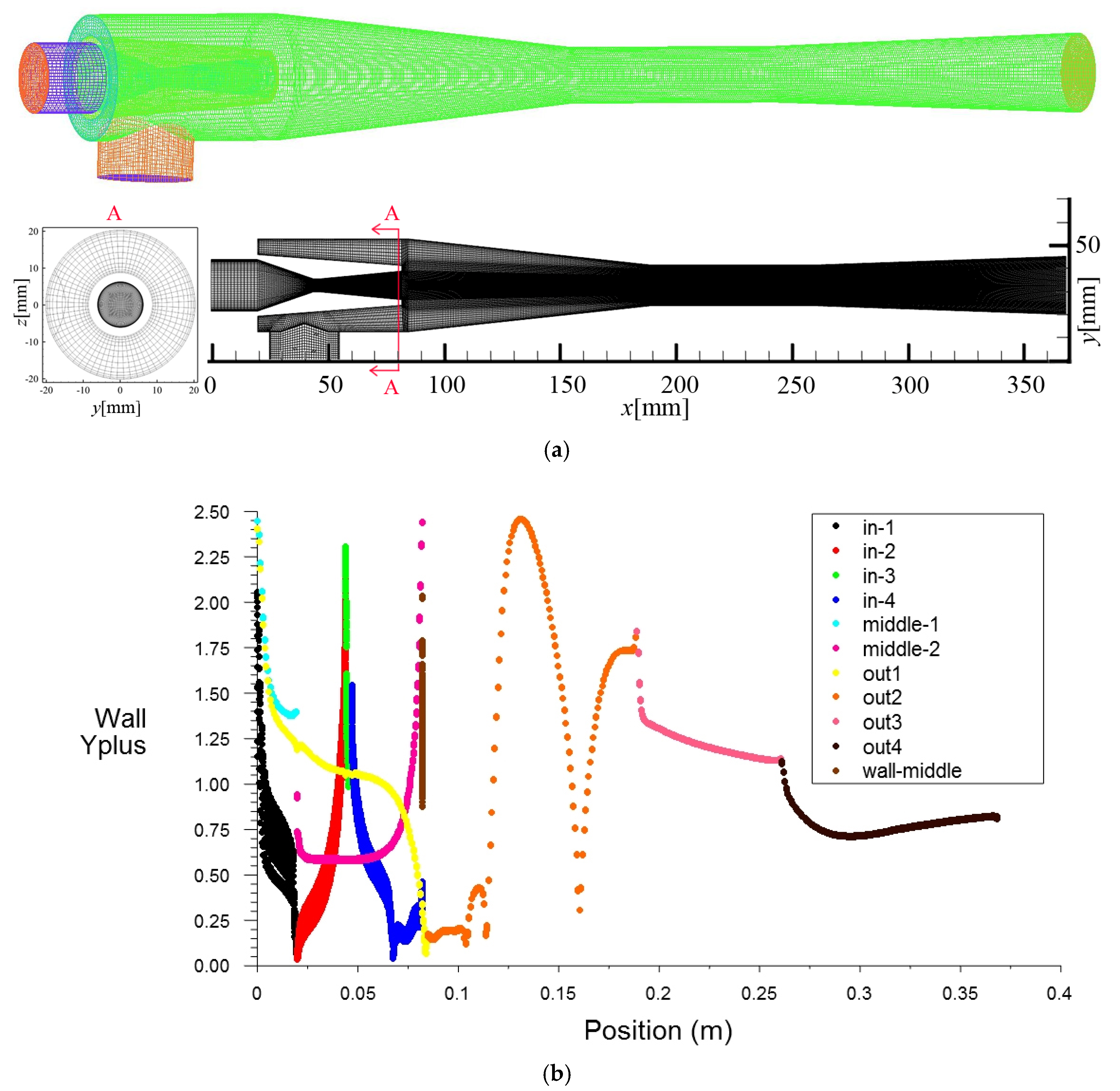
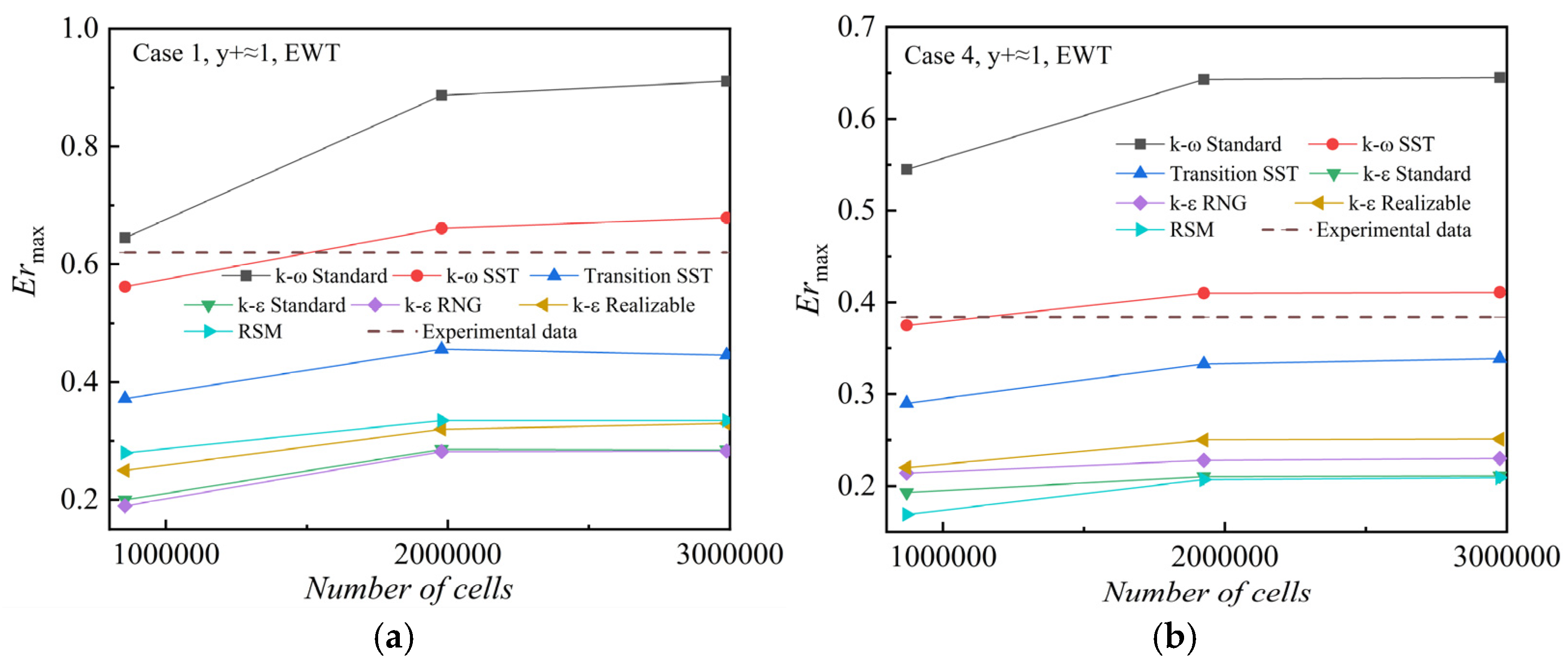
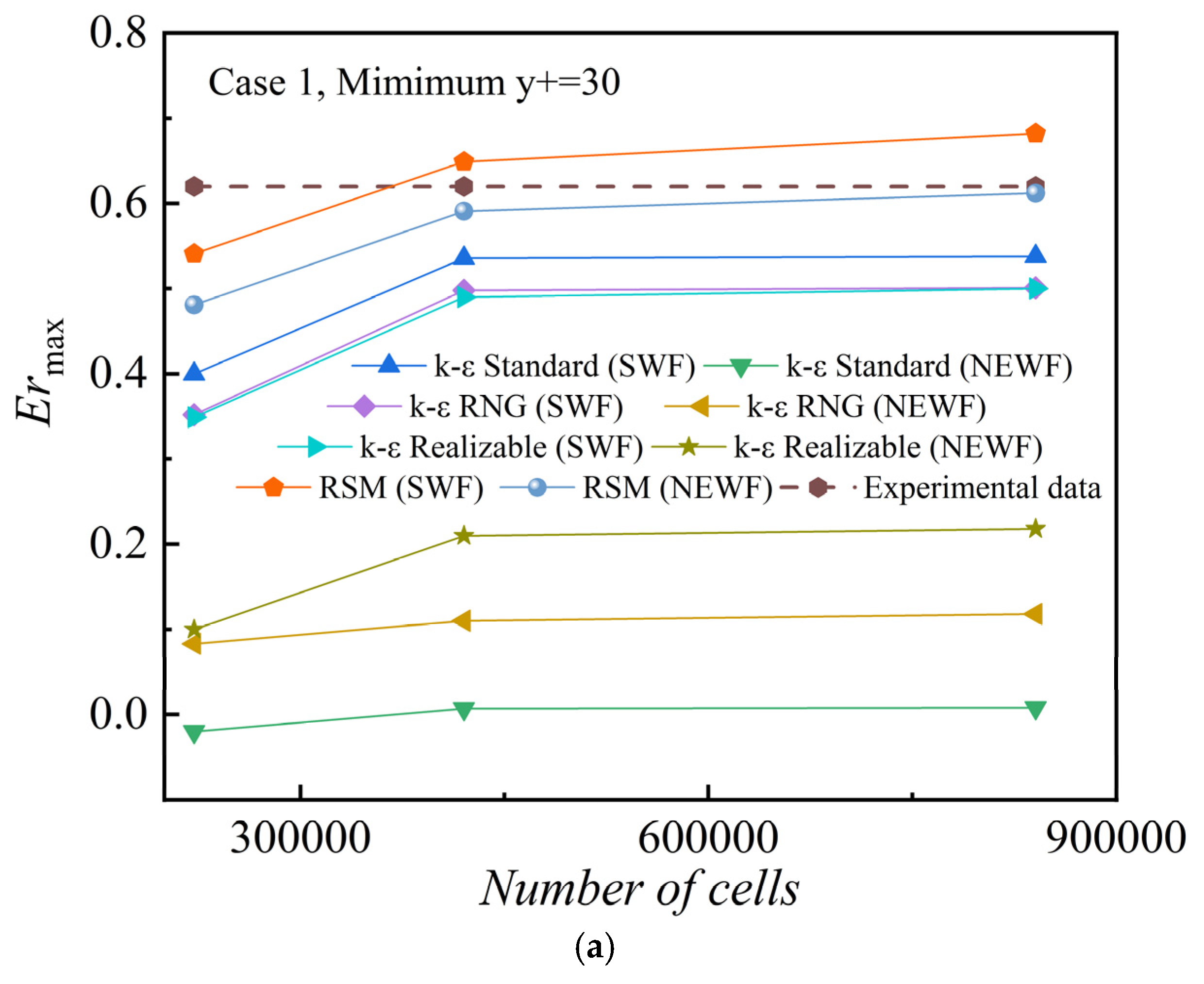


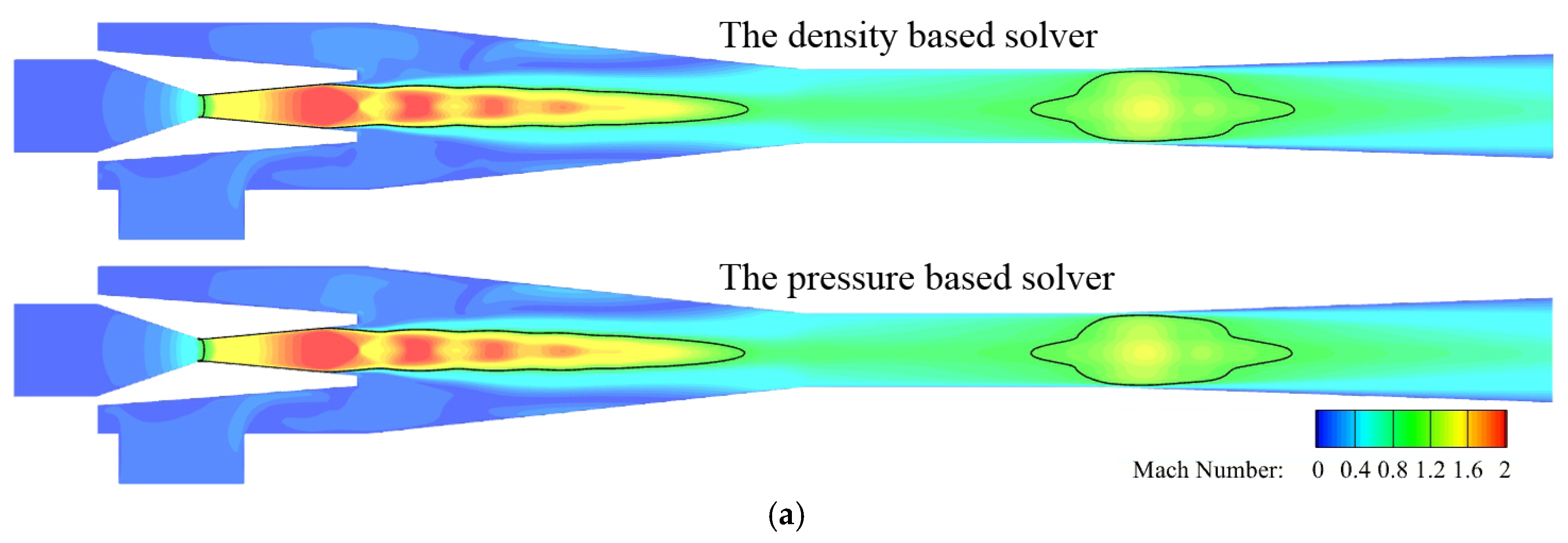
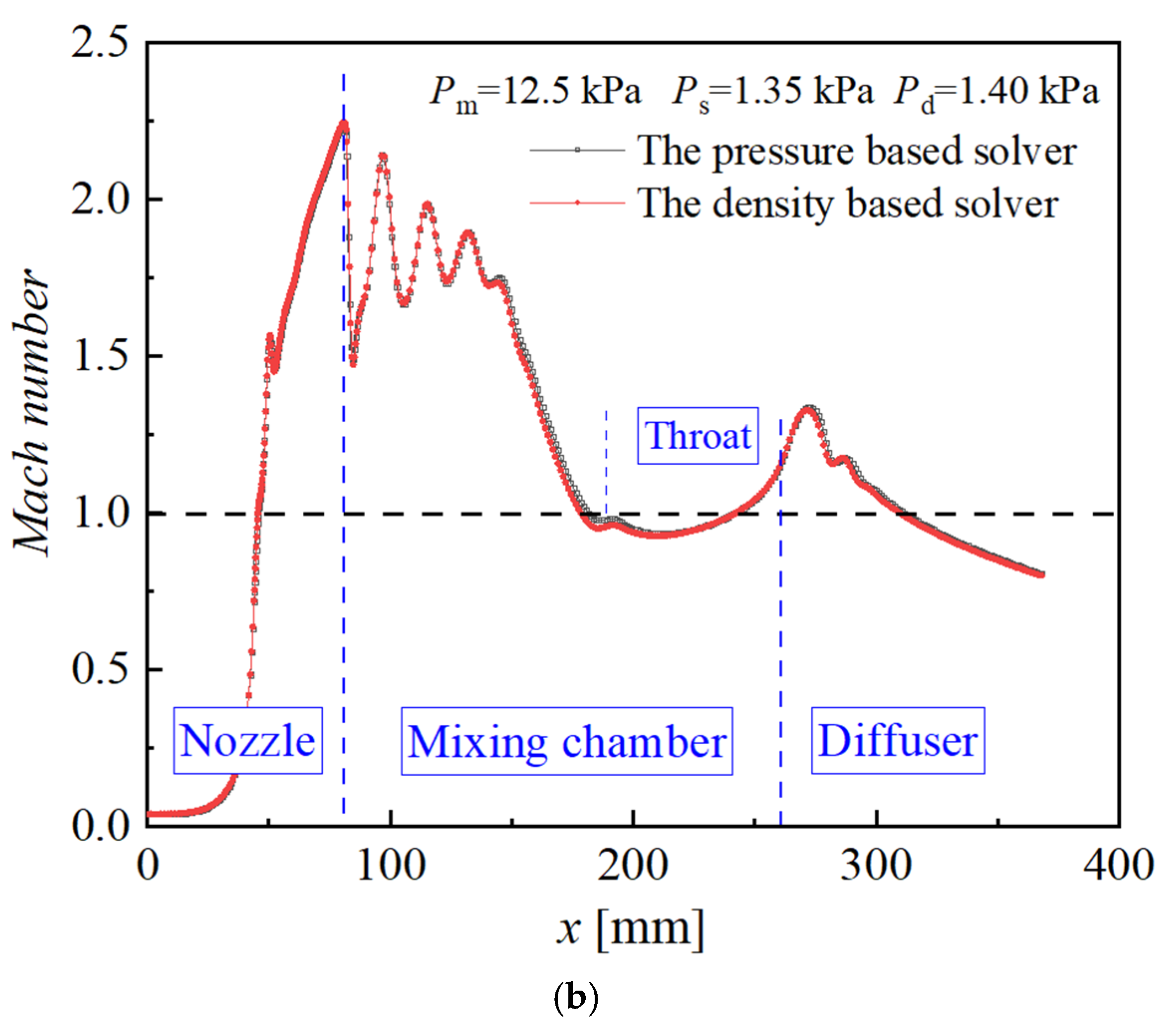
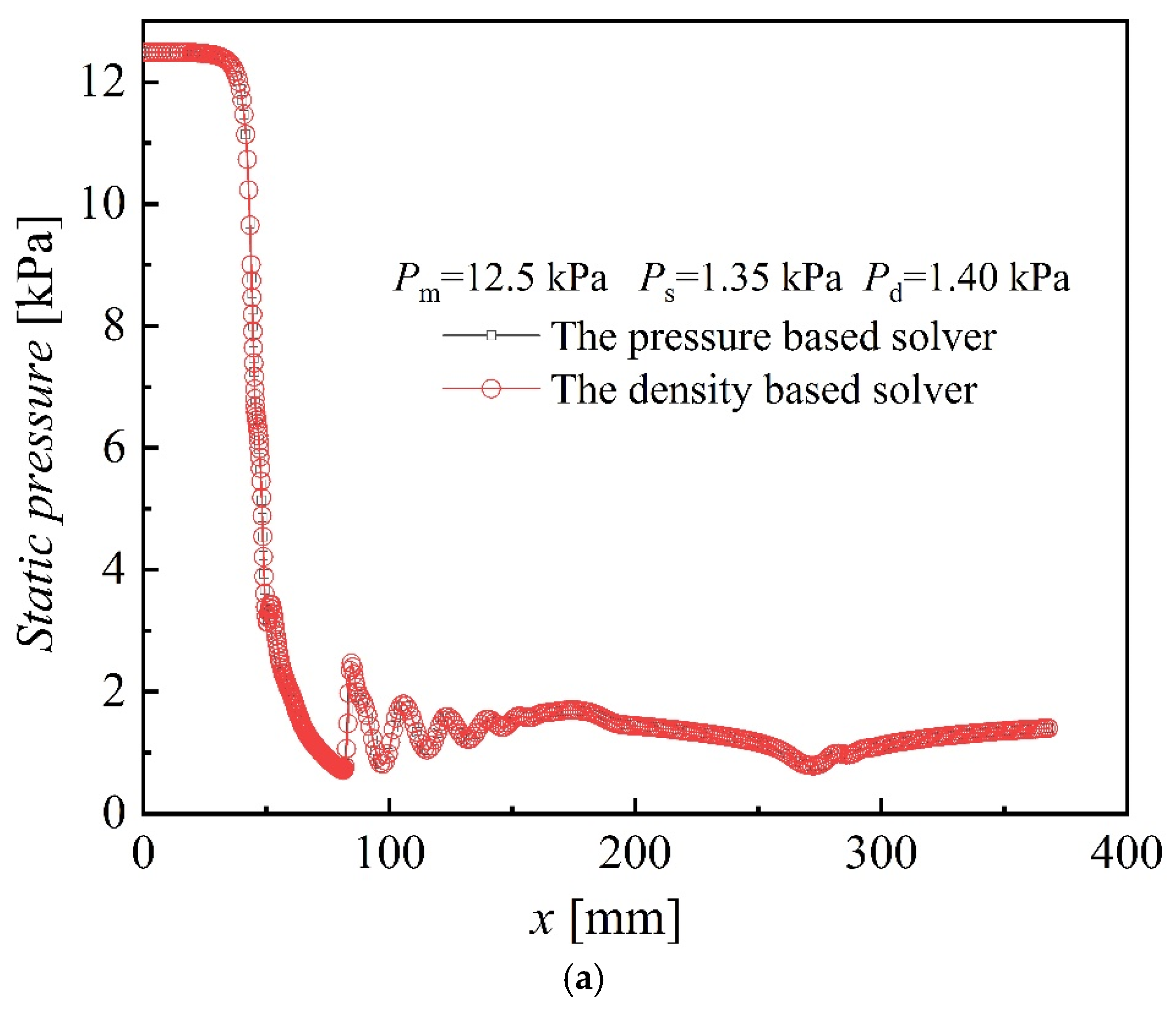
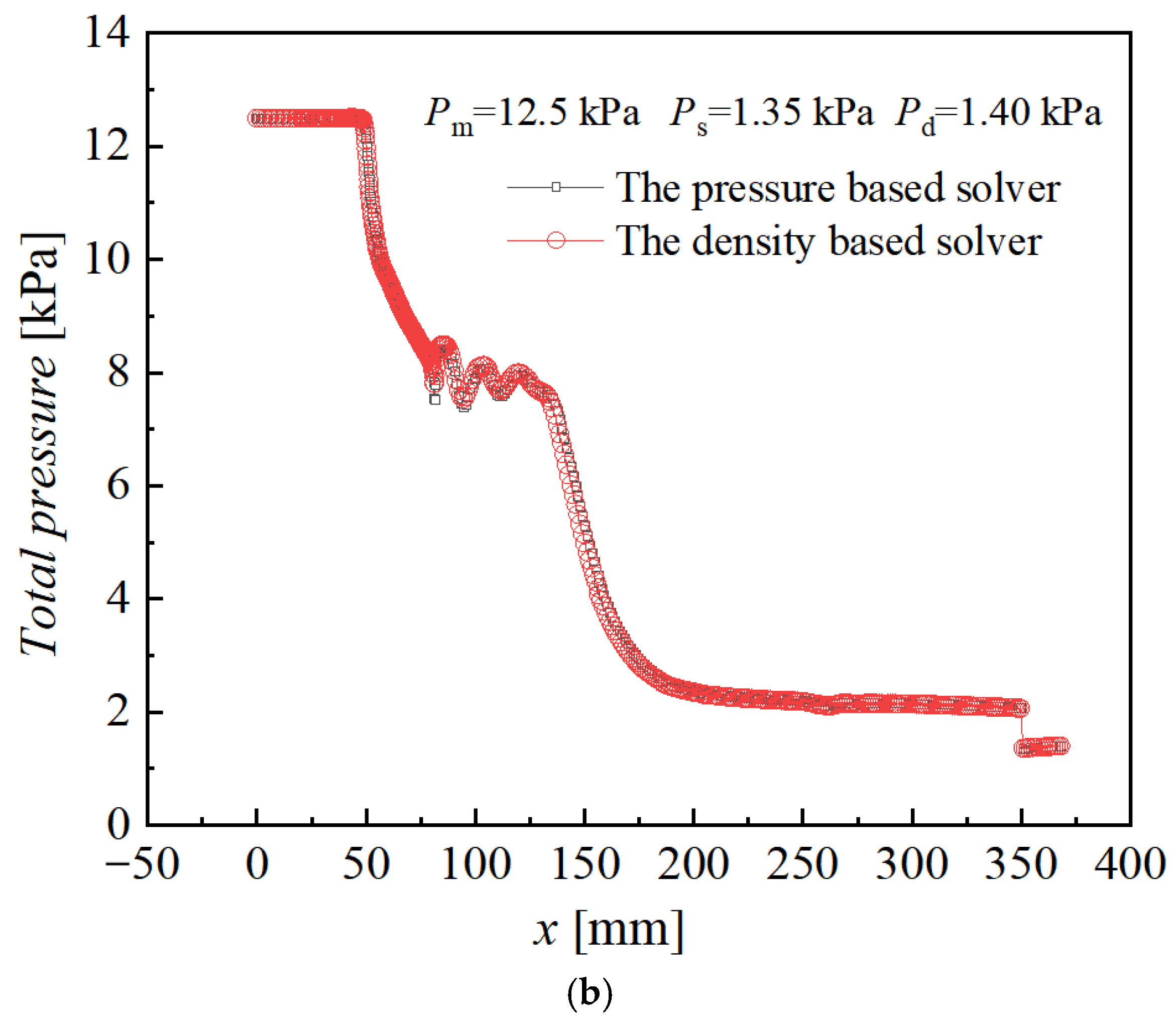
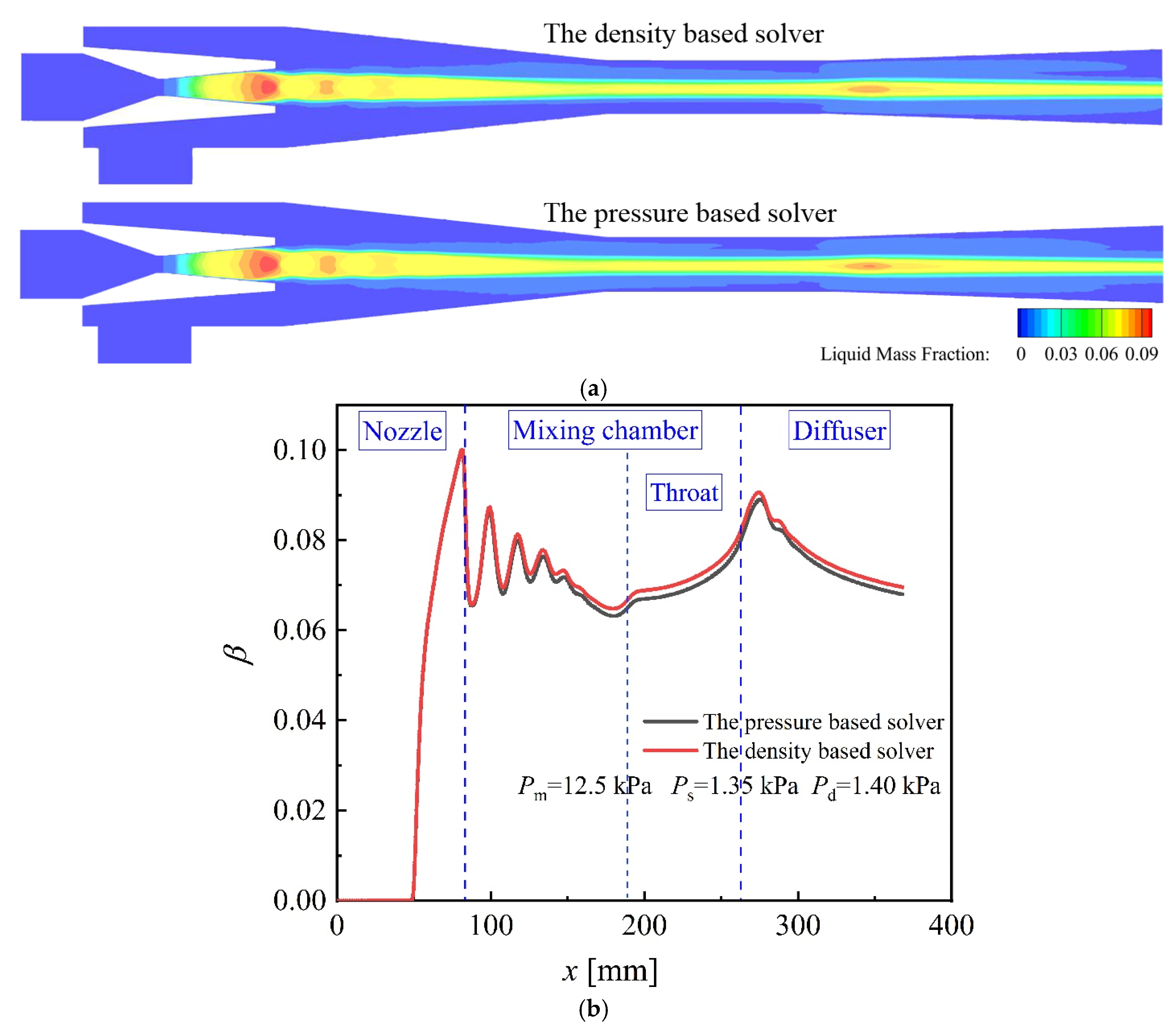
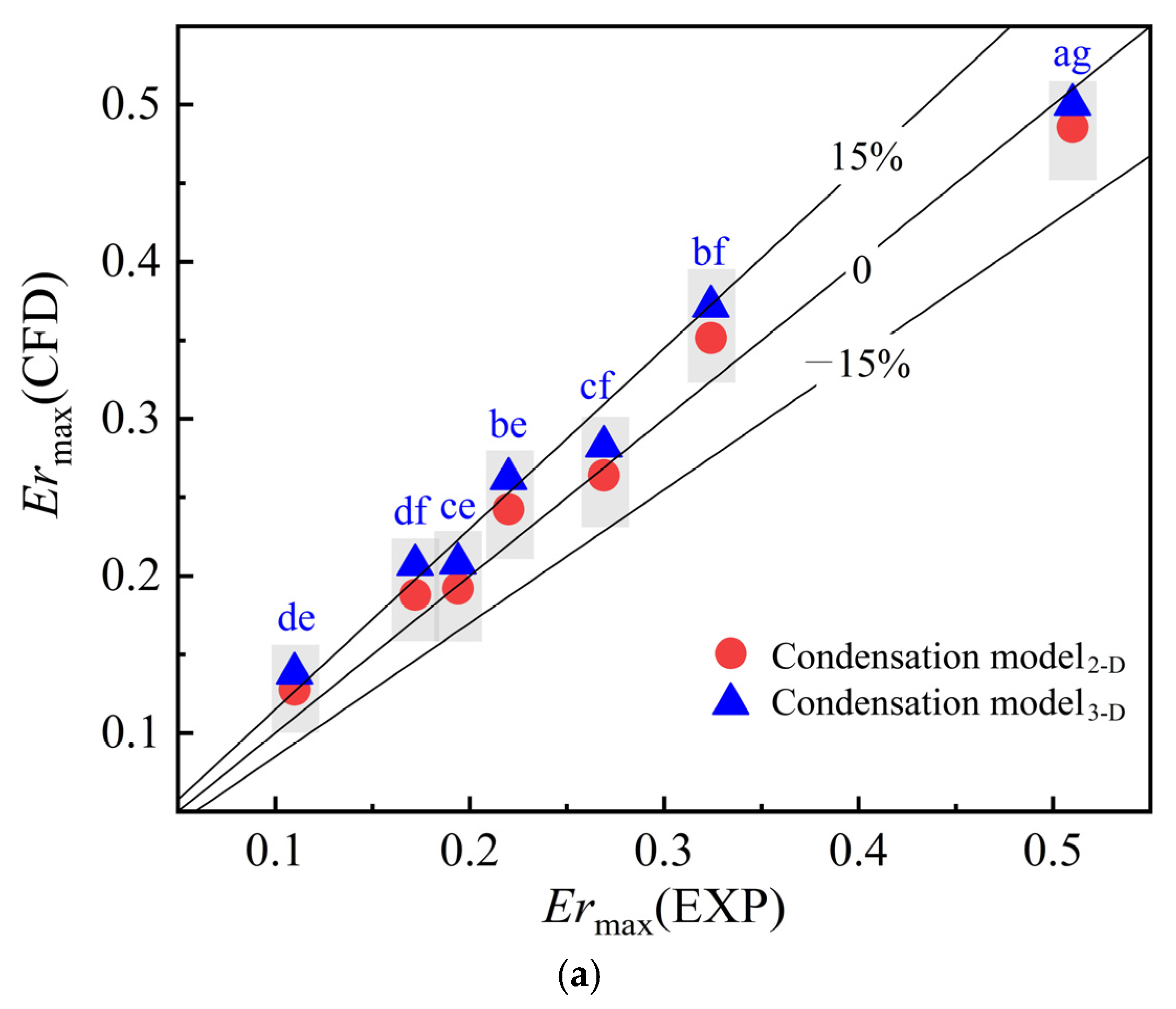

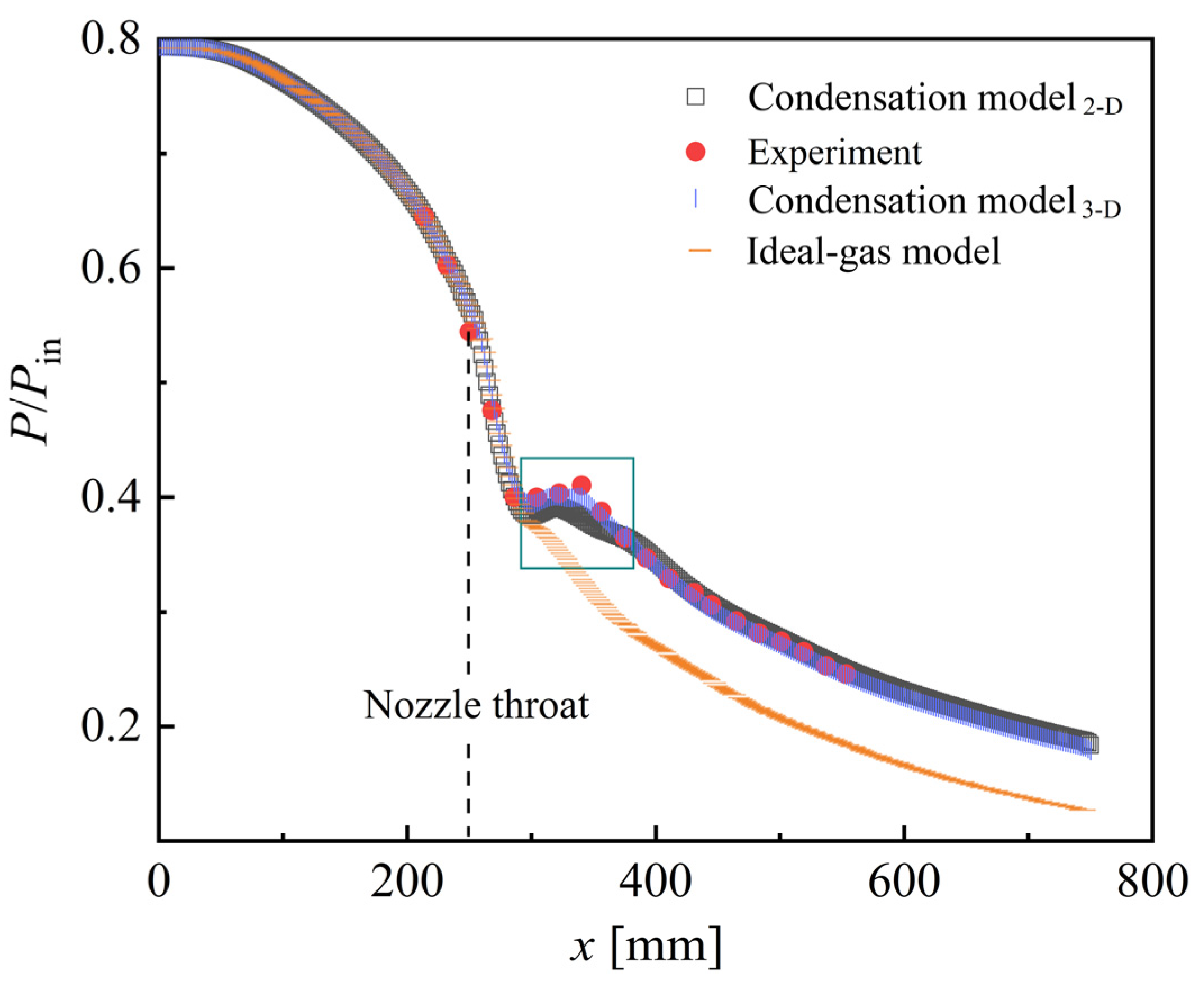
| Size | Case | Pm [kPa] | Tm [°C] | Ps [kPa] | Ts [°C] | Pd [kPa] |
|---|---|---|---|---|---|---|
| E1 | 1 | 116.0 | 105.8 | 1.306 | 10.8 | 1.35~2.70 |
| 2 | 153.0 | 114.2 | 1.306 | 10.8 | 1.35~2.90 | |
| 3 | 198.0 | 121.8 | 1.306 | 10.8 | 1.35~3.90 | |
| E2 | 4 | 11.906 | 51.3 | 1.306 | 10.8 | 1.35~1.90 |
| 5 | 15.465 | 56.6 | 1.306 | 10.8 | 1.35~2.40 | |
| 6 | 19.571 | 61.6 | 1.306 | 10.8 | 1.35~2.90 | |
| 7 | 19.571 | 61.6 | 1.813 | 15.8 | 1.85~2.90 | |
| 8 | 12.5 | 52.2 | 1.35 | 11.4 | 1.4 | |
| ag | 11.906 | 51.3 | 1.813 | 15.8 | 1.85~2.00 | |
| bf | 15.465 | 56.2 | 1.306 | 10.8 | 1.35~2.40 | |
| cf | 19.571 | 61.6 | 1.306 | 10.8 | 1.35~2.90 | |
| df | 24.837 | 66.8 | 1.306 | 10.8 | 1.35~3.20 | |
| be | 15.465 | 56.2 | 1.0 | 13.2 | 1.1~2.2 | |
| ce | 19.571 | 61.6 | 1.0 | 13.2 | 1.1~2.6 | |
| de | 24.837 | 66.8 | 1.0 | 13.2 | 1.1~3.3 |
| Type1, y+ ≈ 1 | Type2, Minimum y+ = 30 | |||||
|---|---|---|---|---|---|---|
| Mesh Level | Coarse | Medium | Fine | Coarse | Medium | Fine |
| Number [million] | 0.8 | 2.0 | 2.9 | 0.2 | 0.4 | 0.9 |
| Model | e(Ermax) | |||||||
|---|---|---|---|---|---|---|---|---|
| Case | k-ω Standard (EWT) | k-ω SST (EWT) | Transition SST (EWT) | k-ε Standard (SWF) | k-ε RNG (SWF) | k-ε Realizable (SWF) | Linear RSM (SWF) | |
| 1 | 43% | 7% | −26% | −24% | −20% | −21% | 5% | |
| 2 | 47% | 11% | −38% | −38% | −36% | −28% | 11% | |
| 3 | 28% | 2% | −31% | −40% | −37% | −30% | −19% | |
| 4 | 42% | 9% | −13% | −10% | −5% | −6% | −2% | |
| 5 | 21% | 6% | −49% | −62% | −52% | −38% | −19% | |
| 6 | 22% | −5% | −27% | −76% | −74% | −55% | −10% | |
| 7 | 38% | −2% | −30% | −27% | −32% | −22% | −2% | |
| (Ermax) | 34.5% | 4.0% | −30.6% | −39.5% | −36.5% | −28.6% | −5.2% | |
| m | s | ||
|---|---|---|---|
| Case | |||
| 1 | 8% | 67% | |
| 2 | 2% | 93% | |
| 3 | 5% | 88% | |
| 4 | 4% | 55% | |
| 5 | 7% | 96% | |
| 6 | 2% | 129% | |
| 7 | 7% | 80% | |
| average | 5% | 87% | |
| k-ω Standard (EWT) | k-ω SST (EWT) | Transition SST (EWT) | k-ε Standard (EWT) | k-ε RNG (EWT) | k-ε Realizable (EWT) | RSM (EWT) |
|---|---|---|---|---|---|---|
| 1.3 | 1.6 | 3.6 | 1 | 1.5 | 1.4 | 4.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Huang, H.; Duan, D.; Shen, S.; Zhou, D.; Liu, S. Non-Condensation Turbulence Models with Different Near-Wall Treatments and Solvers Comparative Research for Three-Dimensional Steam Ejectors. Energies 2024, 17, 5586. https://doi.org/10.3390/en17225586
Li Y, Huang H, Duan D, Shen S, Zhou D, Liu S. Non-Condensation Turbulence Models with Different Near-Wall Treatments and Solvers Comparative Research for Three-Dimensional Steam Ejectors. Energies. 2024; 17(22):5586. https://doi.org/10.3390/en17225586
Chicago/Turabian StyleLi, Yiqiao, Hao Huang, Dingli Duan, Shengqiang Shen, Dan Zhou, and Siyuan Liu. 2024. "Non-Condensation Turbulence Models with Different Near-Wall Treatments and Solvers Comparative Research for Three-Dimensional Steam Ejectors" Energies 17, no. 22: 5586. https://doi.org/10.3390/en17225586
APA StyleLi, Y., Huang, H., Duan, D., Shen, S., Zhou, D., & Liu, S. (2024). Non-Condensation Turbulence Models with Different Near-Wall Treatments and Solvers Comparative Research for Three-Dimensional Steam Ejectors. Energies, 17(22), 5586. https://doi.org/10.3390/en17225586






