Research on the Mechanism and Prediction Model of Pressure Drive Recovery in Low-Permeability Oil Reservoirs
Abstract
1. Introduction
2. Materials and Methods
2.1. Mathematical Model of Oil-Water Seepage in Low-Permeability Reservoirs
2.2. Model of Fracture Permeability
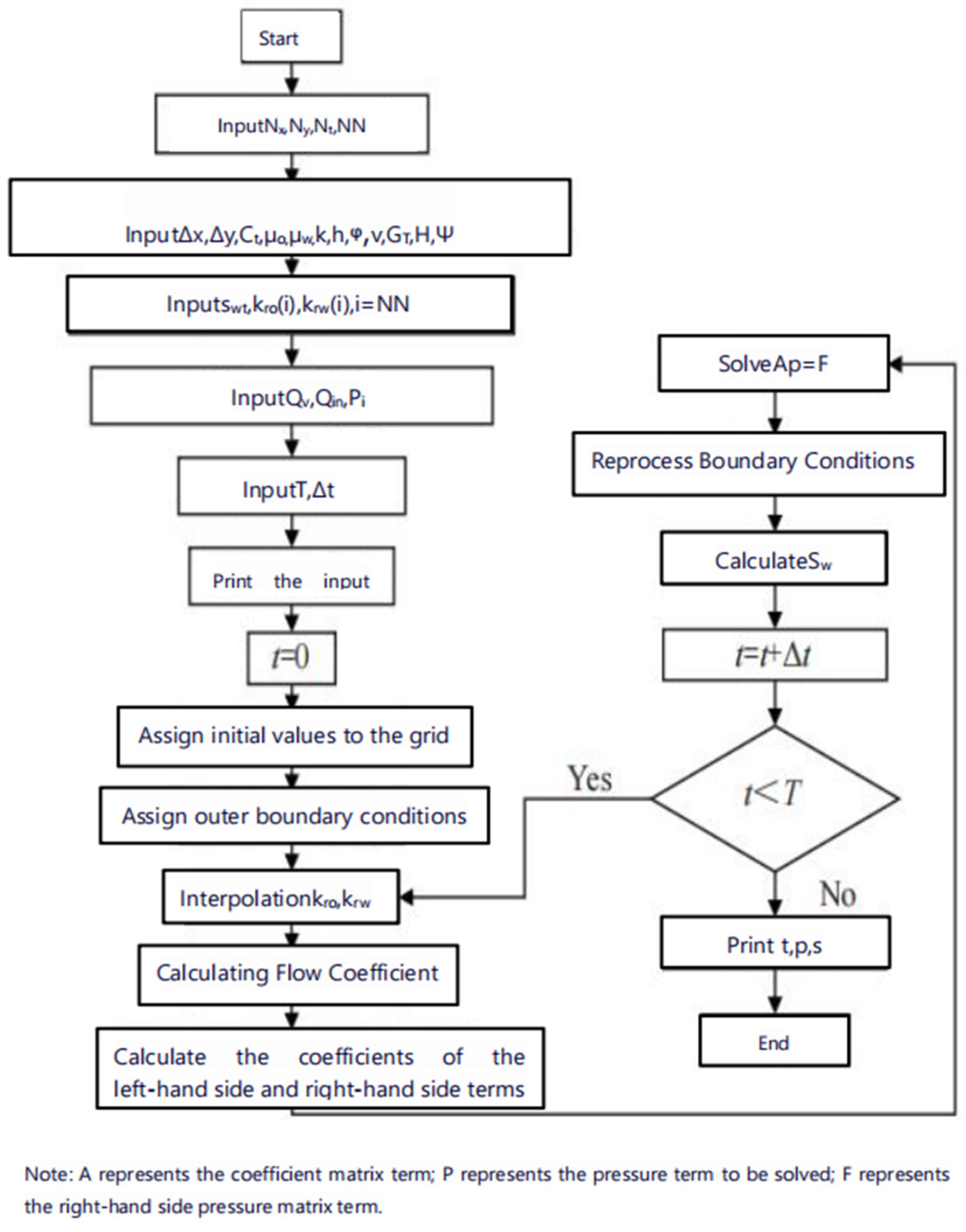
2.3. Solution of Pressure-Driven Model
- (1)
- Input Basic Parameters: Initially, the fundamental parameters required by the model are input. These parameters may include rock and fluid properties, well specifications, and operational conditions.
- (2)
- Initialization and Boundary Conditions: Each grid cell is assigned an initial value, and the outer boundary conditions of the model are specified. These boundary conditions define the pressure or flow conditions at the edges of the simulated reservoir.
- (3)
- Calculation of kro and krw: Using interpolation methods, the relative perm of oil (kro) and water (krw) are determined for each grid cell. These values are crucial in determining the flow behavior of the fluids within the reservoir.
- (4)
- Calculation of Flow Coefficients: Based on the reservoir’s fundamental parameters and the derived pressure-driven water injection well pressure analysis model, the flow coefficients for each grid cell are computed. These coefficients reflect the ease of fluid flow through the porous medium.
- (5)
- Formation of the Five-Diagonal Equation System: A system of five-diagonal equations is formulated, where each equation represents the pressure balance at a specific grid cell. This system encapsulates the governing equations of fluid flow and the interactions between adjacent grid cells.
- (6)
- Solution of the Equation System: The five-diagonal equation system is solved numerically to obtain the pressure values at different grid nodes. This step is crucial in determining the pressure distribution within the reservoir under the influence of the water injection well.
- (7)
- Explicit Saturation Calculation and Iteration: Following the pressure calculation, the saturations are updated explicitly using the new pressure values. This step involves applying the appropriate saturation–pressure relationships for the oil and water phases. The updated saturations are then used in the next iteration of the simulation.
- (8)
- Iteration and Simulation Completion: The above steps are repeated in a loop until the end of the simulation time is reached. Each iteration refines the pressure and saturation distributions, providing a more accurate representation of the reservoir’s response to the water injection well.
3. Mechanism of Enhanced Oil Recovery Through Pressure-Driven Technology
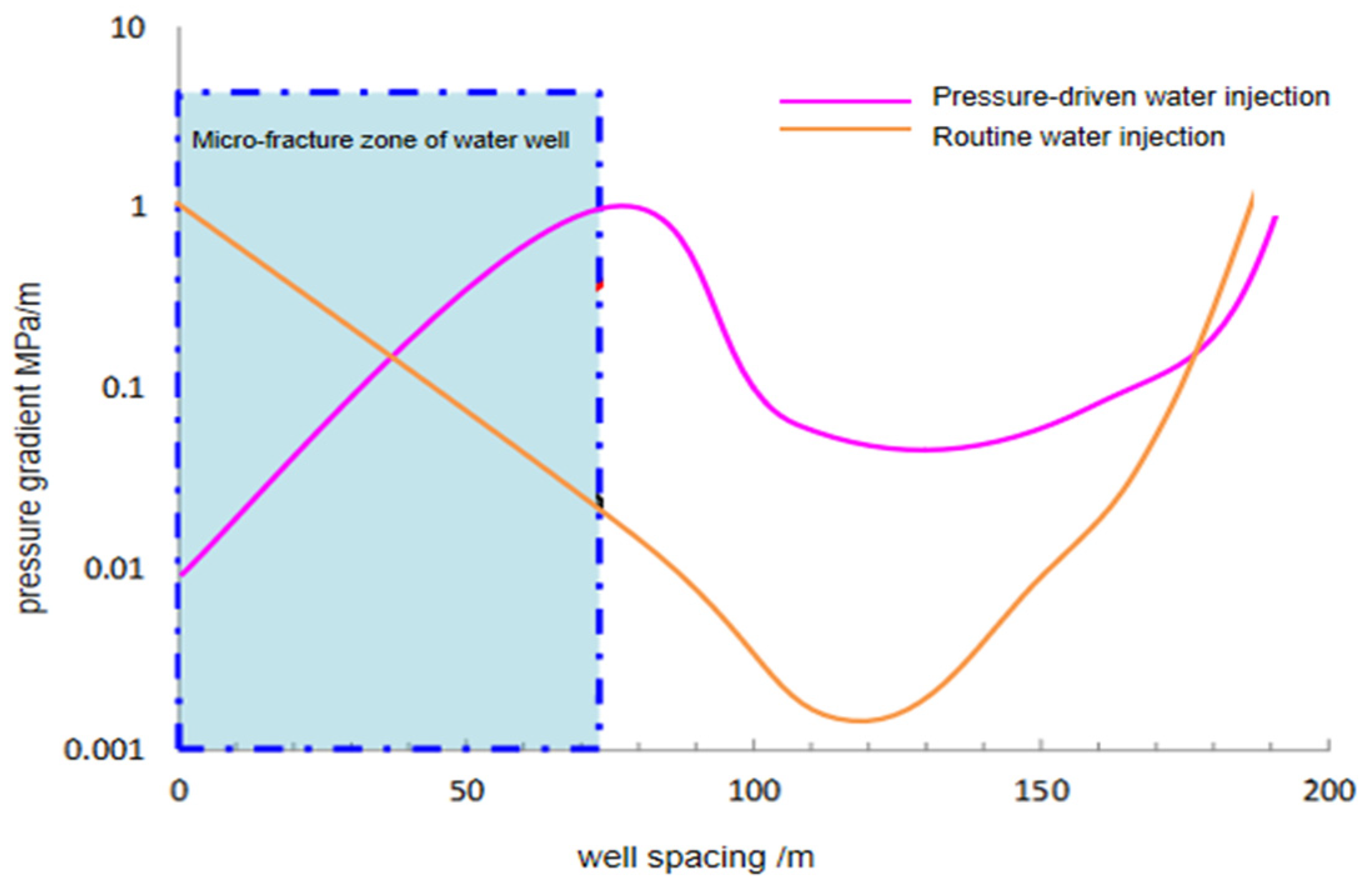
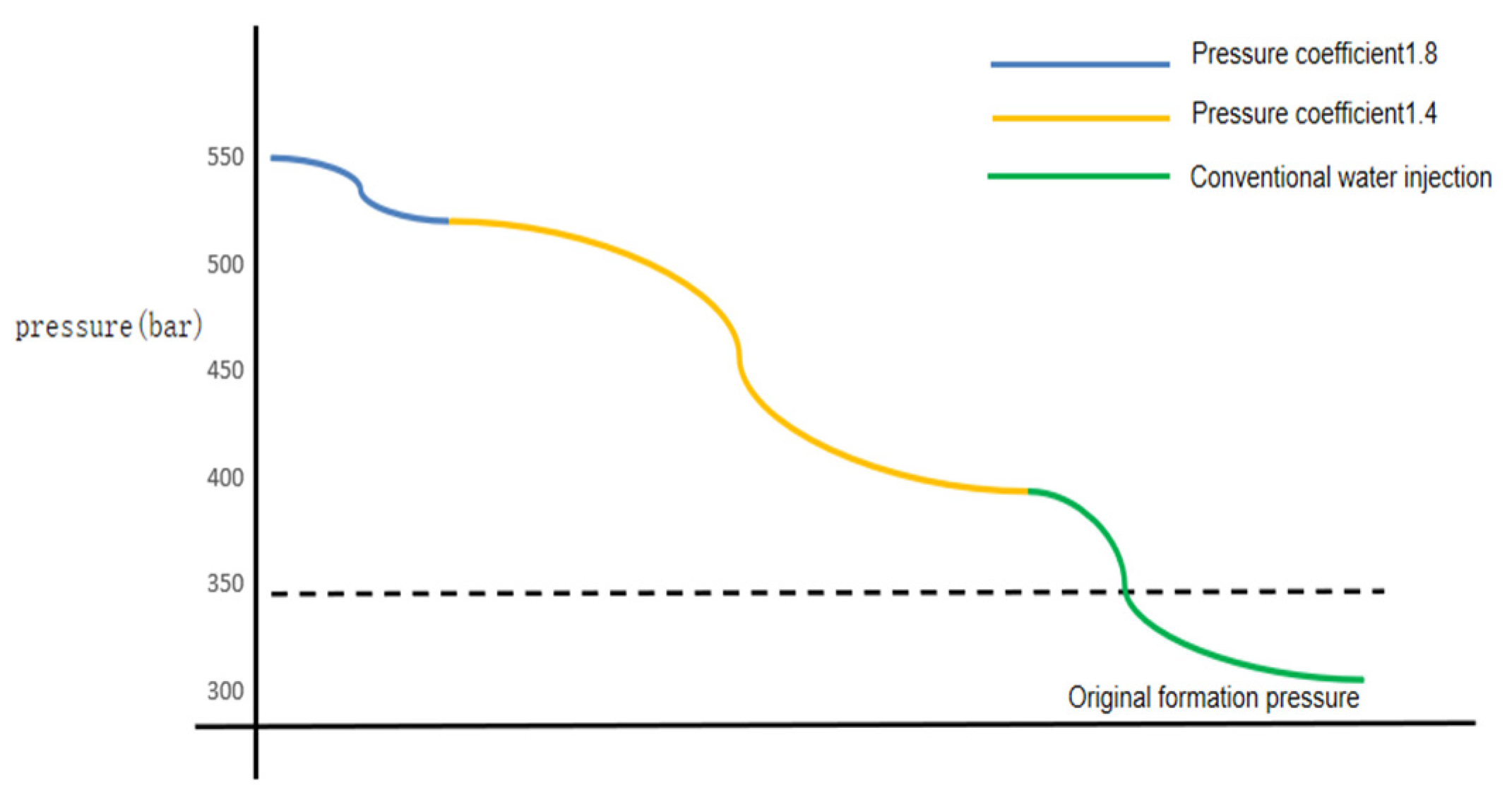
3.1. High Pressure Coefficient: The Key to Establishing a Stable and Continuous Pressure Profile for Long-Term Stable Production
- (1)
- Fluid dynamics effect: As the well spacing increases, the flow path of the fluid becomes longer, leading to an increase in fluid resistance. In this case, using pressure-driven water injection can overcome this resistance, allowing the fluid to pass through the formation more effectively.
- (2)
- Influence of microfracture zones: In the area of microfracture zones between wells, the permeability of the formation will change. Pressure-driven water injection can activate these microfractures by increasing the injection pressure, thereby further improving the fluid flow capacity.
- (3)
- Influence of matrix properties: Factors such as matrix permeability and well spacing may affect the change in pressure gradient. Higher matrix permeability may make it easier for fluids to flow through the formation, while longer well spacing may require higher pressure to maintain the same flow rate.
- η: Pressure Transmission Coefficient.
- k: Permeability, with units expressed in Darcies (Darcy, darcies) or millidarcies (mD).
- μ: Dynamic Viscosity, quantified in units of Pascal-seconds (Pa·s) or centipoise (cP), where 1 Pa·s is equivalent to 1000 cP.
- φ: Porosity, which represents the ratio of pore space to the total volume, is a dimensionless value ranging from 0 to 1.
- Ct: Total compressibility factor, encompassing the compressibility of both the fluid and the rock matrix, measured in units of reciprocal Pascals (1/Pa).
- K: Permeability, units: Darcy (Darcy, darcies) or millidarcies (millidarcies, mD).
- μ: Dynamic Viscosity, units: Pascal-seconds (Pa·s) or centipoise (centipoise, cP), where 1 Pa·s = 1000 cP.
- Δp: Pressure Gradient, units: Pascals (Pa) or bars (bar), where 1 bar ≈ 100,000 Pa.
- v: Fluid Flow Velocity, units: meters per second (m/s) or other velocity units.
- L: Medium length, meters (m).
3.2. Sequential Pressure Drive Followed by Fracturing Facilitates the Formation of Complex Redirected Fracture Networks
- (1)
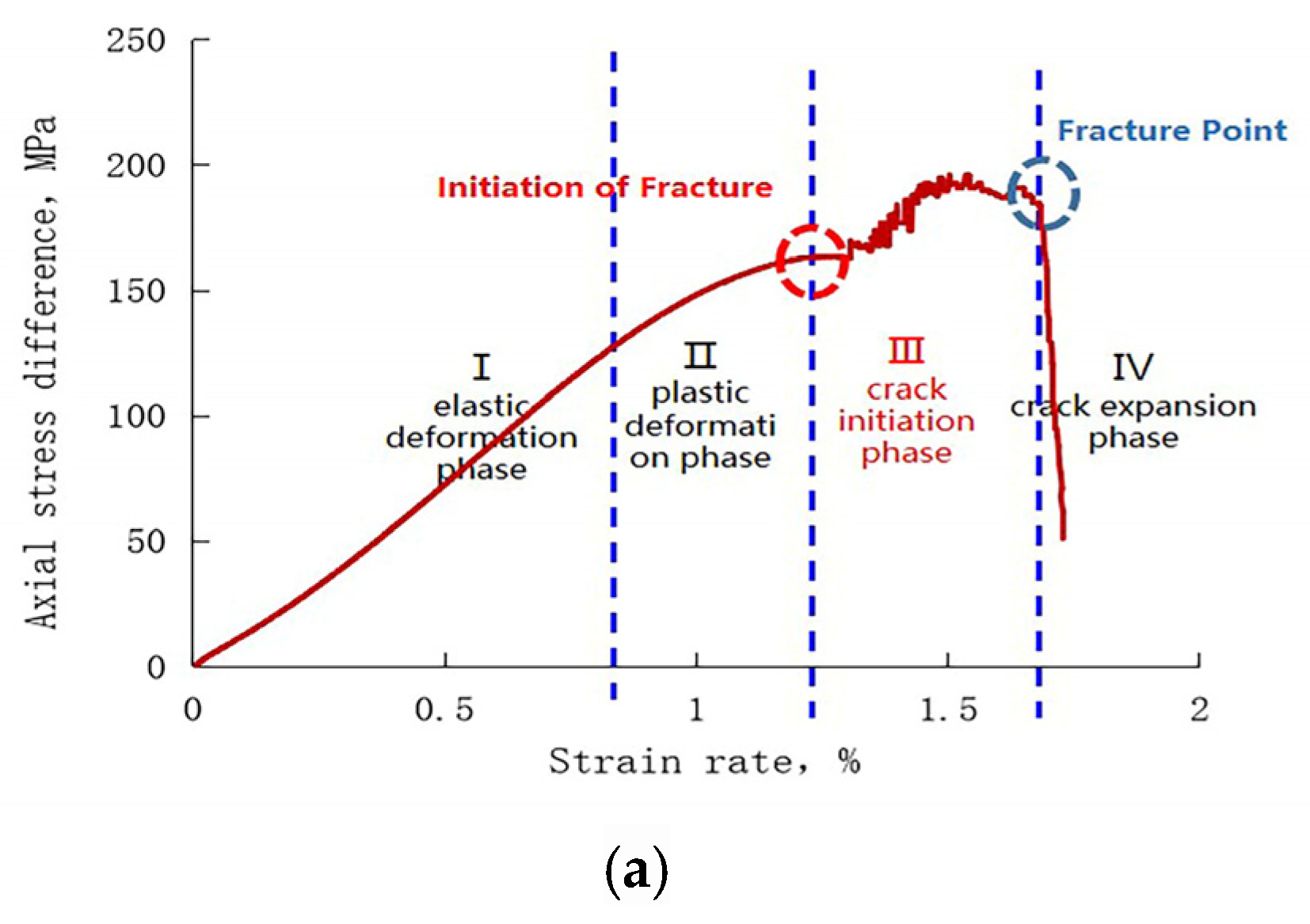
- Influence of Pore Pressure: The increase in pore pressure leads to a decrement in the compressive strength of the rock, rendering it more susceptible to fracturing. This is corroborated by Figure 6, wherein the stress differential curves under varying pore pressures illustrate a progressive decline in the rock’s load-bearing capacity as pore pressure intensifies.
- (2)
- Variations in Formation Stress: The alteration of the lithostatic ratio impacts the effective stress state of the formation. When the formation is under-compacted (with a lithostatic ratio less than 1), the rock may exhibit higher compressive strength; conversely, as the lithostatic ratio approaches or exceeds unity, the increment in pore fluid pressure results in a reduction in the rock’s effective stress, thereby diminishing its resistance to fracturing.
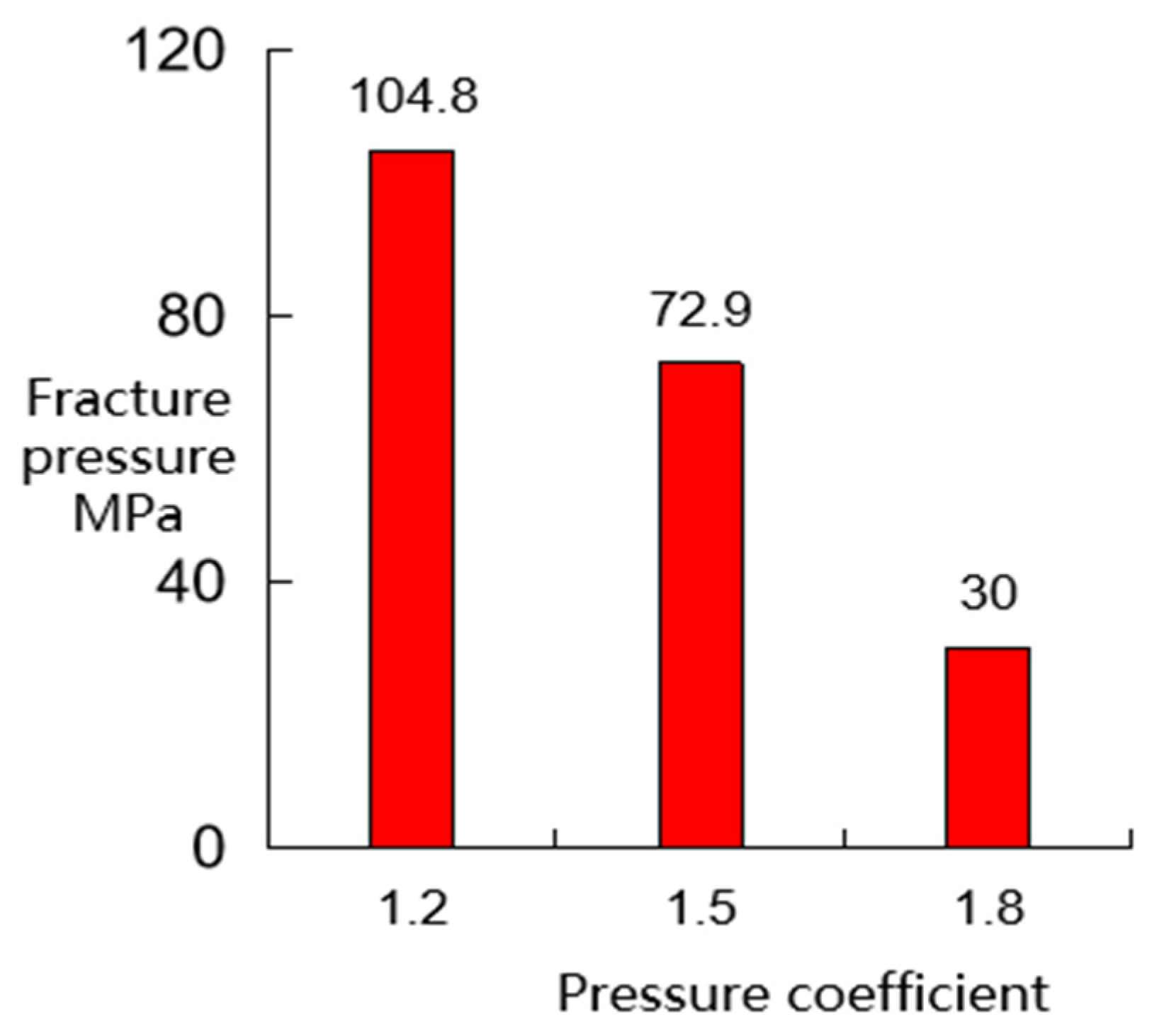
- (3)
- Support from Physical Simulation Experimentation: The relationship between the lithostatic ratio and fracturing pressure depicted in Figure 8 further endorses this perspective. As the lithostatic ratio increases from 1.0 to 1.8, a marked decrease in the rock’s fracturing pressure is observed, with a significant drop to 72.9 MPa at a lithostatic ratio of 1.5, and a further decline to 30 MPa when the ratio is 1.2.
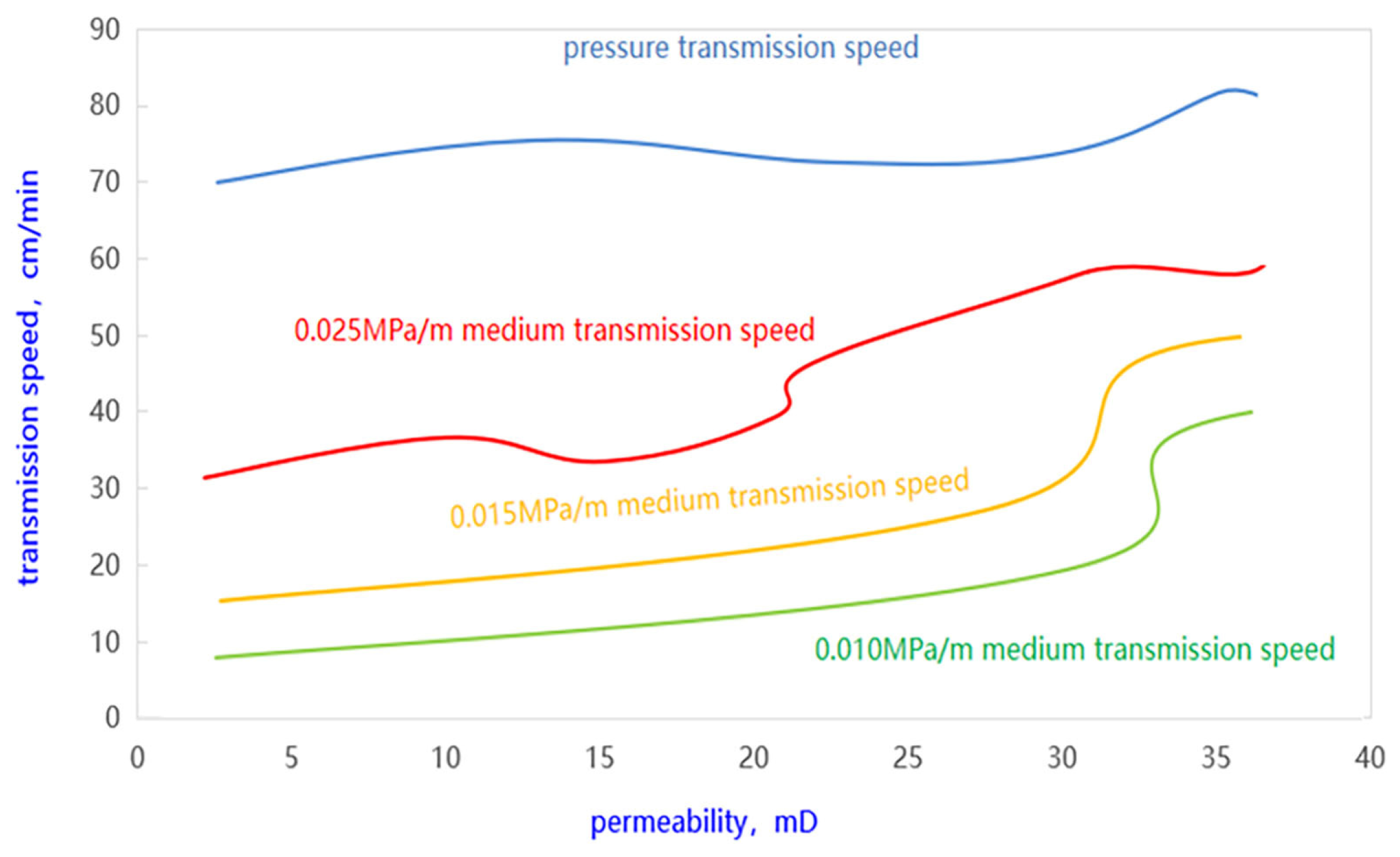
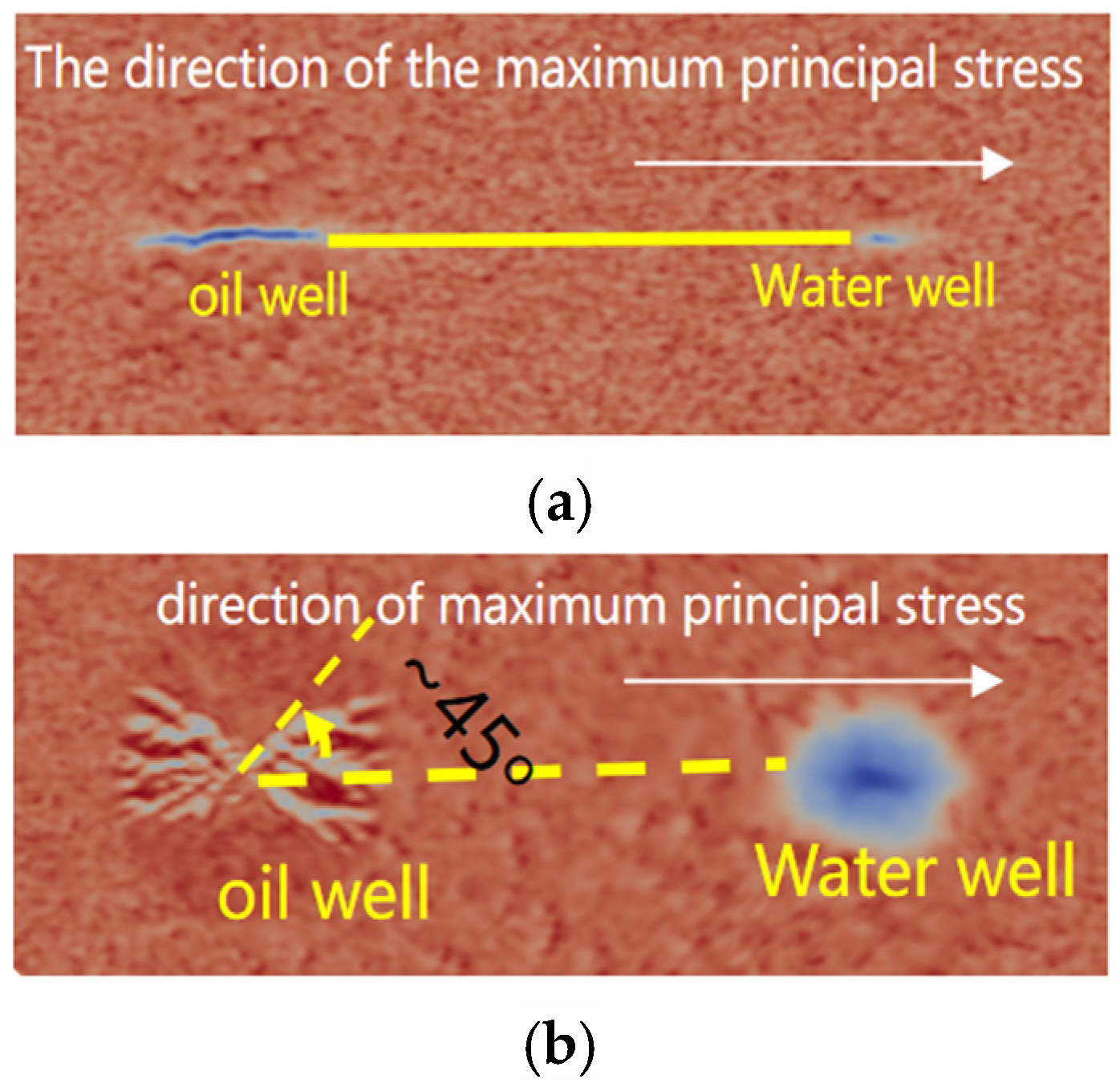
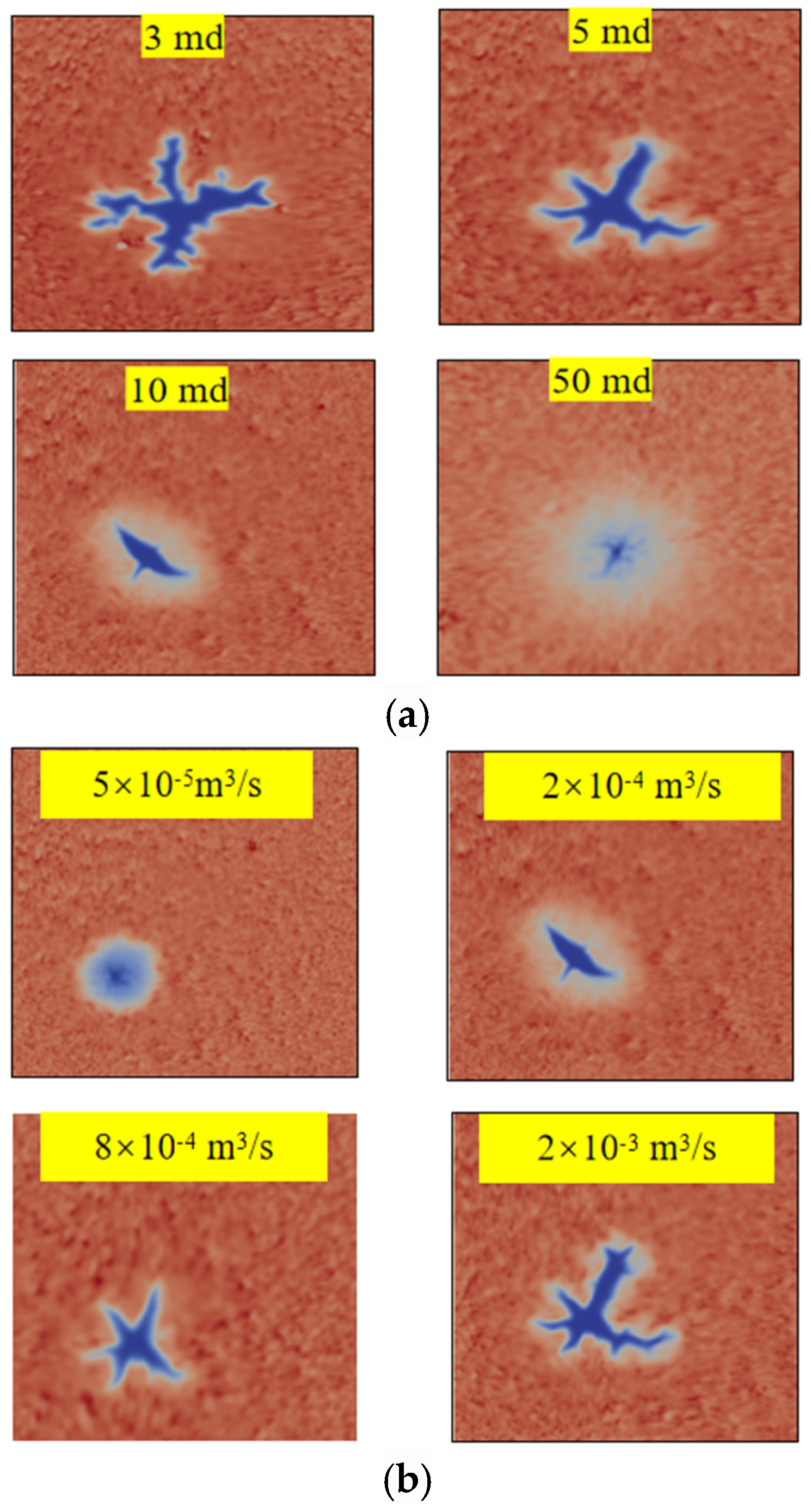
3.3. Reservoir Physical Properties and Injection Displacement Are the Main Controlling Factors Affecting the Morphology and Extension Range of Fracture Network
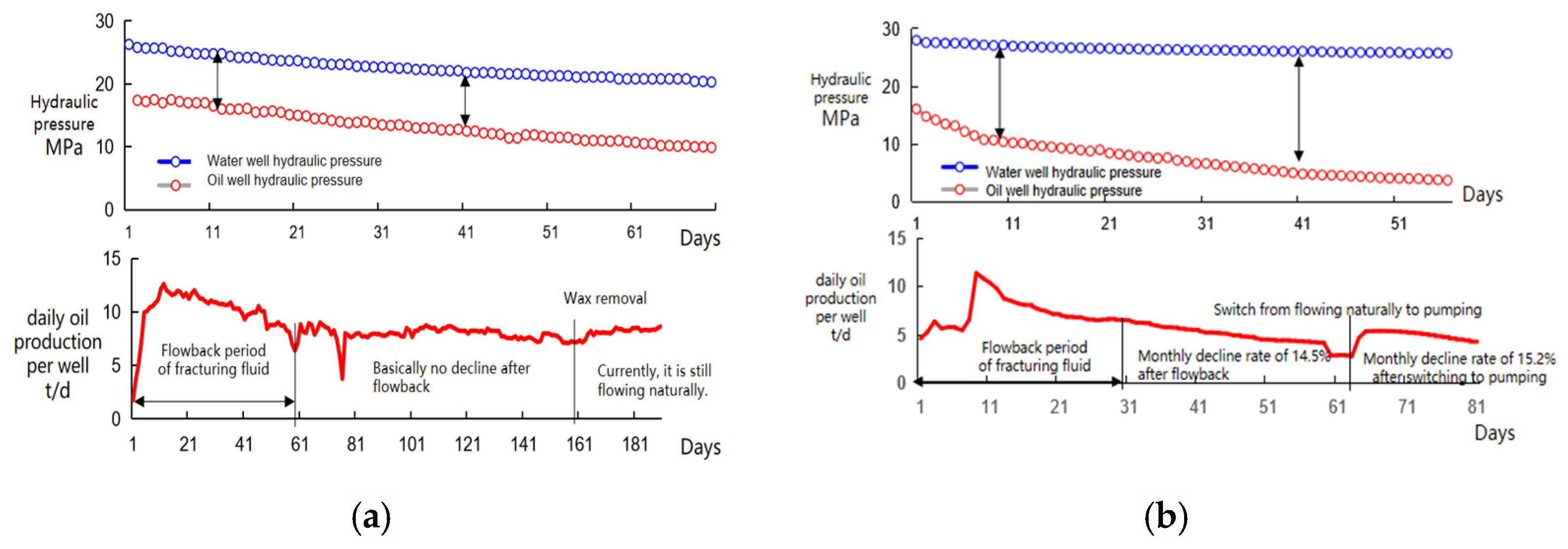
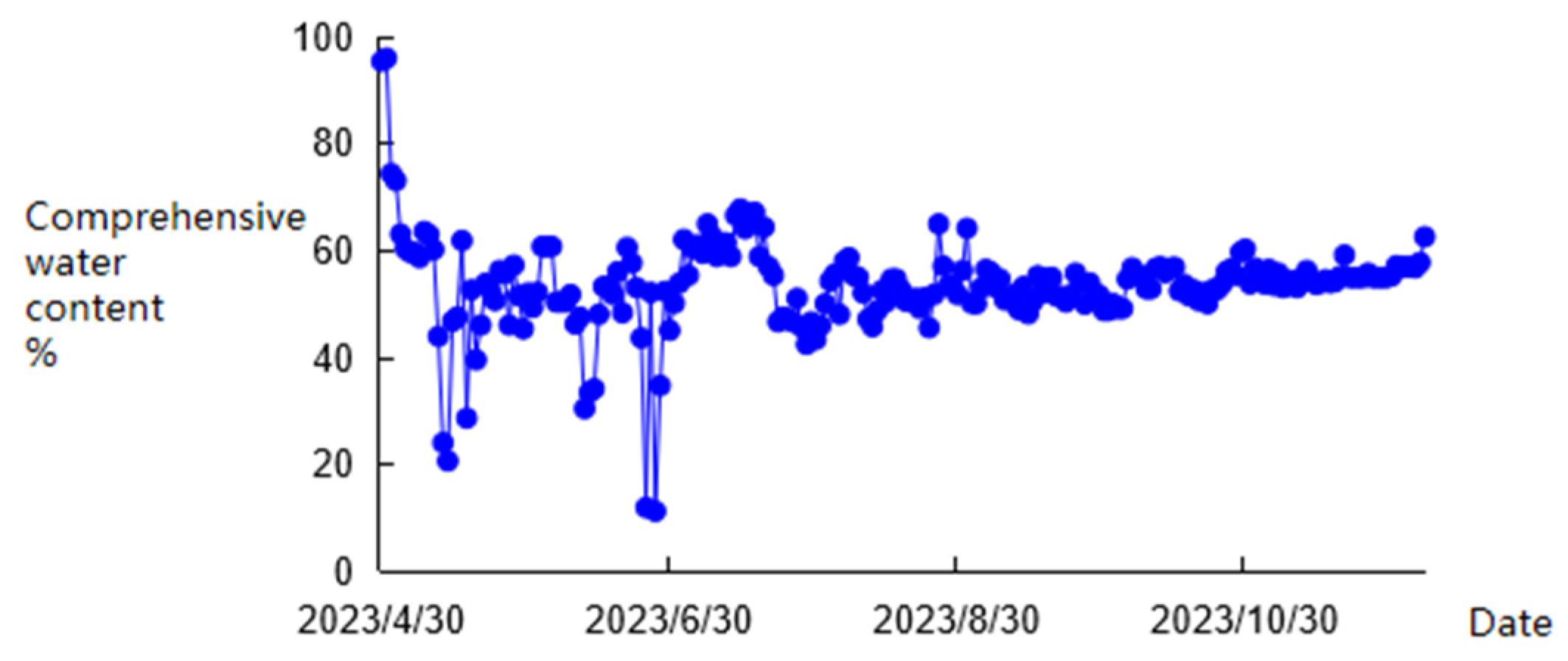
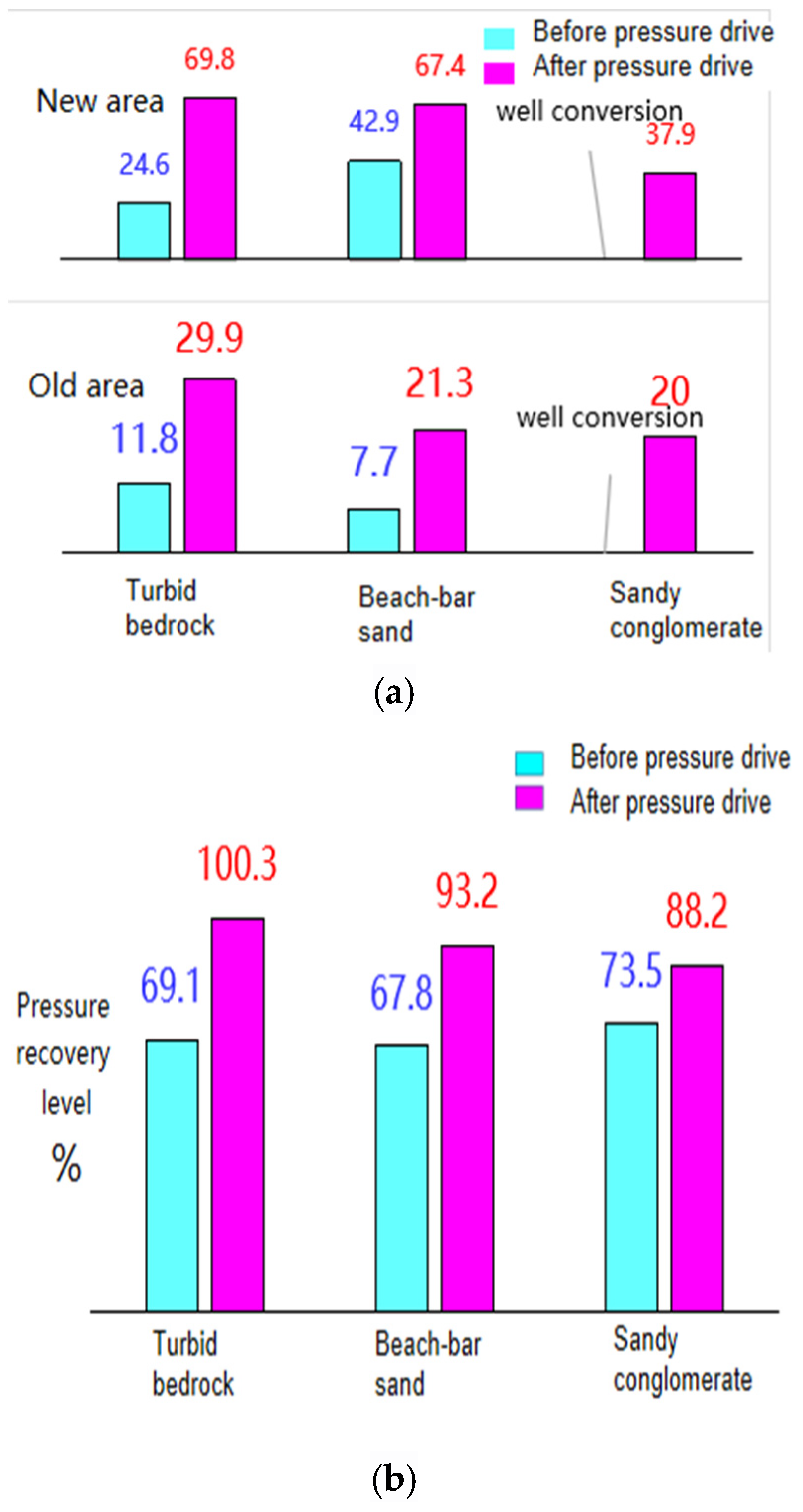
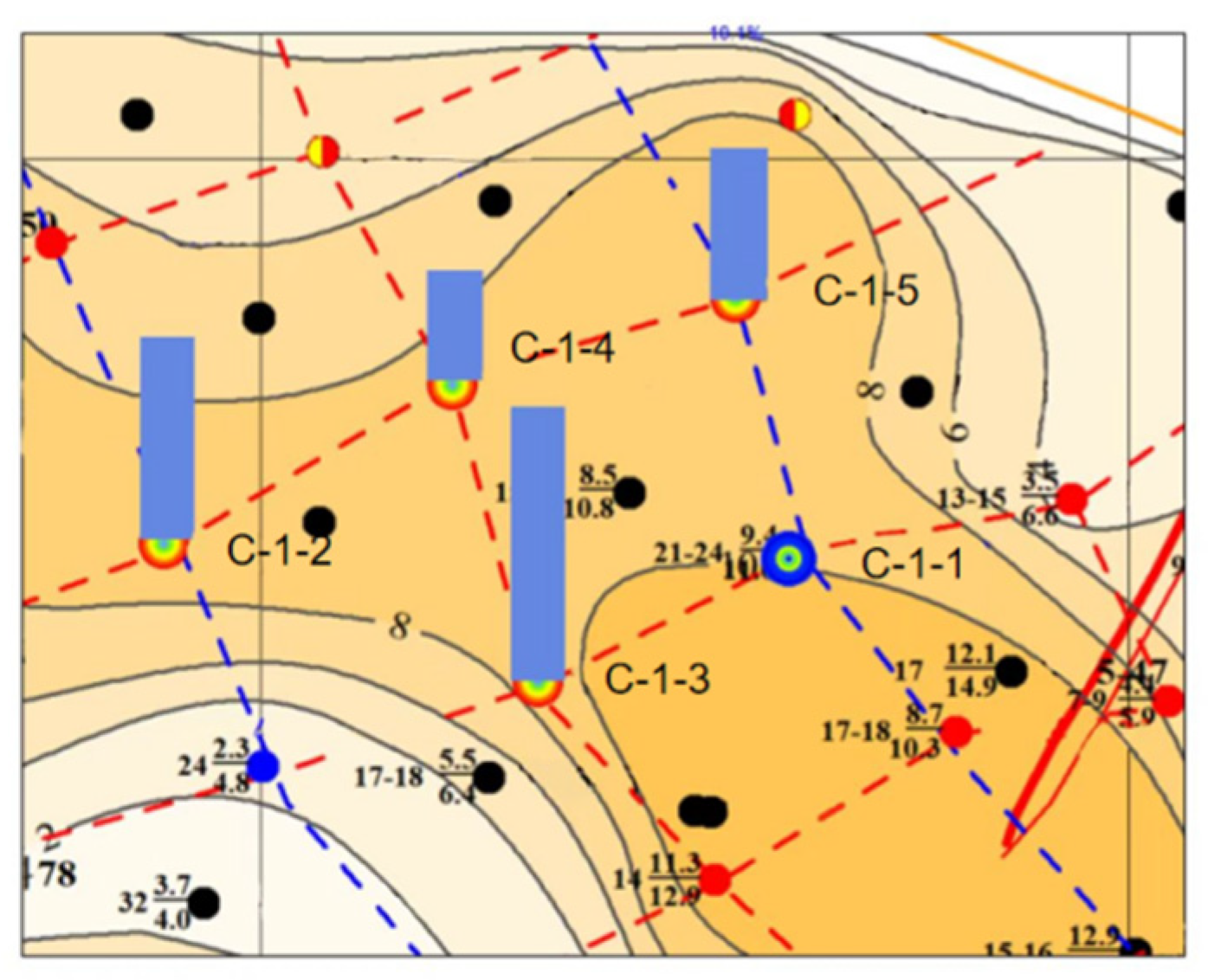
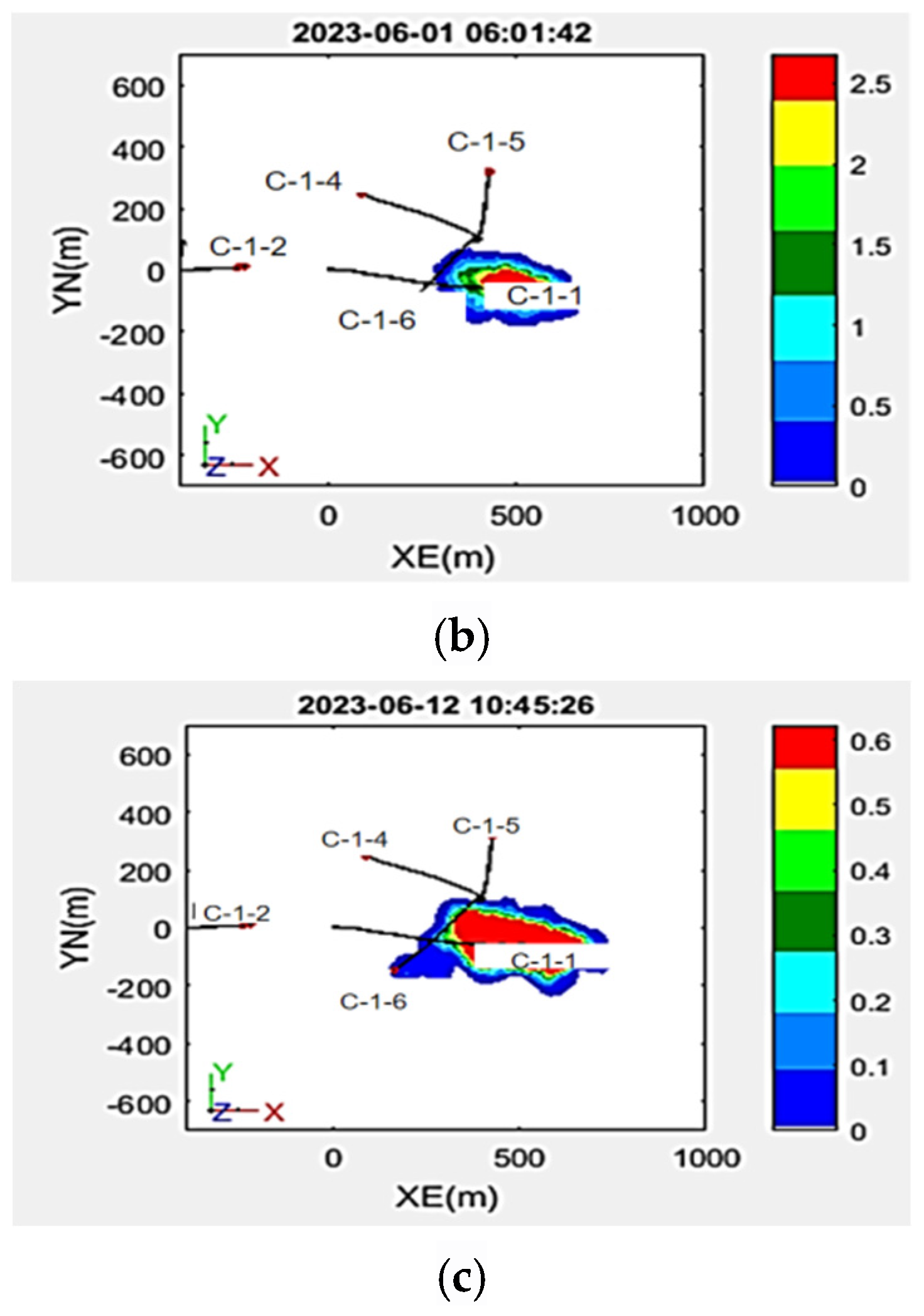
4. Research on Production Characteristics of Pressure Drive in Field Operations
5. Identify the Main Controlling Factors of Pressure-Driven Technology
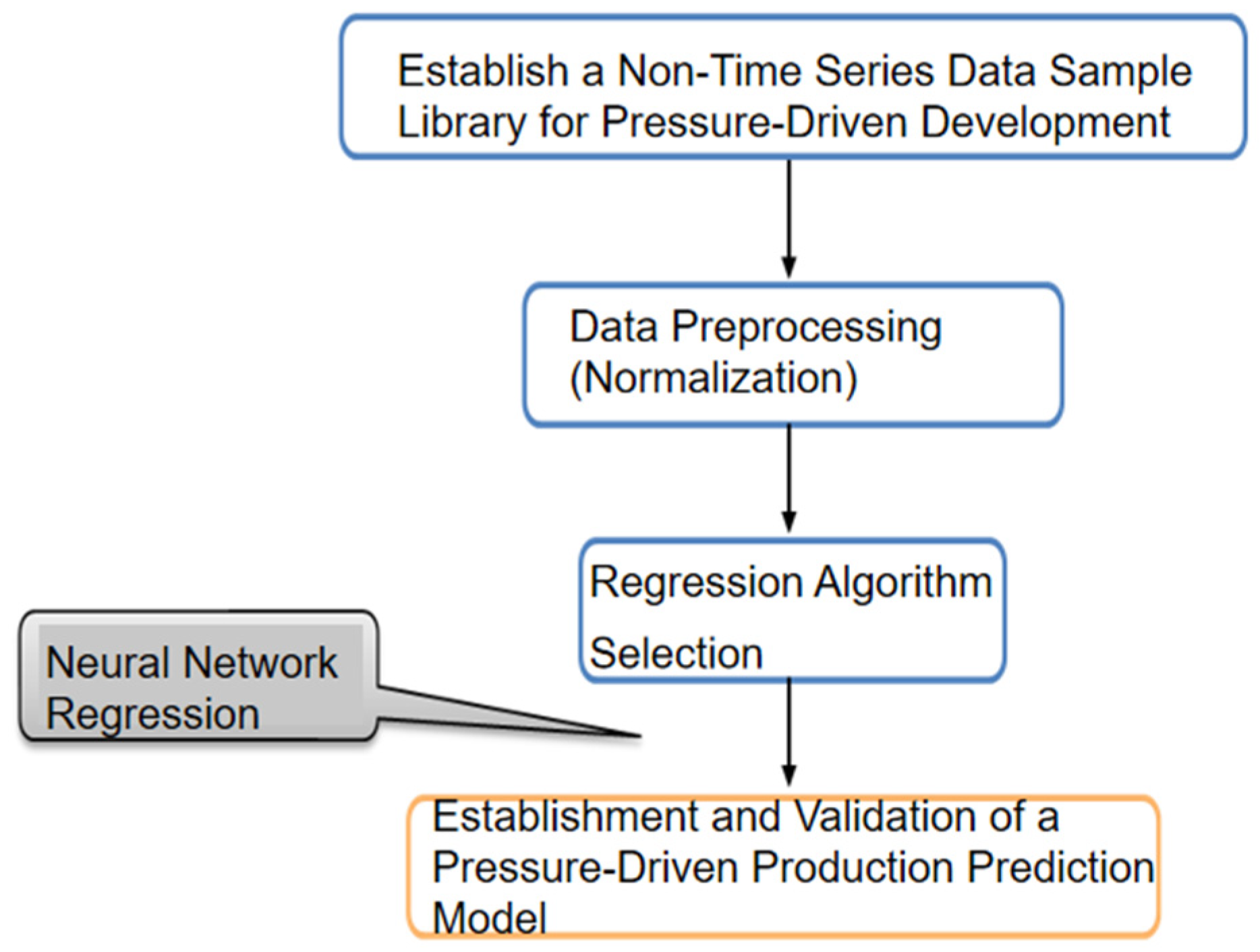
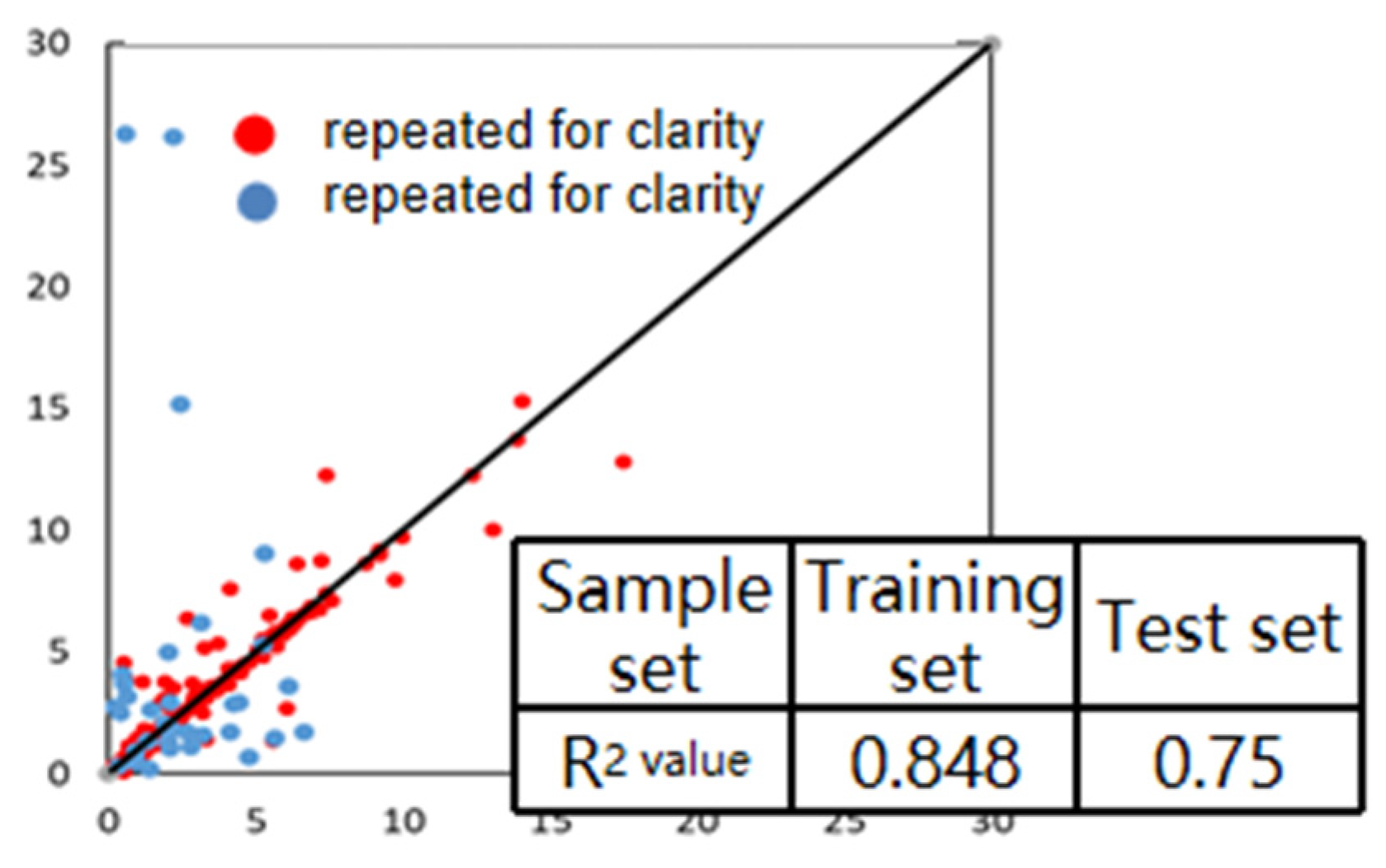
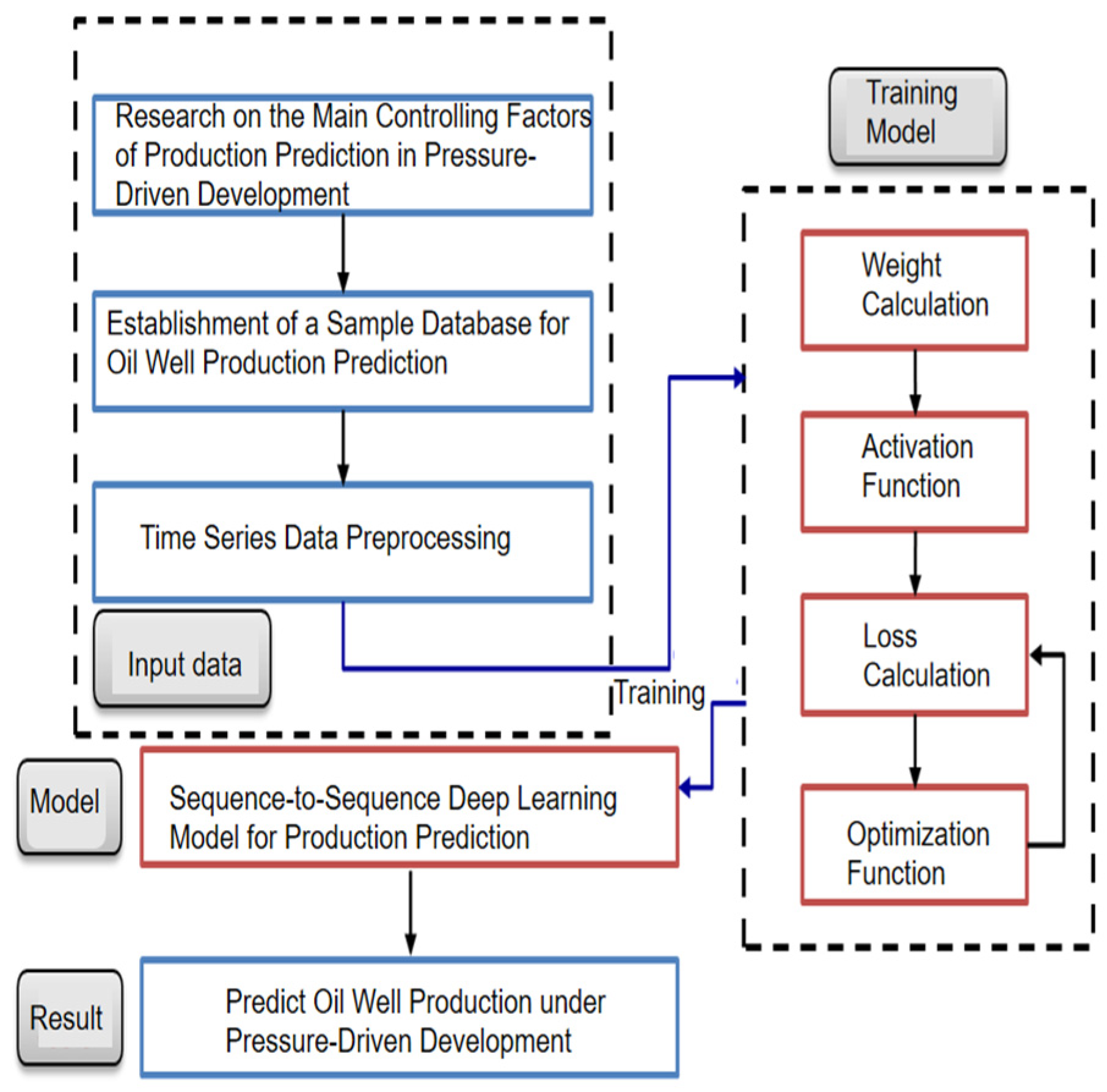
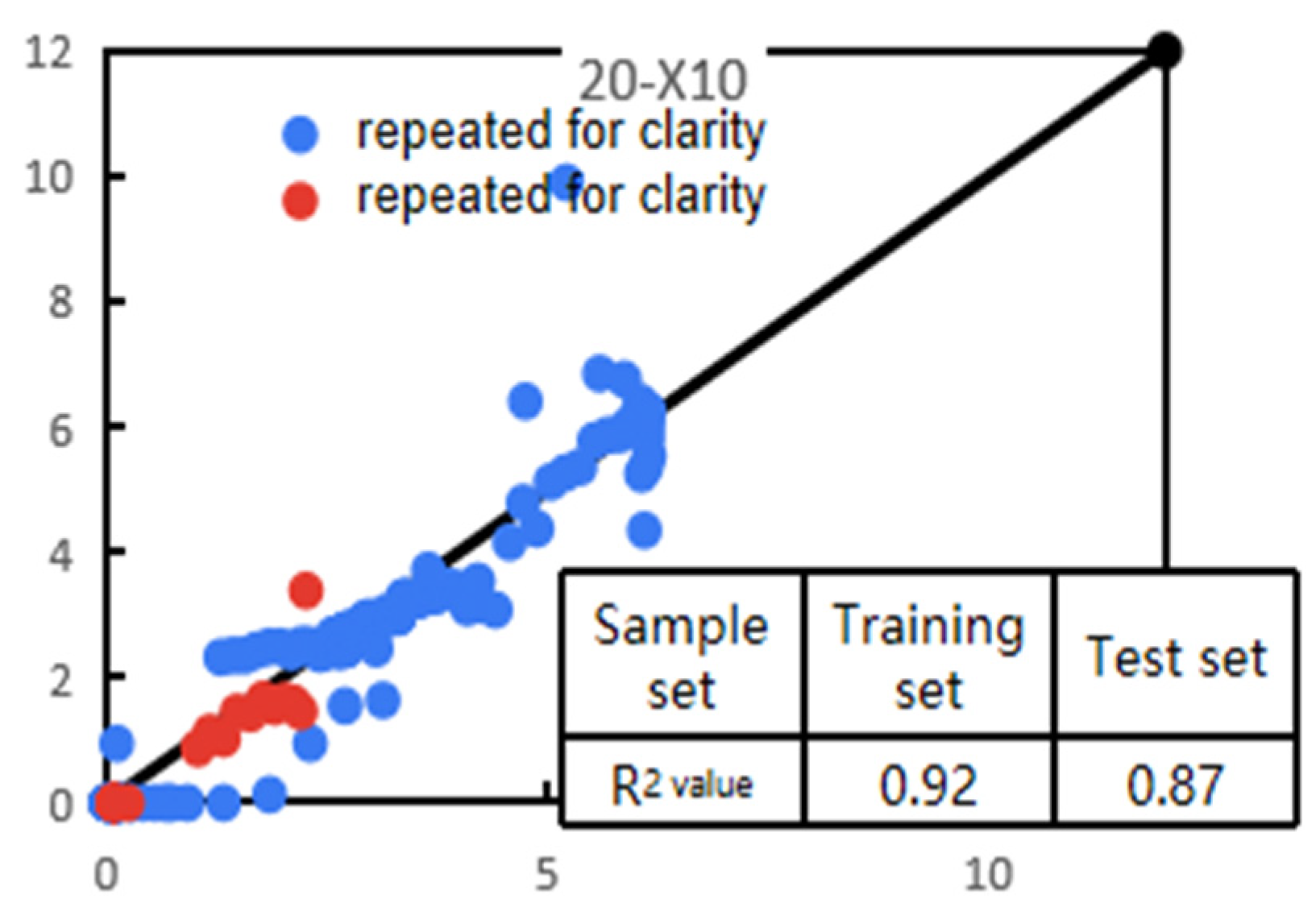
6. Prediction Model for Pressure Drive Effectiveness
- z(l) represents the activation output of the l $-th layer.
- W(l) denotes the weight matrix associated with the l $-th layer.
- a(l) is the activation output of the l-1 layer, which also serves as the input to the l layer.
- b(l) is the bias vector for the l layer.
- c is the constant term.
- ϕi is the coefficient of the autoregressive term, indicating the influence of past values of the target variable on the current value.
- p is the order of the autoregressive model.
- θ is the coefficient of the pressure term, representing the impact of pressure on the target variable.
- Pt is the pressure at the current time.
- εt is the error term, assumed to be a white noise process with a mean of zero.
7. Conclusions
- (1)
- An innovative approach to complex fracture networks was developed by investigating the strategy of pressure drive prior to fracturing, revealing that establishing a stable and continuous pressure profile with a high pressure coefficient is crucial for achieving long-term stable production, and also facilitates the formation of complex and branched fracture networks.
- (2)
- Based on the varying physical properties of reservoirs, we innovatively developed a three-dimensional pressure drive method, optimizing different injection rates to control the propagation patterns of pressure-driven fractures, ultimately leading to high-pressure leak-off and the creation of complex fracture networks.
- (3)
- The analysis identifies reservoir physical properties and injection displacement as the main controlling factors affecting the morphology and extension range of the fracture network.
- (4)
- We conducted field-scale studies on the production characteristics of pressure drive operations, utilizing big data analytic tools such as SHAP analysis and correlation analysis to retrospectively evaluate the primary controlling factors of pressure drive in both new and established fields.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Qing, L.; Yuan, C.; Qiang, L. Establishment and evaluation of strength criterion for clayey silt hydrate-bearing sediments. Energy Sources Part A Recovery Util. Environ. Eff. 2018, 40, 742–750. [Google Scholar]
- Li, Q.; Wang, Y.; Wang, F. Effect of thickener and reservoir parameters on the filtration property of CO2 fracturing fluid. Energy Sources Part A Recovery Util. Environ. Eff. 2019, 42, 1705–1715. [Google Scholar] [CrossRef]
- Guo, H.; Cheng, L.; Wang, P.; Jia, P. Water flooding experiment and law of carbonate reservoir cores with different fracture occurrences. Pet. Geol. Recovery Effic. 2022, 29, 105–112. [Google Scholar]
- Yi, Z.; Yong, Y.; Zhi, S. Physical simulation of fracturing-flooding and quantitative characterization of fractures in low-permeability oil reservoirs. Pet. Geol. Recovery Effic. 2022, 29, 143–149. [Google Scholar]
- Li, C. Principles of Reservoir Engineering; Petroleum Industry Press: Beijing, China, 2011; pp. 190–197. [Google Scholar]
- Feng, Z. The Mechanism and Parameters-Optimization of Injection Fracture Pressure Propagation for Low Permeability Oil Field. Ph.D. Thesis, China University of Petroleum, Qingdao, China, 2009. [Google Scholar]
- Jie, C.; Bin, J.; Jia, W. A novel numerical simulation of CO2 immiscible flooding coupled with viscosity and starting pressure gradient modeling in ultra-low permeability reservoir. Front. Earth Sci. 2023, 17, 884–898. [Google Scholar]
- Jie, C.; Jia, W. A new calculation method on the critical well spacing of CO2 miscible flooding in ultra-low permeability reservoirs. J. Porous Media 2021, 24, 59–79. [Google Scholar]
- Guan, Z.; Xiao, X.; Qing, Z. Study on hydraulic fracture propagation mechanism of pore-elastic media based on time-step linear superposition method. Drill. Prod. Technol. 2021, 44, 88–92. [Google Scholar]
- Joseph, C.; Figueroa, A.A.; Ignacio, L.J. Self Adjusting Pressure Drive Shaft. Patent US20030226874A1, 11 December 2002. [Google Scholar]
- Stines, J.R. Rotational Pressure Drive for a Medical Syringe. Patent US07/960022, 1 March 1994. [Google Scholar]
- Pu, C.; Liu, Z.; Pu, G. On the Factors of Impact Pressure in Supercritical CO2 Phase-Transition Blasting—A Numerical Study. Energies 2022, 15, 8599. [Google Scholar] [CrossRef]
- Chang, X.; Yong, Z. Analysis of Oil Production and Fracturing Technologies for Low-Permeability Reservoirs. Petrochem. Technol. 2024, 31, 100–102. [Google Scholar]
- Ze, R. High-efficient Development of Low-permeability Reservoir with Geology and Engineering Integration: A Case Study of N25 Block in Dongying Sag. Drill. Prod. Technol. 2024, 47, 90–96. [Google Scholar]
- Shu, L.; Ding, Z.; Yong, W. Experimental Study on Micro-Nano Emulsion Injection Enhancement Technology for Low-Permeability Reservoirs. Petrochem. Technol. 2024, 53, 553–558. [Google Scholar]
- Duo, P. Research on Enhanced Oil Recovery Technologies for Low-Permeability Reservoirs. Petrochem. Technol. 2023, 30, 50–52. [Google Scholar]
- Liu, J.; Yao, Y.B.; Elsworth, D. Morphological complexity and azimuthal disorder of evolving pore space in low-maturity oil shale during in-situ thermal upgrading and impacts on permeability. Pet. Sci. 2024, 1, 1–20. [Google Scholar] [CrossRef]
- Jin, Y. Fracturing Technology and Development Trends in Low-Permeability Oilfields. China Pet. Chem. Stand. Qual. 2023, 43, 175–177. [Google Scholar]
- Yong, Y.; Shi, Z.; Xiao, C. Practice and understanding of pressure drive development technology for low-permeability reservoirs in Shengli Oilfield. Pet. Geol. Recovery Effic. 2023, 30, 61–71. [Google Scholar]
- Bai, X.F.; Li, J.H.; Liu, X.; Wang, R.; Ma, S.; Yang, F.; Li, X.; Liu, J. Evolution of the Anisotropic Thermo-physical Performance for LowMaturity Oil Shales at an Elevated Temperature and Its Implications for Re-storing Oil Development. Energy Fuels 2024, 38, 15216–15224. [Google Scholar] [CrossRef]
- Zhang, S.Q.; Liu, J.; Li, L.; Kassabi, N.; Hamdi, E. Petrophysical and Geochemical Investigation-Based Methodology for Analysis of the Multilithology of the Permian Longtan Formation in Southeastern Sichuan Basin, SW China. Energies 2024, 17, 766. [Google Scholar] [CrossRef]
- Li, L.; Ma, S.; Liu, X.; Liu, J.; Lu, Y.; Zhao, P.; Kassabi, N.; Elsworth, D. Coal measure gas resources matter in China: Review, challenges, and perspective. Phys. Fluids 2024, 36, 071301. [Google Scholar] [CrossRef]
- Chuan, C.; Huai, L.; Zhong, W. Analysis of pressures in water injection wells considering fracture influence induced by pressure-drive water injection. Pet. Reserv. Eval. Dev. 2023, 13, 686–694. [Google Scholar]
- Yi, L.; Feng, W.; Yu, W. Mechanism of Enhanced Oil Recovery by Pressure Driving in Medium-Low Permeability Reservoirs. Pet. Explor. Dev. 2022, 49, 752–759. [Google Scholar]
- Xiao, C. Practice and Understanding of Pressure-Driven Water Injection Technology in Binnan. Inn. Mong. Petrochem. Ind. 2024, 50, 43–46. [Google Scholar]
- Feng, W.; He, X.; Yi, L. Mechanism of Enhanced Oil Recovery by Pressure Driving Technology with High Pressure Drop Adsorption. Acta Pet. Sin. 2024, 45, 403–411. [Google Scholar]
- Qi, H.; Guo, P.; Yan, L. Pressure-Driven Water Injection Technology and Development Directions for Low-Permeability Reservoirs. Contemp. Petrochem. 2023, 31, 26–29. [Google Scholar]
- Liu, Y.; Yamada, Y. The Characteristics and Design of Hybrid Pressure Drive System with Turbofan and Switch Valve for Laminated Foam-based Soft Actuator. In Proceedings of the JSME annual Conference on Robotics and Mechatronics (Robomec), Osaka, Japan, 6–8 June 2021; pp. 2A1–D02. [Google Scholar] [CrossRef]
- Chiodini, G.; Paonita, A.; Aiuppa, A. Magmas near the critical degassing pressure drive volcanic unrest towards a critical state. Nat. Commun. 2016, 7, 13712. [Google Scholar] [CrossRef] [PubMed]
- Velarde, E.; Ezcurra, E.; Horn, M.H. Warm oceanographic anomalies and fishing pressure drive seabird nesting north. Sci. Adv. 2015, 1, e1400210. [Google Scholar] [CrossRef]
- Ishizuka, S.; Hamasaki, T.; Koumura, K. Measurements of flame speeds in combustible vortex rings: Validity of the back-pressure drive flame propagation mechanism. Proc. Symp. Combust 1999, 27, 727–734. [Google Scholar] [CrossRef]
- Nakazawa, H.; Yokota, S.; Kita, Y. A Constant Pressure Drive System for Engine-Flywheel Hybrid Vehicles (First Report, Simulations for Fuel Saving Analysis of Hybrid Vehicles Using a Flywheel Pump/motor). J. Jpn. Hydraul. Pneum. Soc. 1996, 27, 513–518. [Google Scholar] [CrossRef]
- Zhang, Z.; Xu, S.; Gou, Q.; Li, Q. Reservoir Characteristics and Resource Potential of Marine Shale in South China: A Review. Energies 2022, 15, 8696. [Google Scholar] [CrossRef]
- Han, Z.; Dong, M.A.; Hou, B.W. Post-earthquake hydraulic analyses of urban water supply network based on pressure drive demand model. Sci. Sin. Technol. 2019, 49, 351–362. [Google Scholar] [CrossRef]
- Jie, C.; JU, B.; Lyu, G. A computational method of critical well spacing of CO2 miscible and immiscible concurrent flooding. Pet. Explor. Dev. Online 2017, 44, 815–823. [Google Scholar]
- Jie, C.; Bin, J.; Wen, C. Laboratory simulation of CO2 immiscible gas flooding and characterization of seepage resistance. Front. Earth Sci. 2023, 17, 797–817. [Google Scholar]
- Jun, Z.; Peng, Y.; Su, W. 3D numerical simulation of fracture dynamic propagation in hydraulic fracturing of low-permeability reservoir. Acta Pet. Sin. 2010, 31, 119–123. [Google Scholar]
- Shuai, T.; Yong, H.; Jie, Z. Reasonable pattern well spacing deployment of lens lithologic reservoirs with low permeability. Lithol. Reserv. 2018, 30, 116–123. [Google Scholar]
- Ji, H. Application of advanced water injection inflow production relation model in low-permeability reservoir. Spec. Oil Gas Reserv. 2020, 27, 92–97. [Google Scholar]
- Quan, Z.; Ming, L.; Zi, Z. Application of volume fracturing technology in tight oil reservoirs of Shengli oilfield. China Pet. Explor. 2019, 24, 233–240. [Google Scholar]
- Song, F.; Ding, H.; Wang, Y.; Zhang, S.; Yu, J. A Well Production Prediction Method of Tight Reservoirs Based on a Hybrid Neural Network. Energies 2023, 16, 2904. [Google Scholar] [CrossRef]








Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, H.; Ju, B. Research on the Mechanism and Prediction Model of Pressure Drive Recovery in Low-Permeability Oil Reservoirs. Energies 2024, 17, 5253. https://doi.org/10.3390/en17215253
Liu H, Ju B. Research on the Mechanism and Prediction Model of Pressure Drive Recovery in Low-Permeability Oil Reservoirs. Energies. 2024; 17(21):5253. https://doi.org/10.3390/en17215253
Chicago/Turabian StyleLiu, Haicheng, and Binshan Ju. 2024. "Research on the Mechanism and Prediction Model of Pressure Drive Recovery in Low-Permeability Oil Reservoirs" Energies 17, no. 21: 5253. https://doi.org/10.3390/en17215253
APA StyleLiu, H., & Ju, B. (2024). Research on the Mechanism and Prediction Model of Pressure Drive Recovery in Low-Permeability Oil Reservoirs. Energies, 17(21), 5253. https://doi.org/10.3390/en17215253




