Machine Learning-Aided Dual-Function Microfluidic SIW Sensor Antenna for Frost and Wildfire Detection Applications
Abstract
1. Introduction
- In general, the contributions discussed in previous works have primarily focused on detecting high temperatures, such as in [23], where the detection range was 50 °C to 1050 °C. In addition, efforts were applied to non-weather-related applications, making their approach more generalized. While the system in [17] detected frost within a temperature range of 0 °C to 20 °C, it had an open structure, making it susceptible to coupling and interference, as will be explained in the following point.
- Open structures, such as patch antennas, make them susceptible to the coupling and interference of adjacent elements and environmental influences. Previous designs were mainly patch [26,31], loop [30], or slot [17,29]. Hence, a SIW antenna structure was selected for this work. The SIW antenna is considered a closed structure because it confines electromagnetic waves within the substrate, limiting energy leakage to the surrounding environment. This is achieved through the use of metalized vias or posts, which form sidewalls analogous to the metallic walls in a traditional rectangular waveguide. These vias act as boundaries, guiding the waves within the substrate and preventing radiation losses.
- Evaluations were based only on testing the antenna resonance shift. This brings a considerable level of uncertainty. Hence, a ML model was developed to increase the certainty of predictions by providing comprehensive information, capturing distinctive signatures, reducing ambiguity, enhancing robustness to noise, and improving generalization capabilities. This leads to more confident and reliable predictions regarding environmental states like frost or wildfire.
- Non-antenna sensors are limited by their functionality of sensing only, which means that an antenna must also be used with them. This increases hardware and power consumption since the sensors and antennas are separate, each consuming energy independently. The energy usage can be higher due to the combined needs of both components. Moreover, antennas can be also developed to harvest energy.
- Unfortunately, all of these challenges are amplified at low temperatures, where the complex permittivity of water increases, causing small changes in resonance frequency. Consequently, manually extracting the environmental state becomes limited and difficult.
- To begin with the wireless sensor system, the proposed sensor antenna uses a 5.7 GHz band as the operating frequency. The decision to select such a frequency was made after careful consideration of its performance under various climatic conditions, especially those associated with frost and wildfire detection with low power consumption. In general, the 5.7 GHz band lies within the sub-6 band (<6 GHz); such a band offers a favorable balance between stable performance, availability, simplicity, and energy management, making it an appropriate choice for wireless sensor antenna applications compared with high-frequency bands. Unlike antennas operating in relatively low-frequency bands, such as the sub-6 band, high-frequency antennas increase power consumption due to the greater heat generated. As a result, energy systems must continuously adapt to manage this higher consumption, which becomes particularly challenging in complex or harsh environments [43,44]. Therefore, the selection of the sub-6 band can be attributed to several factors. Firstly, (1) the sub-6 band falls within the industrial, scientific, and medical (ISM) band, which is widely allocated for non-licensed use globally. This regulatory framework facilitates easier deployment and operational flexibility across different geographical regions. Furthermore, sub-6 GHz aligns with existing standards and technologies commonly employed in wireless sensor networks and IoT applications [40]. This compatibility ensures interoperability with other sensor systems and infrastructure, facilitating seamless integration into broader disaster management frameworks and data analytics contexts. Secondly, (2) the sub-6 GHz band’s frequencies can effectively propagate through the atmosphere while providing sufficient penetration for detection in conditions like fog, snow, and smoke, which are common in frost and wildfire scenarios [37,44]. Unlike high-frequency bands (e.g., mm wave bands), the sub-6 GHz band has lower interference and minimal atmospheric absorption, making the overall sensor system more robust to noise [45]. This is particularly advantageous in environments prone to electromagnetic interference from natural and human-made sources, thereby minimizing false alarms and improving detection accuracy. Lastly, (3) although lower frequencies are efficient, choosing very low frequencies increases the size of the antenna, complicating its installation process and thus increasing the complexity of the system. Therefore, in this study, the proposed design utilizes the upper frequency range within the sub-6 GHz band at 5.7 GHz.
- Regarding the antenna/resonator design, this study is the first to adopt the SIW cavity for wireless frost and wildfire detection applications. By doing so, this sensor antenna provides a self-isolated system with low losses, eliminating the coupling and interference of the adjacent elements and environmental influences. This ensures that the decision-making and monitoring processes of the sensed values are reliable and highly accurate.
- In terms of material under test (MUT), the proposed design utilizes a fixed microscale water volume of only 50 μL using microfluidic technology. Unlike study [31], such a configuration enhances the penetration and interaction between the electric field distributions and the water sample. Microfluidic sensors can perform detection processes on a small scale, resulting in efficient use of resources and energy while preventing MUT wastage and leakage.
- Regarding the sensing area, the sensor antenna employs interdigital capacitor approaches [12], creating a large distributed capacitance that maximizes the sensitivity and interaction with the water sample. Additionally, the conductive fingers of the interdigital capacitors are arranged transversely to ensure uniform interaction with different parts of the water sample while occupying a small area. This arrangement enhances and linearizes the sensory response of the antenna’s parameters in the region of interest.
- Regarding the sensing range, the proposed sensor can measure and detect a wide range of temperatures starting from 0 °C. This range represents frost and wildfire, while also responding to the negative temperature range that makes ice accumulation possible. In addition, using water as the material under test significantly enhances the sensing range, as water can monitor both low and high temperatures, ranging from 0 °C to 50 °C. This contrasts with the solid materials mentioned in previous studies, which are limited to specific temperature ranges. Water’s broad sensing capabilities make it a highly suitable choice for early warning detection systems.
- Our study adopts several machine learning models based on classification tasks—artificial neural networks (ANNs), random forest (RF), decision trees (DTs), support vector machines (SVMs), and Gaussian process (GP)—to convert the simulated SIW parameters (resonance frequency, upper frequency, and lower frequency) into three categories (Early Frost, Normal, Early Wildfire). Including resonance frequency, upper frequency, and lower frequency features in the training of these models can increase the certainty of predictions by providing comprehensive information, capturing distinctive signatures, reducing ambiguity, enhancing robustness to noise, and improving generalization capabilities. This leads to more confident and reliable predictions regarding environmental states like frost or wildfire.
- In terms of the single multi-function sensor antenna: despite the low likelihood of frost during an active wildfire, and because frost and wildfire represent contrasting climatic extremes (hot versus cold), there are several practical reasons for proposing this sensor. This sensor provides year-round utility in monitoring environmental changes, especially for those regions that experience frost in the winter and wildfires in the summer [2]. Therefore, having a single sensor for frost in colder months and wildfire in warmer months helps ensuring early detection, enabling preventive measures to mitigate damage. This dual capability underlines the valuable contribution of creating a sensor that is adaptable to a wide range of temperature-sensitive scenarios (not only for crop risks), providing enhanced reliability and resilience in various industrial and environmental applications [3].
- Regarding low power consumption, the proposed sensor can utilize low-power wireless communication protocols such as LoRaWAN, Zigbee, or Bluetooth Low Energy (BLE). These protocols are specifically designed to use minimal power while transmitting small amounts of data over long distances. Compared to traditional temperature sensors (thermometers) that are collaborated with an external RF system, the proposed sensor antenna simultaneously senses and transmits data, eliminating the energy overhead typically required for separate data storage and later transmission [9]. In addition, traditional temperature sensors need external circuits for modulation, demodulation, and digital-to-analog converter systems; such a configuration raises the need for power.
- This study offers promising solutions for smart IoT systems, particularly for those interested in remotely monitoring environmental conditions to prevent frost and wildfire disasters and optimize energy systems. It provides reliability and the ability to integrate with smart grid systems. Additionally, this design is a first step for those interested in predictive maintenance and optimizing the operation of renewable energy sources, such as protecting solar panels from frost and low temperatures. The proposed sensors can be utilized for the real-time monitoring of environmental conditions, providing accurate data on energy use and environmental impact to help optimize energy management strategies. Furthermore, integrating these sensors into smart grid systems can enhance the monitoring of energy flows and distribution, leading to more efficient energy management.
2. Sensor Design and Near-Field Operation Principle
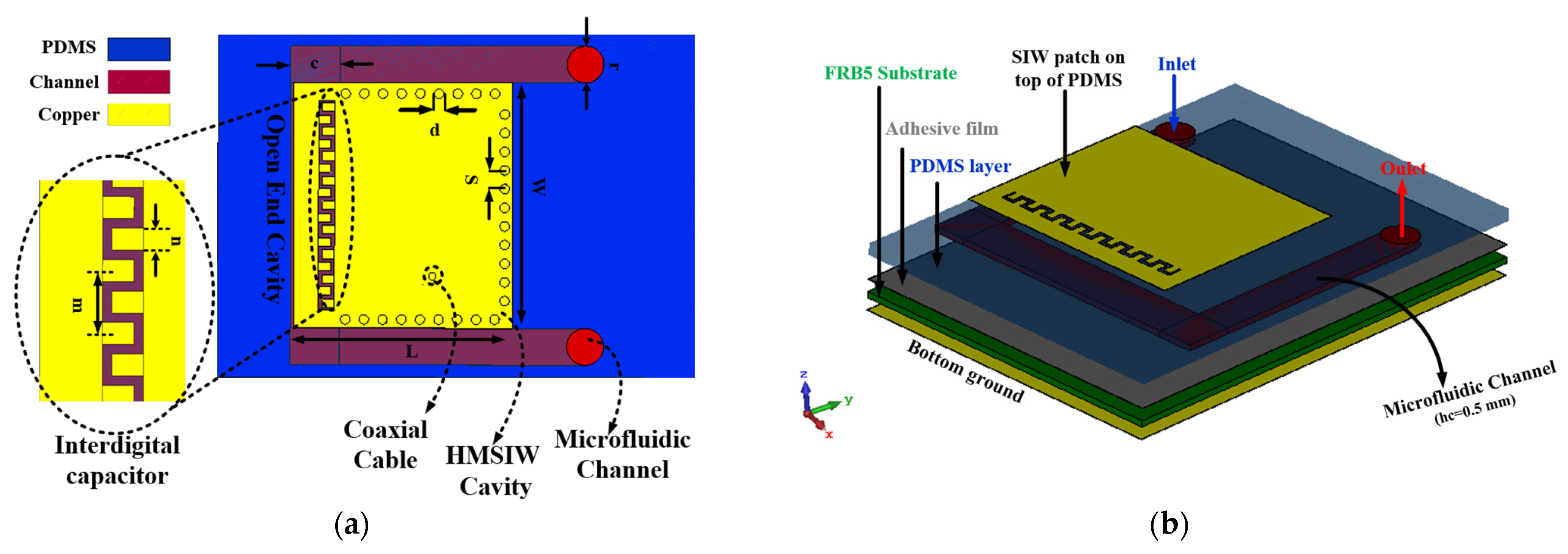
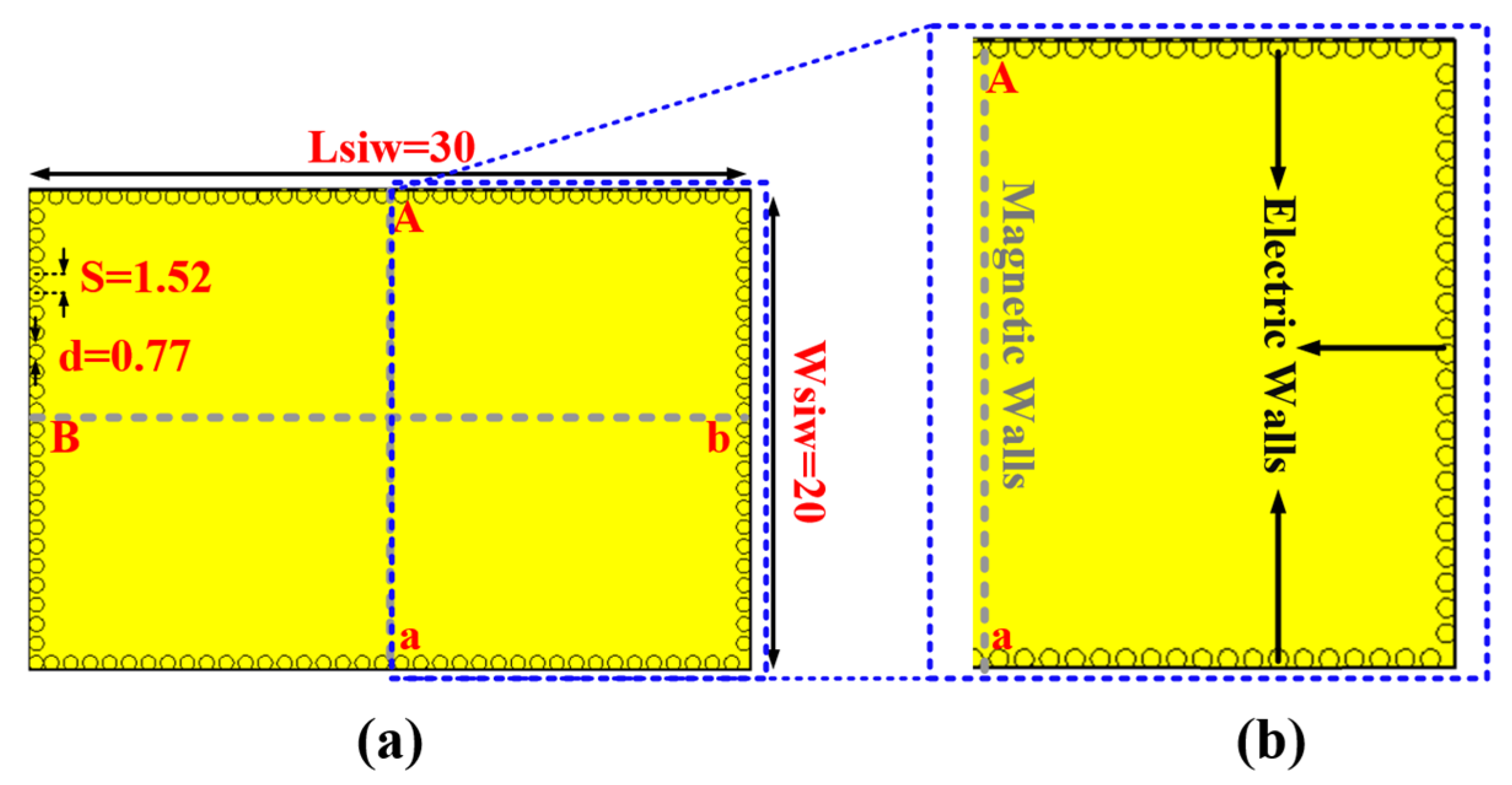
2.1. Design Configuration
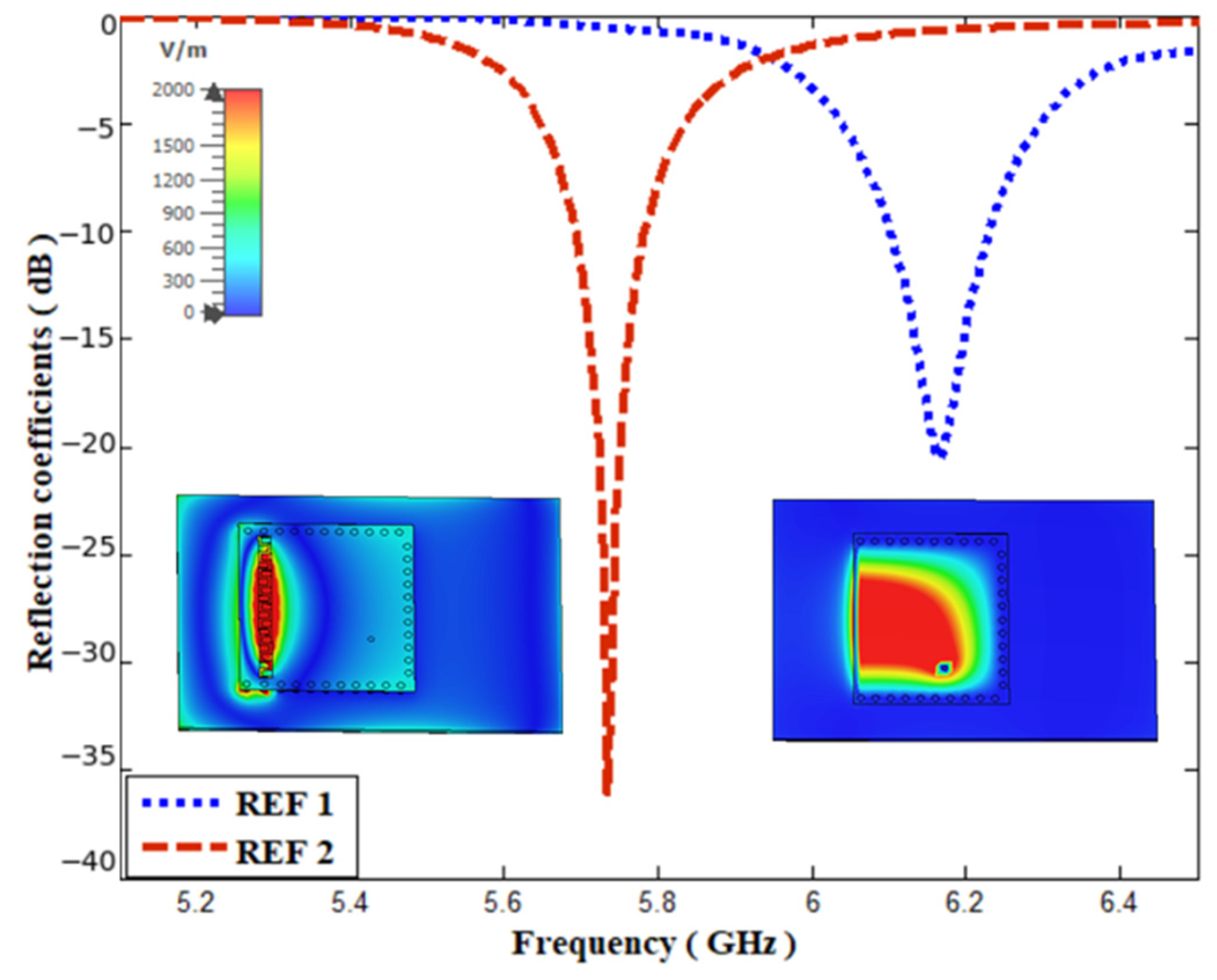
2.2. Evolution Process
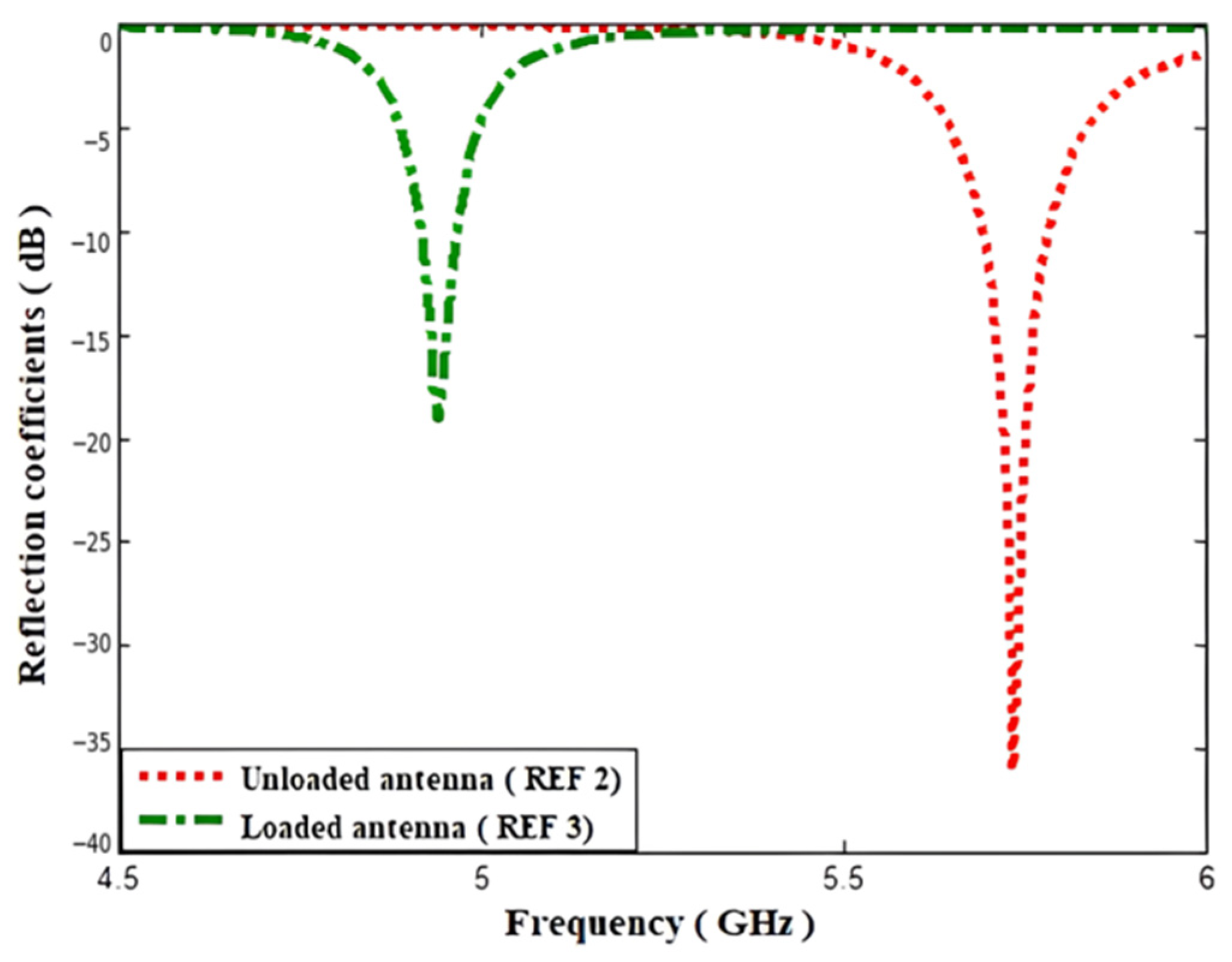
2.3. Description of Sensor Performance during Loading
- Employ samples with diverse water temperatures ), ranging from 0 °C to 50 °C, for classification into frost and wildfire monitoring purposes.
- Calculate the variation in the effective permittivity with the addition of each water sample’s temperature degree. This is achieved by calculating the dielectric constant of water over the range from 0 °C to 50 °C using Equation (5) [30]. This provides an approximation for calculating the effective permittivity of water based on the water temperature change in degrees:where is the effective permittivity of the water and is the temperature in degrees Celsius. In our case, = 78.6, = = , and = 67.736, while = 3.2 (at temperature below 0 °C). The sensor’s antenna response can be described as follows: = 5.5 MHz/ε, and, = 1.83 MHz/°C.
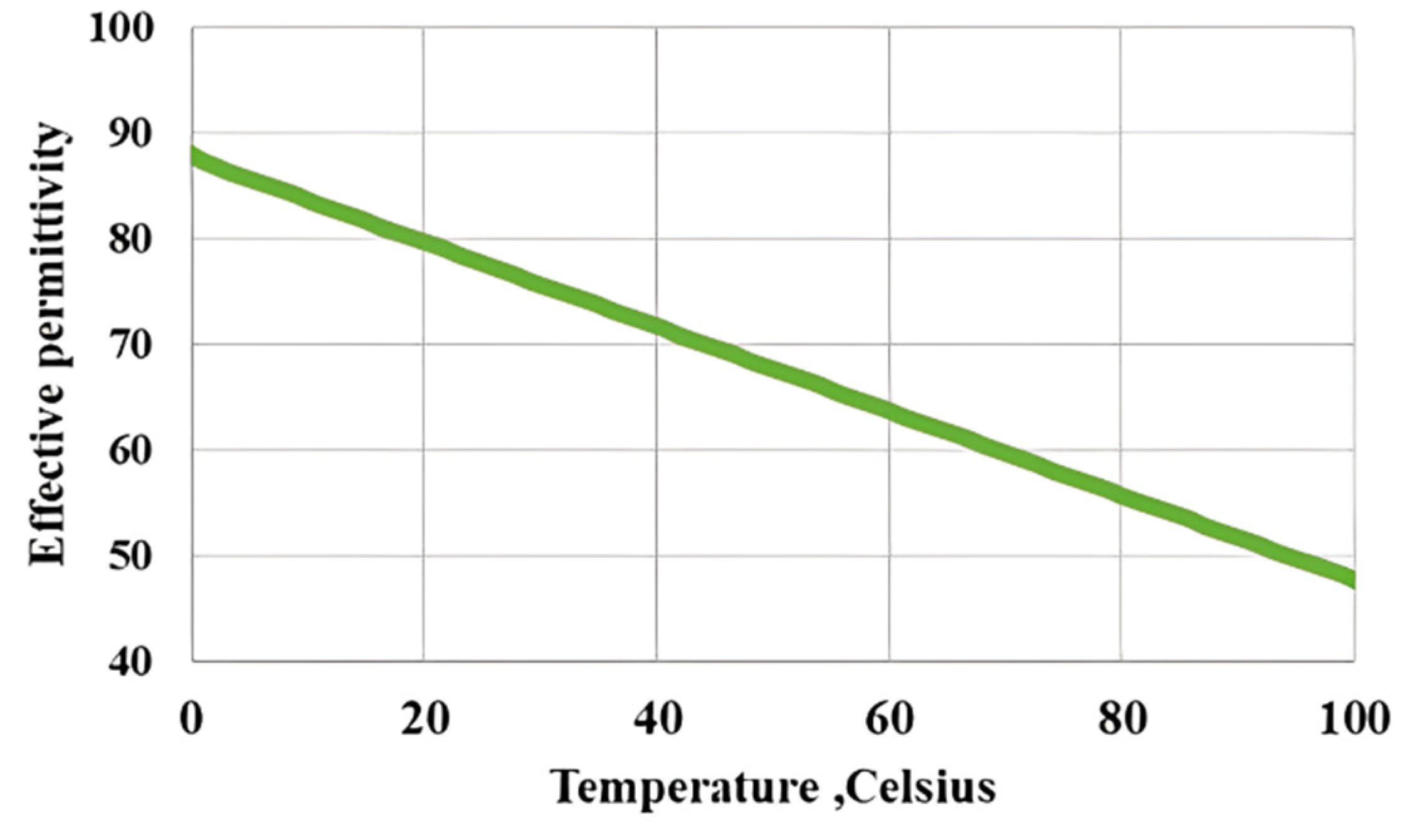
- Investigate the relationship between the resonance frequency and water temperature. This is achieved by examining the relationship between the effective permittivity and water temperature at each degree. Figure 8 demonstrates that the effective permittivity increases with a decrease in water temperature (linear regression). On the other hand, the resonance frequency shifts downward with a decrease in water temperature, corresponding to an increase in effective permittivity, as shown in Figure 9a, demonstrating that the antenna sensor is able to distinguish medium temperatures from low to high; this reflects the ability of this design to detect and forecast frost and wildfires over the sensing region at an early stage. Furthermore, this sensor is capable of distinguishing the presence of ice when = 3.2, as shown in Figure 9b. Meanwhile, the simulated return loss displays a high sensitivity to water temperature changes over the sensing region and to the presence of ice. However, the antenna’s resonance frequency response is more reliable because the resonance frequency is not sensitive to the losses between the sensor antenna and the receiver side. In contrast, the resonance amplitude would be significantly impacted by the distance between two transmitting and receiving antennas. Table 1 presents the simulated resonance frequency with respect to each water sample’s temperature.
3. Far-Field Performance
4. Proposed Smart Sensor Antenna
4.1. Problem Description
4.2. Data Generation and Preparation
5. Proposed Machine Learning Approach
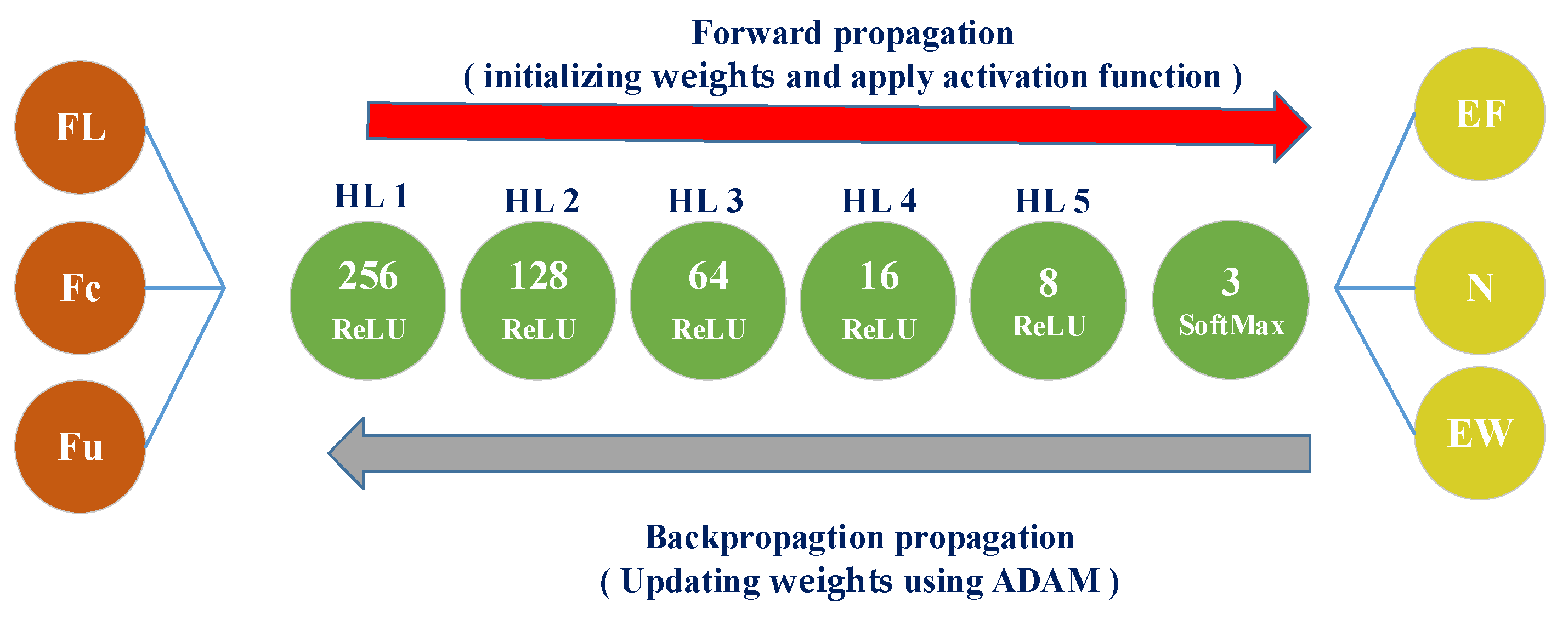
5.1. Perception-Based Approach
5.2. Non-Parametric-Based Approach
5.2.1. Random Forest (RF)
5.2.2. Support Vector Classification (SVC)
5.2.3. Gaussian Process (GP)
6. Performance Measurement Metrics
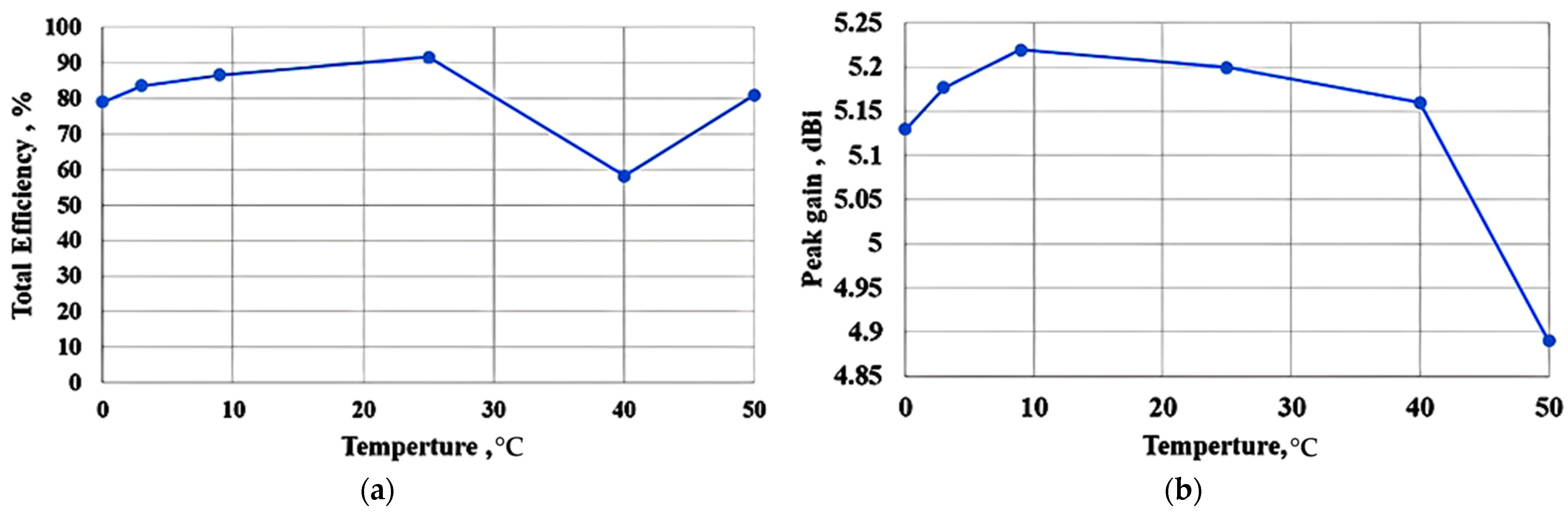
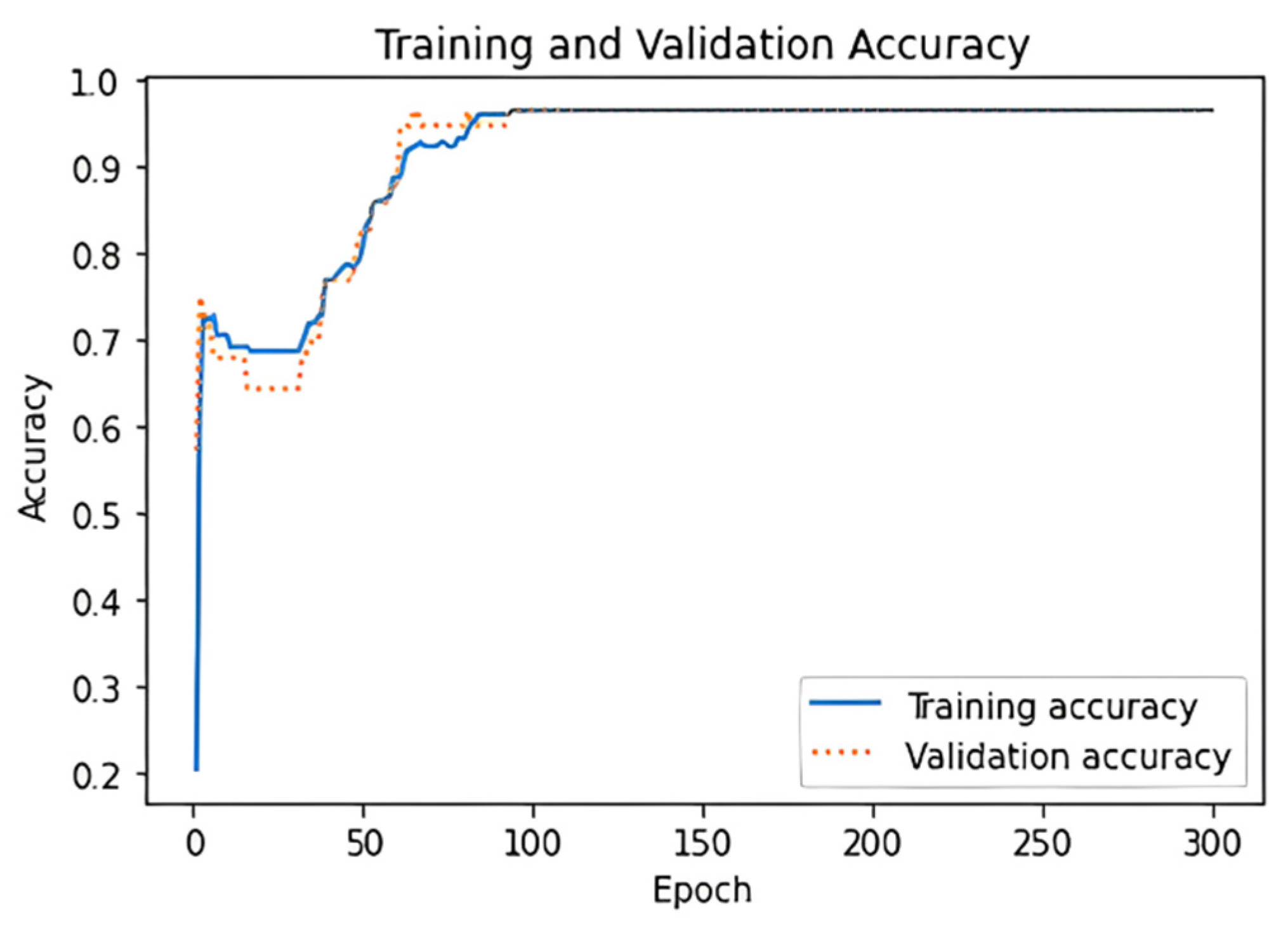
6.1. Performance on the Test Set
6.2. Performance on the Test Set Examples
7. State-of-the-Art-Comparison
8. Conclusions
9. Future Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhou, I.; Lipman, J.; Abolhasan, M.; Shariati, N.; Lamb, D.W. Frost monitoring cyber–physical system: A survey on prediction and active protection methods. IEEE Internet Things J. 2020, 7, 6514–6527. [Google Scholar] [CrossRef]
- Calfire. Cal FIRE. Available online: https://www.fire.ca.gov/ (accessed on 21 August 2024).
- Wei, K.; Yang, Y.; Zuo, H.; Zhong, D. A review on ice detection technology and ice elimination technology for wind turbine. Wind. Energy 2020, 23, 433–457. [Google Scholar] [CrossRef]
- Red Cross. The Climate Crisis: Why the World Must Act Now. Available online: https://www.redcross.org.uk/stories/disasters-and-emergencies/world/the-climate-crisis (accessed on 2 July 2024).
- The National Center for Security and Crisis Mangament (NCSCM). Jordan National Natural Disaster Risk Reduction Stratagy. 26 March 2019. Available online: https://www.preventionweb.net/files/68511_nationalnatrualdisasterriskreduciot.pdf (accessed on 2 July 2024).
- Kobziar, L.N.; Thompson, G.R. Wildfire smoke, a potential infectious agent. Science 2020, 370, 1408–1410. [Google Scholar] [CrossRef]
- National Weather Service. Wildfire Information and Safety Rules. Available online: https://www.weather.gov/otx/Wildfires (accessed on 2 July 2024).
- Somov, A. Wildfire safety with Wireless Sensor Networks. ICST Trans. Ambient. Syst. 2011, 11, e4. [Google Scholar] [CrossRef]
- Oolin, D.M.; Sitar, N. Wireless sensors forwildfire monitoring. In Proceedings of the Conference on Sensors and Smart Structures Technologies for Civil, Mechanical, and Aerospace Systems, San Diego, CA, USA, 7–10 March 2005; pp. 477–484. [Google Scholar]
- Leblon, B. Monitoring forest fire danger withremote sensing. Nat. Hazards 2005, 35, 343–359. [Google Scholar] [CrossRef]
- Jiang, X.; Taneja, J.; Ortiz, J.; Tavakoli, A.; Dutta, P.; Jeong, J.; Culler, D.; Levis, P.; Shenker, S. An architecture forenergy management in wireless sensor networks. ACM Sigbed Rev. 2007, 4, 31–36. [Google Scholar] [CrossRef]
- Ebrahimi, A.; Beziuk, G.; Scott, J.; Ghorbani, K. Microwave diferential frequency splitting sensor using magnetic-LC resonators. Sensors 2020, 20, 1066. [Google Scholar] [CrossRef]
- Su, L.; Muñoz-Enano, J.; Vélez, P.; Gil-Barba, M.; Casacuberta, P.; Martin, F. Highly sensitive refective-mode phase-variation permittivity sensor based on a coplanar waveguide terminated with an open complementary split ring resonator (OCSRR). IEEE Access 2021, 9, 27928–27944. [Google Scholar] [CrossRef]
- Malyuskin, O. Microplastic detection in soil and water using resonance microwave spectroscopy: A feasibility study. IEEE Sens. J. 2020, 20, 14817–14826. [Google Scholar] [CrossRef]
- Jha, A.K.; Mrozowski, M.; Delmonte, N.; Lamecki, A.; Bozzi, M. Planar microwave bragg refector resonant dielectric sensor. In Proceedings of the IMWS-AMP 2019—2019 IEEE MTT-S International Microwave Workshop Series on Advanced Materials and Processes for RF and THz Applications, Bochum, Germany, 16–18 July 2019; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2019; pp. 160–162. [Google Scholar] [CrossRef]
- Gil, M.; Velez, P.; Aznar-Ballesta, F.; Munoz-Enano, J.; Martin, F. Diferential sensor based on electroinductive wave transmission lines for dielectric constant measurements and defect detection. IEEE Trans. Antennas Propag. 2020, 68, 1876–1886. [Google Scholar] [CrossRef]
- Kozak, R.; Khorsand, K.; Zarifi, T.; Golovin, K.; Zarifi, M.H. Patch antenna sensor for wireless ice and Frost Detection. Sci. Rep. 2021, 11, 13707. [Google Scholar] [CrossRef] [PubMed]
- Qiao, Q.; Zhang, L.; Yang, F.; Yue, Z.; Elsherbeni, A.Z. Reconfgurable sensing antenna with novel HDPE-BST material for temperature monitoring. IEEE Antennas Wirel. Propag. Lett. 2013, 12, 1420–1423. [Google Scholar] [CrossRef]
- Mohammad, I.; Huang, H. An antenna sensor for crack detection and monitoring. Adv. Struct. Eng. 2011, 14, 47–53. [Google Scholar] [CrossRef]
- Zainud-Deen, S.H.; Malhat, H.A.E.A.; El-Refaay, E.A.A. A. InSb based microstrip patch antenna temperature sensor for terahertz applications. Wirel. Pers. Commun. 2020, 115, 893–908. [Google Scholar] [CrossRef]
- Yan, D.; Yang, Y.; Hong, Y.; Liang, T.; Yao, Z.; Chen, X.; Xiong, J. AlN-based ceramic patch antenna-type wireless passive high-temperature sensor. Micromachines 2017, 8, 301. [Google Scholar] [CrossRef]
- Lu, F.; Wang, H.; Guo, Y.; Tan, Q.; Zhang, W.; Xiong, J. Microwave backscatter-based wireless temperature sensor fabricated by an alumina-backed au slot radiation patch. Sensors 2018, 18, 242. [Google Scholar] [CrossRef] [PubMed]
- Cheng, H.; Ebadi, S.; Ren, X.; Gong, X. Wireless passive high-temperature sensor based on multifunctional reflective patch antenna up to 1050 degrees centigrade. Sens. Actuators A Phys. 2015, 222, 204–211. [Google Scholar] [CrossRef]
- Xiong, J.; Wu, G.; Tan, Q.; Wei, T.; Wu, D.; Shen, S.; Dong, H.; Zhang, W. Dielectrically-loaded cylindrical resonator-based wireless passive high-temperature sensor. Sensors 2016, 16, 2037. [Google Scholar] [CrossRef]
- Tan, Q.; Guo, Y.; Zhang, L.; Lu, F.; Dong, H.; Xiong, J. Substrate integrated waveguide (SIW)-based wireless temperature sensor for harsh environments. Sensors 2018, 18, 1406. [Google Scholar] [CrossRef]
- Li, Y.; Bowler, N.; Johnson, D.B. A resonant microwave patch sensor for detection of layer thickness or permittivity variations in multilayered dielectric structures. IEEE Sens. J. 2011, 11, 5–15. [Google Scholar] [CrossRef]
- Meyne, N.; Fuge, G.; Zeng, A.P.; Jacob, A.F. Resonant microwave sensors for picoliter liquid characterization and nondestructive detection of single biological cells. IEEE J. Electromagn. RF Microw. Med. Biol. 2017, 1, 98–104. [Google Scholar] [CrossRef]
- Saeed, K.; Guyette, A.C.; Hunter, I.C.; Pollard, R.D. Microstrip resonator technique for measuring dielectric permittivity of liquid solvents and for solution sensing. In Proceedings of the 2007 IEEE/MTT-S International Microwave Symposium, Honolulu, HI, USA, 3–8 June 2007; IEEE: Piscataway, NJ, USA, 2007; pp. 1185–1188. [Google Scholar]
- T, M.S.K.; Ansari, M.A.H.; Jha, A.K.; Akhtar, M.J. Design of SRR-based microwave sensor for characterization of magnetodielectric substrates. IEEE Microw. Wirel. Compon. Lett. 2017, 27, 524–526. [Google Scholar]
- Kunte, A.; Gaikwad, A. Adulteration Detection in Petroleum Liquids using Stacked Multi Ring Resonator. In Proceedings of the 2018 Third International Conference on Electrical, Electronics, Communication, Computer Technologies and Optimization Techniques (ICEECCOT), Msyuru, India, 14–15 December 2018. [Google Scholar]
- Foundazi, A.; Donnell, K.M. Design of a Microstrip Patch Antenna for Microwave Sensing of Petroleum Production Lines. In Proceedings of the 2017 United States National Committee of URSI National Radio Science Meeting (USNC-URSI NRSM), Boulder, CO, USA, 4–7 January 2017. [Google Scholar]
- Da Cunha, M.P.; Lad, R.; Davulis, P.; Canabal, A.; Moonlight, T.; Moulzolf, S.; Frankel, D.; Pollard, T.; McCann, D.; Dudzik, E.; et al. Wireless acoustic wave sensors and systems for harsh environment applications. In Proceedings of the 2011 IEEE Topical Conference on Wireless Sensors and Sensor Networks, Phoenix, AZ, USA, 16–19 January 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 41–44. [Google Scholar]
- Altakhaineh, A.T.; Alia’afreh, S.S. Machine Learning-Enhanced Microfluidic SIW Sensor for Water-in-Fuel Detection Applications. In Proceedings of the 2023 14th International Conference on Information and Communication Systems (ICICS), Irbid, Jordan, 21–23 November 2023; pp. 1–5. [Google Scholar] [CrossRef]
- Salim, A.; Memon, M.U.; Lim, S. Simultaneous detection of two chemicals using a TE20-mode substrate-integrated waveguide resonator. Sensors 2018, 18, 811. [Google Scholar] [CrossRef] [PubMed]
- Salim, A.; Lim, S. TM02 quarter-mode substrate-integrated waveguide resonator for dual detection of chemicals. Sensors 2018, 18, 1964. [Google Scholar] [CrossRef] [PubMed]
- Salim, A.; Kim, S.H.; Park, J.Y.; Lim, S. Microfluidic biosensor based on microwave substrate-integrated waveguide cavity resonator. J. Sens. 2018, 2018, 1324145. [Google Scholar] [CrossRef]
- Salim, A.; Memon, M.U.; Jeong, H.; Lim, S. Simplified approach to detect dielectric constant using a low-cost microfluidic quarter mode substrate-integrated waveguide. Sensors 2020, 20, 4985. [Google Scholar] [CrossRef]
- Memon, M.U.; Lim, S. Microfluidic high-Q circular substrate-integrated waveguide (SIW) cavity for radio frequency (RF) chemical liquid sensing. Sensors 2018, 18, 143. [Google Scholar] [CrossRef]
- Kiani, S.; Rezaei, P.; Karami, M.; Sadeghzadeh, R.A. Band-stop filter sensor based on SIW cavity for the non-invasive measuring of blood glucose. IET Wirel. Sens. Syst. 2019, 9, 1–5. [Google Scholar] [CrossRef]
- Jankovic, N.; Radonic, V. A Microwave Microfluidic Sensor Based on a Dual-Mode Resonator for Dual-Sensing Applications. Sensors 2017, 17, 2713. [Google Scholar] [CrossRef] [PubMed]
- Chen, Q.; Long, Z.; Shinohara, N.; Liu, C. A Substrate Integrated Waveguide Resonator Sensor for Dual-Band Complex Permittivity Measurement. Processes 2022, 10, 708. [Google Scholar] [CrossRef]
- Prakash, D.; Gupta, N. CSRR Based Metamaterial Inspired Sensor for Liquid Concentration Detection Using Machine Learning. Prog. Electromagn. Res. C 2023, 13, 255–267. [Google Scholar] [CrossRef]
- Haider, Z.; Modolo, J.; Liberti, M.; Apollonio, F.; Zhadobov, M. Millimeter-wave induced heating of cutaneous nerves and capillaries. IEEE J. Microw. 2023, 3, 170–180. [Google Scholar] [CrossRef]
- Rochman, M.I.; Fernandez, D.; Nunez, N.; Sathya, V.; Ibrahim, A.S.; Ghosh, M.; Payne, W. Impact of device thermal performance on 5G MMWAVE Communication Systems. In Proceedings of the 2022 IEEE International Workshop Technical Committee on Communications Quality and Reliability (CQR), Arlington, VA, USA, 13–15 September 2022. [Google Scholar]
- Alizadeh, A.; Vu, M.; Rappaport, T.S. A study of interference distributions in millimeter wave cellular networks. In Proceedings of the 2019 IEEE International Conference on Microwaves, Antennas, Communications and Electronic Systems (COMCAS), Tel-Aviv, Israel, 4–6 November 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Caufield, C. When Should I Cover? A Guide to Frost. Backyard Harvest Project. 18 May 2022. Available online: https://www.backyardharvestproject.com/blog/when-should-i-cover-a-guide-to-frost (accessed on 21 September 2024).
- Mohapatra, A.; Trinh, T. Early Wildfire Detection Technologies in Practice—A Review. Sustainability 2022, 14, 12270. [Google Scholar] [CrossRef]
- Develi, I. Application of multilayer perceptron networks to laser diodenonlinearity determination for radio-over-fibre mobile communicat-ions. Microw. Opt. Technol. Lett. 2004, 42, 425–427. [Google Scholar] [CrossRef]
- Haykin, S.S. Neural Networks: A Comprehensive Foundation; Macmil-lan: New York, NY, USA, 1994. [Google Scholar]
- Jang, J.-S.R. Self-learning fuzzy controllers based on temporal back propagation. IEEE Trans. Neural Netw. 1992, 3, 714–723. [Google Scholar] [CrossRef]
- Sharma, Y.; Zhang, H.H.; Xin, H. Machine learning techniques for optimizing design of double T-shaped monopole antenna. IEEE Trans. Antennas Propag. 2020, 68, 5658–5663. [Google Scholar] [CrossRef]
- Haque, A.; Rahman, A.; Al-Bawri, S.S.; Yusoff, Z.; Sharker, A.H.; Abdulkawi, W.M.; Saha, D.; Paul, L.C.; Zakariya, M.A. Machine learning-based technique for gain and resonance prediction of mid band 5G Yagi antenna. Sci. Rep. 2023, 13, 12590. [Google Scholar] [CrossRef]
- Naous, T.; Al Merie, A.; Al Khatib, S.K.; Al-Husseini, M.; Shubair, R.M.; El Misilmani, H.M. Machine learning-aided design of dielectric-filled slotted waveguide antennas with specified sidelobe levels. IEEE Access 2022, 10, 30583–30595. [Google Scholar] [CrossRef]
- Awad, M.; Khanna, R. Support vector regression. In Efficient Learning Machines; Apress: Berkeley, CA, USA, 2015; pp. 67–80. [Google Scholar]
- Hossin, M.; Sulaiman, M.N. A review on evaluation metrics for data classification evaluations. Int. J. Data Min. Knowl. Manag. Process 2015, 5, 1. [Google Scholar]






| , GHz | , °C | State | |
|---|---|---|---|
| 87.74 | 4.9186 | 0 | Frost |
| 86.5 | 4.9235 | 3 | Normal |
| 84.1 | 4.9298 | 9 | Normal |
| 78.6 | 4.9425 | 25 | Normal |
| 71.7 | 4.9599 | 40 | High Temperature |
| 67.7 | 4.9722 | 50 | High Temperature |
| 3.2 | 5.69 | <0 | Ice |
| Layers | Units | Activation | Kernel Initializer |
|---|---|---|---|
| 1 | 256 | ReLU | glorot_normal |
| 2 | 128 | ReLU | glorot_normal |
| 3 | 64 | ReLU | glorot_normal |
| 4 | 16 | ReLU | glorot_normal |
| 5 | 8 | ReLU | glorot_normal |
| 6 | 3 | SoftMax | - |
| Layers | Inputs, GHz | ML Models | Predicted | Actual | ||
|---|---|---|---|---|---|---|
| Sample 1 6 °C | 4.9243 | 4.9243 | 4.9497 | ANN | EF | EF |
| RF | EF | EF | ||||
| SVC | EF | EF | ||||
| GP | EF | EF | ||||
| Sample 2 8 °C | 4.927 | 4.927 | 4.9522 | ANN | N | N |
| RF | N | N | ||||
| SVC | N | N | ||||
| GP | N | N | ||||
| Sample 2 33.8 °C | 4.96 | 4.96 | 4.99 | ANN | EW | EW |
| RF | EW | EW | ||||
| SVC | EW | EW | ||||
| GP | EW | EW | ||||
| Ref. | Antenna Mode/Type | MUTP | #PUT | DM | ML | App |
|---|---|---|---|---|---|---|
| [21] | Passive, ML | Solid | 1 | permittivity | No | HT |
| [22] | Passive, ML | Solid | 1 | permittivity | No | HT |
| [23] | Passive, ML | Solid | 1 | permittivity | No | HT |
| [24] | Passive, ML | Solid | 1 | permittivity | No | HT |
| [25] | Passive, ML | Solid | 1 | permittivity | No | HT |
| [26] | Passive, ML | Solid | 1 | permittivity | No | HT |
| [27] | Active, ML | Ice | 1 | Thickness | No | Frost |
| [*] | ML | Liquid | 3 | permittivity | Yes | ATR 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Altakhaineh, A.T.; Alrawashdeh, R.; Zhou, J. Machine Learning-Aided Dual-Function Microfluidic SIW Sensor Antenna for Frost and Wildfire Detection Applications. Energies 2024, 17, 5208. https://doi.org/10.3390/en17205208
Altakhaineh AT, Alrawashdeh R, Zhou J. Machine Learning-Aided Dual-Function Microfluidic SIW Sensor Antenna for Frost and Wildfire Detection Applications. Energies. 2024; 17(20):5208. https://doi.org/10.3390/en17205208
Chicago/Turabian StyleAltakhaineh, Amjaad T., Rula Alrawashdeh, and Jiafeng Zhou. 2024. "Machine Learning-Aided Dual-Function Microfluidic SIW Sensor Antenna for Frost and Wildfire Detection Applications" Energies 17, no. 20: 5208. https://doi.org/10.3390/en17205208
APA StyleAltakhaineh, A. T., Alrawashdeh, R., & Zhou, J. (2024). Machine Learning-Aided Dual-Function Microfluidic SIW Sensor Antenna for Frost and Wildfire Detection Applications. Energies, 17(20), 5208. https://doi.org/10.3390/en17205208








