Novel Multi-Criteria Decision Analysis Based on Performance Indicators for Urban Energy System Planning
Abstract
1. Introduction
2. Case Study, Materials and Methods
2.1. Case Study
2.2. Background Information
2.3. Decision Analysis Methodology
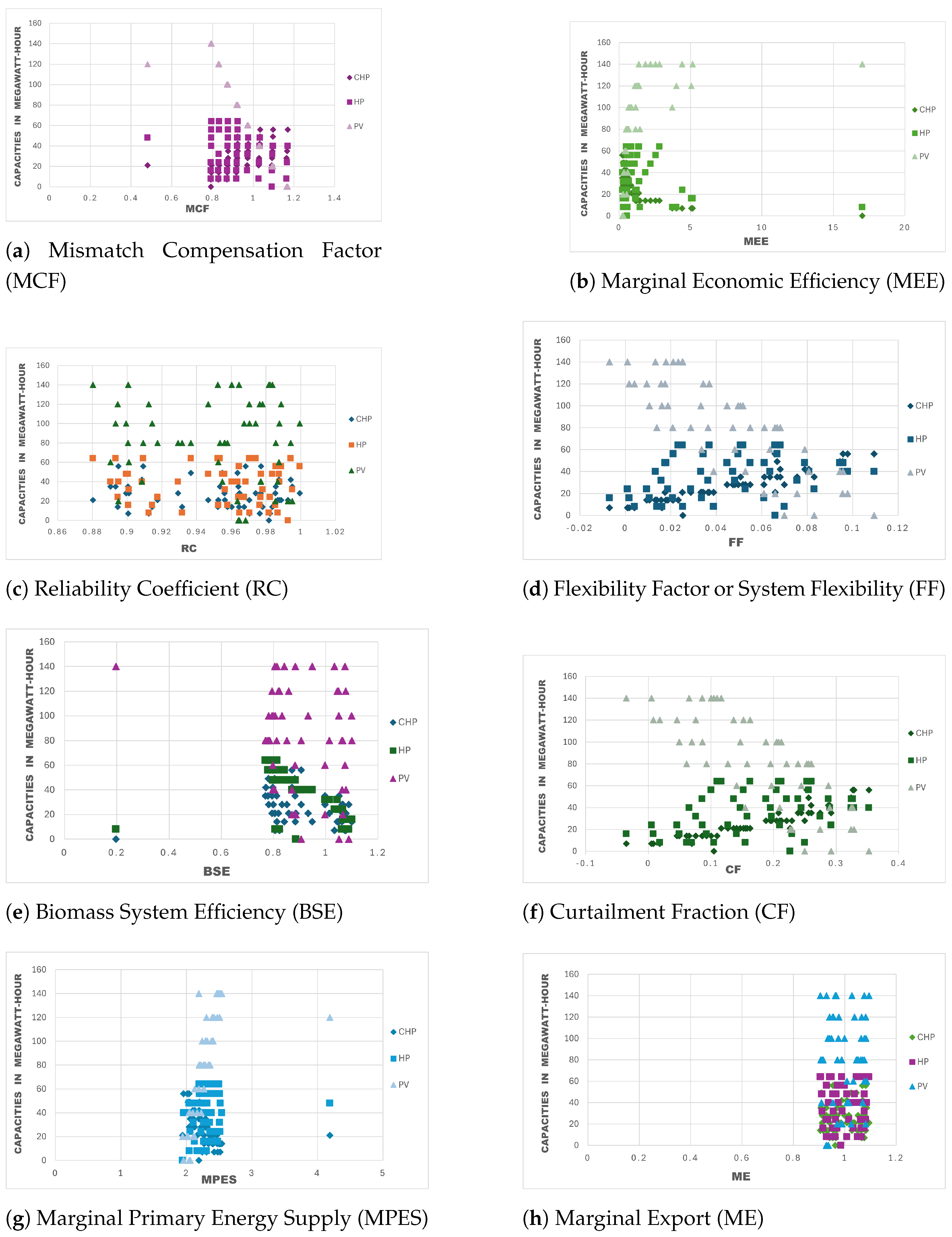
2.3.1. Technical Targets
- Relocation Coefficient (RC) is defined as the measure of comparison between the ability of different technologies in the supply system flexibility. It is the ratio between the net electricity exchange between the plant and system and the electricity demand minus intermittent electricity production. This indicator essentially helps evaluate how well the energy system can adjust to changes in energy demand and production, particularly when integrating renewable energy sources that may have fluctuating output. Its formula is reported as follows:
- Flexibility Factor or System Flexibility (FF) is an indicator first described by Paul Denholm and Robert M. Margolis to be the lowest hourly value over the year divided by the maximum hourly value with regard to the output of a simulation [63]. Thus, this indicator was used to assess the flexibility of the system over the year used in the simulation. We gave it a range between 0 and 1 with a value close to 0, which means the system is not flexible, and a value close to 1 means the system is flexible. In general terms, this metric helps determine how well the energy system can maintain consistent performance despite fluctuations in energy production and demand throughout the year.
- Biomass System Efficiency (BSE) is used to assess the importance of biomass in the energy system without the transportation system [64]. This indicator was helpful in this work since it could help in the quantification and reduction of biomass in the system. To attain this, the output from synthetic fuel is subtracted from the production of all the fuel by biomass, which is then divided by the biomass used for transportation subtracted from the input amount of biomass. Essentially, this efficiency metric shows how effectively the system uses biomass resources, helping to minimize waste and maximize energy output from the available biomass.
2.3.2. Economic Targets
- Mismatch Compensation Factor (MCF) was developed by Lund et al. [65] with respect to zero-energy buildings. It relates cost balance (i.e., the installed capacity of renewable energy sources where the import costs and export incomes are balanced) to energy balance (i.e., the installed capacity of renewable energy source (RES) balancing aggregated annual imports to exports from the energy system). This indicator helps measure how well the energy system can balance its energy production with its costs, ensuring that it produces enough renewable energy to meet its own needs while minimizing external energy purchases.
- Marginal Economic Efficiency (MEE) shows how the added cost of RES contributes to the total cost of the system. It is expressed by dividing the change in the total system cost by the change in the cost of RES [60]. In simpler terms, this indicator helps assess how cost-effective the system is when adding renewable energy sources, showing whether the investment in renewable technologies leads to efficient use of resources and overall cost savings.
2.3.3. Environmental Targets
- When a system is not able to hold excess production of RES within a given period, the percentage of the RES production lost by the technology is called Curtailment Fraction (CF). When the percentage is equal to , we say the system has the capacity to integrate the excess RES produced and vice versa. It is calculated by subtracting the realized RES production from the potential RES production, and the results are divided by the potential RES production. This indicator practically measures how much renewable energy is wasted because the system cannot fully utilize or store it, with higher curtailment indicating greater energy loss.
- Marginal Primary Energy Supply (MPES) compares the different RES where the factors may be determined by marginal effects. Specifically, the MPES indicates how the marginal Primary Energy Supply (PES) of the system is affected by a marginal change in the PES from RES. If it is less than 1, the system cannot fully integrate marginal RES production [60]. In other therms, this indicator shows how efficiently the system can incorporate small increases in renewable energy supply, helping to assess the system’s ability to handle additional renewable energy without performance losses. This is represented by the formula below.
- Marginal Export (ME) is used to determine the relationship between marginal export and marginal changes in PES, which are biomass-based [64].
2.4. TOPSIS-Based MCDA Approach
- Construct the assessment matrix: first, compile the quantitative evaluations for each alternative i across each criterion j. This matrix provides a comprehensive overview of how each alternative performs under each criterion.
- Compute the normalized matrix, with the generic element representing the normalized evaluation of alternative i under criterion j as:Normalize the matrix: next, standardize the values in the assessment matrix to make them comparable across criteria. The normalized value for each alternative i and criterion j is calculated as:This step removes the units of measurement and scales the data, ensuring that each criterion contributes equally to the analysis.
- Calculate the weighted normalized matrix: Apply the assigned weights to the normalized values to reflect the importance of each criterion. The weighted normalized value is given by:where is the weight assigned to criterion j. This step adjusts the normalized values according to the significance of each criterion.
- Determine the ideal solutions: identify the best possible (positive ideal) and worst possible (negative ideal) values for each criterion. The positive ideal solution and the negative ideal solution are defined as:where includes criteria to be maximized and includes criteria to be minimized. These ideal solutions serve as reference points for comparison.
- Calculate the distances to the ideal solutions: measure the distances of each alternative from the positive and negative ideal solutions. The distances and for each alternative i are computed as:These distances quantify how far each alternative is from the ideal solutions.
- Calculate the closeness coefficient: determine the closeness coefficient for each alternative i, which indicates its relative proximity to the ideal solutions. The closeness coefficient is calculated as:This coefficient shows how closely an alternative aligns with the best possible scenario while avoiding the worst.
- Rank the alternatives: finally, rank the alternatives based on their closeness coefficients in descending order. For example, in comparison between two generic alternatives i and z, if , then alternative i is preferred over alternative z. This ranking helps in making informed decisions by highlighting the most favorable options.
3. Results and Discussion
3.1. Performance Indicators of the Energy Scenarios
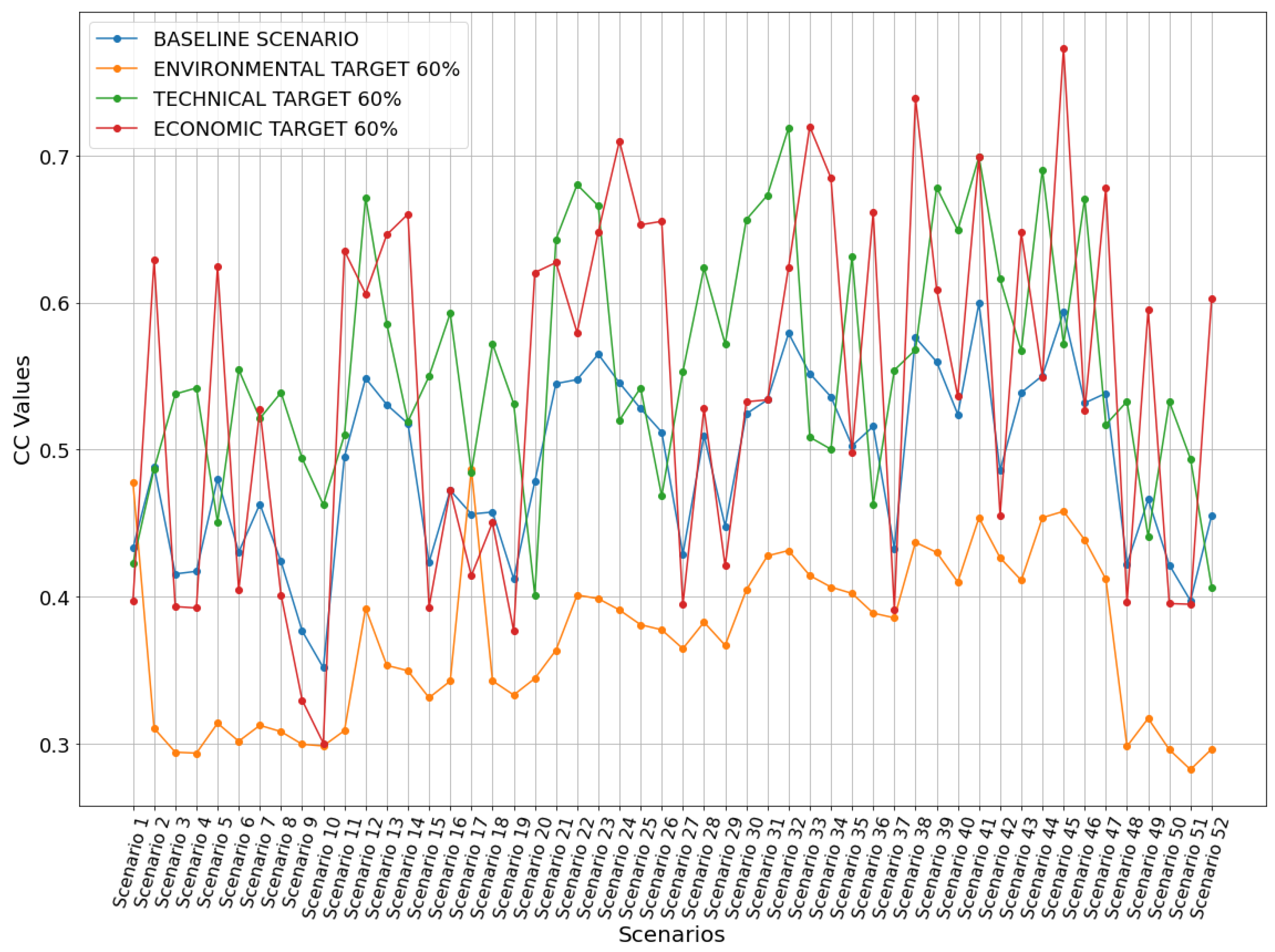
3.2. Multi-Criteria Decision Analysis (MCDA) and Sensitivity Analysis
4. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gonçalves, A.C.; Costoya, X.; Nieto, R.; Liberato, M.L. Extreme weather events on energy systems: A comprehensive review on impacts, mitigation, and adaptation measures. Sustain. Energy Res. 2024, 11, 4. [Google Scholar] [CrossRef]
- Xu, L.; Feng, K.; Lin, N.; Perera, A.; Poor, H.V.; Xie, L.; Ji, C.; Sun, X.A.; Guo, Q.; O’Malley, M. Resilience of renewable power systems under climate risks. Nat. Rev. Electr. Eng. 2024, 1, 53–66. [Google Scholar] [CrossRef]
- Cheikh, N.B.; Zaied, Y.B. Renewable energy deployment and geopolitical conflicts. J. Environ. Manag. 2023, 344, 118561. [Google Scholar] [CrossRef] [PubMed]
- Yasmeen, R.; Shah, W.U.H. Energy Uncertainty, Geopolitical Conflict, and Militarization Matters for Renewable and Non-renewable Energy Development: Perspectives from G7 Economies. Energy 2024, 306, 132480. [Google Scholar] [CrossRef]
- Ibekwe, K.I.; Etukudoh, E.A.; Nwokediegwu, Z.Q.S.; Umoh, A.A.; Adefemi, A.; Ilojianya, V.I. Energy security in the global context: A comprehensive review of geopolitical dynamics and policies. Eng. Sci. Technol. J. 2024, 5, 152–168. [Google Scholar] [CrossRef]
- Frilingou, N.; Xexakis, G.; Koasidis, K.; Nikas, A.; Campagnolo, L.; Delpiazzo, E.; Chiodi, A.; Gargiulo, M.; McWilliams, B.; Koutsellis, T.; et al. Navigating through an energy crisis: Challenges and progress towards electricity decarbonisation, reliability, and affordability in Italy. Energy Res. Soc. Sci. 2023, 96, 102934. [Google Scholar] [CrossRef]
- Adelekan, O.A.; Ilugbusi, B.S.; Adisa, O.; Obi, O.C.; Awonuga, K.F.; Asuzu, O.F.; Ndubuisi, N.L. Energy transition policies: A global review of shifts towards renewable sources. Eng. Sci. Technol. J. 2024, 5, 272–287. [Google Scholar] [CrossRef]
- Ahmed, N.; Ore Areche, F.; Saenz Arenas, E.R.; Cosio Borda, R.F.; Javier-Vidalón, J.L.; Silvera-Arcos, S.; Ober, J.; Kochmańska, A. Natural disasters and energy innovation: Unveiling the linkage from an environmental sustainability perspective. Front. Energy Res. 2023, 11, 1256219. [Google Scholar] [CrossRef]
- Wu, D.; Xie, Y.; Liu, D. Rethinking the complex effects of the clean energy transition on air pollution abatement: Evidence from China’s coal-to-gas policy. Energy 2023, 283, 128413. [Google Scholar] [CrossRef]
- Dincer, I.; Aydin, M.I. New paradigms in sustainable energy systems with hydrogen. Energy Convers. Manag. 2023, 283, 116950. [Google Scholar] [CrossRef]
- Johansson, B.; Jonsson, D.K.; Veibäck, E.; Sonnsjö, H. Assessing the capabilites to manage risks in energy systems–analytical perspectives and frameworks with a starting point in Swedish experiences. Energy 2016, 116, 429–435. [Google Scholar] [CrossRef]
- Cuisinier, E.; Bourasseau, C.; Ruby, A.; Lemaire, P.; Penz, B. Techno-economic planning of local energy systems through optimization models: A survey of current methods. Int. J. Energy Res. 2021, 45, 4888–4931. [Google Scholar] [CrossRef]
- Hasselqvist, H.; Renström, S.; Strömberg, H.; Håkansson, M. Household energy resilience: Shifting perspectives to reveal opportunities for renewable energy futures in affluent contexts. Energy Res. Soc. Sci. 2022, 88, 102498. [Google Scholar] [CrossRef]
- Lund, H. Renewable energy strategies for sustainable development. Energy 2007, 32, 912–919. [Google Scholar] [CrossRef]
- Kalair, A.; Abas, N.; Saleem, M.S.; Kalair, A.R.; Khan, N. Role of energy storage systems in energy transition from fossil fuels to renewables. Energy Storage 2021, 3, e135. [Google Scholar] [CrossRef]
- Lopion, P.; Markewitz, P.; Robinius, M.; Stolten, D. A review of current challenges and trends in energy systems modeling. Renew. Sustain. Energy Rev. 2018, 96, 156–166. [Google Scholar] [CrossRef]
- Kotzur, L.; Nolting, L.; Hoffmann, M.; Groß, T.; Smolenko, A.; Priesmann, J.; Büsing, H.; Beer, R.; Kullmann, F.; Singh, B.; et al. A modeler’s guide to handle complexity in energy systems optimization. Adv. Appl. Energy 2021, 4, 100063. [Google Scholar] [CrossRef]
- Ervural, B.C.; Evren, R.; Delen, D. A multi-objective decision-making approach for sustainable energy investment planning. Renew. Energy 2018, 126, 387–402. [Google Scholar] [CrossRef]
- Thompson, S. Strategic analysis of the renewable electricity transition: Power to the world without carbon emissions? Energies 2023, 16, 6183. [Google Scholar] [CrossRef]
- Rozhkov, A. Applying graph theory to find key leverage points in the transition toward urban renewable energy systems. Appl. Energy 2024, 361, 122854. [Google Scholar] [CrossRef]
- Adanma, U.M.; Ogunbiyi, E.O. Assessing the economic and environmental impacts of renewable energy adoption across different global regions. Eng. Sci. Technol. J. 2024, 5, 1767–1793. [Google Scholar] [CrossRef]
- Moriarty, P.; Honnery, D. Feasibility of a 100% global renewable energy system. Energies 2020, 13, 5543. [Google Scholar] [CrossRef]
- Akpan, J.; Olanrewaju, O. Towards a common methodology and modelling tool for 100% renewable energy analysis: A review. Energies 2023, 16, 6598. [Google Scholar] [CrossRef]
- Elazab, R.; Dahab, A.A.; Adma, M.A.; Hassan, H.A. Reviewing the frontier: Modeling and energy management strategies for sustainable 100% renewable microgrids. Discov. Appl. Sci. 2024, 6, 168. [Google Scholar] [CrossRef]
- Meschede, H.; Bertheau, P.; Khalili, S.; Breyer, C. A review of 100% renewable energy scenarios on islands. Wiley Interdiscip. Rev. Energy Environ. 2022, 11, e450. [Google Scholar] [CrossRef]
- Marocco, P.; Novo, R.; Lanzini, A.; Mattiazzo, G.; Santarelli, M. Towards 100% renewable energy systems: The role of hydrogen and batteries. J. Energy Storage 2023, 57, 106306. [Google Scholar] [CrossRef]
- O’malley, M. Towards 100% renewable energy system. IEEE Trans. Power Syst. 2022, 37, 3187–3189. [Google Scholar] [CrossRef]
- Dahab, A.A.; Elazab, R.; Adma, M.A.A.; Hassan, H.F. Global Challenges and Economic Feasibility in Achieving 100% Renewable Energy. Adv. Electr. Electron. Eng. 2024, in press. [CrossRef]
- Sahoo, G.S.; Mathur, M.; Zaidi, T.; Sharma, R. Comprehensive Assessment of Land Requirements for 100% Solar Energy Transition in Smart Cities. In Proceedings of the E3S Web of Conferences, EDP Sciences, Singapore, 7–9 June 2024; Volume 540, p. 04006. [Google Scholar]
- Ulpiani, G.; Vetters, N.; Shtjefni, D.; Kakoulaki, G.; Taylor, N. Let’s hear it from the cities: On the role of renewable energy in reaching climate neutrality in urban Europe. Renew. Sustain. Energy Rev. 2023, 183, 113444. [Google Scholar] [CrossRef]
- Li, L.; Wang, J.; Zhong, X.; Lin, J.; Wu, N.; Zhang, Z.; Meng, C.; Wang, X.; Shah, N.; Brandon, N.; et al. Combined multi-objective optimization and agent-based modeling for a 100% renewable island energy system considering power-to-gas technology and extreme weather conditions. Appl. Energy 2022, 308, 118376. [Google Scholar] [CrossRef]
- Tian, X.; Zhou, Y.; Morris, B.; You, F. Sustainable design of Cornell University campus energy systems toward climate neutrality and 100% renewables. Renew. Sustain. Energy Rev. 2022, 161, 112383. [Google Scholar] [CrossRef]
- Cong, R.; Fujiyama, A.; Matsumoto, T. An Optimal Scheme Assists the Municipalities in Fukuoka, Japan in Achieving their Goal of 100% Renewable Energy Supply and Future Decarbonization. Energy Nexus 2024, 13, 100277. [Google Scholar] [CrossRef]
- Liu, S.; Duffy, A.H.; Whitfield, R.I.; Boyle, I.M. Integration of decision support systems to improve decision support performance. Knowl. Inf. Syst. 2010, 22, 261–286. [Google Scholar] [CrossRef]
- Prina, M.G.; Johannsen, R.M.; Sparber, W.; Østergaard, P.A. Evaluating near-optimal scenarios with EnergyPLAN to support policy makers. Smart Energy 2023, 10, 100100. [Google Scholar] [CrossRef]
- Prina, M.G.; Lionetti, M.; Manzolini, G.; Sparber, W.; Moser, D. Transition pathways optimization methodology through EnergyPLAN software for long-term energy planning. Appl. Energy 2019, 235, 356–368. [Google Scholar] [CrossRef]
- Ren, J. Waste-to-Energy: Multi-Criteria Decision Analysis for Sustainability Assessment and Ranking; Academic Press: Cambridge, MA, USA, 2020. [Google Scholar]
- Brodny, J.; Tutak, M. Assessing the energy security of European Union countries from two perspectives–A new integrated approach based on MCDM methods. Appl. Energy 2023, 347, 121443. [Google Scholar] [CrossRef]
- Kumar, A.; Sah, B.; Singh, A.R.; Deng, Y.; He, X.; Kumar, P.; Bansal, R.C. A review of multi criteria decision making (MCDM) towards sustainable renewable energy development. Renew. Sustain. Energy Rev. 2017, 69, 596–609. [Google Scholar] [CrossRef]
- Kandakoglu, M.; Walther, G.; Ben Amor, S. The use of multi-criteria decision-making methods in project portfolio selection: A literature review and future research directions. Ann. Oper. Res. 2024, 332, 807–830. [Google Scholar] [CrossRef]
- Manoj, V.; Pilla, R.; Kumar, Y.N.; Sinha, C.; Prasad, S.V.; Chakravarthi, M.K.; Bhogi, K.K. Towards Efficient Energy Solutions: MCDA-Driven Selection of Hybrid Renewable Energy Systems. Int. J. Electr. Electron. Eng. Telecommun. 2024, 13, 98–111. [Google Scholar] [CrossRef]
- Islam, M.R.; Aziz, M.T.; Alauddin, M.; Kader, Z.; Islam, M.R. Site suitability assessment for solar power plants in Bangladesh: A GIS-based analytical hierarchy process (AHP) and multi-criteria decision analysis (MCDA) approach. Renew. Energy 2024, 220, 119595. [Google Scholar] [CrossRef]
- Halder, B.; Bandyopadhyay, J.; Sandhyaki, S. Impact assessment of environmental disturbances triggering aquaculture land suitability mapping using AHP and MCDA techniques. Aquac. Int. 2024, 32, 2039–2075. [Google Scholar] [CrossRef]
- Więckowski, J.; Kizielewicz, B.; Sałabun, W. A multi-dimensional sensitivity analysis approach for evaluating the robustness of renewable energy sources in European countries. J. Clean. Prod. 2024, 143225. [Google Scholar] [CrossRef]
- Benítez, J.; Carpitella, S.; Certa, A.; Izquierdo, J. Management of uncertain pairwise comparisons in AHP through probabilistic concepts. Appl. Soft Comput. 2019, 78, 274–285. [Google Scholar] [CrossRef]
- Aljburi, M.T.; Albahri, A.; Albahri, O.; Alamoodi, A.; Mohammed, S.M.; Deveci, M.; Tomášková, H. Exploring decision-making techniques for evaluation and benchmarking of energy system integration frameworks for achieving a sustainable energy future. Energy Strategy Rev. 2024, 51, 101251. [Google Scholar] [CrossRef]
- Alamoodi, A.H.; Garfan, S.; Al-Zuhairi, O.; Zaidan, B.; Zaidan, A.; Albahri, O.S.; Ahmaro, I.Y.; Albahri, A.S.; Yussof, S.; Magableh, A.A. Exploring the integration of multi criteria decision analysis in the clean energy biodiesels applications: A systematic review and gap analysis. Eng. Appl. Artif. Intell. 2024, 133, 108023. [Google Scholar] [CrossRef]
- Anchieta, T.; Meirelles, G.; Carpitella, S.; Brentan, B.; Izquierdo, J. Water distribution network expansion: An evaluation from the perspective of complex networks and hydraulic criteria. J. Hydroinform. 2023, 25, 628–644. [Google Scholar] [CrossRef]
- Brentan, B.; Carpitella, S.; Zanfei, A.; Gabriel Souza, R.; Menapace, A.; Meirelles, G.; Righetti, M.; Izquierdo, J. Multi-criteria analysis applied to ranking rehabilitation strategies of water distribution networks. Math. Methods Appl. Sci. 2023. [Google Scholar] [CrossRef]
- Chatterjee, S.; Chakraborty, S. A study on the effects of objective weighting methods on TOPSIS-based parametric optimization of non-traditional machining processes. Decis. Anal. J. 2024, 11, 100451. [Google Scholar] [CrossRef]
- Yazo-Cabuya, E.J.; Ibeas, A.; Herrera-Cuartas, J.A. Integration of Sustainability in Risk Management and Operational Excellence through the VIKOR Method Considering Comparisons between Multi-Criteria Decision-Making Methods. Sustainability 2024, 16, 4585. [Google Scholar] [CrossRef]
- Menapace, A.; Thellufsen, J.Z.; Pernigotto, G.; Roberti, F.; Gasparella, A.; Righetti, M.; Baratieri, M.; Lund, H. The design of 100% renewable smart urb an energy systems: The case of Bozen-Bolzano. Energy 2020, 207, 118198. [Google Scholar] [CrossRef]
- Battini, F.; Menapace, A.; Stradiotti, G.; Zanfei, A.; Nicolosi, F.F.; Dalla Torre, D.; Renzi, M.; Pernigotto, G.; Ravazzolo, F.; Righetti, M.; et al. Technical, economic and environmental optimization of renewable urban energy systems in a climate change scenario. Smart Energy, 2024; in press. [Google Scholar]
- ISTAT. Popolazione Residente al 1 Gennaio: Provincia Autonoma Bolzano/Bozen. 2023. Available online: http://dati.istat.it (accessed on 26 August 2024).
- Grazieschi, G.; Zubaryeva, A.; Sparber, W. Energy and greenhouse gases life cycle assessment of electric and hydrogen buses: A real-world case study in Bolzano Italy. Energy Rep. 2023, 9, 6295–6310. [Google Scholar] [CrossRef]
- Pinamonti, M.; Prada, A.; Baggio, P. Rule-based control strategy to increase photovoltaic self-consumption of a modulating heat pump using water storages and building mass activation. Energies 2020, 13, 6282. [Google Scholar] [CrossRef]
- Hunter, G.W.; Vettorato, D.; Sagoe, G. Creating smart energy cities for sustainability through project implementation: A case study of Bolzano, Italy. Sustainability 2018, 10, 2167. [Google Scholar] [CrossRef]
- Prina, M.G.; Cozzini, M.; Garegnani, G.; Moser, D.; Oberegger, U.F.; Vaccaro, R.; Sparber, W. Smart energy systems applied at urban level: The case of the municipality of Bressanone-Brixen. Int. J. Sustain. Energy Plan. Manag. 2016, 10, 33–52. [Google Scholar]
- Fedak, W.; Anweiler, S.; Ulbrich, R.; Jarosz, B. The concept of autonomous power supply system fed with renewable energy sources. J. Sustain. Dev. Energy Water Environ. Syst. 2017, 5, 579–589. [Google Scholar] [CrossRef]
- stergaard, P.A. Reviewing EnergyPLAN simulations and performance indicator applications in EnergyPLAN simulations. Appl. Energy 2015, 154, 921–933. [Google Scholar] [CrossRef]
- stergaard, P.A.; Lund, H.; Thellufsen, J.Z.; Sorknæs, P.; Mathiesen, B.V. Review and validation of EnergyPLAN. Renew. Sustain. Energy Rev. 2022, 168, 112724. [Google Scholar] [CrossRef]
- Akpahou, R.; Mensah, L.D.; Quansah, D.A.; Kemausuor, F. Energy planning and modeling tools for sustainable development: A systematic literature review. Energy Rep. 2024, 11, 830–845. [Google Scholar] [CrossRef]
- Denholm, P.; Margolis, R.M. Evaluating the limits of solar photovoltaics (PV) in traditional electric power systems. Energy Policy 2007, 35, 2852–2861. [Google Scholar] [CrossRef]
- Kwon, P.S.; Østergaard, P.A. Priority order in using biomass resources–Energy systems analyses of future scenarios for Denmark. Energy 2013, 63, 86–94. [Google Scholar] [CrossRef]
- Lund, H.; Marszal, A.; Heiselberg, P. Zero energy buildings and mismatch compensation factors. Energy Build. 2011, 43, 1646–1654. [Google Scholar] [CrossRef]



| Before Normalization | ||||||||
| Scenarios | RC | FF | CF | MCF | MPES | MEE | ME | BSE |
| Scenario 1 | 0.981722 | 0.025282 | 0.104913 | 0.792006 | 2.189719 | 17.02612 | 0.963444 | 0.196561 |
| Scenario 2 | 0.914448 | 0.010581 | 0.049434 | 0.871856 | 2.395090 | 1.176235 | 1.064378 | 1.098251 |
| Scenario 3 | 0.957826 | 0.020870 | 0.092879 | 0.917171 | 2.333604 | 1.151019 | 0.915653 | 1.099818 |
| Scenario 4 | 0.967399 | 0.018738 | 0.086294 | 0.871856 | 2.406525 | 1.152334 | 0.934797 | 1.049301 |
| Scenario 5 | 0.894655 | 0.009454 | 0.045639 | 0830840 | 2.470161 | 1.210174 | 1.081707 | 1.048504 |
| Scenario 6 | 0.977985 | 0.015756 | 0.075988 | 0.830840 | 2.506582 | 1.408031 | 0.955969 | 1.043592 |
| Scenario 7 | 0.960285 | 0.013243 | 0.065025 | 0.793491 | 2.537576 | 1.840971 | 1.027957 | 0.947787 |
| Scenario 8 | 0.983609 | 0.017858 | 0.086074 | 0.793491 | 2.518343 | 2.206353 | 0.967219 | 0.883702 |
| Scenario 9 | 0.964461 | 0.021068 | 0.100287 | 0.793491 | 2.505681 | 2.551852 | 0.928922 | 0.840727 |
| Scenario 10 | 0.952290 | 0.023275 | 0.109848 | 0.793491 | 2.496894 | 2.835778 | 0.904580 | 0.812299 |
| After Normalization | ||||||||
| Scenarios | RC | FF | CF | MCF | MPES | MEE | ME | BSE |
| Scenario 1 | 0.850946 | 0.277390 | 0.361767 | 0.451797 | 0.111556 | 1.000000 | 0.309250 | 0.000000 |
| Scenario 2 | 0.286335 | 0.151160 | 0.218751 | 0.567825 | 0.202887 | 0.056067 | 0.839516 | 0.998265 |
| Scenario 3 | 0.650396 | 0.239502 | 0.330747 | 0.633672 | 0.175544 | 0.054565 | 0.058171 | 1.000000 |
| Scenario 4 | 0.730733 | 0.221197 | 0.313773 | 0.567825 | 0.207973 | 0.054643 | 0.158749 | 0.944072 |
| Scenario 5 | 0.120217 | 0.141479 | 0.208970 | 0.508226 | 0.236273 | 0.058088 | 0.930552 | 0.943190 |
| Scenario 6 | 0.819577 | 0.195596 | 0.287204 | 0.508226 | 0.252470 | 0.069871 | 0.269977 | 0.937751 |
| Scenario 7 | 0.671030 | 0.174015 | 0.258943 | 0.453955 | 0.266253 | 0.095655 | 0.648173 | 0.831685 |
| Scenario 8 | 0.866785 | 0.213642 | 0.313203 | 0.453955 | 0.257700 | 0.117415 | 0.329079 | 0.760737 |
| Scenario 9 | 0.706079 | 0.241208 | 0.349842 | 0.453955 | 0.252069 | 0.137991 | 0.127884 | 0.713158 |
| Scenario 10 | 0.603932 | 0.260161 | 0.374491 | 0.453955 | 0.248161 | 0.154900 | 0.000000 | 0.681686 |
| BS | CC | ENV 60% | CC | TEC 60% | CC | ECO 60% | CC |
|---|---|---|---|---|---|---|---|
| Scenario 41 | 0.5994 | Scenario 17 | 0.4868 | Scenario 32 | 0.7190 | Scenario 45 | 0.7729 |
| Scenario 45 | 0.5936 | Scenario 1 | 0.4777 | Scenario 41 | 0.6992 | Scenario 38 | 0.7389 |
| Scenario 32 | 0.5790 | Scenario 45 | 0.4580 | Scenario 44 | 0.6903 | Scenario 33 | 0.7197 |
| Scenario 38 | 0.5762 | Scenario 44 | 0.4537 | Scenario 22 | 0.6802 | Scenario 24 | 0.7098 |
| Scenario 23 | 0.5648 | Scenario 41 | 0.4536 | Scenario 39 | 0.6783 | Scenario 41 | 0.6993 |
| Scenario 39 | 0.5596 | Scenario 46 | 0.4385 | Scenario 31 | 0.6730 | Scenario 34 | 0.6847 |
| Scenario 33 | 0.5517 | Scenario 38 | 0.4369 | Scenario 12 | 0.6715 | Scenario 47 | 0.6781 |
| Scenario 44 | 0.5502 | Scenario 32 | 0.4313 | Scenario 46 | 0.6708 | Scenario 36 | 0.6613 |
| Scenario 12 | 0.5485 | Scenario 39 | 0.4300 | Scenario 23 | 0.6657 | Scenario 14 | 0.6601 |
| Scenario 22 | 0.5476 | Scenario 31 | 0.4277 | Scenario 30 | 0.6564 | Scenario 26 | 0.6552 |
| BS | CC | ENV 60% | CC | TEC 60% | CC | ECO 60% | CC |
|---|---|---|---|---|---|---|---|
| Scenario 8 | 0.4238 | Scenario 8 | 0.3081 | Scenario 2 | 0.4868 | Scenario 50 | 0.3952 |
| Scenario 15 | 0.4233 | Scenario 6 | 0.3016 | Scenario 17 | 0.4847 | Scenario 51 | 0.3948 |
| Scenario 48 | 0.4223 | Scenario 9 | 0.2995 | Scenario 26 | 0.4683 | Scenario 27 | 0.3945 |
| Scenario 50 | 0.4215 | Scenario 10 | 0.2984 | Scenario 36 | 0.4627 | Scenario 3 | 0.3932 |
| Scenario 4 | 0.4172 | Scenario 48 | 0.2981 | Scenario 10 | 0.4624 | Scenario 15 | 0.3929 |
| Scenario 3 | 0.4154 | Scenario 52 | 0.2962 | Scenario 5 | 0.4506 | Scenario 4 | 0.3922 |
| Scenario 19 | 0.4121 | Scenario 50 | 0.2959 | Scenario 49 | 0.4407 | Scenario 37 | 0.3914 |
| Scenario 51 | 0.3972 | Scenario 3 | 0.2941 | Scenario 1 | 0.4226 | Scenario 19 | 0.3768 |
| Scenario 9 | 0.3766 | Scenario 4 | 0.2935 | Scenario 52 | 0.4064 | Scenario 9 | 0.3295 |
| Scenario 10 | 0.3516 | Scenario 51 | 0.2823 | Scenario 20 | 0.4010 | Scenario 10 | 0.3003 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nimako, B.K.; Carpitella, S.; Menapace, A. Novel Multi-Criteria Decision Analysis Based on Performance Indicators for Urban Energy System Planning. Energies 2024, 17, 5207. https://doi.org/10.3390/en17205207
Nimako BK, Carpitella S, Menapace A. Novel Multi-Criteria Decision Analysis Based on Performance Indicators for Urban Energy System Planning. Energies. 2024; 17(20):5207. https://doi.org/10.3390/en17205207
Chicago/Turabian StyleNimako, Benjamin Kwaku, Silvia Carpitella, and Andrea Menapace. 2024. "Novel Multi-Criteria Decision Analysis Based on Performance Indicators for Urban Energy System Planning" Energies 17, no. 20: 5207. https://doi.org/10.3390/en17205207
APA StyleNimako, B. K., Carpitella, S., & Menapace, A. (2024). Novel Multi-Criteria Decision Analysis Based on Performance Indicators for Urban Energy System Planning. Energies, 17(20), 5207. https://doi.org/10.3390/en17205207







