Recurrence Multilinear Regression Technique for Improving Accuracy of Energy Prediction in Power Systems
Abstract
1. Introduction
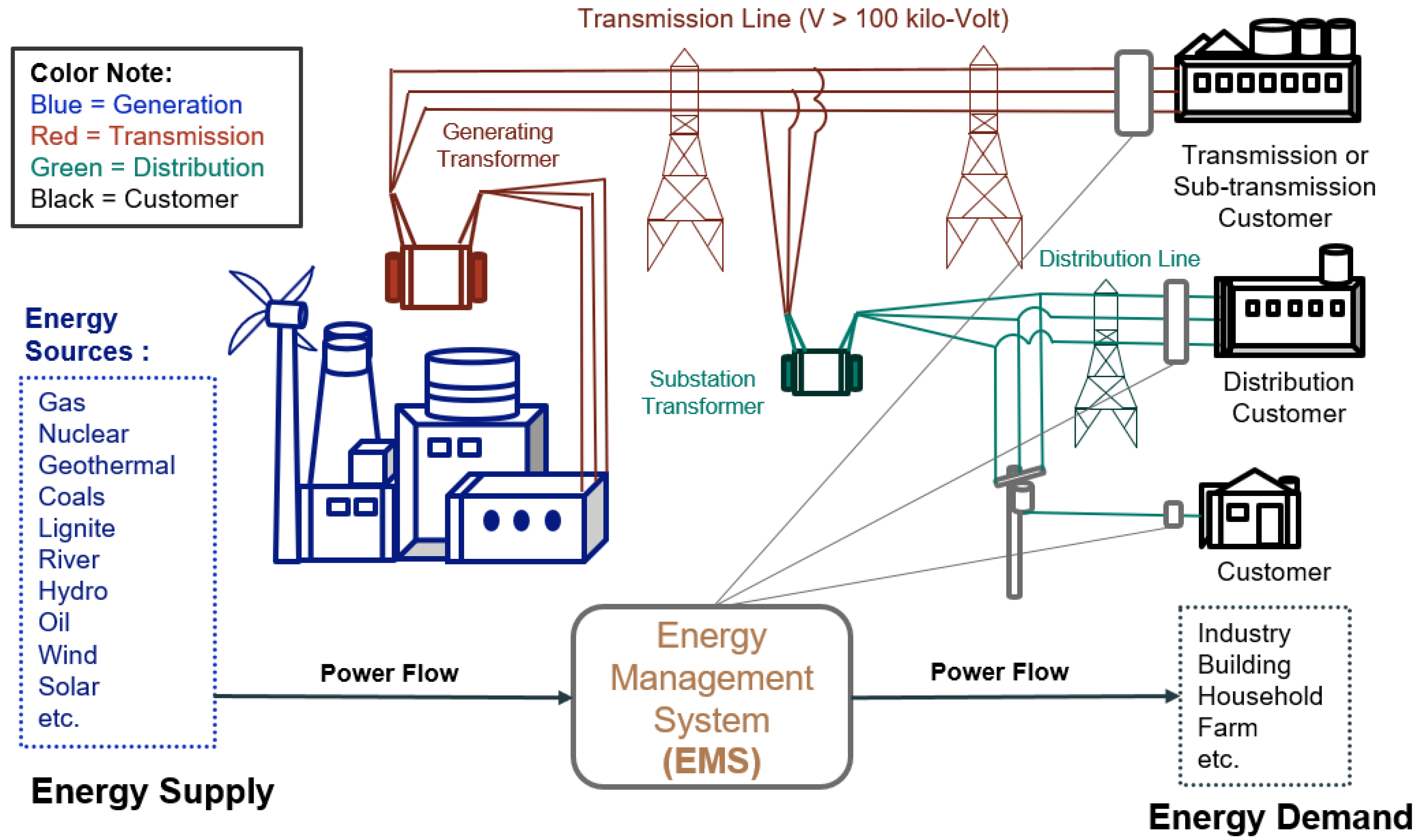
- This paper proposes the energy supply (production) as an input data model (coal, gas, oil, nuclear, river, wind, solar, etc.) to predict energy demand (consumption).
- It develops a multilinear regression model from a single linear regression to implement a multivariate input model.
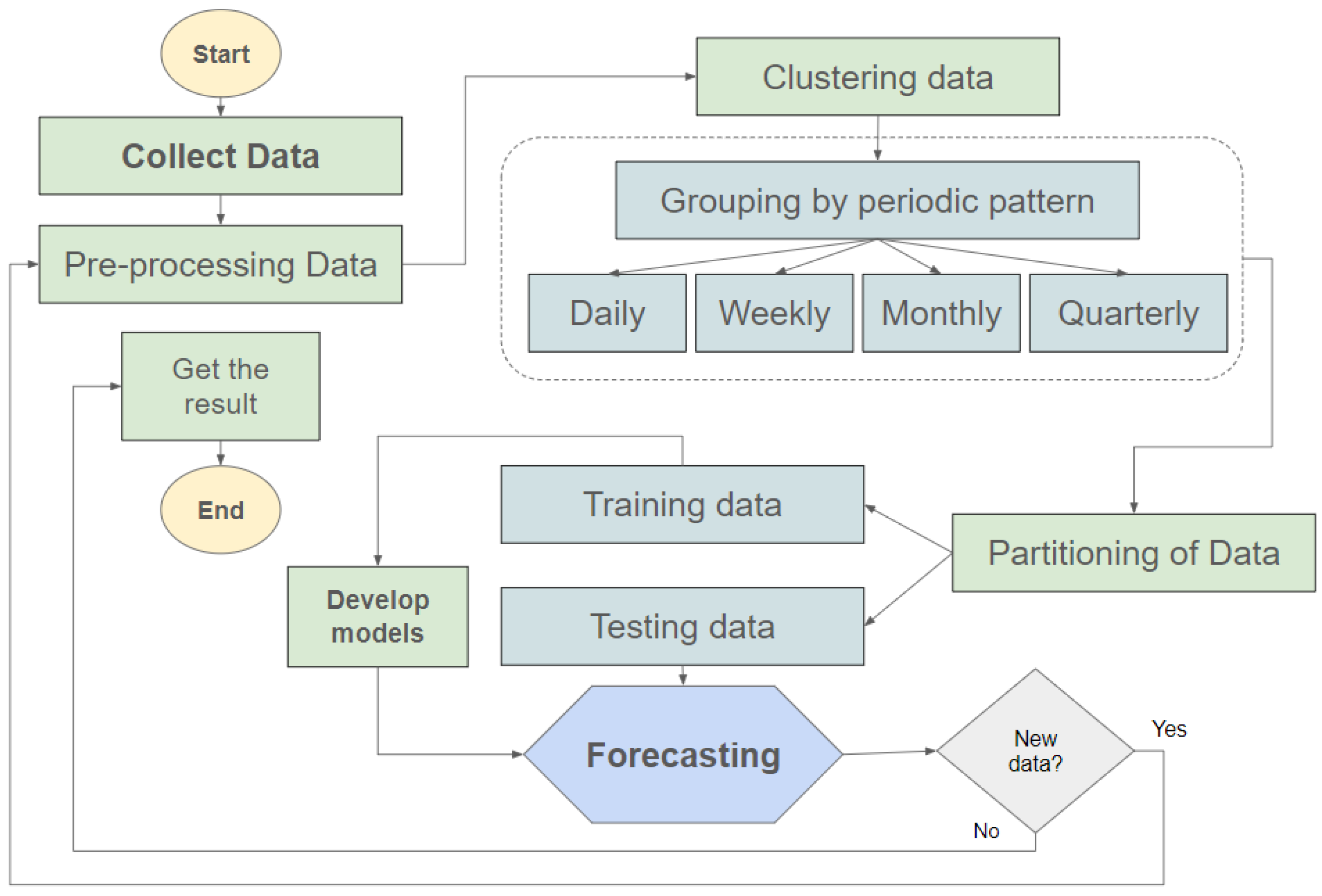
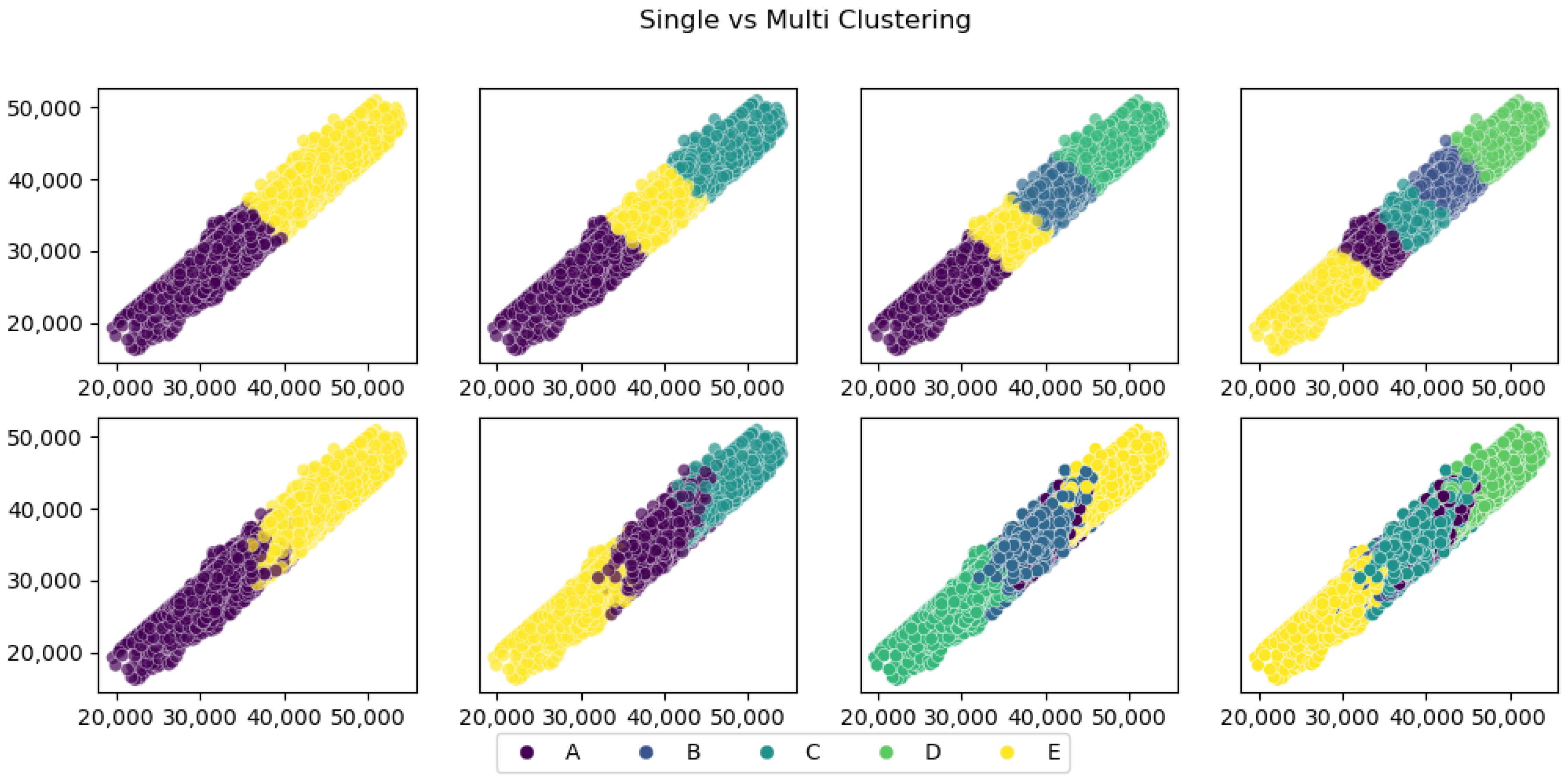
- It also combined the K-Means clustering algorithm and multilinear regression to make fewer errors.
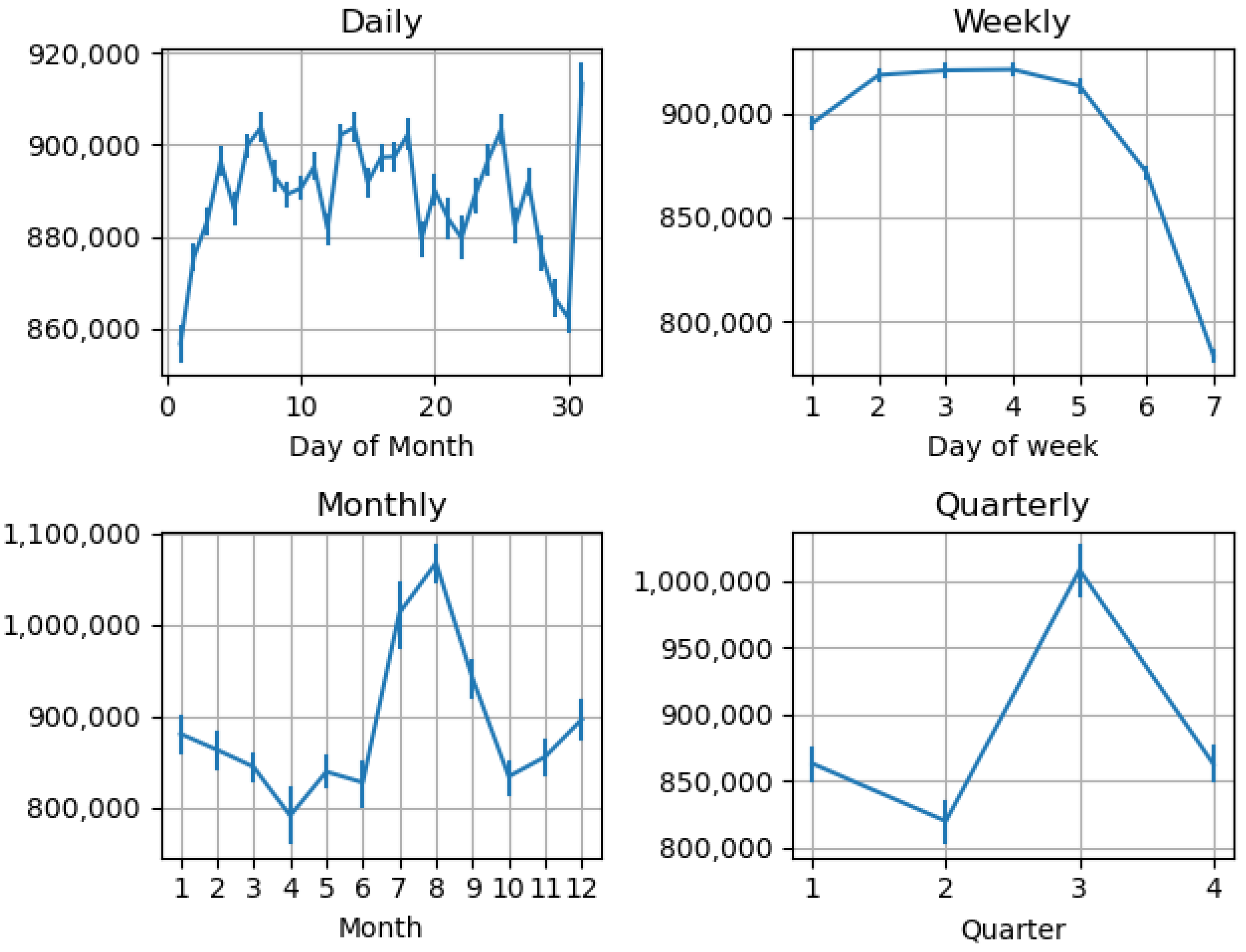
- It uses periodic daily, weekly, monthly, and quarterly patterns to improve the accuracy of energy prediction.
2. Proposed RMLR Model and Evaluation
2.1. The Proposed RMLR Techniques
| Algorithm 1 Clustering RMLR algorithm |
 |
2.2. Model Performance Evaluation
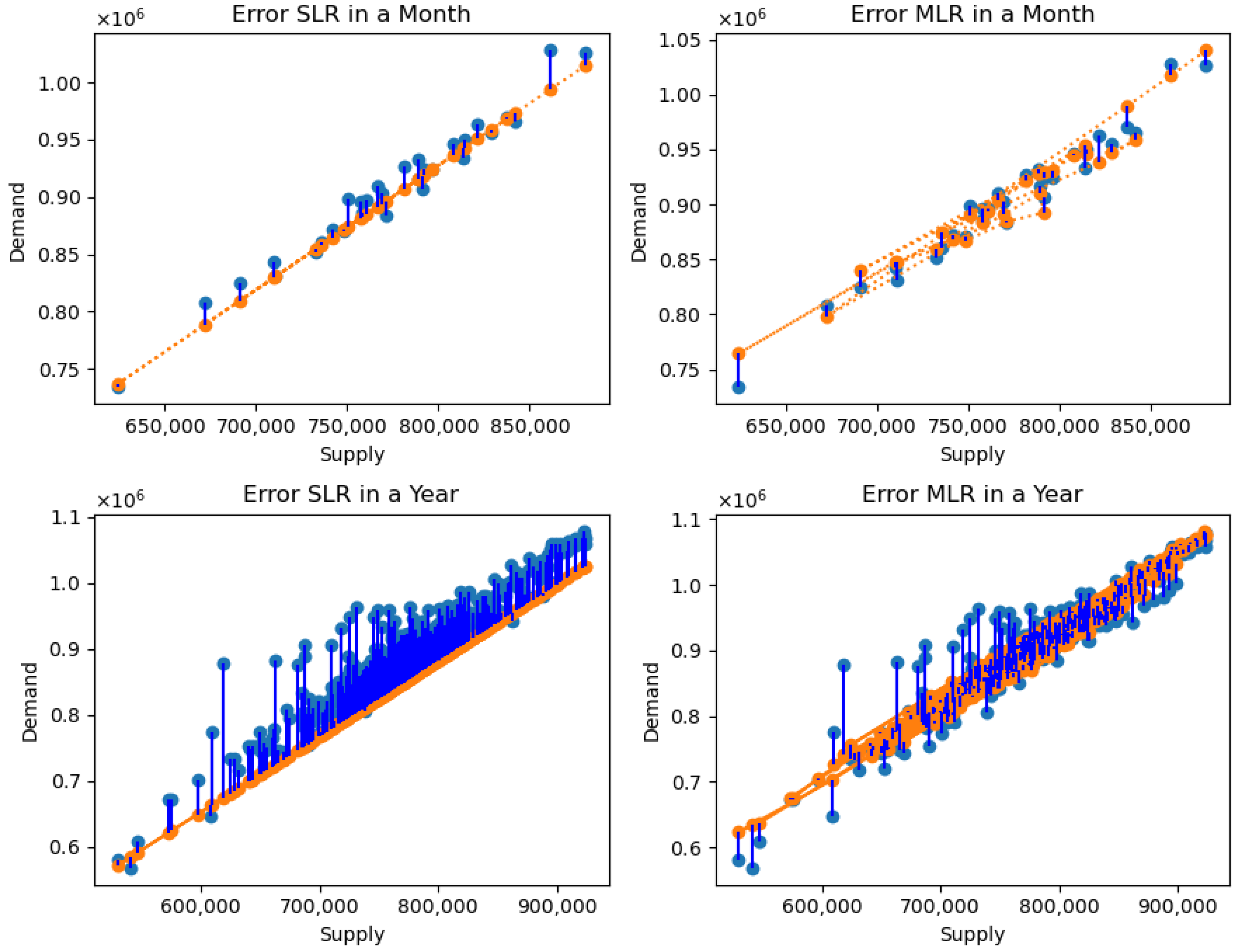
- All calculated errors are divided by the square root of the mean to obtain the RMSE. The forecast error is a measure of prediction accuracy, measured as the difference between forecast and actual data.
- The MAE represents the average error of all the forecasting results from the training data. The error is calculated based on a comparison between the predicted and actual electricity demand.
- Using data from forecast results, the MAPE can be used to calculate the average error as a percentage. For the error percentage, the mean value of the prediction results compared to the actual electricity demand is multiplied by 100%.
- The mean absolute percentage accuracy is the model prediction accuracy value. MAPA is obtained after calculating the error percentage value with a perfect accuracy of 100% minus the total average error percentage obtained.
3. Simulation Results
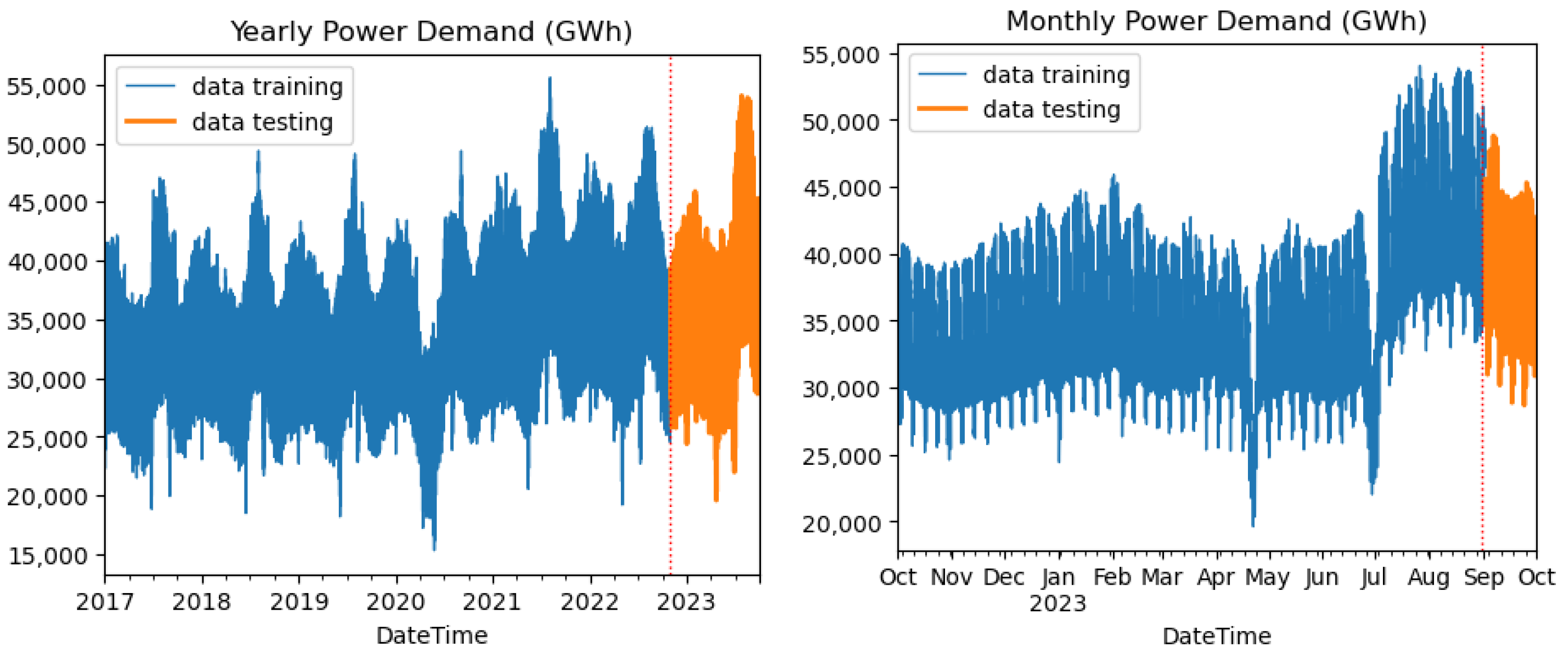
3.1. Data Preprocessing
3.2. Clustering Multilinear Regression
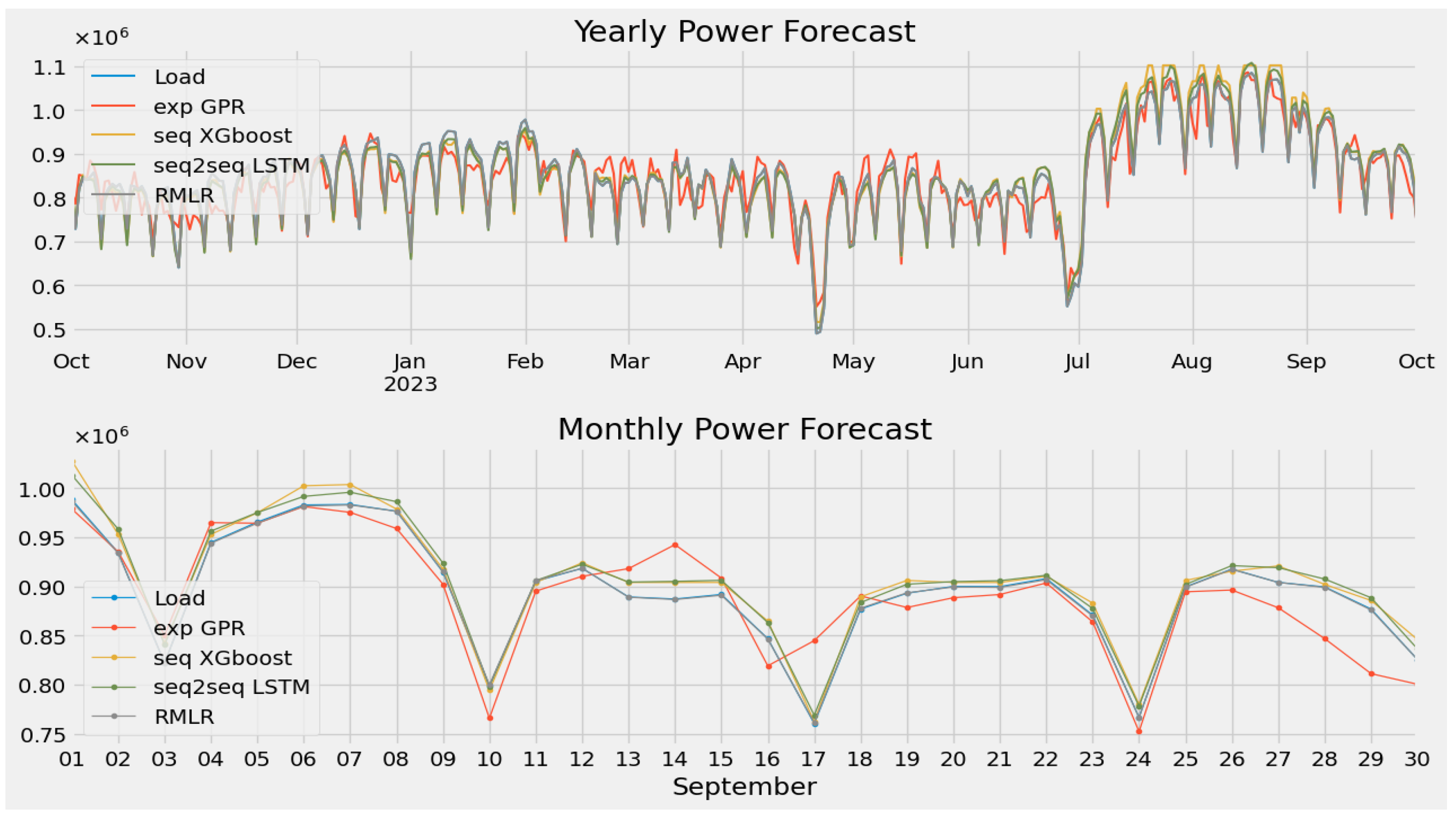
3.3. Comparison with Other Methods
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Aurangzeb, K.; Alhussein, M. Deep learning framework for short term power load forecasting, a case study of individual household energy customer. In Proceedings of the International Conference on Advances in the Emerging Computing Technologies (AECT), Madinah, Saudi Arabia, 10 February 2020; pp. 1–5. Available online: https://ieeexplore.ieee.org/abstract/document/9194153 (accessed on 20 September 2023).
- Parkash, B.; Lie, T.T.; Li, W.; Tito, S.R. End-to-End Top-Down Load Forecasting Model for Residential Consumers. Energies 2024, 17, 2550. [Google Scholar] [CrossRef]
- Tang, L.; Yi, Y.; Peng, Y. An ensemble deep learning model for short-term load forecasting based on ARIMA and LSTM. In Proceedings of the IEEE International Conference on Communications, Control, and Computing Technologies for Smart Grids (SmartGridComm), Beijing, China, 21–23 October 2019; pp. 1–6. Available online: https://ieeexplore.ieee.org/abstract/document/8909756 (accessed on 20 September 2023).
- Sias, Q.A.; Lim, S.; Gantassi, R.; Choi, Y. Implementation of Single and Multi Linear Regression for Prediction of Energy Consumption based on Previous Data of Energy Production. In Proceedings of the 2023 International Conference on Artificial Intelligence in Information and Communication (ICAIIC), Bali, Indonesia, 20–23 February 2023; pp. 830–832. Available online: https://ieeexplore.ieee.org/document/10066989 (accessed on 20 September 2023).
- Alquthami, T.; Zulfiqar, M.; Kamran, M.; Milyani, A.H.; Rasheed, M.B. A Performance Comparison of Machine Learning Algorithms for Load Forecasting in Smart Grid. IEEE Access 2022, 10, 48419–48433. [Google Scholar] [CrossRef]
- Zhu, J.; Dong, H.; Zheng, W.; Li, S.; Huang, Y.; Xi, L. Review and prospect of data-driven techniques for load forecasting in integrated energy systems. Appl. Energy 2022, 321, 119269. [Google Scholar] [CrossRef]
- Habbak, H.; Mahmoud, M.; Metwally, K.; Fouda, M.M.; Ibrahem, M.I. Load Forecasting Techniques and Their Applications in Smart Grids. Energies 2023, 16, 1480. [Google Scholar] [CrossRef]
- Lindberg, K.B.; Seljom, P.; Madsen, H.; Fischer, D.; Korpås, M. Long-term electricity load forecasting: Current and future trends. Util. Policy 2019, 58, 102–119. [Google Scholar] [CrossRef]
- Alkawaz, A.N.; Abdellatif, A.; Kanesan, J.; Khairuddin, A.S.M.; Gheni, H.M. Day-Ahead Electricity Price Forecasting Based on Hybrid Regression Model. IEEE Access 2022, 10, 108021–108033. [Google Scholar] [CrossRef]
- Sharma, A.; Jain, S.K. A novel seasonal segmentation approach for day-ahead load forecasting. Energy 2022, 257, 124752. [Google Scholar] [CrossRef]
- Huy, P.C.; Minh, N.Q.; Tien, N.D.; Quynh, T. Short-term Electricity Load forecasting based on Temporal Fusion Transformer Model. IEEE Access 2022, 10, 106296–106304. [Google Scholar] [CrossRef]
- Madhukumar, M.; Sebastian, A.; Liang, X.; Jamil, M.; Khan, S. Regression Model-Based Short-Term Load Forecasting for University Campus Load. IEEE Access 2022, 10, 8891–8905. [Google Scholar] [CrossRef]
- Lee, G.-C. Regression-Based Methods for Daily Peak Load Forecasting in South Korea. Sustainability 2022, 14, 3984. [Google Scholar] [CrossRef]
- Kareem, S.; Akpinar, M. Removing Seasonal Effect on City Based Daily Electricity Load Forecasting with Linear Regression. In Proceedings of the International Symposium on Networks, Computers and Communications (ISNCC), Dubai, United Arab Emirates, 31 October–2 November 2021; pp. 1–6. Available online: https://ieeexplore.ieee.org/abstract/document/9615873 (accessed on 26 October 2023).
- Ardiansyah; Masood, Z.; Choi, D.; Choi, Y. Seq2Seq regression learning-based multivariate and multistep SOC forecasting of BESS in frequency regulation service. Sustain. Energy Grids Netw. 2022, 32, 100939. [Google Scholar] [CrossRef]
- Selvi, M.V.; Mishra, S. Investigation of Performance of Electric Load Power Forecasting in Multiple Time Horizons with New Architecture Realized in Multivariate Linear Regression and Feed-Forward Neural Network Techniques. IEEE Trans. Ind. Appl. 2020, 56, 5603–5612. [Google Scholar] [CrossRef]
- Sias, Q.A.; Gantassi, R.; Choi, Y.; Afandi, A. Recurrence Multi Linear Regression of Historical Energy Supply for Energy Demand Forecaster. In Proceedings of the 2023 8th International Conference on Electrical, Electronics and Information Engineering (ICEEIE), Malang City, Indonesia, 28–29 September 2023; pp. 1–4. Available online: https://ieeexplore.ieee.org/abstract/document/10334912 (accessed on 26 October 2023).
- Mohammadi, E.; Alizadeh, M.; Asgarimoghaddam, M.; Wang, X.; Simões, M.G. A Review on Application of Artificial Intelligence Techniques in Microgrids. IEEE J. Emerg. Sel. Top. Ind. Electron. 2022, 3, 878–890. [Google Scholar] [CrossRef]
- Patel, R.K.; Kumari, A.; Tanwar, S.; Hong, W.-C.; Sharma, R. AI-Empowered Recommender System for Renewable Energy Harvesting in Smart Grid System. IEEE Access 2022, 10, 24316–24326. [Google Scholar] [CrossRef]
- Cai, H.; Shen, S.; Lin, Q.; Li, X.; Xiao, H. Predicting the Energy Consumption of Residential Buildings for Regional Electricity Supply-Side and Demand-Side Management. IEEE Access 2019, 7, 30386–30397. [Google Scholar] [CrossRef]
- Zhang, T.; Zhang, X.; Rubasinghe, O.; Liu, Y.; Chow, Y.H.; Iu, H.H.C.; Fernando, T. Long-term Energy and Peak Power Demand Forecasting based on Sequential-XGBoost. IEEE Trans. Power Syst. 2023, 39, 3088–3104. [Google Scholar] [CrossRef]
- Suresh, V.; Aksan, F.; Janik, P.; Sikorski, T.; Revathi, B.S. Probabilistic LSTM-Autoencoder Based Hour-Ahead Solar Power Forecasting Model for Intra-Day Electricity Market Participation: A Polish Case Study. IEEE Access 2022, 10, 110628–110638. [Google Scholar] [CrossRef]
- Neeraj; Mathew, J.; Behera, R.K. EMD-Att-LSTM: A Data-driven Strategy Combined with Deep Learning for Short-term Load Forecasting. J. Mod. Power Syst. Clean Energy 2022, 10, 1229–1240. [Google Scholar] [CrossRef]
- Qi, Y.; Luo, H.; Luo, Y.; Liao, R.; Ye, L. Adaptive Clustering Long Short-Term Memory Network for Short-Term Power Load Forecasting. Energies 2023, 16, 6230. [Google Scholar] [CrossRef]
- Masood, Z.; Gantassi, R.; Ardiansyah; Choi, Y. A Multi-Step Time-Series Clustering-Based Seq2Seq LSTM Learning for a Single Household Electricity Load Forecasting. Energies 2022, 15, 2623. [Google Scholar] [CrossRef]
- Shafique, T.; Gantassi, R.; Soliman, A.-H.; Amjad, A.; Hui, Z.-Q.; Choi, Y. A Review of Energy Hole Mitigating Techniques in Multi-Hop Many to One Communication and its Significance in IoT Oriented Smart City Infrastructure. IEEE Access 2023, 11, 121340–121367. [Google Scholar] [CrossRef]
- Dong, X.; Deng, S.; Wang, D. A short-term power load forecasting method based on k-means and SVM. J. Ambient. Intell. Humaniz. Comput. 2022, 13, 5253–5267. [Google Scholar] [CrossRef]
- Mamun, A.A.; Sohel, M.; Mohammad, N.; Sunny, M.S.H.; Dipta, D.R.; Hossain, E. A Comprehensive Review of the Load Forecasting Techniques Using Single and Hybrid Predictive Models. IEEE Access 2020, 8, 134911–134939. [Google Scholar] [CrossRef]
- Asghar, Z.; Hafeez, K.; Sabir, D.; Ijaz, B.; Syed; Ro, J. RECLAIM: Renewable Energy Based Demand-Side Management Using Machine Learning Models. IEEE Access 2023, 11, 3846–3857. [Google Scholar] [CrossRef]
- Mehedi, I.M.; Bassi, H.M.; Rawa, M.; Ajour, M.N. Intelligent Machine Learning with Evolutionary Algorithm Based Short Term Load Forecasting in Power Systems. IEEE Access 2021, 9, 100113–100124. [Google Scholar] [CrossRef]
- Permata, R.P.; Prastyo, D.D.; Wibawati. Hybrid dynamic harmonic regression with calendar variation for Turkey short-term electricity load forecasting. Procedia Comput. Sci. 2022, 197, 25–33. [Google Scholar] [CrossRef]
- Wang, W.; Feng, B.; Huang, G.; Guo, C.; Liao, W.; Chen, Z. Conformal asymmetric multi-quantile generative transformer for day-ahead wind power interval prediction. Appl. Energy 2023, 333, 120634. [Google Scholar] [CrossRef]
- Wang, L.; Mao, M.; Xie, J.; Liao, Z.; Zhang, H.; Li, H. Accurate solar PV power prediction interval method based on frequency-domain decomposition and LSTM model. Energy 2023, 262, 125592. [Google Scholar] [CrossRef]
- Sluijterman, L.; Cator, E.; Heskes, T. How to evaluate uncertainty estimates in machine learning for regression? Neural Netw. 2024, 173, 106203. [Google Scholar] [CrossRef]
- Zhang, Y.; Wen, H.; Wu, Q.; Ai, Q. Optimal adaptive prediction intervals for electricity load forecasting in distribution systems via reinforcement learning. IEEE Trans. Smart Grid 2022, 14, 3259–3270. [Google Scholar] [CrossRef]
- Sleiman, A.; Su, W. Combined K-Means Clustering with Neural Networks Methods for PV Short-Term Generation Load Forecasting in Electric Utilities. Energies 2024, 17, 1433. [Google Scholar] [CrossRef]
- Zeng, W.; Li, J.; Sun, C.; Cao, L.; Tang, X.; Shu, S.; Zheng, J. Ultra Short-Term Power Load Forecasting Based on Similar Day Clustering and Ensemble Empirical Mode Decomposition. Energies 2023, 16, 1989. [Google Scholar] [CrossRef]



| Error | Model | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Single-variable clustering | |||||
| MAE | SLR | 46.167 | 46.058 | 47.136 | 48.002 |
| MLR | 19.019 | 21.340 | 19.870 | 24.500 | |
| RMSE | SLR | 54.692 | 54.223 | 56.058 | 56.239 |
| MLR | 28.846 | 31.496 | 30.176 | 34.517 | |
| MAPE | SLR | 0.0548 | 0.0547 | 0.0533 | 0.0533 |
| MLR | 0.0219 | 0.0249 | 0.0231 | 0.0278 | |
| Multivariate clustering | |||||
| MAE | SLR | 48.263 | 46.755 | 46.243 | 49.043 |
| MLR | 16.337 | 20.183 | 30.090 | 26.048 | |
| RMSE | SLR | 55.246 | 52.286 | 51.704 | 54.825 |
| MLR | 25.819 | 27.441 | 37.187 | 34.520 | |
| MAPE | SLR | 0.0540 | 0.0529 | 0.0525 | 0.0553 |
| MLR | 0.0185 | 0.0233 | 0.0349 | 0.0295 |
| Model | RMSE | MAE | MAPE | MAPA | Time |
|---|---|---|---|---|---|
| Daily | |||||
| exp GPR | 99.849 | 123.533 | 0.109 | 99.890 | 1.986 |
| seq XGboost | 101.325 | 122.679 | 0.109 | 99.890 | 0.127 |
| seq2seq LSTM | 100.665 | 119.157 | 0.109 | 99.891 | 22.243 |
| RMLR | 92.726 | 91.855 | 0.047 | 99.953 | 0.24 |
| Weekly | |||||
| exp GPR | 91.293 | 111.049 | 0.100 | 99.900 | 2.124 |
| seq XGboost | 92.441 | 111.439 | 0.099 | 99.910 | 0.212 |
| seq2seq LSTM | 96.526 | 109.518 | 0.105 | 99.895 | 22.873 |
| RMLR | 91.304 | 91.201 | 0.034 | 99.966 | 0.37 |
| Monthly | |||||
| exp GPR | 96.889 | 112.894 | 0.107 | 99.893 | 1.337 |
| seq XGboost | 102.172 | 115.396 | 0.036 | 99.964 | 0.098 |
| seq2seq LSTM | 98.324 | 111.620 | 0.107 | 99.893 | 20.991 |
| RMLR | 91.613 | 91.325 | 0.036 | 99.964 | 0.004 |
| Quarterly | |||||
| exp GPR | 100.604 | 117.050 | 0.110 | 99.890 | 1.549 |
| seq XGboost | 101.661 | 117.046 | 0.108 | 99.892 | 0.103 |
| seq2seq LSTM | 106.171 | 119.174 | 0.114 | 99.886 | 21.461 |
| RMLR | 91.511 | 91.365 | 0.038 | 99.962 | 0.011 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sias, Q.A.; Gantassi, R.; Choi, Y.; Bae, J.H. Recurrence Multilinear Regression Technique for Improving Accuracy of Energy Prediction in Power Systems. Energies 2024, 17, 5186. https://doi.org/10.3390/en17205186
Sias QA, Gantassi R, Choi Y, Bae JH. Recurrence Multilinear Regression Technique for Improving Accuracy of Energy Prediction in Power Systems. Energies. 2024; 17(20):5186. https://doi.org/10.3390/en17205186
Chicago/Turabian StyleSias, Quota Alief, Rahma Gantassi, Yonghoon Choi, and Jeong Hwan Bae. 2024. "Recurrence Multilinear Regression Technique for Improving Accuracy of Energy Prediction in Power Systems" Energies 17, no. 20: 5186. https://doi.org/10.3390/en17205186
APA StyleSias, Q. A., Gantassi, R., Choi, Y., & Bae, J. H. (2024). Recurrence Multilinear Regression Technique for Improving Accuracy of Energy Prediction in Power Systems. Energies, 17(20), 5186. https://doi.org/10.3390/en17205186








